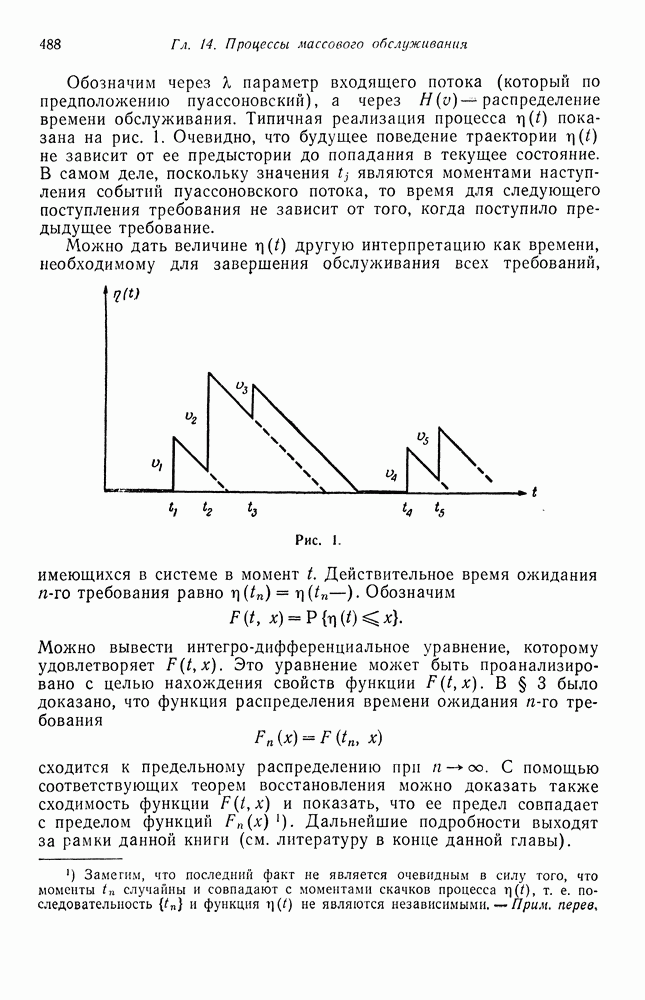
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЦЕПЕЙ МАРКОВА, ПОРОЖДЕННЫХ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
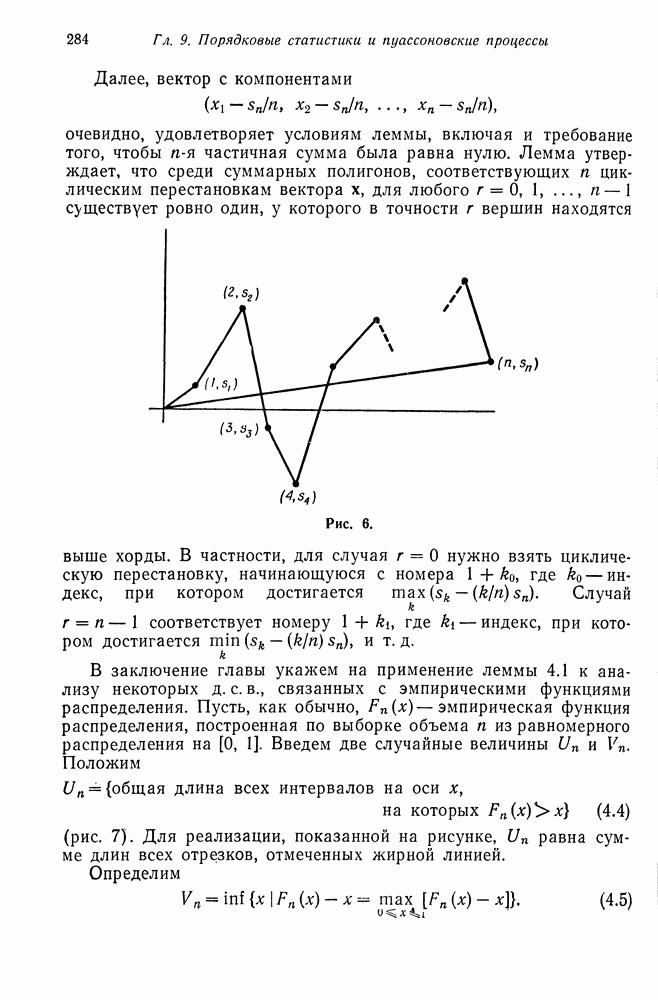
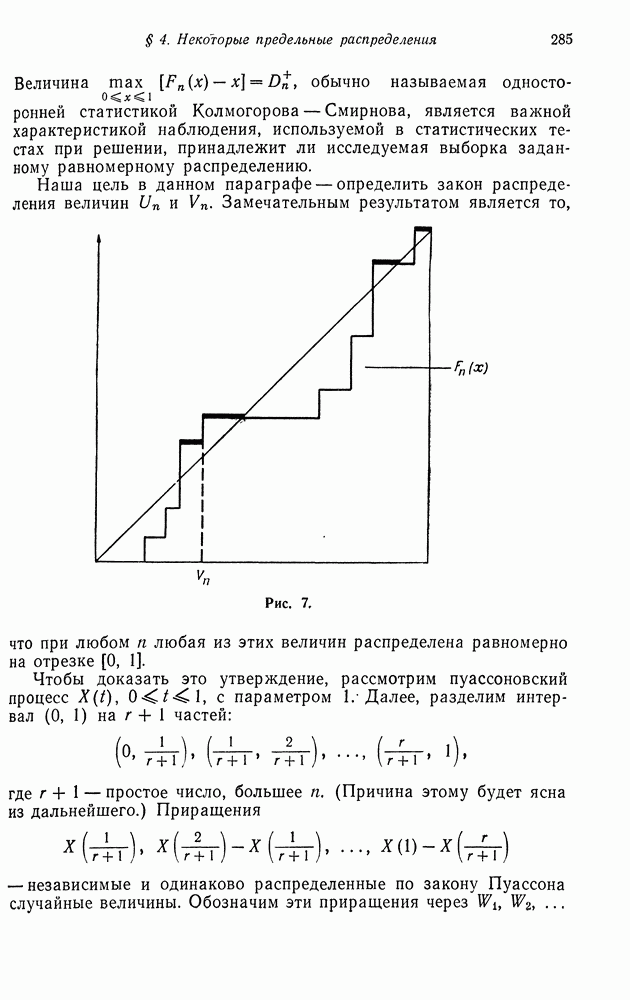
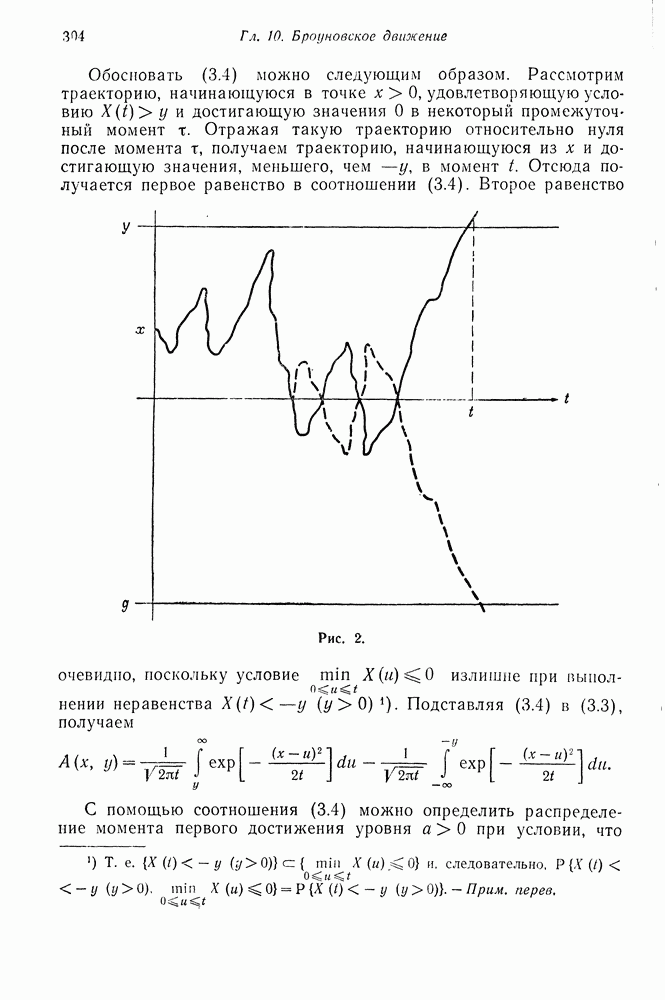
В предыдущих двух параграфах мы рассмотрели несколько цепей Маркова, связанных с ветвящимися процессами. В настоящем параграфе мы изучим некоторые вопросы, относящиеся к структуре этих цепей. Более точно, будет найдено все множество собственных значений и описаны некоторые свойства соответствующих векторов. В § 8 мы укажем на различные применения и интерпретации этих результатов.
Пусть задана производящая функция

Рассмотрим порожденную цепь Маркова с матрицей переходных вероятностей  где
где

Для того чтобы найти собственные значения матрицы  проанализируем производящую функцию вероятностей
проанализируем производящую функцию вероятностей 

Дифференцируя  по
по  получим
получим

Полагая  имеем
имеем

где

Таким образом, если мы будем трактовать  как матрицу, задающую линейное преобразование в линейном пространстве размерности
как матрицу, задающую линейное преобразование в линейном пространстве размерности  то из соотношения (6.5) следует, что
то из соотношения (6.5) следует, что  где
где  Таким образом,
Таким образом,  является собственным вектором матрицы
является собственным вектором матрицы  соответствующим собственному значению
соответствующим собственному значению  Очевидно,
Очевидно,  где
где  , поскольку
, поскольку  при всех
при всех  Эти два результата являются частным проявлением формулы
Эти два результата являются частным проявлением формулы

где  является полиномом степени
является полиномом степени  При
При  имеем
имеем 
Наша цель теперь — доказать формулу (6.6) для всех  Для этого продифференцируем (6.4) еще раз по
Для этого продифференцируем (6.4) еще раз по 

Положим  тогда
тогда

Пусть

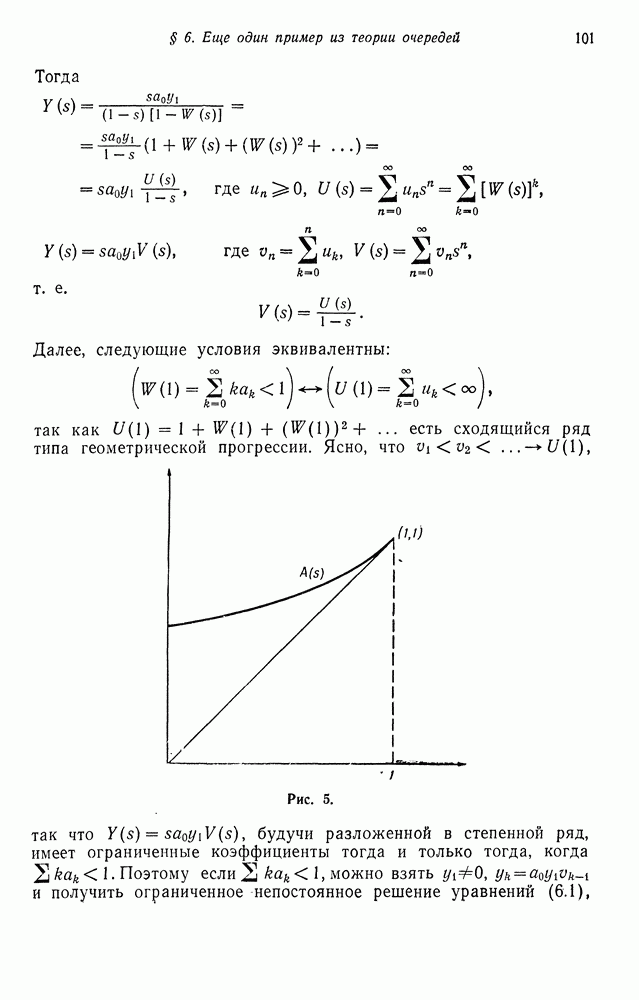
Тогда

где

Таким образом,

Следовательно, нами установлена формула

где  полином степени
полином степени  по крайней мере для
по крайней мере для  . В действительности же справедлив следующий более общий результат.
. В действительности же справедлив следующий более общий результат.
Теорема 6.1. Пусть 

Тогда

где  полином степени
полином степени  по
по  (Условимся) что полином степени —1 есть тождественный нуль.)
(Условимся) что полином степени —1 есть тождественный нуль.)
Доказательство. Если продифференцировать  раз, левая часть примет вид
раз, левая часть примет вид

где  полином степени
полином степени  Если продифференцировать
Если продифференцировать  в правой части
в правой части  раз по
раз по  , то получим
, то получим

Первый член появляется при последовательном дифференцировании  раз. Оставшиеся члены возникают при дифференцировании других сомножителей, таких, как
раз. Оставшиеся члены возникают при дифференцировании других сомножителей, таких, как  и т. д., которые появляются в процессе дифференцирования исходного выражения. Степени этих возникающих сомножителей не зависят от
и т. д., которые появляются в процессе дифференцирования исходного выражения. Степени этих возникающих сомножителей не зависят от  Это означает, что результат указанных операций дифференцирования есть линейная комбинация различных степеней
Это означает, что результат указанных операций дифференцирования есть линейная комбинация различных степеней  коэффициенты которой содержат в качестве сомножителей максимум
коэффициенты которой содержат в качестве сомножителей максимум  из чисел
из чисел  коэффициенты являются полиномами степени не выше
коэффициенты являются полиномами степени не выше  по отношению к переменной
по отношению к переменной  Каждое слагаемое второго члена выражения (6.10) зависит от
Каждое слагаемое второго члена выражения (6.10) зависит от  через выражение вида
через выражение вида

при некотором 
Группируя члены в равенстве (6.10), получим

где  — полином от переменной
— полином от переменной  степени не выше
степени не выше  при
при  Фактически при
Фактически при  степени члена
степени члена  складываются, и зависимость от
складываются, и зависимость от  сохраняется лишь в коэффициентах при
сохраняется лишь в коэффициентах при 
Предположим, что равенство (6.8) доказано для всех степеней  Тогда в силу гипотезы индукции
Тогда в силу гипотезы индукции

где  — полиномы степеней не выше
— полиномы степеней не выше  силу
силу

Сравнивая (6.12) и (6.13), видим, что утверждение индукции выполняется и для  Это завершает доказательство формулы (6.8).
Это завершает доказательство формулы (6.8).
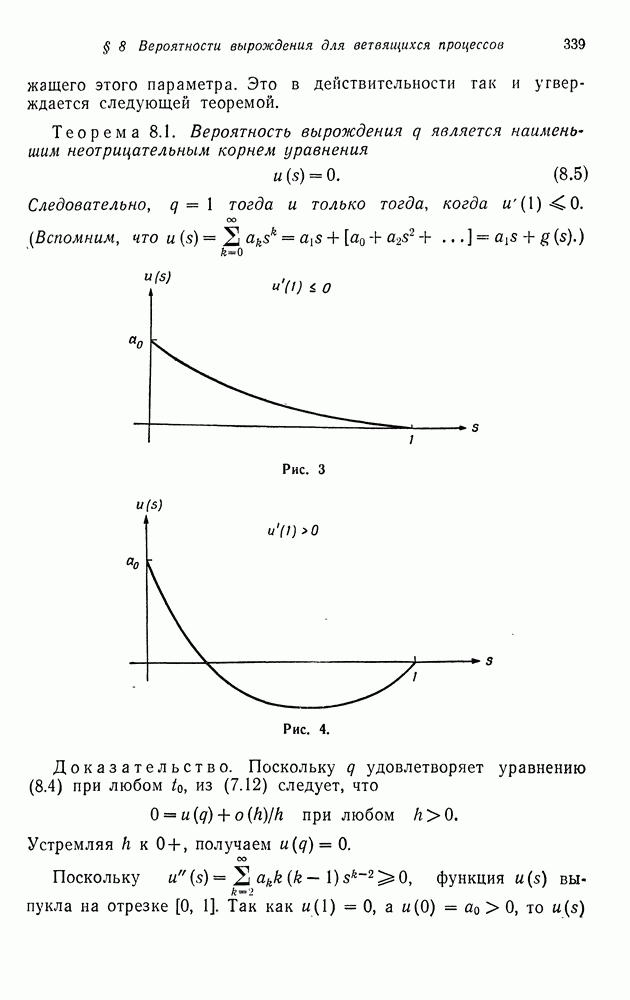
Докажем теперь основную теорему данного параграфа, которая раскрывает природу собственных значений матрицы 
Теорема 6.2. (1) Собственными значениями матрицы  являются числа
являются числа  определяемые равенством (6.7). Более того,
определяемые равенством (6.7). Более того,
(2) числа  удовлетворяют соотношению
удовлетворяют соотношению  если
если  где
где 
Доказательство. (1) Введем базис из  векторов размерности
векторов размерности  где
где  Эти векторы, очевидно, линейно независимы, поскольку в противном случае мы могли бы построить полипом
Эти векторы, очевидно, линейно независимы, поскольку в противном случае мы могли бы построить полипом  степени, имеющий
степени, имеющий  корней, что невозможно.
корней, что невозможно.
Найдем теперь вид матрицы  в специально выбранном базисе
в специально выбранном базисе  Понятно, что
Понятно, что  столбец матрицы
столбец матрицы  состоит из коэффициентов вектора
состоит из коэффициентов вектора  который представлен в виде линейной комбинации векторов
который представлен в виде линейной комбинации векторов 
Из соотношения (6.8) следует, что матрица  в новом базисе имеет вид
в новом базисе имеет вид

где элементы, обозначенные  соответствуют полиному
соответствуют полиному  в (6 8). Таким образом, матрица
в (6 8). Таким образом, матрица  представленная в новом базисе, является треугольной и ее собственные значения, очевидно, равны
представленная в новом базисе, является треугольной и ее собственные значения, очевидно, равны  Поскольку собственные значения инвариантны относительно выбора базиса, доказательство пункта (1) закончено.
Поскольку собственные значения инвариантны относительно выбора базиса, доказательство пункта (1) закончено.
(2) Заметим, что для любого степенного ряда  коэффициент при сом, очевидно, равен
коэффициент при сом, очевидно, равен  [коэффициент при
[коэффициент при  в разложении
в разложении  Полагая
Полагая  получим
получим

Если разделить обе части на коэффициент при  в разложении
в разложении  то, вспоминая определение
то, вспоминая определение  получим соотношение
получим соотношение

При  второе слагаемое в правой части, очевидно, равно 0, таким образом,
второе слагаемое в правой части, очевидно, равно 0, таким образом, 
Поскольку  вероятностная производящая функция, то ее коэффициенты неотрицательны. Следовательно, коэффициент при
вероятностная производящая функция, то ее коэффициенты неотрицательны. Следовательно, коэффициент при  в разложении
в разложении  неотрицателен, так что
неотрицателен, так что
всегда  Из предположения о том, что
Из предположения о том, что  непосредственно вытекает, что второе слагаемое в
непосредственно вытекает, что второе слагаемое в  положительно при
положительно при  самом деле достаточны гораздо более слабые предположения.) Поэтому
самом деле достаточны гораздо более слабые предположения.) Поэтому  что и требовалось доказать.
что и требовалось доказать.
Из теоремы 6.2 известны все собственные значения матрицы (6.2). В предположениях пункта (2), т. е.  где
где

собственные значения  все различны. Обратимся теперь к задаче описания собственных векторов, соответствующих этим собственным значениям.
все различны. Обратимся теперь к задаче описания собственных векторов, соответствующих этим собственным значениям.
Мы уже показали, что собственному значению  соответствует пара правых собственных векторов
соответствует пара правых собственных векторов  Интуитивно более привлекательна пара векторов, являющихся линейной комбинацией указанных, а именно
Интуитивно более привлекательна пара векторов, являющихся линейной комбинацией указанных, а именно  Для компонент векторов, представленных в такой форме, можно дать вероятностную интерпретацию (см. § 2 гл. 4).
Для компонент векторов, представленных в такой форме, можно дать вероятностную интерпретацию (см. § 2 гл. 4).
Анализ выражения для показывает, что матрица  имеет
имеет

откуда с очевидностью следует, что  поглощающие состояния. Более того, из предположения о том, что
поглощающие состояния. Более того, из предположения о том, что  следует, что
следует, что  достижимы за один переход из каждого состояния
достижимы за один переход из каждого состояния  с положительной вероятностью. Следовательно,
с положительной вероятностью. Следовательно,  единственные поглощающие состояния.
единственные поглощающие состояния.
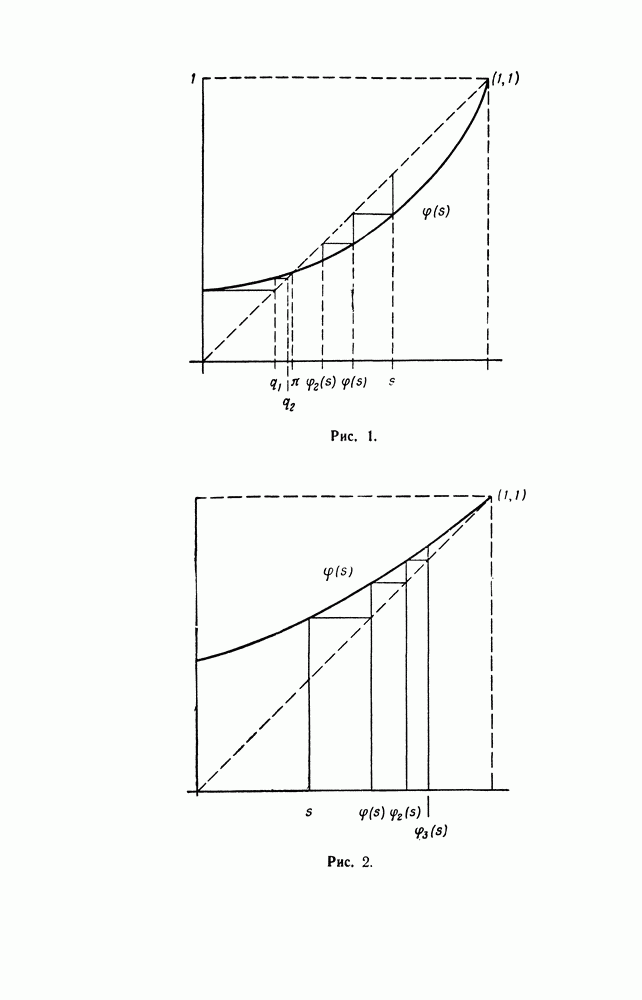
Следующая теорема характеризует правые собственные векторы, соответствующие собственным значениям 
Теорема 6.3. Существуют полиномы  степени
степени  для которых
для которых

(Вектор  равен
равен  )
)
Доказательство. Теорема уже доказана при  Если
Если  мы знаем, что
мы знаем, что

где  — полином степени
— полином степени  Выберем
Выберем  в виде
в виде

где постоянные  нужно подобрать. Необходимо выбрать
нужно подобрать. Необходимо выбрать  так, чтобы соотношение
так, чтобы соотношение

выполнялось при всех  Приравнивая коэффициенты при
Приравнивая коэффициенты при  в обеих частях равенства, получим условие
в обеих частях равенства, получим условие

Поскольку  при
при  можно найти такое число
можно найти такое число  чтобы равенство (6.16) удовлетворялось. Затем, приравнивая коэффициенты при
чтобы равенство (6.16) удовлетворялось. Затем, приравнивая коэффициенты при  в обеих частях (6.15) и используя то обстоятельство, что
в обеих частях (6.15) и используя то обстоятельство, что  известно, получим соотношение вида
известно, получим соотношение вида

Найдем  из (6.17). Это возможно, поскольку
из (6.17). Это возможно, поскольку  Продолжая процедуру таким же образом, можно вычислить последовательно все коэффициенты
Продолжая процедуру таким же образом, можно вычислить последовательно все коэффициенты  так, чтобы (6.15) выполнялось тождественно по
так, чтобы (6.15) выполнялось тождественно по 
Вышеприведенное построение доказывает существование полного базиса из собственных векторов специального вида (т. е. полученных с помощью полиномов). Из теории матриц (см. стр. 505) следует, что существует полная система левых собственных векторов. Предположим, что мы записали правые собственные векторы в следующем порядке:

где  полином, определенный в теореме 6.3,
полином, определенный в теореме 6.3,
Обозначим биортогональную систему левых собственных векторов через

По-видимому, довольно трудно выразить  в замкнутом виде. Тем не менее
в замкнутом виде. Тем не менее  может быть в принципе вычислен рекуррентно (фактически с помощью того же метода, который использовался при доказательстве теоремы 6.3).
может быть в принципе вычислен рекуррентно (фактически с помощью того же метода, который использовался при доказательстве теоремы 6.3).
Для вычисления  также можно предложить рекуррентный метод. Можно доказать, что компоненты вектора
также можно предложить рекуррентный метод. Можно доказать, что компоненты вектора  имеют вид
имеют вид

где  полином степени
полином степени  который можно найти рекуррентным образом.
который можно найти рекуррентным образом.
Мы завершим параграф несколькими конкретными примерами. Примеры.  Тогда при
Тогда при 

Значение  для этих частных случаев представляет интерес, поскольку оно характеризует скорость приближения системы к поглощающему состоянию или, в генетической терминологии, скорость приближения к гомозиготному состоянию. Для примера (А)
для этих частных случаев представляет интерес, поскольку оно характеризует скорость приближения системы к поглощающему состоянию или, в генетической терминологии, скорость приближения к гомозиготному состоянию. Для примера (А)

Для примера (Б)

следовательно, асимптотически по 

Аналогично для случая (В)

так что асимптотически

Заметим, что в пуассоновском случае значение  (для больших
(для больших  является промежуточным между соответствующими значениями для биномиального распределения потомков и отрицательного биномиального распределения.
является промежуточным между соответствующими значениями для биномиального распределения потомков и отрицательного биномиального распределения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 1. СВОДКА ОСНОВНЫХ ТЕРМИНОВ И СВОЙСТВ СЛУЧАЙНЫХ ВЕЛИЧИН И ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
- А. Совместные функции распределения
- Б. Условные распределения и плотности
- В. Бесконечные семейства случайных величин
- Г. Характеристические функции
- Д. Производящие функции
- Е. Примеры функций распределения
- Ж. Предельные теоремы
- § 2. ДВА ПРОСТЫХ ПРИМЕРА СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 3. КЛАССИФИКАЦИЯ ОБЩИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- ЗАМЕЧАНИЯ
- Глава 2. МАРКОВСКИЕ ЦЕПИ
- § 2. ПРИМЕРЫ МАРКОВСКИХ ЦЕПЕЙ
- Б. Одномерные случайные блуждания
- В. Дискретная марковская цепь, описывающая очередь
- Г. Модель из теории запасов
- Д. Серии успехов
- Е. Ветвящиеся процессы
- Ж. Марковские цепи в генетике
- 3. Генетическая модель II
- § 3. МАТРИЦЫ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ МАРКОВСКОЙ ЦЕПИ
- § 4. КЛАССИФИКАЦИЯ СОСТОЯНИЙ МАРКОВСКОЙ ЦЕПИ
- § 5. ВОЗВРАТНОСТЬ
- § 6. ПРИМЕРЫ ВОЗВРАТНЫХ МАРКОВСКИХ ЦЕПЕЙ
- § 7. ЕЩЕ О ВОЗВРАТНОСТИ
- Глава 3. ОСНОВНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ МАРКОВСКИХ ЦЕПЕЙ И ИХ ПРИЛОЖЕНИЯ
- § 2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 1.1
- § 3. ВЕРОЯТНОСТИ ПОГЛОЩЕНИЯ
- § 4. КРИТЕРИИ ВОЗВРАТНОСТИ
- § 5. ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
- § 6. ЕЩЕ ОДИН ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
- § 7. СЛУЧАЙНОЕ БЛУЖДАНИЕ
- Глава 4. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ МАРКОВСКИХ ЦЕПЕЙ
- § 2. СВЯЗЬ МЕЖДУ СОБСТВЕННЫМИ ЗНАЧЕНИЯМИ И КЛАССАМИ ВОЗВРАТНЫХ СОСТОЯНИЙ
- § 3. ПЕРИОДИЧЕСКИЕ КЛАССЫ
- § 4. СПЕЦИАЛЬНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ ДЛЯ МАРКОВСКИХ ЦЕПЕЙ
- § 5. ПРИМЕРЫ
- § 6. ПРИЛОЖЕНИЯ К БРОСАНИЯМ МОНЕТЫ
- Глава 5. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ И ИХ ПРИЛОЖЕНИЯ
- § 1. ВЕРОЯТНОСТИ ПЕРЕХОДА С ЗАПРЕЩЕНИЕМ
- § 2. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ
- § 3. СУЩЕСТВОВАНИЕ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ РАСПРЕДЕЛЕНИЙ
- § 4. ИНТЕРПРЕТАЦИЯ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ РАСПРЕДЕЛЕНИЙ
- § 5. РЕГУЛЯРНЫЕ, СУПЕРРЕГУЛЯРНЫЕ И СУБРЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТЬ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН КАК МАРКОВСКАЯ ЦЕПЬ
- § 1. СВОЙСТВА ВОЗВРАТНОСТИ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- § 2. ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
- § 3. ПРАВЫЕ РЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
- Глава 7. КЛАССИЧЕСКИЕ ПРИМЕРЫ ЦЕПЕЙ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 1. ОБЩИЕ ПРОЦЕССЫ ЧИСТОГО РОЖДЕНИЯ (РАЗМНОЖЕНИЯ) И ПУАССОНОВСКИЕ ПРОЦЕССЫ
- Б. Примеры пуассоновских процессов
- В. Процесс чистого рождения
- Г. Процесс Юла
- § 2. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О ПУАССОНОВСКИХ ПРОЦЕССАХ
- § 3. МОДЕЛЬ СЧЕТЧИКА
- § 4. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛИ
- § 5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
- § 6. ПРИМЕРЫ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
- § 7. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛЙ С ПОГЛОЩАЮЩИМИ СОСТОЯНИЯМИ
- § 8. ЦЕПИ МАРКОВА С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ И НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- Глава 8. ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 1. СВОЙСТВА ДИФФЕРЕНЦИРУЕМОСТИ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ
- § 2. КОНСЕРВАТИВНЫЕ ПРОЦЕССЫ. ПРЯМЫЕ И ОБРАТНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПОСТРОЕНИЕ ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ С ПОМОЩЬЮ ЕЕ ИНФИНИТЕЗИМАЛЬНЫХ ПАРАМЕТРОВ
- § 4. СТРОГО МАРКОВСКОЕ СВОЙСТВО
- Глава 9. ПОРЯДКОВЫЕ СТАТИСТИКИ, ПУАССОНОВСКИЕ ПРОЦЕССЫ И ИХ ПРИЛОЖЕНИЯ
- § 1. ПОРЯДКОВЫЕ СТАТИСТИКИ И ИХ СВЯЗЬ С ПУАССОНОВСКИМИ ПРОЦЕССАМИ
- § 2. ЗАДАЧА О БАЛЛОТИРОВКЕ
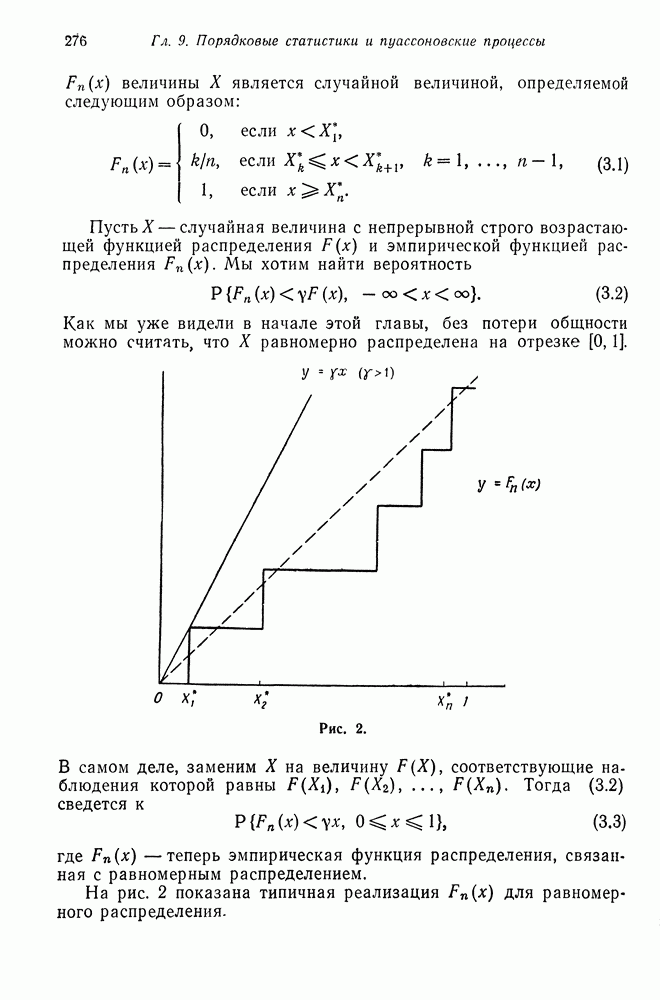
- § 3. ЭМПИРИЧЕСКИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПОРЯДКОВЫЕ СТАТИСТИКИ
- § 4. НЕКОТОРЫЕ ПРЕДЕЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ДЛЯ ЭМПИРИЧЕСКИХ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
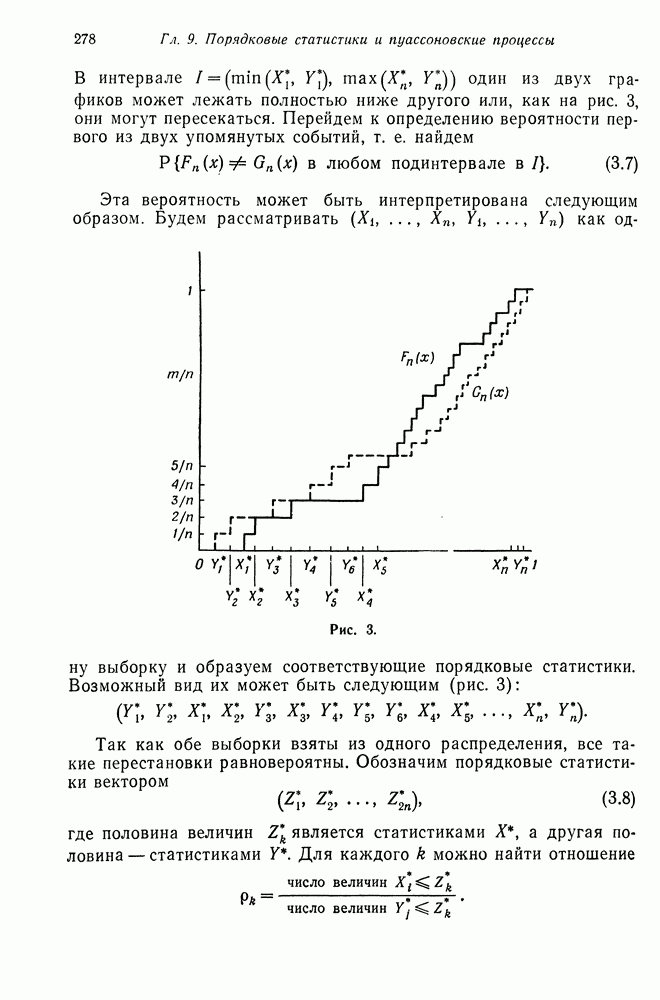
- Глава 10. БРОУНОВСКОЕ ДВИЖЕНИЕ
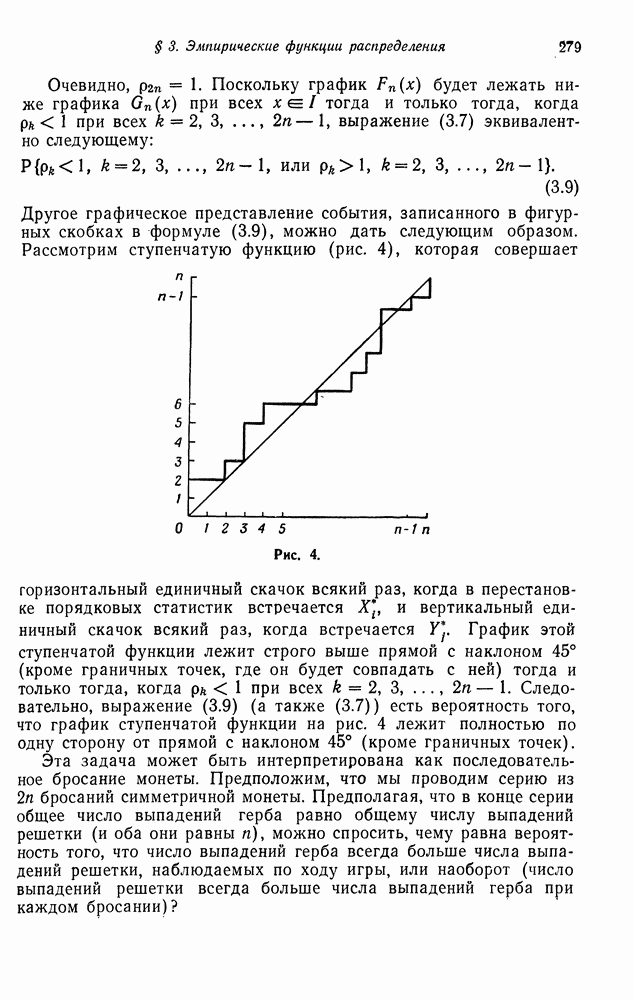
- § 2. СОВМЕСТНЫЕ ВЕРОЯТНОСТИ ДЛЯ БРОУНОВСКОГО ДВИЖЕНИЯ
- § 3. НЕПРЕРЫВНОСТЬ ТРАЕКТОРИЙ И ИХ МАКСИМАЛЬНЫЕ ЗНАЧЕНИЯ
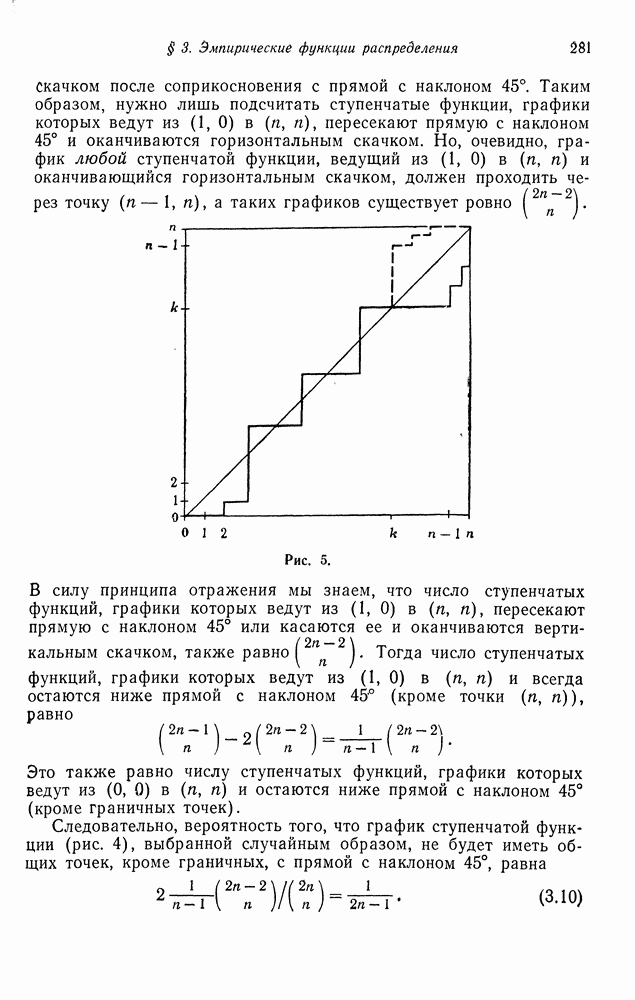
- Глава 11. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ
- § 1. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
- § 2. СООТНОШЕНИЯ ДЛЯ ПРОИЗВОДЯЩЕЙ ФУНКЦИИ, ОПИСЫВАЮЩЕЙ ВЕТВЯЩИЙСЯ ПРОЦЕСС
- § 3. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ
- § 4. ПРИМЕРЫ
- § 5. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДВУМЯ ТИПАМИ ЧАСТИЦ
- § 6. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕСКОЛЬКИМИ ТИПАМИ ЧАСТИЦ
- § 7. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 8. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 10. ВЕТВЯЩИЙСЯ ПРОЦЕСС С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ И ДВУМЯ ТИПАМИ ЧАСТИЦ
- § 11. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ, ЗАВИСЯЩИЕ ОТ ВОЗРАСТА
- Глава 12. СОСТАВНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- § 1. МНОГОМЕРНЫЕ ОДНОРОДНЫЕ ПУЛССОНОВСКИЕ ПРОЦЕССЫ
- § 2. ПРИМЕНЕНИЕ МНОГОМЕРНЫХ ПУАССОНОВСКИХ ПРОЦЕССОВ В АСТРОНОМИИ
- § 3. ИММИГРАЦИЯ И РОСТ ПОПУЛЯЦИЙ
- § 4. ВЕРОЯТНОСТНЫЕ МОДЕЛИ МУТАЦИИ И РОСТА
- § 5. ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ ОДНОМЕРНОЙ ПОПУЛЯЦИИ
- § 6. ВЕРОЯТНОСТНАЯ МОДЕЛЬ РОСТА ПОПУЛЯЦИИ В ПРОСТРАНСТВЕ И ВРЕМЕНИ
- § 7. ДЕТЕРМИНИРОВАННЫЙ РОСТ ПОПУЛЯЦИИ С РАСПРЕДЕЛЕНИЕМ ПО ВОЗРАСТАМ
- § 8. ДИСКРЕТНАЯ ВОЗРАСТНАЯ МОДЕЛЬ
- Глава 13. ДЕТЕРМИНИРОВАННЫЕ И СЛУЧАЙНЫЕ ГЕНЕТИЧЕСКИЕ И ЭКОЛОГИЧЕСКИЕ ПРОЦЕССЫ
- § 1. ГЕНЕТИЧЕСКИЕ МОДЕЛИ. ОПИСАНИЕ ГЕНЕТИЧЕСКОГО МЕХАНИЗМА
- § 2. ИНБРИДИНГ
- Б. Спаривание сибсов
- В. Гены, идентичные по происхождению
- Г. Бесконечная диплоидная популяция и коэффициент инбридинга
- Д. Популяция с самооплодотворением и случайным спариванием
- § 3. ПОЛИПЛОИДЫ
- § 4. МАРКОВСКИЕ ПРОЦЕССЫ, ПОРОЖДАЕМЫЕ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
- § 5. МОДЕЛИ РОСТА ПОПУЛЯЦИЙ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
- § 6. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЦЕПЕЙ МАРКОВА, ПОРОЖДЕННЫХ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
- § 7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МОДЕЛИ МУТАЦИИ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
- § 8. ВЕРОЯТНОСТНЫЙ СМЫСЛ СОБСТВЕННЫХ ЗНАЧЕНИЙ
- Глава 14. ПРОЦЕССЫ МАССОВОГО ОБСЛУЖИВАНИЯ
- § 2. ПРОСТЕЙШИЕ ПРОЦЕССЫ ОБСЛУЖИВАНИЯ (М/М/1)
- § 3. НЕКОТОРЫЕ ОБЩИЕ МОДЕЛИ ОБСЛУЖИВАНИЯ ОДНИМ ПРИБОРОМ
- § 4. МЕТОД ВЛОЖЕННЫХ ЦЕПЕЙ МАРКОВА ПРИМЕНИТЕЛЬНО К МОДЕЛИ ОБСЛУЖИВАНИЯ (M/G/1)
- § 5. ЭКСПОНЕНЦИАЛЬНО РАСПРЕДЕЛЕННОЕ ВРЕМЯ ОБСЛУЖИВАНИЯ (G/М/1)
- § 6. ГАММА-РАСПРЕДЕЛЕНИЕ ИНТЕРВАЛОВ МЕЖДУ ПОСТУПЛЕНИЯМИ И ОБОБЩЕНИЯ (Ek/М/1)
- § 7. ЭКСПОНЕНЦИАЛЬНОЕ ОБСЛУЖИВАНИЕ s ПРИБОРОВ (GI/M/s)
- § 8. ВИРТУАЛЬНОЕ ВРЕМЯ ОЖИДАНИЯ И ПЕРИОД ЗАНЯТОСТИ
- ПРИЛОЖЕНИЕ § 1. СПЕКТРАЛЬНАЯ ТЕОРЕМА
- § 2. ТЕОРИЯ ФРОБЕНИУСА ПОЛОЖИТЕЛЬНЫХ МАТРИЦ
- РАЗЛИЧНЫЕ ЗАДАЧИ