| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
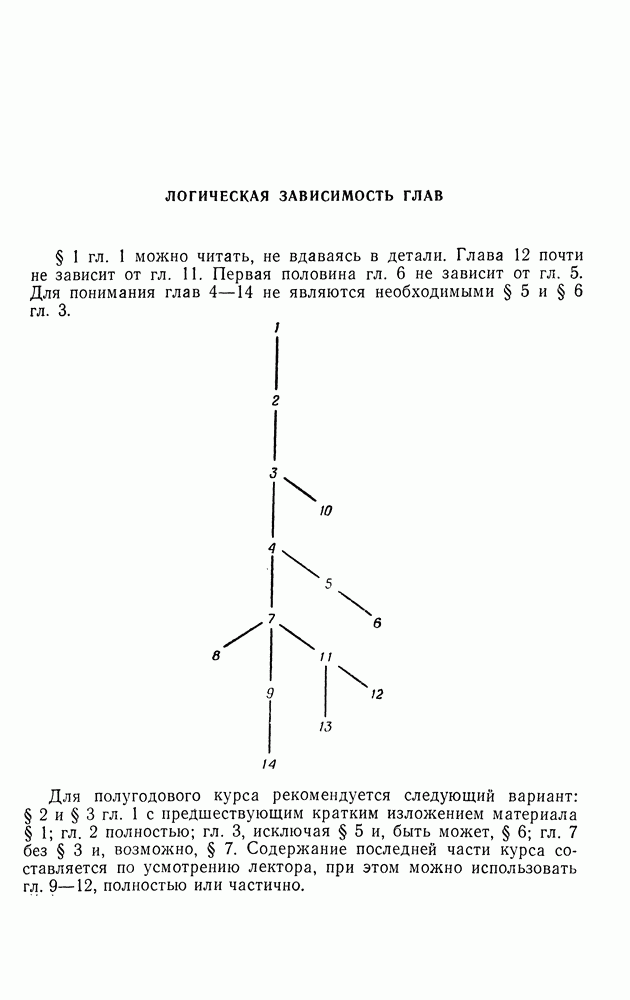
§ 5. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДВУМЯ ТИПАМИ ЧАСТИЦ
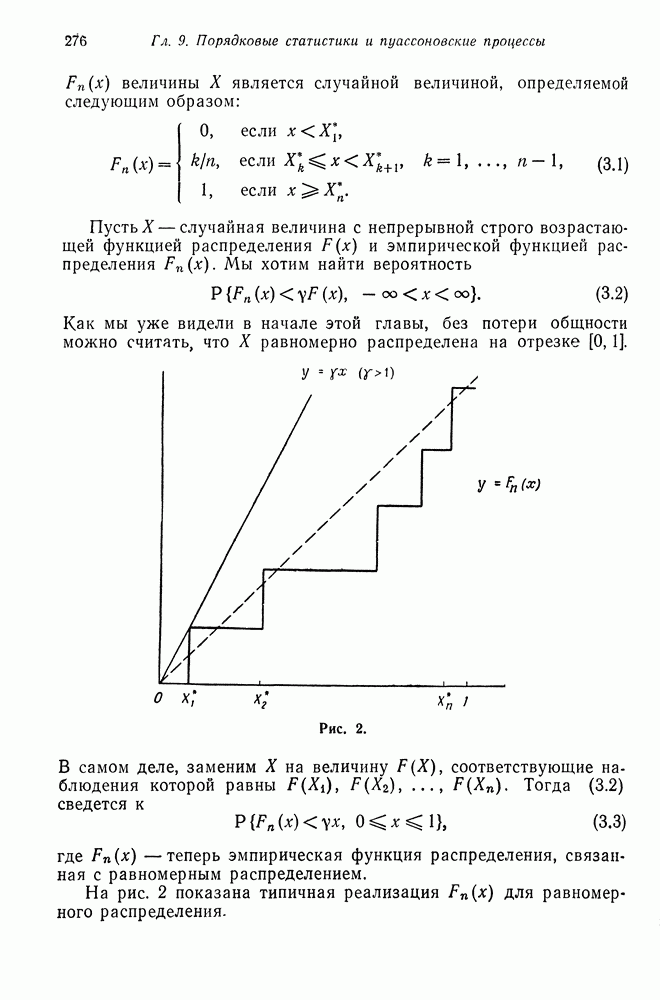
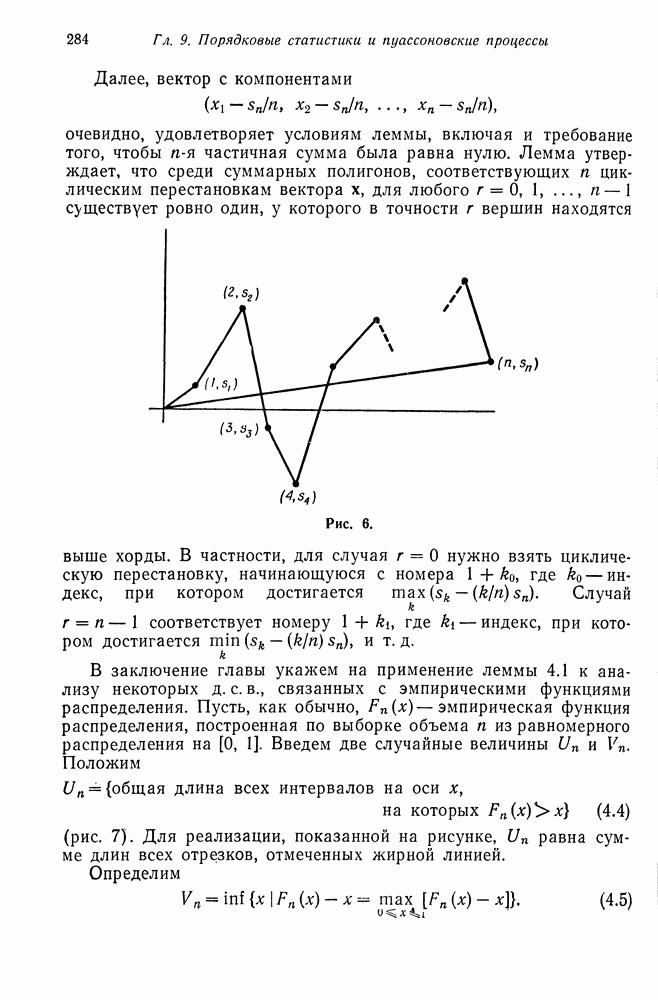
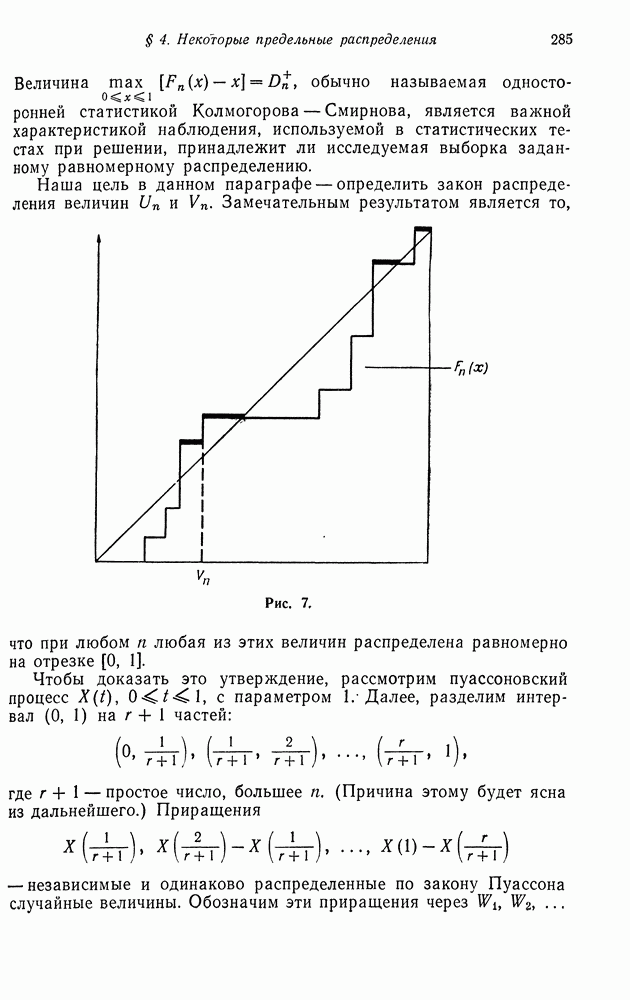
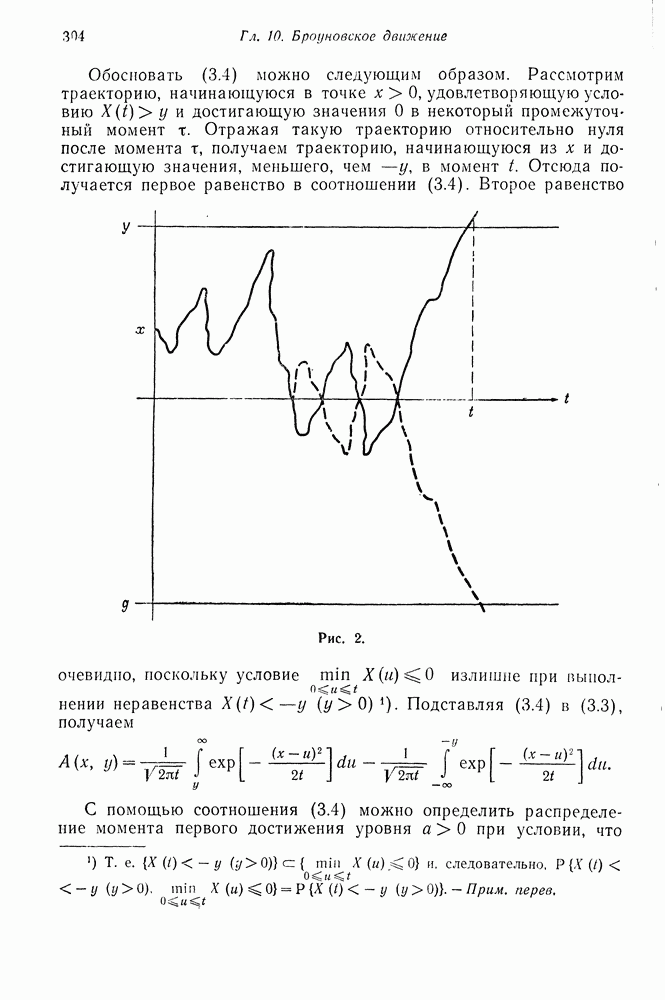
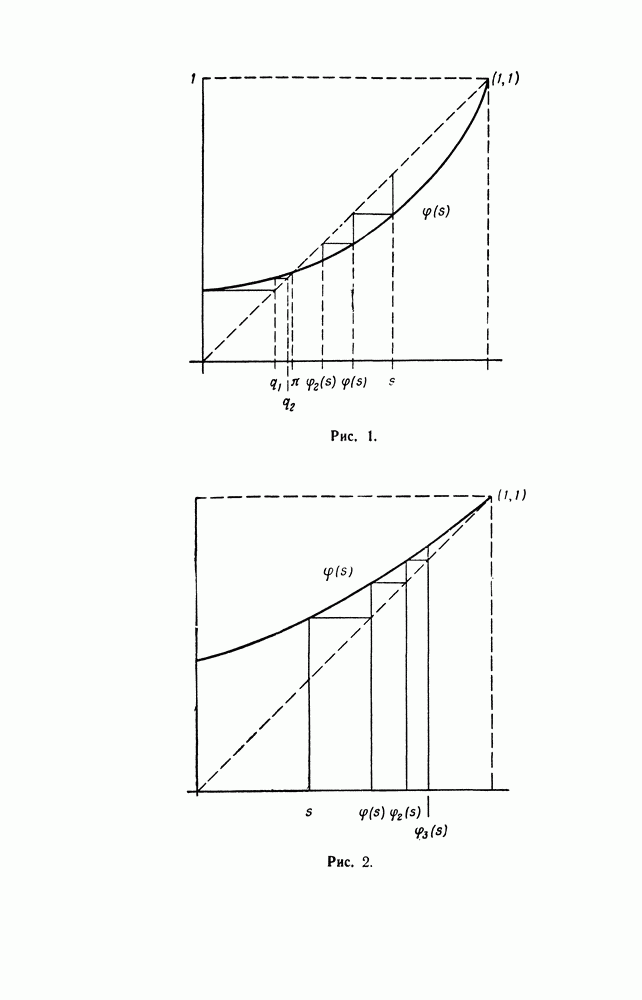
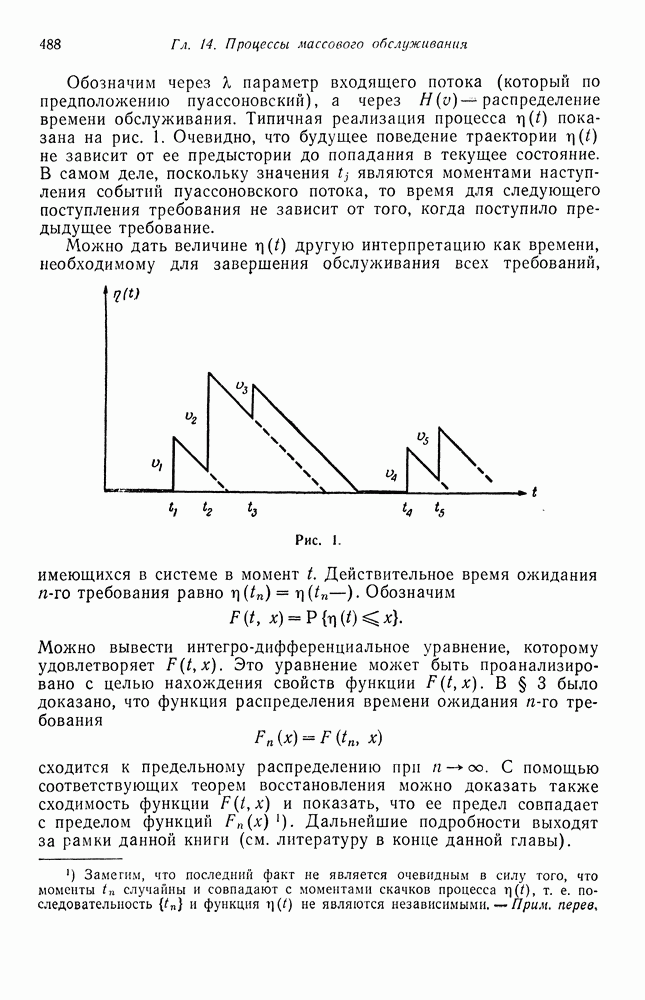
Обобщим развитую выше теорию на случай двух измерений. Рассмотрим популяцию организмов или объектов, в которой различаются два типа этих объекюв. Индивидуумы каждого типа могут в общем случае порождать потомков обоих типов независимо от других индивидуумов. Пусть  число индивидуумов типов I и II соответственно в
число индивидуумов типов I и II соответственно в  поколении. Можно записать
поколении. Можно записать

где  независимые одинаково распределенные случайные векторы с распределением
независимые одинаково распределенные случайные векторы с распределением

Здесь 

Другими словами,  вероятности того, что индивидуум типа I или II соответственно порождает
вероятности того, что индивидуум типа I или II соответственно порождает  прямых потомков, из которых
прямых потомков, из которых  имеют тип I и
имеют тип I и  - тип II.
- тип II.
Предположим, что процесс начинается, когда имеется один индивидуум, т. е. предположим, что

или

Введем две двумерные производящие функции

Производящая функция распределения (5.1) имеет вид

а распределения (5.2) —

Кроме того,

Обобщая метод, примененный для одномерного случая, можно показать, что

Это двумерный аналог формулы (2.3).
Чтобы обобщить формулу (3.5), введем следующие обозначения. Пусть  двумерный вектор с компонентами
двумерный вектор с компонентами  Положим
Положим

и введем матрицу математических ожиданий

Таким образом,  средние количества потомков типов I и II соответственно, порожденных единственным родителем типа
средние количества потомков типов I и II соответственно, порожденных единственным родителем типа  Тогда обобщением (3.5) является матричное равенство
Тогда обобщением (3.5) является матричное равенство

Доказательство его для  проводится непосредственно:
проводится непосредственно:

Предположим теперь, что соотношение (5.4) выполняется для  и докажем его для
и докажем его для  . В силу того что последовательность
. В силу того что последовательность  образует цепь Маркова, имеем
образует цепь Маркова, имеем

Тем самым (5.4) доказано.
Введем следующие вероятности поглощения для двумерного ветвящегося процесса:

«Одномерная» теория распространяется на этот случай с той лишь разницей, что роль математического ожидания  здесь играет наибольшее собственное значение
здесь играет наибольшее собственное значение  матрицы
матрицы 
Мы отсылаем читателя к приложению и, в частности, к теореме Фробениуса относительно матриц с неотрицательными элементами. Там доказано, что если  матрица с положительными элементами (что условимся обозначать
матрица с положительными элементами (что условимся обозначать  то собственное значение, максимальное по модулю, является положительным и, следовательно, действительным. Это собственное значение будет обозначаться через
то собственное значение, максимальное по модулю, является положительным и, следовательно, действительным. Это собственное значение будет обозначаться через 
Удобно ввести следующие векторные обозначения:

Теперь можно доказать такую теорему.
Теорема 5.1. Предположим, что компоненты вектора  не являются линейными функциями
не являются линейными функциями  (все элементы матрицы
(все элементы матрицы  положительны). Тогда
положительны). Тогда  если максимальное собственное значение
если максимальное собственное значение  матрицы
матрицы  не превышает 1, и 1, если
не превышает 1, и 1, если  (Обозначение
(Обозначение  означает, что вектор
означает, что вектор  и имеет положительные (неотрицательные) компоненты.) В случае
и имеет положительные (неотрицательные) компоненты.) В случае  наименьшее неотрицательное решение уравнения
наименьшее неотрицательное решение уравнения

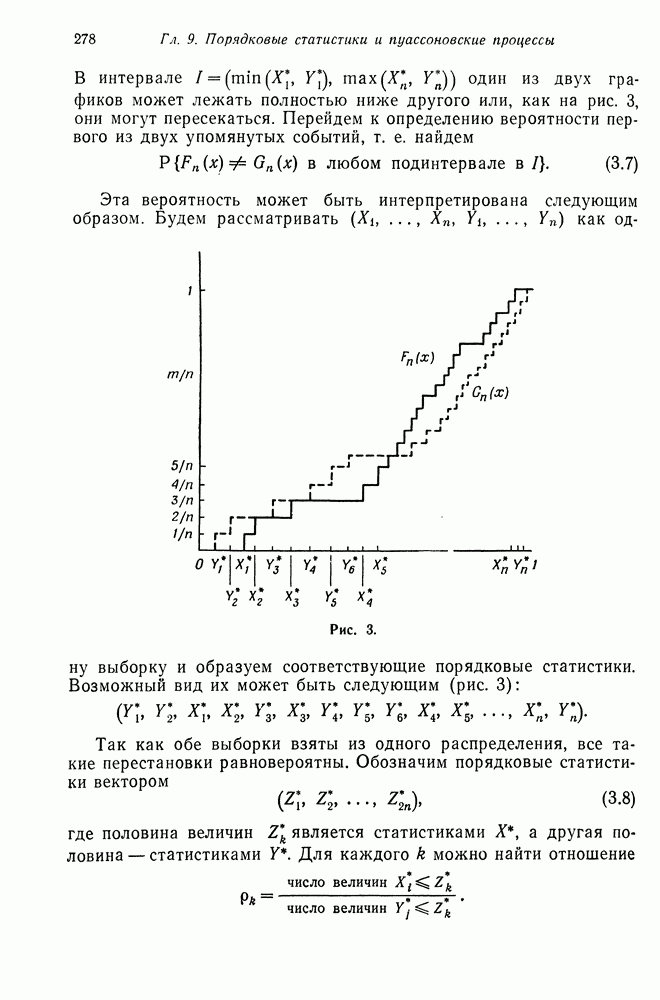
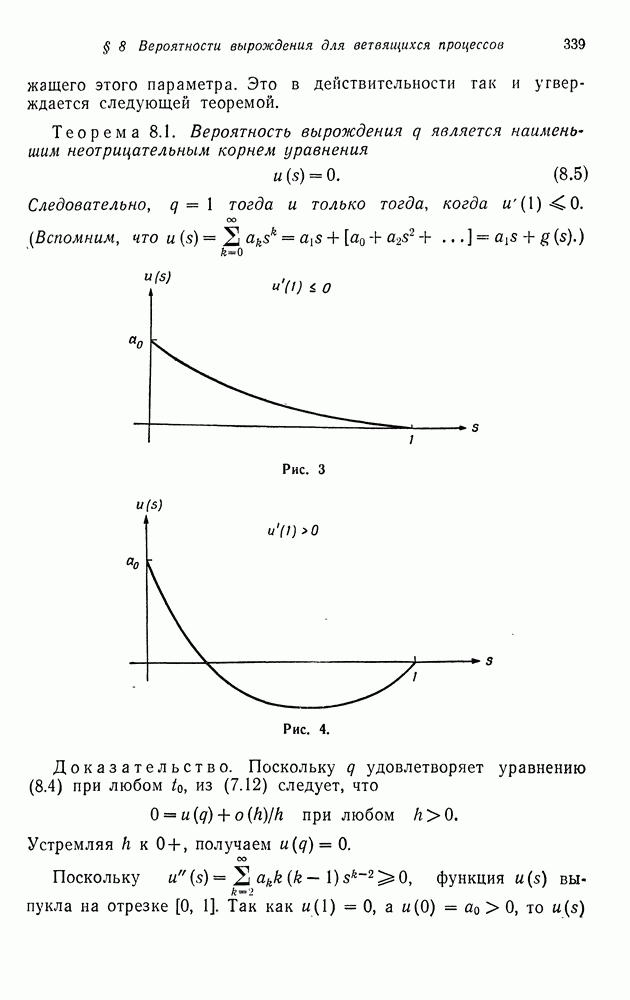
Доказательство. Рассмотрим случай  . В соответствии с общей теорией цепей Маркова мы знаем, что если цепь имеет единственное поглощающее состояние, то все состояния, из которых оно может быть достигнуто, — переходные (невозвратные). Двумерный процесс
. В соответствии с общей теорией цепей Маркова мы знаем, что если цепь имеет единственное поглощающее состояние, то все состояния, из которых оно может быть достигнуто, — переходные (невозвратные). Двумерный процесс  является как раз таким процессом: начало координат является единственным поглощающим состоянием, и оно может быть достигнуто из любого другого. Это является следствием того факта, что
является как раз таким процессом: начало координат является единственным поглощающим состоянием, и оно может быть достигнуто из любого другого. Это является следствием того факта, что  не имеет линейных компонент и
не имеет линейных компонент и  Таким образом, все состояния, за
Таким образом, все состояния, за
исключением начала координат, невозвратны. Следовательно,

для любого положительного  (см. теорему 7.1 гл. 2). Это означает, что
(см. теорему 7.1 гл. 2). Это означает, что

Из формулы (5.4) имеем  Но из теоремы 2.3 приложения следует, что
Но из теоремы 2.3 приложения следует, что  сходится покомпонентно при
сходится покомпонентно при  . Следовательно, в случае
. Следовательно, в случае  компоненты векторов
компоненты векторов  остаются ограниченными при
остаются ограниченными при  Отсюда следует, что событие
Отсюда следует, что событие  происходит с вероятностью 0. Следовательно,
происходит с вероятностью 0. Следовательно,  или, что то же,
или, что то же,  при
при  с вероятностью 1. Таким образом, если
с вероятностью 1. Таким образом, если  то
то

Рассмотрим теперь случай  Из формулы (5.3) при
Из формулы (5.3) при  имеем
имеем

Пусть

Тогда (5.6) можно переписать в виде

Поскольку  является возрастающей функцией
является возрастающей функцией  (причем если увеличиваются обе эти переменные одновременно, то — строго возрастающей) и поскольку
(причем если увеличиваются обе эти переменные одновременно, то — строго возрастающей) и поскольку  то имеем, очевидно,
то имеем, очевидно,

Тогда по индукции

Следовательно,  при любом
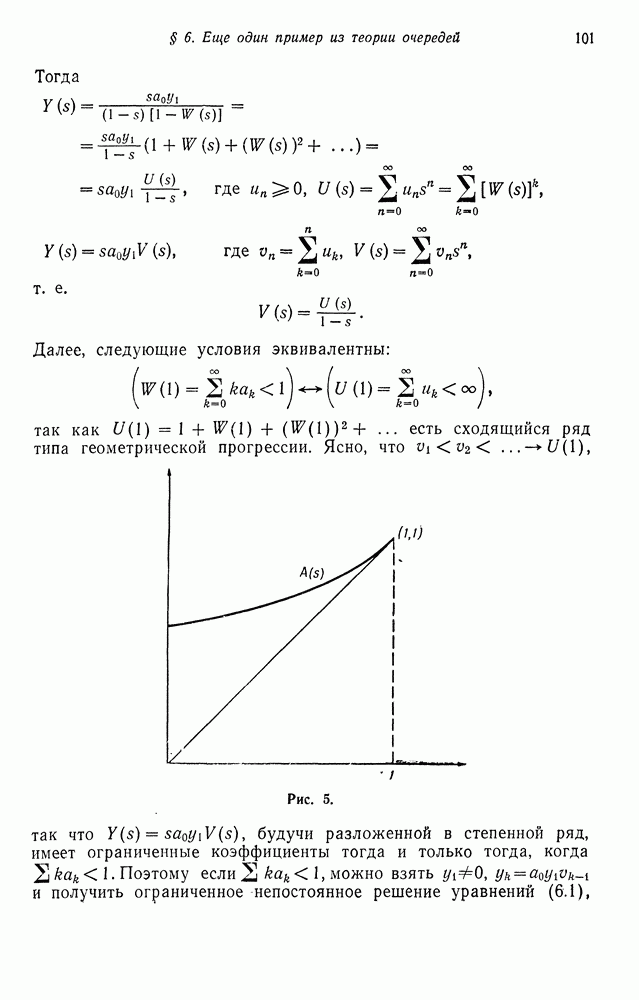
при любом  монотонно возрастающая последовательность, ограниченная сверху числом 1, и
монотонно возрастающая последовательность, ограниченная сверху числом 1, и

Пусть в соотношении  Тогда
Тогда

или, в векторных обозначениях,  Докажем теперь, что
Докажем теперь, что  и что это — единственное решение уравнения (5.5) при указанных условиях. Раскладывая
и что это — единственное решение уравнения (5.5) при указанных условиях. Раскладывая  по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  получаем выражение
получаем выражение

которое справедливо при  и достаточно малых
и достаточно малых  Символ
Символ  означает, что
означает, что  при
при  Очевидно,
Очевидно,

Перепишем (5.8) в векторной форме

где

 Из соотношения
Из соотношения  следует, что
следует, что  Пусть норма вектора
Пусть норма вектора  определяется как сумма абсолютных значений его координат:
определяется как сумма абсолютных значений его координат:  Докажем теперь, что для достаточно больших
Докажем теперь, что для достаточно больших 

при условии, что и 0. Действительно, в соответствии с теоремой 2,3 приложения

где  максимальное собственное значение
максимальное собственное значение  а
а  — отвечающие ему единственные (с точностью до постоянного множителя) соответственно левый и правый собственные векторы, нормированные таким образом, что
— отвечающие ему единственные (с точностью до постоянного множителя) соответственно левый и правый собственные векторы, нормированные таким образом, что  Обозначение
Обозначение  является обобщением общепринятого. Именно
является обобщением общепринятого. Именно  вектор, каждый элемент которого стремится к 0 при
вектор, каждый элемент которого стремится к 0 при  Множитель
Множитель  не зависит от
не зависит от  . Он равен разности между
. Он равен разности между  и его предельным (при
и его предельным (при  значением. Перепишем вышеприведенное выражение в виде
значением. Перепишем вышеприведенное выражение в виде

Если  , то получим очевидную оценку
, то получим очевидную оценку

Поскольку  то при достаточно большом
то при достаточно большом  получим неравенство (5.10). Комбинируя (5.9) и (5.10), получаем
получим неравенство (5.10). Комбинируя (5.9) и (5.10), получаем

при условии, что  достаточно мал, а
достаточно мал, а  достаточно велико, скажем
достаточно велико, скажем  Пусть
Пусть  . Тогда
. Тогда

при всех  удовлетворяющих условию
удовлетворяющих условию  Используем (5.11) для того, чтобы доказать, что
Используем (5.11) для того, чтобы доказать, что  . Предположим, что
. Предположим, что  т. е.
т. е.  для
для  Тогда величина
Тогда величина  стремится
стремится  при
при  Из (5.3) следует, что
Из (5.3) следует, что

Используя (5.11), где  имеем
имеем

если  а этого можно добиться, выбрав
а этого можно добиться, выбрав  достаточно большим. Однако соотношение (5.12) противоречит предположению о том, что
достаточно большим. Однако соотношение (5.12) противоречит предположению о том, что  при
при  Таким образом, равенство
Таким образом, равенство  невозможно. Предположим теперь, что
невозможно. Предположим теперь, что  Тогда
Тогда

и

Таким образом, имеем

где  Поскольку
Поскольку  монотонна по
монотонна по  должна быть постоянной на отрезке
должна быть постоянной на отрезке 

и, следовательно,

что противоречит сделанному предположению о том, что  Аналогичным образом можно доказать, что случай
Аналогичным образом можно доказать, что случай  невозможен. Таким образом, установлено, что
невозможен. Таким образом, установлено, что  Проверка того, что
Проверка того, что  меньше любой другой положительной неподвижной точки, производится следующим образом. Пусть вектор
меньше любой другой положительной неподвижной точки, производится следующим образом. Пусть вектор  удовлетворяет уравнению
удовлетворяет уравнению  . В силу монотонности имеем
. В силу монотонности имеем  Итерируя, получаем
Итерируя, получаем  переходя к пределу, находим, что
переходя к пределу, находим, что 
Мы можем усилить результат теоремы 5.1 следующим образом.
Теорема 5.2. В предположениях теоремы 5.1 для любого вектора  из единичного квадрата, отличного от 1,
из единичного квадрата, отличного от 1,

Доказательство. Предположим сначала, что  . Если
. Если  положительное целое число, то разложение Тейлора функции
положительное целое число, то разложение Тейлора функции  имеет вид
имеет вид

Последняя сумма ограничена величиной

которая при  стремится к 0, поскольку
стремится к 0, поскольку 
Каждый коэффициент первой суммы стремится к нулю при  поскольку
поскольку  стремится либо к 0, либо к
стремится либо к 0, либо к  Этот факт базируется на том, что все конечные состояния, не совпадающие с (0,0), невозвратны. Отсюда следует, что при фиксированном
Этот факт базируется на том, что все конечные состояния, не совпадающие с (0,0), невозвратны. Отсюда следует, что при фиксированном  первая сумма стремится к 0. Следовательно,
первая сумма стремится к 0. Следовательно,

как и утверждается в теореме. Аналогично

Если одна из величин  равна 1, но не обе одновременно, то
равна 1, но не обе одновременно, то  является положительным вектором, каждая компонента которого строго меньше 1. Применяя предыдущие рассуждения к
является положительным вектором, каждая компонента которого строго меньше 1. Применяя предыдущие рассуждения к  получаем
получаем

Следствие 5.1. Единственными решениями уравнения (5.5) являются 1 и  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 1. СВОДКА ОСНОВНЫХ ТЕРМИНОВ И СВОЙСТВ СЛУЧАЙНЫХ ВЕЛИЧИН И ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
- А. Совместные функции распределения
- Б. Условные распределения и плотности
- В. Бесконечные семейства случайных величин
- Г. Характеристические функции
- Д. Производящие функции
- Е. Примеры функций распределения
- Ж. Предельные теоремы
- § 2. ДВА ПРОСТЫХ ПРИМЕРА СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 3. КЛАССИФИКАЦИЯ ОБЩИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- ЗАМЕЧАНИЯ
- Глава 2. МАРКОВСКИЕ ЦЕПИ
- § 2. ПРИМЕРЫ МАРКОВСКИХ ЦЕПЕЙ
- Б. Одномерные случайные блуждания
- В. Дискретная марковская цепь, описывающая очередь
- Г. Модель из теории запасов
- Д. Серии успехов
- Е. Ветвящиеся процессы
- Ж. Марковские цепи в генетике
- 3. Генетическая модель II
- § 3. МАТРИЦЫ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ МАРКОВСКОЙ ЦЕПИ
- § 4. КЛАССИФИКАЦИЯ СОСТОЯНИЙ МАРКОВСКОЙ ЦЕПИ
- § 5. ВОЗВРАТНОСТЬ
- § 6. ПРИМЕРЫ ВОЗВРАТНЫХ МАРКОВСКИХ ЦЕПЕЙ
- § 7. ЕЩЕ О ВОЗВРАТНОСТИ
- Глава 3. ОСНОВНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ МАРКОВСКИХ ЦЕПЕЙ И ИХ ПРИЛОЖЕНИЯ
- § 2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 1.1
- § 3. ВЕРОЯТНОСТИ ПОГЛОЩЕНИЯ
- § 4. КРИТЕРИИ ВОЗВРАТНОСТИ
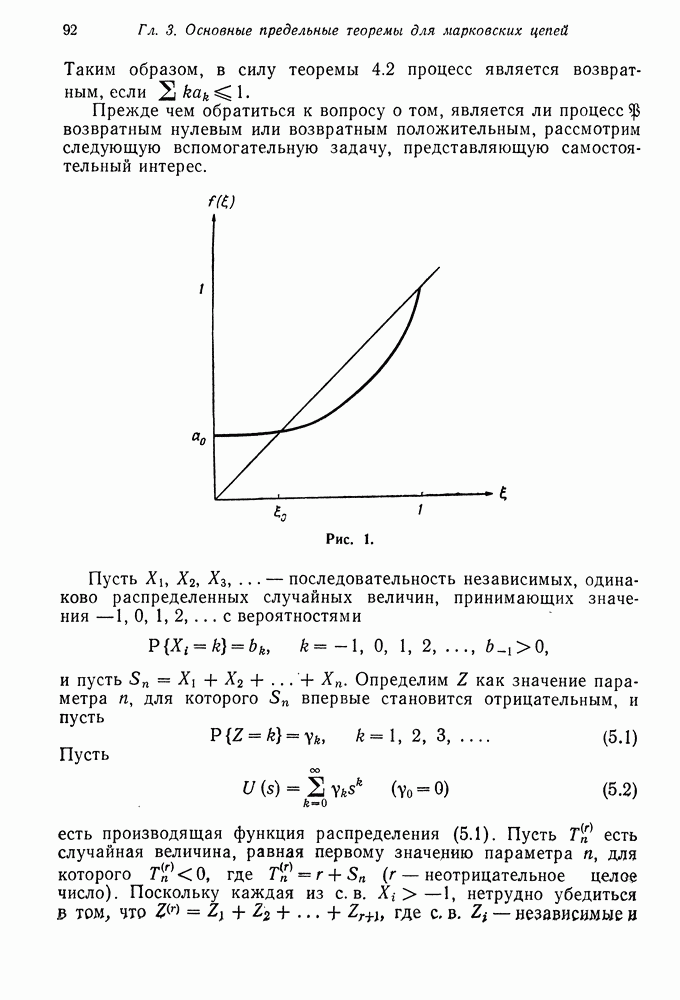
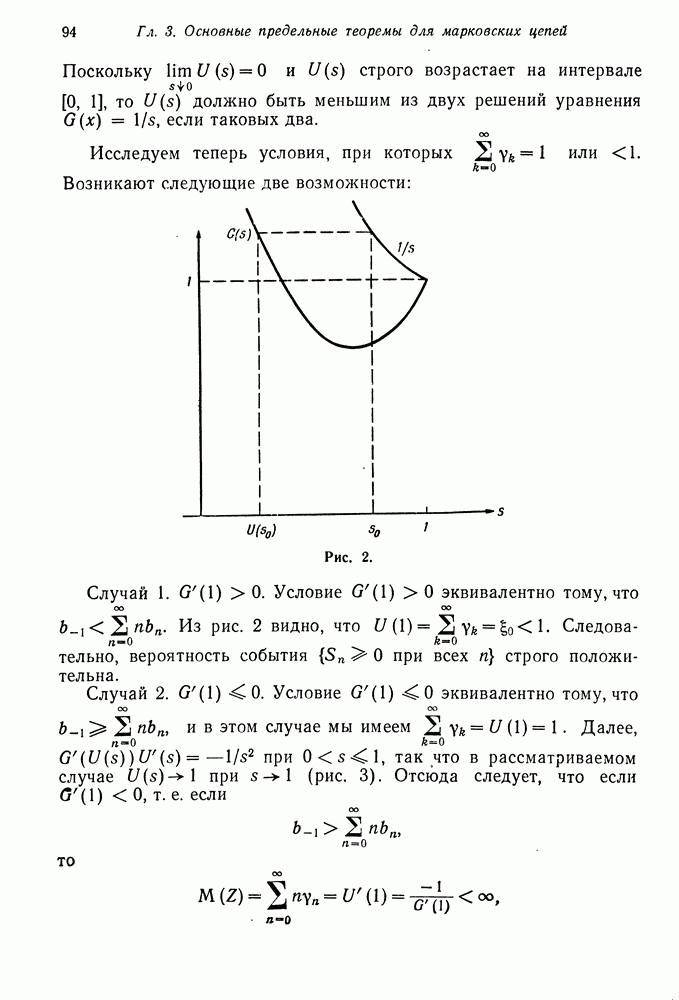
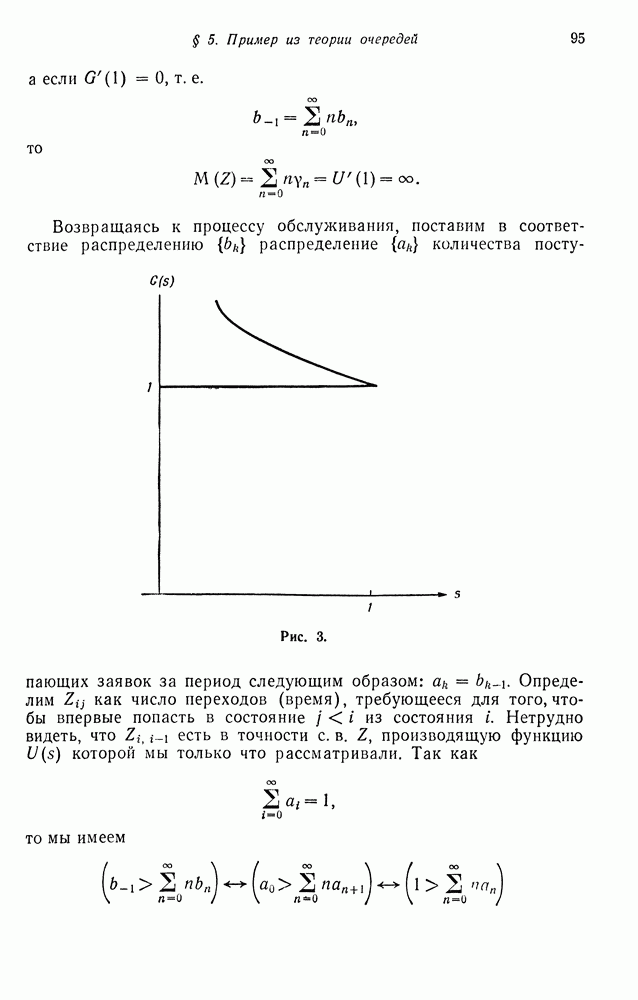
- § 5. ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
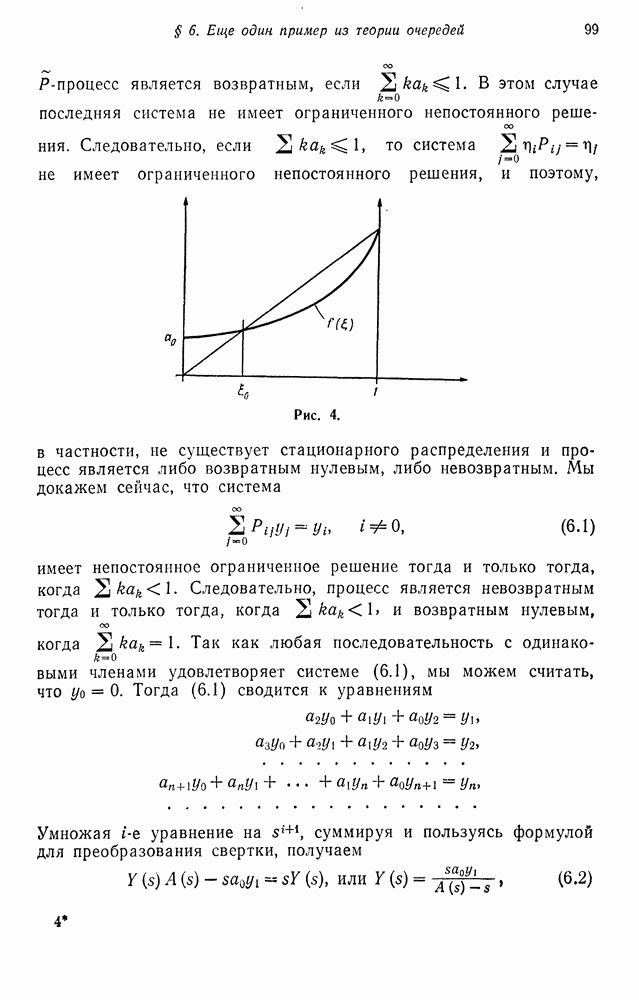
- § 6. ЕЩЕ ОДИН ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
- § 7. СЛУЧАЙНОЕ БЛУЖДАНИЕ
- Глава 4. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ МАРКОВСКИХ ЦЕПЕЙ
- § 2. СВЯЗЬ МЕЖДУ СОБСТВЕННЫМИ ЗНАЧЕНИЯМИ И КЛАССАМИ ВОЗВРАТНЫХ СОСТОЯНИЙ
- § 3. ПЕРИОДИЧЕСКИЕ КЛАССЫ
- § 4. СПЕЦИАЛЬНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ ДЛЯ МАРКОВСКИХ ЦЕПЕЙ
- § 5. ПРИМЕРЫ
- § 6. ПРИЛОЖЕНИЯ К БРОСАНИЯМ МОНЕТЫ
- Глава 5. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ И ИХ ПРИЛОЖЕНИЯ
- § 1. ВЕРОЯТНОСТИ ПЕРЕХОДА С ЗАПРЕЩЕНИЕМ
- § 2. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ
- § 3. СУЩЕСТВОВАНИЕ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ РАСПРЕДЕЛЕНИЙ
- § 4. ИНТЕРПРЕТАЦИЯ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ РАСПРЕДЕЛЕНИЙ
- § 5. РЕГУЛЯРНЫЕ, СУПЕРРЕГУЛЯРНЫЕ И СУБРЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТЬ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН КАК МАРКОВСКАЯ ЦЕПЬ
- § 1. СВОЙСТВА ВОЗВРАТНОСТИ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- § 2. ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
- § 3. ПРАВЫЕ РЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
- Глава 7. КЛАССИЧЕСКИЕ ПРИМЕРЫ ЦЕПЕЙ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 1. ОБЩИЕ ПРОЦЕССЫ ЧИСТОГО РОЖДЕНИЯ (РАЗМНОЖЕНИЯ) И ПУАССОНОВСКИЕ ПРОЦЕССЫ
- Б. Примеры пуассоновских процессов
- В. Процесс чистого рождения
- Г. Процесс Юла
- § 2. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О ПУАССОНОВСКИХ ПРОЦЕССАХ
- § 3. МОДЕЛЬ СЧЕТЧИКА
- § 4. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛИ
- § 5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
- § 6. ПРИМЕРЫ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
- § 7. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛЙ С ПОГЛОЩАЮЩИМИ СОСТОЯНИЯМИ
- § 8. ЦЕПИ МАРКОВА С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ И НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- Глава 8. ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 1. СВОЙСТВА ДИФФЕРЕНЦИРУЕМОСТИ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ
- § 2. КОНСЕРВАТИВНЫЕ ПРОЦЕССЫ. ПРЯМЫЕ И ОБРАТНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПОСТРОЕНИЕ ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ С ПОМОЩЬЮ ЕЕ ИНФИНИТЕЗИМАЛЬНЫХ ПАРАМЕТРОВ
- § 4. СТРОГО МАРКОВСКОЕ СВОЙСТВО
- Глава 9. ПОРЯДКОВЫЕ СТАТИСТИКИ, ПУАССОНОВСКИЕ ПРОЦЕССЫ И ИХ ПРИЛОЖЕНИЯ
- § 1. ПОРЯДКОВЫЕ СТАТИСТИКИ И ИХ СВЯЗЬ С ПУАССОНОВСКИМИ ПРОЦЕССАМИ
- § 2. ЗАДАЧА О БАЛЛОТИРОВКЕ
- § 3. ЭМПИРИЧЕСКИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПОРЯДКОВЫЕ СТАТИСТИКИ
- § 4. НЕКОТОРЫЕ ПРЕДЕЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ДЛЯ ЭМПИРИЧЕСКИХ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
- Глава 10. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 2. СОВМЕСТНЫЕ ВЕРОЯТНОСТИ ДЛЯ БРОУНОВСКОГО ДВИЖЕНИЯ
- § 3. НЕПРЕРЫВНОСТЬ ТРАЕКТОРИЙ И ИХ МАКСИМАЛЬНЫЕ ЗНАЧЕНИЯ
- Глава 11. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ
- § 1. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
- § 2. СООТНОШЕНИЯ ДЛЯ ПРОИЗВОДЯЩЕЙ ФУНКЦИИ, ОПИСЫВАЮЩЕЙ ВЕТВЯЩИЙСЯ ПРОЦЕСС
- § 3. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ
- § 4. ПРИМЕРЫ
- § 5. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДВУМЯ ТИПАМИ ЧАСТИЦ
- § 6. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕСКОЛЬКИМИ ТИПАМИ ЧАСТИЦ
- § 7. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 8. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 10. ВЕТВЯЩИЙСЯ ПРОЦЕСС С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ И ДВУМЯ ТИПАМИ ЧАСТИЦ
- § 11. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ, ЗАВИСЯЩИЕ ОТ ВОЗРАСТА
- Глава 12. СОСТАВНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- § 1. МНОГОМЕРНЫЕ ОДНОРОДНЫЕ ПУЛССОНОВСКИЕ ПРОЦЕССЫ
- § 2. ПРИМЕНЕНИЕ МНОГОМЕРНЫХ ПУАССОНОВСКИХ ПРОЦЕССОВ В АСТРОНОМИИ
- § 3. ИММИГРАЦИЯ И РОСТ ПОПУЛЯЦИЙ
- § 4. ВЕРОЯТНОСТНЫЕ МОДЕЛИ МУТАЦИИ И РОСТА
- § 5. ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ ОДНОМЕРНОЙ ПОПУЛЯЦИИ
- § 6. ВЕРОЯТНОСТНАЯ МОДЕЛЬ РОСТА ПОПУЛЯЦИИ В ПРОСТРАНСТВЕ И ВРЕМЕНИ
- § 7. ДЕТЕРМИНИРОВАННЫЙ РОСТ ПОПУЛЯЦИИ С РАСПРЕДЕЛЕНИЕМ ПО ВОЗРАСТАМ
- § 8. ДИСКРЕТНАЯ ВОЗРАСТНАЯ МОДЕЛЬ
- Глава 13. ДЕТЕРМИНИРОВАННЫЕ И СЛУЧАЙНЫЕ ГЕНЕТИЧЕСКИЕ И ЭКОЛОГИЧЕСКИЕ ПРОЦЕССЫ
- § 1. ГЕНЕТИЧЕСКИЕ МОДЕЛИ. ОПИСАНИЕ ГЕНЕТИЧЕСКОГО МЕХАНИЗМА
- § 2. ИНБРИДИНГ
- Б. Спаривание сибсов
- В. Гены, идентичные по происхождению
- Г. Бесконечная диплоидная популяция и коэффициент инбридинга
- Д. Популяция с самооплодотворением и случайным спариванием
- § 3. ПОЛИПЛОИДЫ
- § 4. МАРКОВСКИЕ ПРОЦЕССЫ, ПОРОЖДАЕМЫЕ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
- § 5. МОДЕЛИ РОСТА ПОПУЛЯЦИЙ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
- § 6. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЦЕПЕЙ МАРКОВА, ПОРОЖДЕННЫХ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
- § 7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МОДЕЛИ МУТАЦИИ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
- § 8. ВЕРОЯТНОСТНЫЙ СМЫСЛ СОБСТВЕННЫХ ЗНАЧЕНИЙ
- Глава 14. ПРОЦЕССЫ МАССОВОГО ОБСЛУЖИВАНИЯ
- § 2. ПРОСТЕЙШИЕ ПРОЦЕССЫ ОБСЛУЖИВАНИЯ (М/М/1)
- § 3. НЕКОТОРЫЕ ОБЩИЕ МОДЕЛИ ОБСЛУЖИВАНИЯ ОДНИМ ПРИБОРОМ
- § 4. МЕТОД ВЛОЖЕННЫХ ЦЕПЕЙ МАРКОВА ПРИМЕНИТЕЛЬНО К МОДЕЛИ ОБСЛУЖИВАНИЯ (M/G/1)
- § 5. ЭКСПОНЕНЦИАЛЬНО РАСПРЕДЕЛЕННОЕ ВРЕМЯ ОБСЛУЖИВАНИЯ (G/М/1)
- § 6. ГАММА-РАСПРЕДЕЛЕНИЕ ИНТЕРВАЛОВ МЕЖДУ ПОСТУПЛЕНИЯМИ И ОБОБЩЕНИЯ (Ek/М/1)
- § 7. ЭКСПОНЕНЦИАЛЬНОЕ ОБСЛУЖИВАНИЕ s ПРИБОРОВ (GI/M/s)
- § 8. ВИРТУАЛЬНОЕ ВРЕМЯ ОЖИДАНИЯ И ПЕРИОД ЗАНЯТОСТИ
- ПРИЛОЖЕНИЕ § 1. СПЕКТРАЛЬНАЯ ТЕОРЕМА
- § 2. ТЕОРИЯ ФРОБЕНИУСА ПОЛОЖИТЕЛЬНЫХ МАТРИЦ
- РАЗЛИЧНЫЕ ЗАДАЧИ