| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. ТЕОРИЯ ФРОБЕНИУСА ПОЛОЖИТЕЛЬНЫХ МАТРИЦ
Теория положительных матриц, развитая Фробениусом, играет важную роль во многих разделах теории вероятностей, в частности в анализе матриц переходных вероятностей цепей Маркова.
Предварительные замечания
Если каждый элемент  некоторой квадратной матрицы
некоторой квадратной матрицы  неотрицателен, то мы будем писать
неотрицателен, то мы будем писать
 если
если  и по крайней мере один элемент
и по крайней мере один элемент  то мы будем писать
то мы будем писать  и называть А положительной матрицей. Если все
и называть А положительной матрицей. Если все  то этот факт мы будем обозначать
то этот факт мы будем обозначать  . Такими же обозначениями мы будем пользоваться и для векторов. Именно если
. Такими же обозначениями мы будем пользоваться и для векторов. Именно если  означает, что
означает, что  для всех
для всех  означает, что
означает, что  хотя бы для одного I, и, наконец,
хотя бы для одного I, и, наконец,  означает, что
означает, что  для всех
для всех  Мы также будем писать
Мы также будем писать  если
если  Ясно, что из
Ясно, что из  следует, что
следует, что  а из
а из  следует, что
следует, что 
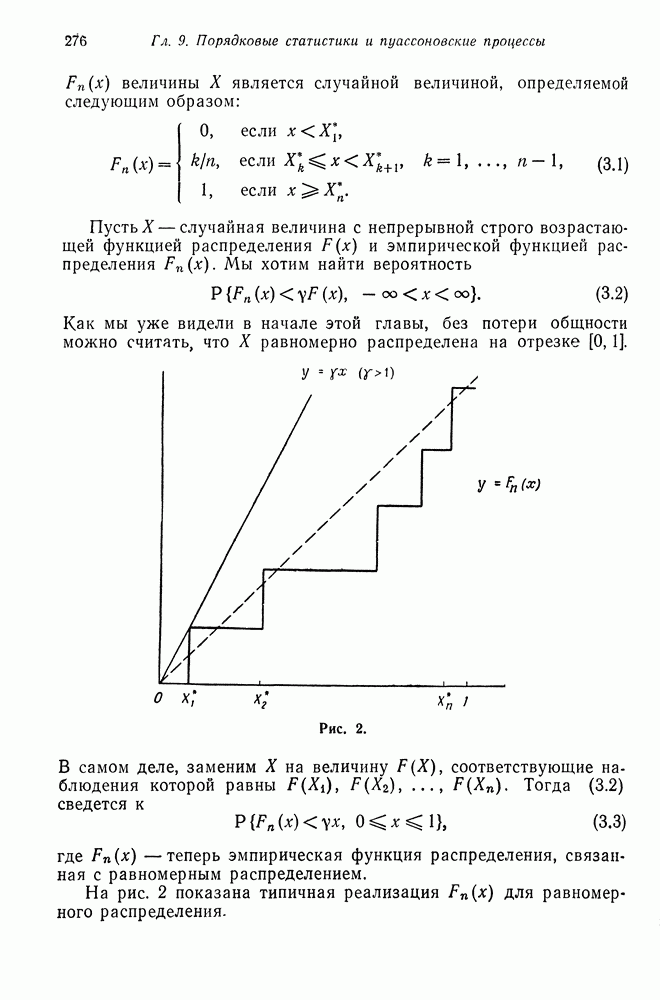
Пусть  рассмотрим множество
рассмотрим множество  всех действительных чисел
всех действительных чисел  , каждому из которых соответствует вектор
, каждому из которых соответствует вектор  такой, что
такой, что

Пусть  легко показать, что
легко показать, что  конечно, а в случае когда
конечно, а в случае когда  , еще и положительно. В самом деле, если
, еще и положительно. В самом деле, если  то из условий
то из условий  следует, что
следует, что  а также что
а также что  хотя бы для одного
хотя бы для одного  Отсюда получаем неравенство
Отсюда получаем неравенство  Если
Если  то
то  ; это означает, что число
; это означает, что число  (Ему соответствует вектор
(Ему соответствует вектор 
Предположим теперь, что  для матрицы
для матрицы  Для
Для  соотношение
соотношение  невозможно, так как
невозможно, так как  . С другой стороны, из равенства
. С другой стороны, из равенства  для некоторого
для некоторого  следует, что
следует, что  Таким образом, существует вектор
Таким образом, существует вектор  такой, что
такой, что  Пусть
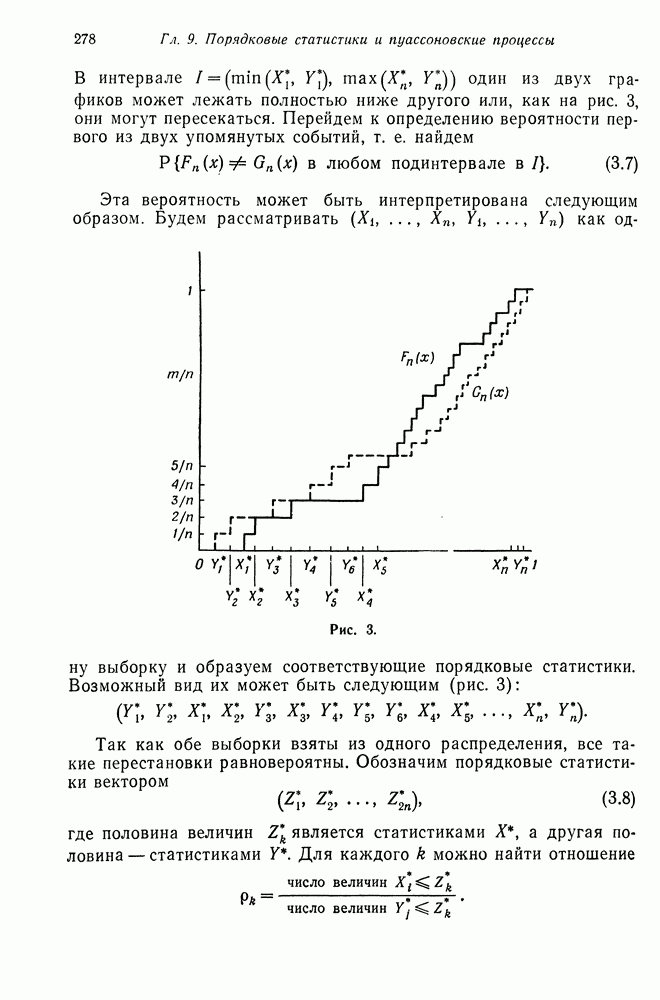
Пусть  множество индексов положительных элементов вектора
множество индексов положительных элементов вектора  очевидно,
очевидно,  не зависит от выбора вектора
не зависит от выбора вектора  Пусть вектор
Пусть вектор  таков, что
таков, что  если
если  если
если  Определим
Определим  как множество индексов положительных координат вектора
как множество индексов положительных координат вектора  это множество не зависит от выбора вектора у и, кроме того,
это множество не зависит от выбора вектора у и, кроме того,  Поскольку
Поскольку  то
то  Рассуждая точно так же, легко убедиться, что
Рассуждая точно так же, легко убедиться, что

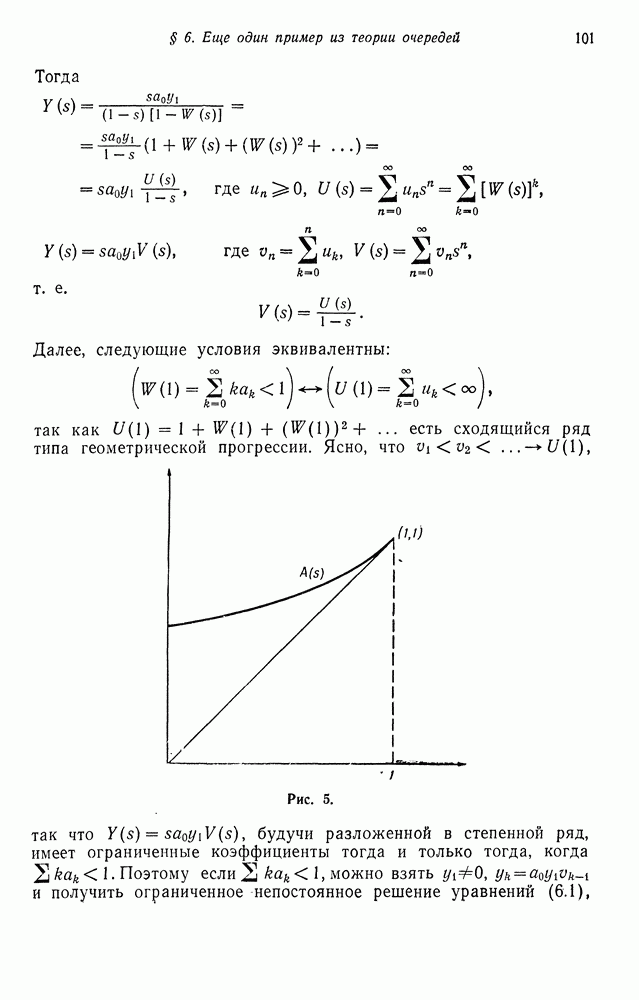
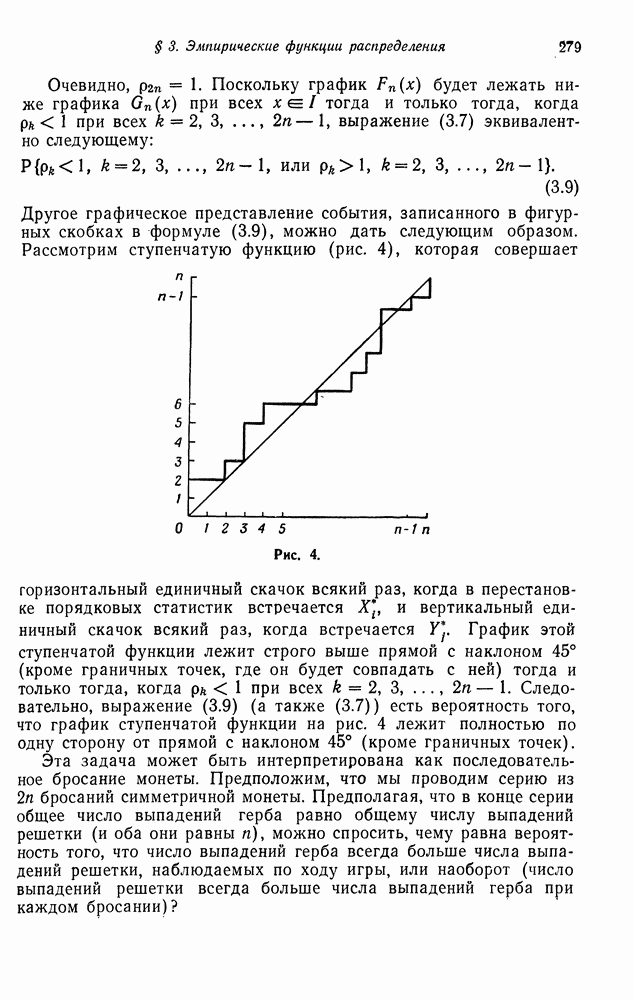
причем здесь все включения являются строгими. Теперь уже не составляет труда показать, что  Действительно,
Действительно,  для
для  но так как любой вектор может быть представлен как разность двух строго положительных векторов, то
но так как любой вектор может быть представлен как разность двух строго положительных векторов, то  для любого
для любого  что эквивалентно равенству нулю матрицы
что эквивалентно равенству нулю матрицы 
Первая теорема Фробениуса
Теорема 2.1. Если  , то (а) существует вектор
, то (а) существует вектор  такой, что
такой, что  для всех собственных значений X матрицы А, отличных от
для всех собственных значений X матрицы А, отличных от  правые собственные векторы матрицы А, соответствующие
правые собственные векторы матрицы А, соответствующие  образуют одномерное подпространство, т. е.
образуют одномерное подпространство, т. е. 
Доказательство, (а) По определению  существует последовательность
существует последовательность  и векторы
и векторы  такие, что
такие, что

Так как значения компонент всех векторов х принадлежат отрезку [0, 1], то с помощью процесса диагонализации мы можем построить последовательность положительных целых чисел  такую, что
такую, что

где  Из (2.1) следует, что
Из (2.1) следует, что  Кроме того, если мы заменим в неравенстве
Кроме того, если мы заменим в неравенстве  индекс
индекс  на
на  и устремим
и устремим  то придем к неравенству
то придем к неравенству  Мы покажем, что на самом деле
Мы покажем, что на самом деле  Действительно, если это не так, то
Действительно, если это не так, то  Умножая обе части этого неравенства слева на А, получаем неравенство
Умножая обе части этого неравенства слева на А, получаем неравенство  где
где  Это неравенство сохранится и тогда, когда мы прибавим к
Это неравенство сохранится и тогда, когда мы прибавим к  достаточно малое положительное число
достаточно малое положительное число  Нормируя вектор
Нормируя вектор  так, чтобы сумма его координат равнялась единице, мы убеждаемся в том, что
так, чтобы сумма его координат равнялась единице, мы убеждаемся в том, что  принадлежит множеству
принадлежит множеству  Но последнее противоречит определению
Но последнее противоречит определению  Таким образом,
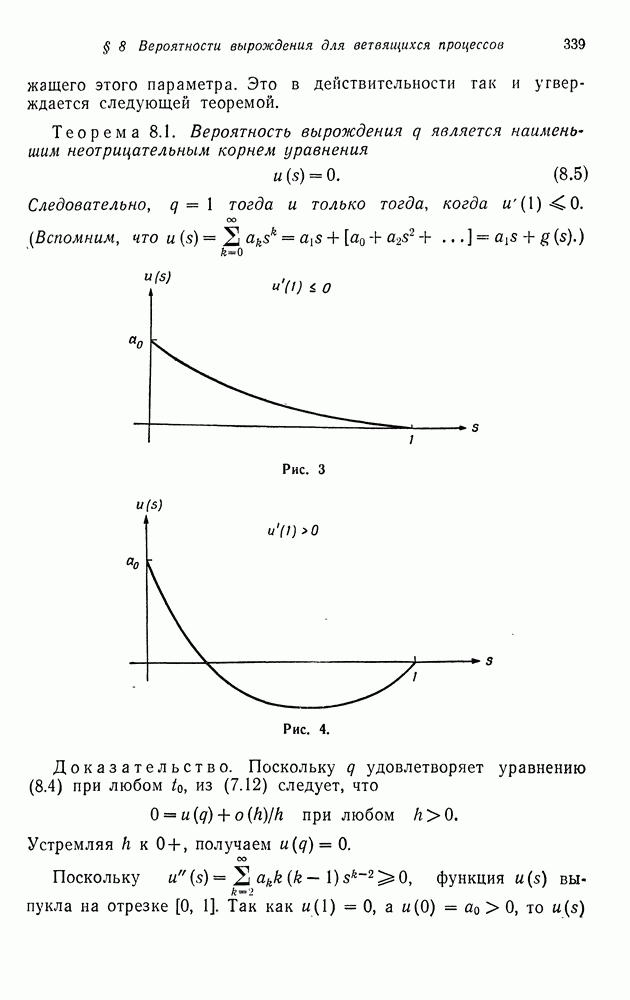
Таким образом,  Поскольку
Поскольку  то
то  т. е.
т. е.  Этим завершается доказательство утверждения
Этим завершается доказательство утверждения 
(б) Пусть  где
где  Координатная запись равенства
Координатная запись равенства  имеет вид
имеет вид

Отсюда для абсолютных величин имеем

т. е.

Нормируя вектор  так, чтобы сумма его координат равнялась единице (напомним, что
так, чтобы сумма его координат равнялась единице (напомним, что  мы видим, что
мы видим, что  принадлежит
принадлежит  Тогда по определению
Тогда по определению  имеем
имеем  Чтобы показать,
Чтобы показать,
что  введем матрицу
введем матрицу  где I — единичная матрица,
где I — единичная матрица,  положительное число, малое настолько, что
положительное число, малое настолько, что  Поскольку
Поскольку  наибольшее по абсолютной величине положительное собственное значение матрицы А, то
наибольшее по абсолютной величине положительное собственное значение матрицы А, то  является таковым для матрицы
является таковым для матрицы  Повторяя те же рассуждения, что и при доказательстве неравенства
Повторяя те же рассуждения, что и при доказательстве неравенства  для матрицы
для матрицы  и ее собственного значения
и ее собственного значения  получаем неравенство
получаем неравенство  Но, с другой стороны,
Но, с другой стороны,

так что из  следует
следует  Последнее означает, что X действительно и положительно. Таким образом, имеет место равенство
Последнее означает, что X действительно и положительно. Таким образом, имеет место равенство  что противоречит исходному предположению (
что противоречит исходному предположению ( Предположим, что
Предположим, что  и не существует такой константы с, что
и не существует такой константы с, что  Поскольку А — действительная матрица, векторы
Поскольку А — действительная матрица, векторы  координатами которых служат соответственно действительные и мнимые части координат вектора у, являются собственными векторами матрицы А, соответствующими
координатами которых служат соответственно действительные и мнимые части координат вектора у, являются собственными векторами матрицы А, соответствующими  Поскольку
Поскольку  для всех констант с, то по крайней мере один из векторов и или
для всех констант с, то по крайней мере один из векторов и или  не представим в виде
не представим в виде  Поэтому мы можем считать вектор у действительным. Так как
Поэтому мы можем считать вектор у действительным. Так как  можно выбрать такое число
можно выбрать такое число  что
что  но не
но не  при этом
при этом  Отсюда
Отсюда  как и в доказательстве утверждения
как и в доказательстве утверждения  с необходимостью получаем:
с необходимостью получаем:  Это противоречит выбору
Это противоречит выбору 
Отметим попутно несколько простых фактов. Если  то можно утверждать, что существует вектор
то можно утверждать, что существует вектор  такой, что
такой, что  а подпространство левых собственных векторов, соответствующих
а подпространство левых собственных векторов, соответствующих  одномерно. Следуя доказательству теоремы 2.1, положим
одномерно. Следуя доказательству теоремы 2.1, положим  где
где  для некоторого
для некоторого  Легко убедиться в существовании вектора
Легко убедиться в существовании вектора  такого, что
такого, что  в одномерности подпространства левых собственных векторов, отвечающих А, а также в том, что если А — любое собственное значение матрицы А, не равное А, то
в одномерности подпространства левых собственных векторов, отвечающих А, а также в том, что если А — любое собственное значение матрицы А, не равное А, то  Но отсюда следует, что
Но отсюда следует, что  если
если  тогда как по теореме
тогда как по теореме  если собственное значение А отлично от
если собственное значение А отлично от  Следовательно,
Следовательно, 
Теорема 2.2. Если матрица  такова, что
такова, что  для некоторого целого числа
для некоторого целого числа  то для нее остаются справедливыми утвероюдения предыдущей теоремы.
то для нее остаются справедливыми утвероюдения предыдущей теоремы.
Доказательство. Как и в доказательстве теоремы 2.1, мы можем найти вектор  такой, что
такой, что  Если
Если
 то
то  Умножая обе части этого неравенства слева на
Умножая обе части этого неравенства слева на  приходим к соотношению
приходим к соотношению  где
где  Это противоречит определению
Это противоречит определению  доказательство теоремы 2.1); следовательно,
доказательство теоремы 2.1); следовательно,  Отсюда получаем соотношение
Отсюда получаем соотношение  Так как
Так как  то
то 
Для доказательства неравенства  в пункте (б) теоремы 2.1 нам было бы достаточно положительности (не строгой) матрицы А. Поэтому это неравенство выполняется и в условиях настоящей теоремы. Предположим, что
в пункте (б) теоремы 2.1 нам было бы достаточно положительности (не строгой) матрицы А. Поэтому это неравенство выполняется и в условиях настоящей теоремы. Предположим, что  для некоторого вектора
для некоторого вектора  Тогда
Тогда  Если мы покажем, что
Если мы покажем, что  является наибольшим по модулю положительным собственным значением матрицы
является наибольшим по модулю положительным собственным значением матрицы  то теорема 2.1 сразу же приведет нас к противоречию. Так как
то теорема 2.1 сразу же приведет нас к противоречию. Так как  то
то  имеет наибольшее по модулю положительное собственное значение по теореме 2.1, которому соответствует собственный вектор с положительными компонентами. В таком случае, если
имеет наибольшее по модулю положительное собственное значение по теореме 2.1, которому соответствует собственный вектор с положительными компонентами. В таком случае, если  не является наибольшим по модулю положительным собственным значением матрицы
не является наибольшим по модулю положительным собственным значением матрицы  то матрица
то матрица  имеет по крайней мере два положительных собственных значения
имеет по крайней мере два положительных собственных значения  которым соответствуют собственные векторы
которым соответствуют собственные векторы  Но это невозможно; действительно, пусть
Но это невозможно; действительно, пусть  таково, что
таково, что  но не 0. Тогда
но не 0. Тогда  . С другой стороны,
. С другой стороны,  Поскольку вектор
Поскольку вектор  имеет по крайней мере одну нулевую компоненту, в то время как все компоненты вектора
имеет по крайней мере одну нулевую компоненту, в то время как все компоненты вектора  положительны, мы приходим к противоречию.
положительны, мы приходим к противоречию.
Тот факт, что все собственные векторы матрицы А являются собственными векторами матрицы  сводит доказательство утверждения (в) к повторению доказательства утверждения (в) теоремы 2.1.
сводит доказательство утверждения (в) к повторению доказательства утверждения (в) теоремы 2.1.
Продолжая изучение матриц  для которых
для которых  при некотором целом
при некотором целом  введем матрицу ранга 1 по формуле
введем матрицу ранга 1 по формуле

где  правый собственный вектор, введенный в доказательстве теоремы
правый собственный вектор, введенный в доказательстве теоремы  левый собственный вектор, принадлежащий
левый собственный вектор, принадлежащий  и нормированный условием
и нормированный условием  Такая матрица обладает следующими свойствами:
Такая матрица обладает следующими свойствами:

Первые два свойства проверяются непосредственно; что же касается третьего, то заметим, что для любого вектора х имеем

так что  аналогично
аналогично  т. е.
т. е. 
Приведем без доказательства следующий факт. Пусть В — квадратная матрица; положим

где  элементы матрицы В. Матрица В имеет собственное значение Я, такое, что
элементы матрицы В. Матрица В имеет собственное значение Я, такое, что  для всех других собственных значений Я матрицы В имеет место неравенство
для всех других собственных значений Я матрицы В имеет место неравенство 
 часто называют спектральным радиусом матрицы. Мы воспользуемся этим понятием при доказательстве следующей теоремы.
часто называют спектральным радиусом матрицы. Мы воспользуемся этим понятием при доказательстве следующей теоремы.
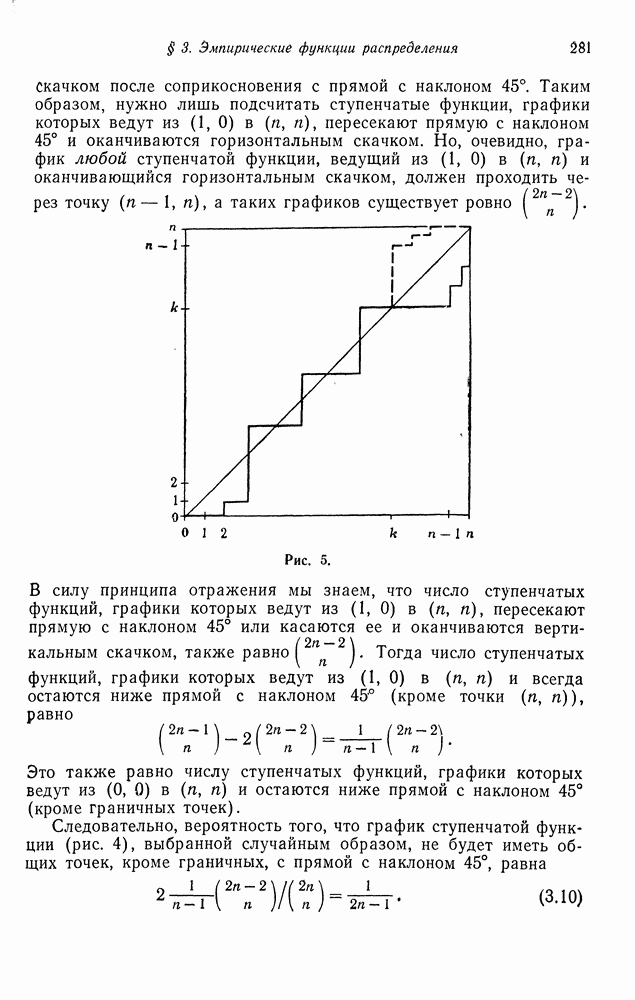
Теорема 2.3. Если  для некоторого целого
для некоторого целого  то
то

где  и
и  имеют прежний смысл.
имеют прежний смысл.
Доказательство. Покажем сначала, что если Я является собственным значением матрицы  то
то  Действительно, предположим, что
Действительно, предположим, что  при некотором
при некотором  ; тогда
; тогда

откуда следует, что всякое собственное значение матрицы В является собственным значением матрицы  то же можно сказать о собственных векторах. Из теоремы 2.2 следует, что либо
то же можно сказать о собственных векторах. Из теоремы 2.2 следует, что либо  либо
либо  Предположим, что
Предположим, что  тогда в силу одномерности собственного подпространства, соответствующего
тогда в силу одномерности собственного подпространства, соответствующего  матрицы А, а следовательно, и матрицы В имеет место соотношение
матрицы А, а следовательно, и матрицы В имеет место соотношение  С другой стороны,
С другой стороны,  Получаем противоречие. Значит, спектральный радиус
Получаем противоречие. Значит, спектральный радиус  матрицы В удовлетворяет неравенству
матрицы В удовлетворяет неравенству  Пусть
Пусть  положительное число, такое, что
положительное число, такое, что  поскольку
поскольку

то  для достаточно больших
для достаточно больших  Используя свойства (II) и (III) матрицы
Используя свойства (II) и (III) матрицы  получаем
получаем

или

Так как  для достаточно больших
для достаточно больших  то
то

а следовательно, 
Вторая теорема Фробениуса
Теорема 2.4. Пусть  имеет тот же смысл, что и в теореме 2.1; тогда:
имеет тот же смысл, что и в теореме 2.1; тогда:  является собственным значением матрицы А и ему соответствует собственный вектор
является собственным значением матрицы А и ему соответствует собственный вектор  если
если  — любое другое собственное значение матрицы А, то
— любое другое собственное значение матрицы А, то  среднее
среднее

сходится, если  если X — собственное значение матрицы
если X — собственное значение матрицы  то
то  является корнем из единицы, а
является корнем из единицы, а  суть собственные значения матрицы А.
суть собственные значения матрицы А.
Доказательство, (а) Пусть  матрица, все элементы которой равны единице; тогда
матрица, все элементы которой равны единице; тогда  при любом
при любом  Пусть
Пусть  Выберем
Выберем  таким, что
таким, что  тогда из
тогда из  следует, что
следует, что

Таким образом, если  значение
значение  соответствующее матрице
соответствующее матрице  то
то  является возрастающей функцией аргумента 6. Заметим, что
является возрастающей функцией аргумента 6. Заметим, что  есть значение
есть значение  соответствующее самой матрице А. По теореме 2.1 существует вектор
соответствующее самой матрице А. По теореме 2.1 существует вектор  нормированный условием такой, что
нормированный условием такой, что

Пусть  последовательность положительных чисел, сходящаяся к нулю. Как и при доказательстве теоремы 2.1, мы
последовательность положительных чисел, сходящаяся к нулю. Как и при доказательстве теоремы 2.1, мы
можем выделить последовательность целых чисел  такую, что
такую, что  где вектор
где вектор  Ясно, что
Ясно, что  Поскольку
Поскольку

в пределе при  получаем равенство
получаем равенство  Но из доказательства пункта (б) теоремы 2.1 следует, что
Но из доказательства пункта (б) теоремы 2.1 следует, что  значит,
значит, 
Доказательство утверждения (б) совпадает с доказательством для случая 
Доказывая утверждения (в) и  мы можем предположить без потери общности, что
мы можем предположить без потери общности, что 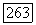 так как если
так как если 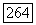 то можно разделить каждый элемент матрицы А на
то можно разделить каждый элемент матрицы А на 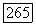 Так как
Так как 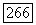 то
то 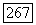 Записав это соотношение в координатной форме, мы сразу же найдем, что
Записав это соотношение в координатной форме, мы сразу же найдем, что

Таким образом, элементы матриц 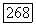 равномерно ограничены.
равномерно ограничены.
Пусть 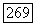 для некоторого
для некоторого 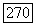 т. е.
т. е. 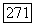 есть линейное пространство неподвижных точек матрицы
есть линейное пространство неподвижных точек матрицы 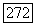 линейное пространство, совпадающее с областью значений матрицы
линейное пространство, совпадающее с областью значений матрицы 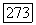 Положим еще
Положим еще

Ясно, что 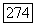 является замкнутым линейным пространством, таким, что для каждого х из
является замкнутым линейным пространством, таким, что для каждого х из 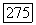

и следовательно, 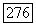 Мы покажем также, что
Мы покажем также, что 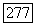 сходится для каждого х из К и что
сходится для каждого х из К и что 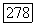 -мерное векторное пространство можно представить в виде прямой суммы пространств
-мерное векторное пространство можно представить в виде прямой суммы пространств 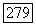
Этим мы докажем утверждение 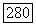
Покажем сначала, что 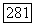 для всякого
для всякого 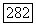 Поскольку
Поскольку 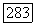 при некотором х,
при некотором х,

стремится к 0 при  в силу того, что элементы матриц
в силу того, что элементы матриц 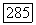 равномерно ограничены.
равномерно ограничены.
Чтобы показать, что каждый вектор х можно представить в виде суммы вектора из 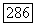 и вектора из К, разложим х в сумму вида
и вектора из К, разложим х в сумму вида

Так как элементы матриц 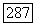 равномерно ограничены, то ограничены и компоненты векторов
равномерно ограничены, то ограничены и компоненты векторов  Поэтому существует последовательность положительных целых чисел
Поэтому существует последовательность положительных целых чисел 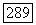 и вектор
и вектор 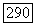 такие, что
такие, что

Поскольку

то

Кроме того,

откуда следует, что  Так как К — замкнутое линейное пространство и элементы векторов
Так как К — замкнутое линейное пространство и элементы векторов 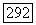 равномерно ограничены, то
равномерно ограничены, то 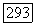 при
при 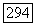 Итак,
Итак, 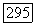 где
где 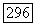 и доказательство утверждения (в) закончено.
и доказательство утверждения (в) закончено.
(г) Мы знаем, что существует вектор 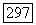 такой, что
такой, что 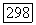 Предположим сначала, что
Предположим сначала, что 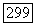 Пусть теперь
Пусть теперь 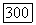 при некотором
при некотором  тогда
тогда

и, таким образом,

Но если  Итак,
Итак,  следовательно,
следовательно,

Это означает, что существуют такие константы  что
что

Обозначим через  вектор
вектор  . Умножая соотношение
. Умножая соотношение  на
на  и суммируя по
и суммируя по  получаем
получаем

В то же время суммирование по  приводит к равенству
приводит к равенству

откуда следует, что

Далее,

откуда следует, что  Итак,
Итак,  является собственным значением матрицы А при
является собственным значением матрицы А при  Поскольку число собственных значений матрицы А конечно, Я должно быть корнем из единицы.
Поскольку число собственных значений матрицы А конечно, Я должно быть корнем из единицы.
Пусть теперь  но не
но не  Проведя в случае надобности перенумерацию строк и столбцов матрицы А, мы можем считать, что
Проведя в случае надобности перенумерацию строк и столбцов матрицы А, мы можем считать, что  , где
, где  Так как
Так как  то из соотношения
то из соотношения  вытекает, что
вытекает, что

где порядки квадратных матриц  равны соответственно
равны соответственно  Вектор
Вектор  является левым собственным вектором матрицы
является левым собственным вектором матрицы  Пусть
Пусть  — собственное значение матрицы
— собственное значение матрицы  тогда, если Я является собственным значением матрицы
тогда, если Я является собственным значением матрицы  то задача сводится к рассмотренному выше случаю. Если же Я не является собственным значением матрицы
то задача сводится к рассмотренному выше случаю. Если же Я не является собственным значением матрицы  то оно должно быть собственным значением матрицы
то оно должно быть собственным значением матрицы  Но собственные значения матрицы
Но собственные значения матрицы  являются собственными значениями матрицы А и поэтому не превышают по модулю единицы. В то же время, так как
являются собственными значениями матрицы А и поэтому не превышают по модулю единицы. В то же время, так как  то она имеет наибольшее положительное собственное значение, являющееся верхней границей для абсолютных величин всех остальных ее собственных значений. Так как
то она имеет наибольшее положительное собственное значение, являющееся верхней границей для абсолютных величин всех остальных ее собственных значений. Так как  то наибольшее собственное значение матрицы
то наибольшее собственное значение матрицы  равно единице. Теперь предыдущие рассуждения применимы к матрице
равно единице. Теперь предыдущие рассуждения применимы к матрице  именно: либо
именно: либо  имеет левый собственный вектор со всеми положительными координатами, соответствующий собственному значению 1, либо
имеет левый собственный вектор со всеми положительными координатами, соответствующий собственному значению 1, либо 
имеет вид (после соответствующей перенумерации строк и столбцов)

Продолжая таким образом, мы придем за конечное число шагов к ситуации, когда существует левый собственный вектор  соответствующий собственному значению 1.
соответствующий собственному значению 1.
Приводимые ниже следствия содержат полезную информацию относительно спектрального радиуса  положительной матрицы А. Первое из них представляет собой другую формулировку утверждений (а) и (б) теоремы 2.4.
положительной матрицы А. Первое из них представляет собой другую формулировку утверждений (а) и (б) теоремы 2.4.
Следствие 2.1. Если  то наибольшее по абсолютной величине собственное значение
то наибольшее по абсолютной величине собственное значение  является действительным неотрицательным и может быть охарактеризовано как
является действительным неотрицательным и может быть охарактеризовано как  где
где

Следствие 2.2. Если  и существует вектор
и существует вектор  что
что  то
то  является верхней границей для
является верхней границей для 
Доказательство. Умножая слева на А обе части неравенства  получаем
получаем  Легко видеть, что и в общем случае
Легко видеть, что и в общем случае

откуда сразу же следует неравенство

Это неравенство приводит к оценке

Следствие 2.3. Если  то
то 
Доказательство. Так как из  следует, что
следует, что  то
то

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 1. СВОДКА ОСНОВНЫХ ТЕРМИНОВ И СВОЙСТВ СЛУЧАЙНЫХ ВЕЛИЧИН И ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
- А. Совместные функции распределения
- Б. Условные распределения и плотности
- В. Бесконечные семейства случайных величин
- Г. Характеристические функции
- Д. Производящие функции
- Е. Примеры функций распределения
- Ж. Предельные теоремы
- § 2. ДВА ПРОСТЫХ ПРИМЕРА СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 3. КЛАССИФИКАЦИЯ ОБЩИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- ЗАМЕЧАНИЯ
- Глава 2. МАРКОВСКИЕ ЦЕПИ
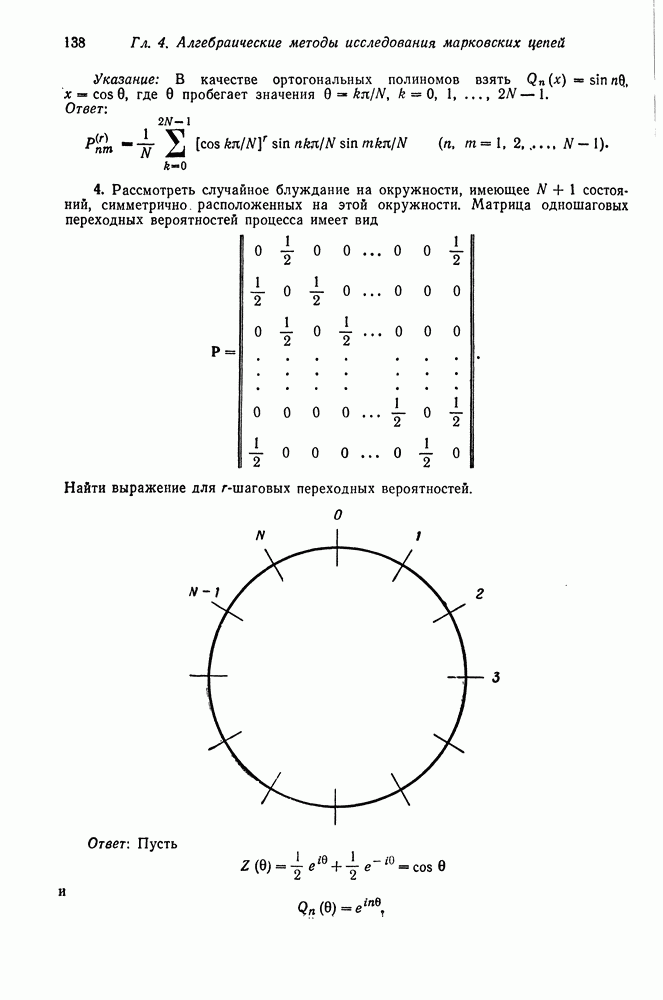
- § 2. ПРИМЕРЫ МАРКОВСКИХ ЦЕПЕЙ
- Б. Одномерные случайные блуждания
- В. Дискретная марковская цепь, описывающая очередь
- Г. Модель из теории запасов
- Д. Серии успехов
- Е. Ветвящиеся процессы
- Ж. Марковские цепи в генетике
- 3. Генетическая модель II
- § 3. МАТРИЦЫ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ МАРКОВСКОЙ ЦЕПИ
- § 4. КЛАССИФИКАЦИЯ СОСТОЯНИЙ МАРКОВСКОЙ ЦЕПИ
- § 5. ВОЗВРАТНОСТЬ
- § 6. ПРИМЕРЫ ВОЗВРАТНЫХ МАРКОВСКИХ ЦЕПЕЙ
- § 7. ЕЩЕ О ВОЗВРАТНОСТИ
- Глава 3. ОСНОВНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ МАРКОВСКИХ ЦЕПЕЙ И ИХ ПРИЛОЖЕНИЯ
- § 2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 1.1
- § 3. ВЕРОЯТНОСТИ ПОГЛОЩЕНИЯ
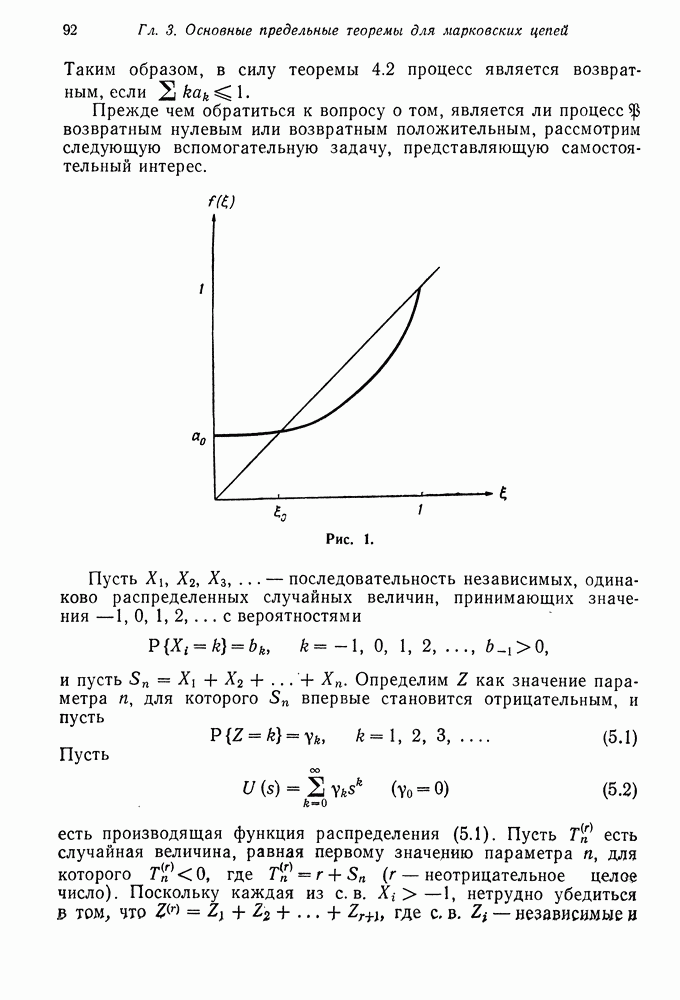
- § 4. КРИТЕРИИ ВОЗВРАТНОСТИ
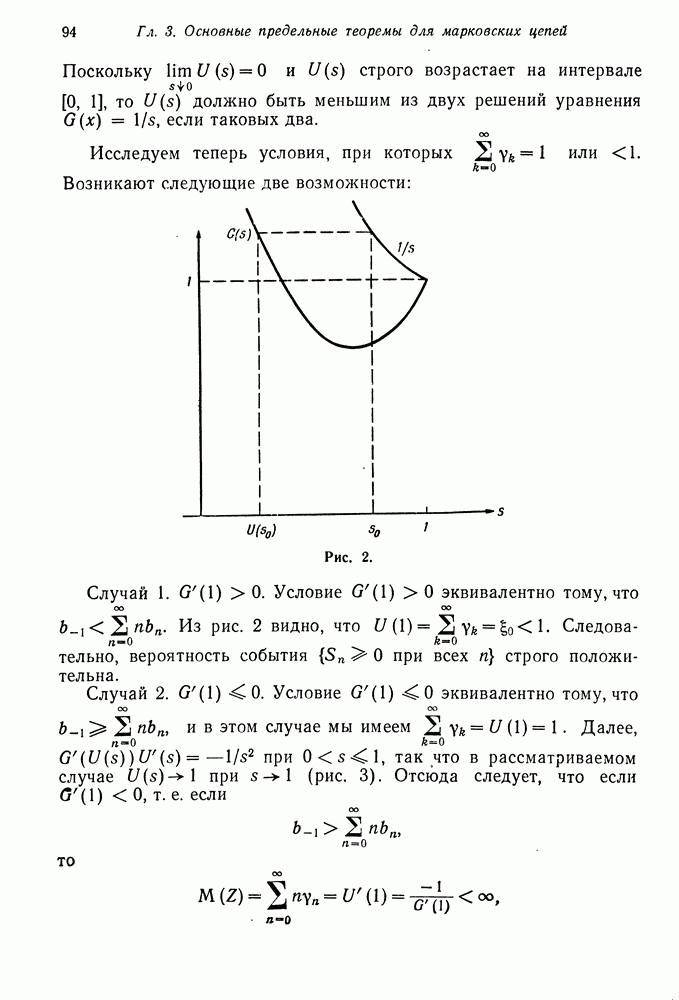
- § 5. ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
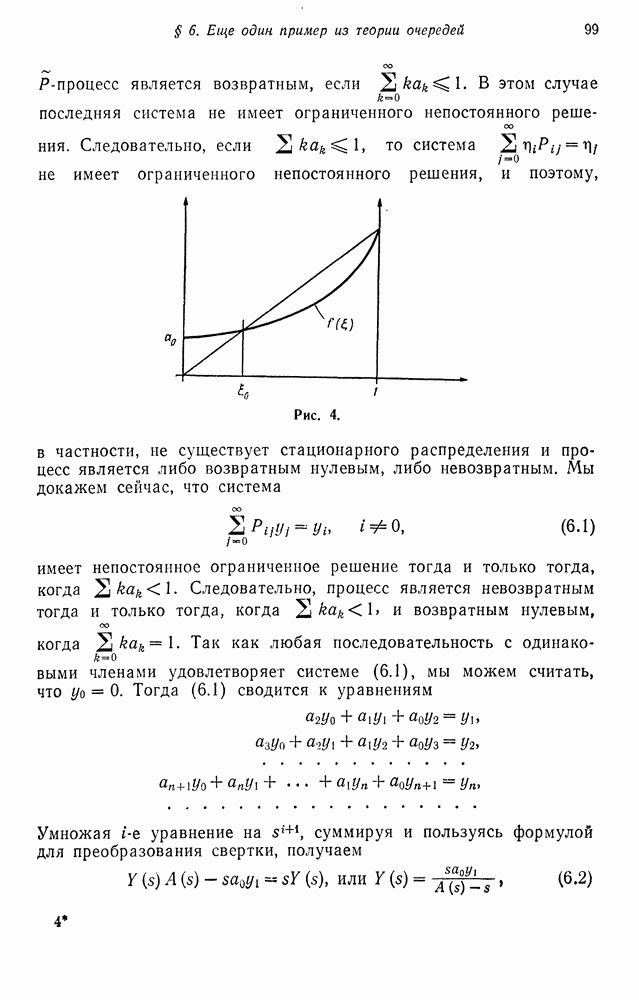
- § 6. ЕЩЕ ОДИН ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
- § 7. СЛУЧАЙНОЕ БЛУЖДАНИЕ
- Глава 4. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ МАРКОВСКИХ ЦЕПЕЙ
- § 2. СВЯЗЬ МЕЖДУ СОБСТВЕННЫМИ ЗНАЧЕНИЯМИ И КЛАССАМИ ВОЗВРАТНЫХ СОСТОЯНИЙ
- § 3. ПЕРИОДИЧЕСКИЕ КЛАССЫ
- § 4. СПЕЦИАЛЬНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ ДЛЯ МАРКОВСКИХ ЦЕПЕЙ
- § 5. ПРИМЕРЫ
- § 6. ПРИЛОЖЕНИЯ К БРОСАНИЯМ МОНЕТЫ
- Глава 5. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ И ИХ ПРИЛОЖЕНИЯ
- § 1. ВЕРОЯТНОСТИ ПЕРЕХОДА С ЗАПРЕЩЕНИЕМ
- § 2. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ
- § 3. СУЩЕСТВОВАНИЕ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ РАСПРЕДЕЛЕНИЙ
- § 4. ИНТЕРПРЕТАЦИЯ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ РАСПРЕДЕЛЕНИЙ
- § 5. РЕГУЛЯРНЫЕ, СУПЕРРЕГУЛЯРНЫЕ И СУБРЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТЬ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН КАК МАРКОВСКАЯ ЦЕПЬ
- § 1. СВОЙСТВА ВОЗВРАТНОСТИ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- § 2. ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
- § 3. ПРАВЫЕ РЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
- Глава 7. КЛАССИЧЕСКИЕ ПРИМЕРЫ ЦЕПЕЙ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 1. ОБЩИЕ ПРОЦЕССЫ ЧИСТОГО РОЖДЕНИЯ (РАЗМНОЖЕНИЯ) И ПУАССОНОВСКИЕ ПРОЦЕССЫ
- Б. Примеры пуассоновских процессов
- В. Процесс чистого рождения
- Г. Процесс Юла
- § 2. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О ПУАССОНОВСКИХ ПРОЦЕССАХ
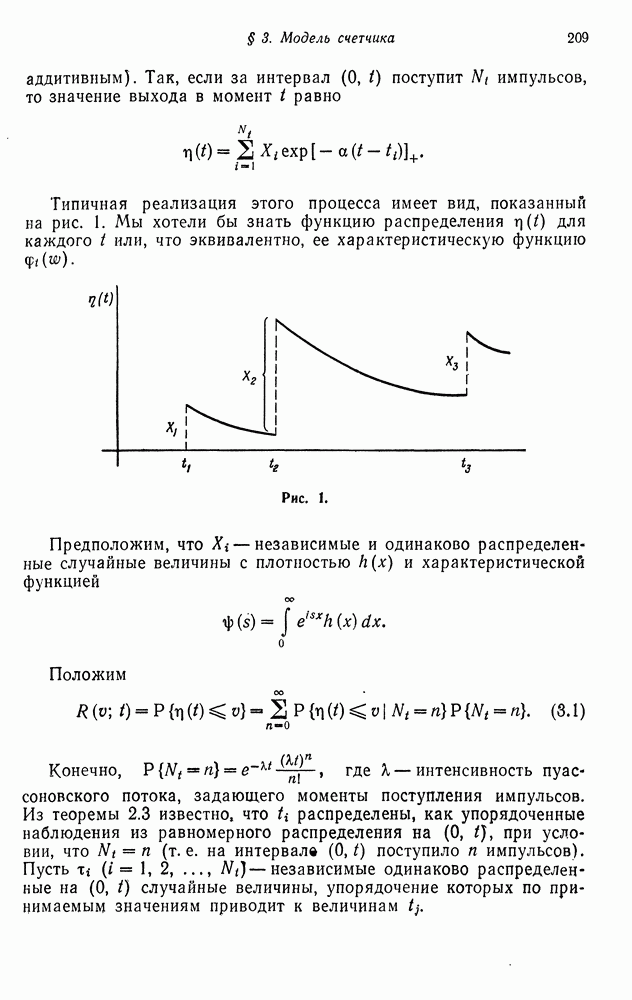
- § 3. МОДЕЛЬ СЧЕТЧИКА
- § 4. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛИ
- § 5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
- § 6. ПРИМЕРЫ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
- § 7. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛЙ С ПОГЛОЩАЮЩИМИ СОСТОЯНИЯМИ
- § 8. ЦЕПИ МАРКОВА С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ И НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- Глава 8. ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 1. СВОЙСТВА ДИФФЕРЕНЦИРУЕМОСТИ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ
- § 2. КОНСЕРВАТИВНЫЕ ПРОЦЕССЫ. ПРЯМЫЕ И ОБРАТНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПОСТРОЕНИЕ ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ С ПОМОЩЬЮ ЕЕ ИНФИНИТЕЗИМАЛЬНЫХ ПАРАМЕТРОВ
- § 4. СТРОГО МАРКОВСКОЕ СВОЙСТВО
- Глава 9. ПОРЯДКОВЫЕ СТАТИСТИКИ, ПУАССОНОВСКИЕ ПРОЦЕССЫ И ИХ ПРИЛОЖЕНИЯ
- § 1. ПОРЯДКОВЫЕ СТАТИСТИКИ И ИХ СВЯЗЬ С ПУАССОНОВСКИМИ ПРОЦЕССАМИ
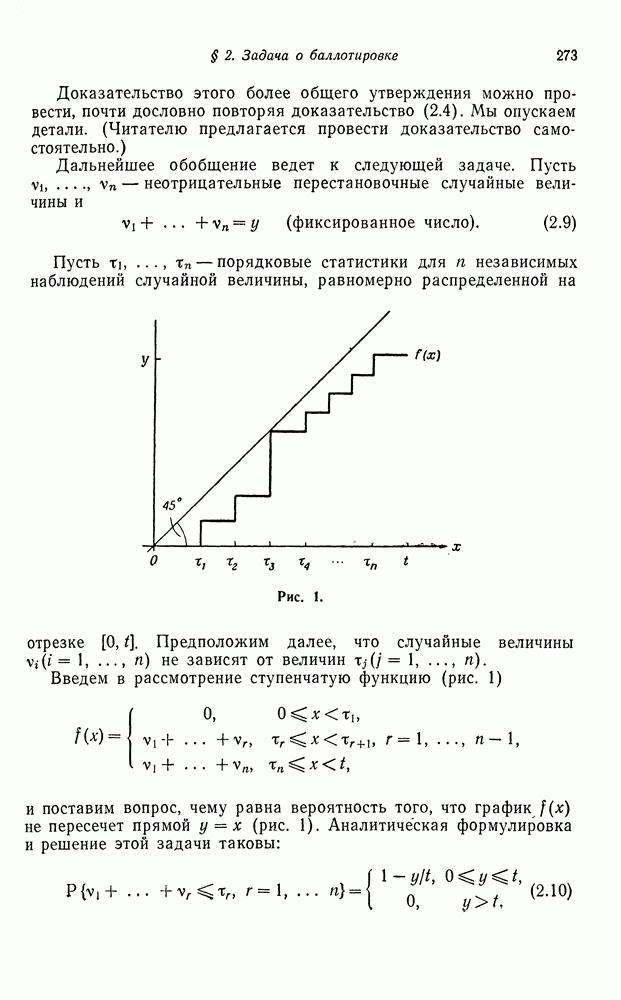
- § 2. ЗАДАЧА О БАЛЛОТИРОВКЕ
- § 3. ЭМПИРИЧЕСКИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПОРЯДКОВЫЕ СТАТИСТИКИ
- § 4. НЕКОТОРЫЕ ПРЕДЕЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ДЛЯ ЭМПИРИЧЕСКИХ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
- Глава 10. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 2. СОВМЕСТНЫЕ ВЕРОЯТНОСТИ ДЛЯ БРОУНОВСКОГО ДВИЖЕНИЯ
- § 3. НЕПРЕРЫВНОСТЬ ТРАЕКТОРИЙ И ИХ МАКСИМАЛЬНЫЕ ЗНАЧЕНИЯ
- Глава 11. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ
- § 1. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
- § 2. СООТНОШЕНИЯ ДЛЯ ПРОИЗВОДЯЩЕЙ ФУНКЦИИ, ОПИСЫВАЮЩЕЙ ВЕТВЯЩИЙСЯ ПРОЦЕСС
- § 3. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ
- § 4. ПРИМЕРЫ
- § 5. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДВУМЯ ТИПАМИ ЧАСТИЦ
- § 6. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕСКОЛЬКИМИ ТИПАМИ ЧАСТИЦ
- § 7. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 8. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 10. ВЕТВЯЩИЙСЯ ПРОЦЕСС С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ И ДВУМЯ ТИПАМИ ЧАСТИЦ
- § 11. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ, ЗАВИСЯЩИЕ ОТ ВОЗРАСТА
- Глава 12. СОСТАВНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- § 1. МНОГОМЕРНЫЕ ОДНОРОДНЫЕ ПУЛССОНОВСКИЕ ПРОЦЕССЫ
- § 2. ПРИМЕНЕНИЕ МНОГОМЕРНЫХ ПУАССОНОВСКИХ ПРОЦЕССОВ В АСТРОНОМИИ
- § 3. ИММИГРАЦИЯ И РОСТ ПОПУЛЯЦИЙ
- § 4. ВЕРОЯТНОСТНЫЕ МОДЕЛИ МУТАЦИИ И РОСТА
- § 5. ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ ОДНОМЕРНОЙ ПОПУЛЯЦИИ
- § 6. ВЕРОЯТНОСТНАЯ МОДЕЛЬ РОСТА ПОПУЛЯЦИИ В ПРОСТРАНСТВЕ И ВРЕМЕНИ
- § 7. ДЕТЕРМИНИРОВАННЫЙ РОСТ ПОПУЛЯЦИИ С РАСПРЕДЕЛЕНИЕМ ПО ВОЗРАСТАМ
- § 8. ДИСКРЕТНАЯ ВОЗРАСТНАЯ МОДЕЛЬ
- Глава 13. ДЕТЕРМИНИРОВАННЫЕ И СЛУЧАЙНЫЕ ГЕНЕТИЧЕСКИЕ И ЭКОЛОГИЧЕСКИЕ ПРОЦЕССЫ
- § 1. ГЕНЕТИЧЕСКИЕ МОДЕЛИ. ОПИСАНИЕ ГЕНЕТИЧЕСКОГО МЕХАНИЗМА
- § 2. ИНБРИДИНГ
- Б. Спаривание сибсов
- В. Гены, идентичные по происхождению
- Г. Бесконечная диплоидная популяция и коэффициент инбридинга
- Д. Популяция с самооплодотворением и случайным спариванием
- § 3. ПОЛИПЛОИДЫ
- § 4. МАРКОВСКИЕ ПРОЦЕССЫ, ПОРОЖДАЕМЫЕ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
- § 5. МОДЕЛИ РОСТА ПОПУЛЯЦИЙ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
- § 6. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЦЕПЕЙ МАРКОВА, ПОРОЖДЕННЫХ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
- § 7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МОДЕЛИ МУТАЦИИ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
- § 8. ВЕРОЯТНОСТНЫЙ СМЫСЛ СОБСТВЕННЫХ ЗНАЧЕНИЙ
- Глава 14. ПРОЦЕССЫ МАССОВОГО ОБСЛУЖИВАНИЯ
- § 2. ПРОСТЕЙШИЕ ПРОЦЕССЫ ОБСЛУЖИВАНИЯ (М/М/1)
- § 3. НЕКОТОРЫЕ ОБЩИЕ МОДЕЛИ ОБСЛУЖИВАНИЯ ОДНИМ ПРИБОРОМ
- § 4. МЕТОД ВЛОЖЕННЫХ ЦЕПЕЙ МАРКОВА ПРИМЕНИТЕЛЬНО К МОДЕЛИ ОБСЛУЖИВАНИЯ (M/G/1)
- § 5. ЭКСПОНЕНЦИАЛЬНО РАСПРЕДЕЛЕННОЕ ВРЕМЯ ОБСЛУЖИВАНИЯ (G/М/1)
- § 6. ГАММА-РАСПРЕДЕЛЕНИЕ ИНТЕРВАЛОВ МЕЖДУ ПОСТУПЛЕНИЯМИ И ОБОБЩЕНИЯ (Ek/М/1)
- § 7. ЭКСПОНЕНЦИАЛЬНОЕ ОБСЛУЖИВАНИЕ s ПРИБОРОВ (GI/M/s)
- § 8. ВИРТУАЛЬНОЕ ВРЕМЯ ОЖИДАНИЯ И ПЕРИОД ЗАНЯТОСТИ
- ПРИЛОЖЕНИЕ § 1. СПЕКТРАЛЬНАЯ ТЕОРЕМА
- § 2. ТЕОРИЯ ФРОБЕНИУСА ПОЛОЖИТЕЛЬНЫХ МАТРИЦ
- РАЗЛИЧНЫЕ ЗАДАЧИ