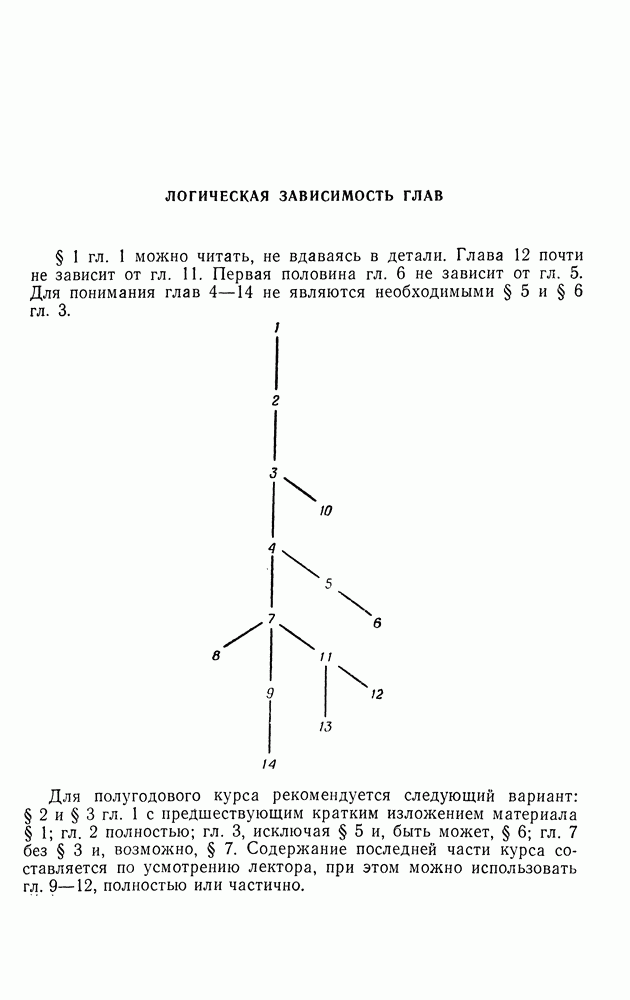
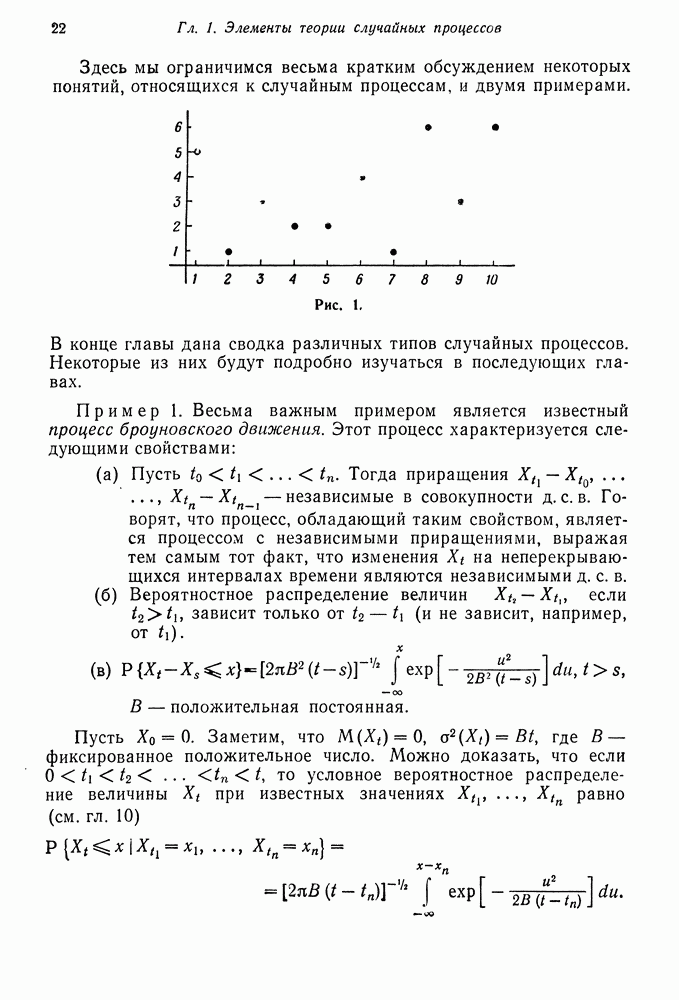
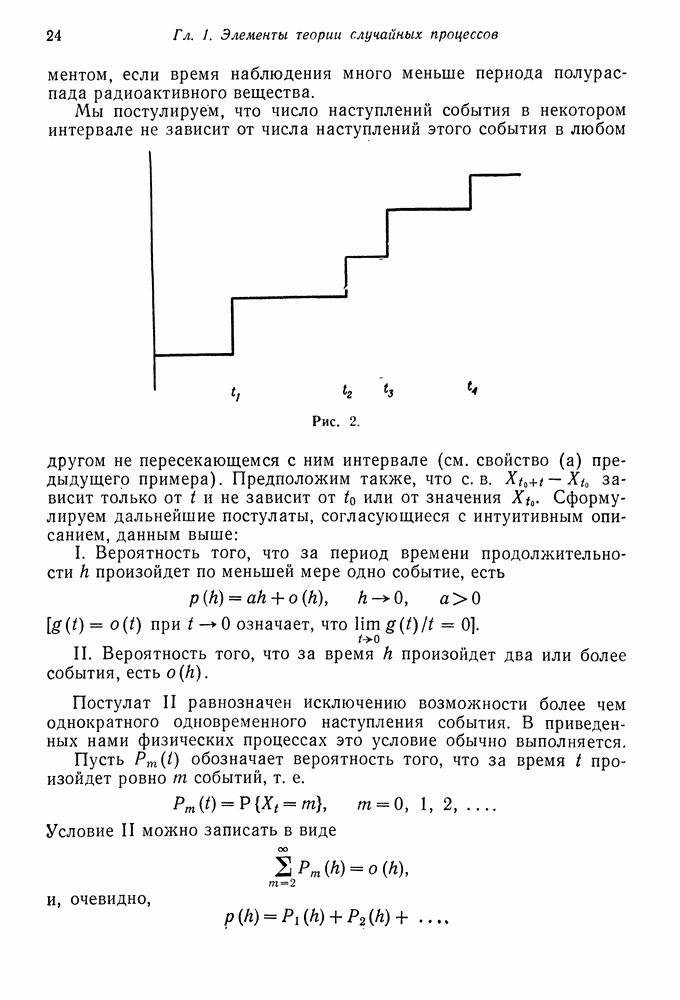
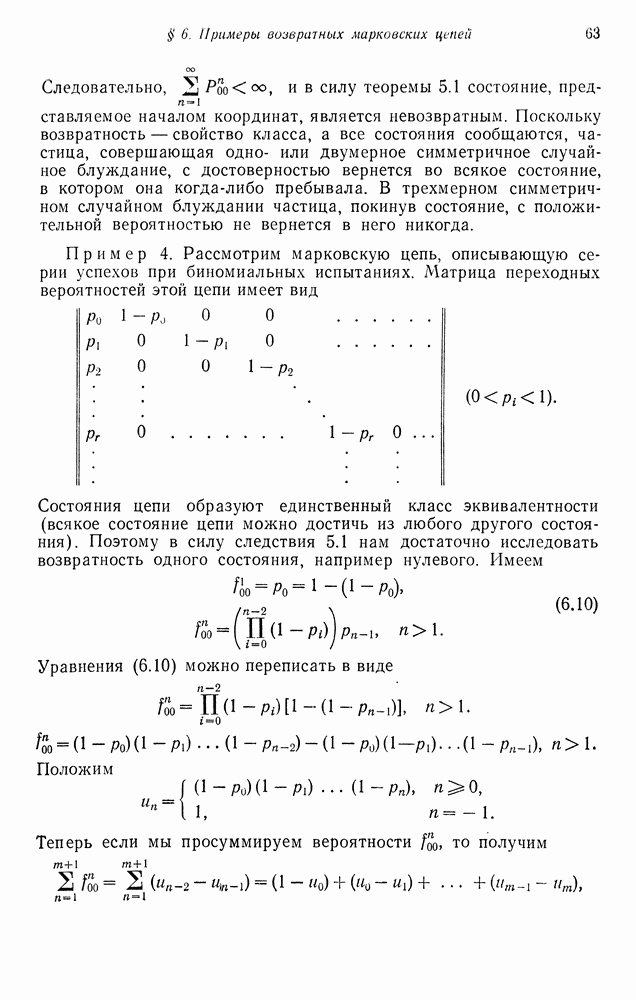
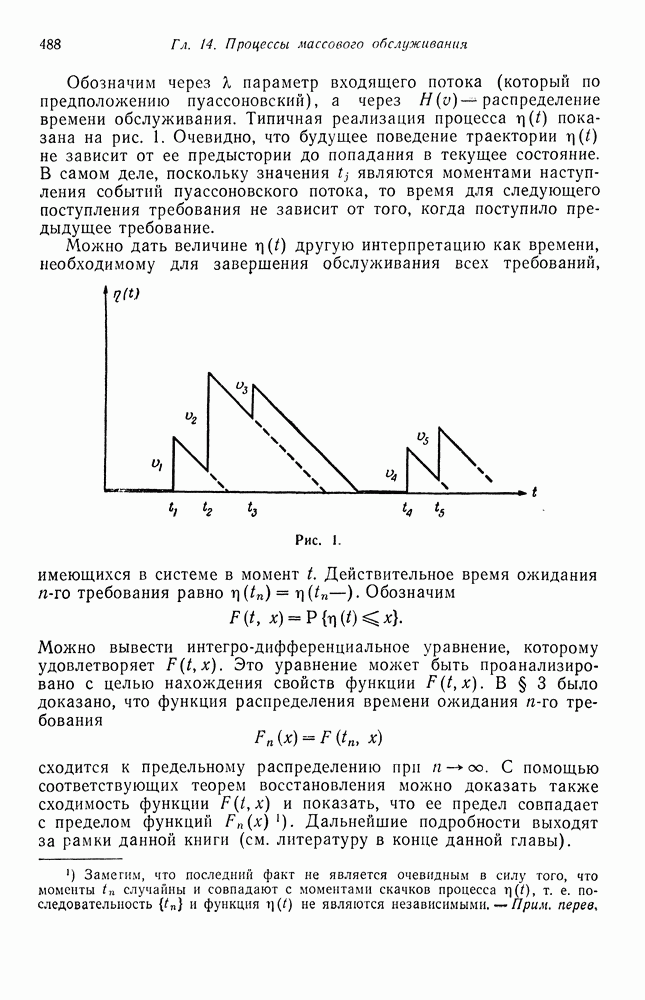
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
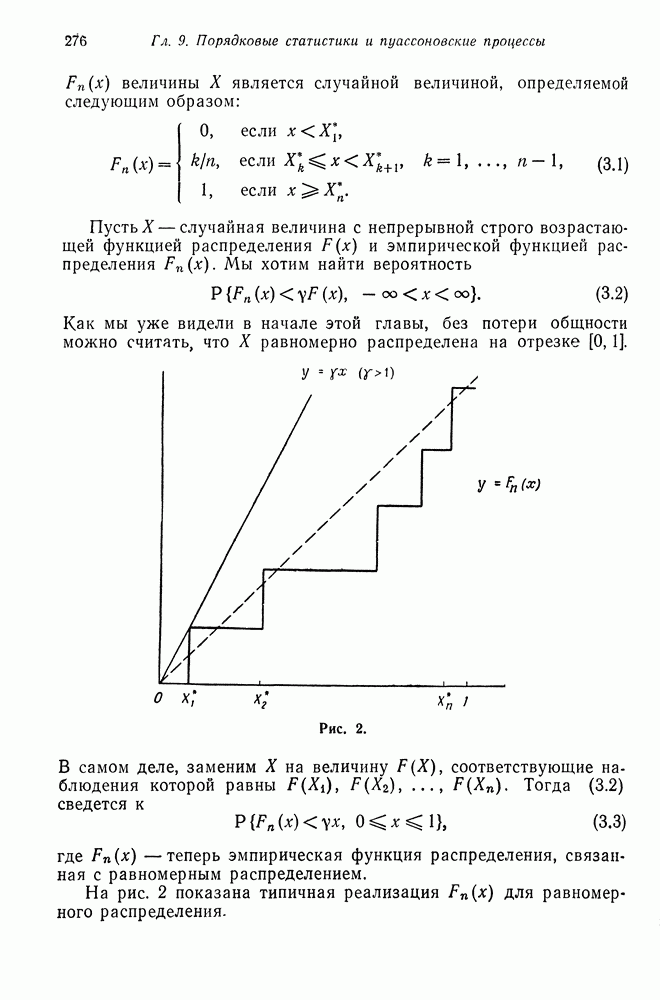
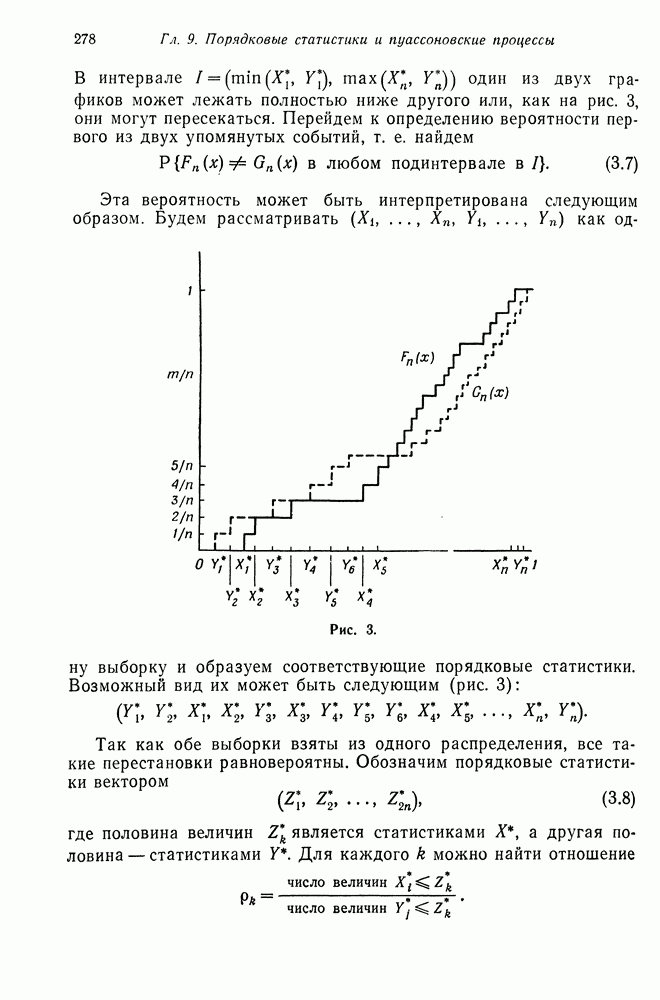
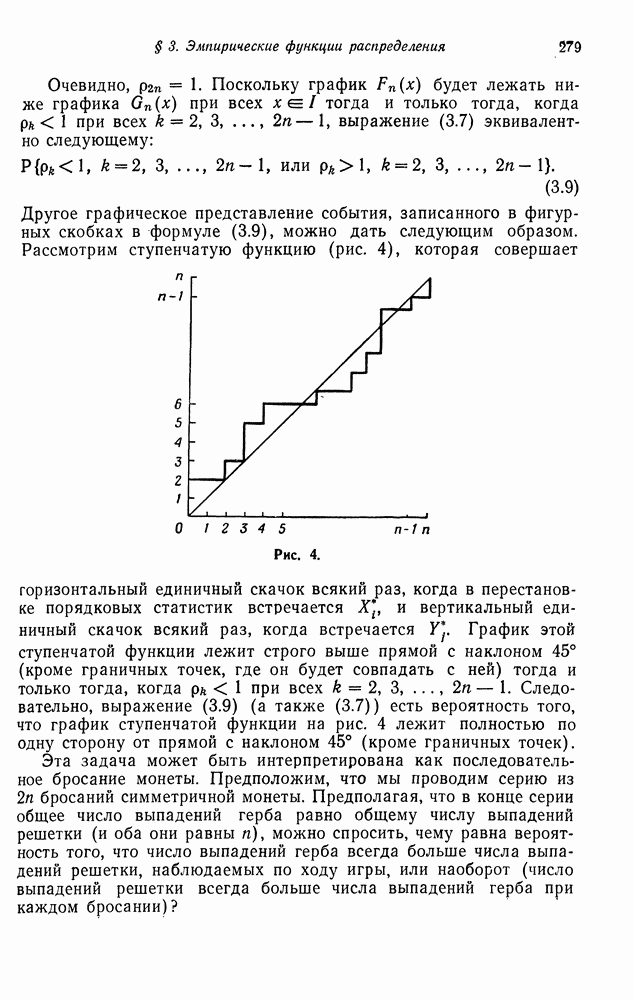
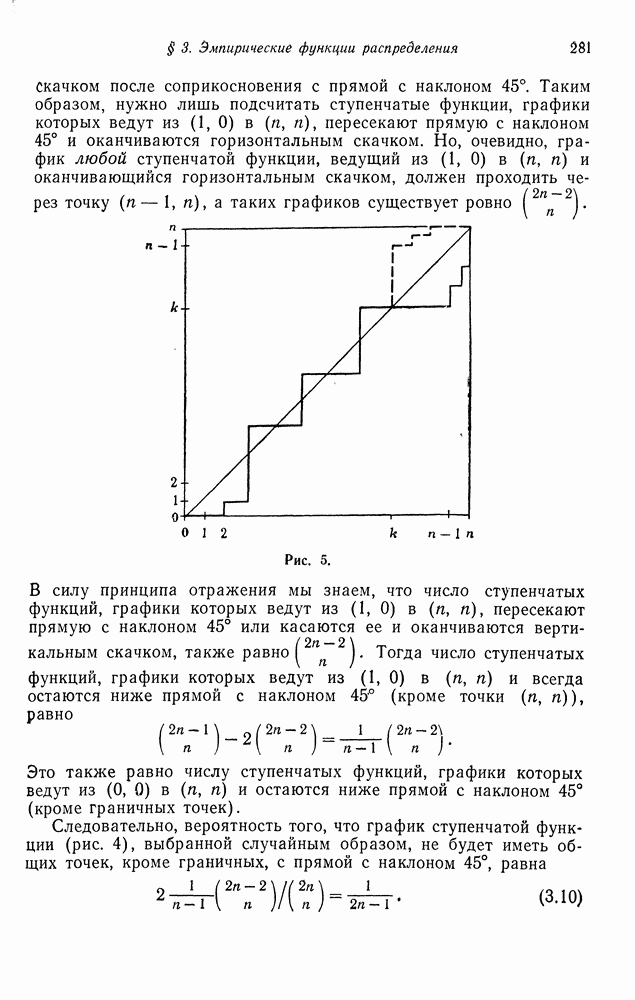
§ 3. ПРАВЫЕ РЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
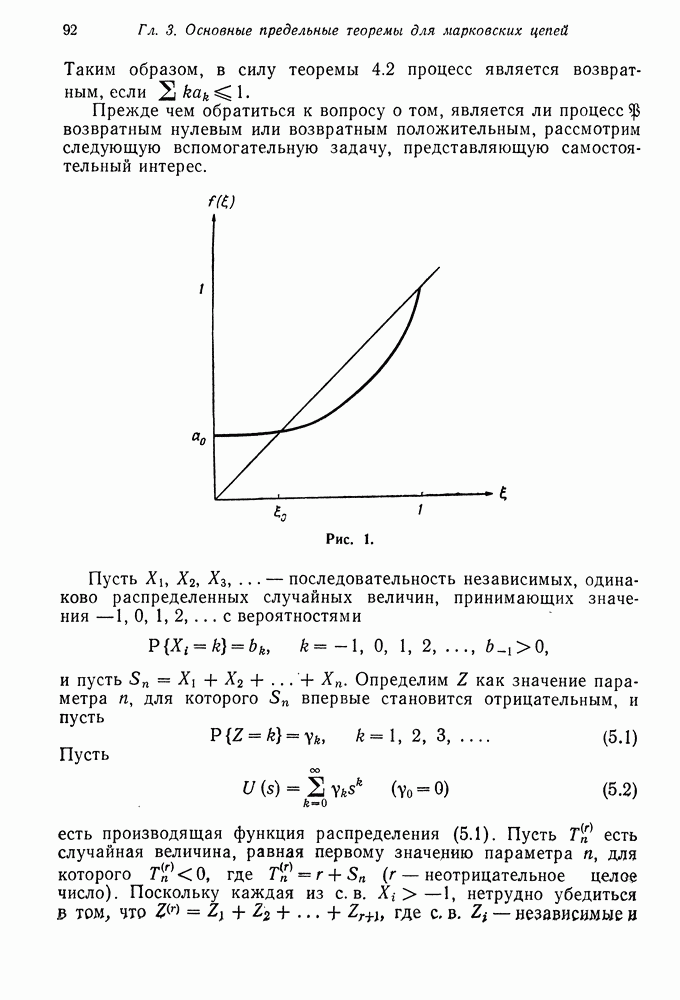
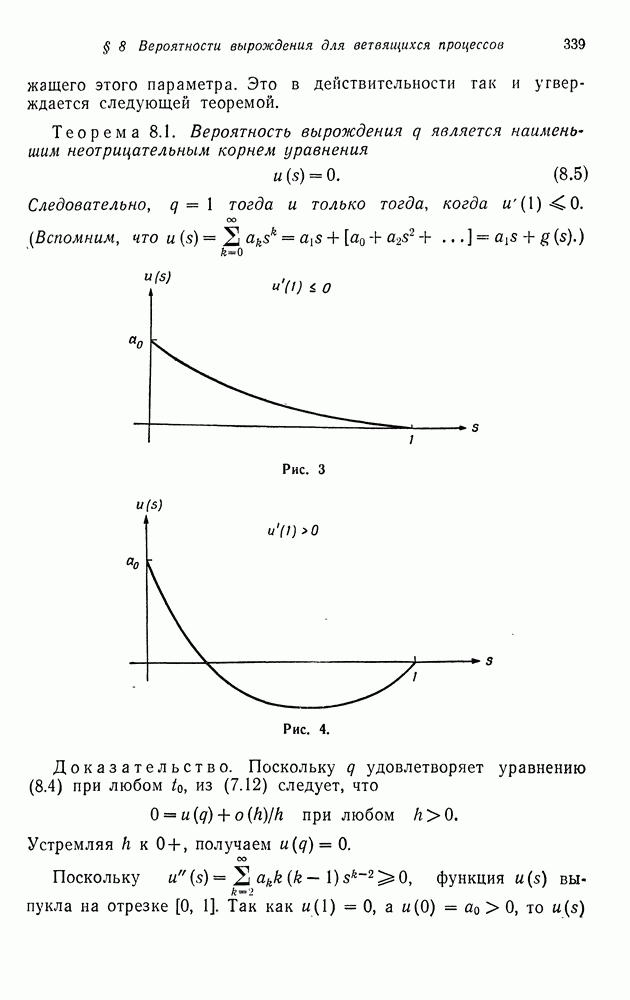
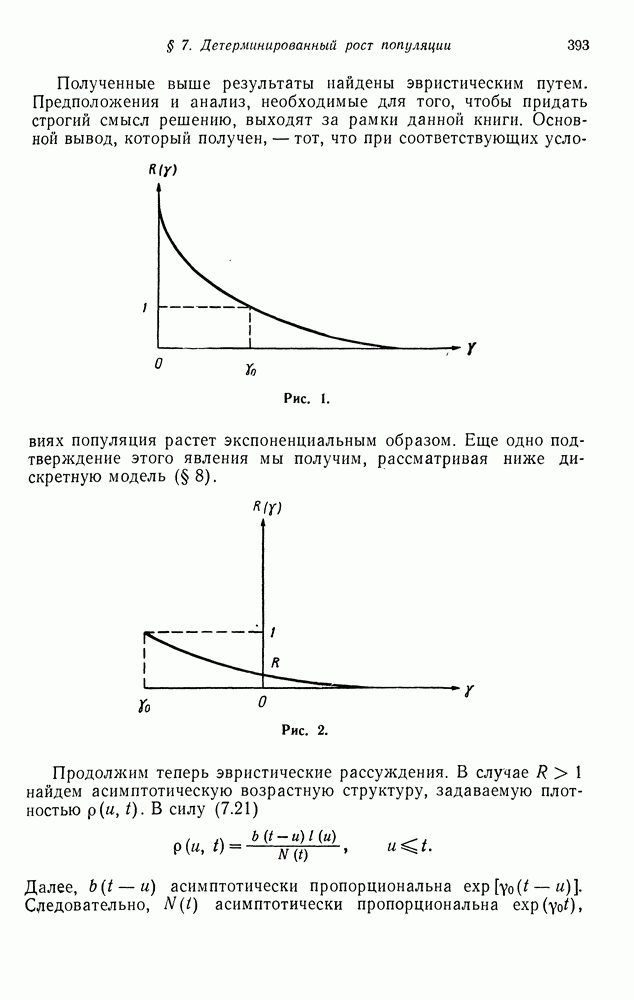
Для специальных классов марковских цепей обычно удается получить более сильные результаты, касающиеся свойства возвратности, задач о времени пребывания, нахождения законов распределения различных функционалов от процессов и др. В этом параграфе мы получим уточнение свойств правых регулярных последовательностей (теорема 5.2 гл. 5) для марковской цепи 
Если марковская цепь является неприводимой и возвратной, то единственным правым регулярным вектором является постоянный вектор (теорема 5.2 гл. 5). Если же марковская цепь описывает последовательность сумм независимых случайных величин, то этот результат можно распространить на непериодический невозвратный случай, если мы потребуем, чтобы правый регулярный вектор был ограниченным. Более точно, мы докажем следующее.
Теорема 3.1. Если марковская цепь  с матрицей переходных вероятностей
с матрицей переходных вероятностей  неприводима, и если последовательность
неприводима, и если последовательность  правая регулярная, т. е.
правая регулярная, т. е.  удовлетворяет условиям
удовлетворяет условиям

и

причем  ограничена, то
ограничена, то  при всех
при всех 
Доказательство. Пусть ограниченная последовательность  удовлетворяет условиям (3.1) и (3.2). Пусть
удовлетворяет условиям (3.1) и (3.2). Пусть  любое состояние, отличное от нулевого и достижимое из него. Тогда существует такое
любое состояние, отличное от нулевого и достижимое из него. Тогда существует такое  , что
, что  . Зафиксируем
. Зафиксируем  и положим
и положим

Используя пространственную однородность процесса, мы можем написать

т. е. последовательность  также удовлетворяет
также удовлетворяет  Следовательно,
Следовательно,  удовлетворяет условиям (3.2). Очевидно,
удовлетворяет условиям (3.2). Очевидно,  ограничена, поскольку ограничена
ограничена, поскольку ограничена  Пусть
Пусть

Так как  ограничена, мы можем выбрать последовательность целых чисел
ограничена, мы можем выбрать последовательность целых чисел  для которой
для которой

Опять же в силу ограниченности  из последовательности
из последовательности  можно выбрать подпоследовательность
можно выбрать подпоследовательность  такую, что существует
такую, что существует  и). В свою очередь из
и). В свою очередь из  можно выбрать подпоследовательность для которой существует предел
можно выбрать подпоследовательность для которой существует предел  Затем из
Затем из  выбираем подпоследовательность
выбираем подпоследовательность  такую, что существует
такую, что существует  Продолжая таким образом, мы получим ряд последовательностей
Продолжая таким образом, мы получим ряд последовательностей  каждая из которых является подпоследовательностью предыдущей. Существует последовательность, а именно
каждая из которых является подпоследовательностью предыдущей. Существует последовательность, а именно  которая является подпоследовательностью каждой из последовательностей
которая является подпоследовательностью каждой из последовательностей

начиная с некоторого члена. Действительно,  является подпоследовательностью последовательности
является подпоследовательностью последовательности  начиная по крайней мере с
начиная по крайней мере с  (Построение последовательности
(Построение последовательности  носит название процесса диагонализации.) В силу этого свойства
носит название процесса диагонализации.) В силу этого свойства  и факта существования соответствующих пределов мы можем утверждать, что
и факта существования соответствующих пределов мы можем утверждать, что

существует для каждого 
По построению  (см. (3.4)) имеем
(см. (3.4)) имеем

а в силу (3.3)

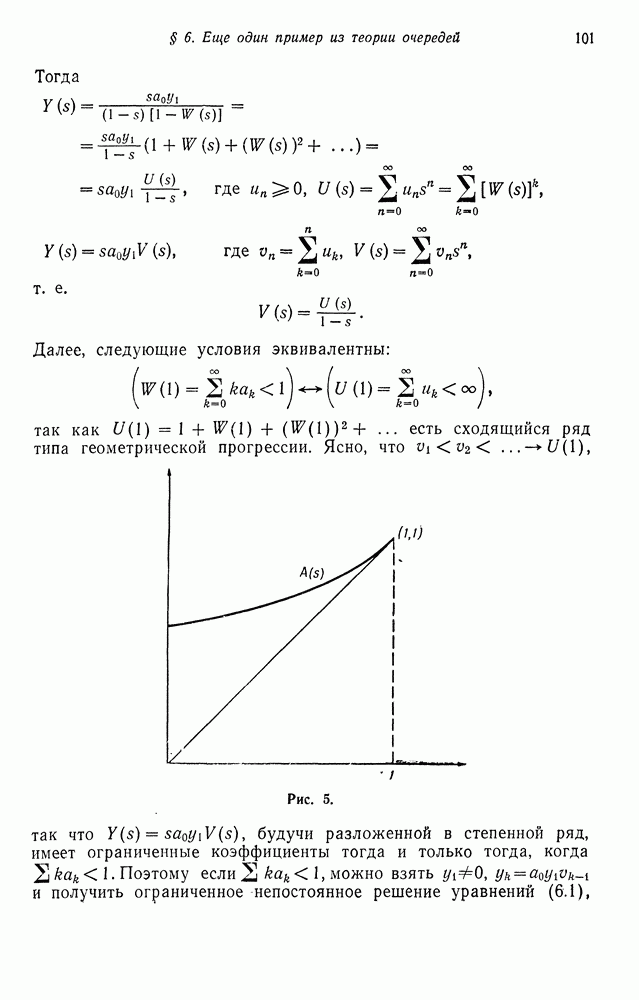
Как мы уже видели,

Переходя к пределу в обеих частях при  получаем
получаем

Мы сейчас покажем, что в правой части соотношения (3.7) можно перейти к пределу под знаком суммы. Для этого нам нужно показать, что для любого заданного  существует целое число
существует целое число  такое, что
такое, что

при условии, что  Выберем
Выберем  настолько большим, что
настолько большим, что

Затем выберем  таким, что
таким, что

при  и всех
и всех  Тогда при
Тогда при 

Установив правомерность перехода к пределу под знаком суммы, из (3.7) получаем

т. е. 2. удовлетворяет условию (3.2), хотя не обязательно условию (3.1). Последовательно применяя соотношение (3.8), получаем

Обращаясь к (3.6), мы видим, что предыдущее соотношение при

Левая часть в (3.9) представляет собой взвешенное среднее чисел, каждое из которых  Поэтому равенство (3.9) может иметь место только в том случае, если для всех
Поэтому равенство (3.9) может иметь место только в том случае, если для всех  таких, что
таких, что  при некотором
при некотором  величина
величина  равна
равна  . В частности, по определению
. В частности, по определению 

для любого положительного целого  . В силу
. В силу  можно выбрать таким, чтобы все неравенства
можно выбрать таким, чтобы все неравенства

выполнялись одновременно. Складывая эти неравенства, получаем 

Так как  ограничены, то существует такое
ограничены, то существует такое  что
что  для всех
для всех  Тогда, очевидно,
Тогда, очевидно,

Поскольку это неравенство должно выполняться при любом целом  и любом
и любом  с необходимостью должно быть отрицательным либо равным нулю. Таким образом,
с необходимостью должно быть отрицательным либо равным нулю. Таким образом,  или
или

для всех  и любого
и любого  достижимого из нуля.
достижимого из нуля.
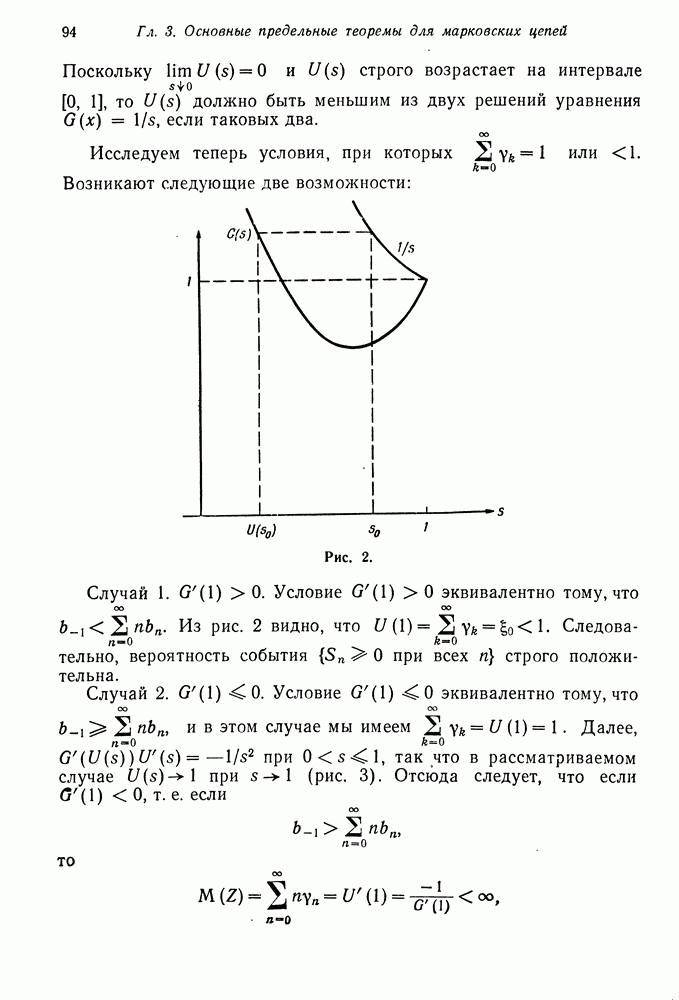
До сих пор мы нигде не использовали условия (3.1), т. е. того факта, что  Нам потребовалось только, чтобы
Нам потребовалось только, чтобы  были ограничены. Следовательно, мы можем провести все предыдущие рассуждения для последовательности
были ограничены. Следовательно, мы можем провести все предыдущие рассуждения для последовательности  у которой
у которой  Разумеется,
Разумеется,  остается ограниченной и удовлетворяет (3.2). В этом случае
остается ограниченной и удовлетворяет (3.2). В этом случае

для всех  и всех состояний ко, достижимых из нулевого состояния. Сравнивая (3.10) и (3.11), получаем
и всех состояний ко, достижимых из нулевого состояния. Сравнивая (3.10) и (3.11), получаем

для всех  и всех состояний ко, достижимых из нулевого состояния. В частности,
и всех состояний ко, достижимых из нулевого состояния. В частности,

для всех состояний ко, достижимых из нулевого состояния. Теперь мы впервые за все доказательство воспользуемся предположением о неприводимости марковской цепи. Это предположение гарантирует, что все состояния достижимы из нулевого состояния. Следовательно, (3.12) выполняется для всех  и все члены последовательности
и все члены последовательности  равны константе
равны константе 
В заключение этой главы мы применим теорему 3.1 для доказательства обобщенной теоремы восстановления для сумм независимых одинаково распределенных целочисленных случайных величин. Мы будем далее предполагать, что суммы  являются непериодическими д. с. в., т. е. что наименьшая аддитивная группа, порождаемая целыми числами
являются непериодическими д. с. в., т. е. что наименьшая аддитивная группа, порождаемая целыми числами  для которых
для которых  есть группа всех целых чисел.
есть группа всех целых чисел.
Мы дадим прямое доказательство теоремы восстановления; однако несколько вспомогательных результатов, получаемых попутно, представляют самостоятельный интерес, а методы их доказательства типичны для задач о флуктуациях в теории сумм независимых д. с. в.
Теорема 3.2. Если  являются непериодическими
являются непериодическими  то
то

Для удобства разобьем доказательство на несколько этапов. Для любой величины а положим  и
и  Пусть
Пусть

Поскольку последовательность  не возрастает, предел
не возрастает, предел

существует, хотя возможно, что  Однако, поскольку
Однако, поскольку  усиленный закон больших чисел гарантирует нам, что
усиленный закон больших чисел гарантирует нам, что

Следовательно,  конечно с вероятностью 1.
конечно с вероятностью 1.
Далее,

Так как  независимы и одинаково распределены, то последнее слагаемое есть не что иное, как
независимы и одинаково распределены, то последнее слагаемое есть не что иное, как
Устремляя  получаем
получаем

(Читателю рекомендуется доказать возможность перехода к пределу под знаком математического ожидания.) Очевидно,

откуда с учетом (3.16) получаем

Наши рассуждения имеют одно слабое место: мы не знаем a priori, что  а только в этом случае соотношение (3.16) имеет смысл.
а только в этом случае соотношение (3.16) имеет смысл.
Чтобы восполнить этот пробел, нам понадобится следующая теорема, имеющая и самостоятельный интерес.
Теорема 3.3. Пусть  неотрицательная целочисленная с. в., т. е.
неотрицательная целочисленная с. в., т. е.  ее характеристическая функция. Предположим, что
ее характеристическая функция. Предположим, что  сходится к а
сходится к а  при
при  Тогда
Тогда 
Доказательство. Выделяя действительную и мнимую части выражения  мы заключаем, что
мы заключаем, что

Для любого фиксированного  найдем наибольшее целое число
найдем наибольшее целое число  удовлетворяющее условию
удовлетворяющее условию 
В силу (3.18) сумма  равномерно ограничена при достаточно но малых 0. Представим эту сумму в виде
равномерно ограничена при достаточно но малых 0. Представим эту сумму в виде

Оценим снизу  используя тот факт, что
используя тот факт, что  является убывающей функцией при
является убывающей функцией при  (см. стр. 178):
(см. стр. 178):

Из определения  следует, что
следует, что  при
при  Тогда предыдущее неравенство дает
Тогда предыдущее неравенство дает

С другой стороны, для второй суммы в (3.19) имеем

Но  для всех
для всех  таких, что
таких, что  Следовательно,
Следовательно,

Но  при
при  в соответствии с (3.18), и поэтому ее среднее значение стремится к нулю:
в соответствии с (3.18), и поэтому ее среднее значение стремится к нулю:

(Читателю следует доказать это.)
Из полученных оценок следует, что вторая сумма в (3.19) стремится к нулю при  Поэтому сумма
Поэтому сумма

равномерно ограничена при  Очевидно,
Очевидно,  возрастает до бесконечности при
возрастает до бесконечности при  отсюда и следует сходимость ряда
отсюда и следует сходимость ряда  Чтобы
Чтобы
завершить доказательство теоремы 3.3, мы должны показать, что

Для этого зададим  и выберем
и выберем  таким, что
таким, что  Последнее возможно, поскольку, как мы уже показали, ряд
Последнее возможно, поскольку, как мы уже показали, ряд  сходится. Далее,
сходится. Далее,

Так как  то вторая и третья суммы ограничены величиной
то вторая и третья суммы ограничены величиной  Отсюда
Отсюда

При фиксированном  сумма в правой части стремится к нулю, так как каждое ее слагаемое стремится к нулю. Поэтому
сумма в правой части стремится к нулю, так как каждое ее слагаемое стремится к нулю. Поэтому

Выражение в левой части представляет собой фиксированное неотрицательное число;  можно выбрать произвольно малым. Отсюда вытекает справедливость соотношения (3.20).
можно выбрать произвольно малым. Отсюда вытекает справедливость соотношения (3.20).
Теперь мы можем дать строгое доказательство соотношения (3.17). Введем характеристические функции случайных величин 

и

Отметим, что случайная величина может принимать только неотрицательные целые значения. Очевидно, с. в.  независимы. Кроме того,
независимы. Кроме того,  и одинаково распределены, так как определяется через
и одинаково распределены, так как определяется через  точно так же, как
точно так же, как  определяется через
определяется через 
Так как  соотношение неявно фигурирует в (3.15)), то
соотношение неявно фигурирует в (3.15)), то

Из определений следует, что  и при
и при  (сходимость понимается как сходимость в смысле распределений). В силу критерия сходимости
(сходимость понимается как сходимость в смысле распределений). В силу критерия сходимости  Леви (стр. 16) имеем
Леви (стр. 16) имеем

Но

Так как

мы можем записать предыдущее соотношение в виде

Подставляя это соотношение в (3.21), получаем

Поделив обе части на  и устремив
и устремив  получаем
получаем

так как  (Формальное доказательство этого предельного соотношения проводится так же, как и доказательство соотношения (3.20) в теореме 3.3.) Очевидно,
(Формальное доказательство этого предельного соотношения проводится так же, как и доказательство соотношения (3.20) в теореме 3.3.) Очевидно,  и из (3.22) следует, что
и из (3.22) следует, что 

Так как  неотрицательная д. с. в., мы можем воспользоваться теоремой 3.3, из которой следует, что предел в (3.23) равен
неотрицательная д. с. в., мы можем воспользоваться теоремой 3.3, из которой следует, что предел в (3.23) равен  таким образом,
таким образом, 
Нам потребуется следующая лемма.
Лемма 3.1. Пусть  есть вероятность того, что процесс
есть вероятность того, что процесс  отправляясь из состояния
отправляясь из состояния  на первом шаге окажется в одном из положительных
на первом шаге окажется в одном из положительных
состояний и после этого никогда не окажется ни в одном отрицательном состоянии. При  вероятности
вероятности  полагаются равными нулю. Тогда
полагаются равными нулю. Тогда

Доказательство. Из самого определения вероятностей  следует, что
следует, что 

Далее,

Лемма доказана. 
Пусть

т. е.  есть вероятность, отправляясь из состояния
есть вероятность, отправляясь из состояния  оказаться на положительной оси.
оказаться на положительной оси.
Рассмотрим те реализации процесса, которые выходят из состояния  и включают в себя неположительные состояния. По условию теоремы
и включают в себя неположительные состояния. По условию теоремы  поэтому в силу закона больших чисел такая реализация с вероятностью 1 может быть в неположительных состояниях лишь конечное число раз. Вероятность того, что процесс в последний раз находился в неположительном состоянии на
поэтому в силу закона больших чисел такая реализация с вероятностью 1 может быть в неположительных состояниях лишь конечное число раз. Вероятность того, что процесс в последний раз находился в неположительном состоянии на  шаге, равна
шаге, равна  последнее равенство следует из определения ей для
последнее равенство следует из определения ей для  Перебирая все возможности, связанные с последним моментом пребывания в неположительных состояниях, получаем важное соотношение:
Перебирая все возможности, связанные с последним моментом пребывания в неположительных состояниях, получаем важное соотношение:

( - символ Кронекера). Теперь мы можем доказать теорему восстановления. Доказательство теоремы 3.2. Из определения
- символ Кронекера). Теперь мы можем доказать теорему восстановления. Доказательство теоремы 3.2. Из определения  следует, что
следует, что

Так как  (лемма 1.1), то с помощью диагонализации (см. доказательство теоремы 3.1) мы можем выделить подпоследовательность
(лемма 1.1), то с помощью диагонализации (см. доказательство теоремы 3.1) мы можем выделить подпоследовательность  такую, что предел
такую, что предел

существует для каждого 
В соотношении (3.25) перейдем к пределу при  стремящемся к бесконечности по значениям подпоследовательности это даст
стремящемся к бесконечности по значениям подпоследовательности это даст

причем  ограниченная последовательность. (Читателю рекомендуется самостоятельно убедиться в возможности предельного перехода под знаком суммы.)
ограниченная последовательность. (Читателю рекомендуется самостоятельно убедиться в возможности предельного перехода под знаком суммы.)
В силу теоремы 3.1 ограниченная регулярная последовательность  является постоянной; пусть все ее члены равны константе а. Из (3.24) имеем
является постоянной; пусть все ее члены равны константе а. Из (3.24) имеем

Так как  и Ряд
и Ряд  сходится, то
сходится, то

Но, очевидно,  Следовательно,
Следовательно,  Если имеется другая последовательность
Если имеется другая последовательность  обладающая тем свойством, что
обладающая тем свойством, что  сходится при всех
сходится при всех  то точно так же можно показать, что предел
то точно так же можно показать, что предел  Таким образом, мы установили справедливость соотношения (3.13). Предельное соотношение (3.14) доказывается аналогичным образом.
Таким образом, мы установили справедливость соотношения (3.13). Предельное соотношение (3.14) доказывается аналогичным образом.
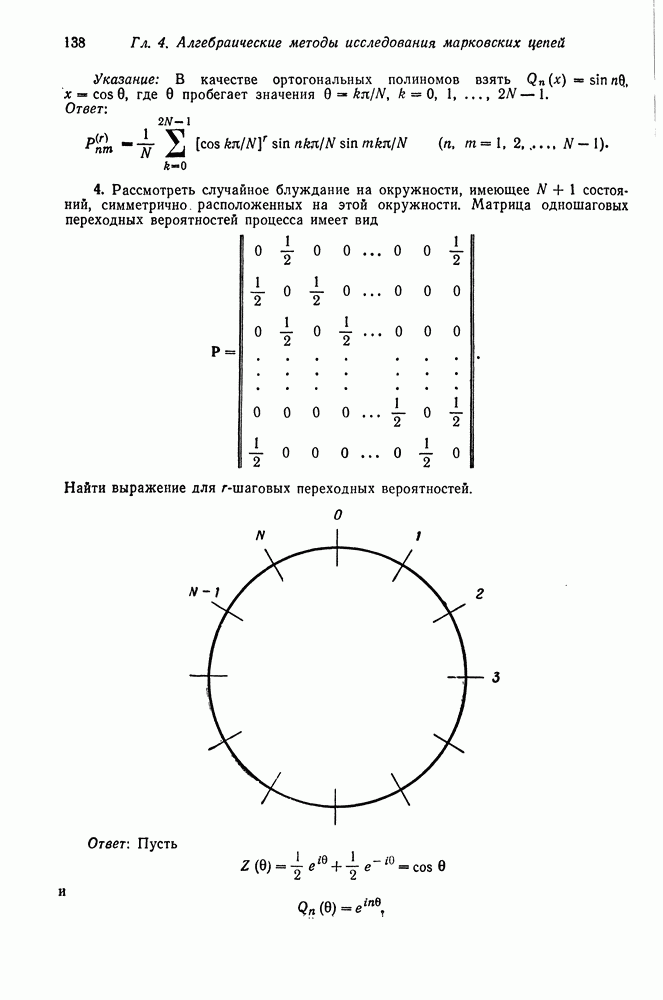
ЗАДАЧИ
(см. скан)
(см. скан)
(см. скан)
(см. скан)
(см. скан)
ЗАМЕЧАНИЯ
В значительной степени источником материала этой главы послужила элегантная книга Спицера [1]. Превосходными руководствами по теории вероятностей, содержащими изложение предельных теорем для сумм независимых случайных величин на значительно более высоком уровне, являются монографии Гнеденко и
Колмогорова [2], Лоэва [3] и Реньи [4]. Современное полное изложение предельных теорем теории вероятностей в различных аспектах читатель найдет во втором томе Книги Феллера [5].
ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 1. СВОДКА ОСНОВНЫХ ТЕРМИНОВ И СВОЙСТВ СЛУЧАЙНЫХ ВЕЛИЧИН И ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
- А. Совместные функции распределения
- Б. Условные распределения и плотности
- В. Бесконечные семейства случайных величин
- Г. Характеристические функции
- Д. Производящие функции
- Е. Примеры функций распределения
- Ж. Предельные теоремы
- § 2. ДВА ПРОСТЫХ ПРИМЕРА СЛУЧАЙНЫХ ПРОЦЕССОВ
- § 3. КЛАССИФИКАЦИЯ ОБЩИХ СЛУЧАЙНЫХ ПРОЦЕССОВ
- ЗАМЕЧАНИЯ
- Глава 2. МАРКОВСКИЕ ЦЕПИ
- § 2. ПРИМЕРЫ МАРКОВСКИХ ЦЕПЕЙ
- Б. Одномерные случайные блуждания
- В. Дискретная марковская цепь, описывающая очередь
- Г. Модель из теории запасов
- Д. Серии успехов
- Е. Ветвящиеся процессы
- Ж. Марковские цепи в генетике
- 3. Генетическая модель II
- § 3. МАТРИЦЫ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ МАРКОВСКОЙ ЦЕПИ
- § 4. КЛАССИФИКАЦИЯ СОСТОЯНИЙ МАРКОВСКОЙ ЦЕПИ
- § 5. ВОЗВРАТНОСТЬ
- § 6. ПРИМЕРЫ ВОЗВРАТНЫХ МАРКОВСКИХ ЦЕПЕЙ
- § 7. ЕЩЕ О ВОЗВРАТНОСТИ
- Глава 3. ОСНОВНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ МАРКОВСКИХ ЦЕПЕЙ И ИХ ПРИЛОЖЕНИЯ
- § 2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 1.1
- § 3. ВЕРОЯТНОСТИ ПОГЛОЩЕНИЯ
- § 4. КРИТЕРИИ ВОЗВРАТНОСТИ
- § 5. ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
- § 6. ЕЩЕ ОДИН ПРИМЕР ИЗ ТЕОРИИ ОЧЕРЕДЕЙ
- § 7. СЛУЧАЙНОЕ БЛУЖДАНИЕ
- Глава 4. АЛГЕБРАИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ МАРКОВСКИХ ЦЕПЕЙ
- § 2. СВЯЗЬ МЕЖДУ СОБСТВЕННЫМИ ЗНАЧЕНИЯМИ И КЛАССАМИ ВОЗВРАТНЫХ СОСТОЯНИЙ
- § 3. ПЕРИОДИЧЕСКИЕ КЛАССЫ
- § 4. СПЕЦИАЛЬНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ ДЛЯ МАРКОВСКИХ ЦЕПЕЙ
- § 5. ПРИМЕРЫ
- § 6. ПРИЛОЖЕНИЯ К БРОСАНИЯМ МОНЕТЫ
- Глава 5. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ И ИХ ПРИЛОЖЕНИЯ
- § 1. ВЕРОЯТНОСТИ ПЕРЕХОДА С ЗАПРЕЩЕНИЕМ
- § 2. ТЕОРЕМЫ ОБ ОТНОШЕНИЯХ
- § 3. СУЩЕСТВОВАНИЕ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ РАСПРЕДЕЛЕНИЙ
- § 4. ИНТЕРПРЕТАЦИЯ ОБОБЩЕННЫХ СТАЦИОНАРНЫХ РАСПРЕДЕЛЕНИЙ
- § 5. РЕГУЛЯРНЫЕ, СУПЕРРЕГУЛЯРНЫЕ И СУБРЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТЬ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН КАК МАРКОВСКАЯ ЦЕПЬ
- § 1. СВОЙСТВА ВОЗВРАТНОСТИ СУММ НЕЗАВИСИМЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
- § 2. ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
- § 3. ПРАВЫЕ РЕГУЛЯРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ МАРКОВСКИХ ЦЕПЕЙ
- Глава 7. КЛАССИЧЕСКИЕ ПРИМЕРЫ ЦЕПЕЙ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 1. ОБЩИЕ ПРОЦЕССЫ ЧИСТОГО РОЖДЕНИЯ (РАЗМНОЖЕНИЯ) И ПУАССОНОВСКИЕ ПРОЦЕССЫ
- Б. Примеры пуассоновских процессов
- В. Процесс чистого рождения
- Г. Процесс Юла
- § 2. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О ПУАССОНОВСКИХ ПРОЦЕССАХ
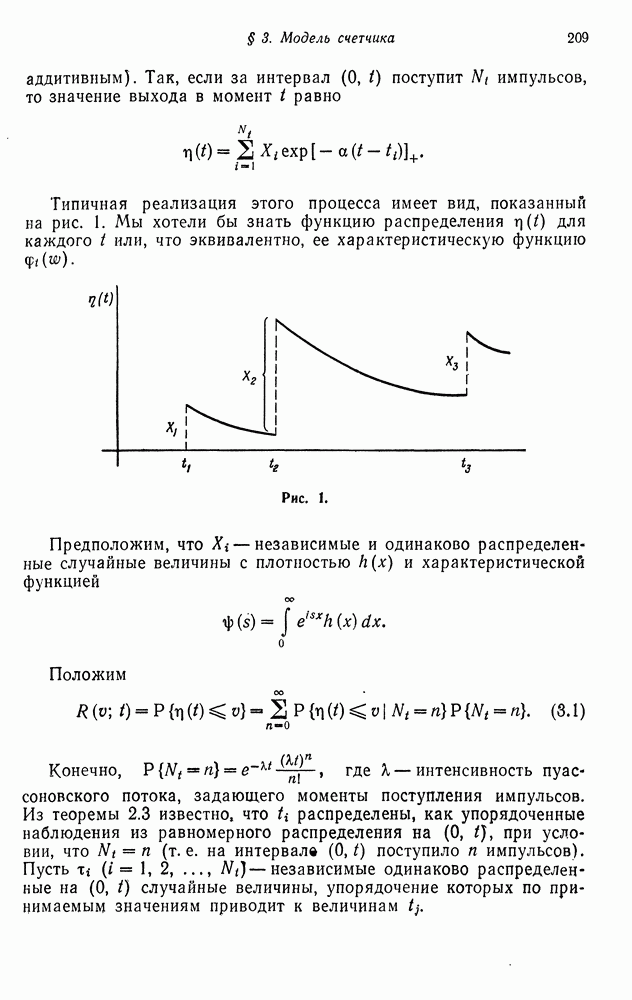
- § 3. МОДЕЛЬ СЧЕТЧИКА
- § 4. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛИ
- § 5. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
- § 6. ПРИМЕРЫ ПРОЦЕССОВ РОЖДЕНИЯ И ГИБЕЛИ
- § 7. ПРОЦЕССЫ РОЖДЕНИЯ И ГИБЕЛЙ С ПОГЛОЩАЮЩИМИ СОСТОЯНИЯМИ
- § 8. ЦЕПИ МАРКОВА С КОНЕЧНЫМ ЧИСЛОМ СОСТОЯНИЙ И НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- Глава 8. ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 1. СВОЙСТВА ДИФФЕРЕНЦИРУЕМОСТИ ПЕРЕХОДНЫХ ВЕРОЯТНОСТЕЙ
- § 2. КОНСЕРВАТИВНЫЕ ПРОЦЕССЫ. ПРЯМЫЕ И ОБРАТНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 3. ПОСТРОЕНИЕ ЦЕПИ МАРКОВА С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ С ПОМОЩЬЮ ЕЕ ИНФИНИТЕЗИМАЛЬНЫХ ПАРАМЕТРОВ
- § 4. СТРОГО МАРКОВСКОЕ СВОЙСТВО
- Глава 9. ПОРЯДКОВЫЕ СТАТИСТИКИ, ПУАССОНОВСКИЕ ПРОЦЕССЫ И ИХ ПРИЛОЖЕНИЯ
- § 1. ПОРЯДКОВЫЕ СТАТИСТИКИ И ИХ СВЯЗЬ С ПУАССОНОВСКИМИ ПРОЦЕССАМИ
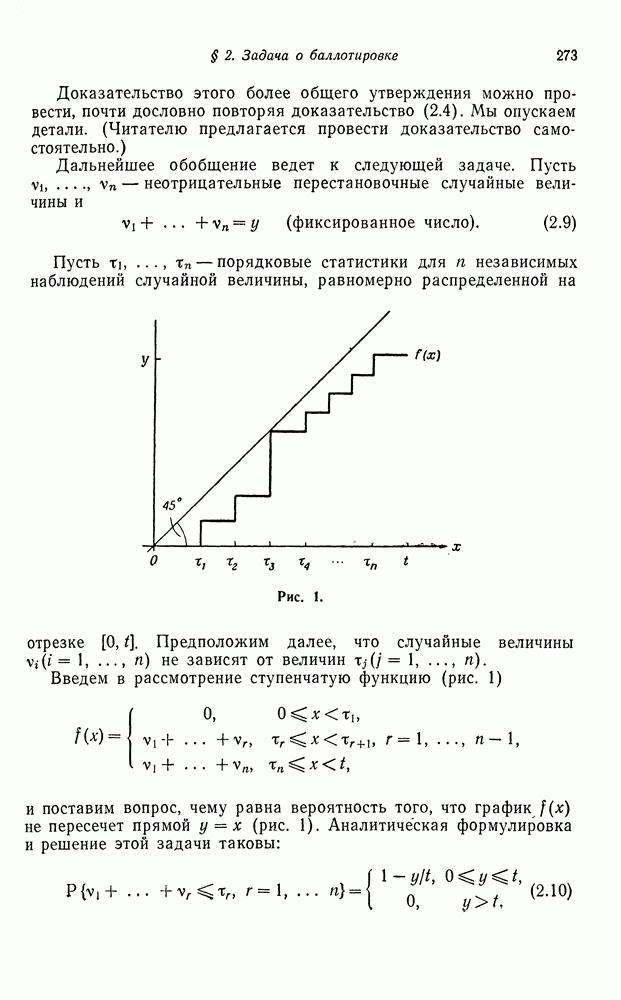
- § 2. ЗАДАЧА О БАЛЛОТИРОВКЕ
- § 3. ЭМПИРИЧЕСКИЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПОРЯДКОВЫЕ СТАТИСТИКИ
- § 4. НЕКОТОРЫЕ ПРЕДЕЛЬНЫЕ РАСПРЕДЕЛЕНИЯ ДЛЯ ЭМПИРИЧЕСКИХ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ
- Глава 10. БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 2. СОВМЕСТНЫЕ ВЕРОЯТНОСТИ ДЛЯ БРОУНОВСКОГО ДВИЖЕНИЯ
- § 3. НЕПРЕРЫВНОСТЬ ТРАЕКТОРИЙ И ИХ МАКСИМАЛЬНЫЕ ЗНАЧЕНИЯ
- Глава 11. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ
- § 1. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
- § 2. СООТНОШЕНИЯ ДЛЯ ПРОИЗВОДЯЩЕЙ ФУНКЦИИ, ОПИСЫВАЮЩЕЙ ВЕТВЯЩИЙСЯ ПРОЦЕСС
- § 3. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ
- § 4. ПРИМЕРЫ
- § 5. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С ДВУМЯ ТИПАМИ ЧАСТИЦ
- § 6. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕСКОЛЬКИМИ ТИПАМИ ЧАСТИЦ
- § 7. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 8. ВЕРОЯТНОСТИ ВЫРОЖДЕНИЯ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ ВЕТВЯЩИХСЯ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
- § 10. ВЕТВЯЩИЙСЯ ПРОЦЕСС С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ И ДВУМЯ ТИПАМИ ЧАСТИЦ
- § 11. ВЕТВЯЩИЕСЯ ПРОЦЕССЫ, ЗАВИСЯЩИЕ ОТ ВОЗРАСТА
- Глава 12. СОСТАВНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
- § 1. МНОГОМЕРНЫЕ ОДНОРОДНЫЕ ПУЛССОНОВСКИЕ ПРОЦЕССЫ
- § 2. ПРИМЕНЕНИЕ МНОГОМЕРНЫХ ПУАССОНОВСКИХ ПРОЦЕССОВ В АСТРОНОМИИ
- § 3. ИММИГРАЦИЯ И РОСТ ПОПУЛЯЦИЙ
- § 4. ВЕРОЯТНОСТНЫЕ МОДЕЛИ МУТАЦИИ И РОСТА
- § 5. ЭКСПОНЕНЦИАЛЬНЫЙ РОСТ ОДНОМЕРНОЙ ПОПУЛЯЦИИ
- § 6. ВЕРОЯТНОСТНАЯ МОДЕЛЬ РОСТА ПОПУЛЯЦИИ В ПРОСТРАНСТВЕ И ВРЕМЕНИ
- § 7. ДЕТЕРМИНИРОВАННЫЙ РОСТ ПОПУЛЯЦИИ С РАСПРЕДЕЛЕНИЕМ ПО ВОЗРАСТАМ
- § 8. ДИСКРЕТНАЯ ВОЗРАСТНАЯ МОДЕЛЬ
- Глава 13. ДЕТЕРМИНИРОВАННЫЕ И СЛУЧАЙНЫЕ ГЕНЕТИЧЕСКИЕ И ЭКОЛОГИЧЕСКИЕ ПРОЦЕССЫ
- § 1. ГЕНЕТИЧЕСКИЕ МОДЕЛИ. ОПИСАНИЕ ГЕНЕТИЧЕСКОГО МЕХАНИЗМА
- § 2. ИНБРИДИНГ
- Б. Спаривание сибсов
- В. Гены, идентичные по происхождению
- Г. Бесконечная диплоидная популяция и коэффициент инбридинга
- Д. Популяция с самооплодотворением и случайным спариванием
- § 3. ПОЛИПЛОИДЫ
- § 4. МАРКОВСКИЕ ПРОЦЕССЫ, ПОРОЖДАЕМЫЕ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
- § 5. МОДЕЛИ РОСТА ПОПУЛЯЦИЙ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
- § 6. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЦЕПЕЙ МАРКОВА, ПОРОЖДЕННЫХ ПРЯМЫМ ПРОИЗВЕДЕНИЕМ ВЕТВЯЩИХСЯ ПРОЦЕССОВ
- § 7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ДЛЯ МОДЕЛИ МУТАЦИИ С НЕСКОЛЬКИМИ ТИПАМИ ИНДИВИДУУМОВ
- § 8. ВЕРОЯТНОСТНЫЙ СМЫСЛ СОБСТВЕННЫХ ЗНАЧЕНИЙ
- Глава 14. ПРОЦЕССЫ МАССОВОГО ОБСЛУЖИВАНИЯ
- § 2. ПРОСТЕЙШИЕ ПРОЦЕССЫ ОБСЛУЖИВАНИЯ (М/М/1)
- § 3. НЕКОТОРЫЕ ОБЩИЕ МОДЕЛИ ОБСЛУЖИВАНИЯ ОДНИМ ПРИБОРОМ
- § 4. МЕТОД ВЛОЖЕННЫХ ЦЕПЕЙ МАРКОВА ПРИМЕНИТЕЛЬНО К МОДЕЛИ ОБСЛУЖИВАНИЯ (M/G/1)
- § 5. ЭКСПОНЕНЦИАЛЬНО РАСПРЕДЕЛЕННОЕ ВРЕМЯ ОБСЛУЖИВАНИЯ (G/М/1)
- § 6. ГАММА-РАСПРЕДЕЛЕНИЕ ИНТЕРВАЛОВ МЕЖДУ ПОСТУПЛЕНИЯМИ И ОБОБЩЕНИЯ (Ek/М/1)
- § 7. ЭКСПОНЕНЦИАЛЬНОЕ ОБСЛУЖИВАНИЕ s ПРИБОРОВ (GI/M/s)
- § 8. ВИРТУАЛЬНОЕ ВРЕМЯ ОЖИДАНИЯ И ПЕРИОД ЗАНЯТОСТИ
- ПРИЛОЖЕНИЕ § 1. СПЕКТРАЛЬНАЯ ТЕОРЕМА
- § 2. ТЕОРИЯ ФРОБЕНИУСА ПОЛОЖИТЕЛЬНЫХ МАТРИЦ
- РАЗЛИЧНЫЕ ЗАДАЧИ