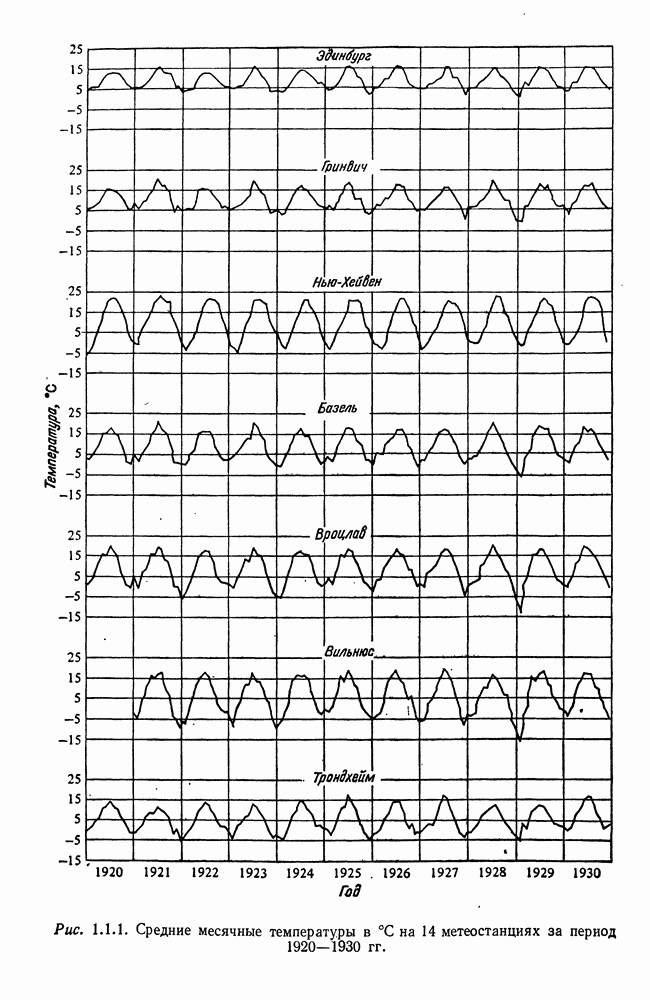
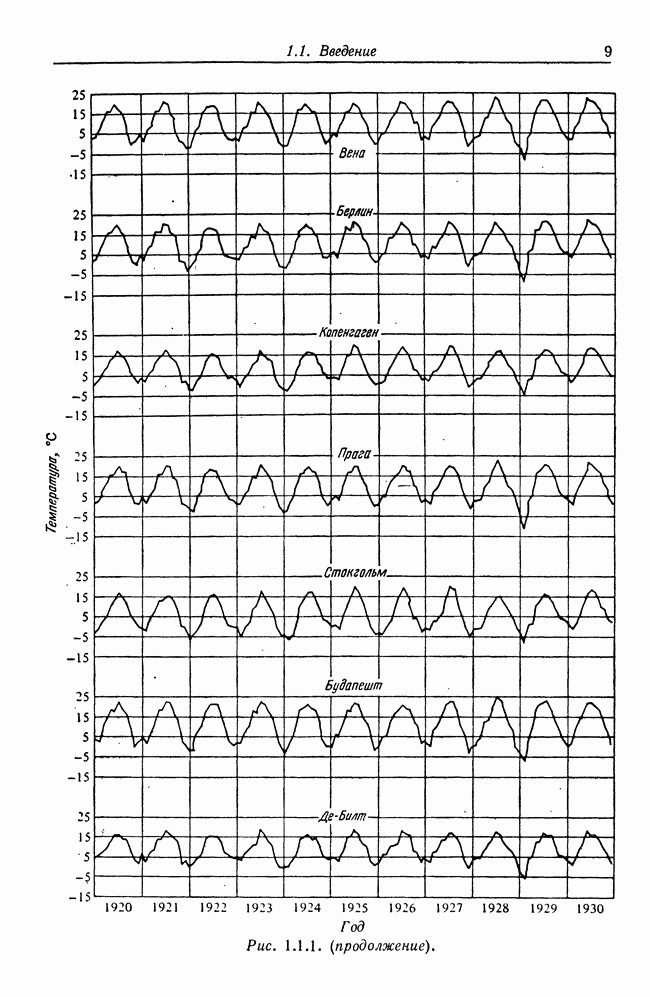
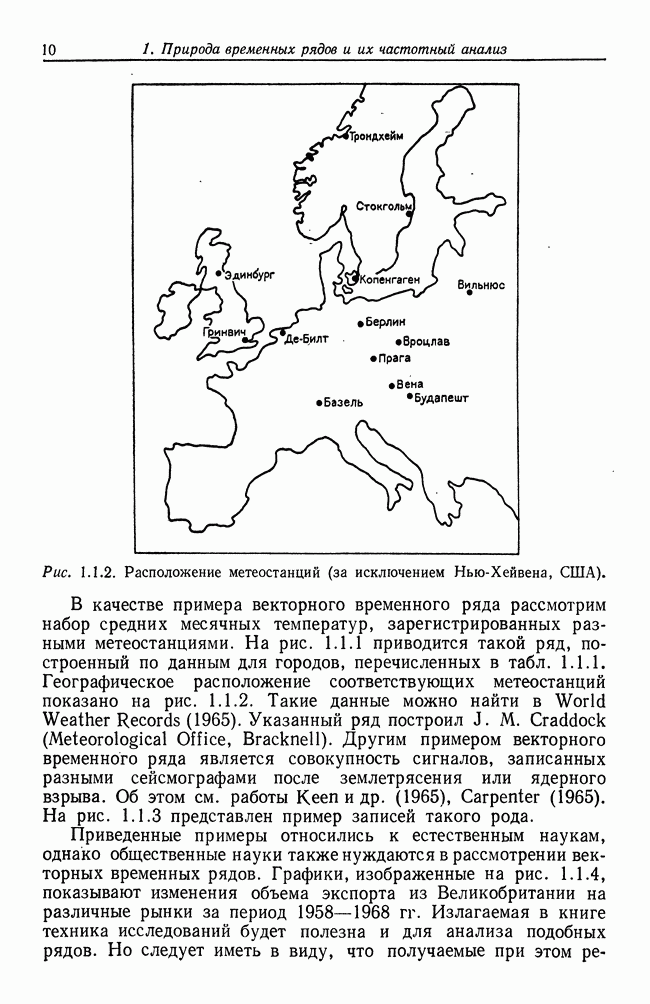
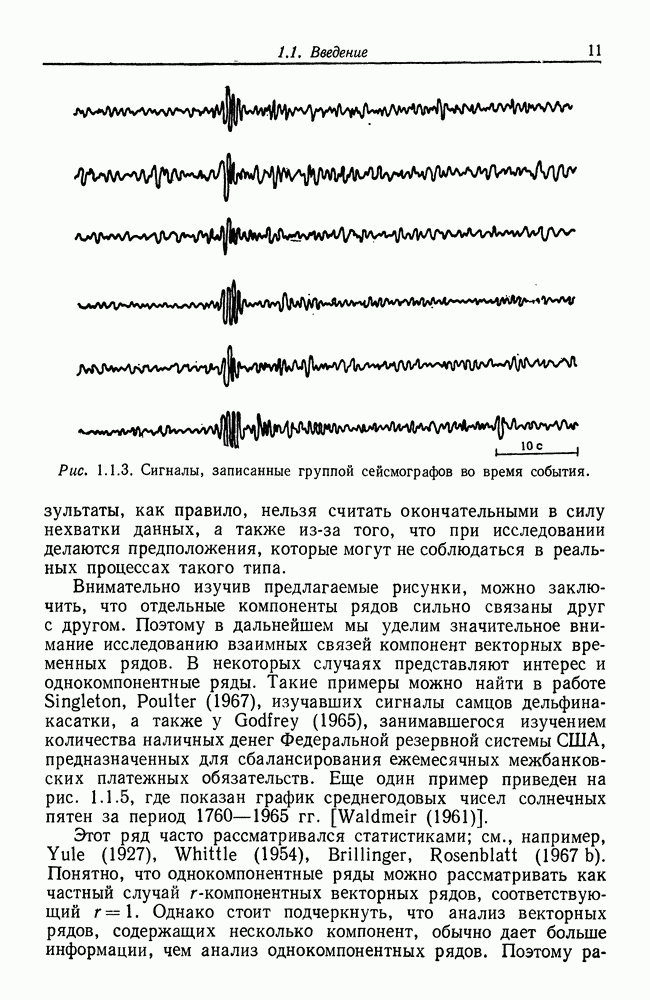
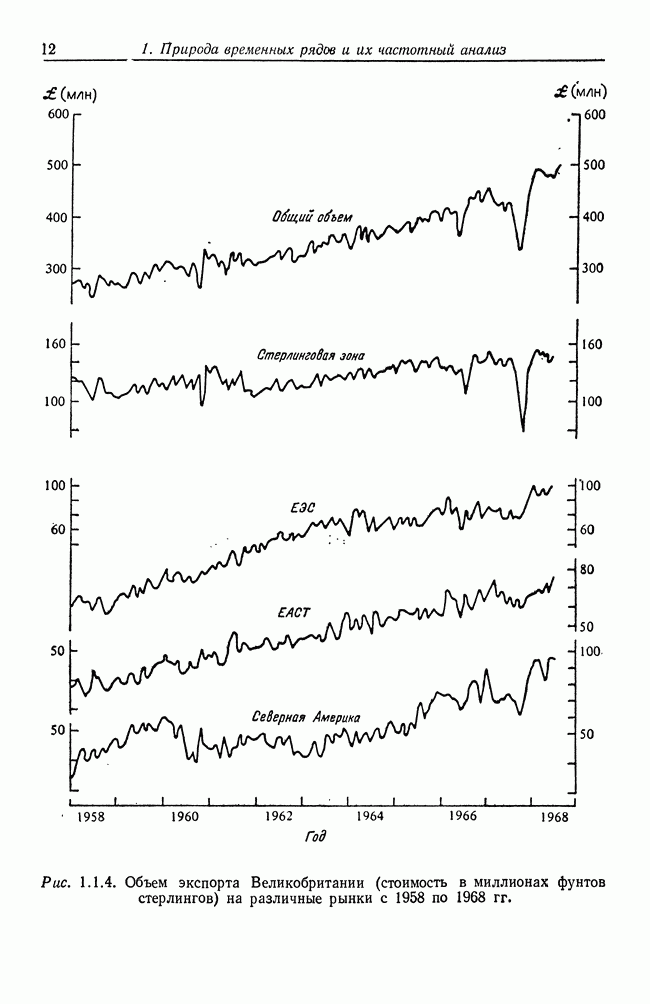
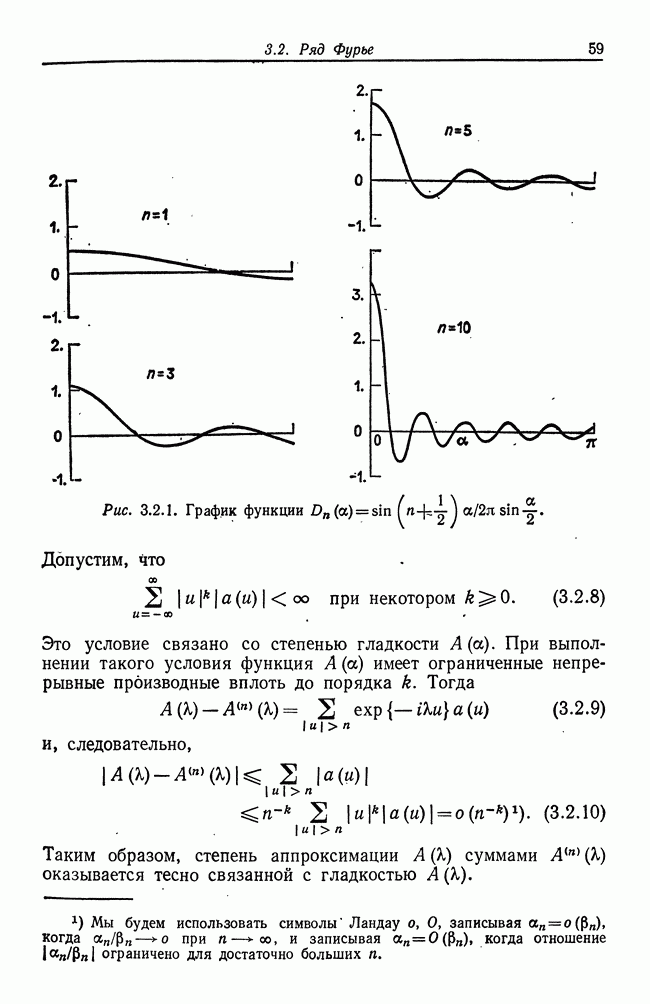
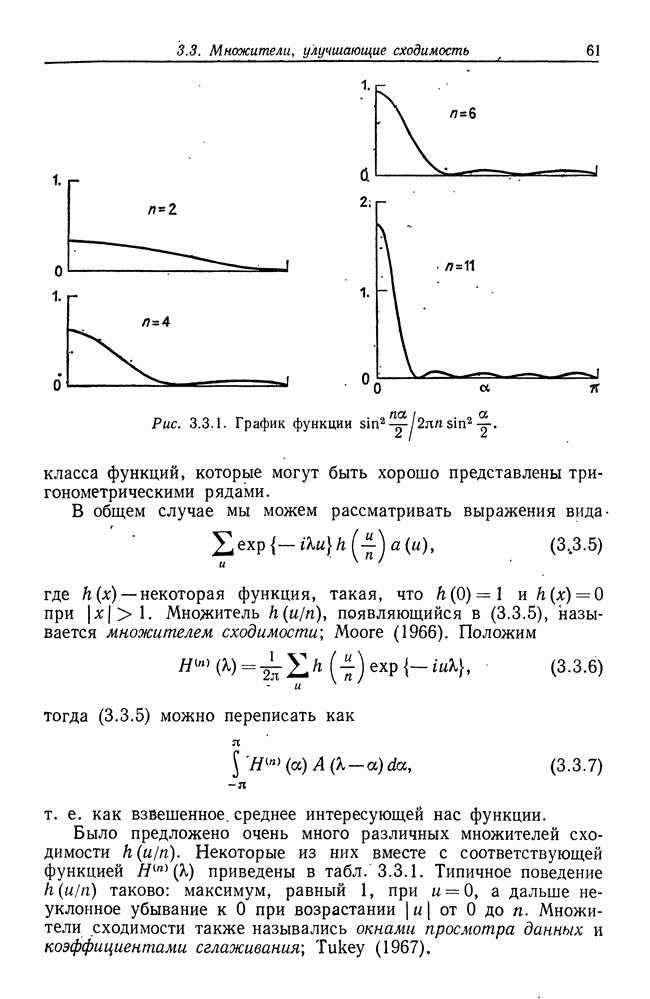
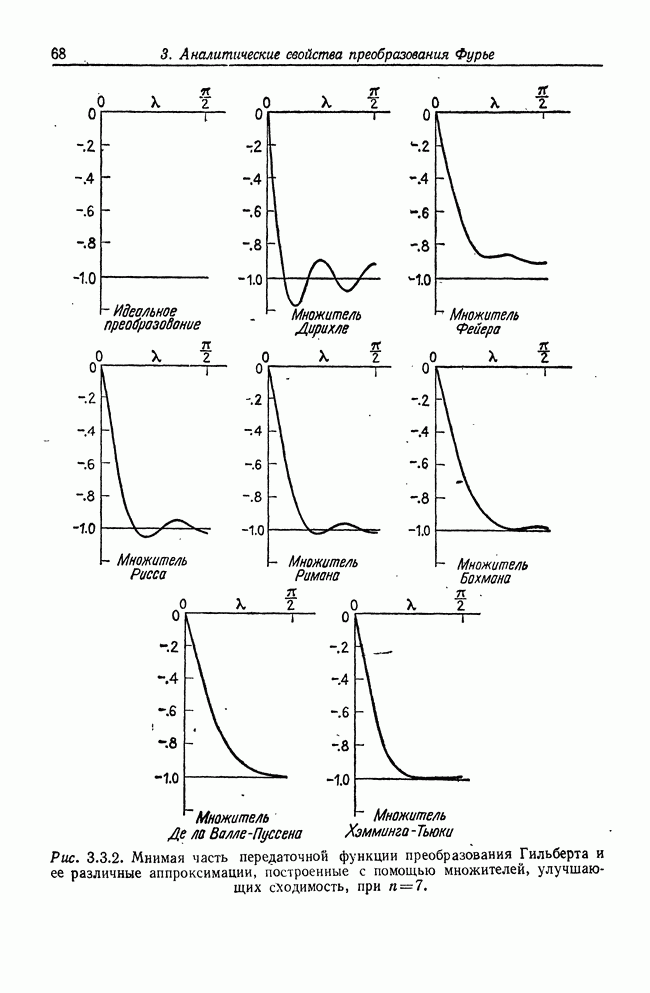
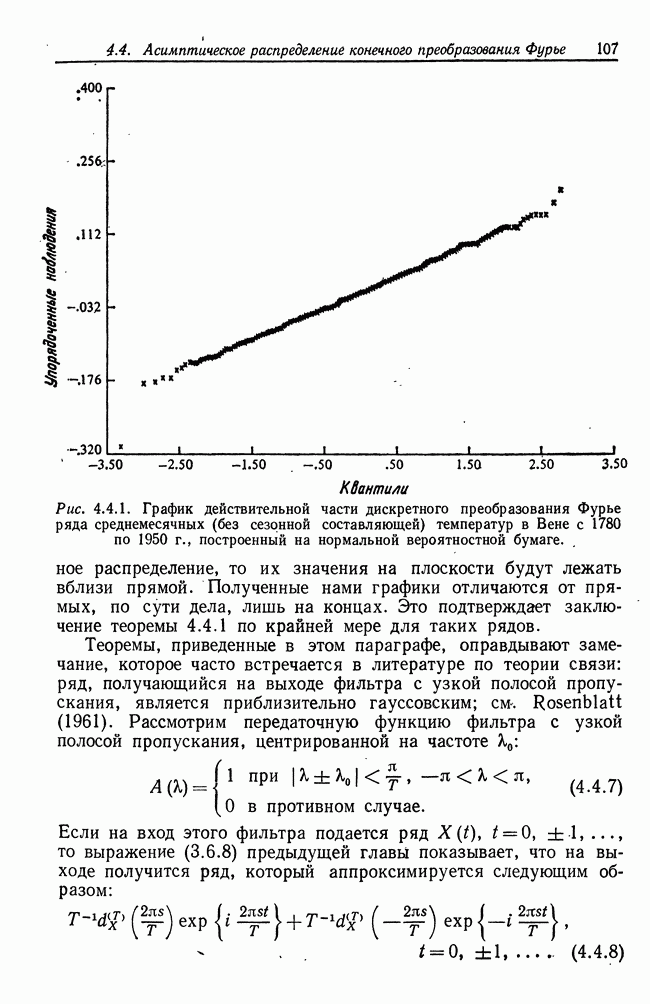
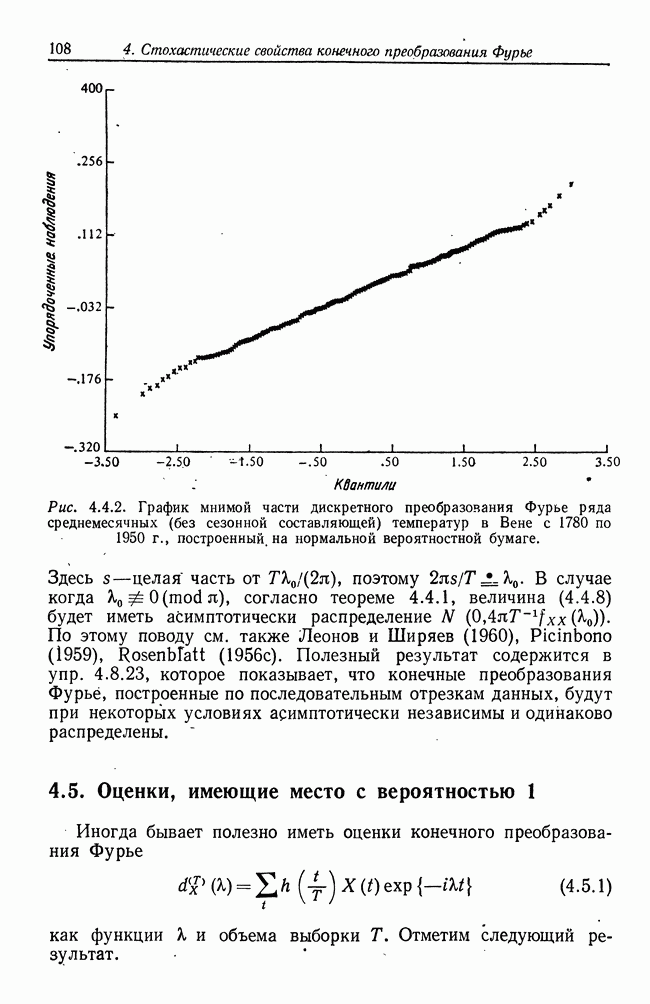
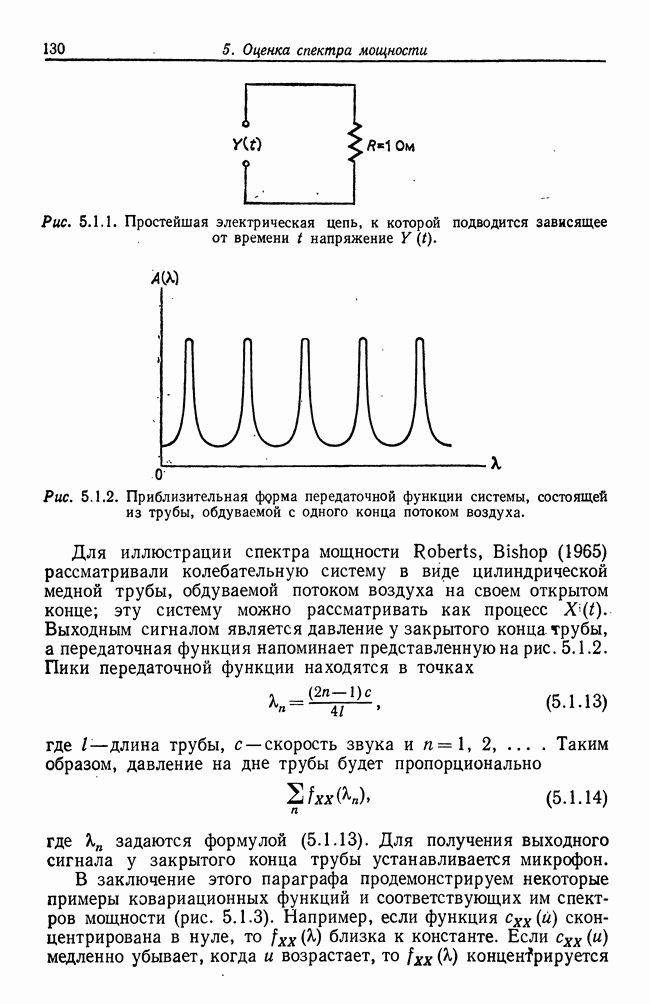
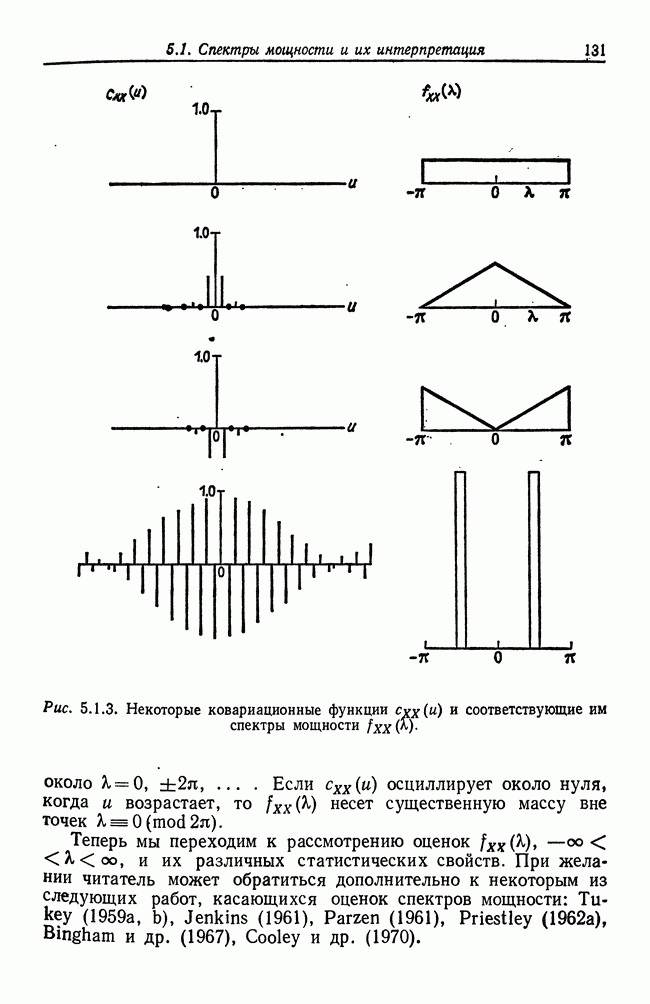
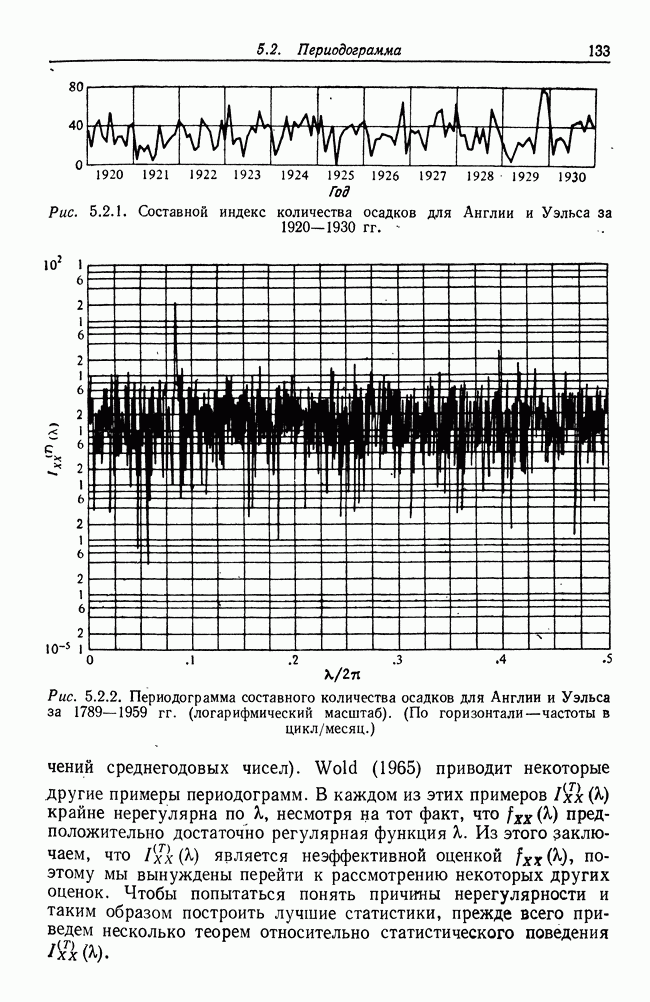
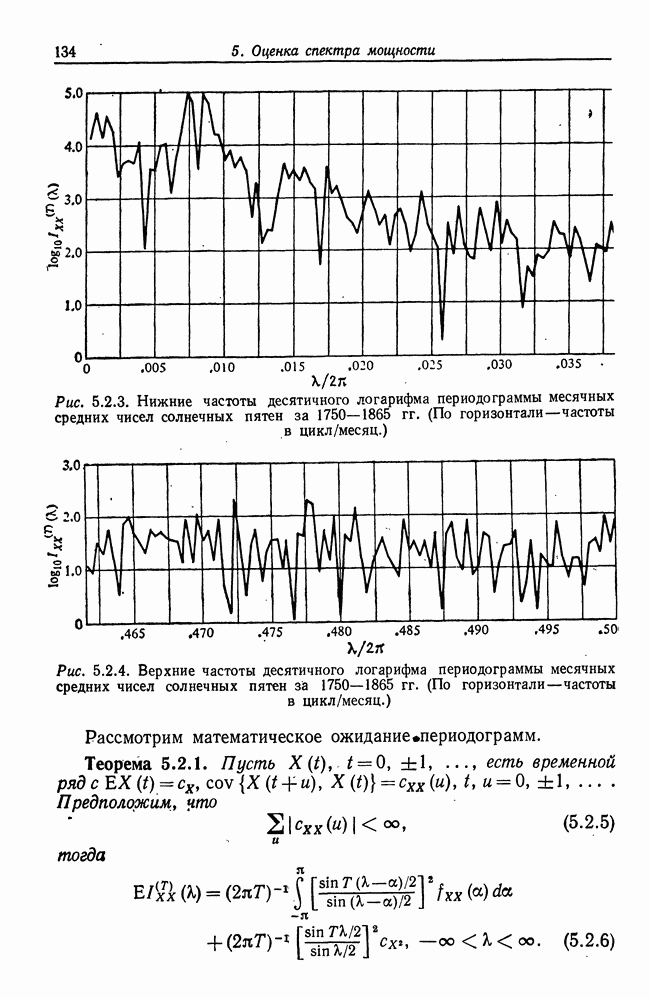
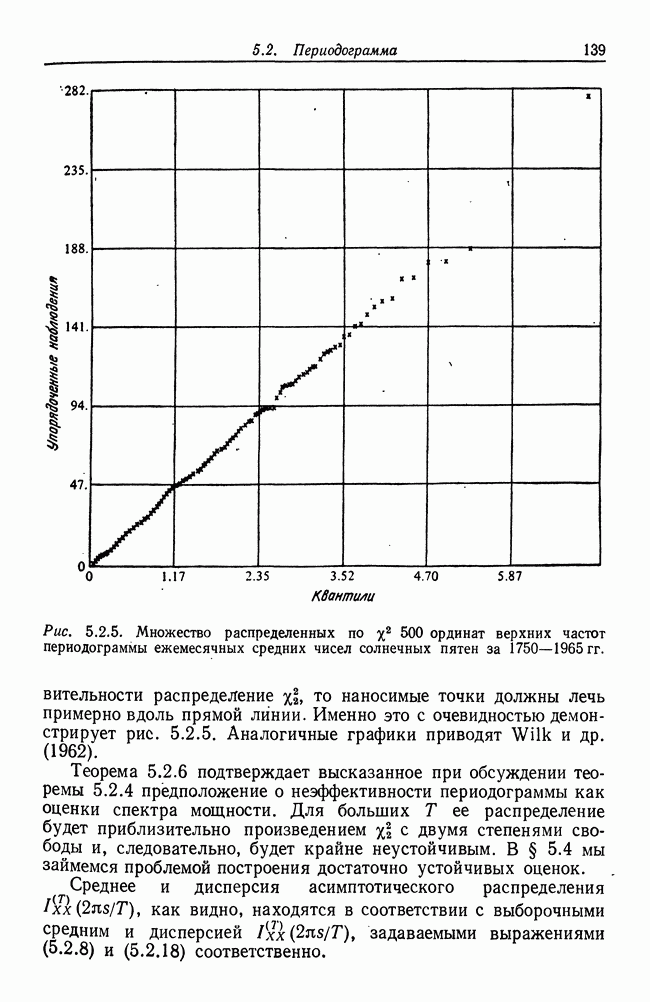
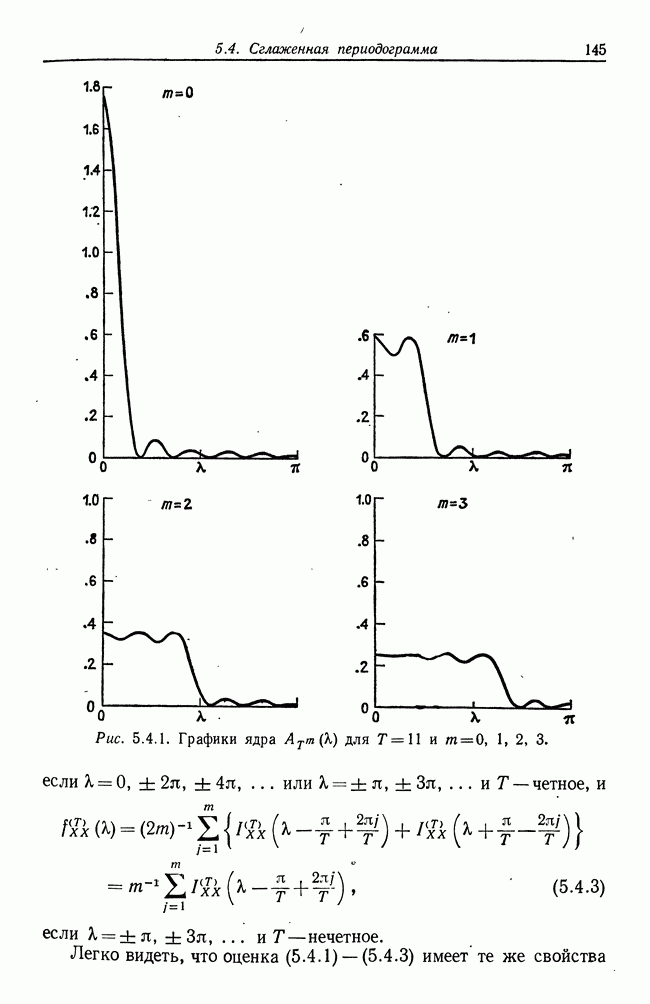
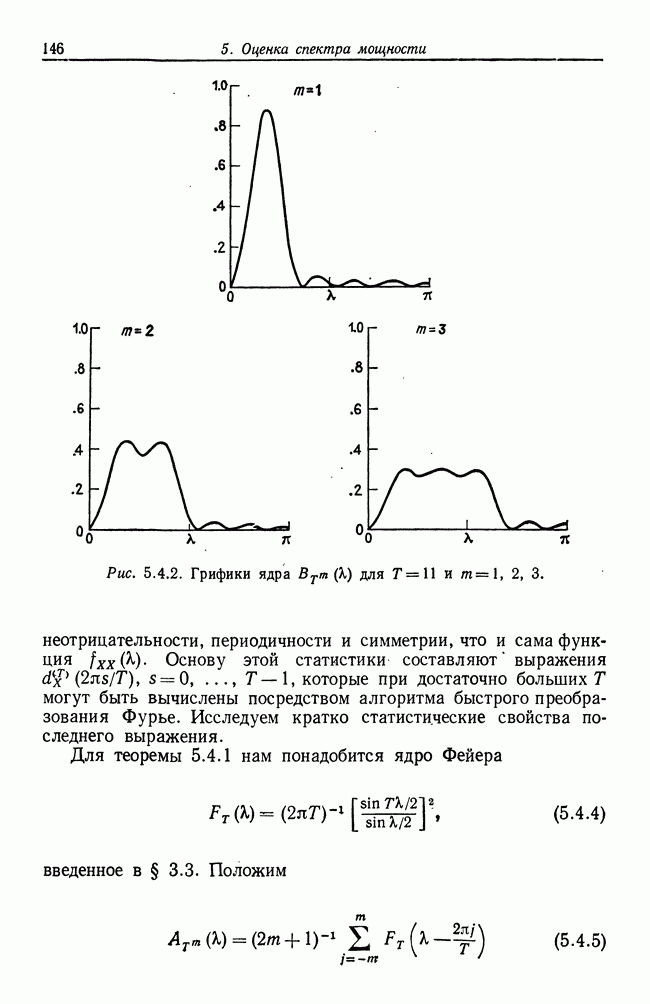
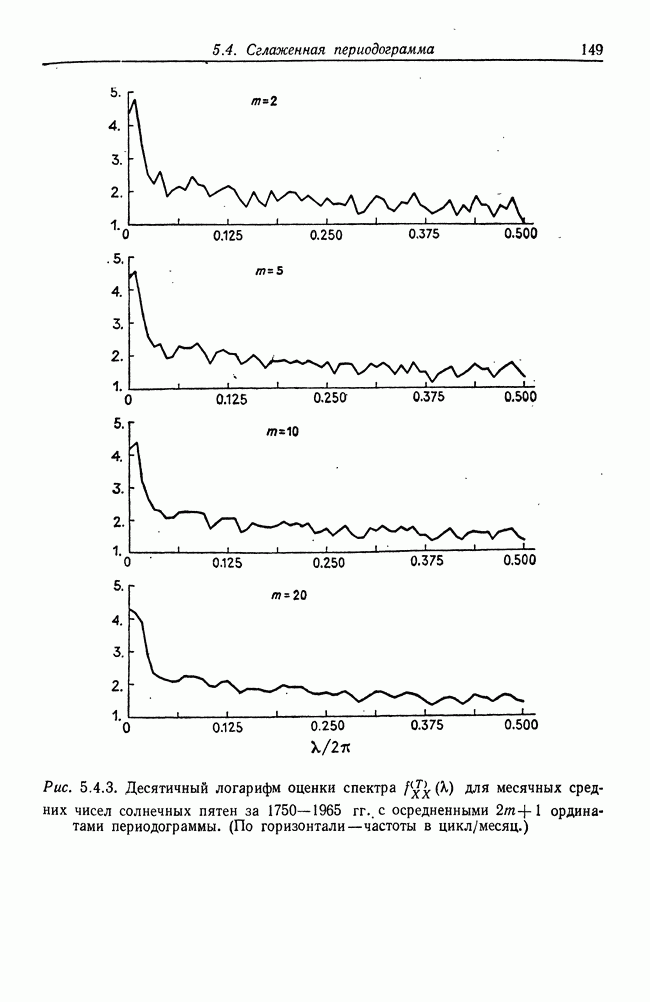
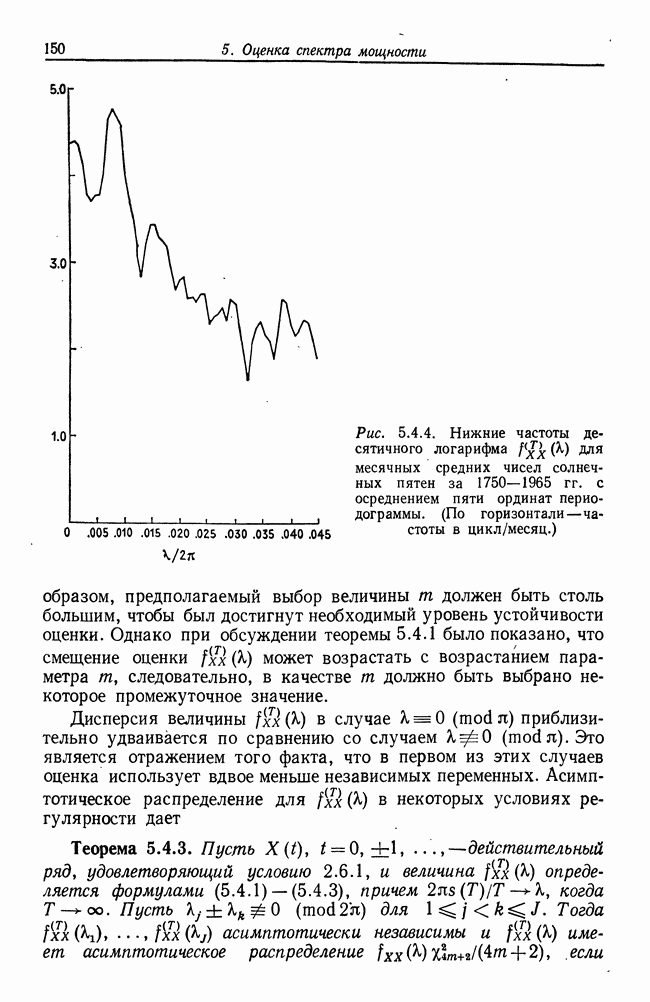
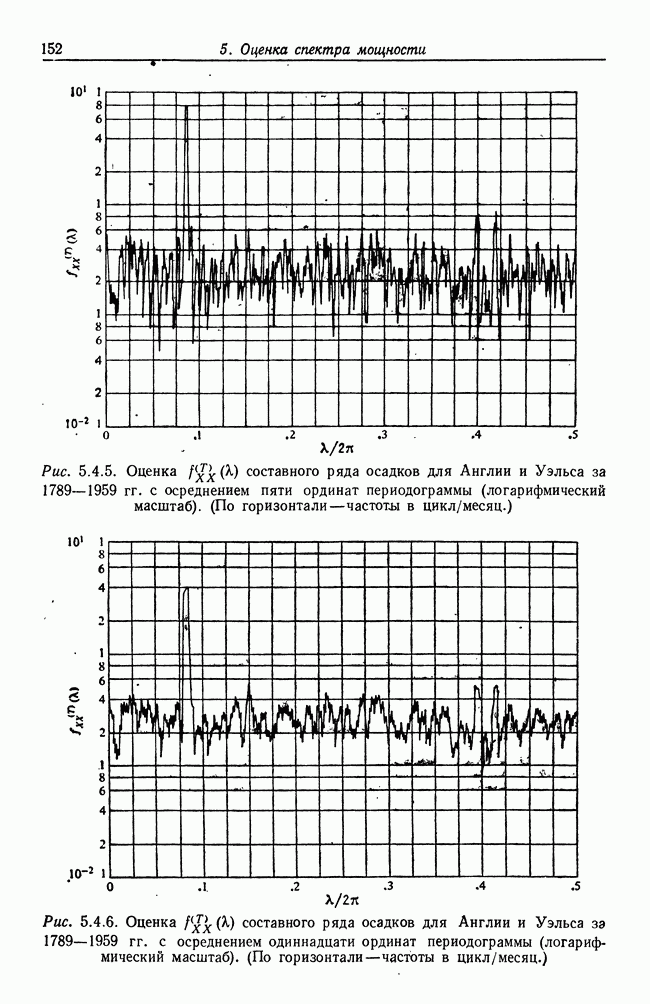
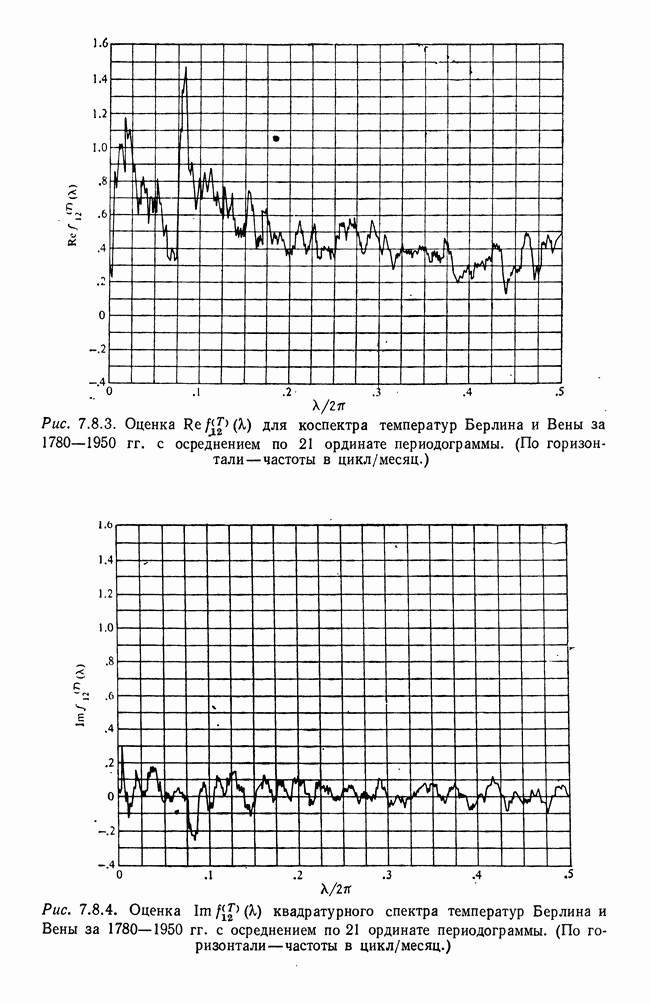
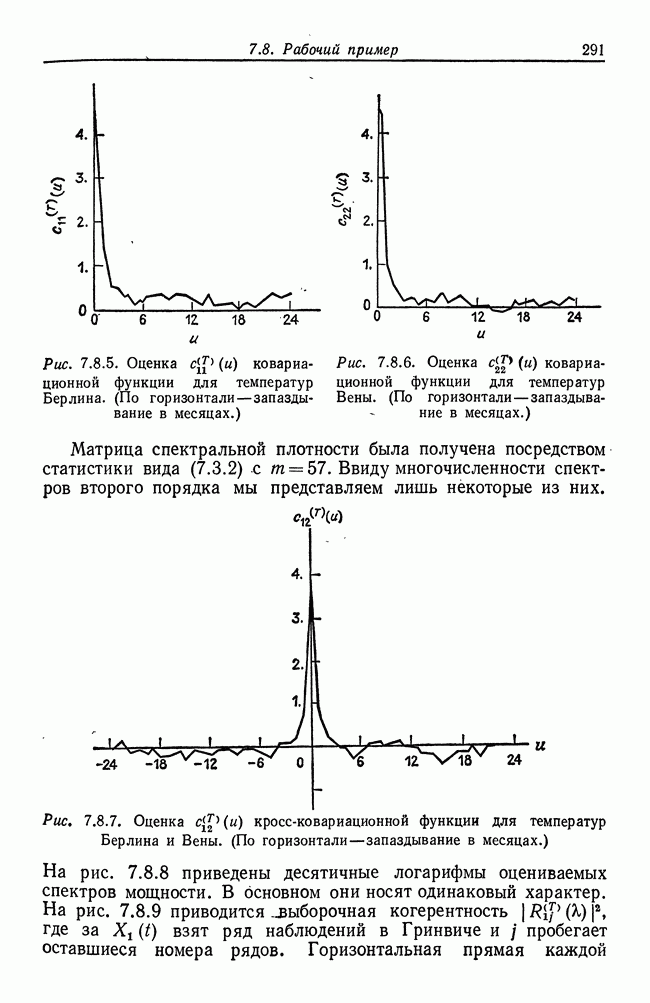
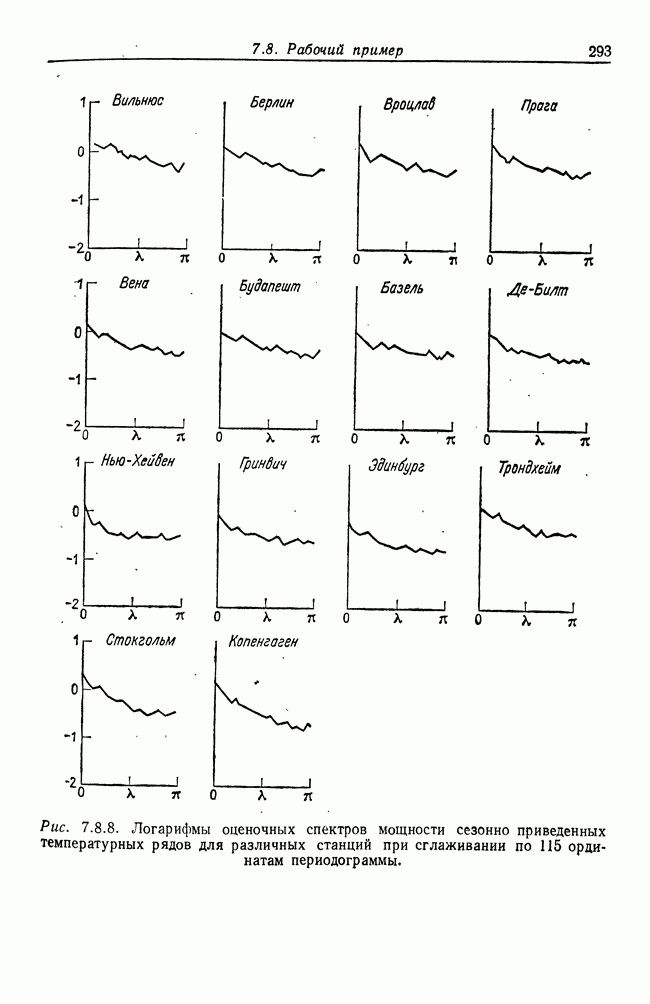
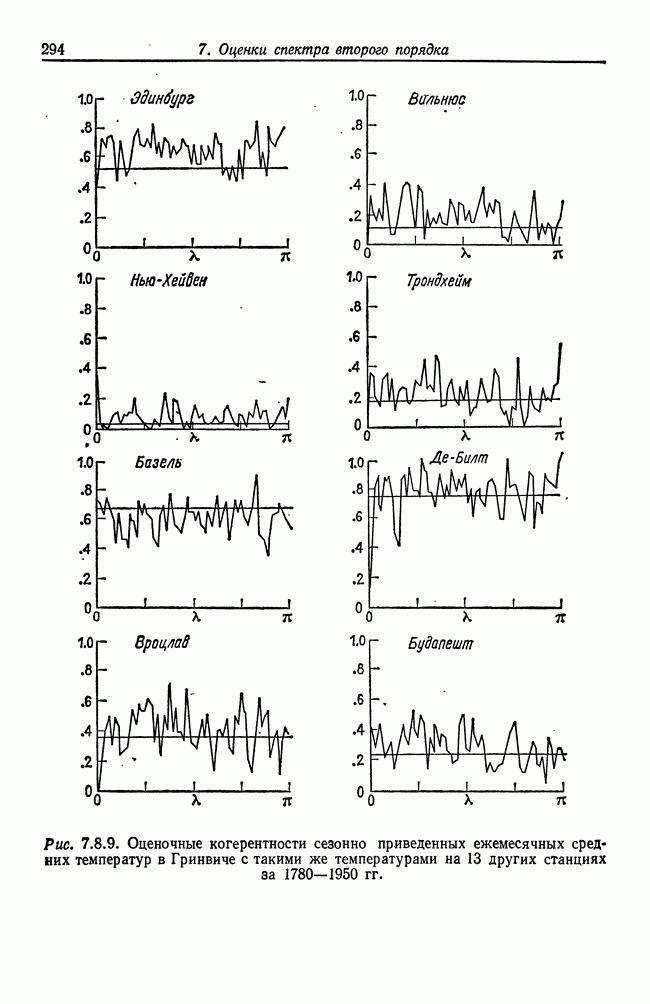
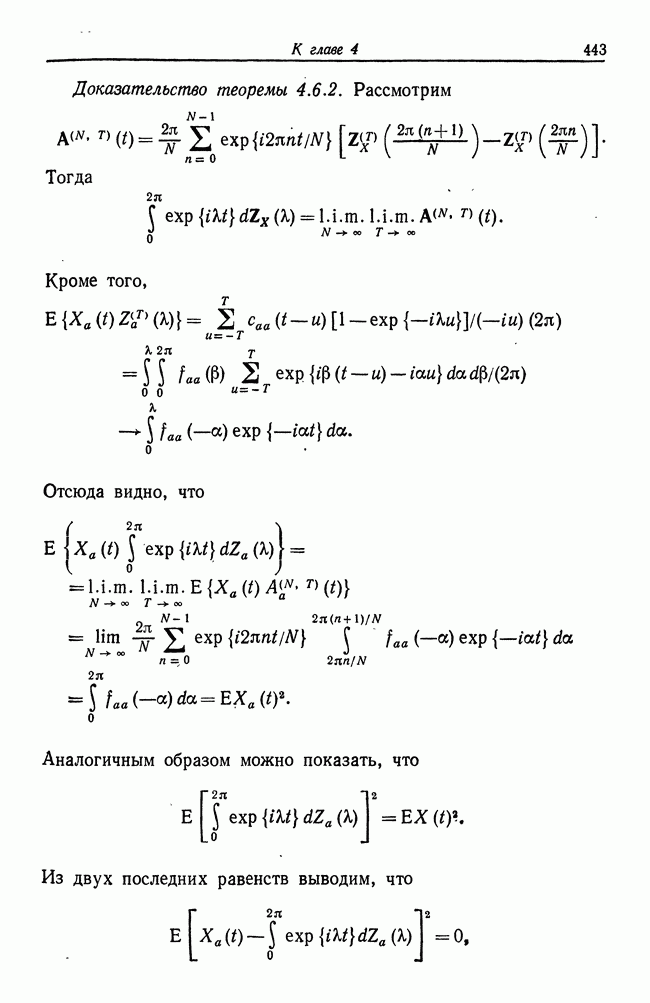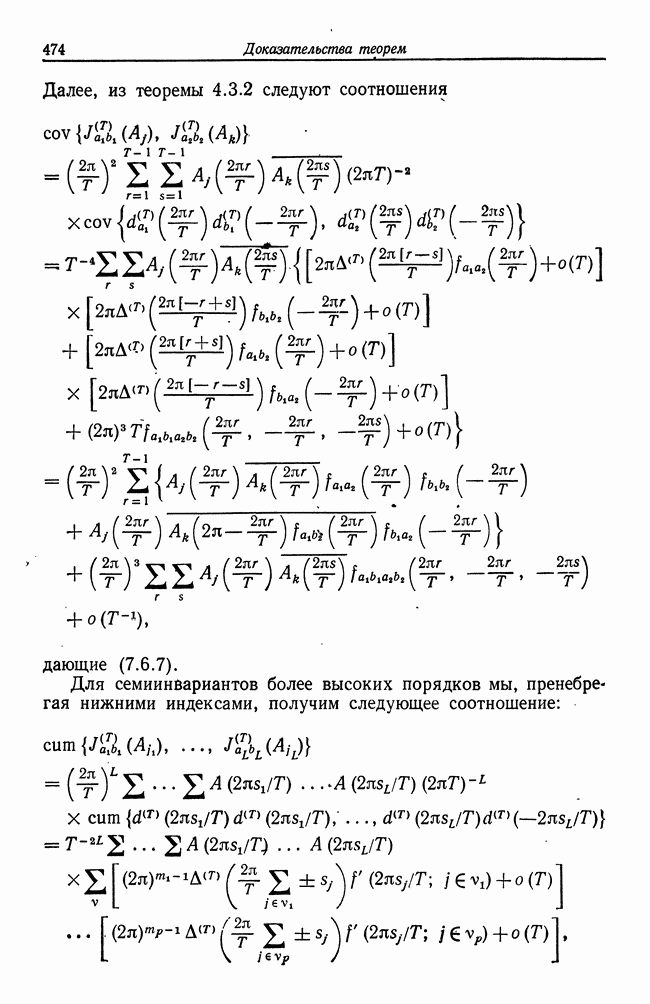| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.2. Результаты для многомерных случайных величин
Напомним читателю, что в множестве эрмитовых матриц вводится частичное упорядочение
 (8.2.1)
(8.2.1)
означающее, что матрица  неотрицательно определена. Это отношение порядка обсуждается, например, в книгах: Bellman (1960), Гельфанд и др. (1960) и Siotani (1967). Среди следствий неравенства (8.2.1) отметим такие:
неотрицательно определена. Это отношение порядка обсуждается, например, в книгах: Bellman (1960), Гельфанд и др. (1960) и Siotani (1967). Среди следствий неравенства (8.2.1) отметим такие:
 (8.2.2)
(8.2.2)
и

здесь  обозначают
обозначают  в порядке возрастания собственные значения А и В соответственно.
в порядке возрастания собственные значения А и В соответственно.
Далее, когда в формулировке теоремы речь пойдет о минимизации эрмитовой матричной функции А (0) аргумента 0, под этим будет подразумеваться отыскание такого значения  что
что
 (8.2.6)
(8.2.6)
при всех 0. Значение  называется минимальным значением
называется минимальным значением  Заметим что если
Заметим что если  минимизирует
минимизирует  то из (8.2.2) — (8.2.5) вытекает, что
то из (8.2.2) — (8.2.5) вытекает, что  минимизирует одновременно функционалы
минимизирует одновременно функционалы 
Введем еще некоторые новые обозначения. Пусть Z — произвольная матрица со столбцами  Тогда вектор-столбец, составленный из столбцов матрицы Z, помещенных один под другим, обозначим
Тогда вектор-столбец, составленный из столбцов матрицы Z, помещенных один под другим, обозначим
 (8.2.7)
(8.2.7)
Для любых матриц U и V назовем их кронекеровым произведением матрицу  составленную из блоков по следующему правилу: если V имеет размеры
составленную из блоков по следующему правилу: если V имеет размеры  то
то
 (8.2.8)
(8.2.8)
Два вновь введенных объекта связаны важным соотношением
 (8.2.9)
(8.2.9)
(предполагается, что матрицы, фигурирующие здесь, имеют надлежащие размеры), см. упр. 8.16.26. Neudecker (1968) и Nissen (1968j рассматривают приложения этих определений в статистике.
Займемся теперь поисками минимума. Пусть случайные векторы X и Y имеют соответственно  и s компонент. Рассмотрим
и s компонент. Рассмотрим  -мерный вектор
-мерный вектор
 (8.2.10)
(8.2.10)
Допустим, что (8.2.10) имеет среднее значение

и ковариационную матрицу
 (8.2.12)
(8.2.12)
Если мы хотим найти  -компонентный вектор
-компонентный вектор  -матрицу а, минимизирующие
-матрицу а, минимизирующие  -эрмитову матрицу
-эрмитову матрицу
 (8.2.13)
(8.2.13)
то решение этой задачи дает
Теорема 8.2.1. Пусть задан  случайный вектор (8.2.10) со средним (8.2.11) и ковариационной матрицей (8.2.12). Предположим, что матрица
случайный вектор (8.2.10) со средним (8.2.11) и ковариационной матрицей (8.2.12). Предположим, что матрица  невырожденна. Тогда (8.2.13) минимизируют величины
невырожденна. Тогда (8.2.13) минимизируют величины
 (8.2.15)
(8.2.15)
и

Соответствующее минимальное значение равно

Назовем величину а, определенную формулой (8.2.15), коэффициентом регрессии Y на X. Случайный вектор
 (8.2.17)
(8.2.17)
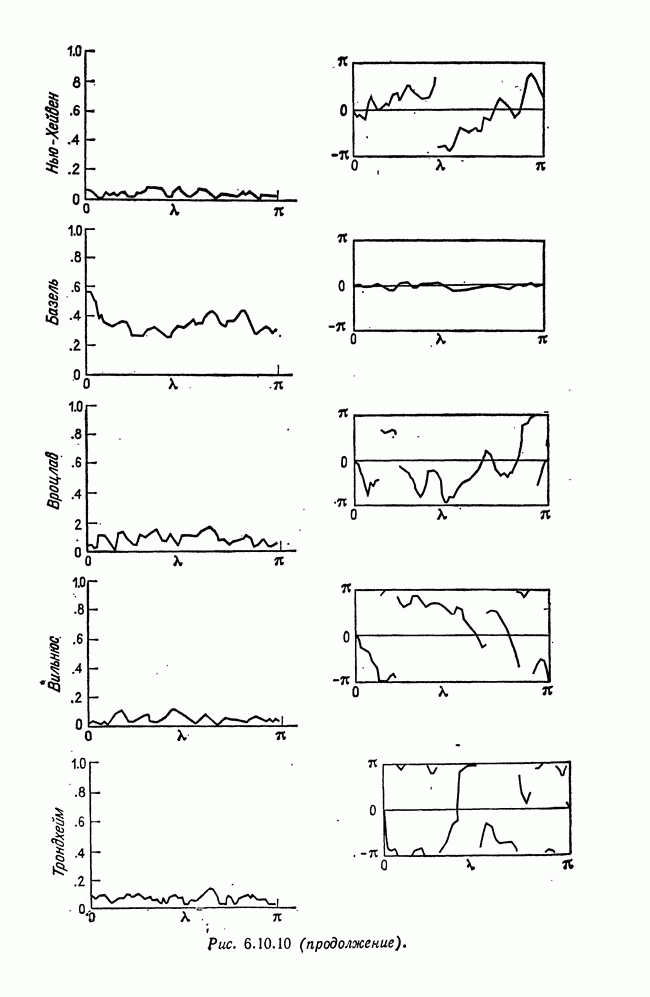
называется наилучшим линейным прогнозом Y, основанным на X. Указанные в теореме  и а доставляют также минимум детерминанту, следу, диагональным элементам и собственным значениям матрицы (8.2.13). Дадим библиографические ссылки на эту теорему: Whittle (1963а, гл. 4), Goldberger (1964, стр. 280), Rao (1965), Khatri (1967). При
и а доставляют также минимум детерминанту, следу, диагональным элементам и собственным значениям матрицы (8.2.13). Дадим библиографические ссылки на эту теорему: Whittle (1963а, гл. 4), Goldberger (1964, стр. 280), Rao (1965), Khatri (1967). При  квадрат коэффициента корреляции Y с его наилучшим линейным прогнозом, именуемый квадратом множественного коэффициента корреляции, имеет вид
квадрат коэффициента корреляции Y с его наилучшим линейным прогнозом, именуемый квадратом множественного коэффициента корреляции, имеет вид
 (8.2.18)
(8.2.18)
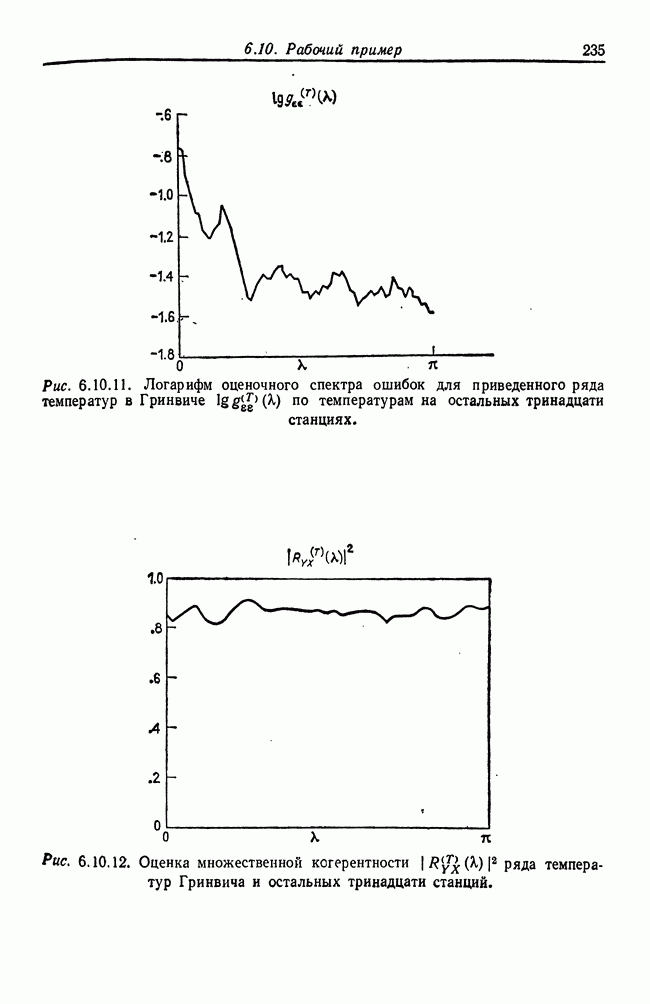
В случае многомерной величины Y рассматривают матрицу с ней мы встретимся при обсуждении  ионических корреляций в гл. 10. Полезными могут оказаться функции этой матрицы, принимающие действительные значения, скажем ее след и детерминант. Эта матрица была введена в работе Khatri (1964). Tate (1966) сделал ряд замечаний о многомерных аналогах коэффициента корреляции, см. также Williams (1967) и Hotelling (1936).
ионических корреляций в гл. 10. Полезными могут оказаться функции этой матрицы, принимающие действительные значения, скажем ее след и детерминант. Эта матрица была введена в работе Khatri (1964). Tate (1966) сделал ряд замечаний о многомерных аналогах коэффициента корреляции, см. также Williams (1967) и Hotelling (1936).
Определим векторную случайную величину
 (8.2.19)
(8.2.19)
которую будем называть ошибкой. Она представляет собой остаточный член при аппроксимации Y лучшим линейным прогнозом, основанным на X. Ковариационная матрица для  задается формулой
задается формулой
 (8.2.20)
(8.2.20)
т. е. совпадает с матрицей (8.2.16). Ковариация величины  называется частной ковариацией
называется частной ковариацией  она выступает в качестве меры линейной зависимости величин
она выступает в качестве меры линейной зависимости величин  , остающейся после удаления линейного влияния X. Аналогичным образом коэффициент корреляции
, остающейся после удаления линейного влияния X. Аналогичным образом коэффициент корреляции  называется частной корреляцией
называется частной корреляцией  Эти параметры рассмотрены в книгах: Kendall, Stuart (1961), гл. 27, и Morrison (1967, гл. 3).
Эти параметры рассмотрены в книгах: Kendall, Stuart (1961), гл. 27, и Morrison (1967, гл. 3).
В том случае, когда величина (8.2.10) имеет многомерное нормальное распределение, ее прогноз, предлагаемый теоремой 8.2.1, оказывается наилучшим в более широком классе прогнозов.
Теорема 8.2.2. Предположим, что многомерная случайная величина (8.2.10) со средним (8.2.11) и дисперсией (8.2.12) распределена по нормальному закону, и пусть матрица невырожденна. Векторная s-компонентная функция Ф (X), имеющая  , которая минимизирует
, которая минимизирует
 (8.2.21)
(8.2.21)
определяется равенством
 (8.2.22)
(8.2.22)
Минимальное значение (8.2.21) равно (8.2.16).
Для нормально распределенных величин условным распределением Y при заданном X будет
 (8.2.23)
(8.2.23)
так что частная корреляция  оказывается условной корреляцией
оказывается условной корреляцией  при заданном X.
при заданном X.
Перейдем к некоторым деталям оценки параметров в сформулированных теоремах. Допустим, что мы располагаем выборкой

 , из значений величины, для которой выполнены условия теоремы 8.2.1. Для удобства будем полагать, что
, из значений величины, для которой выполнены условия теоремы 8.2.1. Для удобства будем полагать, что  Введем
Введем  -матрицу х и
-матрицу х и  -матрицу у:
-матрицу у:
 (8.2.25)
(8.2.25)
Можно оценить ковариационную матрицу (8.2.12), взяв

и

Коэффициент регрессии Y на X можно оценить матрицей
 (8.2.28)
(8.2.28)
а в качестве оценки матрицы (8.2.20) предложим
 (8.2.29)
(8.2.29)
причина замены множителя  на
на  в этой оценке становится ясной при рассмотрении следующей теоремы.
в этой оценке становится ясной при рассмотрении следующей теоремы.
Теорема 8.2.3. Предположим, что (8.2.24),  образует выборку из многомерного нормального распределения со средним 0 и ковариационной матрицей (8.2.12). Пусть а определяется формулой (8.2.28),
образует выборку из многомерного нормального распределения со средним 0 и ковариационной матрицей (8.2.12). Пусть а определяется формулой (8.2.28),  — формулой (8.2.29). Тогда каков бы ни был
— формулой (8.2.29). Тогда каков бы ни был  -мерный вектор а, величина
-мерный вектор а, величина

распределена так же, как  Кроме того,
Кроме того, 
 (8.2.31)
(8.2.31)
и при  оценка а будет асимптотически нормальной величиной, имеющей такие моменты. Матрица
оценка а будет асимптотически нормальной величиной, имеющей такие моменты. Матрица  не зависит от а и распределена по закону
не зависит от а и распределена по закону  . При
. При  величина
величина  имеет плотность распределения
имеет плотность распределения
 (8.2.32)
(8.2.32)
Появляющаяся в (8.2.32) функция — это обобщенная гипергеометрическая функция, см. Abramowitz, Stegun (1964). Процентные точки и моменты  приведены в работах: Amos, Коорmans (1962), Ezekiel, Fox (l959) и Kramer (1963). Olkin, Pratt (1958) построили несмещенную оценку для
приведены в работах: Amos, Коорmans (1962), Ezekiel, Fox (l959) и Kramer (1963). Olkin, Pratt (1958) построили несмещенную оценку для  Распределения других статистик можно определить, пользуясь тем, что случайная матрица
Распределения других статистик можно определить, пользуясь тем, что случайная матрица

имеет распределение

Распределение для а приводит Kshirsagar (1961). Плотность этого распределения пропорциональна
 (8.2.34)
(8.2.34)
Такое распределение является разновидностью многомерного  -распределения, см. Dickey (1967).
-распределения, см. Dickey (1967).
Подобно тому как определялись частные корреляции, можно построить их оценки, основанные на элементах  Например, оценка частной корреляции величин
Например, оценка частной корреляции величин  при отсутствии линейных изменений X имеет вид
при отсутствии линейных изменений X имеет вид
 (8.2.35)
(8.2.35)
где  обозначает элемент матрицы
обозначает элемент матрицы  стоящий на пересечении
стоящий на пересечении  строки и
строки и  столбца.
столбца.
Эта оценка, как видно из распределения для  указанного в теореме 8.2.3, распределена как выборочный коэффициент корреляции
указанного в теореме 8.2.3, распределена как выборочный коэффициент корреляции  основанный на
основанный на  наблюдениях. Функция плотности распределения квадрата этой величины определяется выражением (8.2.32), если заменить в нем
наблюдениях. Функция плотности распределения квадрата этой величины определяется выражением (8.2.32), если заменить в нем  соответственно на
соответственно на  . Большая выборочная дисперсия такого
. Большая выборочная дисперсия такого  приблизительно равняется
приблизительно равняется  Найденные в работе Fisher (1962) распределения коэффициентов корреляции можно так модифицировать, чтобы получить совместное распределение всех частных корреляций. Асимптотику совместных ковариаций можно получить, опираясь на результаты работ Pearson, Filon (1898), Hall (1927) и Hsu (1949). Дальнейшие результаты, а также приближения для законов распределения оценок квадратов коэффициентов корреляции содержатся в работах: Kendall, Stuart (1961), стр. 341, Gajjar (1967), Hodgson (1968), Alexander, Vok (1963), Giri (1965) и Gurland (1966).
Найденные в работе Fisher (1962) распределения коэффициентов корреляции можно так модифицировать, чтобы получить совместное распределение всех частных корреляций. Асимптотику совместных ковариаций можно получить, опираясь на результаты работ Pearson, Filon (1898), Hall (1927) и Hsu (1949). Дальнейшие результаты, а также приближения для законов распределения оценок квадратов коэффициентов корреляции содержатся в работах: Kendall, Stuart (1961), стр. 341, Gajjar (1967), Hodgson (1968), Alexander, Vok (1963), Giri (1965) и Gurland (1966).
Рассмотренные выше теоремы имеют аналоги для комплексных случайных векторов. Например, справедлива
Теорема 8.2.4. Пусть комплексный  -мерный вектор
-мерный вектор
 (8.2.36)
(8.2.36)
со средним 0 таков, что
 (8.2.37)
(8.2.37)
Если матрица невырожденна, то  , минимизирующие
, минимизирующие

таковы:

а само минимальное значение равно
 (8.2.41)
(8.2.41)
Назовем а, определенный формулой (8.2.40), комплексным коэффициентом регрессии Y на X. Указанные  и а будут доставлять минимум, следовательно, и детерминанту, и следу, и диагональным элементам матрицы (8.2.39). При
и а будут доставлять минимум, следовательно, и детерминанту, и следу, и диагональным элементам матрицы (8.2.39). При  выражение для минимума (8.2.41) можно записать в виде
выражение для минимума (8.2.41) можно записать в виде

где по определению

Эта величина, очевидно, представляет собой обобщение на комплексный случай квадрата коэффициента множественной корреляции. Поскольку минимум (8.2.41) должен лежать между и 0, то, значит,  причем значение 1 соответствует минимуму, равному 0. В ряде случаев удобно расщепить
причем значение 1 соответствует минимуму, равному 0. В ряде случаев удобно расщепить  рассматривая порознь
рассматривая порознь

и

здесь  Эти выражения служат мерами линейной связи Y с
Эти выражения служат мерами линейной связи Y с  соответственно.
соответственно.
Вернемся теперь к случаю векторного Y. Явной мерой степени аппроксимации Y линейной функцией от X служит величина ошибки
 (8.2.46)
(8.2.46)
имеющей среднее 0 и такой, что
 (8.2.47)
(8.2.47)
и
 (8.2.48)
(8.2.48)
Аналоги частной ковариации и частной корреляции можно немедленно получить, используя матрицу (8.2.47).
Предположим теперь, что в нашем распоряжении имеется выборка
 (8.2.49)
(8.2.49)
значений вектора, удовлетворяющего условиям теоремы 8.2.4. Определим матрицы х и у формулами (8.2.25) и (8.2.26). Естественно рассмотреть статистики
 (8-2-50)
(8-2-50)
и
 (8.2.51)
(8.2.51)
Для них справедлива
Теорема 8.2.5. Пусть величины (8.2.49),  образуют выборку из многомерного комплексного нормального распределения со средним 0 и ковариационной матрицей (8.2.37).
образуют выборку из многомерного комплексного нормального распределения со средним 0 и ковариационной матрицей (8.2.37).
Если а определяется формулой (8.2.51),  — формулой (8.2.52), то для любого
— формулой (8.2.52), то для любого  -мерного вектора а величина
-мерного вектора а величина

распределена как Кроме того, 
 (8.2.54)
(8.2.54)
и при  величина
величина  распределена асимптотически как
распределена асимптотически как  Далее, матрица
Далее, матрица  не зависит от a и распределена по закону
не зависит от a и распределена по закону  . Наконец, если
. Наконец, если  то величина
то величина  имеет плотность распределения
имеет плотность распределения
 (8.2.55)
(8.2.55)
Отметим, что распределение  в комплексном случае совпадает с распределением в действительном случае при вдвое большем объеме выборки и одновременном увеличении размерности X вдвое. Объяснение этому обстоятельству предлагает эвристический подход, описанный в § 8.4. Полезное же следствие заключается в том, что можно будет применять таблицы и результаты, полученные для действительных величин. Плотность (8.2.55) приводится в работе Goodman (1963); см. также James (1964), формула (112), и Khatri (1965а). При
в комплексном случае совпадает с распределением в действительном случае при вдвое большем объеме выборки и одновременном увеличении размерности X вдвое. Объяснение этому обстоятельству предлагает эвристический подход, описанный в § 8.4. Полезное же следствие заключается в том, что можно будет применять таблицы и результаты, полученные для действительных величин. Плотность (8.2.55) приводится в работе Goodman (1963); см. также James (1964), формула (112), и Khatri (1965а). При  выражение (8.2.55) превращается в
выражение (8.2.55) превращается в

и совпадает с «нулевым» распределением величины (6.2.10), выведенным при условии, что ряд X фиксирован. Поэтому процентные точки в этом случае можно получить из процентных точек  -закона, как в гл. 6. Amos, Koopmans (1962) и Groves, Hannan (1968) нашли много «ненулевых» процентных точек для
-закона, как в гл. 6. Amos, Koopmans (1962) и Groves, Hannan (1968) нашли много «ненулевых» процентных точек для 
Доверительные области для элементов матрицы а можно построить по выражению (8.2.53), действуя как в § 6.2.
По аналогии с (8.2.34) плотность распределения матрицы а будет пропорциональна
 (8.2.57)
(8.2.57)
Wahba (1966) нашел эту плотность в случае 
Иногда представляет интерес рассмотрение следующих комплексных аналогов частных корреляций:

при 1 Естественной оценкой для (8.2.58) служит 

Распределение для  приведенное в теореме 8.2.5, показывает, что последняя оценка распределена одинаково с комплексным выборочным коэффициентом корреляции величин
приведенное в теореме 8.2.5, показывает, что последняя оценка распределена одинаково с комплексным выборочным коэффициентом корреляции величин  основанным на
основанным на  наблюдениях. Квадрат модуля этой оценки имеет плотность распределения (8.2.55), в которой
наблюдениях. Квадрат модуля этой оценки имеет плотность распределения (8.2.55), в которой  заменяются на
заменяются на  соответственно. Асимптотические ковариации пар этих оценок можно вывести из выражения (7.6.16).
соответственно. Асимптотические ковариации пар этих оценок можно вывести из выражения (7.6.16).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- 1. ПРИРОДА ВРЕМЕННЫХ РЯДОВ И ИХ ЧАСТОТНЫЙ АНАЛИЗ
- 1.2. Основания для применения гармонического анализа
- 1.3. Перемешивание
- 1.4. Исторический обзор
- 1.5. Применение частотного анализа
- 1.6. Заключительные замечания
- 1.7. Упражнения
- 2. ОСНОВНЫЕ ПОНЯТИЯ
- 2.2. Стохастические процессы
- 2.3. Кумулянты
- 2.4. Стационарность
- 2.5. Спектр второго порядка
- 2.6. Кумулянтные спектры порядка k
- 2.7. Фильтры
- 2.8. Инвариантные свойства кумулянтного спектра
- 2.9. Примеры стационарных временных рядов
- 2.10. Примеры кумулянтного спектра
- 2.11. Функциональный и стохастический подходы к анализу временных рядов
- 2.12. Тренды
- 2.13. Упражнения
- 3. АНАЛИТИЧЕСКИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ И КОМПЛЕКСНЫЕ МАТРИЦЫ
- 3.2. Ряд Фурье
- 3.3. Множители, улучшающие сходимость
- 3.4. Конечные преобразования Фурье и их свойства
- 3.5. Быстрое преобразование Фурье
- 3.6. Применения дискретного преобразования Фурье
- 3.7. Комплексные матрицы и их экстремальные значения
- 3.8. Функции от преобразования Фурье
- 3.9. Спектральные представления при функциональном подходе к анализу временных рядов
- 3.10. Упражнения
- 4. СТОХАСТИЧЕСКИЕ СВОЙСТВА КОНЕЧНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 4.2. Комплексное нормальное распределение
- 4.3. Стохастические свойства конечного преобразования Фурье
- 4.4. Асимптотическое распределение конечного преобразования Фурье
- 4.5. Оценки, имеющие место с вероятностью 1
- 4.6. Представление Крамера
- 4.7. Анализ главных компонент и его связь с представлением Крамера
- 4.8. Упражнения
- 5. ОЦЕНКА СПЕКТРА МОЩНОСТИ
- 5.2. Периодограмма
- 5.3. Дальнейшее изучение периодограммы
- 5.4. Сглаженная периодограмма
- 5.5. Общий класс спектральных оценок
- 5.6. Состоятельные оценки
- 5.7. Доверительные интервалы
- 5.8. Смещения и предварительная фильтрация
- 5.9. Другие оценки спектра мощности
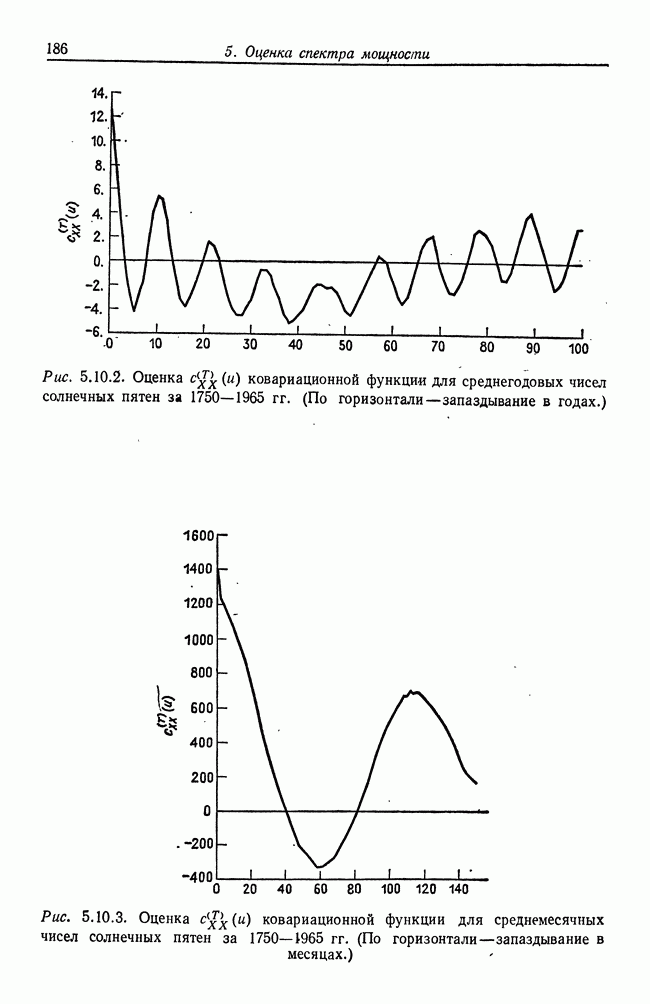
- 5.10. Оценки спектральной меры и ковариационной функции
- 5.11. Отступление от принятых предположений
- 5.12. Использование анализа спектров мощности
- 5.13. Упражнения
- 6. АНАЛИЗ ИНВАРИАНТНЫХ ВО ВРЕМЕНИ ЛИНЕЙНЫХ СООТНОШЕНИЙ МЕЖДУ СТОХАСТИЧЕСКИМИ И НЕКОТОРЫМИ ДЕТЕРМИНИРОВАННЫМИ РЯДАМИ
- 6.2. Метод наименьших квадратов и регрессионная теория
- 6.3. Эвристическое построение оценок
- 6.4. Вид асимптотического распределения
- 6.5. Математические ожидания оценок передаточной функции и спектра ошибок
- 6.6. Асимптотические ковариации предложенных оценок
- 6.7. Асимптотическая нормальность оценок
- 6.8. Оценивание импульсной характеристики
- 6.9. Доверительные области
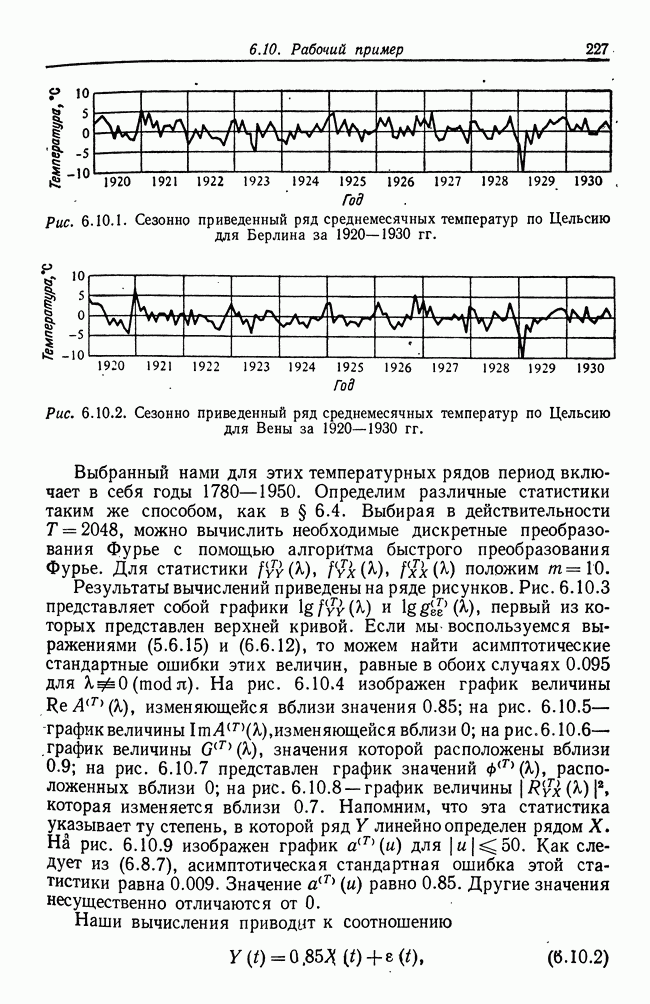
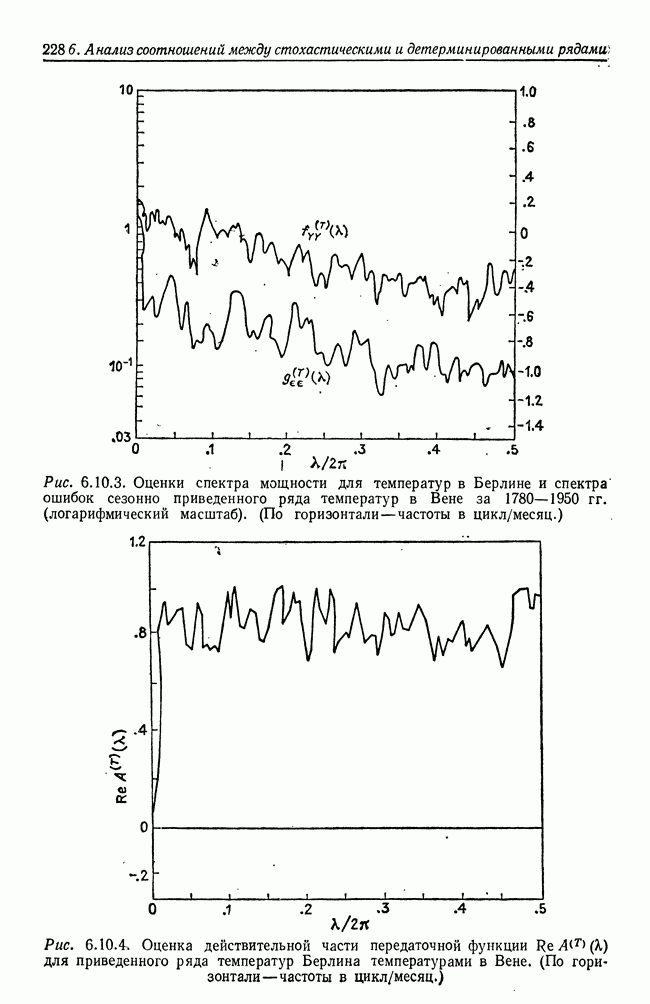
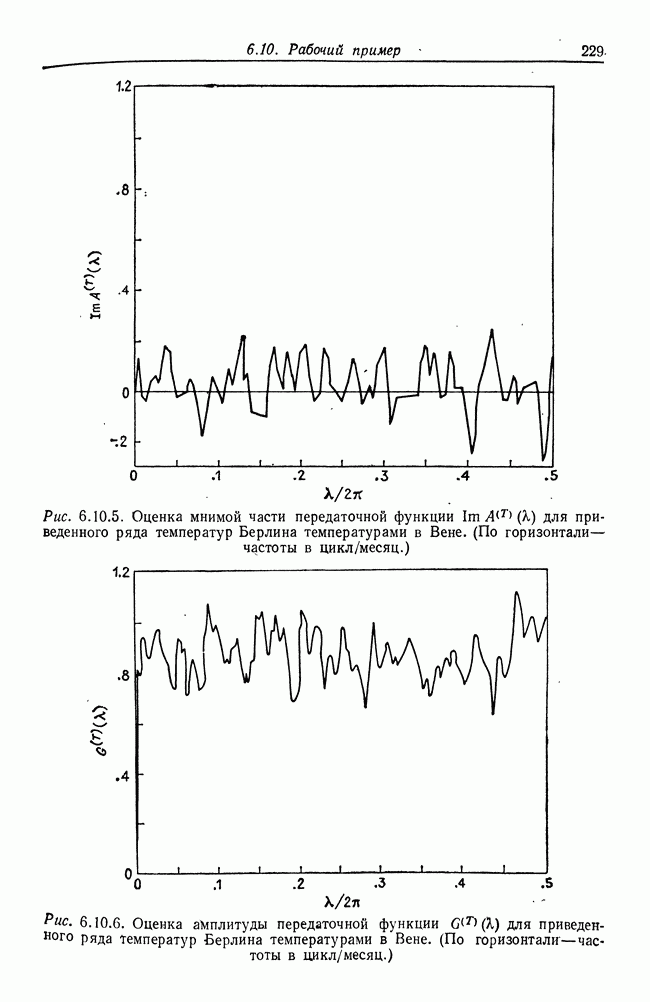
- 6.10. Рабочий пример
- 6.11. Дальнейшие исследования
- 6.12. Сравнение трех оценок импульсной характеристики
- 6.13. Использование предложенных методов
- 6.14. Упражнения
- 7. ОЦЕНКИ СПЕКТРА ВТОРОГО ПОРЯДКА МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
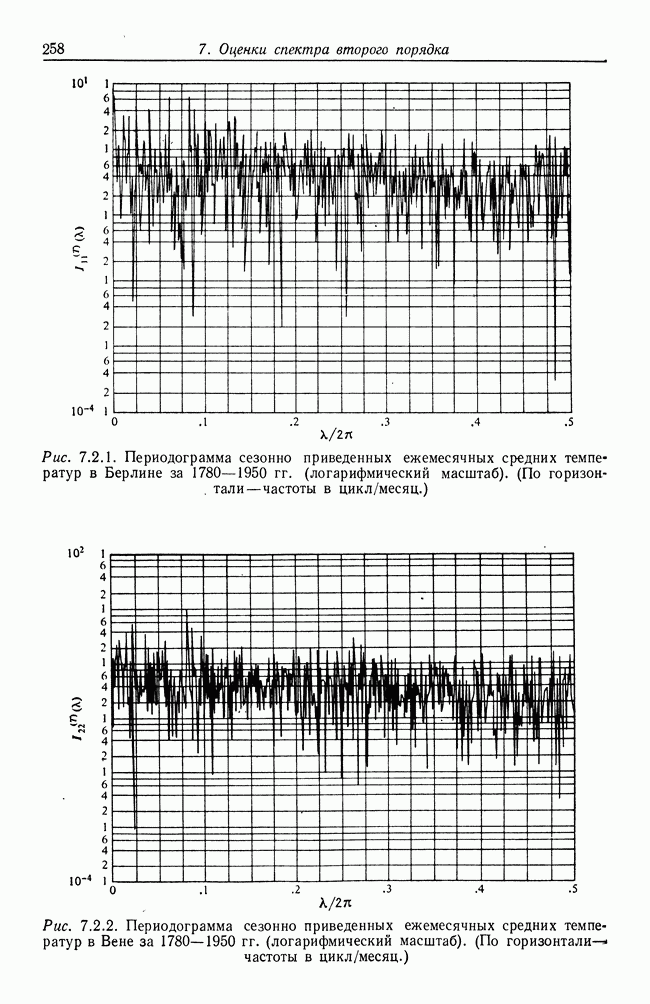
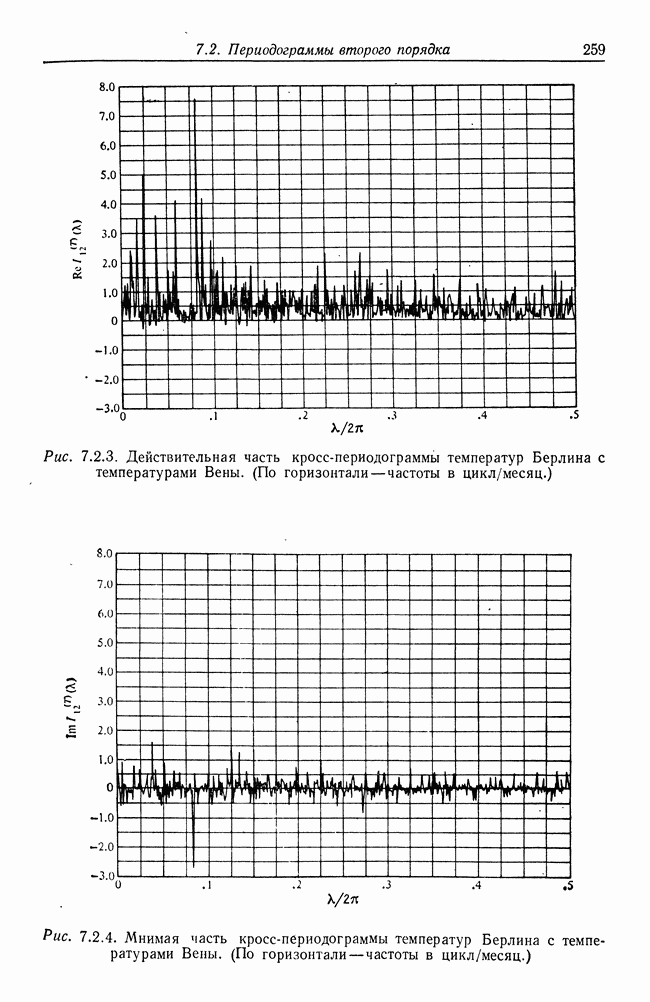
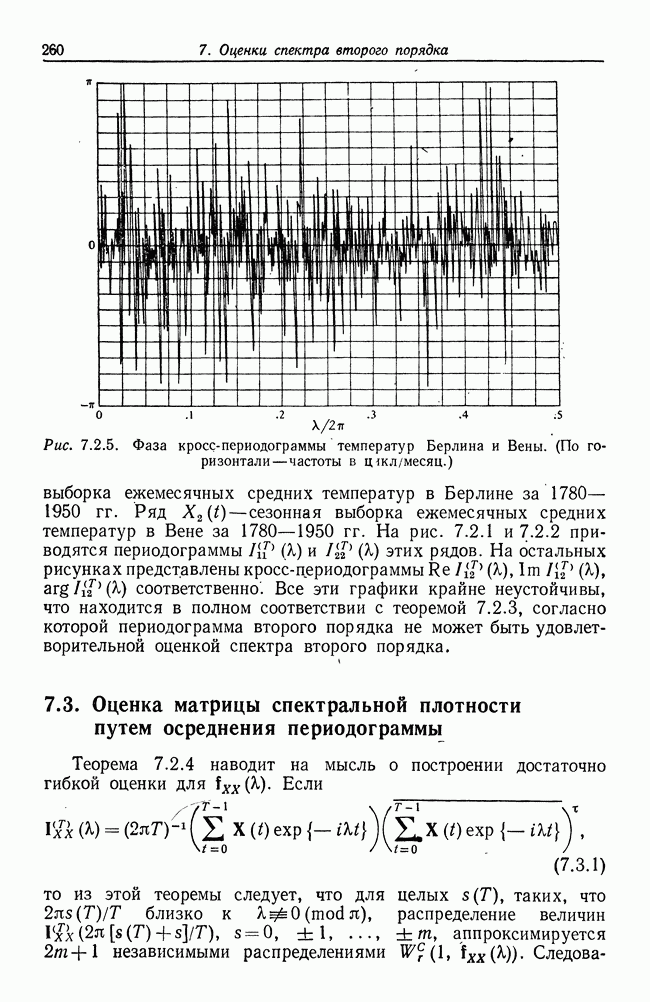
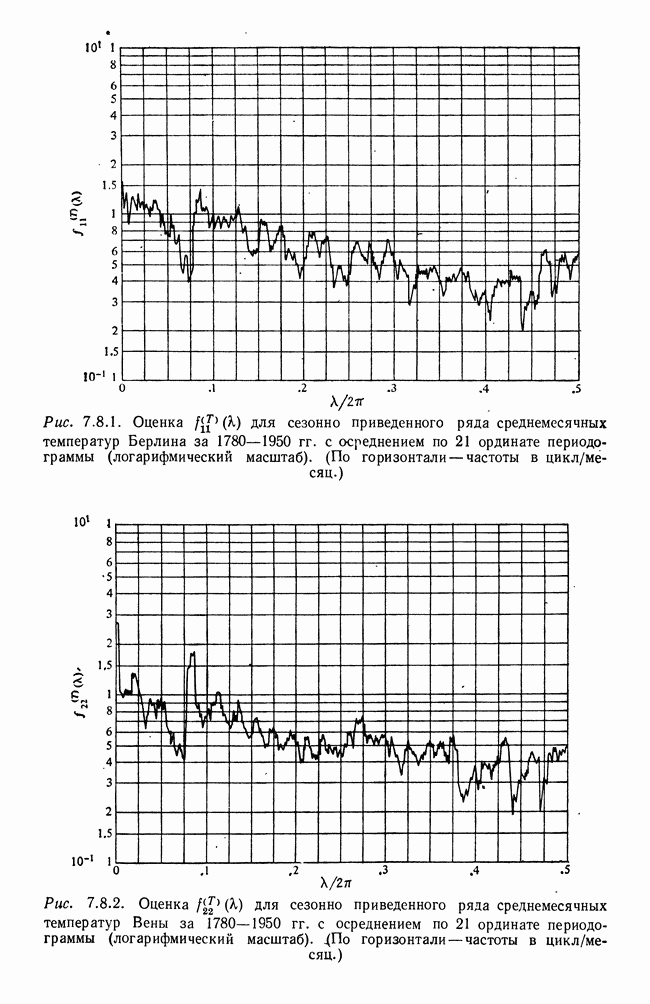
- 7.2. Периодограммы второго порядка
- 7.3. Оценка матрицы спектральной плотности путем осреднения периодограммы
- 7.4. Состоятельные оценки матрицы спектральной плотности
- 7.5. Построение доверительных границ
- 7.6. Оценки родственных величин
- 7.7. Дальнейшее развитие оценок спектра второго порядка
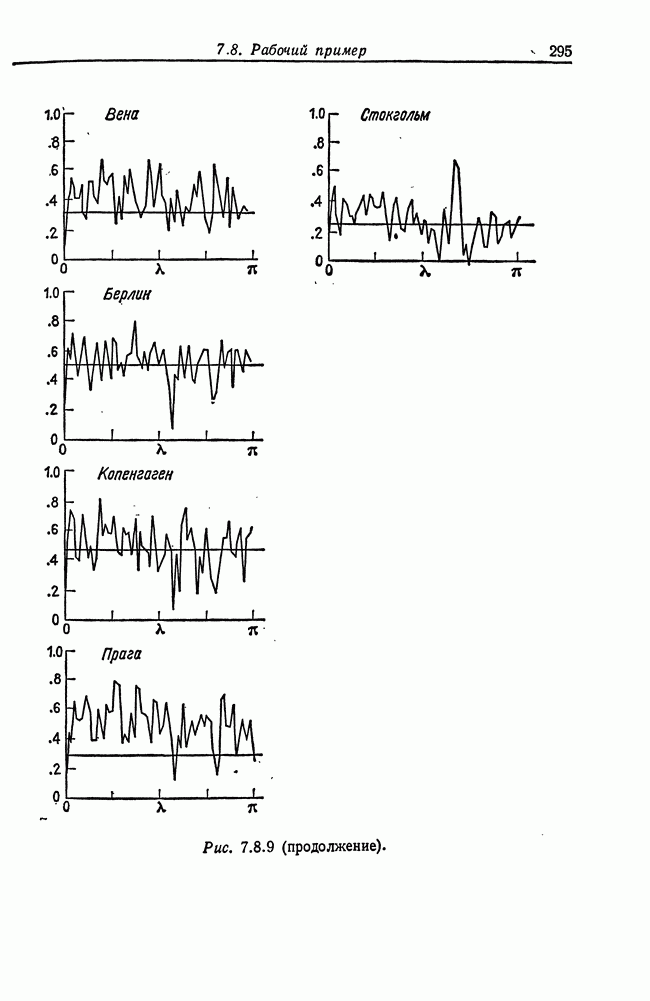
- 7.8. Рабочий пример
- 7.9. Изучение рядов, встречающихся в планировании эксперимента
- 7.10. Упражнения
- 8. АНАЛИЗ ЛИНЕЙНЫХ ИНВАРИАНТНЫХ ВО ВРЕМЕНИ СООТНОШЕНИЙ МЕЖДУ ДВУМЯ МНОГОМЕРНЫМИ СТОХАСТИЧЕСКИМИ РЯДАМИ
- 8.2. Результаты для многомерных случайных величин
- 8.3. Определение оптимального линейного фильтра
- 8.4. Эвристическая интерпретация параметров и построение оценок
- 8.5. Предельное распределение оценок
- 8.6. Класс состоятельных оценок
- 8.7. Асимптотические моменты второго порядка рассмотренных оценок
- 8.8. Асимптотическое распределение оценок
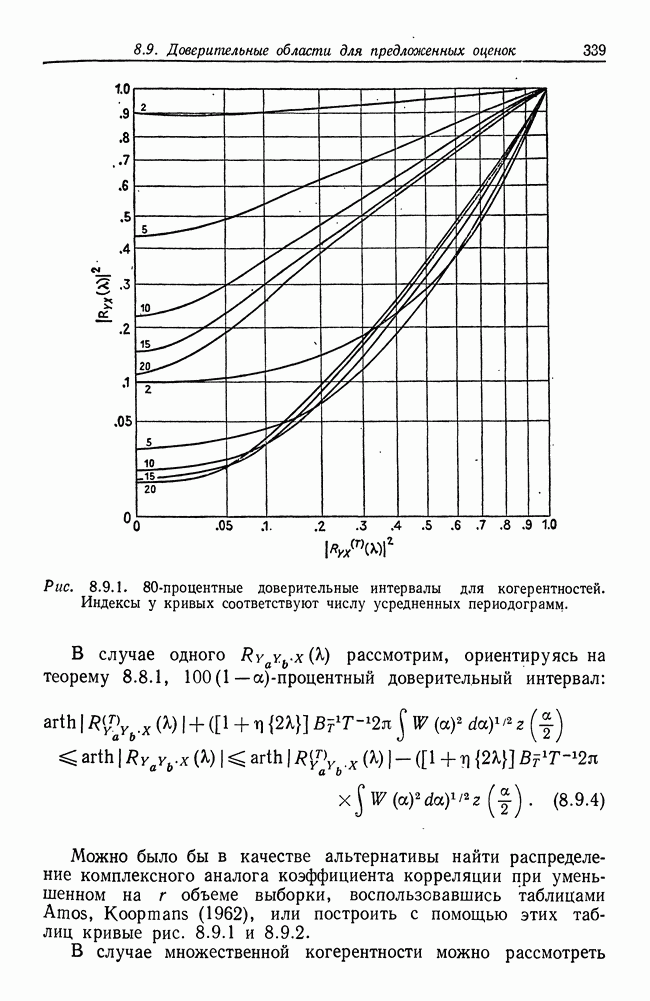
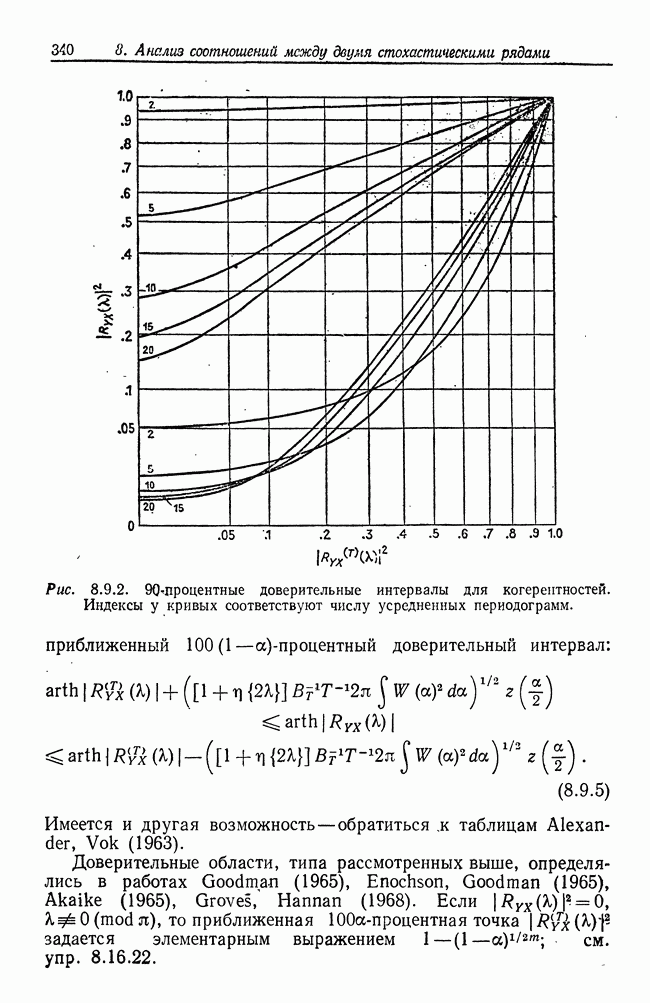
- 8.9. Доверительные области для предложенных оценок
- 8.10. Оценки коэффициентов фильтра
- 8.11. Оценки отклонений, имеющие место с вероятностью 1
- 8.12. Дальнейшее обсуждение
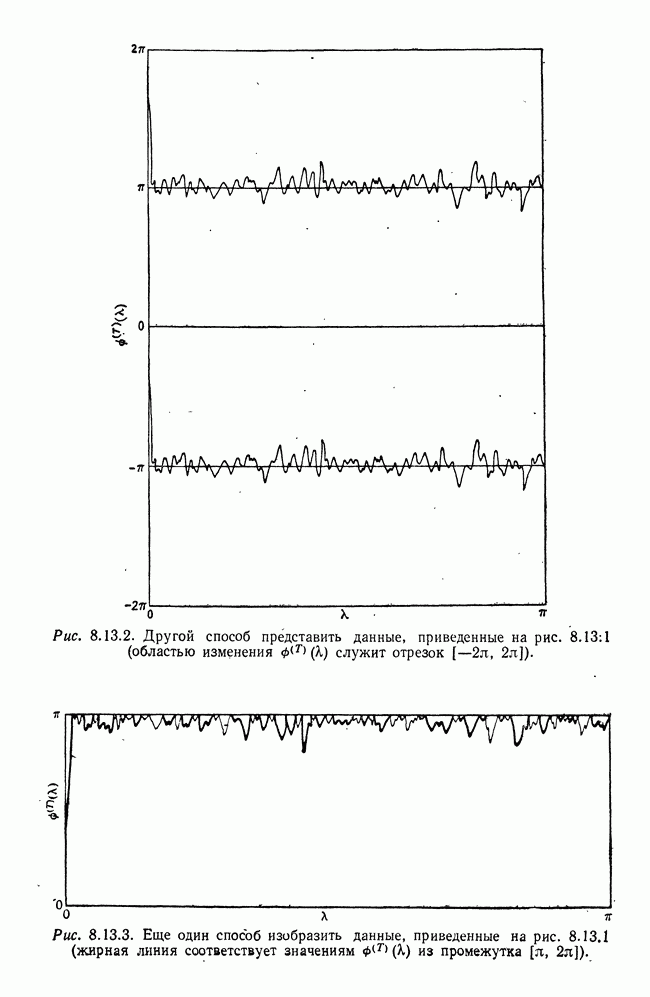
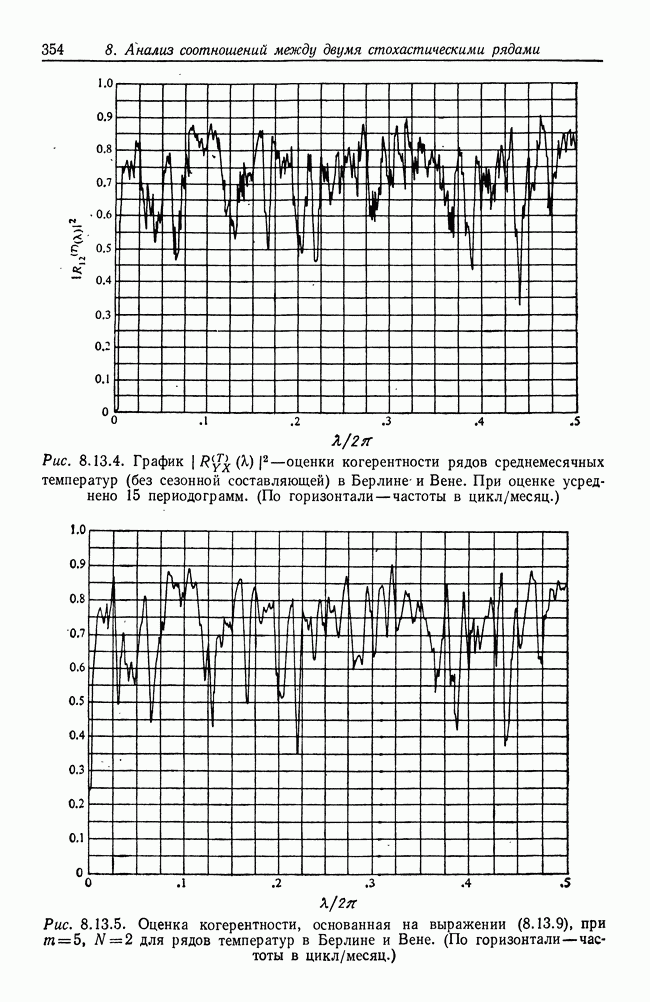
- 8.13. Другие типы оценок
- 8.14. Рабочий пример
- 8.15. Применения материала настоящей главы
- 8.16. Упражнения
- 9. ГЛАВНЫЕ КОМПОНЕНТЫ В ЧАСТОТНОЙ ОБЛАСТИ
- 9.2. Анализ главных компонент векторных величин
- 9.3. Ряды главных компонент
- 9.4. Построение оценок и их асимптотические свойства
- 9.5. Дальнейшие свойства главных компонент
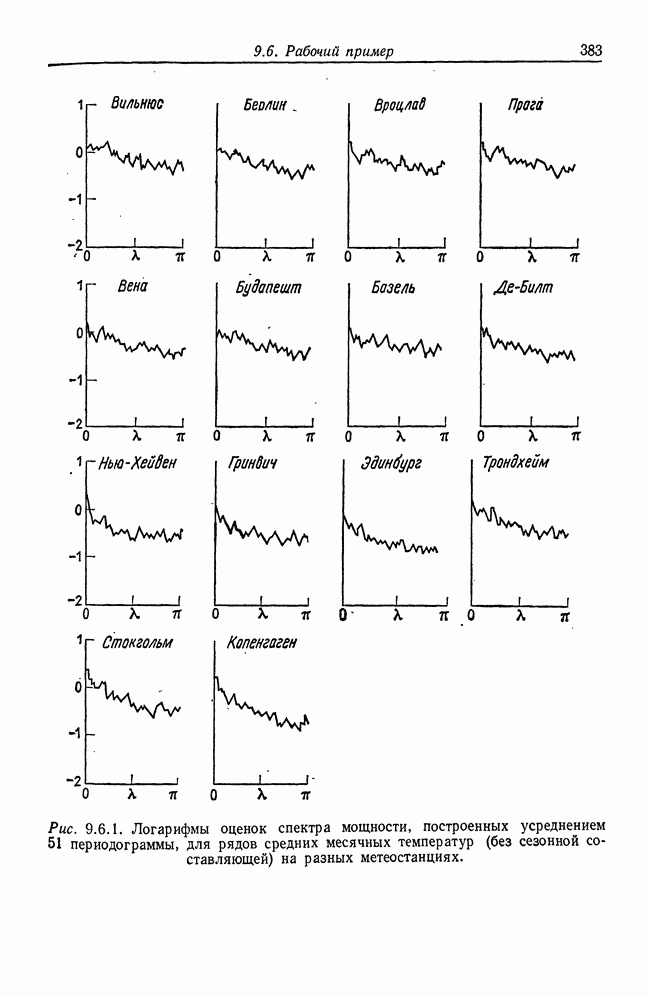
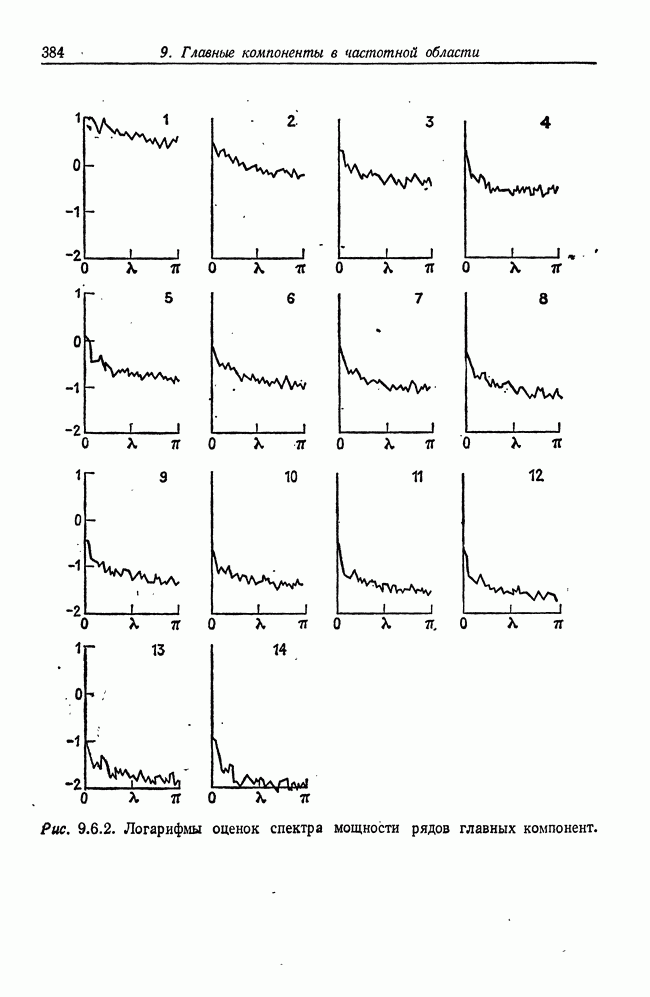
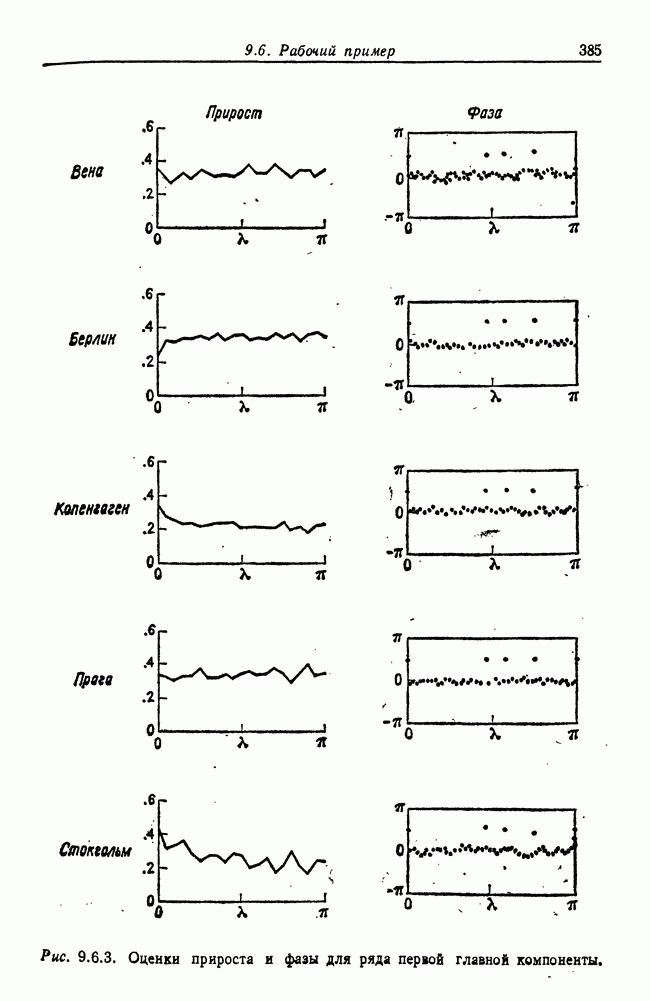
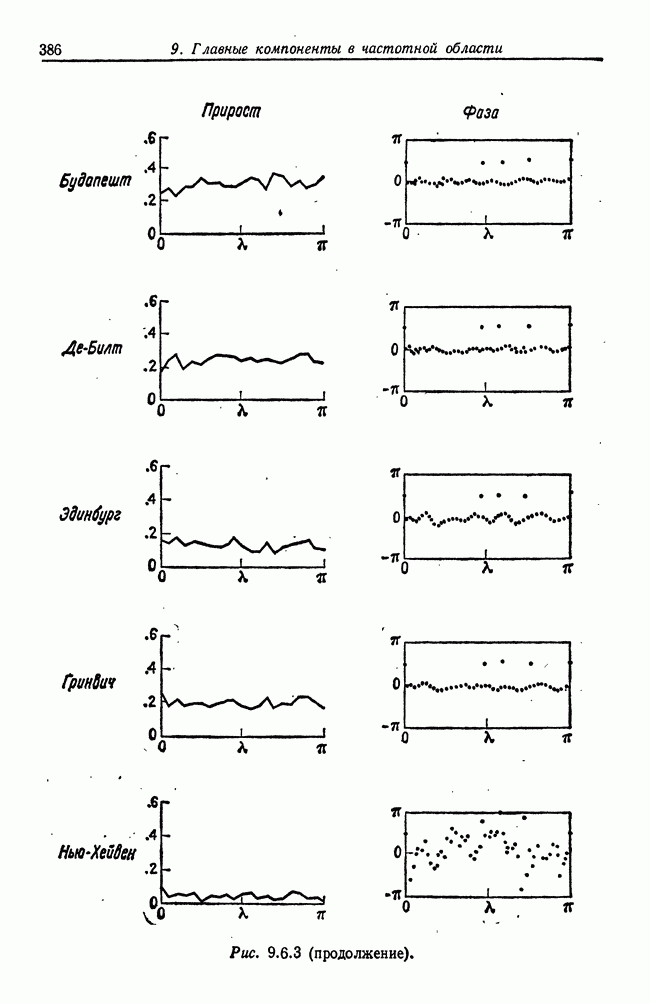
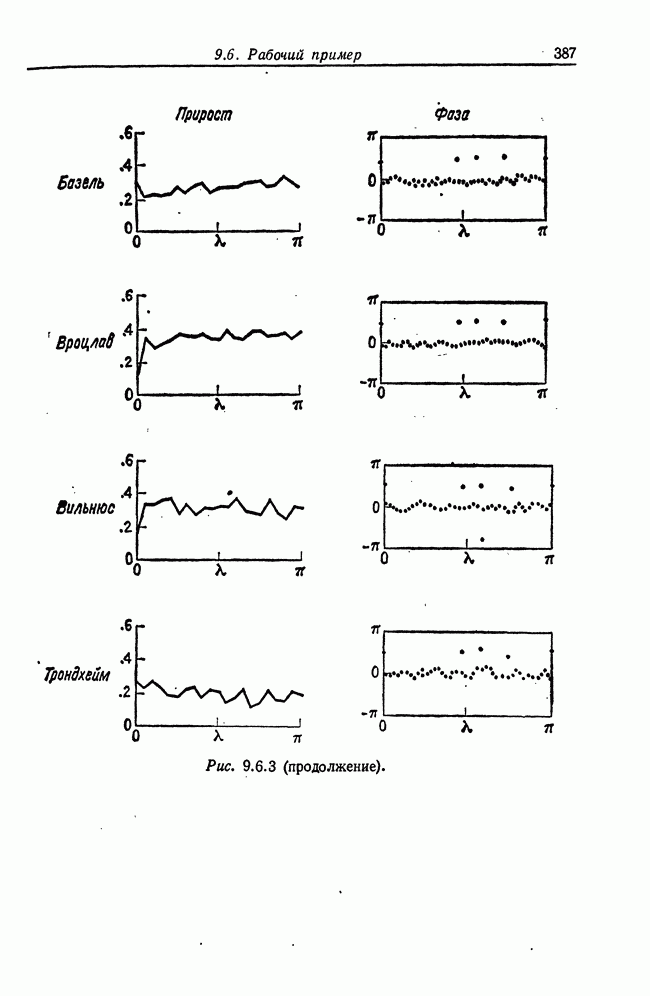
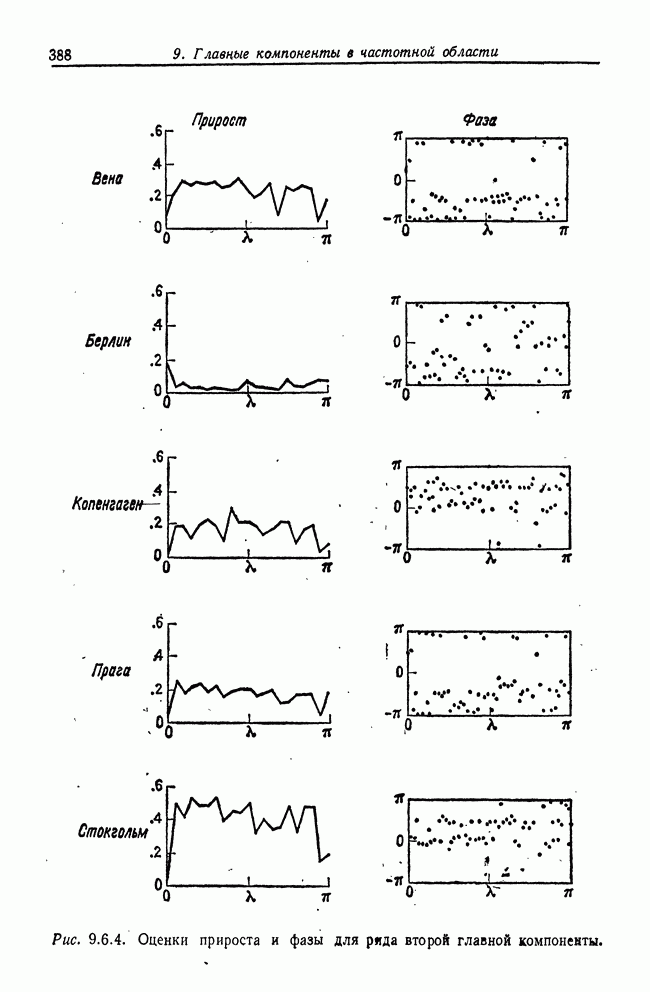
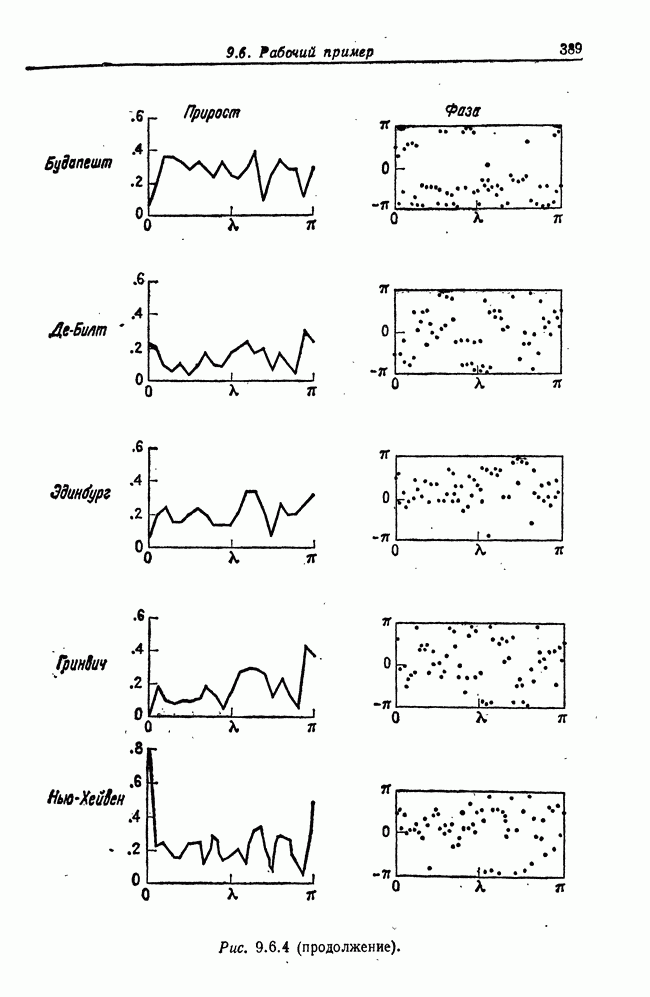
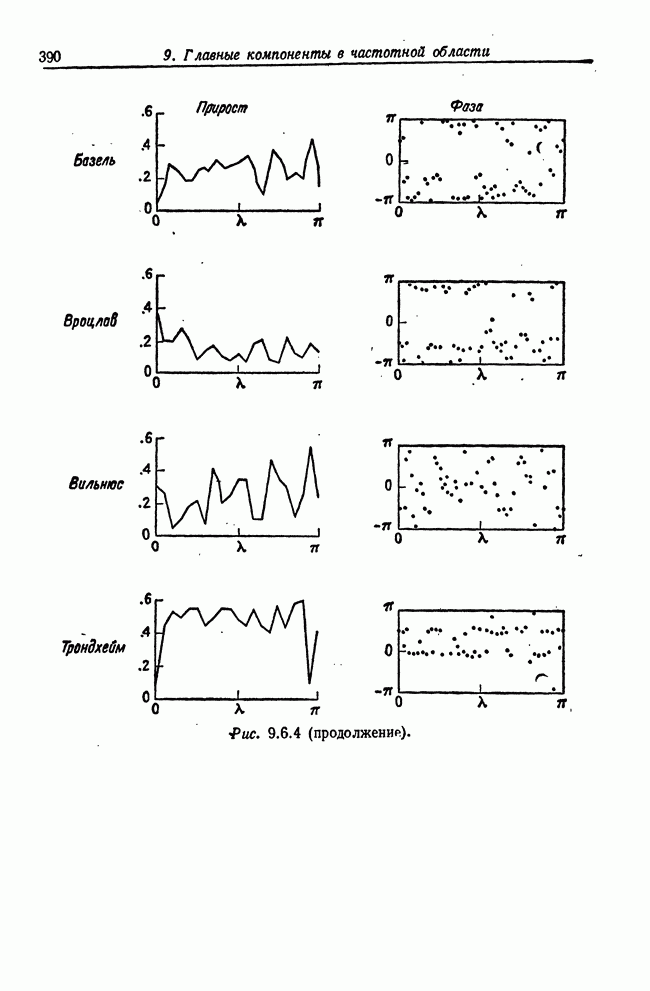
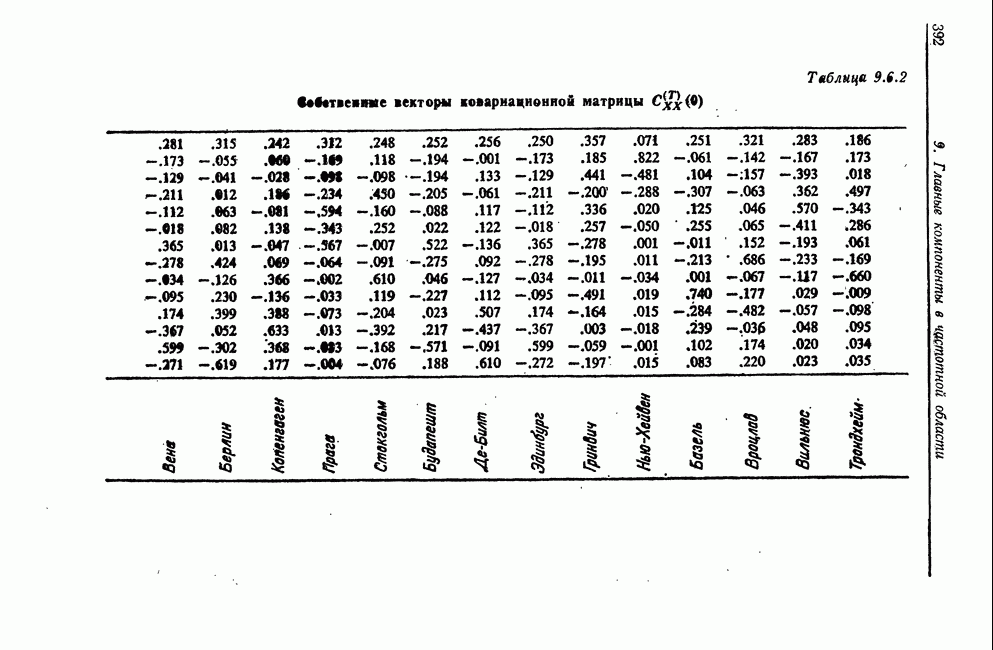
- 9.6. Рабочий пример
- 9.7. Упражнения
- 10. КАНОНИЧЕСКИЙ АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
- 10.2. Канонический анализ векторных случайных величин
- 10.3 Ряды канонических переменных
- 10.4. Построение оценок и их асимптотические свойства
- 10.5. Дальнейшие свойства канонических переменных
- 10.6. Упражнения
- ДОКАЗАТЕЛЬСТВА ТЕОРЕМ
- К главе 3
- К главе 4
- К главе 5
- К главе 6
- К главе 7
- К главе 8
- К главе 9
- К главе 10
- Список литературы