| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
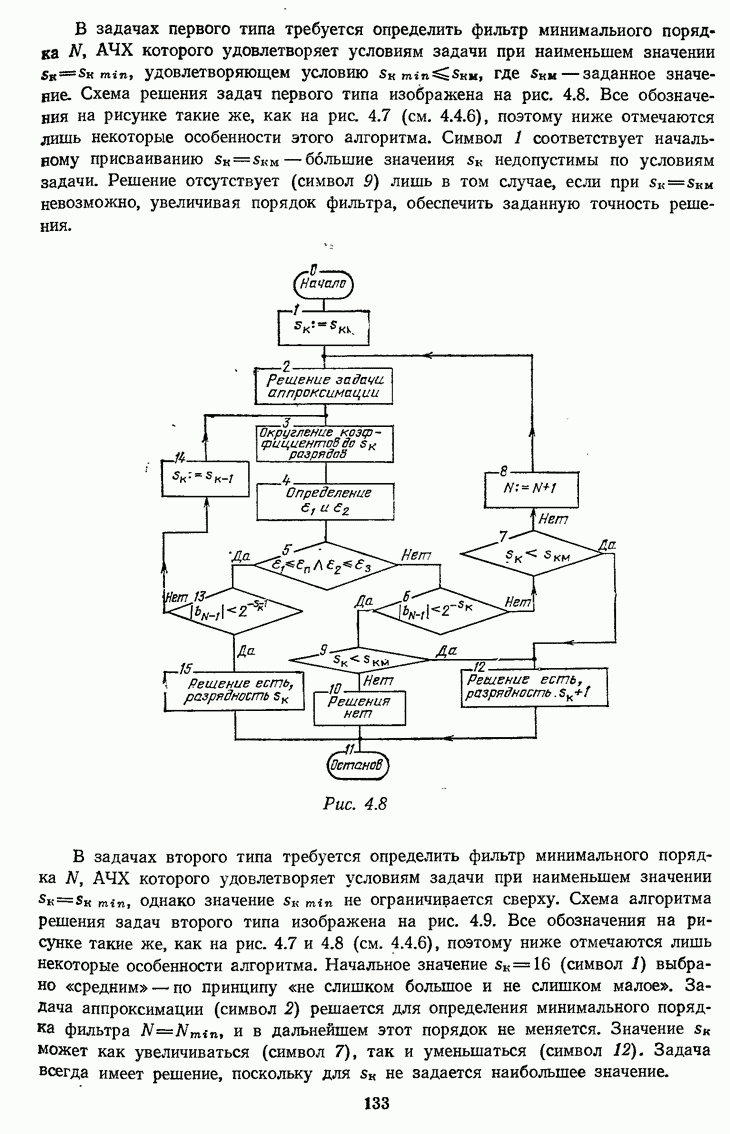
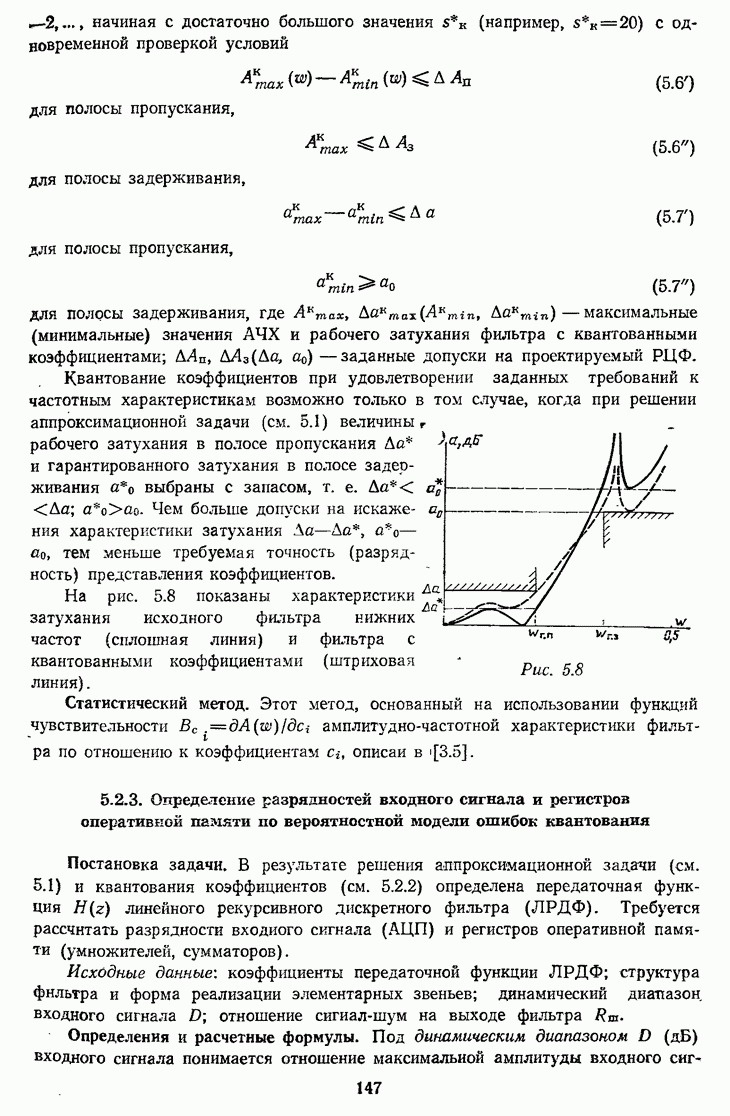
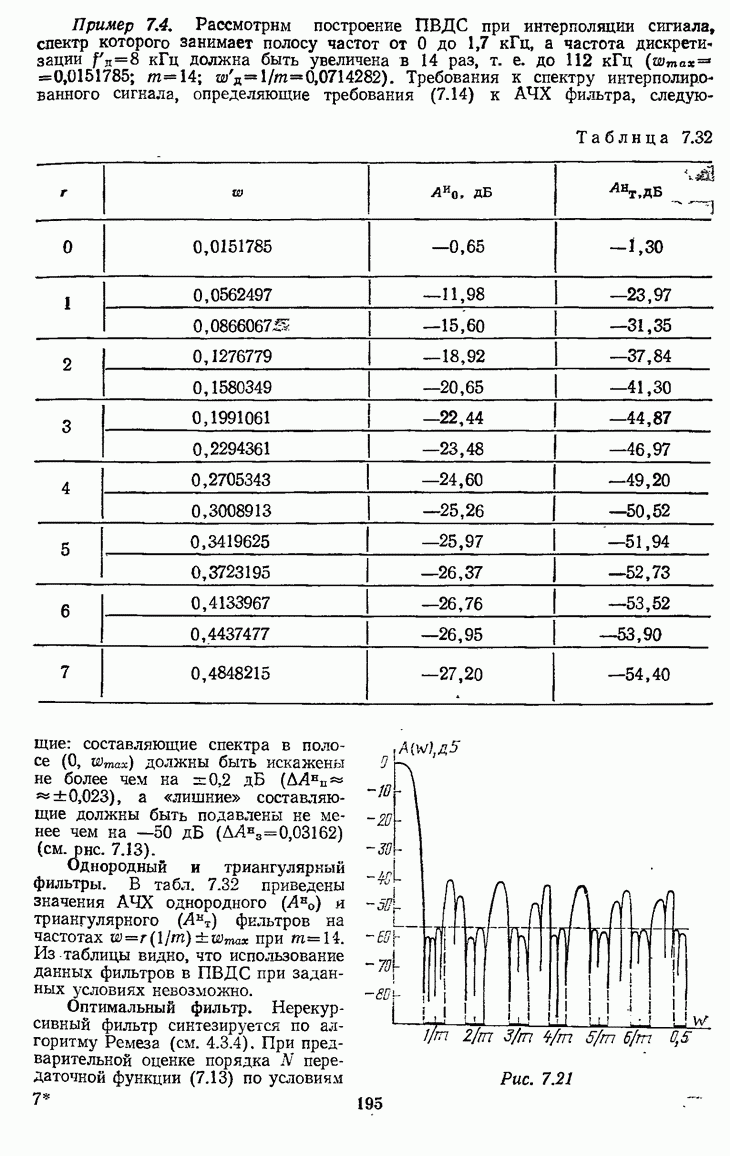
7.4.4. Однородный и триангулярный фильтры при децимации
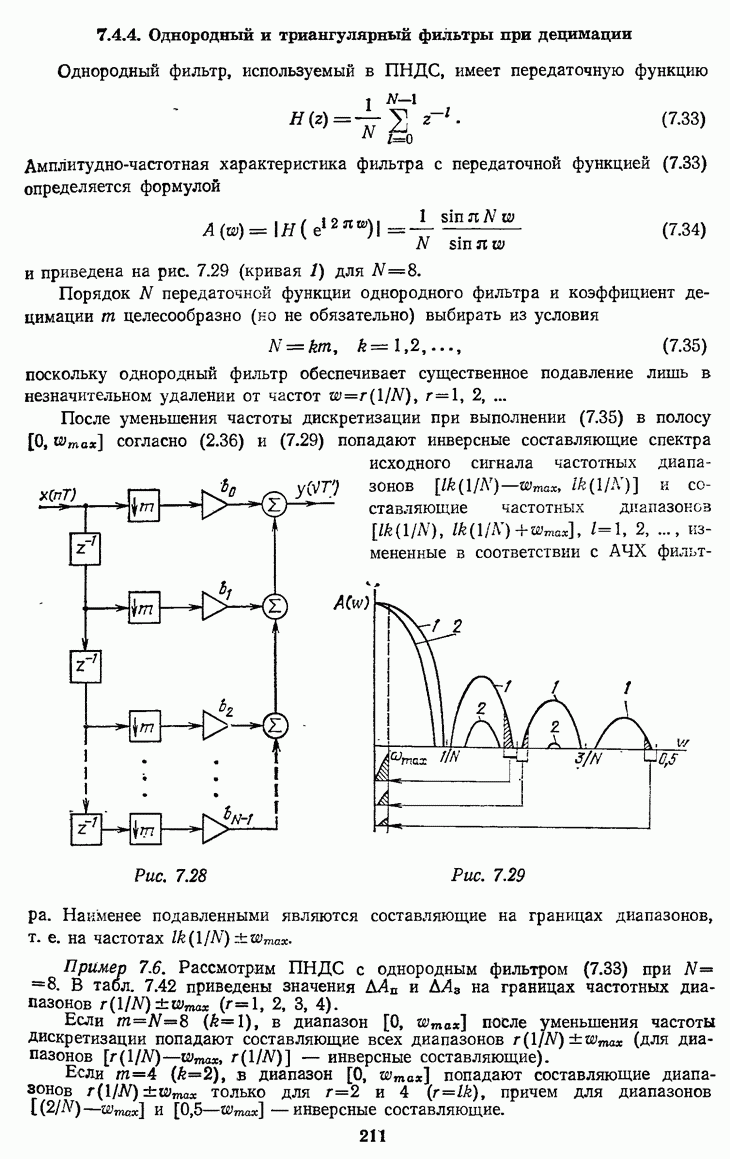
Однородный фильтр, используемый в ПНДС, имеет передаточную функцию

Амплитудно-частотная характеристика фильтра с передаточной функцией (7.33) определяется формулой

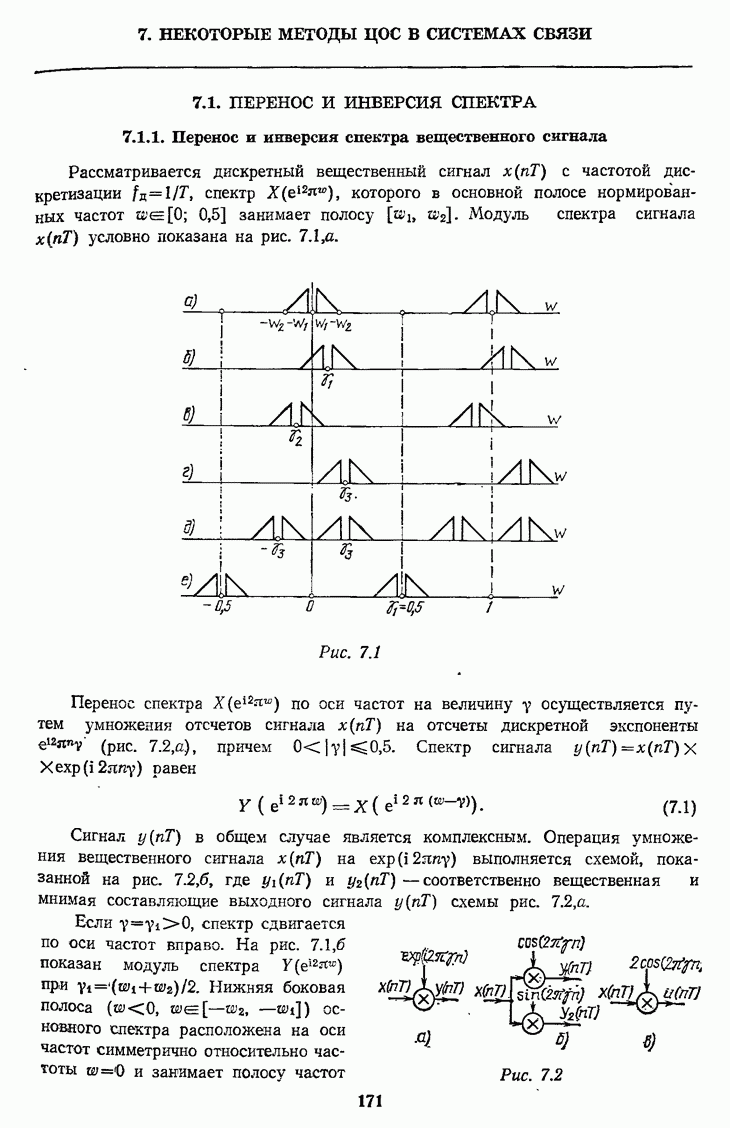
и приведена на рис. 7.29 (кривая 1) для 
Порядок N передаточной функции однородного фильтра и коэффициент децимации  целесообразно (но не обязательно) выбирать из условия
целесообразно (но не обязательно) выбирать из условия

поскольку однородный фильтр обеспечивает существенное подавление лишь в незначительном удалении от частот 
После уменьшения частоты дискретизации при выполнении (7.35) в полосу  согласно (2.36) и (7.29) попадают инверсные составляющие спектра исходного сигнала частотных диапазонов
согласно (2.36) и (7.29) попадают инверсные составляющие спектра исходного сигнала частотных диапазонов  к составляющие частотных диапазонов
к составляющие частотных диапазонов  измененные в соответствии с АЧХ фильтра.
измененные в соответствии с АЧХ фильтра.

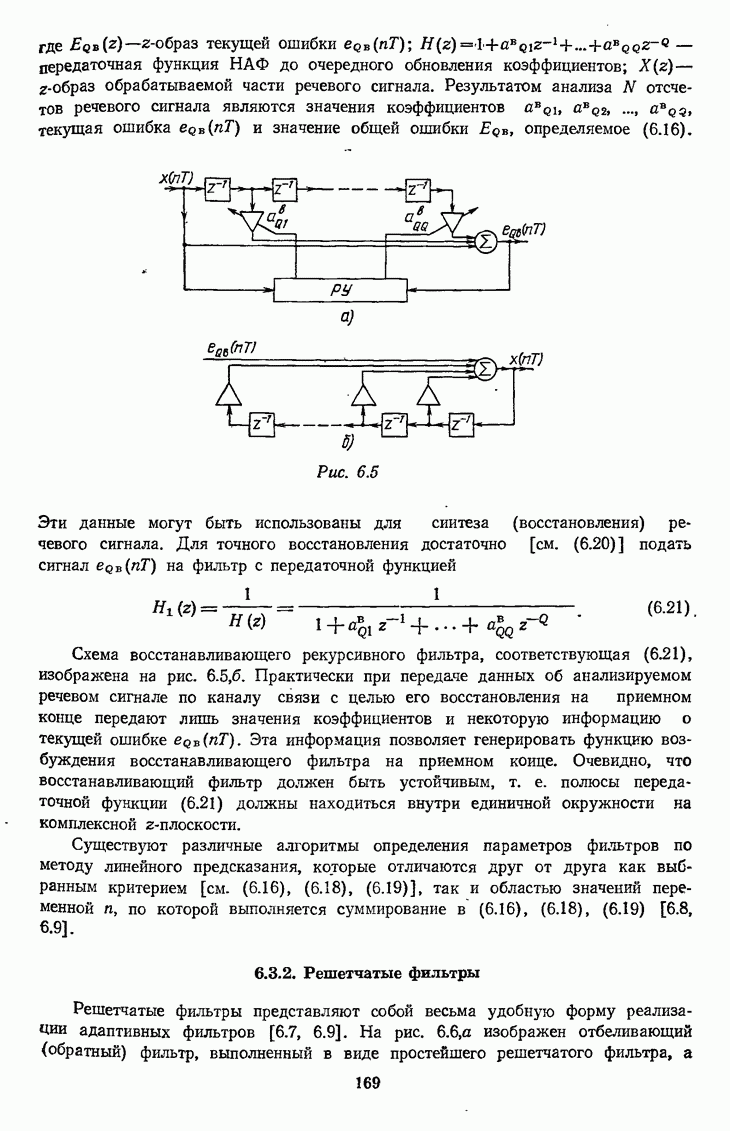
Рис. 7.28

Рис. 7.29
Наименее подавленными являются составляющие на границах диапазонов, т. е. на частотах 
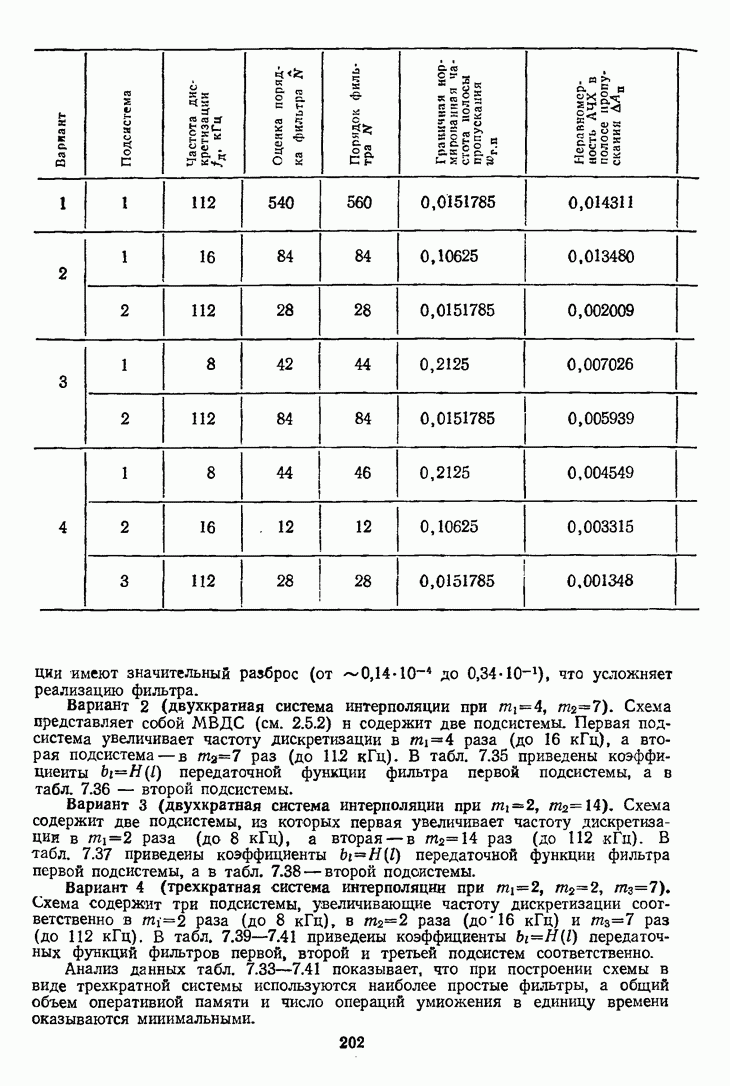
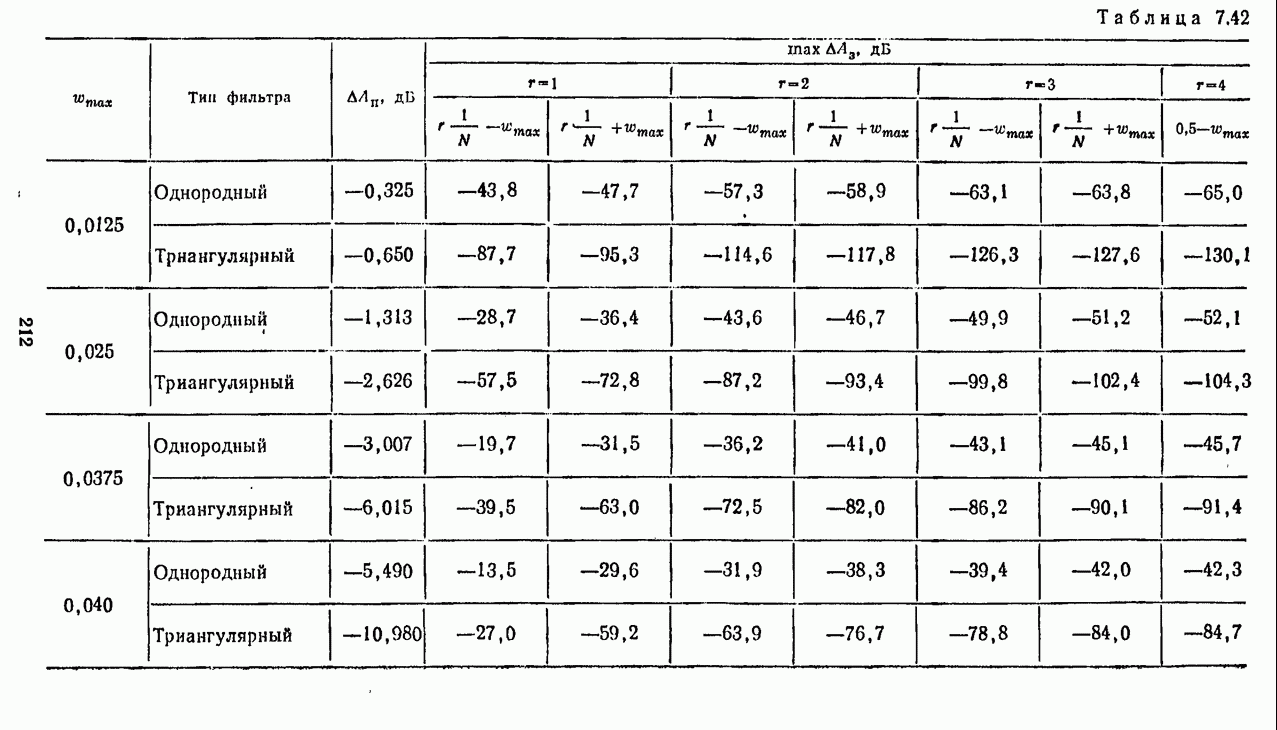
Пример 7.6. Рассмотрим ПНДС с однородным фильтром (7.33) при  . В табл. 7.42 приведены значения
. В табл. 7.42 приведены значения  на границах частотных диапазонов
на границах частотных диапазонов  .
.
Если  в диапазон
в диапазон  после уменьшения частоты дискретизации попадают составляющие всех диапазонов
после уменьшения частоты дискретизации попадают составляющие всех диапазонов  (для диапазонов
(для диапазонов  — инверсные составляющие).
— инверсные составляющие).
Если  в диапазон
в диапазон  попадают составляющие диапазонов
попадают составляющие диапазонов  только для
только для  причем для диапазонов
причем для диапазонов  — инверсные составляющие.
— инверсные составляющие.
На рис. 7.29 условно показаны мвдули составляющих спектров, попадающих в диапазон  при
при 
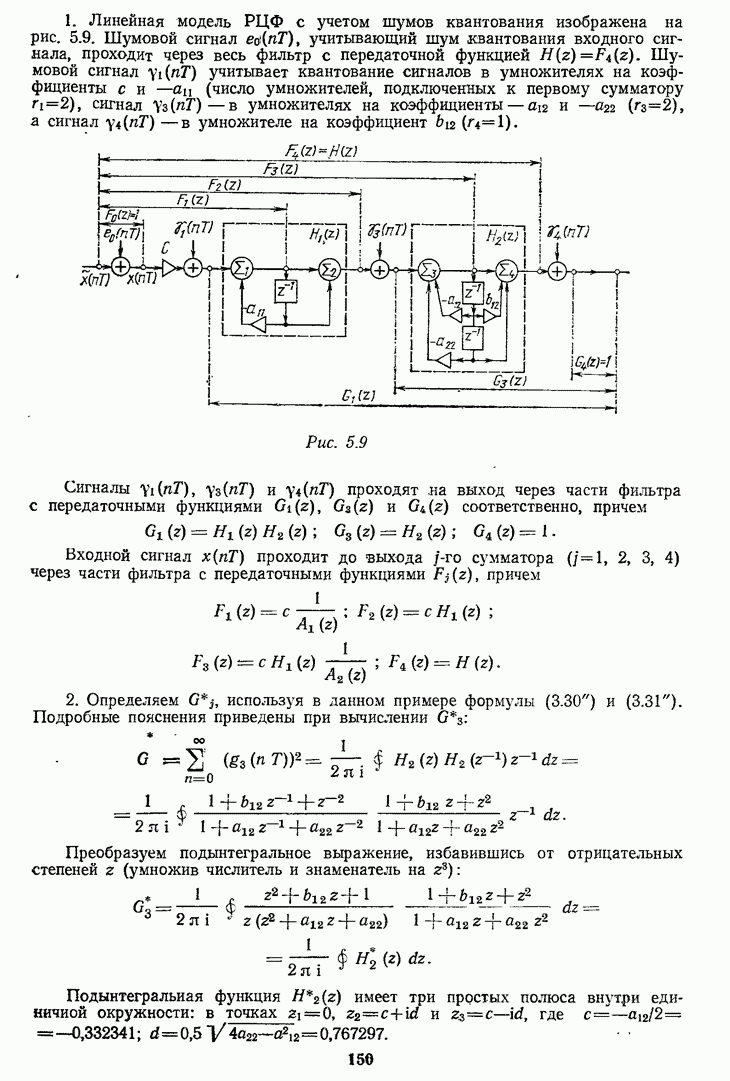
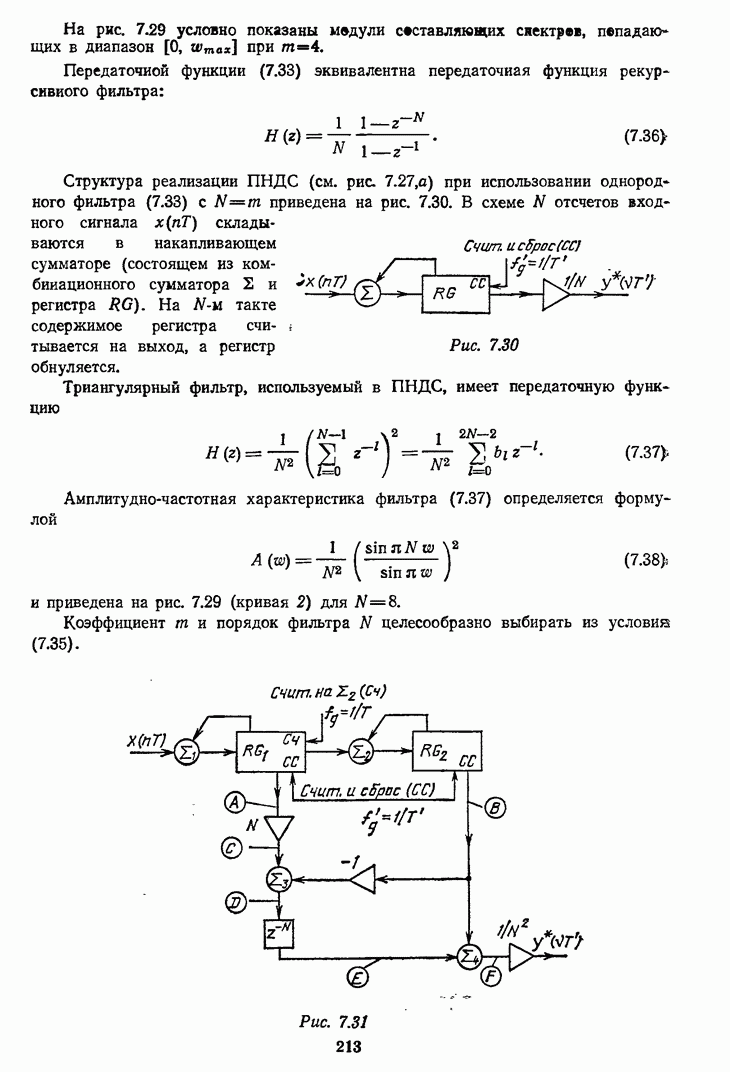
Передаточной функции (7.33) эквивалентна передаточная функция рекурсивного фильтра:

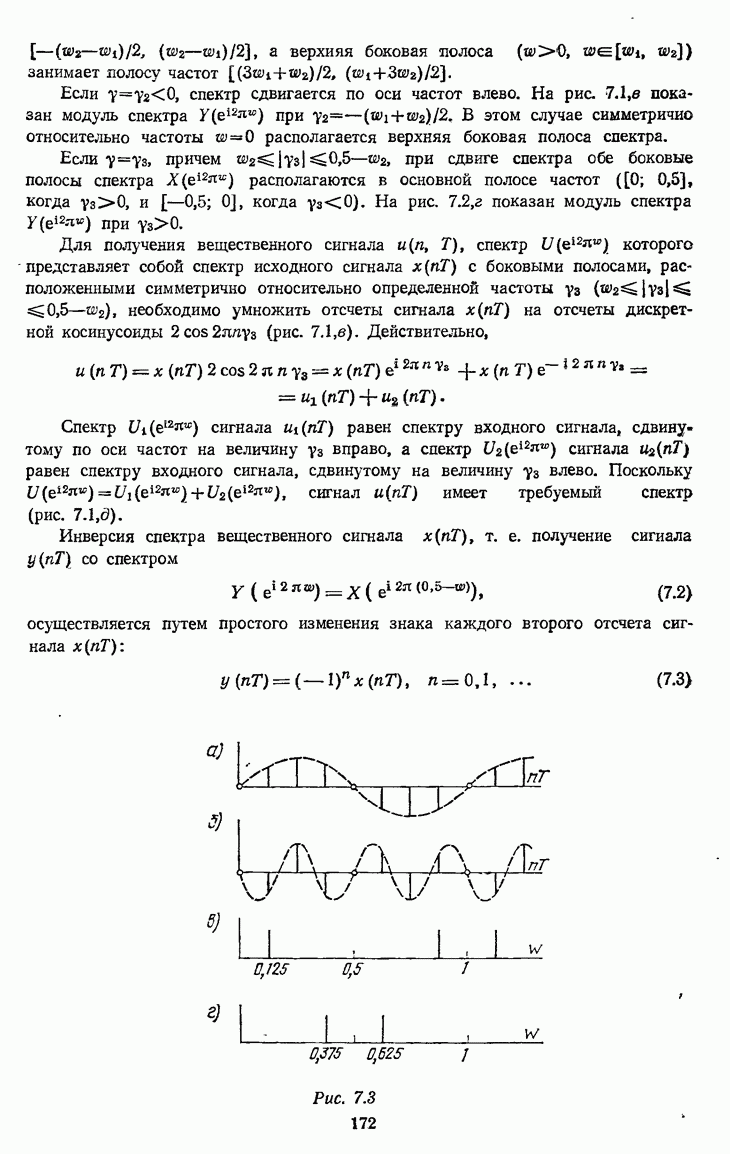
Структура реализации ПНДС (см. рис. 7.27, а) при использовании однородного фильтра (7.33) с  приведена на рис. 7.30. В схеме
приведена на рис. 7.30. В схеме  отсчетов входного сигнала
отсчетов входного сигнала  складываются в накапливающем сумматоре (состоящем из комбинационного сумматора 2 и регистра
складываются в накапливающем сумматоре (состоящем из комбинационного сумматора 2 и регистра  На
На  такте содержимое регистра считывается на выход, а регистр обнуляется.
такте содержимое регистра считывается на выход, а регистр обнуляется.

Рис. 7.30
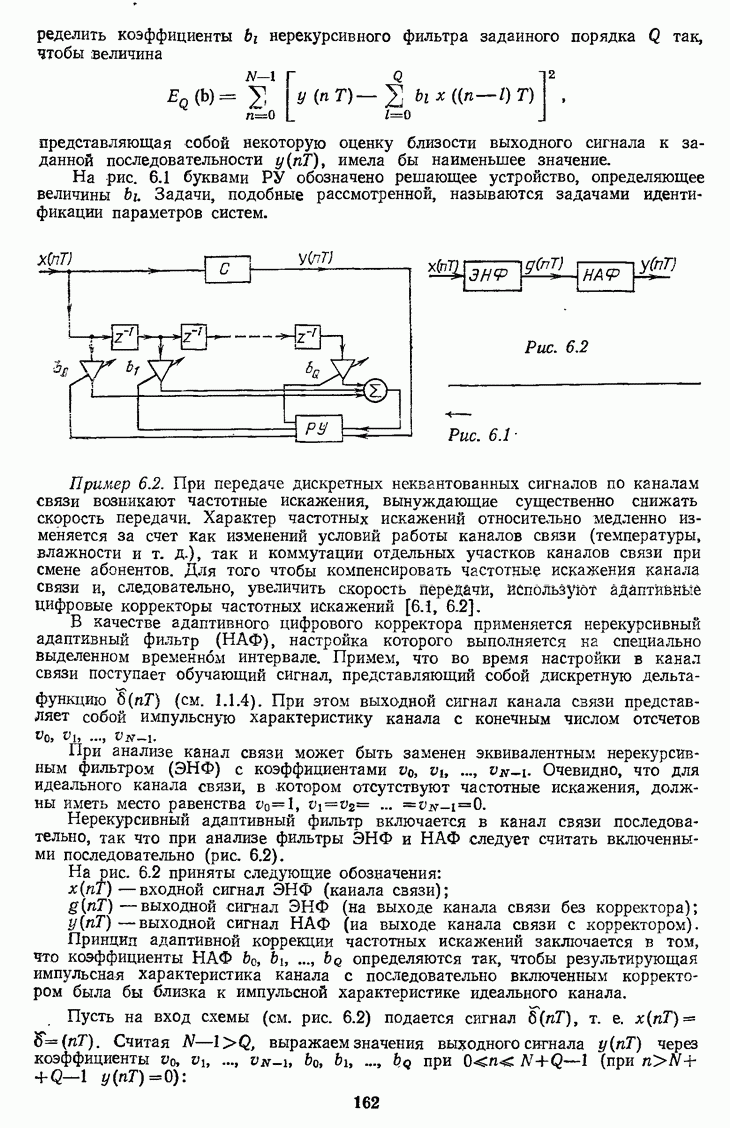
Триангулярный фильтр, используемый в ПНДС, имеет передаточную функцию

Амплитудно-частотная характеристика фильтра (7.37) определяется формулой

и приведена на рис. 7.29 (кривая 2) для 
Коэффициент  и порядок фильтра
и порядок фильтра  целесообразно выбирать из условие (7.35).
целесообразно выбирать из условие (7.35).

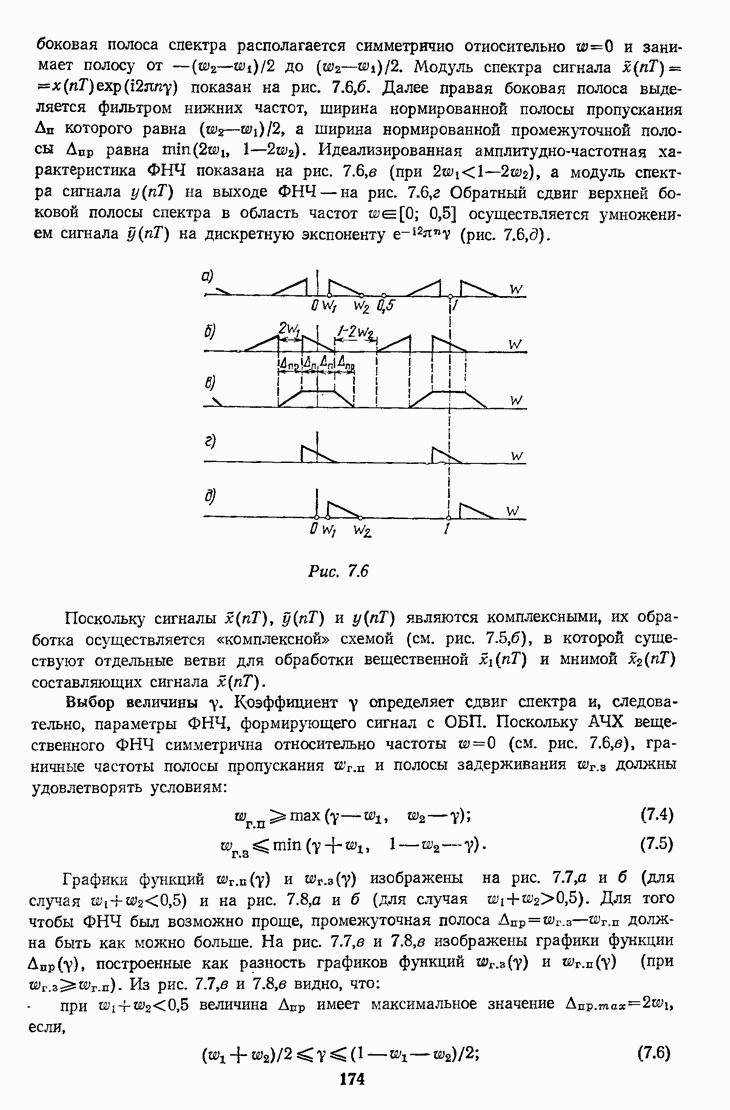
Рис. 7.31
(см. скан)
В табл. 7.42 приведены значения  на границах частотных диапазонов
на границах частотных диапазонов 
Передаточной функции (7.37) эквивалентна передаточная функция рекурсивного фильтра

Структура реализации МНДС (см. рис. 7.27, а) при использовании триангулярного фильтра с  приведена на рис. 7.31 [7.1].
приведена на рис. 7.31 [7.1].
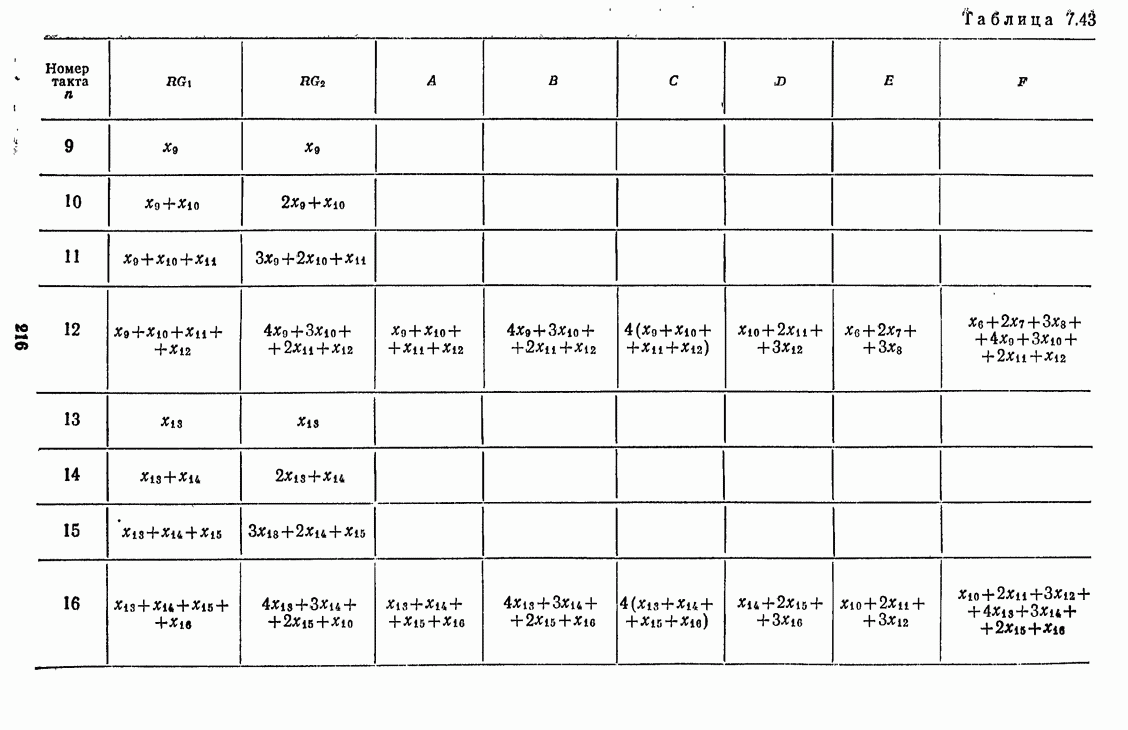
Пример 7.7. Рассмотрим работу схемы (см. рис. 7.31) при  Передаточная функция триангулярного фильтра (7.37) содержит семь коэффициентов:
Передаточная функция триангулярного фильтра (7.37) содержит семь коэффициентов:  Перед тактами
Перед тактами  содержимое всех регистров схемы обнулено (считывание содержимого регистров
содержимое всех регистров схемы обнулено (считывание содержимого регистров  сброс осуществляются на тактах
сброс осуществляются на тактах  . В табл. 7.43 приведены содержимое регистров
. В табл. 7.43 приведены содержимое регистров  и значения сигналов в точках
и значения сигналов в точках  схемы при входном сигнале
схемы при входном сигнале 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- 1. СВОЙСТВА И ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- 1.1. ТИПЫ СИГНАЛОВ. СВЯЗЬ МЕЖДУ СИГНАЛАМИ РАЗЛИЧНЫХ ТИПОВ
- 1.1.2. Связь между аналоговыми и дискретными сигналами
- 1.1.3. Связь между дискретными и цифровыми сигналами
- 1.1.4. Дискретная дельта-функция
- 1.2. Z-ПРЕОБРАЗОВАНИЕ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.3. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ. АЛГОРИТМЫ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.3.2. Свойства дискретного преобразования Фурье
- 1.3.3. Многомерное дискретное преобразование Фурье
- 1.3.4. Алгоритмы БПФ с основанием 2
- 1.3.5. Алгоритмы БПФ для произвольного составного N
- 1.4. ДИСКРЕТНАЯ СВЕРТКА И ЕЕ ВЫЧИСЛЕНИЕ
- 1.4.2. Использование ДПФ для вычисления круговой свертки
- 1.4.3. Линейная свертка
- 1.4.4. Секционированные свертки
- 1.4.5. Методы быстрого вычисления круговой свертки
- 1.4.6. Использование теоретико-числовых преобразований
- 1.4.7. Использование модульной арифметики в кольце полиномов
- 1.5. НЕКОТОРЫЕ ПЕРСПЕКТИВНЫЕ АЛГОРИТМЫ ВЫЧИСЛЕНИЯ ДПФ
- 1.5.2. Алгоритм Винограда с использованием ТЧП
- 1.5.3. Использование эффективных методов поворота вектора (КОРДИК)
- 1.5.4. Специальные виды ДПФ
- 1.6. СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ИХ ХАРАКТЕРИСТИКИ
- 2. ДИСКРЕТНЫЕ СИСТЕМЫ
- 2.1. ДИСКРЕТНЫЕ И ЦИФРОВЫЕ ФИЛЬТРЫ. УСТРОЙСТВА ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ
- 2.1.2. Линейные дискретные фильтры
- 2.1.3. Переход от разностного уравнения к структурной схеме фильтра
- 2.1.4. Цифровые фильтры
- 2.1.5. Устройства цифровой обработки сигналов
- 2.2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ. РАЗЛИЧНЫЕ ФОРМЫ РЕАЛИЗАЦИИ ФИЛЬТРОВ. ПЕРВЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 2.2.2. Соединение фильтров
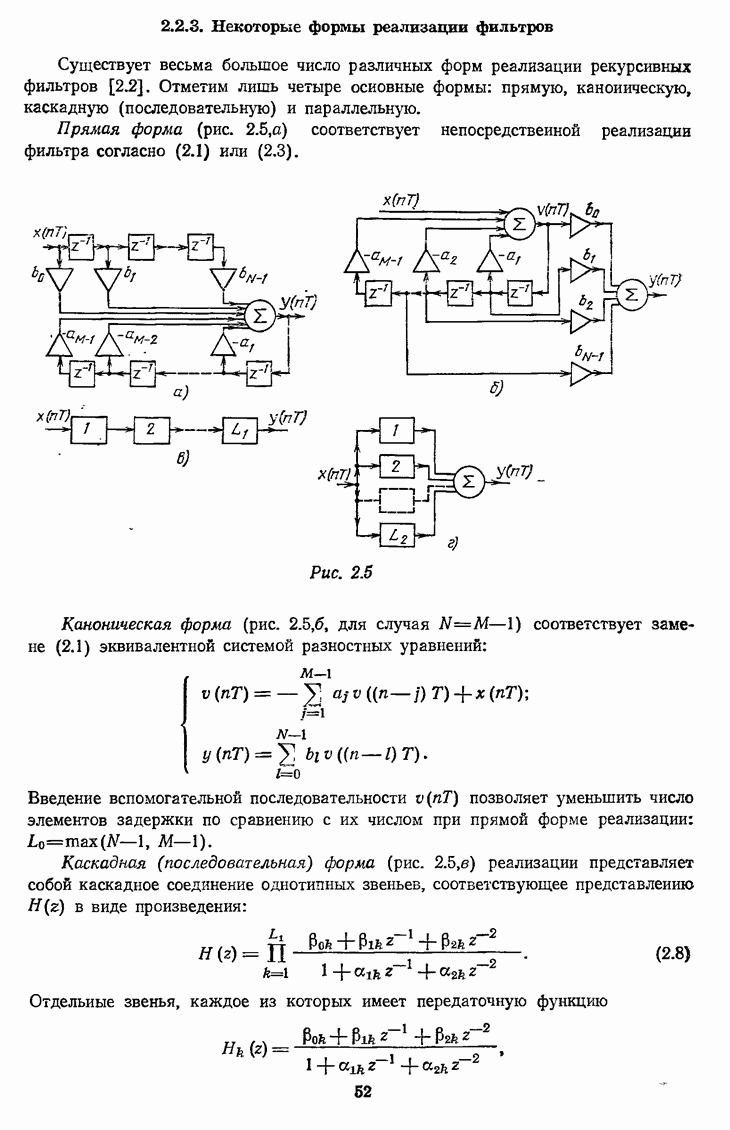
- 2.2.3. Некоторые формы реализации фильтров
- 2.2.4. Реализационные характеристики фильтров
- 2.2.5. Устойчивость фильтров. Первый критерий устойчивости
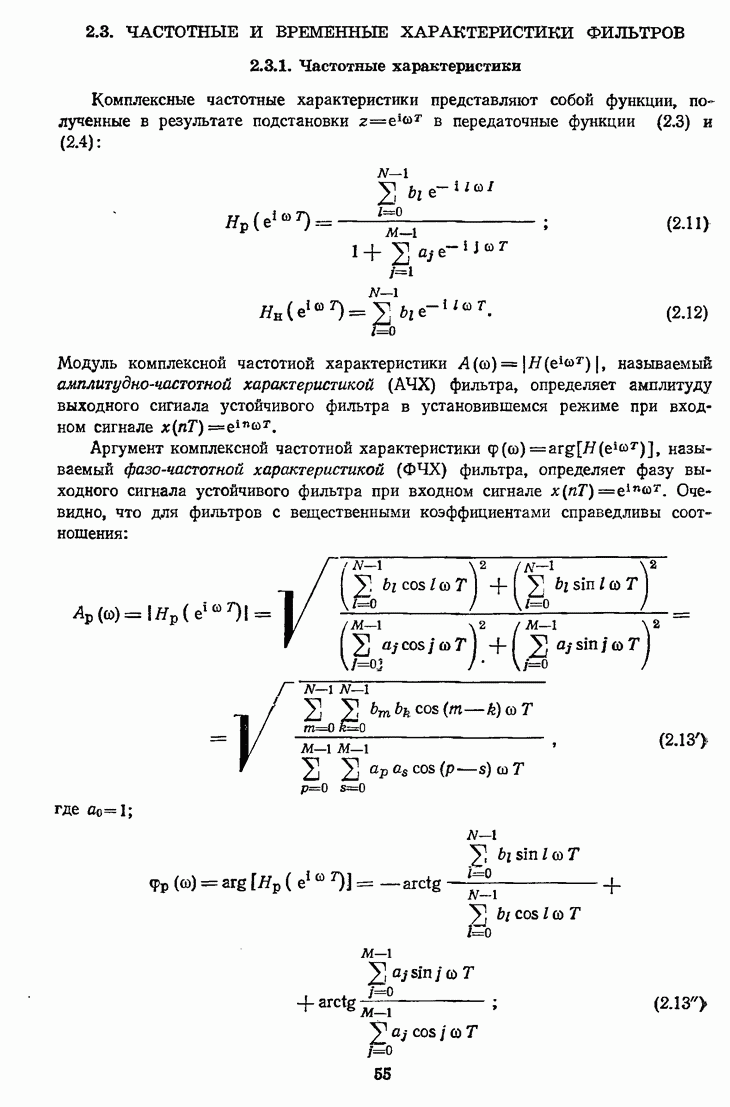
- 2.3. ЧАСТОТНЫЕ И ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ФИЛЬТРОВ
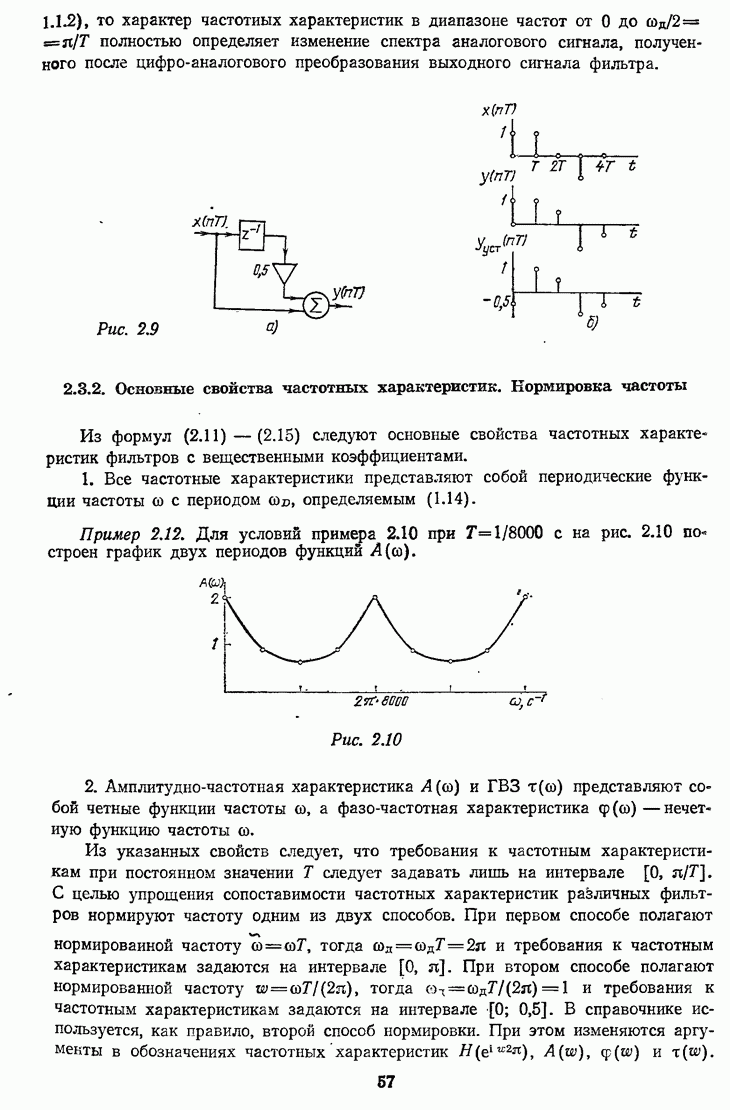
- 2.3.2. Основные свойства частотных характеристик. Нормировка частоты
- 2.3.3. Импульсная характеристика
- 2.3.4. Второй критерий устойчивости фильтров
- 2.3.5. Теорема Парсеваля
- 2.4. АНАЛИЗ ЛИНЕЙНЫХ ЦИФРОВЫХ ЦЕПЕЙ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 2.4.2. Определение Z-образа сигнала по сигнальному графу цепи
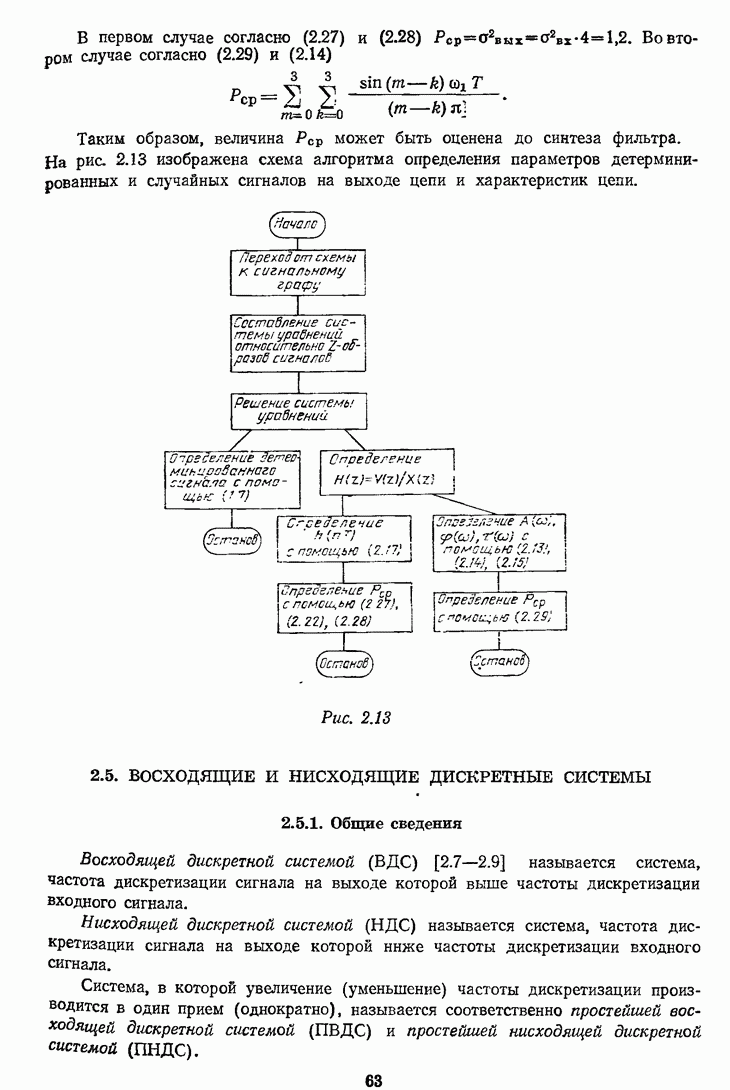
- 2.4.3. Определение характеристик цепи и параметров детерминированных и случайных сигналов на выходе цепи
- 2.5. ВОСХОДЯЩИЕ И НИСХОДЯЩИЕ ДИСКРЕТНЫЕ СИСТЕМЫ
- 2.5.2. Экспандер частоты дискретизации
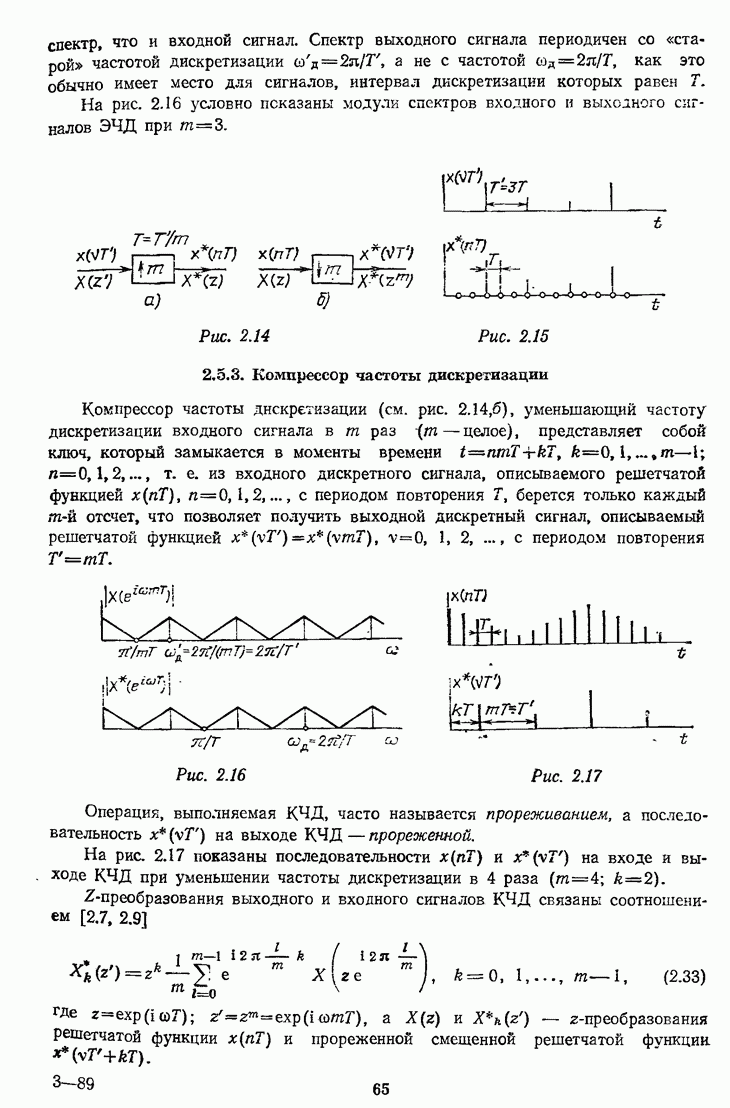
- 2.5.3. Компрессор частоты дискретизации
- 2.5.4. Простейшие восходящие дискретные системы
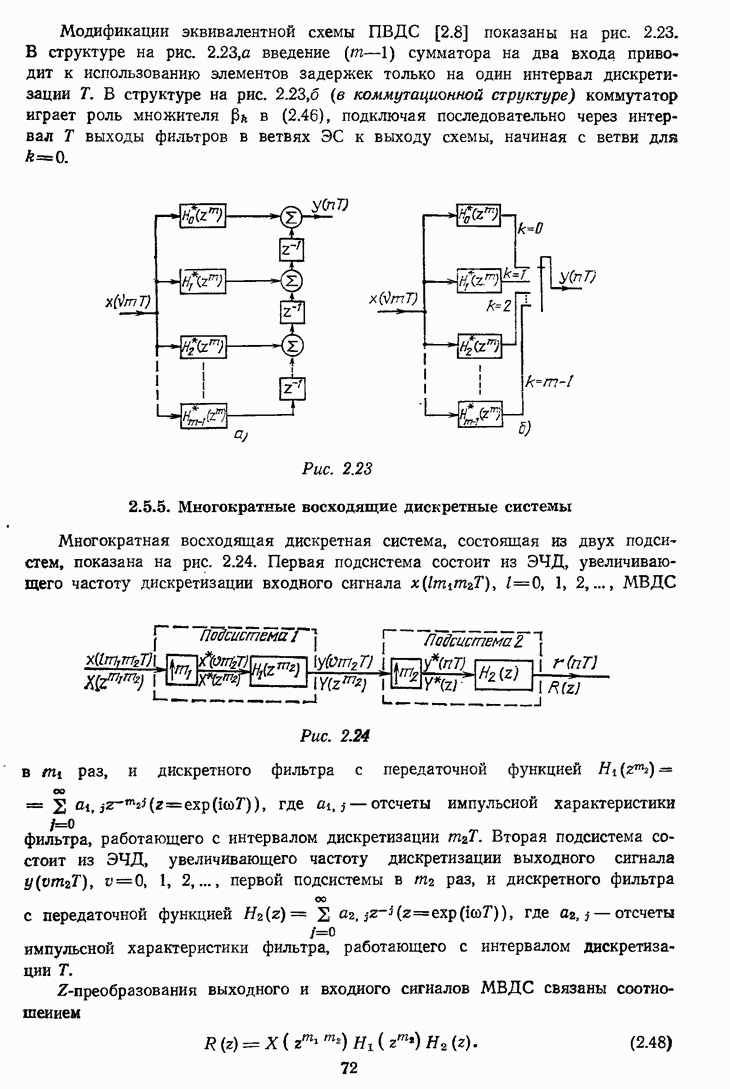
- 2.5.5. Многократные восходящие дискретные системы
- 2.5.6. Простейшие нисходящие дискретные системы
- 2.5.7. Многократные нисходящие дискретные системы
- 3. ЭФФЕКТЫ КВАНТОВАНИЯ СИГНАЛОВ В ЦИФРОВЫХ ФИЛЬТРАХ
- 3.1.2. Перевод чисел из одной ПСС в другую
- 3.2. ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 3.2.2. Плавающая запятая
- 3.3. КОДИРОВАНИЕ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 3.4. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В ЦИФРОВЫХ ФИЛЬТРАХ, ИСПОЛЬЗУЮЩИХ АРИФМЕТИКУ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
- 3.5. КВАНТОВАНИЕ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ, ИСПОЛЬЗУЮЩИХ АРИФМЕТИКУ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
- 3.6. КВАНТОВАНИЕ СИГНАЛОВ В ЦИФРОВЫХ ФИЛЬТРАХ
- 3.7. УЧЕТ КВАНТОВАНИЯ СИГНАЛОВ В СТРУКТУРНЫХ СХЕМАХ ЦИФРОВЫХ ФИЛЬТРОВ
- 3.8. ОБОБЩЕННАЯ ЛИНЕЙНАЯ МОДЕЛЬ ЦИФРОВОГО ФИЛЬТРА
- 3.9. ОЦЕНКИ ОШИБОК (ШУМОВ) КВАНТОВАНИЯ ВЫХОДНОГО СИГНАЛА В ЦИФРОВОМ ФИЛЬТРЕ
- 3.10. ОЦЕНКИ ДИАПАЗОНА ИЗМЕНЕНИЯ СИГНАЛА В ЦИФРОВОМ ФИЛЬТРЕ
- 3.11. ОЦЕНКИ ОШИБОК (ШУМОВ) КВАНТОВАНИЯ И ДИАПАЗОНА ИЗМЕНЕНИЯ СИГНАЛОВ В ВОСХОДЯЩИХ И НИСХОДЯЩИХ ЦИФРОВЫХ СИСТЕМАХ
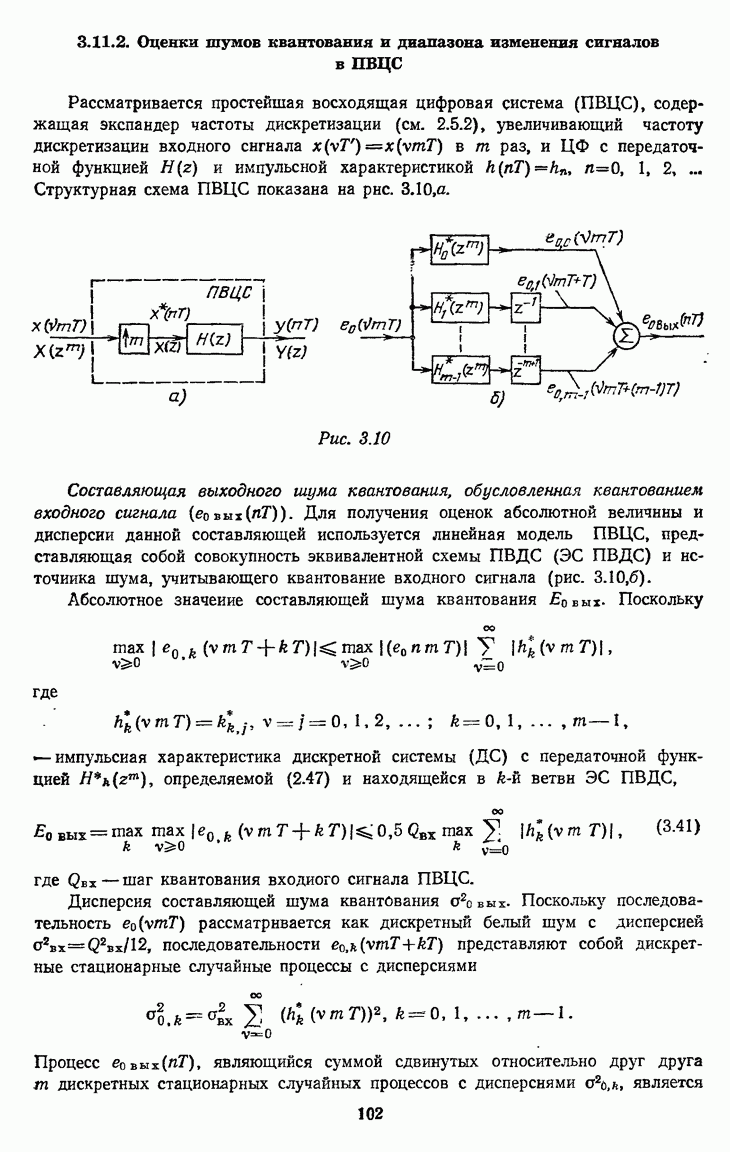
- 3.11.2. Оценки шумов квантования и диапазона изменения сигналов в ПВЦС
- 3.11.3. Оценки шумов квантования и диапазона изменения сигналов в МВЦС
- 3.11.4. Оценки шумов квантования и диапазона изменения сигналов в ПНЦС
- 3.11.5. Оценки шумов квантования и диапазона изменения сигналов в МНДС
- 4. ЭЛЕМЕНТЫ ПРОЕКТИРОВАНИЯ НЕРЕКУРСИВНЫХ ФИЛЬТРОВ
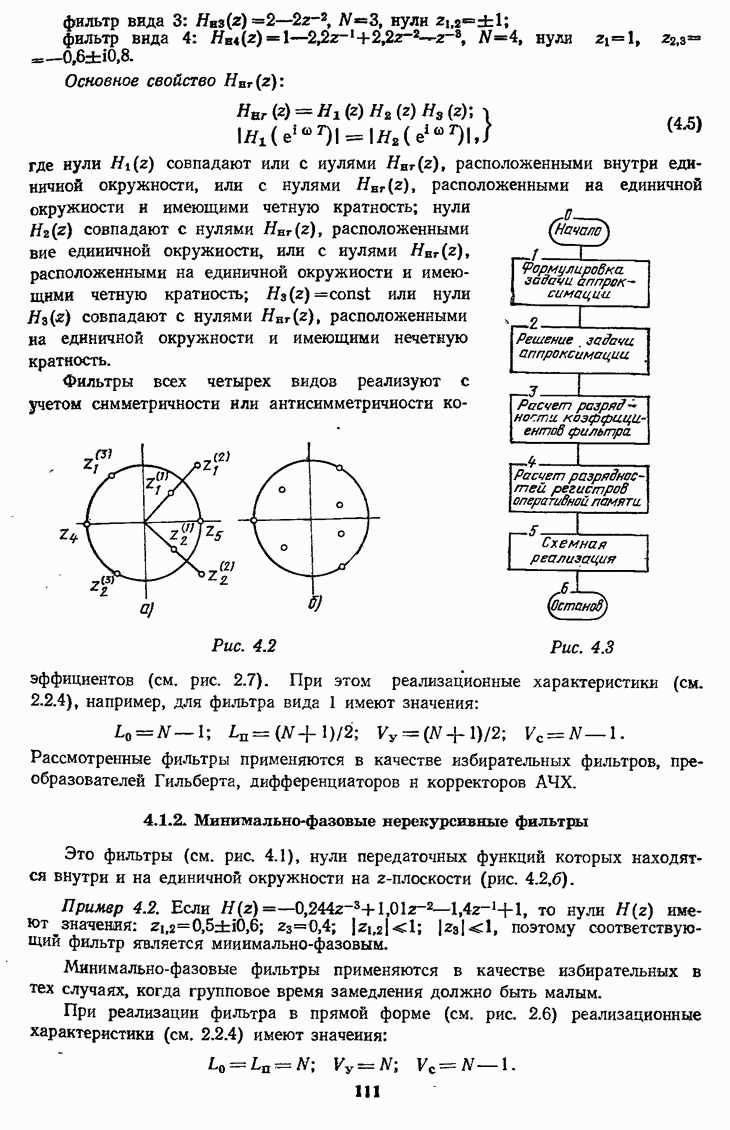
- 4.1.2. Минимально-фазовые нерекурсивные фильтры
- 4.1.3. Основные этапы проектирование нерекурсивных фильтров
- 4.1.4. Сравнение нерекурсивных и рекурсивных фильтров
- 4.2. ФОРМУЛИРОВКИ ЗАДАЧ АППРОКСИМАЦИИ
- 4.2.2. Избирательные фильтры с линейной ФЧХ
- 4.2.3. Равнополосные фильтры с линейной ФЧХ
- 4.2.4. Преобразователи Гильберта
- 4.2.5. Минимально-фазовые фильтры
- 4.3. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ АППРОКСИМАЦИИ
- 4.3.3. Метод наименьших квадратов
- 4.3.4. Метод наилучшей равномерной (чебышевской) аппроксимации. Алгоритм Ремеза
- 4.3.5. Решение чебышевской аппроксимационной задачи для фильтра с линейной ФЧХ с помощью алгоритма Ремеза
- 4.3.6. Решение чебышевской аппроксимационной задачи для минимально-фазового фильтра
- 4.3.7. Решение аппроксимационной задачи для амплитуднофазового корректора по методу наименьших квадратов
- 4.3.8. Оценка погрешности аппроксимации
- 4.3.9. Сравнение возможностей фильтров с линейной ФЧХ и минимально-фазовых фильтров
- 4.3.10. Сравнение методов решения аппроксимационных задач
- 4.4. РАСЧЕТ РАЗРЯДНОСТЕЙ КОЭФФИЦИЕНТОВ ФИЛЬТРОВ И РЕГИСТРОВ ОПЕРАТИВНОЙ ПАМЯТИ
- 4.4.6. Алгоритм расчета разрядности коэффициентов фильтра, реализуемого на специализированном микропроцессоре
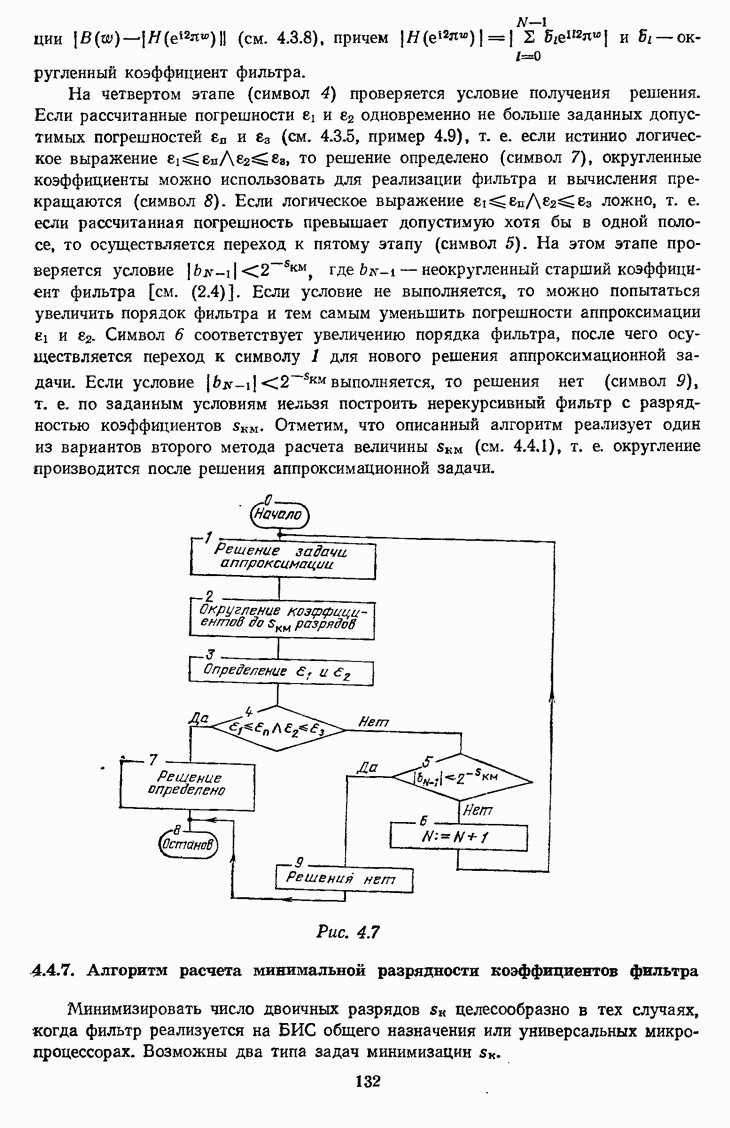
- 4.4.7. Алгоритм расчета минимальной разрядности коэффициентов фильтра
- 4.4.8. Расчет разрядностей регистров оперативной памяти по заданному динамическому диапазону и отношению сигнал-шум
- 4.4.9. Априорная оценка разрядности входного сигнала фильтра
- 5. ЭЛЕМЕНТЫ ПРОЕКТИРОВАНИЯ РЕКУРСИВНЫХ ЦИФРОВЫХ ФИЛЬТРОВ
- 5.1.2. Типы аналоговых фильтров
- 5.1.3. Билинейное преобразование
- 5.1.4. Обобщенное билинейное преобразование
- 5.1.5. Определение передаточной функции цифрового ФНЧ (ФВЧ) по справочнику [5.1]
- 5.1.6. Определение передаточной функции цифрового полосового (режекторного) фильтра по справочнику [5.1]
- 5.1.7. Определение передаточной функции параллельной структуры РЦФ
- 5.1.8. Определение передаточной функции РЦФ с помощью билинейного преобразования на ЭВМ
- 5.2. РАСЧЕТ РАЗРЯДНОСТЕЙ КОЭФФИЦИЕНТОВ ФИЛЬТРА И РЕГИСТРОВ ОПЕРАТИВНОЙ ПАМЯТИ
- 5.2.2. Определение разрядности коэффициентов
- 5.2.3. Определение разрядностей входного сигнала и регистров оперативной памяти по вероятностной модели ошибок квантования
- 5.2.4. Определение разрядностей входного сигнала и регистров оперативной памяти по детерминированной модели ошибок квантования
- 5.3. РАСЧЕТ МАСШТАБНЫХ МНОЖИТЕЛЕЙ
- 5.4. РАССТАНОВКА ЗВЕНЬЕВ В КАСКАДНЫХ СТРУКТУРАХ РЦФ
- 5.5. УСТОЙЧИВОСТЬ РЕКУРСИВНЫХ ЦИФРОВЫХ ФИЛЬТРОВ
- 5.5.2. Определение устойчивости и класса входных сигналов РЦФ
- 5.5.3. Устойчивость положения равновесия
- 5.5.4. Устойчивость процессов
- 6. АДАПТИВНЫЕ ДИСКРЕТНЫЕ И ЦИФРОВЫЕ ФИЛЬТРЫ
- 6.1.2. Критерии настройки адаптивных фильтров и методы определения значений их параметров
- 6.2. АДАПТИВНЫЙ ФИЛЬТР-КОМПЕНСАТОР ПОМЕХ
- 6.2.2. Точный алгоритм настройки нерекурсивного адаптивного фильтра по минимуму СКО
- 6.2.3. Настройка нерекурсивного адаптивного фильтра по минимуму СКО с помощью градиентного метода
- 6.3. АДАПТИВНЫЙ ФИЛЬТР — ЛИНЕЙНОЕ ПРЕДСКАЗЫВАЮЩЕЕ УСТРОЙСТВО
- 6.3.2. Решетчатые фильтры
- 7. НЕКОТОРЫЕ МЕТОДЫ ЦОС В СИСТЕМАХ СВЯЗИ
- 7.2. ФОРМИРОВАНИЕ СИГНАЛА С ОДНОЙ БОКОВОЙ ПОЛОСОЙ (ОБП)
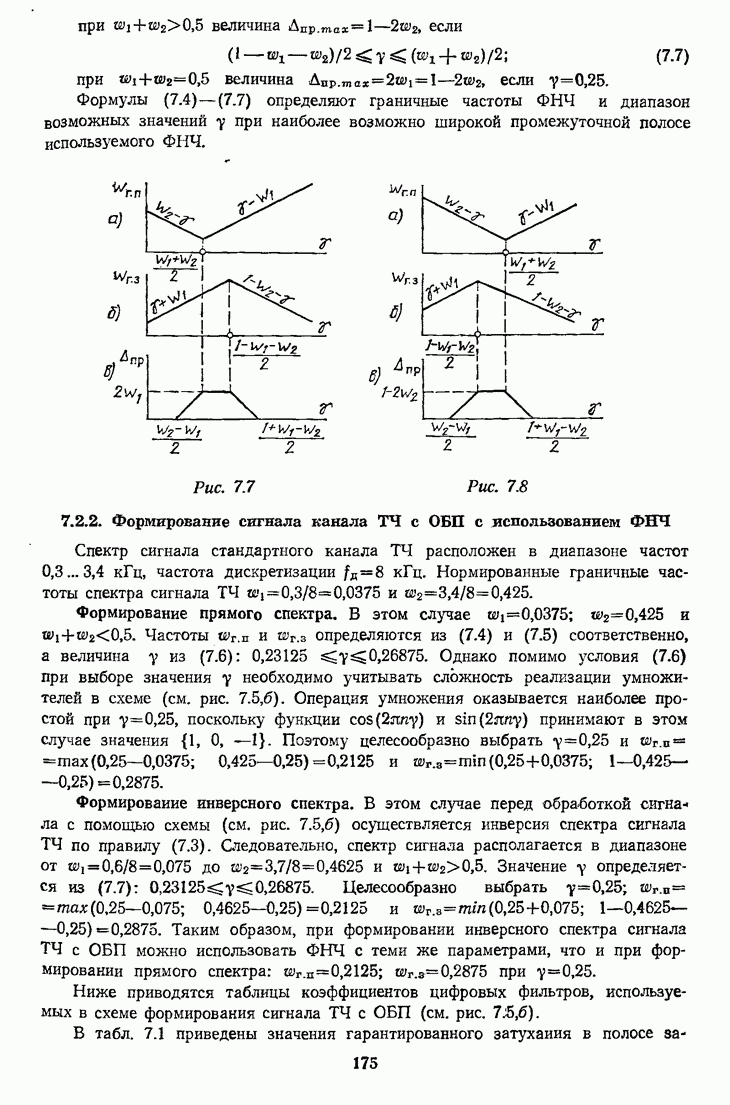
- 7.2.2. Формирование сигнала канала ТЧ с ОБП с использованием ФНЧ
- 7.2.3. Формирование сигнала с ОБП с использованием преобразователя Гильберта
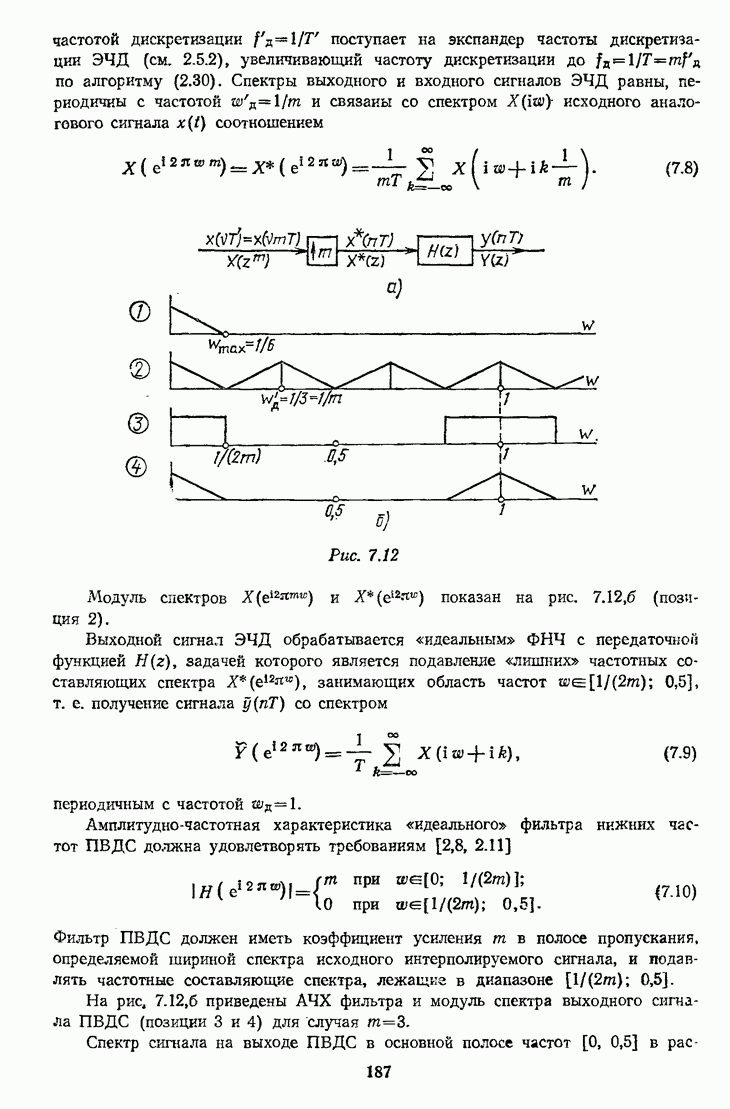
- 7.3. УВЕЛИЧЕНИЕ ЧАСТОТЫ ДИСКРЕТИЗАЦИИ (ИНТЕРПОЛЯЦИЯ) СИГНАЛА
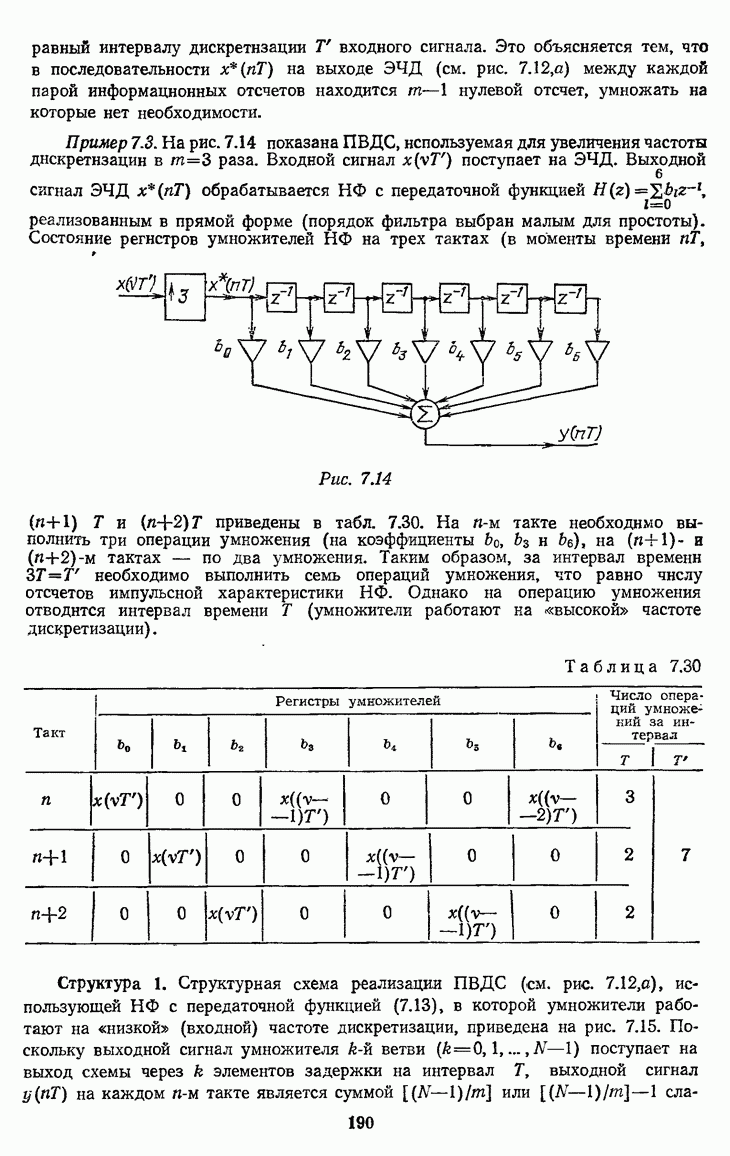
- 7.3.2. Интерполяция сигнала с помощью ПВДС
- 7.3.3. Особенности использования НФ и РФ при интерполяции
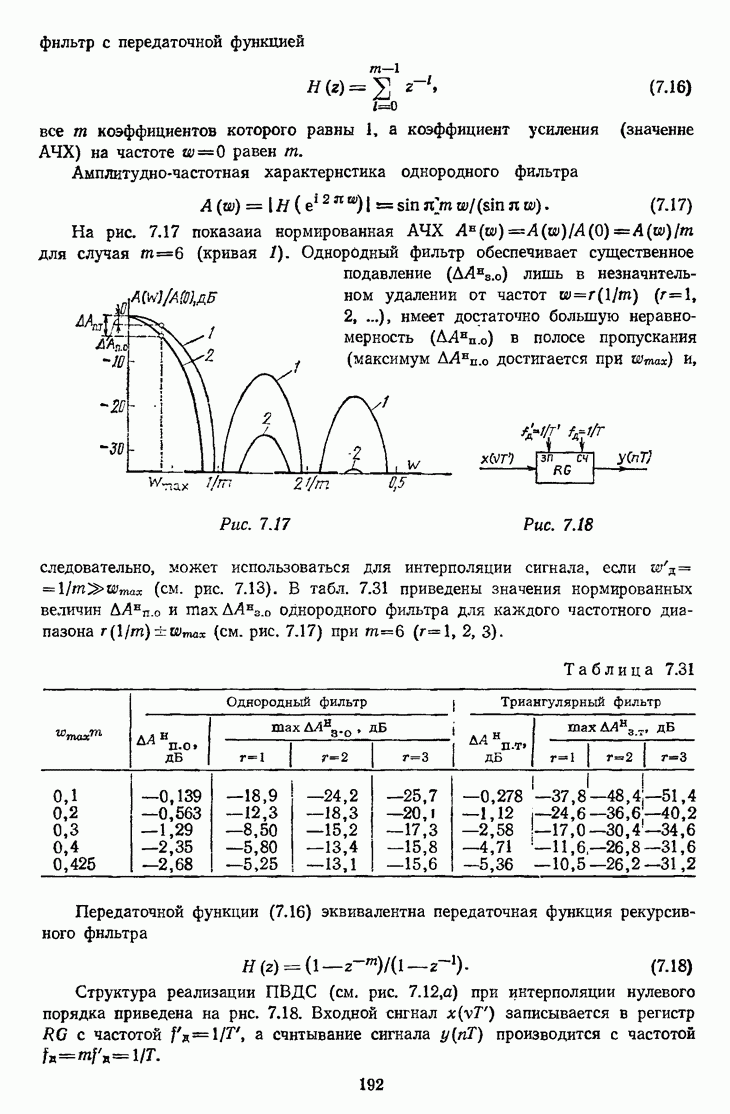
- 7.3.4. Характеристики фильтров реальных ПВДС
- 7.3.5. Структуры ПВДС при интерполяции
- 7.3.6. Цифровая фильтрация при полиномиальной интерполяции
- 7.3.7. Простейшие ВДС с оптимальными фильтрами
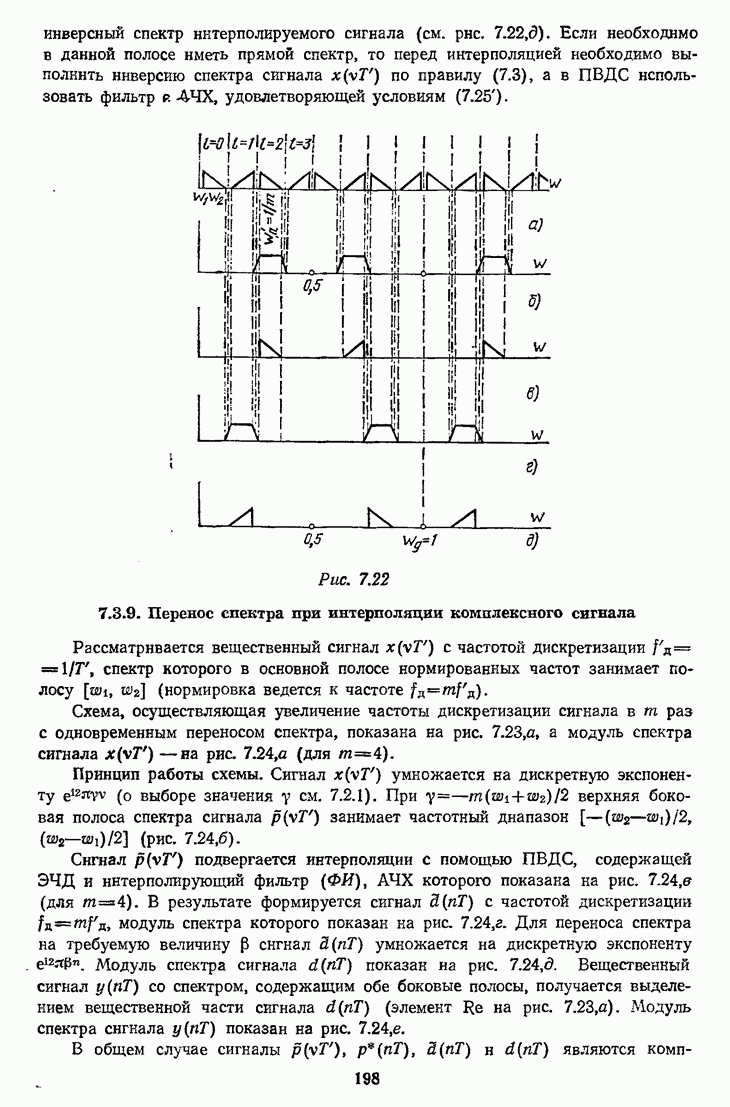
- 7.3.8. Перевес спектра при интерполяция
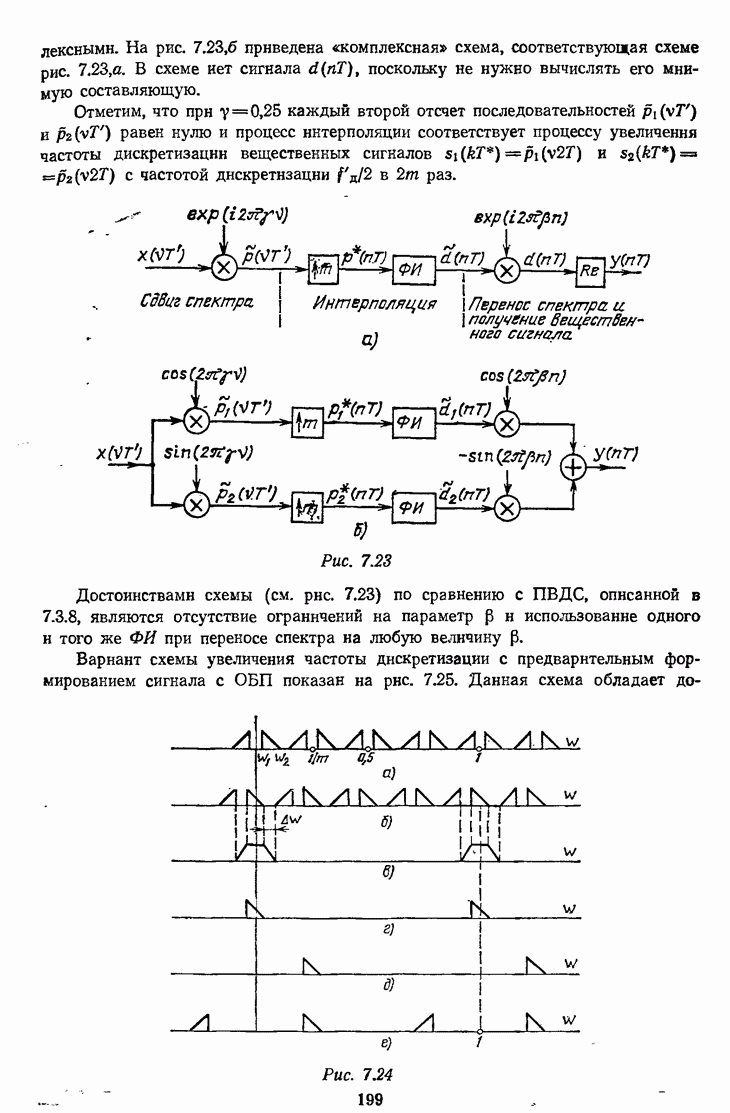
- 7.3.9. Перенос спектра при интерполяции комплексного сигнала
- 7.3.10. Интерполяция сигнала с помощью МВДС
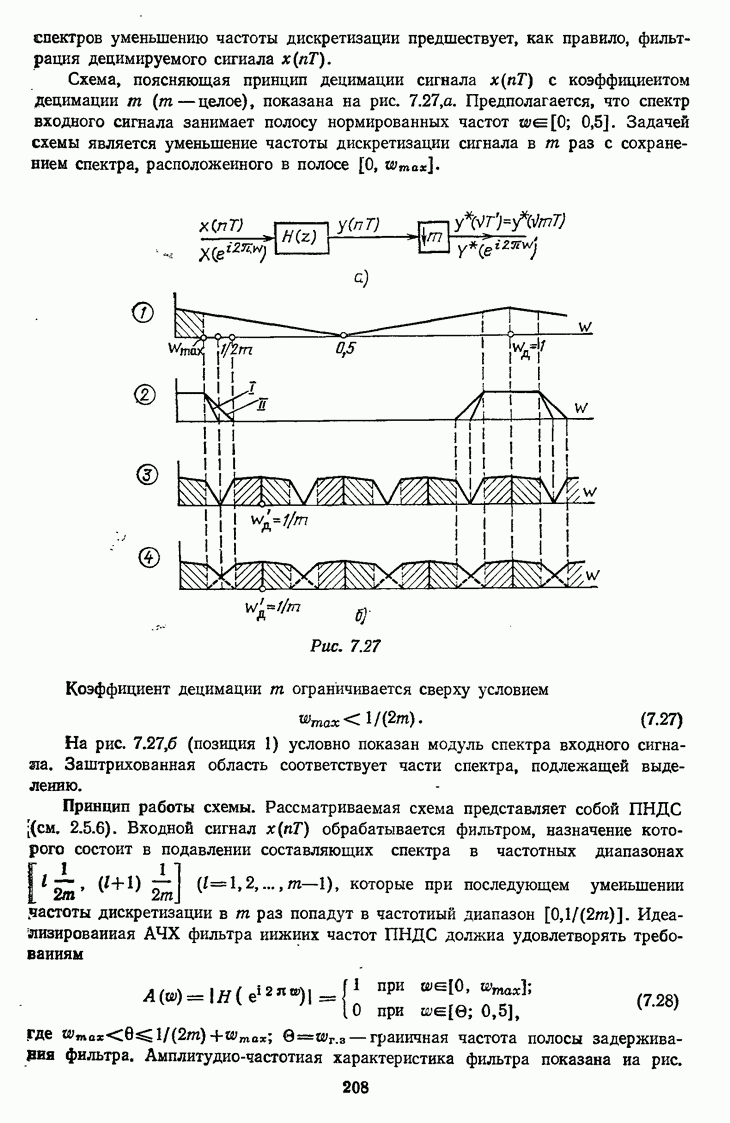
- 7.4. УМЕНЬШЕНИЕ ЧАСТОТЫ ДИСКРЕТИЗАЦИИ (ДЕЦИМАЦИЯ) СИГНАЛА
- 7.4.2. Особенности использования НФ и РФ при децимации
- 7.4.3. Структуры ПНДС при децимации сигнала
- 7.4.4. Однородный и триангулярный фильтры при децимации
- 7.4.5. Простейшая НДС с оптимальными фильтрами
- 7.4.6. Перенос спектра при полосовой фильтрации с уменьшением частоты дискретизации
- 7.4.7. Перенос спектра при децимации комплексного сигнала
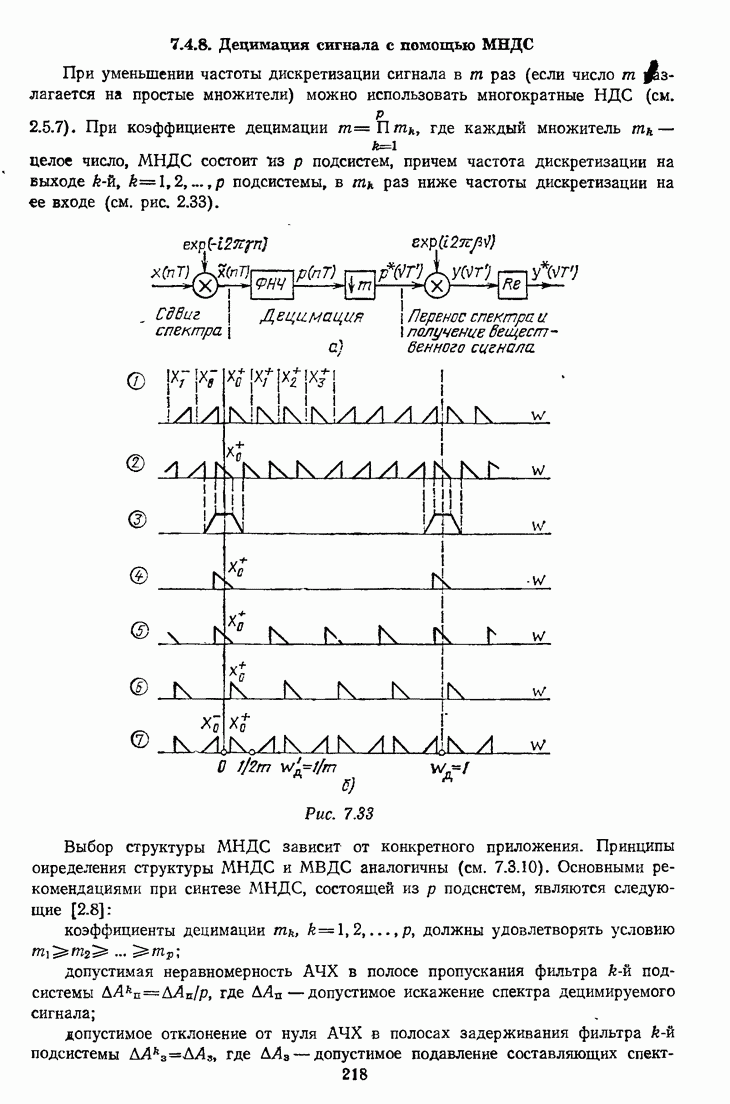
- 7.4.8. Децимация сигнала с помощью МНДС
- 8. ЦИФРОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
- 8.2. МЕТОД ПЕРИОДОГРАММ
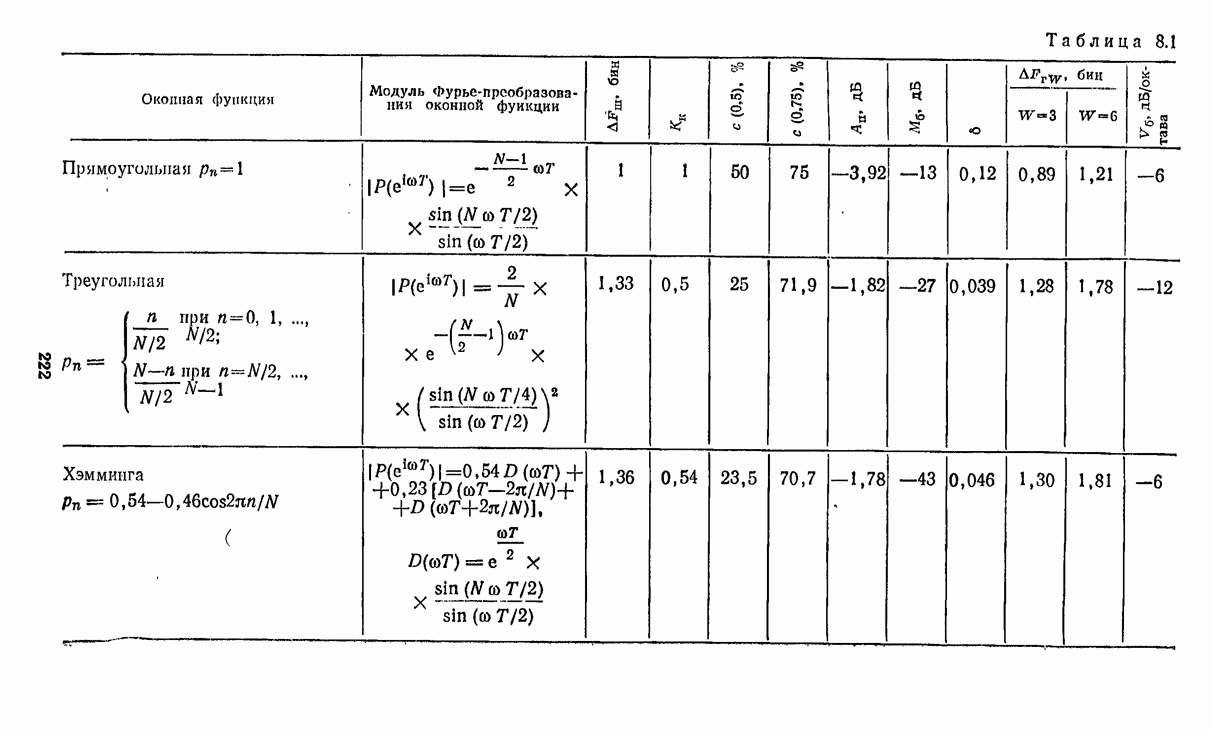
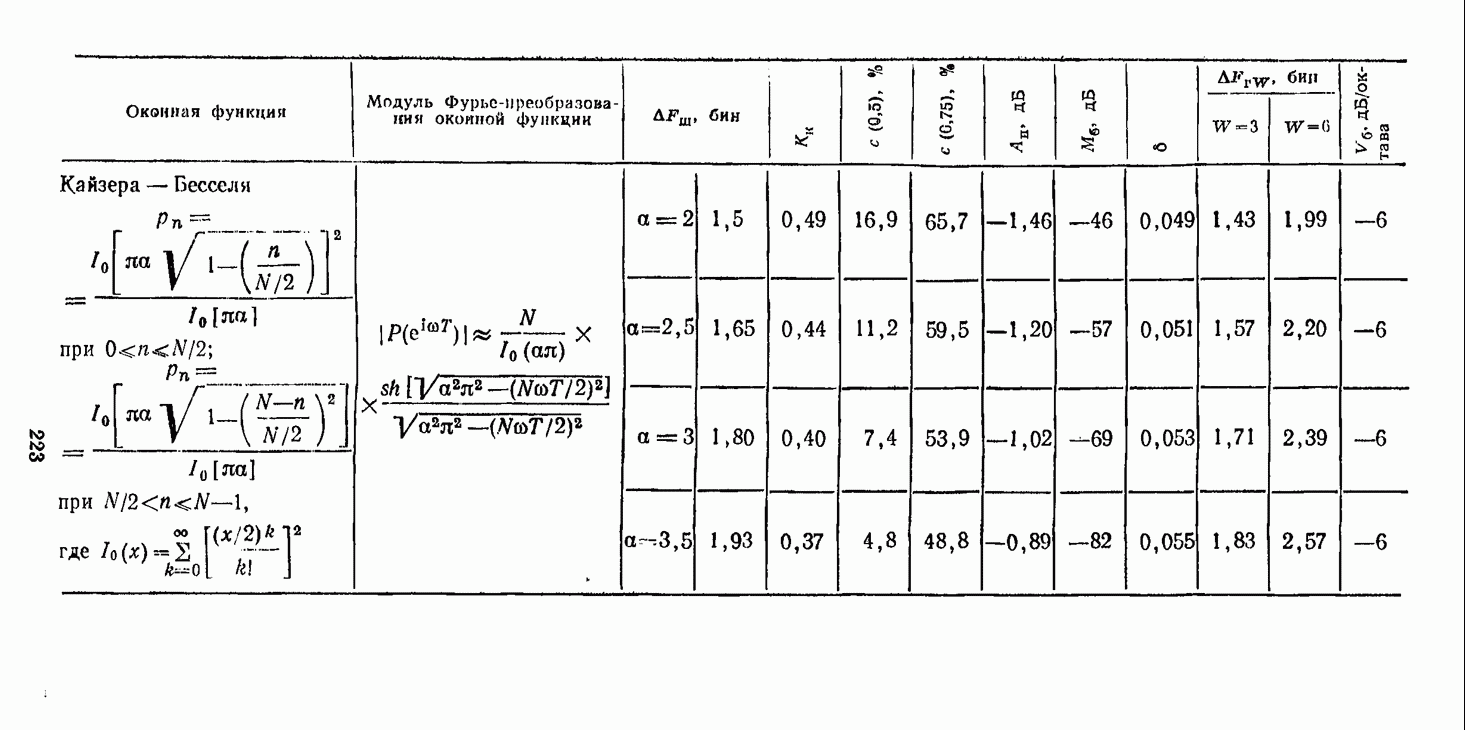
- 8.2.2. Основные свойства оконных функций
- 8.2.3. Принципы выбора оконной функции
- 8.3. МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА, ОСНОВАННЫЕ НА ЛИНЕЙНОМ МОДЕЛИРОВАНИИ
- 8.3.2. Определение параметров АР-модели по известной автокорреляционной функции последовательности
- 8.3.3. Определение параметров АР-модели по анализируемым данным
- 8.3.4. Определение порядка АР-модели
- 9. ТРАНСМУЛЬТИПЛЕКСОРЫ
- 9.2. ОДНОУРОВНЕВЫЕ СТРУКТУРЫ ТМ БЕЗ ДОПОЛНИТЕЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- 9.2.2. Структура ТМ с комплексными сигналами и однократным изменением частоты дискретизации
- 9.2.3. Структура ТМ с комплексными сигналами, однократным изменением частоты дискретизации и дополнительными ФНЧ
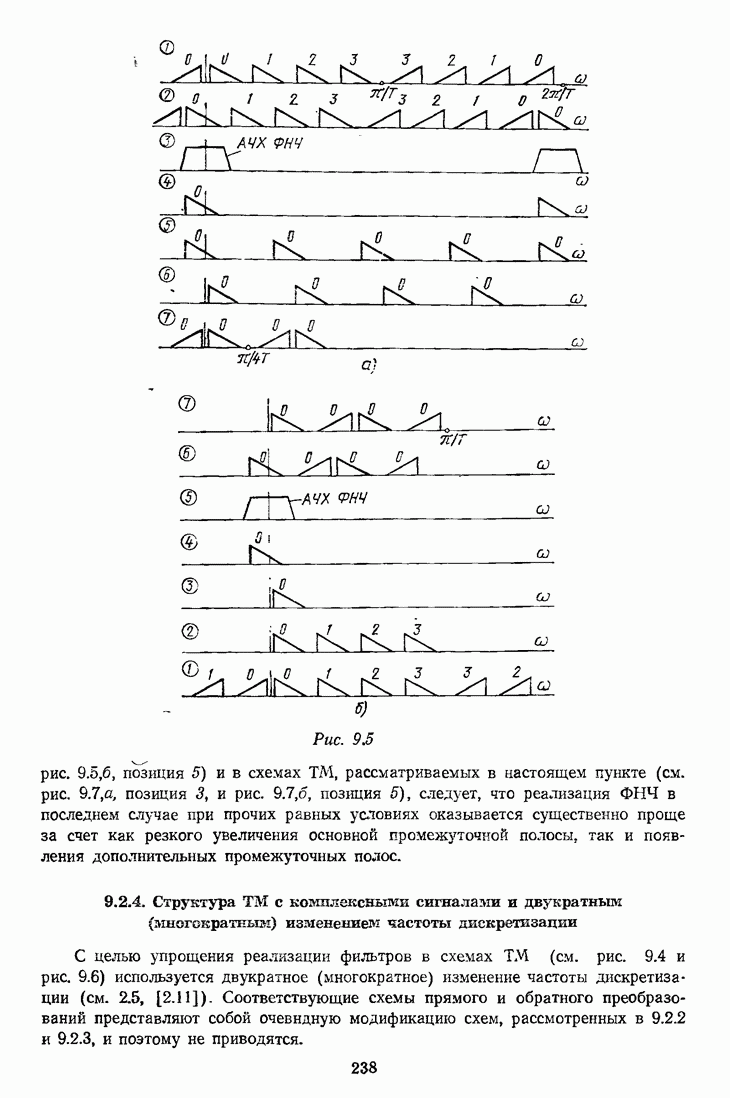
- 9.2.4. Структура ТМ с комплексными сигналами и двукратным (многократным) изменением частоты дискретизации
- 9.3. МНОГОУРОВНЕВЫЕ СТРУКТУРЫ ТМ БЕЗ ДОПОЛНИТЕЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- 9.4. ТРАНСМУЛЬТИПЛЕКСОРЫ С ДОПОЛНИТЕЛЬНЫМИ ПРЕОБРАЗОВАНИЯМИ