| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.2. ФОРМУЛИРОВКИ ЗАДАЧ АППРОКСИМАЦИИ
4.2.1. Требования к аппроксимируемой функции. Критерии аппроксимации
Целью решения аппроксимационной задачи является определение коэффициентов  передаточной функции фильтра. Аппроксимирующая функция
передаточной функции фильтра. Аппроксимирующая функция  должна удовлетворять следующим требованиям:
должна удовлетворять следующим требованиям:
вектор с должен быть связан простой зависимостью с вектором коэффициентов 
функция  должна достаточно просто зависеть от вектора с;
должна достаточно просто зависеть от вектора с;
при заданных значениях  должно выполняться (4.6).
должно выполняться (4.6).
Наиболее простой и удобной для решения задачи аппроксимации является линейная зависимость функции  от вектора с:
от вектора с:

Существуют два основных критерия аппроксимации, уточняющие смысл (4.6): среднеквадратический критерий

и наилучший равномерный (чебышевский) критерий

Критерии (4.8) и (4.9) могут применяться совместно — каждый для определенной области частот. Выбор критерия аппроксимации определяется физическим смыслом задачи.
Общий принцип определения значений весовой функции  состоит в следующем: чем точнее должно выполняться (4.6) при
состоит в следующем: чем точнее должно выполняться (4.6) при  тем больше должно быть значение
тем больше должно быть значение  При использовании критерия (4.9) для отдельных подынтервалов частот
При использовании критерия (4.9) для отдельных подынтервалов частот  задаются значения
задаются значения  такие, чтобы на этих подынтервалах выполнялось неравенство
такие, чтобы на этих подынтервалах выполнялось неравенство

Тогда для  подынтервала
подынтервала

где  — произвольная константа (нормирующий множитель), общая для всех подынтервалов.
— произвольная константа (нормирующий множитель), общая для всех подынтервалов.
Пример 4.3. Пусть при использовании критерия  Примем
Примем  тогда
тогда

В соответствии с (4.9) и (4.11) определяется оптимальная функция  , удовлетворяющая (4.10).
, удовлетворяющая (4.10).
Критерий оптимальности формулируется следующим образом [4.2]: пусть в соответствии с (4.9) и (4.11) построены функции  порядка
порядка  порядка К [см. (4.7)], при этом
порядка К [см. (4.7)], при этом  удовлетворяет (4.10),
удовлетворяет (4.10),  - нет. Тогда не существует функции
- нет. Тогда не существует функции  порядка, меньшего К, удовлетворяющей (4.10), т. е. построенная функция
порядка, меньшего К, удовлетворяющей (4.10), т. е. построенная функция  среди всех функций
среди всех функций  , удовлетворяющих (4.10), имеет наименьший порядок и
, удовлетворяющих (4.10), имеет наименьший порядок и  .
.
Соотношение (4.11) можно использовать совместно с (4.8). Однако в этом случае (4.11) следует рассматривать лишь как эвристическую рекомендацию. Иногда требования к функции  задаются в следующей форме:
задаются в следующей форме:

В этом случае [2.11] следует принять:

и определять оптимальную функцию  в соответствии со сформулированным выше критерием оптимальности.
в соответствии со сформулированным выше критерием оптимальности.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- 1. СВОЙСТВА И ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- 1.1. ТИПЫ СИГНАЛОВ. СВЯЗЬ МЕЖДУ СИГНАЛАМИ РАЗЛИЧНЫХ ТИПОВ
- 1.1.2. Связь между аналоговыми и дискретными сигналами
- 1.1.3. Связь между дискретными и цифровыми сигналами
- 1.1.4. Дискретная дельта-функция
- 1.2. Z-ПРЕОБРАЗОВАНИЕ И ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- 1.3. ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ. АЛГОРИТМЫ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- 1.3.2. Свойства дискретного преобразования Фурье
- 1.3.3. Многомерное дискретное преобразование Фурье
- 1.3.4. Алгоритмы БПФ с основанием 2
- 1.3.5. Алгоритмы БПФ для произвольного составного N
- 1.4. ДИСКРЕТНАЯ СВЕРТКА И ЕЕ ВЫЧИСЛЕНИЕ
- 1.4.2. Использование ДПФ для вычисления круговой свертки
- 1.4.3. Линейная свертка
- 1.4.4. Секционированные свертки
- 1.4.5. Методы быстрого вычисления круговой свертки
- 1.4.6. Использование теоретико-числовых преобразований
- 1.4.7. Использование модульной арифметики в кольце полиномов
- 1.5. НЕКОТОРЫЕ ПЕРСПЕКТИВНЫЕ АЛГОРИТМЫ ВЫЧИСЛЕНИЯ ДПФ
- 1.5.2. Алгоритм Винограда с использованием ТЧП
- 1.5.3. Использование эффективных методов поворота вектора (КОРДИК)
- 1.5.4. Специальные виды ДПФ
- 1.6. СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ИХ ХАРАКТЕРИСТИКИ
- 2. ДИСКРЕТНЫЕ СИСТЕМЫ
- 2.1. ДИСКРЕТНЫЕ И ЦИФРОВЫЕ ФИЛЬТРЫ. УСТРОЙСТВА ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ
- 2.1.2. Линейные дискретные фильтры
- 2.1.3. Переход от разностного уравнения к структурной схеме фильтра
- 2.1.4. Цифровые фильтры
- 2.1.5. Устройства цифровой обработки сигналов
- 2.2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ. РАЗЛИЧНЫЕ ФОРМЫ РЕАЛИЗАЦИИ ФИЛЬТРОВ. ПЕРВЫЙ КРИТЕРИЙ УСТОЙЧИВОСТИ
- 2.2.2. Соединение фильтров
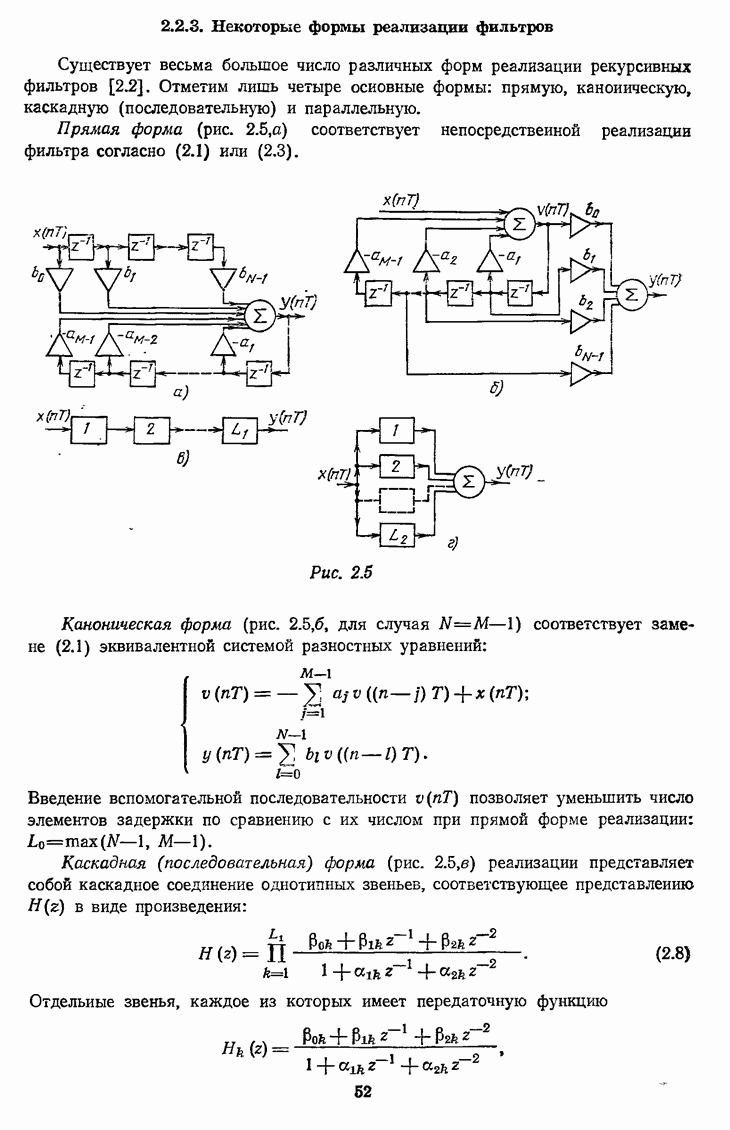
- 2.2.3. Некоторые формы реализации фильтров
- 2.2.4. Реализационные характеристики фильтров
- 2.2.5. Устойчивость фильтров. Первый критерий устойчивости
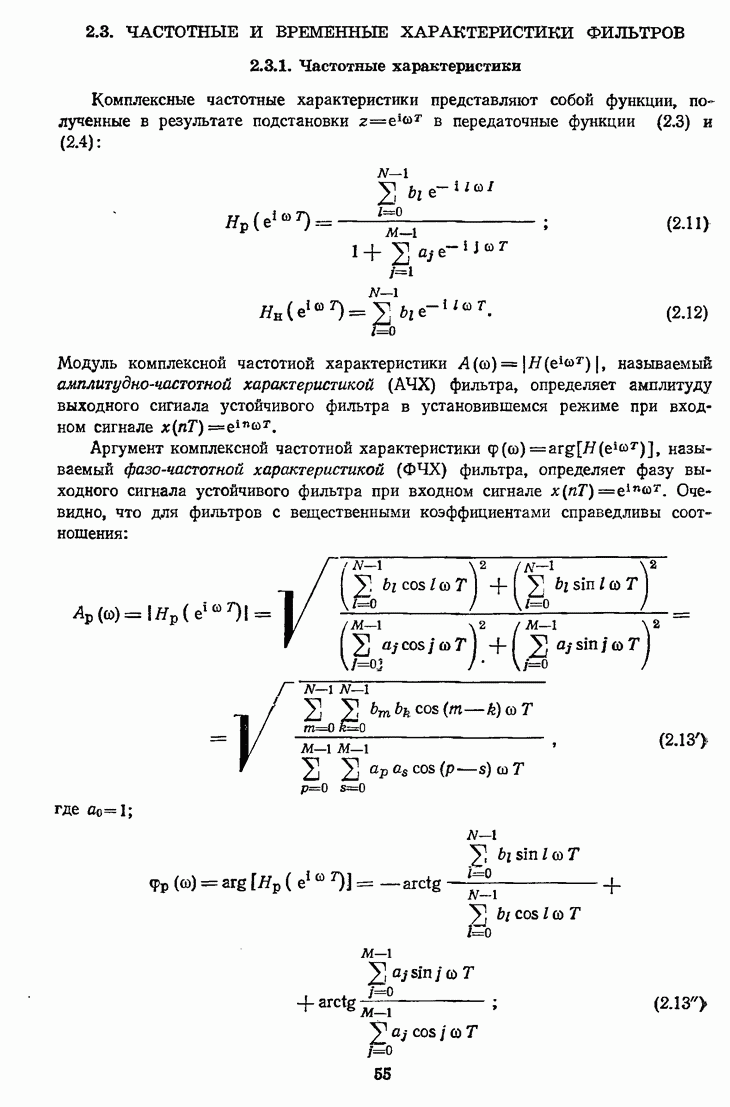
- 2.3. ЧАСТОТНЫЕ И ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ФИЛЬТРОВ
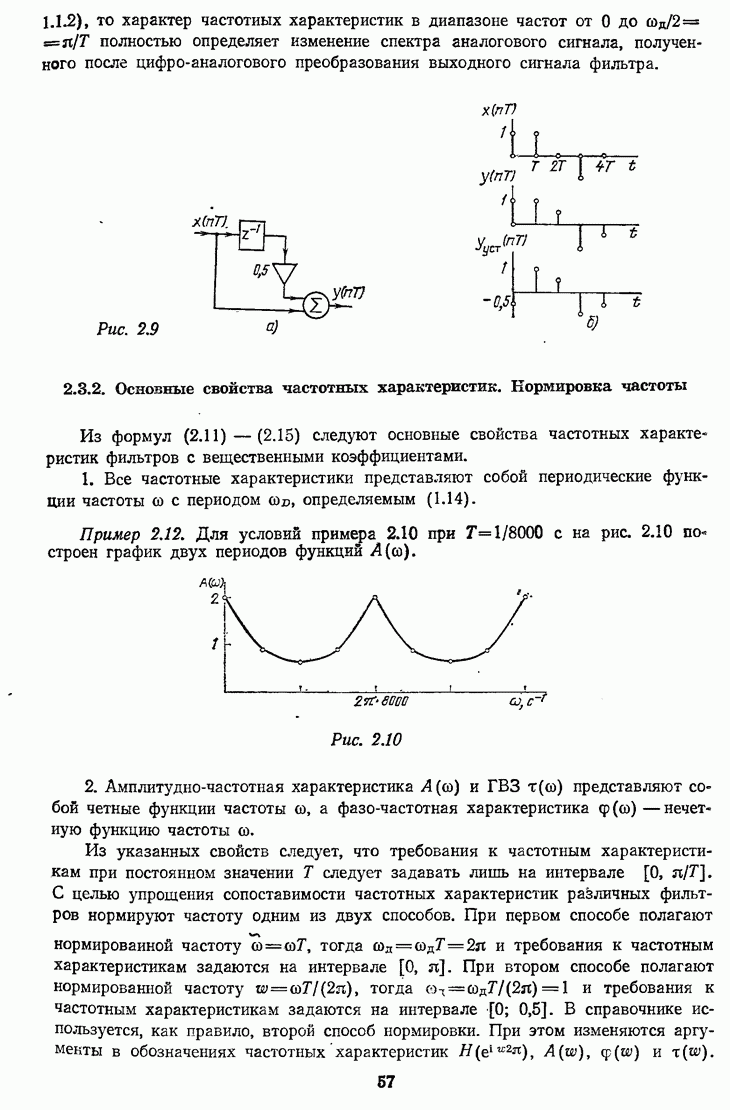
- 2.3.2. Основные свойства частотных характеристик. Нормировка частоты
- 2.3.3. Импульсная характеристика
- 2.3.4. Второй критерий устойчивости фильтров
- 2.3.5. Теорема Парсеваля
- 2.4. АНАЛИЗ ЛИНЕЙНЫХ ЦИФРОВЫХ ЦЕПЕЙ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
- 2.4.2. Определение Z-образа сигнала по сигнальному графу цепи
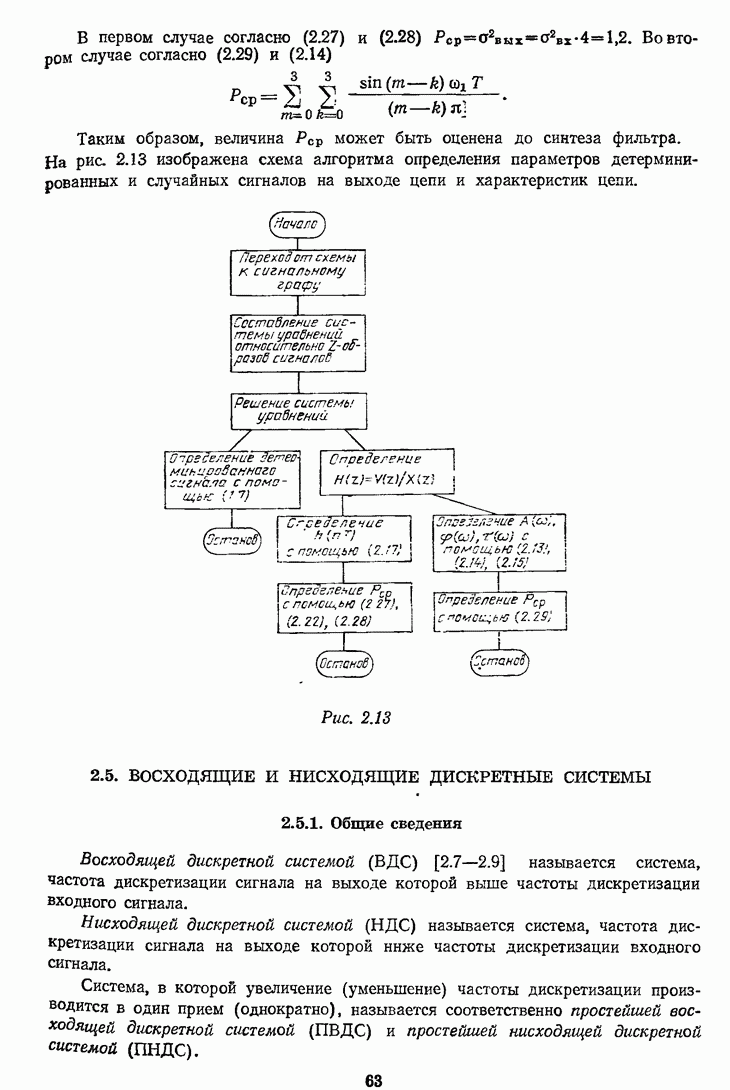
- 2.4.3. Определение характеристик цепи и параметров детерминированных и случайных сигналов на выходе цепи
- 2.5. ВОСХОДЯЩИЕ И НИСХОДЯЩИЕ ДИСКРЕТНЫЕ СИСТЕМЫ
- 2.5.2. Экспандер частоты дискретизации
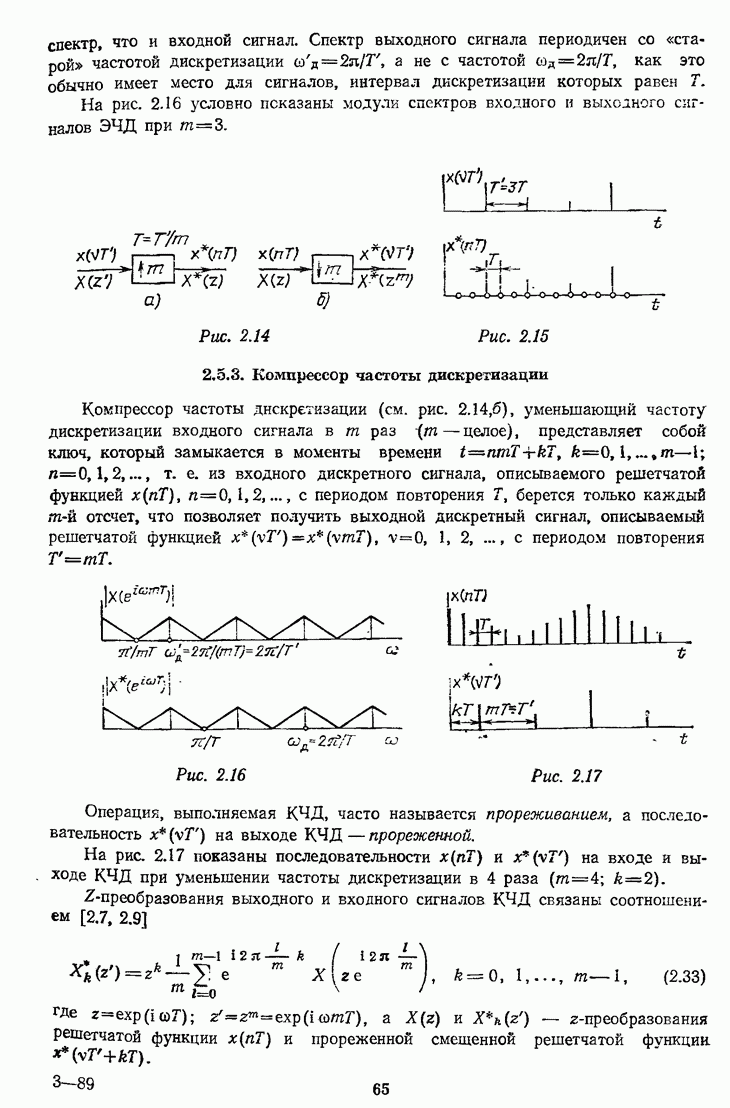
- 2.5.3. Компрессор частоты дискретизации
- 2.5.4. Простейшие восходящие дискретные системы
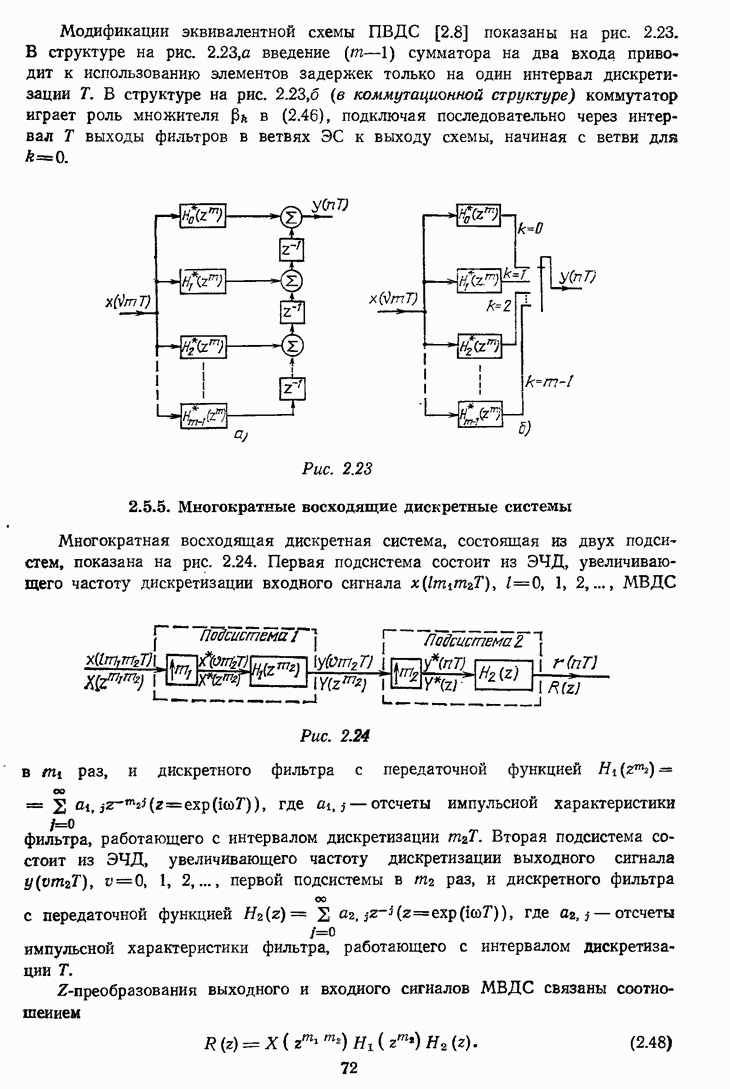
- 2.5.5. Многократные восходящие дискретные системы
- 2.5.6. Простейшие нисходящие дискретные системы
- 2.5.7. Многократные нисходящие дискретные системы
- 3. ЭФФЕКТЫ КВАНТОВАНИЯ СИГНАЛОВ В ЦИФРОВЫХ ФИЛЬТРАХ
- 3.1.2. Перевод чисел из одной ПСС в другую
- 3.2. ФОРМЫ ПРЕДСТАВЛЕНИЯ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 3.2.2. Плавающая запятая
- 3.3. КОДИРОВАНИЕ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ
- 3.4. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ В ЦИФРОВЫХ ФИЛЬТРАХ, ИСПОЛЬЗУЮЩИХ АРИФМЕТИКУ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
- 3.5. КВАНТОВАНИЕ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ, ИСПОЛЬЗУЮЩИХ АРИФМЕТИКУ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
- 3.6. КВАНТОВАНИЕ СИГНАЛОВ В ЦИФРОВЫХ ФИЛЬТРАХ
- 3.7. УЧЕТ КВАНТОВАНИЯ СИГНАЛОВ В СТРУКТУРНЫХ СХЕМАХ ЦИФРОВЫХ ФИЛЬТРОВ
- 3.8. ОБОБЩЕННАЯ ЛИНЕЙНАЯ МОДЕЛЬ ЦИФРОВОГО ФИЛЬТРА
- 3.9. ОЦЕНКИ ОШИБОК (ШУМОВ) КВАНТОВАНИЯ ВЫХОДНОГО СИГНАЛА В ЦИФРОВОМ ФИЛЬТРЕ
- 3.10. ОЦЕНКИ ДИАПАЗОНА ИЗМЕНЕНИЯ СИГНАЛА В ЦИФРОВОМ ФИЛЬТРЕ
- 3.11. ОЦЕНКИ ОШИБОК (ШУМОВ) КВАНТОВАНИЯ И ДИАПАЗОНА ИЗМЕНЕНИЯ СИГНАЛОВ В ВОСХОДЯЩИХ И НИСХОДЯЩИХ ЦИФРОВЫХ СИСТЕМАХ
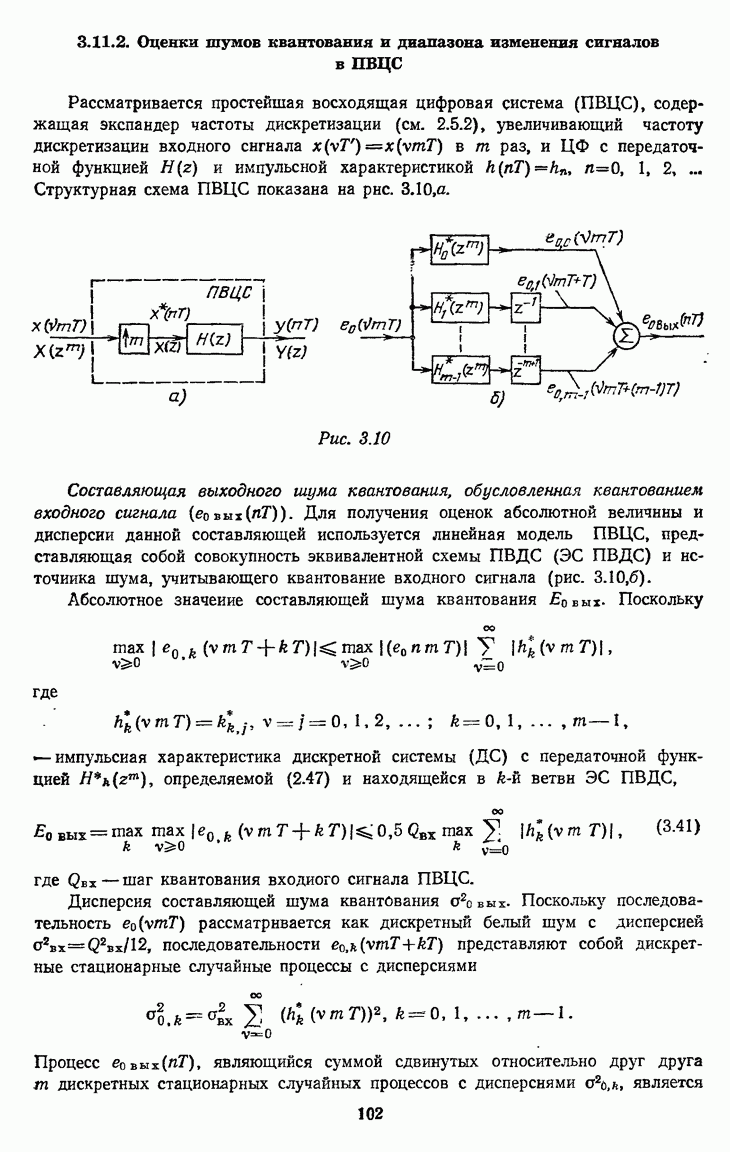
- 3.11.2. Оценки шумов квантования и диапазона изменения сигналов в ПВЦС
- 3.11.3. Оценки шумов квантования и диапазона изменения сигналов в МВЦС
- 3.11.4. Оценки шумов квантования и диапазона изменения сигналов в ПНЦС
- 3.11.5. Оценки шумов квантования и диапазона изменения сигналов в МНДС
- 4. ЭЛЕМЕНТЫ ПРОЕКТИРОВАНИЯ НЕРЕКУРСИВНЫХ ФИЛЬТРОВ
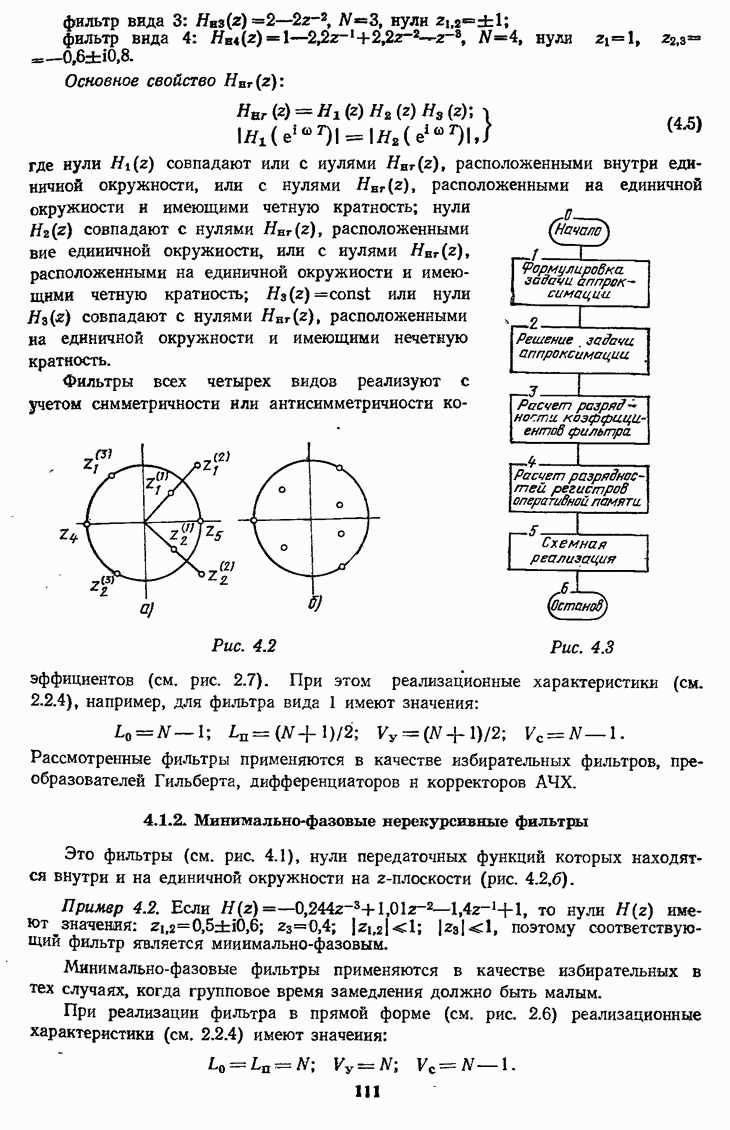
- 4.1.2. Минимально-фазовые нерекурсивные фильтры
- 4.1.3. Основные этапы проектирование нерекурсивных фильтров
- 4.1.4. Сравнение нерекурсивных и рекурсивных фильтров
- 4.2. ФОРМУЛИРОВКИ ЗАДАЧ АППРОКСИМАЦИИ
- 4.2.2. Избирательные фильтры с линейной ФЧХ
- 4.2.3. Равнополосные фильтры с линейной ФЧХ
- 4.2.4. Преобразователи Гильберта
- 4.2.5. Минимально-фазовые фильтры
- 4.3. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ АППРОКСИМАЦИИ
- 4.3.3. Метод наименьших квадратов
- 4.3.4. Метод наилучшей равномерной (чебышевской) аппроксимации. Алгоритм Ремеза
- 4.3.5. Решение чебышевской аппроксимационной задачи для фильтра с линейной ФЧХ с помощью алгоритма Ремеза
- 4.3.6. Решение чебышевской аппроксимационной задачи для минимально-фазового фильтра
- 4.3.7. Решение аппроксимационной задачи для амплитуднофазового корректора по методу наименьших квадратов
- 4.3.8. Оценка погрешности аппроксимации
- 4.3.9. Сравнение возможностей фильтров с линейной ФЧХ и минимально-фазовых фильтров
- 4.3.10. Сравнение методов решения аппроксимационных задач
- 4.4. РАСЧЕТ РАЗРЯДНОСТЕЙ КОЭФФИЦИЕНТОВ ФИЛЬТРОВ И РЕГИСТРОВ ОПЕРАТИВНОЙ ПАМЯТИ
- 4.4.6. Алгоритм расчета разрядности коэффициентов фильтра, реализуемого на специализированном микропроцессоре
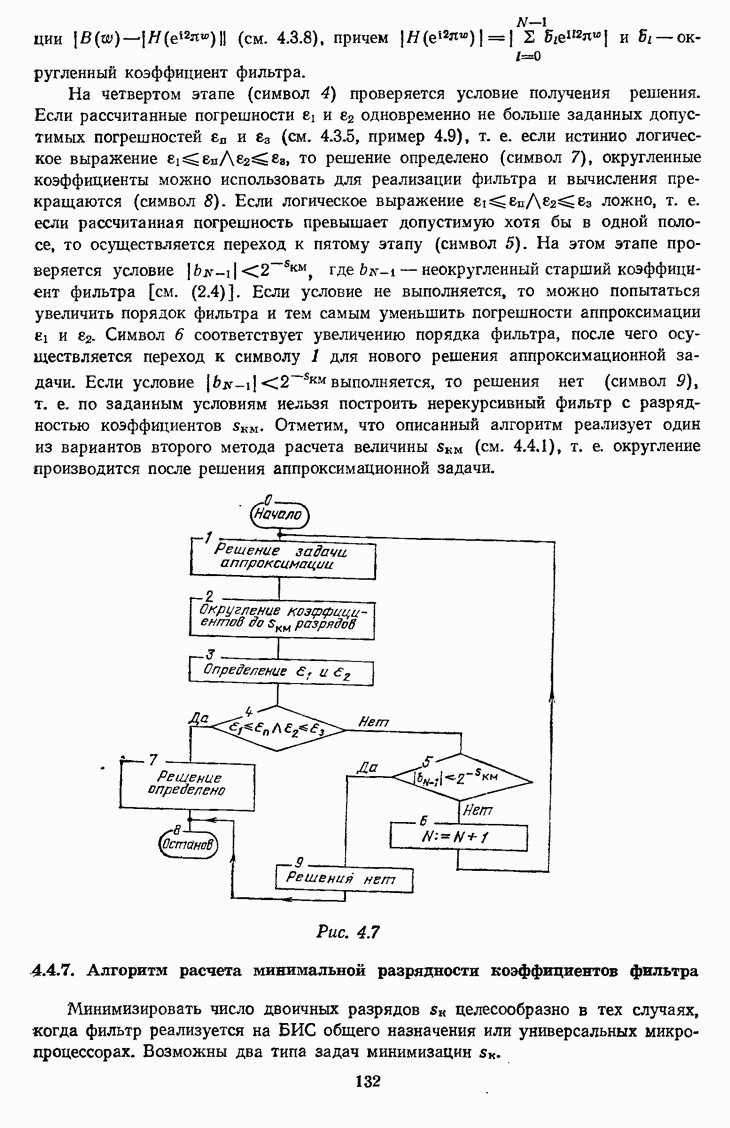
- 4.4.7. Алгоритм расчета минимальной разрядности коэффициентов фильтра
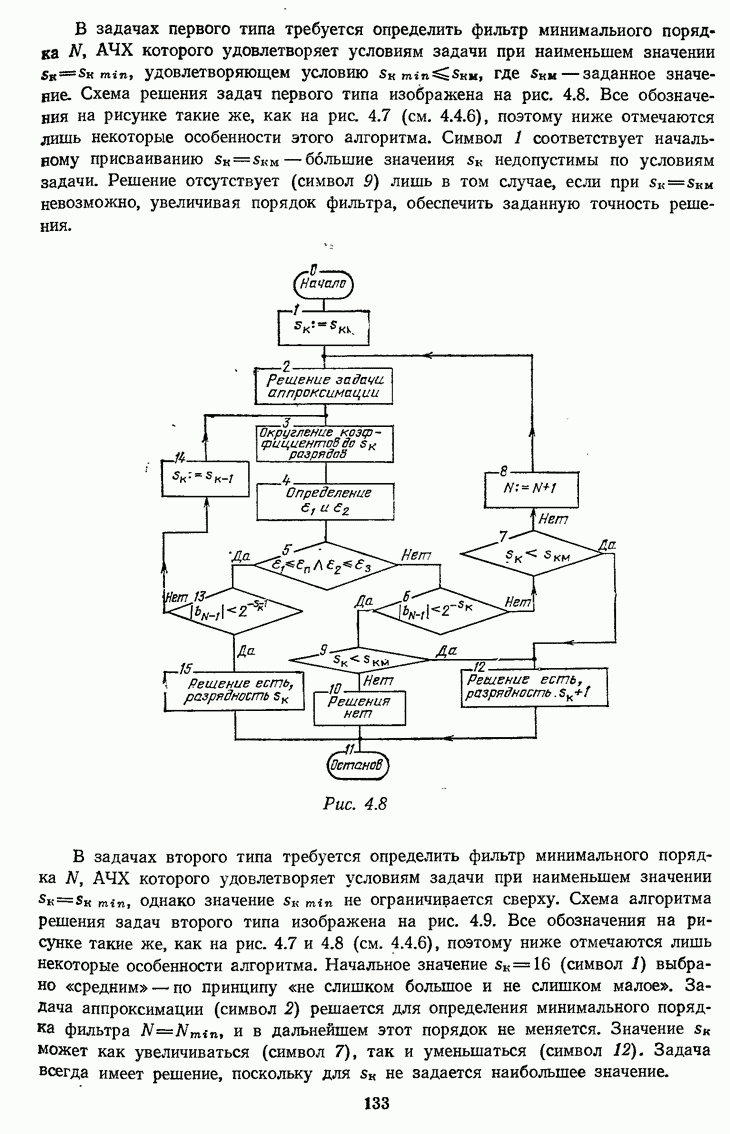
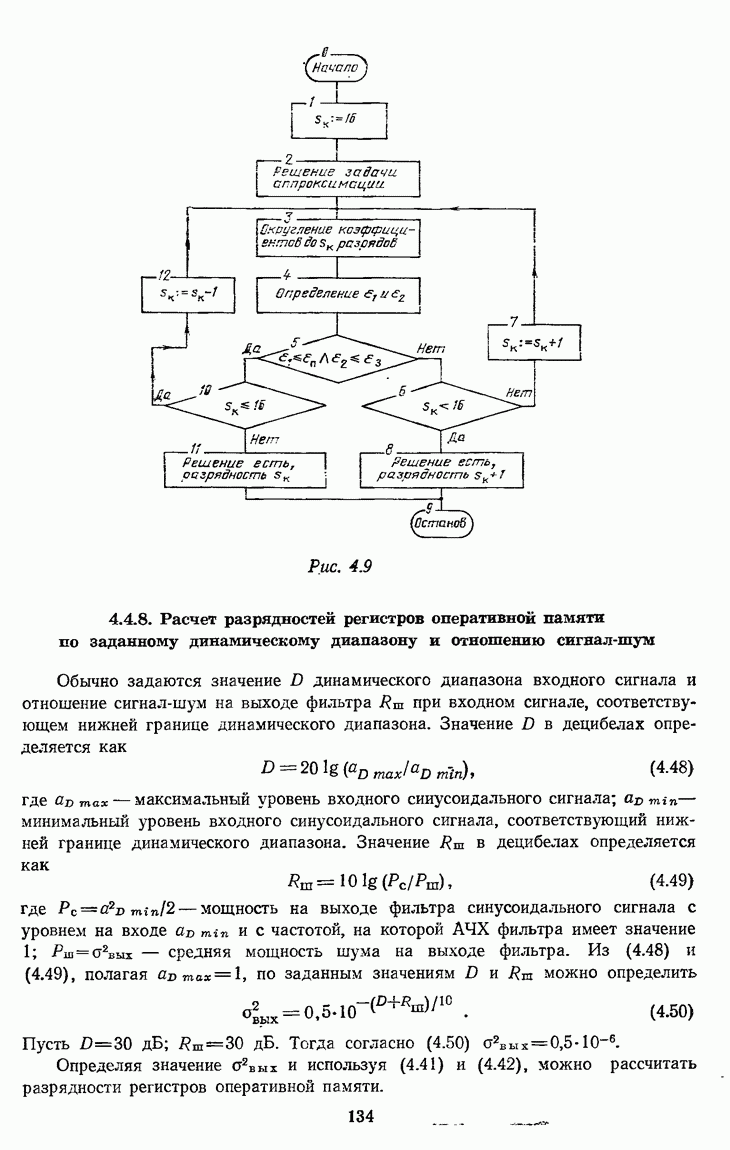
- 4.4.8. Расчет разрядностей регистров оперативной памяти по заданному динамическому диапазону и отношению сигнал-шум
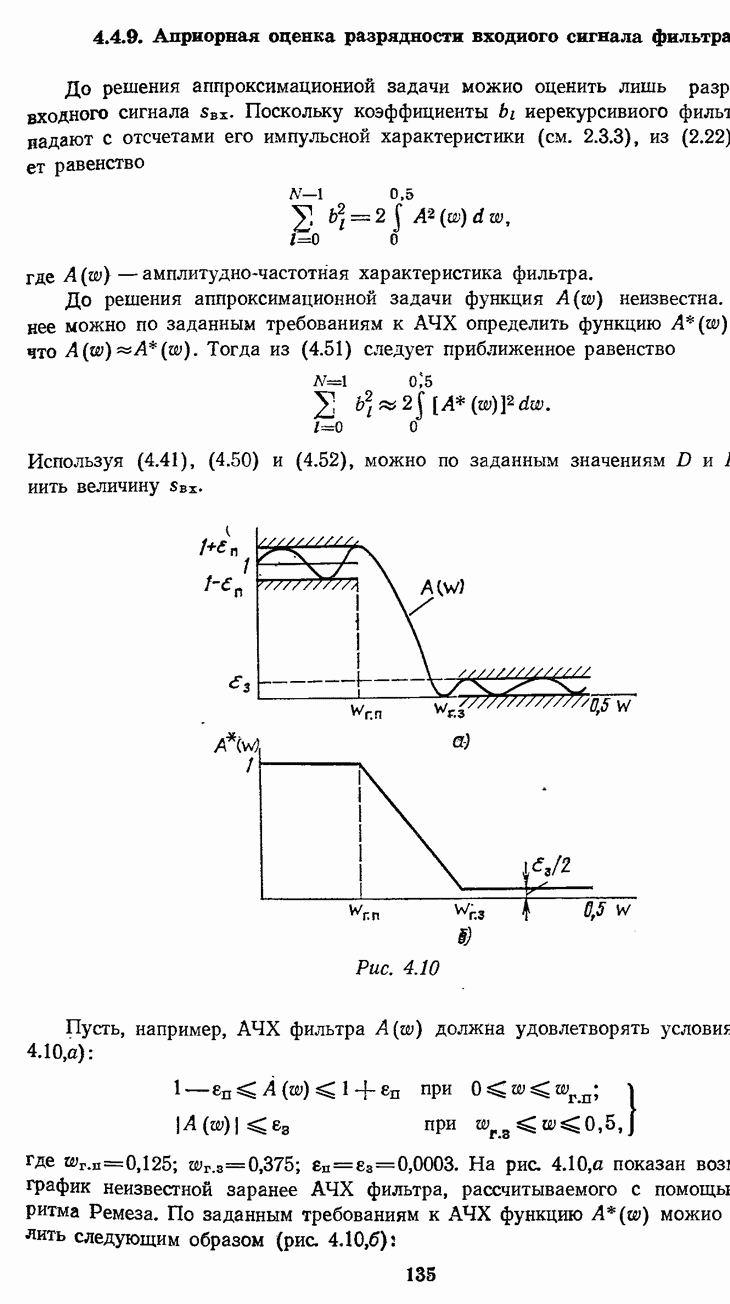
- 4.4.9. Априорная оценка разрядности входного сигнала фильтра
- 5. ЭЛЕМЕНТЫ ПРОЕКТИРОВАНИЯ РЕКУРСИВНЫХ ЦИФРОВЫХ ФИЛЬТРОВ
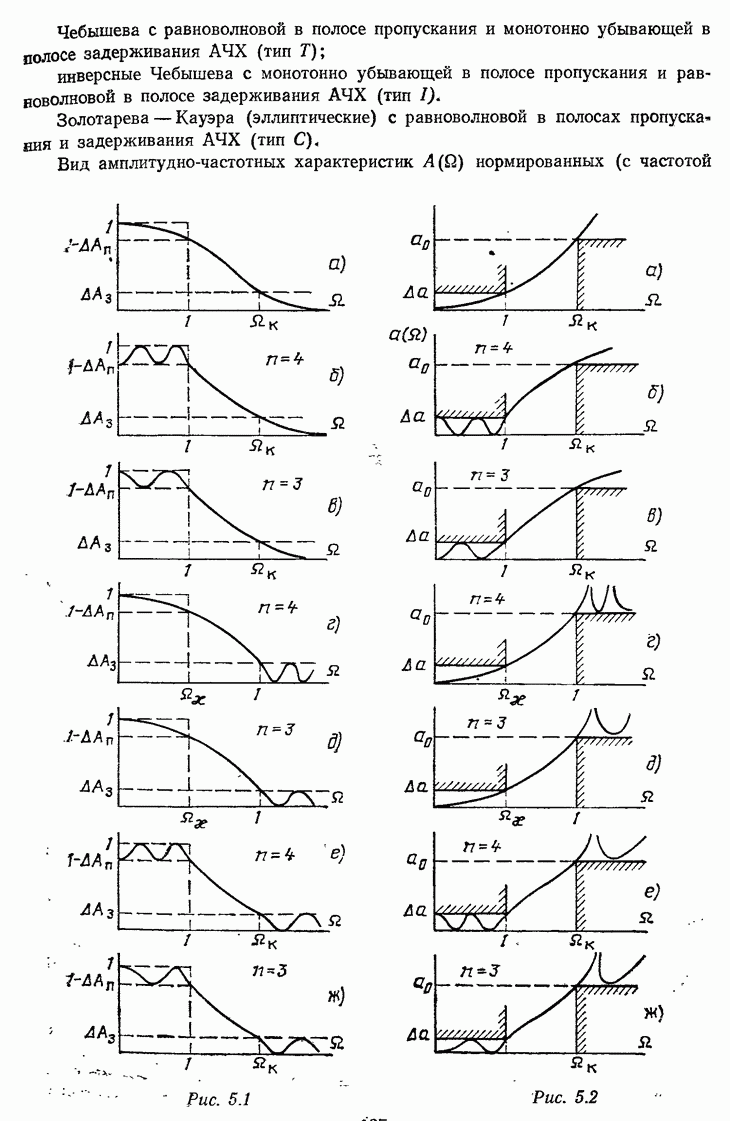
- 5.1.2. Типы аналоговых фильтров
- 5.1.3. Билинейное преобразование
- 5.1.4. Обобщенное билинейное преобразование
- 5.1.5. Определение передаточной функции цифрового ФНЧ (ФВЧ) по справочнику [5.1]
- 5.1.6. Определение передаточной функции цифрового полосового (режекторного) фильтра по справочнику [5.1]
- 5.1.7. Определение передаточной функции параллельной структуры РЦФ
- 5.1.8. Определение передаточной функции РЦФ с помощью билинейного преобразования на ЭВМ
- 5.2. РАСЧЕТ РАЗРЯДНОСТЕЙ КОЭФФИЦИЕНТОВ ФИЛЬТРА И РЕГИСТРОВ ОПЕРАТИВНОЙ ПАМЯТИ
- 5.2.2. Определение разрядности коэффициентов
- 5.2.3. Определение разрядностей входного сигнала и регистров оперативной памяти по вероятностной модели ошибок квантования
- 5.2.4. Определение разрядностей входного сигнала и регистров оперативной памяти по детерминированной модели ошибок квантования
- 5.3. РАСЧЕТ МАСШТАБНЫХ МНОЖИТЕЛЕЙ
- 5.4. РАССТАНОВКА ЗВЕНЬЕВ В КАСКАДНЫХ СТРУКТУРАХ РЦФ
- 5.5. УСТОЙЧИВОСТЬ РЕКУРСИВНЫХ ЦИФРОВЫХ ФИЛЬТРОВ
- 5.5.2. Определение устойчивости и класса входных сигналов РЦФ
- 5.5.3. Устойчивость положения равновесия
- 5.5.4. Устойчивость процессов
- 6. АДАПТИВНЫЕ ДИСКРЕТНЫЕ И ЦИФРОВЫЕ ФИЛЬТРЫ
- 6.1.2. Критерии настройки адаптивных фильтров и методы определения значений их параметров
- 6.2. АДАПТИВНЫЙ ФИЛЬТР-КОМПЕНСАТОР ПОМЕХ
- 6.2.2. Точный алгоритм настройки нерекурсивного адаптивного фильтра по минимуму СКО
- 6.2.3. Настройка нерекурсивного адаптивного фильтра по минимуму СКО с помощью градиентного метода
- 6.3. АДАПТИВНЫЙ ФИЛЬТР — ЛИНЕЙНОЕ ПРЕДСКАЗЫВАЮЩЕЕ УСТРОЙСТВО
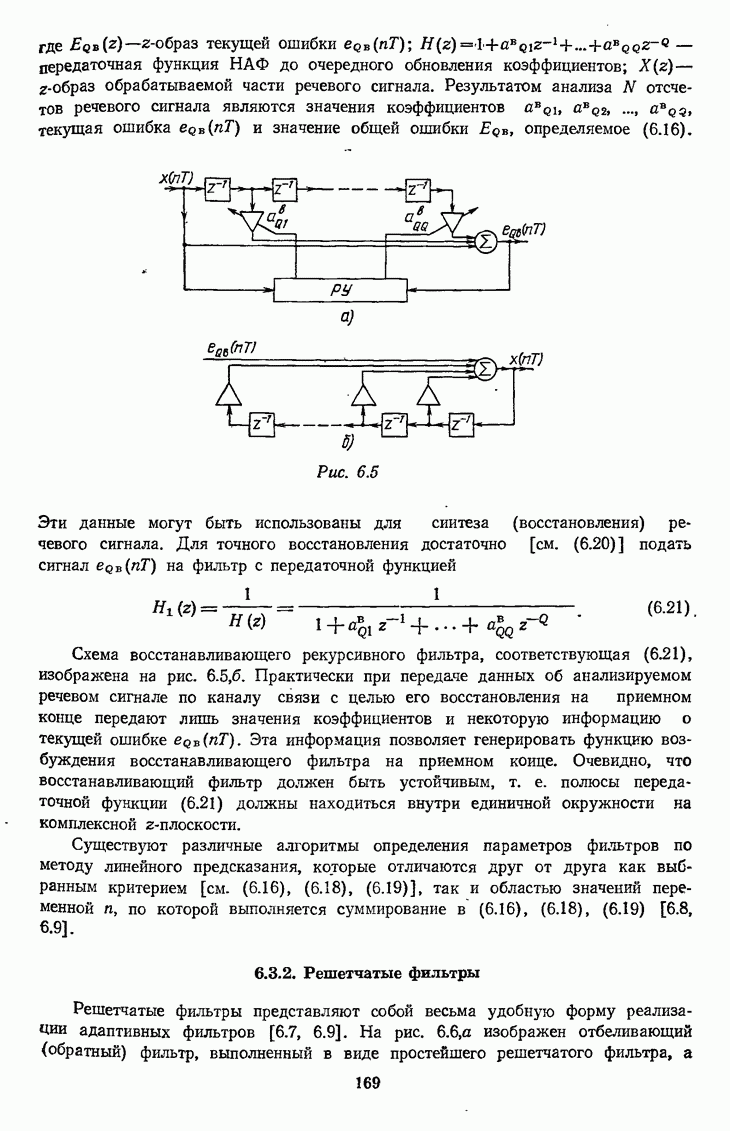
- 6.3.2. Решетчатые фильтры
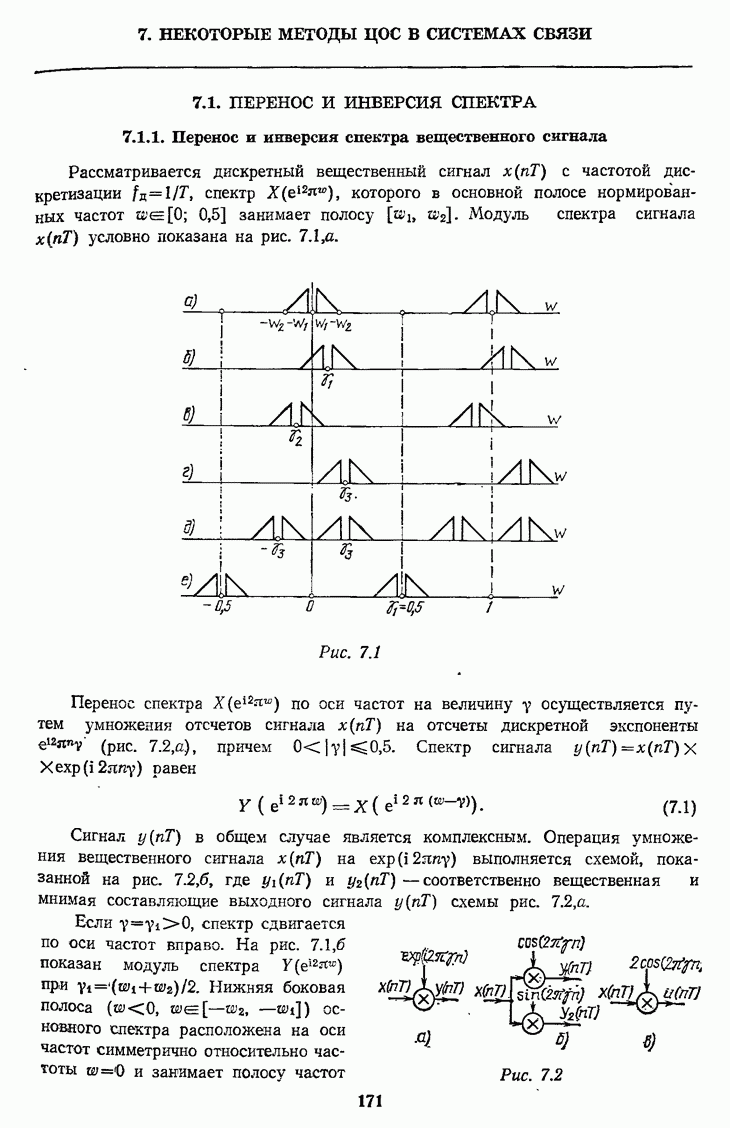
- 7. НЕКОТОРЫЕ МЕТОДЫ ЦОС В СИСТЕМАХ СВЯЗИ
- 7.2. ФОРМИРОВАНИЕ СИГНАЛА С ОДНОЙ БОКОВОЙ ПОЛОСОЙ (ОБП)
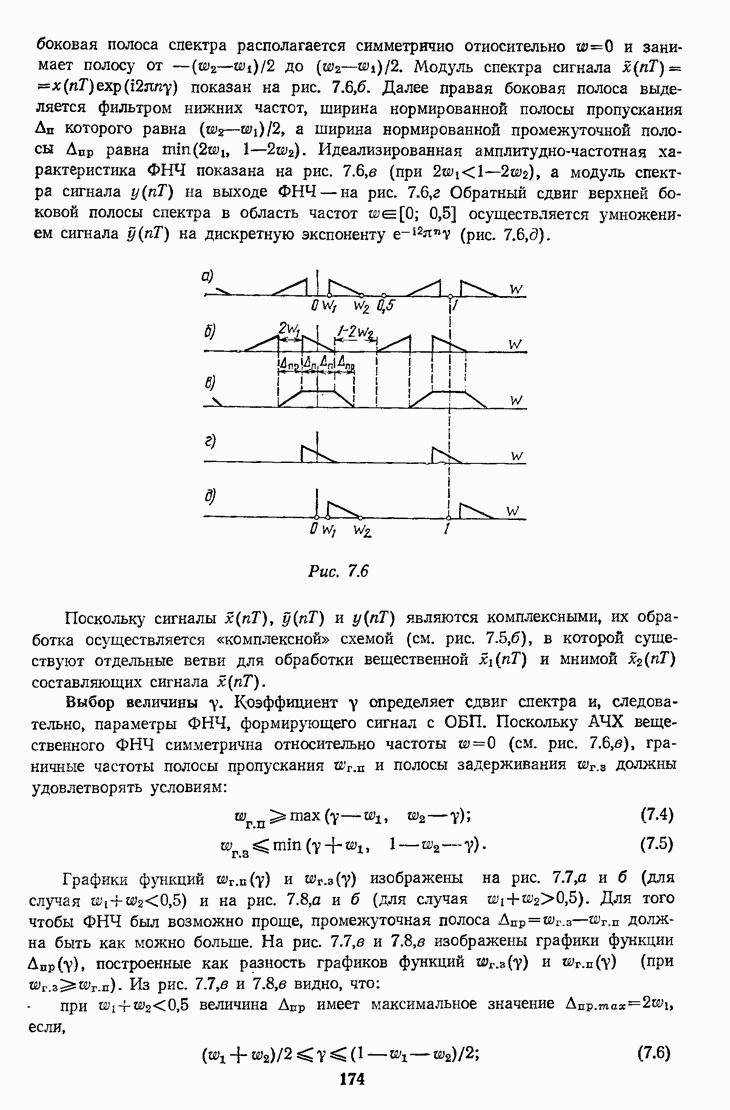
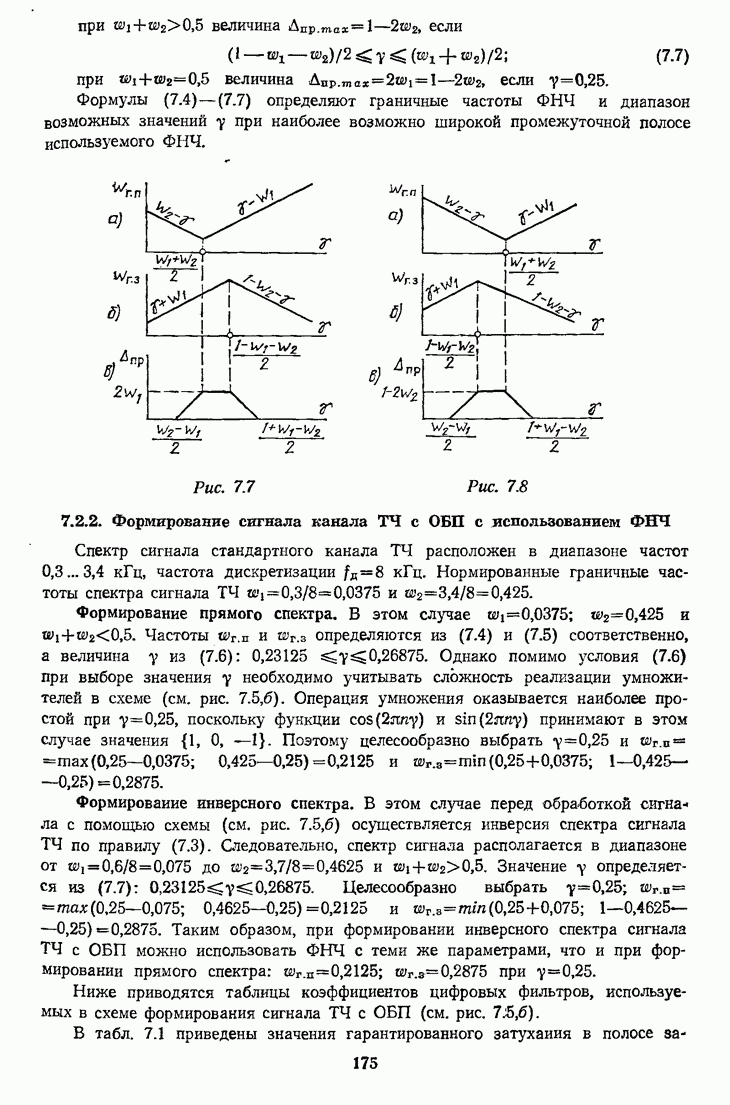
- 7.2.2. Формирование сигнала канала ТЧ с ОБП с использованием ФНЧ
- 7.2.3. Формирование сигнала с ОБП с использованием преобразователя Гильберта
- 7.3. УВЕЛИЧЕНИЕ ЧАСТОТЫ ДИСКРЕТИЗАЦИИ (ИНТЕРПОЛЯЦИЯ) СИГНАЛА
- 7.3.2. Интерполяция сигнала с помощью ПВДС
- 7.3.3. Особенности использования НФ и РФ при интерполяции
- 7.3.4. Характеристики фильтров реальных ПВДС
- 7.3.5. Структуры ПВДС при интерполяции
- 7.3.6. Цифровая фильтрация при полиномиальной интерполяции
- 7.3.7. Простейшие ВДС с оптимальными фильтрами
- 7.3.8. Перевес спектра при интерполяция
- 7.3.9. Перенос спектра при интерполяции комплексного сигнала
- 7.3.10. Интерполяция сигнала с помощью МВДС
- 7.4. УМЕНЬШЕНИЕ ЧАСТОТЫ ДИСКРЕТИЗАЦИИ (ДЕЦИМАЦИЯ) СИГНАЛА
- 7.4.2. Особенности использования НФ и РФ при децимации
- 7.4.3. Структуры ПНДС при децимации сигнала
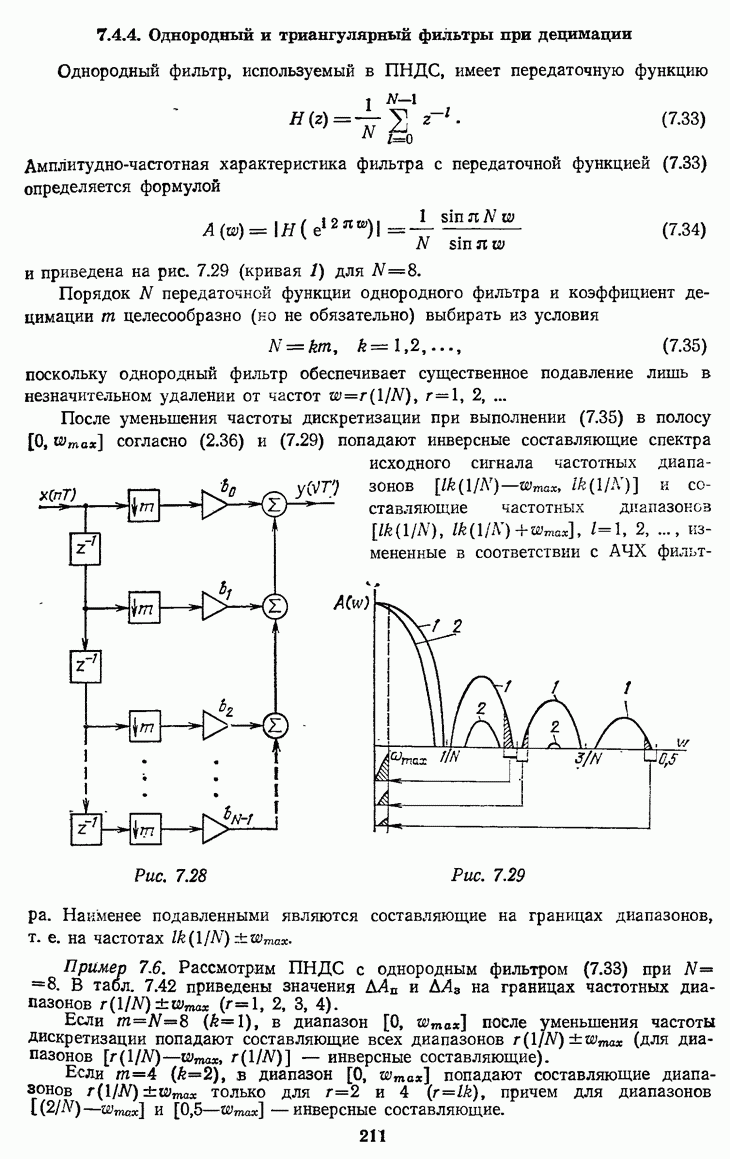
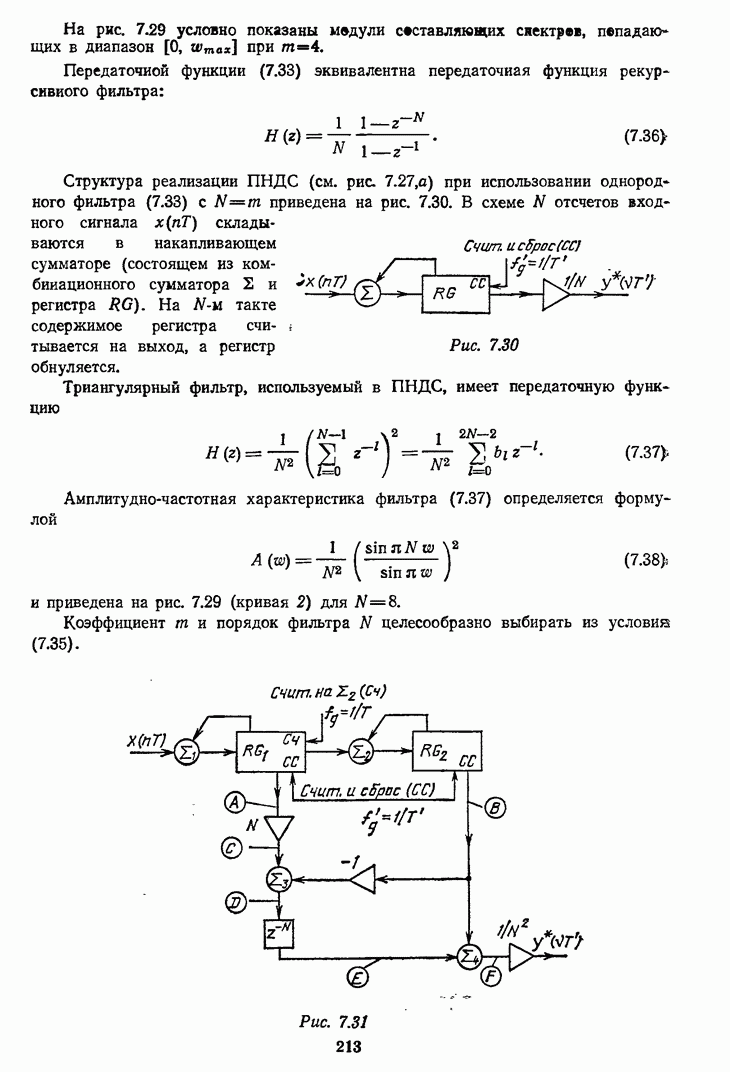
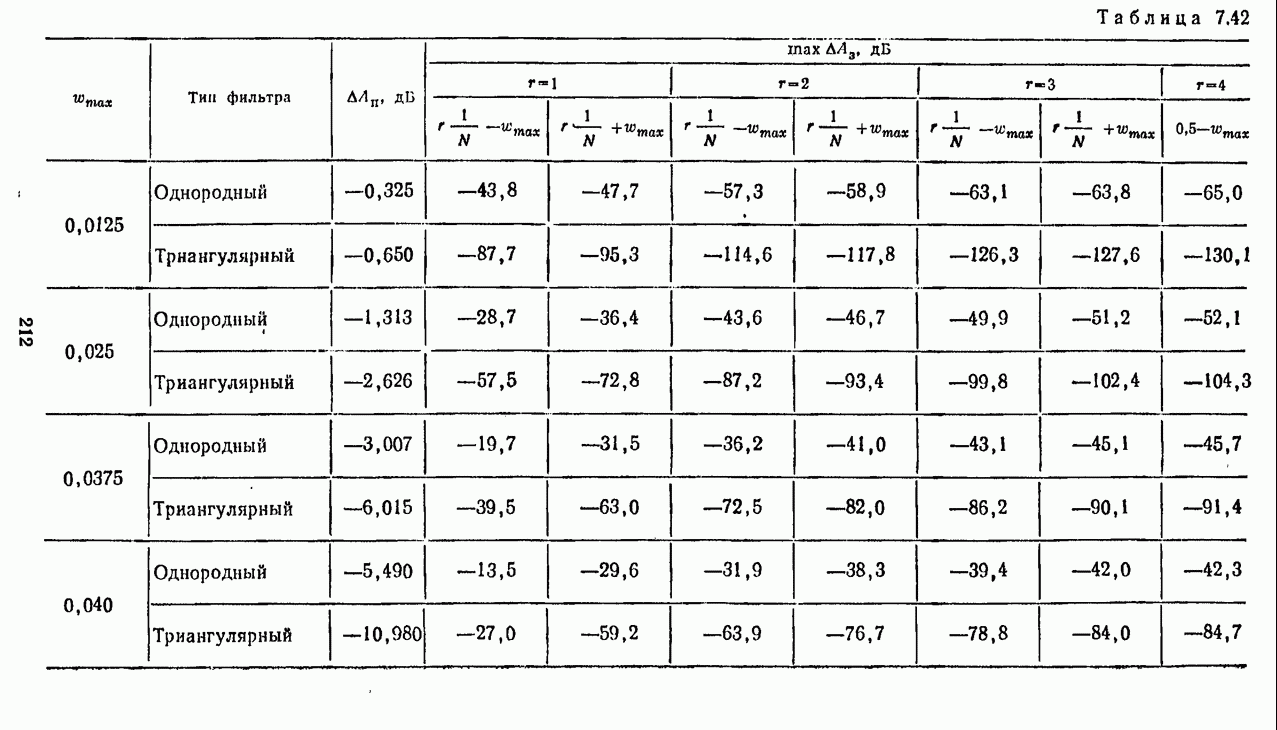
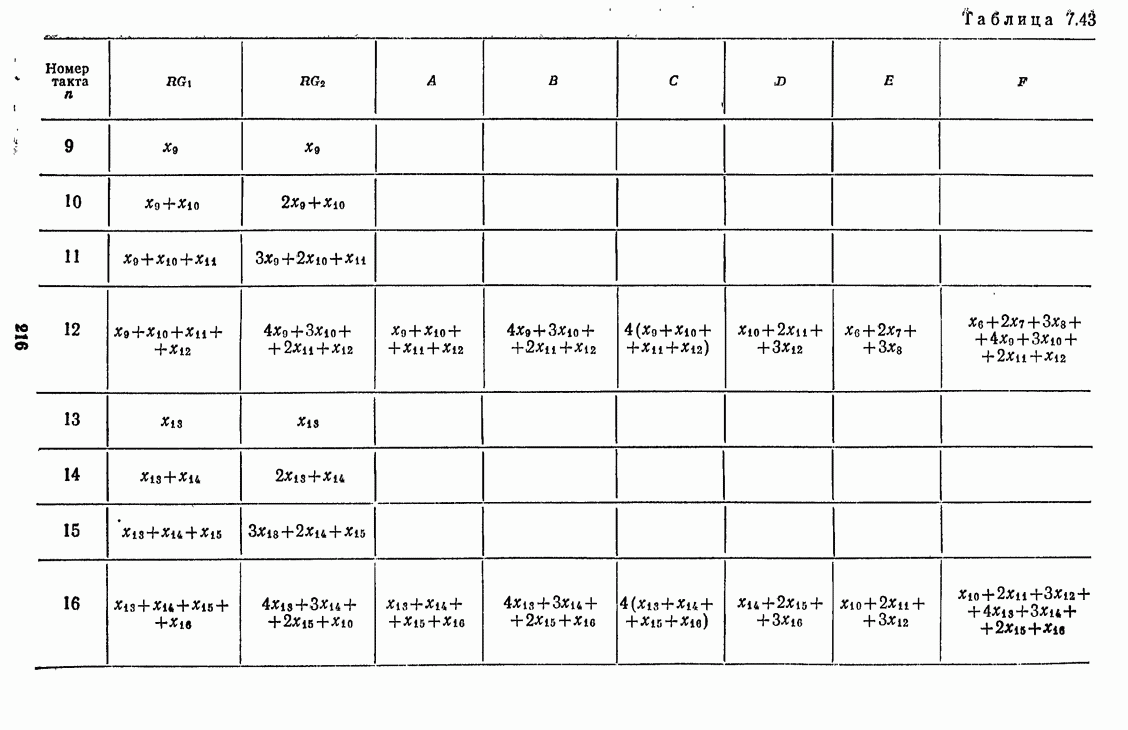
- 7.4.4. Однородный и триангулярный фильтры при децимации
- 7.4.5. Простейшая НДС с оптимальными фильтрами
- 7.4.6. Перенос спектра при полосовой фильтрации с уменьшением частоты дискретизации
- 7.4.7. Перенос спектра при децимации комплексного сигнала
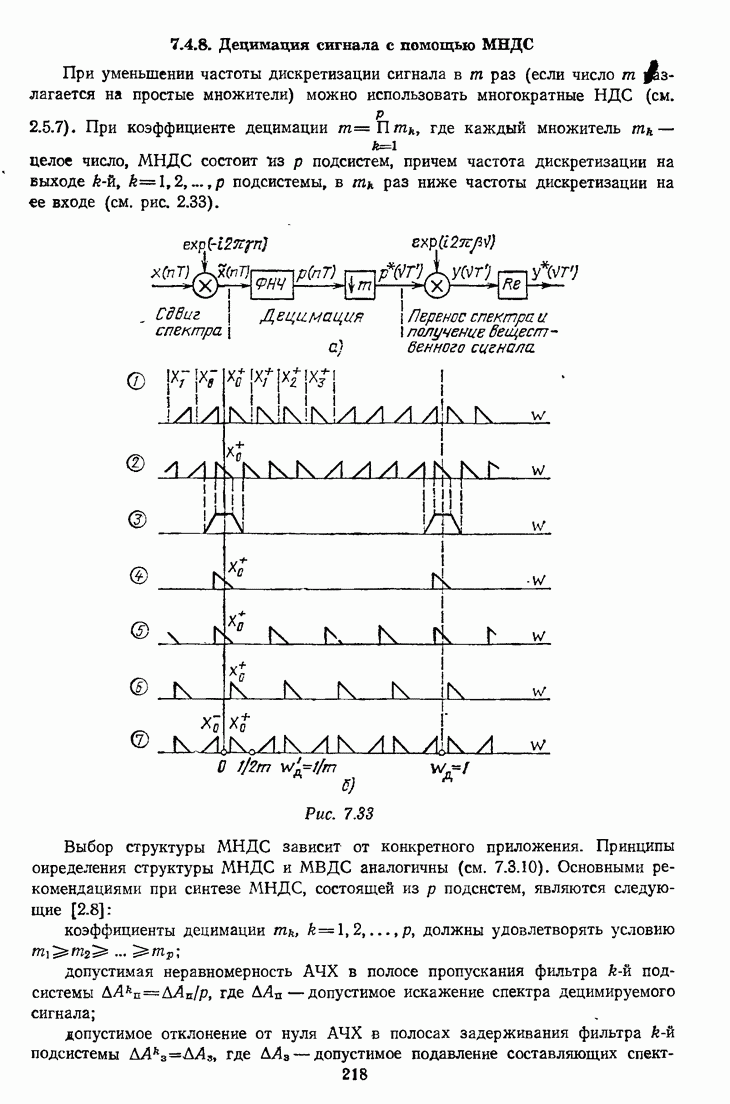
- 7.4.8. Децимация сигнала с помощью МНДС
- 8. ЦИФРОВЫЕ МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА
- 8.2. МЕТОД ПЕРИОДОГРАММ
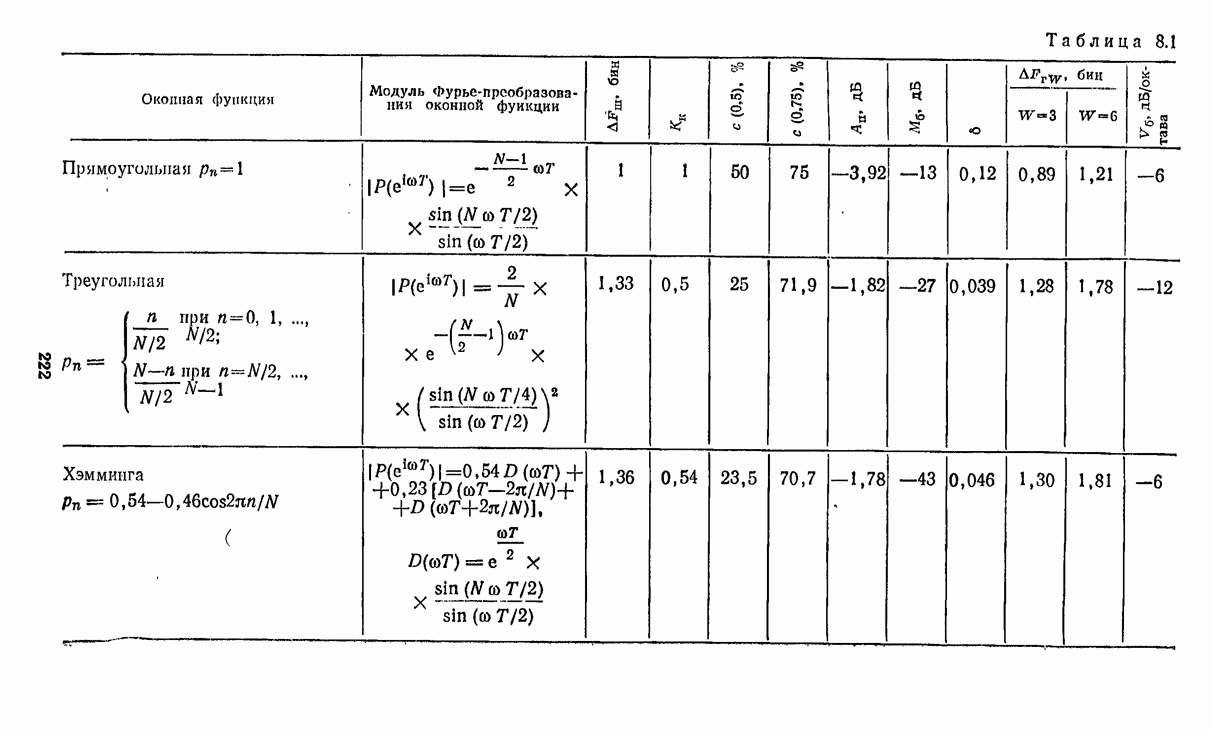
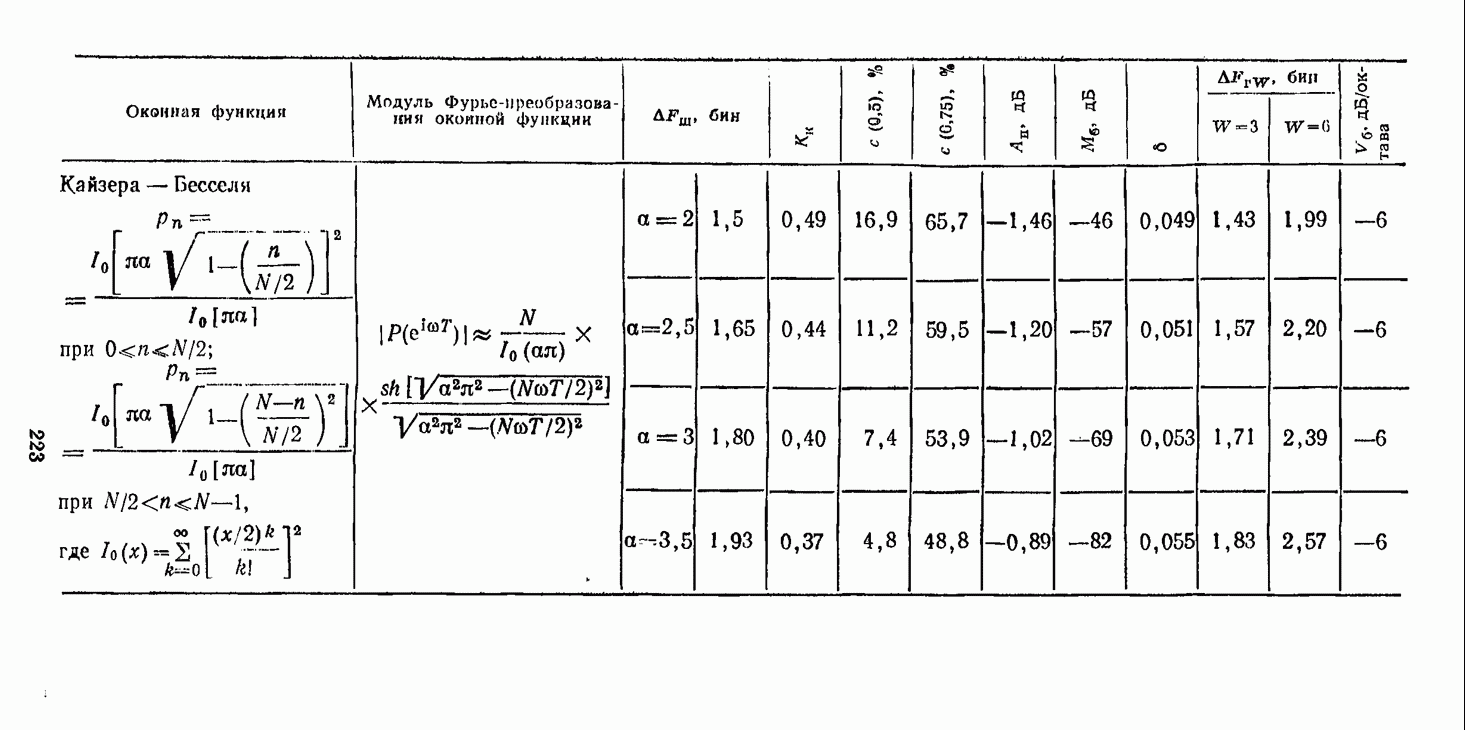
- 8.2.2. Основные свойства оконных функций
- 8.2.3. Принципы выбора оконной функции
- 8.3. МЕТОДЫ СПЕКТРАЛЬНОГО АНАЛИЗА, ОСНОВАННЫЕ НА ЛИНЕЙНОМ МОДЕЛИРОВАНИИ
- 8.3.2. Определение параметров АР-модели по известной автокорреляционной функции последовательности
- 8.3.3. Определение параметров АР-модели по анализируемым данным
- 8.3.4. Определение порядка АР-модели
- 9. ТРАНСМУЛЬТИПЛЕКСОРЫ
- 9.2. ОДНОУРОВНЕВЫЕ СТРУКТУРЫ ТМ БЕЗ ДОПОЛНИТЕЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- 9.2.2. Структура ТМ с комплексными сигналами и однократным изменением частоты дискретизации
- 9.2.3. Структура ТМ с комплексными сигналами, однократным изменением частоты дискретизации и дополнительными ФНЧ
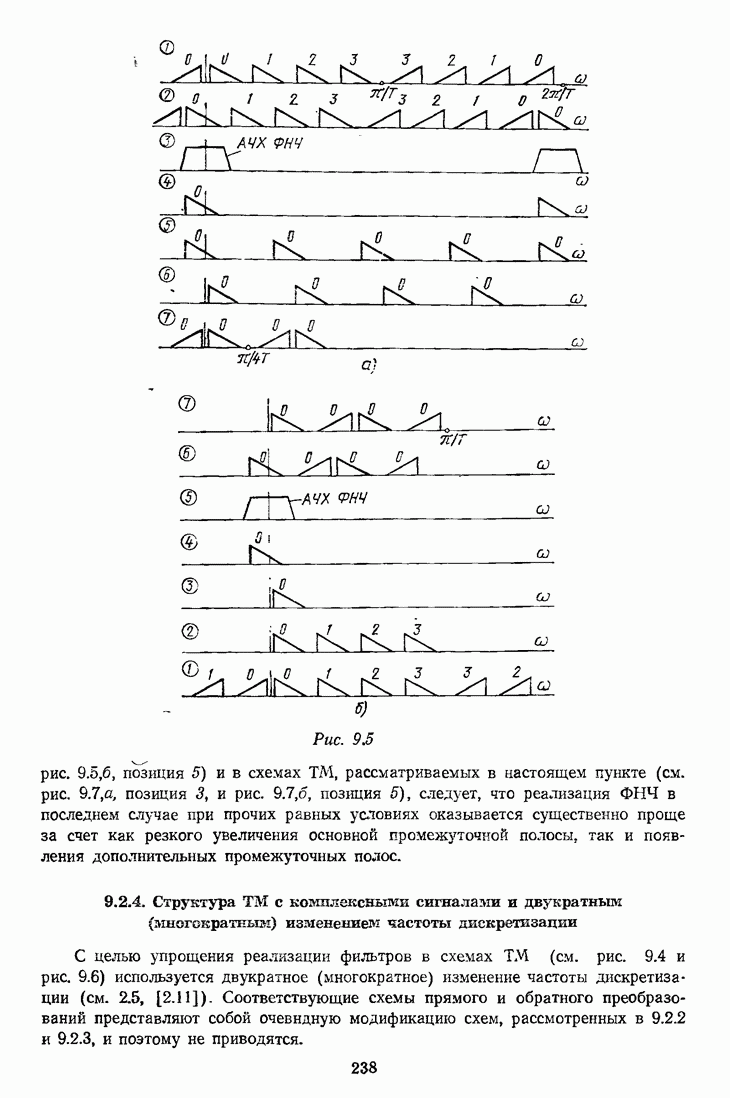
- 9.2.4. Структура ТМ с комплексными сигналами и двукратным (многократным) изменением частоты дискретизации
- 9.3. МНОГОУРОВНЕВЫЕ СТРУКТУРЫ ТМ БЕЗ ДОПОЛНИТЕЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- 9.4. ТРАНСМУЛЬТИПЛЕКСОРЫ С ДОПОЛНИТЕЛЬНЫМИ ПРЕОБРАЗОВАНИЯМИ