| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Голоморфные функции
6. Простейшие свойства.
В предыдущем параграфе был отмечен ряд свойств голоморфных функций нескольких переменных, которые являются распространением соответствующих свойств функций одного переменного (интегральная формула Коши для поликругов, разложимость в степенной ряд, бесконечная дифференцируемость, неравенства Коши). Здесь мы продолжим изучение таких свойств.
Начнем с теоремы единственности. В формулировке п. 21 ч. I она на пространственный случай не распространяется: функция  голоморфная в
голоморфная в  и не равная тождественно нулю, обращается в нуль на множестве с предельными точками (аналитических плоскостях
и не равная тождественно нулю, обращается в нуль на множестве с предельными точками (аналитических плоскостях  Верна такая
Верна такая
Теорема 1 (единственности). Если функция  в некоторой точке
в некоторой точке  области
области  обращается в нуль вместе со всеми частными производными, то
обращается в нуль вместе со всеми частными производными, то 
Все коэффициенты тейлоровского разложения  в точке
в точке  равны 0, следовательно,
равны 0, следовательно,  в некоторой окрестности этой точки. Обозначим
в некоторой окрестности этой точки. Обозначим  открытое ядро W (совокупность внутренних точек этого множества). Множество
открытое ядро W (совокупность внутренних точек этого множества). Множество  открыто и непусто (оно содержит
открыто и непусто (оно содержит  как и в
как и в  доказывается, что оно замкнуто в
доказывается, что оно замкнуто в  поэтому
поэтому 
В доказанной теореме, по существу, требуется, чтобы  обращалась в нуль в
обращалась в нуль в  -мерной окрестности точки
-мерной окрестности точки  Даже из обращения в нуль в
Даже из обращения в нуль в  -мерной окрестности точки, вообще говоря, не следует тождественного обращения функции в нуль (пример:
-мерной окрестности точки, вообще говоря, не следует тождественного обращения функции в нуль (пример:  обращается в нуль на
обращается в нуль на  -мерном множестве
-мерном множестве  Имеются, однако, случаи, когда обращение функции в нуль в
Имеются, однако, случаи, когда обращение функции в нуль в  -мерной окрестности точки влечет за собой тождественное ее равенство нулю:
-мерной окрестности точки влечет за собой тождественное ее равенство нулю:
Если функция  обращается в нуль в действительной окрестности точки
обращается в нуль в действительной окрестности точки  т. е. на множестве
т. е. на множестве  то
то 
В некотором поликруге с центром  функция
функция  разлагается в ряд
разлагается в ряд

Полагая здесь  найдем, что
найдем, что

для всех  Дифференцируя это тождество по
Дифференцируя это тождество по  а затем полагая
а затем полагая  найдем, что все
найдем, что все  По теореме 1 тогда
По теореме 1 тогда 
Теорема 2 (принцип максимума модуля).  функция
функция  достигает максимума в некоторой точке
достигает максимума в некоторой точке  то
то 
Рассмотрим любую аналитическую прямую  проходящую через точку а. Сужение
проходящую через точку а. Сужение  на эту прямую — функция
на эту прямую — функция  голоморфно в некотором круге
голоморфно в некотором круге  достигает максимума при
достигает максимума при  По принципу максимума модуля для функций одного переменного
По принципу максимума модуля для функций одного переменного  -постоянная, зависящая от со. Но
-постоянная, зависящая от со. Но  не зависит от
не зависит от  , поэтому
, поэтому  окрестности точки а. По теореме 1
окрестности точки а. По теореме 1  в D
в D
Если  голоморфна в области
голоморфна в области  и непрерывна в
и непрерывна в  то максимум
то максимум  достигается на границе
достигается на границе  Однако в
Однако в  при
при  существуют такие области, в которых
существуют такие области, в которых  для любой
для любой
 непрерывной в
непрерывной в  фактически достигается не на всей
фактически достигается не на всей  а лишь на некотором ее подмножестве. Наименьшее такое замкнутое подмножество называется границей Шилова области
а лишь на некотором ее подмножестве. Наименьшее такое замкнутое подмножество называется границей Шилова области  Точнее, границей Шилова области
Точнее, границей Шилова области  называется такое замкнутое множество
называется такое замкнутое множество  что: 1) для любой
что: 1) для любой  непрерывной в В,
непрерывной в В,

и 2) любое замкнутое множество  обладающее свойством 1), Содержит
обладающее свойством 1), Содержит 
Примеры.
1. Шар  Покажем, что здесь граница Шилова совпадает с топологической границей. Для этого возьмем произвольную точку и построим функцию
Покажем, что здесь граница Шилова совпадает с топологической границей. Для этого возьмем произвольную точку и построим функцию  голоморфную в В, непрерывную в В и такую, что
голоморфную в В, непрерывную в В и такую, что  Для всех
Для всех  Обозначим через
Обозначим через

скалярное произведение векторов  в комплексном пространстве
в комплексном пространстве  По неравенству Буняковскош — Шварца
По неравенству Буняковскош — Шварца

ибо  причем равенство
причем равенство  достигается в В лишь при
достигается в В лишь при  Поэтому функция
Поэтому функция  обладает нужным свойством.
обладает нужным свойством.
2. Поликруг  Здесь граница Шилова составляет лишь
Здесь граница Шилова составляет лишь  -мерную часть
-мерную часть  -мерной топологической границы, именно, она совпадает с остовом поликруга. Для доказательства рассмотрим любую функцию
-мерной топологической границы, именно, она совпадает с остовом поликруга. Для доказательства рассмотрим любую функцию  голоморфную в
голоморфную в  и непрерывную в
и непрерывную в  Прежде всего заметим, что функция
Прежде всего заметим, что функция  Для любого фиксированного
Для любого фиксированного  является голоморфной функцией
является голоморфной функцией  в поликруге
в поликруге  . В самом деле, ее можно представить как предел последовательности функций
. В самом деле, ее можно представить как предел последовательности функций  где
где  какая-либо последовательность точек круга
какая-либо последовательность точек круга  сходящаяся к точке Так как
сходящаяся к точке Так как  то все
то все  голоморфны в
голоморфны в  а в силу равномерной непрерывности
а в силу равномерной непрерывности  последовательность
последовательность  сходится равномерно в
сходится равномерно в  . По теореме Вейерштрасса (см. ниже, теорема 4) отсюда и следует сделанное утверждение. Точно так же доказывается, что все функции
. По теореме Вейерштрасса (см. ниже, теорема 4) отсюда и следует сделанное утверждение. Точно так же доказывается, что все функции  где
где  при фиксированных
при фиксированных  по модулю равных 1, голоморфны по
по модулю равных 1, голоморфны по  в соответствующих поликругах.
в соответствующих поликругах.
Пусть  достигается в некоторой точке
достигается в некоторой точке  которая принадлежит одному из множеств
которая принадлежит одному из множеств  перенумеровывая в случае надобности переменные, можно считать, что оно совпадает с
перенумеровывая в случае надобности переменные, можно считать, что оно совпадает с  . Либо
. Либо  либо по принципу максимума модуля (он применим по доказанному выше)
либо по принципу максимума модуля (он применим по доказанному выше)  постоянна по переменному
постоянна по переменному  и тогда значение
и тогда значение  достигается в некоторой точке, две последние координаты которой по модулю равны 1. Продолжая это рассуждение, мы получим, что значение
достигается в некоторой точке, две последние координаты которой по модулю равны 1. Продолжая это рассуждение, мы получим, что значение  достигается на остове поликруга
достигается на остове поликруга  Таким образом, граница Шилова поликруга
Таким образом, граница Шилова поликруга  принадлежит
принадлежит 
Но для любой точки  найдется функция
найдется функция  голоморфная в
голоморфная в  и непрерывная в
и непрерывная в  для которой
для которой  для всех
для всех  в качестве такой функции можно взять произведение
в качестве такой функции можно взять произведение  Таким образом, граница Шилова совпадает с
Таким образом, граница Шилова совпадает с 
Теорема 3 (Лиувилль). Если функция  голоморфна в
голоморфна в  и ограничена, то она постоянна.
и ограничена, то она постоянна.
Воспользуемся индукцией по  При
При  теорема доказана в первой части, пусть она верна для функций
теорема доказана в первой части, пусть она верна для функций  переменного. Возьмем произвольные точки
переменного. Возьмем произвольные точки  так как функция
так как функция  по индуктивному предположению постоянна, то
по индуктивному предположению постоянна, то  Но функция
Но функция  также постоянна, следовательно,
также постоянна, следовательно,  Таким образом,
Таким образом,  т. е. теорема верна для функций
т. е. теорема верна для функций  переменных
переменных
В дальнейшем теорема будет усилена (см. п. 18, а также задачу 9).
Теорема 4 (Вейерштрасс). Пусть последовательность функций  сходится к функции
сходится к функции  равномерно на каждом компактном подмножестве
равномерно на каждом компактном подмножестве  тогда
тогда  и для любого
и для любого 

на любом 
По теореме  функция голоморфна по каждому переменному в любой точке
функция голоморфна по каждому переменному в любой точке  и по теореме Хартогса принадлежит
и по теореме Хартогса принадлежит  Вторую часть теоремы достаточно доказать для окрестности произвольной точки
Вторую часть теоремы достаточно доказать для окрестности произвольной точки  и производной по одному переменному
и производной по одному переменному  Возьмем поликруг
Возьмем поликруг  и воспользуемся формулой Коши
и воспользуемся формулой Коши

где  остов
остов  Так как
Так как  равномерно на
равномерно на  то для любого
то для любого  найдется
найдется  такое, что
такое, что  Для всех
Для всех  Если
Если  то из (3) будем иметь для всех
то из (3) будем иметь для всех  до
до 

 отсюда следует, что -
отсюда следует, что - -равномерно на
-равномерно на 
Приведем теперь наиболее содержательное из обобщений на пространственный случай свойство голоморфных функций — так называемую подготовительную теорему (Vorbereitungsatz) Вейерштрасса. Эта теорема обобщает известное свойство голоморфных функций одного переменного обращаться в нуль как целые степени  : если
: если  (но
(но  ), то в некоторой окрестности точки
), то в некоторой окрестности точки 

где  голоморфна и не обращается в нуль.
голоморфна и не обращается в нуль.
Теорема 5. Пусть функция  голоморфна в некоторой окрестности
голоморфна в некоторой окрестности  точки
точки  но
но  тогда в некоторой окрестности V этой точки
тогда в некоторой окрестности V этой точки

где  -порядок нуля
-порядок нуля  в точке
в точке  функции
функции  голоморфны в
голоморфны в  голоморфна в V и не обращается там в нуль.
голоморфна в V и не обращается там в нуль.
Без ограничения общности считаем, что  По теореме единственности для функций одного переменного можно выбрать
По теореме единственности для функций одного переменного можно выбрать  так, чтобы
так, чтобы  при
при  непре рывности
непре рывности  найдется поликруг
найдется поликруг  такой, что
такой, что  при
при  Для любого фиксированного
Для любого фиксированного  число ну лей функции
число ну лей функции  в круге
в круге  равно
равно

ибо левая часть (6) — целочисленная и непрерывная функция точки  следовательно, постоянная, а при
следовательно, постоянная, а при  она равна порядку нуля функции
она равна порядку нуля функции  в точке
в точке  т. е.
т. е. 
Фиксируем  обозначим через
обозначим через  нули функции
нули функции  в круге
в круге  и построим многочлен относительно
и построим многочлен относительно 

имеющий эти нули своими корнями. Его коэффициенты голоморфны в  . В самом деле, для любой голоморфной в
. В самом деле, для любой голоморфной в  функции
функции  по обобщенному принципу аргумента (см. задачу 1 к гл. IV ч. I)
по обобщенному принципу аргумента (см. задачу 1 к гл. IV ч. I)

откуда видно, что суммы в левой части — голоморфные функции переменного  в V (мы учитываем, что
в V (мы учитываем, что  при
при  Полагая здесь о
Полагая здесь о  найдем, что суммы
найдем, что суммы  степеней корней многочлена (7) голоморфны в V, а через эти суммы (как известно из алгебры) рационально выражаются его коэффициенты, следовательно,
степеней корней многочлена (7) голоморфны в V, а через эти суммы (как известно из алгебры) рационально выражаются его коэффициенты, следовательно,  При
При  все
все  корней многочлена равны нулю, поэтому и все
корней многочлена равны нулю, поэтому и все 
Функция

при любом фиксированном  является голоморфной функцией
является голоморфной функцией  в круге
в круге  и не обращается в нуль, ибо
и не обращается в нуль, ибо  обращается в нуль того же порядка лишь в точках
обращается в нуль того же порядка лишь в точках  в которых и
в которых и  При фиксированном
При фиксированном  имеем
имеем

а так как  на
на  (ибо там
(ибо там  ), то правая часть, а значит и
), то правая часть, а значит и  голоморфно зависит от
голоморфно зависит от  По теореме Хартогса
По теореме Хартогса  голоморфна в поликруге
голоморфна в поликруге 
Подготовительная теорема Вейерштрасса показывает, что голоморфная функция обращается в нуль как многочлен относительно переменного  с коэффициентами из кольца
с коэффициентами из кольца  функций от
функций от  голоморфных в точке а. Точнее, все коэффициенты,
голоморфных в точке а. Точнее, все коэффициенты,
кроме старшего, принадлежат идеалу, который образуют в  функции, обращающиеся в нуль в этой точке. Таким образом, эта теорема позволяет привлечь для исследования множества нулей голоморфных функций алгебраические методы.
функции, обращающиеся в нуль в этой точке. Таким образом, эта теорема позволяет привлечь для исследования множества нулей голоморфных функций алгебраические методы.
Замечание. Если и выполняются все условия теоремы Вейерштрасса, кроме условия  то существует линейная замена переменных
то существует линейная замена переменных  или, в подробной записи,
или, в подробной записи,

после которой  переходит в функцию
переходит в функцию  такую, что
такую, что  .
.
Для доказательства выпишем группу членов

тейлоровского разложения  в точке а наименьшего порядка
в точке а наименьшего порядка  при котором не все коэффициенты группы равны 0. Сделаем в ней замену переменных (8), причем матрицу
при котором не все коэффициенты группы равны 0. Сделаем в ней замену переменных (8), причем матрицу  подберем так, чтобы
подберем так, чтобы  и чтобы коэффициент при
и чтобы коэффициент при 

После такой замены  перейдет в функцию
перейдет в функцию  для которой
для которой  что и требуется.
что и требуется.
Заметим еще, что при  разложению Вейерштрасса функции О можно придать вид
разложению Вейерштрасса функции О можно придать вид 

для которого условие  не требуется (здесь
не требуется (здесь  голоморфные в точке а
голоморфные в точке а  функции,
функции,  и I — целые числа,
и I — целые числа,  голоморфная в точке
голоморфная в точке  функция, не обращающаяся в нуль). В самом деле, если
функция, не обращающаяся в нуль). В самом деле, если  то мы имеем разложение (9) с
то мы имеем разложение (9) с  если же
если же  то из тейлоровского разложения мы получим, что
то из тейлоровского разложения мы получим, что  где уже
где уже  и, применяя теорему к функции
и, применяя теорему к функции  придем к разложению (9).
придем к разложению (9).
В заключение этого пункта докажем лемму о голоморфной зависимости интегралов от параметра, которой мы несколько раз пользовались при доказательстве подготовительной теоремы
Вейерштрасса. Мы рассмотрим ее в несколько более общей ситуации.
Лемма. Пусть  - спрямляемая кривая в плоскости
- спрямляемая кривая в плоскости  область в
область в  пусть
пусть  Если функция
Если функция  непрерывна на
непрерывна на  голоморфна по
голоморфна по  при любом
при любом  и имеет на
и имеет на  непрерывные частные производные
непрерывные частные производные 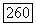 то интеграл
то интеграл

голоморфен в D и

Для любого 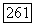 выберем
выберем 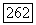 так, чтобы поликруг
так, чтобы поликруг 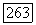 пусть
пусть 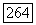 вектор, у которого все координаты, кроме
вектор, у которого все координаты, кроме 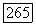 равны 0. Имеем
равны 0. Имеем

и, следовательно,

В силу того, что 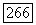 при фиксированном
при фиксированном 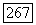 равномерно непрерывна на компактном множестве
равномерно непрерывна на компактном множестве 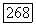 то для любого
то для любого 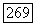 можно выбрать
можно выбрать 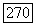 столь малым, что для всех
столь малым, что для всех 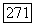 при
при 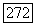 будет
будет

Поэтому, оценивая последовательно интегралы в правой части (12), мы найдем, что левая часть этого равенства 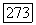
не превосходит по модулю 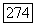 Таким образом, в каждой точке
Таким образом, в каждой точке 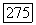 все частные производные
все частные производные 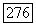 существуют и выражаются формулами
существуют и выражаются формулами 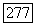
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ГОЛОМОРФНЫЕ ФУНКЦИИ
- 1. Комплексные числа.
- 2. Топология комплексной плоскости.
- 3. Пути и кривые.
- 4. Области.
- § 2. Функции комплексного переменного
- 6. Дифференцируемость.
- 7. Геометрическая и гидродинамическая интерпретация.
- § 3. Элементарные функции
- 9. Геометрические свойства.
- 10. Дробно-линейные изоморфизмы и автоморфизмы.
- 11. Некоторые рациональные функции.
- 12. Показательная функция.
- 13. Тригонометрические функции.
- ГЛАВА II. СВОЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ
- 15. Первообразная.
- 16. Гомотопия. Теорема Коши.
- 17. Обобщения теоремы Коши.
- 18. Интегральная формула Коши.
- § 5. Ряды Тейлора
- 20. Свойства голоморфных функций.
- 21. Теорема единственности.
- 22. Теорема Вейерштрасса
- § 6. Ряды Лорана и особые точки
- 24. Изолированные особые точки.
- 25. Вычеты.
- ГЛАВА III. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
- § 7. Понятие аналитического продолжения
- 27. Продолжение вдоль пути.
- § 8. Понятие аналитической функции
- 29. Элементарные функции.
- 30. Особые точки.
- § 9. Понятие римановой поверхности
- ГЛАВА IV. ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ
- § 10. Геометрические принципы
- 34. Принцип сохранения области.
- 35. Принцип максимума модуля и лемма Шварца.
- § 11. Теорема Римана
- 37. Принцип компактности.
- 38. Теорема Римана.
- § 12. Соответствие границ и принцип симметрии
- 40. Принцип симметрии.
- 41. Эллиптический синус и модулярная функция.
- ГЛАВА V. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ
- § 13. Разложения целых и мероморфных функций
- 43. Теорема Вейерштрасса.
- § 14. Гармонические и субгармонические функции
- 45. Задача Дирихле.
- 46. Субгармонические функции.
- ГЛАВА I. ГОЛОМОРФНЫЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. Простейшие области.
- § 2. Понятие голоморфности
- 4. Плюригармонические функции.
- 5. Основная теорема Хартогса.
- § 3. Голоморфные функции
- 7. Степенные ряды.
- ГЛАВА II. ИНТЕГРИРОВАНИЕ
- § 4. Многообразия и формы
- 11. Понятие интеграла от формы.
- § 5. Теорема Коши — Пуанкаре
- 13. Дифференцирование форм.
- 14. Формула Стокса.
- 15. Теорема Коши — Пуанкаре.
- § 6. Интегральные представления
- 17. Теорема Севери.
- 18. Формула Вейля.
- ГЛАВА III. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
- § 7. Области голоморфности
- 20. Понятие области голоморфности.
- 21. Голоморфная выпуклость.
- 22. Свойства областей голоморфности.
- § 8. Псевдовыпуклость
- 24. Выпуклость в смысле Леви.
- 25. Плюрисубгармонические функции.
- 26. Псевдовыпуклые области.
- § 9. Оболочки голоморфности
- 28. Области наложения.
- 29. Многолистные оболочки голоморфности.
- ГЛАВА IV. МЕРОМОРФНЫЕ ФУНКЦИИ И ПРОБЛЕМЫ КУЗЕНА
- § 10. Мероморфные функции
- 31. Первая проблема Кузена.
- 32. Решение для поликругов.
- 33. Применения. Вторая проблема Кузена.
- § 11. Методы теории пучков
- 35. Группы когомологий.
- § 12. Применения
- 37. Решение первой проблемы Кузена.
- 38. Решение второй проблемы Кузена.
- 39. Решение д-проблемы и проблемы Леви.
- ГЛАВА V. ОСОБЕННОСТИ И ВЫЧЕТЫ
- § 13. Многомерные вычеты
- 40. Теория Мартинелли.
- 41. Теория Лере.
- 42. Логарифмический вычет.
- § 14. Аналитические множества
- 44. Локальное обращение голоморфных функций.
- § 15. Аналитичность множества особенностей
- 46. Существенно особые точки.
- 47. Теорема о вложенном ребре.
- ГЛАВА VI. ГОЛОМОРФНЫЕ ОТОБРАЖЕНИЯ
- § 16. Автоморфизмы простейших областей
- 49. Автоморфизмы пространства.
- 50. Автоморфизмы некоторых областей.
- § 17. Инвариантная метрика
- 52. Метрика Бергмана.
- 53. Поведение кернфункции на границе.


















































































































































































































































































































































































































































































































































































