39. Решение д-проблемы и проблемы Леви.

В начале этого параграфа мы сформулировали теорему II, которая решает для областей голоморфности так называемую -проблему. В общем случае постановка этой проблемы такова:

-проблема. Пусть область на комплексном многообразии и дифференциальная форма бистепени класса для которой

Требуется найти форму бистпени класса такую, что

Так как то условие (1) является необходимым для разрешимости проблемы.

Мы будем решать эту проблему для областей в два шага: сначала решим ее для форм с коэффициентами из пространства затем сгладим полученные решения. Для простоты ограничимся наиболее важным для приложений случаем в общем случае доказательство аналогично

Для первого шага нам понадобятся некоторые обозначения. Через где открытое множество в и мы обозначаем пространство всех дифференциальных форм бистепени с коэффициентами из пространства по мере где мера Лебега в Скалярное произведение

превращает в гильбертово пространство с нормой

1. Сведение к оценкам. Оператор заданный на гладких формах, определяет оператор с плотной областью определения по определению принадлежит если все Аналогичный оператор обозначим через . Так как то Это значит, что множество значений оператора содержится в пространстве нулей оператора и -проблема сводится к установлению равенства

Обозначим через оператор сопряженный Т:

Из этого равенства видно, что ортогонально его замыкание будет ортогональным дополнением к если плотно в . В этом случае отыскание формы из равенства (2) сводится к отысканию формы такой, что

Так как и то в этом равенстве можно ограничиться формами Если мы докажем оценку

где с — константа, не зависящая от А, то из неравенства

будет следовать ограниченность линейного функционала определенного на Из общего вида ограниченного линейного функционала в гильбертовом пространстве вытекает существование формы удовлетворяющей (4). Эта форма будет решением -проблемы и будет удовлетворять дополнительному требованию если плотно в ибо

Итог наших рассуждений подводит

Лемма 1. Если множество плотно в плотно в и выполняется оценка (5), то для любой формы найдется единственная форма такая, что Оператор линеен и непрерывен, имеет место оценка

с той же постоянной с, что и в (5).

Ввиду (5) пространство замкнуто; согласно доказанному выше существует удовлетворяющая (2) и (6). Единственность следует из того, что при выполнении условия леммы является ортогональным дополнением к Линейность оператора обратного к следует из линейности его непрерывность вытекает из (6)

I. Мы докажем сейчас, что при некоторых ограничениях на функцию условие плотности выполняется. Сначала найдем явное выражение оператора для форм равных нулю вне какого-нибудь компакта из Так как

то

где

и . Таким образом,

содержит все формы класса Следовательно плотно в а для доказательства того, что плотно в нам достаточно любую форму приблизить формами класса по норме Возможность такого приближения устанавливается в следующей лемме.

Обозначим и потребуем, чтобы была положительной в и так быстро убывала на что

где

Лемма 2. Если удовлетворяет условию (9), то формы класса плотны в если имеет какие-нибудь частные производные, принадлежащие то найдется последовательность которая сходится к вместе с этими производными.

Обозначим через характеристическую функцию множества Усредним ее с помощью ядра неотрицательной 0 функции из равной нулю вне единичного шара; именно положим

Функция она равна 1 на и 0 вне любая производная от порядка а не превосходит по модулю где постоянная не зависит от Формы

принадлежат и сходятся в Так как

то

где получилось в результате дифференцирования произведения по правилу Лейбница; является линейной комбинацией производных от порядка а. Так как где постоянная с не зависит от то мы получаем ввиду (9), что в

Так как операторы и линейно выражаются через первые производные, то мы получаем

Следствие. Если удовлетворяет (9), то формы класса плотны в пространстве по норме и плотны в по норме Из последнего следует, что плотно в

Таким образом, оценку (5) достаточно получить для форм из .

II. Оценки в псевдовыпуклых областях. Для оценки нормы оператора воспользуемся легко проверяемым коммутационным соотношением

где определены в (7). Интегрируя по частям выражение

и пользуясь (11), мы получаем

Перебрасывая в последнем интеграле на мы находим, что

где вектор Под знаком второго интеграла стоит выражение, равное где модуль вектора из коэффициентов формы коэффициент через где мы обозначаем форму Леви Поэтому

и мы теперь можем доказать следующую теорему существования:

Теорема 1 (Хёрмандер). Пусть псевдовыпуклая область в такова, что где а — положительная константа, Тогда для любой такой, что найдется такая, что

Если область ограничена и то найдется решение удовлетворяющее условию

где диаметр области (Здесь ).

Обозначим через А, функцию класса плюрисубгармоническую в и стремящуюся к на (см. курс Хёрмандера, стр. 74); если достаточно гладкая, то в качестве I можно взять — если функцию Заменяя X на мы можем считать, что добавляя

получаем, что при Заменяя теперь Я функ цией и о Я, где выпуклая достаточно быстро растущая функция класса мы можем считать, что условие (9) выполнено для любой функции плюрисубгармоничность Я от этих замен не нарушается. Скалярное произведение в мы будем обозначать символом норму в этом пространстве — символом соответствующие обозначения

Из равенства (12), где вместо надо писать мы получаем, что по лемме 1 существует такая, что Таким образом, последовательность ограничена так как Из нее можно выделить подпоследовательность слабо сходящуюся в этом пространстве (см. Иосида, стр. 180); это значит, что для любого предел существует. Линейный функционал ограничен и потому представим некоторым элементом т. е. Так как а так как если Наконец, из того, что мы получаем

и первая часть теоремы доказана.

Если область ограничена, то мы можем считать, что и в качестве взять Для найденного выше получаем

Функция достигает минимума по а при и мы получаем оптимальную оценку

Замечание. Последовательность элементов ортогональна к в этом пространстве и тоже слабо сходится к Поэтому принадлежит ортогональному дополнению к

и этим условием форма определена однозначно. Как и в лемме 1, линейный оператор обратный к и решающий -проблему, ограничен; его норма не превосходит Наконец, если удовлетворяет условию (9), то т. е. для некоторой формы Гладкость решения. Пусть правая часть (2) принадлежит мы хотим найти решение тоже принадлежащее Сначала мы индукцией по а будем доказывать существование у специально подобранного решения всех производных порядка а, которые принадлежат на компактных лодмножествах это свойство мы будем записывать так:

Лемма 3. Если функция имеет компактный носитель и если то тоже принадлежит

Пусть область содержит носитель последовательность усреднений (10). Так как

и если носитель содержится в то последовательность сходится в . В самом

так как

Случай Подберем функцию так, чтобы для некоторой константы и воспользуемся теоремой 1. Если X — произвольная функция из то поэтому согласно лемме 3 все Так как в порядок дифференцирования не влияет на результат, то это рассуждение можно применить к и получить, что и т. д. Значит, для

любого а функция суммируема с квадратом на каждом компакте, где Ввиду произвольности к это и есть свойство (15).

Случай Воспользуемся тем, что в равенстве (12) форма и потому можно взять равной 1 на носителе Равенство принимает вид

где норма берется в Заменяя на 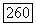мы получаем, что

Это равенство справедливо для любой формы со, у которой 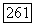для таких форм существование 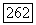вытекает из (17).

Подберем 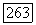так, чтобы для нее выполнялось условие теоремы 1, а для 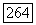условие (9). Решение уравнения (2) возьмем в пространстве 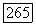это значит, что 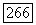для некоторой 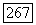Так как 1, то можно определить оператор 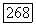, сопряженный оператору 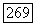его явный вид задается формулой (8). Так как 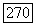(ввиду равенств 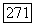то и 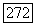Поэтому для 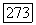где 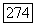мы получаем следующее выражение:

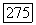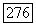Таким образом, если то Так как 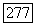то из 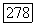следует, что 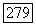а тогда ввиду 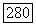для всех 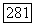Согласно лемме 3 все 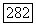Так как 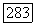то мы доказали по индукции, что для любых 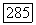суммируемы с квадратом на каждом компакте, где к 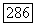Ввиду произвольности 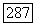это и есть свойство (15).

Согласно лемме Соболева о вложении) всякая форма, удовлетворяющая (15), совпадает в с некоторой формой класса 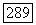Таким образом, доказав (15) для специально подобранных решений 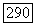мы доказали следующую теорему, которая и решает -проблему:

Теорема 2 (Хёрмандер). Если область 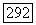псевдовыпукла, то уравнение 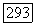имеет решение 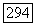бистепени 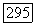для всякой формы 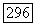бистепени 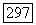такой, что 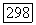Для 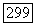всякое решение обладает этим свойством.

Эта теорема справедлива и для областей на многообразиях Штейна, причем для форм любой бистепени 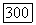доказательство можно найти в книге Хёрмандера, цит. на стр. 463.

Замечание 1. Как видно из доказательства, мы брали Согласно лемме 1 этим условием форма определена однозначно и она линейно зависит от Используя более сильную лемму Соболева о непрерывности вложения, мы получаем, что оператор обратный непрерывен в следующем смысле:

Для любого компакта и любого найдутся (33 а, постоянная и компакт такие, что

где

Замечание 2. Так как всякая область голоморфности является псевдовыпуклой то теорема II, сформулированная в начале параграфа, является следствием теоремы 2.

В заключение приведем решение проблемы Леви, которая связывает локальные и глобальные свойства областей голоморфности (см. п. 24).

Как мы убедились в п. 26, для решения этой проблемы нужно доказать, что любая псевдовыпуклая область является областью голоморфности; на основании теоремы 2 это вытекает из следующей теоремы:

Теорема 3 (Хёрмандер). Пусть область в такая, что уравнение имеет решение бистепени для всякой формы бистепени такой, что Тогда является областью голоморфности.

Мы будем доказывать это индукцией по При утверждение тривиально, ибо любая плоская область является

областью голоморфности; предположим, что оно справедливо для областей из

Нам нужно доказать, что для любого шара граница которого содержит хотя бы одну точку найдется функция не продолжаемая голоморфно в точку . Без ограничения общности можно считать, что и что непусто. Тогда непусто и открытое множество которое мы рассматриваем в пространстве точек а 0 является его граничной точкой. Мы обозначим через проекцию и через вложение множества так что мы рассматриваем как подмножество Пусть совокупность -форм класса Для любой формы от переменной мы обозначим через ту же , рассматриваемую как форму от на множестве

Символом будем обозначать форму от которая получится из формы если положить в последней таким образом,

Рис. 115.

Прежде всего докажем, что система

разрешима в классе для любой замкнутой формы

Для этого рассмотрим множество заштрихованное на схематическом рис. 115. Так как оно не пересекается с и оба этих множества относительно замкнуты в О, то можно построить функцию равную 1 на и 0 на . С ее помощью мы преобразуем в форму (которая полагается равной 0 на хотя там и не определена); очевидно, Далее полагаем где подбирается так, чтобы было Этот подбор осуществим, ибо последнее равенство переписывается в виде системы в правой части которой стоит форма — замкнутая в силу замкнутости а такая система разрешима в классе по условию. Очевидно, мы имеем Так как то по условию существует форма Полагая мы найдем, что и

что а является искомым решением системы (18).

Так как открытое множество в то по индуктивному предположению из доказанной разрешимости системы (18) следует, что состоит из областей голоморфности. Поэтому существует функция не продолжаемая голоморфно в окрестность замкнутого шара Рассматривая как замкнутую форму из мы, как и в предыдущем абзаце, найдем форму такую, что Построенная F является голоморфной функцией в а так как сужение то F не продолжаема голоморфно в окрестность замкнутого шара

Таким образом, доказана

Теорема (Ока). Любая псевдовыпуклая область является областью голоморфности.

Как показывает теорема 3, условие псевдовыпуклости области является не только достаточным, но и необходимым условием для разрешимости -проблемы для форм любой бистепени

Мы закончим этот параграф доказательством еще одного критерия для областей голоморфности.

Теорема 4. Область является областью голоморфности тогда и только тогда, когда

Согласно теореме Поэтому из тривиальности всех этих групп когомологий следует разрешимость -проблемы в области для форм любой бистепени По теореме является областью голоморфности. Обратное утверждение составляет содержание следствия п. 37

ЗАДАЧИ

(см. скан)

(см. скан)

(см. скан)

(см. скан)