28. Области наложения.

Выше не раз отмечалась необходимость рассмотрения многолистных областей, аналогичных римановым поверхностям над комплексной плоскостью. Здесь мы изложим основные определения и некоторые результаты, связанные с этим понятием.

Каждое комплексное многообразие размерности посредством локальных координат локально гомеоморфно отображается в пространство Однако локальные координаты не

определены глобально на многообразии, т. е. не являются на нем функциями в смысле п. 9.

Мы выделим специальный класс многообразий условием существования глобально определенного непрерывного отображения в всюду локально гомеоморфного. Такие многообразия вместе с заданными на них отображениями в и будут предметом нашего изучения в этом пункте.

Определение. Многообразием наложения над пространством (короче: многообразием над мы будем называть пару где многообразие, а локально гомеоморфное отображение, которое называется проектированием. Если связно, то называется областью наложения над

Это определение распространяет на пространственный случай определение римановой поверхности над С (см. п. 32 ч. I). Как и в плоском случае, проектирование позволяет перенести на многообразия понятия, введенные в Так, мы назовем поликругом на с центром в точке и радиусом множество точек содержащее которое гомеоморфно преобразует в точки поликруга где проекция точки

Объединение всех поликругов на с данным центром также является поликругом, который называется максимальным; радиус этого поликруга (конечный или бесконечный) называется расстоянием до границы и обозначается через Под расстоянием до границы некоторого множества понимается

Если комплексно аналитическое многообразие (см. п. 9), то на можно ввести понятие голоморфной функции. Именно, функция называется голоморфной на если для любого поликруга на функция голоморфна в поликруге Очевидно, что это определение голоморфности совпадает с принятым в п. 9. В частности, на будут голоморфными все локальные координаты: которые коротко обозначаются через

Кольцо всех функций, голоморфных в области над мы будем обозначать через

Важный пример комплексно аналитического многообразия над доставляет процесс аналитического продолжения

голоморфных функций. В случае нескольких переменных он проводится в точности так же, как в плоском случае, и мы ограничимся его кратким описанием. Будем исходить из какого-либо элемента совокупности поликруга и голоморфной в этом поликруге функции Точно так, как в случае одного переменного, определяется непосредственное аналитическое продолжение, аналитическое продолжение и аналитическое продолжение вдоль пути отображение у задается непрерывными комплексными функциями Доказывается, что аналитическое продолжение вдоль пути (если оно возможно) не зависит от выбора промежуточных точек, а также не меняется при замене пути у гомотопным ему путем с теми же концами, если вдоль всех путей осуществляющих гомотопию, продолжение начального элемента возможно. Приведем теперь основное

Определение. Аналитической функцией комплексных переменных называется совокупность элементов некоторое множество индексов), каждый из которых получается из любого другого аналитическим продолжением вдоль какого-либо пути.

Построим теперь комплексно аналитическое многообразие над связанное с аналитическими функциями. Рассмотрим множество точками которого служат пары где точка и функция

голоморфна в некотором поликруге с центром в а, который для определенности будем считать поликругом сходимости ряда Введем в 9 топологию следующим образом: под окрестностью точки понимается совокупность точек таких, что: 1) и 2) элемент является непосредственным аналитическим

продолжением элемента Мы предоставляем читателю доказать, что эта топология превращает в хаусдорфово пространство.

Определим теперь проекцию в отображением

Нетрудно видеть, что локальный гомеоморфизм и что это отображение определяет на структуру комплексно аналитического многообразия комплексной размерности (ср. п. 32 ч. I); мы будем называть римановым многообразием.

Таким образом, пара является комплексно аналитическим многообразием над (окрестности оказываются на нем поликругами). Примером голоморфной на функции является функция

сопоставляющая точке свободный член ряда (2).

Риманово многообразие очевидно, несвязно. Однако подмножества его точек таких, что элементы принадлежат одной аналитической функции (т. е. являются аналитическим продолжением друг друга вдоль какого-либо пути), связны. Такие множества являются областями в мы будем называть их римановыми поверхностями. Очевидно, каждой области соответствует аналитическая функция и, обратно, каждой аналитической функции соответствует область

Рис. 111.

Пусть какая-либо риманова поверхность; через обозначим соответственно сужения на отображений (3) и (4). Локально гомеоморфное отображение не обязано быть в целом гомеоморфизмом, поэтому оно может переводить в одну течку несколько точек (рис. 111). Функция однозначная на будет тогда многозначной, если ее рассматривать в зависимости от Таким образом, и в случае многих переменных мы можем рассматривать (многозначные) аналитические функции как (однозначные) голоморфные функции, если вместо областей в перейдем к областям над т. е. римановым поверхностям.

Кроме областей рассматриваются и другие модели римановых поверхностей, эквивалентные этим областям (понятие эквивалентности мы сейчас определим). Мы будем далее заниматься расширением областей наложения и, чтобы можн» было сравнивать между собой различные модели, введем

понятия вложения многообразий и сужения функций, связав их с возможностью отображения одного многообразия на другое.

Определение 1. Пусть даны два многообразия над ; если существует такое непрерывное отображение что на

то говорят, что первое многообразие (слабо) -вложено во второе, и пишут: Если при этом является взаимно однозначным отображением то говорят, что сильно -вложено в Если еще гомеоморфизм на то называются эквивалентными.

Это определение обобщает обычное понятие включения: если в обычном смысле, то является сужением функции на и в качестве можно принять естественное отображение вложения где переводит каждую точку в ту же точку рассматриваемую как точка Очевидно, что эквивалентные многообразия сильно вложены друг в друга (одно — посредством другое . В случае слабого вложения первое многообразие может оказаться «более разветвленным», чем второе. Так, риманова поверхность функции над оказывается слабо вложенной в риманову поверхность (в качестве надо принять отображение, склеивающие пары точек первой поверхности, в которых принимает одинаковые значения). Всякое многообразие над является -вложенным в

Обобщая понятие функции, голоморфной на многообразии, введем понятие голоморфного отображения многообразий. Пусть даны два комплексно аналитических многообразия соответственно над пространствами и отображение называется голоморфным, если оно непрерывно и все функции

голоморфны на Если еще гомеоморфизм на (тогда непременно и обратное отображение также голоморфно, то называется голоморфным

изоморфизмом (короче, голоморфизмом) или биголоморфным отображением.

Отметим, что если одно комплексно аналитическое многообразие -вложено в другое такое же, то отображение вложения непременно является голоморфным. В самом деле, по определению вложения функции (6)

а последние голоморфны, ибо комплексно аналитическое многообразие. Эквивалентность многообразий в этом случае сводится к голоморфной эквивалентности.

Определение 2. Пусть функция на втором многообразии; функцию будем называть -сужением функции на первое многообразие (обозначение: если на

функцию тогда будем называть -расширением

Если естественное отображение вложения, то мы имеем обычное сужение

Покажем, что построенное выше риманово многообразие является «универсальной моделью» многообразий над т. е. что любое комплексно аналитическое многообразие над можно -вложить в риманово многообразие. Точнее, имеет место

Теорема 1. Пусть связное комплексно аналитическое многообразие, область наложения над — голоморфная на функция-, существуют связная компонента и отображение такие, что

где и сужения на отображений (3) и (4).

Для любой точки обозначим через совокупность точки и голоморфной функции (разложения в ряд Тейлора с центром в а функции Пусть образ области при построенном отображении; так как непрерывно, связно, то связной компоненте По построению так что имеет место

Теперь мы хотим ввести понятие многолистных областей голоморфности. Определим их как области над в которых существует голоморфная функция, не расширяемая на области, неэквивалентные данной. Иными словами, примем такое

Определение. Область наложения называется областью голоморфности, если существует функция обладающая следующим свойством: из того, что некоторая область и функция является -расширением функции следует, что эквивалентна (т. е. что взаимно однозначно отображает на

В этом определении, по существу, используется, что эквивалентность областей наложения сводится к голоморфной эквивалентности, и постулируется инвариантность областей голоморфности при биголоморфных отображениях (для однолистных областей голоморфности это свойство было доказано в .

Важные примеры многолистных областей голоморфности представляют максимальные связные компоненты риманова многообразия Для доказательства нам понадобится Лемма. Если отображение вложения области над в себя имеет хотя бы одну неподвижную точку, то оно тождественно.

Множество всех неподвижных точек отображения замкнуто (ибо непрерывное отображение хаусдорфова пространства в себя) и по условию непусто. Покажем, что оно открыто. Пусть неподвижная точка поликруг на Обозначим это — открытое множество на (в силу непрерывности содержащее причем проекция гомеоморфна на По определению -вложения на имеем а так как на V отображение гомеоморфно, то отсюда следует, что при т. е. все точки из V неподвижные. Итак, множество неподвижных точек отображения непусто и одновременно замкнуто и открыто; так как связно, то это множество совпадает с

Теорема 2. Любая область риманова многообразия где максимальная связная компонента является областью голоморфности.

Функция голоморфна на причем функция голоморфна на надо показать, что в этой ситуации является взаимно однозначным отображением на Так как то по теореме 1 существует -вложение в многообразие для которого По построению этого -вложения для имеем следовательно, отображение имеет в неподвижные точки. По лемме о всюду в откуда видно, что взаимно однозначно отображает на

Чтобы сформулировать необходимые и достаточные условия для областей голоморфности над условимся называть область голоморфно отделимой, если для любых двух различных точек найдется функция разделяющая эти точки, т. е. такая, что

Для однолистных областей условие голоморфной отделимости выполняется автоматически, ибо в качестве разделяющей функции всегда можно взять одну из координат. Для многолистных областей это не так: вот соответствующий пример. Пусть — тор в возьмем область над диаграмма Рейнхарта которой изображена на рис. 112. Эта диаграмма представляет собой лежащую над первым квадрантом плоскости часть двулистной римановой поверхности функции с точками ветвления над

Рис. 112.

Рассмотрим произвольную функцию 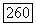голоморфную на 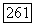Ее значения на любом из двух «листов» 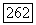голоморфны вне шара 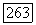ибо многообразие ветвления (тор Г) лежит на сфере 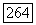вне шара область не разветвлена. По теореме Осгуда — Брауна 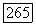эти значения продолжаются до целых функций, а так как на 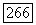они должны совпадать, то они совпадают тождественно (см. задачу 15 к гл. I). Таким образом, значения 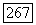в точках различных листов области 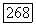лежащих над одной точкой 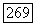должны совпадать: точки 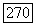с одинаковой проекцией не отделимы голоморфно.

Теорема 3 (Картан — Туллен). Область наложения 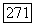тогда и только тогда является областью голоморфности, когда она голоморфно выпукла и голоморфно отделима.

Мы не будем подробно излагать доказательство, опишем лишь изменения, которые нужно внести в многолистном случае.

Необходимость. Доказательство теоремы об одновременном продолжении без существенных изменений

переносится на многомерный случай, а из этой теоремы вытекает голоморфная выпуклость области голоморфности

Для доказательства голоморфной отделимости возьмем на функцию 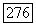описанную в определении области голоморфности, и по теореме 1 построим соответствующее ей 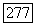-вложение 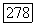в риманово многообразие 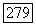Из того же определения следует, что отображение 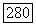взаимно однозначно, т. е. что Для различных точек 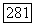Пусть 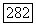; из (8) и (7) имеем 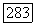а так как из определения функции 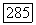следует, что в точках 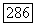значения функции 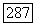или какой-либо ее производной различны (в противном случае Это и означает голоморфную отделимость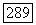

Достаточность. Пусть 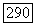компактное исчерпывание области (напомним, что 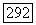является многообразием, а по нашему определению в 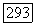каждое многообразие счетно исчерпываемо). Пользуясь голоморфной выпуклостью 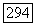мы можем считать, что 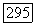Покроем 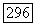конечным числом поликругов и в пересечении каждого из них с 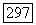возьмем по точке 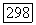через обозначим функцию из такую, что

Функция

Пользуясь голоморфной отделимостью, можно исправить функцию так, чтобы она, оставаясь голоморфной в и удовлетворяя неравенству (9), имела в любых двух различных точках с одинаковой проекцией различные элементы (о том, как осуществить такое исправление, см. книгу Б. А. Фукса, стр. 193).

Покажем, что является областью голоморфности (исправленной) функции Пусть имеется -расширение функции в область требуется доказать, что взаимно однозначно отображает на Если то согласно а согласно Отсюда по построению вытекает, что т. е. взаимно однозначно. Кроме того, ибо в противном случае область

имела бы в граничную точку, а в этой точке функция в силу неравенств (9) не может быть голоморфной

Замечание. К. Ока доказал в 1953 г., что всякая голоморфно выпуклая область над голоморфно отделима. Поэтому условия в теореме 3 не являются независимыми.

Области наложения над которые являются областями голоморфности, мы будем называть еще многообразиями Штейна. Заметим, что обычно этот термин трактуется шире: многообразием Штейна называется любое комплексно аналитическое многообразие X комплексной размерности обладающее следующими тремя свойствами: 1) X голоморфно выпукло, 2) X голоморфно отделимо, 3) для любой точки существует функций голоморфных на X, которые образуют локальные координаты в этой точке.