41. Теория Лере.

Здесь мы рассмотрим другой метод вычисления интегралов, принадлежащий Ж. Лере. В ряде случаев этот метод позволяет свести вычисление интеграла от формы со степени по -мерному циклу а к вычислению интеграла от формы степени называемой формой-вычетом, по некоторому -мерному циклу, лежащему на многообразии особенностей формы со. Метод Лере также можно рассматривать как обобщение классического метода вычетов,

который соответствует случаю и сводит вычисление интегралов от форм по замкнутым кривым к вычислению значений вычетов в особых точках нульмерных интегралов от по этим точкам). Мы изложим этот метод в его простейшем варианте 2).

Пусть на -мерном комплексном многообразии задано -мерное комплексное подмногообразие , которое в окрестности каждой своей точки 2° задается как множество нулей голоморфной в этой окрестности функции такой, что

Пусть на задана дифференциальная форма степени класса имеющая на полярную особенность первого порядка. Последнее условие означает, что в каждой произведение продолжается до -формы на

Лемма. Форма тогда и только тогда представима в окрестности точки в виде 2)

где когда в этой окрестности

Примем за одну из локальных координат, определяющих в окрестности скажем за переменную 2, (это возможно в силу условий, наложенных выше на Выражение для а в этих координатах можно разбить на два слагаемых:

где содержит (как всегда, мы полагаем Таким образом, если а представима в виде (2) при то а значит, и т. е. (3) выполняется. Обратно, если то и а так как а не содержит то это может быть лишь при

Теорема 1. Если форма имеющая на полярную особенность первого порядка, замкнута в то

в окрестности произвольной точки вне она представима в виде

где формы При этом сужение не зависит от выбора функции и является замкнутой формой.

Так как у нас то но на имеем (ибо замкнута), значит, по непрерывности всюду в Таким образом, продолжается на до формы и по лемме найдется форма такая, что

Умножив это равенство на найдем где значит, по той же лемме существует форма такая, что Это равенство вне равносильно (4).

Покажем, что сужение однозначно определяется формой и. Предположим сначала, что функция определяющая полярное множество задана, и докажем, что из равенства

следует равенство Но из (5) мы получаем откуда а так как функция, отличная от нуля в то там в силу того, что последнее равенство справедливо и всюду в Мы можем применить лемму, по которой найдется форма такая, что Подставляя это в (5), находим по той же лемме где Отсюда и видно, что сужение ибо на у нас

Теперь докажем независимость и от выбора функции, определяющей полярное множество. Пусть это множество (в пределах окрестности определяется еще функцией тогда частное голоморфно и отлично от нуля в (см. п. 33). Пусть мы имеем

где . Подставляя сюда найдем

здесь и по доказанному выше

Остается доказать замкнутость формы Но вне в силу замкнутости мы имеем причем в силу непрерывности это равенство справедливо всюду в . В силу доказанной выше единственности заключаем, что

Определение 1. Формой-вычетом замкнутой формы имеющей на полярную особенность первого порядка, называется замкнутая форма, которая в окрестности каждой точки равна сужению на формы в разложении (4):

Таким образом, оператор преобразует группу замкнутых -форм степени в группу замкнутых -форм степени :

Замечание. Если форма голоморфна на то и голоморфна на Это следует из того, что в случае голоморфности формы и , при доказательстве теоремы 1 также можно выбрать голоморфными.

Пример. Пусть равно (комплексной) размерности многообразия а форма голоморфна на и в локальных координатах действующих в окрестности точки она представляется в виде

где Тогда можно написать

откуда видно, что

При мы получаем обычную формулу для вычета в полюсе первого порядка:

Перейдем к описанию так называемого пограничного оператора Лере который каждой точке сопоставляет гомеоморф окружности (и таким образом увеличивает действительную размерность на 1).

Рис. 120.

Этот оператор должен обладать следующими свойствами:

1. В некоторой окрестности существуют локальные координаты с началом в которых определяется уравнением и определяется уравнением

2. Совокупность образует в непрерывную поверхность.

3. При линии не имеют общих точек.

Таким образом, совокупность составляет границу трубчатой окрестности многообразия (см. схематический рис. 120, где изображено линией, а М - трехмерным пространством). В принятых выше условиях построение такого оператора всегда возможно, ибо действительные размерности и отличаются на две единицы.

Пусть теперь цикл на действительной размерности мы предположим, что носитель этого цикла (т. е. соответствующий ему полиэдр) компактно принадлежит Обозначим

мы можем рассматривать как -мерную цепь на если введем в ней естественную ориентацию, соответствующую ориентации . Для этого достаточно ввести ориентацию на каждой линии , например так: будем считать, что ориентация в окрестности задается порядком следования локальных

координат а на многообразии - порядком ; тогда положительный обход на будет соответствовать возрастанию в представлении окружности (см. свойство 1 оператора ).

Легко видеть, что оператор коммутирует с оператором взятия границ поэтому он переводит циклы снова в циклы и циклы, гомологичные нулю, в такие же. Таким образом, устанавливает гомоморфизм групп гомологий

(см. п. 12; значок в обозначении групп указывает на то, что рассматриваются компактные гомологии, т. е. принимаются во внимание лишь цепи с компактными носителями).

Следующая теорема является обобщением теоремы Коши о вычетах из

Теорема 2. Пусть -мерный цикл и замкнутая форма степени имеющая своим полярным множеством первого порядка; тогда

где пограничный оператор Лере.

Обозначим через оператор, который обладает свойствами 1—3 оператора с той лишь разницей, что в 1 уравнение заменено уравнением и при трубчатая окрестность ограниченная поверхностью стягивается в . По формуле Стокса для любых имеем

в силу замкнутости формы, так что интеграл от со по бест не зависит от

Теперь покроем конечной системой окрестностей в каждой из которых действует теорема 1 и, как выше, можно принять Построим для этого покрытия разбиение единицы (см. п. 11) и применим в каждой теорему 1, в которой положено мы получим

Здесь

при левая часть (12) не зависит от и равна интегралу по а вторая сумма в правой части стремится к нулю при Поэтому, переходя в (12) к пределу при мы будем иметь

Заметим, что если заменить о другие циклом , принадлежащим тому же классу компактных гомологий на (это означает, что ограничивает некоторую -мерную цепь, компактно принадлежащую то в силу замкнутости формы интегралы от нее по с и а по формуле Стокса совпадают. Учитывая еще, что согласно (10) оператор сохраняет гомологии, мы можем заменить в (11) циклы о и любыми представителями соответствующих классов Поэтому формулу (11) можно переписать в виде

Ясно, далее, что если к добавить точную в форму (т. е. являющуюся дифференциалом некоторой формы степени то интегралы в (13) не изменятся. Класс форм, отличающихся от на точные формы, является классом когомологий, содержащим , а совокупность таких классов для всех замкнутых форм степени из группой когомологий (см. п. 13). Мы видим, что класс когомологий из содержащий зависит только от класса когомологий из содержащего форму

Определение 2. Пусть — некоторая замкнутая форма, представляющая класс класс когомологий из содержащий форму называется классом-вычетом и обозначается символом

Формулу (13) теперь можно переписать в виде

Можно убедиться в том, что оператор устанавливает гомоморфизм соответствующих групп когомологий:

Опишем в общих чертах случай полярных особенностей выше первого порядка. Пусть опять на -мерном комплексном многообразии задается многообразие локально описываемое как множество нулей голоморфной функции для которой Будем говорить, что форма имеет на полярную особенность порядка если произведение продолжается до -формы на где не продолжается.

Приведем без доказательства теорему, которая сводит вычисление интегралов от замкнутых форм, имеющих на полярную особенность выше первого порядка, к уже рассмотренному случаю (см. книгу Лере, цит. на стр. 493):

Для любой замкнутой формы имеющей на полярную особенность, найдется когомологичная ей форма которая имеет на особенность первого порядка.

Класс когомологий из содержащий т. е. класс называется классом-вычетом формы ; он определяется лишь классом когомологий из содержащим .

В плоском случае переход от формы состоит в замене функцией имеющей в точке а полюс первого порядка и тот же вычет, что и Отметим, что в пространственном случае для голоморфной форма не обязана быть голоморфной и вообще класс-вычет голоморфной формы со может не содержать голоморфных форм. Этим и объясняется необходимость рассматривать в теории Лере не только голоморфные, но и формы класса

Для практики важен также случай, когда форма имеет несколько полярных многообразий порядков соответственно Предполагается, что находятся в общем положении, т. е. что во всех точках их пересечений матрицы, составленные из производных функций, определяющих эти многообразия, по локальным координатам имеют наивысший возможный ранг. Мы обозначим

и рассмотрим последовательность гомоморфизмов которые ставят в соответствие циклам принадлежащим классам компактных гомологий из циклы принадлежащие классам из

Циклы расслаиваются на гомеоморфы окружностей, обходящие и принадлежащие Как и выше, этой последовательности двойственна последовательность гомоморфизмов групп когомологий, которая определяет сложный класс-вычет:

Последовательным применением формулы (14) получается следующее утверждение:

Для любого -мерного цикла о из класса гомологий и любой замкнутой 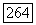-формы со степени 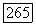из класса когомологий 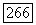имеет место формула вычета

В заключение отметим, что если форма 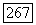обращается в нуль на некотором 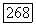-мерном комплексном многообразии 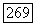то интегралы от нее и от 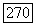по пересечениям 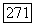и исчезают. Это дает возможность рассматривать вместо групп гомологий и когомологий группы относительных гомологий и когомологий. Поясним эти понятия на примере группы относительных гомологий. Будем рассматривать прдмногообразие некоторого многообразия как его подкомплекс; через обозначим группы -мерных цепей на этих комплексах (как всегда, с целыми коэффициентами). Цепь будем называть циклом относительно если ее граница до с (в частности, равна нулю). Группа 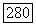является подгруппой 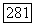факторгруппу

будем называть группой относительных цепей. Цепь 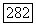называется относительной границей, если существует цепь

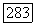такая, что Относительные границы образуют подгруппу 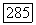группы 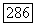всех: относительных циклов; факторгруппа

называется группой относительных гомологий.

При рассмотрении форм 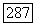имеющих полярную особенность первого порядка на многообразии и обращающихся в нуль на многообразии (они предполагаются находящимися в общем положении), можно несколько уточнить описанную выше кон струкцию. Именно, к свойствам 1—3 кограничного оператора Лере можно добавить еще свойство:

Тогда этот оператор каждый относительный цикл 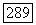преобразует в относительный цикл 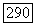Легко убедиться в том, что он устанавливает гомоморфизм соответствующих групп относительных гомологий:

Формула вычета (13) для классов относительных гомологий сохраняется.

Примеры применения метода Лере для вычисления интегралов, имеющих важное значение в теоретической физике, можно найти в книге: Р. Хуа и В. Теплиц, Гомология и фейнмановские интегралы, «Мир», М., 1969.