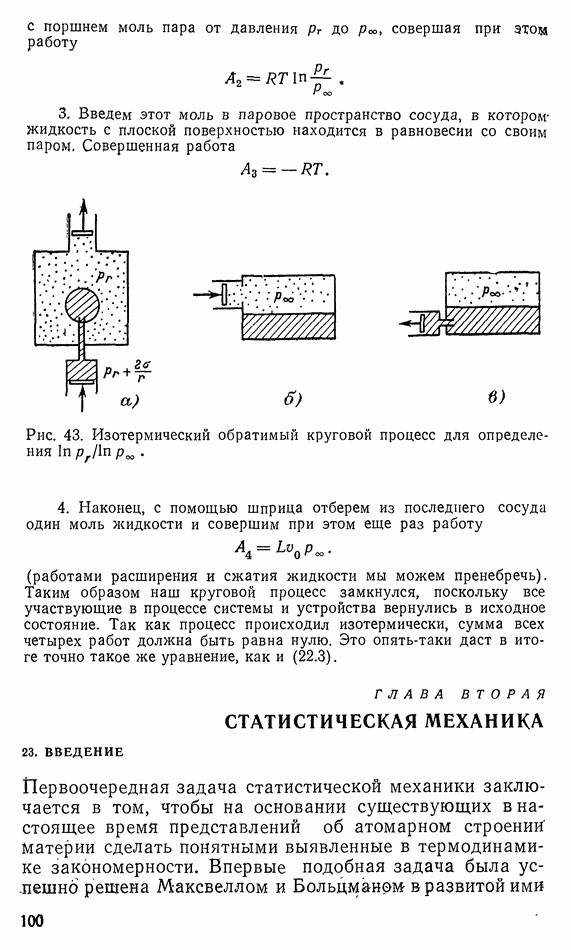
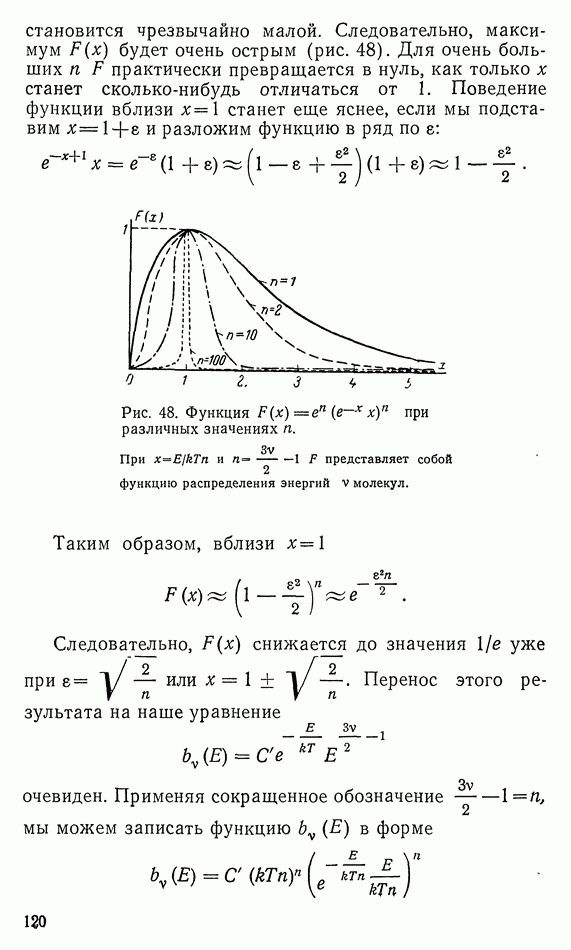
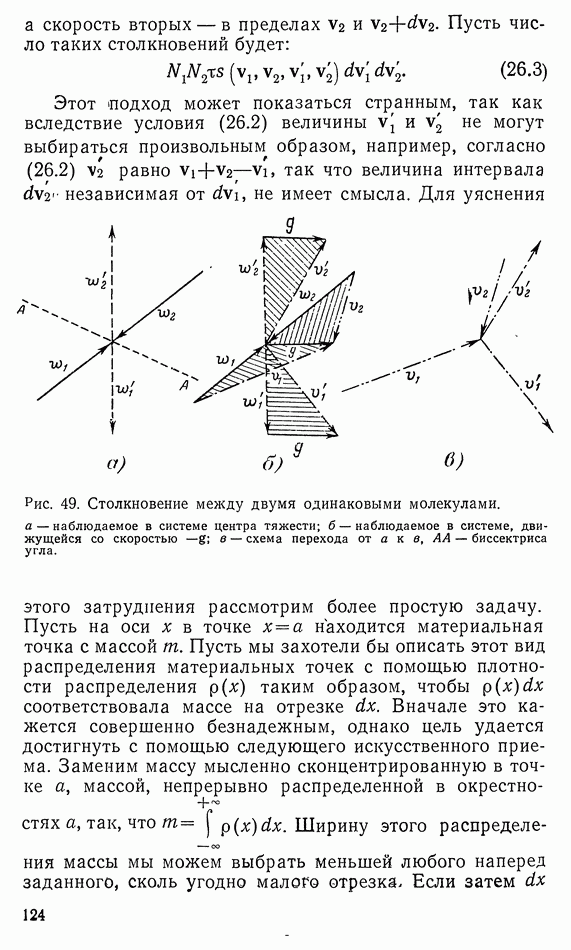
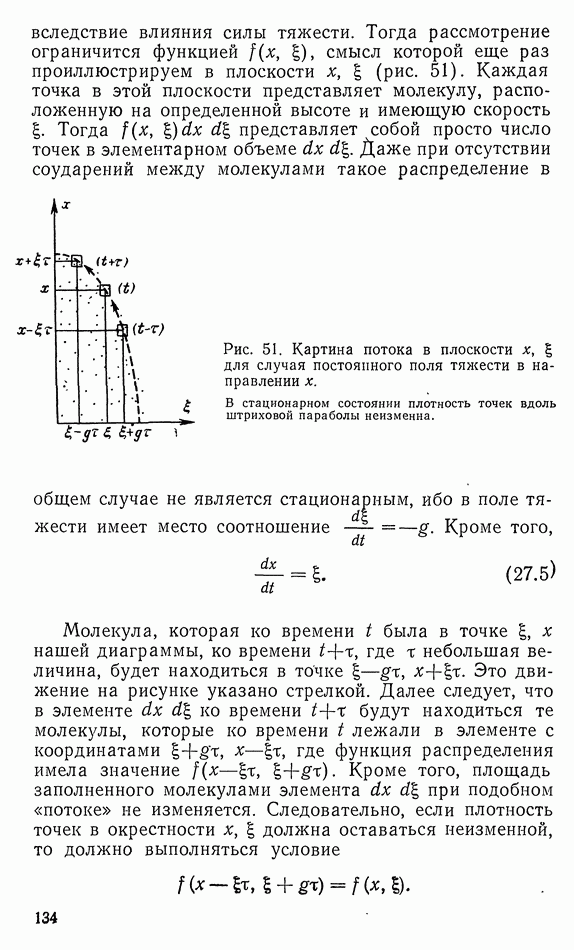
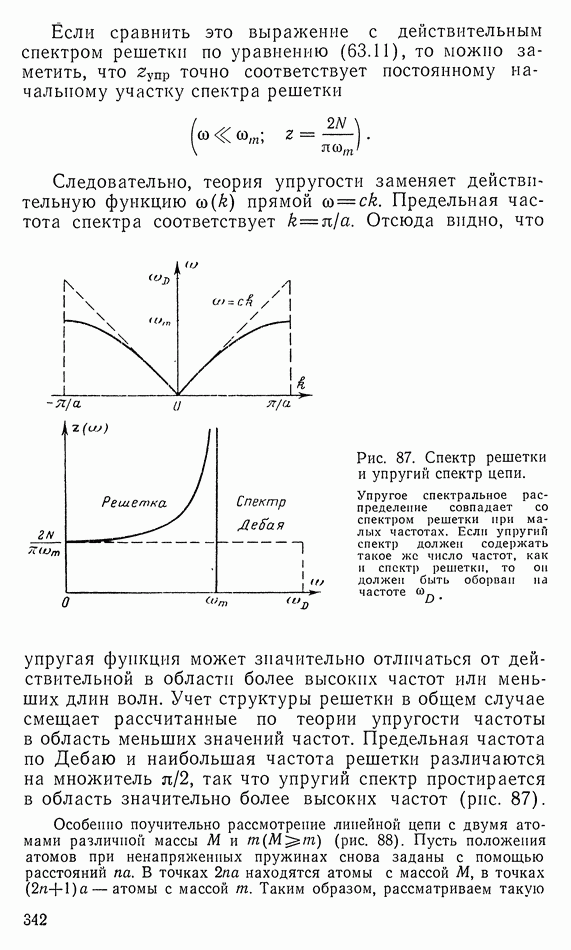
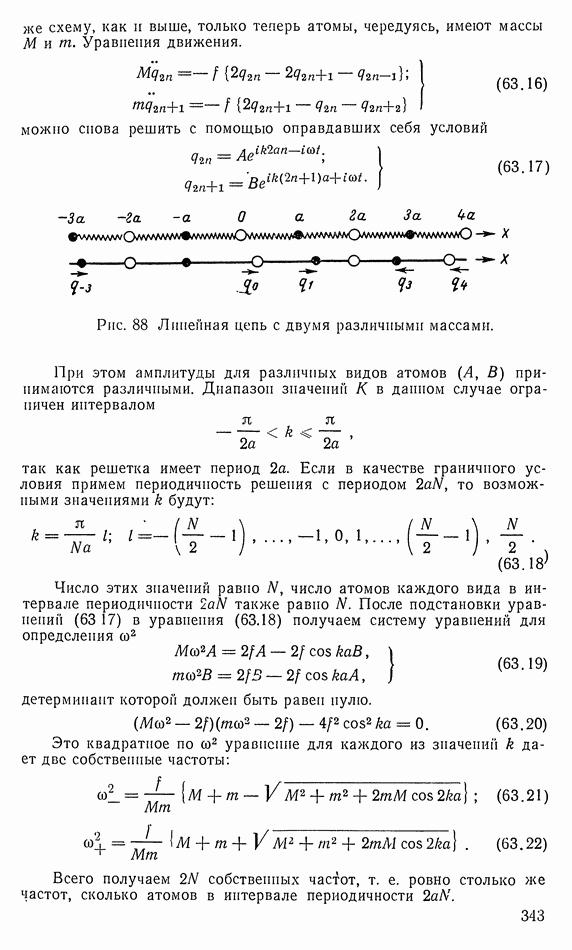
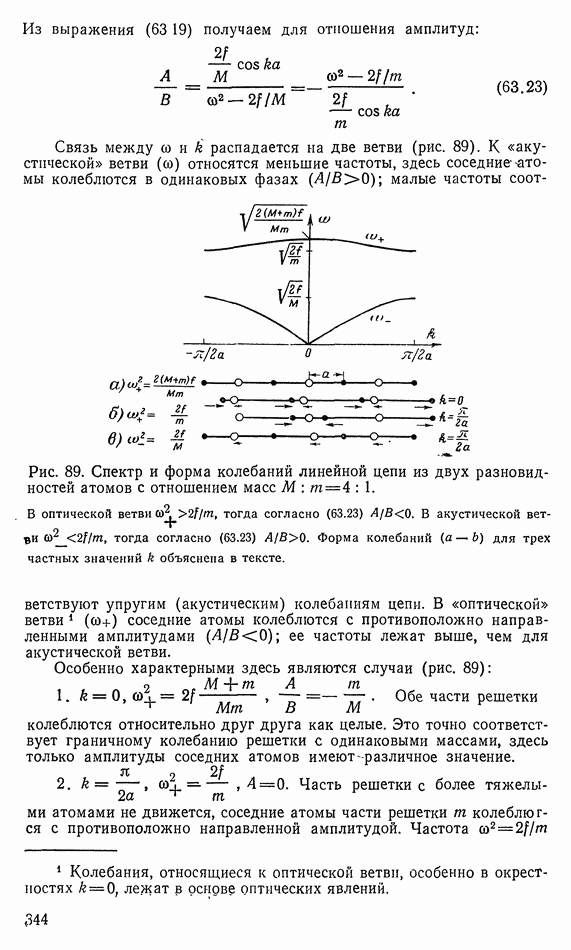
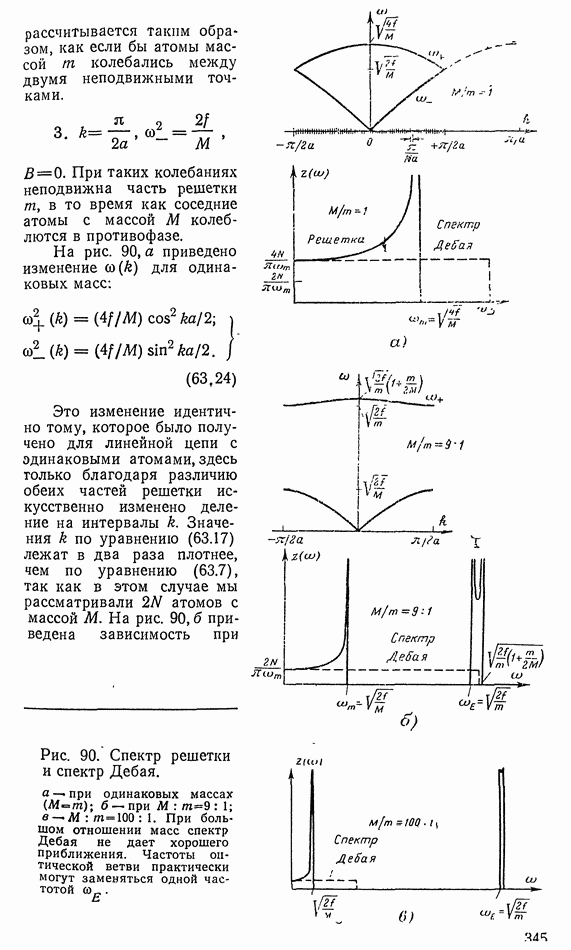
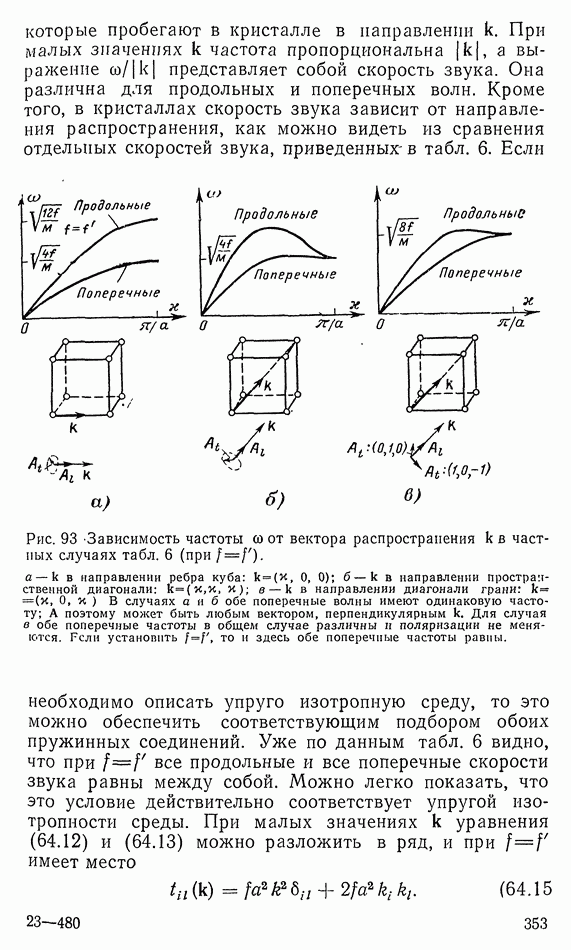
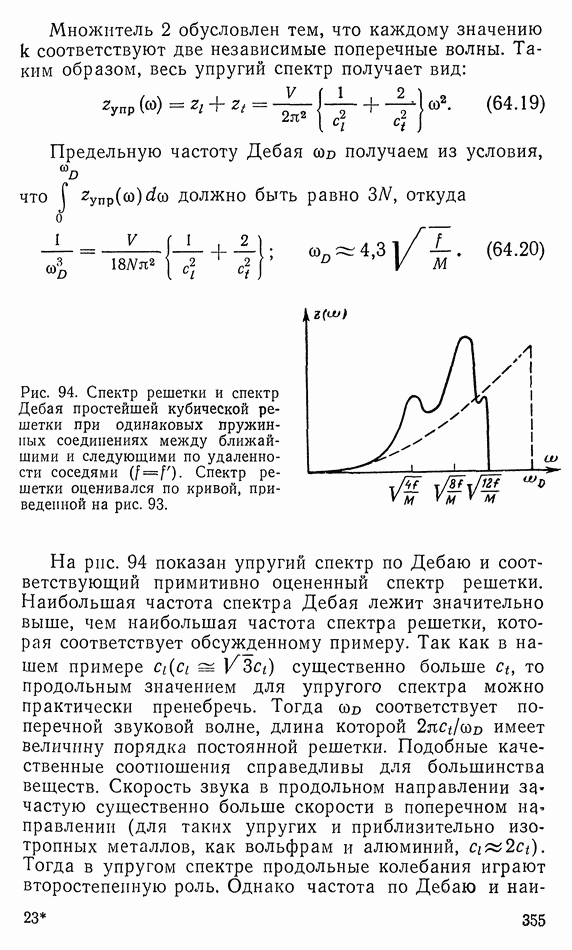
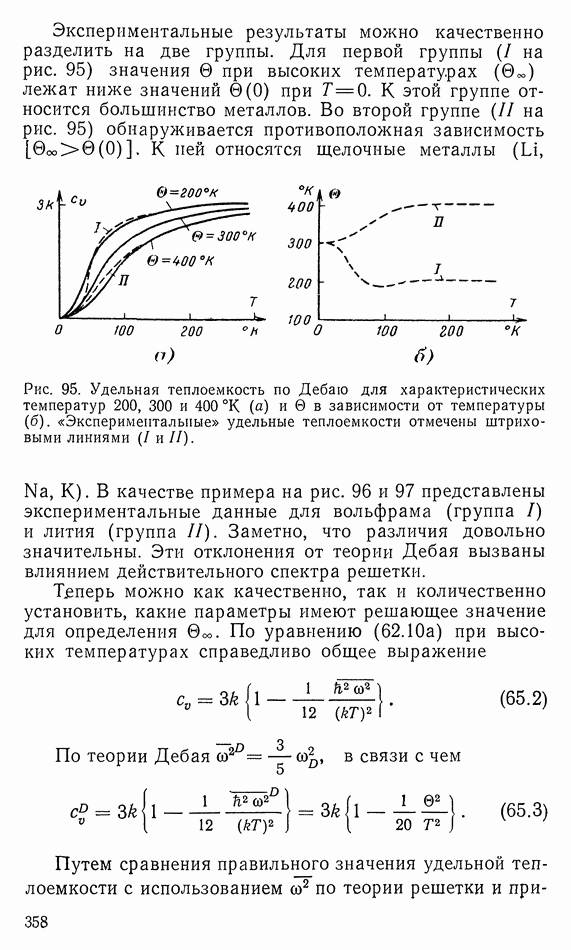
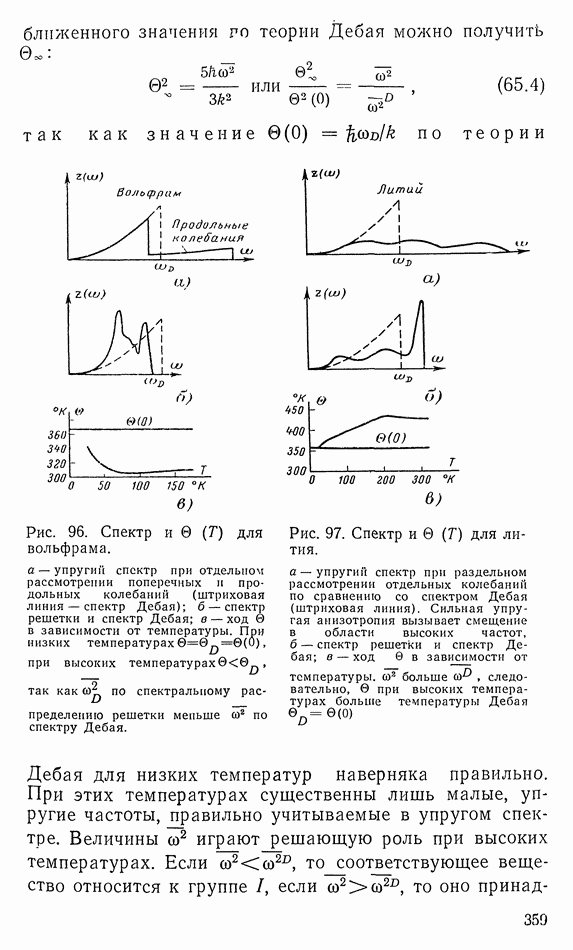
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Б. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ
30. УРАВНЕНИЯ ДВИЖЕНЙЯ ГАМИЛЬТОНА
а) Вариационное исчисление, уравнения движения в форме Лагранжа и Гамильтона
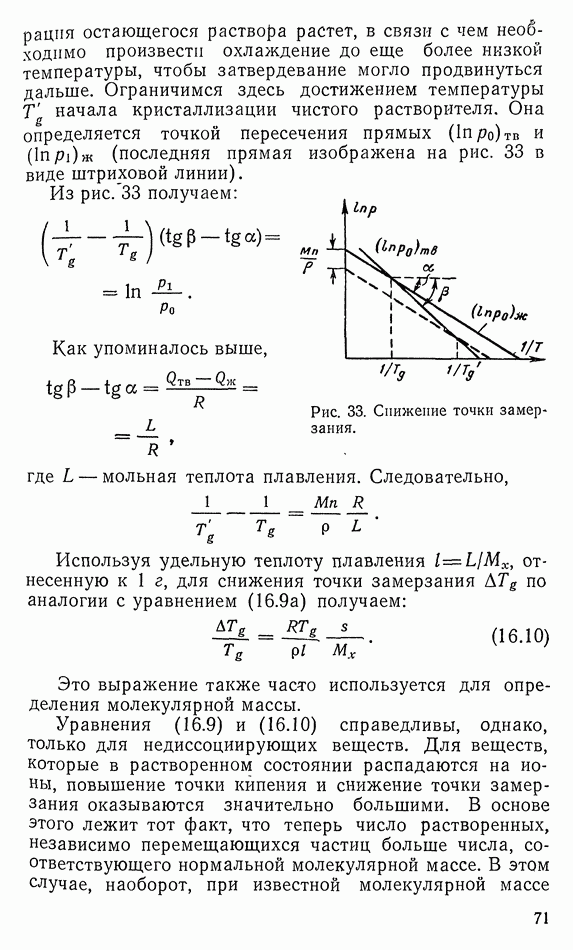
Естественный подход к теории Гамильтона обеспечивается вариационным исчислением. Здесь нам потребуется лишь один простой закон, а именно относящиеся к проблемам вариационного исчисления уравнения Эйлера. Сформулируем эту чисто математическую теорему вначале для одной координаты 
Пусть будет задана известная под названием «функции Лагранжа» функция  координаты х и скорости х. Как х, так и х представляют собой функции времени
координаты х и скорости х. Как х, так и х представляют собой функции времени  Рассмотрим интеграл от
Рассмотрим интеграл от  до
до 

Будем искать такую функцию  для которой
для которой  заданных «краевых значениях»
заданных «краевых значениях»  интеграл
интеграл  имеет экстремальные значения.
имеет экстремальные значения.
Заменим кривую  проварьированной кривой
проварьированной кривой  со значениями
со значениями  При этом а пусть будет неким числом. Для такой кривой
При этом а пусть будет неким числом. Для такой кривой  становится функцией а:
становится функцией а:

Наше условие экстремума означает теперь, что  для любого
для любого  при
при  равно 0.
равно 0.
Выполнение дифференцирования дает:

Очевидно, что

Интегрирование первого слагаемого даст нуль, так как  при краевых значениях равно 0. Таким образом, остается
при краевых значениях равно 0. Таким образом, остается

Для того чтобы этот интеграл для любой функции  был равен нулю, выражение в фигурных скобках должно всегда быть равным нулю, но это, однако, означает, что искомая функция
был равен нулю, выражение в фигурных скобках должно всегда быть равным нулю, но это, однако, означает, что искомая функция  должна удовлетворять уравнению Эйлера:
должна удовлетворять уравнению Эйлера:

Определим относящийся к х импульс  с помощью выражения
с помощью выражения

и представим себе, что данное уравнение решено относительно х таким образом, что х оказывается функцией  Введем далее функцию Гамильтона
Введем далее функцию Гамильтона

где в правой части вместо х следует подставить только что упомянутую функцию переменных  Для частных производных функции
Для частных производных функции  справедливы равенства
справедливы равенства

или

Уравнение (30.3), определяющее  позволяет исключить в правой части все члены с частными производными от х. С учетом выражения (30.2) получим окончательно уравнения Гамильтона:
позволяет исключить в правой части все члены с частными производными от х. С учетом выражения (30.2) получим окончательно уравнения Гамильтона:

Отсюда для производной по времени функции  следует:
следует:

Численное значение  не зависит от
не зависит от 
Переход от одной переменной  к нескольким, например
к нескольким, например  переменным
переменным  представляет собой чисто механическую работу по вышеприведенной схеме, если задана функция Лагранжа
представляет собой чисто механическую работу по вышеприведенной схеме, если задана функция Лагранжа

Будем искать такую функцию  -для которой интеграл
-для которой интеграл

имеет экстремум при заданных значениях  для
для  Заменим ее проварьированной функцией
Заменим ее проварьированной функцией

и потребуем, чтобы  для
для  и для всех становящихся равным нулю на границах
и для всех становящихся равным нулю на границах  временного интервала функций
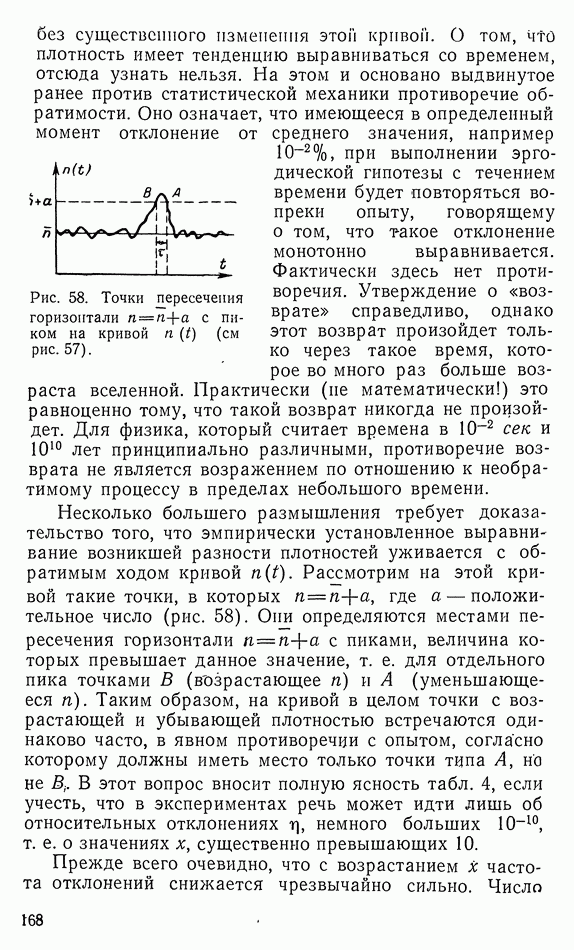
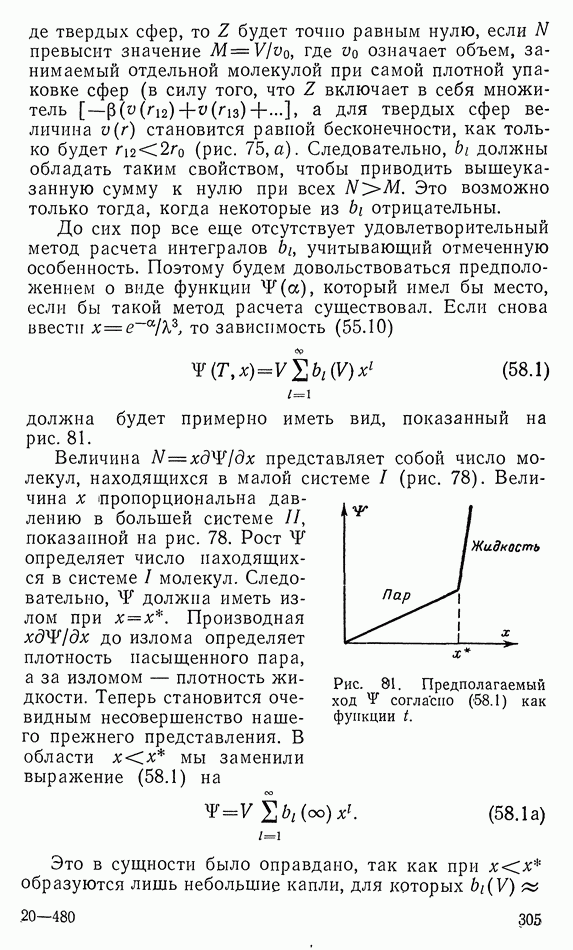
временного интервала функций 
Как и ранее, получаем уравнения Эйлера:

Используя импульсы

определяем как функцию Гамильтона

где все  следует понимать как функции
следует понимать как функции 
Запишем уравнения Гамильтона

Отсюда снова следует закон сохранения:

Параметры  производные по времени от которых заданы с помощью условий (30.11), называют также «канонически сопряженными переменными».
производные по времени от которых заданы с помощью условий (30.11), называют также «канонически сопряженными переменными».
Изменение во времени какой-либо физической величины, которая задана как функция координат, импульсов и времени, составляет:

После подстановки уравнений Гамильтона получаем: 

Сумма в правой части уравнения сокращенно обозначается  и называется «скобками Пуассона». Она играет большую роль в современной теоретической физике.
и называется «скобками Пуассона». Она играет большую роль в современной теоретической физике.
Изложенная таким образом математическая схема приобретает физическое содержание, если для данной интересующей нас системы функция Лагранжа  выбрана так, что дифференциальные уравнения (30.8) или (30.11) отображают действительные уравнения движения. В простейшем случае система состоит из материальных точек, которые подвержены воздействию сил, имеющих потенциал. Если для материальной точки с массой
выбрана так, что дифференциальные уравнения (30.8) или (30.11) отображают действительные уравнения движения. В простейшем случае система состоит из материальных точек, которые подвержены воздействию сил, имеющих потенциал. Если для материальной точки с массой  ввести координаты
ввести координаты  то для случая нерелятивистской механики уравнения движения относительно координаты
то для случая нерелятивистской механики уравнения движения относительно координаты  будут иметь вид:
будут иметь вид:

Соответствующие уравнения справедливы и для  Уравнения Ньютона (30.13) фактически представляют собой уравнения Эйлера для вариационной задачи:
Уравнения Ньютона (30.13) фактически представляют собой уравнения Эйлера для вариационной задачи:

Следовательно, в этом случае

3N уравнений (30.13) эквивалентны следующему требованию: движение происходит так, что величина 
имеет экстремальное значение, когда конфигураций  начале (ко времени
начале (ко времени  и в конце (ко времени
и в конце (ко времени  имеет определенные заданные значения. Но это требование совершенно независимо от системы координат. Отсюда следует: если вместо
имеет определенные заданные значения. Но это требование совершенно независимо от системы координат. Отсюда следует: если вместо  координат
координат  выбрать какие-либо другие параметры
выбрать какие-либо другие параметры  которые взаимнооднозначным образом являются функциями
которые взаимнооднозначным образом являются функциями  параметров
параметров  и выразить кинетическую энергию К и потенциальную энергию
и выразить кинетическую энергию К и потенциальную энергию  через
через  то образованные в виде
то образованные в виде

уравнения Эйлера также являются правильными уравнениями движения. Знак  в аргументе здесь и ниже означает сокращенное обозначение
в аргументе здесь и ниже означает сокращенное обозначение  То же самое справедливо и для
То же самое справедливо и для 
Так как кинетическая энергия одновременно квадратична в переменных  то такова же она и при переменных
то такова же она и при переменных  Относящиеся к
Относящиеся к  импульсы
импульсы

поэтому линейно однородны в переменных  Далее справедливо
Далее справедливо

Отсюда полученная в выражении (30.10) функция Гамильтона

равна сумме кинетической и потенциальной энергии. Таким образом, уравнение (30.12) представляет собой закон сохранения энергии.
При изменении формы уравнений движения (30.8) на каноническую форму (30.11) переходят от  дифференциальных уравнений второго порядка для
дифференциальных уравнений второго порядка для  функций от времени
функций от времени  дифференциальных уравнений первого порядка для
дифференциальных уравнений первого порядка для  функций от времени
функций от времени 
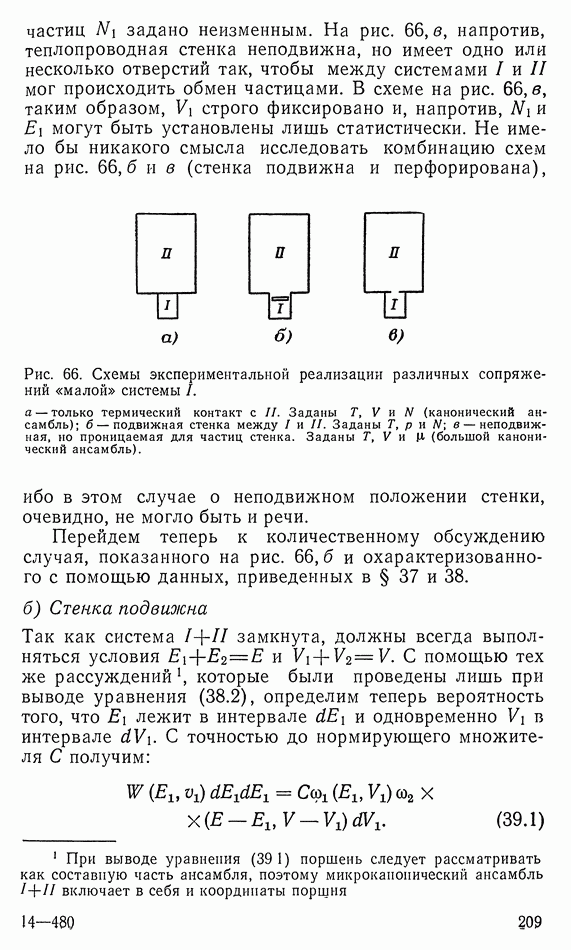
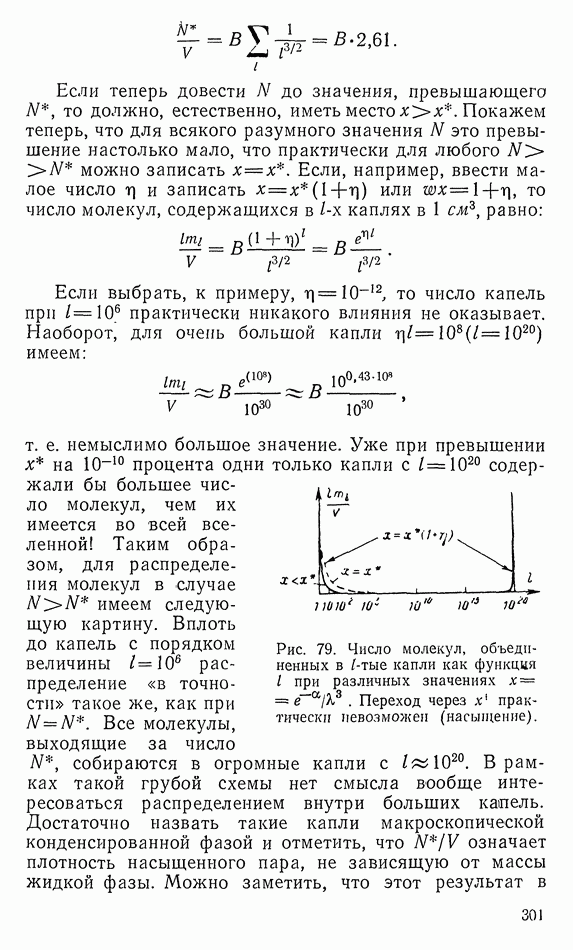
б) Канонические преобразования
Канонические уравнения можно также Вывести непосредственно из вариационного принципа К Если подставить  из (30.10) в (30-7а), то получим вариационную задачу
из (30.10) в (30-7а), то получим вариационную задачу 

с функцией Лагранжа

в которой  мы рассматриваем как независимые переменные.
мы рассматриваем как независимые переменные.  должно быть экстремумом относительно всех вариаций функций
должно быть экстремумом относительно всех вариаций функций  для которых установлены начальные и конечные значения. Тогда действительны уравнения Эйлера
для которых установлены начальные и конечные значения. Тогда действительны уравнения Эйлера

в точности дают канонические уравнения (30.11). Здесь введен «модифицированный принцип Гамильтона» (30.18), поскольку он удобен для обсуждения той части теории канонических преобразований, которые понадобятся ниже.
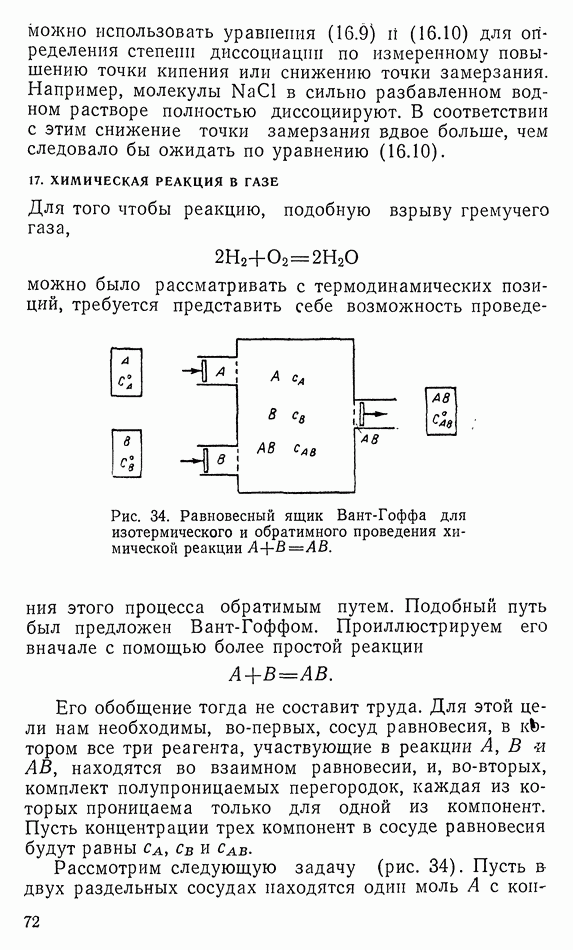
Из элементарной механики известно, что решение многих задач облегчается, если уравнения движения записать не в декартовых координатах, а преобразовать в другую систему координат. Имея в виду, что переменные  выступают в уравнении (30.18), эквивалентным образом рассмотрим теперь более общие преобразования:
выступают в уравнении (30.18), эквивалентным образом рассмотрим теперь более общие преобразования:

Назовем каноническим такое преобразование, когда существует функция  для которой уравнения движения в новых переменных
для которой уравнения движения в новых переменных  снова имеют каноническую форму:
снова имеют каноническую форму:

Благодаря (30.21) в новых переменных также должен выполняться модифицированный принцип Гамильтона:

Функция  должна выбираться так, чтобы при подстановка экстремалей (30.18) в (30.20) получались экстремали (30.22). Из этого еще не следует, что подынтегральные функции обоих вариационных принципов после выражения новых переменных через старые с помощью соотношений (30 20) должны совпадать. Напротив, они еще могут отличаться на производную по времени любой функции
должна выбираться так, чтобы при подстановка экстремалей (30.18) в (30.20) получались экстремали (30.22). Из этого еще не следует, что подынтегральные функции обоих вариационных принципов после выражения новых переменных через старые с помощью соотношений (30 20) должны совпадать. Напротив, они еще могут отличаться на производную по времени любой функции  всех переменных
всех переменных  ведь
ведь

при вариации не дает никакого вклада, так как начальные и конечные значения  твердо устанавливаются. Выберем
твердо устанавливаются. Выберем

Хотя вследствие (30.20) среди  параметров
параметров  только
только  независимы, это не является каким-либо ограничением. Для того чтобы экстремали обоих вариационных принципов совпадали, должно теперь выполняться условие
независимы, это не является каким-либо ограничением. Для того чтобы экстремали обоих вариационных принципов совпадали, должно теперь выполняться условие

или

С другой стороны, дифференцирование  по времени дает:
по времени дает:

Оба этих уравнения выполняются, когда

Первые уравнения означают, что преобразование (30.20) каноническое, коль скоро его можно вывести из преобразующей функции  согласно (30.24). Второе уравнение указывает, что новую функцию Гамильтона получают, разрешая уравнения преобразования относительно
согласно (30.24). Второе уравнение указывает, что новую функцию Гамильтона получают, разрешая уравнения преобразования относительно  и подставляя значения в старую функцию Гамильтона.
и подставляя значения в старую функцию Гамильтона.
Детерминант функционала, произведенного с помощью преобразования (30.20), равен единице:

Для доказательства выпишем вначале необходимые частные производные;  следует понимать как функции
следует понимать как функции 
Используя (30.24) и обозначения  получаем:
получаем:

Вычисляя частные производные от второго из уравнений (30.24) по  или
или  получаем:
получаем:

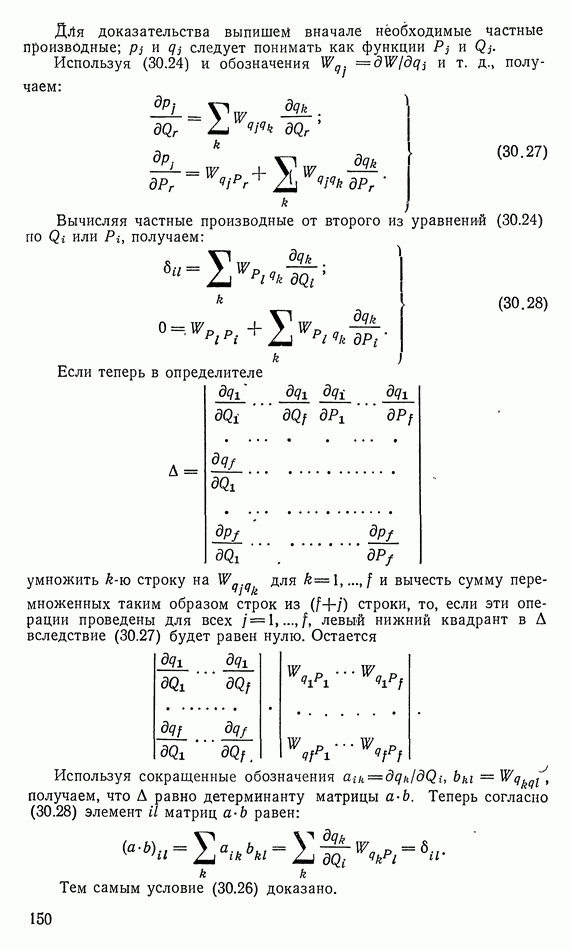
Если теперь в определителе

умножить  строку на для
строку на для  и вычесть сумму перемноженных таким образом строк из
и вычесть сумму перемноженных таким образом строк из  строки, то, если эти операции проведены для всех
строки, то, если эти операции проведены для всех  левый нижний квадрант в
левый нижний квадрант в  вследствие (30.27) будет равен нулю. Остается
вследствие (30.27) будет равен нулю. Остается

Используя сокращенные обозначения  получаем, что
получаем, что  равно детерминанту матрицы
равно детерминанту матрицы  Теперь согласно (30.28) элемент
Теперь согласно (30.28) элемент  матриц
матриц  равен:
равен:

Тем самым условие (30.26) доказано.
В заключение рассмотрим преобразование (30.24) для случая, когда разница между новыми и старыми координатами и импульсами

бесконечно мала. Так как тождественное преобразование выполняется с помощью выражения

то в качестве преобразующей функции для бесконечно малого преобразования есть основания принять.

где  бесконечно мало. Тем самым в соответствии с (30.24) будут иметь место соотношения
бесконечно мало. Тем самым в соответствии с (30.24) будут иметь место соотношения

В предельном случае  мы можем в
мы можем в  заменить
заменить  на
на  в результате чего получим:
в результате чего получим:

Если заменить здесь  на и выбрать в качестве
на и выбрать в качестве  функцию Гамильтона
функцию Гамильтона  то последние уравнения станут идентичными уравнениям движения. Таким образом, действительное изменение координат и импульсов за время
то последние уравнения станут идентичными уравнениям движения. Таким образом, действительное изменение координат и импульсов за время  описано с помощью бесконечно малого канонического преобразования, для которого преобразующей является функция Гамильтона. Так как последовательность канонических преобразований также дает каноническое преобразование, то значения
описано с помощью бесконечно малого канонического преобразования, для которого преобразующей является функция Гамильтона. Так как последовательность канонических преобразований также дает каноническое преобразование, то значения  в какой-либо момент времени связаны с начальными значениями
в какой-либо момент времени связаны с начальными значениями  через канонические преобразования. Теорема (30.26) о детерминанте функционала оказывается, таким образом, эквивалентной по значению обсуждаемой в следующем параграфе теореме Лиувилля.
через канонические преобразования. Теорема (30.26) о детерминанте функционала оказывается, таким образом, эквивалентной по значению обсуждаемой в следующем параграфе теореме Лиувилля.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА ПЕРВАЯ. ТЕРМОДИНАМИКА
- 1. ПОНЯТИЕ ТЕМПЕРАТУРЫ И УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- 2. ПАРАМЕТРЫ СОСТОЯНИЯ
- 3. ПЕРВЫЙ ОСНОВНОЙ ЗАКОН
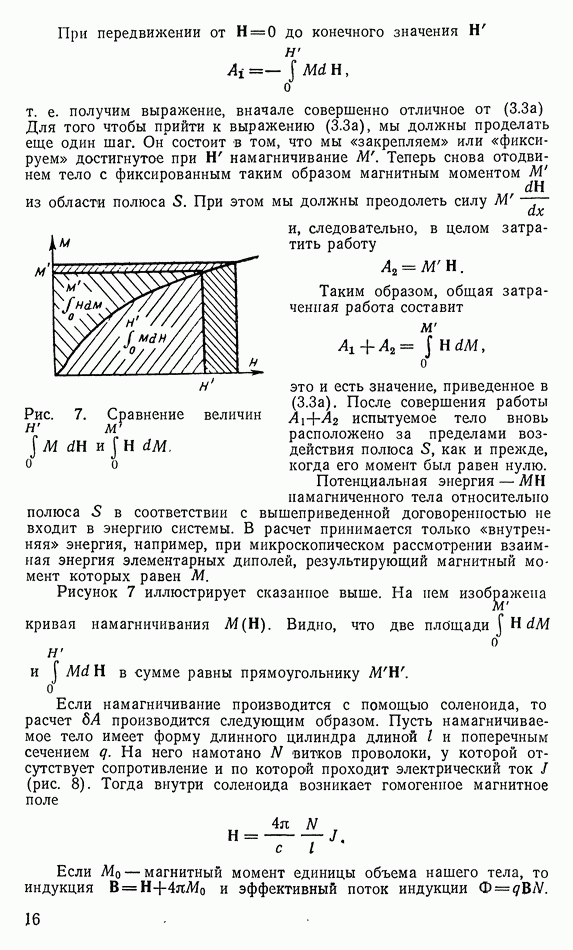
- б) Намагничивание
- в) Энергия идеального газа
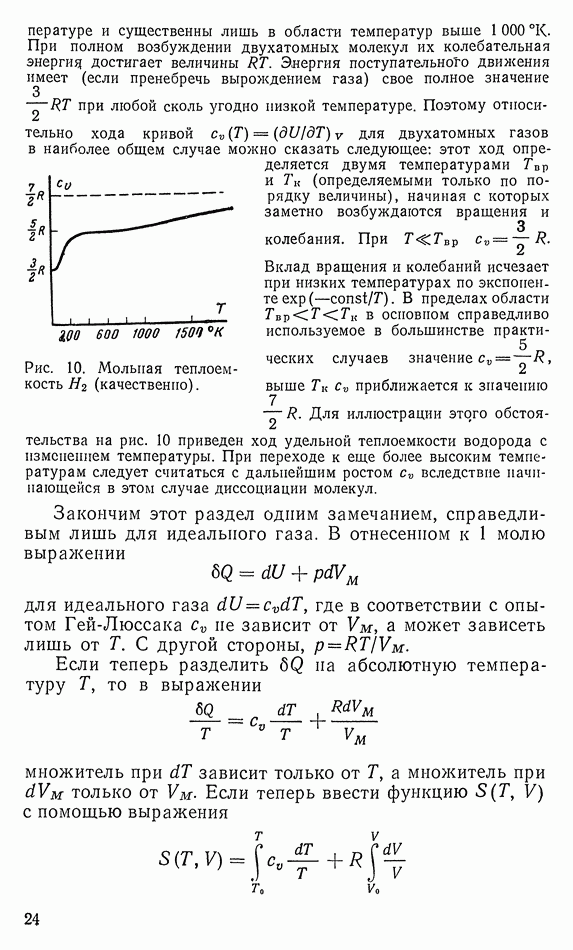
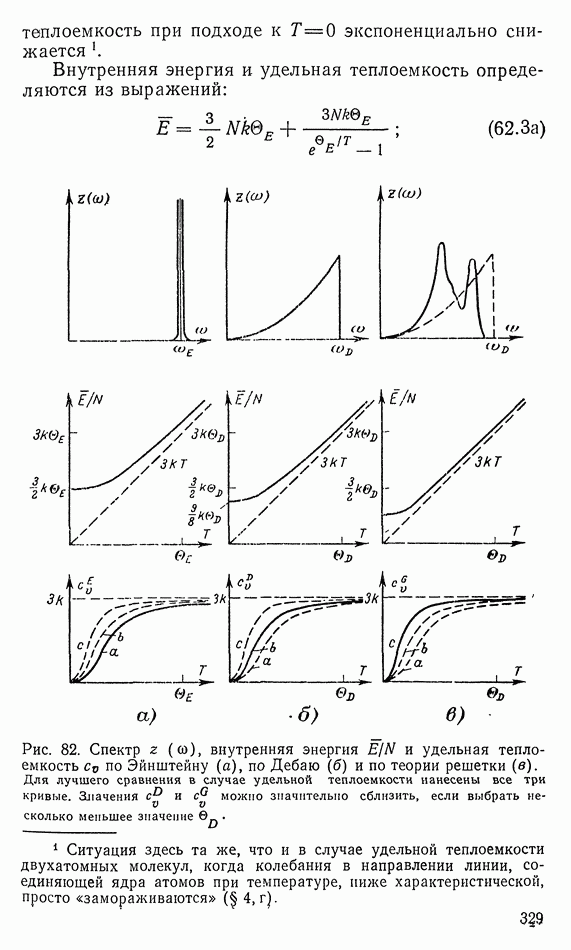
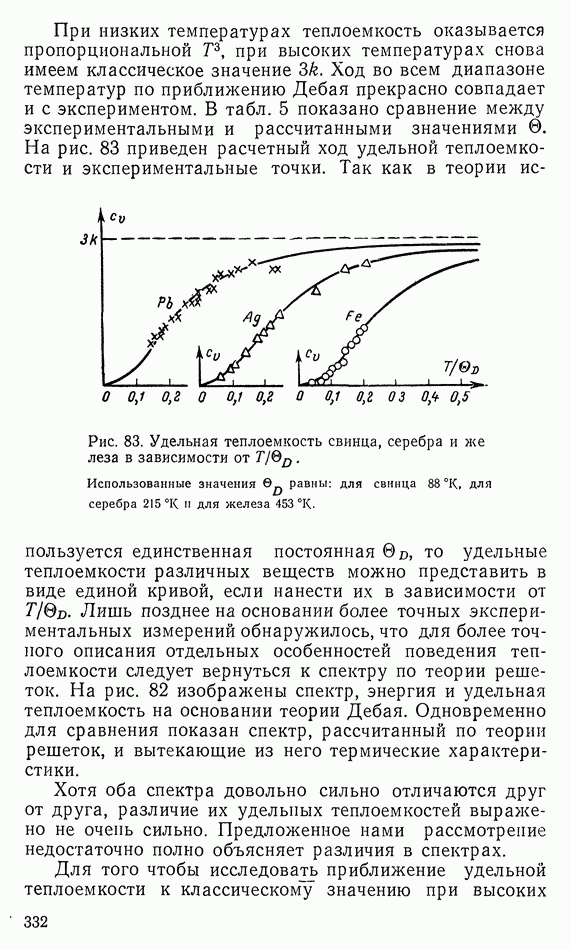
- 4. УДЕЛЬНАЯ ТЕПЛОЕМКОСТЬ
- б) Адиабатный процесс
- в) Применение для расчета скорости звука
- г) Энергия и удельная теплоемкость идеального газа
- 5. ВТОРОЙ ОСНОВНОЙ ЗАКОН
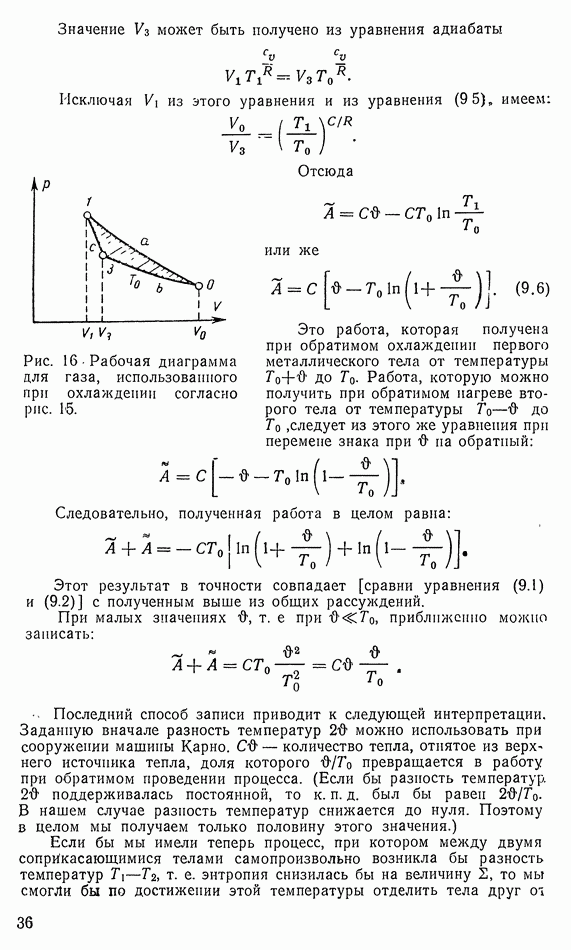
- 6. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ КАРНО
- 7. ОБЩИЙ СЛУЧАЙ МАШИНЫ КАРНО И ОПРЕДЕЛЕНИЕ АБСОЛЮТНОЙ ТЕМПЕРАТУРЫ
- Б. ЭНТРОПИЯ
- 8. ЭНТРОПИЯ КАК ФУНКЦИЯ СОСТОЯНИЯ
- 9. РОСТ ЭНТРОПИИ В ИЗОЛИРОВАННОЙ СИСТЕМЕ
- 10. ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА
- В. НЕКОТОРЫЕ ПРИМЕНЕНИЯ
- 11. СВОБОДНАЯ ЭНЕРГИЯ
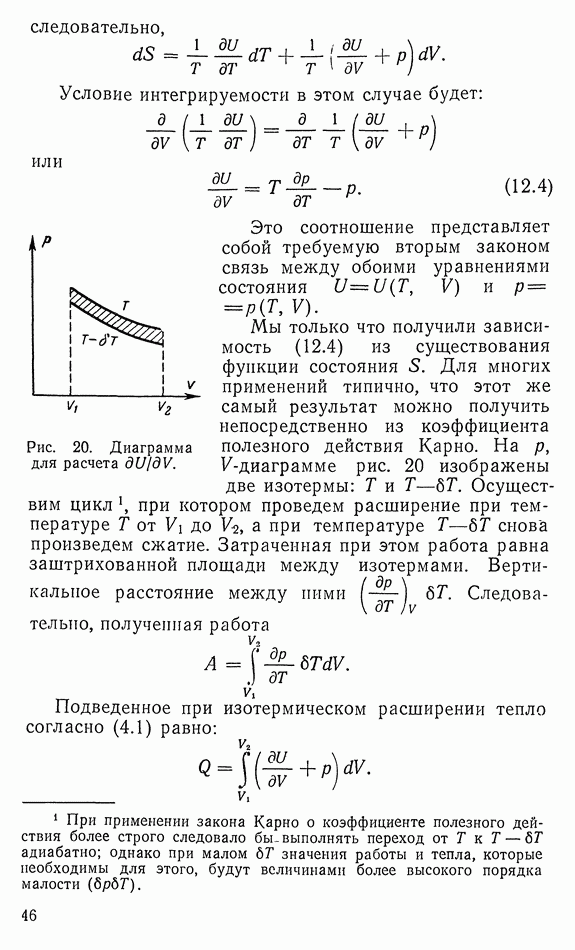
- 12. УРАВНЕНИЕ СОСТОЯНИЯ И УСЛОВИЕ ИНТЕГРИРУЕМОСТИ
- 13. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- 14. ЭФФЕКТ ДЖОУЛЯ — ТОМСОНА
- Г. МЕТОД КРУГОВЫХ ПРОЦЕССОВ
- 15. ДАВЛЕНИЕ ПАРА (ФОРМУЛА КЛАУЗИУСА — КЛАПЕЙРОНА)
- 16. РАСТВОРЫ
- 17. ХИМИЧЕСКАЯ РЕАКЦИЯ В ГАЗЕ
- 18. ПРИМЕР ИЗ СВЕРХПРОВОДИМОСТИ
- Д. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ И ОБЩЕЕ РАВНОВЕСИЕ
- 19. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ И ИХ ПРИМЕНЕНИЕ К ГОМОГЕННЫМ ФАЗАМ
- 20. ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ
- 21. ХИМИЧЕСКИЙ ПОТЕНЦИАЛ ИДЕАЛЬНОГО ГАЗА
- 22. ДАВЛЕНИЕ ПАРА НАД НЕБОЛЬШОЙ КАПЛЕЙ
- ГЛАВА ВТОРАЯ. СТАТИСТИЧЕСКАЯ МЕХАНИКА
- А. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
- 24. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- 25. МАКСВЕЛЛОВСКОЕ РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ
- 26. ОБОСНОВАНИЕ БОЛЬЦМАНОМ РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ МАКСВЕЛЛА И Н-TEOPEMA
- 27. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
- 28. ТЕОРЕМА О ВИРИАЛЕ
- 29. РАЗРЕЖЕННЫЙ НЕИДЕАЛЬНЫЙ ГАЗ
- Б. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ
- 30. УРАВНЕНИЯ ДВИЖЕНЙЯ ГАМИЛЬТОНА
- 31. Г-ПРОСТРАНСТВО
- В. МИКРОКАНОНИЧЕСКИЙ АНСАМБЛЬ
- 32. УСРЕДНЕНИЕ ПО ВРЕМЕНИ И ПО АНСАМБЛЮ
- 33. ПРОСТЕЙШИЕ ПРИМЕНЕНИЯ
- 34. ЭНТРОПИЯ
- 35. ДЕЛЕНИЕ НА N1 И ДЕЙСТВИТЕЛЬНЫЙ ФАЗОВЫЙ ОБЪЕМ
- Г. КАНОНИЧЕСКИЙ АНСАМБЛЬ
- 37. КАНОНИЧЕСКИЙ АНСАМБЛЬ
- 38. МАКРОСКОПИЧЕСКОЕ ТЕЛО
- Д. ДВА ДРУГИХ АНСАМБЛЯ
- 39. СВОБОДНАЯ ЭНТАЛЬПИЯ
- 40. БОЛЬШОЙ КАНОНИЧЕСКИЙ АНСАМБЛЬ (T, V, «мю» ЗАДАНЫ)
- 41. ЗАКЛЮЧЕНИЕ
- ГЛАВА ТРЕТЬЯ. КВАНТОВАЯ СТАТИСТИКА
- 42. ПРЕДВАРИТЕЛЬНОЕ РАССМОТРЕНИЕ НЕКОТОРЫХ РЕЗУЛЬТАТОВ
- 43. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ КВАНТОВОЙ ТЕОРИИ
- 44. АНСАМБЛЬ ИЛИ СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ
- 45. ЭНТРОПИЯ ТЕРМИЧЕСКИ ИЗОЛИРОВАННОЙ СИСТЕМЫ
- 46. КАНОНИЧЕСКИЙ АНСАМБЛЬ
- ГЛАВА ЧЕТВЕРТАЯ. ИДЕАЛЬНЫЕ И РЕАЛЬНЫЕ ГАЗЫ А. ИДЕАЛЬНЫЙ ГАЗ И ВЫРОЖДЕНИЕ ГАЗА
- 47. СТАТИСТИЧЕСКИЙ ИНТЕГРАЛ И СТАТИСТИЧЕСКАЯ СУММА ДЛЯ ЧАСТИЦ
- 48. N ОДИНАКОВЫХ НЕВЗАИМОДЕЙСТВУЮЩИХ ЧАСТИЦ
- 49. СИСТЕМА ИЗОЛИРОВАНА
- 50. СИСТЕМА НАХОДИТСЯ В ТЕРМОСТАТЕ
- 51. БОЛЬШОЙ КАНОНИЧЕСКИЙ АНСАМБЛЬ
- 52. ПРЕДЕЛЬНЫЙ СЛУЧАЙ СИЛЬНОГО РАЗРЕЖЕНИЯ
- 53. ГАЗ ФЕРМИ
- 54. ГАЗ БОЗЕ
- Б. РЕАЛЬНЫЕ ГАЗЫ И КОНДЕНСАЦИЯ
- 56. ОБЛАСТЬ НЕНАСЫЩЕННОГО ПАРА
- 57. КОНДЕНСАЦИЯ
- 58. ЖИДКАЯ ФАЗА
- 59. АНАЛОГИЯ МЕЖДУ ИДЕАЛЬНЫМ ГАЗОМ БОЗЕ И РЕАЛЬНЫМ ГАЗОМ
- 60. ОБРАЗОВАНИЕ ЗАРОДЫШЕЙ
- ГЛАВА ПЯТАЯ. ТВЕРДОЕ ТЕЛО
- 62. КВАНТОВОМЕХАНИЧЕСКОЕ РАССМОТРЕНИЕ И ОБЩИЙ ОБЗОР
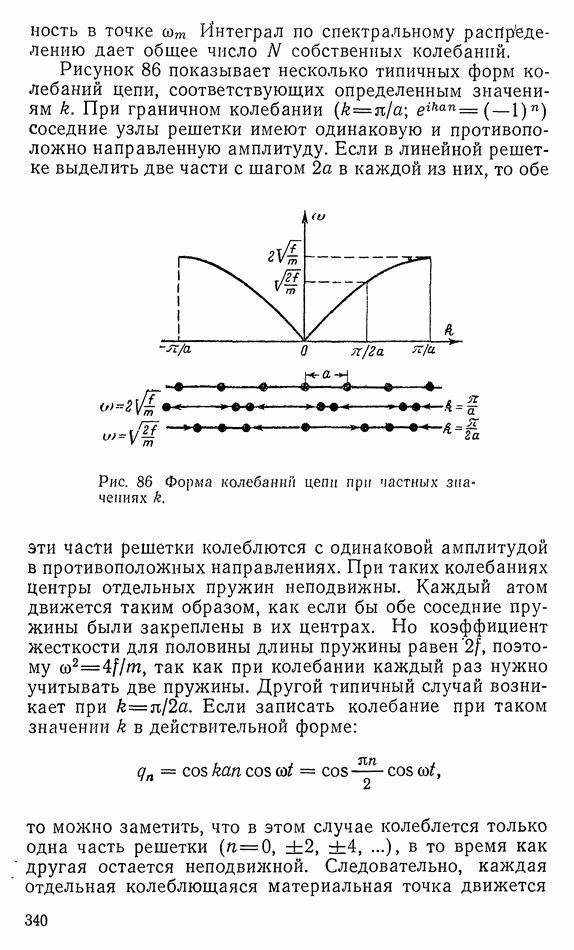
- 63. ЛИНЕЙНАЯ ЦЕПЬ
- 64. КОЛЕБАНИЯ ПРОСТРАНСТВЕННОЙ РЕШЕТКИ
- 65. ОБСУЖДЕНИЕ ХОДА УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ
- Б. УПОРЯДОЧЕННАЯ И НЕУПОРЯДОЧЕННАЯ КРИСТАЛЛИЧЕСКАЯ РЕШЕТКА
- 67. СТАТИСТИЧЕСКИЙ МЕТОД
- 68. СВЕРХСТРУКТУРА
- 60. РАЗДЕЛЕНИЕ ФАЗ («фи» ПОЛОЖИТЕЛЬНО)
- 70. ФЕРРОМАГНЕТИЗМ
- 71. ПРИБЛИЖЕНИЕ БЭТЕ ДЛЯ МОДЕЛИ ИЗИНГА
- 72. ЛИНЕИНАЯ И ПЛОСКАЯ РЕШЕТКИ ПО МЕТОДУ МАТРИЦ
- ГЛАВА ШЕСТАЯ. ФЛУКТУАЦИИ И БРОУНОВСКОЕ ДВИЖЕНИЕ
- 74. ЯВЛЕНИЯ ФЛУКТУАЦИЙ
- Б. БРОУНОВСКОЕ ДВИЖЕНИЕ
- 76. ПОДВИЖНОСТЬ И ДИФФУЗИЯ
- 77. УРАВНЕНИЕ ЛАНЖЕВЕНА
- 78. МЕТОД ЭЙНШТЕЙНА И ХОПФА
- 79. УСТАНОВЛЕНИЕ РАСПРЕДЕЛЕНИЯ МАКСВЕЛЛА
- 80. НЕКОТОРЫЕ СВЕДЕНИЯ О СЛУЧАЙНОМ ДВИЖЕНИИ
- 81. КОРРЕЛЯЦИЯ ДЛЯ СТАТИСТИЧЕСКИ ИЗМЕНЯЮЩЕЙСЯ ФУНКЦИИ
- 82. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ФОККЕРА — ПЛАНКА
- 83. СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ СТАТИСТИЧЕСКОЙ ФУНКЦИИ
- 84. СЛАБО ДЕМПФИРОВАННЫЙ ОСЦИЛЛЯТОР С ЗАТУХАНИЕМ, ЗАВИСЯЩИМ ОТ ЧАСТОТЫ
- 85. ФОРМУЛА НАЙКВИСТА
- 86. ДРОБОВОЙ ЭФФЕКТ
- ГЛАВА СЕДЬМАЯ. ТЕРМОДИНАМИКА НЕОБРАТИМЫХ ПРОЦЕССОВ
- 88. НЕОБРАТИМЫЕ ПРОЦЕССЫ В СТАТИСТИЧЕСКОЙ МЕХАНИКЕ
- 89. ОДНОВРЕМЕННОЕ НАБЛЮДЕНИЕ НЕСКОЛЬКИХ МАКРОСКОПИЧЕСКИХ ВЕЛИЧИН
- 90. МЕТОД КОКСА
- 91. ОБМЕН ТЕПЛОМ И ЧАСТИЦАМИ
- 92. НЕКОТОРЫЕ ПРИМЕНЕНИЯ
- 93. МЕТОД ТОМСОНА И ЕГО ПОДТВЕРЖДЕНИЕ СООТНОШЕНИЯМИ ОНЗАГЕРА
- 94. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ. ВЫВОД ТОМСОНА
- 95. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ. ОБСУЖДЕНИЕ С ПОМОЩЬЮ СООТНОШЕНИЯ ВЗАИМНОСТИ ОНЗАГЕРА