| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
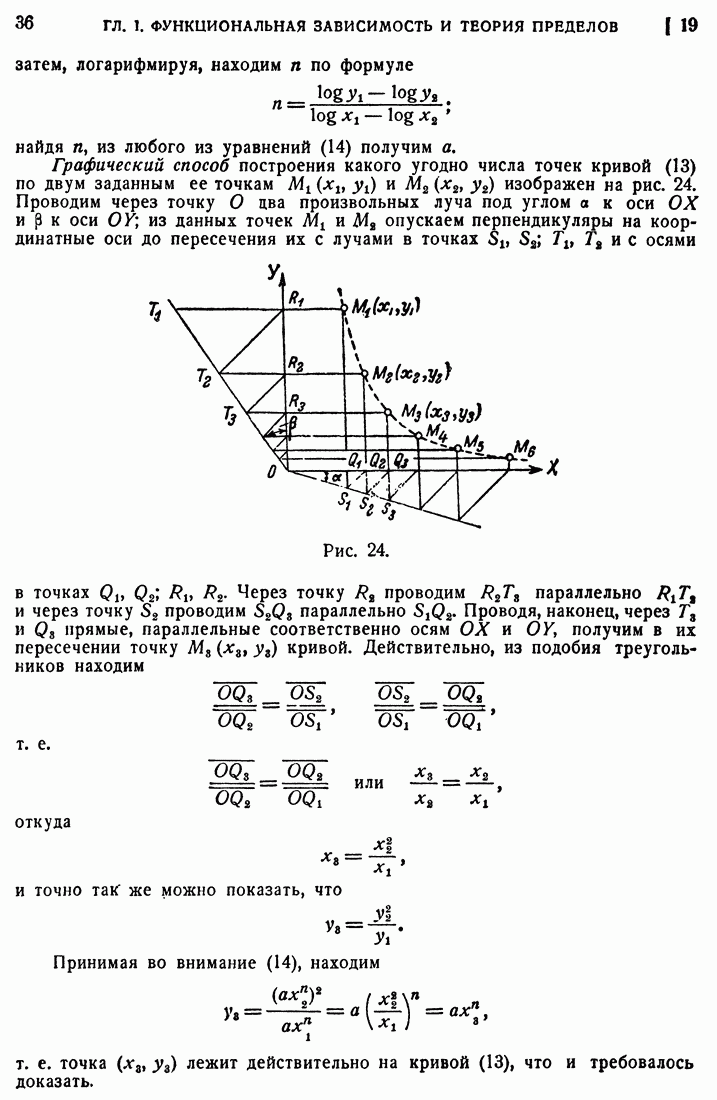
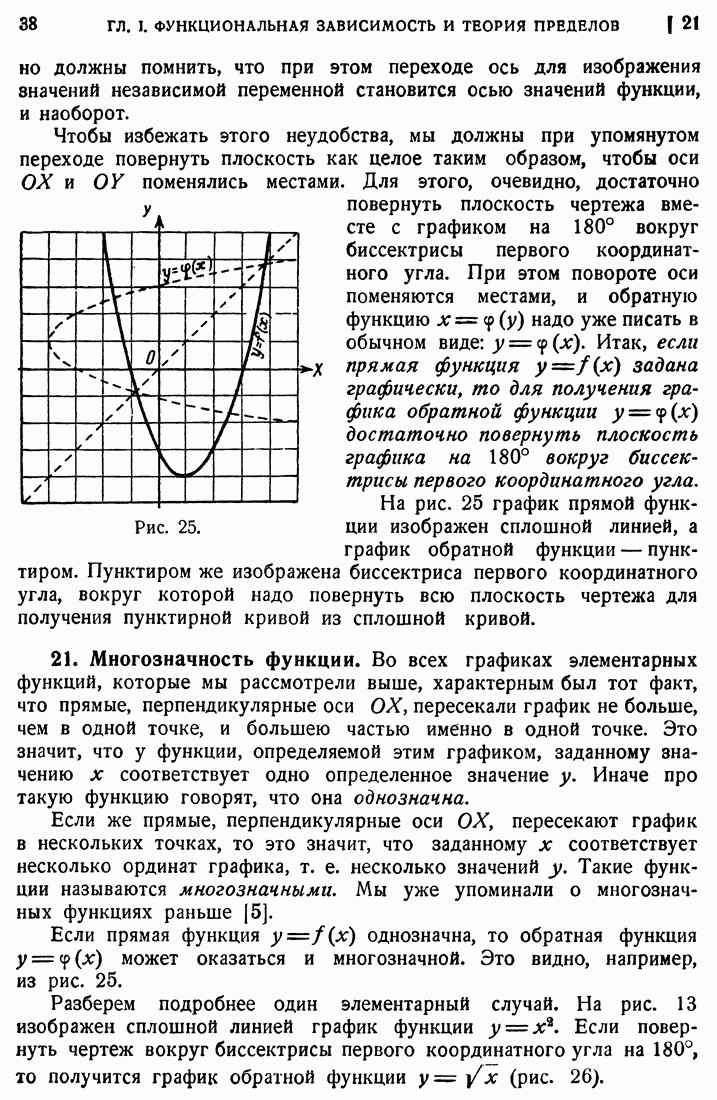
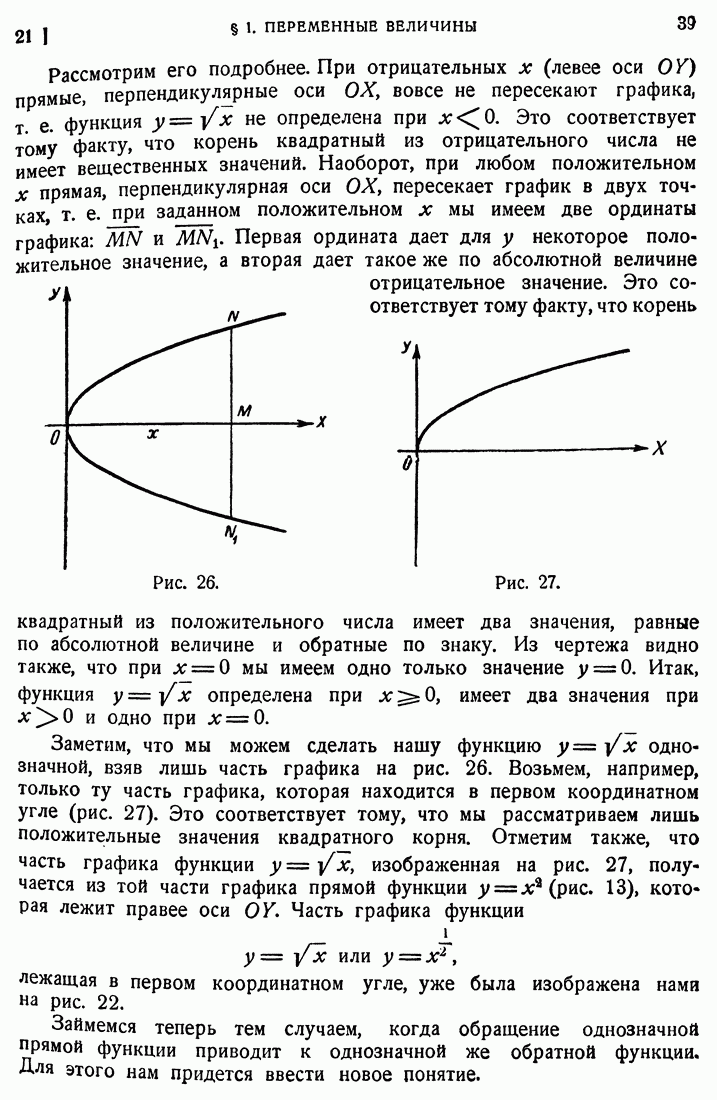
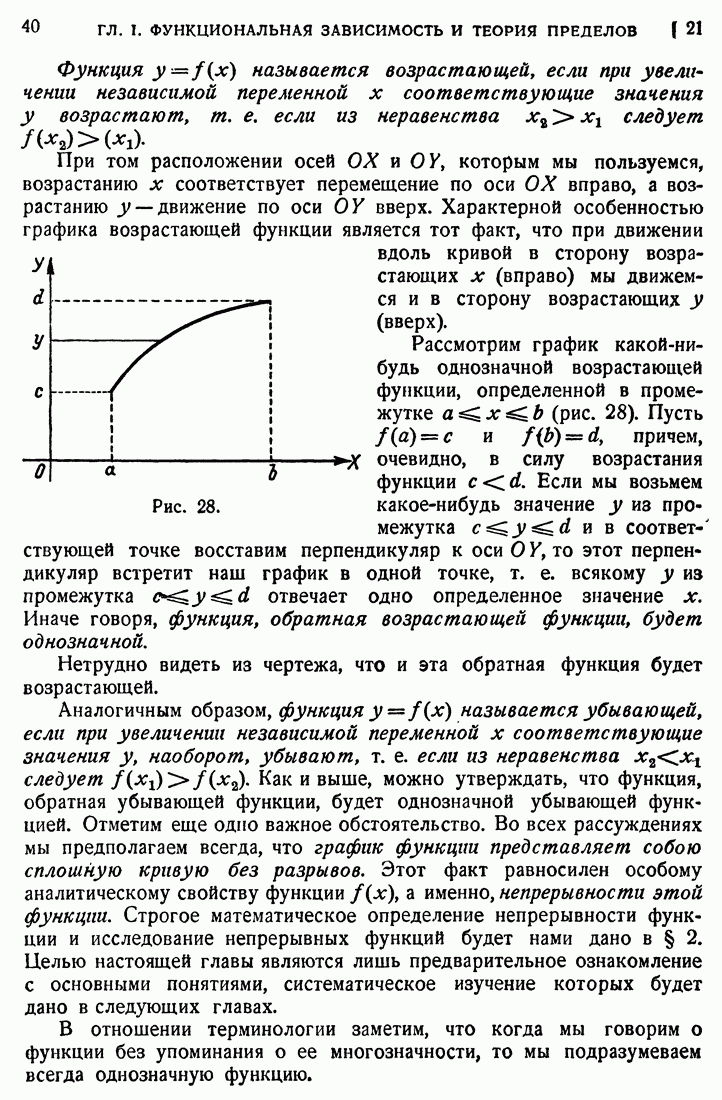
60. Наибольшее и наименьшее значения функций.
Пусть рассматриваются значения функции  при значениях независимой переменной
при значениях независимой переменной  из промежутка (а, b), т. е. при
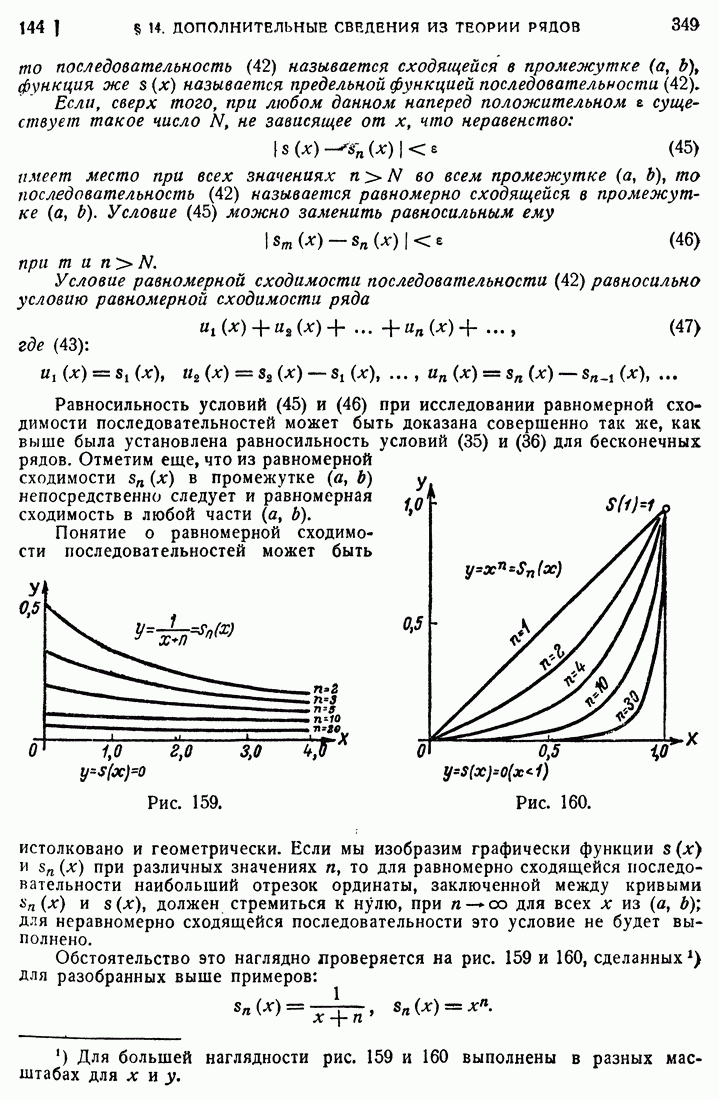
из промежутка (а, b), т. е. при  , и пусть требуется найти наибольшее и наименьшее из этих значений. При указанном условии функция f(x) будет достигать наибольшего и наименьшего значения [35], т. е. соответствующий этой функции график будет иметь в упомянутом промежутке наибольшую и наименьшую ординаты.
, и пусть требуется найти наибольшее и наименьшее из этих значений. При указанном условии функция f(x) будет достигать наибольшего и наименьшего значения [35], т. е. соответствующий этой функции график будет иметь в упомянутом промежутке наибольшую и наименьшую ординаты.
Согласно приведенным выше правилам, мы сможем найти все максимумы и минимумы функции, заключающиеся внутри промежутка  . Если функция
. Если функция  имеет свою наибольшую ординату внутри этого промежутка, то эта наибольшая ордината будет, очевидно, совпадать с наибольшим максимумом функции внутри промежутка
имеет свою наибольшую ординату внутри этого промежутка, то эта наибольшая ордината будет, очевидно, совпадать с наибольшим максимумом функции внутри промежутка  Но может оказаться, что наибольшая ордината находится не внутри промежутка, а на одном из его концов
Но может оказаться, что наибольшая ордината находится не внутри промежутка, а на одном из его концов  или
или  Поэтому для нахождения, например, наибольшего значения функции недостаточно сравнить все ее максимумы внутри промежутка и взять наибольший, но необходимо также принять во внимание и значение функции на концах промежутка. Точно так же для определения наименьшего значения функции надо взять все ее минимумы, лежащие внутри промежутка, и граничные значения функции при
Поэтому для нахождения, например, наибольшего значения функции недостаточно сравнить все ее максимумы внутри промежутка и взять наибольший, но необходимо также принять во внимание и значение функции на концах промежутка. Точно так же для определения наименьшего значения функции надо взять все ее минимумы, лежащие внутри промежутка, и граничные значения функции при  Заметим при этом, что максимумы и минимумы могут вовсе отсутствовать, а наибольшее и наименьшее значения у непрерывной функции в ограниченном промежутке
Заметим при этом, что максимумы и минимумы могут вовсе отсутствовать, а наибольшее и наименьшее значения у непрерывной функции в ограниченном промежутке  обязательно будут существовать.
обязательно будут существовать.
Отметим некоторые частные случаи, когда нахождение наименьших и наибольших значений производится наиболее просто. Если, например, функция f(x) возрастает в промежутке  то, очевидно, при
то, очевидно, при  она будет принимать наименьшее, а при
она будет принимать наименьшее, а при  наибольшее значение. Для убывающей функции картина будет противоположной.
наибольшее значение. Для убывающей функции картина будет противоположной.

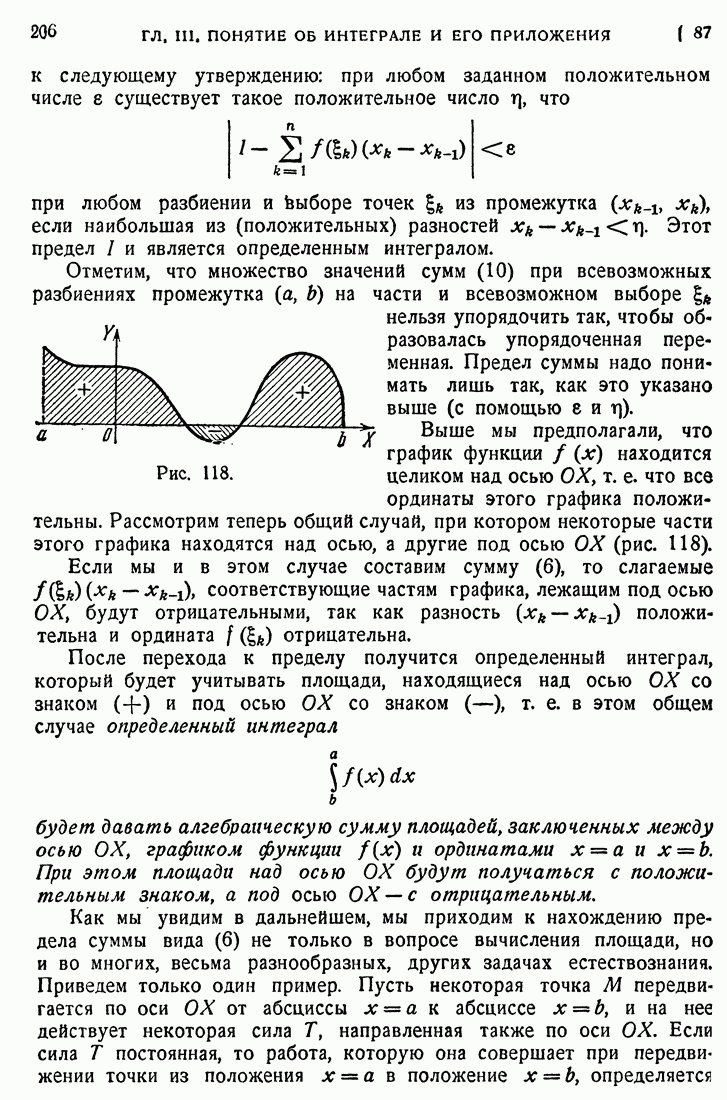
Рис. 63.
Если функция имеет внутри промежутка один максимум и не имеет минимумов, то этот единственный максимум и дает наибольшее значение функции (рис. 63), так что в этом случае для определения наибольшего значения функции вовсе не надо определять значений функций на концах промежутка. Точно так же, если функция имеет внутри промежутка один минимум и не имеет вовсе максимумов, то упомянутый единственный минимум и дает наименьшее значение функции. Указанные только что обстоятельства будут иметь место в первых из четырех изложенных ниже задач.
1. Дан отрезок длины l. Требуется разделить его на две часта так, чтобы площадь прямоугольника, построенного на них, была наибольшей.
Пусть  длина одной из частей отрезка,
длина одной из частей отрезка,  длина другой его части. Принимая во внимание, что площадь прямоугольника равна произведению его соседних сторон, видим, что задача сводится к нахождению тех начений
длина другой его части. Принимая во внимание, что площадь прямоугольника равна произведению его соседних сторон, видим, что задача сводится к нахождению тех начений  при которых функция
при которых функция

достигает наибольшего значения в промежутке  изменения
изменения 
Составим производные первого и второго порядка

Приравнивая первую производную нулю, получим единственное значение  которому и соответствует максимум, так как
которому и соответствует максимум, так как  постоянно отрицательна. Таким образом, наибольшая площадь будет у квадрата со стороною
постоянно отрицательна. Таким образом, наибольшая площадь будет у квадрата со стороною

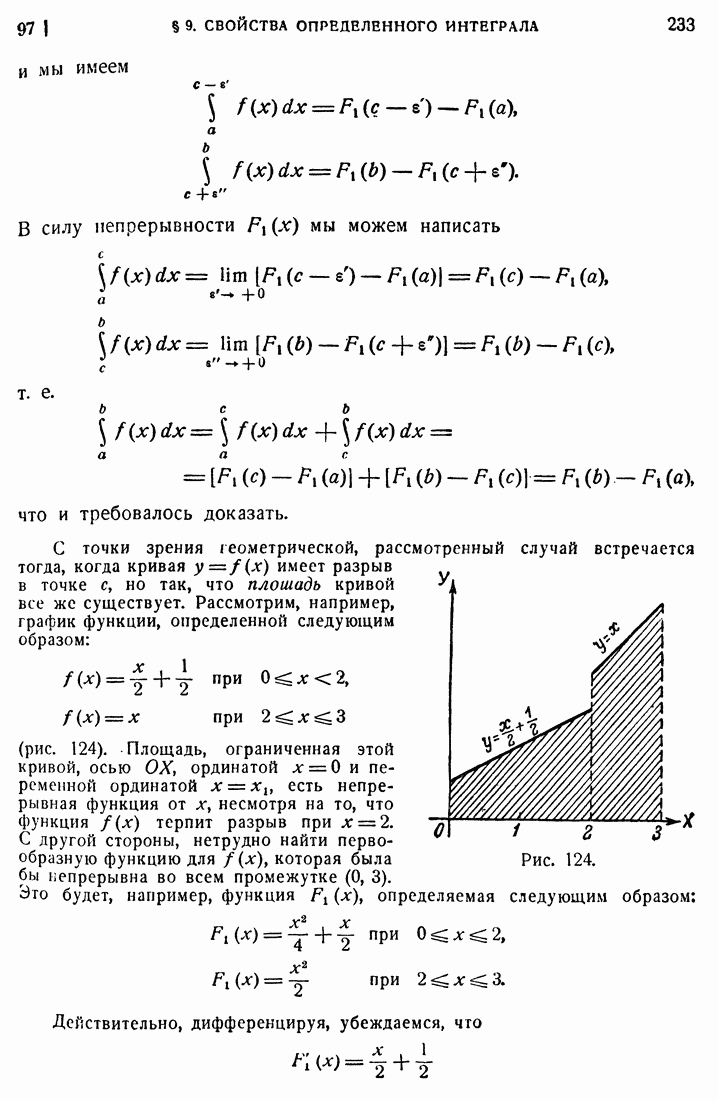
Рис. 64.
2. Из круга радиуса R вырезается сектор и из оставшейся части круга склеивается конус. Требуется определить угол вырезанного сектора так, чтобы объем конуса был наибольшим.
Примем за независимую переменную  не угол вырезанного сектора, а его дополнение до
не угол вырезанного сектора, а его дополнение до  , т. е. угол оставшегося сектора. При значениях
, т. е. угол оставшегося сектора. При значениях  близких к 0 и
близких к 0 и  объем конуса будет близок к нулю, и, очевидно, внутри промежутка
объем конуса будет близок к нулю, и, очевидно, внутри промежутка  будет существовать такое значение
будет существовать такое значение  при котором этот объем будет наибольшим.
при котором этот объем будет наибольшим.
При склеивании оставшейся части круга в конус (рис. 64) получится такой конус, у которого образующая равна  , длина окружности основания равна
, длина окружности основания равна  радиус основания
радиус основания  и высота
и высота

Объем этого конуса будет

При отыскании наибольшего значения этой функции мы можем не обращать внимания на постоянный множитель  Оставшееся произведение
Оставшееся произведение  положительно и, следовательно, будет достигать наибольшего значения при тех же значениях при которых достигает наибольшего значения его квадрат. Таким образом, мы можем рассматривать функцию
положительно и, следовательно, будет достигать наибольшего значения при тех же значениях при которых достигает наибольшего значения его квадрат. Таким образом, мы можем рассматривать функцию

внутри промежутка  ). Составляем первую производную
). Составляем первую производную

Она существует, при всех значениях  Приравнивая ее нулю, получим три значения:
Приравнивая ее нулю, получим три значения:

Первые два значения не лежат внутри промежутка  . Остается единственное значение
. Остается единственное значение  лежащее внутри этого промежутка; но выше мы видели, что наибольшее значение внутри этого промежутка должно встретиться, а следовательно, и не исследуя значения 3, можем утверждать, что ему будет соответствовать наибольший объем конуса.
лежащее внутри этого промежутка; но выше мы видели, что наибольшее значение внутри этого промежутка должно встретиться, а следовательно, и не исследуя значения 3, можем утверждать, что ему будет соответствовать наибольший объем конуса.
3. Прямою L плоскость разделена на две части (среды) I и II. Точка двигается в среде I со скоростью  в среде II — со скоростью
в среде II — со скоростью  По какому пути должна двигаться точка, чтобы возможно скорее попасть из точки А среды I в точку В среды II?
По какому пути должна двигаться точка, чтобы возможно скорее попасть из точки А среды I в точку В среды II?
Пусть  перпендикуляры из точек А и В на прямую L. Введем следующие обозначения:
перпендикуляры из точек А и В на прямую L. Введем следующие обозначения:  и на прямой L будем отсчитывать абсциссы в направлении
и на прямой L будем отсчитывать абсциссы в направлении 

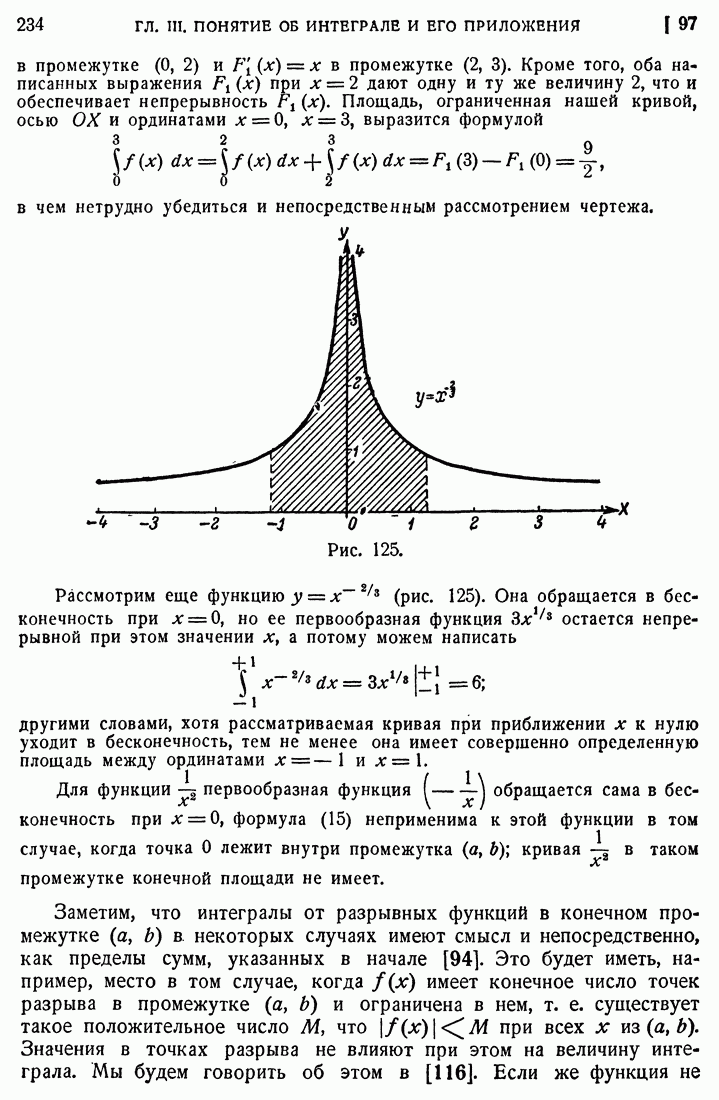
Рис. 65.
Ясно, что как в среде  так и в среде II путь точки должен быть прямолинейным, но путь по прямой АВ не будет, вообще говоря, „скорейшим путем". Итак, „скорейший путь будет состоять из двух прямолинейных отрезков AM и MB, причем точка М должна лежать на прямой L. За независимую переменную
так и в среде II путь точки должен быть прямолинейным, но путь по прямой АВ не будет, вообще говоря, „скорейшим путем". Итак, „скорейший путь будет состоять из двух прямолинейных отрезков AM и MB, причем точка М должна лежать на прямой L. За независимую переменную  выберем абсциссу точки М:
выберем абсциссу точки М:  Время
Время  наименьшее значение которого ищется, определится по формуле
наименьшее значение которого ищется, определится по формуле

в промежутке  Составим производные первого и второго порядков:
Составим производные первого и второго порядков:

Обе производные существуют при всех значениях  всегда имеет знак
всегда имеет знак  Следовательно,
Следовательно,  возрастает в промежутке
возрастает в промежутке  и не может обратиться в нуль более одного раза. Но
и не может обратиться в нуль более одного раза. Но

и

а потому уравнение

имеет единственный корень  между 0 и с, которому соответствует единственный минимум функции
между 0 и с, которому соответствует единственный минимум функции  так как
так как  . Абсциссы 0 и с соответствуют точкам
. Абсциссы 0 и с соответствуют точкам  а потому искомая точка М будет находиться между точками
а потому искомая точка М будет находиться между точками  что можно было бы показать и из элементарных геометрических соображений.
что можно было бы показать и из элементарных геометрических соображений.
Поясним геометрический смысл полученного решения. Обозначим через  углы, составленные отрезками
углы, составленные отрезками  и ВМ с перпендикуляром, восставленным из точки М к L. Абсцисса
и ВМ с перпендикуляром, восставленным из точки М к L. Абсцисса  искомой точки М должна обращать Б пуль
искомой точки М должна обращать Б пуль  , т. е. должна удовлетворять уравнению
, т. е. должна удовлетворять уравнению

которое можно переписать так:

или

„скорейший путь" будет тот, при котором отношение синусов углов а и  будет равно отношению скоростей в средах
будет равно отношению скоростей в средах  . Результат этот дает нам известный закон преломления света, и, следовательно, преломление света совершается так, как будто луч света выбирает „скорейший путь" из точек одной среды в точки другой.
. Результат этот дает нам известный закон преломления света, и, следовательно, преломление света совершается так, как будто луч света выбирает „скорейший путь" из точек одной среды в точки другой.
4. Положим, что экспериментально определяется величина  одинаково тщательно произведенных наблюдений дают для нее
одинаково тщательно произведенных наблюдений дают для нее  значений
значений

неодинаковых ввиду неточности инструментов. „Наиболее вероятным" значением величины  будем считать то, при котором сумма квадратов ошибок будет наименьшей. Таким образом, нахождение этого значения приводится к нахождению
будем считать то, при котором сумма квадратов ошибок будет наименьшей. Таким образом, нахождение этого значения приводится к нахождению  из условия наименьшего значения функции
из условия наименьшего значения функции

в промежутке  . Составляем производные первого и второго порядков
. Составляем производные первого и второго порядков

Приравнивая первую производную нулю, получим единственное значение

которому будет соответствовать минимум ввиду положительности второй производной. Таким образом „наиболее вероятным значением х является среднее арифметическое значений, полученных из наблюдений.
5. Найти кратчайшее расстояние точки М до окружности.
Примем за начало координат центр окружности О, за ось ОХ — прямую ОМ. Пусть  и пусть R есть радиус окружности. Уравнение окружности будет
и пусть R есть радиус окружности. Уравнение окружности будет

а расстояние точки М с координатами  до любой точки окружности
до любой точки окружности

Будем искать наибольшее значение квадрата этого расстояния. Подставив вместо  его выражение
его выражение  из уравнения окружности, мы получим функцию
из уравнения окружности, мы получим функцию

где независимая переменная  может изменяться в промежутке
может изменяться в промежутке  Так как первая производная
Так как первая производная

отрицательна при всех значениях  то функция
то функция  убывает и достигает, следовательно, наименьшего значения при
убывает и достигает, следовательно, наименьшего значения при  на правом конце промежутка.
на правом конце промежутка.
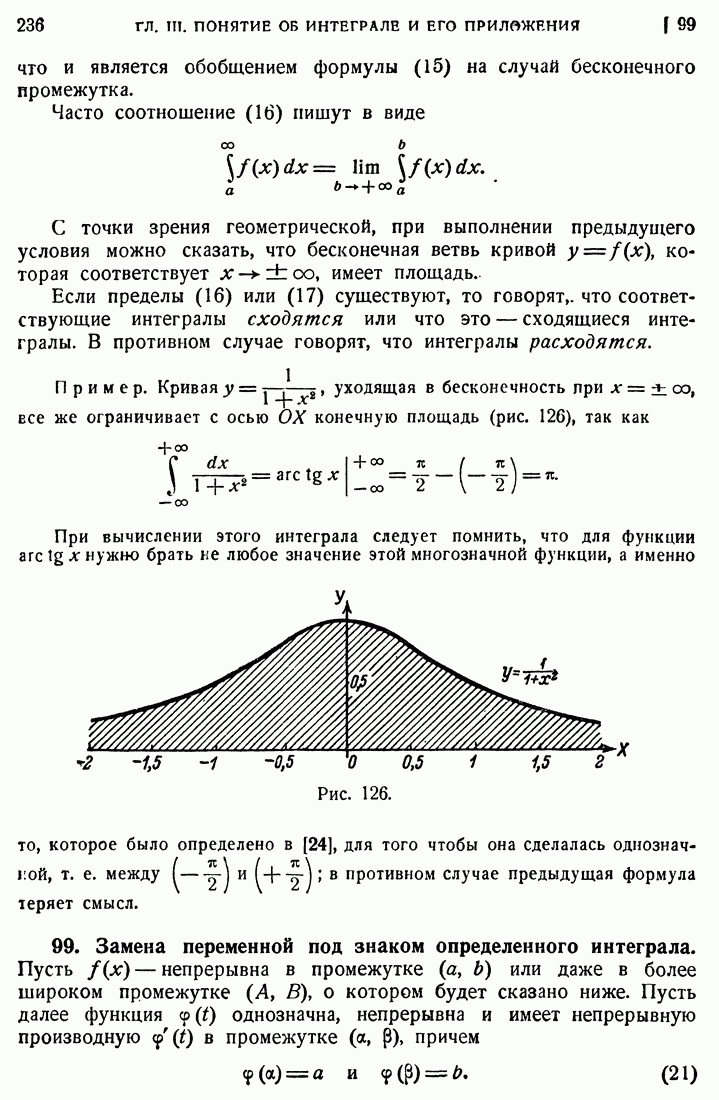
Кратчайшим расстоянием будет длина отрезка РМ (рис. 66).
6. В прямой круговой конус вписать прямой круговой цилиндр (с основанием  лежащим в основании конуса) так, чтобы его полная поверхность была наибольшей.
лежащим в основании конуса) так, чтобы его полная поверхность была наибольшей.

Рис. 66.

Рис. 67.
Обозначим радиус основания и высоту конуса буквами R и H, а радиус основания и высоту цилиндра-—буквами  и h. Функция, наибольшее значение которой ищется, будет в данном случае
и h. Функция, наибольшее значение которой ищется, будет в данном случае

Переменные величины  и h связаны между собой тем условием, что цилиндр вписан в данный конус. Из подобия треугольников ABD и AMN имеем (рис. 67):
и h связаны между собой тем условием, что цилиндр вписан в данный конус. Из подобия треугольников ABD и AMN имеем (рис. 67):

откуда

Подставляя это значение h в выражение для S, получим

Таким образом, S оказывается функцией одной независимой переменной  , которая может изменяться в промежутке
, которая может изменяться в промежутке  . Составим производные первых двух порядков:
. Составим производные первых двух порядков:

Приравнивая нулю получим для  одно значение
одно значение

Для того чтобы это значение находилось внутри промежутка  необходимо выполнение неравенств
необходимо выполнение неравенств

Первое из этих неравенств равносильно тому, что Н должно быть больше R. Умножая обе части второго неравенства на положительную величину  получим
получим

При выполнении этого условия  имеет знак (—); значению (2) соответствуют единственный максимум функции S и наибольшая величина поверхности цилиндра. Эту величину можно легко определить, подставляя значение
имеет знак (—); значению (2) соответствуют единственный максимум функции S и наибольшая величина поверхности цилиндра. Эту величину можно легко определить, подставляя значение  из (2) в выражение для S.
из (2) в выражение для S.
Предположим теперь, что значение (2) не лежит внутри промежутка  т. е. что не выполнено одно из неравенств (3). При этом могут представиться две возможности: или НR или
т. е. что не выполнено одно из неравенств (3). При этом могут представиться две возможности: или НR или  но
но  . Обе они могут быть охарактеризованы одним неравенством
. Обе они могут быть охарактеризованы одним неравенством

Преобразуем выражение для

Из этого выражения видно, что при выполнении условия (4) при  т. е. функция S возрастает в промежутке
т. е. функция S возрастает в промежутке  а потому достигает наибольшего значения при
а потому достигает наибольшего значения при  При этом значении
При этом значении  , очевидно,
, очевидно,  и полученное решение можно рассматривать как сплющенный цилиндр, основание которого совпадает с основанием конуса и вся поверхность которого приводится к
и полученное решение можно рассматривать как сплющенный цилиндр, основание которого совпадает с основанием конуса и вся поверхность которого приводится к 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ
- ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ
- 1. Величина и ее измерение.
- 2. Число.
- 3. Величины постоянные и переменные.
- 4. Промежуток.
- 5. Понятие о функции.
- 6. Аналитический способ задания функциональной зависимости.
- 7. Неявные функции.
- 8. Табличный способ.
- 9. Графический способ изображения чисел.
- 10. Координаты.
- 11. График и уравнение кривой.
- 12. Линейная функция.
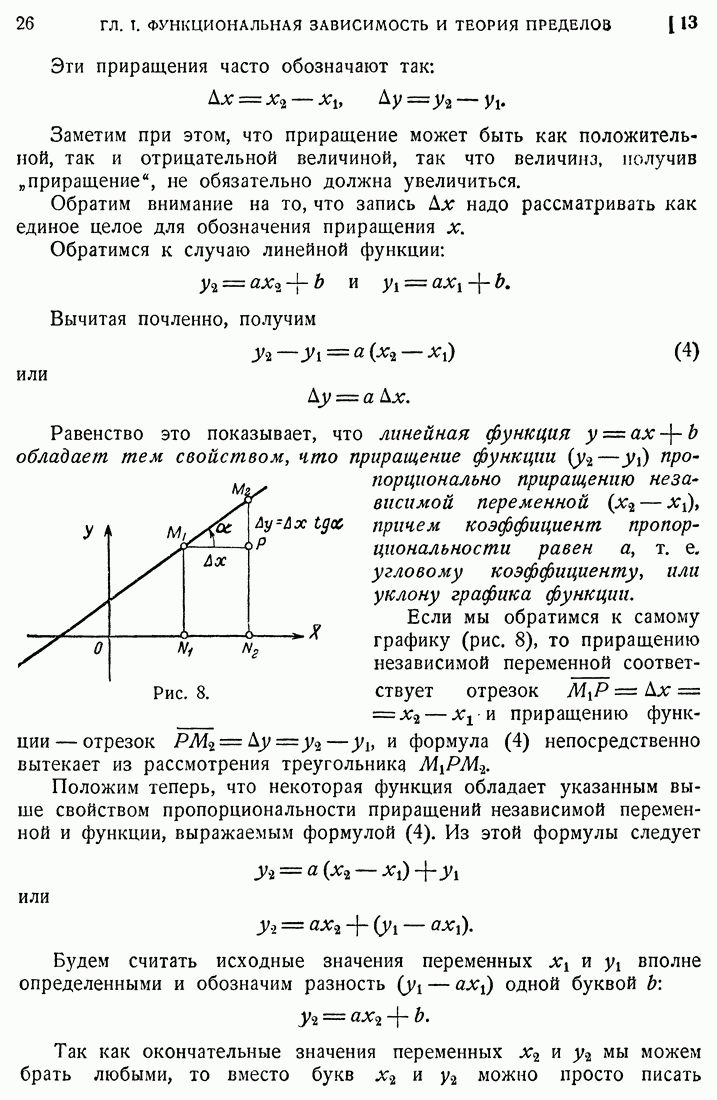
- 13. Приращение. Основное свойство линейной функции.
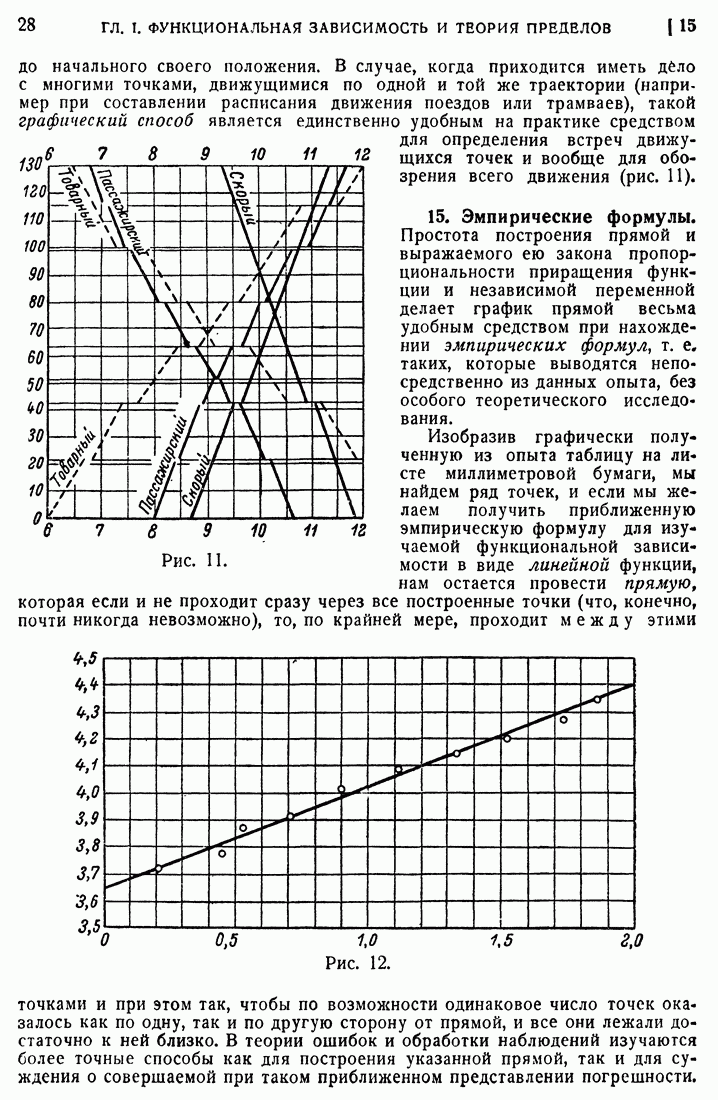
- 14. График равномерного движения.
- 15. Эмпирические формулы.
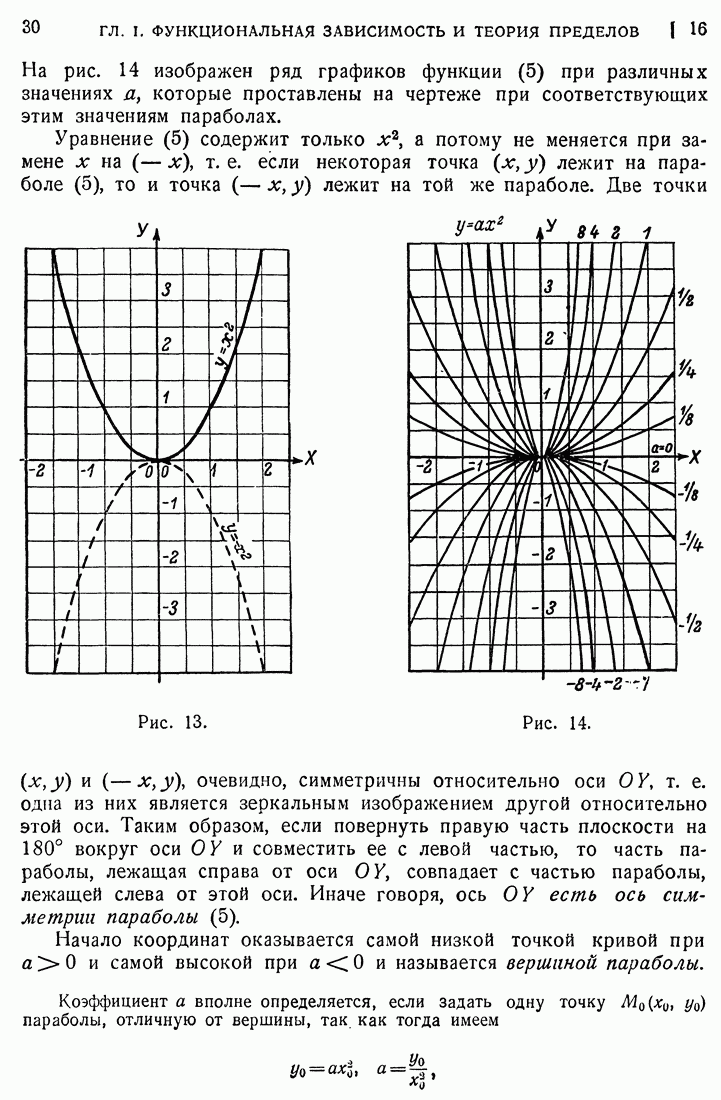
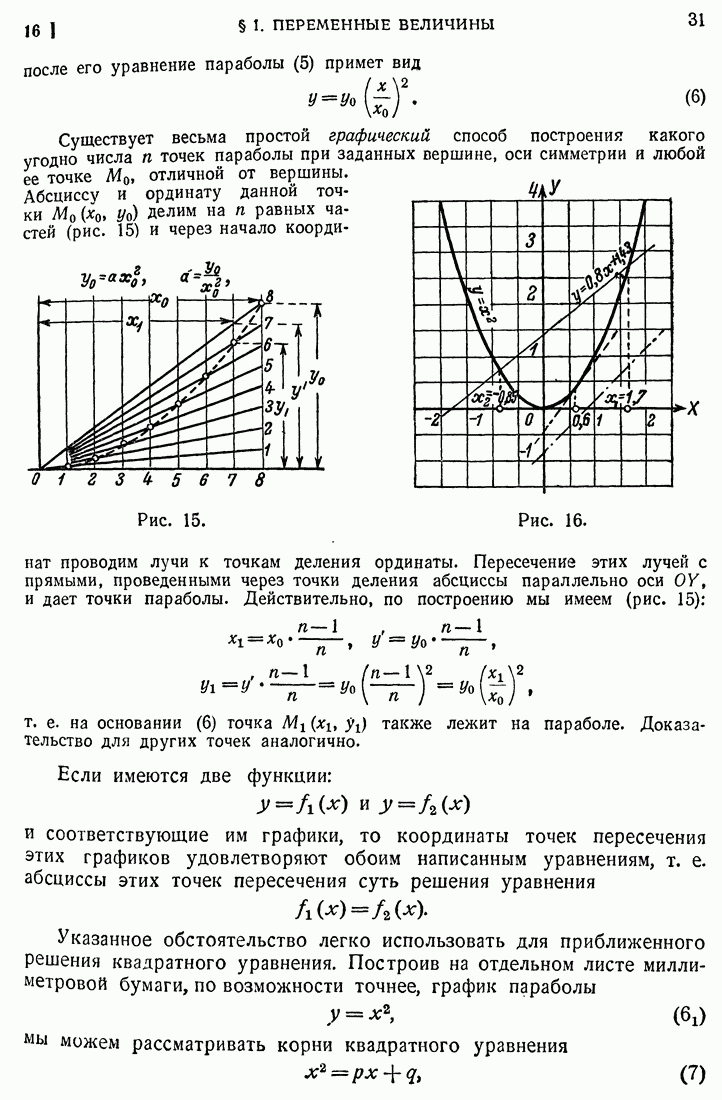
- 16. Парабола второй степени.
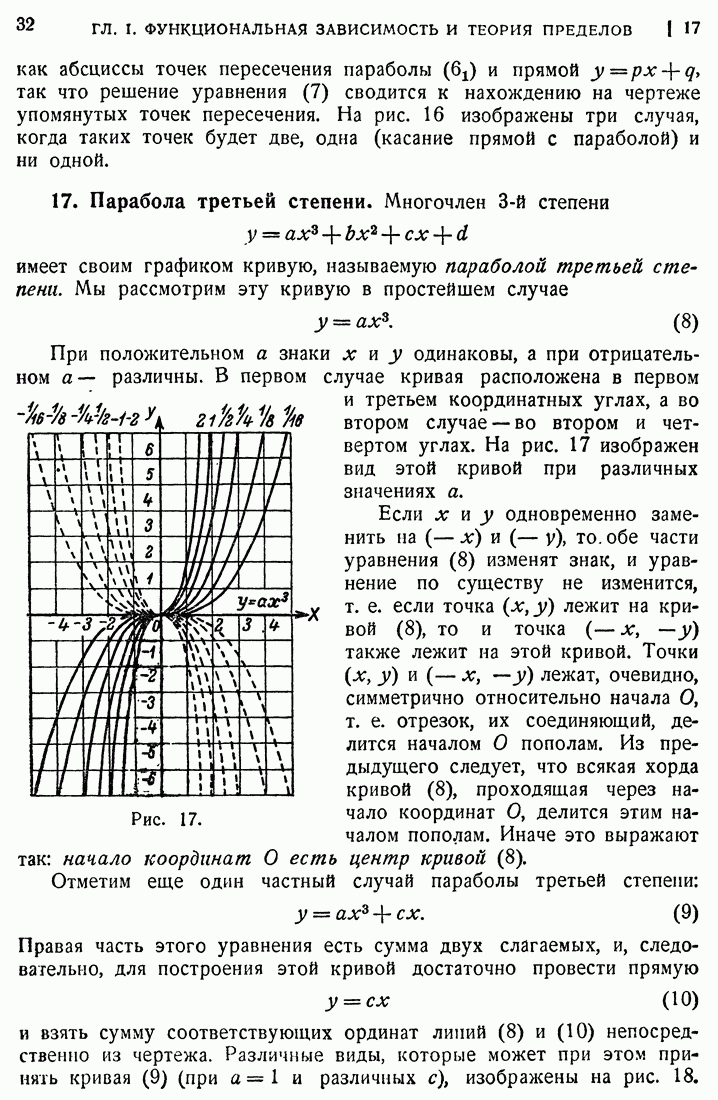
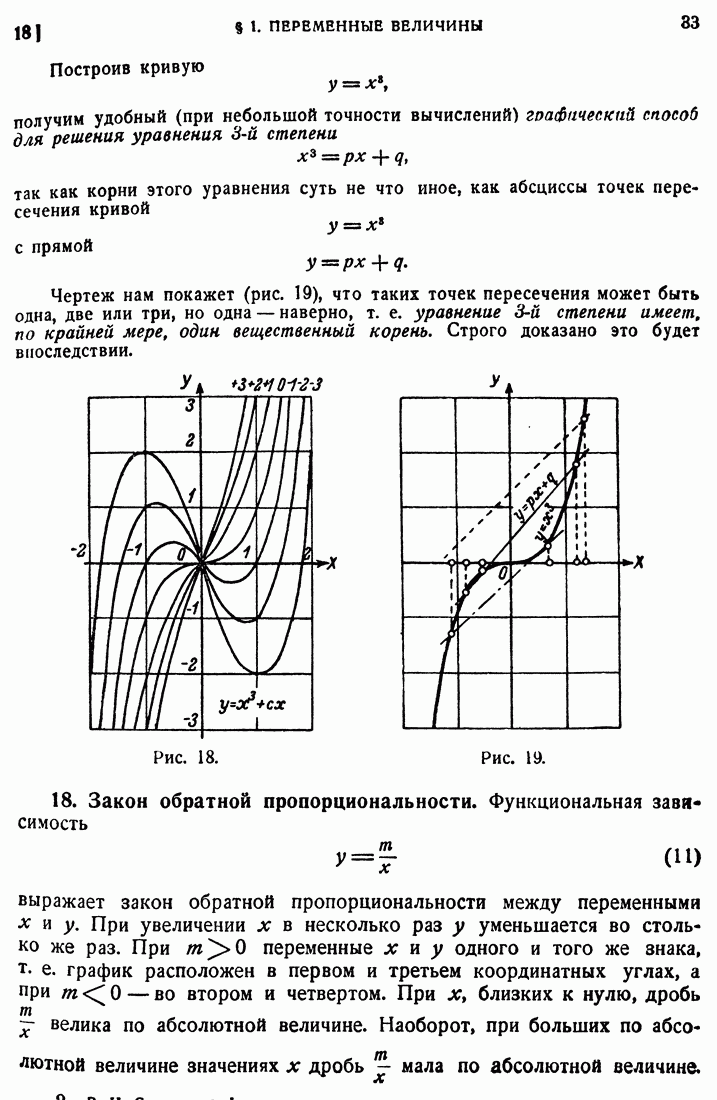
- 17. Парабола третьей степени.
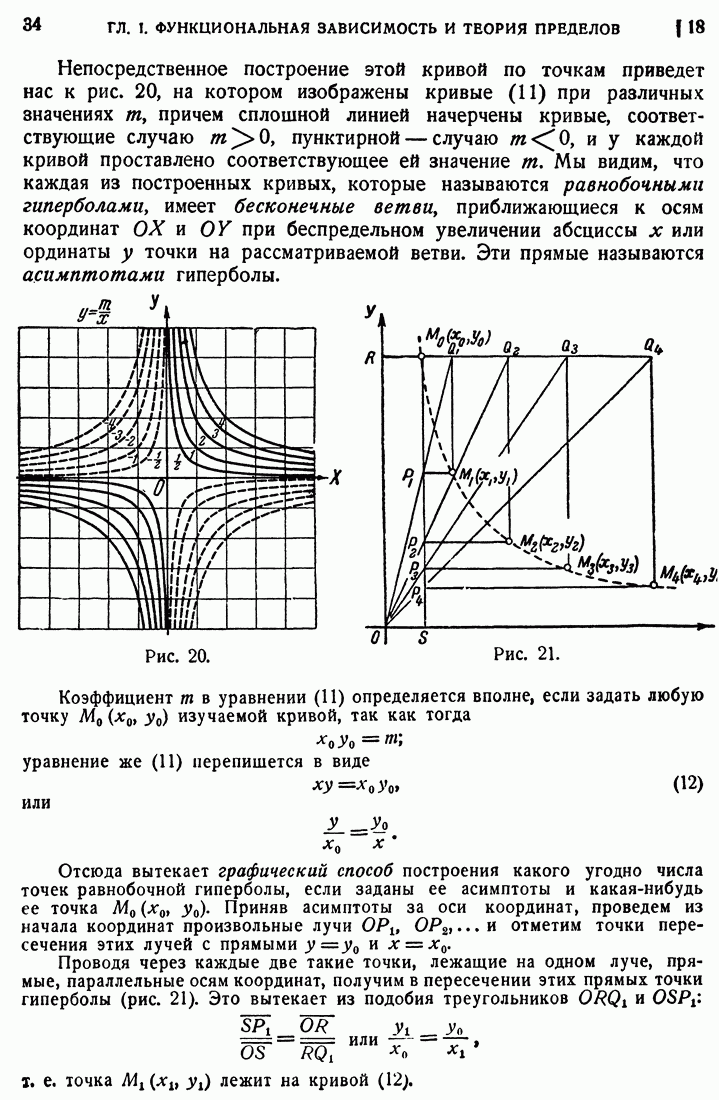
- 18. Закон обратной пропорциональности.
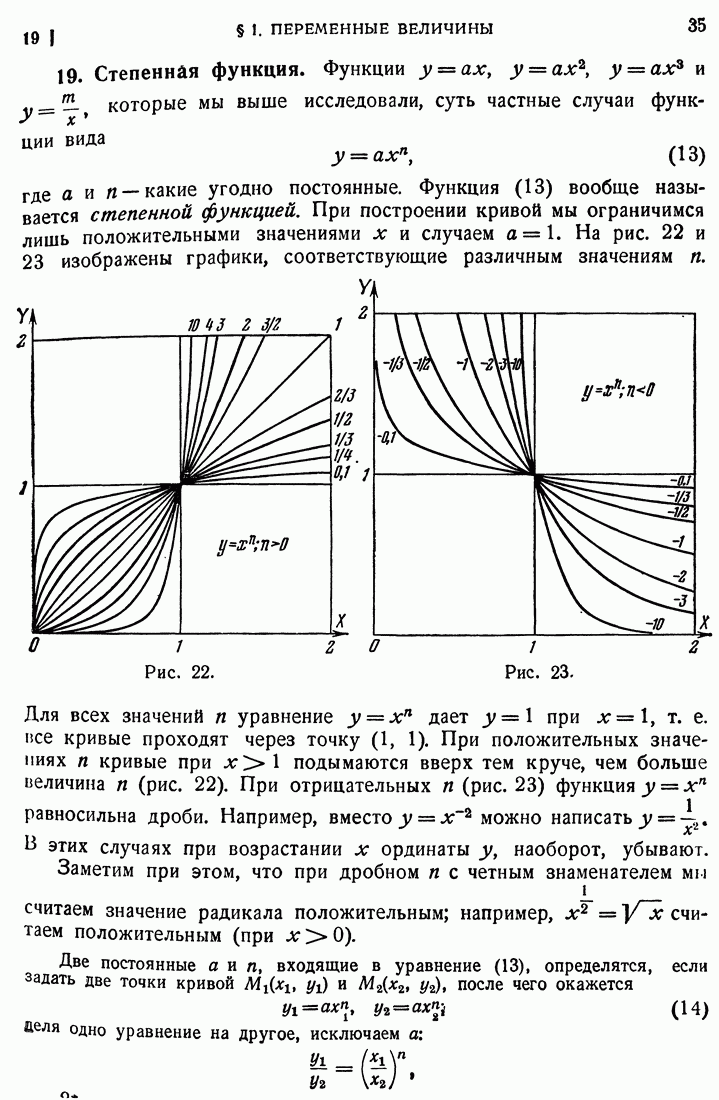
- 19. Степенная функция.
- 20. Обратные функции.
- 21. Многозначность функции.
- 22. Показательная и логарифмическая функции.
- 23. Тригонометрические функции.
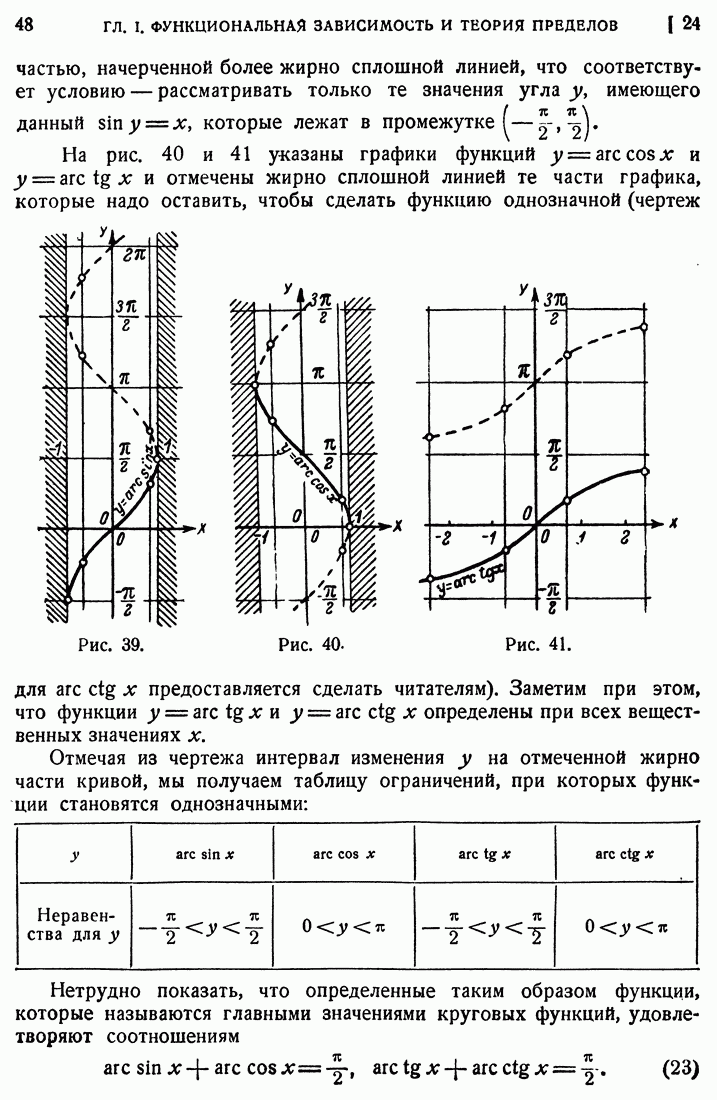
- 24. Обратные тригонометрические, или круговые, функции.
- § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 25. Упорядоченное переменное.
- 26. Величины бесконечно малые.
- 27. Предел переменной величины.
- 28. Основные теоремы.
- 29. Величины бесконечно большие.
- 30. Монотонные переменные.
- 31. Признак Коши существования предела.
- 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью.
- 33. Примеры.
- 34. Непрерывность функции.
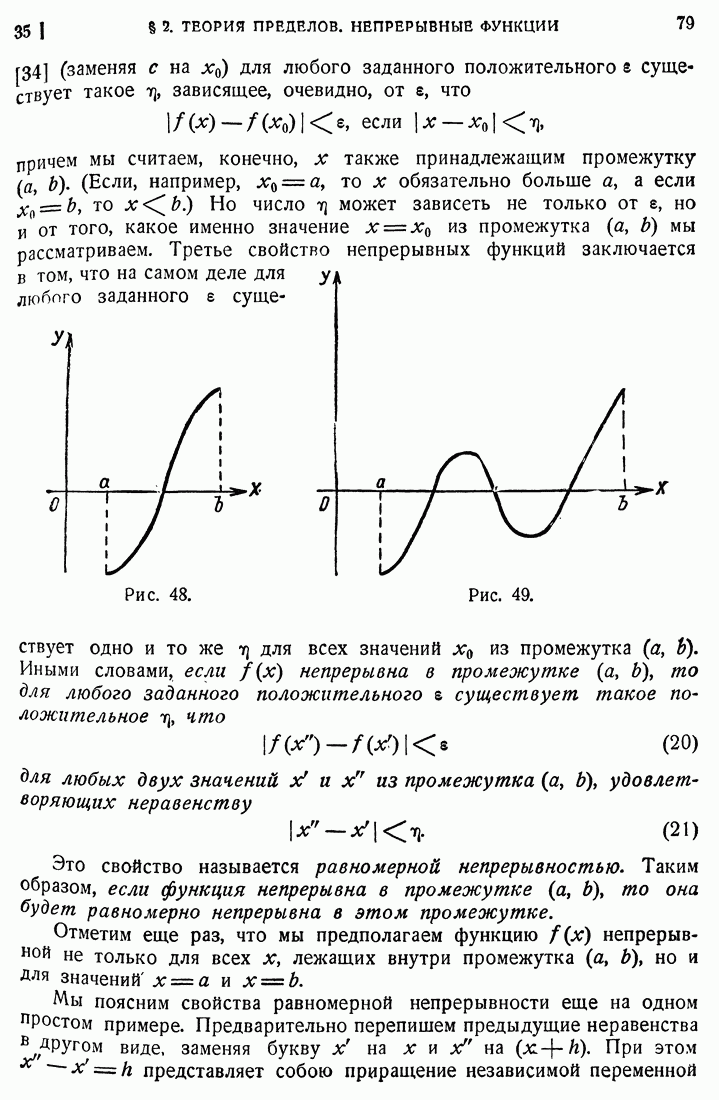
- 35. Свойства непрерывных функций.
- 36. Сравнение бесконечно малых и бесконечно больших величин.
- 37. Примеры.
- 38. Число е.
- 39. Недоказанные предложения.
- 40. Вещественные числа.
- 41. Действия над вещественными числами.
- 42. Точные границы числовых множеств. Признаки существования предела.
- 43. Свойства непрерывных функций.
- 44. Непрерывность элементарных функций.
- ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ
- 45. Понятие о производной.
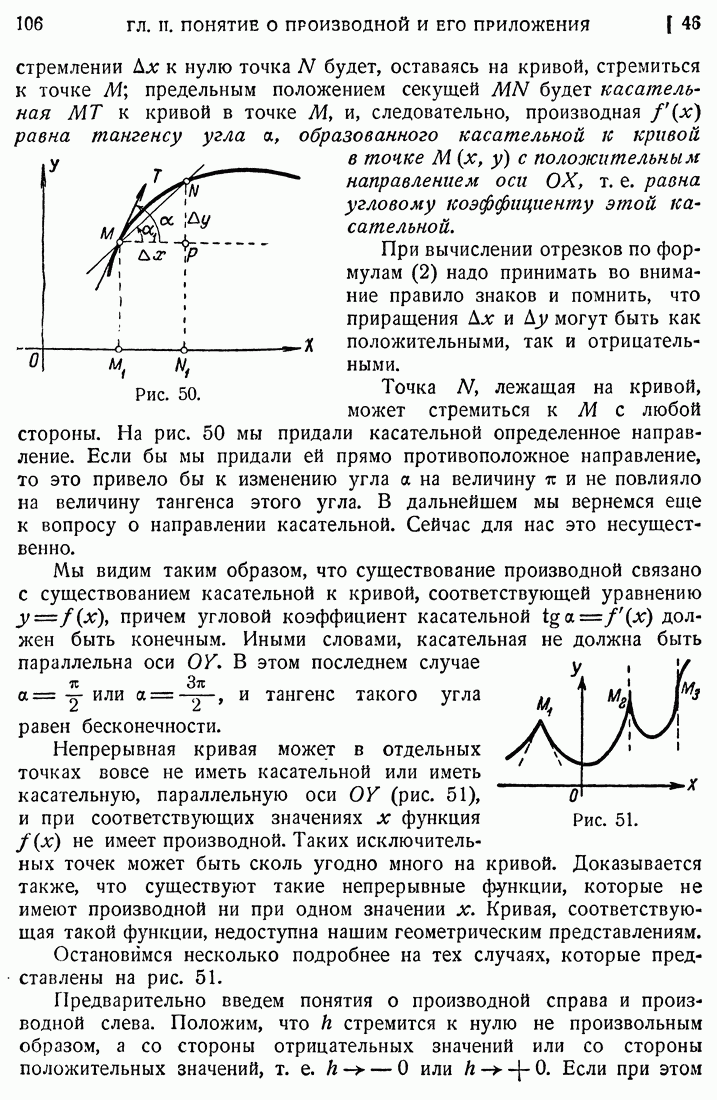
- 46. Геометрическое значение производной.
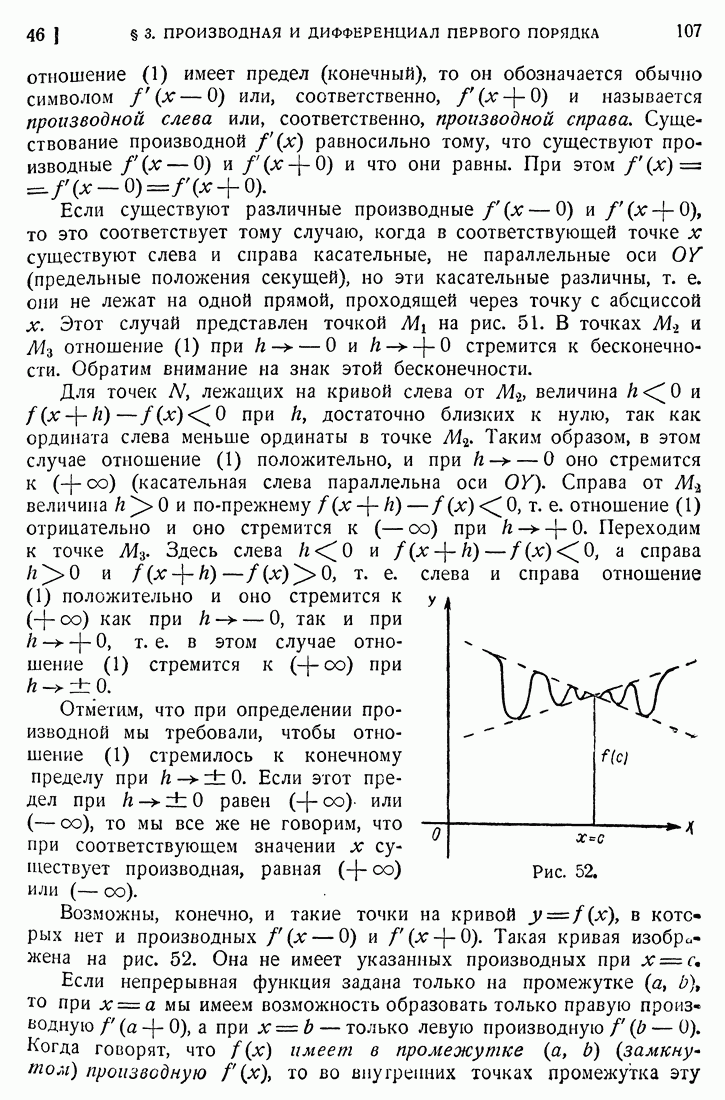
- 47. Производные простейших функций.
- 48. Производные сложных и обратных функций.
- 49. Таблица производных и примеры.
- 50. Понятие о дифференциале.
- 51. Некоторые дифференциальные уравнения.
- 52. Оценка погрешностей.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 53. Производные высших порядков.
- 54. Механическое значение второй производной.
- 55. Дифференциалы высших порядков.
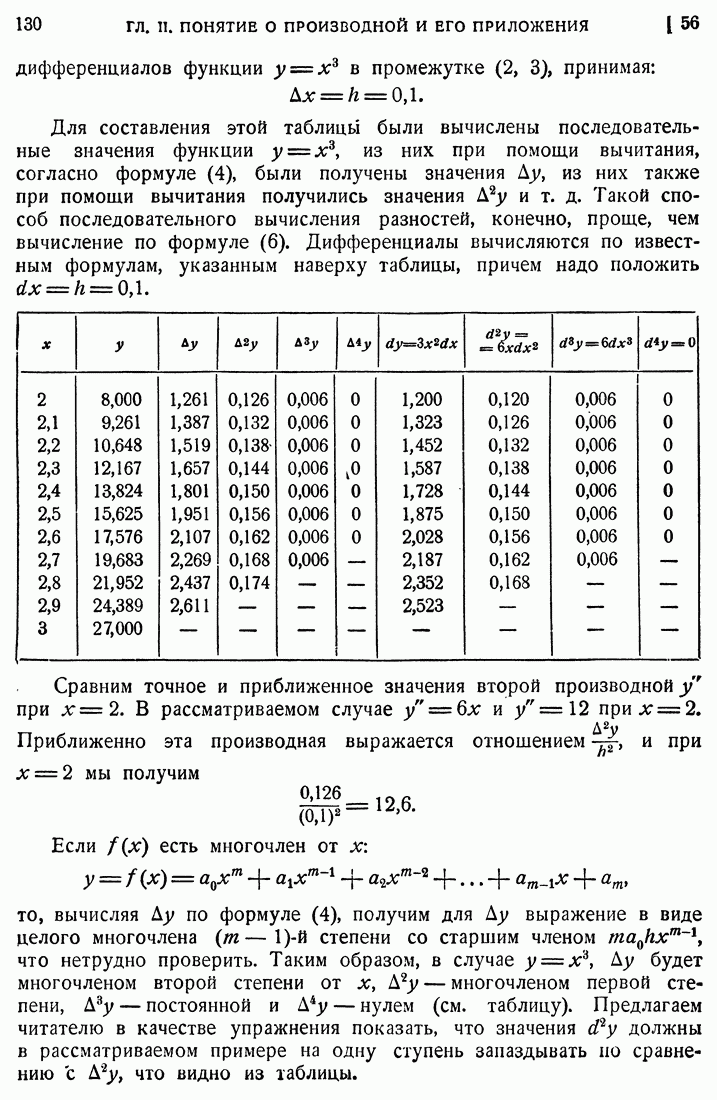
- 56. Разности функций.
- § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ
- 57. Признаки возрастания и убывания функций.
- 58. Максимумы и минимумы функций.
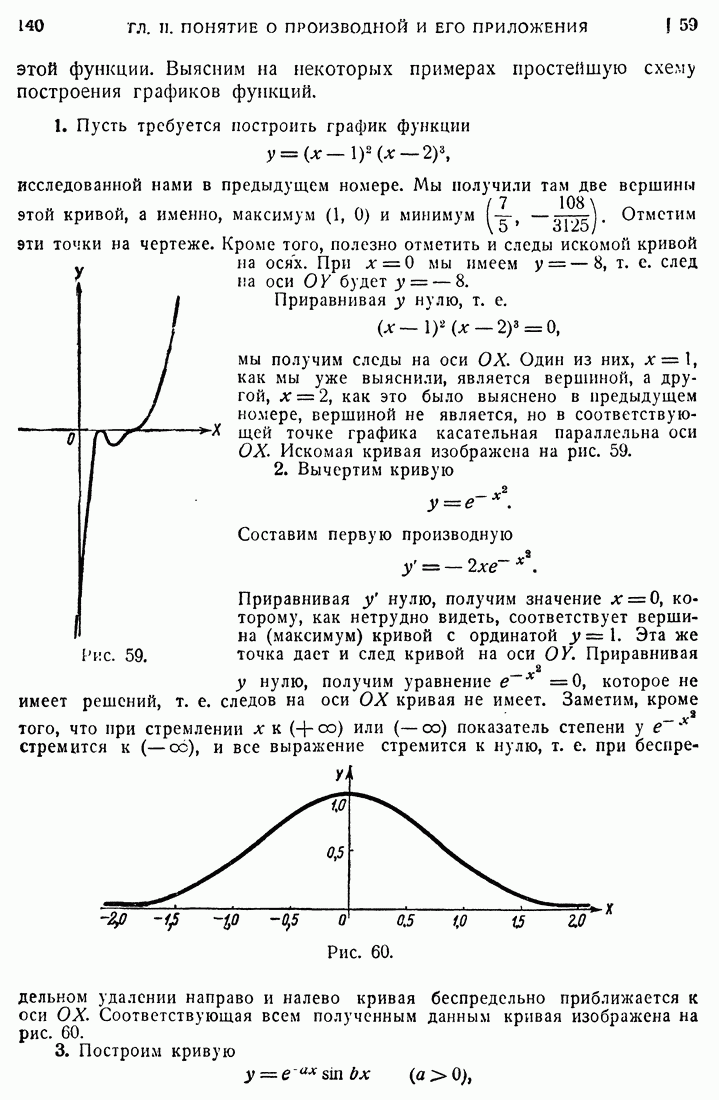
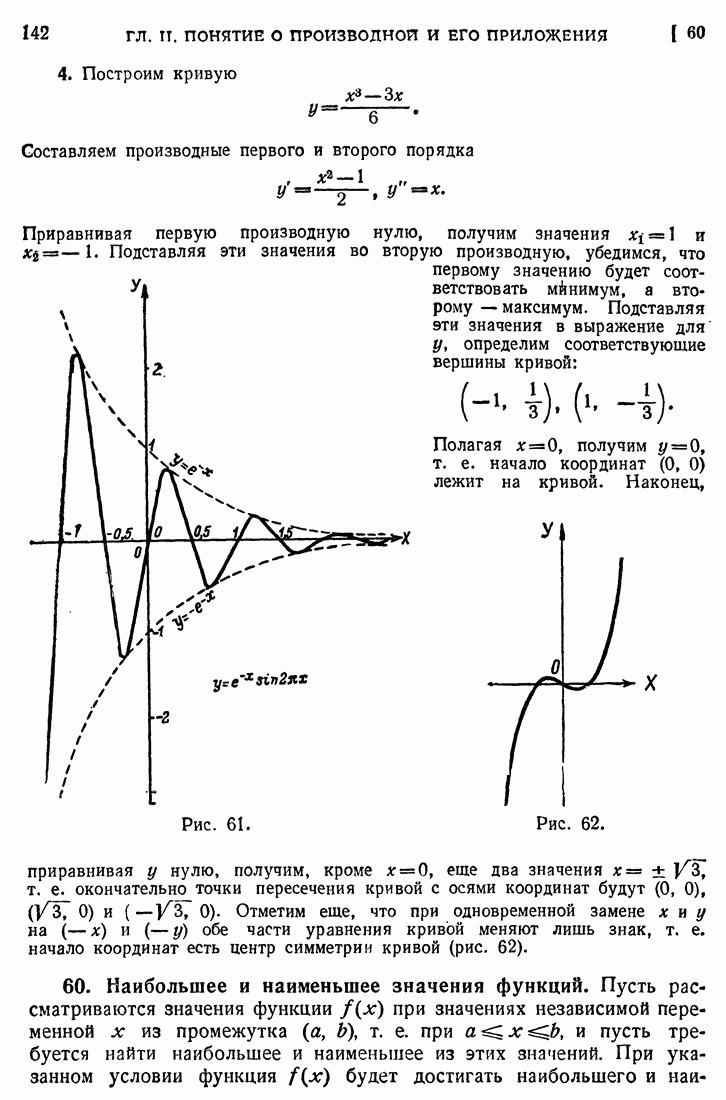
- 59. Построение графиков.
- 60. Наибольшее и наименьшее значения функций.
- 61. Теорема Ферма.
- 62. Теорема Ролля.
- 63. Формула Лагранжа.
- 64. Формула Коши.
- 65. Раскрытие неопределенностей.
- 66. Различные виды неопределенностей.
- § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
- 68. Частные производные и полный дифференциал функции двух независимых переменных.
- 69. Производные сложных и неявных функций.
- § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ
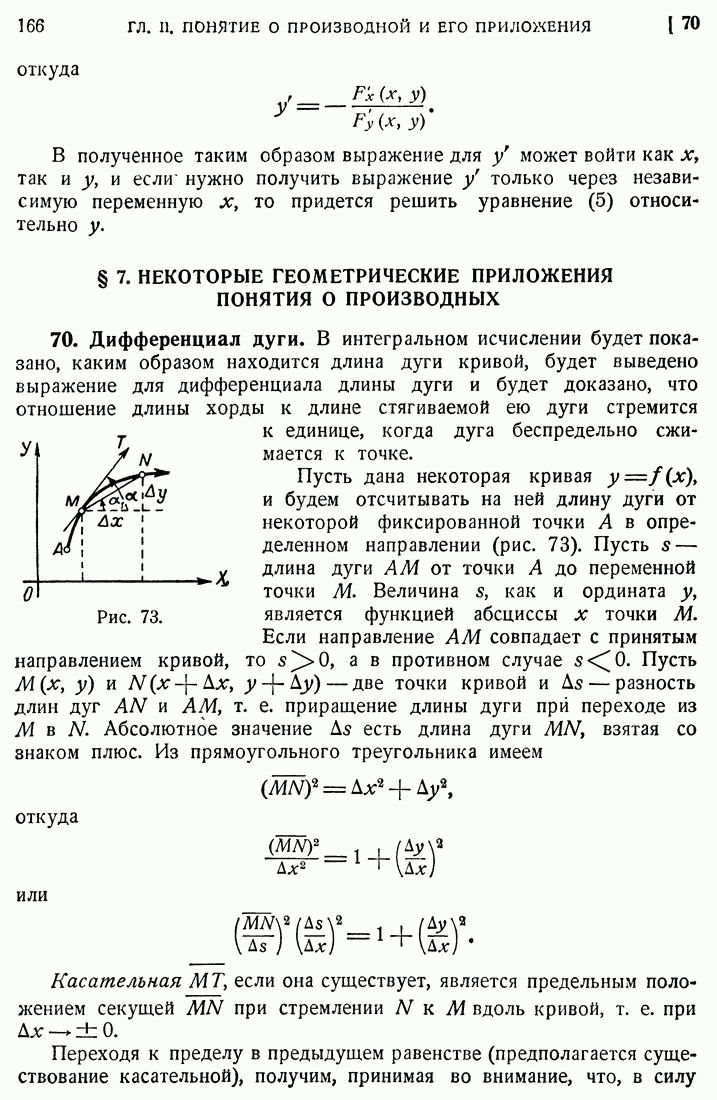
- 70. Дифференциал дуги.
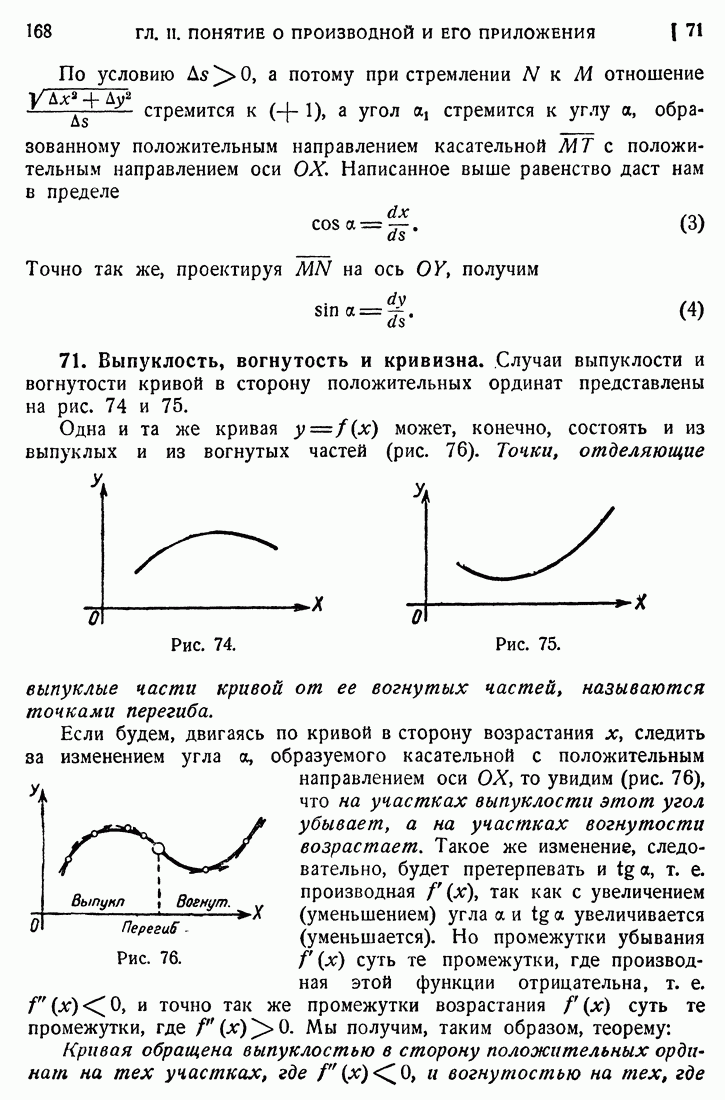
- 71. Выпуклость, вогнутость и кривизна.
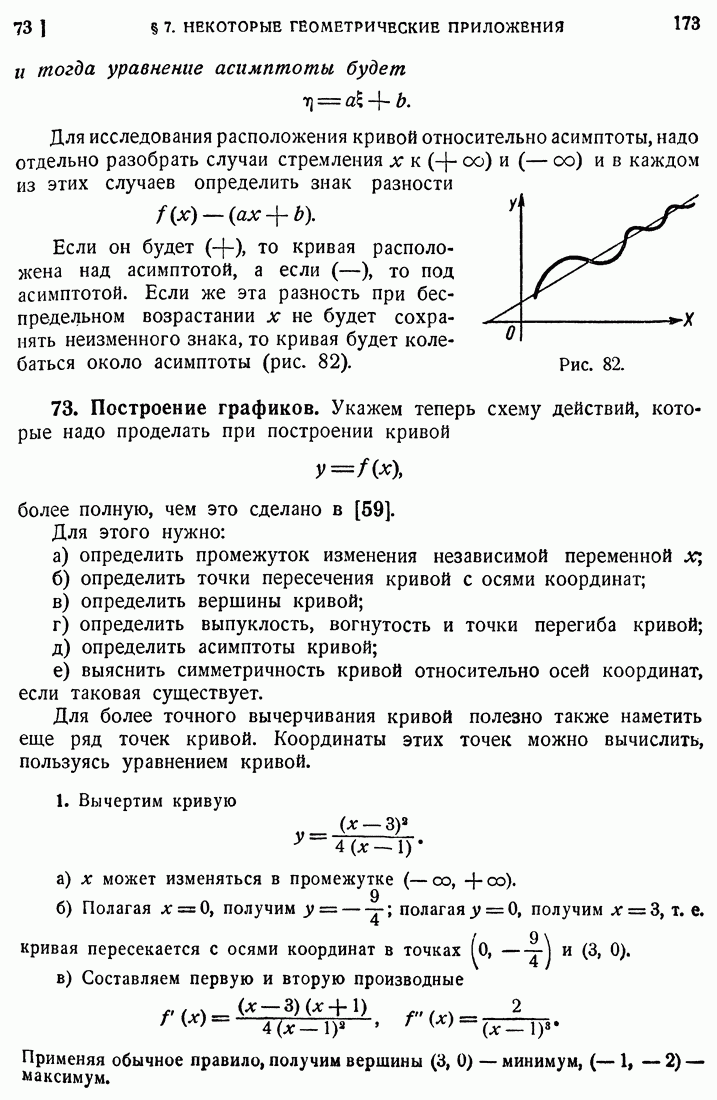
- 72. Асимптоты.
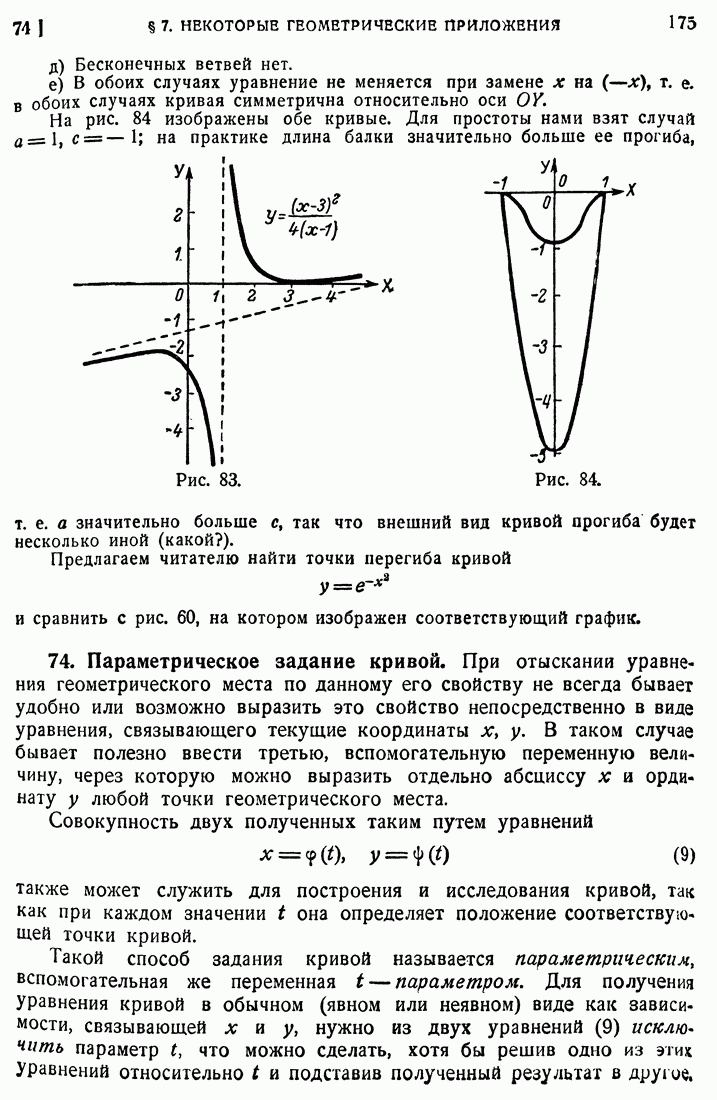
- 73. Построение графиков.
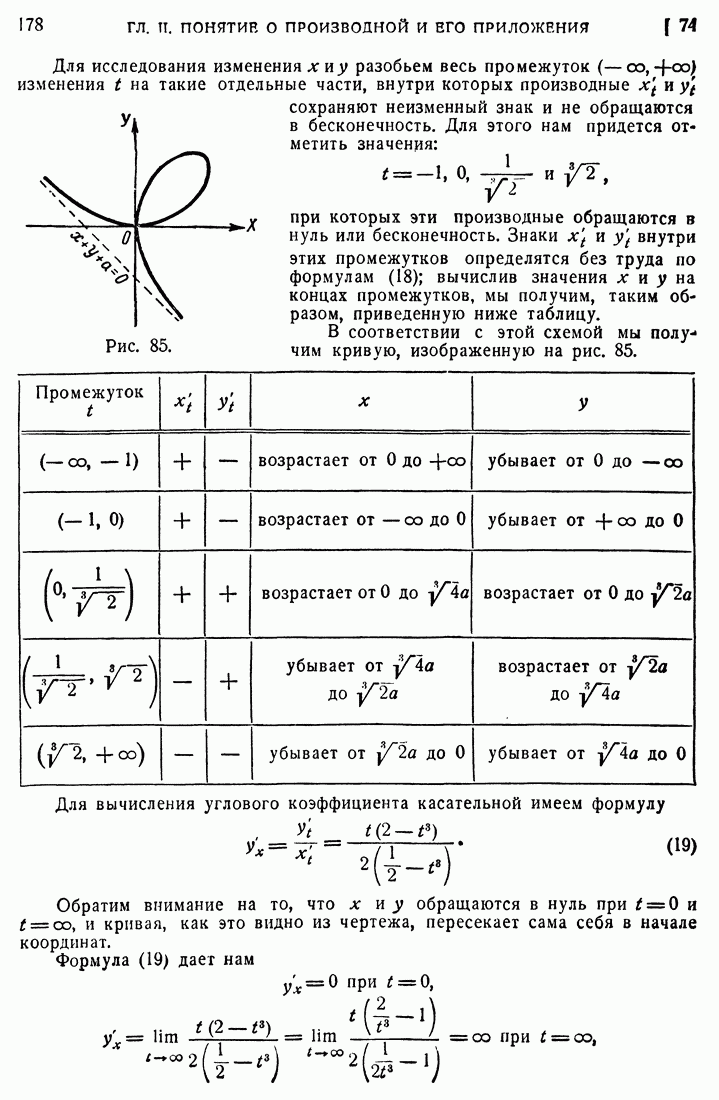
- 74. Параметрическое задание кривой.
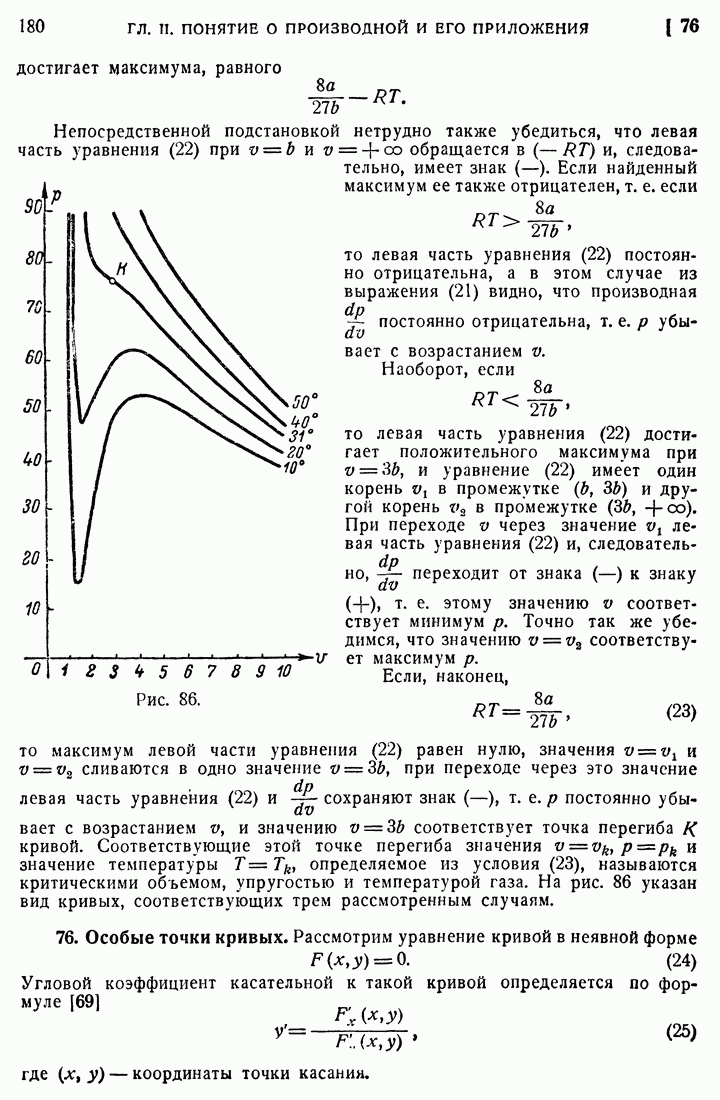
- 75. Уравнение Ван-дер-Ваальса.
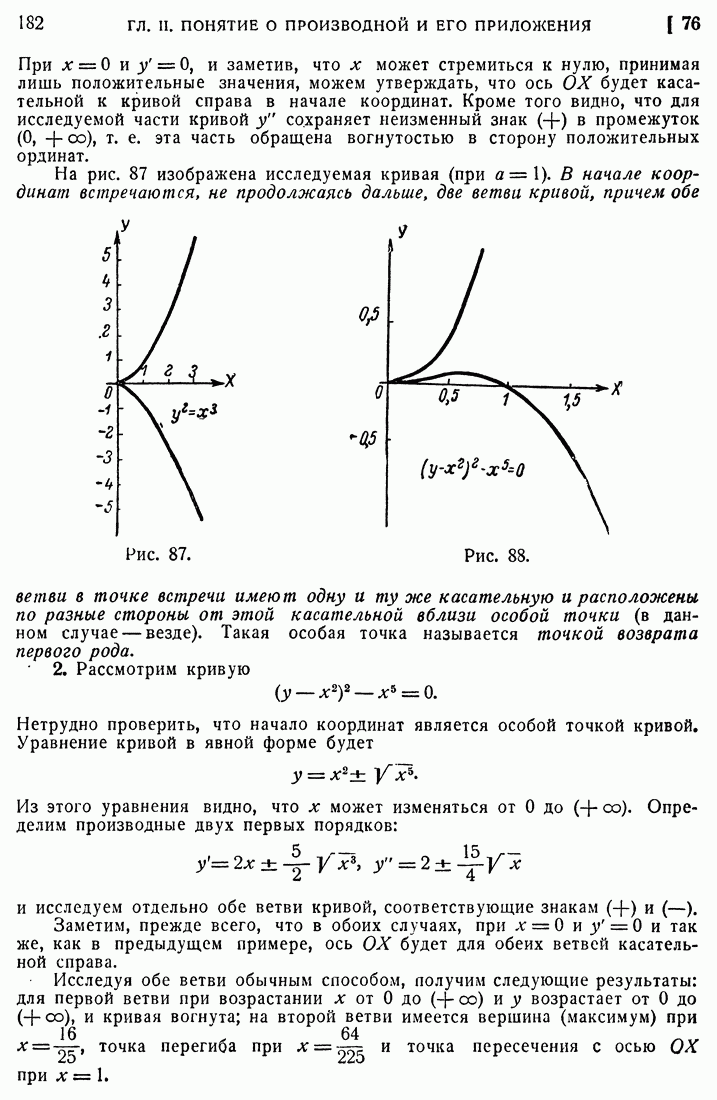
- 76. Особые точки кривых.
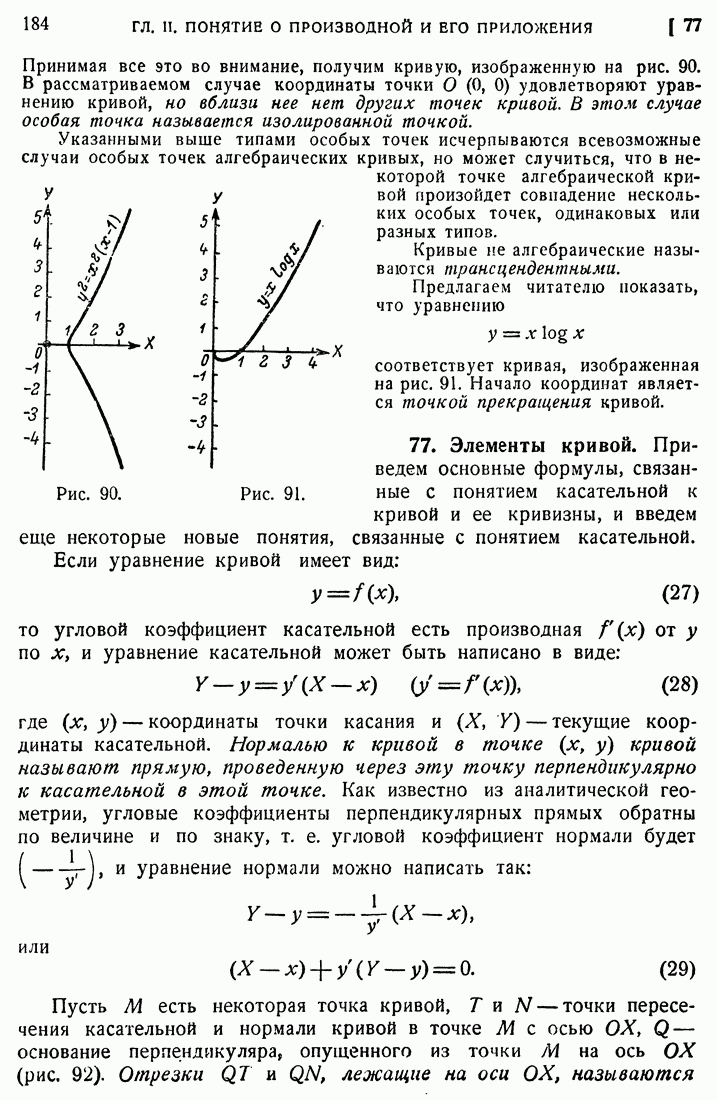
- 77. Элементы кривой.
- 78. Цепная линия.
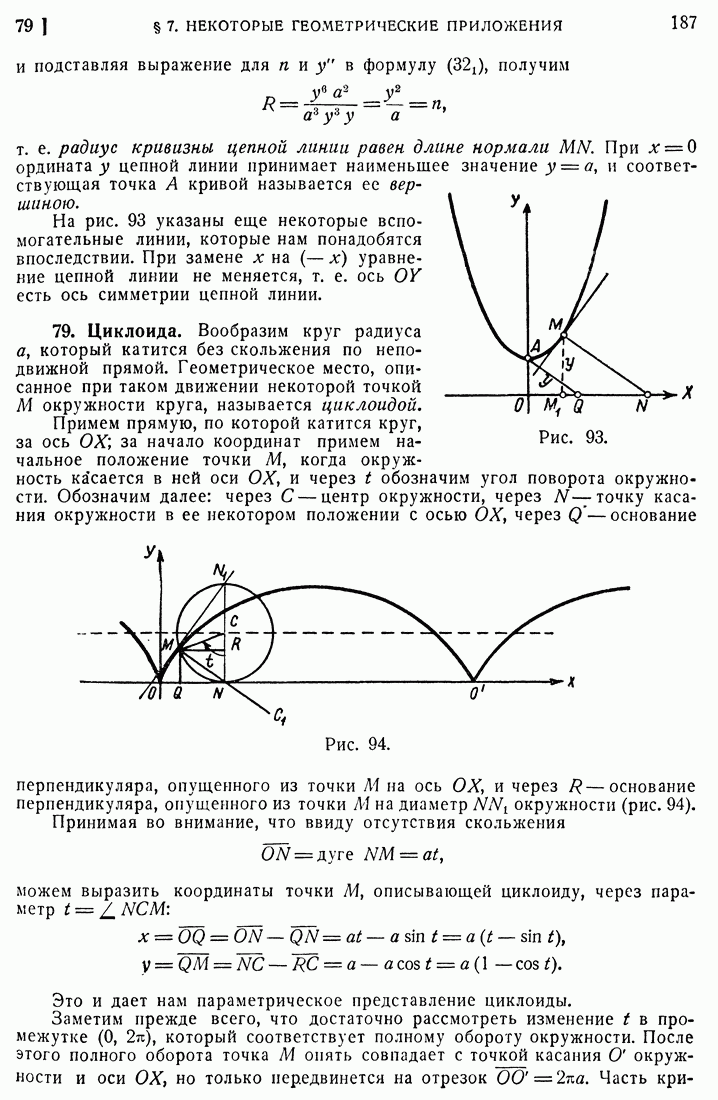
- 79. Циклоида.
- 80. Эпициклоиды и гипоциклоиды.
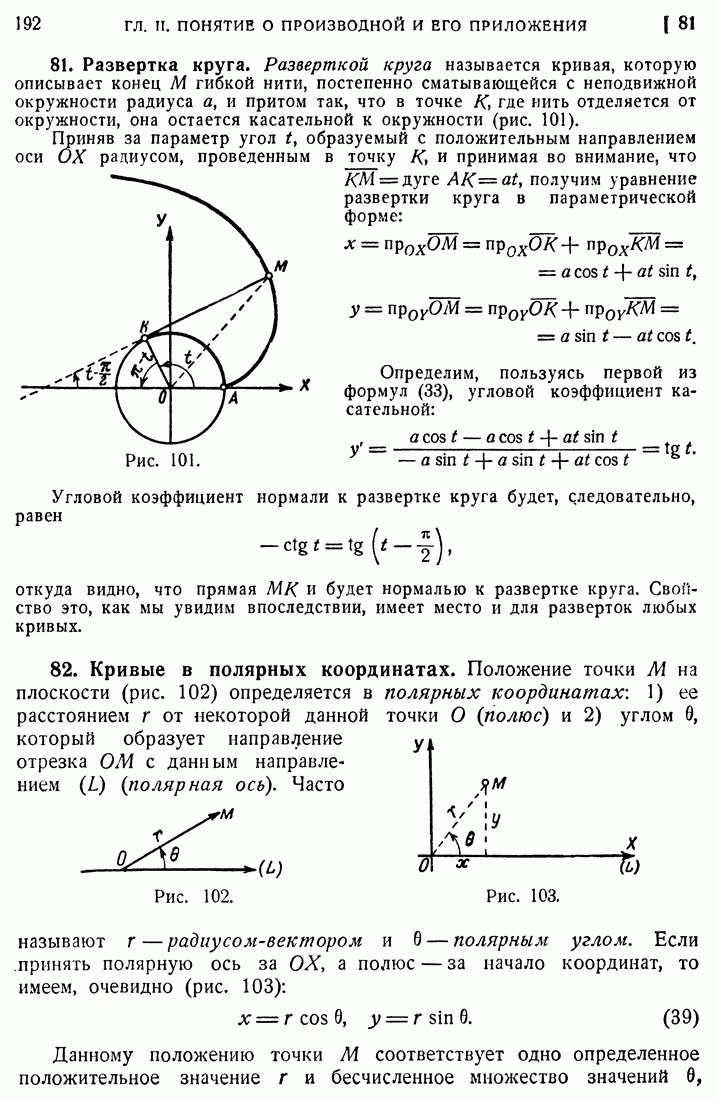
- 81. Развертка круга.
- 82. Кривые в полярных координатах.
- 83. Спирали.
- 85. Овалы Кассини и лемниската.
- ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ
- 86. Понятие о неопределенном интеграле.
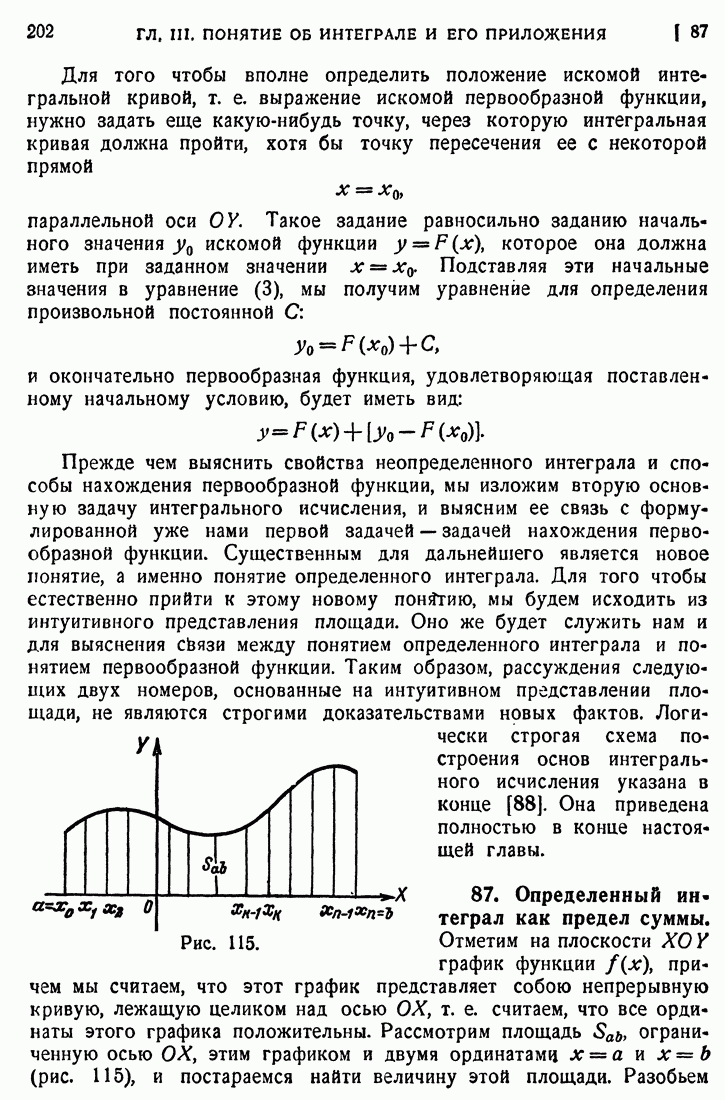
- 87. Определенный интеграл как предел суммы.
- 88. Связь определенного и неопределенного интегралов.
- 89. Свойства неопределенного интеграла.
- 90. Таблица простейших интегралов.
- 91. Правило интегрирования по частям.
- 92. Правило замены переменных. Примеры.
- 93. Примеры дифференциальных уравнений первого порядка.
- § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 94. Основные свойства определенного интеграла.
- 95. Теорема о среднем.
- 96. Существование первообразной функции.
- 97. Разрыв подынтегральной функции.
- 98. Бесконечные пределы.
- 99. Замена переменной под знаком определенного интеграла.
- 100. Интегрирование по частям.
- § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 101. Вычисление площадей.
- 102. Площадь сектора.
- 103. Длина дуги.
- 104. Вычисление объемов тел по их поперечным сечениям.
- 105. Объем тела вращения.
- 106. Поверхность тела вращения.
- 107. Определение центров тяжести. Теоремы Гульдина.
- 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций.
- 109. Формула касательных и формула Понселе.
- 110. Формула Симпсона.
- 111. Вычисление определенного интеграла с переменным верхним пределом.
- 112. Графические способы.
- 113. Площади быстро колеблющихся кривых.
- § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
- 115. Разбиение промежутка на части и образование различных сумм.
- 116. Интегрируемые функции.
- 117. Свойства интегрируемых функций.
- ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 118. Понятие о бесконечном ряде.
- 119. Основные свойства бесконечных рядов.
- 120. Ряды с положительными членами. Признаки сходимости.
- 121. Признаки Коши и Даламбера.
- 122. Интегральный признак сходимости Коши.
- 123. Знакопеременные ряды.
- 124. Абсолютно сходящиеся ряды.
- 125. Общий признак сходимости.
- § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ
- 126. Формула Тейлора.
- 127. Различные виды формулы Тейлора.
- 128. Ряды Тейлора и Маклорена.
- 129. Разложение exp(x).
- 130. Разложение sin x и cos x.
- 131. Бином Ньютона.
- 132. Разложение log(1+x).
- 133. Разложение arctg x.
- 134. Приближенные формулы.
- 135. Максимумы, минимумы и точки перегиба.
- 136. Раскрытие неопределенностей.
- § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ
- 137. Свойства абсолютно сходящихся рядов.
- 138. Умножение абсолютно сходящихся рядов.
- 139. Признак Куммера.
- 140. Признак Гаусса.
- 141. Гипергеометрический ряд.
- 142. Двойные ряды.
- 143. Ряды с переменными членами. Равномерно сходящиеся ряды.
- 144. Равномерно сходящиеся последовательности функций.
- 145. Свойства равномерно сходящихся последовательностей.
- 146. Свойства равномерно сходящихся рядов.
- 147. Признаки равномерной сходимости.
- 148. Степенные ряды. Радиус сходимости.
- 149. Вторая теорема Абеля.
- 150. Дифференцирование и интегрирование степенного ряда.
- ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ
- 152. О предельном переходе.
- 153. Частные производные и полный дифференциал первого порядка.
- 154. Однородные функции.
- 155. Частные производные высших порядков.
- 156. Дифференциалы высших порядков.
- 157. Неявные функции.
- 158. Пример.
- 159. Существование неявных функций.
- 160. Кривые в пространстве и поверхности.
- § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных.
- 162. Необходимые условия максимума и минимума функции.
- 163. Исследование максимума и минимума функции двух независимых переменных.
- 164. Примеры.
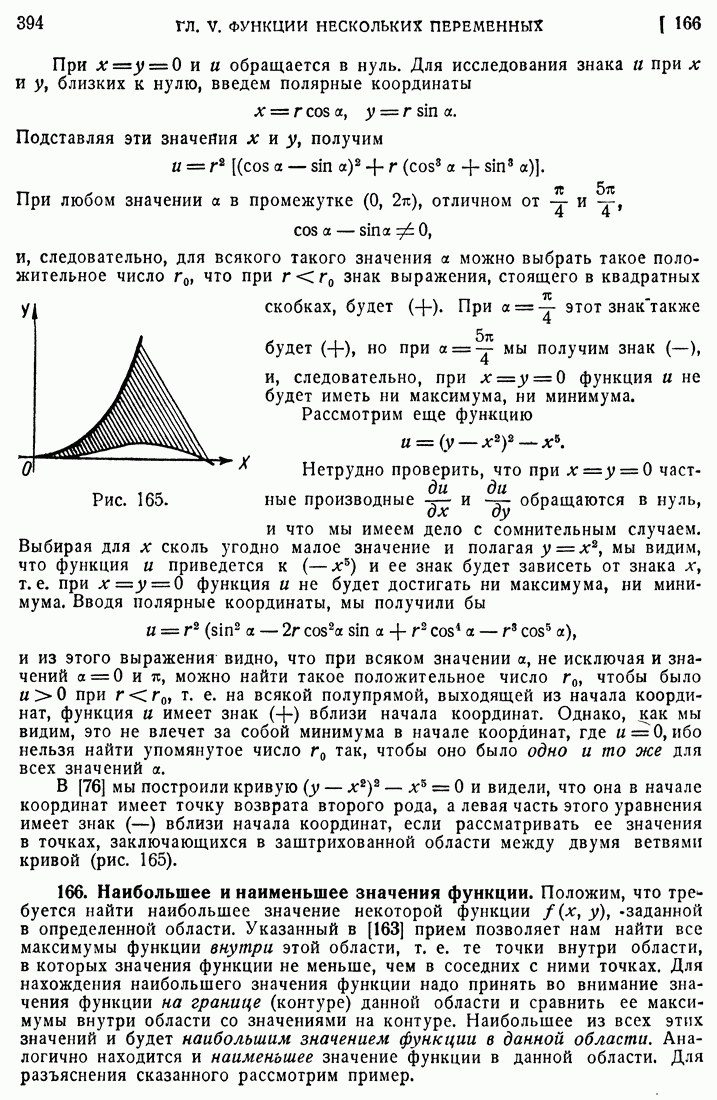
- 165. Дополнительные замечания о нахождении максимумов и минимумов функции.
- 166. Наибольшее и наименьшее значения функции.
- 167. Относительные максимумы и минимумы.
- 168. Дополнительные замечания.
- 169. Примеры.
- ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
- 170. Комплексные числа.
- 171. Сложение и вычитание комплексных чисел.
- 172. Умножение комплексных чисел.
- 173. Деление комплексных чисел.
- 174. Возвышение в степень.
- 175. Извлечение корня.
- 176. Показательная функция.
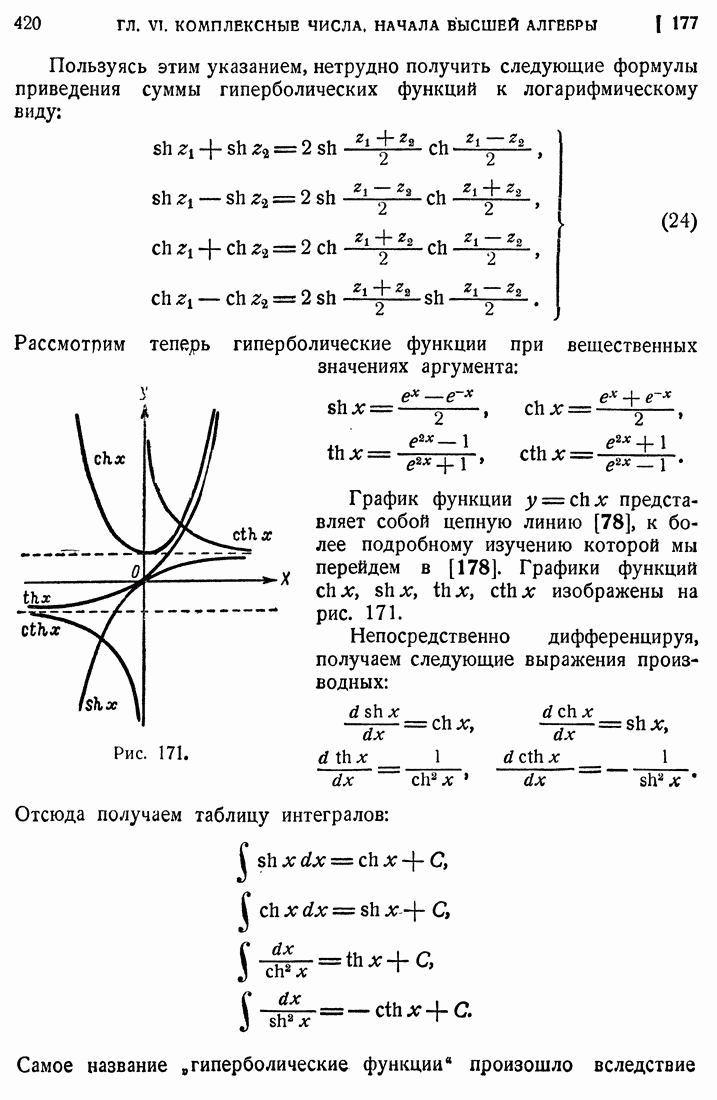
- 177. Тригонометрические и гиперболические функции.
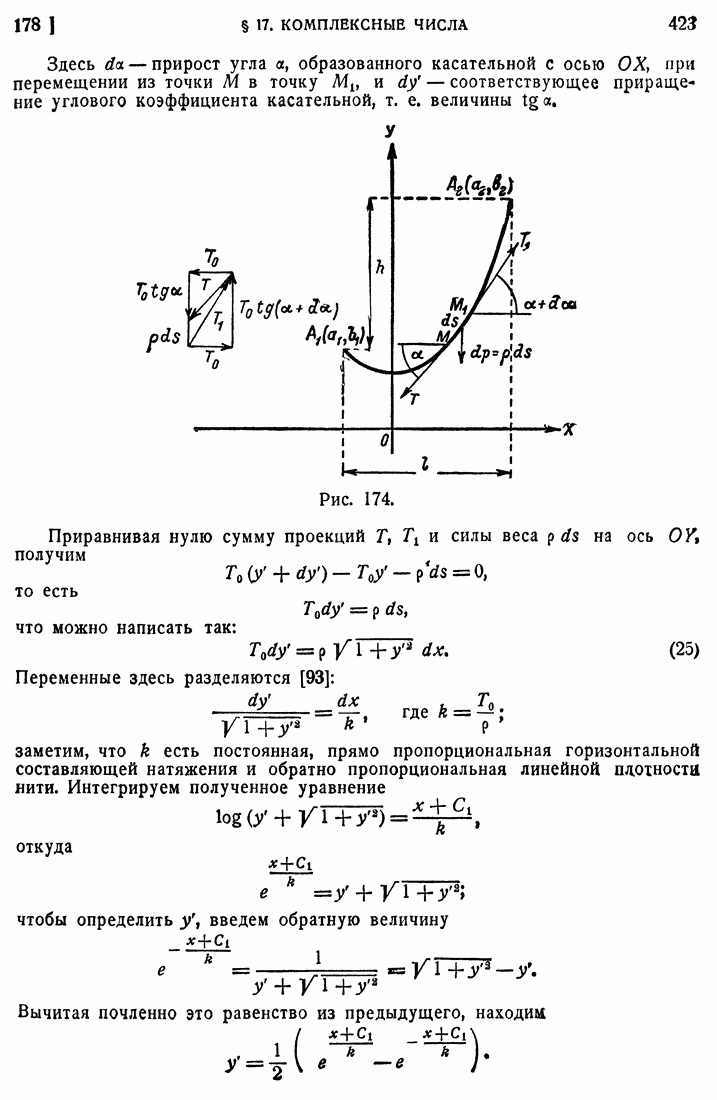
- 178. Цепная линия.
- 179. Логарифмирование.
- 180. Синусоидальные величины и векторные диаграммы.
- 181. Примеры.
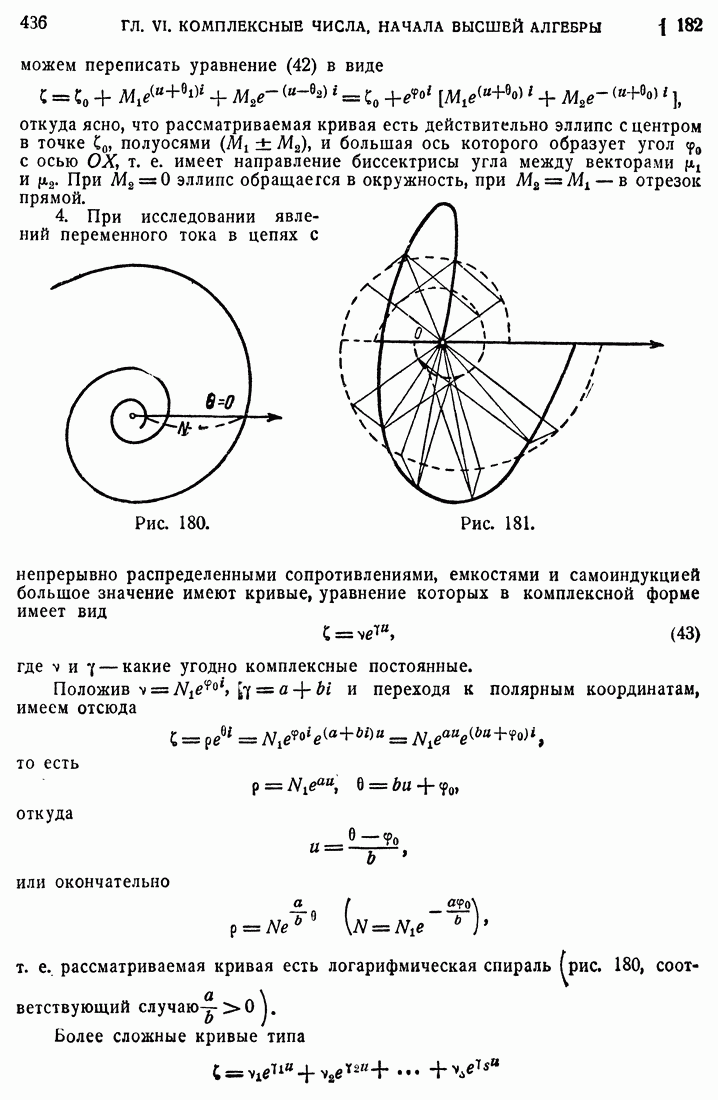
- 182. Кривые в комплексной форме.
- 183. Представление гармонического колебания в комплексной форме.
- § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ
- 185. Разложение многочлена на множители.
- 186. Кратные корни.
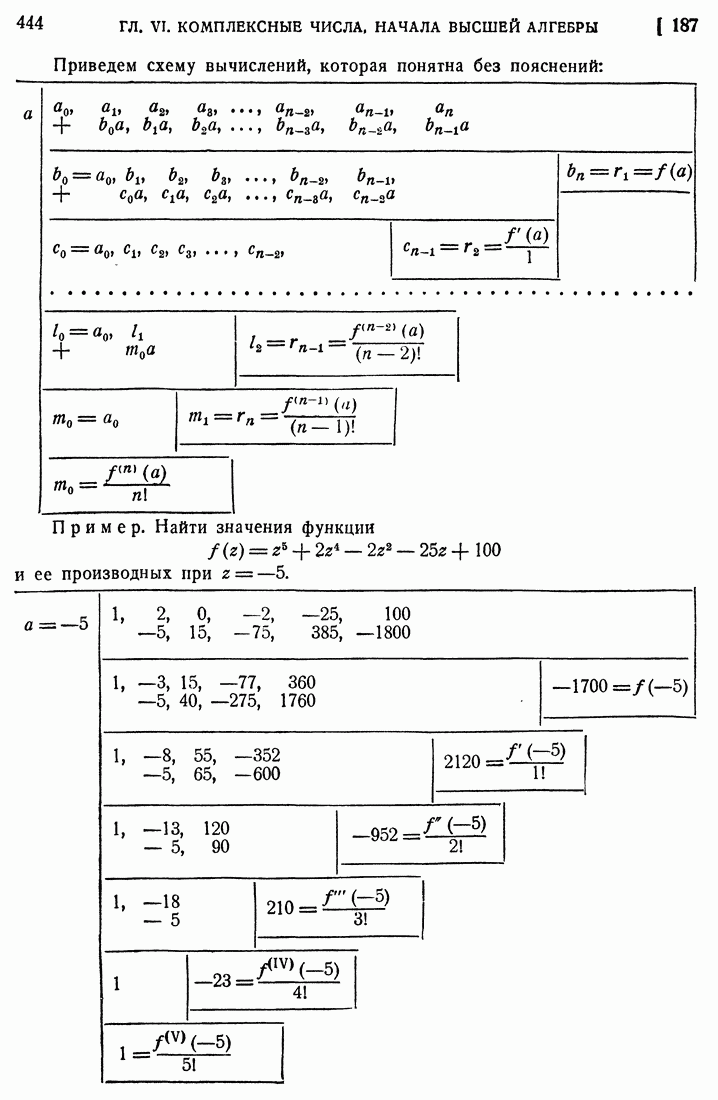
- 187. Правило Горнера.
- 188. Общий наибольший делитель.
- 189. Вещественные многочлены.
- 190. Зависимость между корнями уравнения и его коэффициентами.
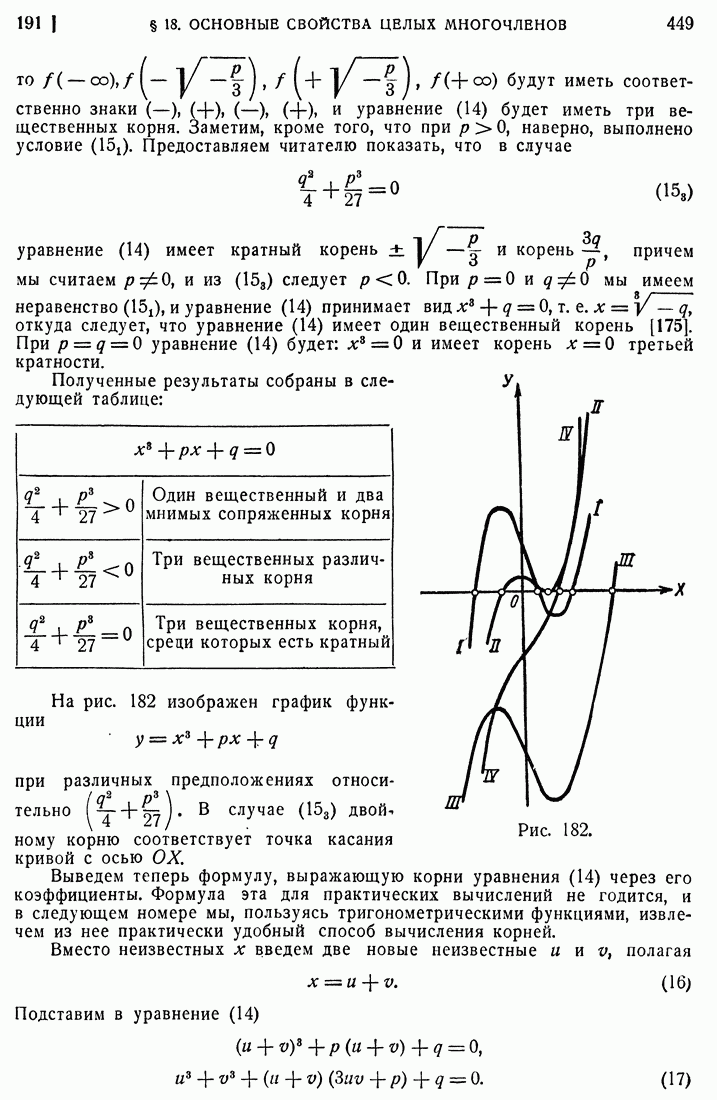
- 191. Уравнение третьей степени.
- 192. Решение кубического уравнения в тригонометрической форме.
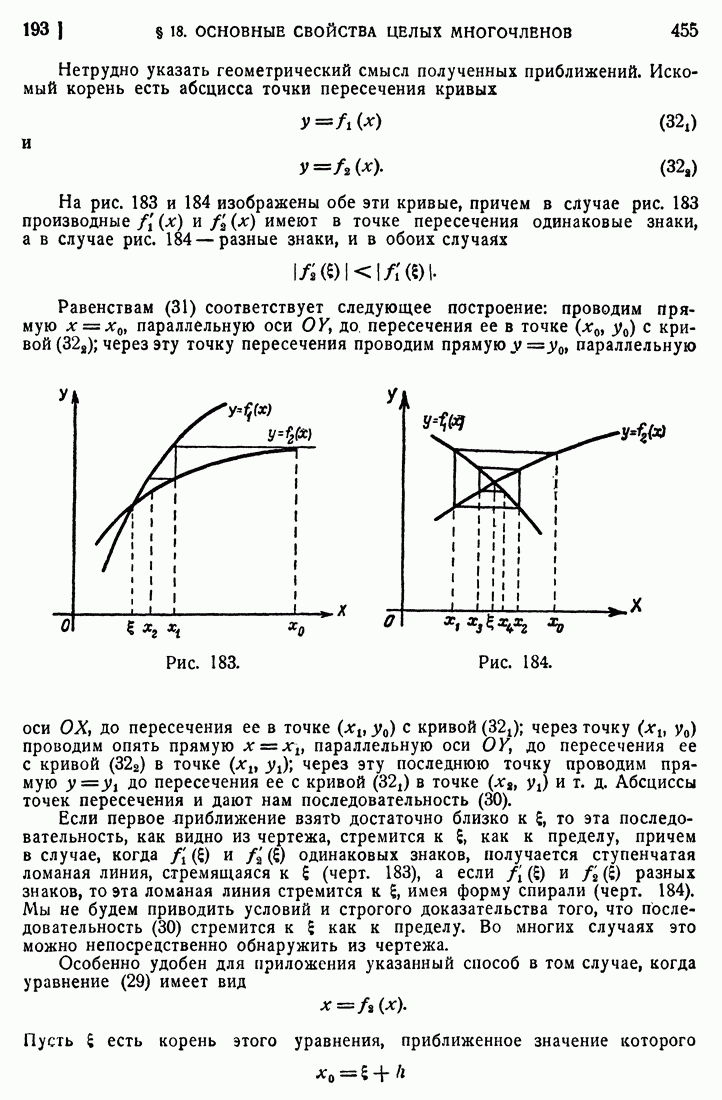
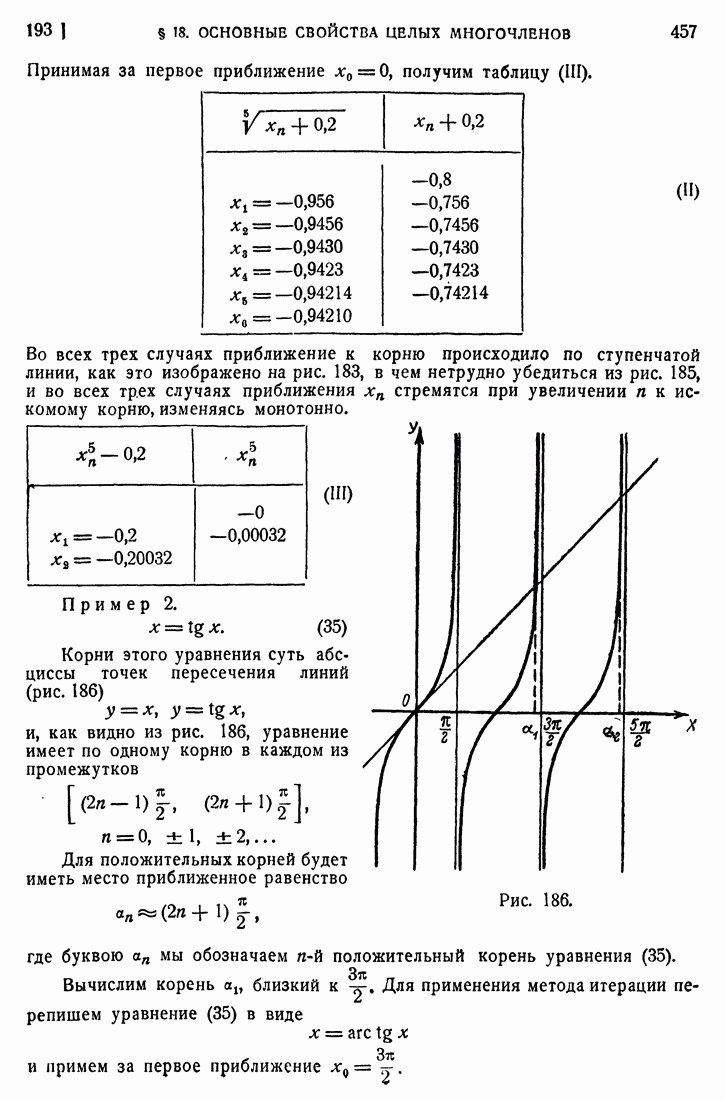
- 193. Способ итерации.
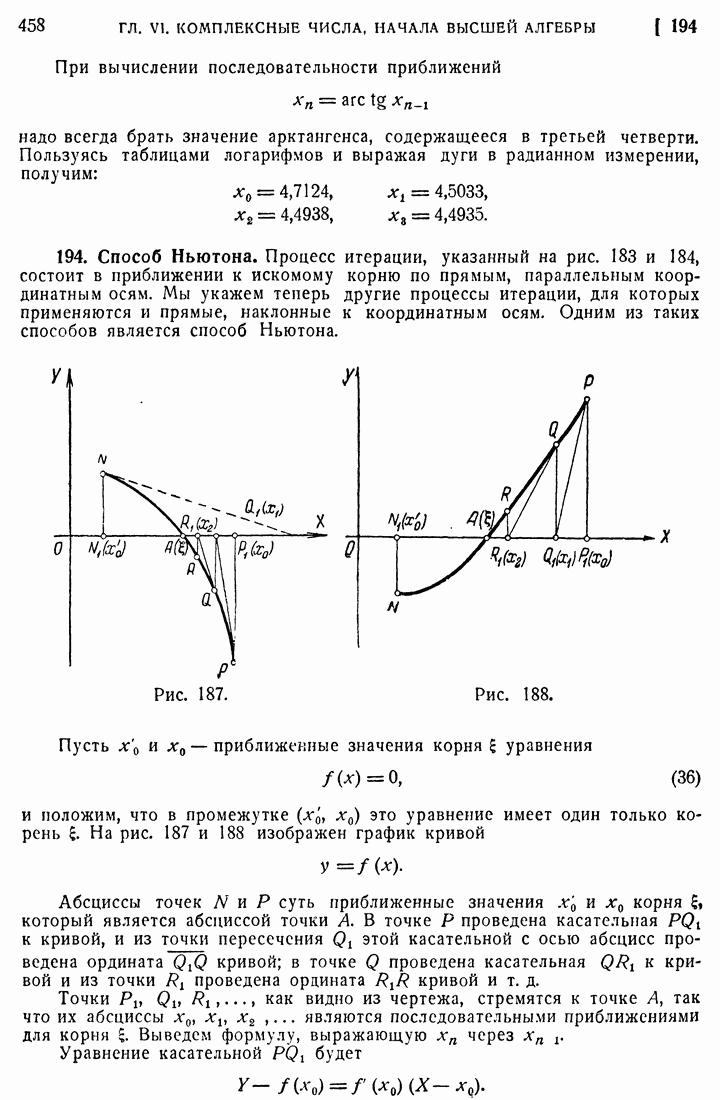
- 194. Способ Ньютона.
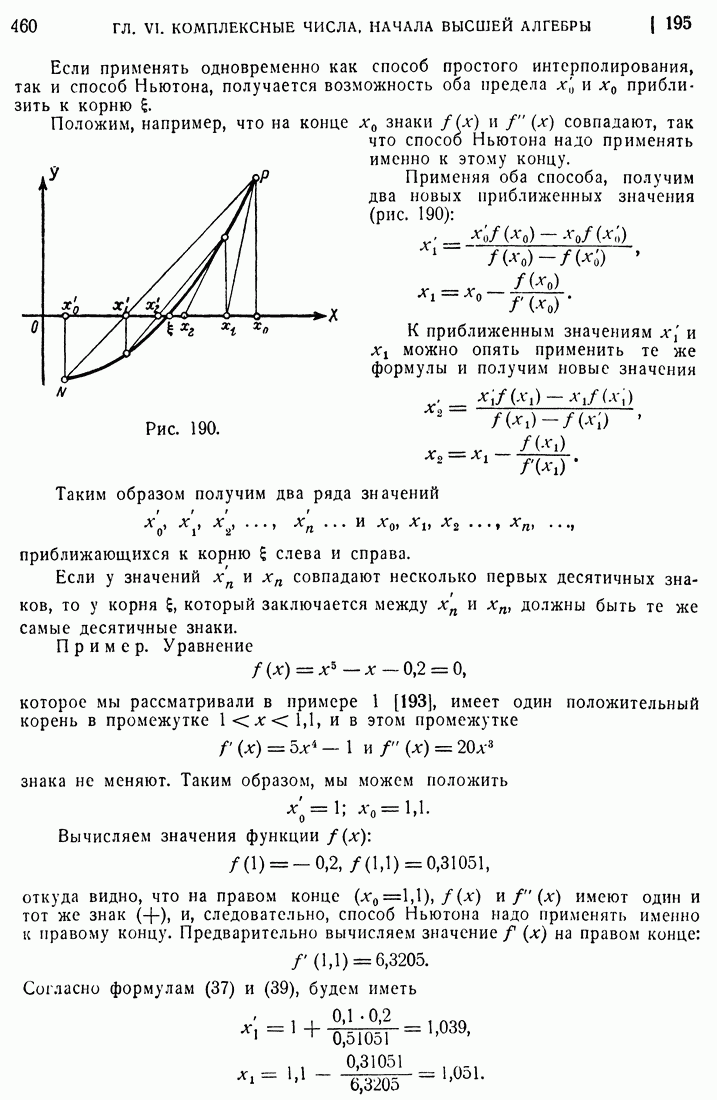
- 195. Способ простого интерполирования.
- § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ
- 196. Разложение рациональной дроби на простейшие.
- 197. Интегрирование рациональной дроби.
- 198. Интеграл от выражений, содержащих радикалы.
- 199. Интегралы вида…
- 200. Интегралы вида…
- 201. Интегралы вида…