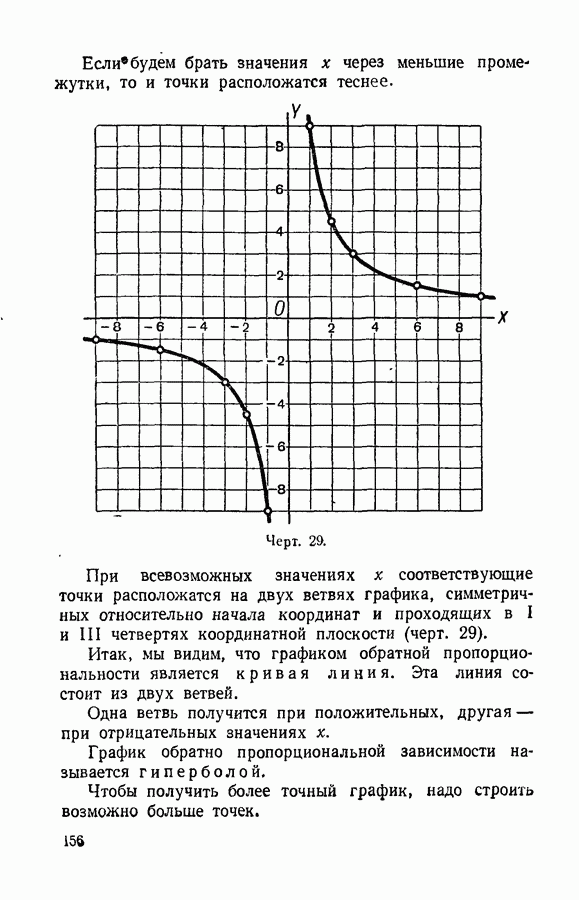
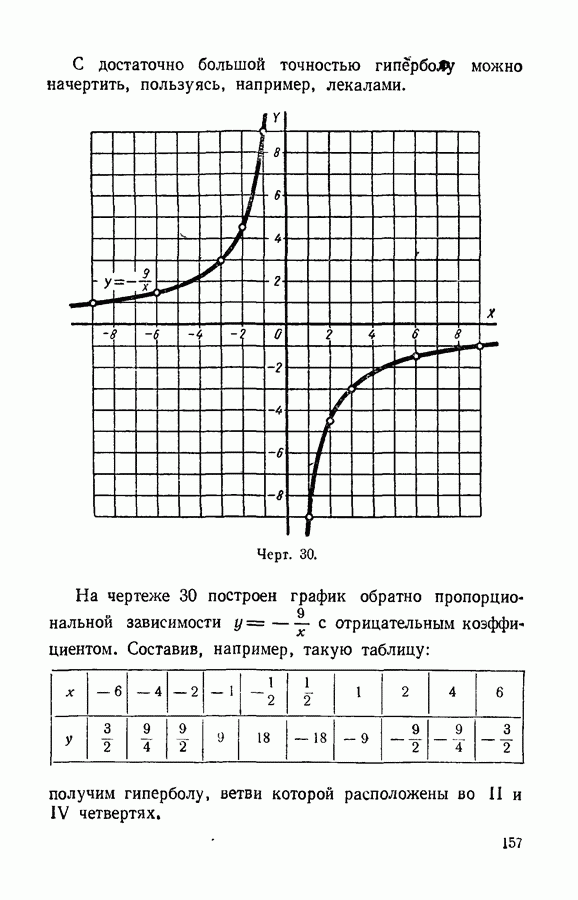
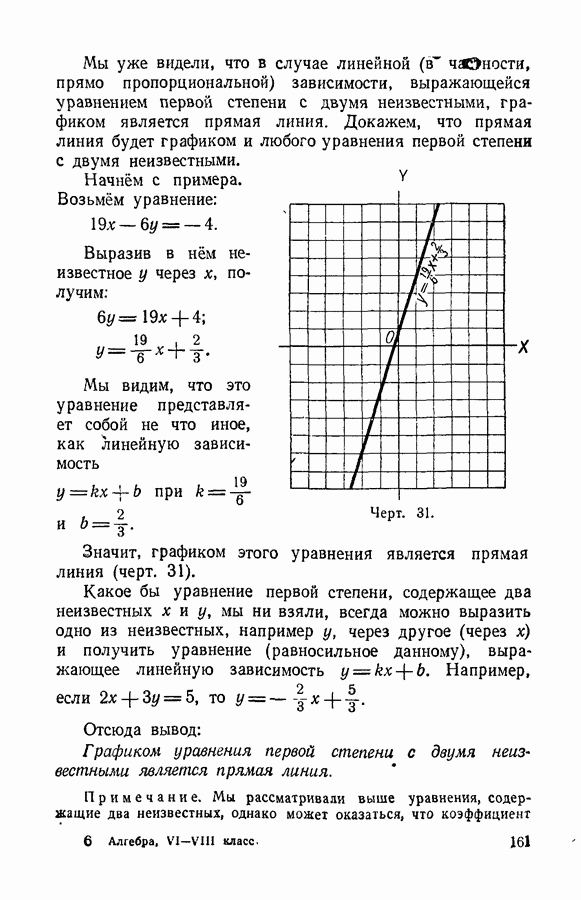
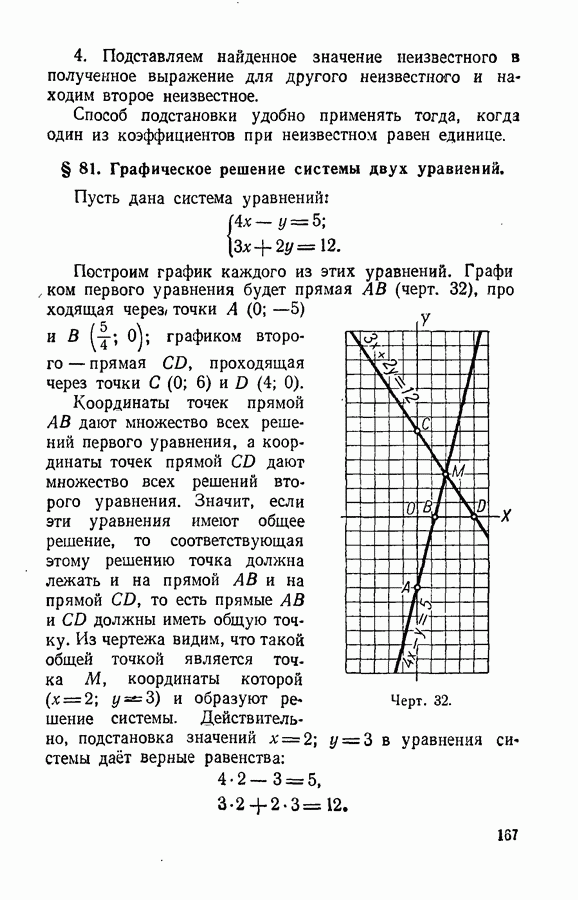
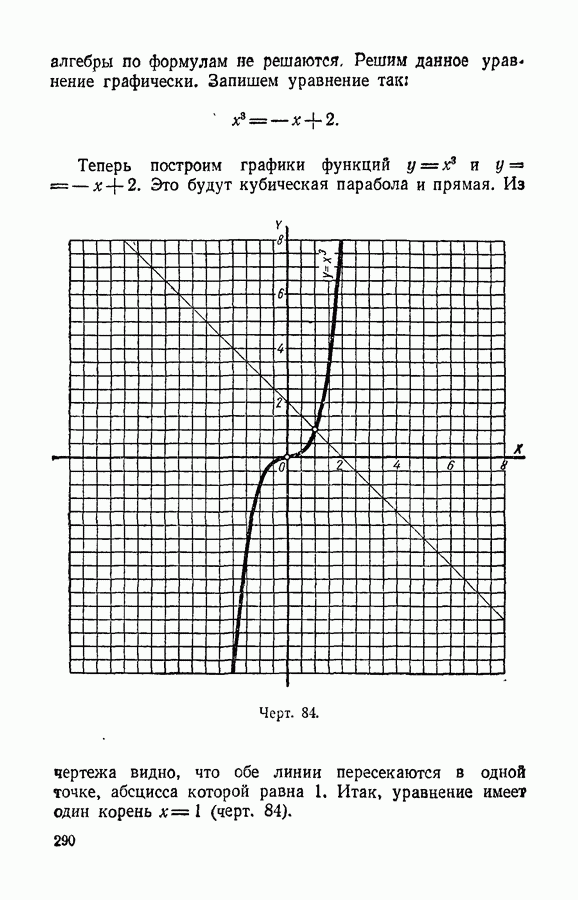
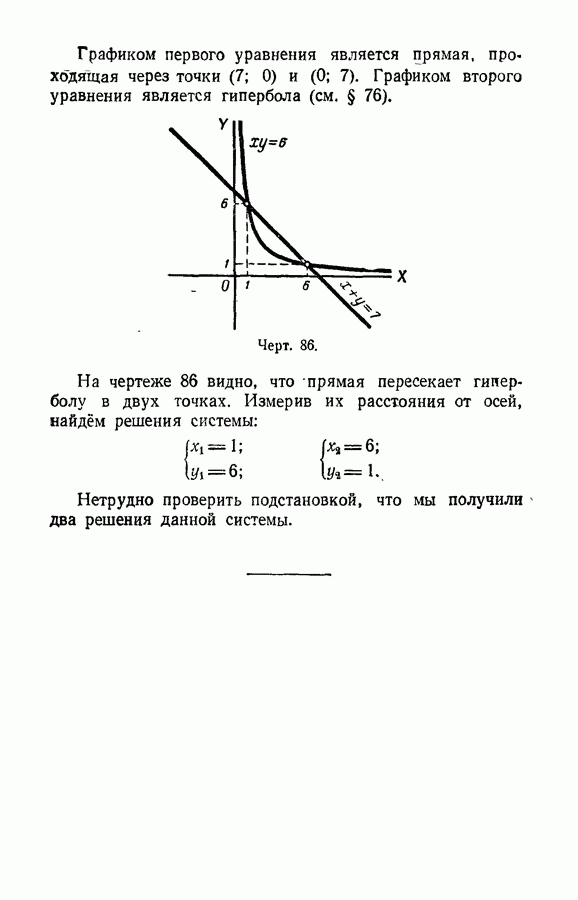
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 103. Уравнение вида ax^2+c=0
Задача. Длина прямоугольного участка земли в 5 раз больше его ширины, а площадь равна  Вычислить длину и ширину участка.
Вычислить длину и ширину участка.
Решение. Обозначим ширину участка через х метров. Тогда длина его будет равна  метрам. Площадь равна
метрам. Площадь равна 
По условию

Получили уравнение с одним неизвестным.
Решим его. Разделив обе части уравнения на 5, получим равносильное ему уравнение:

из которого найдём:

Уравнение имеет два корня:

Но по условию задачи для неизвестного допустимыми являются только положительные значения. Значит, решением задачи будет только 
Ответ. Ширина участка равна  а длина равна
а длина равна 
Пусть вообще имеем уравнение, которое после перенесения всех членов в левую часть и приведения подобных будет иметь вид:

Перенесём свободный член с в правую часть и разделим уравнение на а; тогда получим уравнение

равносильное данному.
Рассмотрим следующие возможные случаи.
Случай 1. Пусть а и с — числа одинакового знака (то есть либо оба положительны, либо оба отрицательны); тогда — есть положительное число, а  отрицательное число. Но мы знаем, что
отрицательное число. Но мы знаем, что  , а потому не может равняться отрицательному числу; в этом случае уравнение (2), а значит, и данное, равносильное ему уравнение (1) не имеют решений.
, а потому не может равняться отрицательному числу; в этом случае уравнение (2), а значит, и данное, равносильное ему уравнение (1) не имеют решений.
Так, например, уравнение  не имеет решений.
не имеет решений.
Это и понятно: левая его часть — положительное число при всех значениях х, а потому не может равняться нулю.
Случай 2. Пусть  Тогда уравнение (2) примет вид:
Тогда уравнение (2) примет вид:  Очевидно, что это равенство будет верным только при
Очевидно, что это равенство будет верным только при  Значит, при
Значит, при  уравнение (1), равносильное
уравнение (1), равносильное  имеет единственное решение
имеет единственное решение 
Случай 3. Числа а и с имеют противоположные знаки (одно из них положительно, а другое отрицательно). Тогда число отрицательно, а противоположное ему число —  положительно.
положительно.
В этом случае уравнение

равносильное данному, имеет два корня:

Следовательно, и уравнение (1) имеет два корня:

Примеры: 
Вычислить  мы всегда можем приближённо с той степенью точности, какая нам требуется.
мы всегда можем приближённо с той степенью точности, какая нам требуется.
Пример.

Следовательно, мы можем записать (см. таблицу В. М. Брадиса)  (с двумя значащими цифрами);
(с двумя значащими цифрами);  (с тремя значащими, цифрами);
(с тремя значащими, цифрами);  (с четырьмя значащими цифрами).
(с четырьмя значащими цифрами).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.
- § 2. Алгебраические выражения.
- § 3. Допустимые значения букв.
- § 4. Порядок действий.
- § 5. Основные законы сложения и умножения.
- § 6. Краткие исторические сведения.
- ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА.
- § 7. Положительные и отрицательные числа.
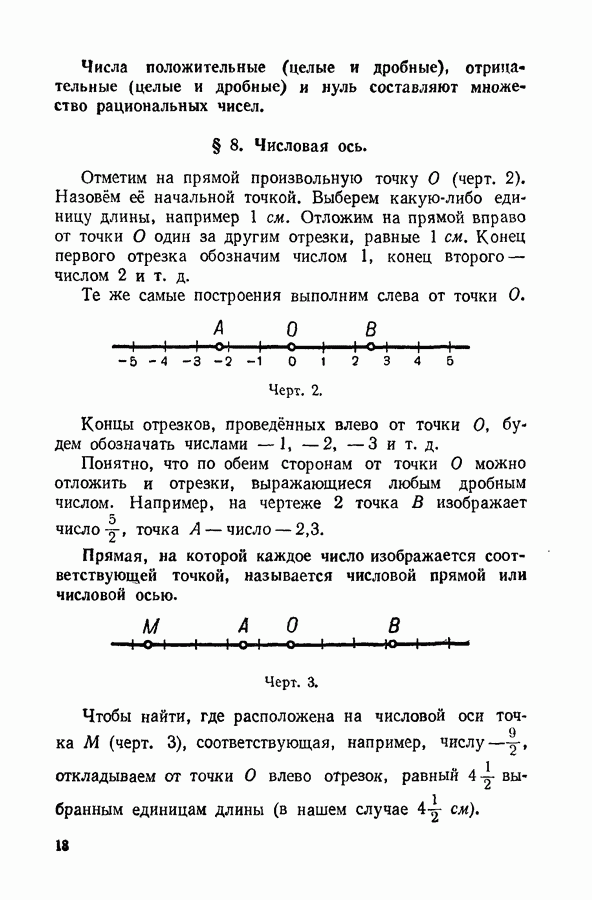
- § 8. Числовая ось.
- § 9. Противоположные числа.
- § 10. Абсолютная величина числа.
- § 11. Сравнение рациональных чисел.
- § 12. Сложение рациональных чисел.
- § 13. Сложение нескольких чисел.
- § 14. Законы сложения.
- § 15. Вычитание рациональных чисел.
- § 16. Алгебраическая сумма.
- § 17. Умножение.
- § 18. Умножение нескольких чисел.
- § 19. Законы умножения.
- § 20. Деление.
- § 21. Свойства деления.
- § 22. Возведение в степень.
- § 23. Порядок выполнения действий.
- § 24. Уравнения.
- § 25. Решение задач с помощью уравнений.
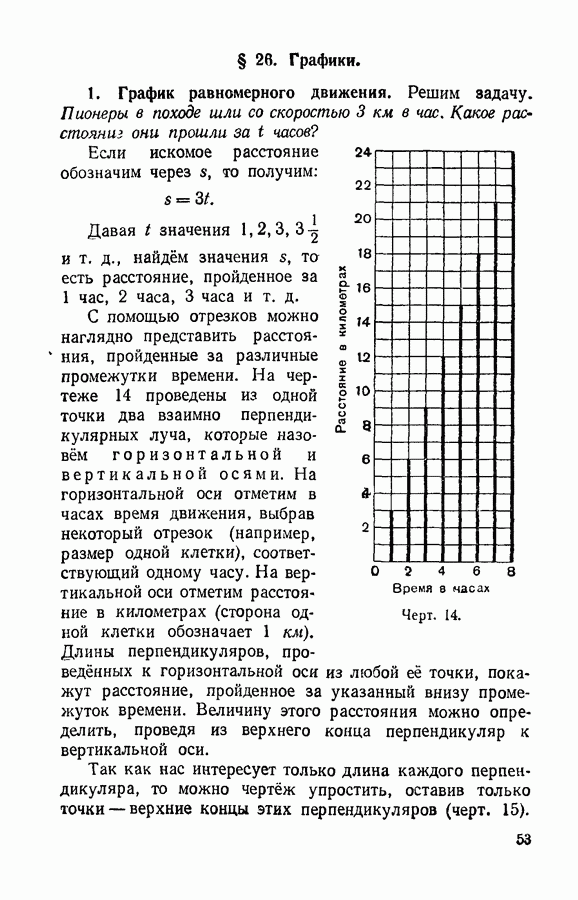
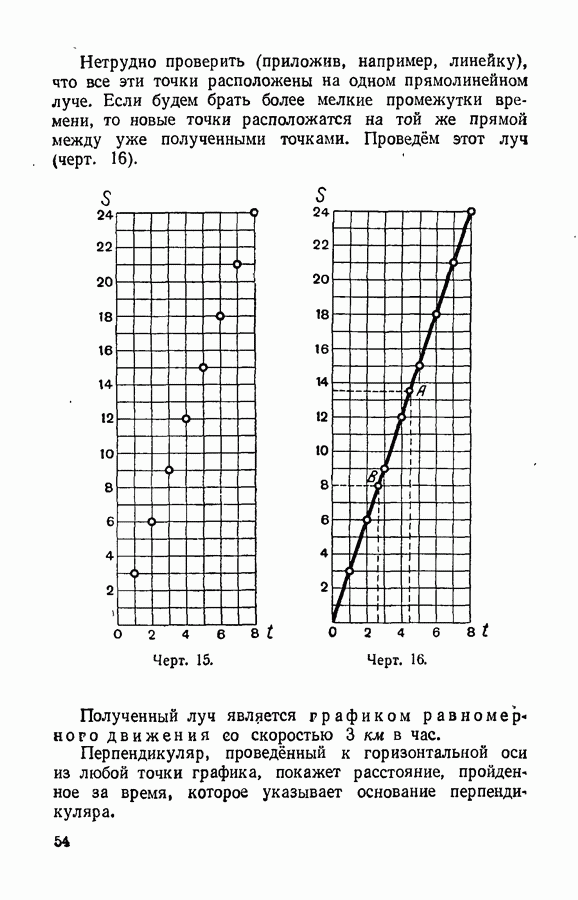
- § 26. Графики.
- § 27. Краткие исторические сведения. (Из истории отрицательных чисел.)
- ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ.
- § 28. Одночлен и многочлен.
- § 29. Тождества и тождественные преобразования.
- § 30. Коэффициент.
- § 31. Расположенные многочлены.
- § 32. Приведение подобных членов.
- § 33. Сложение одночленов и многочленов.
- § 34. Противоположные многочлены.
- § 35. Вычитание одночленов и многочленов
- § 36. Умножение одночленов.
- § 37. Умножение многочлена на одночлен.
- § 38. Умножение многочленов.
- § 39. Умножение расположенных многочленов.
- § 40. Возведение одночленов в степень.
- § 41. Формулы сокращённого умножения.
- § 42. Общие замечания о делении целых алгебраических выражений.
- § 43. Деление одночленов.
- § 44. Деление многочлена на одночлен
- § 45. Примеры решения уравнений.
- ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ.
- § 47. Равносильные уравнения.
- § 48. Два основных свойства уравнений.
- § 49. Уравнения, содержащие неизвестное в обеих частях.
- § 50. Уравнение первой степени с одним неизвестным.
- § 51. Общие указания к решению уравнений.
- § 52. Решение задач с помощью уравнений.
- § 53. Краткие исторические сведения. (Из истории уравнений.)
- ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ.
- § 54. Понятие о разложении на множители.
- § 55. Вынесение за скобки общего множителя.
- § 56. Способ группировки.
- § 57. Применение формул сокращённого умножения.
- § 58. Применение нескольких способов.
- § 59. Деление многочленов при помощи разложения на множители.
- ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ.
- § 60. Понятие об алгебраической дроби.
- § 61. Основное свойство дроби и сокращение дробей.
- § 62. Перемена знака у членов дроби.
- § 63. Целая отрицательная и нулевая степени числа.
- § 64. Приведение дробей к общему знаменателю.
- § 65. Сложение дробей.
- § 66. Вычитание дробей.
- § 67. Умножение дробей.
- § 68. Деление дробей.
- § 69. Возведение дроби в натуральную степень.
- § 70. Дробные уравнения.
- § 71. Примеры решения уравнений с буквенными коэффициентами.
- ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.
- § 72. Координаты точки на плоскости.
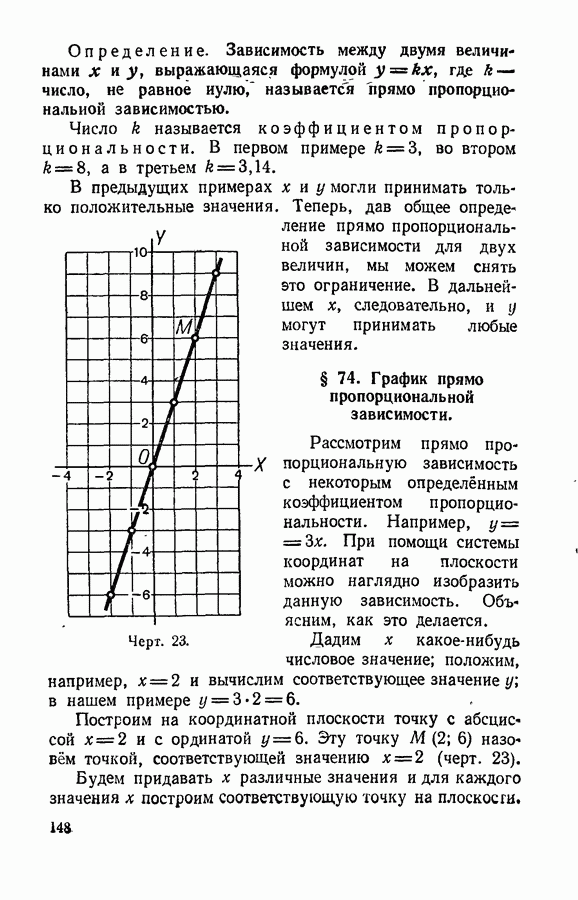
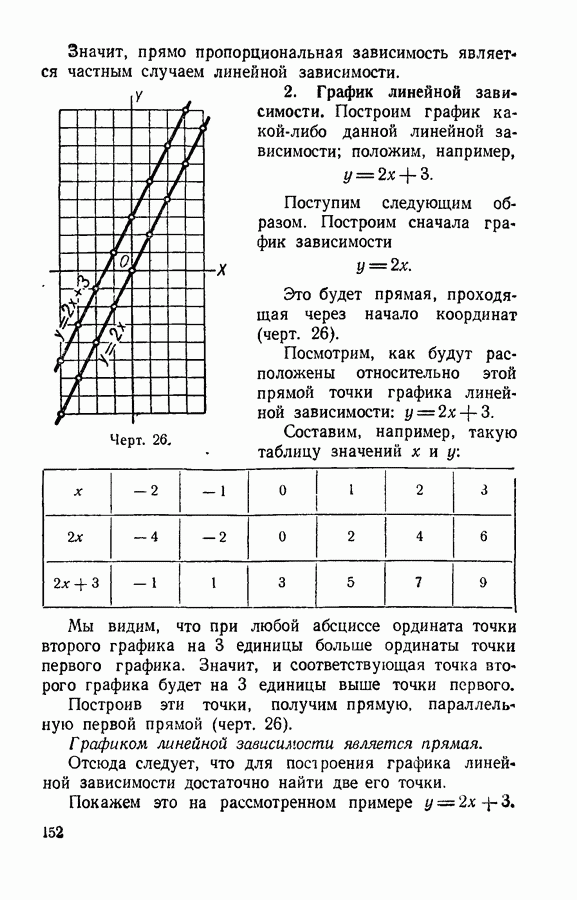
- § 73. Прямо пропорциональная зависимость.
- § 74. График прямо пропорциональной зависимости.
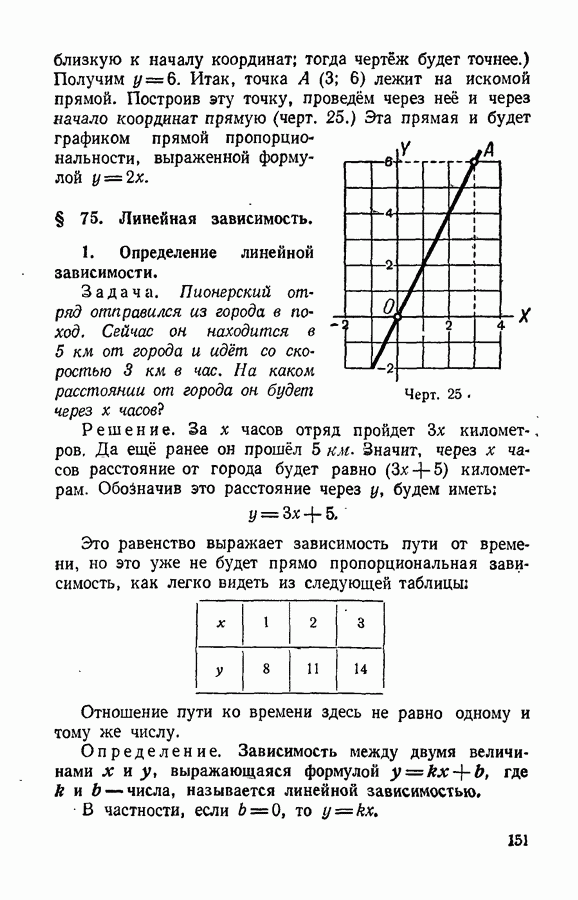
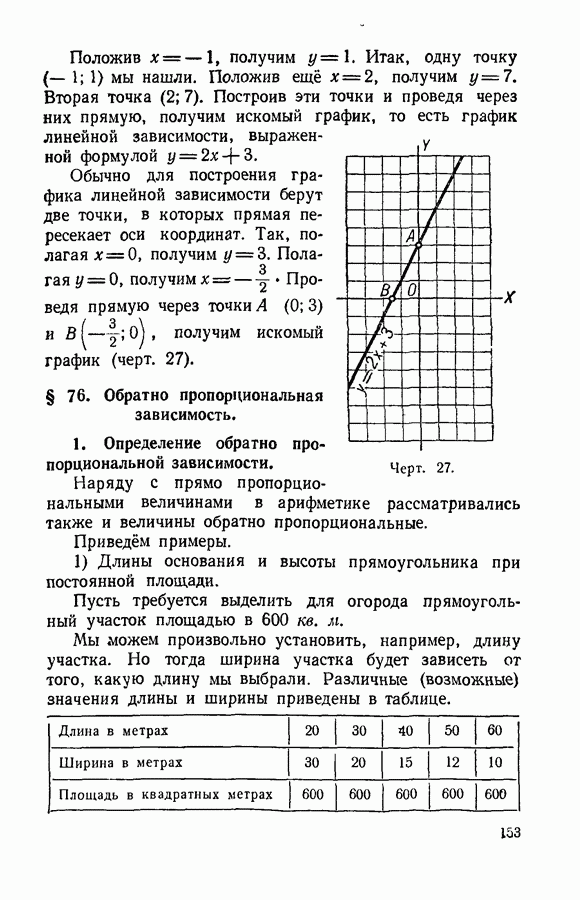
- § 75. Линейная зависимость.
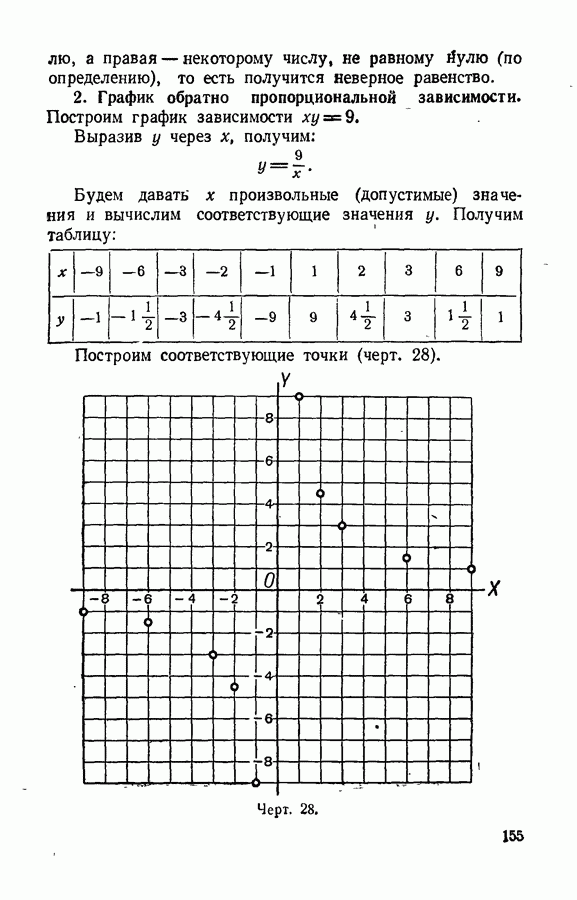
- § 76. Обратно пропорциональная зависимость.
- ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ.
- § 77. Уравнение первой степени с двумя неизвестными.
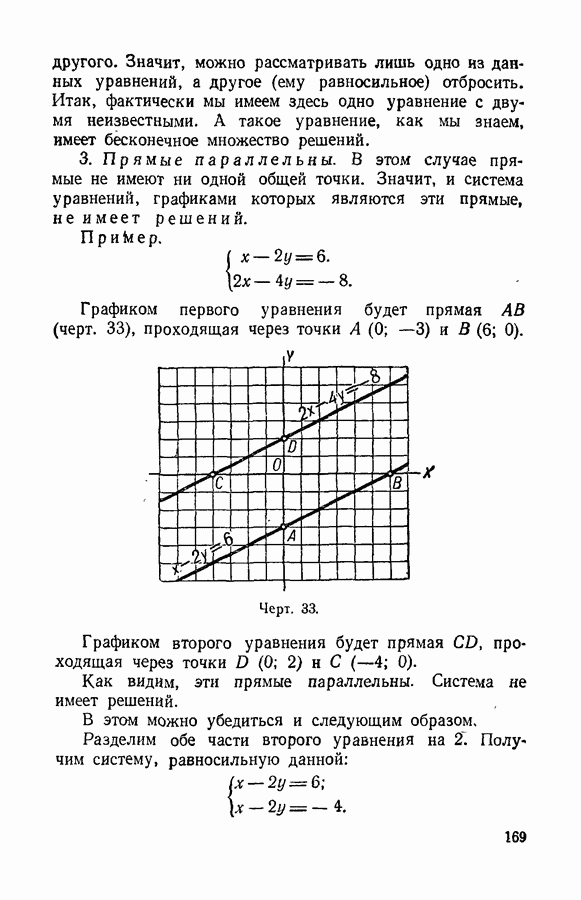
- § 78. Система двух уравнений первой степени с двумя неизвестными.
- § 79. Равносильные системы.
- § 80. Решение систем уравнений.
- § 81. Графическое решение системы двух уравнений.
- § 82. Решение задач.
- § 83. Уравнение с тремя неизвестными.
- § 84. Система трёх уравнений с тремя неизвестными.
- ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА.
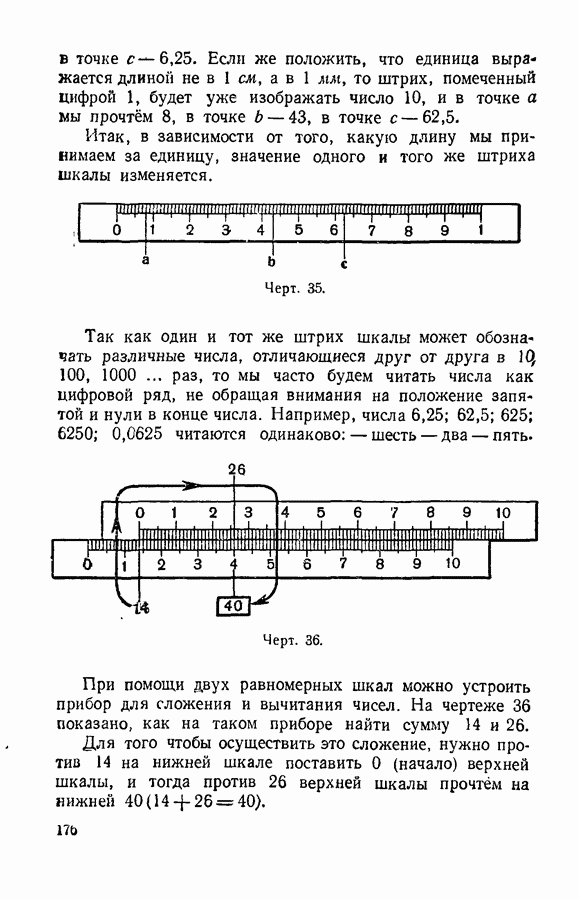
- § 85. Равномерные и неравномерные шкалы.
- § 86. Устройство счётной (логарифмической) линейки.
- § 87. Основная шкала.
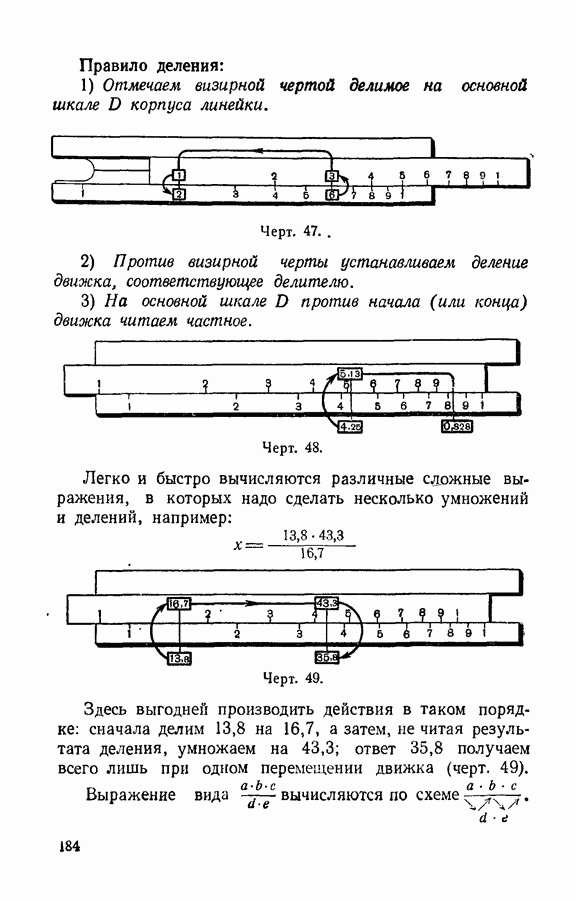
- § 88. Умножение и деление с помощью счётной линейки.
- ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ.
- § 89. Построение графика зависимости y = x^2
- § 90. Вычисление квадратов чисел по таблицам и при помощи счётной линейки.
- § 91. Понятие об извлечении корня. Решим две задачи.
- § 92. Арифметический корень.
- § 93. Приближённый квадратный корень из положительного числа.
- § 94. График зависимости y = sqrt(х).
- § 95. Извлечение квадратного корня из целых чисел.
- § 96. Извлечение корня с точностью до 0,1; 0,01 и т. д.
- § 97. Квадратный корень из произведения, дроби и степени.
- § 98. Простейшие преобразования.
- § 99. Извлечение квадратного корня по таблицам и при помощи счётной линейки.
- § 100. Краткие исторические сведения.
- ГЛАВА ОДИННАДЦАТАЯ. КВАДРАТНЫЕ УРАВНЕНИЯ.
- § 101. Квадратные уравнения.
- § 102. Уравнение вида ax^2+bx=0
- § 103. Уравнение вида ax^2+c=0
- § 104. Приведённое квадратное уравнение.
- § 105. Квадратное уравнение общего вида.
- § 106. Дискриминант.
- § 107. Графическое решение квадратного уравнения.
- § 108. Решение задач, приводящих к квадратным уравнениям.
- § 109. Теорема Виета.
- § 110. Исследование корней квадратного уравнения.
- § 111. Разложение квадратного трёхчлена на множители.
- § 112. Системы двух уравнений, из которых одно второй и одно первой степени.
- § 113. Краткие исторические сведения.
- ГЛАВА ДВЕНАДЦАТАЯ. ФУНКЦИИ И ГРАФИКИ.
- § 114. Переменные величины.
- § 115. Понятие о функциональной зависимости.
- § 116. Аргумент и функция.
- § 117. Способы задания функции.
- § 118. Функция y = kx.
- § 119. Линейная функция.
- § 120. Трехчлен второй степени.
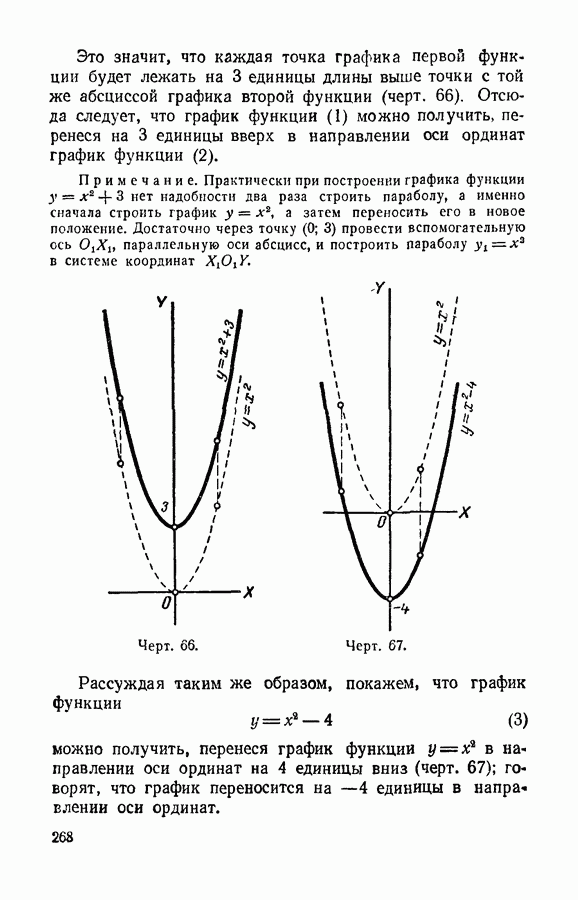
- § 121. График функции y=x^2+n
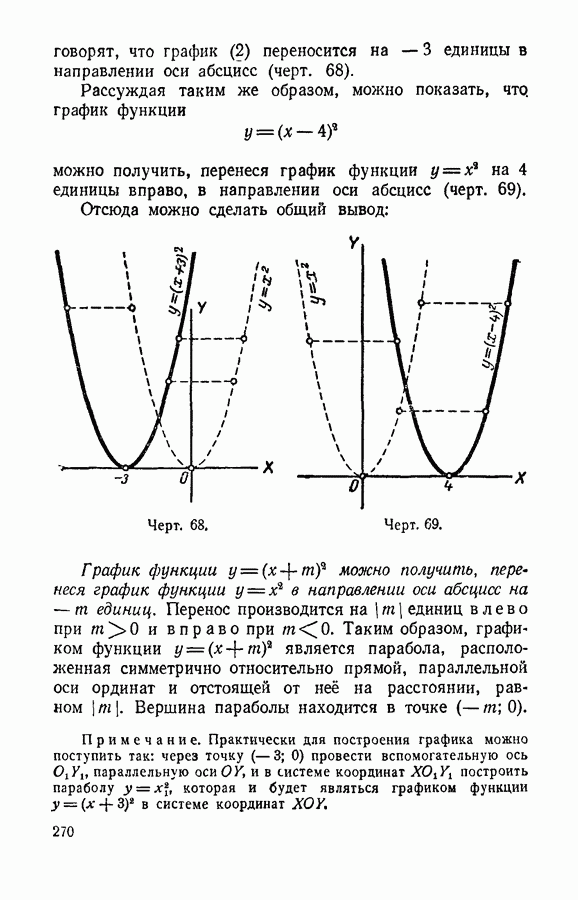
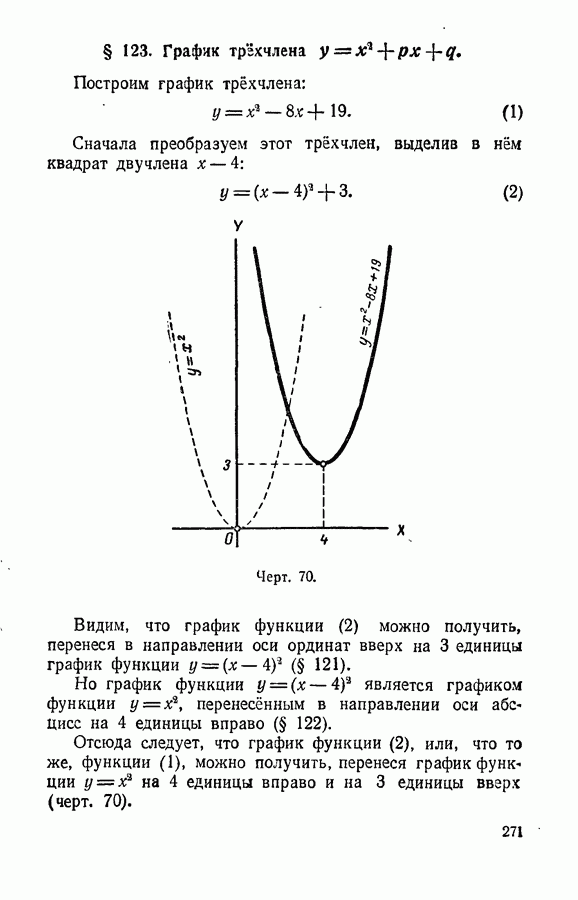
- § 122. График функции y = (x+m)^2
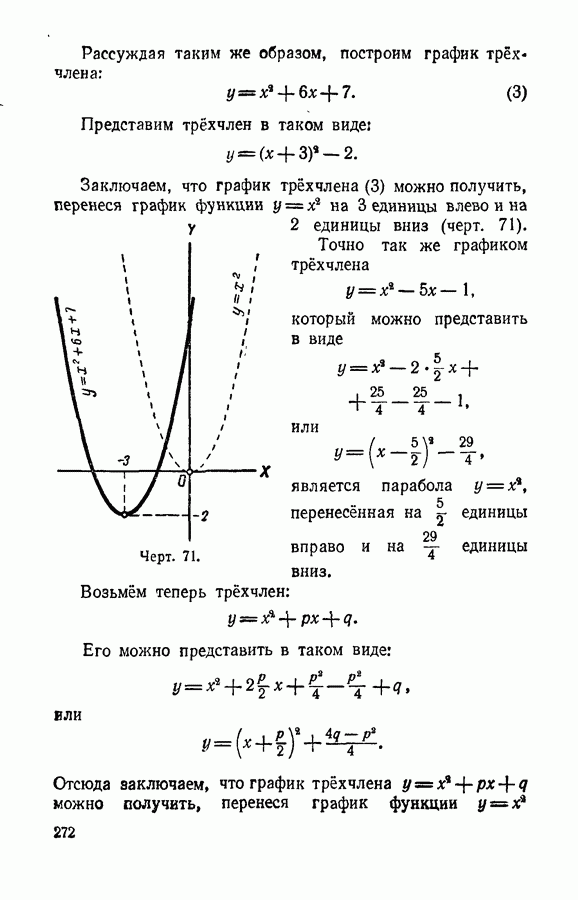
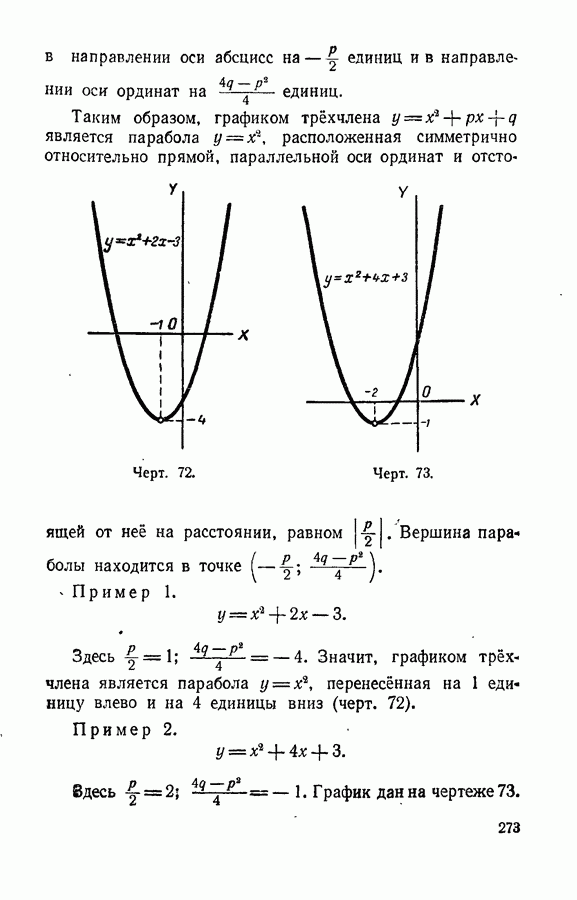
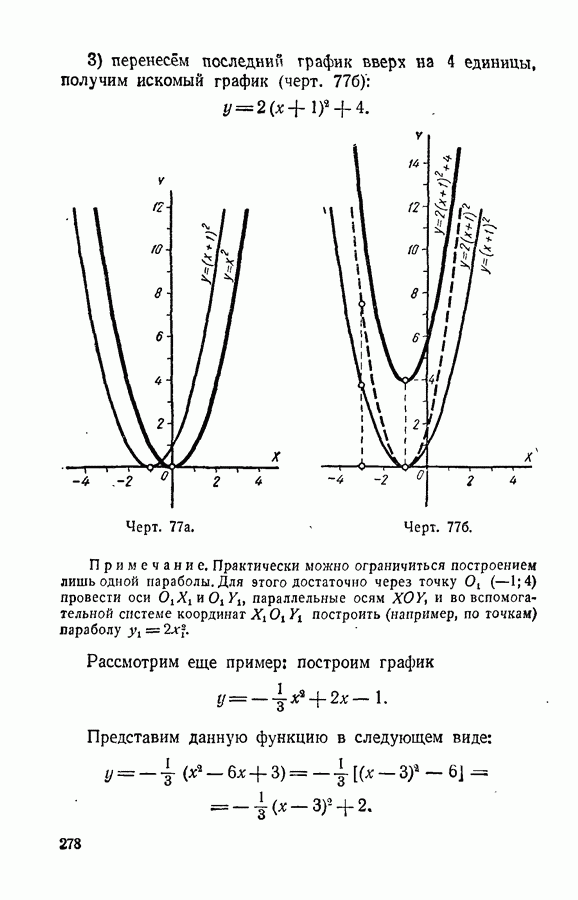
- § 123. График трехчлена y = x^2+px+q
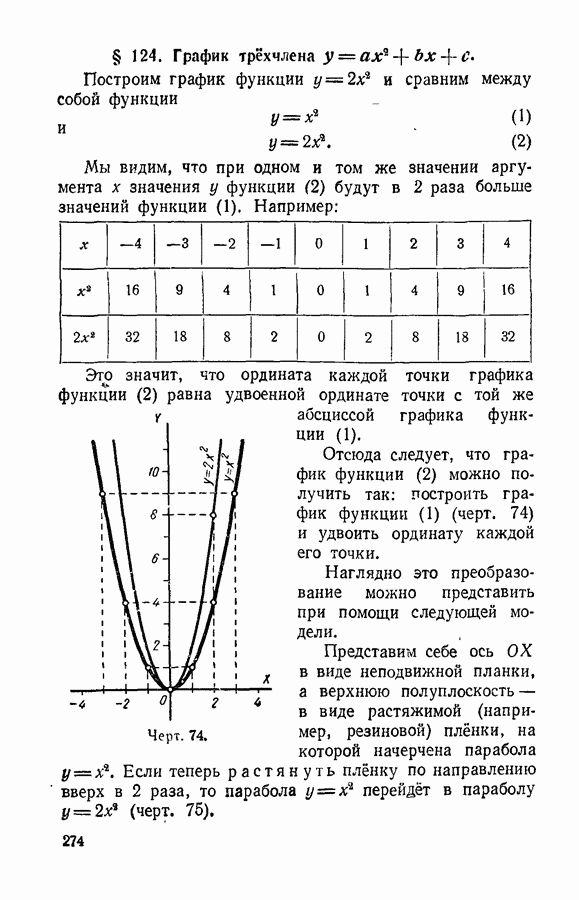
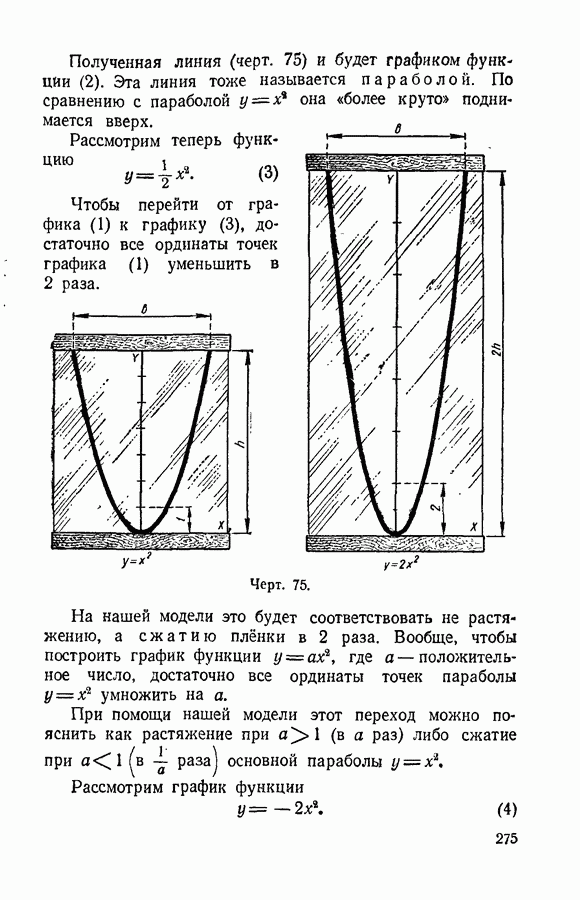
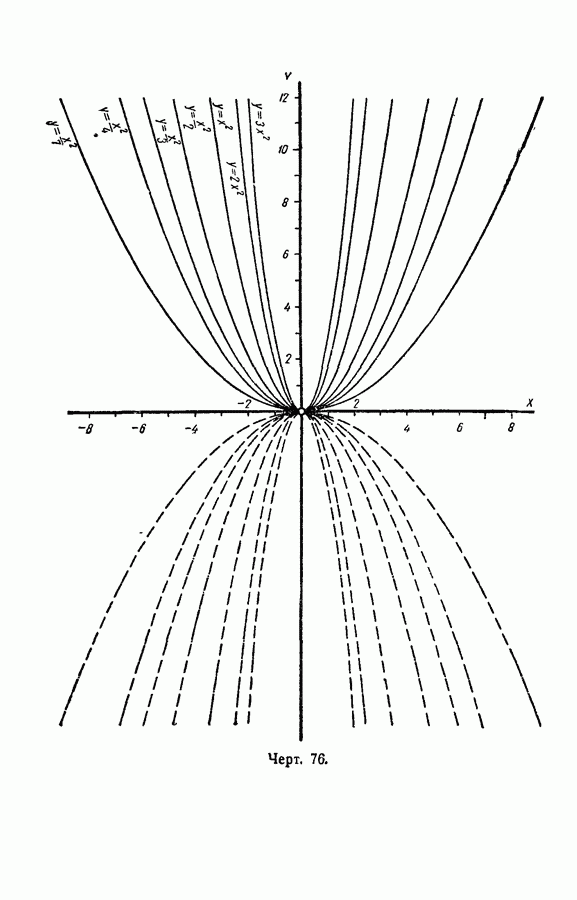
- § 124. График трехчлена y = ax^2+bx+c
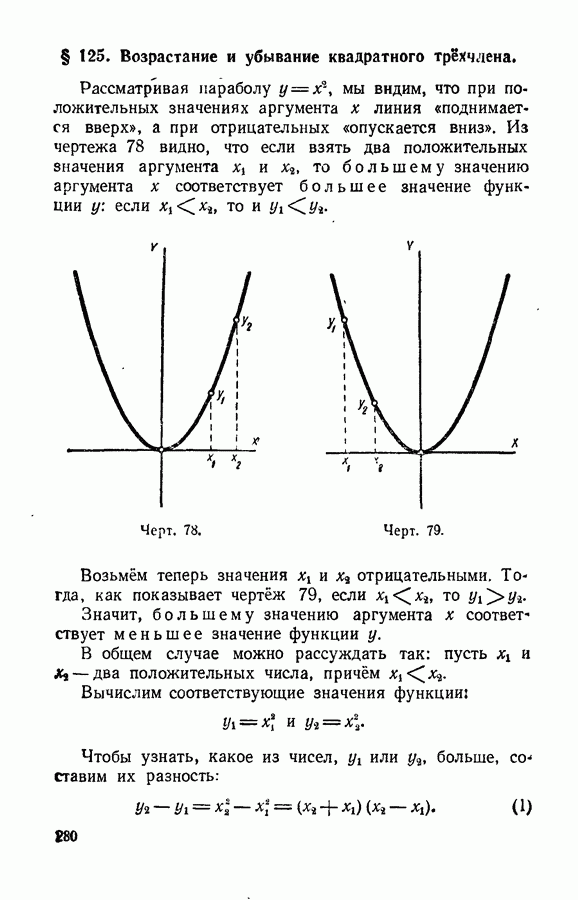
- § 125. Возрастание и убывание квадратного трёхчлена.
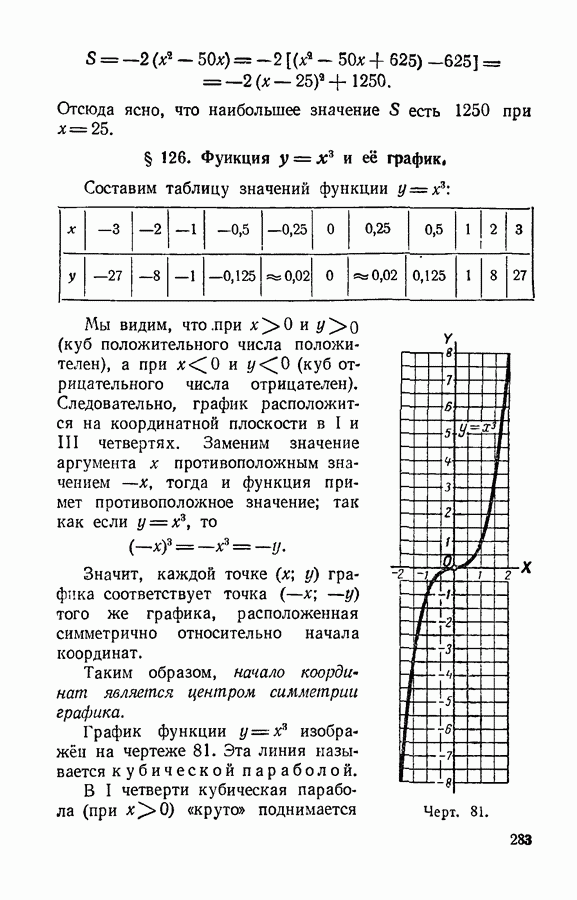
- § 126. Функция у = х^3 и её график.
- § 127. Понятие о кубическом корне.
- § 128. Приближённое извлечение кубического корня.
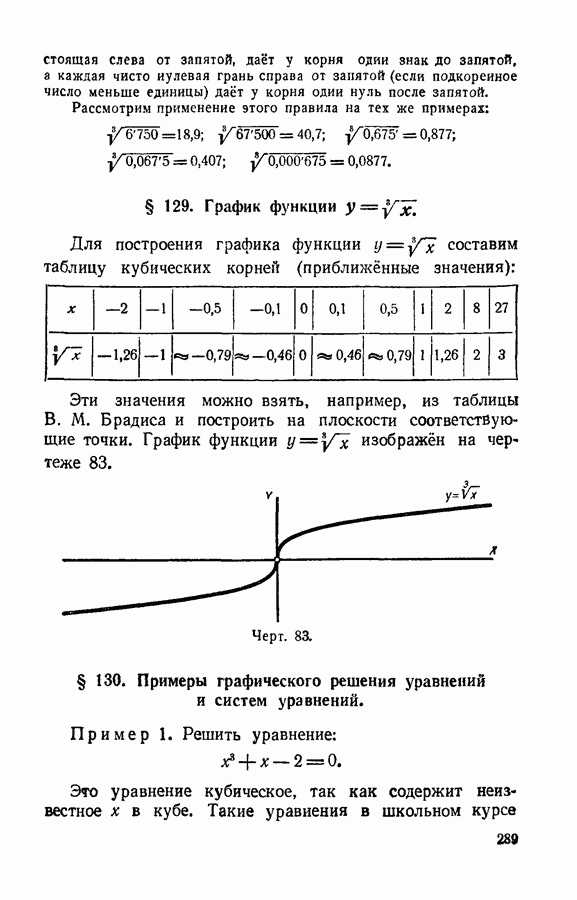
- § 129. График функции y = x^(1/3)
- § 130. Примеры графического решения уравнений и систем уравнений.