| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ.
§ 77. Уравнение первой степени с двумя неизвестными.
В главе IV мы изучали уравнения, содержащие одно неизвестное; однако уравнение может содержать не одно, а несколько неизвестных, обозначенных буквами. Сформулируем определение уравнения в общем виде.
Определение. Уравнением называется равенство, в котором одно или несколько чисел, обозначенных буквами, являются неизвестными.
Пусть, например, сказано, что сумма квадратов двух неизвестных чисел х и у равна 7; это можно записать при помощи следующего уравнения с двумя неизвестными:

Для уравнений с двумя неизвестными остаются справедливыми все те свойства, которые были установлены для уравнений с одним неизвестным (§ 48).
Уравнением первой степени с двумя неизвестными называется уравнение вида

где х и у — неизвестные,  (коэффициенты при неизвестных) - данные числа, не равные оба нулю, с (свободный член) — любое данное число.
(коэффициенты при неизвестных) - данные числа, не равные оба нулю, с (свободный член) — любое данное число.
Примеры уравнений первой степени:

Уравнения:

после переноса членов, содержащих неизвестные, в левую часть, а известных чисел — в правую часть приводятся к виду (1), а потому эти уравнения также являются уравнениями первой степени.
Уравнение (1) называется нормальным видом уравнения первой степени с двумя неизвестными.
Из приведённых примеров видно (примеры 2 и 3), что рассмотренные ранее равенства, выражающие прямо пропорциональную и линейную зависимости, являются уравнениями первой степени с двумя неизвестными.
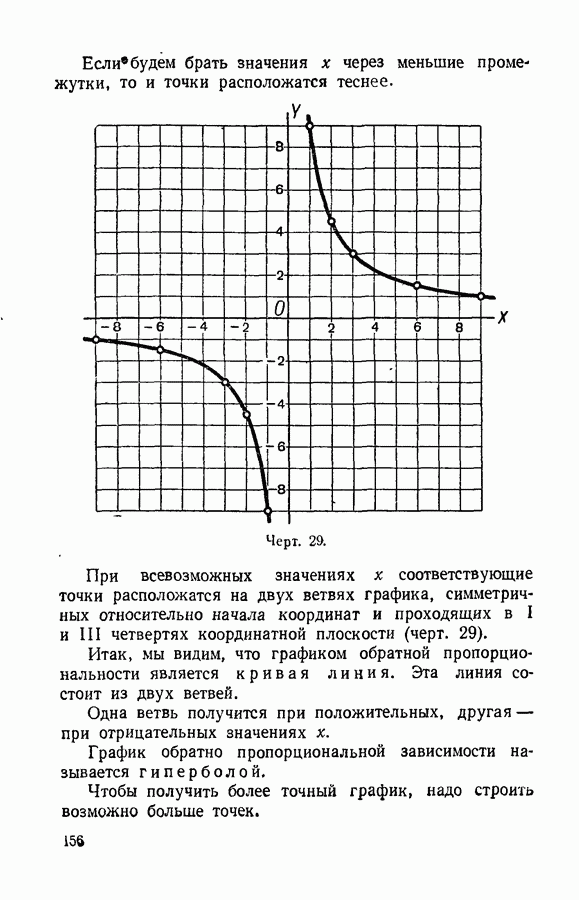
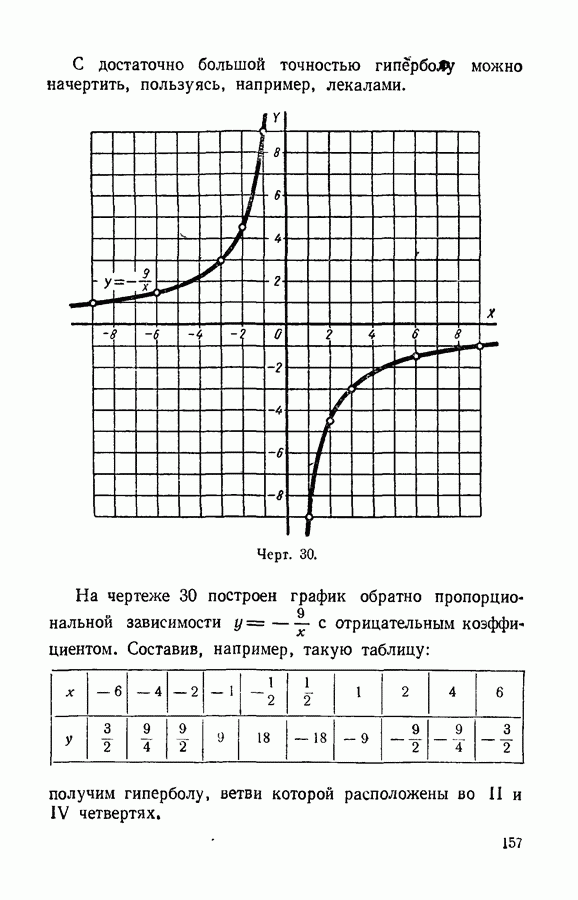
Равенство, выражающее обратно пропорциональную зависимость, например  уже не является уравнением первой степени.
уже не является уравнением первой степени.
Рассмотрим какое-нибудь уравнение с двумя неизвестными, например:

Возьмём какую-либо пару чисел, например:  Подставив эти значения в данное уравнение, получим верное равенство:
Подставив эти значения в данное уравнение, получим верное равенство:

Говорят, что эта пара чисел удовлетворяет данному уравнению или что она (эта пара) есть решение данного уравнения.
Возьмём теперь такую пару чисел: 
Подставив эти значения в данное уравнение, получим в его левой части  При этих значениях левая часть (нуль) оказалась не равной правой части (т. е. числу 3). Говорят, что пара чисел
При этих значениях левая часть (нуль) оказалась не равной правой части (т. е. числу 3). Говорят, что пара чисел  не удовлетворяет данному уравнению или что она не есть решение уравнения.
не удовлетворяет данному уравнению или что она не есть решение уравнения.
Каждая пара значений х и у, подстановка которых в уравнение с двумя неизвестными х и у обращает его в верное равенство, называется решением этого уравнения.
Решим такую задачу.
Задача. Сумма двух чисел равна 6. Чему равно каждое слагаемое?
Обозначим через х и у искомые слагаемые.
Задача приводит к уравнению:

Дадим х какое-либо значение, например  тогда для другого неизвестного у получим уравнение:
тогда для другого неизвестного у получим уравнение:

из которого найдём  Пара чисел
Пара чисел  даёт решение нашей задачи.
даёт решение нашей задачи.
Однако вместо  мы могли бы взять какое-нибудь другое значение для х, например
мы могли бы взять какое-нибудь другое значение для х, например  и тогда мы нашли бы
и тогда мы нашли бы  Значит, мы получили ещё одно решение уравнения:
Значит, мы получили ещё одно решение уравнения: 
В таблице приведено несколько решений данного уравнения: значения х и у записаны друг под другом, а в нижней строчке показано, что сумма этих значений равна 6.

Ясно, что одному из неизвестных (например, х) можно придать любое значение и, подставив его в данное уравнение, найти соответствующее значение другого неизвестного.
Как видим, задача имеет бесконечное множество решений.
Уравнение не даёт определённого ответа на вопрос задачи. Оно лишь указывает на зависимость между двумя неизвестными. На основании этой зависимости, зная значение одного неизвестного, мы могли найти значение и другого.
Итак, уравнение первой степени, содержащее два неизвестных, имеет бесконечное множество решений.
Одному из неизвестных можно придать произвольное значение и из данного уравнения найти соответствующее значение другого неизвестного.
Мы уже видели, что в случае линейной (в частности, прямо пропорциональной) зависимости, выражающейся уравнением первой степени с двумя неизвестными, графиком является прямая линия. Докажем, что прямая линия будет графиком и любого уравнения первой степени с двумя неизвестными.
Начнём с примера.
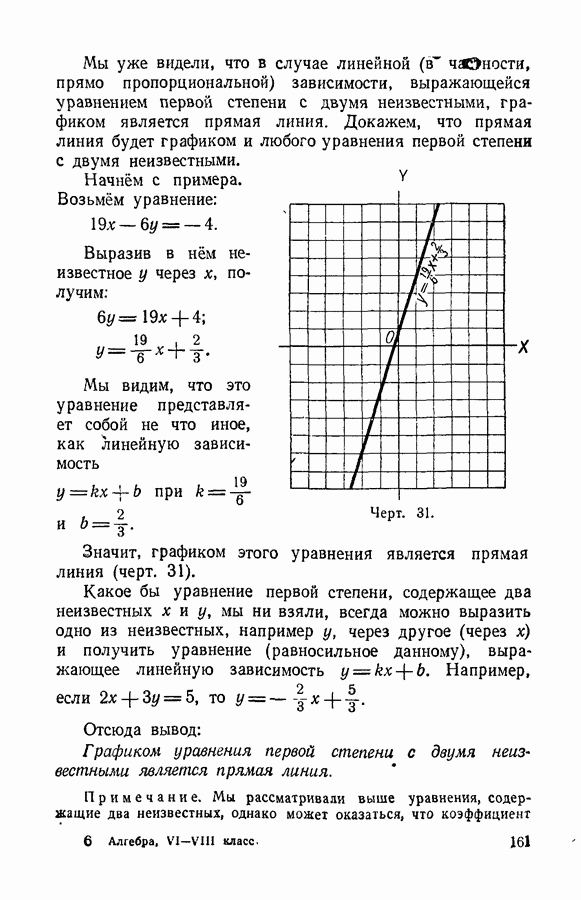
Возьмём уравнение:

Выразив в нём неизвестное у через х, получим:

Мы видим, что это уравнение представляет собой не что иное, как линейную зависимость

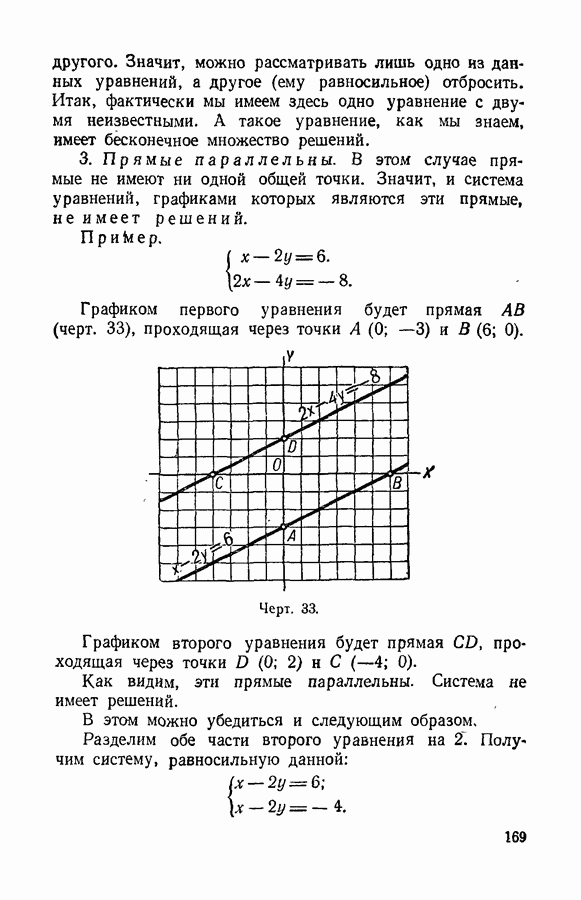
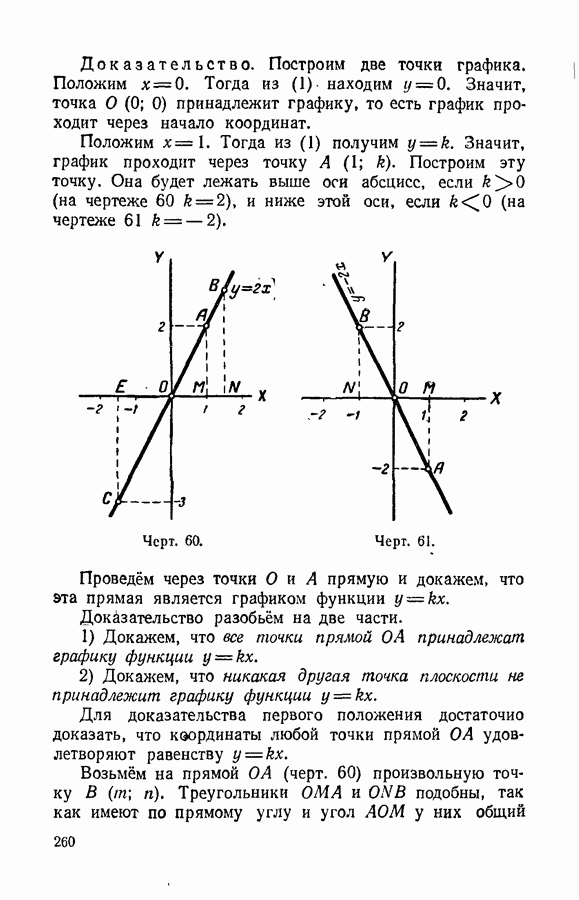
Значит, графиком этого уравнения является прямая линия (черт. 31).

Черт. 31.
Какое бы уравнение первой степени, содержащее два неизвестных х и у, мы ни взяли, всегда можно выразить одно из неизвестных, например у, через другое (через  и получить уравнение (равносильное данному), выражающее линейную зависимость
и получить уравнение (равносильное данному), выражающее линейную зависимость  . Например, если
. Например, если  то
то 
Отсюда вывод:
Графиком уравнения первой степени с двумя неизвестными является прямая линия.
Примечание. Мы рассматривали выше уравнения, содержащие два неизвестных, однако может оказаться, что коэффициент
при одном из неизвестных будет равен нулю, так что уравнение запишется в виде уравнения с одним неизвестным.
Возьмём, например, уравнение:

Приведём это уравнение к нормальному виду:

Это уравнение также имеет бесконечное множество решений; ему удовлетворяет любая пара чисел  , где у — произвольное число. Обычно член
, где у — произвольное число. Обычно член  не пишут и уравнение записывают так:
не пишут и уравнение записывают так: 
| << Предыдущий параграф | Следующий параграф >> |
- ГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.
- § 2. Алгебраические выражения.
- § 3. Допустимые значения букв.
- § 4. Порядок действий.
- § 5. Основные законы сложения и умножения.
- § 6. Краткие исторические сведения.
- ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА.
- § 7. Положительные и отрицательные числа.
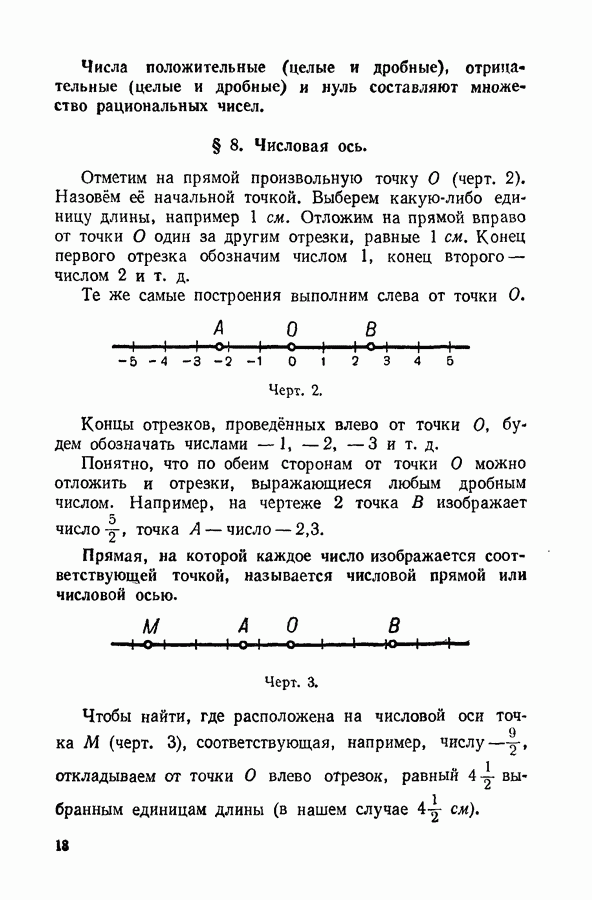
- § 8. Числовая ось.
- § 9. Противоположные числа.
- § 10. Абсолютная величина числа.
- § 11. Сравнение рациональных чисел.
- § 12. Сложение рациональных чисел.
- § 13. Сложение нескольких чисел.
- § 14. Законы сложения.
- § 15. Вычитание рациональных чисел.
- § 16. Алгебраическая сумма.
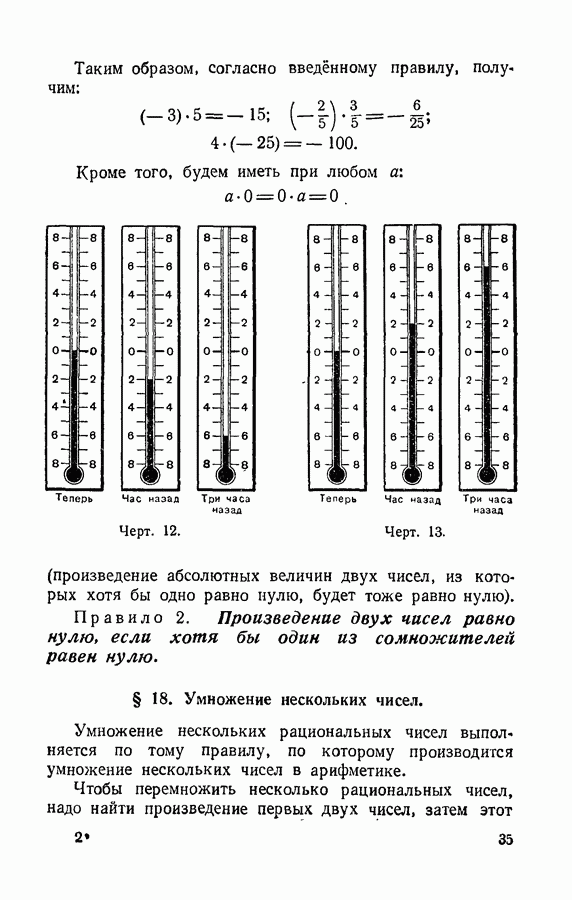
- § 17. Умножение.
- § 18. Умножение нескольких чисел.
- § 19. Законы умножения.
- § 20. Деление.
- § 21. Свойства деления.
- § 22. Возведение в степень.
- § 23. Порядок выполнения действий.
- § 24. Уравнения.
- § 25. Решение задач с помощью уравнений.
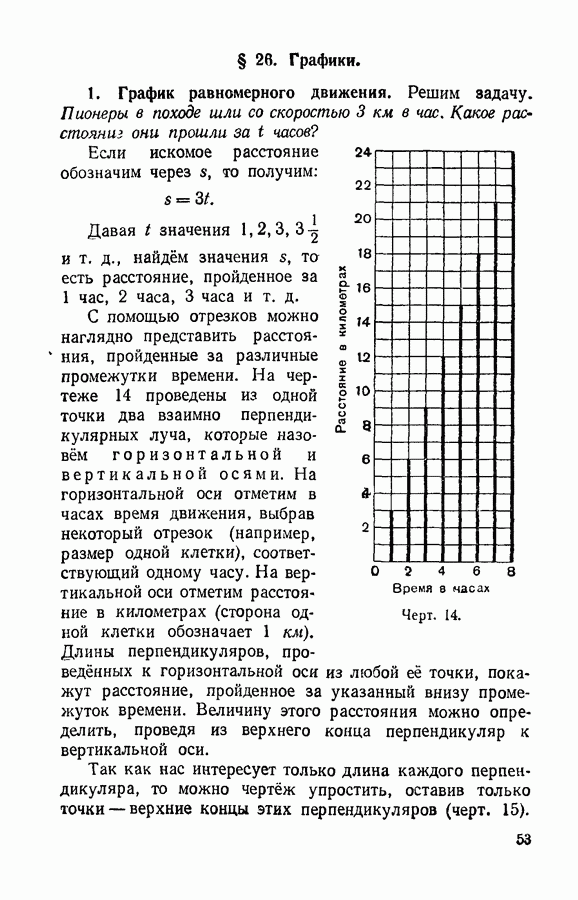
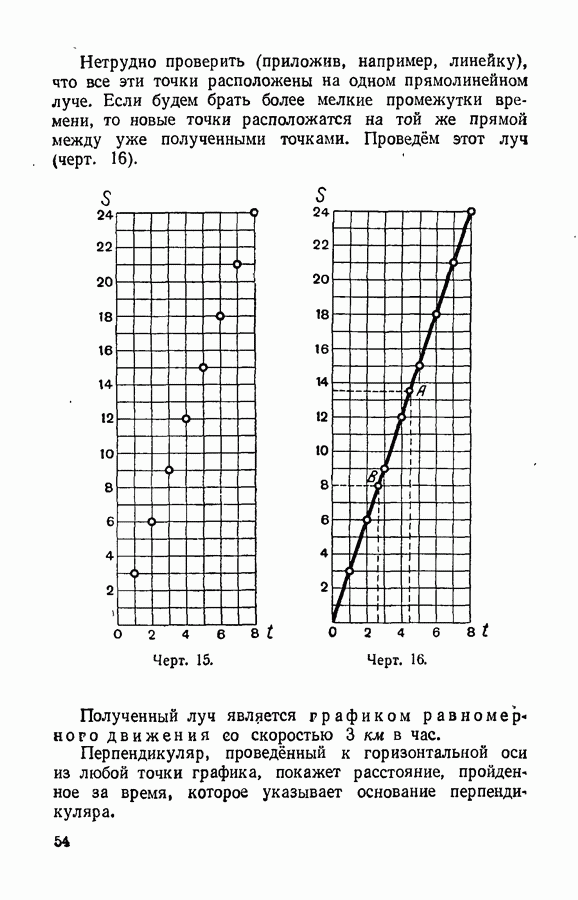
- § 26. Графики.
- § 27. Краткие исторические сведения. (Из истории отрицательных чисел.)
- ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ.
- § 28. Одночлен и многочлен.
- § 29. Тождества и тождественные преобразования.
- § 30. Коэффициент.
- § 31. Расположенные многочлены.
- § 32. Приведение подобных членов.
- § 33. Сложение одночленов и многочленов.
- § 34. Противоположные многочлены.
- § 35. Вычитание одночленов и многочленов
- § 36. Умножение одночленов.
- § 37. Умножение многочлена на одночлен.
- § 38. Умножение многочленов.
- § 39. Умножение расположенных многочленов.
- § 40. Возведение одночленов в степень.
- § 41. Формулы сокращённого умножения.
- § 42. Общие замечания о делении целых алгебраических выражений.
- § 43. Деление одночленов.
- § 44. Деление многочлена на одночлен
- § 45. Примеры решения уравнений.
- ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ.
- § 47. Равносильные уравнения.
- § 48. Два основных свойства уравнений.
- § 49. Уравнения, содержащие неизвестное в обеих частях.
- § 50. Уравнение первой степени с одним неизвестным.
- § 51. Общие указания к решению уравнений.
- § 52. Решение задач с помощью уравнений.
- § 53. Краткие исторические сведения. (Из истории уравнений.)
- ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ.
- § 54. Понятие о разложении на множители.
- § 55. Вынесение за скобки общего множителя.
- § 56. Способ группировки.
- § 57. Применение формул сокращённого умножения.
- § 58. Применение нескольких способов.
- § 59. Деление многочленов при помощи разложения на множители.
- ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ.
- § 60. Понятие об алгебраической дроби.
- § 61. Основное свойство дроби и сокращение дробей.
- § 62. Перемена знака у членов дроби.
- § 63. Целая отрицательная и нулевая степени числа.
- § 64. Приведение дробей к общему знаменателю.
- § 65. Сложение дробей.
- § 66. Вычитание дробей.
- § 67. Умножение дробей.
- § 68. Деление дробей.
- § 69. Возведение дроби в натуральную степень.
- § 70. Дробные уравнения.
- § 71. Примеры решения уравнений с буквенными коэффициентами.
- ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.
- § 72. Координаты точки на плоскости.
- § 73. Прямо пропорциональная зависимость.
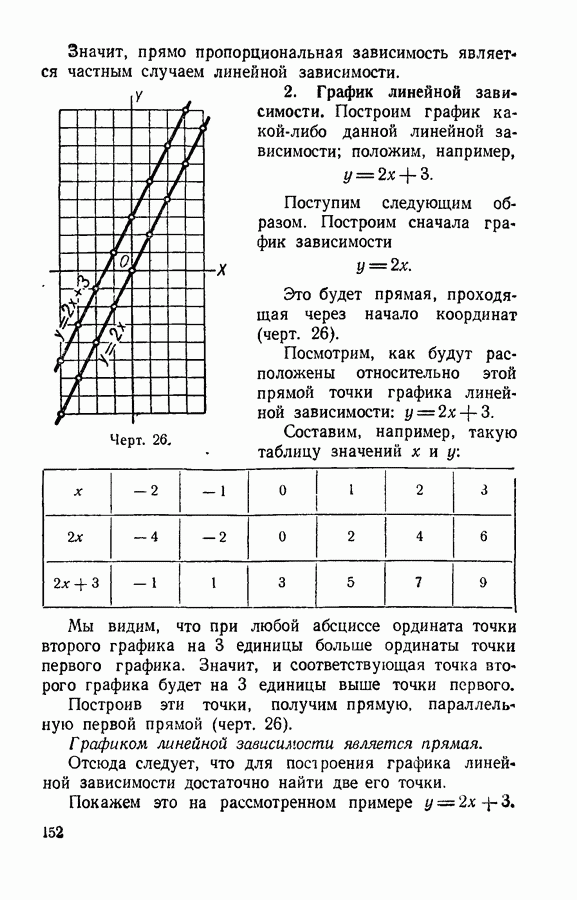
- § 74. График прямо пропорциональной зависимости.
- § 75. Линейная зависимость.
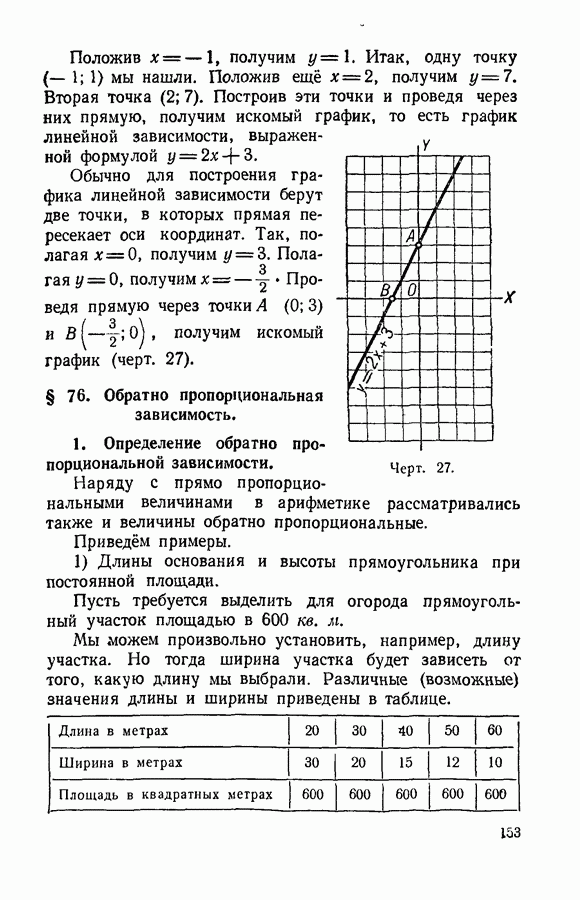
- § 76. Обратно пропорциональная зависимость.
- ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ.
- § 77. Уравнение первой степени с двумя неизвестными.
- § 78. Система двух уравнений первой степени с двумя неизвестными.
- § 79. Равносильные системы.
- § 80. Решение систем уравнений.
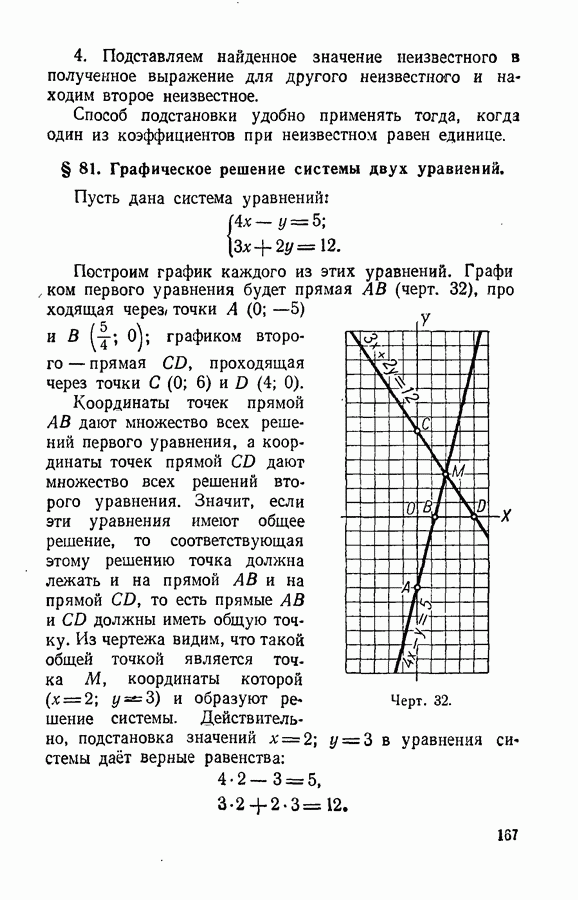
- § 81. Графическое решение системы двух уравнений.
- § 82. Решение задач.
- § 83. Уравнение с тремя неизвестными.
- § 84. Система трёх уравнений с тремя неизвестными.
- ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА.
- § 85. Равномерные и неравномерные шкалы.
- § 86. Устройство счётной (логарифмической) линейки.
- § 87. Основная шкала.
- § 88. Умножение и деление с помощью счётной линейки.
- ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ.
- § 89. Построение графика зависимости y = x^2
- § 90. Вычисление квадратов чисел по таблицам и при помощи счётной линейки.
- § 91. Понятие об извлечении корня. Решим две задачи.
- § 92. Арифметический корень.
- § 93. Приближённый квадратный корень из положительного числа.
- § 94. График зависимости y = sqrt(х).
- § 95. Извлечение квадратного корня из целых чисел.
- § 96. Извлечение корня с точностью до 0,1; 0,01 и т. д.
- § 97. Квадратный корень из произведения, дроби и степени.
- § 98. Простейшие преобразования.
- § 99. Извлечение квадратного корня по таблицам и при помощи счётной линейки.
- § 100. Краткие исторические сведения.
- ГЛАВА ОДИННАДЦАТАЯ. КВАДРАТНЫЕ УРАВНЕНИЯ.
- § 101. Квадратные уравнения.
- § 102. Уравнение вида ax^2+bx=0
- § 103. Уравнение вида ax^2+c=0
- § 104. Приведённое квадратное уравнение.
- § 105. Квадратное уравнение общего вида.
- § 106. Дискриминант.
- § 107. Графическое решение квадратного уравнения.
- § 108. Решение задач, приводящих к квадратным уравнениям.
- § 109. Теорема Виета.
- § 110. Исследование корней квадратного уравнения.
- § 111. Разложение квадратного трёхчлена на множители.
- § 112. Системы двух уравнений, из которых одно второй и одно первой степени.
- § 113. Краткие исторические сведения.
- ГЛАВА ДВЕНАДЦАТАЯ. ФУНКЦИИ И ГРАФИКИ.
- § 114. Переменные величины.
- § 115. Понятие о функциональной зависимости.
- § 116. Аргумент и функция.
- § 117. Способы задания функции.
- § 118. Функция y = kx.
- § 119. Линейная функция.
- § 120. Трехчлен второй степени.
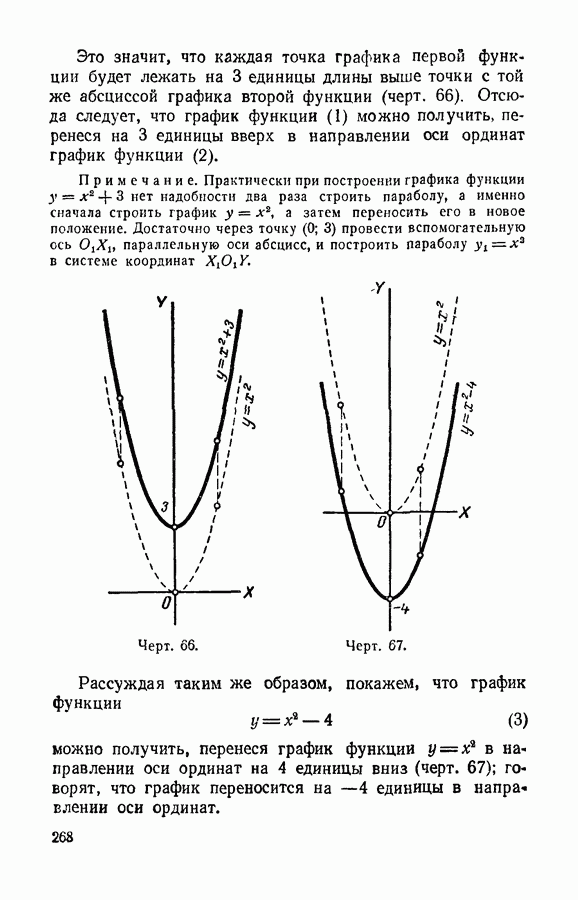
- § 121. График функции y=x^2+n
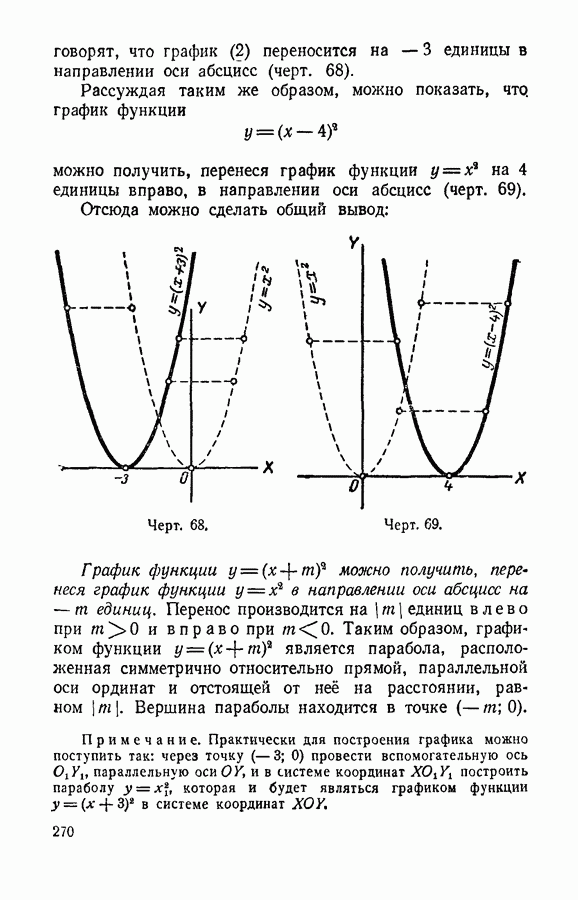
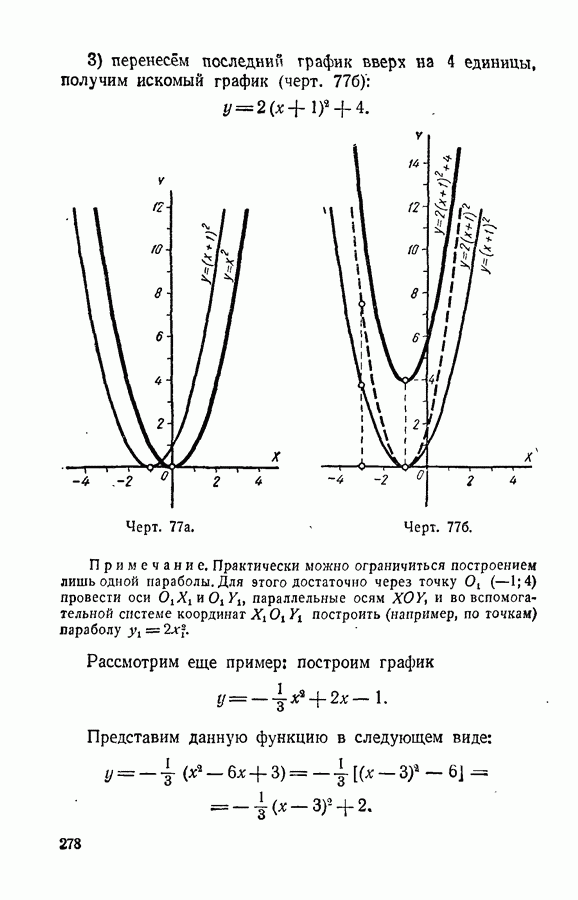
- § 122. График функции y = (x+m)^2
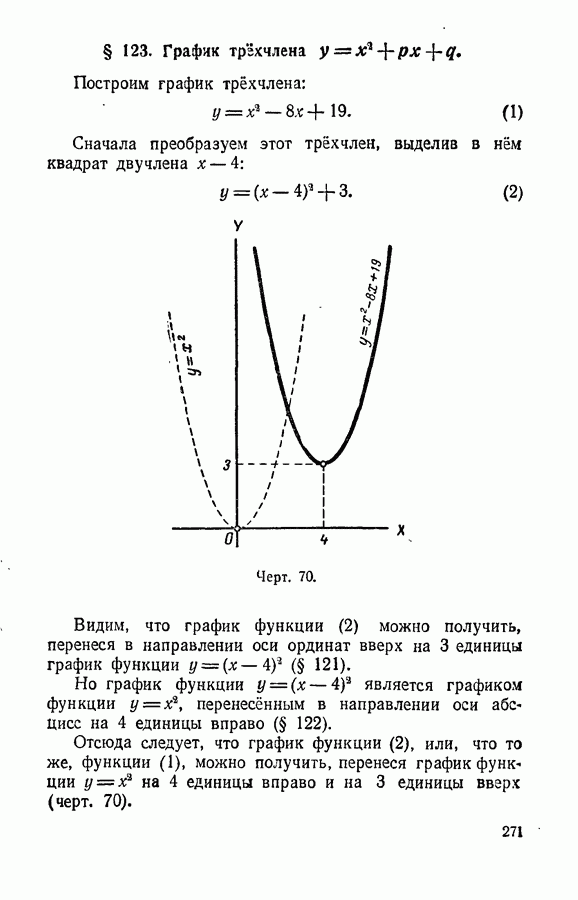
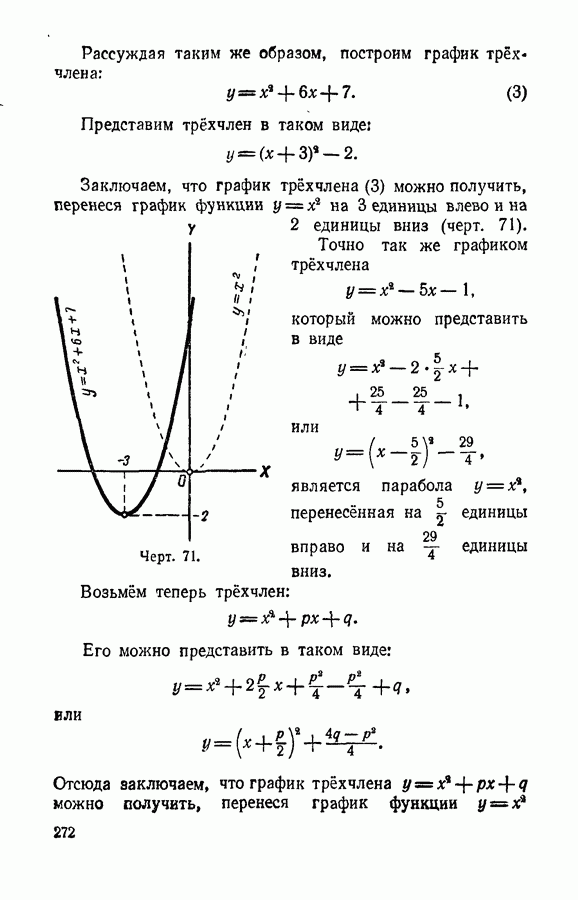
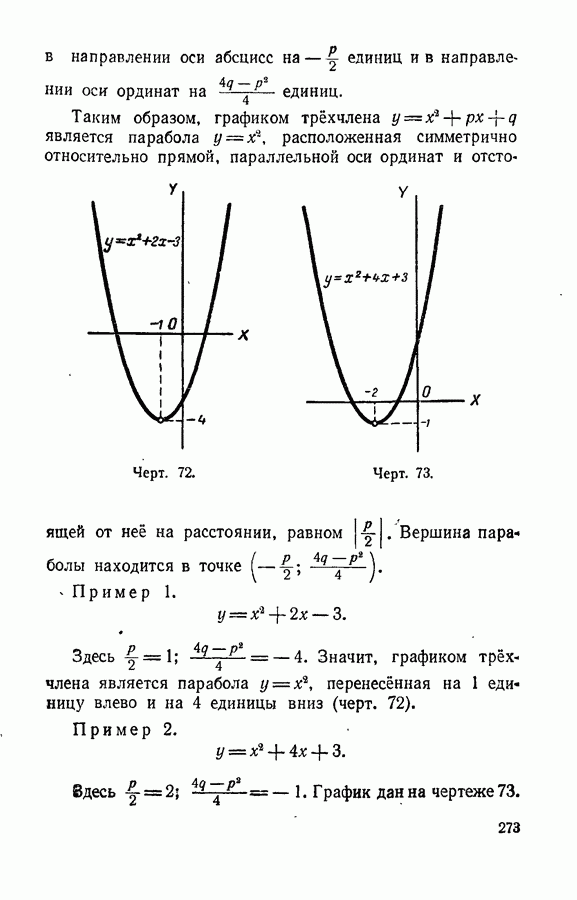
- § 123. График трехчлена y = x^2+px+q
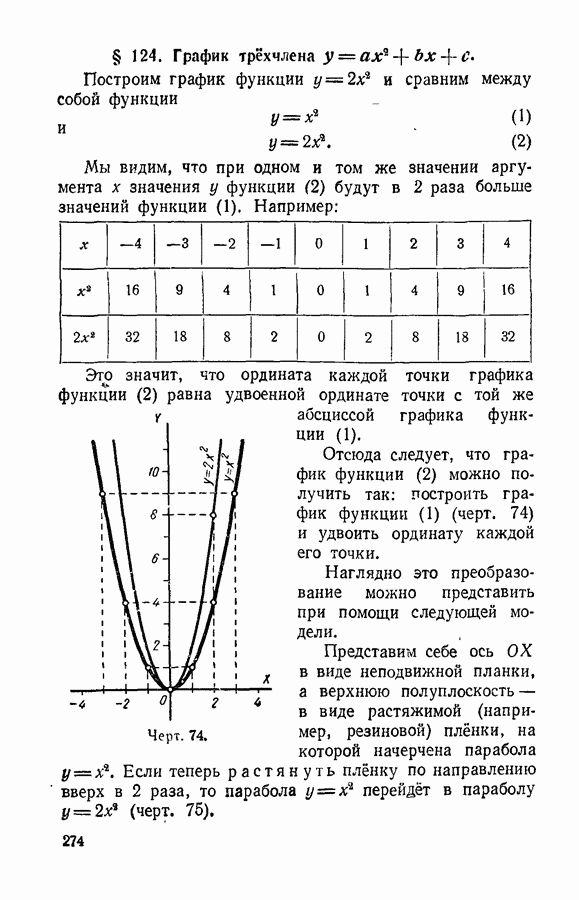
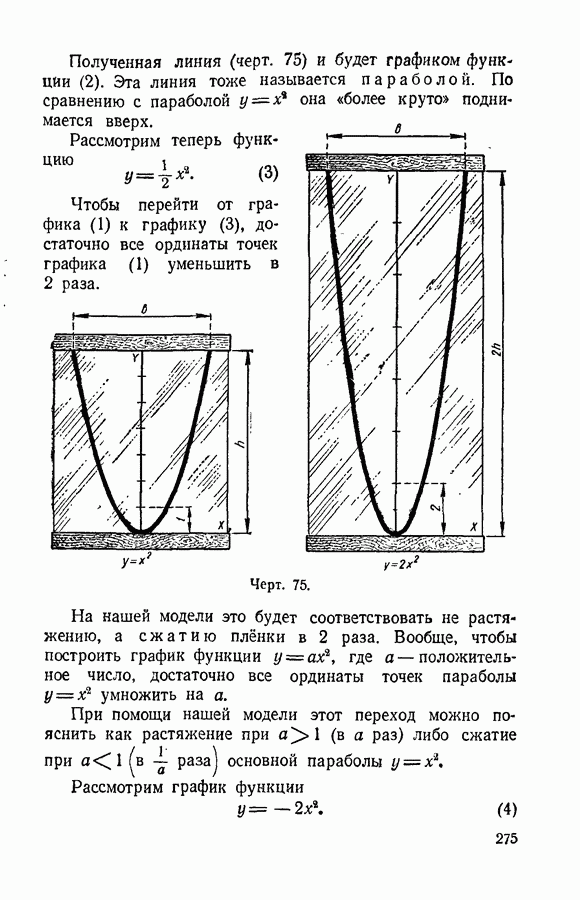
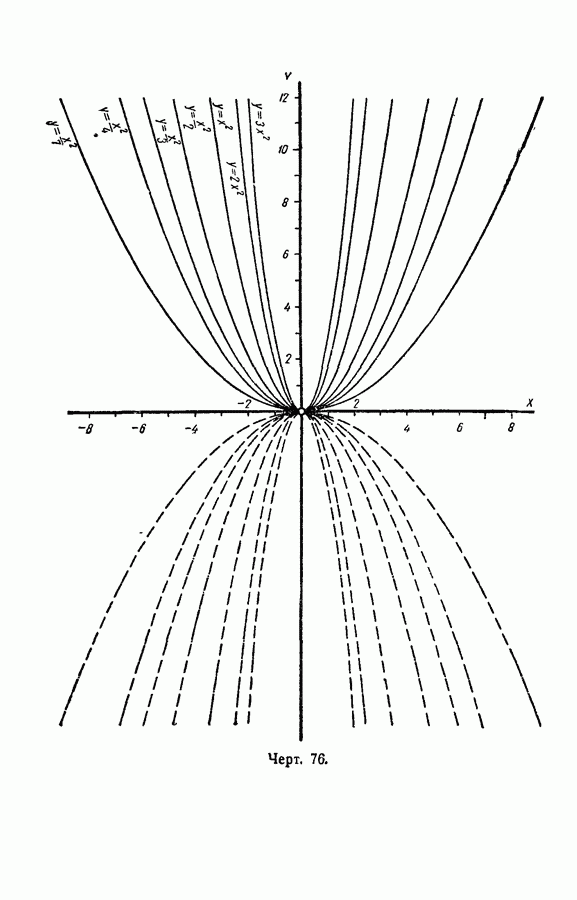
- § 124. График трехчлена y = ax^2+bx+c
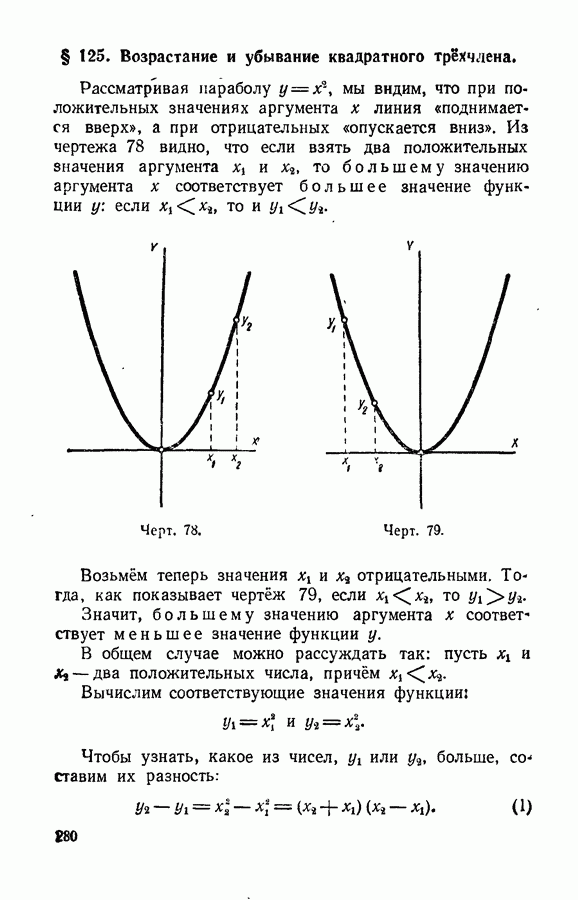
- § 125. Возрастание и убывание квадратного трёхчлена.
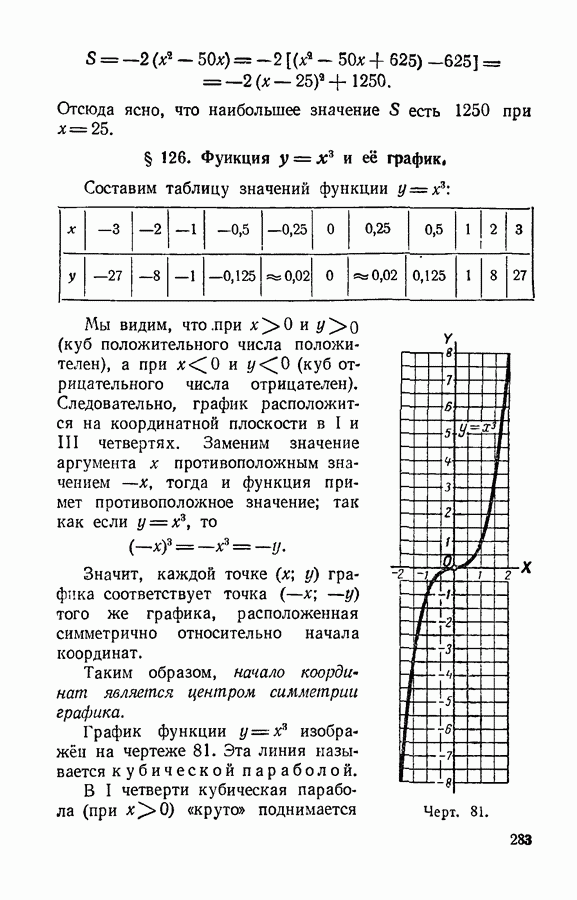
- § 126. Функция у = х^3 и её график.
- § 127. Понятие о кубическом корне.
- § 128. Приближённое извлечение кубического корня.
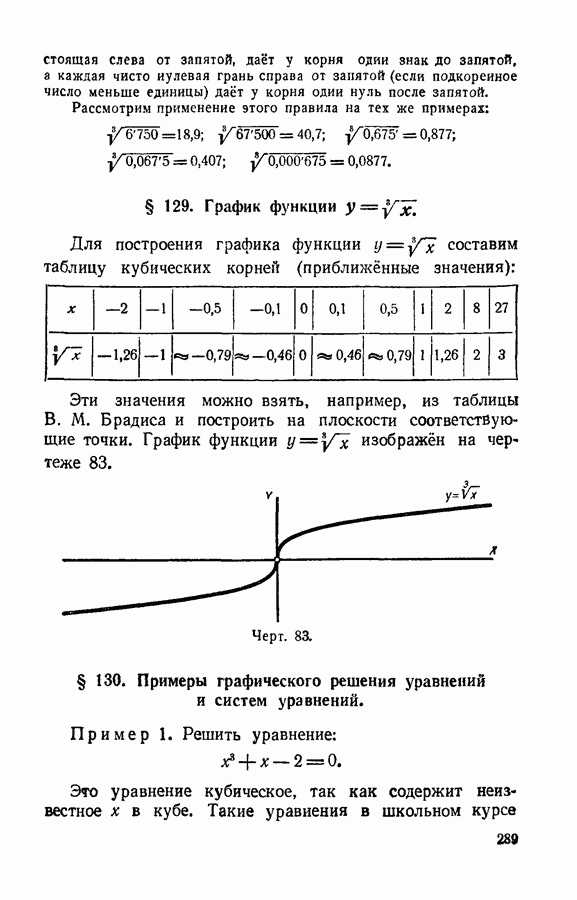
- § 129. График функции y = x^(1/3)
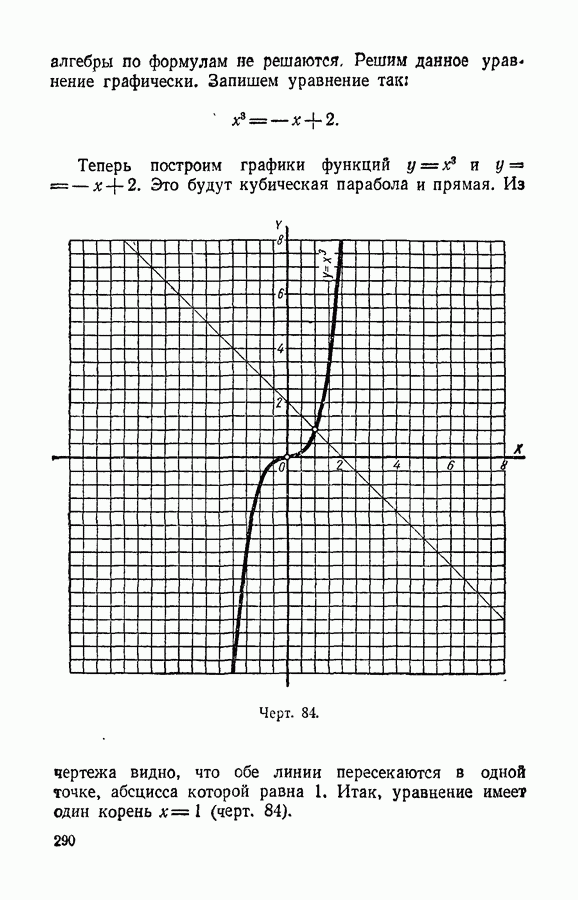
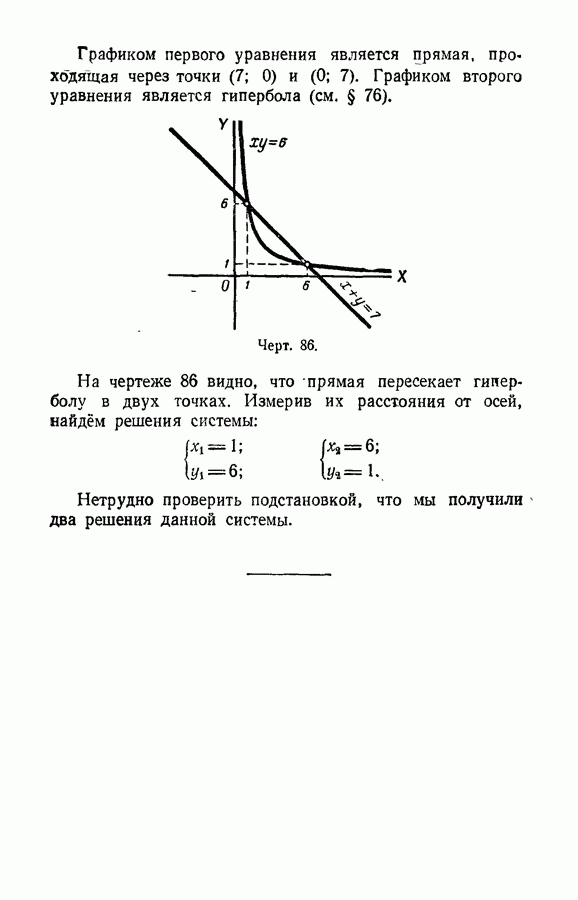
- § 130. Примеры графического решения уравнений и систем уравнений.