| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 65. Сложение дробей.
Задача 1. 5 первом классе роздали а тетрадей, во втором  тетрадей. Каждый ученик получил по
тетрадей. Каждый ученик получил по  тетрадей. Сколько было учеников в обоих классах?
тетрадей. Сколько было учеников в обоих классах?
Решим задачу двумя способами.
1-й способ.
1) Сколько было учеников в первом классе?

2) Сколько было учеников во втором классе?

3) Сколько было учеников в обоих классах?

2-й способ.
1) Сколько роздано тетрадей в обоих классах?

2) Сколько было учеников в обоих классах?

Сравнивая оба ответа, заключаем, что

Справедливость этого равенства для любых рациональных значений  можно показать так.
можно показать так.
Мы знаем свойство деления (§ 21): чтобы разделить сумму на какое-либо число, можно разделить каждое слагаемое на это число и полученные частные сложить. Значит,

Читая это равенство справа налево, получим равенство (1). Значит, сложение выполнено нами верно.
Правило. Чтобы сложить дроби с одинаковыми знаменателями, надо сложить  числители и сумму разделить на их общий знаменатель.
числители и сумму разделить на их общий знаменатель.
При сложении дробей с различными знаменателями надо предварительно привести их к общему знаменателю.
Задача 2. Школьники выехали на экскурсию в город. Они проехали до станции на лошадях а километров со скоростью  км в час, затем поездом
км в час, затем поездом  километров со скоростью, в
километров со скоростью, в  раз большей. Сколько часов школьники находились в пути?
раз большей. Сколько часов школьники находились в пути?
Решение.
1) До станции школьники ехали  часов.
часов.
2) Скорость поезда равна то  км в час.
км в час.
3) Школьники ехали поездом  часов.
часов.
4) Всего школьники пробыли в пути  часов.
часов.
Чтобы упростить полученный ответ, произведём сложение. Так как знаменатели дробей различны, то надо дроби сначала привести к общему знаменателю. Легко видеть, что общий знаменатель  Значит, числитель и знаменатель первой дроби надо умножить на
Значит, числитель и знаменатель первой дроби надо умножить на  . Получим:
. Получим:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ.
- § 2. Алгебраические выражения.
- § 3. Допустимые значения букв.
- § 4. Порядок действий.
- § 5. Основные законы сложения и умножения.
- § 6. Краткие исторические сведения.
- ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА.
- § 7. Положительные и отрицательные числа.
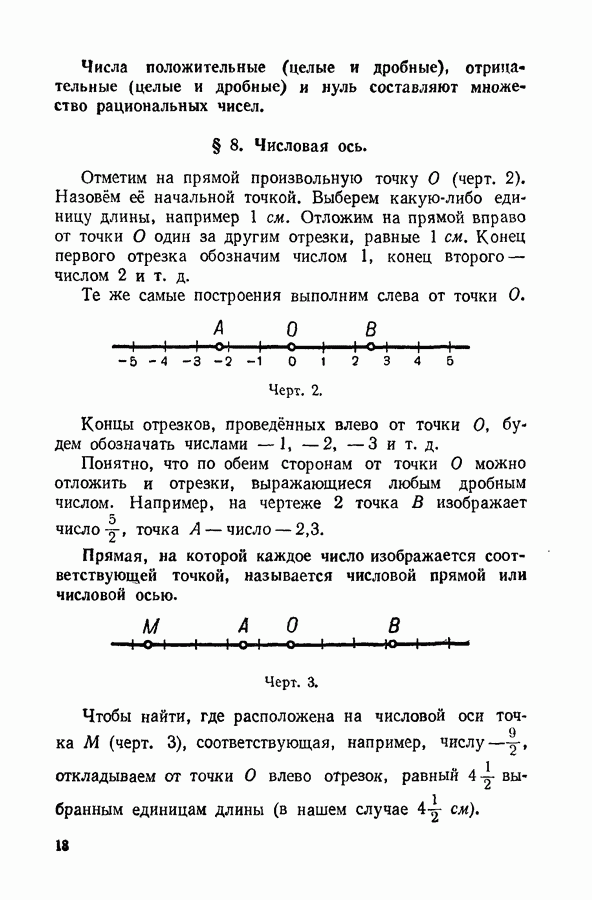
- § 8. Числовая ось.
- § 9. Противоположные числа.
- § 10. Абсолютная величина числа.
- § 11. Сравнение рациональных чисел.
- § 12. Сложение рациональных чисел.
- § 13. Сложение нескольких чисел.
- § 14. Законы сложения.
- § 15. Вычитание рациональных чисел.
- § 16. Алгебраическая сумма.
- § 17. Умножение.
- § 18. Умножение нескольких чисел.
- § 19. Законы умножения.
- § 20. Деление.
- § 21. Свойства деления.
- § 22. Возведение в степень.
- § 23. Порядок выполнения действий.
- § 24. Уравнения.
- § 25. Решение задач с помощью уравнений.
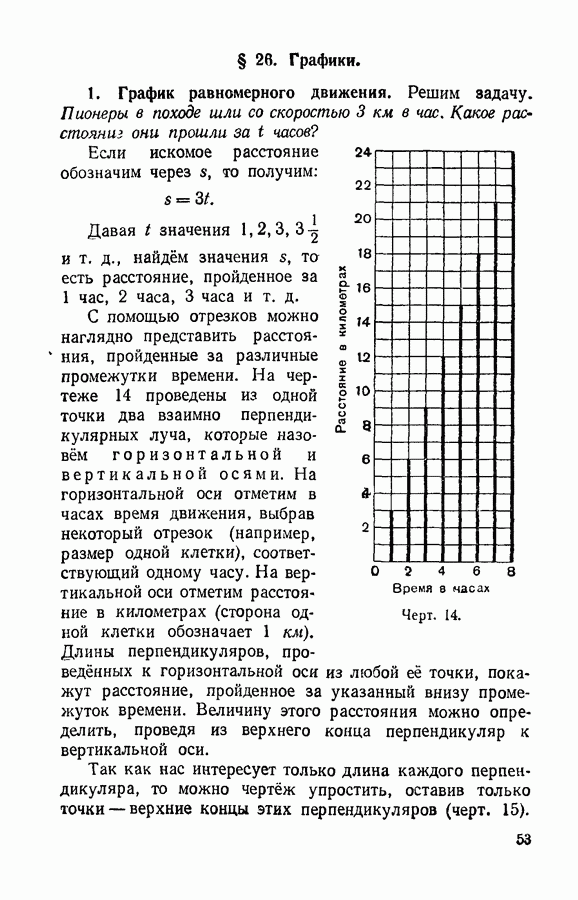
- § 26. Графики.
- § 27. Краткие исторические сведения. (Из истории отрицательных чисел.)
- ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ.
- § 28. Одночлен и многочлен.
- § 29. Тождества и тождественные преобразования.
- § 30. Коэффициент.
- § 31. Расположенные многочлены.
- § 32. Приведение подобных членов.
- § 33. Сложение одночленов и многочленов.
- § 34. Противоположные многочлены.
- § 35. Вычитание одночленов и многочленов
- § 36. Умножение одночленов.
- § 37. Умножение многочлена на одночлен.
- § 38. Умножение многочленов.
- § 39. Умножение расположенных многочленов.
- § 40. Возведение одночленов в степень.
- § 41. Формулы сокращённого умножения.
- § 42. Общие замечания о делении целых алгебраических выражений.
- § 43. Деление одночленов.
- § 44. Деление многочлена на одночлен
- § 45. Примеры решения уравнений.
- ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ.
- § 47. Равносильные уравнения.
- § 48. Два основных свойства уравнений.
- § 49. Уравнения, содержащие неизвестное в обеих частях.
- § 50. Уравнение первой степени с одним неизвестным.
- § 51. Общие указания к решению уравнений.
- § 52. Решение задач с помощью уравнений.
- § 53. Краткие исторические сведения. (Из истории уравнений.)
- ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ.
- § 54. Понятие о разложении на множители.
- § 55. Вынесение за скобки общего множителя.
- § 56. Способ группировки.
- § 57. Применение формул сокращённого умножения.
- § 58. Применение нескольких способов.
- § 59. Деление многочленов при помощи разложения на множители.
- ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ.
- § 60. Понятие об алгебраической дроби.
- § 61. Основное свойство дроби и сокращение дробей.
- § 62. Перемена знака у членов дроби.
- § 63. Целая отрицательная и нулевая степени числа.
- § 64. Приведение дробей к общему знаменателю.
- § 65. Сложение дробей.
- § 66. Вычитание дробей.
- § 67. Умножение дробей.
- § 68. Деление дробей.
- § 69. Возведение дроби в натуральную степень.
- § 70. Дробные уравнения.
- § 71. Примеры решения уравнений с буквенными коэффициентами.
- ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.
- § 72. Координаты точки на плоскости.
- § 73. Прямо пропорциональная зависимость.
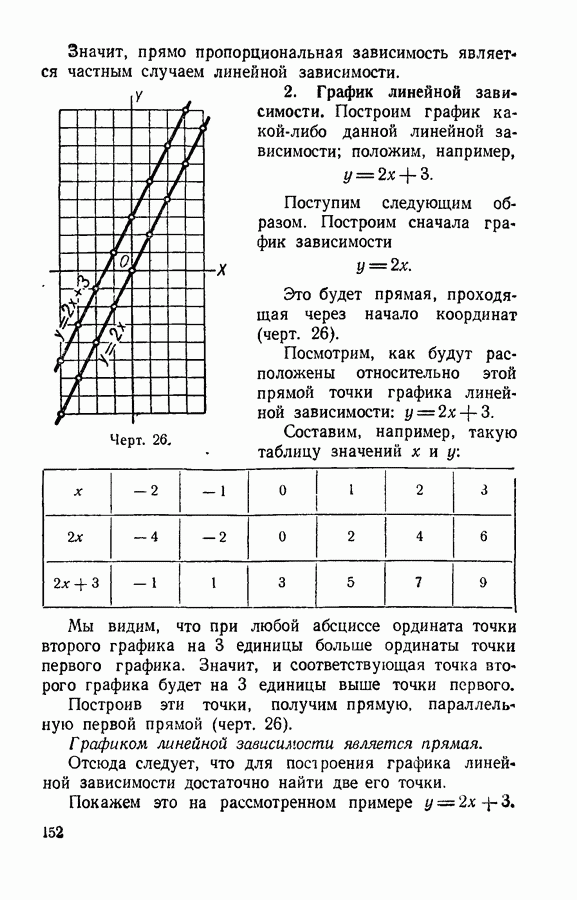
- § 74. График прямо пропорциональной зависимости.
- § 75. Линейная зависимость.
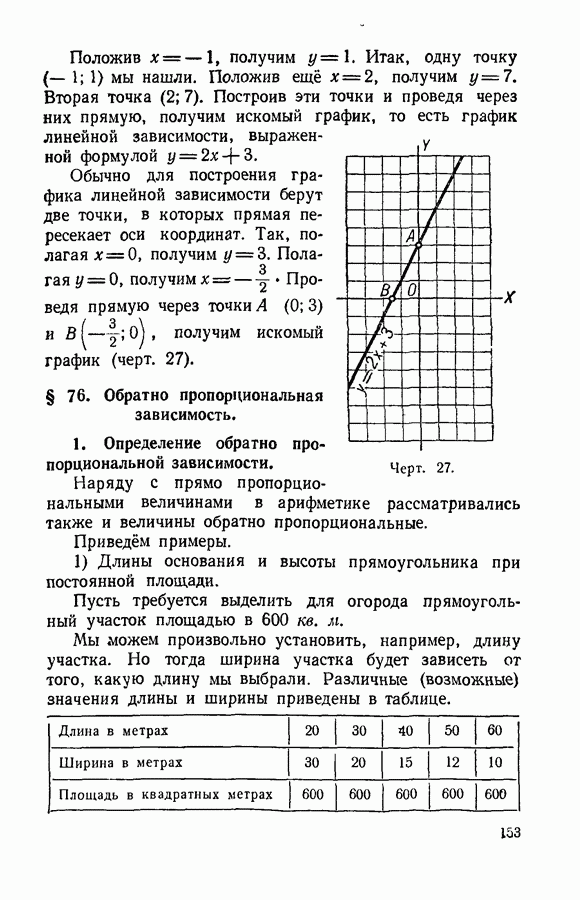
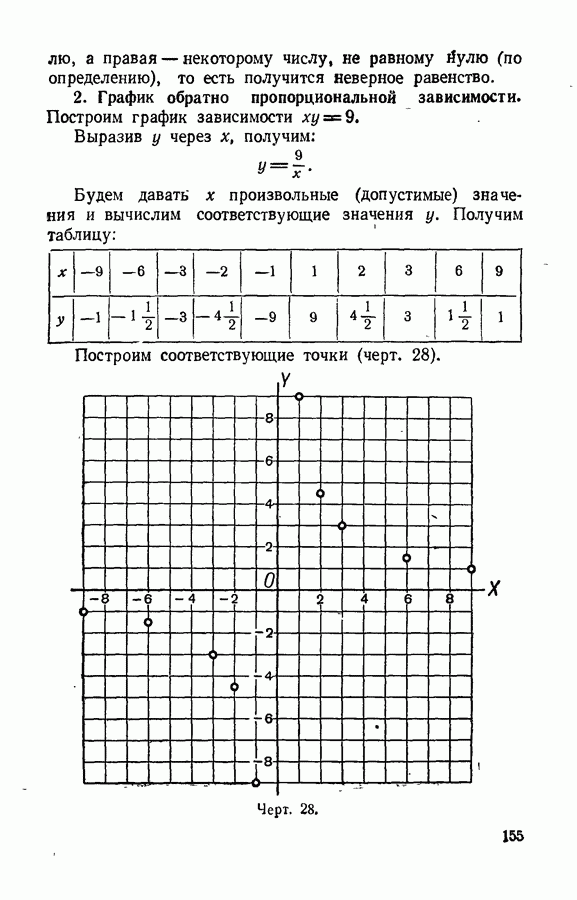
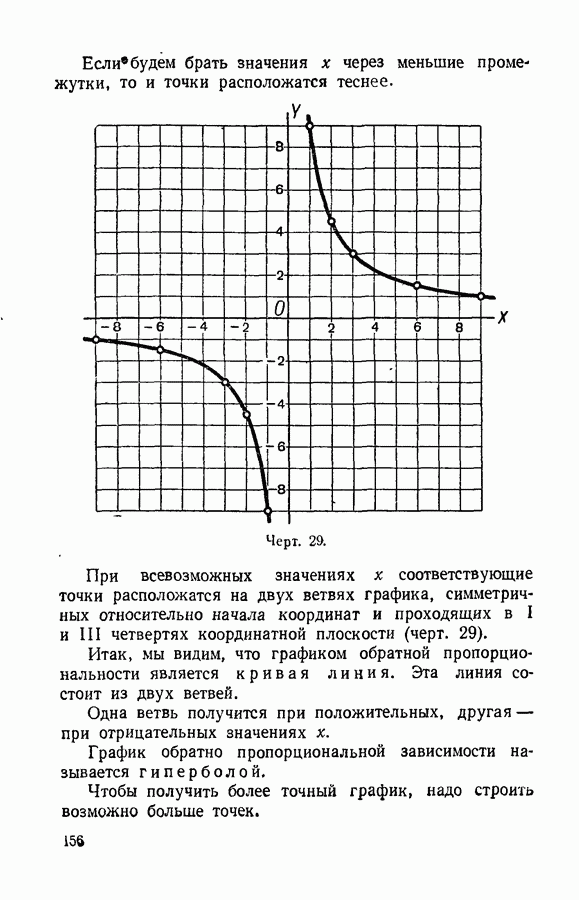
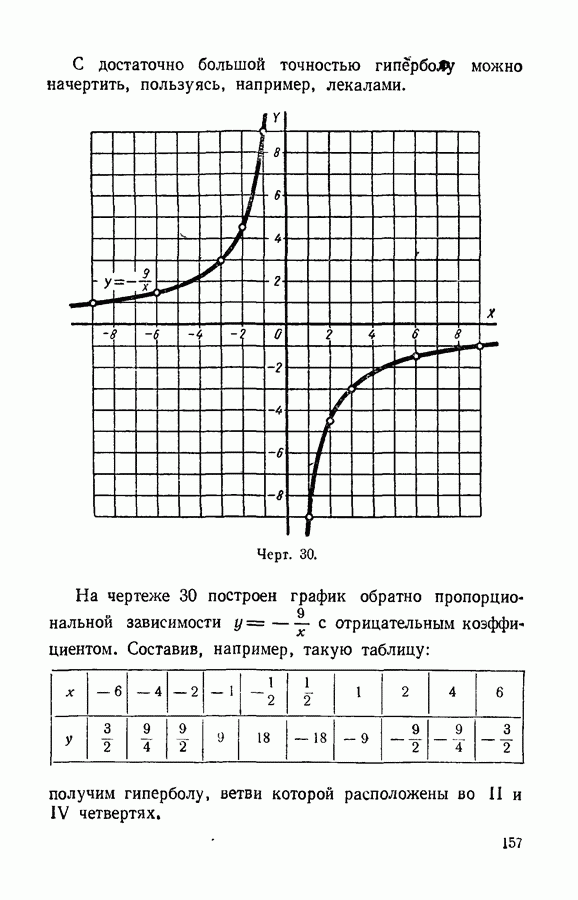
- § 76. Обратно пропорциональная зависимость.
- ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ.
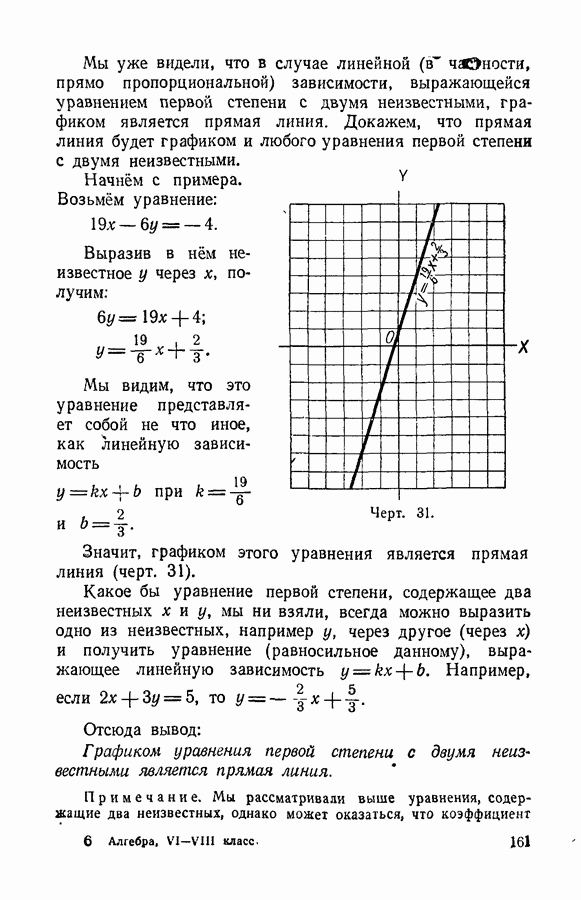
- § 77. Уравнение первой степени с двумя неизвестными.
- § 78. Система двух уравнений первой степени с двумя неизвестными.
- § 79. Равносильные системы.
- § 80. Решение систем уравнений.
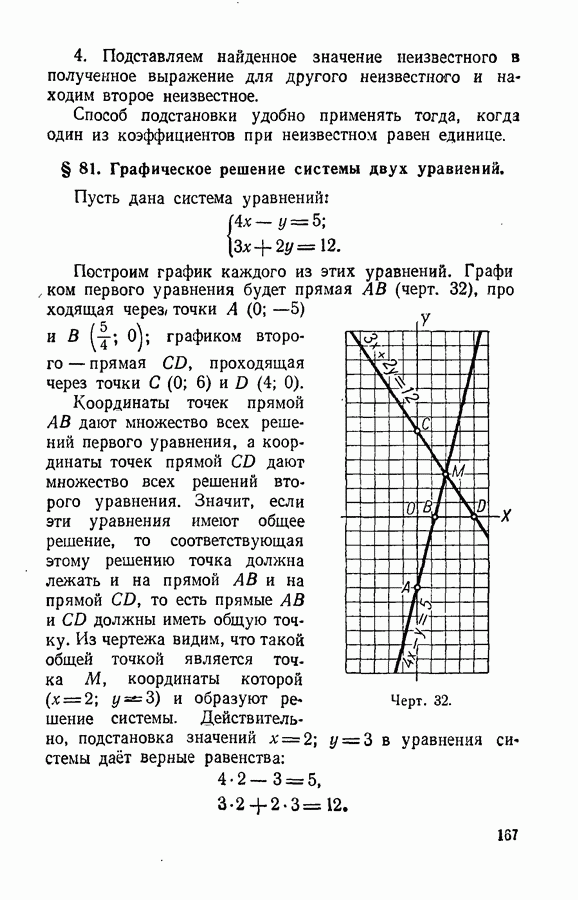
- § 81. Графическое решение системы двух уравнений.
- § 82. Решение задач.
- § 83. Уравнение с тремя неизвестными.
- § 84. Система трёх уравнений с тремя неизвестными.
- ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА.
- § 85. Равномерные и неравномерные шкалы.
- § 86. Устройство счётной (логарифмической) линейки.
- § 87. Основная шкала.
- § 88. Умножение и деление с помощью счётной линейки.
- ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ.
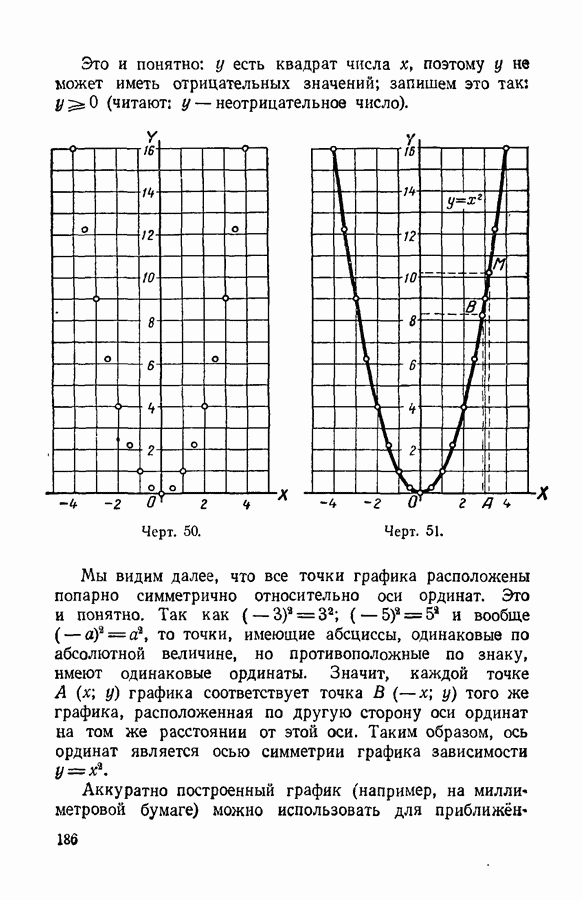
- § 89. Построение графика зависимости y = x^2
- § 90. Вычисление квадратов чисел по таблицам и при помощи счётной линейки.
- § 91. Понятие об извлечении корня. Решим две задачи.
- § 92. Арифметический корень.
- § 93. Приближённый квадратный корень из положительного числа.
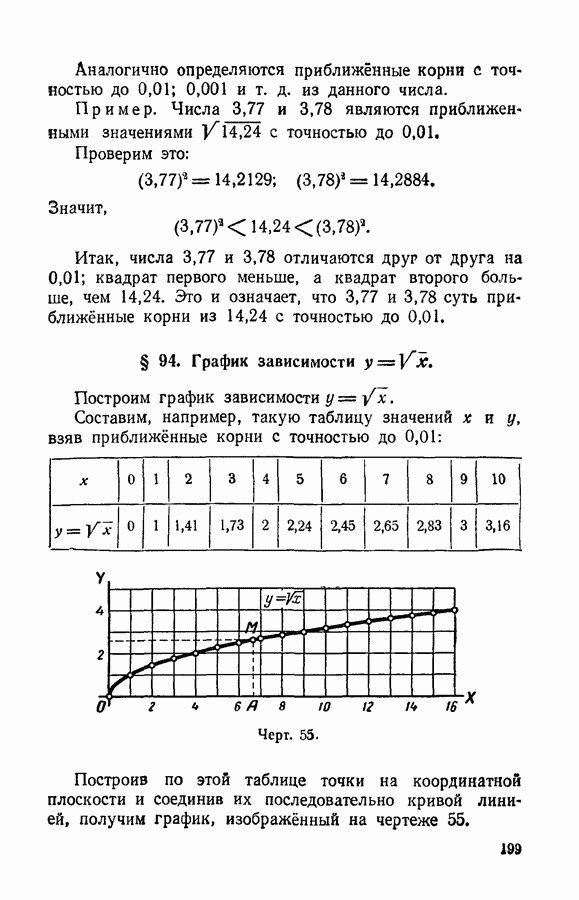
- § 94. График зависимости y = sqrt(х).
- § 95. Извлечение квадратного корня из целых чисел.
- § 96. Извлечение корня с точностью до 0,1; 0,01 и т. д.
- § 97. Квадратный корень из произведения, дроби и степени.
- § 98. Простейшие преобразования.
- § 99. Извлечение квадратного корня по таблицам и при помощи счётной линейки.
- § 100. Краткие исторические сведения.
- ГЛАВА ОДИННАДЦАТАЯ. КВАДРАТНЫЕ УРАВНЕНИЯ.
- § 101. Квадратные уравнения.
- § 102. Уравнение вида ax^2+bx=0
- § 103. Уравнение вида ax^2+c=0
- § 104. Приведённое квадратное уравнение.
- § 105. Квадратное уравнение общего вида.
- § 106. Дискриминант.
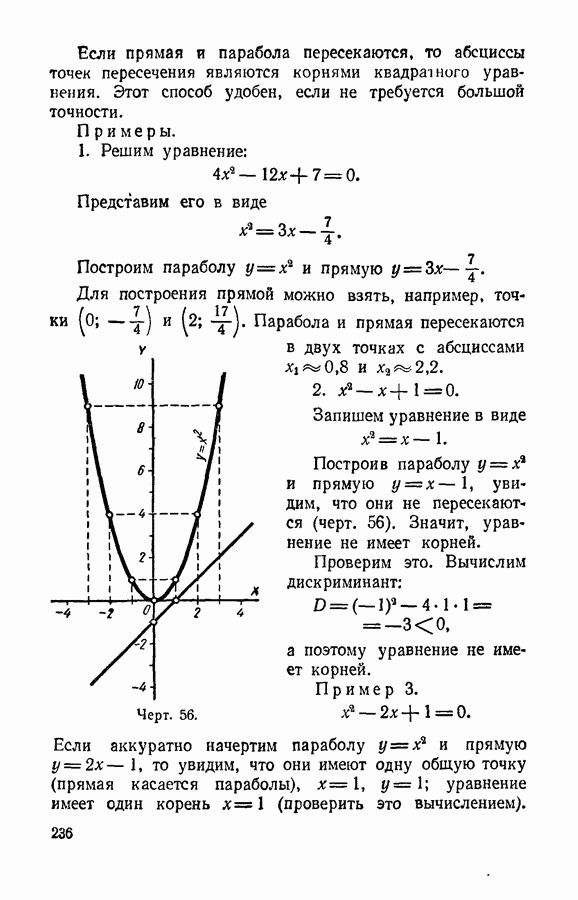
- § 107. Графическое решение квадратного уравнения.
- § 108. Решение задач, приводящих к квадратным уравнениям.
- § 109. Теорема Виета.
- § 110. Исследование корней квадратного уравнения.
- § 111. Разложение квадратного трёхчлена на множители.
- § 112. Системы двух уравнений, из которых одно второй и одно первой степени.
- § 113. Краткие исторические сведения.
- ГЛАВА ДВЕНАДЦАТАЯ. ФУНКЦИИ И ГРАФИКИ.
- § 114. Переменные величины.
- § 115. Понятие о функциональной зависимости.
- § 116. Аргумент и функция.
- § 117. Способы задания функции.
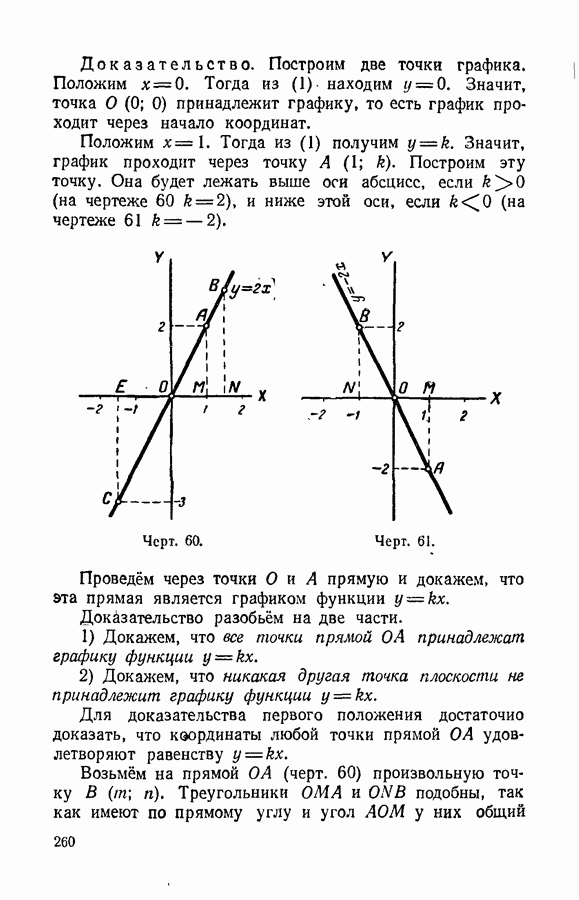
- § 118. Функция y = kx.
- § 119. Линейная функция.
- § 120. Трехчлен второй степени.
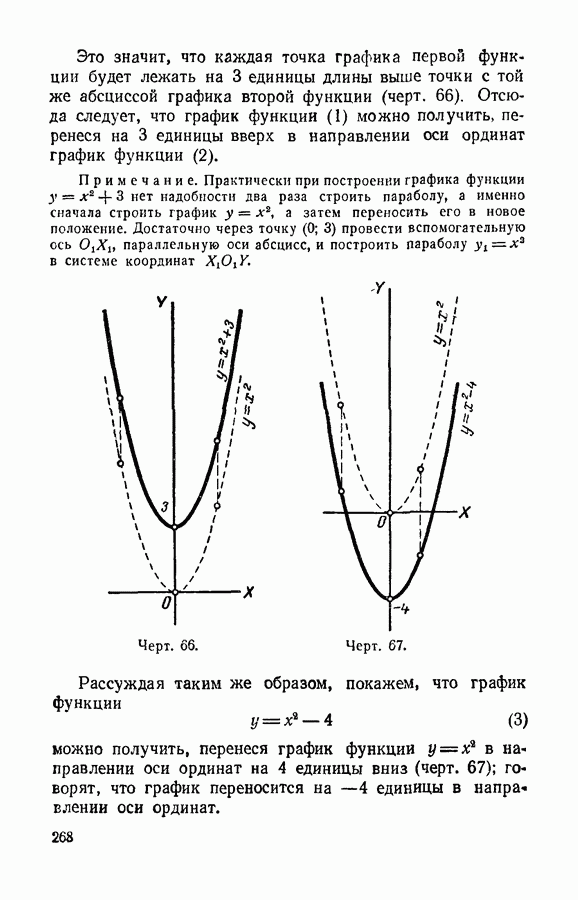
- § 121. График функции y=x^2+n
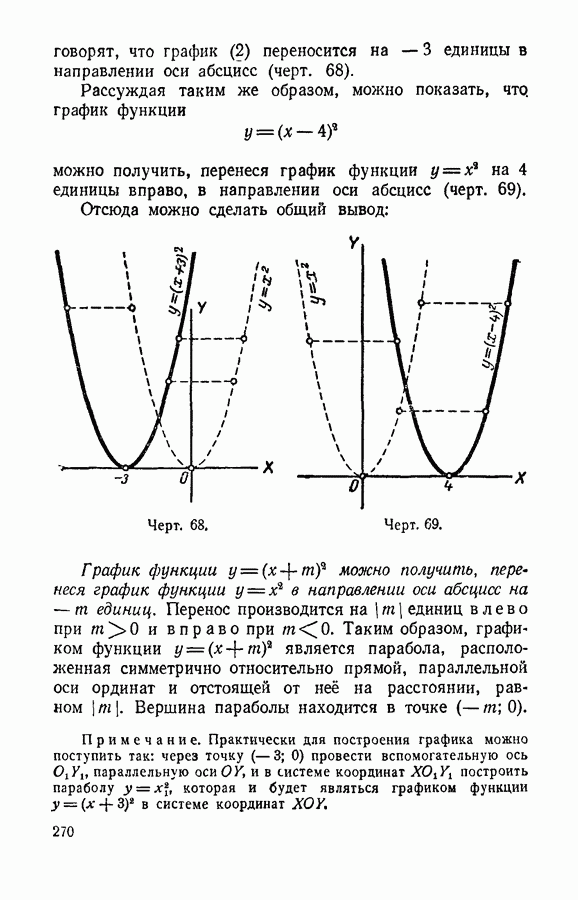
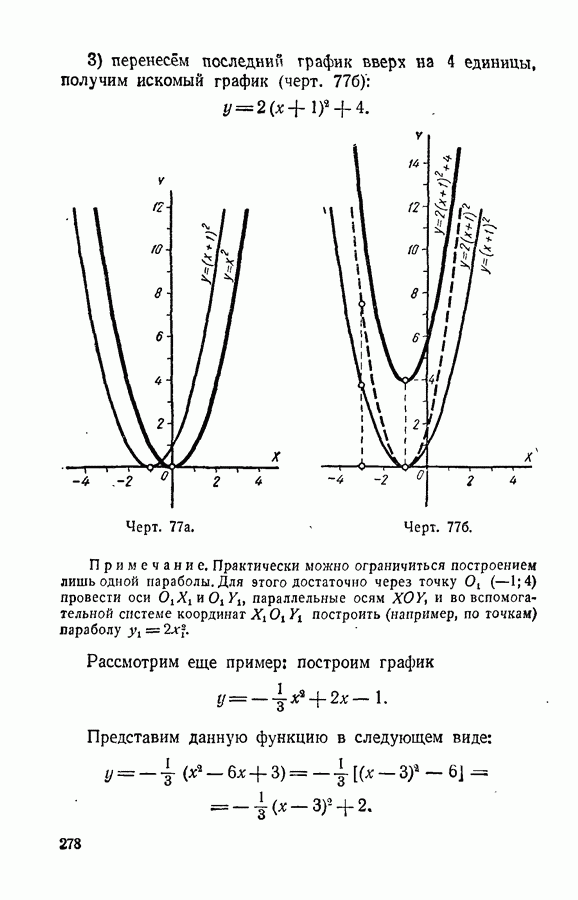
- § 122. График функции y = (x+m)^2
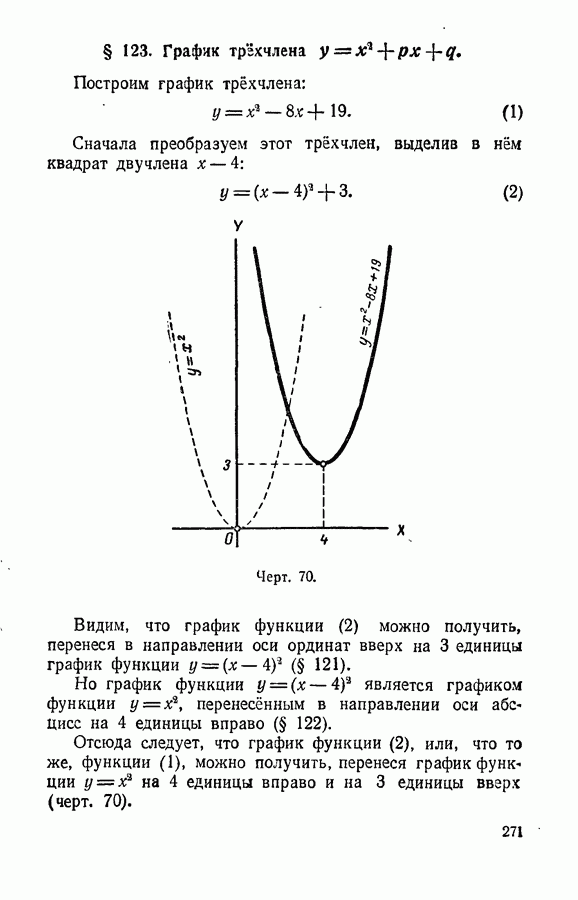
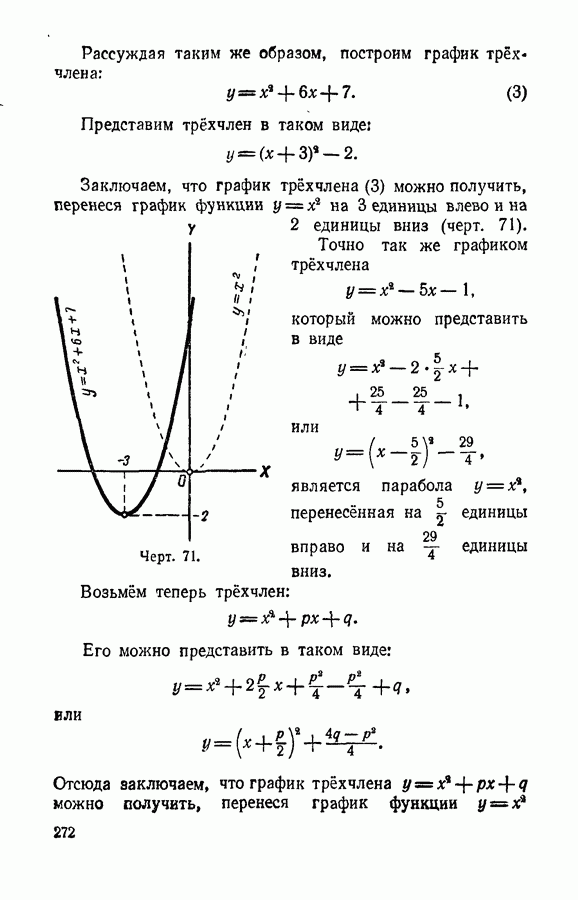
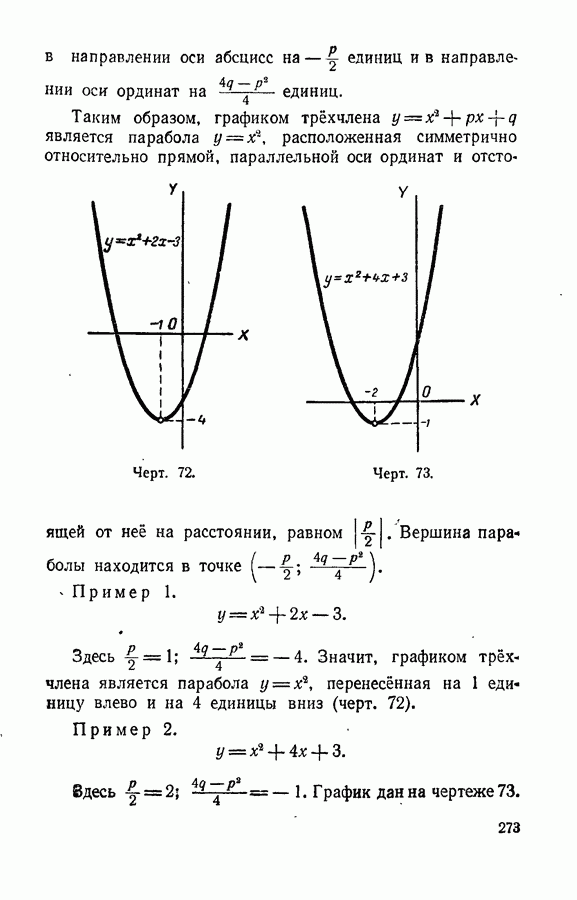
- § 123. График трехчлена y = x^2+px+q
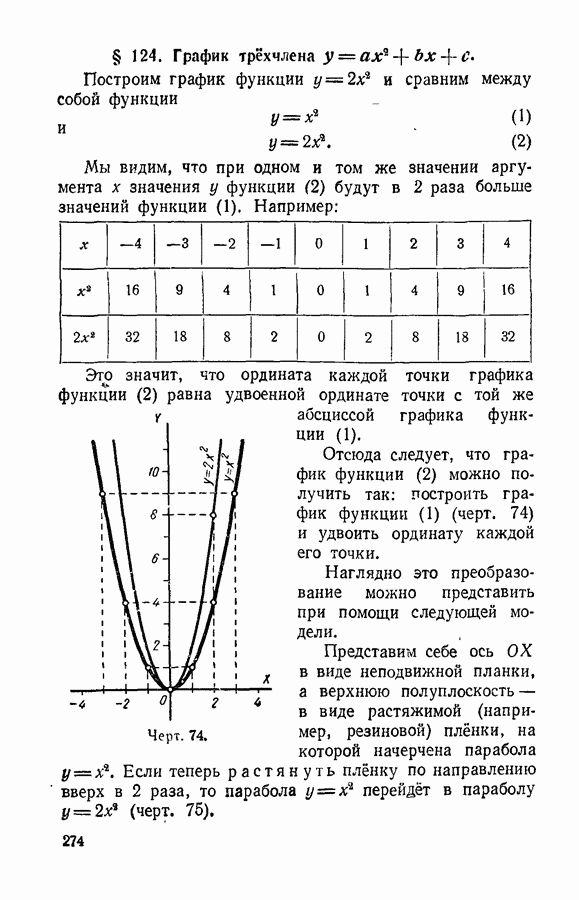
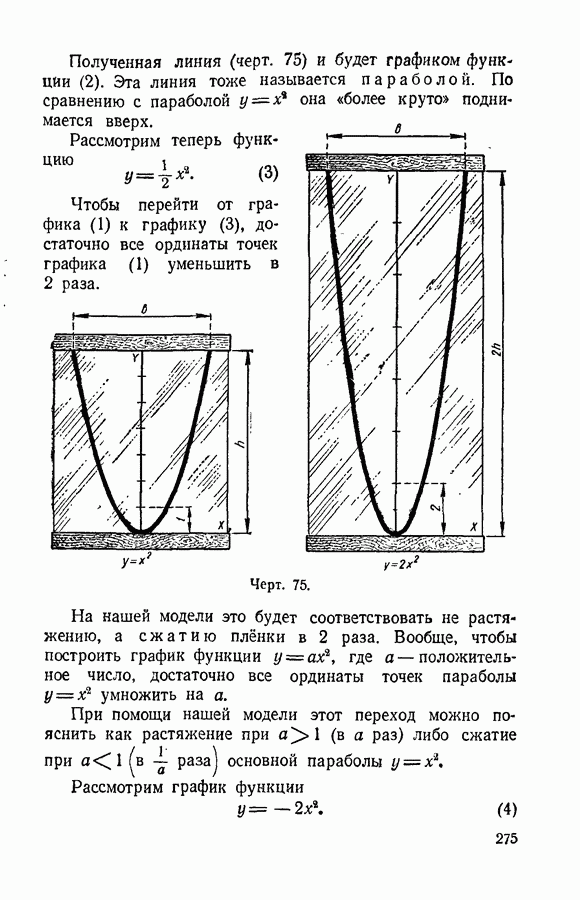
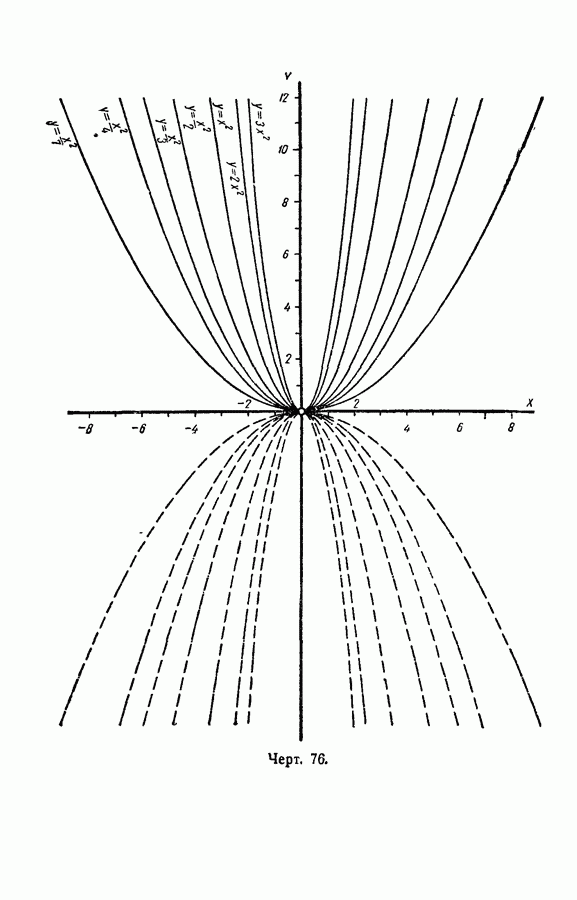
- § 124. График трехчлена y = ax^2+bx+c
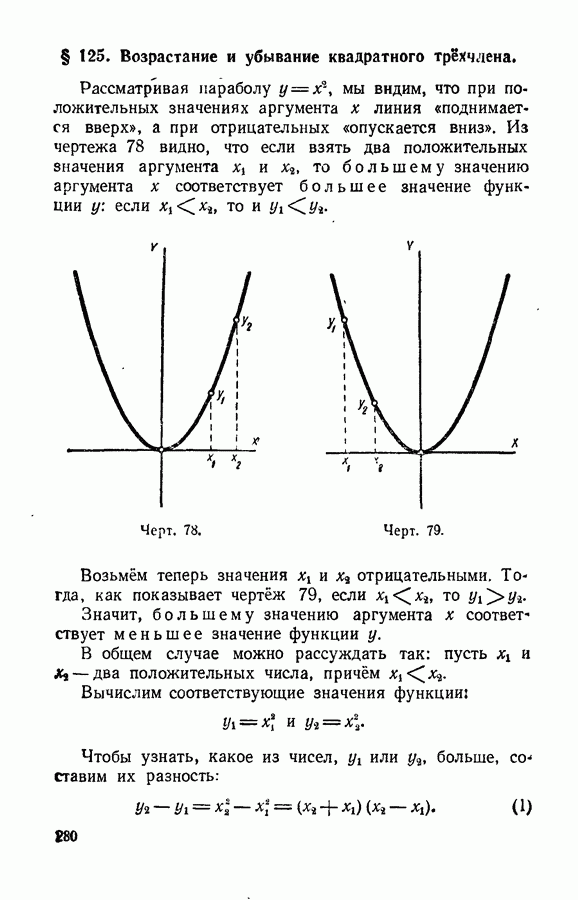
- § 125. Возрастание и убывание квадратного трёхчлена.
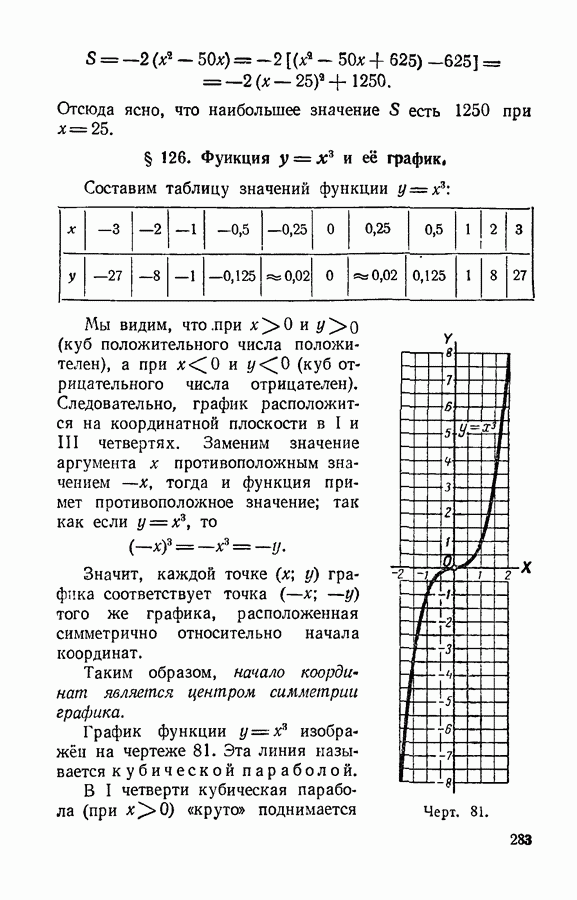
- § 126. Функция у = х^3 и её график.
- § 127. Понятие о кубическом корне.
- § 128. Приближённое извлечение кубического корня.
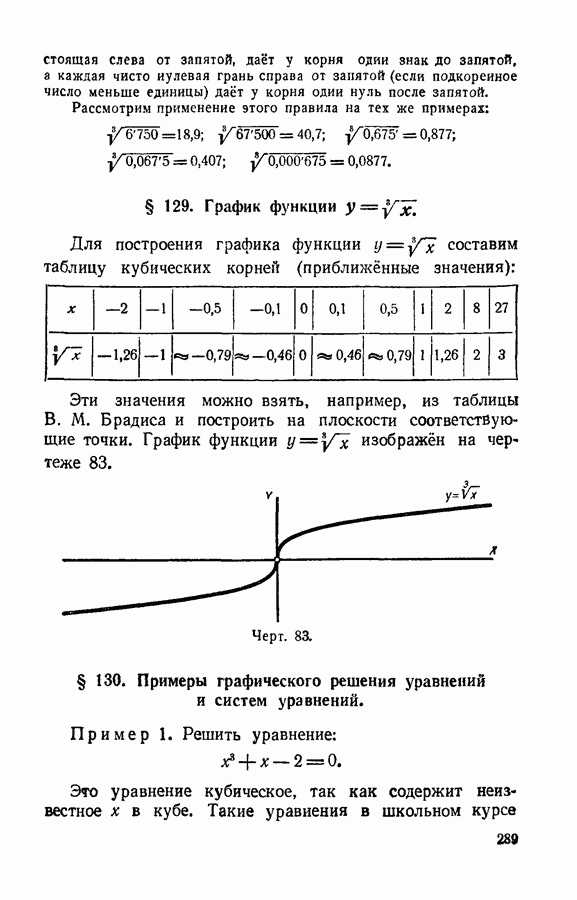
- § 129. График функции y = x^(1/3)
- § 130. Примеры графического решения уравнений и систем уравнений.