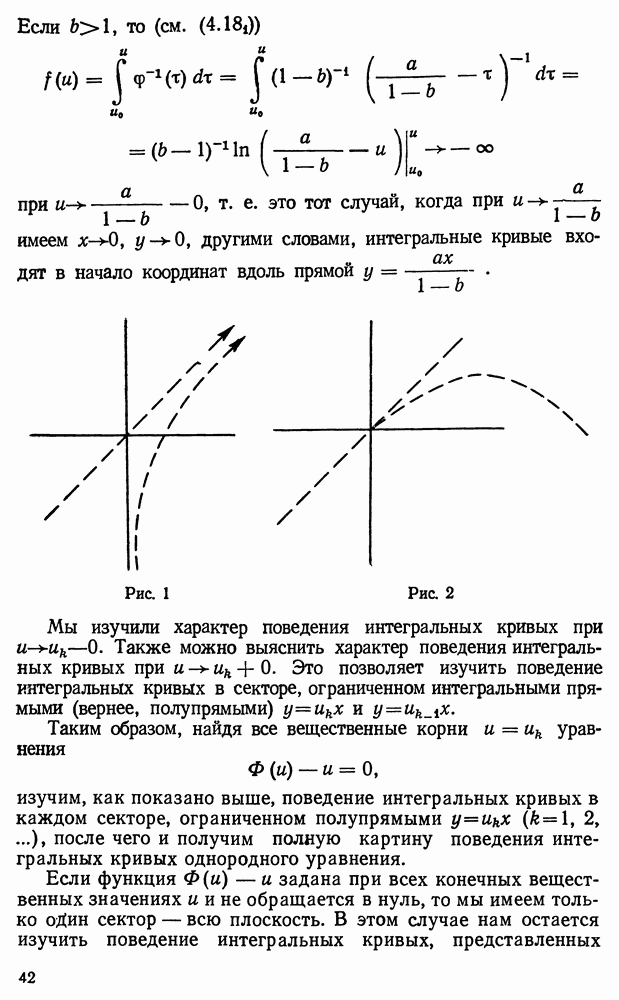
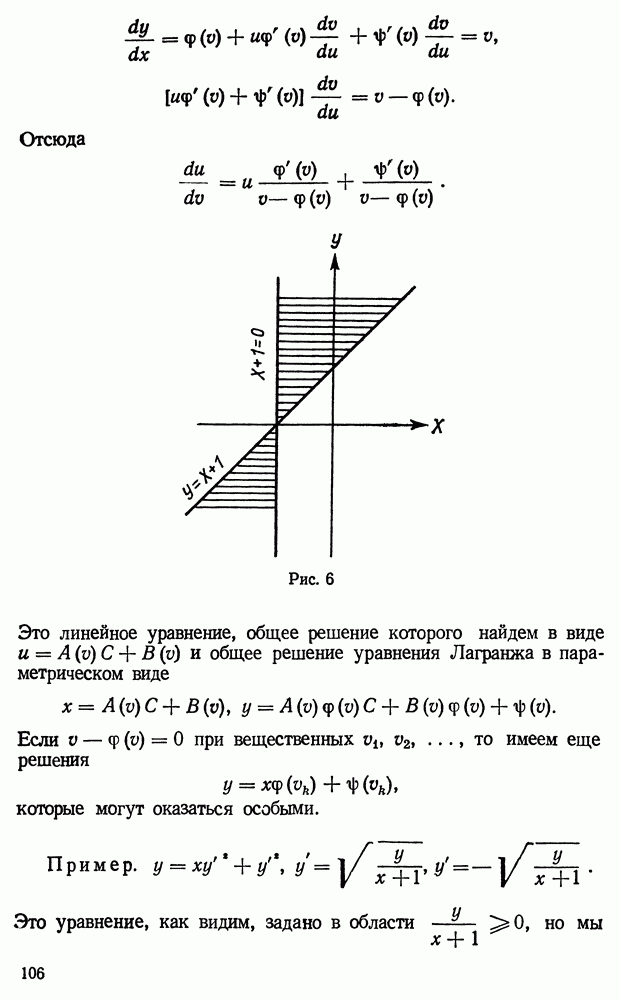
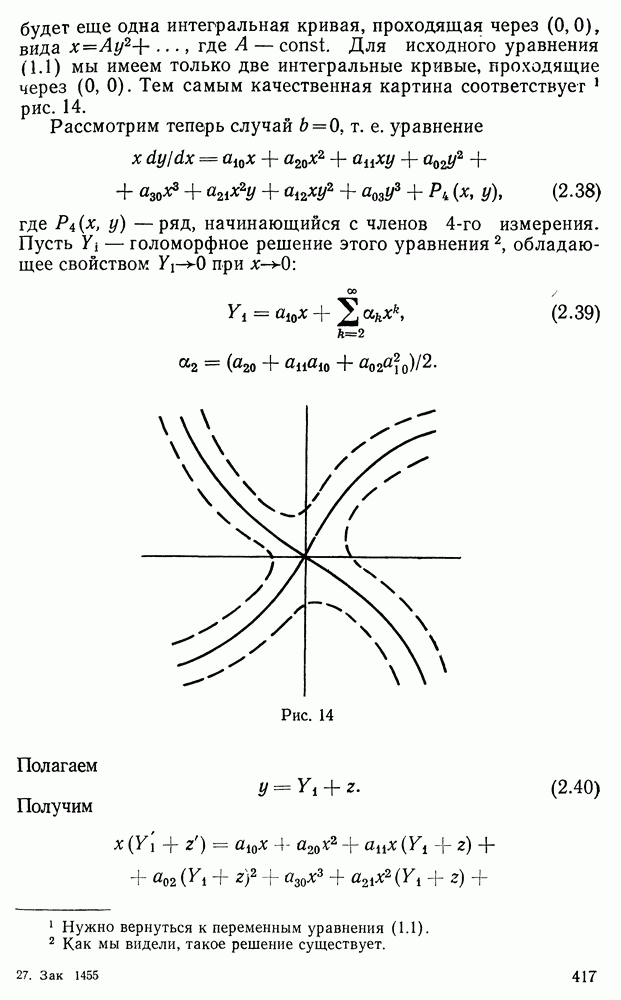
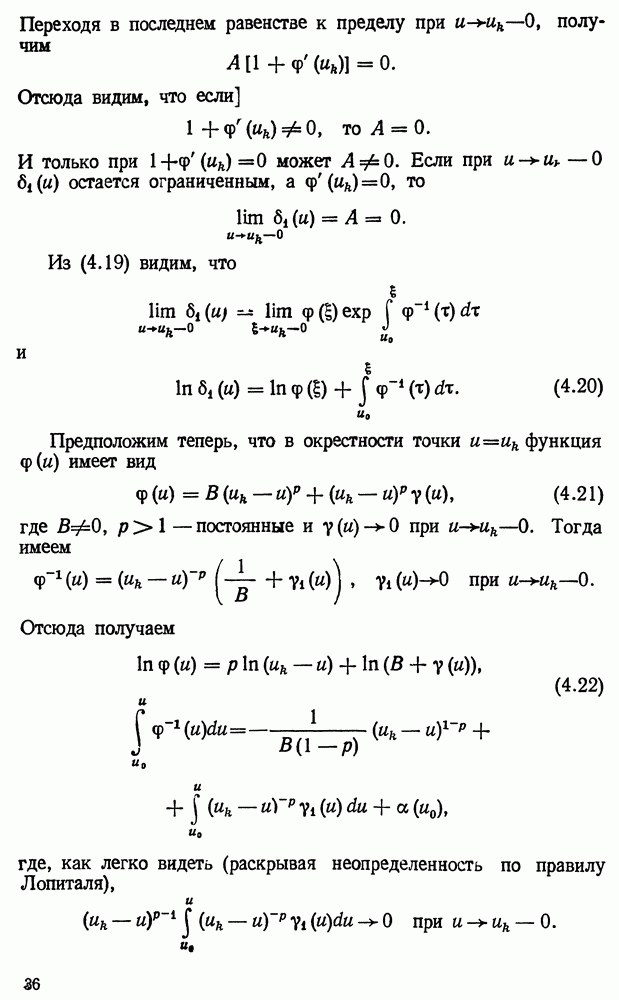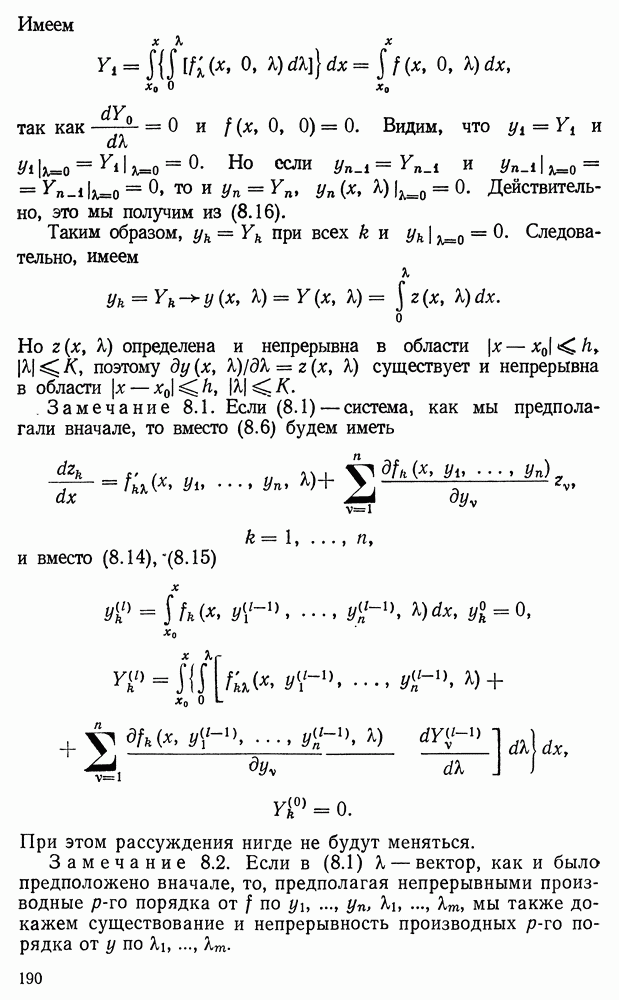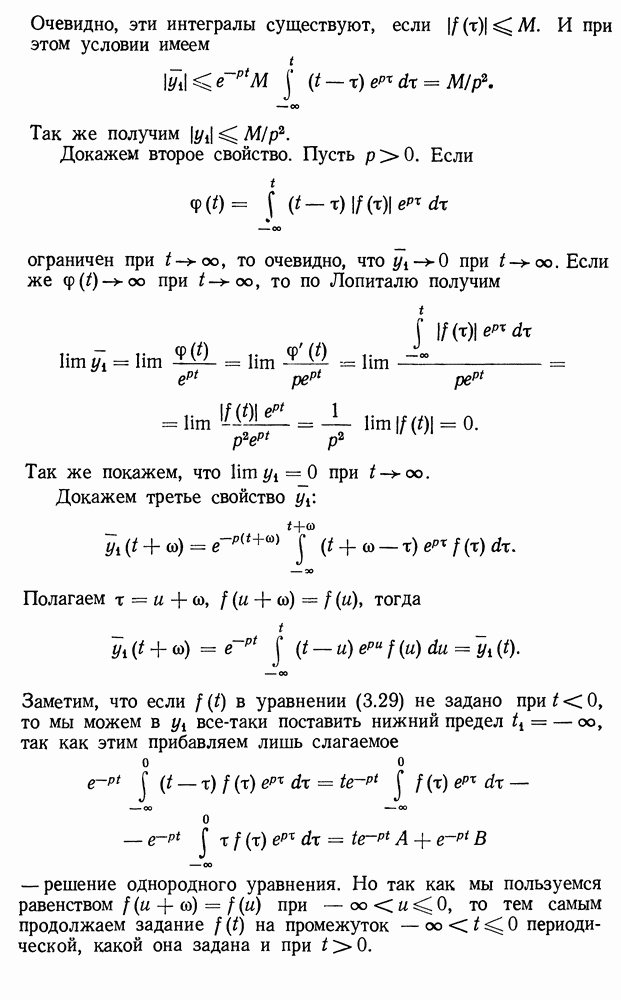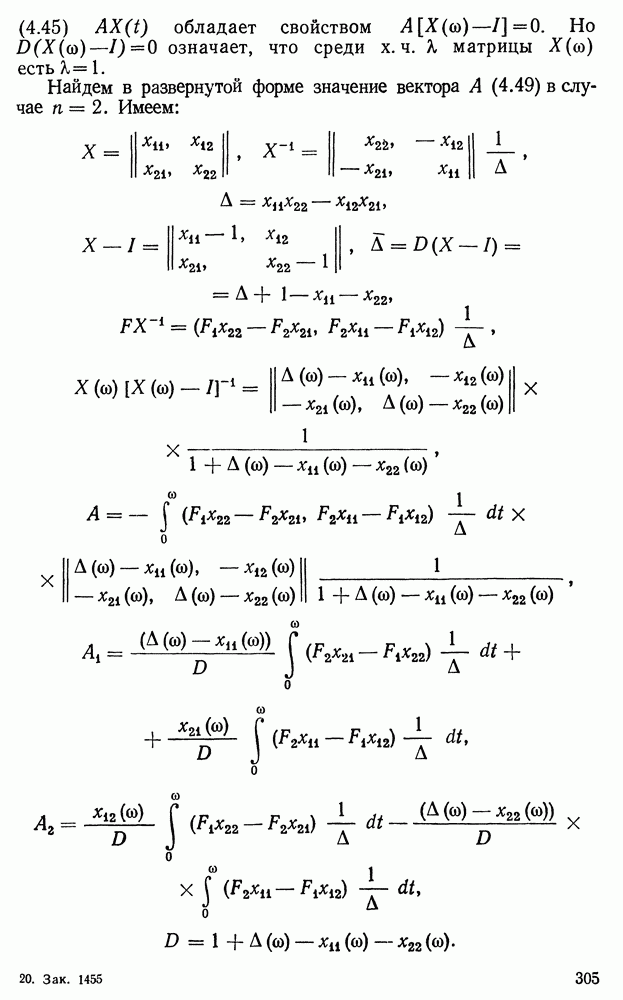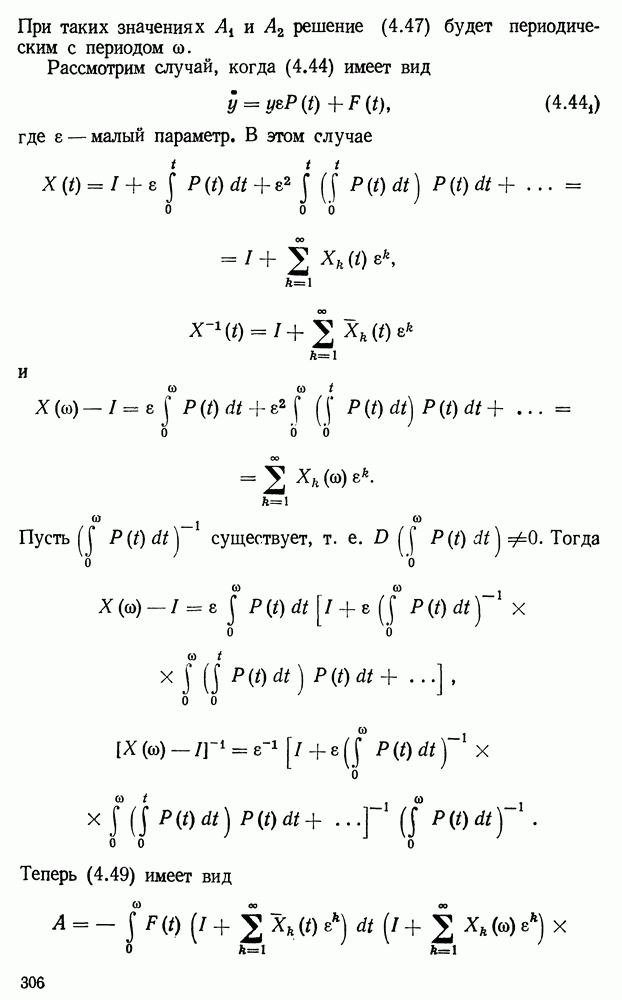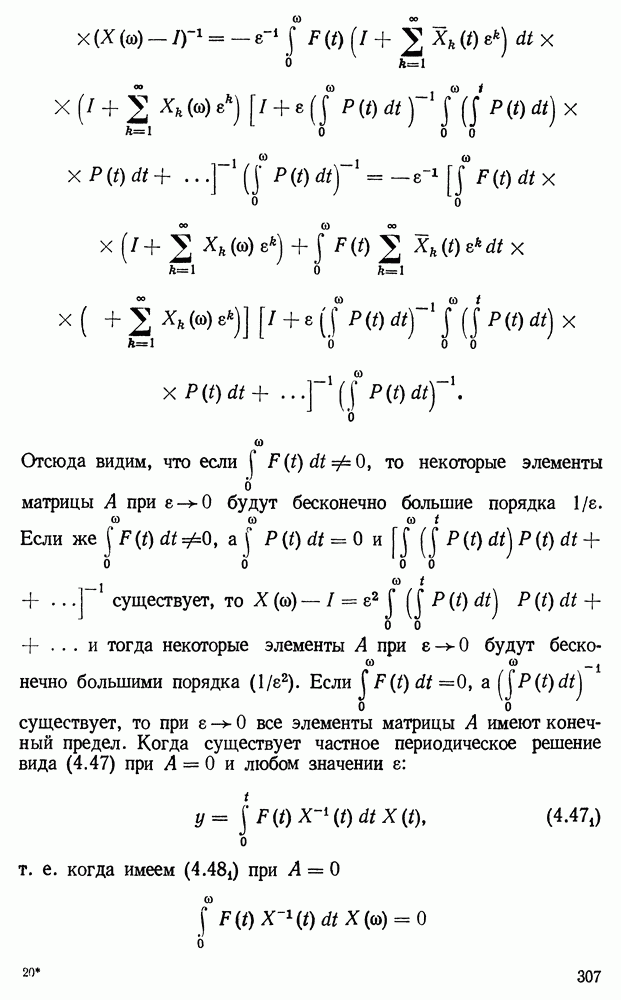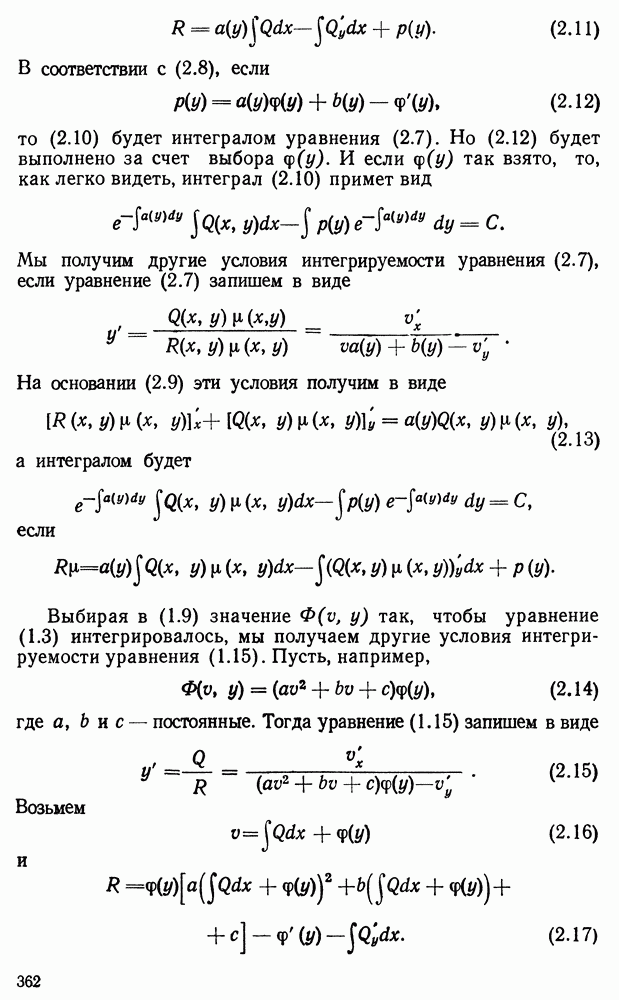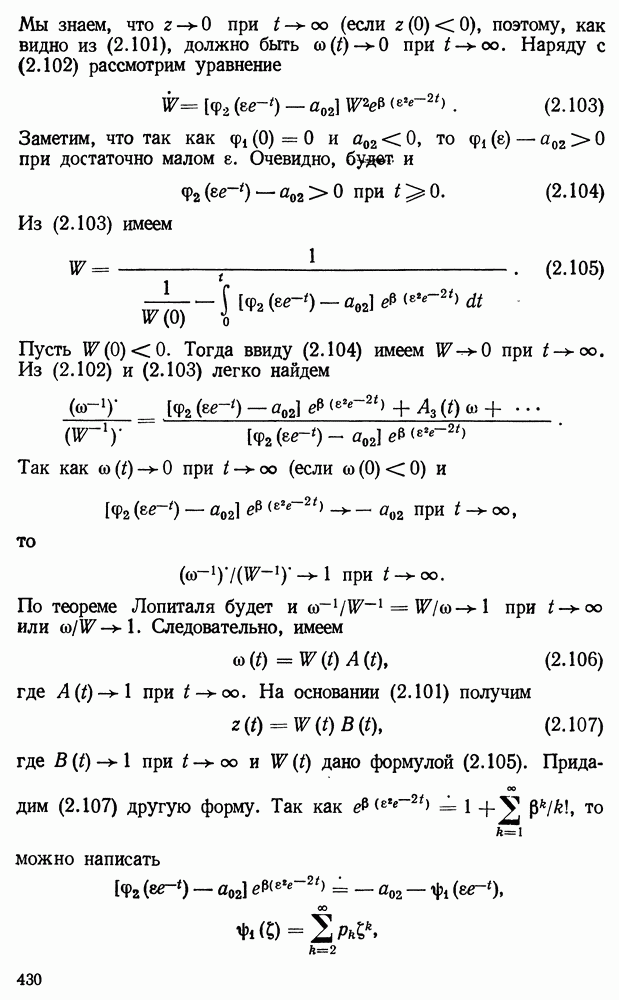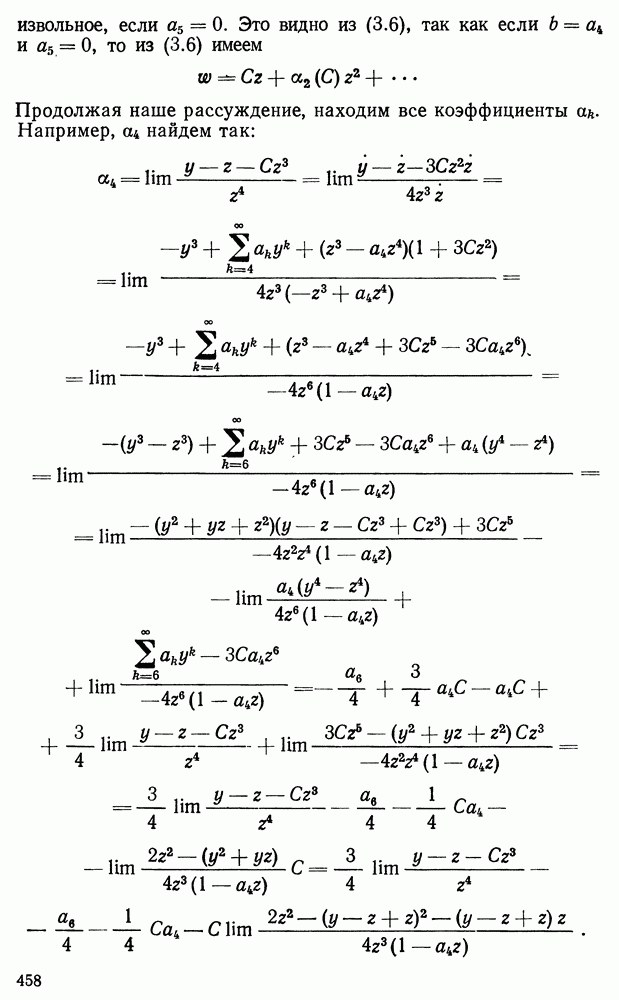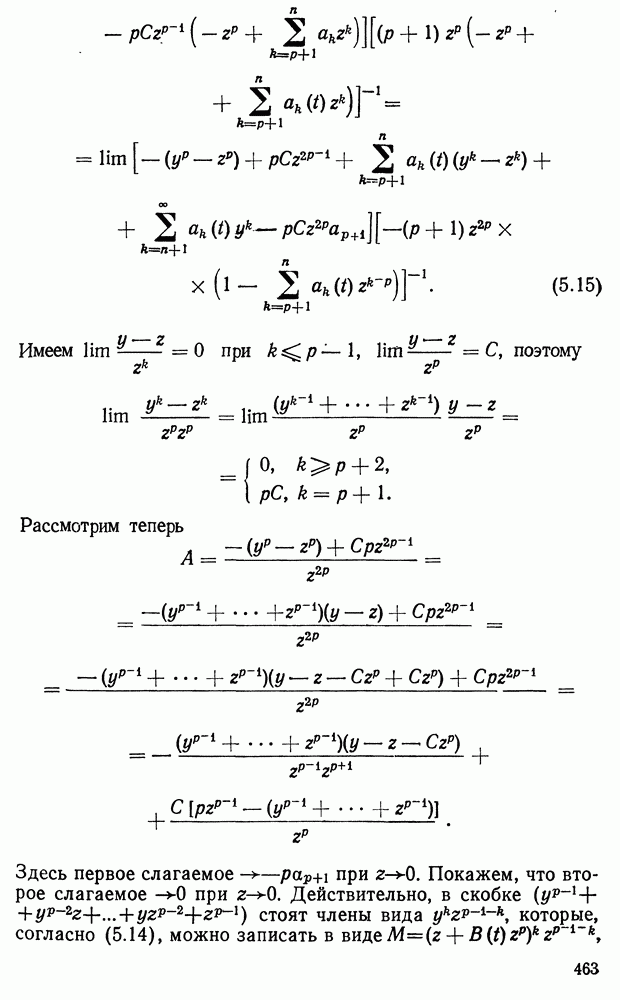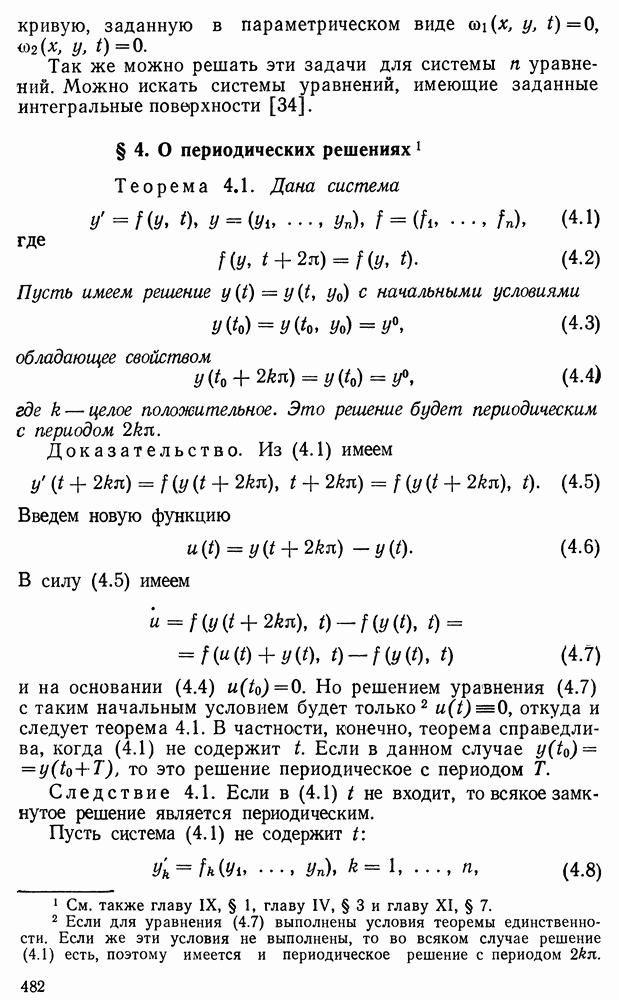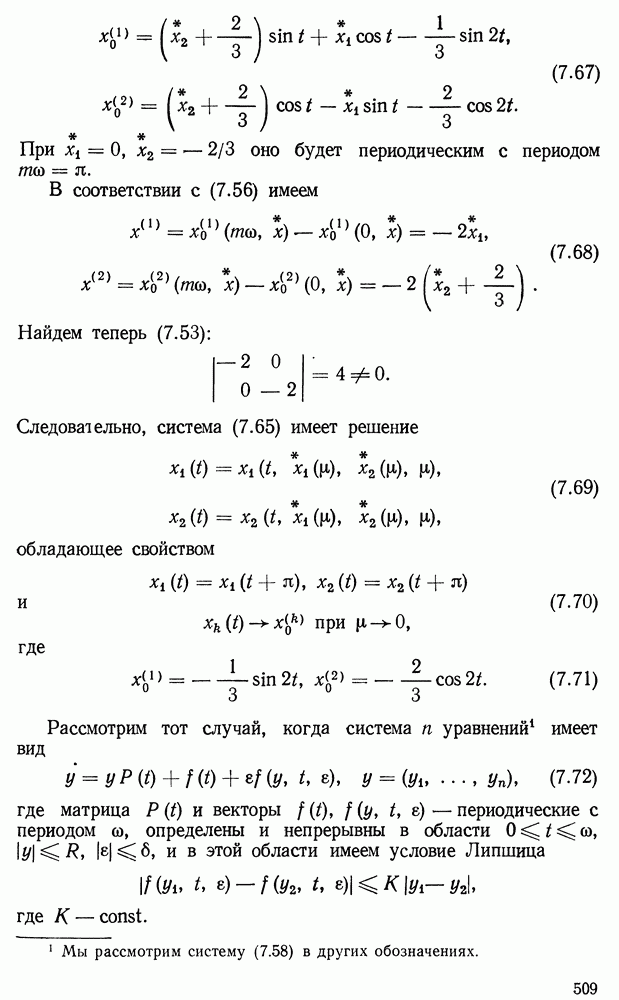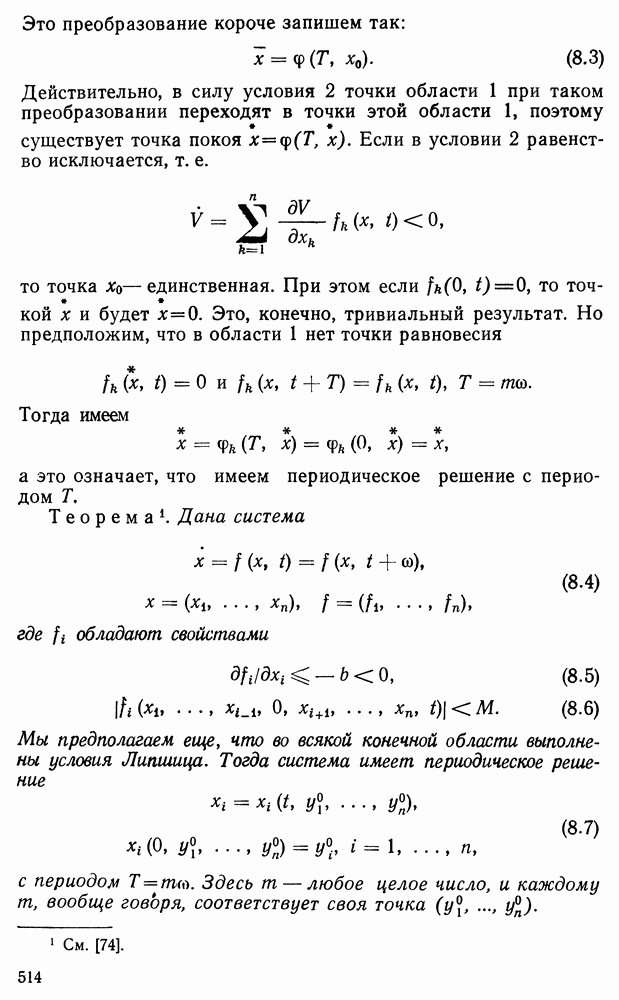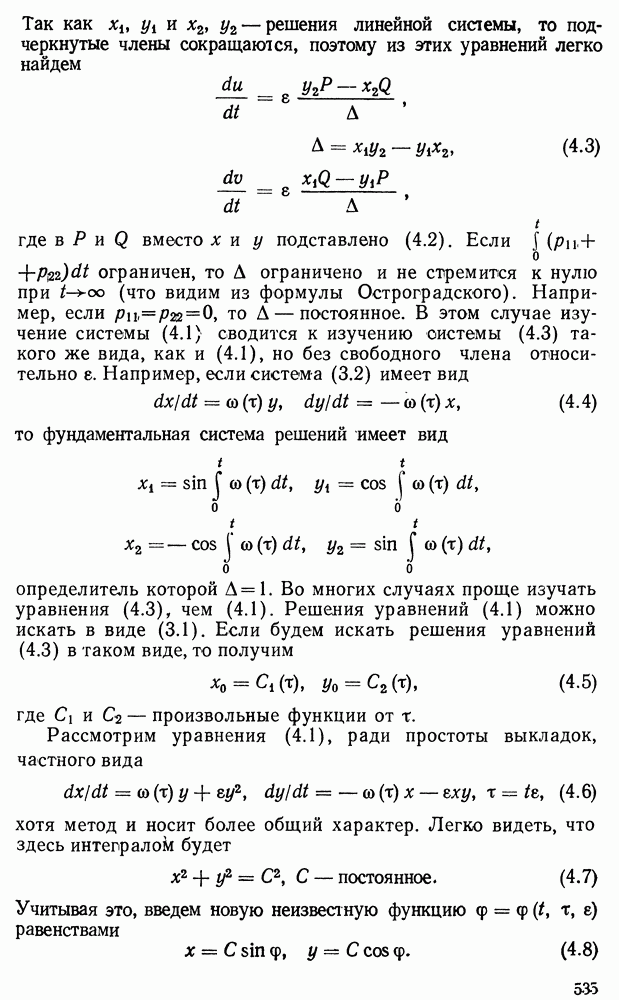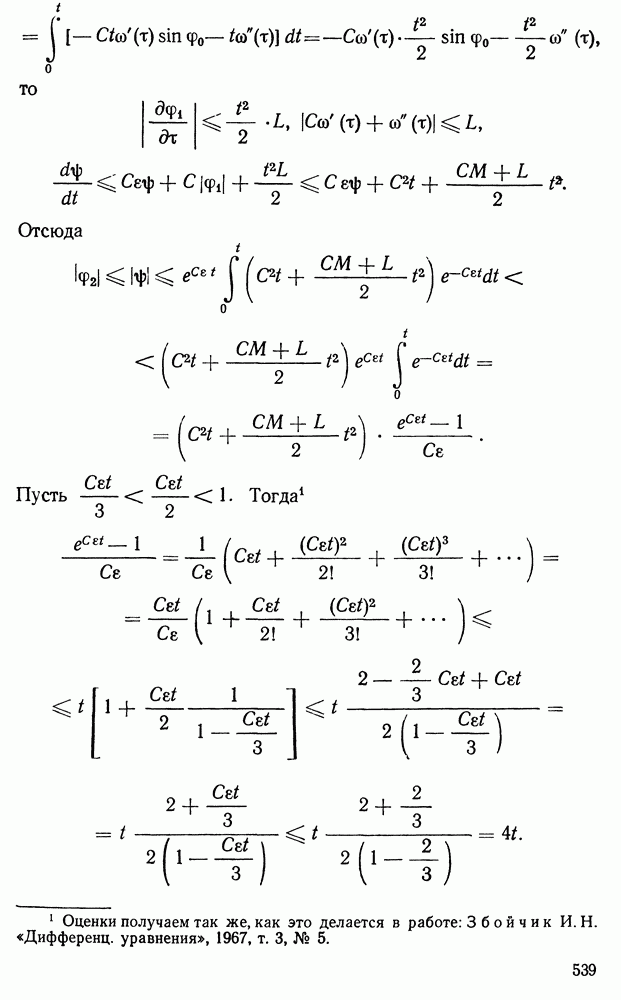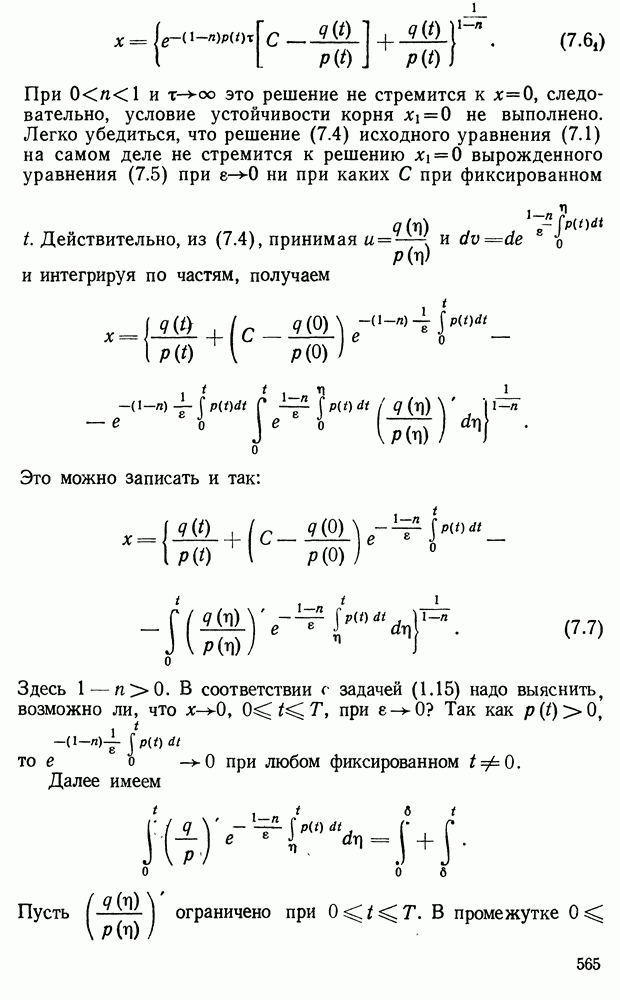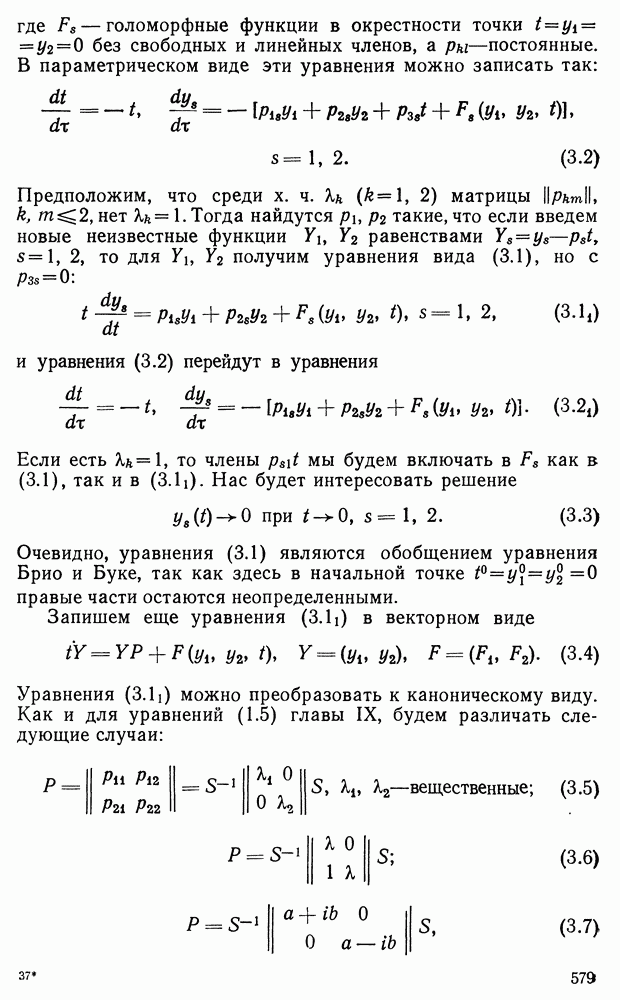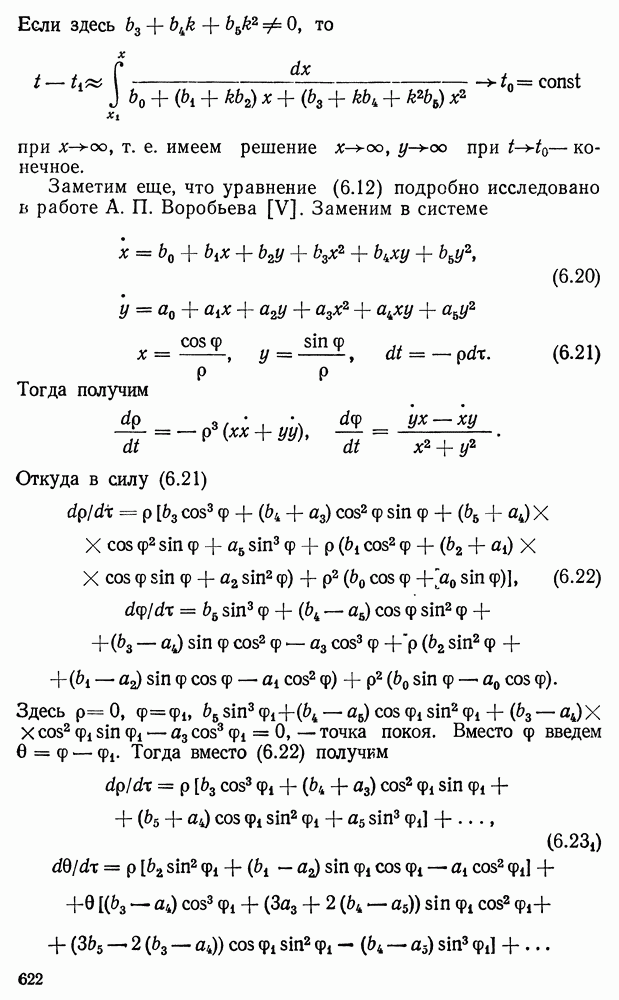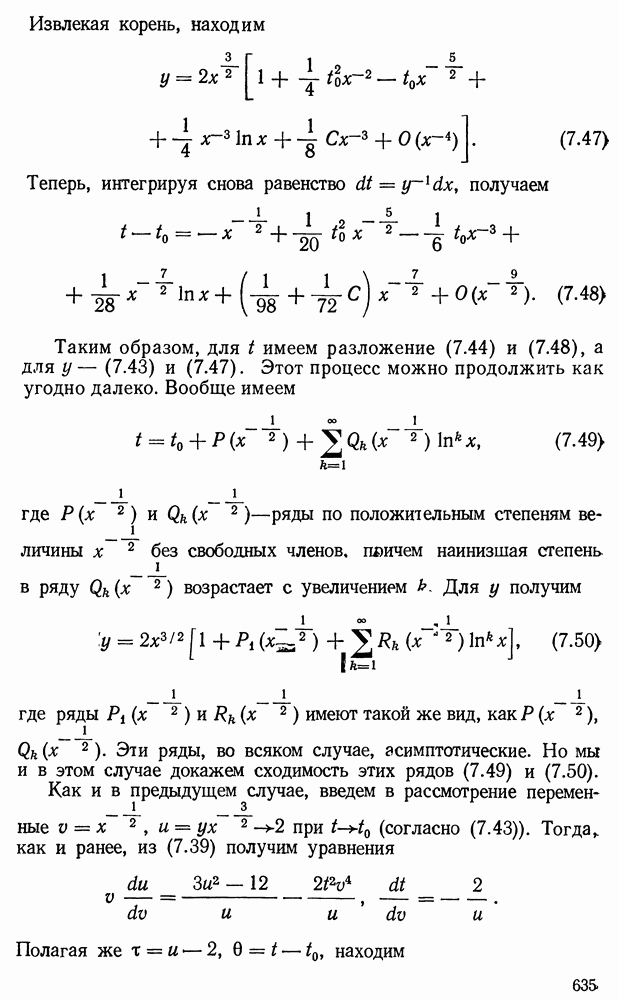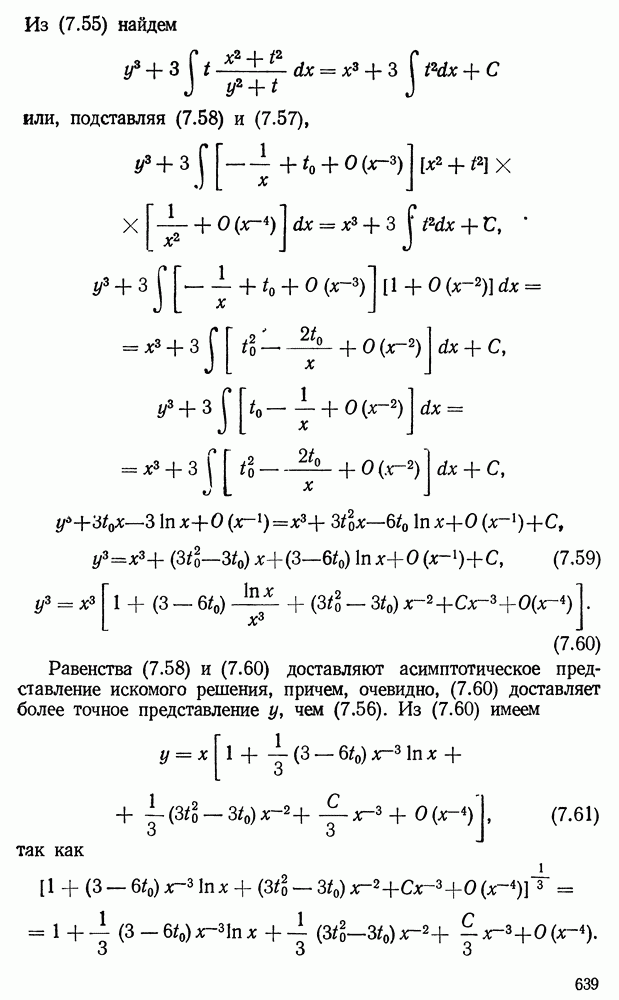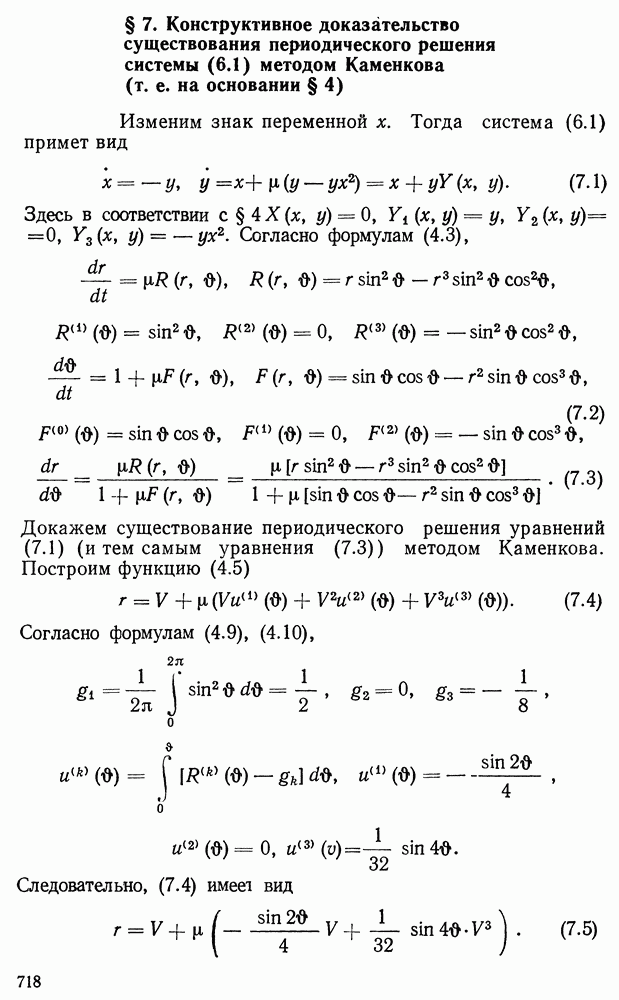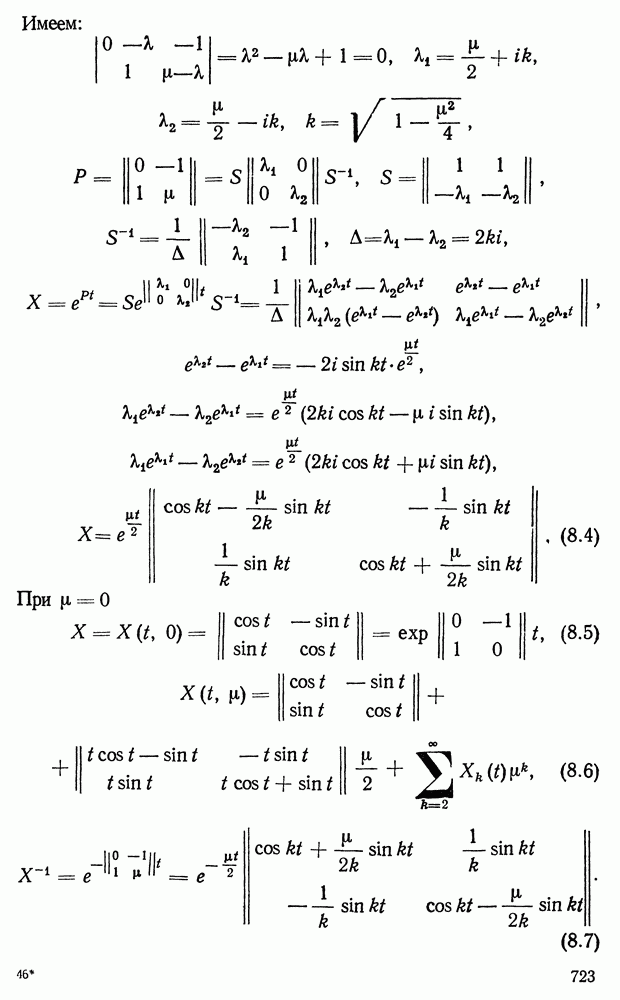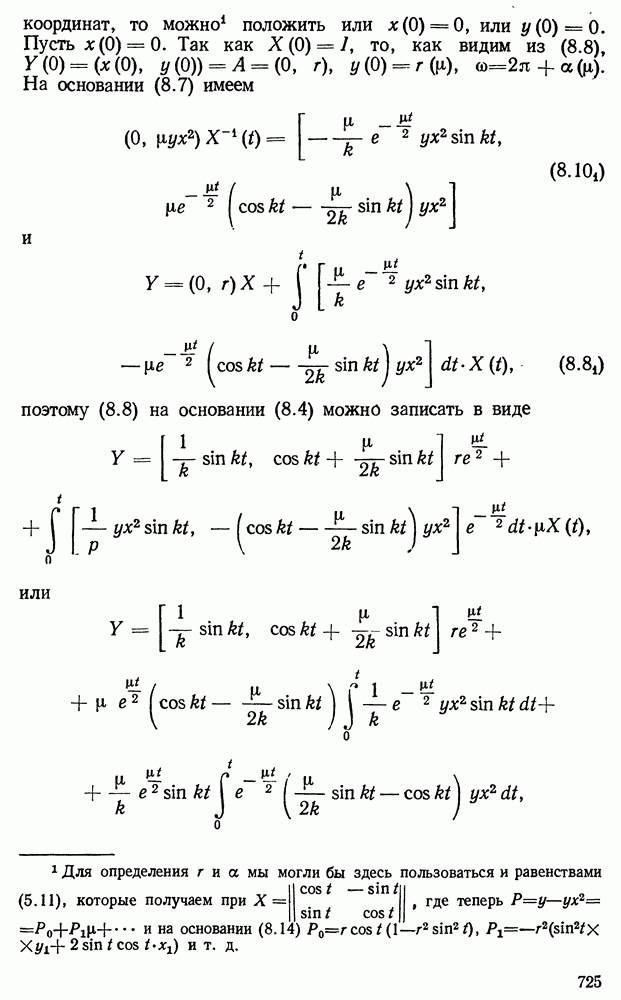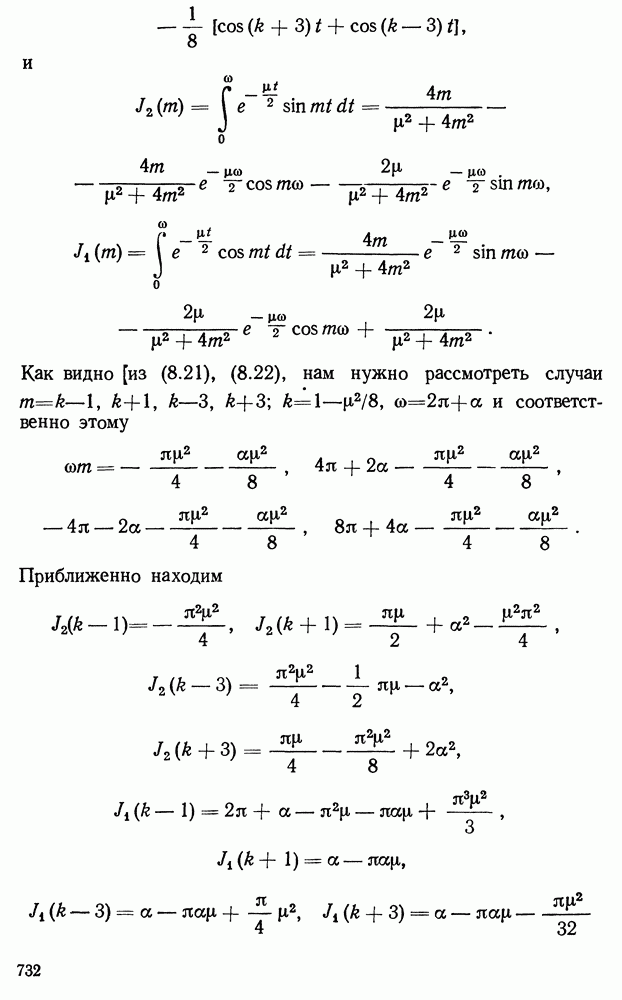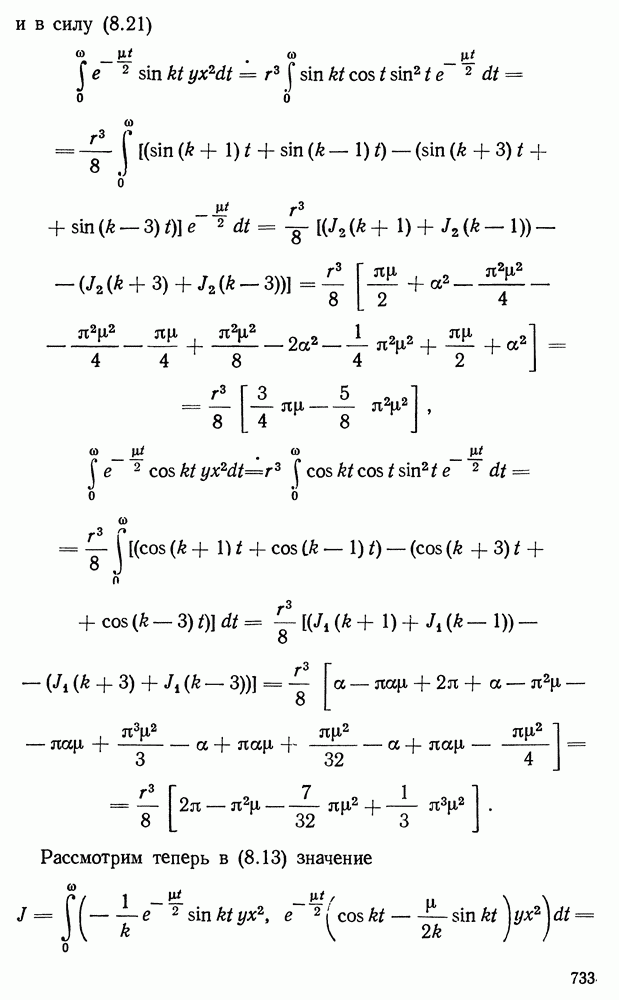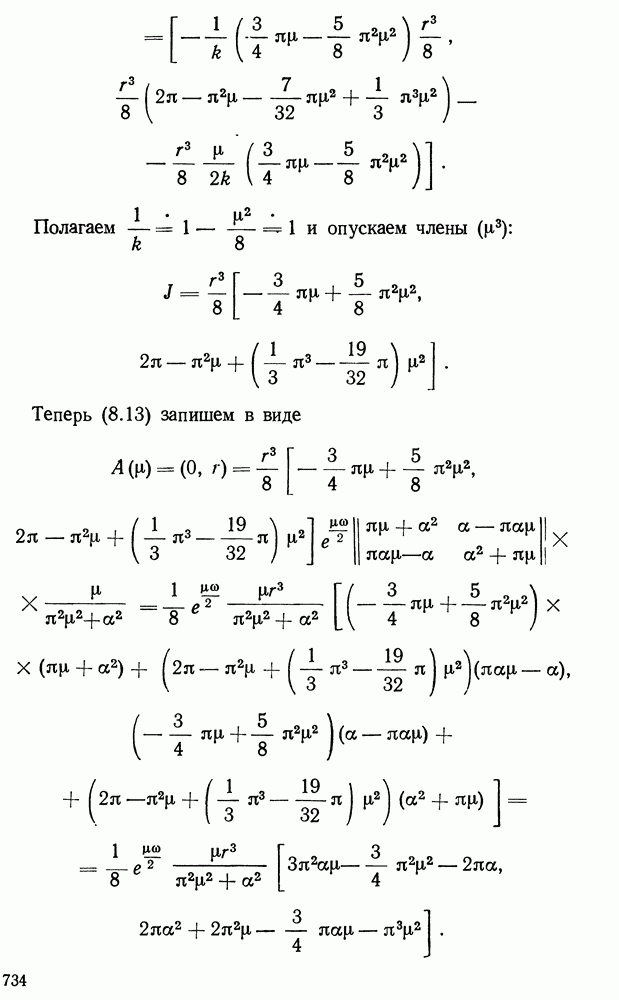| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА III. ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
В предыдущей главе мы видели, что изучение одного уравнения любого порядка или системы уравнений, разрешенных относительно старших производных, всегда можно привести к изучению нормальной системы (1.2) главы II. Такую систему мы в этой главе и будем рассматривать. Здесь будут показаны методы изучения системы дифференциальных уравнений, пригодные для весьма широких классов систем. Речь будет идти о существовании решений и их построении в виде некоторых сходящихся рядов. Будут затронуты и другие вопросы. Остановимся сначала на некоторых вспомогательных предложениях.
§ 1. Голоморфные функции и мажоранты
Функция  называется голоморфной
называется голоморфной  в окрестности точки
в окрестности точки  если в окрестности этой точки она представима в виде сходящегося ряда
если в окрестности этой точки она представима в виде сходящегося ряда

где  — постоянные.
— постоянные.
Пусть дан ряд

с постоянными коэффициентами  сходящийся в области
сходящийся в области

Если

то, как известно, из сходимости ряда (1.2) в области (1.3) следует сходимость ряда (1.1) в той же области, и ряд (1.2)
в этом случае называется мажорантой ряда (1.1). Если ряд (1.1) сходится в области (1.3), то он имеет и мажоранту (1.2) в этой области.
Действительно, если ряд (1.1) сходится в области (1.3), то, как известно, он сходится в этой области и абсолютно, т. е. сходится ряд

в области (1.3). Но тогда (1.5) и есть мажоранта (1.2) для ряда (1.1). Важнее другое. А именно, что для сходящегося ряда (1.1) всегда можно построить мажоранту в виде элементарной функции. Покажем это. Рассмотрим значение функции (1.5) в области

Функция (1.5) непрерывная, а область (1.6) замкнутая, поэтому имеем оценку в области (1.6)

Но тогда имеем и неравенства

или

Заменим в ряде  правыми частями неравенств (1-9). Тогда получим ряд
правыми частями неравенств (1-9). Тогда получим ряд

Этот ряд сходится в области

и является мажорантой для ряда (1.1). Но сумма ряда (1.10) есть

Действительно, перемножая ряды

мы и получаем (1.10).
Приведем пример голоморфной функции от одной независимой переменной. Предположим,

где  — полиномы с вещественными коэффициентами. Пусть
— полиномы с вещественными коэффициентами. Пусть  где а — вещественное число. Согласно известной формуле Тейлора,
где а — вещественное число. Согласно известной формуле Тейлора,

где  — степень полинома
— степень полинома  — вещественные числа. Обозначим через
— вещественные числа. Обозначим через  комплексные и вещественные корни полинома
комплексные и вещественные корни полинома  Тогда, как известно,
Тогда, как известно,

где А — постоянное число, которое можно считать и единицей,  — целые положительные числа.
— целые положительные числа.
Известно, что можно  представить в виде суммы элементарных дробей
представить в виде суммы элементарных дробей  где 4° — постоянные числа, а
где 4° — постоянные числа, а 
— целое.
Имеем

Этот ряд, очевидно, сходится при  Отсюда следует, что все элементарные дроби представимы в виде сходящихся рядов
Отсюда следует, что все элементарные дроби представимы в виде сходящихся рядов  где
где  — расстояние до ближайшего из корней
— расстояние до ближайшего из корней  полинома
полинома  Тем самым имеем и такое разложение
Тем самым имеем и такое разложение

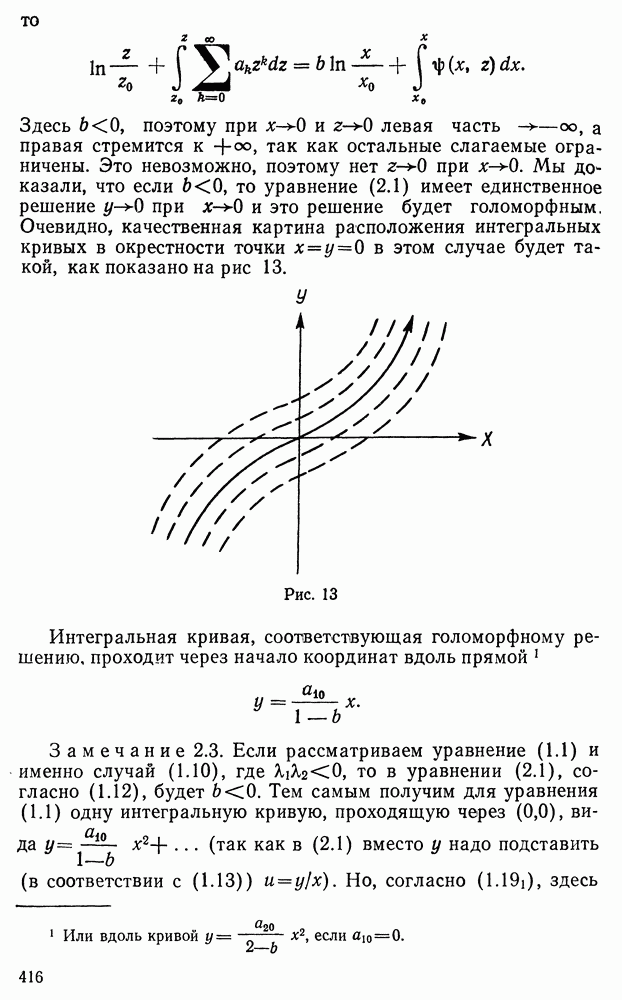
сходящееся при  Так как
Так как  вещественный полином и а — вещественное число, то
вещественный полином и а — вещественное число, то  вещественные числа, так как они определяются как коэффициенты ряда Тейлора по формуле
вещественные числа, так как они определяются как коэффициенты ряда Тейлора по формуле

Мы доказали утверждение: функция (1.13) представима сходящимся рядом

где  и а — вещественные числа,
и а — вещественные числа,  расстояние от а до ближайшего из корней
расстояние от а до ближайшего из корней  (учитывая и комплексные) полинома
(учитывая и комплексные) полинома 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВМЕСТО ПРЕДИСЛОВИЯ
- ГЛАВА I. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ
- § 2. Общее, частное и особое решения
- § 3. Дифференциальное уравнение с разделяющимися переменными
- § 4. Однородные уравнения
- § 5. Уравнения, приводящиеся к однородному
- § 6. Линейное уравнение
- § 7. Уравнение Риккати
- § 8. Дифференциальные уравнения в полных дифференциалах
- § 9. Интегрирующий множитель
- § 10. Строгое определение общего решения
- § 11. Особое решение
- § 12. Интеграл
- § 13. Уравнения, не разрешенные относительно у’
- § 14. Решение в параметрическом виде
- § 15. Частные случаи дифференциальных уравнений, не разрешенных относительно у’
- § 16. Расположение интегральных кривых в окрестности границы области D(x, у)
- ГЛАВА II. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Интегралы системы
- § 3. Уравнение n-го порядка
- § 4. Приведение уравнения n-го порядка к системе n уравнений первого порядка и наоборот
- § 5. Частные случаи уравнения n-го порядка
- ГЛАВА III. ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
- § 2. Теорема Коши
- § 3. Линейные системы
- § 4. Теорема Пикара
- § 5. Частные случаи теоремы Пикара
- § 6. Область существования решения
- § 7. Непрерывная зависимость решений от параметров
- § 8. Дифференцируемость по параметру
- § 9. Теоремы о существовании решений в максимальной области, зависящей от параметра
- § 10. Построение решений во всей области существования
- § 11. Существование общего решения
- § 12. Устойчивость по Ляпунову. Еще об общем решении
- § 13. Существование дифференцируемых полных интегралов
- ГЛАВА IV. ЛИНЕЙНОЕ УРАВНЕНИЕ n-го ПОРЯДКА
- § 2. Однородное уравнение с постоянными вещественными коэффициентами
- § 3. Примеры
- ГЛАВА V. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 2. Неоднородная система
- § 3. Однородные линейные системы с постоянными коэффициентами
- § 4. О матрицах
- § 5. Общее исследование системы (3.1)
- § 6. Матричный метод
- § 7. Теорема о преобразовании системы (6.1) в каноническую вещественную систему
- § 8. Неоднородные линейные системы с постоянными коэффициентами
- ГЛАВА VI. ВОПРОСЫ УСТОЙЧИВОСТИ
- § 1. Устойчивость по Ляпунову
- § 2. Теорема Ляпунова
- § 3. Устойчивость решений линейных систем
- § 4. Линейные однородные системы с периодическими коэффициентами
- § 5. Второй метод Ляпунова
- ГЛАВА VII. ЛИНЕЙНЫЕ УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА
- § 1. Однородное дифференциальное уравнение первого порядка в частных производных
- § 2. Построение решения задачи Коши
- § 3. Решение задачи Коши для однородного уравнения с n независимыми переменными
- § 4. Неоднородное уравнение
- § 5. Задача Коши для неоднородного уравнения
- § 6. Общая задача Коши для неоднородного уравнения
- ГЛАВА VIII. МЕТОД ПРЕОБРАЗОВАНИЙ И МЕТОД ОСОБЫХ РЕШЕНИЙ
- § 2. Признаки интегрируемости уравнения (1.1) в замкнутой форме
- § 3. Метод последовательных преобразований
- § 4. Эвристический метод преобразований
- § 5. Осуществимость преобразований
- § 6. Метод преобразований в системах
- ГЛАВА IX. РЕШЕНИЯ С ОСОБЫМИ НАЧАЛЬНЫМИ ЗНАЧЕНИЯМИ. УРАВНЕНИЕ у’=Р(х, y)/Q(x, у)
- § 1. Уравнение y’ = P(x,y)/Q(x,y)
- § 2. Уравнение Брио и Буке
- § 3. Теорема Пуанкаре
- ГЛАВА X. СРАВНЕНИЕ РЕШЕНИЙ ПОЛНОГО И УКОРОЧЕННОГО ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Случай, когда y(t) и z(t) — решения дифференциальных уравнений
- § 3. Представление решений полного уравнения через измененное укороченное
- § 4. Общий метод доказательства существования разложения (1.1)
- § 5. Продолжение § 4
- ГЛАВА XI. РАЗНОТЕМНЫЕ ЗАМЕЧАНИЯ
- § 1. О стационарных интегралах
- § 2. Интегралы системы (1.1), не зависящие от t
- § 3. Построение систем дифференциальных уравнений, имеющих заданную интегральную кривую
- § 4. О периодических решениях
- § 5. Гамильтоновы системы двух уравнений
- § 6. Система Гамильтона, варьированная относительно системы (5.22)
- § 7. Задачи Пуанкаре о периодических решениях
- § 8. Метод неподвижных точек
- § 9. Принцип кольца
- § 10. Предельные циклы и построение решений вблизи предельных циклов
- § 11. Уравнение Риккати
- ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С МАЛЫМ ПАРАМЕТРОМ
- § 2. Замечания о преобразованиях рядов
- § 3. Система …
- § 4. Нелинейные уравнения
- § 5. Уравнение …
- § 6. Уравнения с малым параметром при старшей производной
- § 7. Примеры тихоновских систем
- ГЛАВА XIII. ТЕОРИЯ ПОДВИЖНЫХ ОСОБЫХ ТОЧЕК В ВЕЩЕСТВЕННОЙ ОБЛАСТИ
- § 1. Системы, решения которых существуют в области …
- § 2. Поведение решений при t->оо
- § 3. О решениях систем двух дифференциальных уравнений типа Брио и Буке
- § 4. Особые случаи системы (3.1)
- § 5. Подвижные особые точки решений системы двух уравнений
- § 6. Случай …
- § 7. Построение решений (5.10)
- § 8. Случай …
- § 10. Заключительный
- ГЛАВА XIV. ФРАГМЕНТЫ ИЗ ЭЛЕМЕНТАРНОЙ КОНСТРУКТИВНОЙ ТЕОРИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ АВТОНОМНОЙ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 1. Периодические решения вокруг центра (Ляпунов)
- § 2. Замечания
- § 3. Периодические решения вокруг центра (Пуанкаре)
- § 4. Доказательство существования и построение предельных циклов по методу Каменкова
- § 5. Существование и построение изолированных периодических решений уравнения …
- § 6. Уравнение Ван дер Поля. Качественная теория
- § 7. Конструктивное доказательство существования периодического решения системы (6.1) методом Каменкова (т. е. на основании § 4)
- § 8. Уравнение. Построение предельного цикла
- ЛИТЕРАТУРА