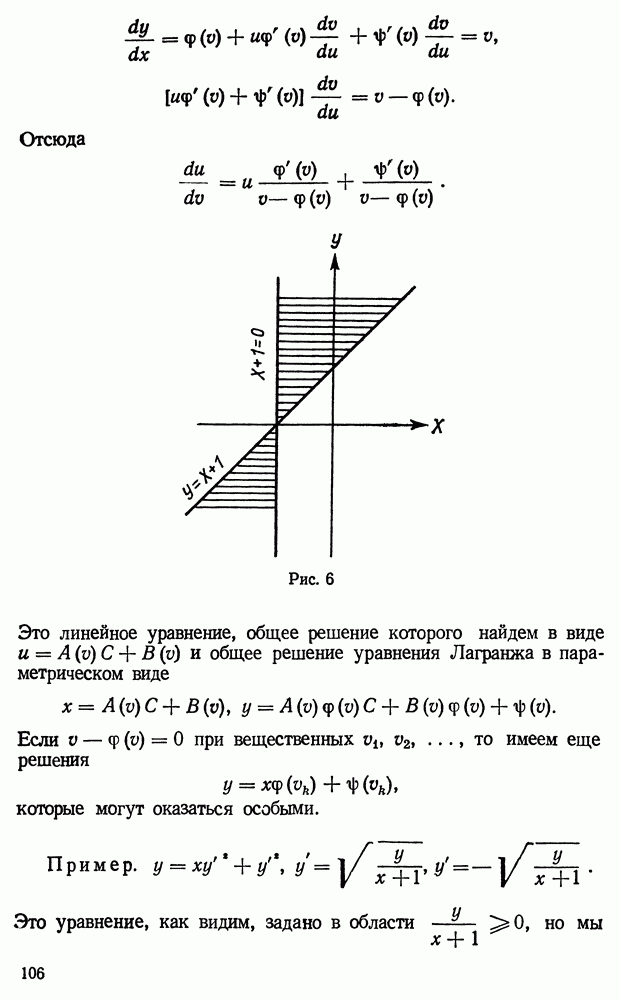
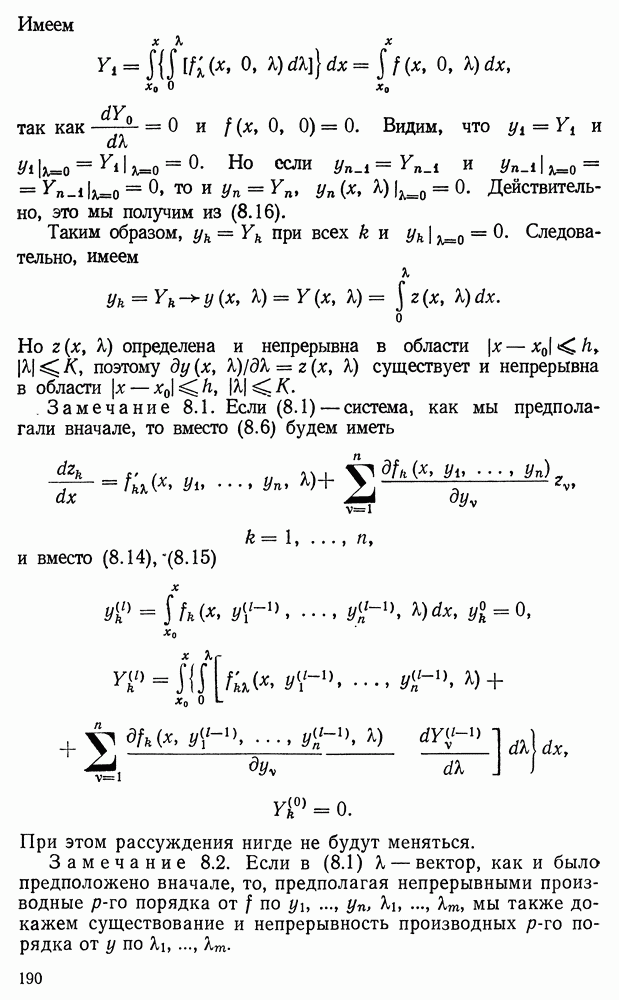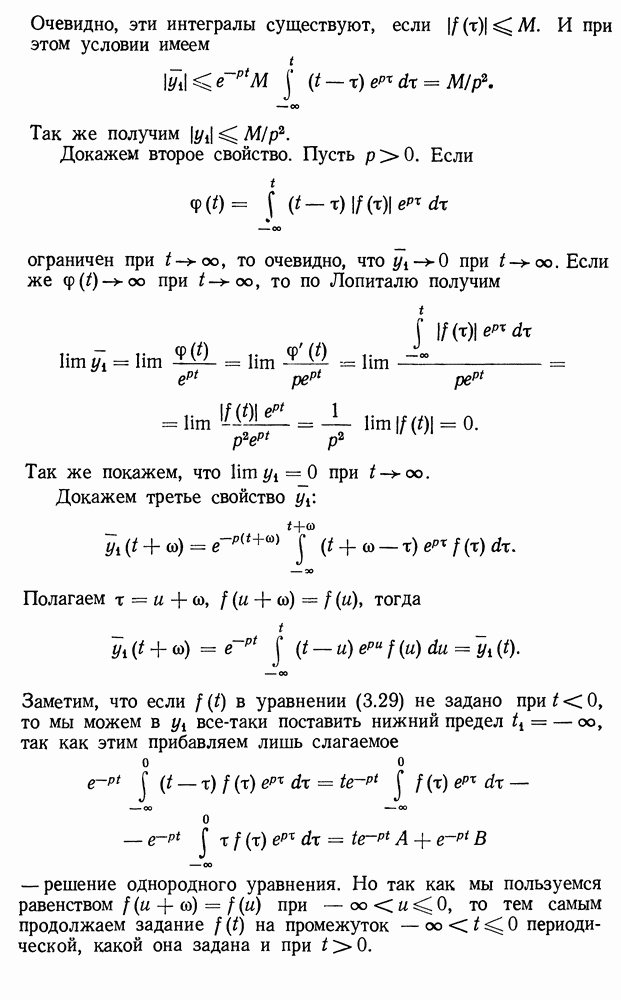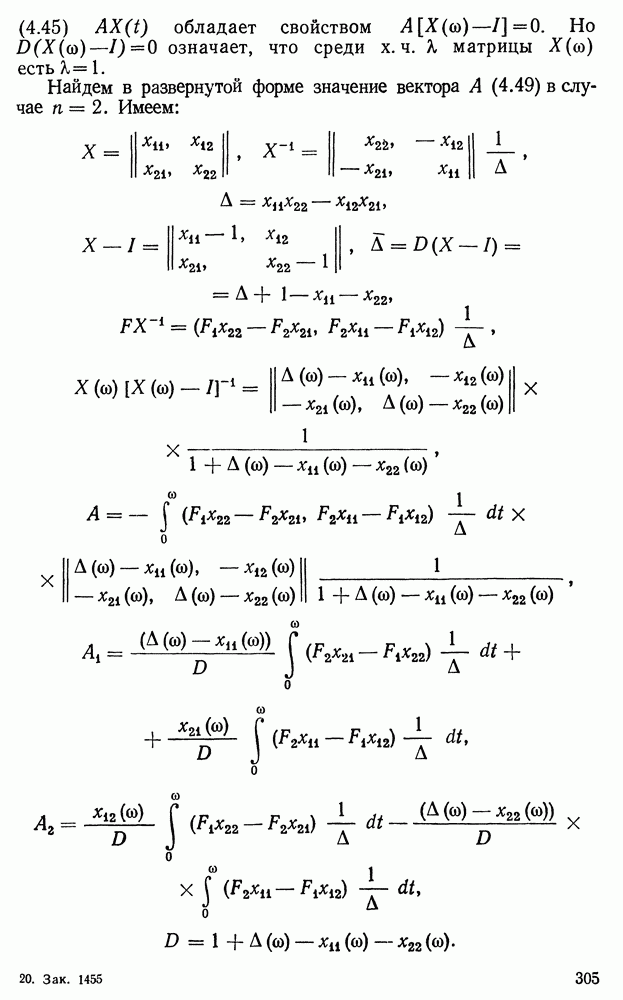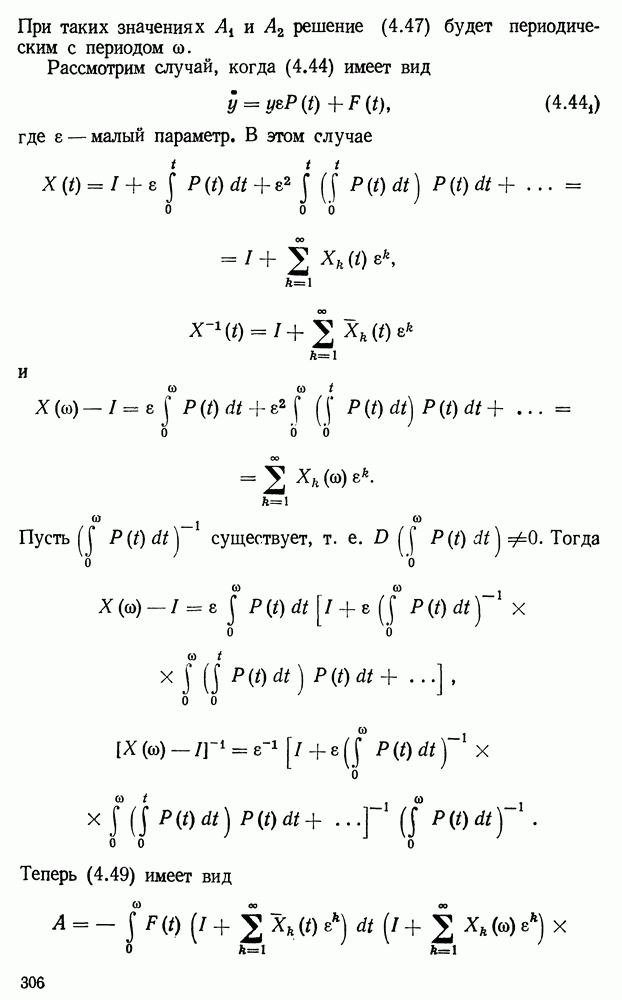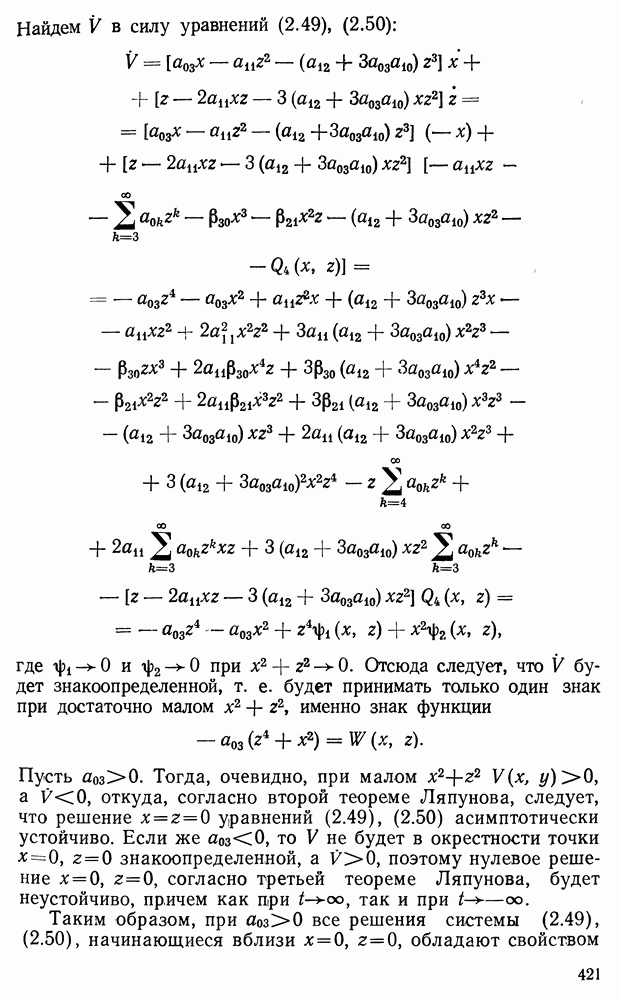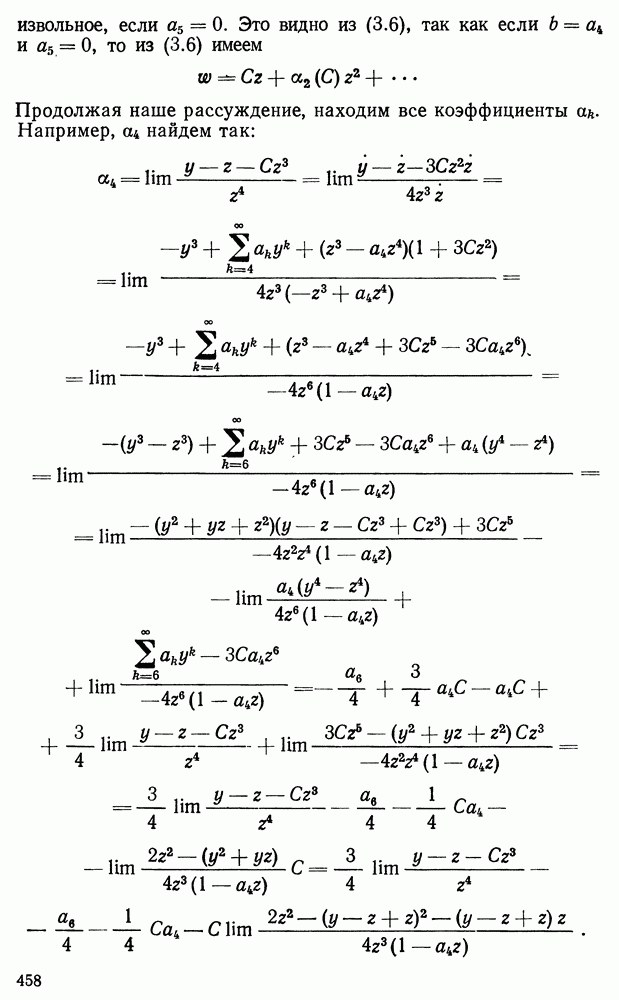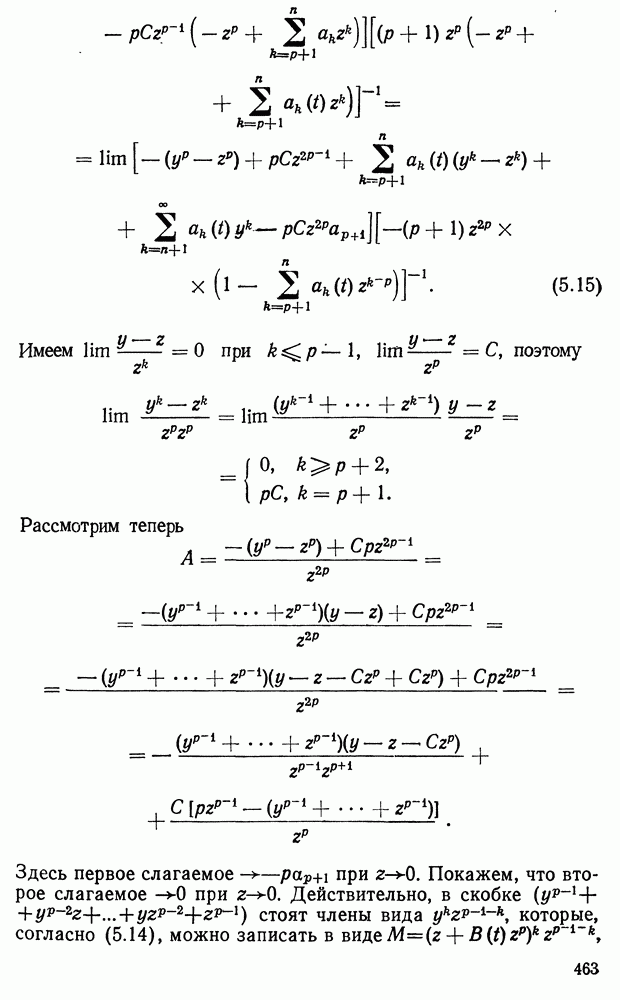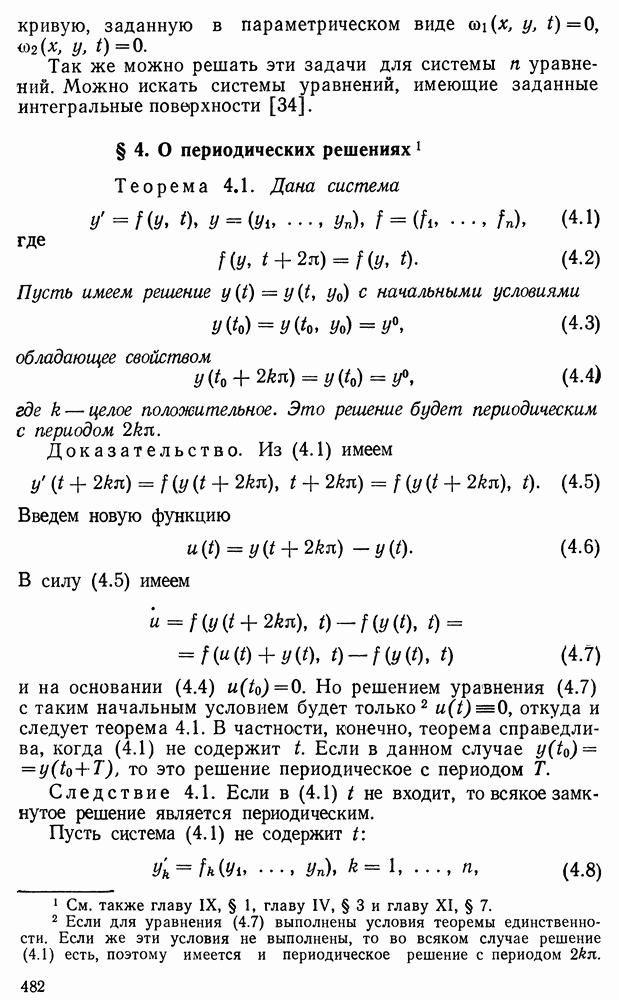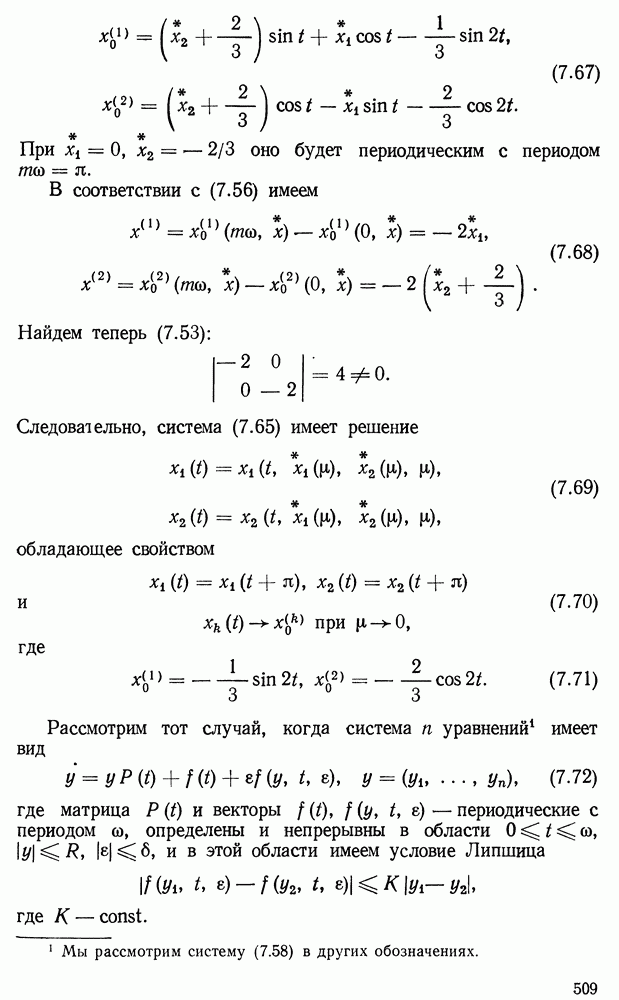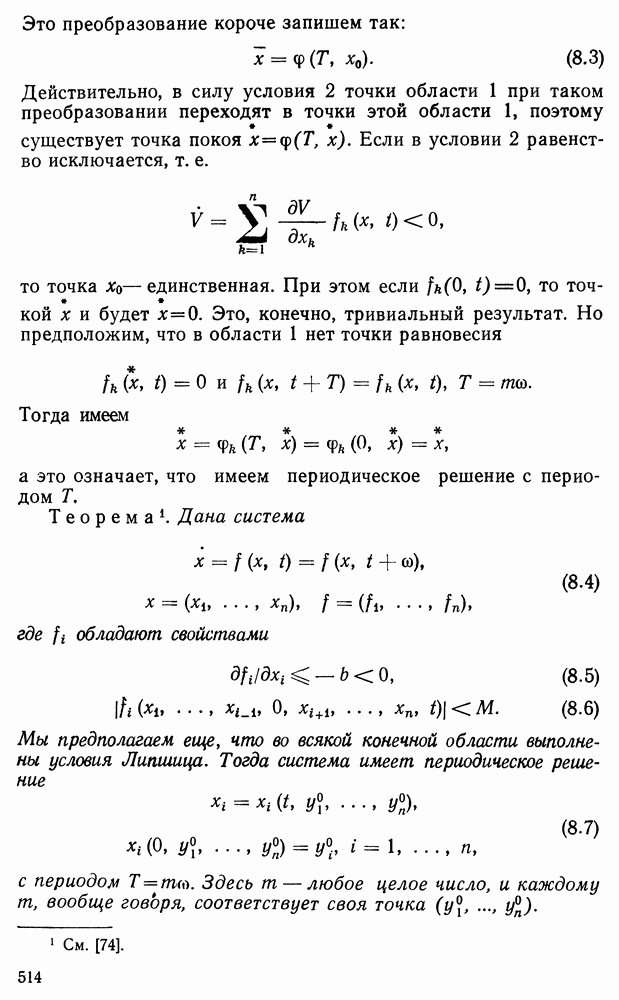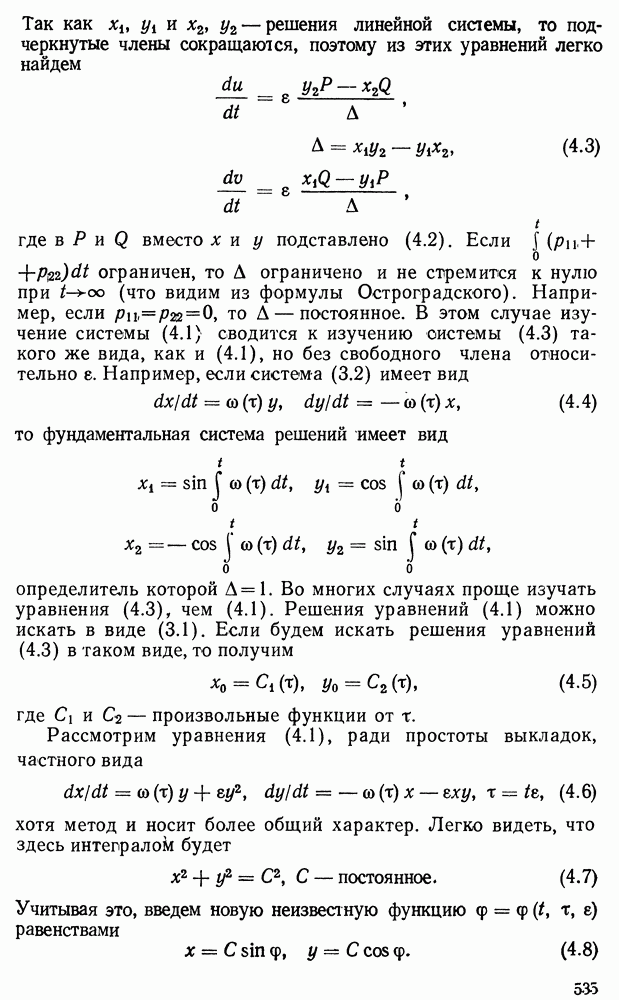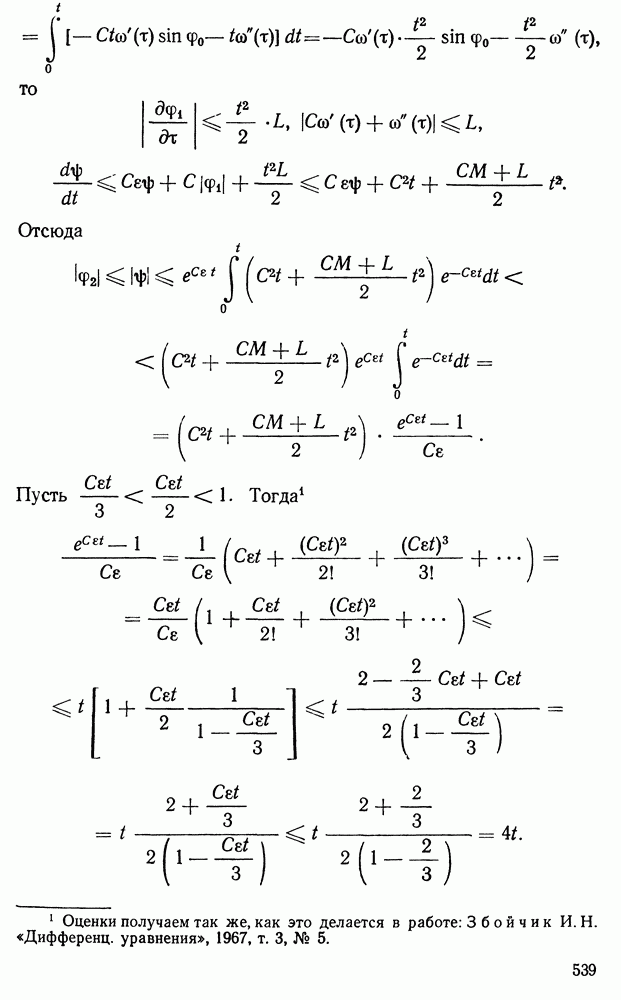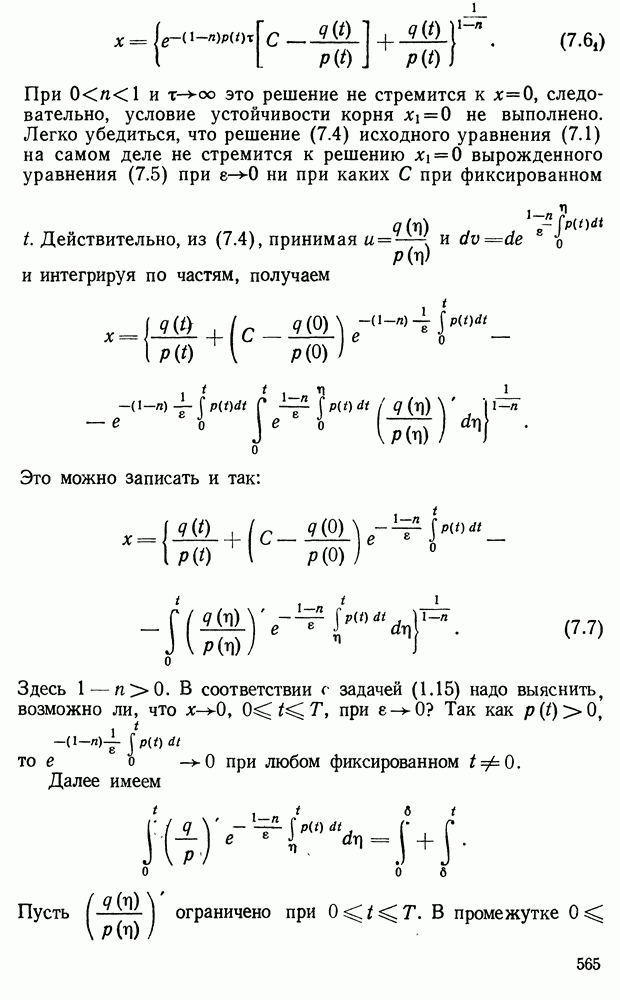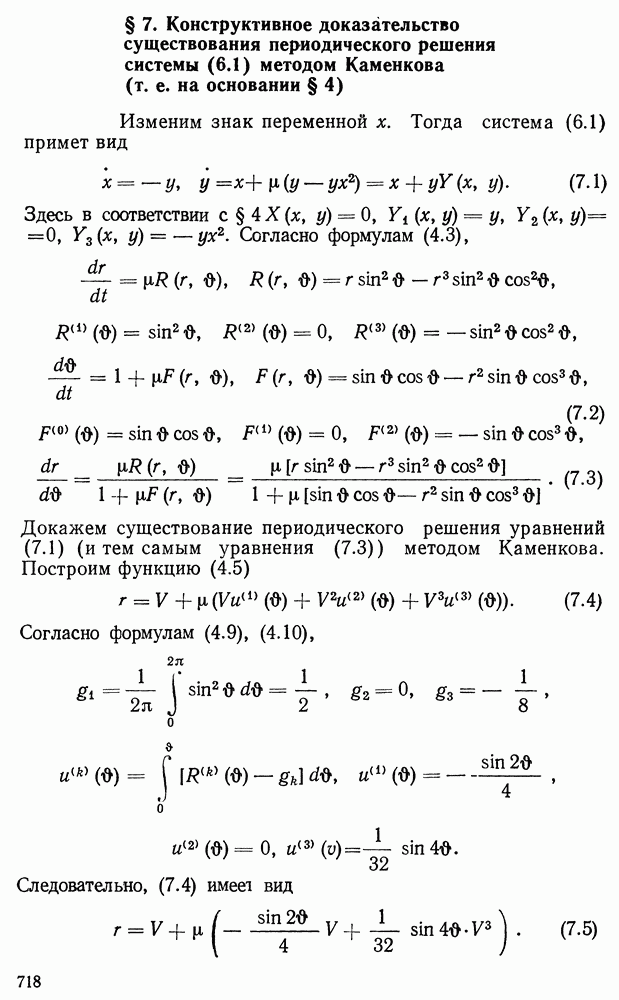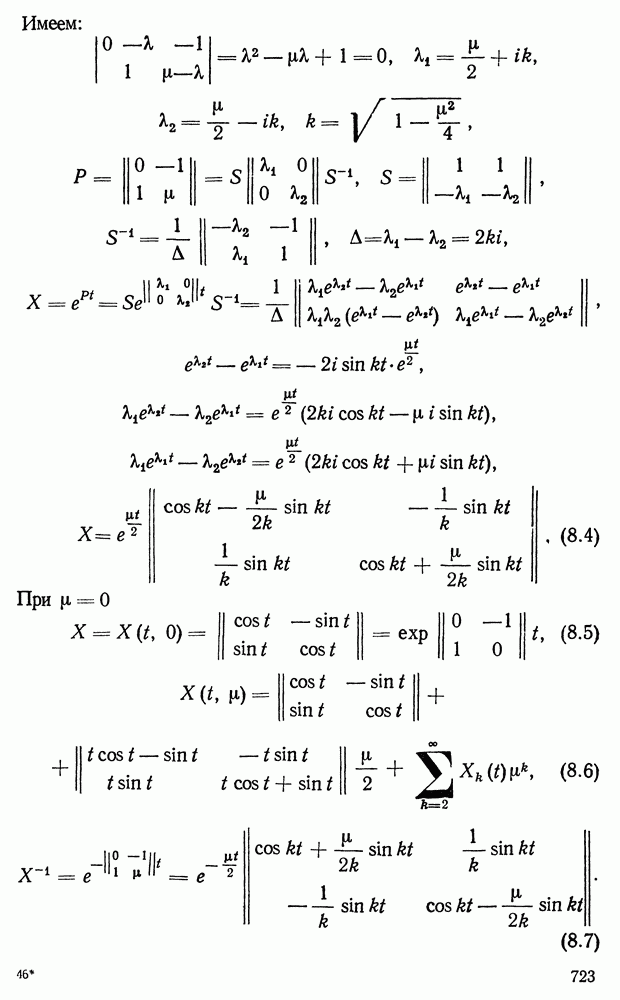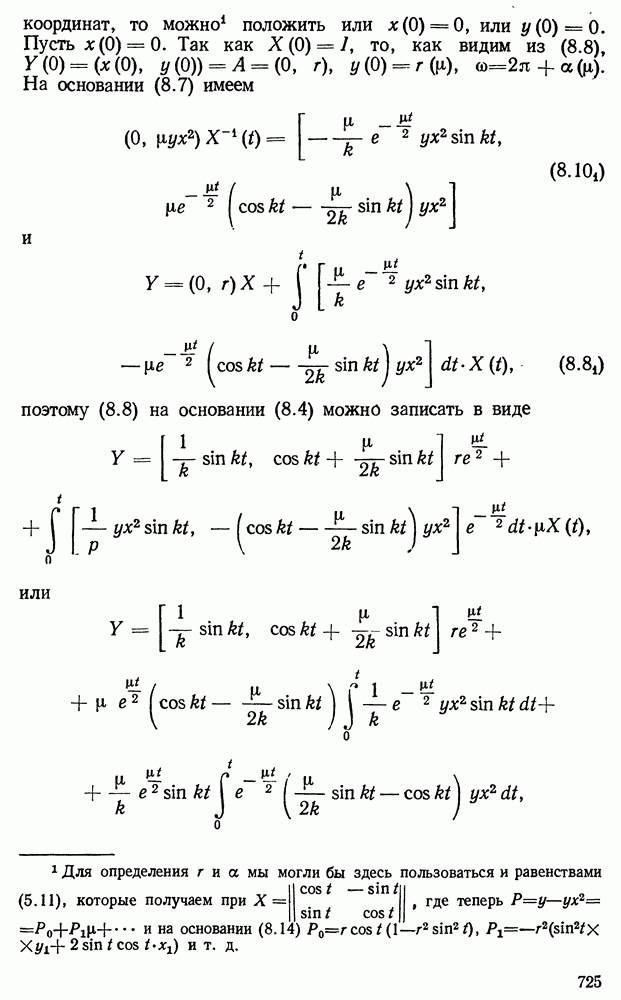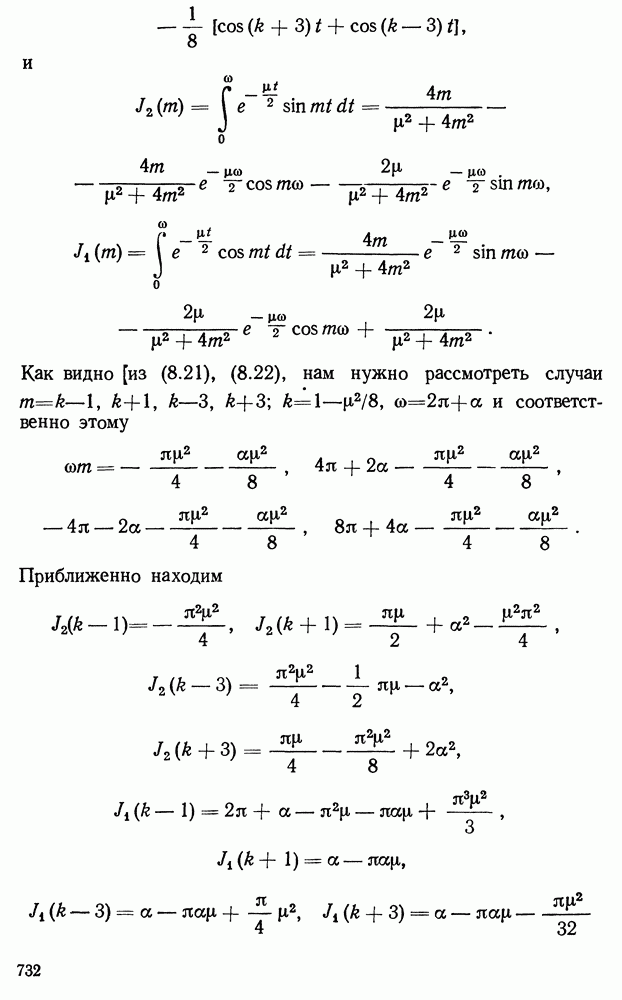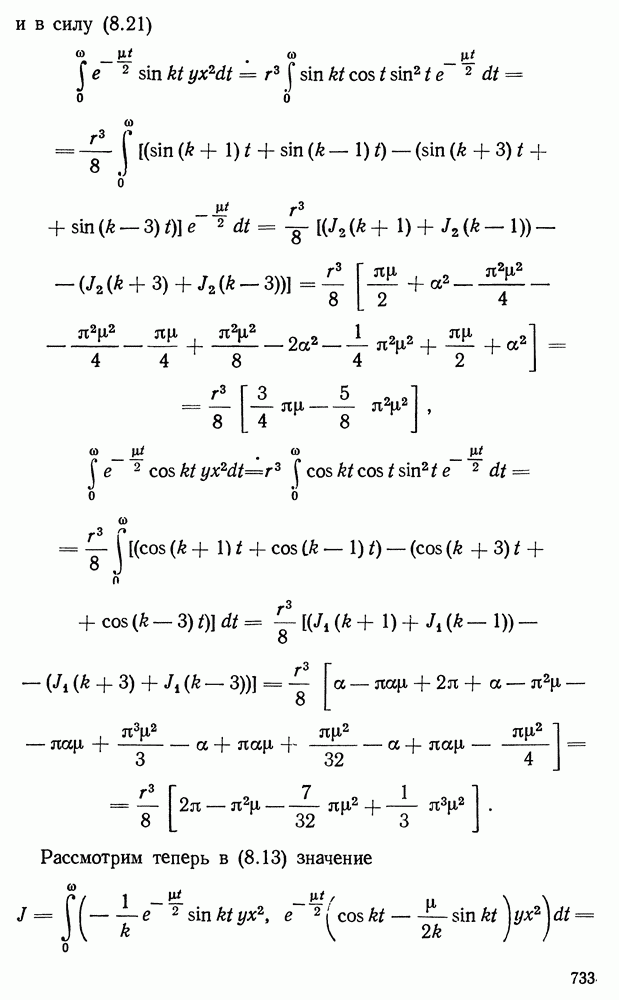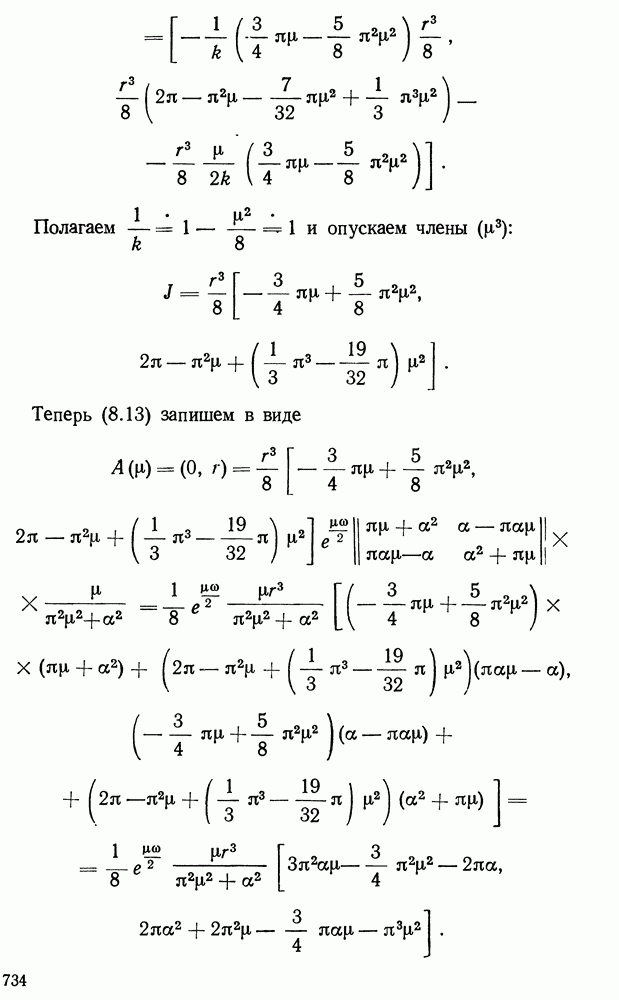| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА IV. ЛИНЕЙНОЕ УРАВНЕНИЕ n-го ПОРЯДКА
§ 1. Общая теория линейного уравнения

Если  то уравнение называется однородным:
то уравнение называется однородным:

Здесь  называется линейным оператором и означает совокупность операций над у, указанных формулой (1.2).
называется линейным оператором и означает совокупность операций над у, указанных формулой (1.2).
В главе III мы видели, что если  непрерывны в области
непрерывны в области

то существует единственное решение уравнения (1.1) с начальными условиями

где  — произвольные числа. Это решение непрерывно в области (1.3).
— произвольные числа. Это решение непрерывно в области (1.3).
Замечание 1.1. Решение уравнения (1.2) с начальными условиями  единственно и
единственно и 
Сначала рассмотрим уравнение (1.2). Три свойства оператора 

Здесь  — произвольные постоянные. Доказательства очевидны. Отсюда следует
— произвольные постоянные. Доказательства очевидны. Отсюда следует
Теорема 1.1. Если  — решения уравнения (1.2), то и
— решения уравнения (1.2), то и  — также решение уравнения (1.2) при произвольных
— также решение уравнения (1.2) при произвольных  .
.
Линейно независимые функции. Пусть  — функции, заданные в промежутке а
— функции, заданные в промежутке а  Функции
Функции  называются линейно зависимыми в этом промежутке, если существуют постоянные
называются линейно зависимыми в этом промежутке, если существуют постоянные  не
не
все равные нулю, для которых имеем

Если таких постоянных  нет, то
нет, то  называются линейно независимыми.
называются линейно независимыми.
Необходимое условие линейной зависимости  Пусть
Пусть  — линейно зависимые, т. е. имеем (1.5), где не все
— линейно зависимые, т. е. имеем (1.5), где не все  — нули (и m=n). Дифференцируя тождество
— нули (и m=n). Дифференцируя тождество  раз, получаем
раз, получаем

Уравнениям (1.5) и (1.6) удовлетворяют  не все равные нулю. Но тогда, как известно из алгебры, имеем
не все равные нулю. Но тогда, как известно из алгебры, имеем

Определитель  называется определителем Вронского, или вронскианом. Равенство (1.7) и есть необходимое условие линейной зависимости функций
называется определителем Вронского, или вронскианом. Равенство (1.7) и есть необходимое условие линейной зависимости функций 
Покажем теперь, что если в  решения уравнения (1.2), то это условие является и достаточным для линейной зависимости
решения уравнения (1.2), то это условие является и достаточным для линейной зависимости 
Теорема 1.2. Если  — решения уравнения (1.2)
— решения уравнения (1.2)

то

 — линейно зависимые решения в промежутке а
— линейно зависимые решения в промежутке а
Доказательство. Рассмотрим уравнения 

с неизвестными  Определитель этой линейной однородной алгебраической системы равен нулю согласно (1.8).
Определитель этой линейной однородной алгебраической системы равен нулю согласно (1.8).
В силу известной теоремы из алгебры система (1.10) имеет ненулевое решение

т. е. здесь не все  равны нулю. При таких
равны нулю. При таких  рассмотрим функцию
рассмотрим функцию

Согласно теореме 1.1, это решение уравнения (1.2), а согласно (1.10) и замечанию 1.1, это решение есть

А это означает, что  линейно зависимые. А тогда имеем и (1.9). Теорема 1.2 доказана.
линейно зависимые. А тогда имеем и (1.9). Теорема 1.2 доказана.
Теорема 1.3. Для того чтобы решения  уравнения (1.2) были линейно независимые, необходимо и достаточно, чтобы в какой-нибудь точке
уравнения (1.2) были линейно независимые, необходимо и достаточно, чтобы в какой-нибудь точке  было
было  И если
И если  то и
то и  если же
если же  то и
то и 
Достаточность. Пусть  . Тогда и
. Тогда и  так как если бы оказалось
так как если бы оказалось  то было бы, согласно теореме 1.2, и равенство (1.9), т. е.
то было бы, согласно теореме 1.2, и равенство (1.9), т. е.  чего нет.
чего нет.
Необходимость. Пусть  линейно независимые решения уравнения (1.2). Тогда
линейно независимые решения уравнения (1.2). Тогда  так как иначе они, согласно теореме 1.2, будут линейно зависимые. Теорема 1.3 доказана.
так как иначе они, согласно теореме 1.2, будут линейно зависимые. Теорема 1.3 доказана.
Линейно независимые решения  уравнения (1.2) существуют. Действительно, согласно теореме Пикара, существуют решения с начальными условиями
уравнения (1.2) существуют. Действительно, согласно теореме Пикара, существуют решения с начальными условиями

Здесь  что и доказывает утверждение. Очевидно и то, что линейно независимых систем решений бесконечное множество, так как по-разному можно построить решения с такими начальными условиями, чтобы определитель Вронского был отличен от нуля.
что и доказывает утверждение. Очевидно и то, что линейно независимых систем решений бесконечное множество, так как по-разному можно построить решения с такими начальными условиями, чтобы определитель Вронского был отличен от нуля.
Общее решение уравнения (1.2).
Теорема 1.4. Если  — линейно независимые решения уравнения (1.2), то
— линейно независимые решения уравнения (1.2), то

есть общее решение в области

Действительно, так как  , то из равенств
, то из равенств

при любых  при которых решение удовлетворяет заданным условиям задачи Коши. А тогда (1.14) действительно является общим решением уравнения (1.2).
при которых решение удовлетворяет заданным условиям задачи Коши. А тогда (1.14) действительно является общим решением уравнения (1.2).
Существует  линейно независимых решений. Это мы доказали. Но более
линейно независимых решений. Это мы доказали. Но более  таких решений быть не может.
таких решений быть не может.
Доказательство. Пусть  решения уравнения (1.2). Если
решения уравнения (1.2). Если  — линейно независимые, то, согласно теореме 1.4.,
— линейно независимые, то, согласно теореме 1.4.,

 линейно зависимые. Если же
линейно зависимые. Если же  линейно зависимые, то
линейно зависимые, то  где не все
где не все  тогда имеем
тогда имеем  линейно зависимые, так как в этом тождестве не все
линейно зависимые, так как в этом тождестве не все  равны нулю.
равны нулю.
Линейно независимые решения  называются фундаментальной системой решений.
называются фундаментальной системой решений.
Замечание 1.2. Мы показали, что для фундаментальной системы решений  уравнения (1.2) имеем
уравнения (1.2) имеем  при если в этом промежутке
при если в этом промежутке  непрерывны. Но если
непрерывны. Но если  непрерывны лишь в промежутке
непрерывны лишь в промежутке  то может быть, что
то может быть, что  при
при  Или, например, если
Или, например, если  непрерывны в области
непрерывны в области  то может быть, что
то может быть, что  при
при  Это мы увидим позднее.
Это мы увидим позднее.
Неоднородное уравнение (1.1). Уравнение (1.2) называется соответствующим однородным уравнением по отношению к (1.1). Пусть  есть решение уравнения (1.1), т. е.
есть решение уравнения (1.1), т. е.  Положим тогда
Положим тогда

где  — новая неизвестная функция. Подставляя это в (1.1), получаем
— новая неизвестная функция. Подставляя это в (1.1), получаем

В силу  имеем
имеем

 является решением соответствующего однородного уравнения. Если
является решением соответствующего однородного уравнения. Если  фундаментальная система решений уравнения (1.17), то общее решение
фундаментальная система решений уравнения (1.17), то общее решение  общее решение уравнения (1.1) есть
общее решение уравнения (1.1) есть

т. е. общее решение уравнения (1.1) есть сумма частного решения неоднородного уравнения (1.1) и общего решения соответствующего однородного уравнения (1.2). Очевидным является утверждение, что если  и — решения уравнений
и — решения уравнений  то
то  есть решение уравнения
есть решение уравнения

Это несколько упрощает в некоторых случаях нахождение частных решений уравнения (1.1).
Но как найти частное решение неоднородного уравнения  Лагранж дал способ нахождения этого частного решения, если уже найдена фундаментальная система решений
Лагранж дал способ нахождения этого частного решения, если уже найдена фундаментальная система решений  соответствующего однородного уравнения (1.2). Именно формула (1.14) доставляет общее решение однородного уравнения (1.2), если
соответствующего однородного уравнения (1.2). Именно формула (1.14) доставляет общее решение однородного уравнения (1.2), если  -линейно независимые решения. Будем искать и решение неоднородного уравнения (1.1) в форме (1.14), где
-линейно независимые решения. Будем искать и решение неоднородного уравнения (1.1) в форме (1.14), где  считаем неизвестными функциями, которые нужно найти так, чтобы формула (1.14) давала решение неоднородного уравнения. Если подставим у, данное формулой (1.14), в (1.1), то для нахождения
считаем неизвестными функциями, которые нужно найти так, чтобы формула (1.14) давала решение неоднородного уравнения. Если подставим у, данное формулой (1.14), в (1.1), то для нахождения  получим одно уравнение. Но мы имеем
получим одно уравнение. Но мы имеем  неизвестных
неизвестных  Поэтому как-то нужно это уравнение дополнить еще какими-нибудь
Поэтому как-то нужно это уравнение дополнить еще какими-нибудь  уравнениями. Мы эти уравнения, следуя Лагранжу, построим так. Найдем у:
уравнениями. Мы эти уравнения, следуя Лагранжу, построим так. Найдем у:

Потребуем выполнения равенства

После этого

Теперь полагаем

Продолжая так дальше, получаем

и

Подставляя эти значения у и  из (1.14), (1.24) и (1.25) в уравнение (1.1), получаем
из (1.14), (1.24) и (1.25) в уравнение (1.1), получаем

Так как  то последнее равенство имеет вид
то последнее равенство имеет вид

Равенства (1.23) и (1.26) являются  алгебраическими линейными неоднородными уравнениями с
алгебраическими линейными неоднородными уравнениями с  неизвестными
неизвестными  Определитель этой линейной системы есть
Определитель этой линейной системы есть

поэтому мы единственным образом найдем

через  их производные и
их производные и  Отсюда
Отсюда

где  — произвольные постоянные. Подставляя эти значения
— произвольные постоянные. Подставляя эти значения  в (1.14), мы получаем решение неоднородного уравнения (1.1)
в (1.14), мы получаем решение неоднородного уравнения (1.1)

Это общее решение уравнения (1.1). Если же полагаем  то получим частное решение неоднородного уравнения (1.1). Таким образом, для интегрирования уравнения (1.1) надо лишь найти
то получим частное решение неоднородного уравнения (1.1). Таким образом, для интегрирования уравнения (1.1) надо лишь найти  линейно независимых решений однородного уравнения (1.2), после чего легко получить общее решение неоднородного уравнения в виде (1.27). Но мы знаем,
линейно независимых решений однородного уравнения (1.2), после чего легко получить общее решение неоднородного уравнения в виде (1.27). Но мы знаем,
как получить  линейно независимых решений во всей области непрерывности коэффициентов
линейно независимых решений во всей области непрерывности коэффициентов 
Эти решения мы, очевидно, получим в виде сходящихся рядов Пикара. Однако решение в такой форме не всегда нас удовлетворяет, так как не всегда позволяет изучить поведение решения, в особенности при  Поэтому существуют другие способы представления решения линейных уравнений в частных случаях. Далее мы с ними познакомимся.
Поэтому существуют другие способы представления решения линейных уравнений в частных случаях. Далее мы с ними познакомимся.
Покажем теперь, что если известны  линейно независимых решений уравнения
линейно независимых решений уравнения  то интегрирование уравнения (1.2) приводится к интегрированию линейного уравнения
то интегрирование уравнения (1.2) приводится к интегрированию линейного уравнения  -го порядка. Итак, пусть
-го порядка. Итак, пусть  линейно независимые решения уравнения (1.2). Полагаем
линейно независимые решения уравнения (1.2). Полагаем

Отсюда

Подставим это в (1.1). Получим

Так как  то после деления на
то после деления на  полученное равенство можно переписать так:
полученное равенство можно переписать так:

Это уравнение  порядка.
порядка.
Из (1.28) имеем

Здесь  являются линейно независимыми решениями уравнения (1.29). То, что
являются линейно независимыми решениями уравнения (1.29). То, что  -решения уравнения (1.29), понятно. Покажем, что
-решения уравнения (1.29), понятно. Покажем, что  линейно независимы. Действительно, предположим, что
линейно независимы. Действительно, предположим, что  линейно зависимые, т. е.
линейно зависимые, т. е.  где
где  не все равны нулю. Тогда, интегрируя это равенство, на основании (1.28) получаем
не все равны нулю. Тогда, интегрируя это равенство, на основании (1.28) получаем

 — линейно зависимые, что противоречит выбору
— линейно зависимые, что противоречит выбору  Следовательно,
Следовательно,  — линейно независимые
— линейно независимые
решения уравнения (1.29). Отсюда и следует, что после  -кратного введения новой неизвестной функции по формулам типа (1.28) получим уравнение
-кратного введения новой неизвестной функции по формулам типа (1.28) получим уравнение  -го порядка. В частности, если имеем уравнение второго порядка
-го порядка. В частности, если имеем уравнение второго порядка

и нам известно одно нетривиальное (т. е. отличное от  решение
решение  то, полагая
то, полагая

получим для  линейное уравнение
линейное уравнение

откуда найдем

и тем самым найдем общее решение исходного уравнения

Замечание 1.3. Пусть в уравнении  вещественные функции. Будем рассматривать комплексное решение
вещественные функции. Будем рассматривать комплексное решение

где  — вещественные функции. Согласно определению производной, имеем
— вещественные функции. Согласно определению производной, имеем

Подставляя значения этих производных в (1.2), получаем

Полученное равенство выполняется тогда и только тогда, когда

Отсюда видим, что  — решение только в том случае, когда и
— решение только в том случае, когда и  — решения.
— решения.
Замечание 1.4. Если будем искать решение задачи Коши

где  вещественные, то должно быть
вещественные, то должно быть

А тогда, согласно замечанию 1.1, решение 
Два важных примера линейно независимых функций.
1. Функции  — линейно независимые, так как если имеем
— линейно независимые, так как если имеем  где не все
где не все  равны нулю, то имеем бесконечное число различных корней
равны нулю, то имеем бесконечное число различных корней  этого уравнения, что противоречит теореме из алгебры о том, что их должно быть не более
этого уравнения, что противоречит теореме из алгебры о том, что их должно быть не более  различных.
различных.
Рассмотрим функцию  где
где  — комплексное с вещественными а и
— комплексное с вещественными а и  Если X — вещественное, то производные
Если X — вещественное, то производные  . Покажем, что эта формула остается верной и
. Покажем, что эта формула остается верной и  случае комплексного X.
случае комплексного X.
По формулам Эйлера

Легко видеть, что

т. е.

Но тогда, очевидно, имеем

Замечание 1.5. Пусть  где X — постоянное
где X — постоянное  (вещественное или комплексное) и
(вещественное или комплексное) и  — апхп
— апхп  — полином степени
— полином степени  — постоянные. Тогда
— постоянные. Тогда

где  полином степени
полином степени  с коэффициентом, равным
с коэффициентом, равным  при
при 
2. Пусть  — неравные между собой постоянные. Покажем, что функции
— неравные между собой постоянные. Покажем, что функции

где  — положительные целые числа, линейно независимые.
— положительные целые числа, линейно независимые.
Доказательство. Предположим противное, т. е. что они линейно зависимы. Тогда, умножая эти функции на постоянные и складывая, получим

где  — полиномы степени
— полиномы степени  и, по крайней мере, один из них имеет коэффициент, отличный от нуля. Пусть этим полиномом будет
и, по крайней мере, один из них имеет коэффициент, отличный от нуля. Пусть этим полиномом будет  степени
степени  Умножим равенство (1.31) на
Умножим равенство (1.31) на 

Здесь  так как
так как  различны. Дифференцируя это тождество
различны. Дифференцируя это тождество  раз, на основании замечания 1.5 получаем
раз, на основании замечания 1.5 получаем

или после умножения на 

Здесь  полином снова степени
полином снова степени  т. е. коэффициент при старшей степени
т. е. коэффициент при старшей степени  отличен от нуля. Повторяя это рассуждение
отличен от нуля. Повторяя это рассуждение  раз, получаем тождество
раз, получаем тождество

где  полином
полином  -степени. Но это невозможно, так как
-степени. Но это невозможно, так как  только в том случае, когда все коэффициенты равны нулю. Таким образом, функции (1.30) не могут быть линейно зависимыми.
только в том случае, когда все коэффициенты равны нулю. Таким образом, функции (1.30) не могут быть линейно зависимыми.
| << Предыдущий параграф | Следующий параграф >> |
- ВМЕСТО ПРЕДИСЛОВИЯ
- ГЛАВА I. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ
- § 2. Общее, частное и особое решения
- § 3. Дифференциальное уравнение с разделяющимися переменными
- § 4. Однородные уравнения
- § 5. Уравнения, приводящиеся к однородному
- § 6. Линейное уравнение
- § 7. Уравнение Риккати
- § 8. Дифференциальные уравнения в полных дифференциалах
- § 9. Интегрирующий множитель
- § 10. Строгое определение общего решения
- § 11. Особое решение
- § 12. Интеграл
- § 13. Уравнения, не разрешенные относительно у’
- § 14. Решение в параметрическом виде
- § 15. Частные случаи дифференциальных уравнений, не разрешенных относительно у’
- § 16. Расположение интегральных кривых в окрестности границы области D(x, у)
- ГЛАВА II. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Интегралы системы
- § 3. Уравнение n-го порядка
- § 4. Приведение уравнения n-го порядка к системе n уравнений первого порядка и наоборот
- § 5. Частные случаи уравнения n-го порядка
- ГЛАВА III. ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
- § 2. Теорема Коши
- § 3. Линейные системы
- § 4. Теорема Пикара
- § 5. Частные случаи теоремы Пикара
- § 6. Область существования решения
- § 7. Непрерывная зависимость решений от параметров
- § 8. Дифференцируемость по параметру
- § 9. Теоремы о существовании решений в максимальной области, зависящей от параметра
- § 10. Построение решений во всей области существования
- § 11. Существование общего решения
- § 12. Устойчивость по Ляпунову. Еще об общем решении
- § 13. Существование дифференцируемых полных интегралов
- ГЛАВА IV. ЛИНЕЙНОЕ УРАВНЕНИЕ n-го ПОРЯДКА
- § 2. Однородное уравнение с постоянными вещественными коэффициентами
- § 3. Примеры
- ГЛАВА V. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 2. Неоднородная система
- § 3. Однородные линейные системы с постоянными коэффициентами
- § 4. О матрицах
- § 5. Общее исследование системы (3.1)
- § 6. Матричный метод
- § 7. Теорема о преобразовании системы (6.1) в каноническую вещественную систему
- § 8. Неоднородные линейные системы с постоянными коэффициентами
- ГЛАВА VI. ВОПРОСЫ УСТОЙЧИВОСТИ
- § 1. Устойчивость по Ляпунову
- § 2. Теорема Ляпунова
- § 3. Устойчивость решений линейных систем
- § 4. Линейные однородные системы с периодическими коэффициентами
- § 5. Второй метод Ляпунова
- ГЛАВА VII. ЛИНЕЙНЫЕ УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА
- § 1. Однородное дифференциальное уравнение первого порядка в частных производных
- § 2. Построение решения задачи Коши
- § 3. Решение задачи Коши для однородного уравнения с n независимыми переменными
- § 4. Неоднородное уравнение
- § 5. Задача Коши для неоднородного уравнения
- § 6. Общая задача Коши для неоднородного уравнения
- ГЛАВА VIII. МЕТОД ПРЕОБРАЗОВАНИЙ И МЕТОД ОСОБЫХ РЕШЕНИЙ
- § 2. Признаки интегрируемости уравнения (1.1) в замкнутой форме
- § 3. Метод последовательных преобразований
- § 4. Эвристический метод преобразований
- § 5. Осуществимость преобразований
- § 6. Метод преобразований в системах
- ГЛАВА IX. РЕШЕНИЯ С ОСОБЫМИ НАЧАЛЬНЫМИ ЗНАЧЕНИЯМИ. УРАВНЕНИЕ у’=Р(х, y)/Q(x, у)
- § 1. Уравнение y’ = P(x,y)/Q(x,y)
- § 2. Уравнение Брио и Буке
- § 3. Теорема Пуанкаре
- ГЛАВА X. СРАВНЕНИЕ РЕШЕНИЙ ПОЛНОГО И УКОРОЧЕННОГО ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Случай, когда y(t) и z(t) — решения дифференциальных уравнений
- § 3. Представление решений полного уравнения через измененное укороченное
- § 4. Общий метод доказательства существования разложения (1.1)
- § 5. Продолжение § 4
- ГЛАВА XI. РАЗНОТЕМНЫЕ ЗАМЕЧАНИЯ
- § 1. О стационарных интегралах
- § 2. Интегралы системы (1.1), не зависящие от t
- § 3. Построение систем дифференциальных уравнений, имеющих заданную интегральную кривую
- § 4. О периодических решениях
- § 5. Гамильтоновы системы двух уравнений
- § 6. Система Гамильтона, варьированная относительно системы (5.22)
- § 7. Задачи Пуанкаре о периодических решениях
- § 8. Метод неподвижных точек
- § 9. Принцип кольца
- § 10. Предельные циклы и построение решений вблизи предельных циклов
- § 11. Уравнение Риккати
- ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С МАЛЫМ ПАРАМЕТРОМ
- § 2. Замечания о преобразованиях рядов
- § 3. Система …
- § 4. Нелинейные уравнения
- § 5. Уравнение …
- § 6. Уравнения с малым параметром при старшей производной
- § 7. Примеры тихоновских систем
- ГЛАВА XIII. ТЕОРИЯ ПОДВИЖНЫХ ОСОБЫХ ТОЧЕК В ВЕЩЕСТВЕННОЙ ОБЛАСТИ
- § 1. Системы, решения которых существуют в области …
- § 2. Поведение решений при t->оо
- § 3. О решениях систем двух дифференциальных уравнений типа Брио и Буке
- § 4. Особые случаи системы (3.1)
- § 5. Подвижные особые точки решений системы двух уравнений
- § 6. Случай …
- § 7. Построение решений (5.10)
- § 8. Случай …
- § 10. Заключительный
- ГЛАВА XIV. ФРАГМЕНТЫ ИЗ ЭЛЕМЕНТАРНОЙ КОНСТРУКТИВНОЙ ТЕОРИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ АВТОНОМНОЙ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 1. Периодические решения вокруг центра (Ляпунов)
- § 2. Замечания
- § 3. Периодические решения вокруг центра (Пуанкаре)
- § 4. Доказательство существования и построение предельных циклов по методу Каменкова
- § 5. Существование и построение изолированных периодических решений уравнения …
- § 6. Уравнение Ван дер Поля. Качественная теория
- § 7. Конструктивное доказательство существования периодического решения системы (6.1) методом Каменкова (т. е. на основании § 4)
- § 8. Уравнение. Построение предельного цикла
- ЛИТЕРАТУРА