| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА XI. О КРУЧЕНИИ ПОЛЫХ ПРИЗМ
§ 116. Полая эллиптическая призма
Когда цилиндр, эллиптическое основание которого имеет уравнение

подвергается кручению в, то выражение (240) продольного перемещения

которое удовлетворяет, как всякое другое выражение  неопределенному дифференциальному уравнению (238)
неопределенному дифференциальному уравнению (238)  удовлетворяет также определенному уравнению (239).
удовлетворяет также определенному уравнению (239).

или

не только в точках на боковой поверхности, но также во всех точках внутри призмы, так как нет необходимости полагать  или
или  для того,
для того,
чтобы проверить это уравнение, подставляя вместо и его значение (270).
Мы видим, что когда давление на внешней поверхности не имеет продольной составляющей, отсутствует такое же давление на всякой внутренней цилиндрической поверхности с основанием, для которого имели бы также  т. е. с эллиптическим основанием, оси которого находились бы между собой в таком же отношении
т. е. с эллиптическим основанием, оси которого находились бы между собой в таком же отношении  как и оси основания данного цилиндра.
как и оси основания данного цилиндра.
Отсюда следует, что если этот цилиндр имеет полость в виде подобного цилиндра, основание которого имеет тот же центр и то же расположение, как у первого цилиндра, и если он подвергается изнутри, как и снаружи, только атмосферному давлению или давлению любой жидкости, находящейся в состоянии покоя, то продольные перемещения и его точек будут выражены посредством (270), как в сплошном цилиндре.
Отсюда находим:
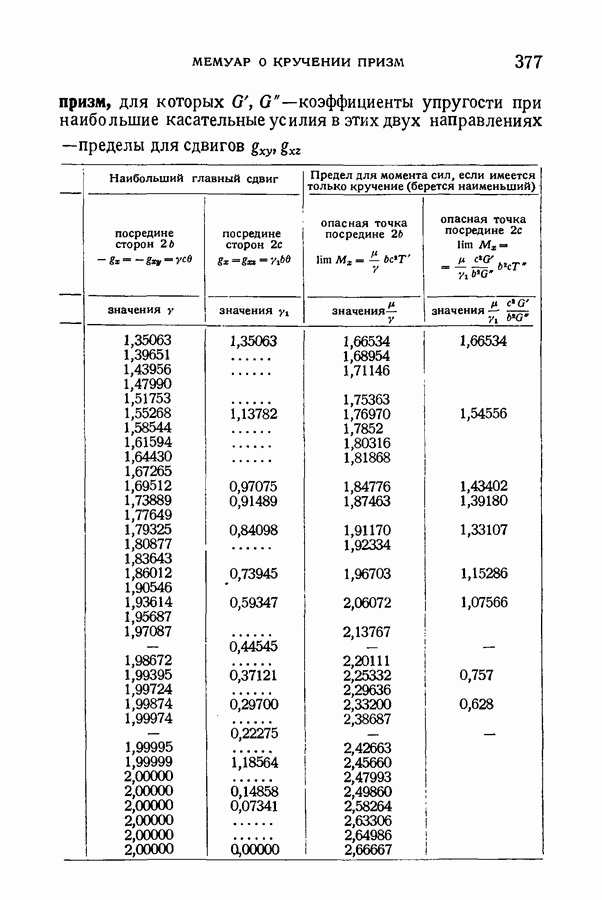
1) что крутящий момент  будет (
будет ( оси основания полости) разностью двух выражений, подобных выражению (242) § 107, т. е. получим:
оси основания полости) разностью двух выражений, подобных выражению (242) § 107, т. е. получим:

2) что точками, наиболее всего подвергающимися опасности разрыва, будут, как в сплошном цилиндре, концы оси  если (§ 108)
если (§ 108)  и Условием прочности всегда будет уравнение
и Условием прочности всегда будет уравнение

посредством которого мы исключим  из предыдущей формулы, дающей допускаемый предел
из предыдущей формулы, дающей допускаемый предел 
Мы не получили бы этих простых выражений для и, крутящего момента  и условий сопротивления, если бы оси
и условий сопротивления, если бы оси  основания полости не находились между собой в таком же соотношении, что и оси
основания полости не находились между собой в таком же соотношении, что и оси  внешнего основания, если бы мы, например, установили с последними только
внешнего основания, если бы мы, например, установили с последними только
отношение равно разностности, чтобы придать сплошной части постоянную толщину.
Но если эта толщина была бы незначительна сравнительно с осями основания, то понятно, что эти выражения могли бы быть приняты в качестве приближенных.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ЖИЗНЬ И НАУЧНАЯ ДЕЯТЕЛЬНОСТЬ Б. СЕН-ВЕНАНА
- МЕМУАР О КРУЧЕНИИ ПРИЗМ
- § 1. Прямые и обратные решения задач о твердых упругих телах
- § 2. Смешанный, или полуобратный, метод
- ГЛАВА II. ФОРМУЛЫ ВНУТРЕННЕГО РАВНОВЕСИЯ УПРУГИХ ТВЕРДЫХ ТЕЛ. КРАТКОЕ НАПОМИНАНИЕ ОБ ИХ ОБОСНОВАНИИ ДЛЯ ПЕРЕМЕЩЕНИЙ ПРОИЗВОЛЬНОЙ ВЕЛИЧИНЫ
- § 3. Средние перемещения малых молекулярных групп
- § 4. Удлинения. Сдвиги
- § 5. Условия, при которых даже значительные перемещения точек упругих тел не изменяют их связности. Очень малые сдвиги
- § 6. Зависимости между сдвигами и удлинениями в различных направлениях. Изменение осей
- § 7. Различные сдвиги относительно прямой или в различных направлениях относительно той же прямой. Главный сдвиг и т. д.
- § 8. Зависимости удлинений и сдвигов от весьма малых перемещений
- § 9. Давления. Их равнодействующая на различных гранях элемента. Их непрерывное изменение
- § 10. Соотношения между давлениями на различные грани, имеющие центр в одной точке
- § 11. Следствия. Изменение плоскостей давления. Плоскостл, слегка наклоненные друг к другу
- § 12. Зависимость составляющих давления от удлинений и сдвигов
- § 13. Соображения о числе отличных друг от друга коэффициентов
- § 14. Однородные тела
- § 15. Тело с тремя плоскостями симметрии или главными плоскостями упругости
- § 16. Выбор осей координат с целью приведения к одной двух касательных составляющих давления. Коэффициент упругости при сдвиге
- § 17. Тело с одинаковой упругостью сдвига во всех направлениях, перпендикулярных к одной прямой или относительно этой прямой и во всех проходящих через нее плоскостях
- § 18. Тело, в котором имеется ось упругости
- § 19. Изотропное тело
- § 20. Соотношения между давлениями и внешними или объемными силами
- § 21. Неопределенные дифференциальные уравнения, справедливые во всех точках тела
- § 22. Определенные уравнения, справедливые только в некоторых точках
- § 23. Применение этих уравнений. Прямые, обратные и смешанные задачи
- § 24. Условия сопротивления последующему разрушению или прогрессирующему и опасному изменению строения тела
- § 25. Установление условий прочности. Опасные точки
- § 26. Условия прочности, когда сдвиги равны нулю или пренебрежимо малы в трех направлениях х, у, z
- § 27. Условия прочности, когда рассматриваются только сдвиги
- § 28. Различные виды разрушений
- ГЛАВА III. ПРИМЕНЕНИЕ ТЕОРИИ В ПРОСТОМ СЛУЧАЕ РАСТЯЖЕНИЯ ИЛИ СЖАТИЯ ПРИЗМЫ С ПРОИЗВОЛЬНЫМ СНОВАНИЕМ
- § 30. Полное решение поставленной задачи
- § 31. Перемещения, не являющиеся очень малыми
- § 32. Более общая задача. Однородная призма без плоскости упругости
- § 33. Применение этих выводов на практике
- ГЛАВА IV. ПРИМЕНЕНИЕ ТЕОРИИ К ИЗГИБУ ПРИЗМЫ
- § 34. Изгиб по дуге окружности. Смешанный, или полуобратный, метод, которым мы воспользуемся
- § 35. Исследование выражений для перемещений
- § 36. Давления. Изгибающий момент
- § 37. Обобщение для случая, когда имеются продольные растяжения, равнодействующая которых не равна нулю и является постоянной
- § 38. Решение предложенной задачи определения перемещений по силам (обратная или отчасти обратная задача по отношению к только что решенной)
- § 39. Распространение этого решения на сколь угодно большой изгиб
- § 40. Неравномерный, или некруговой, изгиб
- § 41. Практические применения. Случай, когда сила или пара сил, изгибающая призму, действует в плоскости, параллельной одной из двух главных осей ее сечений
- § 42. Случай, когда плоскость действия изгибающих сил расположена косо по отношению к главным осям сечений. Определение плоскости действительного изгиба и кривизны. Условие сопротивления
- § 43. Новая форма контура сечения изогнутой призмы
- § 44. Криволинейная форма и наклон к оси первоначально плоских и нормальных сечений при неравномерном, или некруговом, изгибе
- ГЛАВА V. О КРУЧЕНИИ ПРИЗМ. ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 45. Постановка задачи. Условия, относящиеся как к перемещениям, так и к силам. Геометрическое определение движения при кручении
- § 46. Обозначения, используемые в дальнейшем (вместе с обозначениями, приведенными в §§ 4, 6, 8, 11, 15, 18, 21, 22, 24, 27, 30, 36, 40)
- § 47. Характеристические уравнения кручения или выражения для условий относительно перемещений
- § 48. Выражения, относящиеся к силам, т. е. к внешним боковым давлениям
- § 49. Предполагаемая неподвижность одной из точек оси и т. д. Приведение к случаю очень малых перемещений
- § 50. Сдвиги. Крутящие моменты. Неопределенные и определенные уравнения
- § 51. Упрощения для первых решений. Одинаковая упругость при сдвиге. Равенство нулю изгибов, а также продольных и поперечных удлинений
- ГЛАВА VI. КРУЧЕНИЕ ПРИЗМЫ ИЛИ ЦИЛИНДРА С ЭЛЛИПТИЧЕСКИМ ОСНОВАНИЕМ
- § 53. Сдвиги и крутящий момент
- § 54. Поперечные перемещения
- § 55. Давления, которые при этом возникают
- § 56. Решение задачи определения перемещений по данным силам
- § 57. Искривление сечения. Его влияние. Случай кругового сечения, когда искривление отсутствует
- § 58. Практический случай
- § 59. Кручение может иметь место только относительно оси призмы
- § 60. Значительные перемещения, вызванные кручением
- § 61. Наибольший сдвиг. Опасные точки
- § 62. Сравнение с прежней теорией. Объяснение
- § 63. Условие отсутствия разрушения или прочности сцепления
- ГЛАВА VII. ОБЩИЕ ВЫРАЖЕНИЯ ДЛЯ ИНТЕГРАЛОВ НЕОПРЕДЕЛЕННОГО УРАВНЕНИЯ И ВЫТЕКАЮЩИЕ ОТСЮДА ВЫРАЖЕНИЯ СДВИГОВ И КРУТЯЩЕГО МОМЕНТА
- § 65. Случай, когда сечение симметрично, а силы распределены симметрично по отношению к одной из двух осей у или z или по отношению к обеим осям
- § 66. Целое многочленное выражение. Его запись в полярных координатах и распространение на произвольные показатели степени
- § 67. Члены ряда, исчезающие при симметричном сечении. Члены, исчезающие при сечении, одинаковом в обоих направлениях у и z
- ГЛАВА VIII. КРУЧЕНИЕ ПРИЗМЫ С ПРЯМОУГОЛЬНЫМ ОСНОВАНИЕМ
- § 69. Неопределенные и определенные уравнения
- § 70. Решение этих уравнений
- § 71. Сдвиги. Проверка
- § 72. Касательные давления. Крутящий момент. Нормальные давления
- § 73. Задача о перемещениях при заданных силах. Случай из практики
- § 74. Первый пример. Случай, когда одна из сторон прямоугольника очень велика по сравнению с другой
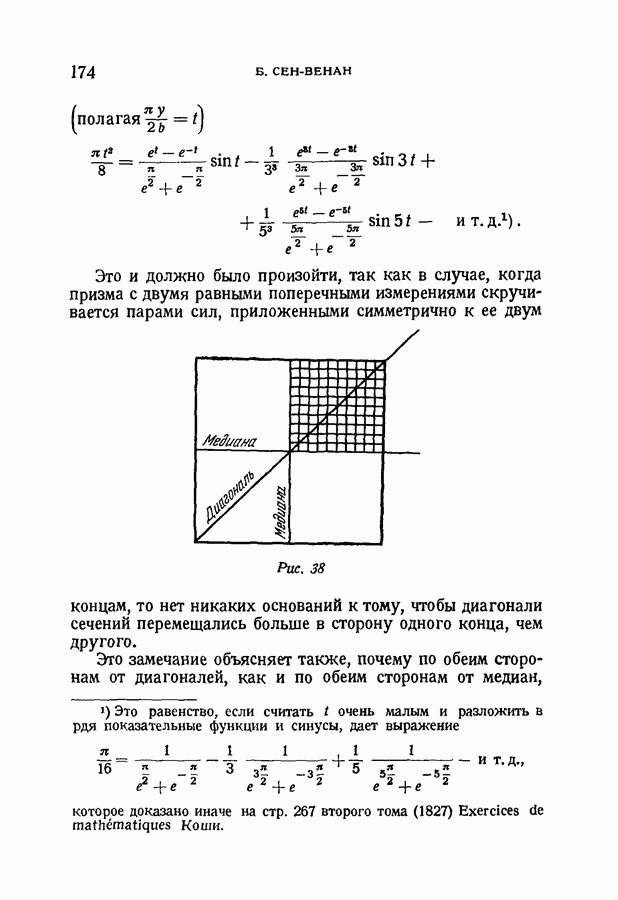
- § 75. Второй пример. Призма с основанием в виде квадрата (рис. 37)
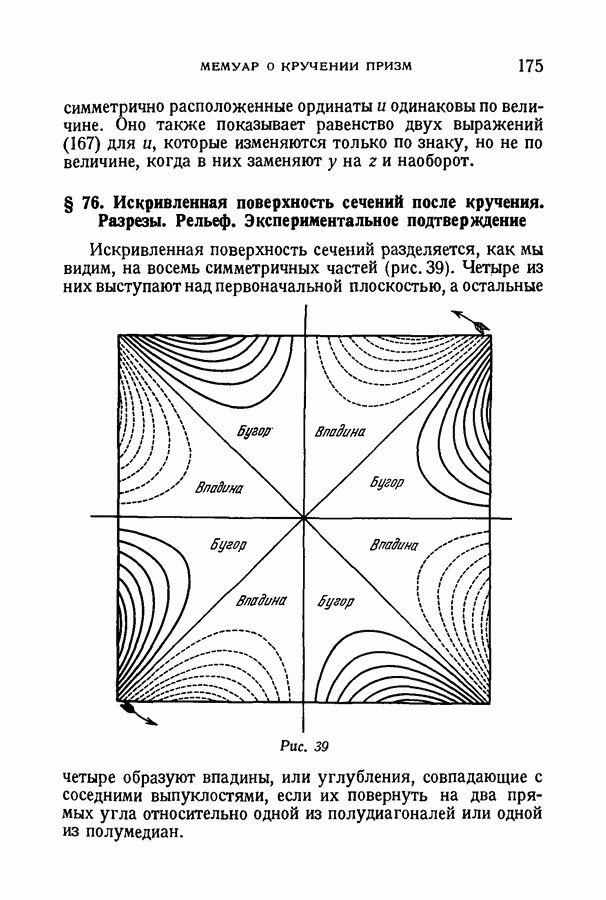
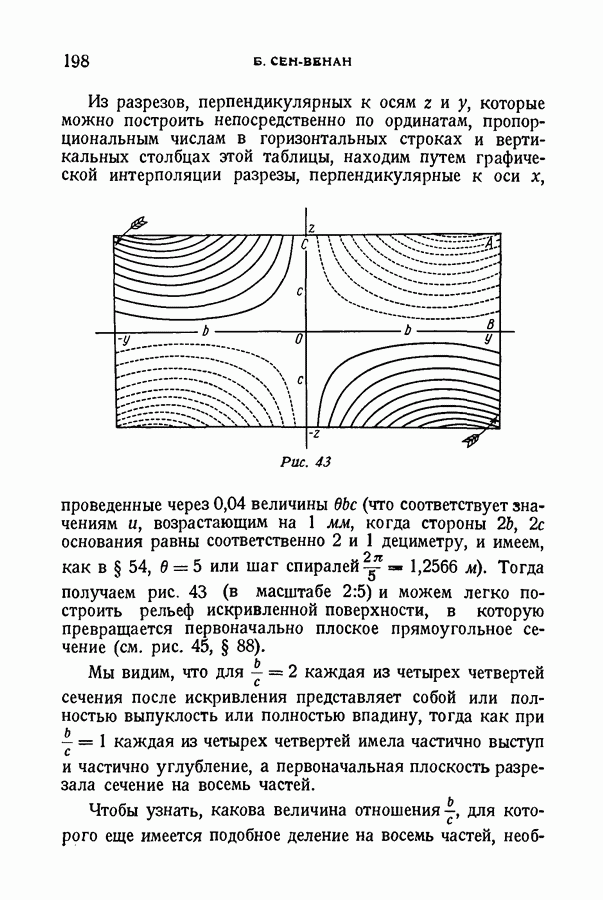
- § 76. Искривленная поверхность сечений после кручения. Разрезы. Рельеф. Экспериментальное подтверждение
- § 77. Крутящий момент для квадратной призмы
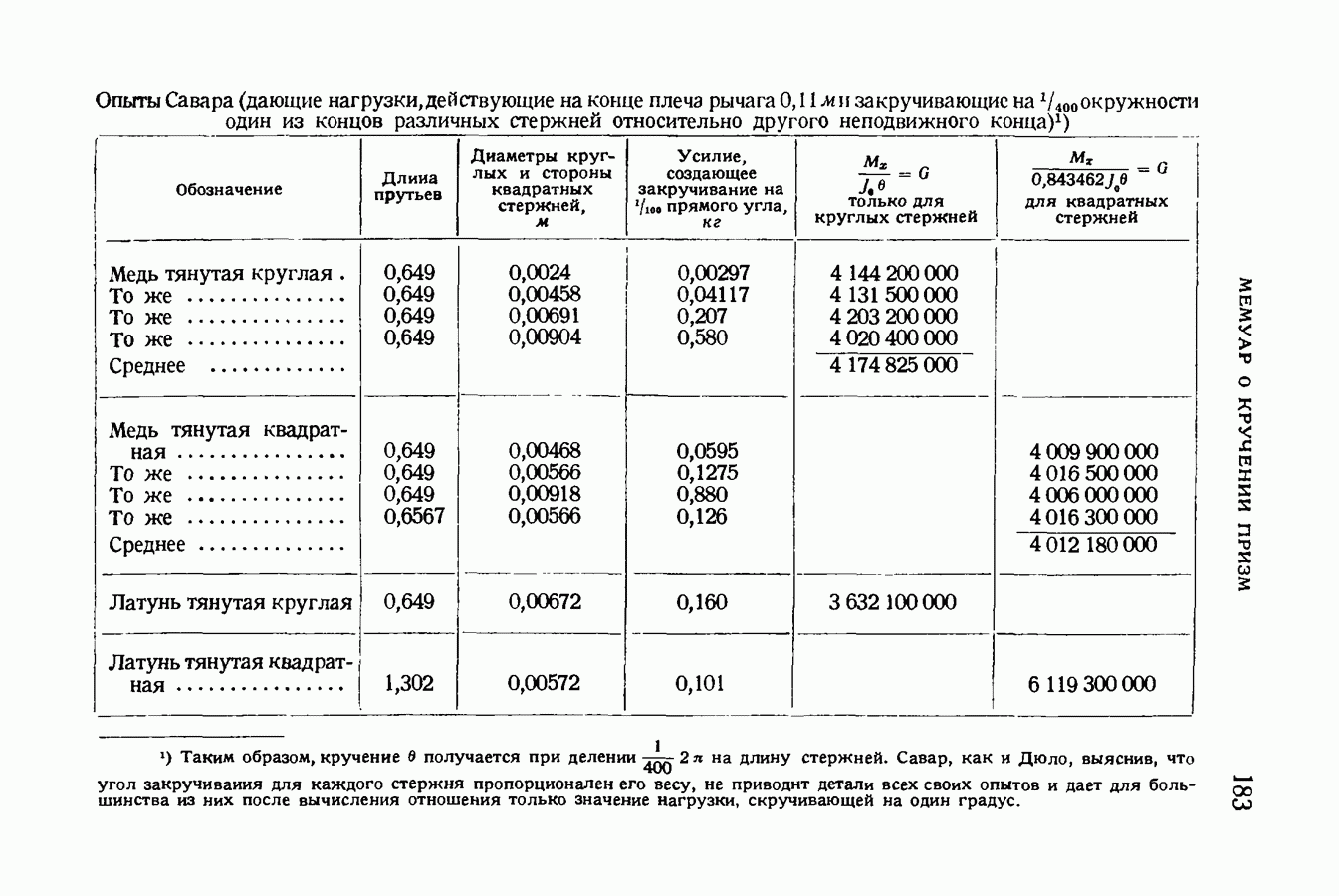
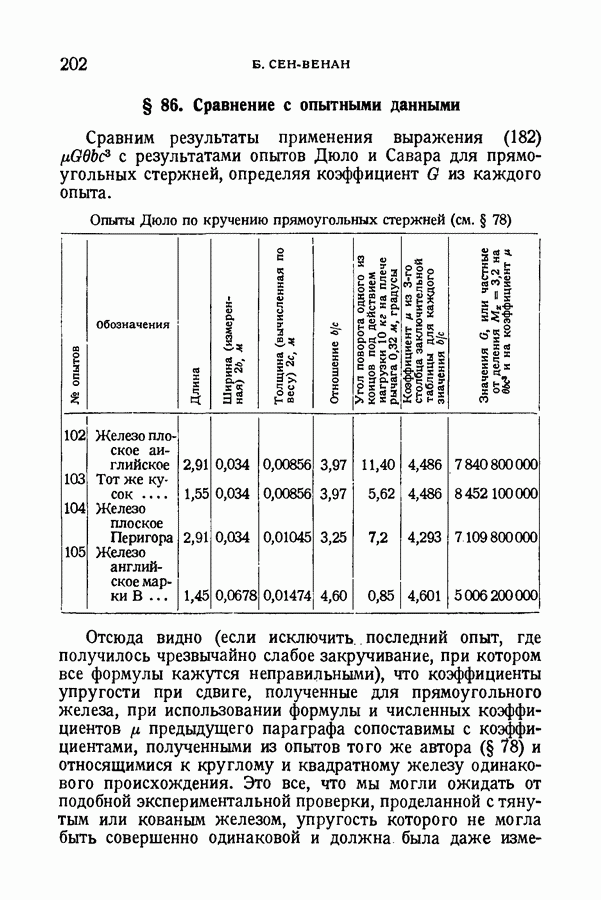
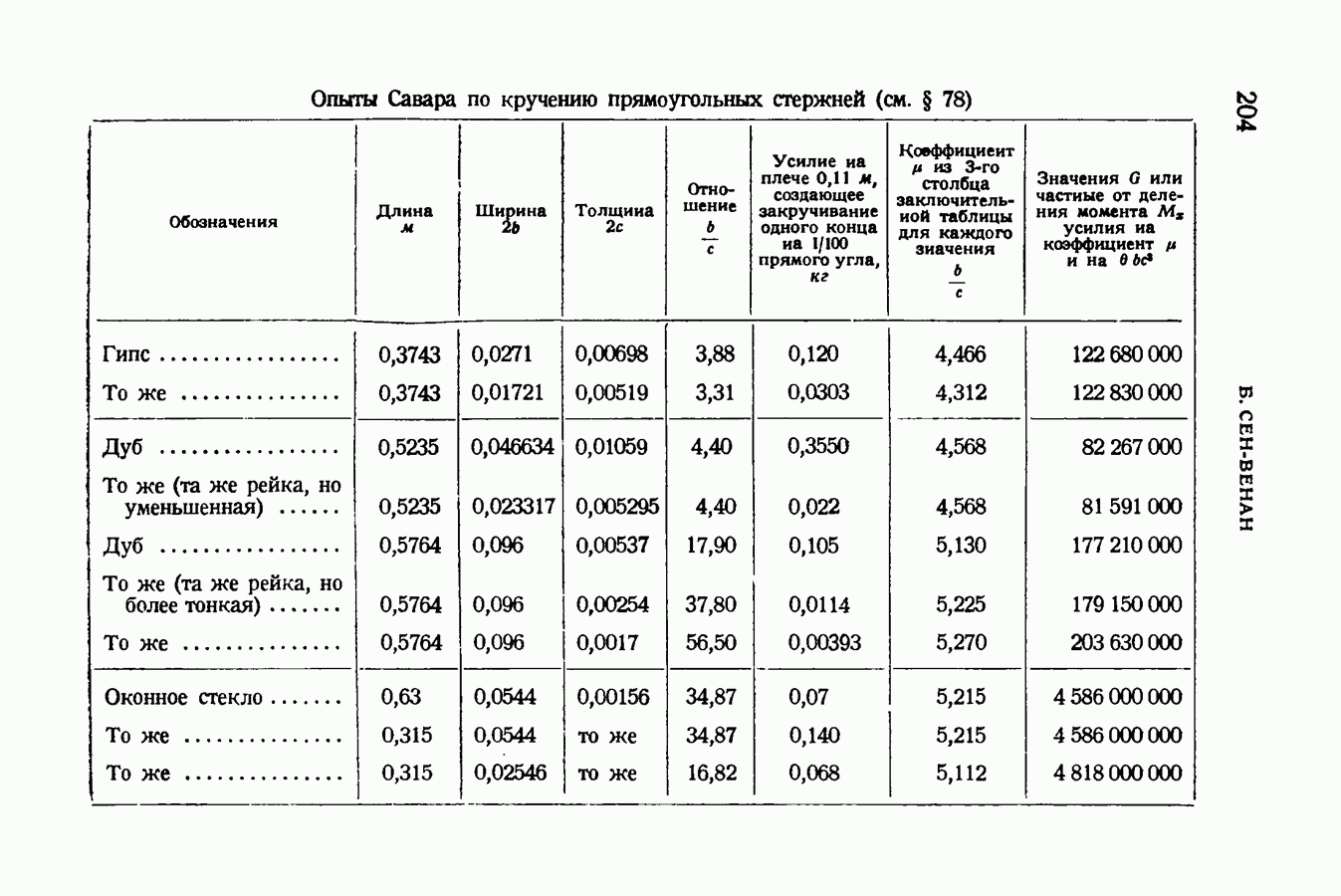
- § 78. Экспериментальное подтверждение
- § 79. Другой способ определения численного соотношения между сопротивлением квадратных призм и сопротивлением круговых цилиндров при одинаковом моменте инерции их оснований
- § 80. Продолжение. Общее целое выражение крутящего момента для прямоугольной призмы
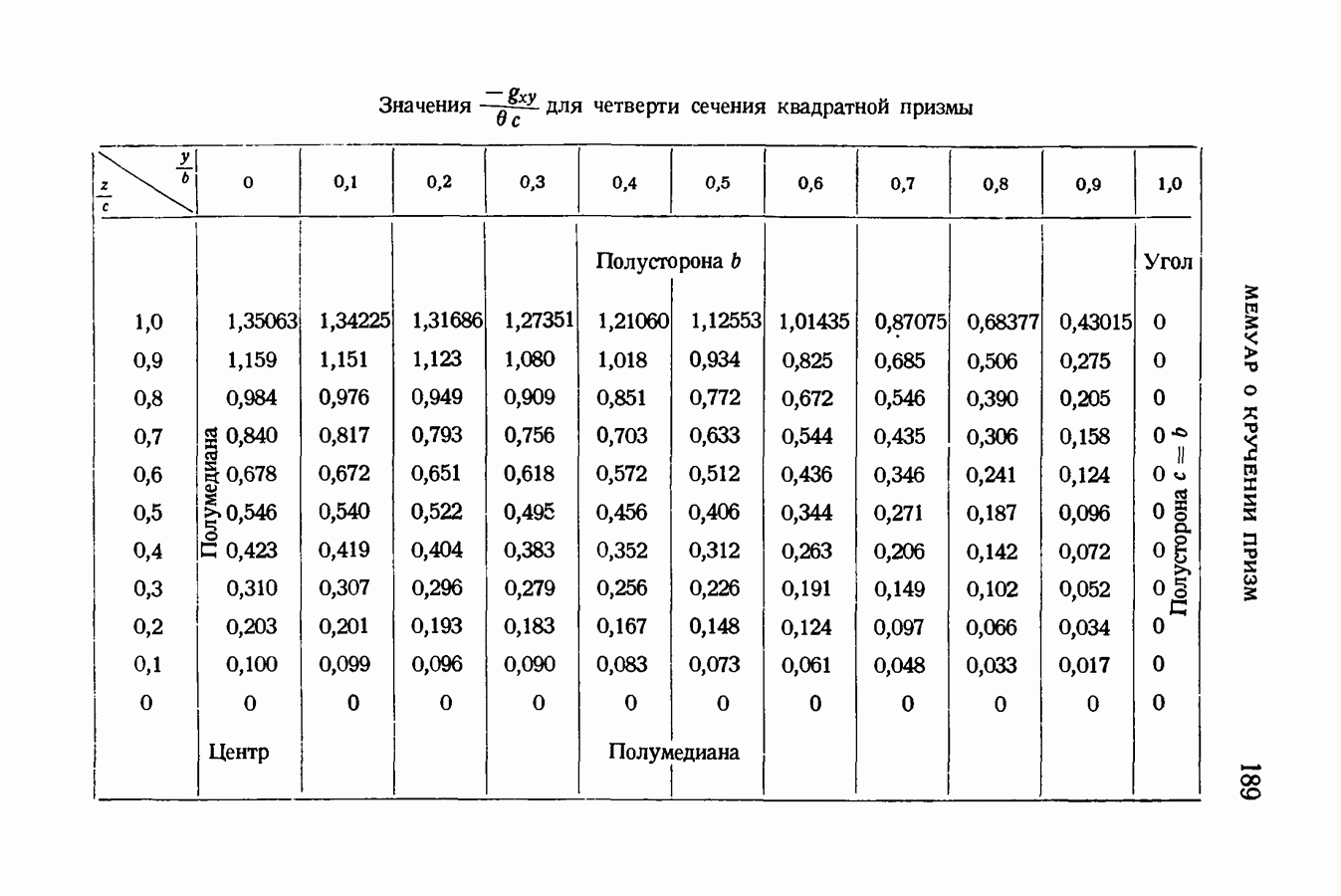
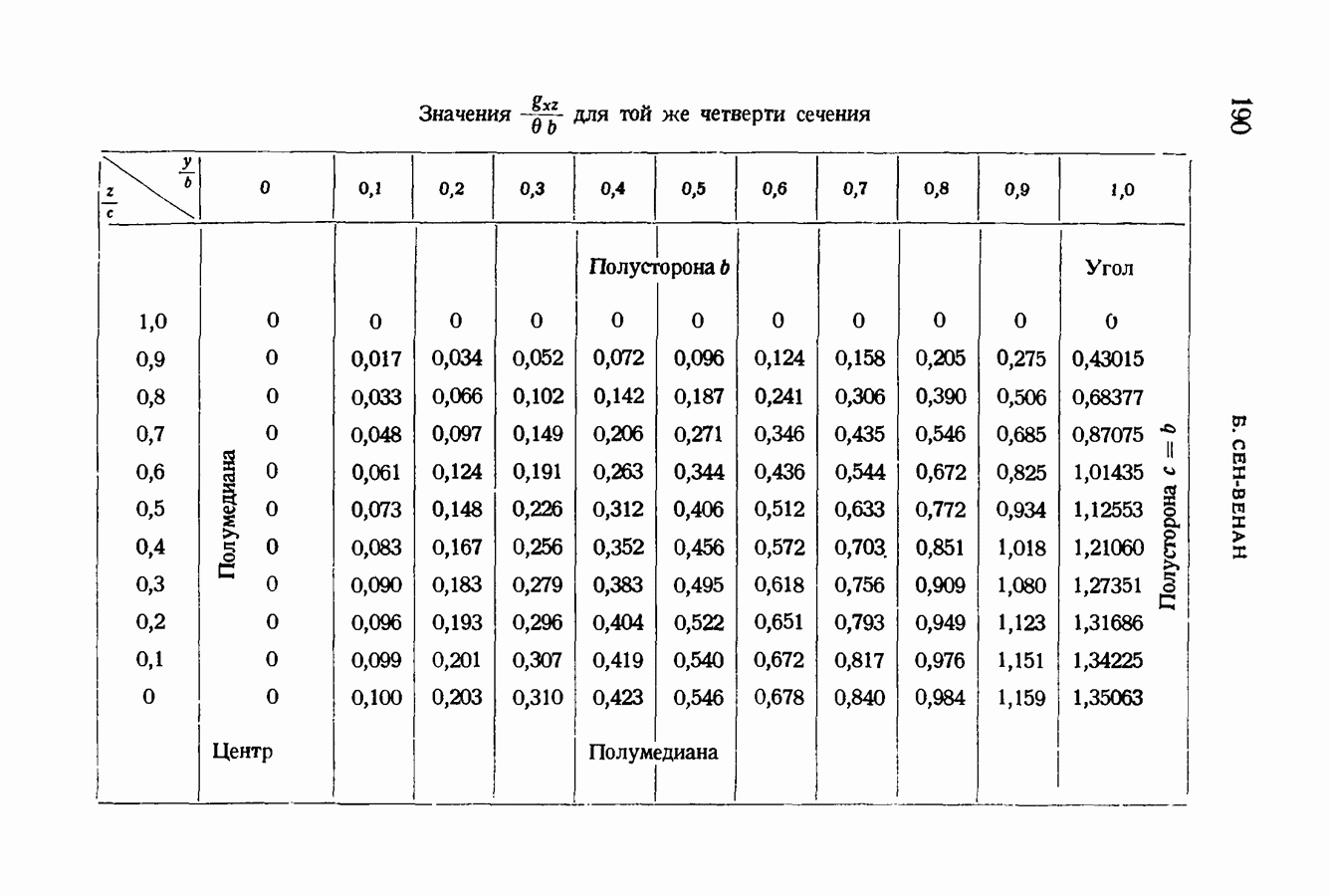
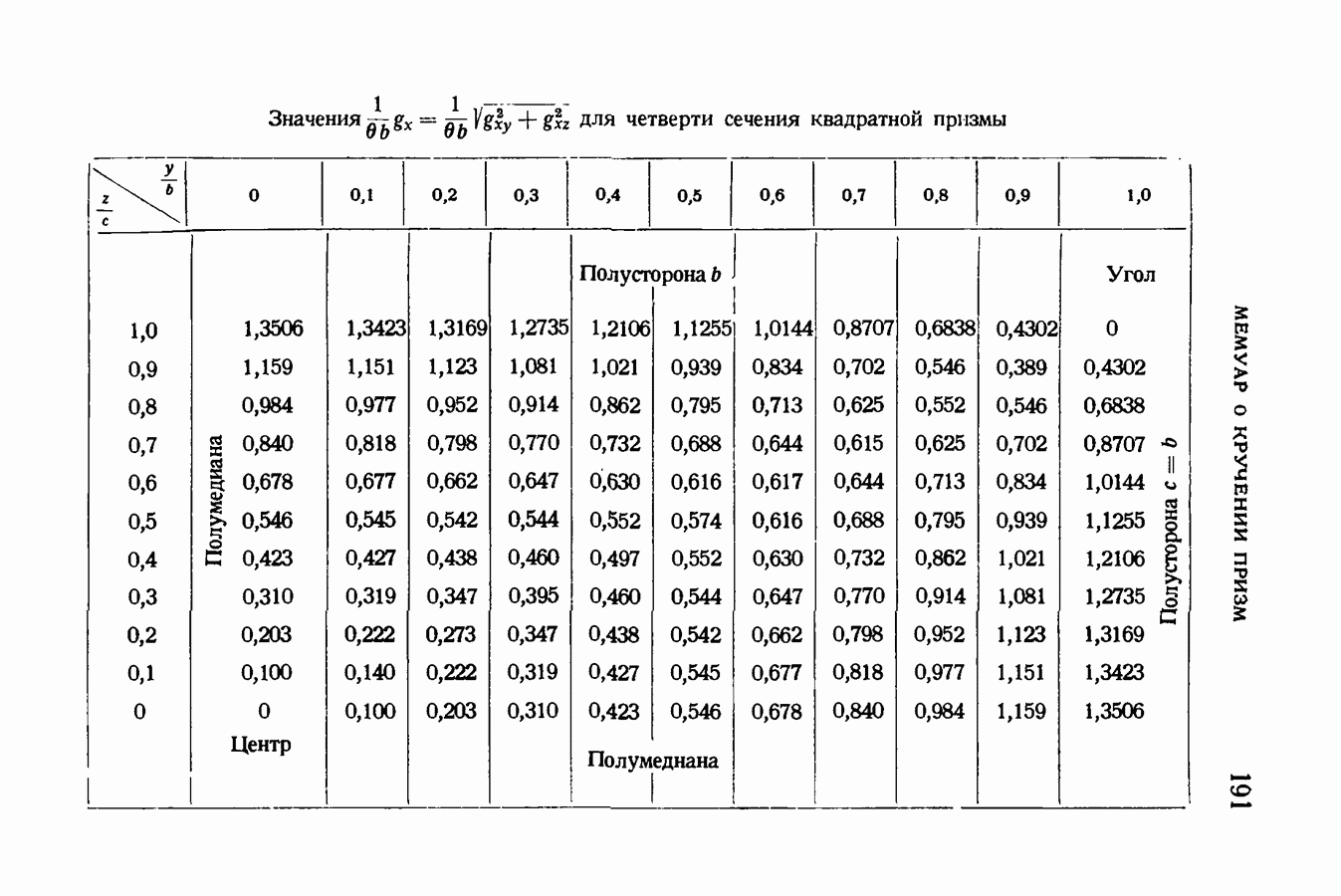
- § 81. Относительные сдвиги волокон призмы с квадратным сечением
- § 82. Опасные точки. Наибольший сдвиг
- § 83. Условие прочности квадратной призмы. Экспериментальное подтверждение
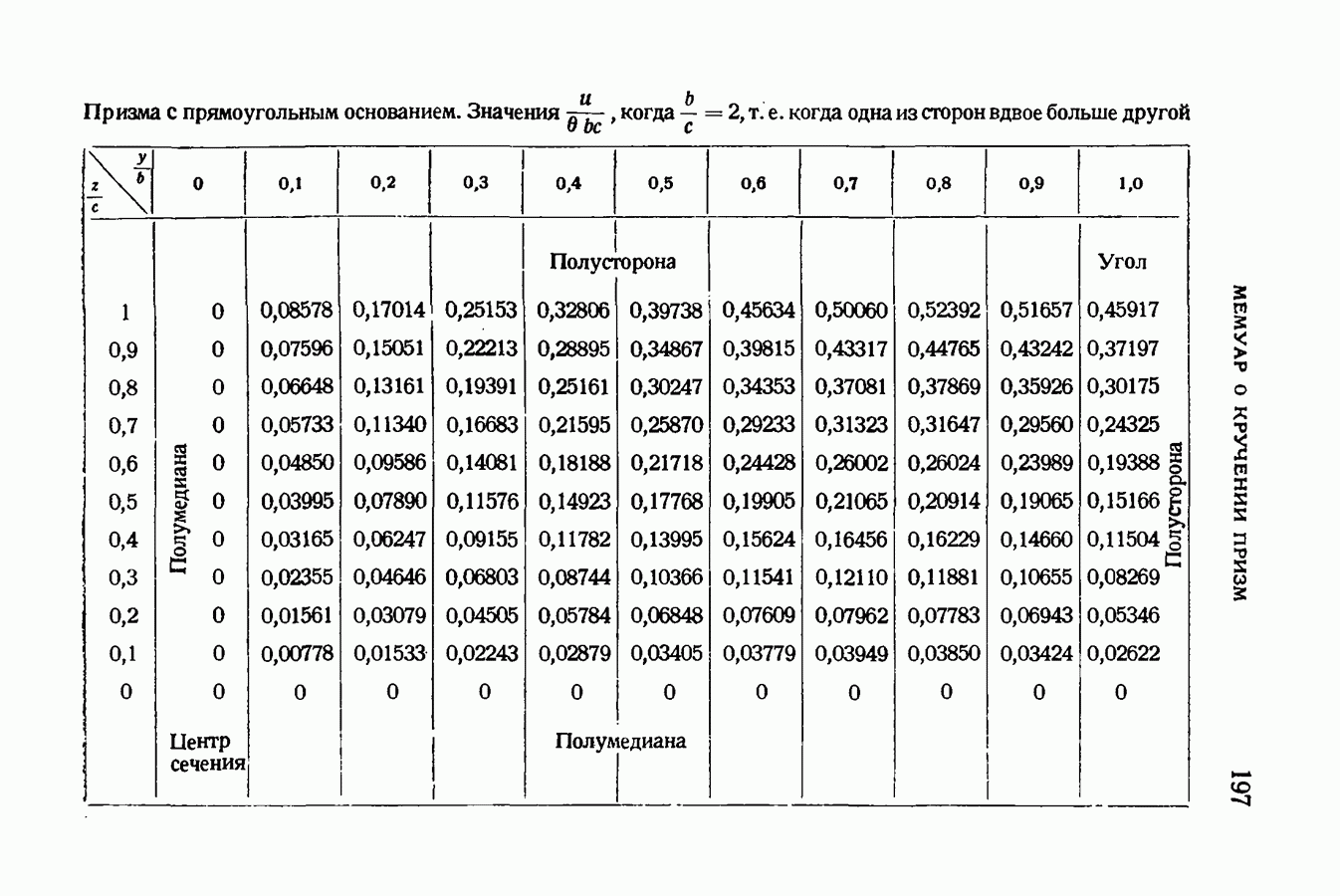
- § 84. Случай любого соотношения между двумя измерениями основания. Вычисление u при b/c=2. Границы случаев, когда искривленное сечение делится на четыре или на восемь частей
- § 85. Крутящий момент для прямоугольных призм
- § 86. Сравнение с опытными данными
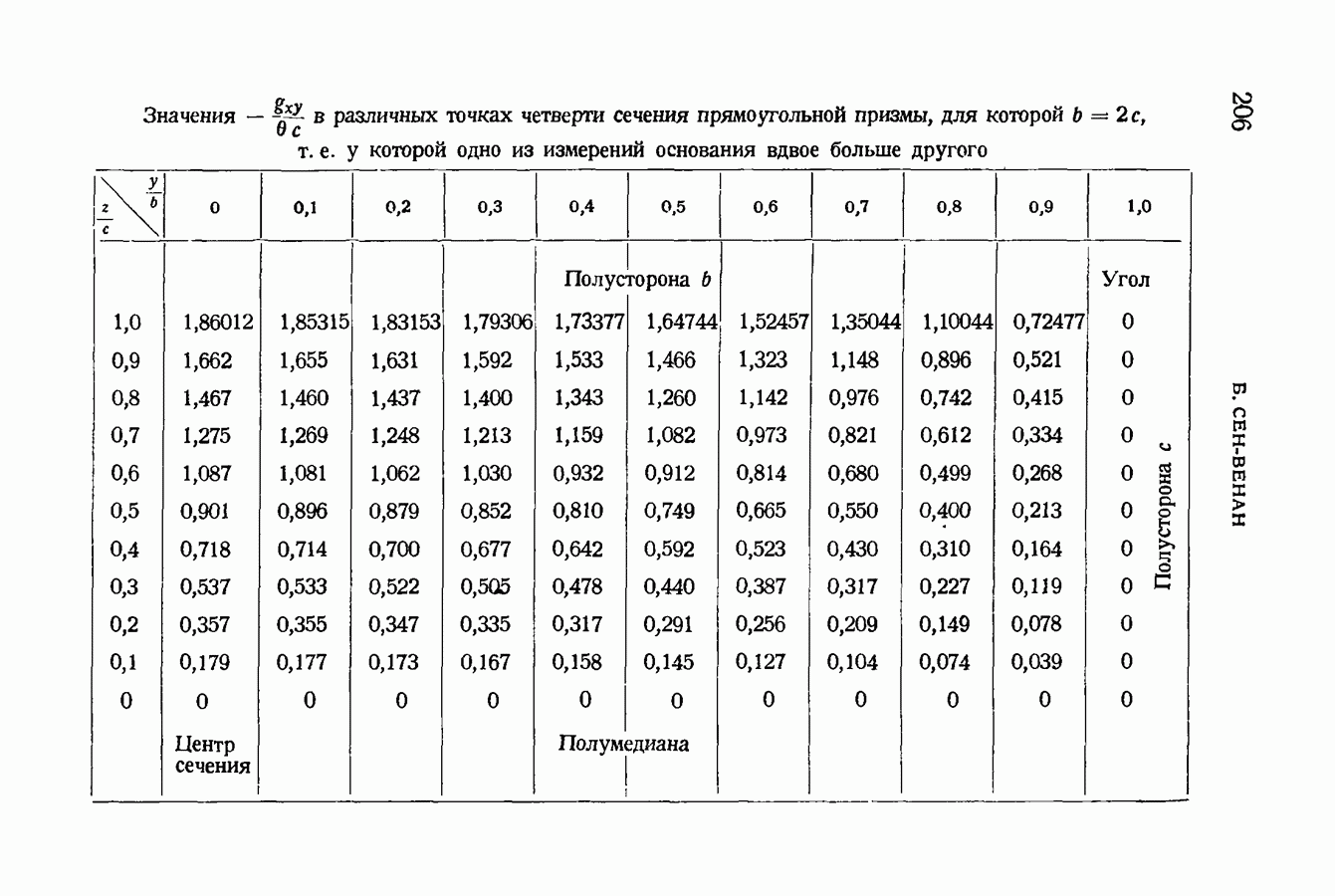
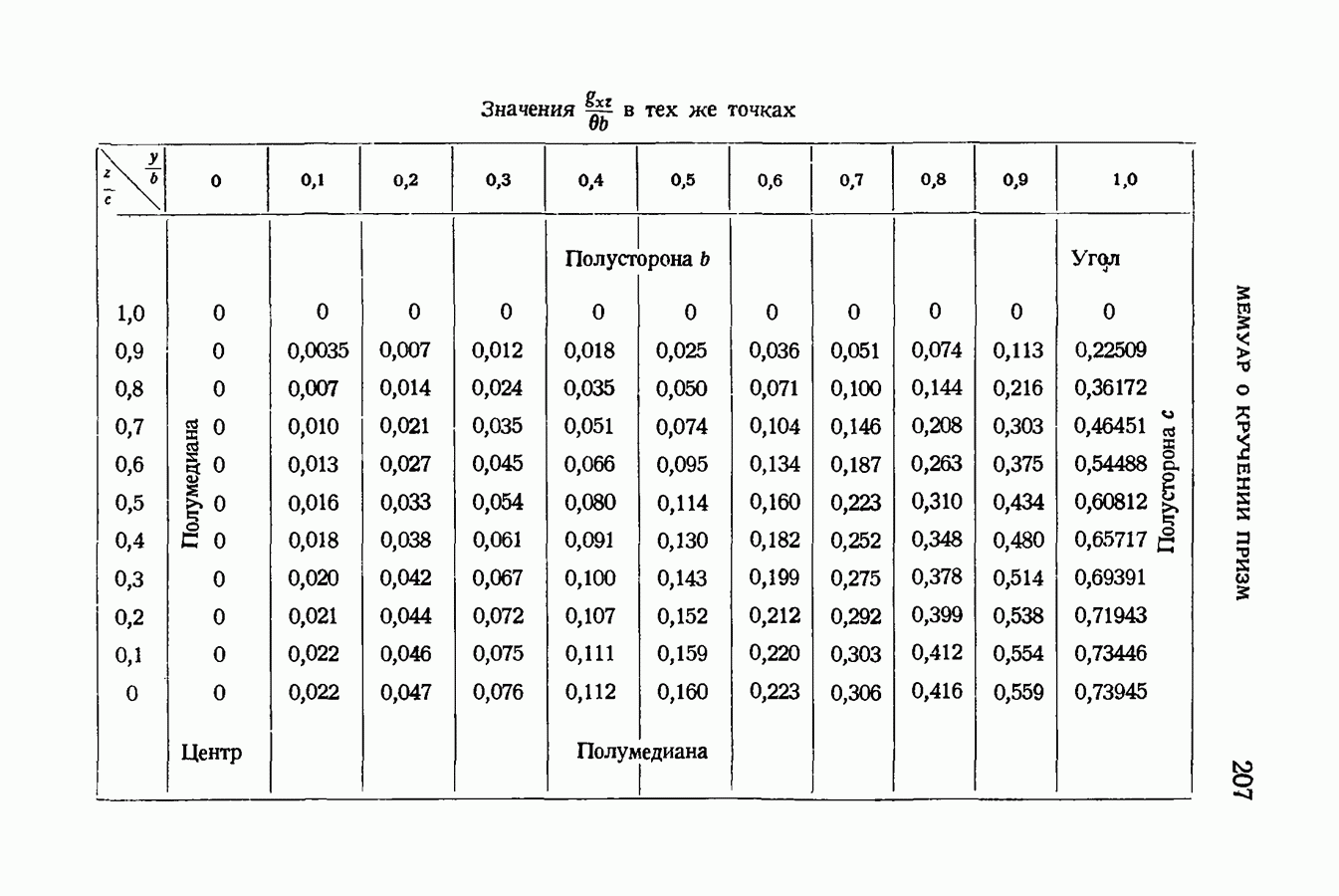
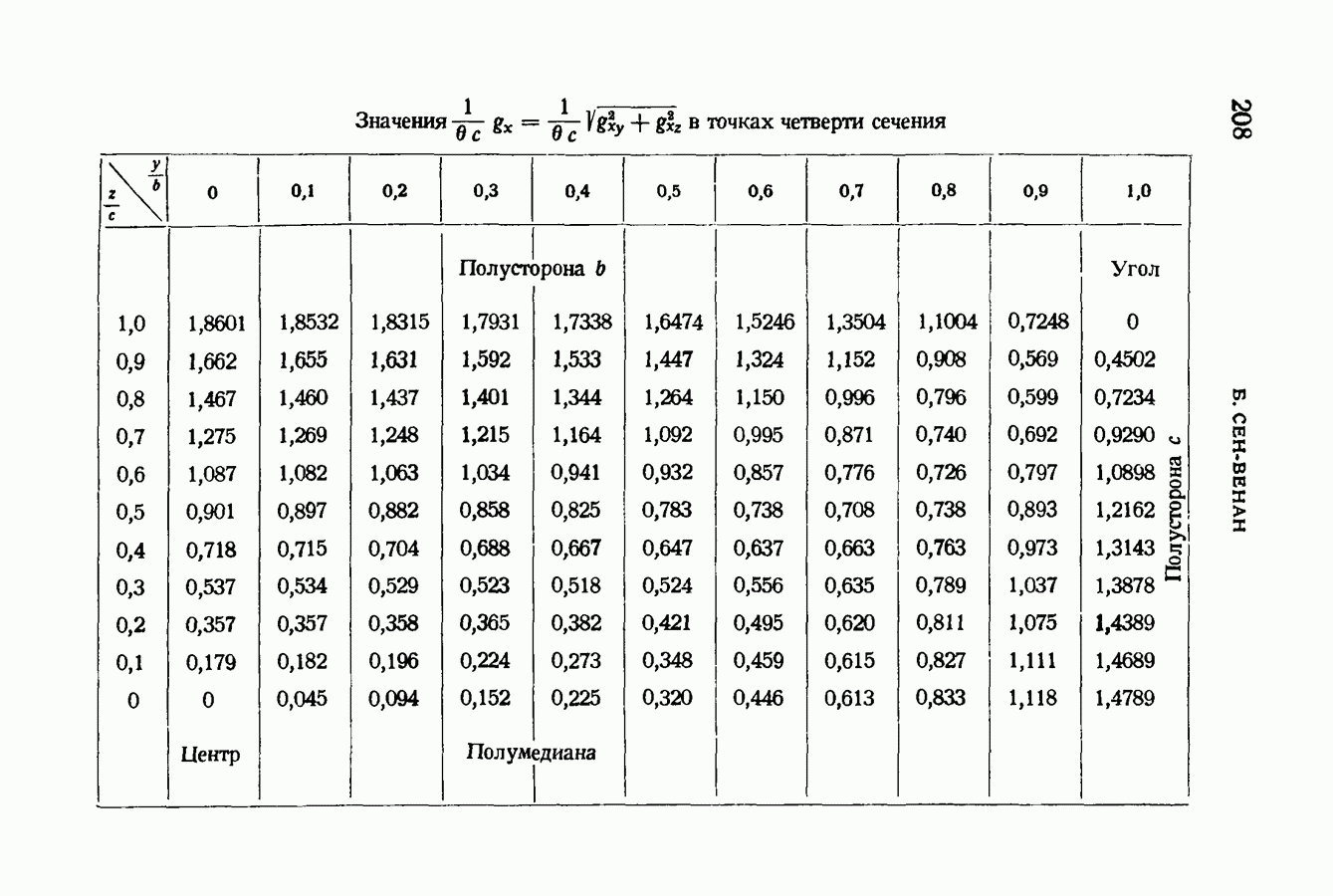
- § 87. Относительные сдвиги волокон для прямоугольных сечений. Наибольшие сдвиги для точек каждой из их сторон
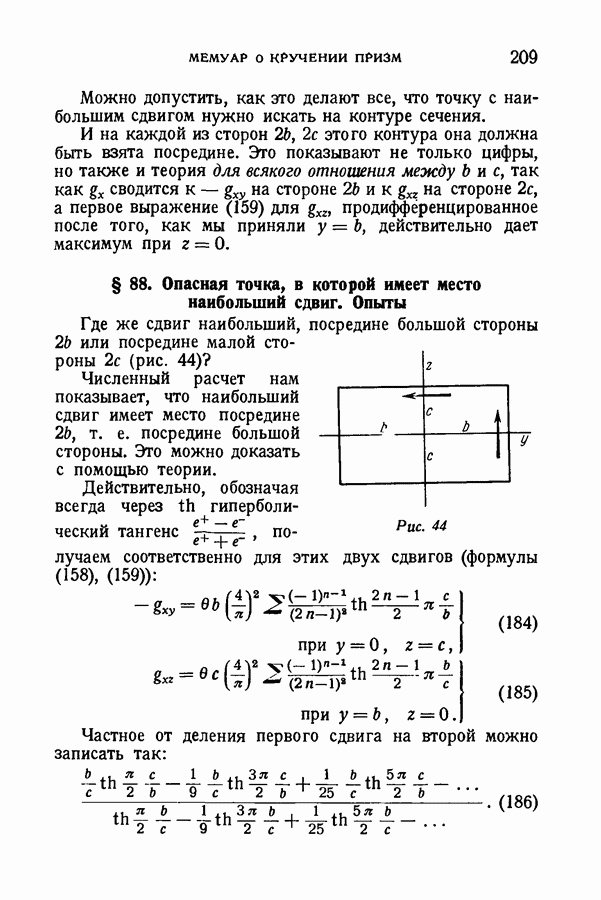
- § 88. Опасная точка, в которой имеет место наибольший сдвиг. Опыты
- § 89. Уравнение отсутствия разрушения или прочности сцепления скрученной призмы. Наибольшие сдвиги
- ГЛАВА IX. КРУЧЕНИЕ ПРИЗМ С ДРУГИМИ ОСНОВАНИЯМИ, НЕ В ВИДЕ ЭЛЛИПСА ИЛИ ПРЯМОУГОЛЬНИКА
- § 90. Бесконечность числа видов уравнения контура сечения и выражений для продольного перемещения u
- § 91. Трансцендентные и алгебраические виды выражения u
- § 92. Симметричные алгебраические кривые. Кривые, одинаковые в двух направлениях
- § 93. Способы, с помощью которых уравнениям придают определенную форму и делают их однородными
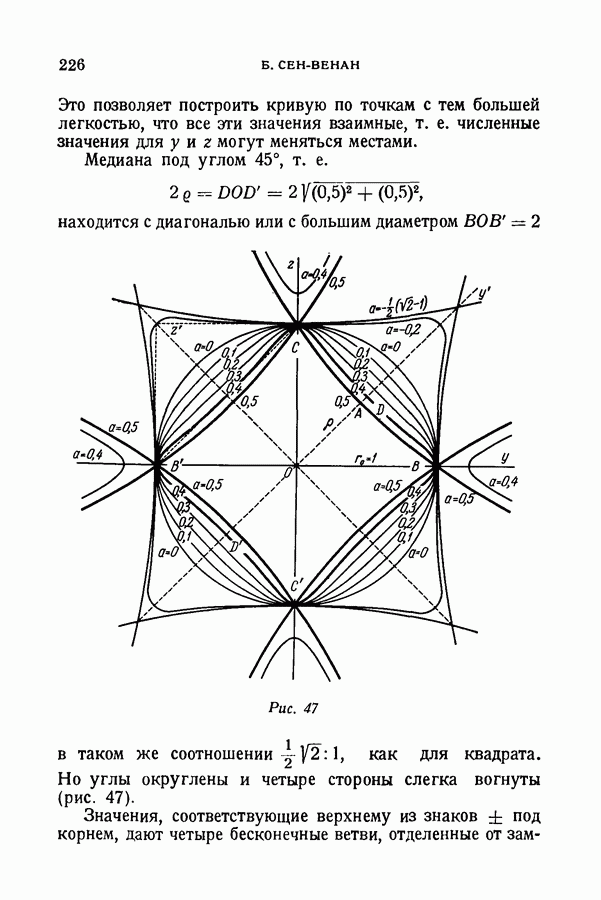
- § 94. Симметричные и равные замкнутые кривые четвертой степени
- § 95. Нахождение этих кривых
- § 96. Кривые восьмой степени, симметричные и одинаковые в двух направлениях
- § 97. Условия, при которых эти кривые замкнуты
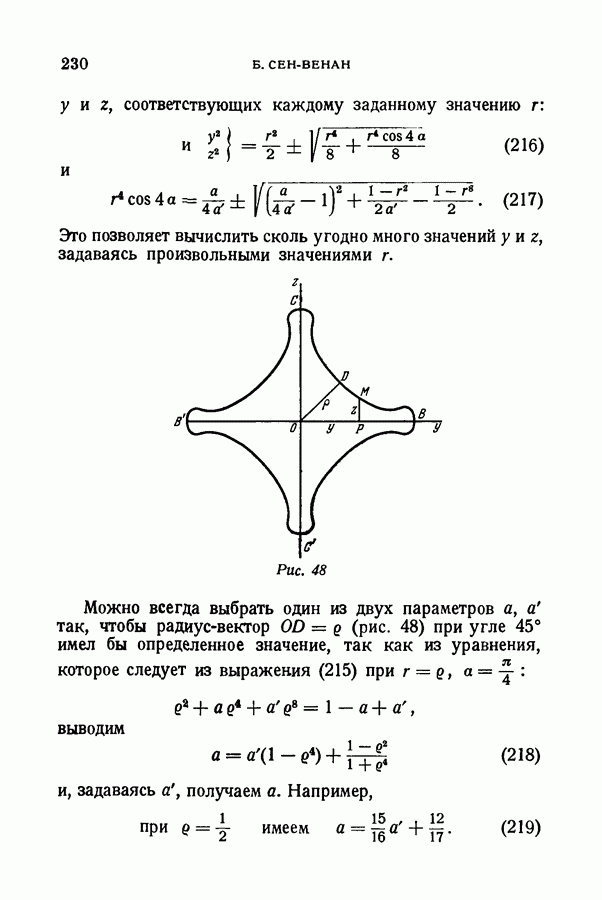
- § 98. Кривые восьмой степени, у которых наименьший диаметр равен половине наибольшего
- § 99. Кривые, представленные уравнениями, в которых радиус-вектор имеет отрицательные показатели степени. Кривые двенадцатой и шестнадцатой степеней и т. д.
- § 100. Сдвиги и крутящий момент в призмах, имеющих основания в виде кривых четвертой и восьмой степеней
- § 101. Вычисление крутящих моментов. Ничтожность влияния выступов сечения или ребер призм
- § 102. Топографические разрезы и рельеф искривленных поверхностей, в которые превращаются сечения
- § 103. Сдвиги, опасные точки и условия прочности для криволинейных квадратов четвертой степени
- § 104. Те же сдвиги и т. д. для криволинейного основания восьмой степени с выступающими ребрами
- § 105. Контуры, неодинаковые относительно осей у и z. Несимметричные контуры. Призма с основанием в виде равностороннего треугольника. Заключение к главе
- ГЛАВА X. СЛУЧАЙ, КОГДА УПРУГОСТЬ ПРИ СДВИГЕ НЕОДИНАКОВА В НАПРАВЛЕНИЯХ ДВУХ ПОПЕРЕЧНЫХ ОСЕЙ
- § 107. Применение формул в случае эллиптического цилиндра или призмы. Частный случай, когда длина осей пропорциональна корням квадратным из упругостей при сдвиге в направлениях этих осей
- § 108. Продолжение. Условие прочности для такой же эллиптической призмы с неодинаковой упругостью
- § 109. Изменения в общих выражениях интегралов неопределенного уравнения главы VII, когда упругость при сдвиге неодинакова
- § 110. Прямоугольная призма с неодинаковой упругостью. Перемещения. Сдвиги. Крутящий момент
- § 111. Случай, когда … очень мало сравнительно с …
- § 112. Случай, когда …
- § 113. Общий случай, когда стороны 2b, 2c прямоугольника с неодинаковой упругостью находятся между собой в любом соотношении
- § 114. Призмы с другими основаниями (кроме эллипса и прямоугольника), аналогичными рассмотренным в главе IX
- § 115. Нормальность сечений, ставших искривленными, к ребрам, превратившимся в спирали
- ГЛАВА XI. О КРУЧЕНИИ ПОЛЫХ ПРИЗМ
- § 116. Полая эллиптическая призма
- § 117. Полая прямоугольная призма
- § 118. Полые призмы с другими основаниями
- ГЛАВА XII. СЛУЧАЙ ОДНОВРЕМЕННОГО КРУЧЕНИЯ, ИЗГИБА, УДЛИНЕНИЙ И ПОПЕРЕЧНЫХ СДВИГОВ. УСЛОВИЯ ПРОЧНОСТИ ПРИ ИХ ОДНОВРЕМЕННОМ ВОЗДЕЙСТВИИ
- § 119. Определение перемещений. Самое простое геометрическое сложение перемещений, вызванных различного рода усилиями
- § 120. Наложение перемещений, вызванных силами, производящими одновременно растяжение, изгиб и кручение призмы
- § 121. Общие условия прочности при различных воздействиях
- § 122. Более частные и более простые условия
- § 123. Простой и непосредственный вывод этих формул
- § 124. Формулы сопротивления в случае замены удлинений и сдвигов их выражениями через внешние силы, действующие на тело
- § 125. Видоизменения, касающиеся сдвигов, для некоторых особых сечений
- § 126. Первое применение. Призма, испытывающая одновременно изгиб и поперечный сдвиг. Случай, когда наиболее подверженное опасности сечение может изгибаться
- § 127. Та же призма. Случай, когда наиболее подверженное опасности сечение вынуждено оставаться плоским. Сомнительный случай
- § 128. Цилиндр с круговым основанием, одновременно изгибаемый, скручиваемый и растягиваемый
- § 129. Вращающийся вал, изгибаемый и скручиваемый посредством двух шестерен или двух приводных ремней. Консоль переменного диаметра, удовлетворяющая условию равного сопротивления
- § 130. Прямоугольная призма, одновременно изогнутая и скрученная. Общие формулы
- § 131. Та же прямоугольная призма. Случай ее изгибания в плоскости наиболее легкого изгиба, т.е. в плоскости, параллельной наименьшим сторонам 2c (см. § 133)
- § 132. Призма с квадратным основанием, изогнутая в любой плоскости и одновременно скрученная
- § 133. Призма с прямоугольным основанием, одна из сторон которого вдвое больше другой, изогнутая в любой плоскости, параллельной или наклоненной к ее граням, и одновременно скрученная
- § 134. Одновременный изгиб и кручение призм с другими основаниями (кроме круга и прямоугольника). Эллиптический цилиндр
- ГЛАВА XIII. РЕЗЮМЕ ЭТОГО МЕМУАРА, КРАТКОЕ ПОВТОРЕНИЕ ФОРМУЛ И ПРАКТИЧЕСКИЕ ПРАВИЛА, ЧИСЛЕННЫЕ ПРИМЕРЫ
- § 136. Краткое повторение формул и практические правила
- § 137. Числовые примеры
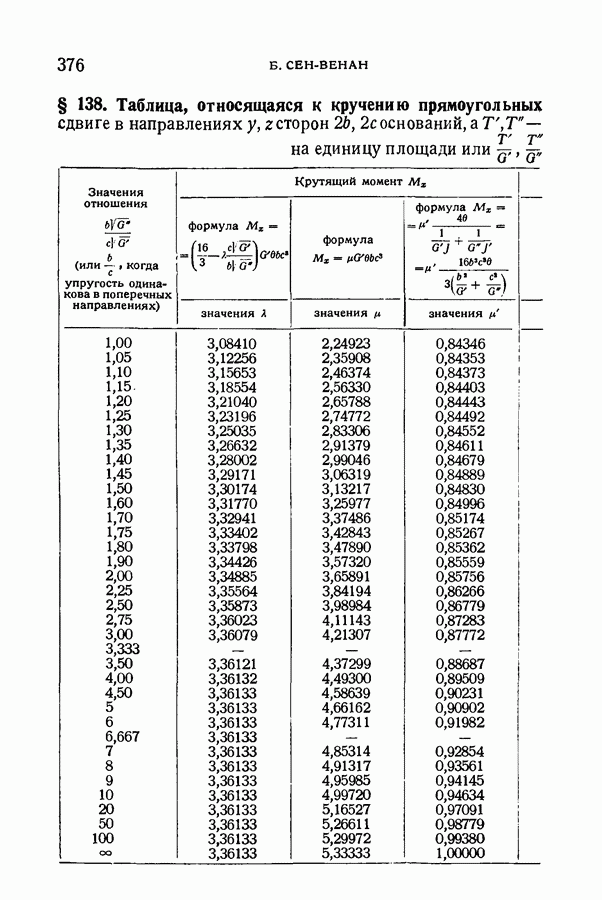
- § 138. Таблица, относящаяся к кручению прямоугольных призм
- МЕМУАР ОБ ИЗГИБЕ ПРИЗМ
- § 1. Прежние исследования по теории изгиба
- § 2. Принятая в настоящее время теория изгиба, вызванного неравномерным продольным растяжением волокон. Гипотезы, на которых она обычно основывается. Ненужность этих гипотез ввиду их неточности для вывода формул
- § 3. Предмет и краткое содержание этого мемуара
- § 4. Краткое разъяснение формул давлений внутри твердых упругих тел. Зависимости между давлениями в различных направлениях в одной точке
- § 5. Продолжение. Удлинения, сдвиги. Линейные выражения для составляющих давления
- § 6. Продолжение. Притяжения и отталкивания, функции молекулярных расстояний. Теорема геометрического сложения сил и малых перемещений
- § 7. Продолжение. Число существенно различных коэффициентов. Его сокращение с тридцати шести до пятнадцати
- § 8. Продолжение. Изменения осей и плоскостей, относительно которых рассматривают давления, удлинения и сдвиги
- § 9. Упрощение формул для составляющих давления в случае тел с различным строением
- § 10. Неопределенные дифференциальные уравнения равновесия упругих твердых тел. Выражения удлинений и сдвигов через очень малые перемещения
- § 11. Определенные уравнения, удовлетворяющиеся только в точках поверхности
- § 12. Применение этих формул к растяжению призмы. Сопровождающие его поперечные сжатия. Коэффициент упругости
- § 13. Применение общих формул Пуассоном и Коши для приближенного решения задачи изгиба
- § 14. Принятые условия и уравнения нашей задачи о неравномерном изгибе призм
- § 15. Первые следствия заданных условий и соотношений
- § 16. Первое интегрирование
- § 17. Распределение сил. Обстоятельства, сопровождающие неравномерный изгиб. Наклон и кривизна сечений. Взаимный наклон волокон. Полная стрела прогиба
- § 18. Кривые контуров сечений, для которых произвольная функция F полностью определяется через у и z. Эллиптический контур и т. д.
- § 19. Способ приложения и распределения внешних сил, уточняющий для различных контуров обычные формулы изгиба, вызванного продольными удлинениями. Значения величины центрального наклона. Сечения эллиптические, круговые, в виде ложного эллипса и т. д.
- § 20. Те же контуры. Полная стрела прогиба при изгибе
- § 21. Те же контуры. Искривленные поверхности, образованные первоначально плоскими сечениями. Их обычная топография
- § 22. Продолжение. Случай, когда каждая искривленная поверхность сечений является общей для бесконечного числа контуров
- § 23. Подробное изложение вопроса для различных сечений. Окружность. Ложный эллипс (овал). Сечения с контуром девятой степени, которые искривляются точно по цилиндрической поверхности с основанием в виде кривой третьей степени, имеющей форму гуська
- § 24. Прямоугольная призма. Преобразование неопределенных и определенных условий
- § 25. Интегрирование с помощью трансцендентного ряда
- § 26. Выражения для перемещений точек прямоугольной призмы
- § 27. Давления … Проверка полученных результатов
- § 28. Центральный сдвиг. Изогнутая ось. Стрела прогиба при изгибе
- § 29. Искривленная поверхность, образованная первоначально плоскими прямоугольными поперечными сечениями
- § 30. Сечения произвольной формы
- § 31. Непосредственное доказательство известных формул изгиба призм, вызванного только их продольными удлинениями
- § 32. Заключение. Общий обзор для случая, когда способ приложения и распределения внешних сил на концах призмы отличен от способа, дающего совершенно точные формулы в соответствии со смешанным методом