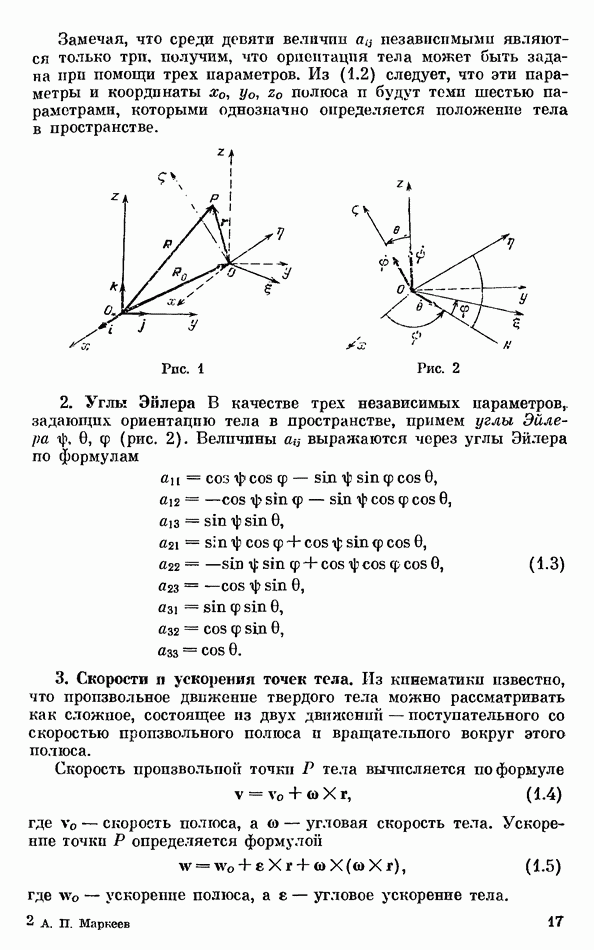
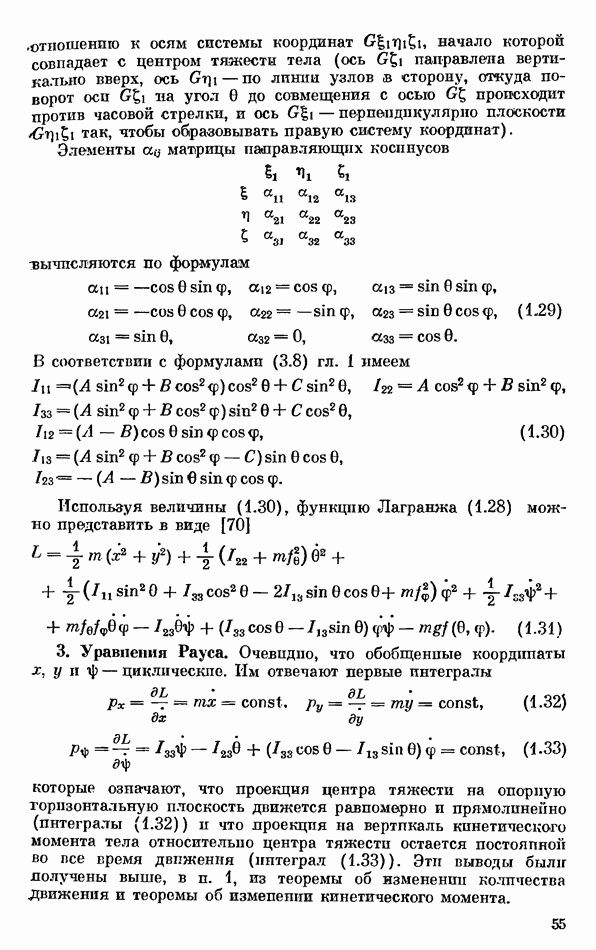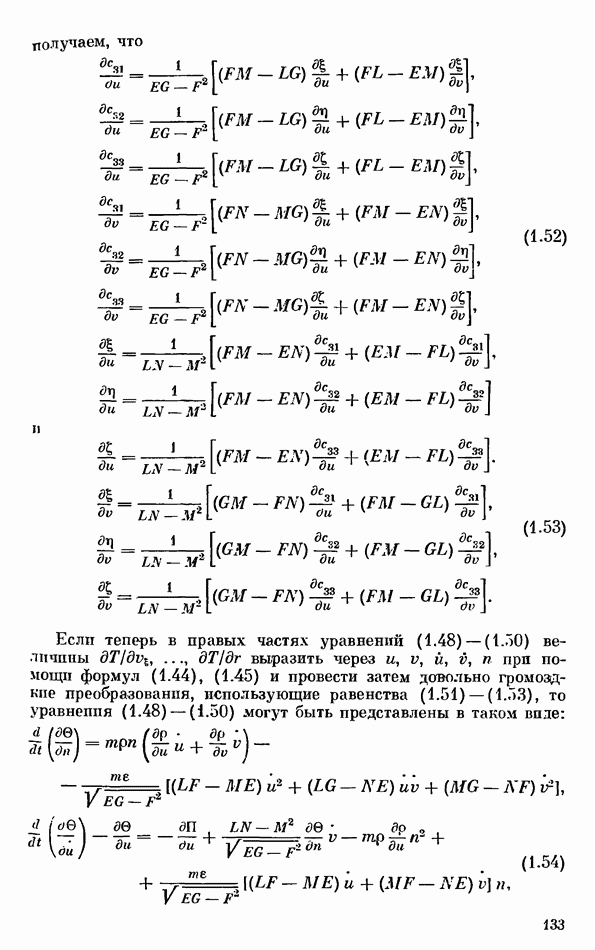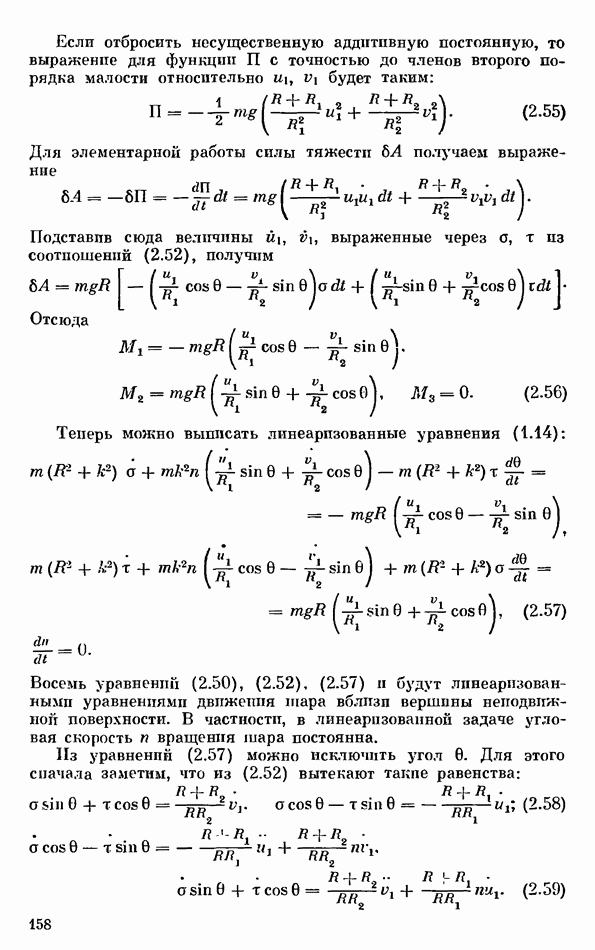| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Стационарные движения неоднородного шара на плоскости с вязким трением.
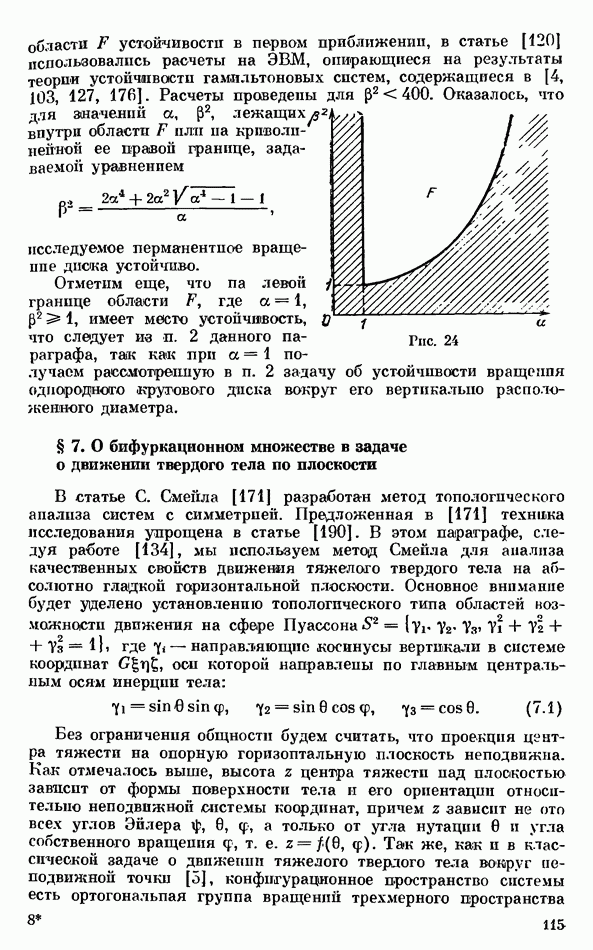
Исследование задачи о существовании и устойчивости стационарных движений тела вращения на неподвижной горизонтальной плоскости при наличии трения скольжения содержится в работах [68, 70, 73—76, 86, 99, 159, 162, 273]. В статье [273] получено необходимое условие устойчивости
вращения тела со сферическим основанием вокруг вертикально направленной оси симметрии; это условие было затем получено еще раз в работе [86], где оно подробно обсуждается в связи с рассмотрением вопроса о стремлении оси симметрии волчка на плоскости с треипем скольжения занять вертикальное положение. Результаты этого обсуждения в краткой форме изложены в монографии [99]. В строгой ыелипейной постановке задача об устойчивости вращения симметричного тела вокруг вертикали на плоскости с вязким трением рассмотрена сначала в [159], а зачтем в [162], где показано, что полученное в [273] необходимое условие устойчивости является и достаточным. Кроме того,  статьях [159, 162] обсуждаются достаточные условия устойчивости при любом законе трения, приводящем к диссипации полной энергии тела. Как замечено в [134] (см. п. 4 § 3 гл. 3), никакой разницы в условиях устойчивости вращения вокруг вертикально направленной оси симметрии для произвольного тела вращения и тела вращения со сферическим основанием нет.
статьях [159, 162] обсуждаются достаточные условия устойчивости при любом законе трения, приводящем к диссипации полной энергии тела. Как замечено в [134] (см. п. 4 § 3 гл. 3), никакой разницы в условиях устойчивости вращения вокруг вертикально направленной оси симметрии для произвольного тела вращения и тела вращения со сферическим основанием нет.
Исследованию второго и третьего типов (см. п. 1) стационарных движений произвольного тела вращения на плоскости с вязким трением посвящена работа [68]; этот же вопрос подробно рассмотрен в диссертации [70].
Стационарные движения динамически симметричного тела вращения, обладающего сферической поверхностью, на плоскости с трением скольжения рассмотрены в недавних статьях А. В. Карапетяна и В. Н. Рубановского [73—76]; закон трения в этих статьях не конкретизируется. Исследованию стационарного вращения тяжелого твердого шара вокруг вертикали при наличии трения скольжения, являющегося весьма произвольной функцией скорости скольжения, посвящена также работа [268]. В данном пункте мы изложим некоторые результаты работ [73—76], полагая для определенности, что трение является вязким.
В работе [73] предложен эффективный метод анализа задачи о существовании и устойчивости стационарных движений неконсервативных механических систем. Он состоит в следующем. Пусть склерономная механическая система допускает не зависящие от времени первые интегралы

а также не зависящую от времени функцию  не возрастающую вдоль движений системы. Функции
не возрастающую вдоль движений системы. Функции 
 предполагаются непрерывно дифференцируемыми по входящим в них переменным
предполагаются непрерывно дифференцируемыми по входящим в них переменным  Сущность предложенного в [73] метода исследования заключена в следующих трех теоремах, являющихся дальнейшим развитием классической теоремы Рауса [77, 150, 285].
Сущность предложенного в [73] метода исследования заключена в следующих трех теоремах, являющихся дальнейшим развитием классической теоремы Рауса [77, 150, 285].
Теорема 1. Если не возрастающая вдоль движений системы функция  имеет строгий локальный минимум при постоянных значениях интегралов
имеет строгий локальный минимум при постоянных значениях интегралов  этой системы, то значения переменных, доставляющие этой функции минимум, отвечают устойчивому действительному (стационарному) движению системы.
этой системы, то значения переменных, доставляющие этой функции минимум, отвечают устойчивому действительному (стационарному) движению системы.
Теорема 2. Если стационарное движение доставляет функции  строгий локальный минимум и изолировано при постоянных значениях интегралов
строгий локальный минимум и изолировано при постоянных значениях интегралов  от движений, вдоль которых функция
от движений, вдоль которых функция  сохраняет постоянное значение, то всякое возмущенное движение, достаточно близкое к не возмущенному, асимптотически при
сохраняет постоянное значение, то всякое возмущенное движение, достаточно близкое к не возмущенному, асимптотически при  стремится к одному из стационарных движений системы, отвечающему строгому локальному минимуму функции
стремится к одному из стационарных движений системы, отвечающему строгому локальному минимуму функции  при возмущенных значениях интегралов
при возмущенных значениях интегралов 
к); в частности, невозмущенное движение асимптотически устойчиво при невозмущенных значениях постоянных используемых интегралов.
Теорема 3. Если стационарное движение не доставляет функции  даже нестрогого минимума и изолировано при постоянных значениях интегралов
даже нестрогого минимума и изолировано при постоянных значениях интегралов  от движений вдоль которых функция
от движений вдоль которых функция  сохраняет постоянное значение, то невозмущенное движение неустойчиво.
сохраняет постоянное значение, то невозмущенное движение неустойчиво.
Следует отметить, что в теоремах 1 и 2 содержатся утверждения об устойчивости, вообще говоря, по отношению не ко  а к части переменных
а к части переменных  именно по отношению к тем из них, изменение которых увеличивает значение функции
именно по отношению к тем из них, изменение которых увеличивает значение функции  при постоянных значениях интегралов
при постоянных значениях интегралов  Заметим также, что утверждение теоремы 2 в известной мере аналогично утверждению теоремы Ляпупова — Малкина об устойчивости в особенном случае критического случая нескольких нулевых корней (см.
Заметим также, что утверждение теоремы 2 в известной мере аналогично утверждению теоремы Ляпупова — Малкина об устойчивости в особенном случае критического случая нескольких нулевых корней (см.  § 5 гл. 3).
§ 5 гл. 3).
Однако ее применение в отличие от теоремы Ляпунова — Малкина не требует анализа характеристического уравнения.
Для динамики симметричного шара справедливы дифференциальные уравнения (2.11) — (2.13). Помимо интеграла  определяемого равенством (2.15), эти уравнения имеют очевидный геометрический иптеграл
определяемого равенством (2.15), эти уравнения имеют очевидный геометрический иптеграл

и не возрастающую в случае трения скольжения функцию (удвоенную полную энергию)  вида
вида

Стационарным движениям шара соответствуют критические точки функции (2.17) при фиксированных значениях интегралов (2.15), (2.16) [77, 156, 285]. В соответствии с процедурой нахождения условного экстремума рассмотрим функцию

где  — неопределенные множители Лагранжа. Функция V принимает стационарные значения, если перемепные
— неопределенные множители Лагранжа. Функция V принимает стационарные значения, если перемепные  и множители
и множители  удовлетворяют системе уравнений (2.15), (2.16) и
удовлетворяют системе уравнений (2.15), (2.16) и

Эта система уравнений имеет следующие три группы решений:

Для решений (2.21) — (2.23) множитель  выражается через
выражается через  соответственно по формулам
соответственно по формулам

а постоянная к интеграла  формулам
формулам 

Для решений  шар совершает вращение с произвольной по времени постоянной угловой скоростью
шар совершает вращение с произвольной по времени постоянной угловой скоростью  вокруг своей оси симметрии, которая неподвижна и занимает
вокруг своей оси симметрии, которая неподвижна и занимает
вертикальное положение; для решения (2.21) центр тяжести шара расположен выше, а для решения  — ниже его геометрического центра. Если
— ниже его геометрического центра. Если  то
то  и решения (2.21), (2.22) отвечают положению равновесия шара.
и решения (2.21), (2.22) отвечают положению равновесия шара.
Группе решений (2.23) отвечают регулярные прецессии: шар вращается с угловой скоростью  вокруг оси симметрии, которая прецессирует с угловой скоростью X вокруг вертикали, проходящей через центр тяжести шара; ось симметрии составляет с вертикалью постоянный угол, косинус которого 73 вычисляется согласно последнему из равенств (2.23).
вокруг оси симметрии, которая прецессирует с угловой скоростью X вокруг вертикали, проходящей через центр тяжести шара; ось симметрии составляет с вертикалью постоянный угол, косинус которого 73 вычисляется согласно последнему из равенств (2.23).
Регулярпые прецессии существуют не при всех угловых скоростях вращепия шара, а только при тех, когда модуль величины  определяемой из (2.23), не превосходит единицы.
определяемой из (2.23), не превосходит единицы.
Компоненты вектора скорости точки касания М шара и опорной плоскости в системе координат определяются из равенств

На стационарпых движениях шара (2.21) — (2.23) скорость точки касания равна нулю, т. е. шар движется без скольжения.
Отметим, что из равенств (2.24) с учетом (2.21) — (2.23) следует, что при каждом значении к иптеграла (2.15) существует не более четырех стационарных движений шара: два вращения вокруг вертикали (2.21), (2.22) и не более двух регулярных прецессий (2.23) (из последнего равенства в (2.24) видно, что одному зпачению к могут отвечать не более двух различных вещественных значений  ).
).
При фиксированном значении к все (в общем случае четыре) стационарные движения шара изолированы одно от другого, если выполняются неравенства

Здесь  — вещественные корни уравнений
— вещественные корни уравнений  соответственно, где
соответственно, где  и определяются соотношениями (2.23) и (2.24):
и определяются соотношениями (2.23) и (2.24):

Покажем, что функция  сохраняет постоянное значение только на стационарных движениях вида (2.21) — (2.23). Функция
сохраняет постоянное значение только на стационарных движениях вида (2.21) — (2.23). Функция  очевидио, сохраняет постоянное значение только на таких движениях, когда скольжение отсутствует, т. е. когда на движениях шара выполняются соотношения
очевидио, сохраняет постоянное значение только на таких движениях, когда скольжение отсутствует, т. е. когда на движениях шара выполняются соотношения

При отсутствии скольжения сила вязкого трения обращается в нуль и реакция плоскости будет направлена по вертикали. Обозначая величину этой нормальной реакции через  получаем из (2.11) -(2.13) уравнения, которым должны удовлетворять движения шара с постоянпым значением
получаем из (2.11) -(2.13) уравнения, которым должны удовлетворять движения шара с постоянпым значением 

На рассматриваемых движениях выполняются соотношения (2.15), (2.16) и, кроме того,

Продифференцировав первые два равенства (2.27) по времени с учетом (2.29), (2.30) и подставив полученные выражения для  и выражения для
и выражения для  из (2.27) в первые два уравнения (2.28), получим следующие два соотношения:
из (2.27) в первые два уравнения (2.28), получим следующие два соотношения:

Если  то из (2.27) — (2.30) сразу следует, что движение тела без скольжения — это только стационарные вращения вокруг вертикали (2.21) и (2.22). Пусть 71 и 72 не равны нулю одновременно. Тогда, умножая первое из равенств (2.33) на 72, а второе на
то из (2.27) — (2.30) сразу следует, что движение тела без скольжения — это только стационарные вращения вокруг вертикали (2.21) и (2.22). Пусть 71 и 72 не равны нулю одновременно. Тогда, умножая первое из равенств (2.33) на 72, а второе на  складывая результаты, получаем
складывая результаты, получаем

Отсюда следует, что либо  либо
либо

(если  то
то  из (2.30) опять следует (2.34)).
из (2.30) опять следует (2.34)).
Если  то из (2.33) и (2.29) получаем
то из (2.33) и (2.29) получаем

Продифференцировав выражение со  по времени с учетом равенств (2.35) и третьего из уравнений (2.30), получим соотношение
по времени с учетом равенств (2.35) и третьего из уравнений (2.30), получим соотношение

из которого следует, что величина  на движениях без скольжения есть функция только одной переменной
на движениях без скольжения есть функция только одной переменной 
Далее, при  равенство (2.32) с учетом (2.27) и (2.30) может быть записано в виде
равенство (2.32) с учетом (2.27) и (2.30) может быть записано в виде

Исключив из равенств (2.31) и (2.37) величину  получим соотношение, связывающее переменную
получим соотношение, связывающее переменную  параметры
параметры  , константы из правых частей равенств (2.31), (2.37) и константу, получающуюся при интегрировании уравнения (2.36) с целью нахождения зависцмости суммы
, константы из правых частей равенств (2.31), (2.37) и константу, получающуюся при интегрировании уравнения (2.36) с целью нахождения зависцмости суммы  . Это соотношение может быть удовлетворено только при постоянном значении угла
. Это соотношение может быть удовлетворено только при постоянном значении угла  Таким образом,
Таким образом,  Отсюда на основании третьего из уравнений (2.30) получаем, что движения шара без скольжения возможны только при выполнении условия (2.34).
Отсюда на основании третьего из уравнений (2.30) получаем, что движения шара без скольжения возможны только при выполнении условия (2.34).
Из (2.34), (2.27), (2.29) и (2.30) вытекает, что при этом должны выполняться соотношения

Из (2.15) следует, что содержащаяся здесь величина X постоянна.
Подставив (2.38) в уравнения (2.28), получим с учетом (2.30)

Умножив  равенства соответственно на
равенства соответственно на  и сложив результаты, получим
и сложив результаты, получим  Следовательно,
Следовательно,

Отсюда и из (2.38), (2.28) — (2.30) следует, что движение шара без скольжения возможно только на стационарных движениях (2.21) — (2.23). Полученный вывод является частным случаем
 результатов работы [135], посвященной задаче исследования предельных движений тяжелого твердого тела на плоскости с вязким трением скольжения. Эта задача будет рассмотрена в § 3.
результатов работы [135], посвященной задаче исследования предельных движений тяжелого твердого тела на плоскости с вязким трением скольжения. Эта задача будет рассмотрена в § 3.
Для исследования устойчивости стационарных движений при помощи теорем 1—3 исследуем характер экстремума функции  на решениях (2.21) — (2.23) при фиксированных значениях интегралов (2.15), (2.16). Рассмотрим решение (2.21). Положим
на решениях (2.21) — (2.23) при фиксированных значениях интегралов (2.15), (2.16). Рассмотрим решение (2.21). Положим

Подставим эти выражения для  в функцию
в функцию  интегралы (2.15), (2.16). Затем при помощи этих интегралов исключим из функции
интегралы (2.15), (2.16). Затем при помощи этих интегралов исключим из функции  переменные
переменные  . В результате получим, что часть функции
. В результате получим, что часть функции  линейная по остальным переменным
линейная по остальным переменным  равна нулю, а квадратичная часть имеет вид
равна нулю, а квадратичная часть имеет вид

Отсюда при помощи критерия Сильвестра получим, что при выполнении условия

стационарное движение (2.21) доставляет функции  строгий минимум при постоянных значениях интегралов (2.15), (2.16) и, следовательно, согласно теореме 1 устойчиво по отношению к переменным
строгий минимум при постоянных значениях интегралов (2.15), (2.16) и, следовательно, согласно теореме 1 устойчиво по отношению к переменным  ; если же
; если же

то стационарное движение (2.21) не доставляет функции  даже нестрогого минимума.
даже нестрогого минимума.
Совершенно аналогично можно получить, что при выполнении условия

стационарное движение (2.22) доставляет функции  строгий минимум и, следовательно, устойчиво, а при условии
строгий минимум и, следовательно, устойчиво, а при условии

не доставляет функции  даже нестрогого минимума.
даже нестрогого минимума.
Для решения (2.23) положим

где  — значение величины
— значение величины  в движении (2.23). При постоянных
в движении (2.23). При постоянных
значениях интегралов (2.15), (2.16) можно исключить из  члены, линейные относительно возмущений, а квадратичная часть
члены, линейные относительно возмущений, а квадратичная часть  будет иметь вид
будет иметь вид

где

Главные миноры первого и второго порядков матрицы квадратичной формы  всегда положительны, а знак главного минора третьего порядка (определителя матрицы), как показывают вычисления, совпадает на движении (2.23) со знаком выражения
всегда положительны, а знак главного минора третьего порядка (определителя матрицы), как показывают вычисления, совпадает на движении (2.23) со знаком выражения  где
где  — функция X, определенная третьим из равенств (2.24).
— функция X, определенная третьим из равенств (2.24).
Учитывая структуру функции  пользуясь критерием Сильвестра, получаем отсюда, что при условии
пользуясь критерием Сильвестра, получаем отсюда, что при условии

стационарное движение (2.23) доставляет функции  строгий минимум при постоянных значениях интегралов (2.15), (2.16) и, следовательно, устойчиво согласно теореме 1 по отношению к переменным
строгий минимум при постоянных значениях интегралов (2.15), (2.16) и, следовательно, устойчиво согласно теореме 1 по отношению к переменным  , а при условии
, а при условии

не доставляет функции  даже нестрогого мпнпмума.
даже нестрогого мпнпмума.
Поскольку выше показано, что функция  постоянна только на стационарных движениях (2.21) - (2.23), а сами стационарные движения изолированы одно от другого
постоянна только на стационарных движениях (2.21) - (2.23), а сами стационарные движения изолированы одно от другого  выполнении условий (2.39)-(2.44) (ср. с условиями (2.26)), то согласно теоремам 2 и 3 получаем, что стационарные вращения шара вокруг вертикали (2.21) и (2.22) устойчивы, причем асимптотически по отношению к переменным
выполнении условий (2.39)-(2.44) (ср. с условиями (2.26)), то согласно теоремам 2 и 3 получаем, что стационарные вращения шара вокруг вертикали (2.21) и (2.22) устойчивы, причем асимптотически по отношению к переменным  выполнении условий (2.39) и (2.41) соответственно, и неустойчивы при выполнении условий (2.40) и (2.42) соответственно. Регулярные
выполнении условий (2.39) и (2.41) соответственно, и неустойчивы при выполнении условий (2.40) и (2.42) соответственно. Регулярные
прецессии (2.23) устойчивы, причем асимптотически  отношению к переменным
отношению к переменным  при выполнении условия (2.43), и неустойчивы при выполнении условия (2.44).
при выполнении условия (2.43), и неустойчивы при выполнении условия (2.44).
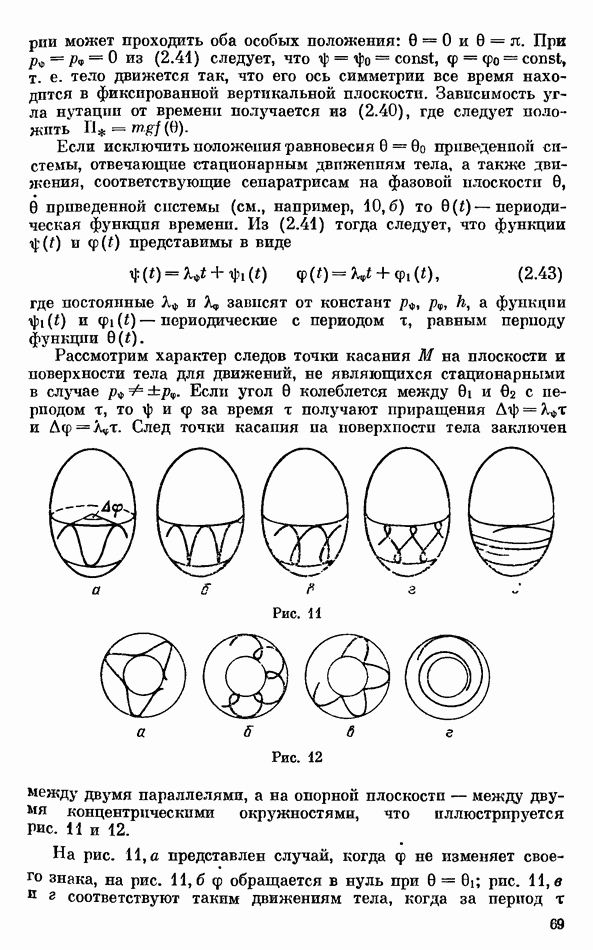
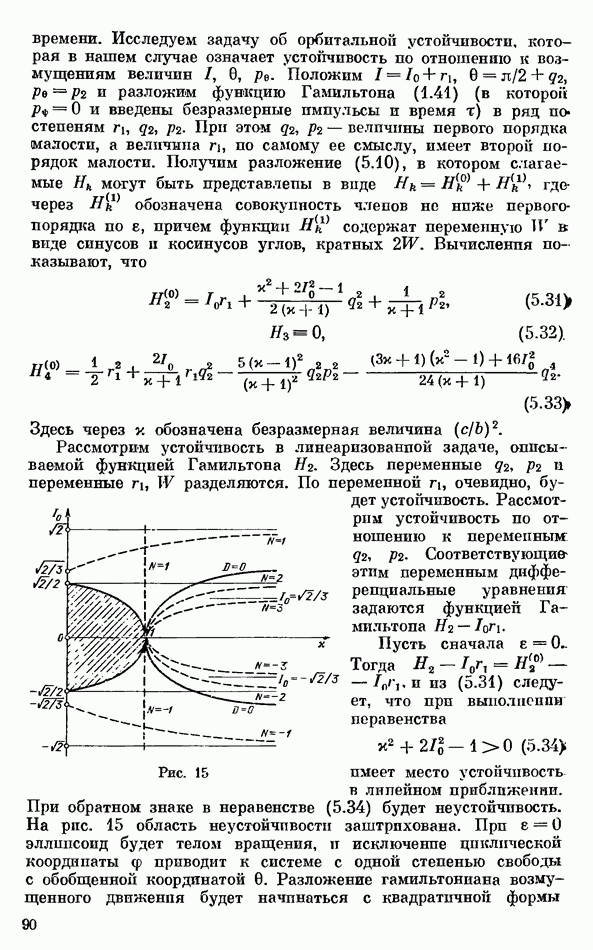
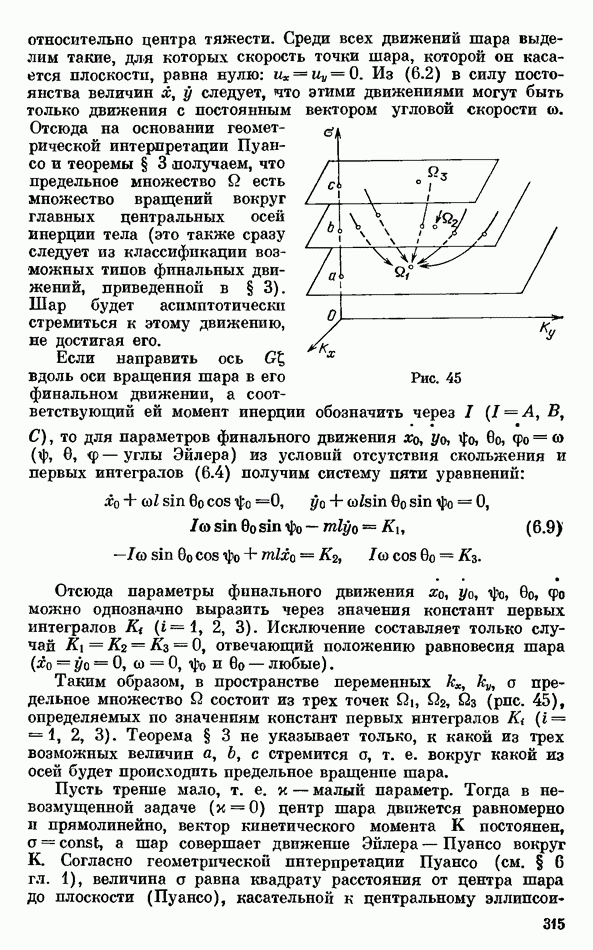
Для геометрической и механической интерпретации полученных результатов рассмотрим, следуя [74, 75], плоскость параметров  (рис. 42). Выделим на этой плоскости следующие области: область
(рис. 42). Выделим на этой плоскости следующие области: область  (ограничена лучами
(ограничена лучами  и кривой
и кривой  в которой при любом фиксированном значении к интеграла Желле (2.15) существует не более одной регулярной прецессии и эта прецессия всегда устойчива; область
в которой при любом фиксированном значении к интеграла Желле (2.15) существует не более одной регулярной прецессии и эта прецессия всегда устойчива; область  (ограничена отрезком прямой
(ограничена отрезком прямой  и кривой
и кривой  в которой при любом фиксированном значении к существует также не более одной регулярной прецессии, но эта прецессия всегда неустойчива; область
в которой при любом фиксированном значении к существует также не более одной регулярной прецессии, но эта прецессия всегда неустойчива; область  (ограничена отрезками прямых
(ограничена отрезками прямых  и кривыми
и кривыми  в которой могут существовать две регулярные прецессии, одна из которых («медленная») устойчива
в которой могут существовать две регулярные прецессии, одна из которых («медленная») устойчива  другая («быстрая») неустойчива
другая («быстрая») неустойчива  Кривые
Кривые  задаются соответственно уравнениями
задаются соответственно уравнениями

и


Рис. 42
Разобьем еще области  и на подобласти
и на подобласти 
Стационарные вращения шара вокруг вертикальной оси симметрии, для которых центр тяжести шара лежит выше его геометрического центра, устойчивы, если параметры шара лежат вне области  и его угловая скорость достаточно велика (выполняется неравенство (2.39)), а в протпвных случаях неустойчивы. Учитывая (2.21), неравенство (2.39) можно записать в впде ограничения на угловую скорость вращения шара:
и его угловая скорость достаточно велика (выполняется неравенство (2.39)), а в протпвных случаях неустойчивы. Учитывая (2.21), неравенство (2.39) можно записать в впде ограничения на угловую скорость вращения шара:

Стационарные вращения шара вокруг вертикальной оси симметрии, для которых центр тяжести лежит ниже его геометрического центра, устойчивы, если параметры шара лежат в областях  или его угловая скорость достаточно мала (выполняется неравенство (2.41)). Учитывая (2.22), неравенство (2.41) можно записать в виде ограничения на угловую скорость вращения шара:
или его угловая скорость достаточно мала (выполняется неравенство (2.41)). Учитывая (2.22), неравенство (2.41) можно записать в виде ограничения на угловую скорость вращения шара:

Если параметры шара лежат вне областей  и
и  а неравенство (2.46) выполняется с обратным знаком, то имеет место неустойчивость.
а неравенство (2.46) выполняется с обратным знаком, то имеет место неустойчивость.
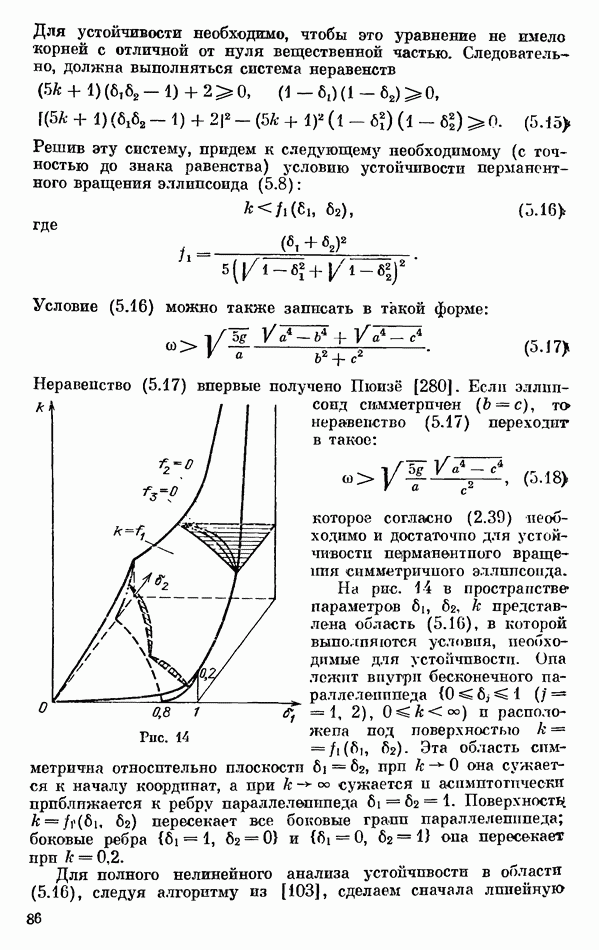
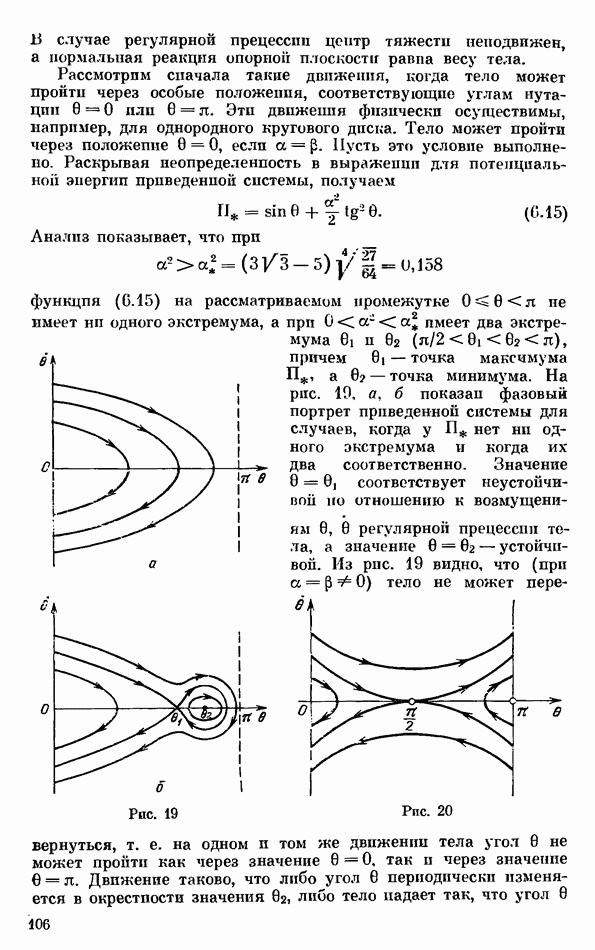
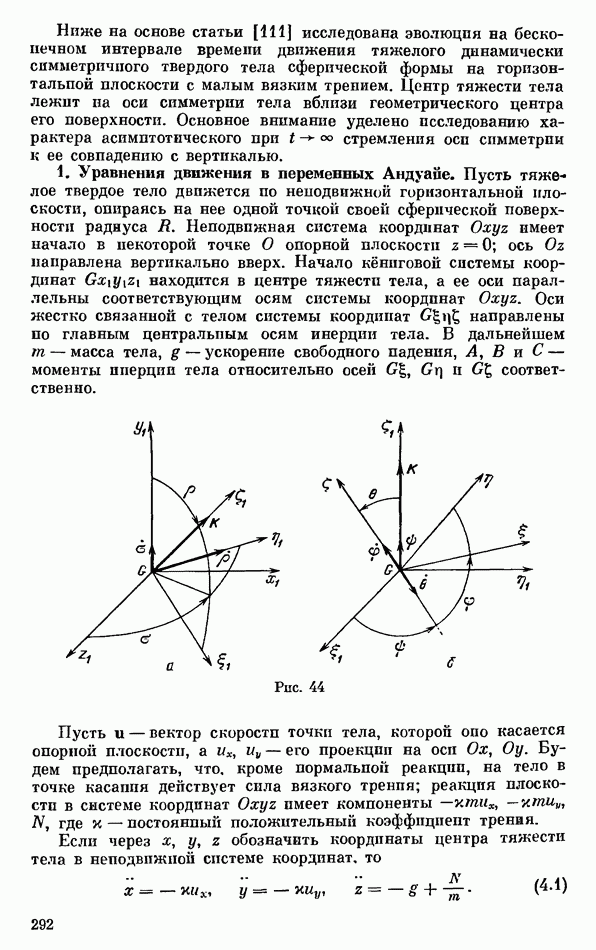
В литературе широко обсуждались [173—175, 218—220, 222, 240—242, 250—253, 255, 273—276, 292] динамические свойства волчка сферической формы, или волчка «тип-топ» (иначе, «китайского волчка», или волчка Томсона), на плоскости с трением скольжения. Конструктивно такой волчок состоит из срезанного шарика с ножкой, расположенной в центре среза; ось симметрии ножки проходит через центры тяжести волчка и части его сферической поверхности (рис. 43). Если волчок расположен ножкой вверх, то его центр тяжести лежит ниже центра кривизны поверхности, так как в устойчивом состоянии покоя волчок опирается на плоскость точкой своей сферической поверхности. За ножку волчок может быть приведен в быстрое вращение; начав вращаться, волчок теряет устойчивость, его ось симметрии отклоняется от ее первоначального вертикального положения; в конце концов волчок переворачивается и продолжает устойчиво вращаться, оипраясь на плоскость своей ножкой.

Рис. 43
Проведенный выше анализ поясняет странное на первый взгляд поведение волчка «тип-топ». Если параметры волчка лежат в областях  то имеет место эффект потери устойчивости вращения волчка с наинизшим расположением центра тяжестп при увеличении его угловой скорости, сопровождающийся стабилизацией вращения волчка с наивысшим расположением центра тяжести. Конечно, проведенный анализ описывает только начальную и конечную стадии переворота волчка. Анализ динамики волчка на всех стадиях его переворота будет проведен ниже, в § 4.
то имеет место эффект потери устойчивости вращения волчка с наинизшим расположением центра тяжестп при увеличении его угловой скорости, сопровождающийся стабилизацией вращения волчка с наивысшим расположением центра тяжести. Конечно, проведенный анализ описывает только начальную и конечную стадии переворота волчка. Анализ динамики волчка на всех стадиях его переворота будет проведен ниже, в § 4.
Как уже отмечалось, результаты исследования устойчивости стационарного вращения шара вокруг вертикали переносятся на случай произвольного тела вращения. Пусть  — расстояние от центра тяжести тела до опорной плоскости
— расстояние от центра тяжести тела до опорной плоскости  — угол нутацпи).
— угол нутацпи).
Необходимое (с точностью до знака равенства) и достаточное условие устойчивости тела вращения вокруг его вертикальной оси симметрии запишется в виде [162]

Индексом 0 здесь обозначены значения функции  и ее второй производной при
и ее второй производной при 
Если  т. е. тело находится в равновесии, то неравенство (2.47) дает
т. е. тело находится в равновесии, то неравенство (2.47) дает  Это означает, что для устойчивости равновесия тела необходимо (с точностью до знака равенства) и достаточно, чтобы его центр тяжести лежал ниже центра кривизны поверхности в точке касания тела с опорной плоскостью.
Это означает, что для устойчивости равновесия тела необходимо (с точностью до знака равенства) и достаточно, чтобы его центр тяжести лежал ниже центра кривизны поверхности в точке касания тела с опорной плоскостью.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА 1. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ МЕХАНИКИ
- § 1. Некоторые понятия и формулы кинематики твердого тела
- § 2. Движение тела по поверхности. Трение
- § 3. Основные динамические величины твердого тела
- § 4. Основные теоремы динамики
- § 5. Уравнения движения твердого тела
- § 6. Движение Эйлера — Пуансо
- § 7. Некоторые дифференциальные уравнения аналитической динамики
- ГЛАВА 2. ИССЛЕДОВАНИЕ ДВИЖЕНИЯ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА НА АБСОЛЮТНО ГЛАДКОЙ ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ
- § 1. Уравнения движения
- 2. Уравнения Лагранжа.
- 3. Уравнения Рауса.
- 4. Уравнения Гамильтона.
- § 2. Движение динамически и геометрически симметричного тела
- 2. Стационарные движения и их устойчивость.
- 3. Пример: стационарные движения динамически симметричного шара
- 4. Движение симметричного тела в общем случае.
- § 3. Качественный анализ движения тела, близкого к симметричному
- § 4. Перманентные вращения твердого тела на гладкой плоскости
- 2. Устойчивость перманентных вращений
- § 5. Некоторые задачи динамики эллипсоида на гладкой плоскости
- 2. Движение, при котором эллипсоид касается плоскости одним из его главных сечений.
- 3. О несуществовании дополнительного интеграла в задаче о движении тела, ограниченного эллипсоидальной поверхностью.
- 4. Качественное исследование движения эллипсоида, близкого к шару.
- § 6. Движение тела с острым краем
- 2. Регулярные прецессии динамически симметричного тела с острым краем в форме окружности.
- 3. Устойчивость движения эллиптического диска.
- § 7. О бифуркационном множестве в задаче о движении твердого тела по плоскости
- ГЛАВА 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ПО НЕПОДВИЖНОЙ АБСОЛЮТНО ШЕРОХОВАТОЙ ПОВЕРХНОСТИ
- 2. Вывод уравнений движения твердого тела, движущегося без скольжения по произвольной неподвижной поверхности.
- 3. Уравнения Воронца движения тяжелого твердого тела, катящегося без скольжения по горизонтальной плоскости.
- 4. Уравнения Эйлера — Лагранжа движения без скольжения твердого тела по произвольной неподвижной поверхности.
- 5. Уравнения Чаплыгина движения без скольжения твердого тела по неподвижной горизонтальной плоскости.
- 6. Уравнения движения твердого тела с острым краем по абсолютно шероховатой поверхности.
- § 2. Движение тела сферической формы по неподвижной поверхности
- 2. Шар Чаплыгина на горизонтальной плоскости.
- 3. Уравнения движения шара по неподвижной поверхности заданной формы.
- 4. Тяжелый шар на неподвижном сфере.
- 5. Устойчивость вращения шара на вершине поверхности двойной кривизны.
- 6. О применении некоторых обобщений теоремы об изменении кинетического момента в задаче о качении твердого тела по неподвижной поверхности.
- § 3. Движение тела вращения по неподвижной поверхности
- 2. Метод Чаплыгина решения задачи о движении тяжелого тела вращения на плоскости.
- 3. Движение тела вращения, ограниченного сферической поверхностью.
- 4. Устойчивость стационарного вращения тела вокруг вертикали.
- 5. Регулярные прецессии.
- 6. Об уравнениях задачи о движении без скольжения тела вращения по поверхности вращения.
- 7. Тяжелое тело вращения с плоским участком поверхности на сфере.
- § 4. Тело с острым краем на неподвижной поверхности
- 2. Общий случай движения диска по абсолютно шероховатой плоскости.
- 3. Дифференциальные уравнения задачи о движении диска по гладкому горизонтальному льду.
- 4. Стационарные движения диска на льду и их устойчивость.
- § 5. Перманентные вращения тяжелого твердого тела на абсолютно шероховатой горизонтальной плоскости
- 2. Устойчивость перманентных вращений.
- 3. О перманентных вращениях неоднородного шара.
- § 6. Динамика кельтского камня
- 2. Устойчивость перманентных вращении тела вокруг главной оси инерции.
- 3. Нормальные координаты для колебании вблизи положения равновесия.
- 4. Нормальная форма нелинейных уравнений возмущенного движения.
- 5. Нелинейные колебания.
- § 7. Простейшие случаи движения однородного эллипсоида по абсолютно шероховатой плоскости
- 2. Случай, когда точка касания описывает одно из главных сечений эллипсоида.
- § 8. Периодические движения эллипсоида, близкого к шару
- 2. Преобразование уравнений движения.
- 3. Существование периодических движений и их построение.
- 4. Кривая, описываемая точкой касания на плоскости.
- 5. Вычисление углов Эйлера.
- 6. Реакция плоскости.
- 7. Устойчивость периодических движений.
- § 9. Асимптотическое решение задачи о движении однородного эллипсоида по абсолютно шероховатой плоскости
- 2. Геометрические свойства усредненного движения.
- 4. Случай эллипсоида вращения.
- 5. Движения, отвечающие полодиям — сепаратрисам.
- 6. Один особый случай движения.
- 7. Случай движения с малой скоростью центра тяжести.
- 8. Об асимптотике движения шара Чаплыгина.
- § 10. К геометрической интерпретации Пуансо движения твердого тела в случае Эйлера
- ГЛАВА 4. ТВЕРДОЕ ТЕЛО НА НЕПОДВИЖНОЙ ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ ПРИ НАЛИЧИИ ТРЕНИЯ СКОЛЬЖЕНИЯ
- 2. Учет трения качения и верчения.
- 3. О движении шара под действием вязкого трения скольжения.
- § 2. Стационарные движения тела вращения
- 2. Теория Контепсу связи между трением скольжения и трением верчения.
- 3. Интеграл Желле.
- 4. Стационарные движения неоднородного шара на плоскости с вязким трением.
- 5. Регулярные прецессии произвольного тела вращения.
- 6. О перманентных вращениях несимметричного тела и их устойчивости.
- § 3. Финальные движения твердого тела на плоскости с вязким трением
- 2. О финальных движениях тела вращения.
- § 4. Эволюция движения волчка сферической формы на плоскости с вязким трением
- 2. Разделение медленных и быстрых движений.
- 3. Эволюция движения волчка на основе приближенной системы уравнений движения.
- 4. Об устойчивости эволюции движения волчка в силу точных уравнений движения.
- § 5. Асимптотический анализ динамики эллипсоида на плоскости с трением скольжения
- 2. Уравнения движения эллипсоида в форме, удобной для применения метода усреднения.
- 4. Геометрическая интерпретация усредненного движения.
- 5. О стремлении эллипсоида вращаться вокруг наибольшей оси.
- 6. Частные решения усредненных уравнений движения.
- 7. О движении эллипсоида по плоскости с вязким трением.
- § 6 Шар Чаплыгина на плоскости с трением скольжения
- 2. Эволюция движения шара на плоскости с вязким трением.
- СПИСОК ЛИТЕРАТУРЫ