| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
Пример 1 [31]. Рассмотрим систему примера 2 § 5 гл. 6, т. е. систему

В гл. 6 эта система рассматривалась при всевозможных значениях параметра  но при некоторых ограничениях на значе-. ние k. Здесь мы рассмотрим изменение качественной структуры системы (1) в зависимости от входящих в нее параметров Яиц при любых
но при некоторых ограничениях на значе-. ние k. Здесь мы рассмотрим изменение качественной структуры системы (1) в зависимости от входящих в нее параметров Яиц при любых 
Напомним, что кривая контактов системы (1) с консервативной системой, соответствующей значению к — 0, есть

т. е. контакт ложный — траектории системы (1) при  образуют с траекториями консервативной системы угол одного знака.
образуют с траекториями консервативной системы угол одного знака.
Заметим, что для двух различных значений параметра  траектории системы с
траектории системы с  пересекают повсюду траектории системы с
пересекают повсюду траектории системы с 
Направление поворота векторного поля определяется знаком  что следует из рассмотрения контактной кривой системы с
что следует из рассмотрения контактной кривой системы с  и системы с
и системы с 

Кроме того, как мы видели, при фиксированном значении параметра  при всех
при всех  начало координат — фокус или узел, точка
начало координат — фокус или узел, точка  -седло, и положение и характер состояний равновесия на экваторе не меняются.
-седло, и положение и характер состояний равновесия на экваторе не меняются.
Разбиение сферы Пуанкаре на траектории при значениях параметра  сохраняет свою качественную структуру при любых значениях
сохраняет свою качественную структуру при любых значениях 
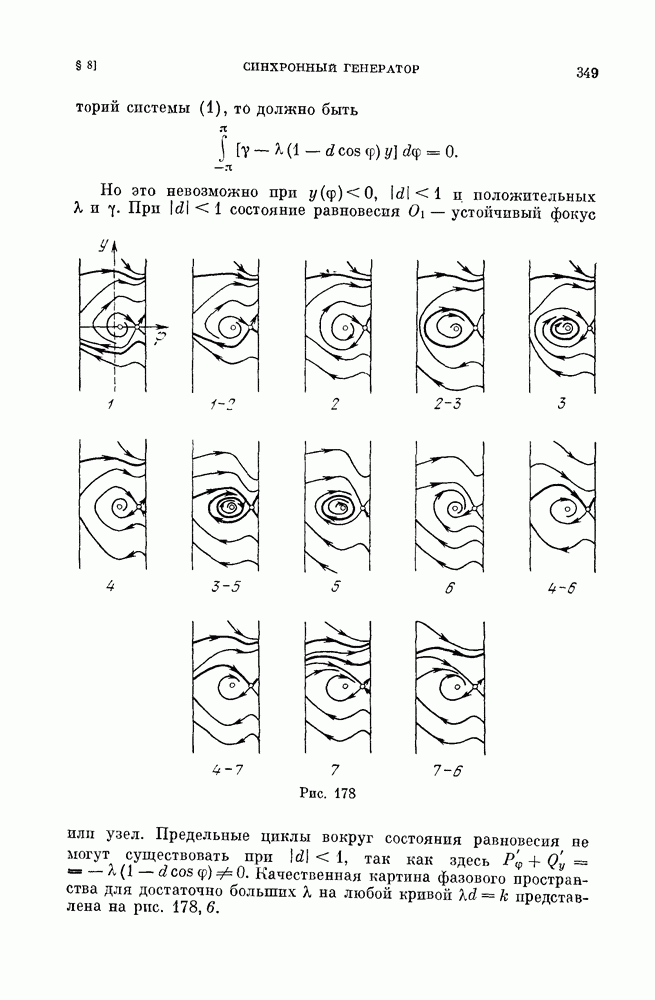
В случаях  качественная картина разбиения сферы Пуанкаре на траектории зависит от величины параметра Я (см. подстрочное примечание на с. 126).
качественная картина разбиения сферы Пуанкаре на траектории зависит от величины параметра Я (см. подстрочное примечание на с. 126).
Рассмотрим случай  При
При  имеет место
имеет место  гл. 6.
гл. 6.
При  поведение сепаратрис седла
поведение сепаратрис седла  попадающих внутрь областей
попадающих внутрь областей  ограниченных сепаратрисами консервативной системы и дугами экватора (эти области не содержат особых точек, лежащих в конечной части плоскости), в силу поворота поля определяется однозначно (см. рис. 87 гл. 6). Поведение
ограниченных сепаратрисами консервативной системы и дугами экватора (эти области не содержат особых точек, лежащих в конечной части плоскости), в силу поворота поля определяется однозначно (см. рис. 87 гл. 6). Поведение  седла, попадающего в область
седла, попадающего в область  ограниченную сепаратрисами и
ограниченную сепаратрисами и  консервативной системы и дугой экватора и содержащую внутри себя особую точку, не определяется однозначно и зависит от параметра Я.
консервативной системы и дугой экватора и содержащую внутри себя особую точку, не определяется однозначно и зависит от параметра Я.
Есть три возможности для поведения этого  седла:
седла:
а) идет в узел  на экваторе;
на экваторе;
б) идет в сложную особую точку  (седло-узел) на экваторе;
(седло-узел) на экваторе;
в) идет в особую точку К (фокус или узел) внутри области 
Вторая возможность имеет место при значении параметра

В этом случае существует интегральная прямая, идущая из седла в особую точку  (седло-узел) на экваторе. Уравнение интегральной прямой будет
(седло-узел) на экваторе. Уравнение интегральной прямой будет

что непосредственно проверяется. Качественная структура разбиения сферы Пуанкаре на траектории определяется теперь 
нозначно и изображена на рис. 124. Значение параметра  очевидно, бифуркационное. При
очевидно, бифуркационное. При  качественная картина будет иметь вид такой же, как на рис. 88 гл. 6, а при
качественная картина будет иметь вид такой же, как на рис. 88 гл. 6, а при  будет иметь место рис. 87 гл. 6. Во всех случаях структура определяется однозначно.
будет иметь место рис. 87 гл. 6. Во всех случаях структура определяется однозначно.
Рассмотрим случай  При
При  имеем качественную картину, изображенную на рис. 84 гл. 6.
имеем качественную картину, изображенную на рис. 84 гл. 6.

Рис. 124

Рис. 125
При  однозначно определяется поведение смещенных сепаратрис, попадающих в области I-III (область I ограничена сепаратрисами
однозначно определяется поведение смещенных сепаратрис, попадающих в области I-III (область I ограничена сепаратрисами  и
и  консервативной системы и близлежащей дугой экватора, область II заполнена замкнутыми кривыми, область III ограничена сепаратрисами
консервативной системы и близлежащей дугой экватора, область II заполнена замкнутыми кривыми, область III ограничена сепаратрисами  и
и  консервативной системы, отрезком
консервативной системы, отрезком  оси х и дугой
оси х и дугой  включающей дугу экватора). Они ведут себя так же, как при малых значениях К.
включающей дугу экватора). Они ведут себя так же, как при малых значениях К.
Поведение сепаратрисы, входящей в область IV (симметричную области III относительно оси  не определяется однозначно и зависит от величины К (аналогично случаю
не определяется однозначно и зависит от величины К (аналогично случаю  здесь имеется три возможности).
здесь имеется три возможности).
1) При  существует интегральная прямая
существует интегральная прямая

идущая из седла  в седло-узел
в седло-узел  на экваторе сферы Пуанкаре — качественная картина изображена на рис. 125;
на экваторе сферы Пуанкаре — качественная картина изображена на рис. 125;  — бифуркационное значение.
— бифуркационное значение.
2) При  поведение сепаратрисы определяется однозначно, и соответственно имеем качественные картины, изображенные на рис. 88, 89 гл. 6.
поведение сепаратрисы определяется однозначно, и соответственно имеем качественные картины, изображенные на рис. 88, 89 гл. 6.
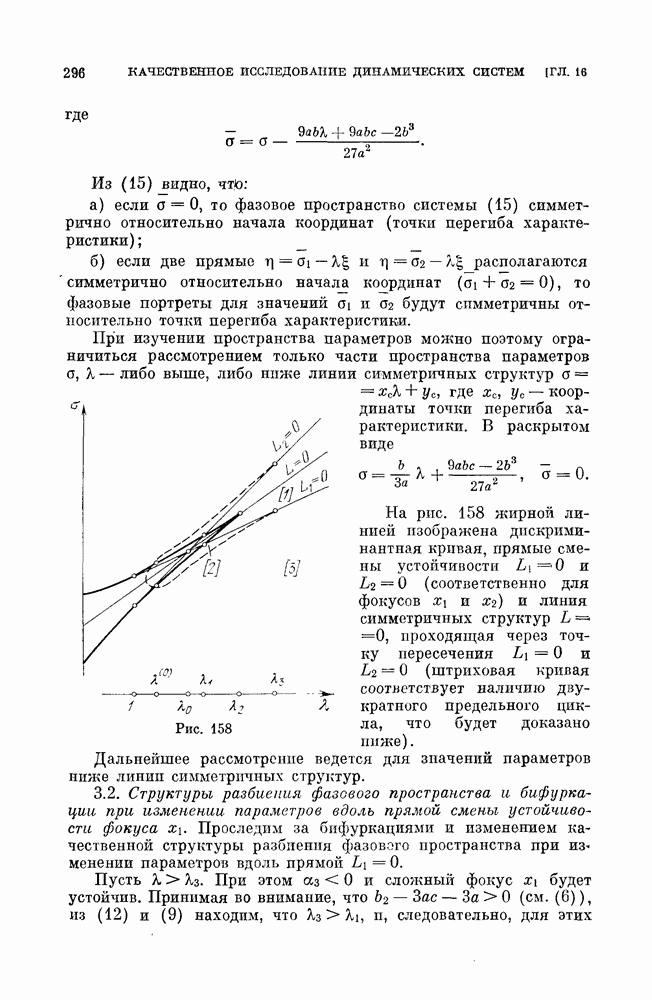
На рис. 126 представлено разбиение пространства параметров  Точкам на осях
Точкам на осях  а также на кривой
а также на кривой  соответствуют бифуркационные структуры.
соответствуют бифуркационные структуры.
3) При  на фазовой плоскости
на фазовой плоскости  существуют области, заполненные замкнутыми кривыми, при
существуют области, заполненные замкнутыми кривыми, при  существуют сепаратрисы, идущие из седла в седло (интегральные прямые), и при
существуют сепаратрисы, идущие из седла в седло (интегральные прямые), и при  сложная особая точка высокого порядка, распадающаяся при изменении параметра
сложная особая точка высокого порядка, распадающаяся при изменении параметра 
Пример 2 [30].

Особые точки фазовой плоскости удовлетворяют системе уравнений


Рис. 126
Умножая первое из этих уравнений на у, второе на а; и вычитая, получим следующее уравнение, которому должны удовлетворять координаты особых точек:

Полагая  мы получаем уравнение для к
мы получаем уравнение для к

Корни этого уравнения действительны в случае, когда

Обозначаем их через  подставляя в одно из уравнений (3), получаем в этом случае пять состояний равновесия:
подставляя в одно из уравнений (3), получаем в этом случае пять состояний равновесия:

Состояние равновесия  , очевидно, простое, если
, очевидно, простое, если  Нетрудно также видеть, что в случае
Нетрудно также видеть, что в случае  остальные состояния равновесия тоже простые. Отметим, кроме того, что при
остальные состояния равновесия тоже простые. Отметим, кроме того, что при  прямые
прямые  являются интегральными прямыми рассматриваемого дифференциального уравнения, так как соотношение
являются интегральными прямыми рассматриваемого дифференциального уравнения, так как соотношение

удовлетворяется тождественно при подстановке  Действительно, мы имеем
Действительно, мы имеем

или

так как выражение в скобках равно нулю  есть корень уравнения (4)). Характер состояния равновесия в начале координат легко может быть определен по корням соответствующего характеристического уравнения. Для исследования остальных состояний равновесия достаточно ограничиться рассмотрением каких-либо двух, не лежащих одновременно на одной и той же прямой
есть корень уравнения (4)). Характер состояния равновесия в начале координат легко может быть определен по корням соответствующего характеристического уравнения. Для исследования остальных состояний равновесия достаточно ограничиться рассмотрением каких-либо двух, не лежащих одновременно на одной и той же прямой  так как векторное поле, определяемое системой (3), симметрично относительно начала координат. (Система (3) не меняется при замене х на
так как векторное поле, определяемое системой (3), симметрично относительно начала координат. (Система (3) не меняется при замене х на  на
на  .) Определение их характера путем вычисления характеристических корней очень громоздко, и это можно сделать проще, воспользовавшись теорией индекса Пуанкаре.
.) Определение их характера путем вычисления характеристических корней очень громоздко, и это можно сделать проще, воспользовавшись теорией индекса Пуанкаре.
Так как при  все состояния равновесия простые, и при изменении знака
все состояния равновесия простые, и при изменении знака  когда корни
когда корни  делаются мнимыми, исчезают (кроме
делаются мнимыми, исчезают (кроме  ), то сумма их индексов должна равняться нулю. Кроме того, ни одно из них не может быть фокусом, так как через них проходят интегральные прямые
), то сумма их индексов должна равняться нулю. Кроме того, ни одно из них не может быть фокусом, так как через них проходят интегральные прямые  Отсюда заключаем, что одно из них — седло, другое — узел.
Отсюда заключаем, что одно из них — седло, другое — узел.
Когда  эти точки сливаются в двойную точку — седло-узел (если при этом
эти точки сливаются в двойную точку — седло-узел (если при этом 
В случае  две симметричные точки сливаются с особой точкой в начале координат в одну и образуют особую точку высшего порядка. Заметив, что при
две симметричные точки сливаются с особой точкой в начале координат в одну и образуют особую точку высшего порядка. Заметив, что при  индекс особой точки в начале координат равен
индекс особой точки в начале координат равен  а при
а при  равен —1, заключаем отсюда, что сумма индексов особых точек, слившихся с началом, равна —2, т. е. эти особые точки — седла, и сложная особая точка имеет характер седла, а оставшиеся две — узлы.
равен —1, заключаем отсюда, что сумма индексов особых точек, слившихся с началом, равна —2, т. е. эти особые точки — седла, и сложная особая точка имеет характер седла, а оставшиеся две — узлы.
В случае, когда

система имеет в начале координат единственную особую точку типа фокус. Постараемся выяснить наличие предельных циклов. Выберем в качестве топографической системы семейство окружностей

Тогда контактная кривая (т. е. кривая, где окружности (6) касаются траектории системы  будет иметь вид
будет иметь вид

или

В полярных координатах

Радиусы  крайних кругов, касающихся кривой контакта, определяются из условия
крайних кругов, касающихся кривой контакта, определяются из условия  которое дает
которое дает  Отсюда находим радиусы крайних кругов топографической системы, касающихся контактной кривой:
Отсюда находим радиусы крайних кругов топографической системы, касающихся контактной кривой:

Предельный цикл лежит в кольцевой области между этими кругами,  будут оба положительными, если
будут оба положительными, если  или
или  Последнее условие совпадает с условием, при котором кривая контактов имеет в начале координат изолированную точку:
Последнее условие совпадает с условием, при котором кривая контактов имеет в начале координат изолированную точку:

Если это условие не выполнено, кривая контактов проходит через начало координат, а величина  становится отрицательной, и можно лишь утверждать, что предельный цикл (если он существует) располагается внутри окружности радиуса
становится отрицательной, и можно лишь утверждать, что предельный цикл (если он существует) располагается внутри окружности радиуса  Нетрудно доказать, что предельный цикл единствен. Воспользуемся с этой целью критерием Дюлака для кольцевой области (см. гл. 6). Очевидно, что функции
Нетрудно доказать, что предельный цикл единствен. Воспользуемся с этой целью критерием Дюлака для кольцевой области (см. гл. 6). Очевидно, что функции

и

удовлетворяют условиям теоремы Дюлака для кольцевой области (см. гл. 6), так как в этом случае  дифференцируема в любой кольцевой области
дифференцируема в любой кольцевой области  окружающей начало координат. Легко проверить, что
окружающей начало координат. Легко проверить, что

не меняет знака в области  Таким образом, цикл один.
Таким образом, цикл один.
Доказанная единственность предельного цикла позволяет утверждать, что при смене устойчивости особой точки в начале координат предельный цикл стягивается в особую точку.
В самом деле, в противном случае должно было бы существовать четное число предельных циклов. Отсюда же следует, что для а  предельных циклов нет.
предельных циклов нет.
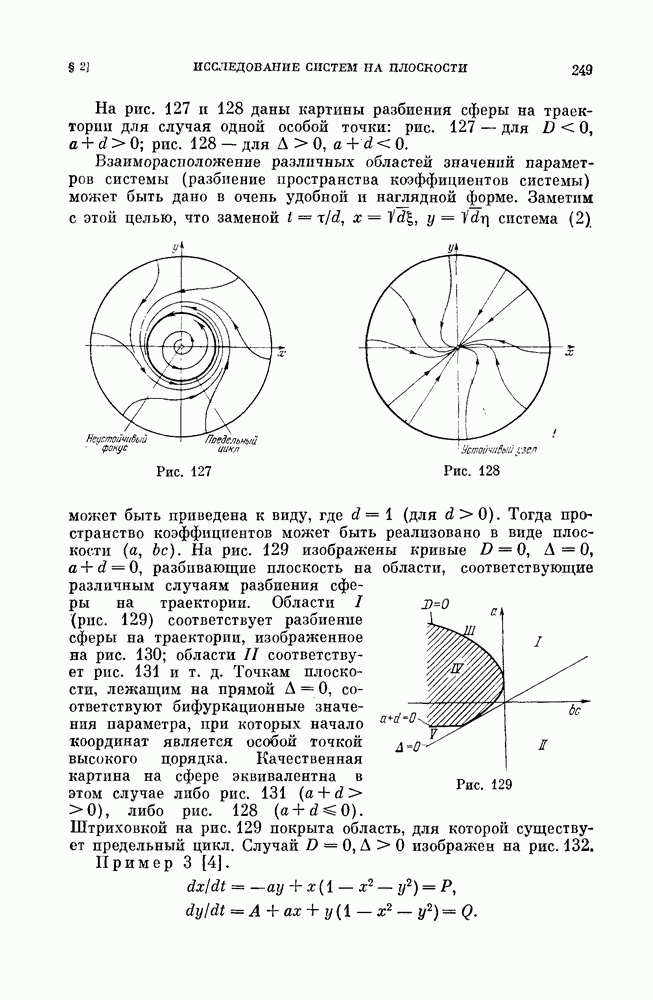
На рис. 127 и 128 даны картины разбиения сферы на траектории для случая одной особой точки: рис. 127 — для  рис. 128 — для
рис. 128 — для  .
.
Взаиморасположение различных областей значений параметров системы (разбиение пространства коэффициентов системы) может быть дано в очень удобной и наглядной форме.

Рис. 127

Рис. 128
Заметим с этой целью, что заменой  система (2) может быть приведена к виду, где
система (2) может быть приведена к виду, где  (для
(для  Тогда пространство коэффициентов может быть реализовано в виде плоскости
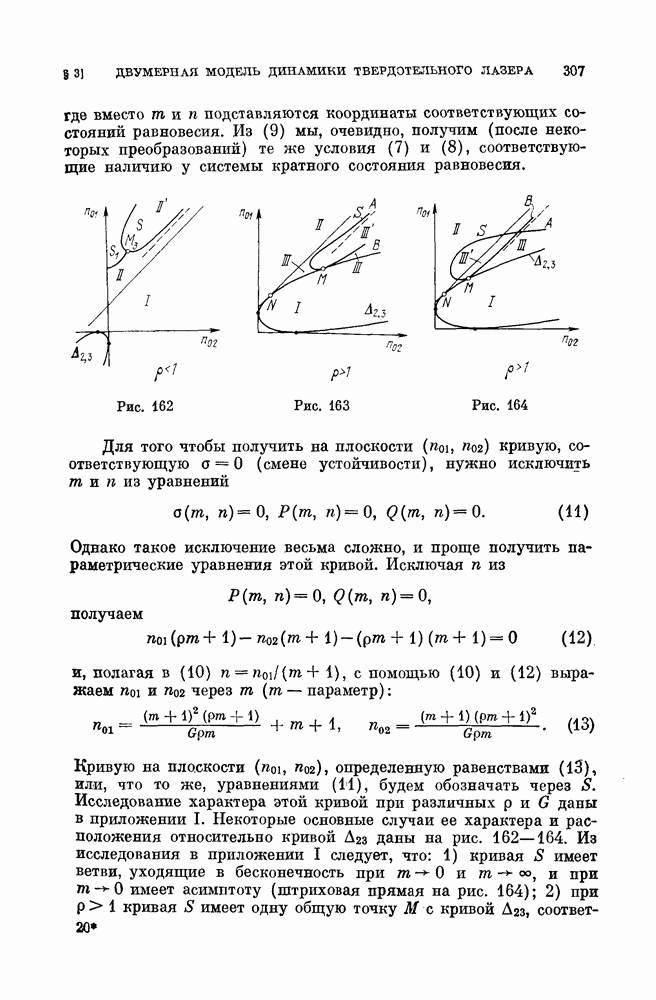
Тогда пространство коэффициентов может быть реализовано в виде плоскости  На рис. 129 изображены кривые
На рис. 129 изображены кривые  разбивающие плоскость на области, соответствующие различным случаям разбиения сферы на траектории. Области I (рис. 129) соответствует разбиение сферы на траектории, изображенное на рис. 130; области II соответствует рис. 131 и т. д. Точкам плоскости, лежащим на прямой
разбивающие плоскость на области, соответствующие различным случаям разбиения сферы на траектории. Области I (рис. 129) соответствует разбиение сферы на траектории, изображенное на рис. 130; области II соответствует рис. 131 и т. д. Точкам плоскости, лежащим на прямой  соответствуют бифуркационные значения параметра, при которых начало координат является особой точкой высокого порядка. Качественная картина на сфере эквивалентна в этом случае либо рис.
соответствуют бифуркационные значения параметра, при которых начало координат является особой точкой высокого порядка. Качественная картина на сфере эквивалентна в этом случае либо рис.  либо рис.
либо рис. 

Рис. 129
Штриховкой на рис. 129 покрыта область, для которой существует предельный цикл. Случай  изображен на рис. 132.
изображен на рис. 132.
Пример 3 [4].

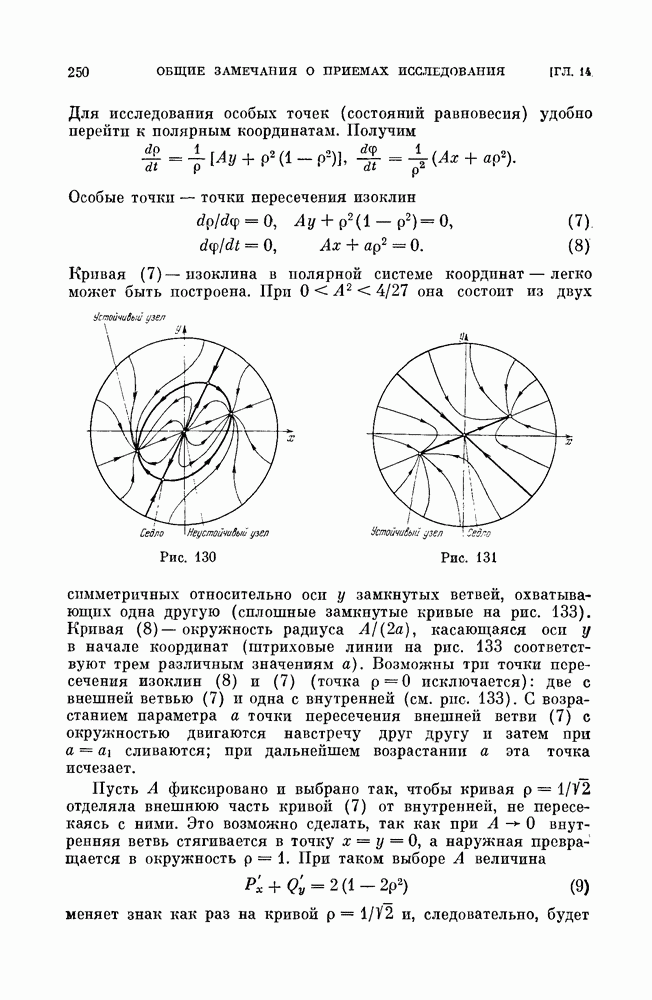
Для исследования особых точек (состояний равновесия) удобно перейти к полярным координатам. Получим

Особые точки — точки пересечения изоклин

Кривая  -изоклина в полярной системе координат — легко может быть построена.
-изоклина в полярной системе координат — легко может быть построена.

Рис. 130

Рис. 131
При  она состоит из двух симметричных относительно оси у замкнутых ветвей, охватывающих одна другую (сплошные замкнутые кривые на рис. 133). Кривая
она состоит из двух симметричных относительно оси у замкнутых ветвей, охватывающих одна другую (сплошные замкнутые кривые на рис. 133). Кривая  -окружность радиуса
-окружность радиуса  касающаяся оси у в начале координат (штриховые линии на рис. 133 соответствуют трем различным значениям а). Возможны три точки пересечения изоклин (8) и (7) (точка
касающаяся оси у в начале координат (штриховые линии на рис. 133 соответствуют трем различным значениям а). Возможны три точки пересечения изоклин (8) и (7) (точка  исключается): две с внешней ветвью (7) и одна с внутренней (см. рис. 133). С возрастанием параметра а точки пересечения внешней ветви (7) с окружностью двигаются навстречу друг другу и затем при
исключается): две с внешней ветвью (7) и одна с внутренней (см. рис. 133). С возрастанием параметра а точки пересечения внешней ветви (7) с окружностью двигаются навстречу друг другу и затем при  сливаются; при дальнейшем возрастании а эта точка исчезает.
сливаются; при дальнейшем возрастании а эта точка исчезает.
Пусть А фиксировано и выбрано так, чтобы кривая  отделяла внешнюю часть кривой (7) от внутренней, не пересекаясь с ними. Это возможно сделать, так как при
отделяла внешнюю часть кривой (7) от внутренней, не пересекаясь с ними. Это возможно сделать, так как при  внутренняя ветвь стягивается в точку
внутренняя ветвь стягивается в точку  а наружная превращается в окружность
а наружная превращается в окружность  При таком выборе А величина
При таком выборе А величина

меняет знак как раз на кривой  следовательно, будет
следовательно, будет
положительной для особой точки на внутренней ветви кривой (7) и отрицательной для особых точек на внешней ветви.
Возьмем в качестве топографической системы Пуанкаре семейство окружностей  и составим производную
и составим производную  вдоль траекторий системы
вдоль траекторий системы

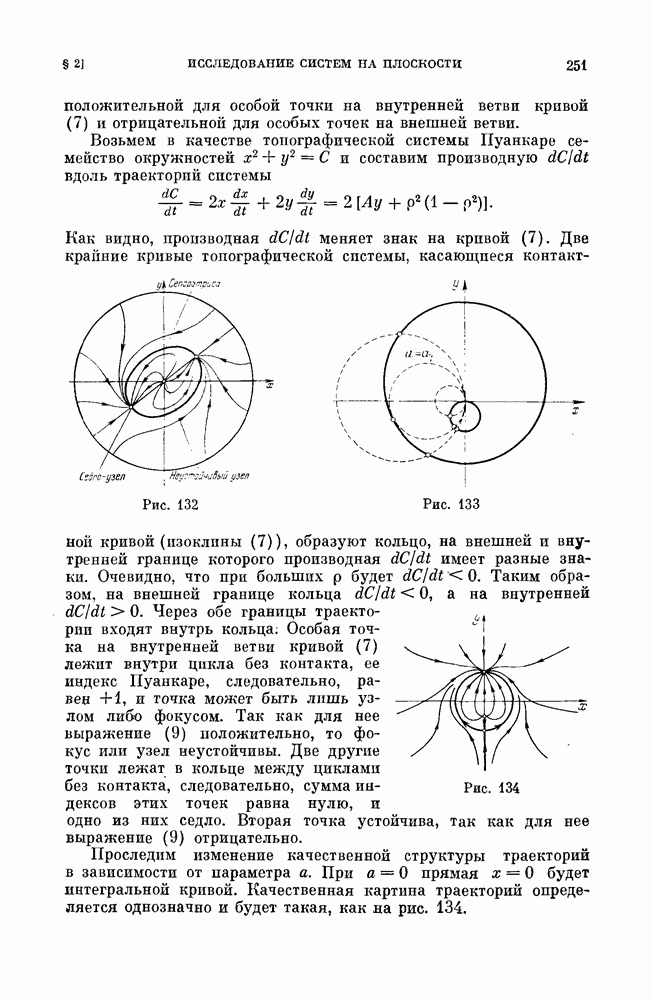
Как видно, производная  меняет знак на кривой (7). Две крайние кривые топографической системы, касающиеся контактной кривой (изоклины (7)), образуют кольцо, на внешней и внутренней границе которого производная
меняет знак на кривой (7). Две крайние кривые топографической системы, касающиеся контактной кривой (изоклины (7)), образуют кольцо, на внешней и внутренней границе которого производная  имеет разные знаки.
имеет разные знаки.

Рис. 132

Рис. 133
Очевидно, что при больших  будет
будет  Таким образом, на внешней границе кольца
Таким образом, на внешней границе кольца  а на внутренней
а на внутренней  Через обе границы траектории входят внутрь кольца: Особая точка на внутренней ветви кривой (7) лежит внутри цикла без контакта, ее индекс Пуанкаре, следовательно, равен
Через обе границы траектории входят внутрь кольца: Особая точка на внутренней ветви кривой (7) лежит внутри цикла без контакта, ее индекс Пуанкаре, следовательно, равен  и точка может быть лишь узлом либо фокусом. Так как для нее выражение (9) положительно, то фокус или узел неустойчивы. Две другие точки лежат в кольце между циклами без контакта, следовательно, сумма индексов этих точек равна нулю, и одно из них седло. Вторая точка устойчива, так как для нее выражение (9) отрицательно.
и точка может быть лишь узлом либо фокусом. Так как для нее выражение (9) положительно, то фокус или узел неустойчивы. Две другие точки лежат в кольце между циклами без контакта, следовательно, сумма индексов этих точек равна нулю, и одно из них седло. Вторая точка устойчива, так как для нее выражение (9) отрицательно.

Рис. 134
Проследим изменение качественной структуры траекторий в зависимости от параметра а. При  прямая
прямая  будет интегральной кривой. Качественная картина траекторий определяется однозначно и будет такая, как на рис. 134.
будет интегральной кривой. Качественная картина траекторий определяется однозначно и будет такая, как на рис. 134.
При возрастании а точки (седло и устойчивый узел) будут сближаться, но до момента слияния качественная структура не может измениться, так как не меняются число и характер особых точек и поведение сепаратрис и так как внутри кольца не могут возникнуть предельные циклы за счет сгущения траекторий. Последнее невозможно, потому что кривая  лежит вне кольца (критерий Дюлака).
лежит вне кольца (критерий Дюлака).

Рис. 135

Рис. 136
При дальнейшем возрастании а точки сливаются и затем исчезают.
Из особой точки седло-узел и сепаратрисы седло-узла (см. гл. 10, И) рождается единственный (так как  в седло-узле) предельный цикл (рис. 135 и 136).
в седло-узле) предельный цикл (рис. 135 и 136).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. АВТОНОМНЫЕ СИСТЕМЫ ВТОРОГО ПОРЯДКА С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- § 1. Автономная динамическая система на плоскости.
- § 2. Теорема существования и единственности решения.
- § 3. Простейшие свойства решений системы (А).
- § 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
- § 5. Сопоставление геометрической интерпретации системы (А) в пространстве (x, y, t) с интерпретацией на фазовой плоскости.
- § 6. Некоторые термины.
- § 7. Теорема о непрерывной зависимости решения от начальных условий.
- § 8. Направление на траекториях. Изменение параметризации.
- § 9. Дифференциальное уравнение, соответствующее динамической системе.
- § 10. Понятие интегральной кривой и интеграла в случае аналитических правых частей Р(х,у) и Q(x,y) системы (А).
- § 11. Что значит «найти решение динамической системы»?
- § 12. Примеры.
- § 13. Замечания по поводу примеров § 12.
- § 14. Математическое определение качественной (топологической) структуры разбиения на траектории и качественного исследования динамической системы.
- ГЛАВА 2. ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ — БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ
- § 2. Цикл без контакта.
- § 3. Предельная точка полутраектории и траектории. Предельная траектория.
- § 4. Основная теорема.
- § 5. Возможные типы полутраекторий и их предельных множеств.
- § 6. Особые и неособые полутраектории и траектории.
- § 7. Возможные типы особых и неособых траекторий.
- § 8. Случай конечного числа особых траекторий. Элементарные ячейки.
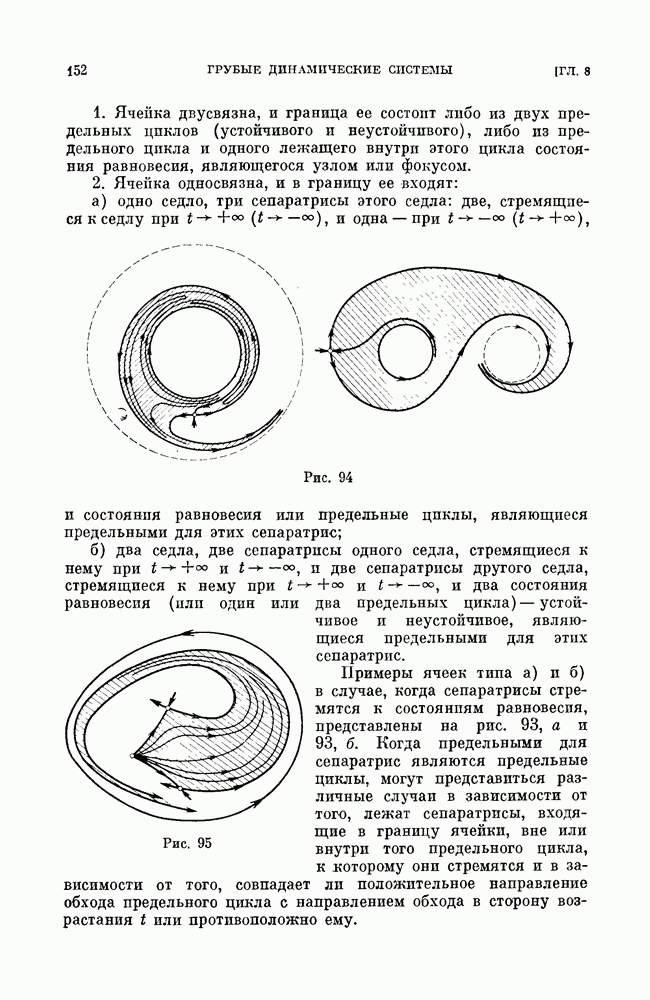
- § 9. Возможные типы ячеек. Односвязные и двусвязные ячейки.
- § 10. Два подхода к описанию качественной структуры.
- § 11. Качественная (топологическая) структура состояния равновесия в случае конечного числа особых траекторий. Схема динамической системы.
- § 12. Устойчивость по Ляпунову.
- ГЛАВА 3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННОЙ СТРУКТУРЫ ОКРЕСТНОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (ОСОБОЙ ТОЧКИ)
- § 2. Приведение динамической системы к каноническому виду.
- § 3. Возможный характер простых состояний равновесия.
- § 4. Замечания о методах установления характера грубых состояний равновесия.
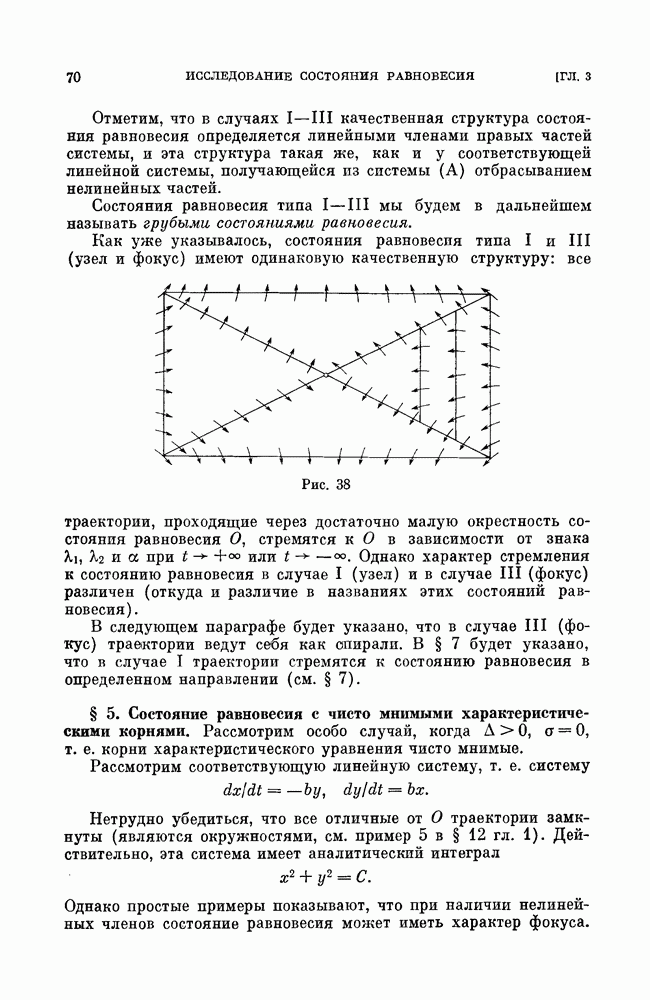
- § 5. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 6. Направления, в которых траектории стремятся к простым состояниям равновесия.
- § 7. Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия.
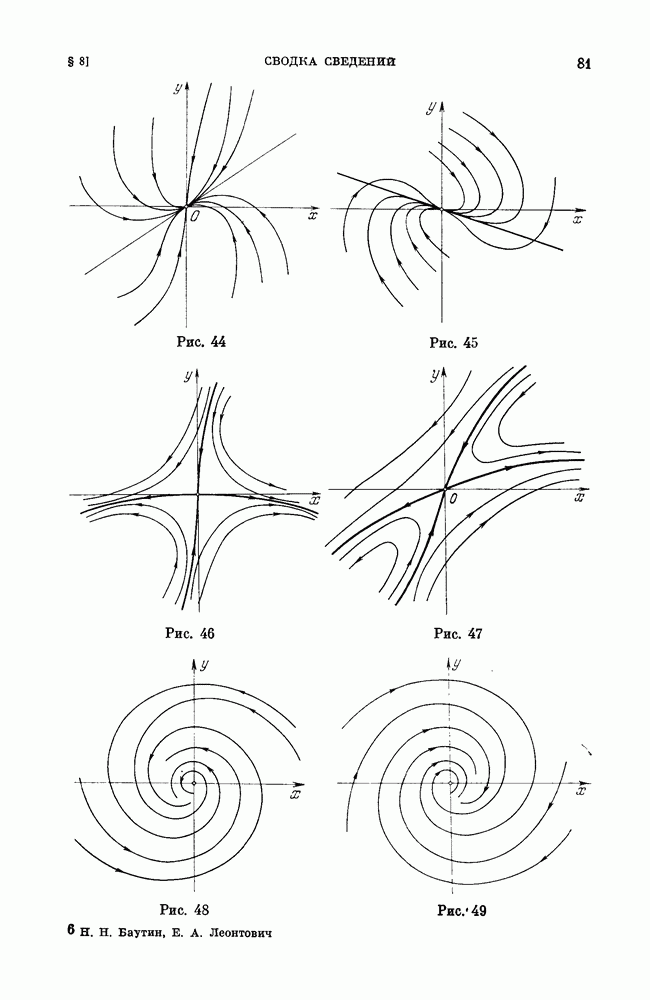
- § 8. Сводка сведений о грубых состояниях равновесия.
- ГЛАВА 4. КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ
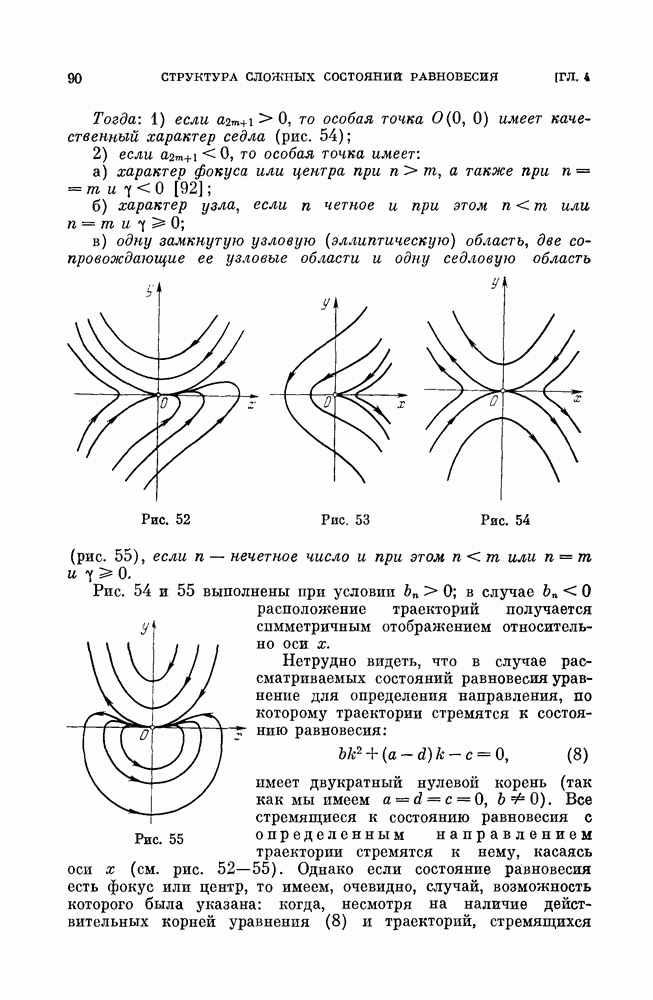
- § 1. Направления, в которых траектории стремятся к сложному состоянию равновесия.
- § 2. Сложное состояние равновесия (особая точка) с нулевыми характеристическими корнями.
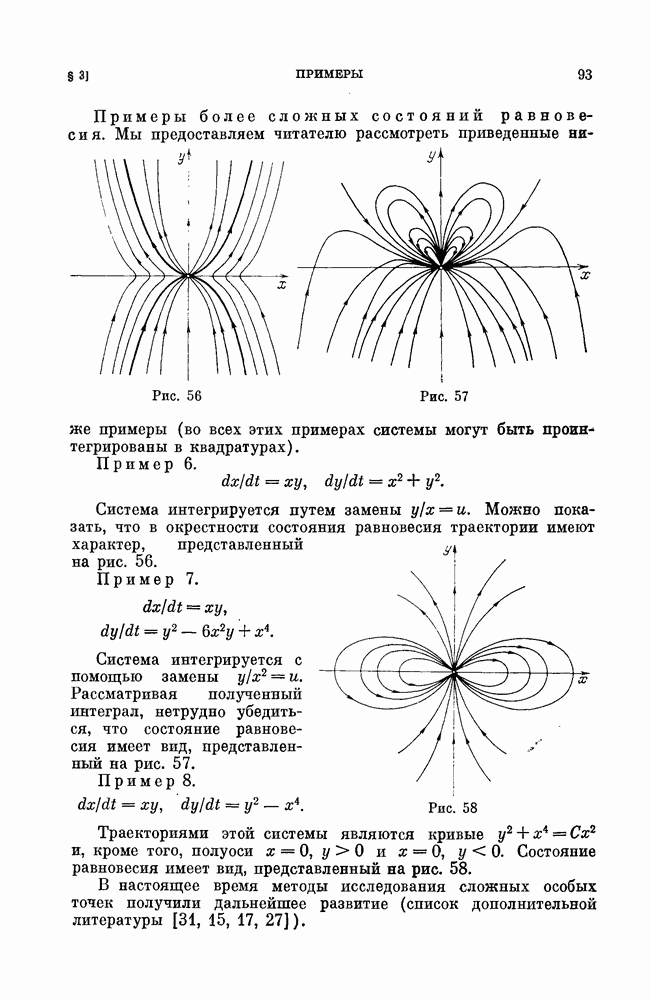
- § 3. Примеры.
- § 4. Нормальные формы.
- ГЛАВА 5. ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ
- § 2. Условия устойчивости и неустойчивости неподвижной точки точечного отображения.
- § 3. Функция соответствия.
- § 4. Изучение окрестности замкнутой траектории. Простые и сложные предельные циклы.
- § 5. Аналитические выражения для коэффициентов функции последования. Характеристический показатель замкнутой траектории.
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЕМЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 2. Изучение поведения интегральных кривых в бесконечности. Сфера Пуанкаре.
- § 3. Примеры исследования в бесконечности [93].
- § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов.
- 1. Некоторые видоизменения критериев Бендиксона и Дюлака.
- 2. Индексы Пуанкаре. Распределение особых точек [77, 117].
- 3. Условия сосуществования замкнутых траекторий и особых точек.
- 4. Две общие теоремы Пуанкаре.
- § 5. Топографическая система Пуанкаре. Функция Ляпунова. Кривые контактов.
- ЧАСТЬ II. ТЕОРИЯ БИФУРКАЦИЙ
- § 1. Свойства консервативных систем на плоскости [2, 3].
- § 2. Динамические системы, характерные для теории колебаний.
- § 3. Измененные системы. Системы, правые части которых зависят от параметра.
- § 4. Основные теоремы о зависимости решения от изменения правых частей динамической системы.
- § 5. Грубость динамической системы и теоремы о непрерывной зависимости решения от изменения правых частей.
- ГЛАВА 8. ГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
- § 2. Состояния равновесия, возможные в грубой динамической системе.
- § 3. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 4. Замкнутые траектории, возможные в грубой системе.
- § 5. Поведение сепаратрис седел в грубых системах.
- § 6. Необходимые условия грубости. Достаточность этих условий для грубости системы.
- § 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем.
- § 8. Понятие грубости при более общих предположениях относительно правых частей динамической системы.
- § 9. Типы особых траекторий и ячеек в грубых системах.
- § 10. Замечания по поводу определения грубой системы.
- ГЛАВА 9. ПРОСТЕЙШИЕ НЕГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ — СИСТЕМЫ ПЕРВОЙ СТЕПЕНИ НЕГРУБОСТИ
- § 2. Системы первой степени негрубости.
- § 3. Состояния равновесия, возможные в системе первой степени негрубости.
- § 4. Замкнутые траектории, возможные в системе первой степени негрубости.
- § 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости.
- § 6. Необходимые и достаточные условия первой степени негрубости.
- § 7. Динамические системы более высокой степени негрубости.
- ГЛАВА 10. БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- § 1. Определение бифуркации.
- § 2. Бифуркации систем первой степени негрубости.
- § 3. Бифуркации некоторых типов сложных особых точек.
- § 4. Бифуркации двукратной точки, для которой …
- § 5. Рождение предельных циклов из особых траекторий степени негрубости выше первой.
- ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
- § 1. Возможный характер зависимости правых частей динамической системы от параметров.
- § 2. Смена качественных структур при изменении параметров.
- § 3. Случай, когда правые части зависят более чем от одного параметра.
- § 4. Бифуркации «от бесконечности».
- § 5. Условия существования седло-узла и сложного фокуса первого порядка.
- § 6. Поворот векторного поля.
- § 7. Метод малого параметра. Метод Понтрягина.
- ГЛАВА 12. ДИНАМИЧЕСКИЕ СИСТЕМЫ С ЦИЛИНДРИЧЕСКОЙ ФАЗОВОЙ ПОВЕРХНОСТЬЮ
- § 1. Цилиндрическая фазовая поверхность и характер траекторий, возможных на цилиндрической фазовой поверхности.
- § 2. Замкнутые траектории, охватывающие цилиндр.
- § 3. Приемы исследования качественной структуры динамической системы на цилиндре.
- § 4. Понятие грубости и степени негрубости для динамических систем на цилиндре. Бифуркации на цилиндре. Поворот поля.
- § 5. Динамические системы на цилиндре, близкие к гамильтоновым (метод Понтрягина).
- ГЛАВА 13. АДЕКВАТНОЕ ИСТОЛКОВАНИЕ НЕЛИНЕЙНЫХ ФИЗИЧЕСКИХ ЯВЛЕНИЙ ФАКТАМИ КАЧЕСТВЕННОЙ ТЕОРИИ И ТЕОРИИ БИФУРКАЦИЙ ДИНАМИЧЕСКИХ СИСТЕМ
- § 1. Мягкий и жесткий режимы.
- § 2. Замечания о границах области устойчивости различных стационарных режимов.
- § 3. Мягкое и жесткое возникновение колебаний.
- § 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
- § 5. Замечания по поводу других границ области устойчивости.
- ЧАСТЬ III. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- ГЛАВА 14. ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 1. Некоторые рецептурные указания.
- § 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
- § 3. Некоторые простые примеры динамических систем на цилиндре.
- ГЛАВА 15. ИССЛЕДОВАНИЕ МЕТОДОМ МАЛОГО ПАРАМЕТРА (МЕТОДОМ ПОНТРЯГИНА)
- § 2. Примеры рассмотрения методом Понтрягина (полное исследование).
- § 3. Исследование методом Понтрягина с привлечением вычислительных методов.
- ГЛАВА 16. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ
- § 2. Электрическая цепь с туннельным диодом.
- § 3. Двумерная модель динамики твердотельного лазера [119].
- § 4. Симметричный полет самолета в вертикальной плоскости (задача Н. Е. Жуковского).
- § 5. Система, описывающая динамику проточного химического реактора.
- § 6. Фазовая автоподстройка частоты.
- § 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов).
- § 8. Синхронный генератор с асинхронной характеристикой.
- ЧАСТЬ IV. КУСОЧНО-СШИТЫЕ СИСТЕМЫ
- ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ
- § 1. Сшитые системы. Доопределение на линиях сшивания.
- § 2. Возможные типы полутраекторий сшитых систем.
- § 3. Особые траектории сшитых систем.
- § 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
- ГЛАВА 18. ИССЛЕДОВАНИЕ КУСОЧНО-СШИТЫХ СИСТЕМ МЕТОДОМ ПОНТРЯГИНА
- § 2. Автоподстройка при кусочно-постоянной аппроксимации характеристики.
- § 3. Автоколебания синхронного мотора.
- ГЛАВА 19. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ
- § 2. Следящая система с люфтом.
- § 3. Электрическая цепь с туннельным диодом.
- § 4. Система со скачками на линии сшивания.
- ГЛАВА 20. ОБ АППРОКСИМАЦИЯХ И ГРУБОСТИ ПРОСТРАНСТВА ПАРАМЕТРОВ [39, 41, 42]
- § 1. Рассмотрение системы (2) при аппроксимациях пилообразными функциями.
- § 2. Рассмотрение системы (2) при аппроксимации, включающей отрезок параболы.
- § 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin f, и пилообразной для cos f функциями.
- § 4. Исследование роли аппроксимаций для уравнения маятникового типа.
- § 5. Динамическая система, описывающая автоколебания синхронного мотора.
- § 6. Динамическая система, описывающая симметричный полет самолета.
- ДОПОЛНЕНИЕ
- § 1. Динамическое системы на двумерных поверхностях.
- § 2. Динамические системы в n-мерном евклидовом пространстве.
- СПИСОК ЛИТЕРАТУРЫ