| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Система со скачками на линии сшивания.
Рассмотрим уравнение [126—128]

в предположении, что характеристика  имеет разрывы типа конечного скачка.
имеет разрывы типа конечного скачка.
Пусть  одна из точек разрыва. Эквивалентная уравнению (1) система
одна из точек разрыва. Эквивалентная уравнению (1) система

не определена на прямой  Поэтому движение изображающей точки системы при попадании ее на эту прямую нуждается в доопределении. Естественно получить его следующим образом. В интервале
Поэтому движение изображающей точки системы при попадании ее на эту прямую нуждается в доопределении. Естественно получить его следующим образом. В интервале  заменим характеристику
заменим характеристику  прямой, соединяющей точки
прямой, соединяющей точки  Тогда на фазовой плоскости в полосе
Тогда на фазовой плоскости в полосе  вместо
вместо
системы (2) будем иметь систему

где

На одной из прямых  зафиксируем какую-нибудь точку с ординатой
зафиксируем какую-нибудь точку с ординатой  Может оказаться, что полутраектория
Может оказаться, что полутраектория  системы (3), начинающаяся при
системы (3), начинающаяся при  в этой точке и проходящая внутри полосы, при всех достаточно малых
в этой точке и проходящая внутри полосы, при всех достаточно малых  вновь выходит из полосы при некотором
вновь выходит из полосы при некотором  в некоторой точке с координатами
в некоторой точке с координатами  В этом случае примем такое доопределение: изображающая точка системы (2), попав в точку
В этом случае примем такое доопределение: изображающая точка системы (2), попав в точку  находится на прямой
находится на прямой  в течение времени
в течение времени  равного пределу
равного пределу  при
при  после чего продолжает движение при
после чего продолжает движение при  (или
(или  в соответствии с системой (2) при начальных условиях
в соответствии с системой (2) при начальных условиях  при
при  Если же рассматриваемая полутраектория системы (3) при всех достаточно малых
Если же рассматриваемая полутраектория системы (3) при всех достаточно малых  целиком лежит в полосе, то примем такое доопределение: изображающая точка системы (2), попав в точку
целиком лежит в полосе, то примем такое доопределение: изображающая точка системы (2), попав в точку  остается на прямой неограниченно долго. Ситуации, которые представятся при вычислениях, исчерпываются двумя указанными.
остается на прямой неограниченно долго. Ситуации, которые представятся при вычислениях, исчерпываются двумя указанными.

Рис. 218
Уравнение движения изображающей точки по прямой  в обоих случаях получим предельным переходом в уравнениях рассматриваемой полутраектории системы (3):
в обоих случаях получим предельным переходом в уравнениях рассматриваемой полутраектории системы (3):  при
при 
Перейдем к вычислениям. Выделим на прямой  полупрямые (рис. 218)
полупрямые (рис. 218)

и на прямой  полупрямые
полупрямые

Траектории системы (3) осуществляют точечные преобразования полупрямой  в полупрямые
в полупрямые  Назовем их соответственно преобразованием
Назовем их соответственно преобразованием  и преобразованием
и преобразованием  Параметрические уравнения функции соответствия будут для преобразования
Параметрические уравнения функции соответствия будут для преобразования 

для преобразования 

Здесь  и
и  параметры (время перехода изображающей точки системы (3) с полупрямой
параметры (время перехода изображающей точки системы (3) с полупрямой  соответственно на полупрямую V или
соответственно на полупрямую V или 
Рассмотрим случаи.
I.  . Состояние равновесия (3) есть седло, расположенное внутри полосы —
. Состояние равновесия (3) есть седло, расположенное внутри полосы —  Соответствующая картина фазовых траекторий приведена на рис. 218, а.
Соответствующая картина фазовых траекторий приведена на рис. 218, а.
Пусть  отрезок, отсекаемый на полупрямой
отрезок, отсекаемый на полупрямой  сепаратрисой, имеющий отрицательный наклон. Величина и
сепаратрисой, имеющий отрицательный наклон. Величина и  при
при  Поэтому, какую бы точку и на интервале
Поэтому, какую бы точку и на интервале  ни фиксировать, при достаточно малых
ни фиксировать, при достаточно малых  она участвует в преобразовании
она участвует в преобразовании  При этом первое из равенств (4) неявно определяет функцию
При этом первое из равенств (4) неявно определяет функцию  время перехода из фиксированного и на полупрямую
время перехода из фиксированного и на полупрямую  Ее предельное значение при
Ее предельное значение при  (приложение I) есть
(приложение I) есть

Во втором из равенств (4) положим  и найдем
и найдем  при
при  Это предельное значение (приложение II) есть
Это предельное значение (приложение II) есть

Фиксируем теперь какую-нибудь точку на интервале  При малых
При малых  она участвует в преобразовании
она участвует в преобразовании  При этом
При этом
первое из равенств (5) неявно определяет функцию  время перехода из фиксированного и на полупрямую
время перехода из фиксированного и на полупрямую  Ее предельное значение при
Ее предельное значение при  (доказательство аналогично доказательству в приложении I) есть
(доказательство аналогично доказательству в приложении I) есть

Во втором из равенств (5) положим  и найдем
и найдем  при 0. Это предельное значение есть
при 0. Это предельное значение есть

Фиксируем теперь и  Рассмотрим изменение отрезка
Рассмотрим изменение отрезка  с уменьшением
с уменьшением  Для этого вычислим
Для этого вычислим

Если  то при малых
то при малых  величина
величина  убывает вместе с
убывает вместе с  и точка
и точка  участвует в преобразовании
участвует в преобразовании  Первое из равенств (5) определяет функцию
Первое из равенств (5) определяет функцию  время перехода из и
время перехода из и  на полупрямую
на полупрямую  Ее предельное значение при
Ее предельное значение при  есть
есть  (это следует из того, что
(это следует из того, что  в равенстве (8) можно сделать как угодно большим, если взять и достаточно близким к
в равенстве (8) можно сделать как угодно большим, если взять и достаточно близким к  и из того, что в
и из того, что в  производная
производная 
Случай  рассматривается аналогично. Величина
рассматривается аналогично. Величина  возрастает с уменьшением
возрастает с уменьшением  и точка
и точка  участвует в преобразовании
участвует в преобразовании  Предельное время есть
Предельное время есть 
При  имеем В этом случае точка
имеем В этом случае точка  при любом
при любом  лежит на сепаратрисе. Время доопределенного движения есть
лежит на сепаратрисе. Время доопределенного движения есть
Для  нужно еще получить уравнения движения изображающей точки по прямой
нужно еще получить уравнения движения изображающей точки по прямой  Для любого и это будет
Для любого и это будет

Полученная схема доопределяемых движений по верхней части прямой  приведена на рис. 219, а. Здесь для наглядности налегающие одна на другую траектории раздвинуты в горизонтальном направлении. Изображающая точка системы (2), попавшая в точку
приведена на рис. 219, а. Здесь для наглядности налегающие одна на другую траектории раздвинуты в горизонтальном направлении. Изображающая точка системы (2), попавшая в точку  совершает мгновенный скачок в соответствии с формулой (7) и продолжает движение при
совершает мгновенный скачок в соответствии с формулой (7) и продолжает движение при  в соответствии с системой (2).
в соответствии с системой (2).
Если  то изображающая точка перескакивает в точку
то изображающая точка перескакивает в точку  находится здесь в течение времени (6) и затем двигается при
находится здесь в течение времени (6) и затем двигается при  При
При  изображающая точка перескакивает в точку
изображающая точка перескакивает в точку  и остается там неограниченно долго. Это движение является вырождением при
и остается там неограниченно долго. Это движение является вырождением при  движения по сепаратрисе седла системы (3).
движения по сепаратрисе седла системы (3).
Если  то изображающая точка мгновенно перескакивает в точку
то изображающая точка мгновенно перескакивает в точку  и находится здесь в течение времени,
и находится здесь в течение времени,
определяемого формулой (8), после чего продолжает движение при 
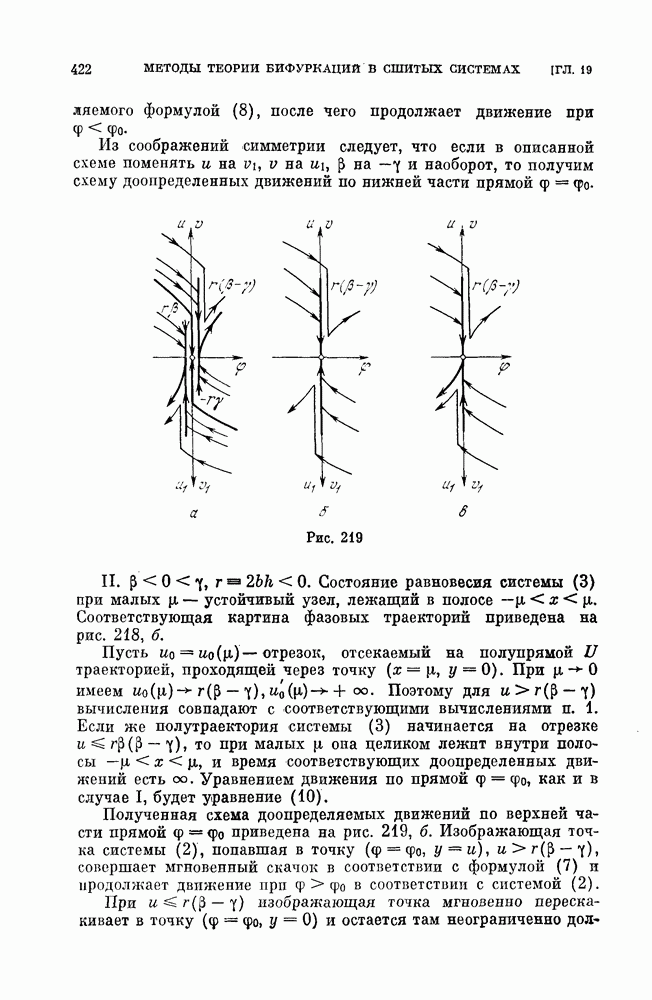
Из соображений симметрии следует, что если в описанной схеме поменять и на  на
на  на
на  и наоборот, то получим схему доопределенных движений по нижней части прямой
и наоборот, то получим схему доопределенных движений по нижней части прямой 

Рис. 219
II.  . Состояние равновесия системы (3) при малых
. Состояние равновесия системы (3) при малых  устойчивый узел, лежащий в полосе
устойчивый узел, лежащий в полосе  Соответствующая картина фазовых траекторий приведена на рис. 218, б.
Соответствующая картина фазовых траекторий приведена на рис. 218, б.
Пусть  отрезок, отсекаемый на полупрямой
отрезок, отсекаемый на полупрямой  траекторией, проходящей через точку
траекторией, проходящей через точку  При
При  имеем
имеем  Поэтому для
Поэтому для  вычисления совпадают с соответствующими вычислениями п. 1. Если же полутраектория системы (3) начинается на отрезке
вычисления совпадают с соответствующими вычислениями п. 1. Если же полутраектория системы (3) начинается на отрезке  то при малых
то при малых  она целиком лежит внутри полосы
она целиком лежит внутри полосы  и время соответствующих доопределенных движений есть
и время соответствующих доопределенных движений есть  Уравнением движения по прямой
Уравнением движения по прямой  как и в случае I, будет уравнение
как и в случае I, будет уравнение 
Полученная схема доопределяемых движений по верхней части прямой  приведена на рис. 219, б. Изображающая точка системы (2), попавшая в точку
приведена на рис. 219, б. Изображающая точка системы (2), попавшая в точку  совершает мгновенный скачок в соответствии с формулой (7) и продолжает движение при
совершает мгновенный скачок в соответствии с формулой (7) и продолжает движение при  в соответствии с системой (2).
в соответствии с системой (2).
При  изображающая точка мгновенно перескакивает в точку
изображающая точка мгновенно перескакивает в точку  и остается там неограниченно
и остается там неограниченно
долго. Будем говорить, что эти движения ведут в состояние равновесия  являющееся вырождением при
являющееся вырождением при  узла системы (3).
узла системы (3).
Из соображений симметрии следует, что если в описанной схеме поменять и на  на
на  то получим схему доопределенных движений по нижней части прямой
то получим схему доопределенных движений по нижней части прямой 
Состояние равновесия системы (3) есть седло, расположенное правее полосы — 
Не приводя вычислений, опишем получающуюся в этом случае схему доопределенных движений (рис. 219, в). Изображающая точка системы (2), попавшая в точку  , совершает мгновенный скачок в соответствии с формулой (7) и продолжает движение при
, совершает мгновенный скачок в соответствии с формулой (7) и продолжает движение при  в соответствии с системой (2).
в соответствии с системой (2).
Если — то изображающая точка мгновенно перескакивает в точку  и находится здесь в течение времени, определяемого формулой (8), после чего продолжает движение при
и находится здесь в течение времени, определяемого формулой (8), после чего продолжает движение при  Изображающая точка системы (2), попавшая в точку
Изображающая точка системы (2), попавшая в точку  совершает мгновенный скачок вверх в соответствии с равенством
совершает мгновенный скачок вверх в соответствии с равенством  продолжает движение при
продолжает движение при  в соответствии с системой (2). Если
в соответствии с системой (2). Если  то изображающая точка мгновенно перескакивает в точку
то изображающая точка мгновенно перескакивает в точку  и остается здесь в течение времени
и остается здесь в течение времени  после чего продолжает движение при
после чего продолжает движение при  за
за  Состояние равновесия системы (3) при малых
Состояние равновесия системы (3) при малых  устойчивый узел, лежащий левее полосы
устойчивый узел, лежащий левее полосы  Схема доопределенных движений та же, что и в
Схема доопределенных движений та же, что и в 
Случай  и случай VI:
и случай VI:  получаются соответственно из случаев IV и III заменами:
получаются соответственно из случаев IV и III заменами:  на
на  , и на
, и на  на
на  и наоборот.
и наоборот.
Из имеющихся шести случаев получим еще шесть, соответствующих изменению знака  заменами:
заменами:  на
на  на
на  и на
и на  на
на  и наоборот.
и наоборот.
Рассматривая точечные преобразования прямых  самих в себя, осуществляемые доопределенными движениями, совместно с точечными преобразованиями прямых
самих в себя, осуществляемые доопределенными движениями, совместно с точечными преобразованиями прямых  самих в себя и одной в другую, осуществляемыми траекториями системы (2), можно провести качественное исследование системы для конкретной характеристики
самих в себя и одной в другую, осуществляемыми траекториями системы (2), можно провести качественное исследование системы для конкретной характеристики  имеющей разрывы.
имеющей разрывы.
Пример 1. Пусть  -функция периода
-функция периода  такая, что
такая, что  при
при  и пусть
и пусть  Этот пример иллюстрирует первый случай доопределения.
Этот пример иллюстрирует первый случай доопределения.
В качестве фазового пространства будем рассматривать полосу, заключенную между прямыми  Точки этих прямых, имеющие одинаковые ординаты, отождествляем. Таким образом, точки разрыва характеристики находятся на линии склейки цилиндрического фазового пространства.
Точки этих прямых, имеющие одинаковые ординаты, отождествляем. Таким образом, точки разрыва характеристики находятся на линии склейки цилиндрического фазового пространства.
Рассмотрим точечное преобразование полупрямой  в полупрямую
в полупрямую  осуществляемое траекториями системы (2). Если обозначить
осуществляемое траекториями системы (2). Если обозначить

то при  параметрические уравнения функции соответствия этого преобразования запишутся в виде
параметрические уравнения функции соответствия этого преобразования запишутся в виде

Ее производные —

Асимптота —

Введем параметр  Для
Для  кривая
кривая  изображена на рис. 220 вместе с ломаной
изображена на рис. 220 вместе с ломаной

являющейся графиком функции соответствия преобразования полупрямой  в себя, осуществляемого доопределенными движениями, и построенной по формуле (7). На рис. 220 изображен случай, когда кривая и ломаная имеют общую точку на горизонтальном участке ломаной. Это означает, что на фазовом цилиндре имеется предельный цикл, при движении по которому изображающая точка имеет остановку в точке
в себя, осуществляемого доопределенными движениями, и построенной по формуле (7). На рис. 220 изображен случай, когда кривая и ломаная имеют общую точку на горизонтальном участке ломаной. Это означает, что на фазовом цилиндре имеется предельный цикл, при движении по которому изображающая точка имеет остановку в точке  на время, определяемое первой строкой формулы (6). Легко видеть, что цикл устойчив и что более одного цикла быть не может. При увеличении
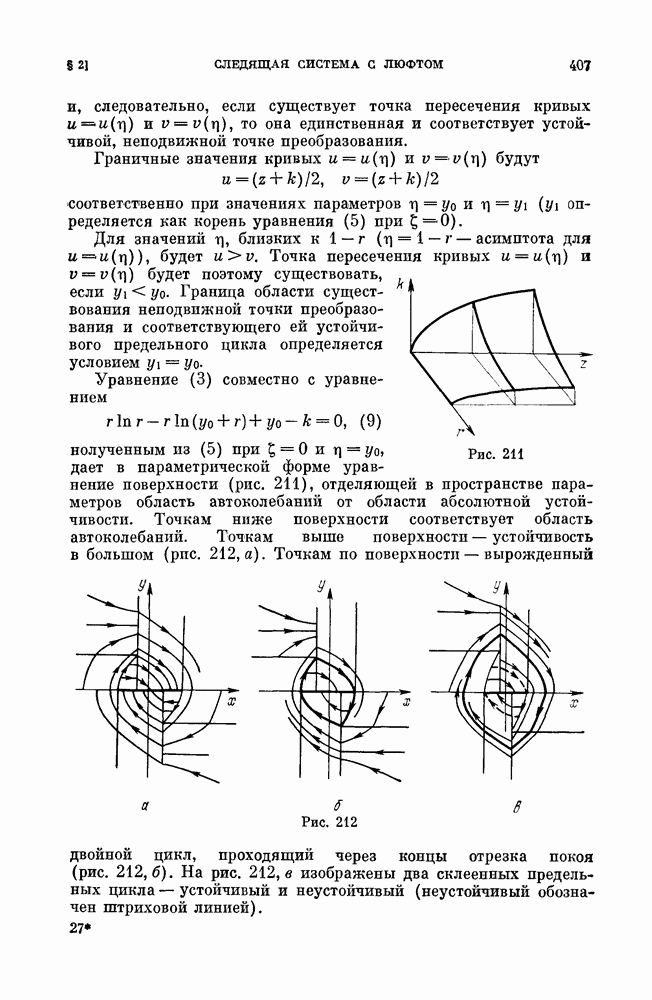
на время, определяемое первой строкой формулы (6). Легко видеть, что цикл устойчив и что более одного цикла быть не может. При увеличении  точка пересечения кривой и ломаной попадает в начальную точку ломаной, что соответствует влипанию цикла в сепаратрису, образующую петлю (сепаратрису, идущую из состояния равновесия
точка пересечения кривой и ломаной попадает в начальную точку ломаной, что соответствует влипанию цикла в сепаратрису, образующую петлю (сепаратрису, идущую из состояния равновесия  в то же самое состояние равновесия). Соответствующая бифуркационная поверхность в пространстве параметров
в то же самое состояние равновесия). Соответствующая бифуркационная поверхность в пространстве параметров  а имеет уравнения
а имеет уравнения  ,
,
 Исключив
Исключив  получим
получим

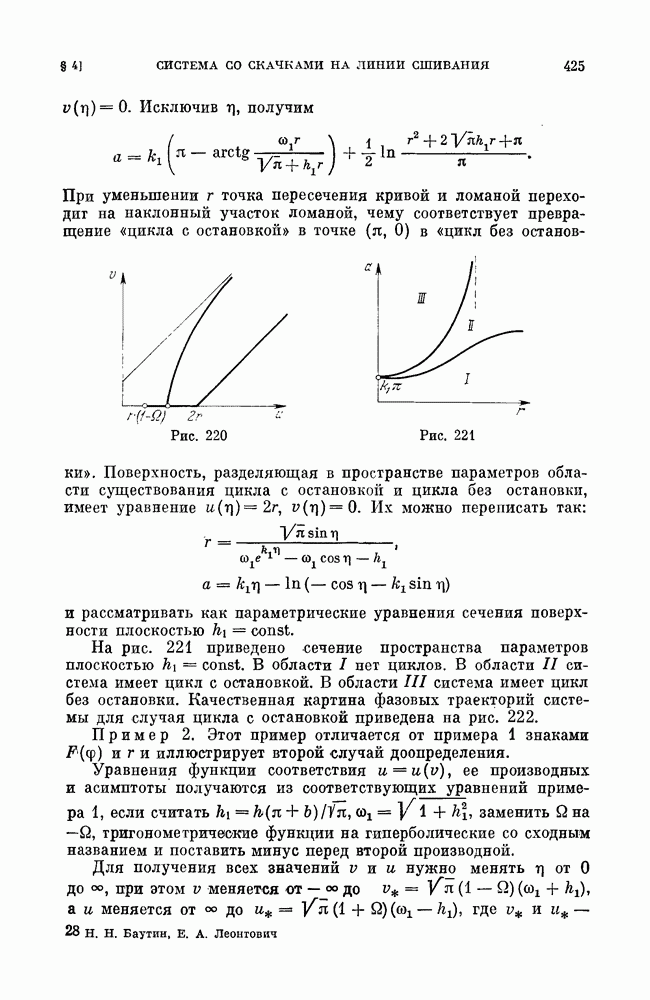
При уменьшении  точка пересечения кривой и ломаной переходит на наклонный участок ломаной, чему соответствует превращение «цикла с остановкой» в точке
точка пересечения кривой и ломаной переходит на наклонный участок ломаной, чему соответствует превращение «цикла с остановкой» в точке  в «цикл без остановки».
в «цикл без остановки».

Рис. 220

Рис. 221
Поверхность, разделяющая в пространстве параметров области существования цикла с остановкой и цикла без остановки, имеет уравнение  Их можно переписать так:
Их можно переписать так:

и рассматривать как параметрические уравнения сечения поверхности плоскостью 
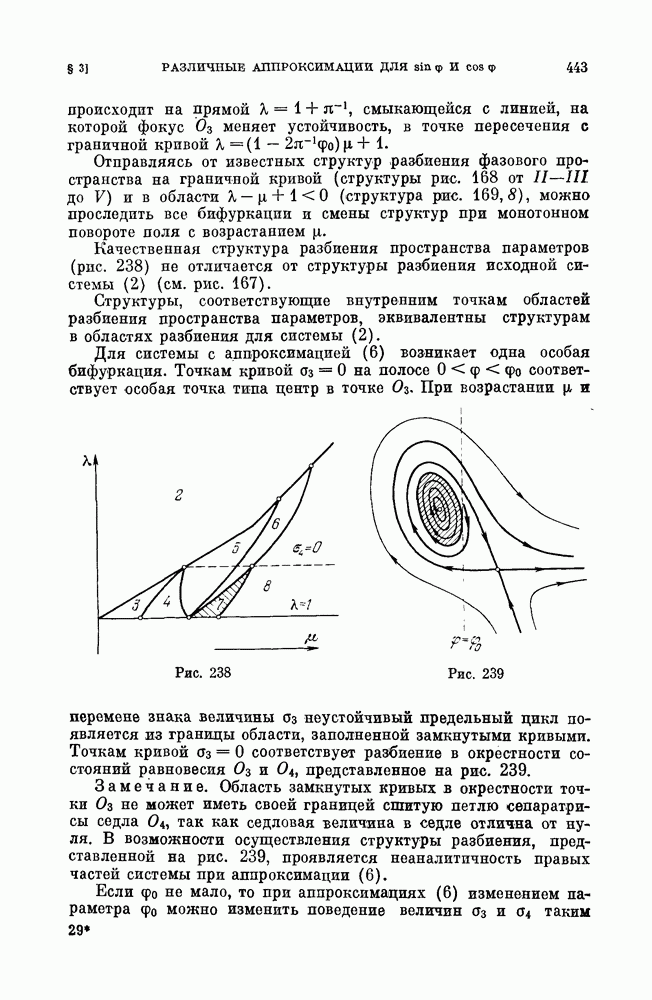
На рис. 221 приведено сечение пространства параметров плоскостью  . В области I нет циклов. В области II система имеет цикл с остановкой. В области III система имеет цикл без остановки. Качественная картина фазовых траекторий системы для случая цикла с остановкой приведена на рис. 222.
. В области I нет циклов. В области II система имеет цикл с остановкой. В области III система имеет цикл без остановки. Качественная картина фазовых траекторий системы для случая цикла с остановкой приведена на рис. 222.
Пример 2. Этот пример отличается от примера 1 знаками  и иллюстрирует второй случай доопределения.
и иллюстрирует второй случай доопределения.
Уравнения функции соответствия  ее производных и асимптоты получаются из соответствующих уравнений примера 1, если считать
ее производных и асимптоты получаются из соответствующих уравнений примера 1, если считать  заменить
заменить  на
на  тригонометрические функции на гиперболические со сходным названием и поставить минус перед второй производной.
тригонометрические функции на гиперболические со сходным названием и поставить минус перед второй производной.
Для получения всех значений  и нужно менять
и нужно менять  от
от  до то, при этом
до то, при этом  меняется от
меняется от  а и меняется от
а и меняется от  до
до  где
где  и
и
отрезки, отсекаемые сепаратрисами седла  соответственно от полупрямых
соответственно от полупрямых  Кривая
Кривая  изображена на рис. 223 вместе с прямой
изображена на рис. 223 вместе с прямой  являющейся графиком функции соответствия при преобразовании полупрямой
являющейся графиком функции соответствия при преобразовании полупрямой  в себя, осуществляемом доопределенными движениями.
в себя, осуществляемом доопределенными движениями.
На рис. 223 изображен случай, когда кривая и прямая имеют точку пересечения. Это означает, что на фазовом цилиндре имеется предельный цикл. Легко видеть, что он устойчив и что более одного цикла быть не может. При уменьшении  прямая передвигается слева направо, и при некотором
прямая передвигается слева направо, и при некотором  точка пересечения попадает в точку
точка пересечения попадает в точку  При этом предельный цикл влипает в сепаратрису седла
При этом предельный цикл влипает в сепаратрису седла  образующую петлю.
образующую петлю.

Рис. 222

Рис. 223

Рис. 224
Соответствующая бифуркационная поверхность в пространстве параметров  имеет уравнение
имеет уравнение

Качественная картина фазовых траекторий системы для случая, когда имеется предельный цикл, приведена на рис. 224.
Приложение I. Пусть  Функцию
Функцию  определяемую первым из равенств (4), не существующую при
определяемую первым из равенств (4), не существующую при  доопределим ее пределом при
доопределим ее пределом при  Получившаяся при этом функция
Получившаяся при этом функция

удовлетворяет следующим условиям: 1) непрерывна, 2) если  ], то
], то  производная
производная 
Следовательно, при зафиксированном на рассмотренном интервале и равенство  определяет в некоторой окрестности точки
определяет в некоторой окрестности точки  однозначную непрерывную функцию
однозначную непрерывную функцию  такую, что
такую, что  . А так как
. А так как  при
при  то
то  при
при 
Пусть теперь — 4). Так как  то функция
то функция  соответствующая фиксированному на рассматриваемом интервале и,
соответствующая фиксированному на рассматриваемом интервале и,
ограничена сверху функцией  соответствующей любому и, фиксированному на интервале
соответствующей любому и, фиксированному на интервале  а предел этой ограничивающей функции при
а предел этой ограничивающей функции при  может быть сделан как угодно близким к нулю, если взять и достаточно близким к
может быть сделан как угодно близким к нулю, если взять и достаточно близким к 
Приложение II. При  Это предельное значение находится непосредственной подстановкой предельного значения
Это предельное значение находится непосредственной подстановкой предельного значения  Если
Если  то положим в равенствах
то положим в равенствах  Первое из них при фиксированном
Первое из них при фиксированном  малых
малых  определяет функцию
определяет функцию  такую, что
такую, что

(Доказательство аналогично доказательству в приложении  Положим теперь во втором из равенств
Положим теперь во втором из равенств  и найдем, что при
и найдем, что при  будет
будет  .
.
Пример 3. Пусть  функция периода
функция периода  такая, что
такая, что


Рис. 225
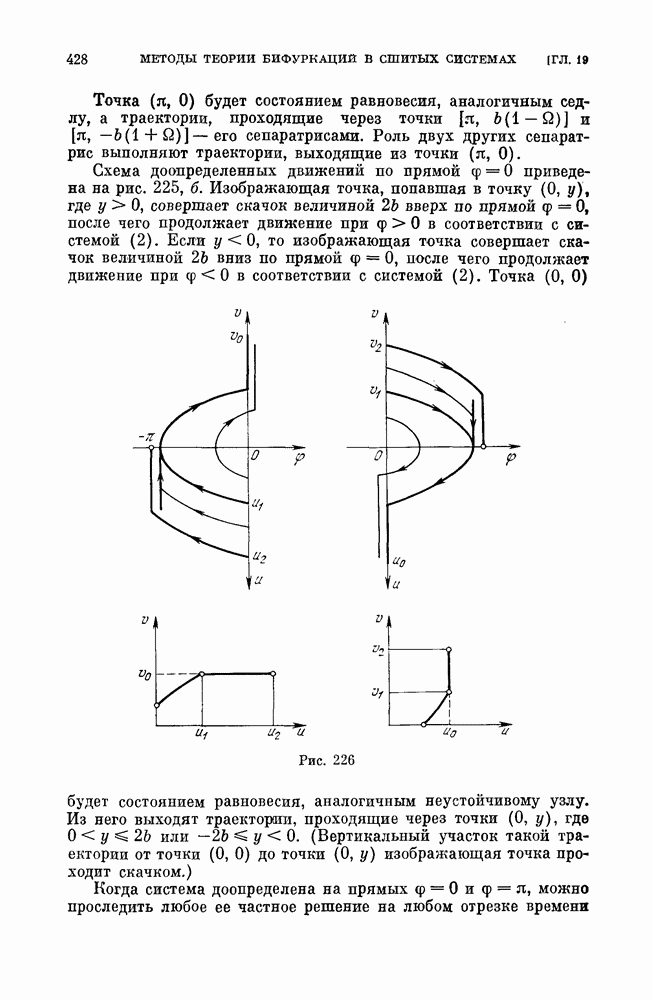
Схема доопределенных движений по прямой  приведена на рис. 225, а (здесь масштаб по оси у уменьшен в
приведена на рис. 225, а (здесь масштаб по оси у уменьшен в  раз). Изображающая точка, попавшая в точку
раз). Изображающая точка, попавшая в точку  где
где  совершает скачок величиной 26 вниз
совершает скачок величиной 26 вниз  прямой
прямой  после чего продолжает движение при
после чего продолжает движение при  в соответствии с системой (2). Если
в соответствии с системой (2). Если  то изображающая точка перескакивает в точку
то изображающая точка перескакивает в точку  и находится в ней в течение времени
и находится в ней в течение времени

после чего продолжает движение при  в соответствии с системой (2). Если
в соответствии с системой (2). Если  то изображающая точка перескакивает и точку
то изображающая точка перескакивает и точку  и остается там неограниченно долго. Если
и остается там неограниченно долго. Если  то изображающая точка перескакивает в точку
то изображающая точка перескакивает в точку  и находится в ней в течение времени
и находится в ней в течение времени

после чего продолжает движение при  Поведение изображающей точки, попавшей на прямую
Поведение изображающей точки, попавшей на прямую  в нижнем полуцилиндре, аналогично (нужно поменять у на
в нижнем полуцилиндре, аналогично (нужно поменять у на  на
на 
Точка  будет состоянием равновесия, аналогичным седлу, а траектории, проходящие через точки
будет состоянием равновесия, аналогичным седлу, а траектории, проходящие через точки  сепаратрисами. Роль двух других сепаратрис выполняют траектории, выходящие из точки
сепаратрисами. Роль двух других сепаратрис выполняют траектории, выходящие из точки 
Схема доопределенных движений по прямой  приведена на рис. 225, б. Изображающая точка, попавшая в точку
приведена на рис. 225, б. Изображающая точка, попавшая в точку  где
где  совершает скачок величиной
совершает скачок величиной  вверх по прямой
вверх по прямой  после чего продолжает движение при
после чего продолжает движение при  в соответствии с системой (2). Если
в соответствии с системой (2). Если  то изображающая точка совершает скачок величиной
то изображающая точка совершает скачок величиной  вниз по прямой
вниз по прямой  после чего продолжает движение при
после чего продолжает движение при  в соответствии с системой (2).
в соответствии с системой (2).

Рис. 226
Точка  будет состоянием равновесия, аналогичным неустойчивому узлу. Из него выходят траектории, проходящие через точки
будет состоянием равновесия, аналогичным неустойчивому узлу. Из него выходят траектории, проходящие через точки  где
где  или
или  (Вертикальный участок такой траектории от точки
(Вертикальный участок такой траектории от точки  до точки
до точки  изображающая точка проходит скачком.)
изображающая точка проходит скачком.)
Когда система доопределена на прямых  можно проследить любое ее частное решение на любом отрезке времени
можно проследить любое ее частное решение на любом отрезке времени
и провести ее качественное псследованпе. Исследование сходно с исследованием в примере 1, поэтому ограничимся лишь изложением результатов, относящихся к предельным циклам, охватывающим состояние равновесия.
Возьмем на прямой  две полуоси: полуось и — вниз от начала координат и полуось
две полуоси: полуось и — вниз от начала координат и полуось  вверх от начала координат. На рис. 226 сверху изображены траектории, осуществляющие отображение
вверх от начала координат. На рис. 226 сверху изображены траектории, осуществляющие отображение  части полуоси и в полуось
части полуоси и в полуось  (слева), и траектории, осуществляющие отображение
(слева), и траектории, осуществляющие отображение  части полуоси
части полуоси  в полуось и (справа). Графики функций
в полуось и (справа). Графики функций  приведены на том же рис. 226 внизу. Для
приведены на том же рис. 226 внизу. Для  функция
функция  находится обычным способом, только с учетом того, что все
находится обычным способом, только с учетом того, что все  нужно сделать больше на величину скачка. Участок
нужно сделать больше на величину скачка. Участок  весь переходит в одну точку
весь переходит в одну точку  Для этих и имеем
Для этих и имеем  Аналогичные соображения можно высказать о функции
Аналогичные соображения можно высказать о функции 
Цикл соответствует точке пересечения линий  На рис. 227 показано изменение взаимного положения линий при изменении параметров. На рис. 228 — соответствующие превращения предельного цикла (соответствующие одна другой картинки на рис. 227 и 228 обозначены одинаковыми буквами). Очевидно, так же, как и в примере 1, расположение траекторий рис. 228 может быть изображено на цилиндре.
На рис. 227 показано изменение взаимного положения линий при изменении параметров. На рис. 228 — соответствующие превращения предельного цикла (соответствующие одна другой картинки на рис. 227 и 228 обозначены одинаковыми буквами). Очевидно, так же, как и в примере 1, расположение траекторий рис. 228 может быть изображено на цилиндре.
Для некоторой области в пространстве параметров линии имеют точку пересечения на кривых участках (рис. 228, а). Цикл не имеет кусков на прямых  При соответствующем изменении параметров точка пересечения передвинется в точку излома линии
При соответствующем изменении параметров точка пересечения передвинется в точку излома линии 

Рис. 227
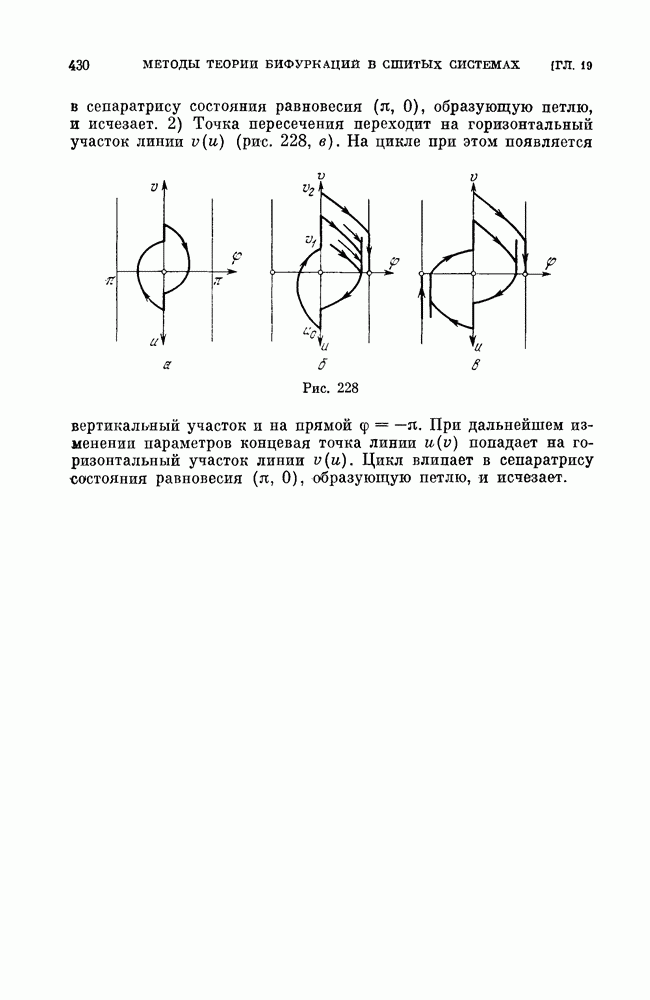
При этом цикл коснется прямой  При дальнейшем изменении параметров точка пересечения переходит на вертикальный участок линии (рис. 228, б). При этом на цикле появляется вертикальный участок на прямой
При дальнейшем изменении параметров точка пересечения переходит на вертикальный участок линии (рис. 228, б). При этом на цикле появляется вертикальный участок на прямой  который изображающая точка проходит скачком, после чего некоторое время стоит в точке
который изображающая точка проходит скачком, после чего некоторое время стоит в точке  прежде чем продолжит движение по циклу. В зависимости от дальнейшего изменения параметров возможны превращения двух типов: 1) концевая точка линии
прежде чем продолжит движение по циклу. В зависимости от дальнейшего изменения параметров возможны превращения двух типов: 1) концевая точка линии  попадает на кривой участок линии
попадает на кривой участок линии  При этом цикл влипает
При этом цикл влипает
в сепаратрису состояния равновесия  образующую петлю, и исчезает. 2) Точка пересечения переходит на горизонтальный участок линии
образующую петлю, и исчезает. 2) Точка пересечения переходит на горизонтальный участок линии  На цикле при этом появляется вертикальный участок и на прямой
На цикле при этом появляется вертикальный участок и на прямой 

Рис. 228
При дальнейшем изменении параметров концевая точка линии  попадает на горизонтальный участок линии и
попадает на горизонтальный участок линии и  Цикл влипает в сепаратрису состояния равновесия
Цикл влипает в сепаратрису состояния равновесия  образующую петлю, и исчезает.
образующую петлю, и исчезает.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. АВТОНОМНЫЕ СИСТЕМЫ ВТОРОГО ПОРЯДКА С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- § 1. Автономная динамическая система на плоскости.
- § 2. Теорема существования и единственности решения.
- § 3. Простейшие свойства решений системы (А).
- § 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
- § 5. Сопоставление геометрической интерпретации системы (А) в пространстве (x, y, t) с интерпретацией на фазовой плоскости.
- § 6. Некоторые термины.
- § 7. Теорема о непрерывной зависимости решения от начальных условий.
- § 8. Направление на траекториях. Изменение параметризации.
- § 9. Дифференциальное уравнение, соответствующее динамической системе.
- § 10. Понятие интегральной кривой и интеграла в случае аналитических правых частей Р(х,у) и Q(x,y) системы (А).
- § 11. Что значит «найти решение динамической системы»?
- § 12. Примеры.
- § 13. Замечания по поводу примеров § 12.
- § 14. Математическое определение качественной (топологической) структуры разбиения на траектории и качественного исследования динамической системы.
- ГЛАВА 2. ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ — БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ
- § 2. Цикл без контакта.
- § 3. Предельная точка полутраектории и траектории. Предельная траектория.
- § 4. Основная теорема.
- § 5. Возможные типы полутраекторий и их предельных множеств.
- § 6. Особые и неособые полутраектории и траектории.
- § 7. Возможные типы особых и неособых траекторий.
- § 8. Случай конечного числа особых траекторий. Элементарные ячейки.
- § 9. Возможные типы ячеек. Односвязные и двусвязные ячейки.
- § 10. Два подхода к описанию качественной структуры.
- § 11. Качественная (топологическая) структура состояния равновесия в случае конечного числа особых траекторий. Схема динамической системы.
- § 12. Устойчивость по Ляпунову.
- ГЛАВА 3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННОЙ СТРУКТУРЫ ОКРЕСТНОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (ОСОБОЙ ТОЧКИ)
- § 2. Приведение динамической системы к каноническому виду.
- § 3. Возможный характер простых состояний равновесия.
- § 4. Замечания о методах установления характера грубых состояний равновесия.
- § 5. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 6. Направления, в которых траектории стремятся к простым состояниям равновесия.
- § 7. Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия.
- § 8. Сводка сведений о грубых состояниях равновесия.
- ГЛАВА 4. КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ
- § 1. Направления, в которых траектории стремятся к сложному состоянию равновесия.
- § 2. Сложное состояние равновесия (особая точка) с нулевыми характеристическими корнями.
- § 3. Примеры.
- § 4. Нормальные формы.
- ГЛАВА 5. ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ
- § 2. Условия устойчивости и неустойчивости неподвижной точки точечного отображения.
- § 3. Функция соответствия.
- § 4. Изучение окрестности замкнутой траектории. Простые и сложные предельные циклы.
- § 5. Аналитические выражения для коэффициентов функции последования. Характеристический показатель замкнутой траектории.
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЕМЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 2. Изучение поведения интегральных кривых в бесконечности. Сфера Пуанкаре.
- § 3. Примеры исследования в бесконечности [93].
- § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов.
- 1. Некоторые видоизменения критериев Бендиксона и Дюлака.
- 2. Индексы Пуанкаре. Распределение особых точек [77, 117].
- 3. Условия сосуществования замкнутых траекторий и особых точек.
- 4. Две общие теоремы Пуанкаре.
- § 5. Топографическая система Пуанкаре. Функция Ляпунова. Кривые контактов.
- ЧАСТЬ II. ТЕОРИЯ БИФУРКАЦИЙ
- § 1. Свойства консервативных систем на плоскости [2, 3].
- § 2. Динамические системы, характерные для теории колебаний.
- § 3. Измененные системы. Системы, правые части которых зависят от параметра.
- § 4. Основные теоремы о зависимости решения от изменения правых частей динамической системы.
- § 5. Грубость динамической системы и теоремы о непрерывной зависимости решения от изменения правых частей.
- ГЛАВА 8. ГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
- § 2. Состояния равновесия, возможные в грубой динамической системе.
- § 3. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 4. Замкнутые траектории, возможные в грубой системе.
- § 5. Поведение сепаратрис седел в грубых системах.
- § 6. Необходимые условия грубости. Достаточность этих условий для грубости системы.
- § 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем.
- § 8. Понятие грубости при более общих предположениях относительно правых частей динамической системы.
- § 9. Типы особых траекторий и ячеек в грубых системах.
- § 10. Замечания по поводу определения грубой системы.
- ГЛАВА 9. ПРОСТЕЙШИЕ НЕГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ — СИСТЕМЫ ПЕРВОЙ СТЕПЕНИ НЕГРУБОСТИ
- § 2. Системы первой степени негрубости.
- § 3. Состояния равновесия, возможные в системе первой степени негрубости.
- § 4. Замкнутые траектории, возможные в системе первой степени негрубости.
- § 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости.
- § 6. Необходимые и достаточные условия первой степени негрубости.
- § 7. Динамические системы более высокой степени негрубости.
- ГЛАВА 10. БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- § 1. Определение бифуркации.
- § 2. Бифуркации систем первой степени негрубости.
- § 3. Бифуркации некоторых типов сложных особых точек.
- § 4. Бифуркации двукратной точки, для которой …
- § 5. Рождение предельных циклов из особых траекторий степени негрубости выше первой.
- ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
- § 1. Возможный характер зависимости правых частей динамической системы от параметров.
- § 2. Смена качественных структур при изменении параметров.
- § 3. Случай, когда правые части зависят более чем от одного параметра.
- § 4. Бифуркации «от бесконечности».
- § 5. Условия существования седло-узла и сложного фокуса первого порядка.
- § 6. Поворот векторного поля.
- § 7. Метод малого параметра. Метод Понтрягина.
- ГЛАВА 12. ДИНАМИЧЕСКИЕ СИСТЕМЫ С ЦИЛИНДРИЧЕСКОЙ ФАЗОВОЙ ПОВЕРХНОСТЬЮ
- § 1. Цилиндрическая фазовая поверхность и характер траекторий, возможных на цилиндрической фазовой поверхности.
- § 2. Замкнутые траектории, охватывающие цилиндр.
- § 3. Приемы исследования качественной структуры динамической системы на цилиндре.
- § 4. Понятие грубости и степени негрубости для динамических систем на цилиндре. Бифуркации на цилиндре. Поворот поля.
- § 5. Динамические системы на цилиндре, близкие к гамильтоновым (метод Понтрягина).
- ГЛАВА 13. АДЕКВАТНОЕ ИСТОЛКОВАНИЕ НЕЛИНЕЙНЫХ ФИЗИЧЕСКИХ ЯВЛЕНИЙ ФАКТАМИ КАЧЕСТВЕННОЙ ТЕОРИИ И ТЕОРИИ БИФУРКАЦИЙ ДИНАМИЧЕСКИХ СИСТЕМ
- § 1. Мягкий и жесткий режимы.
- § 2. Замечания о границах области устойчивости различных стационарных режимов.
- § 3. Мягкое и жесткое возникновение колебаний.
- § 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
- § 5. Замечания по поводу других границ области устойчивости.
- ЧАСТЬ III. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- ГЛАВА 14. ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 1. Некоторые рецептурные указания.
- § 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
- § 3. Некоторые простые примеры динамических систем на цилиндре.
- ГЛАВА 15. ИССЛЕДОВАНИЕ МЕТОДОМ МАЛОГО ПАРАМЕТРА (МЕТОДОМ ПОНТРЯГИНА)
- § 2. Примеры рассмотрения методом Понтрягина (полное исследование).
- § 3. Исследование методом Понтрягина с привлечением вычислительных методов.
- ГЛАВА 16. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ
- § 2. Электрическая цепь с туннельным диодом.
- § 3. Двумерная модель динамики твердотельного лазера [119].
- § 4. Симметричный полет самолета в вертикальной плоскости (задача Н. Е. Жуковского).
- § 5. Система, описывающая динамику проточного химического реактора.
- § 6. Фазовая автоподстройка частоты.
- § 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов).
- § 8. Синхронный генератор с асинхронной характеристикой.
- ЧАСТЬ IV. КУСОЧНО-СШИТЫЕ СИСТЕМЫ
- ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ
- § 1. Сшитые системы. Доопределение на линиях сшивания.
- § 2. Возможные типы полутраекторий сшитых систем.
- § 3. Особые траектории сшитых систем.
- § 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
- ГЛАВА 18. ИССЛЕДОВАНИЕ КУСОЧНО-СШИТЫХ СИСТЕМ МЕТОДОМ ПОНТРЯГИНА
- § 2. Автоподстройка при кусочно-постоянной аппроксимации характеристики.
- § 3. Автоколебания синхронного мотора.
- ГЛАВА 19. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ
- § 2. Следящая система с люфтом.
- § 3. Электрическая цепь с туннельным диодом.
- § 4. Система со скачками на линии сшивания.
- ГЛАВА 20. ОБ АППРОКСИМАЦИЯХ И ГРУБОСТИ ПРОСТРАНСТВА ПАРАМЕТРОВ [39, 41, 42]
- § 1. Рассмотрение системы (2) при аппроксимациях пилообразными функциями.
- § 2. Рассмотрение системы (2) при аппроксимации, включающей отрезок параболы.
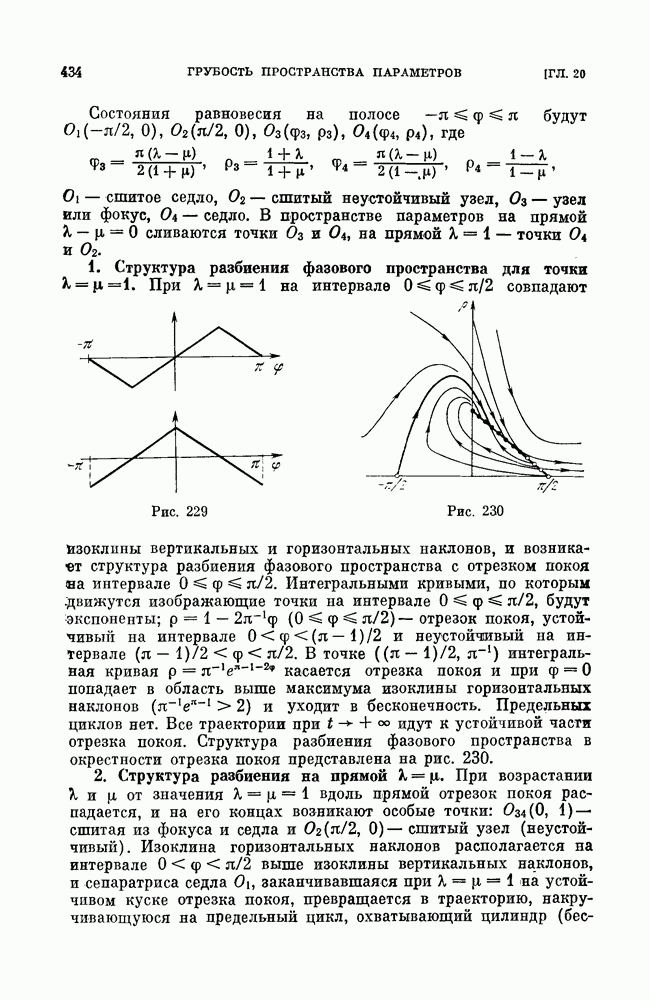
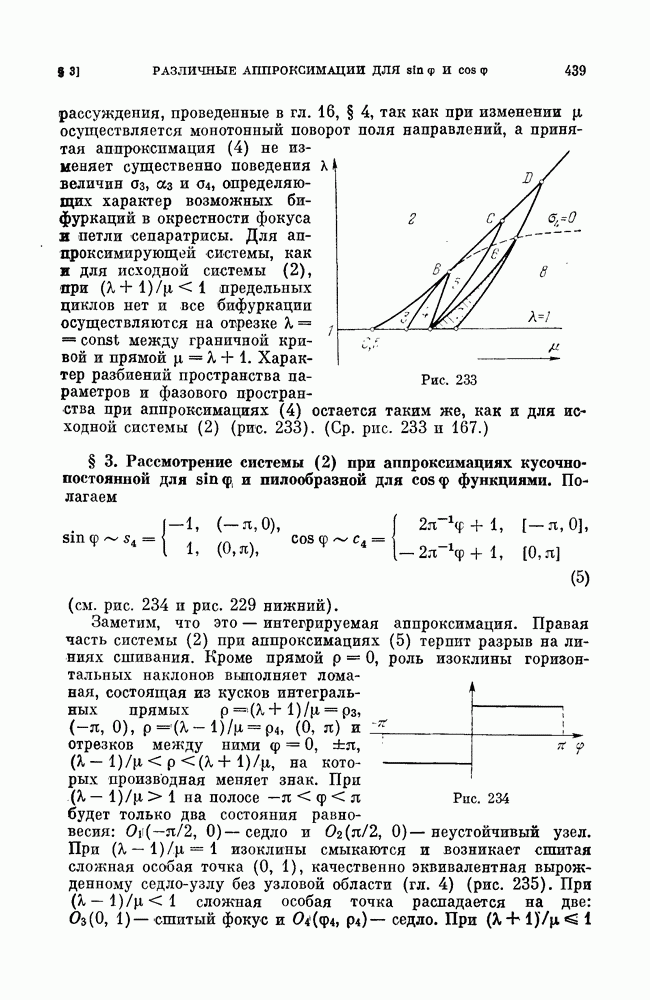
- § 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin f, и пилообразной для cos f функциями.
- § 4. Исследование роли аппроксимаций для уравнения маятникового типа.
- § 5. Динамическая система, описывающая автоколебания синхронного мотора.
- § 6. Динамическая система, описывающая симметричный полет самолета.
- ДОПОЛНЕНИЕ
- § 1. Динамическое системы на двумерных поверхностях.
- § 2. Динамические системы в n-мерном евклидовом пространстве.
- СПИСОК ЛИТЕРАТУРЫ