| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
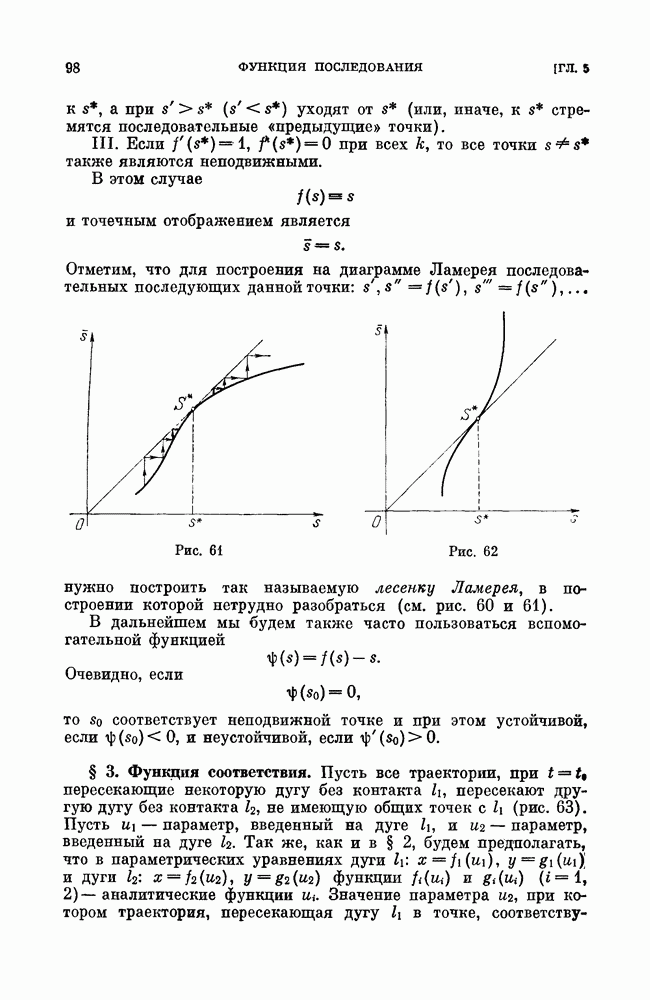
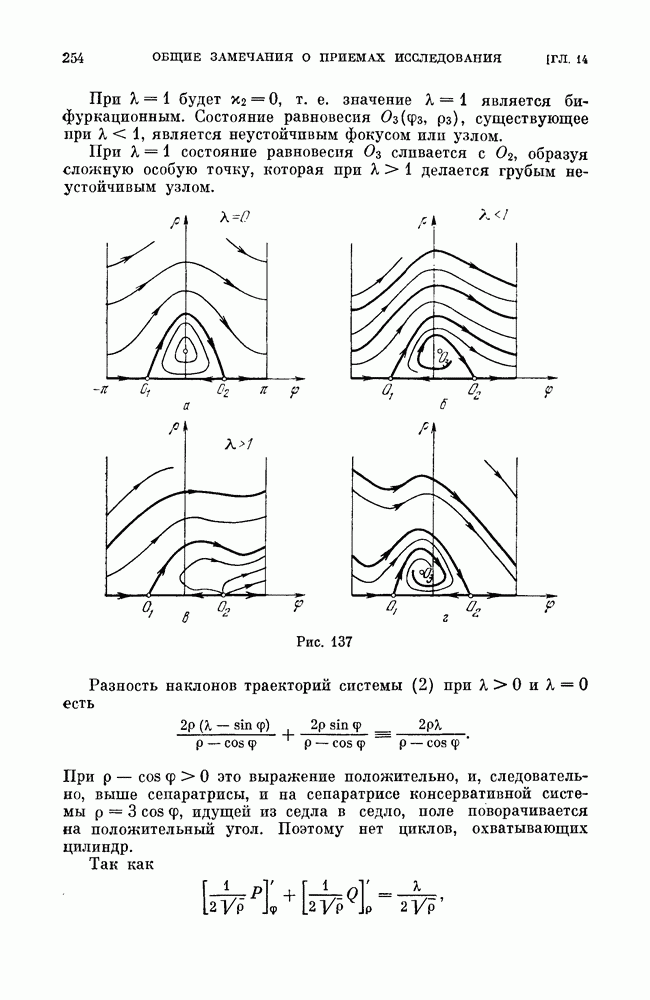
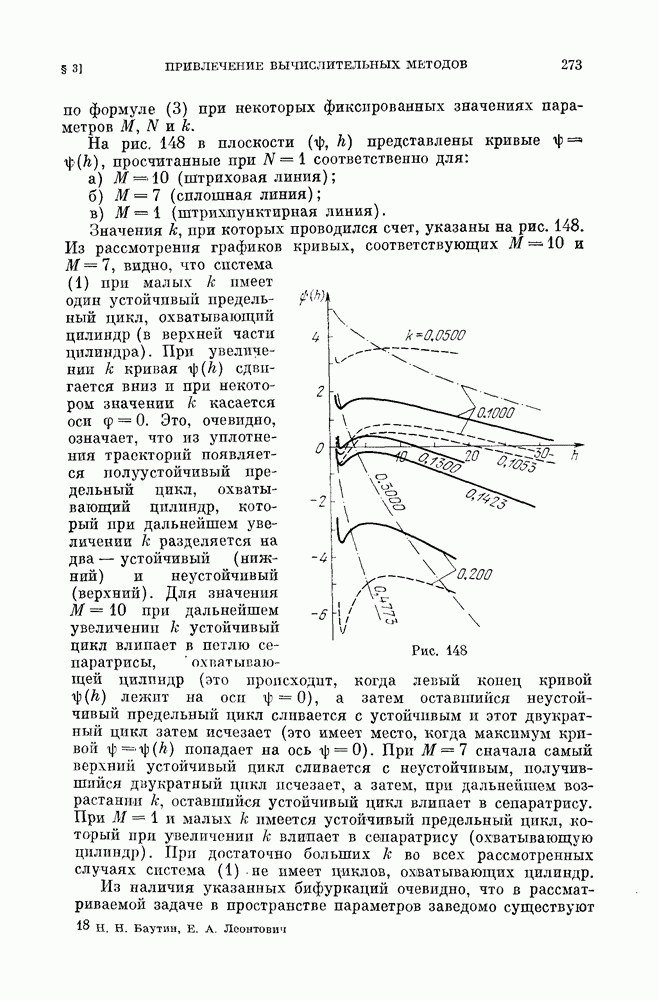
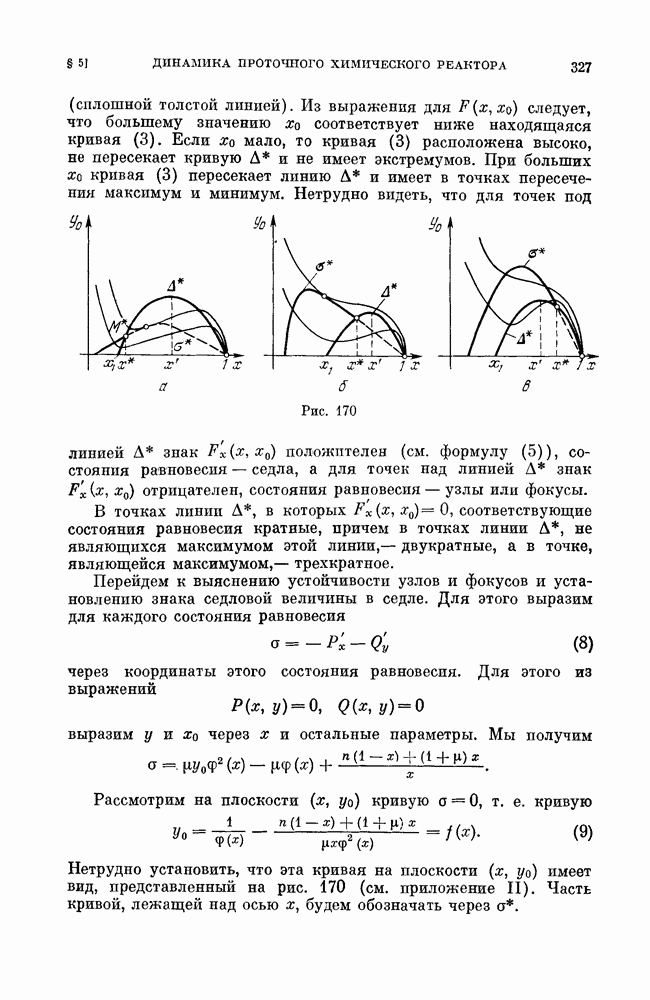
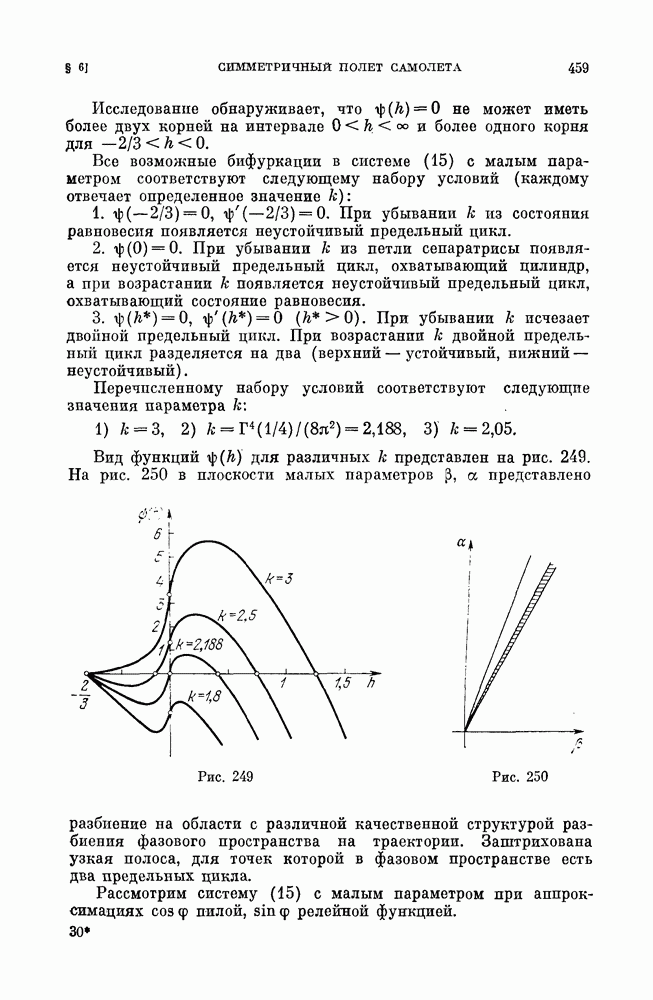
§ 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
Вопрос об устойчивости состояний равновесия (равновесных режимов) возникает при решении многих прикладных задач (из области автоматического регулирования, гироскопической стабилизации, радиотехники, электротехники и т. д.).
Естественно предполагать (см. гл. 8, § 1), что в прикладных задачах соответствующая система дифференциальных уравнений (в частности ее состояния равновесия) грубая и что, следовательно, при анализе устойчивости можно ограничиться тем случаем, когда этот вопрос может быть решен путем отбрасывания всех нелинейных членов и исследования характеристического уравнения (состояние равновесия устойчиво, если действительные части характеристических корней отрицательны).
Исследование вопроса о том, при каких значениях параметров, входящих в правые части динамических систем, рассматриваемое состояние равновесия устойчиво, позволяет выделить область устойчивости этого состояния равновесия в пространстве параметров. Мы будем дальше называть эту область областью Рауса — Гурвица.
Хотя основной интерес для прикладных вопросов (в которых играет роль устойчивость равновесных режимов) имеют такие системы, действительные части корней характеристических уравнений которых отрицательны, т. е. системы со значениями параметров внутри области Рауса — Гурвица, тем не менее для ряда прикладных вопросов представляет интерес выяснение поведения системы в случае, когда изображающая ее в пространстве параметров точка лежит на границе области Рауса — Гурвица или (что физически эквивалентно) достаточно близко к этой границе. Дело в том, что в прикладных вопросах приходится считаться не только с требованиями устойчивости, но и с другими требованиями, относящимися к работе устройства, и может оказаться, что одновременное удовлетворение этих условий наилучшим образом достигается выбором параметров, соответствующих точкам, лежащим в сравнительной близости к границам области Рауса — Гурвица. Таким образом, возникает вопрос о поведении динамической системы вблизи границы области Рауса — Гурвица. Действительно, выбирая значения параметров, близкие к границе этой области, мы никогда не можем быть уверены, что случайные отклонения этих параметров в реальной системе не выведут точку, представляющую систему в пространстве параметров, за границу области Рауса — Гурвица.
Поведение динамической системы при малых отклонениях от границы области Рауса — Гурвица определяет и особенности поведения систем, для которых представляющая их точка в пространстве параметров лежит в области Рауса — Гурвица, но в достаточной близости к границам этой области.
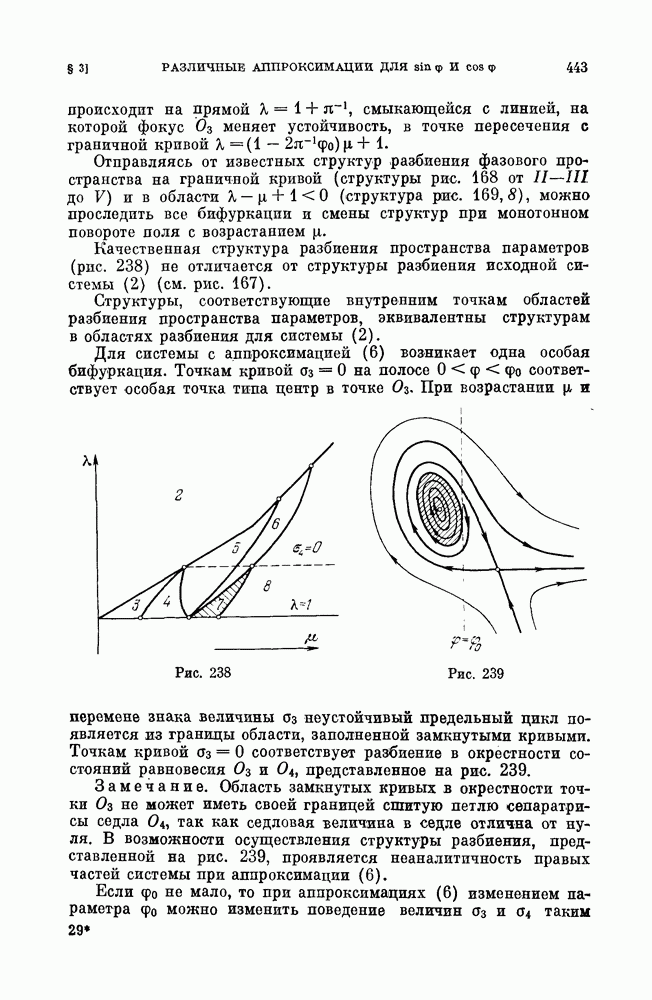
Как мы видели в предыдущем параграфе, вопрос о поведении системы в случае, когда изображающая ее точка в пространстве параметров переходит через границу области Рауса — Гурвица (именно, через границу, соответствующую системе со сложным фокусом), связан с вопросом возбуждения колебаний (мягкого и жесткого самовозбуждений, см. § 3).
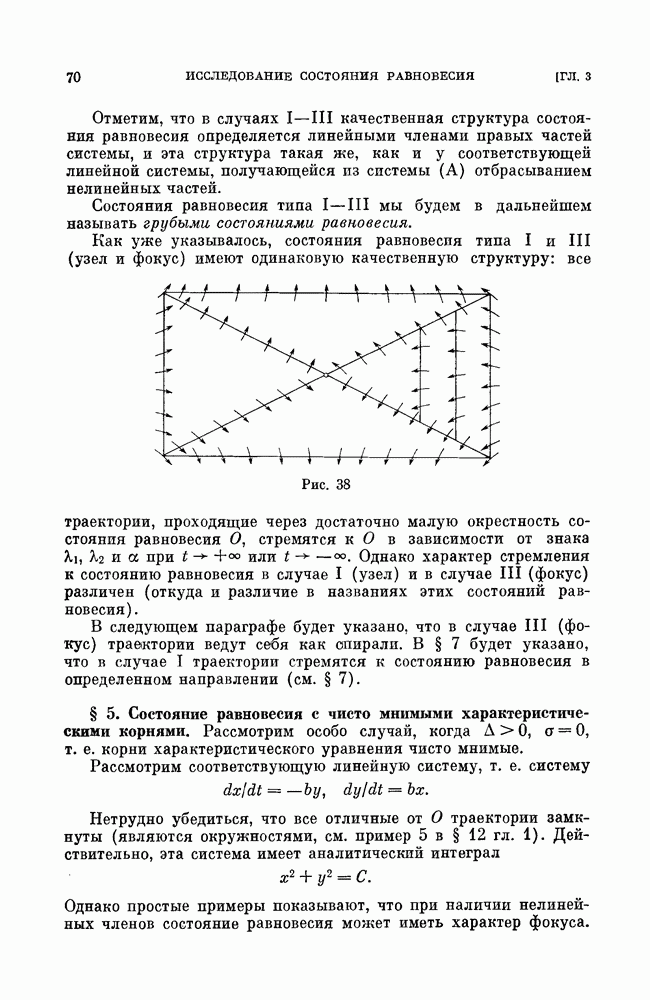
Мы рассмотрим сначала те точки границы области Рауса — Гурвица, которые соответствуют негрубым состояниям равновесия первой степени негрубости — именно, сложному фокусу с
не равной нулю первой ляпуновской величиной (коэффициент  в функции последования) и двукратному состоянию равновесия — седло-узлу.
в функции последования) и двукратному состоянию равновесия — седло-узлу.
В этом случае части границы области Рауса — Гурвица могут быть двоякой природы: безопасные границы — достаточно малое нарушение которых влечет за собой лишь весьма малые (сколь угодно малые при достаточно малых нарушениях) изменения состояния системы; опасные границы — сколь угодно малое нарушение которых повлечет за собой переход системы в новое состояние, которое мы не можем приблизить к исходному выбором достаточно малых нарушений границы.
Иначе говоря, может оказаться, что состояние равновесия измененной системы (сколь угодно мало измененной) будет неустойчиво, но практически система будет вести себя как устойчивая, так как изображающая точка, взятая из некоторой окрестности состояния равновесия, будет для всех  (начиная с начального значения
(начиная с начального значения  оставаться в малой окрестности состояния равновесия (сколь угодно малой при достаточно малых изменениях системы), и, наоборот, мояет оказаться, что, хотя состояние равновесия измененной системы устойчиво, но система практически будет неустойчива, так как изображающую точку, взятую вне малой окрестности состояния равновесия (сколь угодно малой при достаточно малых изменениях системы), нельзя заставить оставаться вблизи состояния равновесия.
оставаться в малой окрестности состояния равновесия (сколь угодно малой при достаточно малых изменениях системы), и, наоборот, мояет оказаться, что, хотя состояние равновесия измененной системы устойчиво, но система практически будет неустойчива, так как изображающую точку, взятую вне малой окрестности состояния равновесия (сколь угодно малой при достаточно малых изменениях системы), нельзя заставить оставаться вблизи состояния равновесия.
Предположим, что рассматриваемое состояние равновесия лежит в начале координат, так что мы можем предполагать систему в виде

где k — параметр.
Рассмотрим подробно два указанных выше случая поведения системы при значениях А, близких к значению  соответствующему сложному фокусу или седло-узлу первой степени негрубости (см. гл. 10).
соответствующему сложному фокусу или седло-узлу первой степени негрубости (см. гл. 10).
1. При  система имеет сложный фокус первого порядка, т. е. состояние равновесия с чисто мнимыми характеристическими корнями, у которого первая ляпуновская величина
система имеет сложный фокус первого порядка, т. е. состояние равновесия с чисто мнимыми характеристическими корнями, у которого первая ляпуновская величина  отлична от нуля. Вводя обозначения
отлична от нуля. Вводя обозначения

 действительная часть характеристических корней), мы, очевидно, будем иметь в рассматриваемом случае
действительная часть характеристических корней), мы, очевидно, будем иметь в рассматриваемом случае

Далее естественно сделать предположение, что  Мы получим наглядную картину поведения системы вблизи
Мы получим наглядную картину поведения системы вблизи
траницы области устойчивости, рассматривая изменение качественной структуры в окрестности состояния равновесия в зависимости от изменения параметра  . Как мы видели (см. гл. 11), возможны следующие случаи:
. Как мы видели (см. гл. 11), возможны следующие случаи:
а)  , сложный фокус устойчив. При переходе через границу
, сложный фокус устойчив. При переходе через границу  от значений
от значений  к значениям
к значениям  появляется единственный устойчивый предельный цикл. При обратном изменении параметра X устойчивый цикл стягивается в точку (в сложный фокус);
появляется единственный устойчивый предельный цикл. При обратном изменении параметра X устойчивый цикл стягивается в точку (в сложный фокус);
б)  , сложный фокус неустойчив. При переходе через границу
, сложный фокус неустойчив. При переходе через границу  от значений
от значений  к значениям
к значениям  к состоянию равновесия стягивается единственный неустойчивый предельный цикл; при обратном изменении параметра из состояния равновесия появляется неустойчивый предельный цикл.
к состоянию равновесия стягивается единственный неустойчивый предельный цикл; при обратном изменении параметра из состояния равновесия появляется неустойчивый предельный цикл.
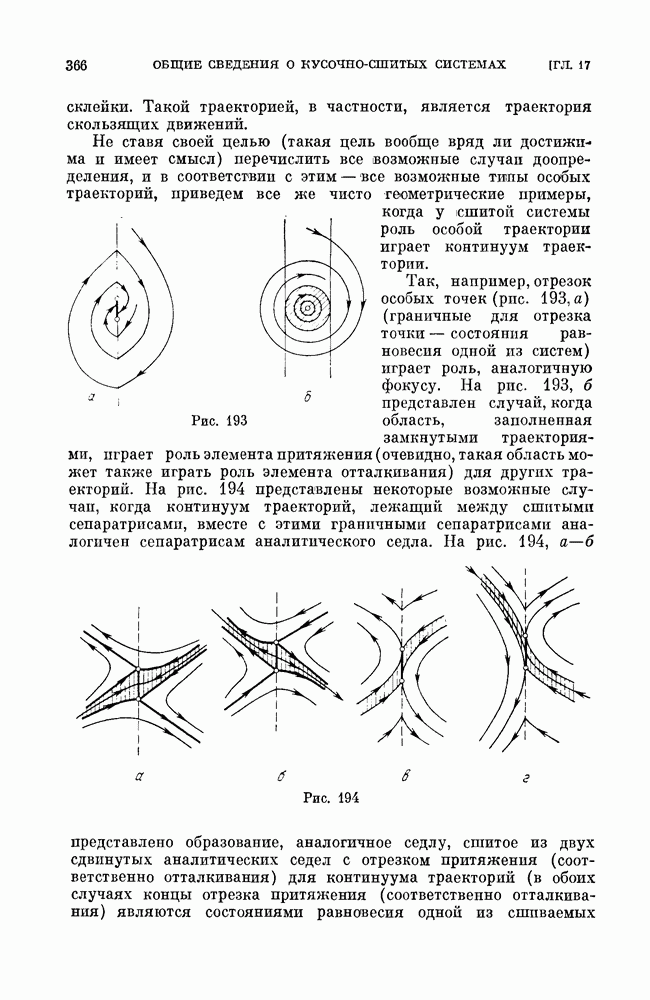
Изменение качественной структуры разбиения окрестности состояния равновесия на траектории для этих двух случаев изображено на рис. 117, 118.

Рис. 117
Штриховкой показана область устойчивости, для которой траектории представляют собой спирали, накручивающиеся на состояние равновесия, или предельный цикл. Область неустойчивости заполнена раскручивающимися спиралями. Рисунки наглядно показывают различие в поведении системы вблизи границы по отношению к случайным толчкам. Сравнивая для  случаи
случаи  видим, что во втором случае возможно выбивание случайным толчком изображающей точки из устойчивого состояния равновесия за границы области устойчивости (внутри рассматриваемой окрестности состояния равновесия), тогда как в первом случае это
видим, что во втором случае возможно выбивание случайным толчком изображающей точки из устойчивого состояния равновесия за границы области устойчивости (внутри рассматриваемой окрестности состояния равновесия), тогда как в первом случае это
невозможно. Рисунки показывают, далее, различие в поведении системы при нарушении условий устойчивости. Переход через границу  в первом случае
в первом случае  соответствует возникновению области неустойчивости внутри устойчивого предельного цикла, которая, однако, остается сколь угодно малой при достаточно малом нарушении условий устойчивости и стягивается в точку при обратном изменении параметра; изображающая точка при этом возвращается в состояние равновесия — система ведет себя обратимо.
соответствует возникновению области неустойчивости внутри устойчивого предельного цикла, которая, однако, остается сколь угодно малой при достаточно малом нарушении условий устойчивости и стягивается в точку при обратном изменении параметра; изображающая точка при этом возвращается в состояние равновесия — система ведет себя обратимо.

Рис. 118
Во втором случае  переход через границу
переход через границу  соответствует исчезновению области устойчивости внутри неустойчивого предельного цикла; изображающая точка при этом срывается с состояния равновесия и уходит за пределы рассматриваемой окрестности состояния равновесия. При обратном изменении параметра изображающая точка не возвращается в состояние равновесия — система ведет себя необратимо.
соответствует исчезновению области устойчивости внутри неустойчивого предельного цикла; изображающая точка при этом срывается с состояния равновесия и уходит за пределы рассматриваемой окрестности состояния равновесия. При обратном изменении параметра изображающая точка не возвращается в состояние равновесия — система ведет себя необратимо.
В § 3 настоящей главы при рассмотрении жесткого возникновения колебаний изображающая точка после срыва уходит на устойчивый предельный цикл, окружающий начало, в силу предположения о специальном характере разбиения плоскости на траектории. Однако при другом виде фазовой плоскости изображающая точка после срыва при  может пойти либо к другому устойчивому состоянию равновесия, либо к предельному циклу, не окружающему начало. Мы вернемся к этому более сложному случаю в следующем параграфе.
может пойти либо к другому устойчивому состоянию равновесия, либо к предельному циклу, не окружающему начало. Мы вернемся к этому более сложному случаю в следующем параграфе.
II. При  система имеет двукратное состояние равновесия — седло-узел, т. е. состояние равновесия, для которого
система имеет двукратное состояние равновесия — седло-узел, т. е. состояние равновесия, для которого

(неравенство нулю  и означает, что точка двукратная).
и означает, что точка двукратная).
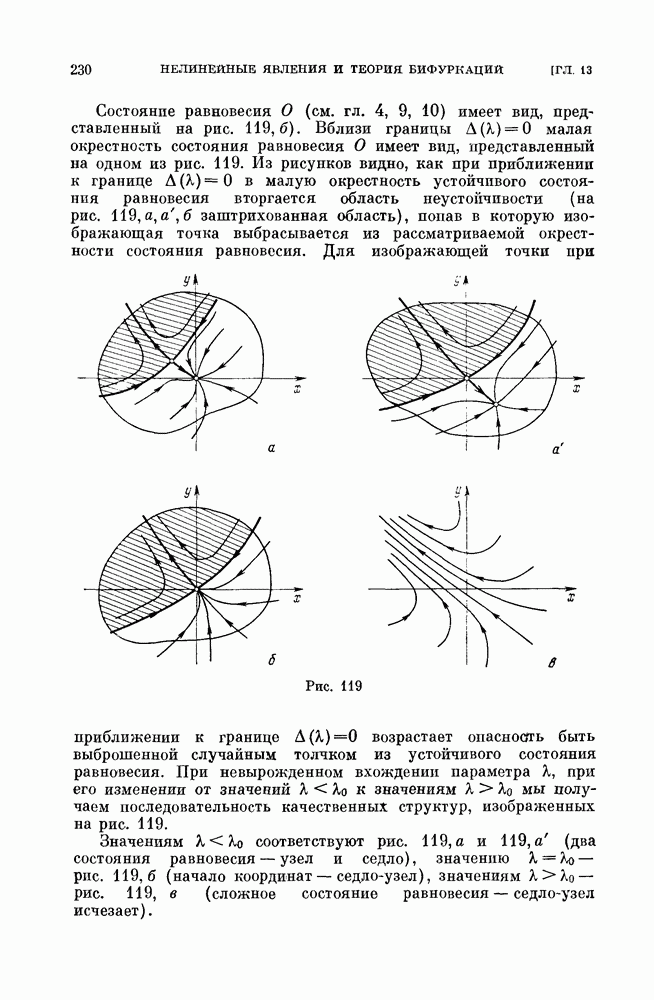
Состояние равновесия О (см. гл. 4, 9, 10) имеет вид, представленный на рис. 119, б). Вблизи границы  малая окрестность состояния равновесия О имеет вид, представленный на одном из рис. 119. Из рисунков видно, как при приближении к границе
малая окрестность состояния равновесия О имеет вид, представленный на одном из рис. 119. Из рисунков видно, как при приближении к границе  в малую окрестность устойчивого состояния равновесия вторгается область неустойчивости (на рис. 119, а, а, б заштрихованная область), попав в которую изображающая точка выбрасывается из рассматриваемой окрестности состояния равновесия.
в малую окрестность устойчивого состояния равновесия вторгается область неустойчивости (на рис. 119, а, а, б заштрихованная область), попав в которую изображающая точка выбрасывается из рассматриваемой окрестности состояния равновесия.

Рис. 119
Для изображающей точки при приближении к границе  возрастает опасность быть выброшенной случайным толчком из устойчивого состояния равновесия. При невырожденном вхождении параметра А, при его изменении от значений
возрастает опасность быть выброшенной случайным толчком из устойчивого состояния равновесия. При невырожденном вхождении параметра А, при его изменении от значений  к значениям
к значениям  мы получаем последовательность качественных структур, изображенных на рис. 119.
мы получаем последовательность качественных структур, изображенных на рис. 119.
Значениям  соответствуют рис. 119, а и 119, а (два состояния равновесия — узел и седло), значению
соответствуют рис. 119, а и 119, а (два состояния равновесия — узел и седло), значению  рис. 119, б (начало координат — седло-узел), значениям
рис. 119, б (начало координат — седло-узел), значениям  рис. 119, в (сложное состояние равновесия — седло-узел исчезает).
рис. 119, в (сложное состояние равновесия — седло-узел исчезает).
Рассмотренная граница области устойчивости, очевидно, является опасной.
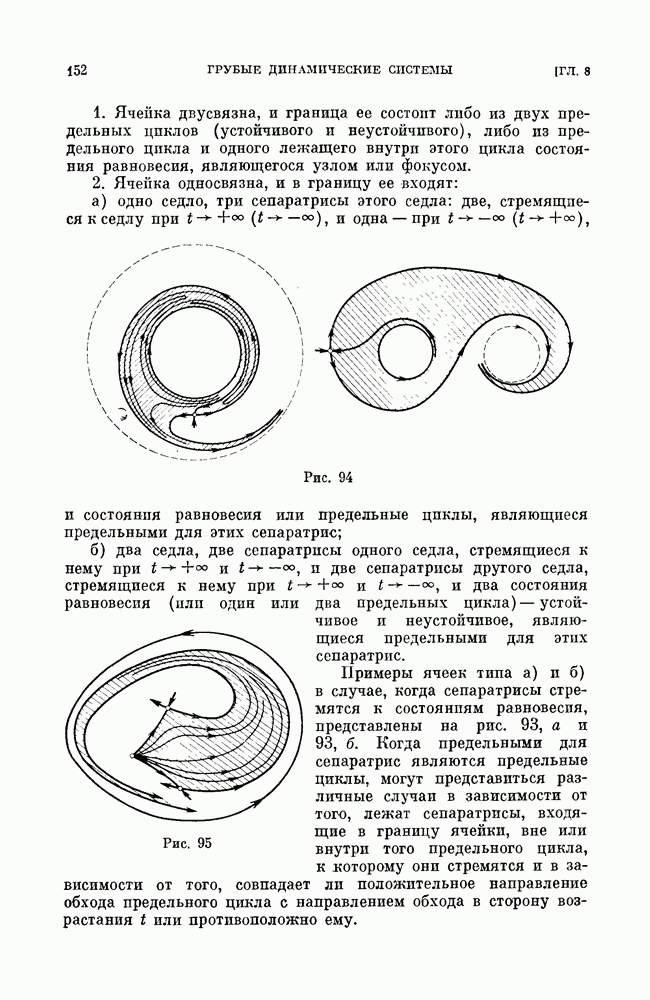
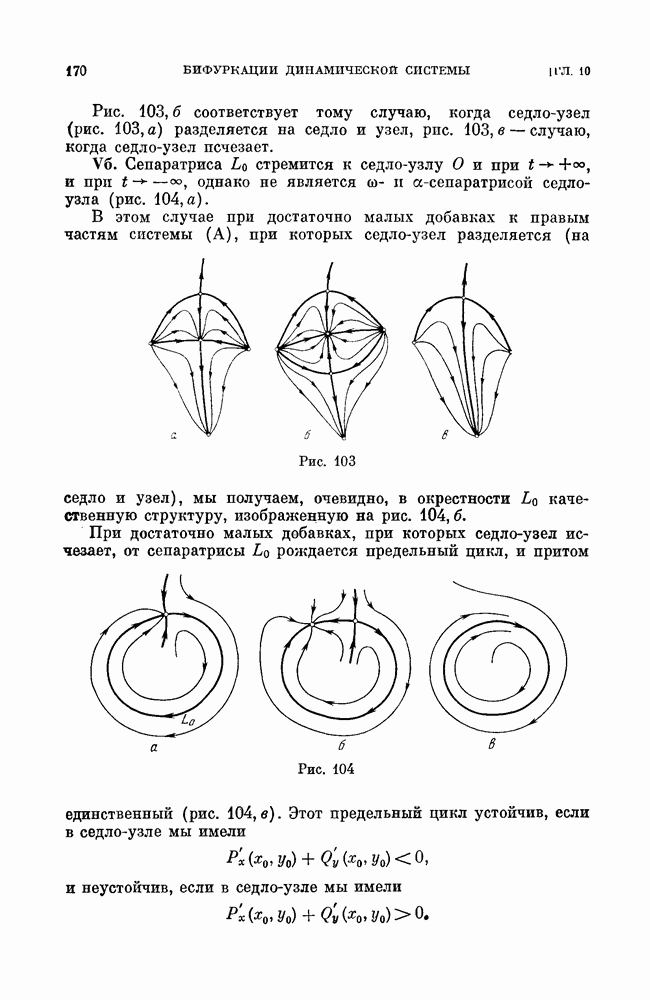
После исчезновения седло-узла изображающая точка либо стремится к устойчивому состоянию равновесия или к устойчивому предельному циклу, близкому к тому, к которому стремилась  -сепаратриса седло-узла (см. рис. 103 гл. 10), либо, в случае, когда сепаратриса седло-узла возвращается в него же, начинает двигаться (сначала с очень большим периодом) по предельному циклу, образовавшемуся из сепаратрисы седло-узла (см. рис. 104 гл. 10). Во всех этих случаях граница области устойчивости опасна.
-сепаратриса седло-узла (см. рис. 103 гл. 10), либо, в случае, когда сепаратриса седло-узла возвращается в него же, начинает двигаться (сначала с очень большим периодом) по предельному циклу, образовавшемуся из сепаратрисы седло-узла (см. рис. 104 гл. 10). Во всех этих случаях граница области устойчивости опасна.
Следует, однако, обратить внимание на то, что если при значениях  изображающая точка двигается по предельному циклу, на котором при
изображающая точка двигается по предельному циклу, на котором при  возникает двукратное состояние равновесия седло-узел, то соответствующая граница, очевидно, является безопасной (изображающая точка не выходит из окрестности цикла).
возникает двукратное состояние равновесия седло-узел, то соответствующая граница, очевидно, является безопасной (изображающая точка не выходит из окрестности цикла).
Рассмотрим еще дополнительно поведение динамических систем вблизи тех точек границы, в которых  где безопасная граница переходит в опасную, т. е. где первая ляпуновская величина
где безопасная граница переходит в опасную, т. е. где первая ляпуновская величина  обращается в нуль. В этом случае поведение системы может быть определено знаком второй ляпуновской величины
обращается в нуль. В этом случае поведение системы может быть определено знаком второй ляпуновской величины  (см. гл. 11, § 5).
(см. гл. 11, § 5).
При рассмотрении этого случая мы предположим, что в систему входит не один, а два параметра  (при наличии только одного параметра картина смазывается), и пусть в некоторой точке
(при наличии только одного параметра картина смазывается), и пусть в некоторой точке  плоскости параметров
плоскости параметров  но
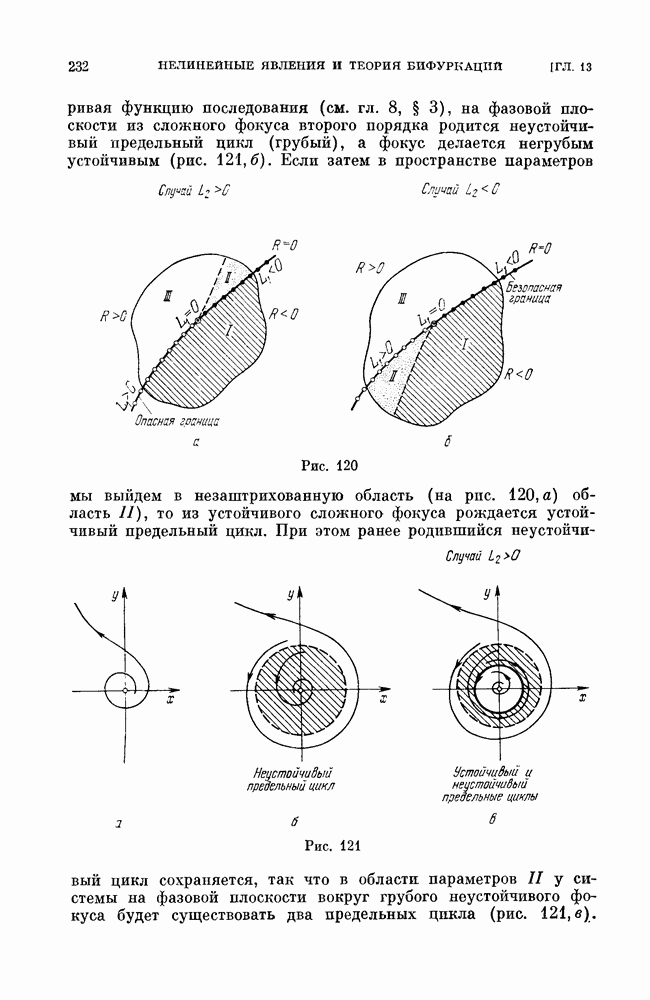
но  На рис. 120 большая точка соответствует точке плоскости параметров, в которой
На рис. 120 большая точка соответствует точке плоскости параметров, в которой  ; в точках части линии
; в точках части линии  обозначенной белыми точками,
обозначенной белыми точками,  (для соответствующих значений параметров система имеет неустойчивый сложный фокус первого порядра); в точках части линии
(для соответствующих значений параметров система имеет неустойчивый сложный фокус первого порядра); в точках части линии  обозначенной черными точками,
обозначенной черными точками,  (система имеет устойчивый сложный фокус).
(система имеет устойчивый сложный фокус).
В заштрихованной части плоскости параметров  в незаштрихованной (но в которой может быть область, обозначенная мелкими штрихами)
в незаштрихованной (но в которой может быть область, обозначенная мелкими штрихами)  Напомним, что при переходе через часть границы
Напомним, что при переходе через часть границы  в которой
в которой  из заштрихованной области в незаштрихованную из сложного фокуса рождается устойчивый предельный цикл, а при переходе через
из заштрихованной области в незаштрихованную из сложного фокуса рождается устойчивый предельный цикл, а при переходе через  где
где  из незаштрихованной в заштрихованную область — неустойчивый цикл.
из незаштрихованной в заштрихованную область — неустойчивый цикл.
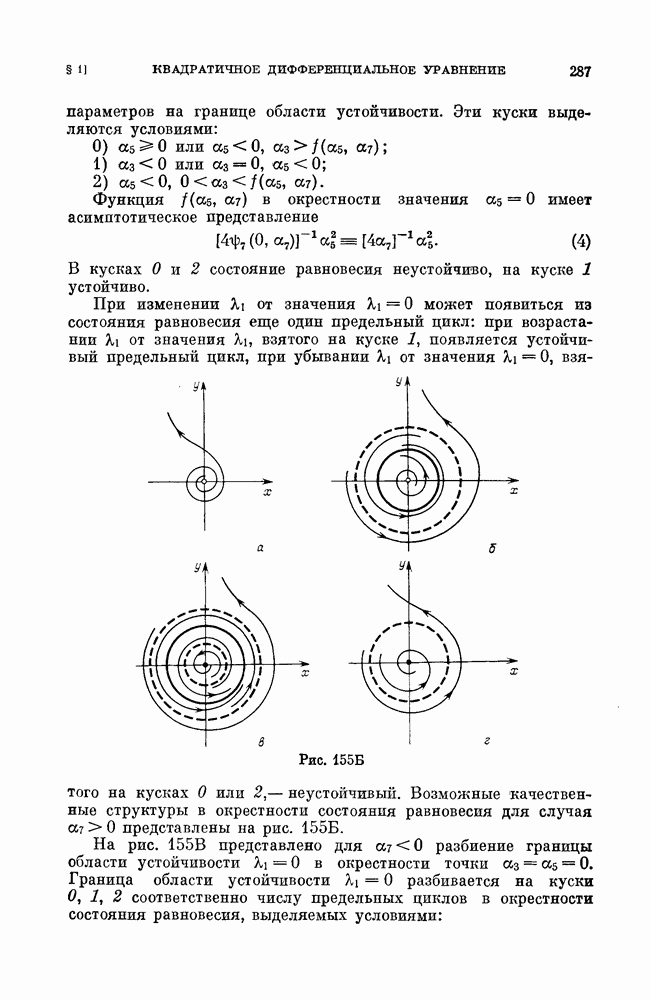
Пусть в точке, в которой  мы имеем
мы имеем  тогда соответствующий сложный фокус (второй степени негрубости) неустойчив (рис. 120, а, 121, а).
тогда соответствующий сложный фокус (второй степени негрубости) неустойчив (рис. 120, а, 121, а).
Если в пространстве параметров мы перейдем по линии  в точки, где
в точки, где  то, как нетрудно показать,
то, как нетрудно показать,
рассматривая функцию последования (см. гл. 8, § 3), на фазовой плоскости из сложного фокуса второго порядка родится неустойчивый предельный цикл (грубый), а фокус делается негрубым устойчивым (рис. 121, б).

Рис. 120
Если затем в пространстве параметров мы выйдем в незаштрихованную область (на рис. 120, а) область II), то из устойчивого сложного фокуса рождается устойчивый предельный цикл.

Рис. 121
При этом ранее родившийся неустойчивый цикл сохраняется, так что в области параметров II у системы на фазовой плоскости вокруг грубого неустойчивого фокуса будет существовать два предельных цикла (рис. 121, в).
С другой стороны, нетрудно показать, что при значениях параметров в области III у системы вокруг неустойчивого фокуса нет предельных циклов. (При переходе из точки, где  на часть линии
на часть линии  где
где  циклы не рождаются, и в силу сделанных выше замечаний не рождаются при переходе в область III.) Но тогда при движении в пространстве параметров из области III в область II непременно должны встретиться бифуркационные значения параметров, при которых у системы существует двукратный цикл. На рис. 120 линия в пространстве параметров, соответствующая двукратным предельным циклам, изображена штрихами. Аналогичное рассмотрение может быть проведено и в случае
циклы не рождаются, и в силу сделанных выше замечаний не рождаются при переходе в область III.) Но тогда при движении в пространстве параметров из области III в область II непременно должны встретиться бифуркационные значения параметров, при которых у системы существует двукратный цикл. На рис. 120 линия в пространстве параметров, соответствующая двукратным предельным циклам, изображена штрихами. Аналогичное рассмотрение может быть проведено и в случае  (рис. 120,6 и рис. 122, а — в).
(рис. 120,6 и рис. 122, а — в).
В рассмотренном случае знак второй ляпуновской величины  играет роль, подобную знаку
играет роль, подобную знаку  увеличивая или уменьшая опасность для изображающей точки быть выброшенной из окрестности состояния равновесия.
увеличивая или уменьшая опасность для изображающей точки быть выброшенной из окрестности состояния равновесия.

Рис. 122
Пусть  (при
(при  и пусть значения параметров достаточно близки к значениям, определяемым этими условиями; тогда в достаточно малой окрестности начала координат в фазовом пространстве может быть одна из структур, изображенных на рис. 121.
и пусть значения параметров достаточно близки к значениям, определяемым этими условиями; тогда в достаточно малой окрестности начала координат в фазовом пространстве может быть одна из структур, изображенных на рис. 121.
При нарушении безопасной границы области устойчивости изображающая точка остается в малой окрестности состояния равновесия вблизи устойчивого предельного цикла, если начальные возмущения не превосходят некоторой малой величины (определяемой размерами второго, неустойчивого предельного цикла, также вторгающегося в малую окрестность начала
координат); при возмущениях, превосходящих эти пределы, изображающую точку нельзя заставить оставаться в малой окрестности состояния равновесия.
С другой стороны, выбивание системы малым толчком из устойчивого состояния равновесия возможно и вблпзи безопасной границы области устойчивости (см. рис. 121).
Пусть  (при
(при  ), и пусть параметры опять мало изменены; тогда в достаточно малой окрестности начала координат может быть одна из структур, изображенных на рис. 122. Здесь даже нарушение опасной границы может оставить изображающую точку в малой окрестности состояния равновесия, если параметры достаточно близки к значениям, определяемым условиями
), и пусть параметры опять мало изменены; тогда в достаточно малой окрестности начала координат может быть одна из структур, изображенных на рис. 122. Здесь даже нарушение опасной границы может оставить изображающую точку в малой окрестности состояния равновесия, если параметры достаточно близки к значениям, определяемым условиями 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. АВТОНОМНЫЕ СИСТЕМЫ ВТОРОГО ПОРЯДКА С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- § 1. Автономная динамическая система на плоскости.
- § 2. Теорема существования и единственности решения.
- § 3. Простейшие свойства решений системы (А).
- § 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
- § 5. Сопоставление геометрической интерпретации системы (А) в пространстве (x, y, t) с интерпретацией на фазовой плоскости.
- § 6. Некоторые термины.
- § 7. Теорема о непрерывной зависимости решения от начальных условий.
- § 8. Направление на траекториях. Изменение параметризации.
- § 9. Дифференциальное уравнение, соответствующее динамической системе.
- § 10. Понятие интегральной кривой и интеграла в случае аналитических правых частей Р(х,у) и Q(x,y) системы (А).
- § 11. Что значит «найти решение динамической системы»?
- § 12. Примеры.
- § 13. Замечания по поводу примеров § 12.
- § 14. Математическое определение качественной (топологической) структуры разбиения на траектории и качественного исследования динамической системы.
- ГЛАВА 2. ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ — БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ
- § 2. Цикл без контакта.
- § 3. Предельная точка полутраектории и траектории. Предельная траектория.
- § 4. Основная теорема.
- § 5. Возможные типы полутраекторий и их предельных множеств.
- § 6. Особые и неособые полутраектории и траектории.
- § 7. Возможные типы особых и неособых траекторий.
- § 8. Случай конечного числа особых траекторий. Элементарные ячейки.
- § 9. Возможные типы ячеек. Односвязные и двусвязные ячейки.
- § 10. Два подхода к описанию качественной структуры.
- § 11. Качественная (топологическая) структура состояния равновесия в случае конечного числа особых траекторий. Схема динамической системы.
- § 12. Устойчивость по Ляпунову.
- ГЛАВА 3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННОЙ СТРУКТУРЫ ОКРЕСТНОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (ОСОБОЙ ТОЧКИ)
- § 2. Приведение динамической системы к каноническому виду.
- § 3. Возможный характер простых состояний равновесия.
- § 4. Замечания о методах установления характера грубых состояний равновесия.
- § 5. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 6. Направления, в которых траектории стремятся к простым состояниям равновесия.
- § 7. Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия.
- § 8. Сводка сведений о грубых состояниях равновесия.
- ГЛАВА 4. КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ
- § 1. Направления, в которых траектории стремятся к сложному состоянию равновесия.
- § 2. Сложное состояние равновесия (особая точка) с нулевыми характеристическими корнями.
- § 3. Примеры.
- § 4. Нормальные формы.
- ГЛАВА 5. ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ
- § 2. Условия устойчивости и неустойчивости неподвижной точки точечного отображения.
- § 3. Функция соответствия.
- § 4. Изучение окрестности замкнутой траектории. Простые и сложные предельные циклы.
- § 5. Аналитические выражения для коэффициентов функции последования. Характеристический показатель замкнутой траектории.
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЕМЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 2. Изучение поведения интегральных кривых в бесконечности. Сфера Пуанкаре.
- § 3. Примеры исследования в бесконечности [93].
- § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов.
- 1. Некоторые видоизменения критериев Бендиксона и Дюлака.
- 2. Индексы Пуанкаре. Распределение особых точек [77, 117].
- 3. Условия сосуществования замкнутых траекторий и особых точек.
- 4. Две общие теоремы Пуанкаре.
- § 5. Топографическая система Пуанкаре. Функция Ляпунова. Кривые контактов.
- ЧАСТЬ II. ТЕОРИЯ БИФУРКАЦИЙ
- § 1. Свойства консервативных систем на плоскости [2, 3].
- § 2. Динамические системы, характерные для теории колебаний.
- § 3. Измененные системы. Системы, правые части которых зависят от параметра.
- § 4. Основные теоремы о зависимости решения от изменения правых частей динамической системы.
- § 5. Грубость динамической системы и теоремы о непрерывной зависимости решения от изменения правых частей.
- ГЛАВА 8. ГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
- § 2. Состояния равновесия, возможные в грубой динамической системе.
- § 3. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 4. Замкнутые траектории, возможные в грубой системе.
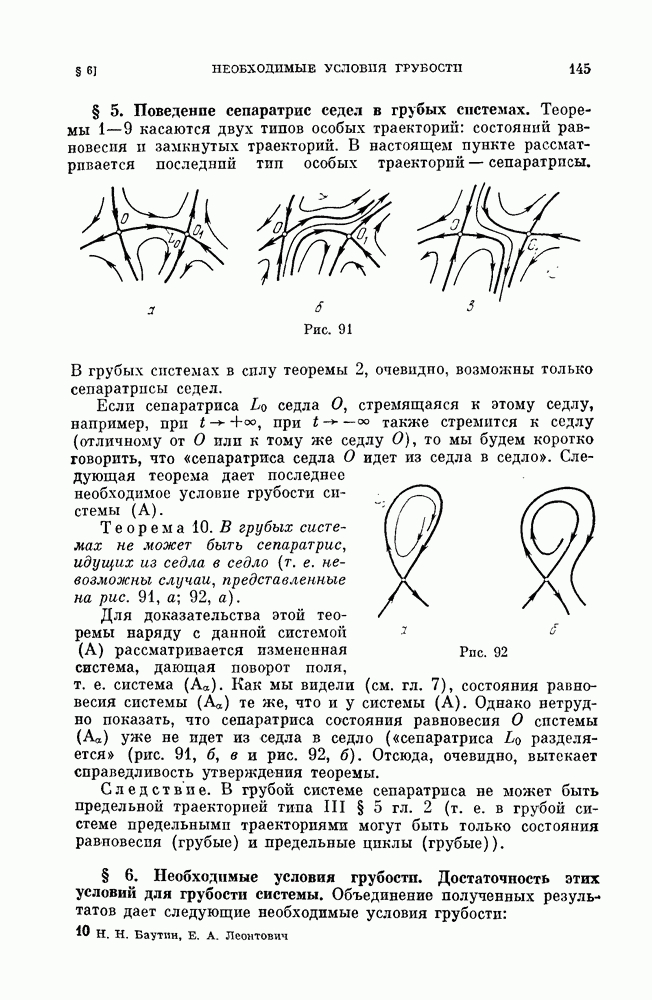
- § 5. Поведение сепаратрис седел в грубых системах.
- § 6. Необходимые условия грубости. Достаточность этих условий для грубости системы.
- § 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем.
- § 8. Понятие грубости при более общих предположениях относительно правых частей динамической системы.
- § 9. Типы особых траекторий и ячеек в грубых системах.
- § 10. Замечания по поводу определения грубой системы.
- ГЛАВА 9. ПРОСТЕЙШИЕ НЕГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ — СИСТЕМЫ ПЕРВОЙ СТЕПЕНИ НЕГРУБОСТИ
- § 2. Системы первой степени негрубости.
- § 3. Состояния равновесия, возможные в системе первой степени негрубости.
- § 4. Замкнутые траектории, возможные в системе первой степени негрубости.
- § 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости.
- § 6. Необходимые и достаточные условия первой степени негрубости.
- § 7. Динамические системы более высокой степени негрубости.
- ГЛАВА 10. БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- § 1. Определение бифуркации.
- § 2. Бифуркации систем первой степени негрубости.
- § 3. Бифуркации некоторых типов сложных особых точек.
- § 4. Бифуркации двукратной точки, для которой …
- § 5. Рождение предельных циклов из особых траекторий степени негрубости выше первой.
- ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
- § 1. Возможный характер зависимости правых частей динамической системы от параметров.
- § 2. Смена качественных структур при изменении параметров.
- § 3. Случай, когда правые части зависят более чем от одного параметра.
- § 4. Бифуркации «от бесконечности».
- § 5. Условия существования седло-узла и сложного фокуса первого порядка.
- § 6. Поворот векторного поля.
- § 7. Метод малого параметра. Метод Понтрягина.
- ГЛАВА 12. ДИНАМИЧЕСКИЕ СИСТЕМЫ С ЦИЛИНДРИЧЕСКОЙ ФАЗОВОЙ ПОВЕРХНОСТЬЮ
- § 1. Цилиндрическая фазовая поверхность и характер траекторий, возможных на цилиндрической фазовой поверхности.
- § 2. Замкнутые траектории, охватывающие цилиндр.
- § 3. Приемы исследования качественной структуры динамической системы на цилиндре.
- § 4. Понятие грубости и степени негрубости для динамических систем на цилиндре. Бифуркации на цилиндре. Поворот поля.
- § 5. Динамические системы на цилиндре, близкие к гамильтоновым (метод Понтрягина).
- ГЛАВА 13. АДЕКВАТНОЕ ИСТОЛКОВАНИЕ НЕЛИНЕЙНЫХ ФИЗИЧЕСКИХ ЯВЛЕНИЙ ФАКТАМИ КАЧЕСТВЕННОЙ ТЕОРИИ И ТЕОРИИ БИФУРКАЦИЙ ДИНАМИЧЕСКИХ СИСТЕМ
- § 1. Мягкий и жесткий режимы.
- § 2. Замечания о границах области устойчивости различных стационарных режимов.
- § 3. Мягкое и жесткое возникновение колебаний.
- § 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
- § 5. Замечания по поводу других границ области устойчивости.
- ЧАСТЬ III. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- ГЛАВА 14. ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 1. Некоторые рецептурные указания.
- § 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
- § 3. Некоторые простые примеры динамических систем на цилиндре.
- ГЛАВА 15. ИССЛЕДОВАНИЕ МЕТОДОМ МАЛОГО ПАРАМЕТРА (МЕТОДОМ ПОНТРЯГИНА)
- § 2. Примеры рассмотрения методом Понтрягина (полное исследование).
- § 3. Исследование методом Понтрягина с привлечением вычислительных методов.
- ГЛАВА 16. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ
- § 2. Электрическая цепь с туннельным диодом.
- § 3. Двумерная модель динамики твердотельного лазера [119].
- § 4. Симметричный полет самолета в вертикальной плоскости (задача Н. Е. Жуковского).
- § 5. Система, описывающая динамику проточного химического реактора.
- § 6. Фазовая автоподстройка частоты.
- § 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов).
- § 8. Синхронный генератор с асинхронной характеристикой.
- ЧАСТЬ IV. КУСОЧНО-СШИТЫЕ СИСТЕМЫ
- ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ
- § 1. Сшитые системы. Доопределение на линиях сшивания.
- § 2. Возможные типы полутраекторий сшитых систем.
- § 3. Особые траектории сшитых систем.
- § 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
- ГЛАВА 18. ИССЛЕДОВАНИЕ КУСОЧНО-СШИТЫХ СИСТЕМ МЕТОДОМ ПОНТРЯГИНА
- § 2. Автоподстройка при кусочно-постоянной аппроксимации характеристики.
- § 3. Автоколебания синхронного мотора.
- ГЛАВА 19. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ
- § 2. Следящая система с люфтом.
- § 3. Электрическая цепь с туннельным диодом.
- § 4. Система со скачками на линии сшивания.
- ГЛАВА 20. ОБ АППРОКСИМАЦИЯХ И ГРУБОСТИ ПРОСТРАНСТВА ПАРАМЕТРОВ [39, 41, 42]
- § 1. Рассмотрение системы (2) при аппроксимациях пилообразными функциями.
- § 2. Рассмотрение системы (2) при аппроксимации, включающей отрезок параболы.
- § 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin f, и пилообразной для cos f функциями.
- § 4. Исследование роли аппроксимаций для уравнения маятникового типа.
- § 5. Динамическая система, описывающая автоколебания синхронного мотора.
- § 6. Динамическая система, описывающая симметричный полет самолета.
- ДОПОЛНЕНИЕ
- § 1. Динамическое системы на двумерных поверхностях.
- § 2. Динамические системы в n-мерном евклидовом пространстве.
- СПИСОК ЛИТЕРАТУРЫ