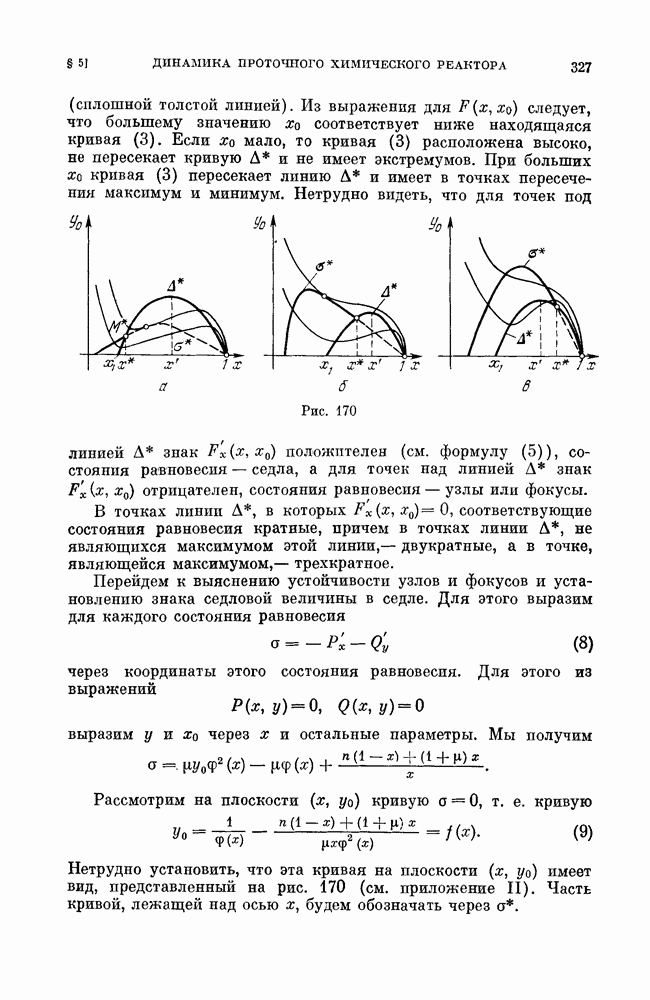
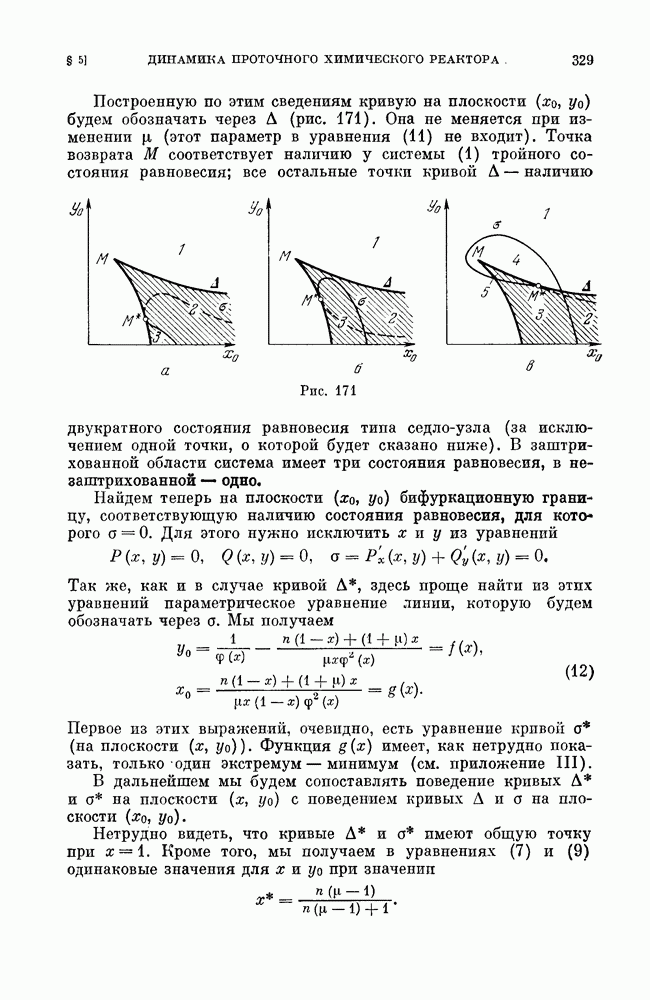
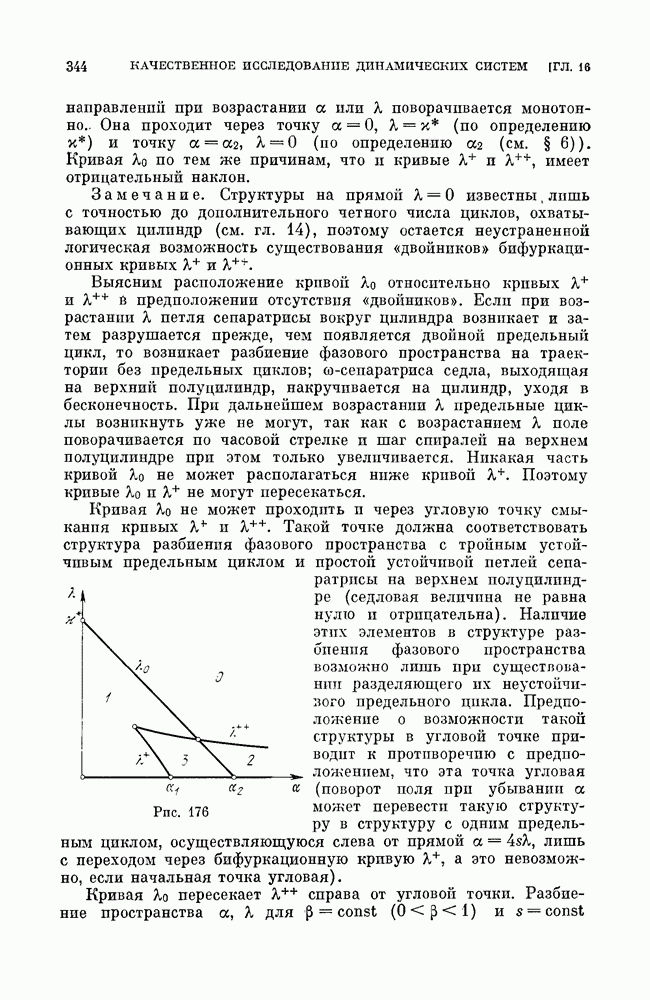
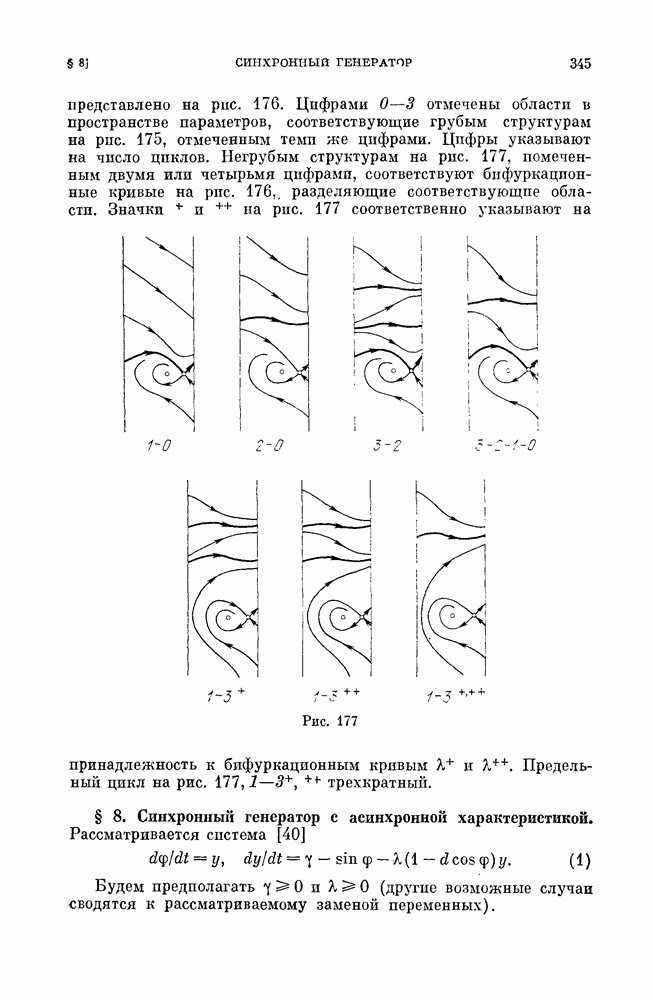
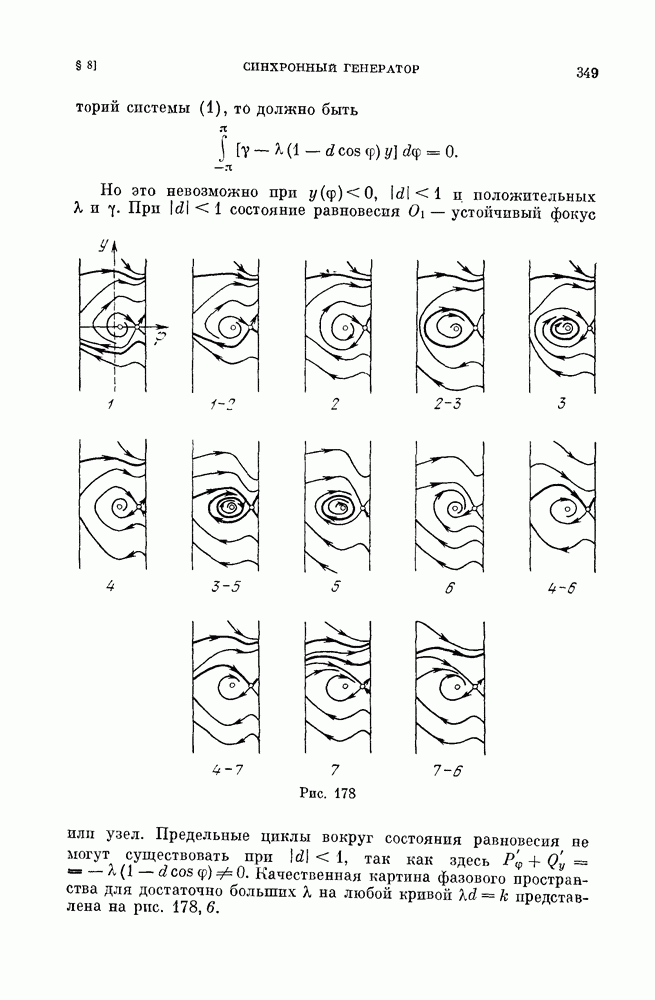
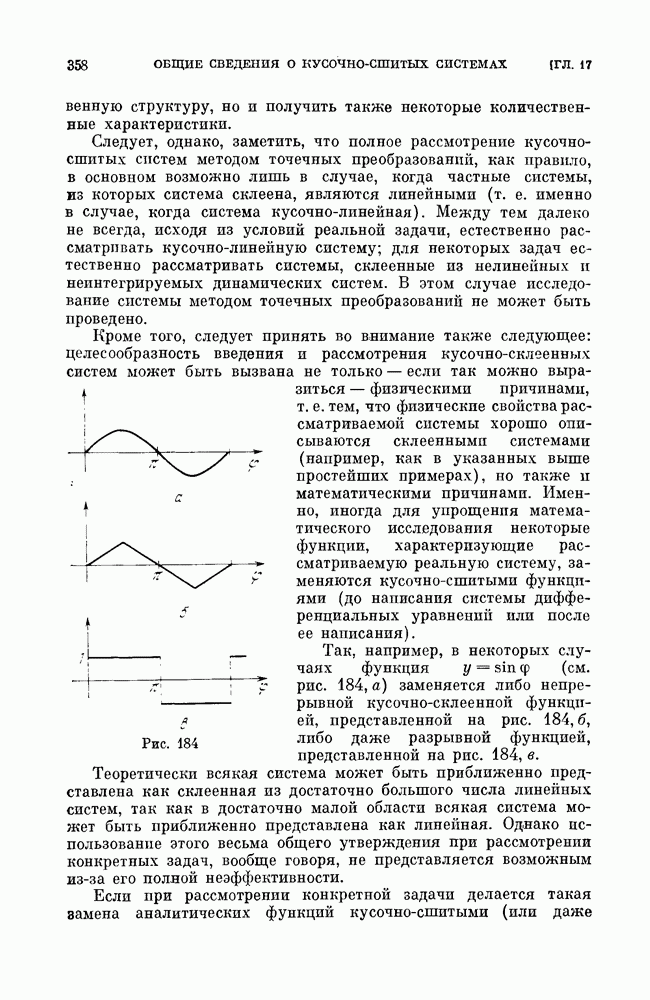
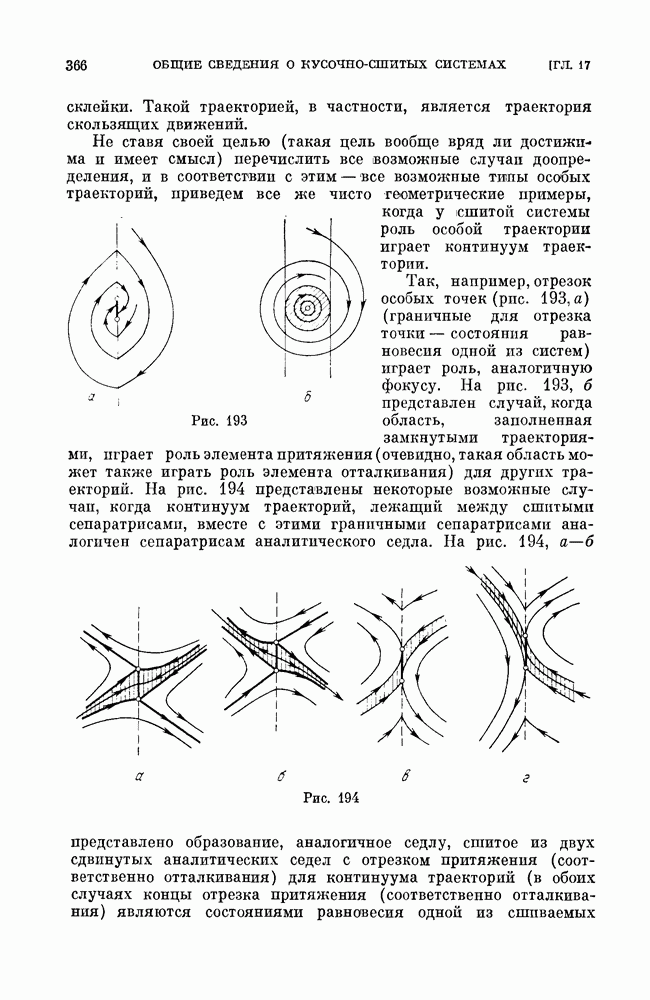
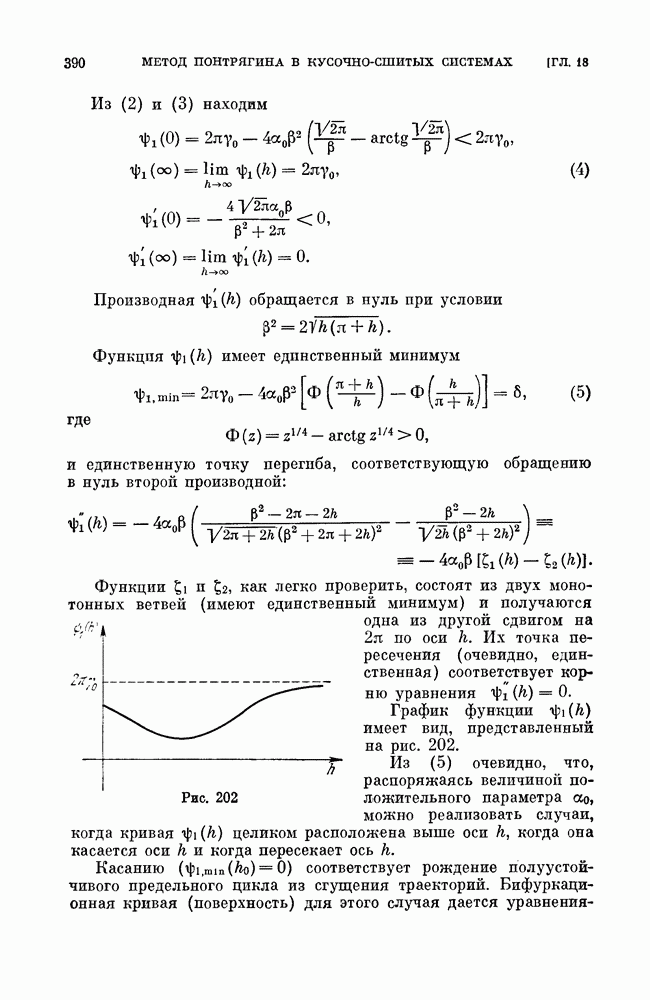
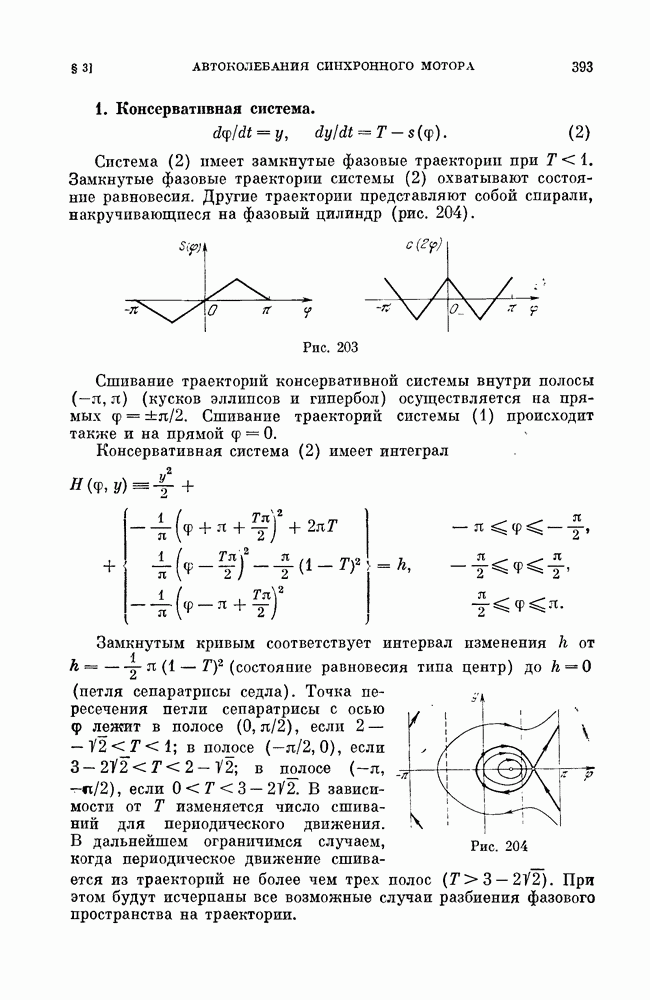
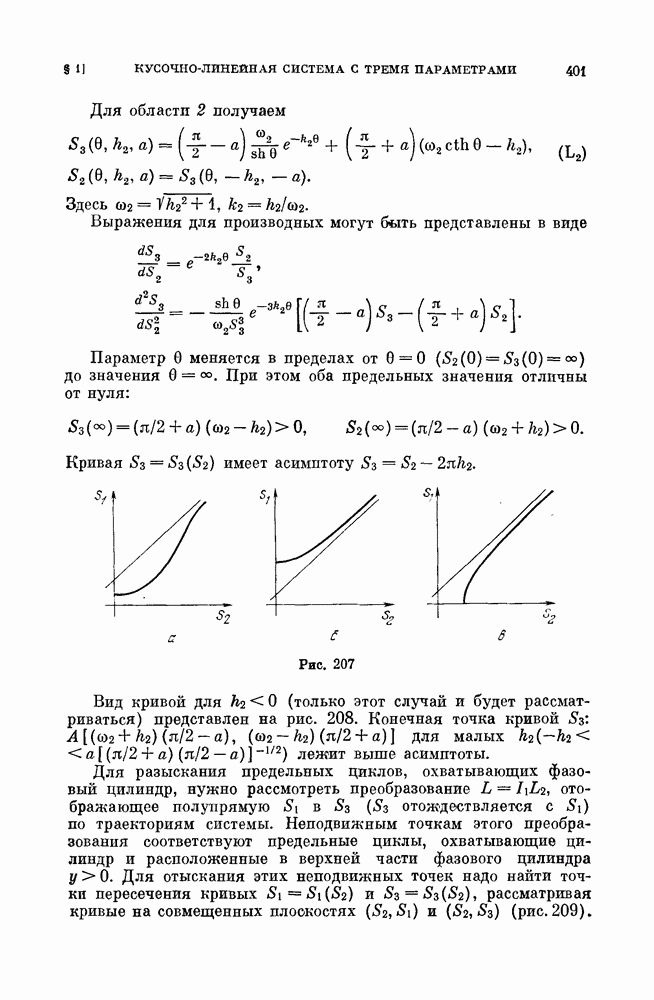
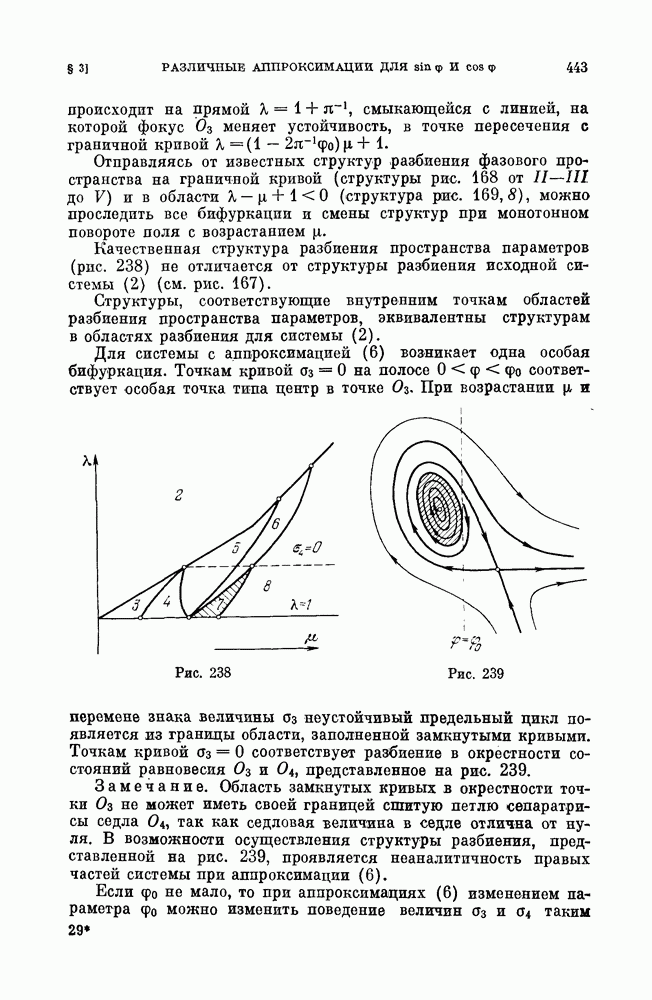
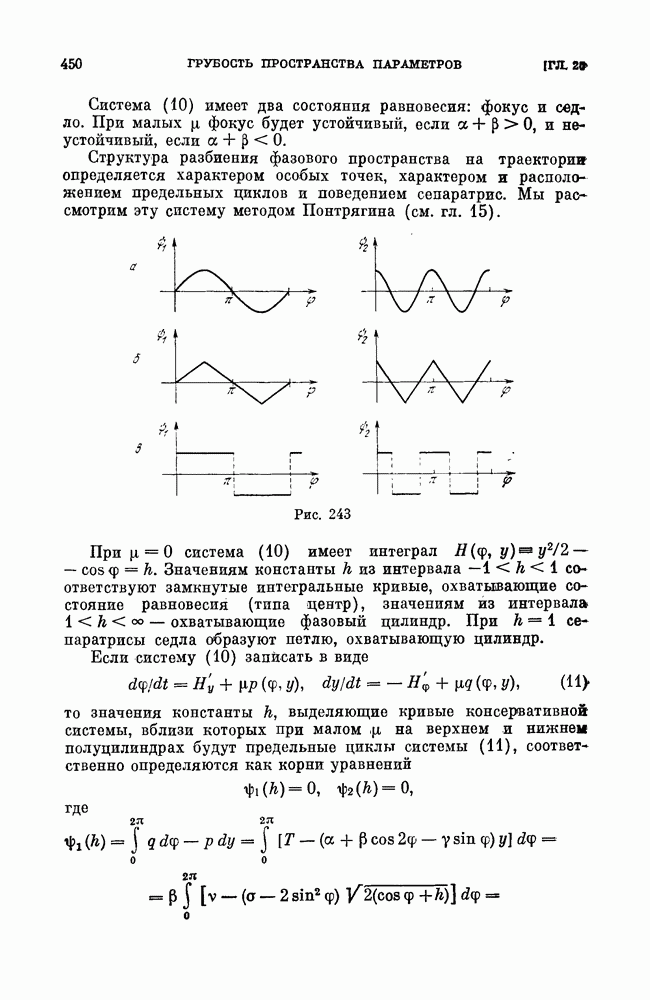
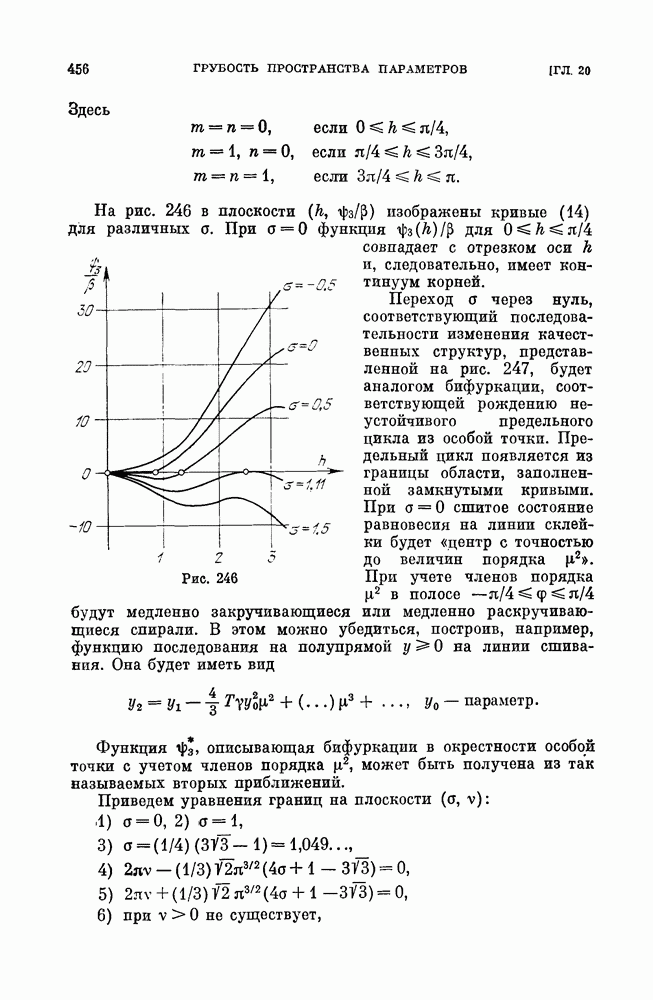
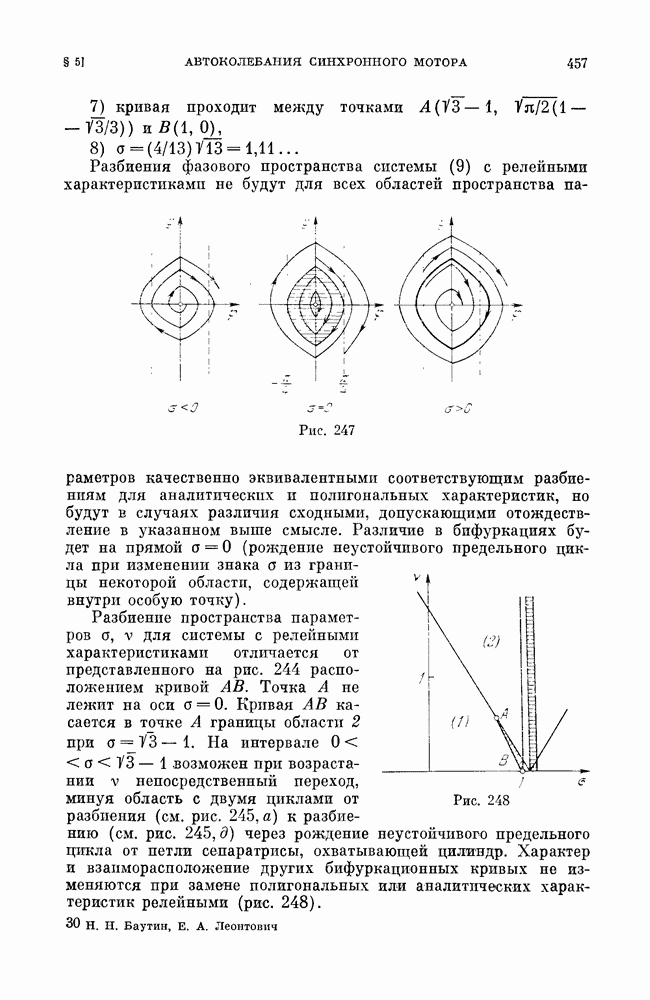
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
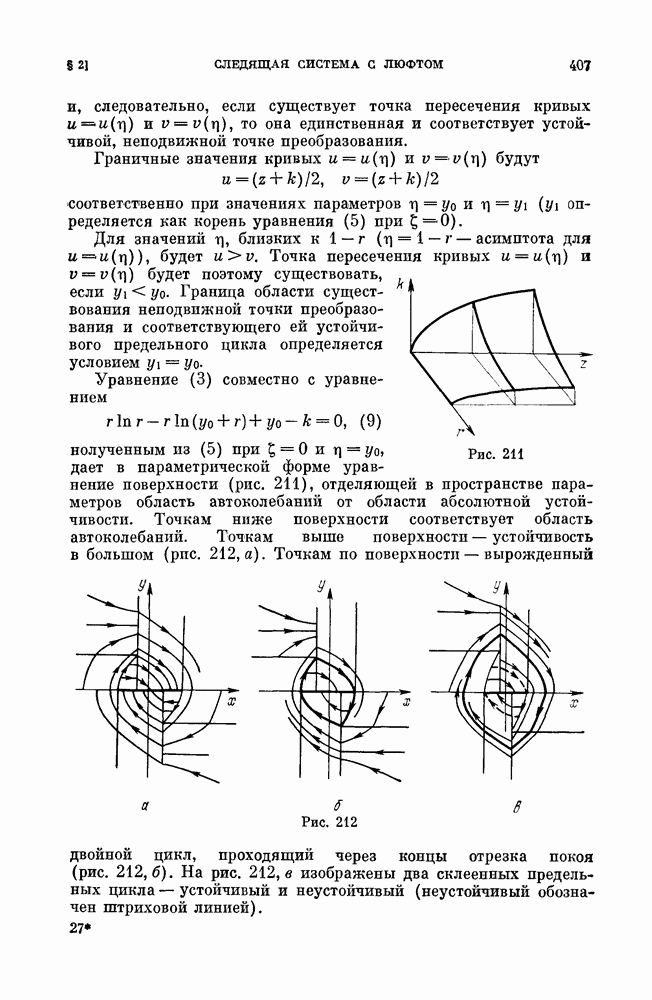
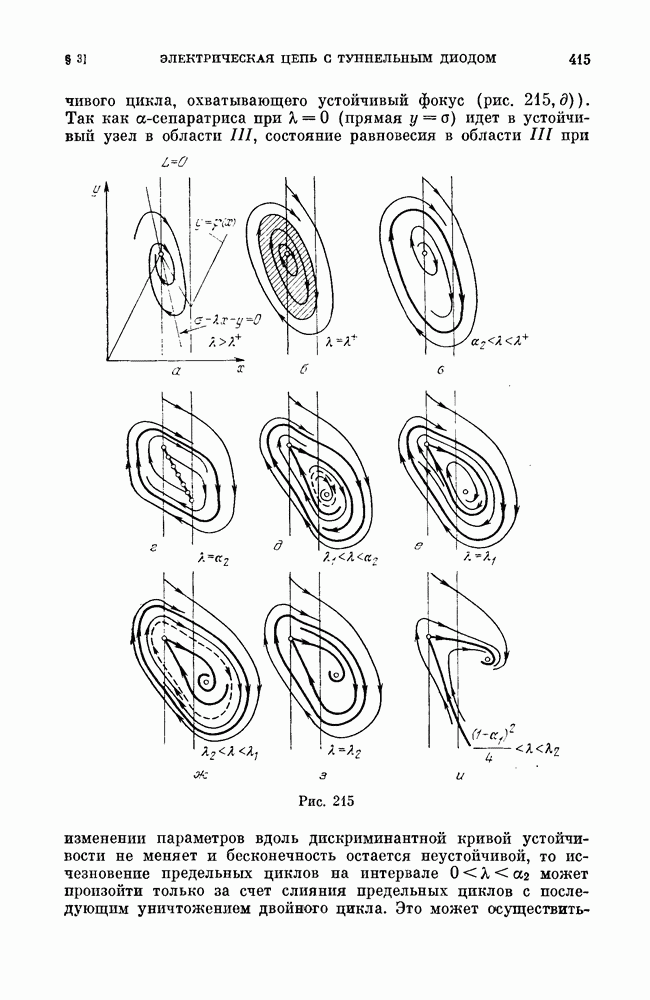
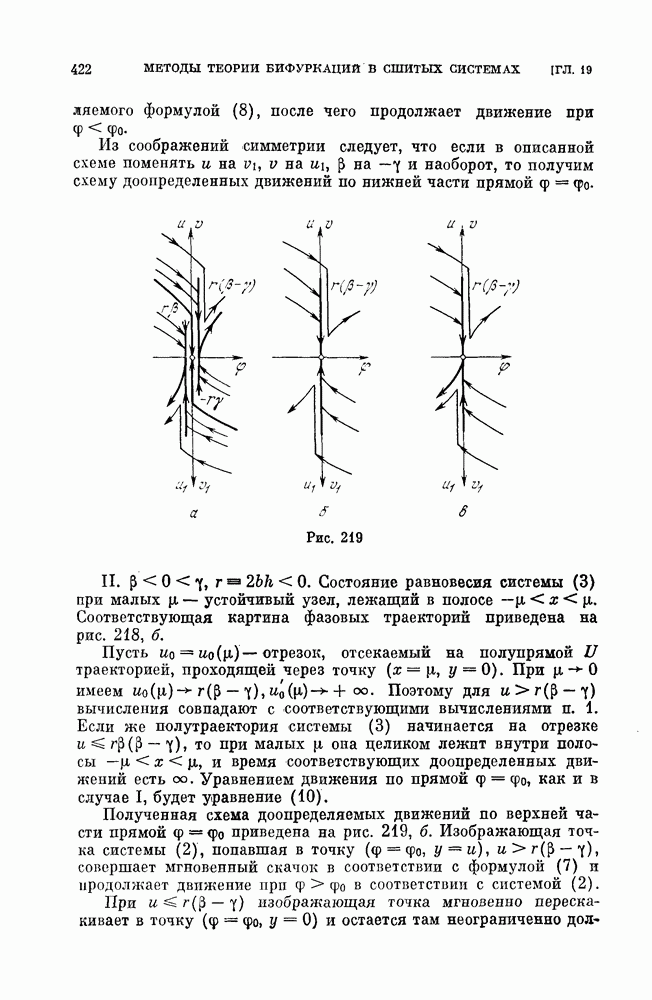
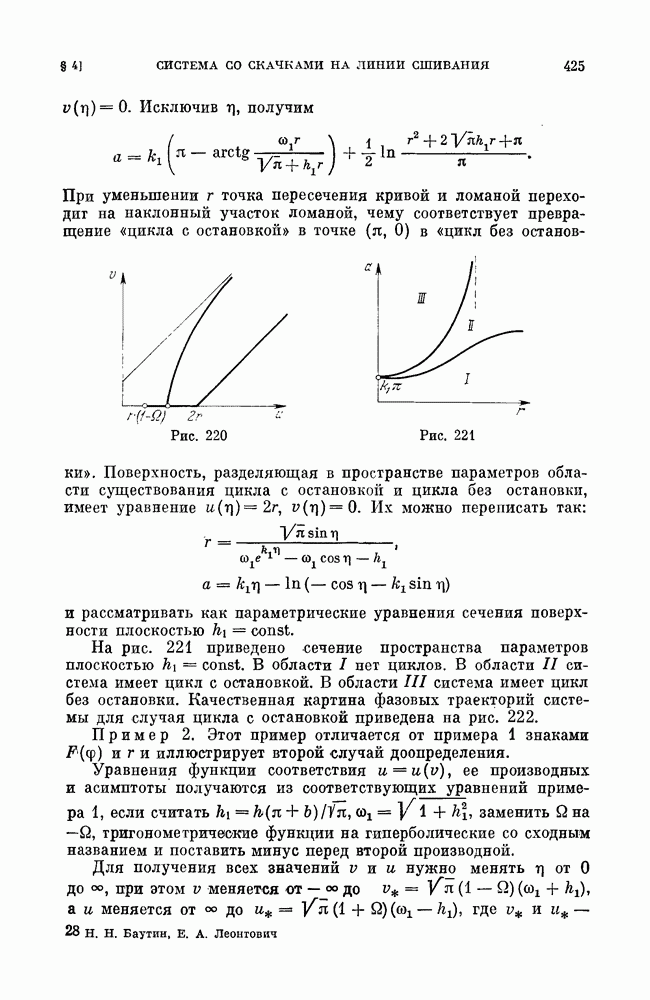
Основная геометрическая интерпретация системы (А) связана не с рассмотрением пространства  рассмотрением плоскости (х,у), которая называется фазовой плоскостью.
рассмотрением плоскости (х,у), которая называется фазовой плоскостью.
В каждой точке области  плоскости
плоскости  (область
(область  может совпадать со всей плоскостью), в которой определены правые части системы (А), рассмотрим вектор
может совпадать со всей плоскостью), в которой определены правые части системы (А), рассмотрим вектор  с компонентами
с компонентами

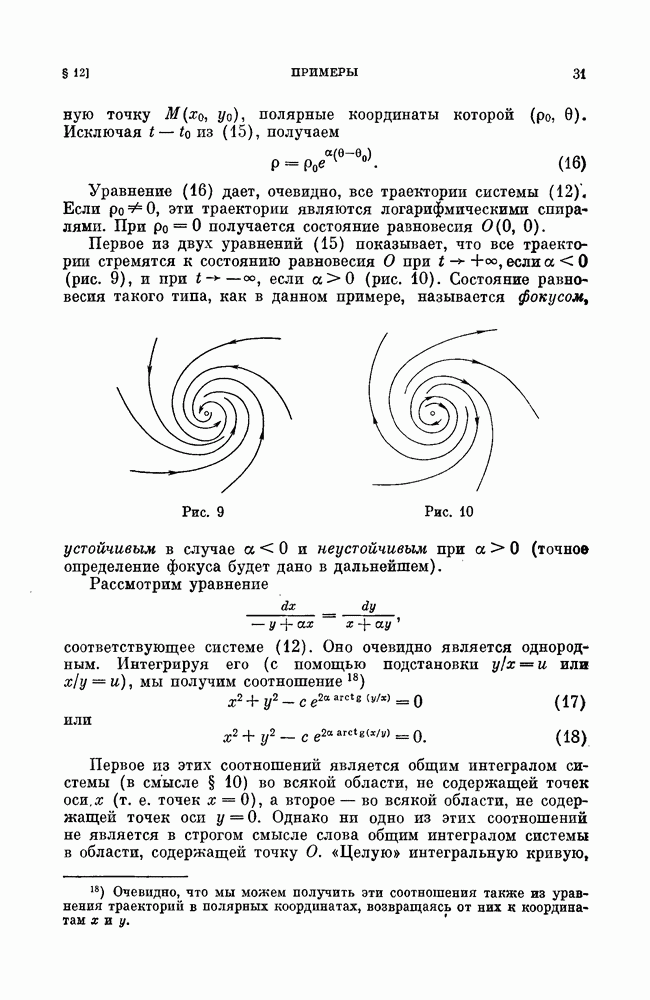
Автономная динамическая система (А) определяет в области  векторное поле. Поэтому система (А) называется также динамической системой на плоскости.
векторное поле. Поэтому система (А) называется также динамической системой на плоскости.
В точках, в которых одновременно

длина вектора обращается в нуль, а направление вектора становится неопределенным. Такие точки называются особыми точками векторного поля или особыми точками системы (А).
Во всякой не особой точке  векторное поле непрерывно в том смысле, что угол между векторами в любых двух достаточно близких к точке
векторное поле непрерывно в том смысле, что угол между векторами в любых двух достаточно близких к точке  точках сколь угодно мал и длины этих векторов сколь угодно мало отличаются друг от друга. Особые точки могут быть точками разрыва векторного поля.
точках сколь угодно мал и длины этих векторов сколь угодно мало отличаются друг от друга. Особые точки могут быть точками разрыва векторного поля.
Пусть

- какое-нибудь решение системы (А).
Множество точек

где  принимает все значения, при которых определено решение (3), называется траекторией, соответствующей данному решению, или траекторией векторного поля, заданного динамической системой (А), а также фазовой траекторией (или просто траекторией данной динамической системы).
принимает все значения, при которых определено решение (3), называется траекторией, соответствующей данному решению, или траекторией векторного поля, заданного динамической системой (А), а также фазовой траекторией (или просто траекторией данной динамической системы).
Уравнения (3) очевидно являются параметрическими уравнениями траектории. Обратно, если дана какая-нибудь траектория, то решение, которому она соответствует, называется решением, соответствующим данной траектории.
В каждой точке  траектории
траектории  не являющейся особой точкой векторного поля, вектор
не являющейся особой точкой векторного поля, вектор  с компонентами
с компонентами  является касательным вектором к траектории
является касательным вектором к траектории 
Пусть  особая точка системы (А), так что
особая точка системы (А), так что

Тогда очевидно, что

есть решение системы (А), и, следовательно, особая точка сама является отдельной траекторией. Такая траектория называется состоянием равновесия.

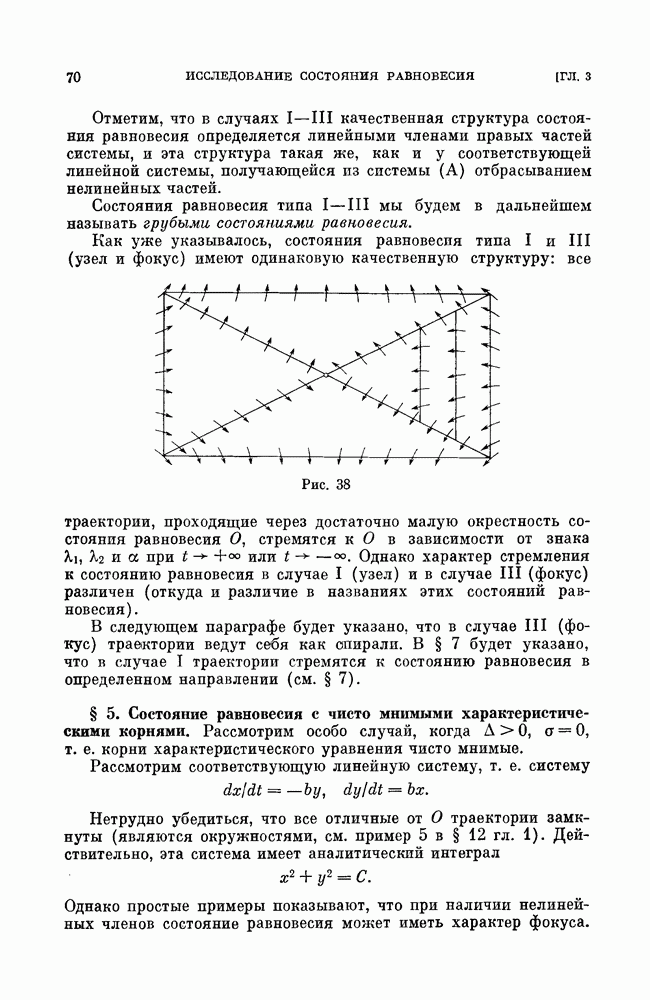
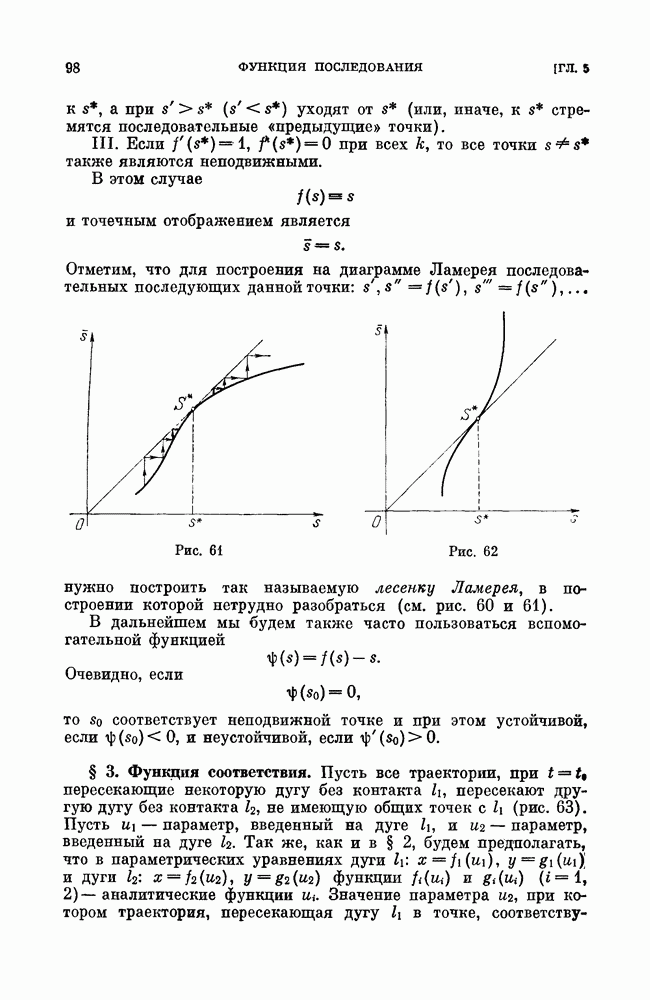
Рис. 1
На траекториях, отличных от состояний равновесия, естественным образом вводится положительное направление движения, именно движение в сторону возрастания  В каждой точке траектории это направление дается соответствующим касательным вектором
В каждой точке траектории это направление дается соответствующим касательным вектором 
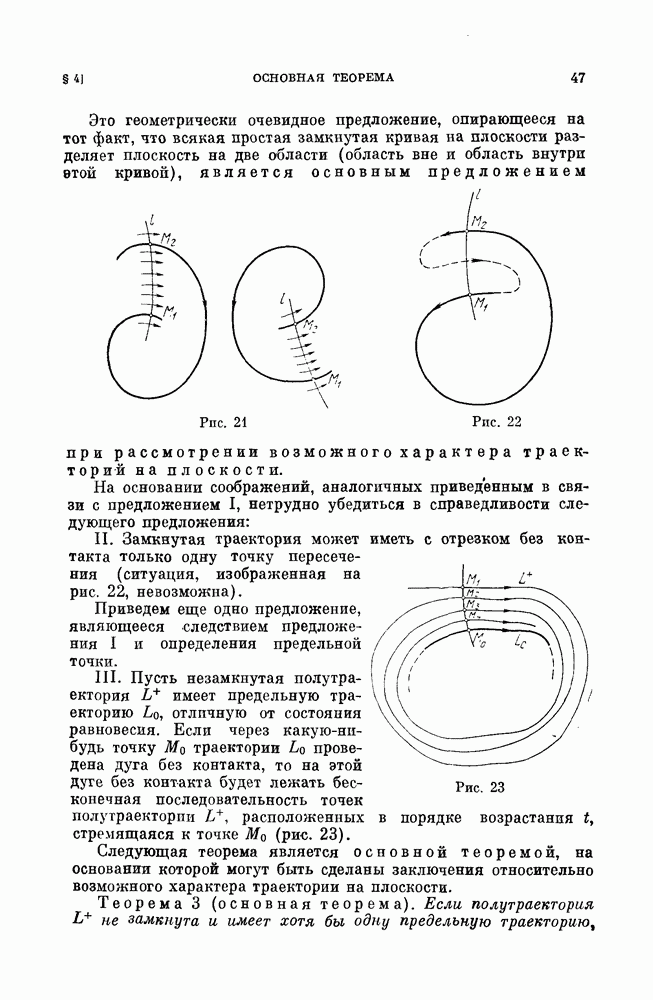
Приведем следующие два основных предложения.
Лемма 1. Пусть траектория  соответствующая решению (3), на интервале
соответствующая решению (3), на интервале  отлична от состояния равновесия, и пусть существуют значения
отлична от состояния равновесия, и пусть существуют значения  такие, что
такие, что

Тогда решение (3) определено при всех значениях  (т. е.
(т. е.  ), функции
), функции  являются периодическими функциями
являются периодическими функциями  а соответствующая траектория — простой гладкой замкнутой кривой.
а соответствующая траектория — простой гладкой замкнутой кривой.
(В силу этого предложения никакая траектория не может «самопересекаться».)
Лемма 2. а) Всяким двум решениям, отличающимся только выбором начального значения  соответствует одна и та же траектория. б) Всякие два различных решения, соответствующие одной и той же траектории, отличаются друг от друга только выбором начального значения
соответствует одна и та же траектория. б) Всякие два различных решения, соответствующие одной и той же траектории, отличаются друг от друга только выбором начального значения 
Замечание. Все решения, соответствующие данной замкнутой траектории, являются периодическими решениями с одним и тем же периодом.
На основании лемм 1 и 2 без труда устанавливается
Теорема 4. Через каждую точку области  (или плоскости) проходит одна и только одна траектория.
(или плоскости) проходит одна и только одна траектория.
Таким образом, задавая в области G (которая может совпадать со всей плоскостью) динамическую систему (А), мы тем самым задаем некоторое семейство траекторий, или, в другой терминологии, разбиение этой области (или плоскости) на траектории.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. АВТОНОМНЫЕ СИСТЕМЫ ВТОРОГО ПОРЯДКА С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- § 1. Автономная динамическая система на плоскости.
- § 2. Теорема существования и единственности решения.
- § 3. Простейшие свойства решений системы (А).
- § 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
- § 5. Сопоставление геометрической интерпретации системы (А) в пространстве (x, y, t) с интерпретацией на фазовой плоскости.
- § 6. Некоторые термины.
- § 7. Теорема о непрерывной зависимости решения от начальных условий.
- § 8. Направление на траекториях. Изменение параметризации.
- § 9. Дифференциальное уравнение, соответствующее динамической системе.
- § 10. Понятие интегральной кривой и интеграла в случае аналитических правых частей Р(х,у) и Q(x,y) системы (А).
- § 11. Что значит «найти решение динамической системы»?
- § 12. Примеры.
- § 13. Замечания по поводу примеров § 12.
- § 14. Математическое определение качественной (топологической) структуры разбиения на траектории и качественного исследования динамической системы.
- ГЛАВА 2. ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ — БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ
- § 2. Цикл без контакта.
- § 3. Предельная точка полутраектории и траектории. Предельная траектория.
- § 4. Основная теорема.
- § 5. Возможные типы полутраекторий и их предельных множеств.
- § 6. Особые и неособые полутраектории и траектории.
- § 7. Возможные типы особых и неособых траекторий.
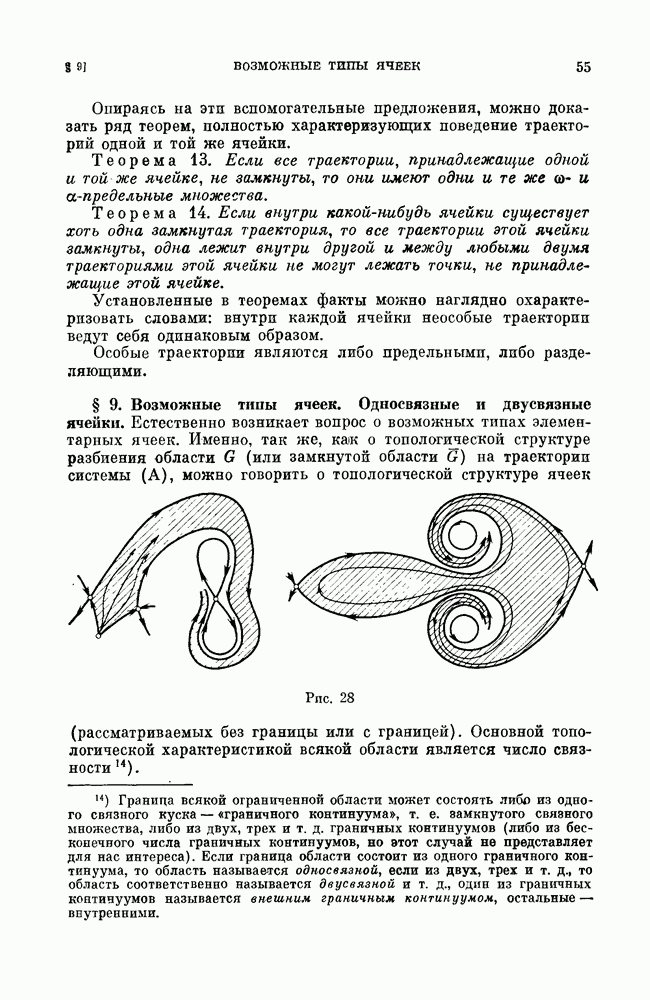
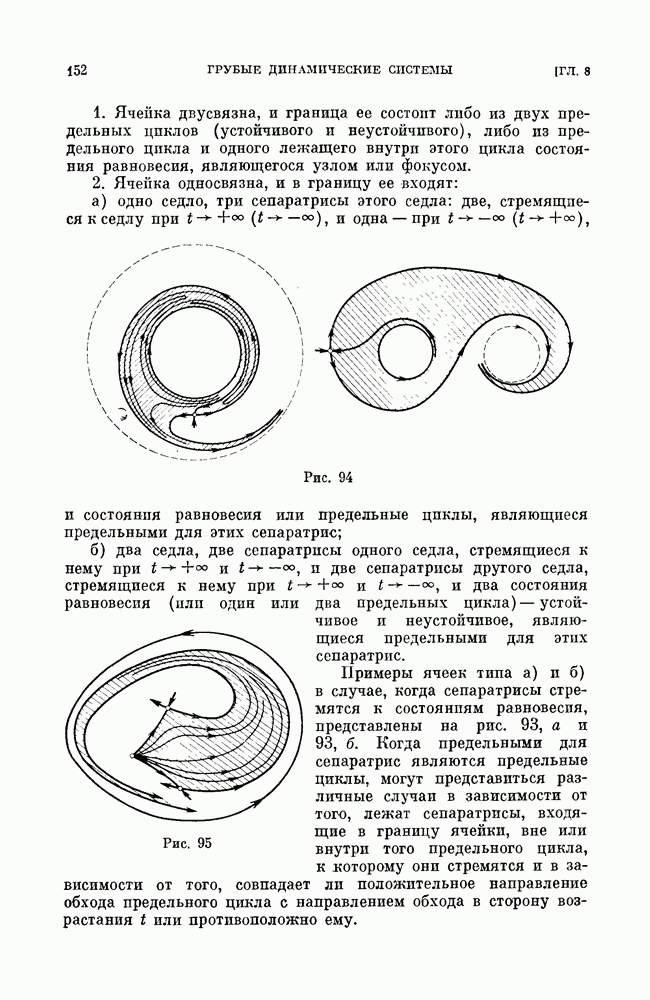
- § 8. Случай конечного числа особых траекторий. Элементарные ячейки.
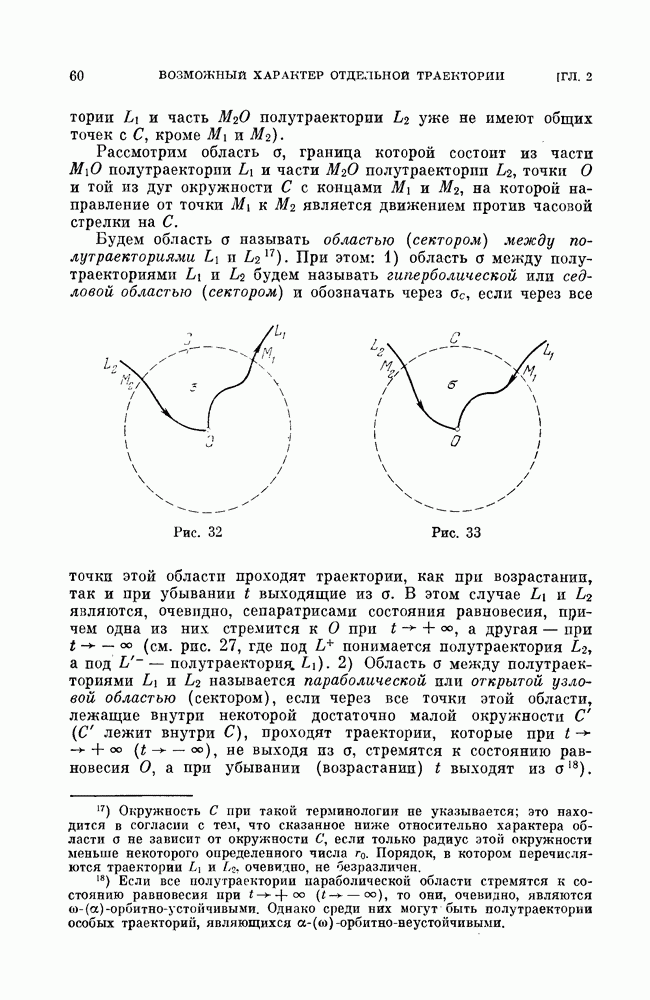
- § 9. Возможные типы ячеек. Односвязные и двусвязные ячейки.
- § 10. Два подхода к описанию качественной структуры.
- § 11. Качественная (топологическая) структура состояния равновесия в случае конечного числа особых траекторий. Схема динамической системы.
- § 12. Устойчивость по Ляпунову.
- ГЛАВА 3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННОЙ СТРУКТУРЫ ОКРЕСТНОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (ОСОБОЙ ТОЧКИ)
- § 2. Приведение динамической системы к каноническому виду.
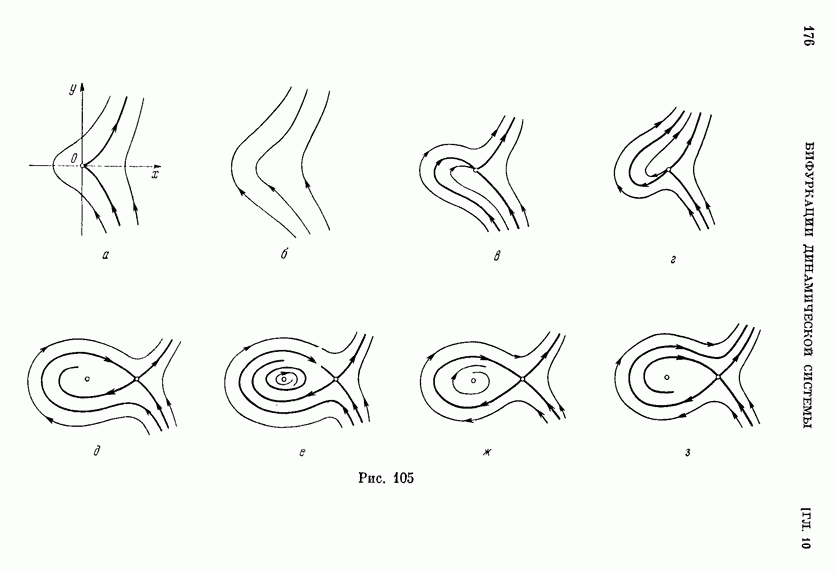
- § 3. Возможный характер простых состояний равновесия.
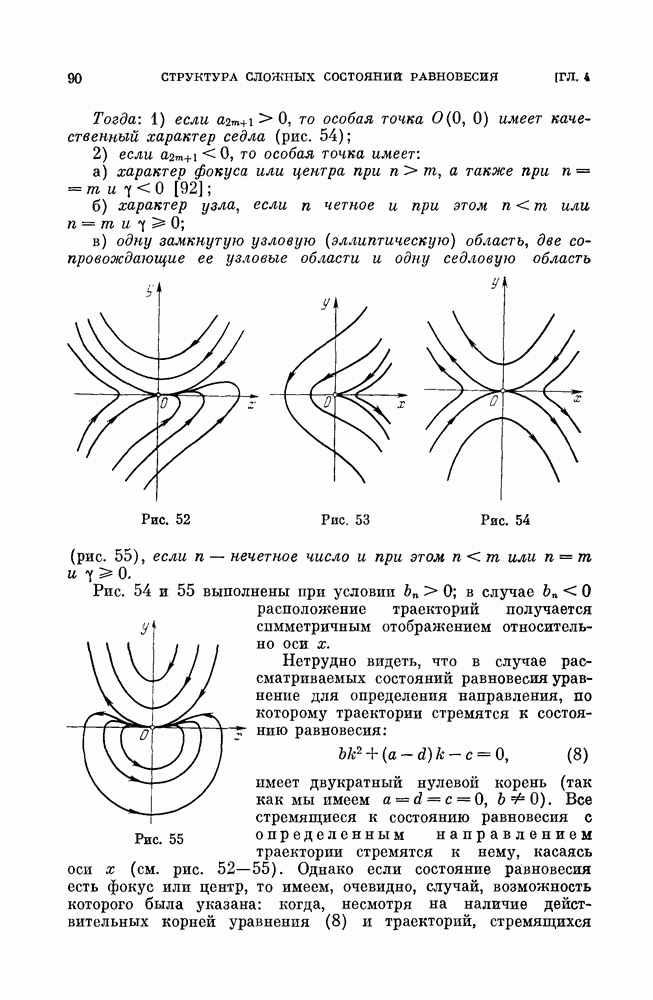
- § 4. Замечания о методах установления характера грубых состояний равновесия.
- § 5. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 6. Направления, в которых траектории стремятся к простым состояниям равновесия.
- § 7. Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия.
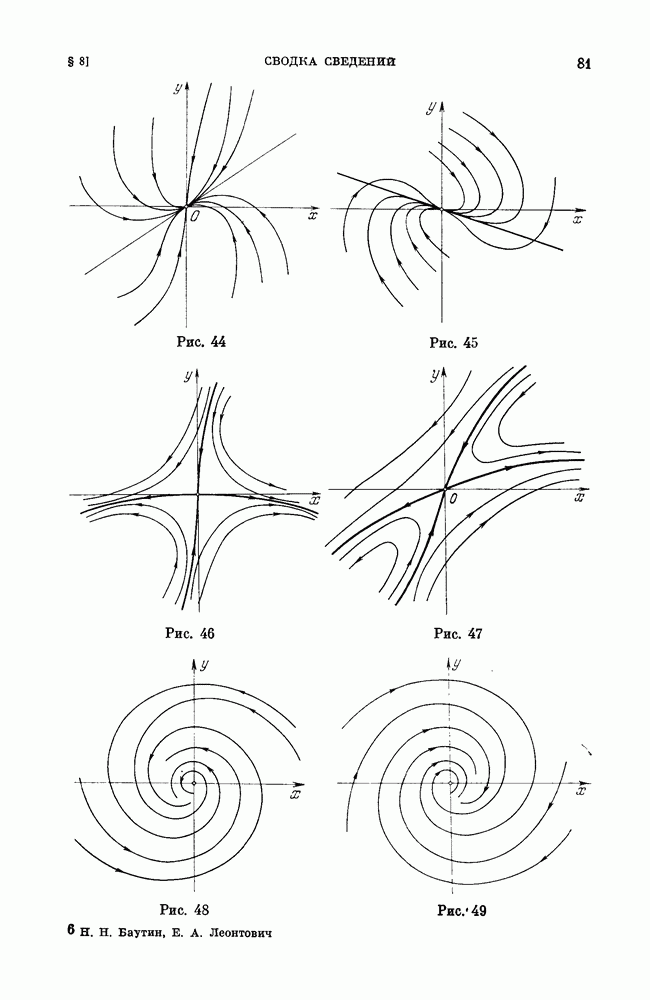
- § 8. Сводка сведений о грубых состояниях равновесия.
- ГЛАВА 4. КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ
- § 1. Направления, в которых траектории стремятся к сложному состоянию равновесия.
- § 2. Сложное состояние равновесия (особая точка) с нулевыми характеристическими корнями.
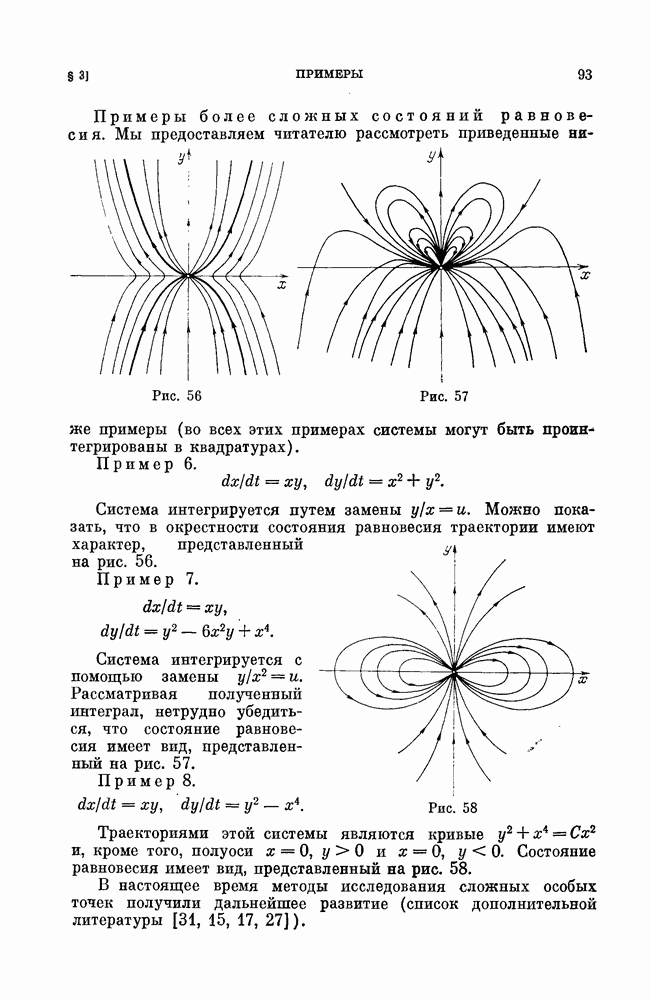
- § 3. Примеры.
- § 4. Нормальные формы.
- ГЛАВА 5. ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ
- § 2. Условия устойчивости и неустойчивости неподвижной точки точечного отображения.
- § 3. Функция соответствия.
- § 4. Изучение окрестности замкнутой траектории. Простые и сложные предельные циклы.
- § 5. Аналитические выражения для коэффициентов функции последования. Характеристический показатель замкнутой траектории.
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЕМЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
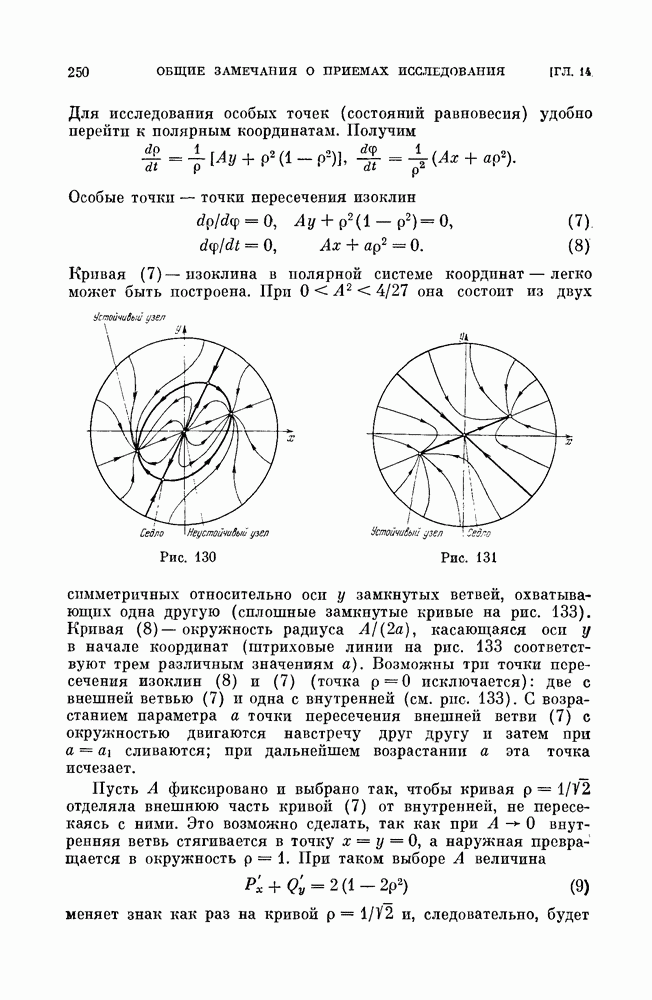
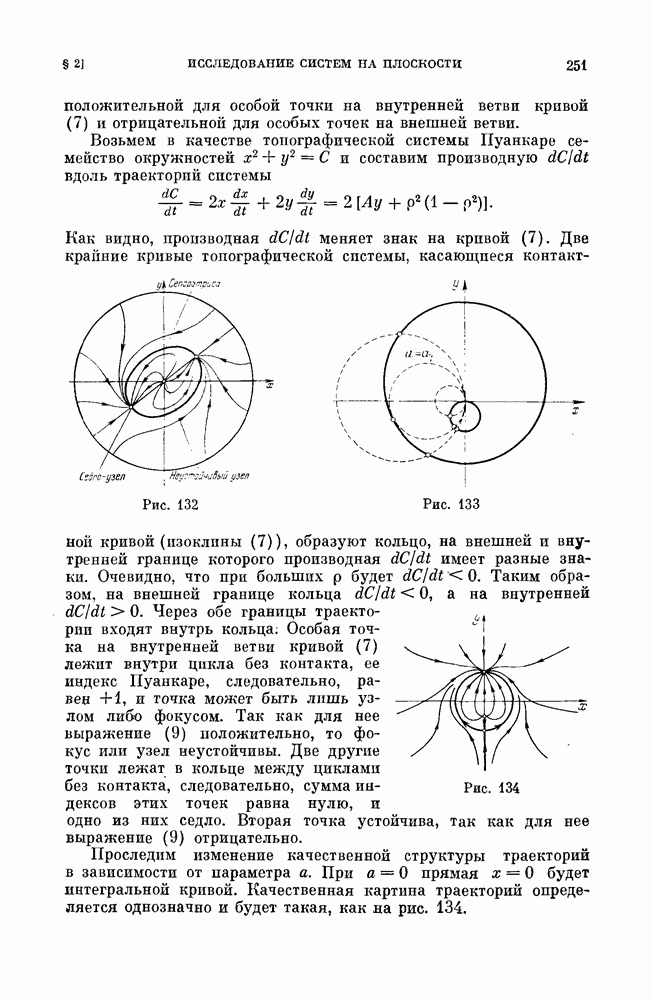
- § 2. Изучение поведения интегральных кривых в бесконечности. Сфера Пуанкаре.
- § 3. Примеры исследования в бесконечности [93].
- § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов.
- 1. Некоторые видоизменения критериев Бендиксона и Дюлака.
- 2. Индексы Пуанкаре. Распределение особых точек [77, 117].
- 3. Условия сосуществования замкнутых траекторий и особых точек.
- 4. Две общие теоремы Пуанкаре.
- § 5. Топографическая система Пуанкаре. Функция Ляпунова. Кривые контактов.
- ЧАСТЬ II. ТЕОРИЯ БИФУРКАЦИЙ
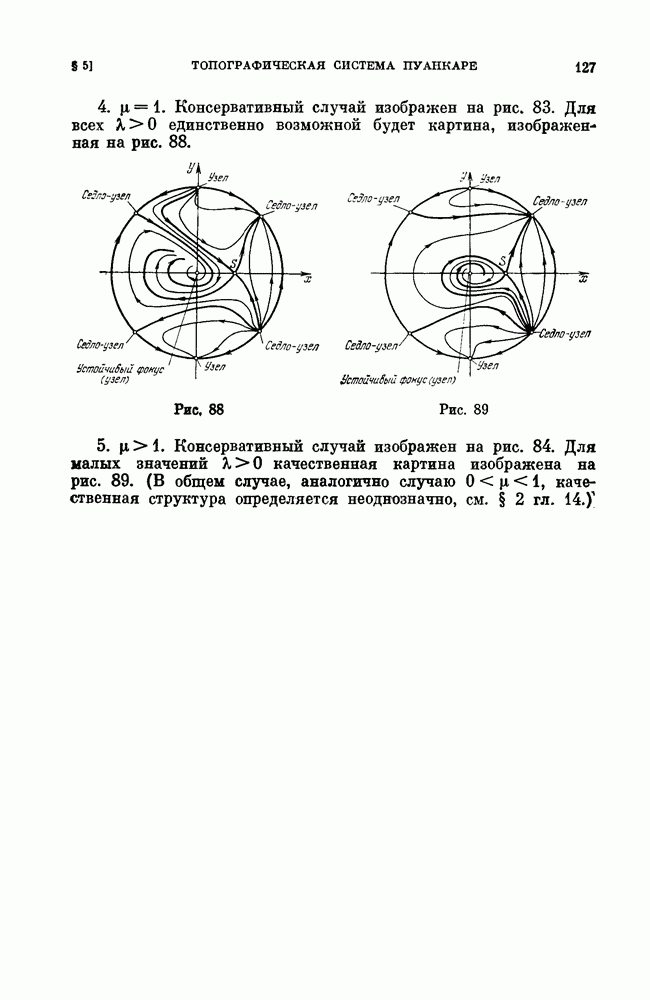
- § 1. Свойства консервативных систем на плоскости [2, 3].
- § 2. Динамические системы, характерные для теории колебаний.
- § 3. Измененные системы. Системы, правые части которых зависят от параметра.
- § 4. Основные теоремы о зависимости решения от изменения правых частей динамической системы.
- § 5. Грубость динамической системы и теоремы о непрерывной зависимости решения от изменения правых частей.
- ГЛАВА 8. ГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
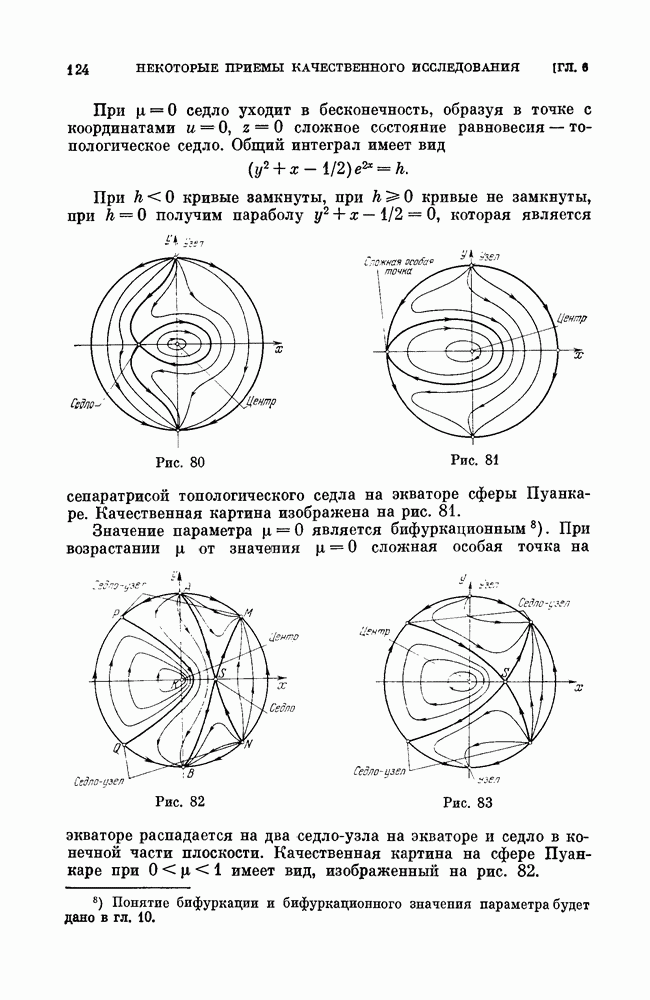
- § 2. Состояния равновесия, возможные в грубой динамической системе.
- § 3. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 4. Замкнутые траектории, возможные в грубой системе.
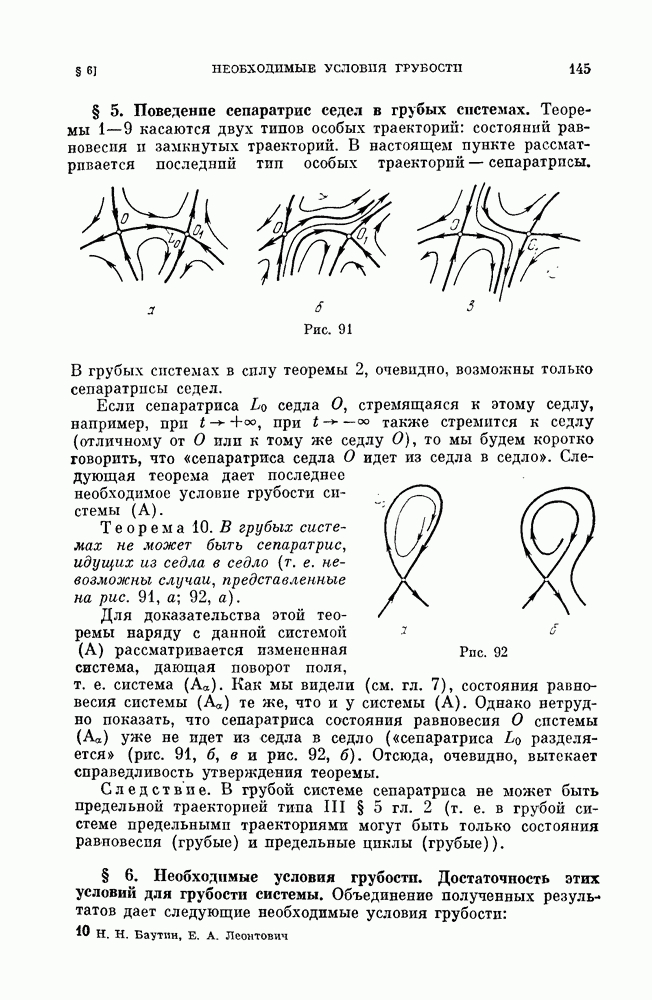
- § 5. Поведение сепаратрис седел в грубых системах.
- § 6. Необходимые условия грубости. Достаточность этих условий для грубости системы.
- § 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем.
- § 8. Понятие грубости при более общих предположениях относительно правых частей динамической системы.
- § 9. Типы особых траекторий и ячеек в грубых системах.
- § 10. Замечания по поводу определения грубой системы.
- ГЛАВА 9. ПРОСТЕЙШИЕ НЕГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ — СИСТЕМЫ ПЕРВОЙ СТЕПЕНИ НЕГРУБОСТИ
- § 2. Системы первой степени негрубости.
- § 3. Состояния равновесия, возможные в системе первой степени негрубости.
- § 4. Замкнутые траектории, возможные в системе первой степени негрубости.
- § 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости.
- § 6. Необходимые и достаточные условия первой степени негрубости.
- § 7. Динамические системы более высокой степени негрубости.
- ГЛАВА 10. БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
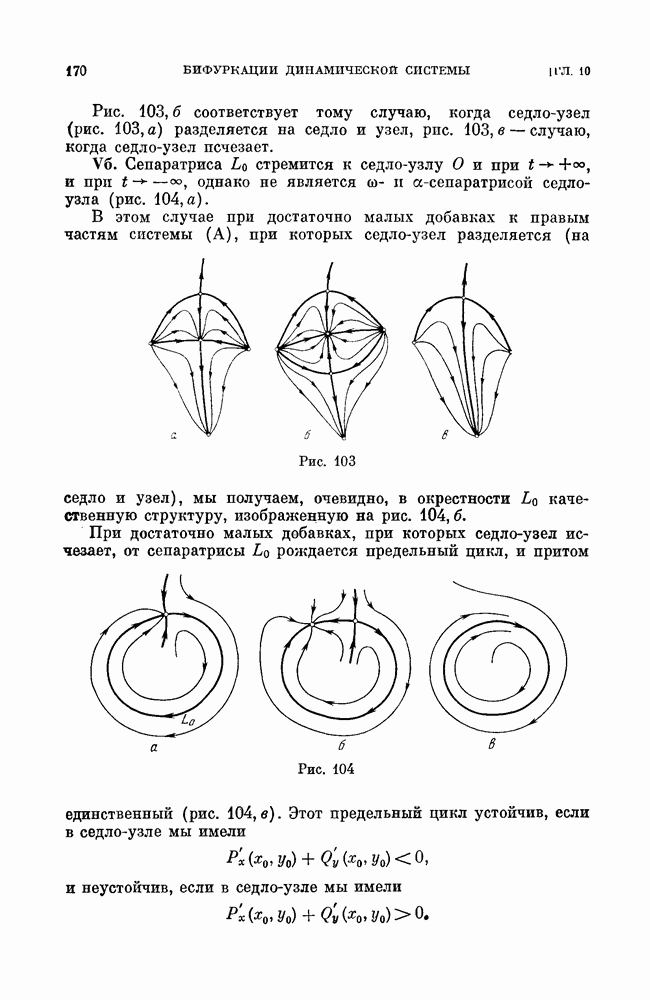
- § 1. Определение бифуркации.
- § 2. Бифуркации систем первой степени негрубости.
- § 3. Бифуркации некоторых типов сложных особых точек.
- § 4. Бифуркации двукратной точки, для которой …
- § 5. Рождение предельных циклов из особых траекторий степени негрубости выше первой.
- ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
- § 1. Возможный характер зависимости правых частей динамической системы от параметров.
- § 2. Смена качественных структур при изменении параметров.
- § 3. Случай, когда правые части зависят более чем от одного параметра.
- § 4. Бифуркации «от бесконечности».
- § 5. Условия существования седло-узла и сложного фокуса первого порядка.
- § 6. Поворот векторного поля.
- § 7. Метод малого параметра. Метод Понтрягина.
- ГЛАВА 12. ДИНАМИЧЕСКИЕ СИСТЕМЫ С ЦИЛИНДРИЧЕСКОЙ ФАЗОВОЙ ПОВЕРХНОСТЬЮ
- § 1. Цилиндрическая фазовая поверхность и характер траекторий, возможных на цилиндрической фазовой поверхности.
- § 2. Замкнутые траектории, охватывающие цилиндр.
- § 3. Приемы исследования качественной структуры динамической системы на цилиндре.
- § 4. Понятие грубости и степени негрубости для динамических систем на цилиндре. Бифуркации на цилиндре. Поворот поля.
- § 5. Динамические системы на цилиндре, близкие к гамильтоновым (метод Понтрягина).
- ГЛАВА 13. АДЕКВАТНОЕ ИСТОЛКОВАНИЕ НЕЛИНЕЙНЫХ ФИЗИЧЕСКИХ ЯВЛЕНИЙ ФАКТАМИ КАЧЕСТВЕННОЙ ТЕОРИИ И ТЕОРИИ БИФУРКАЦИЙ ДИНАМИЧЕСКИХ СИСТЕМ
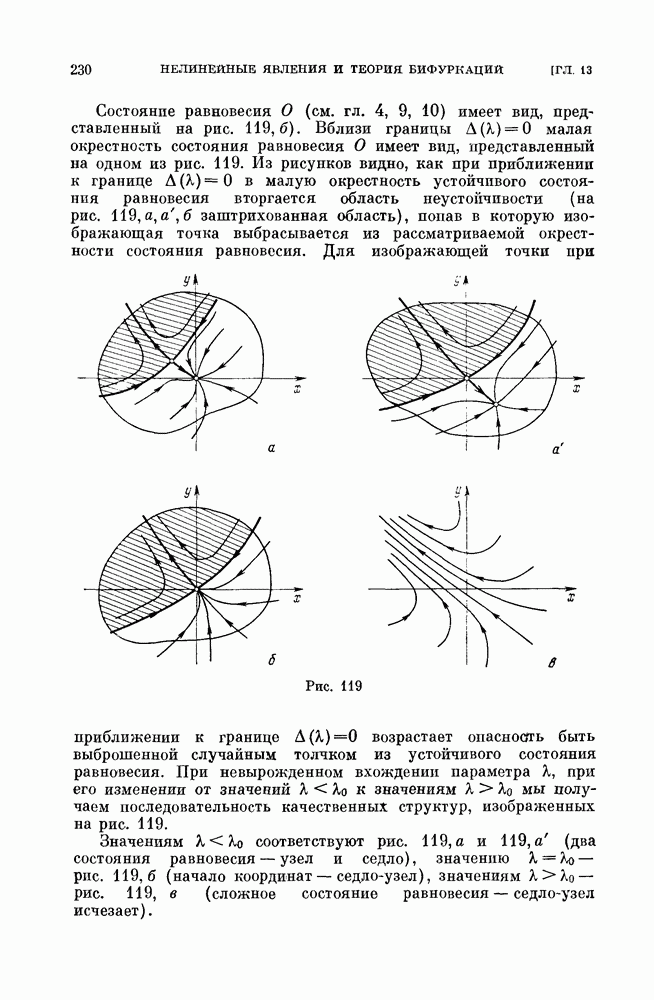
- § 1. Мягкий и жесткий режимы.
- § 2. Замечания о границах области устойчивости различных стационарных режимов.
- § 3. Мягкое и жесткое возникновение колебаний.
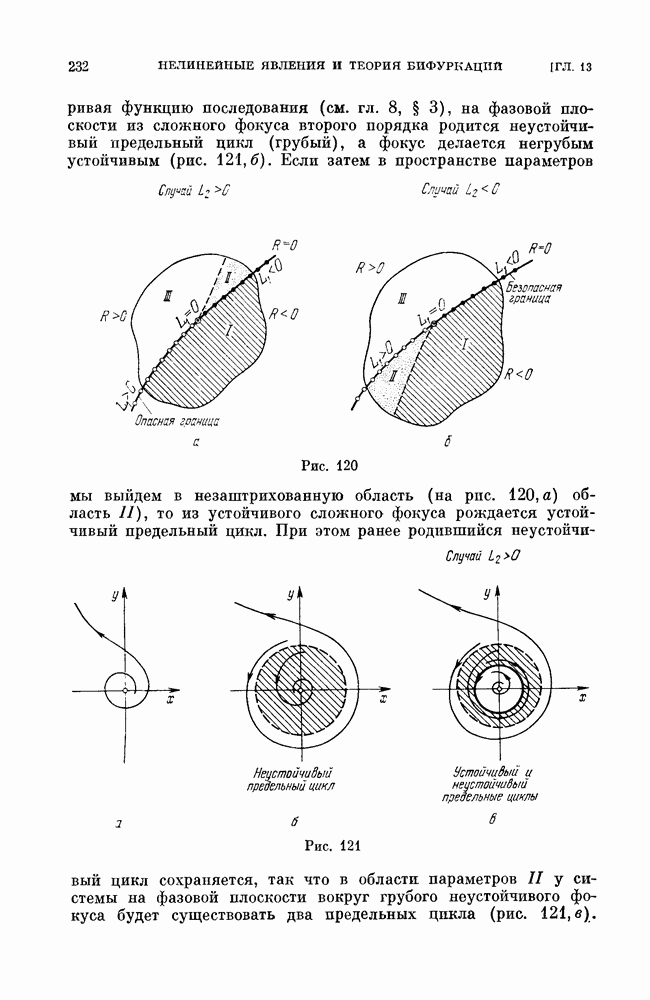
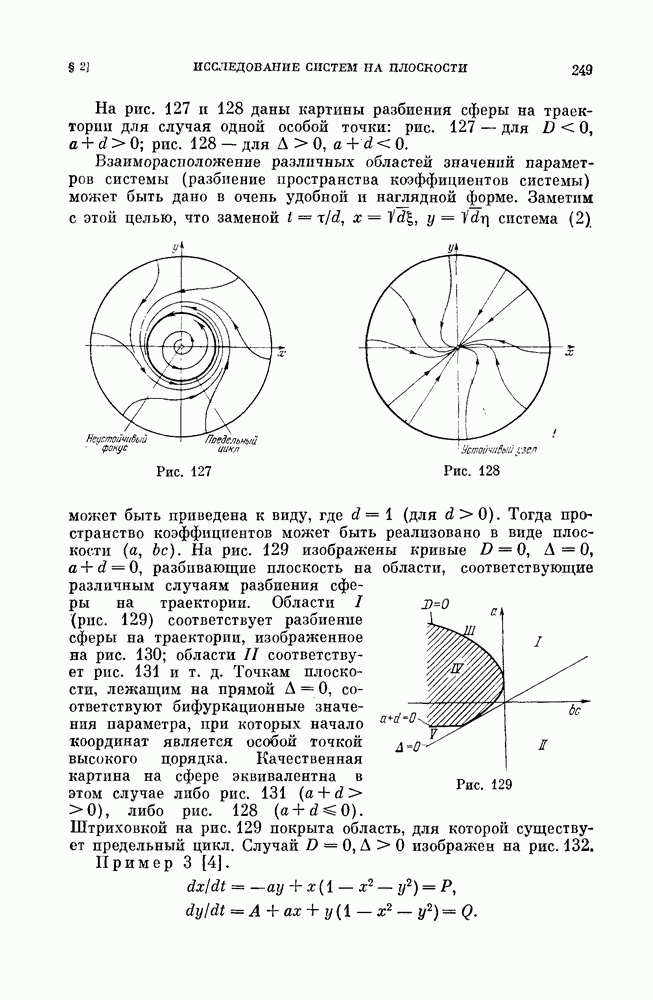
- § 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
- § 5. Замечания по поводу других границ области устойчивости.
- ЧАСТЬ III. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- ГЛАВА 14. ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 1. Некоторые рецептурные указания.
- § 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
- § 3. Некоторые простые примеры динамических систем на цилиндре.
- ГЛАВА 15. ИССЛЕДОВАНИЕ МЕТОДОМ МАЛОГО ПАРАМЕТРА (МЕТОДОМ ПОНТРЯГИНА)
- § 2. Примеры рассмотрения методом Понтрягина (полное исследование).
- § 3. Исследование методом Понтрягина с привлечением вычислительных методов.
- ГЛАВА 16. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ
- § 2. Электрическая цепь с туннельным диодом.
- § 3. Двумерная модель динамики твердотельного лазера [119].
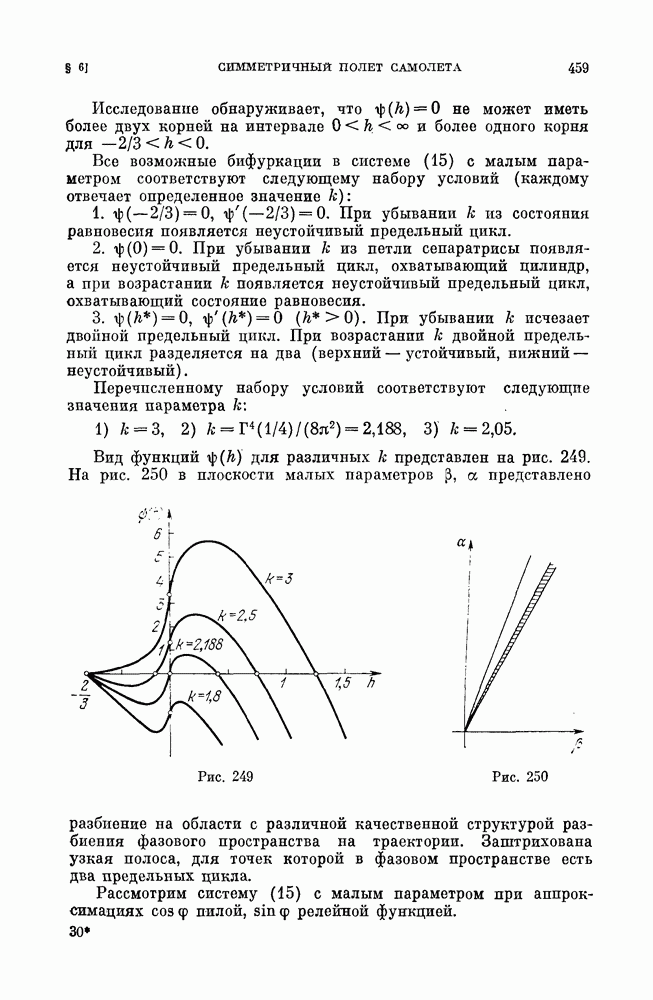
- § 4. Симметричный полет самолета в вертикальной плоскости (задача Н. Е. Жуковского).
- § 5. Система, описывающая динамику проточного химического реактора.
- § 6. Фазовая автоподстройка частоты.
- § 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов).
- § 8. Синхронный генератор с асинхронной характеристикой.
- ЧАСТЬ IV. КУСОЧНО-СШИТЫЕ СИСТЕМЫ
- ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ
- § 1. Сшитые системы. Доопределение на линиях сшивания.
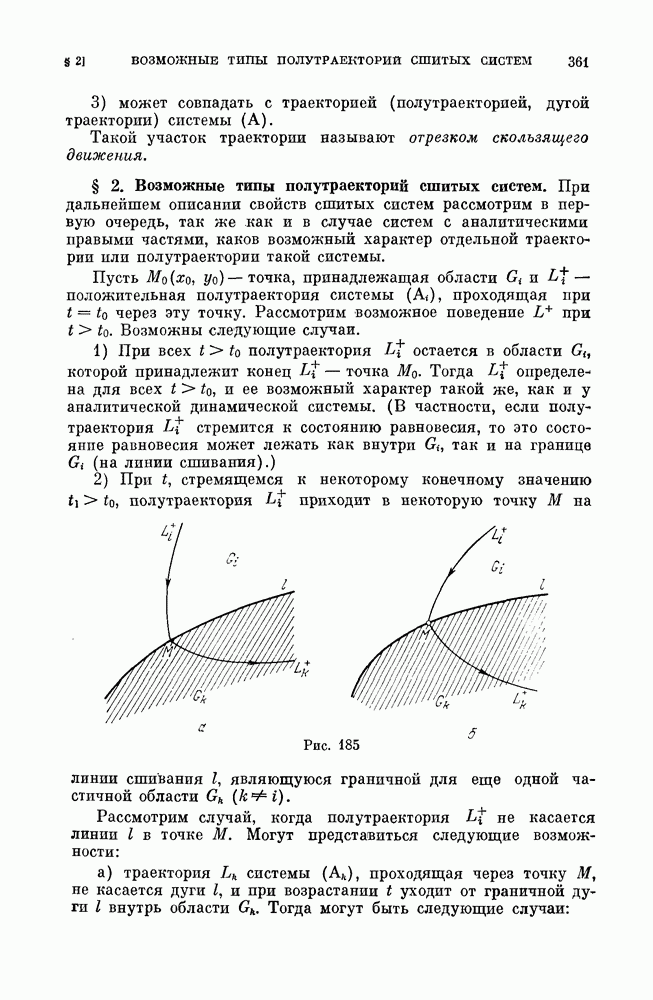
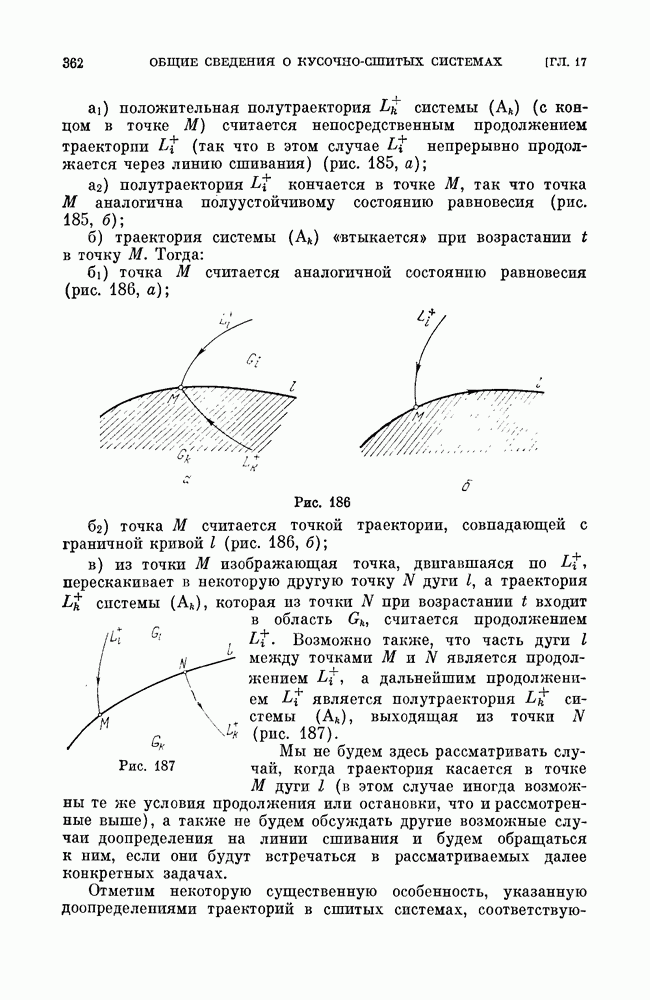
- § 2. Возможные типы полутраекторий сшитых систем.
- § 3. Особые траектории сшитых систем.
- § 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
- ГЛАВА 18. ИССЛЕДОВАНИЕ КУСОЧНО-СШИТЫХ СИСТЕМ МЕТОДОМ ПОНТРЯГИНА
- § 2. Автоподстройка при кусочно-постоянной аппроксимации характеристики.
- § 3. Автоколебания синхронного мотора.
- ГЛАВА 19. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ
- § 2. Следящая система с люфтом.
- § 3. Электрическая цепь с туннельным диодом.
- § 4. Система со скачками на линии сшивания.
- ГЛАВА 20. ОБ АППРОКСИМАЦИЯХ И ГРУБОСТИ ПРОСТРАНСТВА ПАРАМЕТРОВ [39, 41, 42]
- § 1. Рассмотрение системы (2) при аппроксимациях пилообразными функциями.
- § 2. Рассмотрение системы (2) при аппроксимации, включающей отрезок параболы.
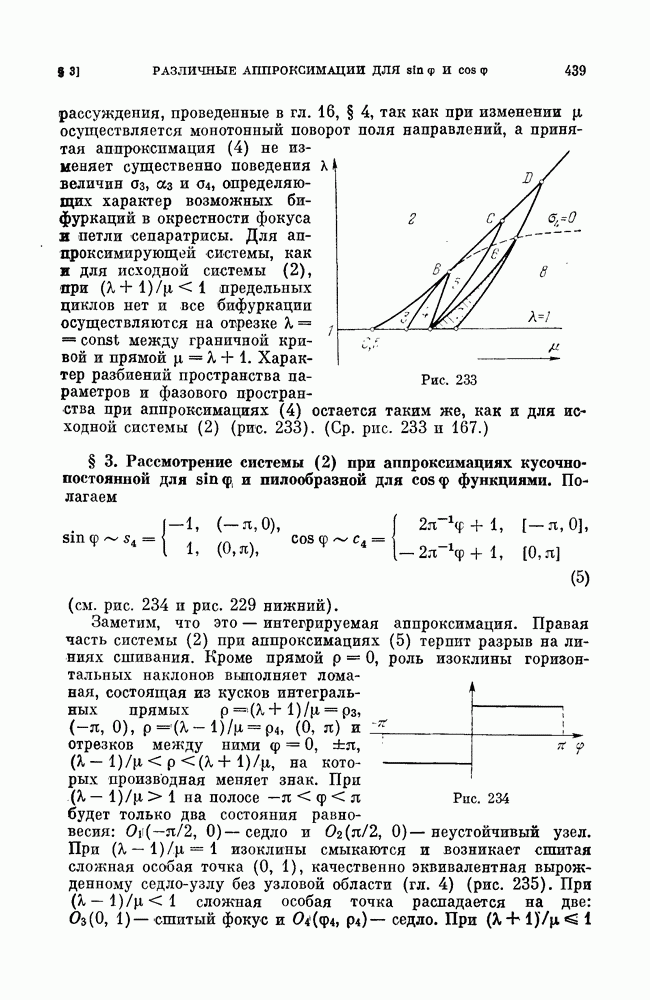
- § 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin f, и пилообразной для cos f функциями.
- § 4. Исследование роли аппроксимаций для уравнения маятникового типа.
- § 5. Динамическая система, описывающая автоколебания синхронного мотора.
- § 6. Динамическая система, описывающая симметричный полет самолета.
- ДОПОЛНЕНИЕ
- § 1. Динамическое системы на двумерных поверхностях.
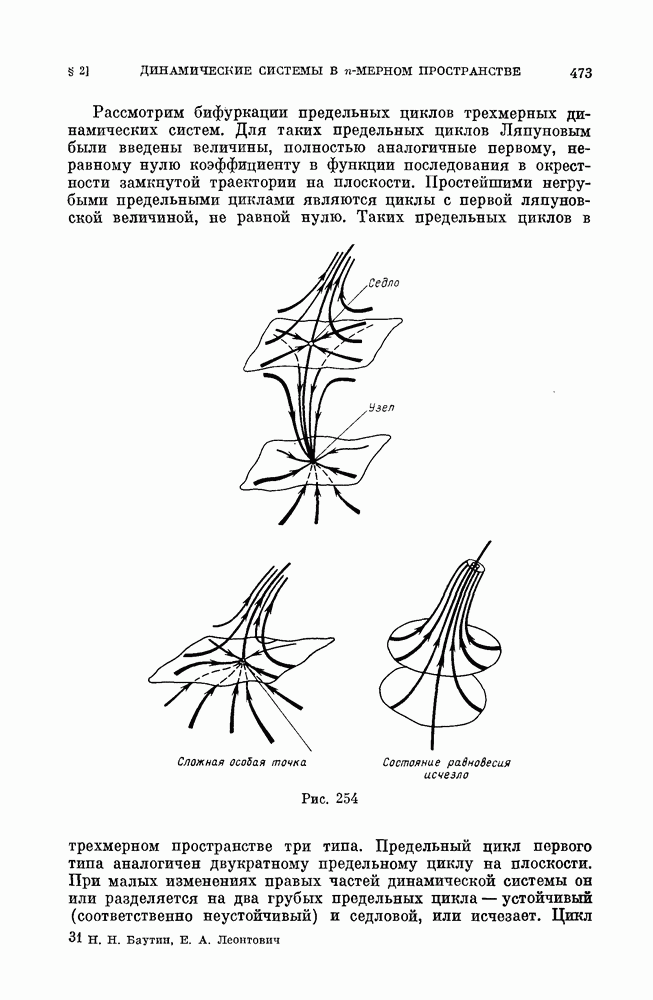
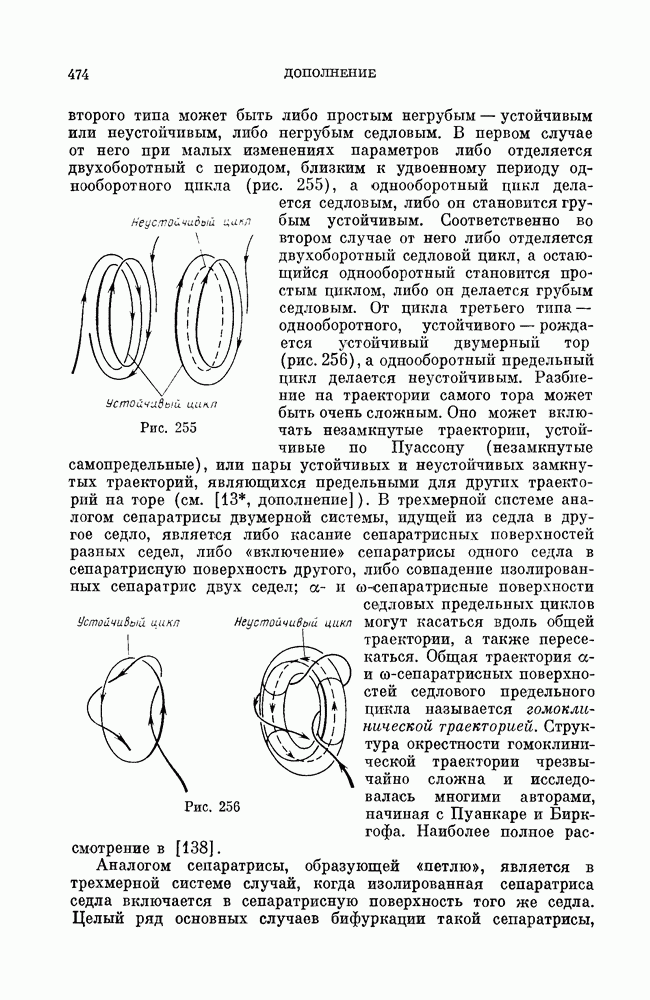
- § 2. Динамические системы в n-мерном евклидовом пространстве.
- СПИСОК ЛИТЕРАТУРЫ