| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 12. Примеры.
В настоящем параграфе мы приведем ряд простых примеров, на которых проиллюстрируем материал предыдущих параграфов. Эти примеры в силу их простоты одновременно являются примерами полного качественного исследования динамической системы. Во всех приведенных примерах динамические системы определены на всей плоскости.
Пример 1.

Траектории — прямые, параллельные оси х

Состояний равновесия, очевидно, нет: все траектории (совпадающие с интегральными кривыми) являются целыми траекториями. Пример 2.

Состояний равновесия нет, траектории не являются целыми траекториями ввиду того, что точки на этих траекториях уходят в бесконечность при  стремящемся к конечному значению. Именно,
стремящемся к конечному значению. Именно,

Пример 3.

где  имеют одинаковые знаки.
имеют одинаковые знаки.
На плоскости  (т. е. на фазовой плоскости системы
(т. е. на фазовой плоскости системы  эта система задает векторное поле, примерно изображенное на рис. 5, а при
эта система задает векторное поле, примерно изображенное на рис. 5, а при  и на рис. 5, б при
и на рис. 5, б при  Прямые на этом рисунке являются изоклинами.
Прямые на этом рисунке являются изоклинами.

Рис. 5
Система (8), очевидно, имеет единственное состояние равновесия  Решая систему (8) как линейную с постоянными коэффициентами, легко видеть, что решение, соответствующее начальным значениям
Решая систему (8) как линейную с постоянными коэффициентами, легко видеть, что решение, соответствующее начальным значениям  имеет вид
имеет вид

Очевидно, что в согласии с леммой 3 это решение является функцией 
Траектории системы (8) проще всего получить, исключая  в уравнениях (9), т. е. переходя к декартовым координатам.
в уравнениях (9), т. е. переходя к декартовым координатам.
Мы получаем

Полагая при  мы получим параболы
мы получим параболы

а при  (когда выражение
(когда выражение  может не иметь смысла)
может не иметь смысла)  При
При  мы получаем
мы получаем 
Перейдем от системы (8) к одному уравнению, например, записанному в виде  или в виде
или в виде

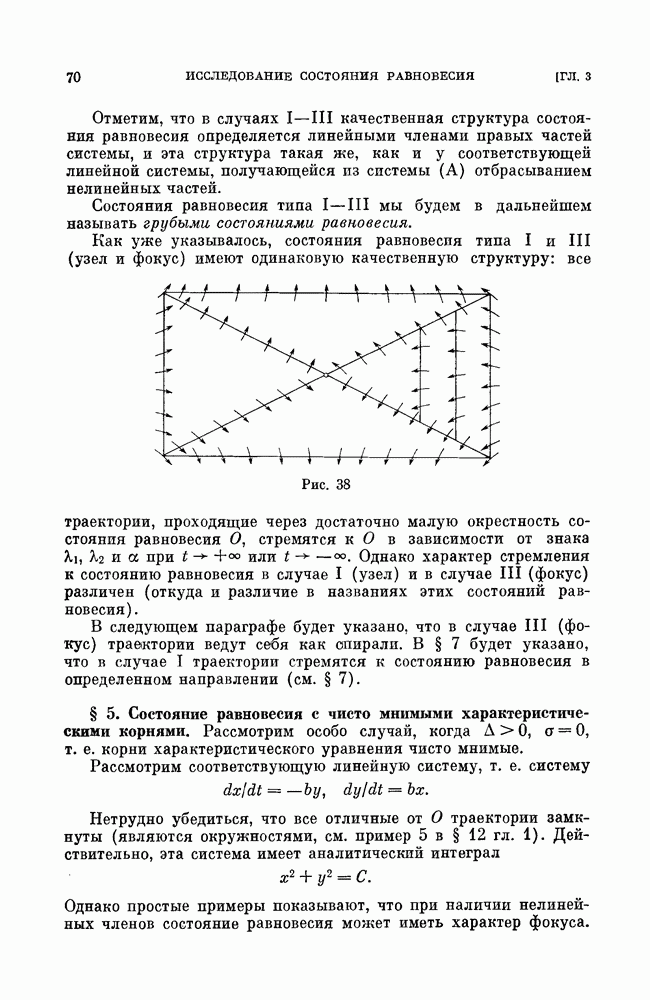
Как было указано, уравнение (11) задает поле линейных элементов, и оно представлено на рис. 6. Если проинтегрировать уравнение (11), то в качестве интегральных кривых в смысле § 10 мы получим параболы (10) и две оси координат.

Рис. 6
Траекториями системы (8) являются те части (половины) парабол (10) и координатных осей  на которые эти кривые разбиваются состоянием равновесия
на которые эти кривые разбиваются состоянием равновесия  Из соотношений (9) видно, что если
Из соотношений (9) видно, что если  то точка на любой отличной от нуля траектории стремится к состоянию равновесия О при
то точка на любой отличной от нуля траектории стремится к состоянию равновесия О при  а если
а если  то при
то при  Напомним (см. § 5), что когда изображающая точка, двигаясь по отличной от состояния равновесия траектории
Напомним (см. § 5), что когда изображающая точка, двигаясь по отличной от состояния равновесия траектории  стремится к некоторому состоянию равновесия
стремится к некоторому состоянию равновесия  то при этом всегда
то при этом всегда 
Таким образом, разбиение на траектории, определенное системой (8) (с указанными на траекториях направлениями), имеет
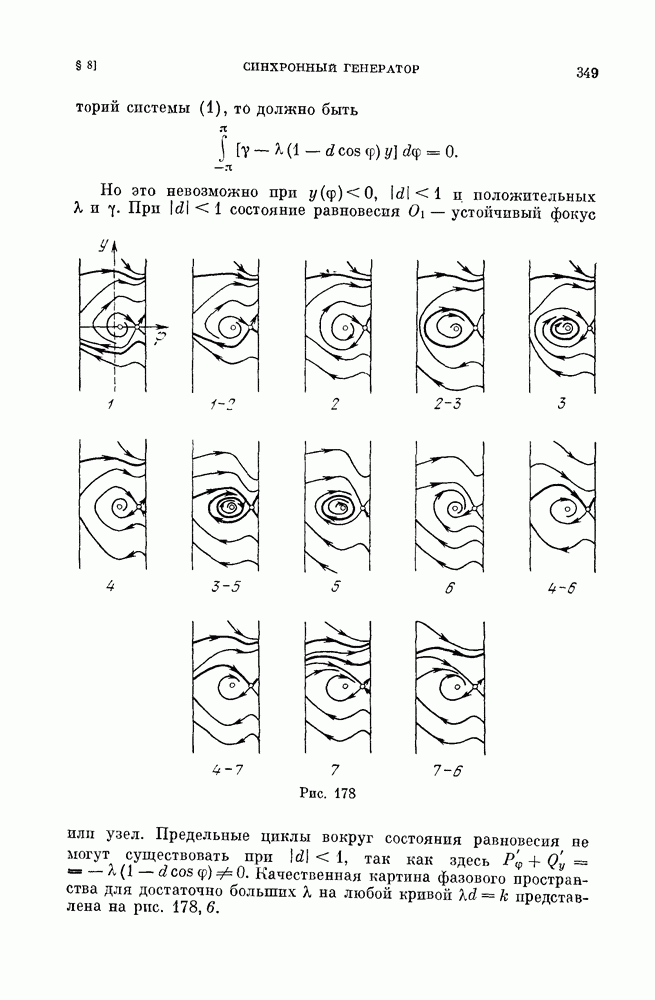
вид, указанный на рис. 7. Состояние равновесия такого типа называется узлом, устойчивым в случае  и неустойчивым в случае
и неустойчивым в случае 
Рассмотрим еще интерпретацию решений системы (8), т. е. интегральные кривые системы (8) в трехмерном пространстве 

Рис. 7
Из формул (9) следует, что интегральными кривыми системы (8) в пространстве  являются:
являются:
1) ось  т. е.
т. е.  (эти уравнения получаются из уравнений (9) при
(эти уравнения получаются из уравнений (9) при  ; она проектируется в состояние равновесия О фазовой плоскости;
; она проектируется в состояние равновесия О фазовой плоскости;
2) показательные кривые

расположенные в координатных полуплоскостях  или
или  и асимптотически стремящиеся к оси
и асимптотически стремящиеся к оси  при
при  если
если  и при
и при  если
если  эти кривые проектируются в положительную и отрицательную полуоси абсцисс, являющиеся траекториями системы;
эти кривые проектируются в положительную и отрицательную полуоси абсцисс, являющиеся траекториями системы;
3) показательные кривые

аналогичные кривым типа 2);
4) кривые

расположенные на параболических цилиндрах  с образующими, параллельными оси
с образующими, параллельными оси  Ось
Ось  разбивает каждый такой цилиндр на две «половины»; каждая интегральная кривая типа 4) лежит целиком в одной половине цилиндра и асимптотически стремится к оси
разбивает каждый такой цилиндр на две «половины»; каждая интегральная кривая типа 4) лежит целиком в одной половине цилиндра и асимптотически стремится к оси  при
при  если
если  и при
и при  если
если  Интегральные кривые типа 4) получаются друг из друга сдвигом вдоль оси
Интегральные кривые типа 4) получаются друг из друга сдвигом вдоль оси  То же справедливо для интегральных кривых типа 2) или 3).
То же справедливо для интегральных кривых типа 2) или 3).
Пример 4.

(а — отличная от нуля постоянная).
Векторное поле, определенное этой системой (при  изображено на рис. 8.
изображено на рис. 8.

Рис. 8
Решая систему (12) как линейную систему с постоянными коэффициентами, мы получим решение, соответствующее начальным значениям  к в следующем виде (оно, очевидно, является функцией
к в следующем виде (оно, очевидно, является функцией  в согласии с
в согласии с  § 3):
§ 3):

Характер траекторий рассматриваемой системы удобнее исследовать, переходя к полярным координатам. Мы получим после элементарных вычислений

Решение этой системы

является, очевидно, уравнением в полярных координатах траектории системы (12), проходящей при  через такую
через такую
начальную точку  полярные координаты которой
полярные координаты которой  Исключая
Исключая  из (15), получаем
из (15), получаем

Уравнение (16) дает, очевидно, все траектории системы (12). Если  эти траектории являются логарифмическими спиралями. При
эти траектории являются логарифмическими спиралями. При  получается состояние равновесия
получается состояние равновесия 
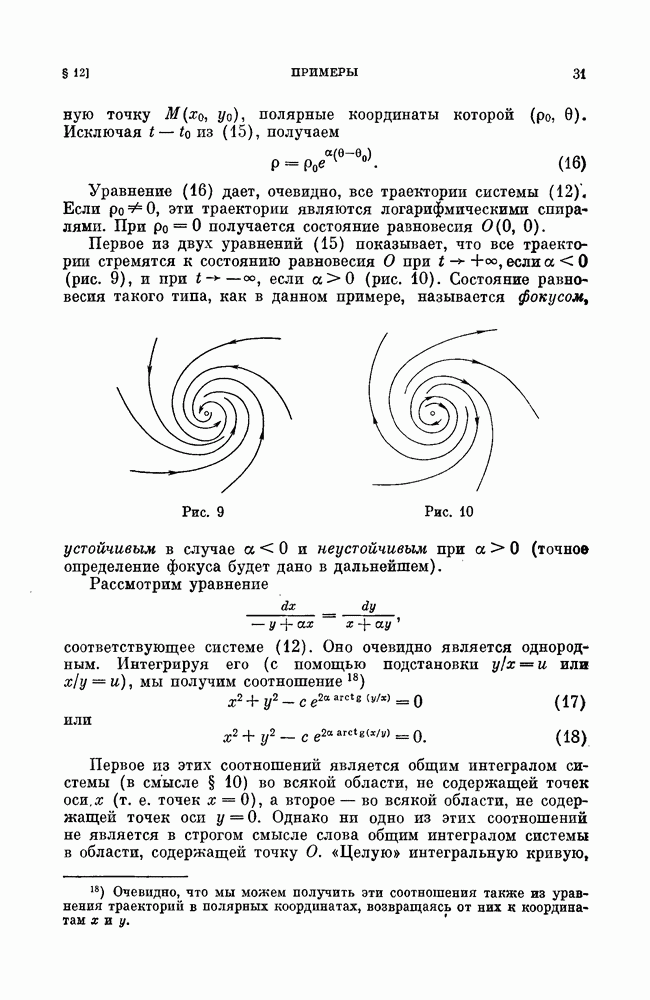
Первое из двух уравнений (15) показывает, что все траектории стремятся к состоянию равновесия О при  если
если  (рис. 9), и при
(рис. 9), и при  если
если  (рис. 10). Состояние равновесия такого типа, как в данном примере, называется фокусом, устойчивым в случае
(рис. 10). Состояние равновесия такого типа, как в данном примере, называется фокусом, устойчивым в случае  и неустойчивым при
и неустойчивым при  (точное определение фокуса будет дано в дальнейшем).
(точное определение фокуса будет дано в дальнейшем).

Рис. 9

Рис. 10
Рассмотрим уравнение

соответствующее системе (12). Оно очевидно является однородным. Интегрируя его (с помощью подстановки  или
или  мы получим соотношение
мы получим соотношение

или

Первое из этих соотношений является общим интегралом системы (в смысле § 10) во всякой области, не содержащей точек  (т. е. точек
(т. е. точек  а второе — во всякой области, не содержащей точек оси
а второе — во всякой области, не содержащей точек оси  Однако ни одно из этих соотношений не является в строгом смысле слова общим интегралом системы в области, содержащей точку О. «Целую» интегральную кривую,
Однако ни одно из этих соотношений не является в строгом смысле слова общим интегралом системы в области, содержащей точку О. «Целую» интегральную кривую,
расположенную в такой области, можно получить, «склеивая» куски кривых (17) и (18).
Рассмотрим интерпретацию в трехмерном пространстве. Как и в предыдущем примере, ось  является интегральной кривой системы (12) в пространстве
является интегральной кривой системы (12) в пространстве  Остальные интегральные кривые расположены на цилиндрических поверхностях, имеющих своими направляющими спирали (16), а образующими — прямые, параллельные оси
Остальные интегральные кривые расположены на цилиндрических поверхностях, имеющих своими направляющими спирали (16), а образующими — прямые, параллельные оси  Эти интегральные кривые асимптотически приближаются к оси
Эти интегральные кривые асимптотически приближаются к оси  при
при  если
если  и при
и при  если
если 

Рис. 11
Отметим, что хотя формы траекторий в примерах 3 и 4 при  соответственно) существенно отличаются, но в некотором смысле поведение траекторий в том и в другом случаях одинаково: именно, в обоих примерах все отличные от состояния равновесия траектории при
соответственно) существенно отличаются, но в некотором смысле поведение траекторий в том и в другом случаях одинаково: именно, в обоих примерах все отличные от состояния равновесия траектории при  стремятся к состоянию равновесия. Пример 5.
стремятся к состоянию равновесия. Пример 5.

Эта система получается как частный случай системы (12) при  Решения, соответствующие начальным значениям
Решения, соответствующие начальным значениям  имеют вид
имеют вид

Непосредственной проверкой (или используя  нетрудно убедиться, что
нетрудно убедиться, что

является общим аналитическим интегралом системы. Таким образом, в этом случае система имеет аналитический интеграл.
Траекториями системы, очевидно, являются состояние равновесия  и замкнутые траектории — концентрические окружности с центром в начале (рис. 11). Решения (20), соответствующие замкнутым траекториям — окружностям, являются периодическими функциями с периодом
и замкнутые траектории — концентрические окружности с центром в начале (рис. 11). Решения (20), соответствующие замкнутым траекториям — окружностям, являются периодическими функциями с периодом 
Интегральными кривыми в трехмерном пространстве  являются ось
являются ось  и винтовые линии, расположенные на круглых цилиндрах с направляющими (21). Шаг каждой винтовой линии равен
и винтовые линии, расположенные на круглых цилиндрах с направляющими (21). Шаг каждой винтовой линии равен 
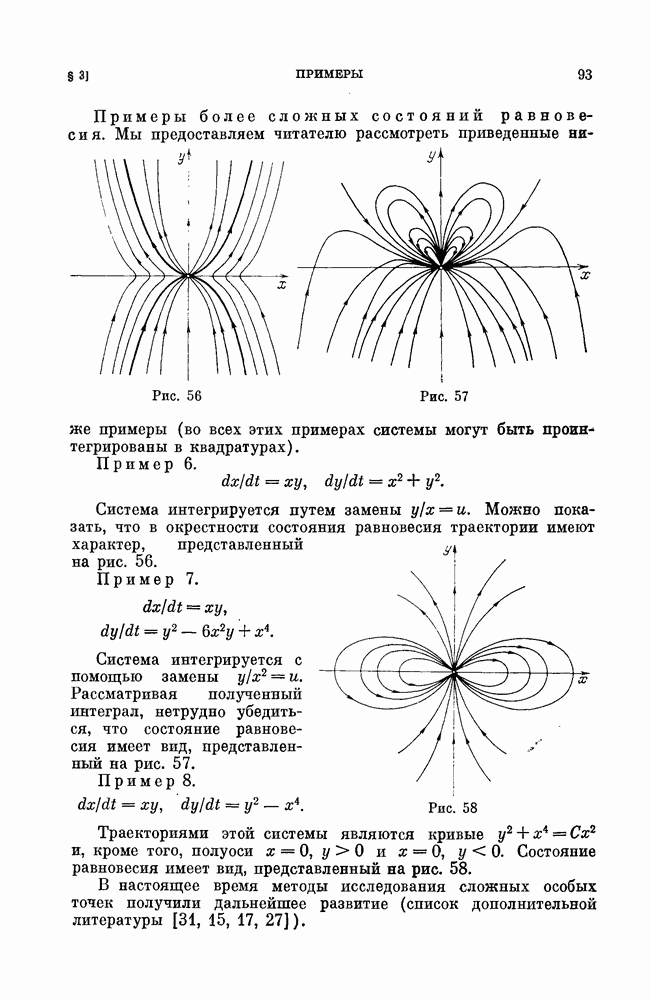
Пример 6.

Векторное поле изображено на рис. 12. Решение системы, соответствующее начальным значениям  имеет вид
имеет вид

Точка  состояние равновесия.
состояние равновесия.
Система имеет аналитический интеграл

Интегральными кривыми являются при  гиперболы (24) и при
гиперболы (24) и при  координатные оси
координатные оси  Каждая гипербола состоит из двух траекторий (ее Еетвей), и каждая из координатных осей — из трех траекторий (состояния равновесия О и двух полуосей).
Каждая гипербола состоит из двух траекторий (ее Еетвей), и каждая из координатных осей — из трех траекторий (состояния равновесия О и двух полуосей).

Рис. 12

Рис. 13
Соответствующее разбиение на траектории указано на рис. 13.
Из выражений (23) очевидно, что траектории, являющиеся полупрямыми оси  (получающиеся из (23) при
(получающиеся из (23) при  стремятся к состоянию равновесия при
стремятся к состоянию равновесия при  а траектории, являющиеся полупрямыми оси
а траектории, являющиеся полупрямыми оси  при
при  Других траекторий, стремящихся к состоянию равновесия О, система не имеет.
Других траекторий, стремящихся к состоянию равновесия О, система не имеет.
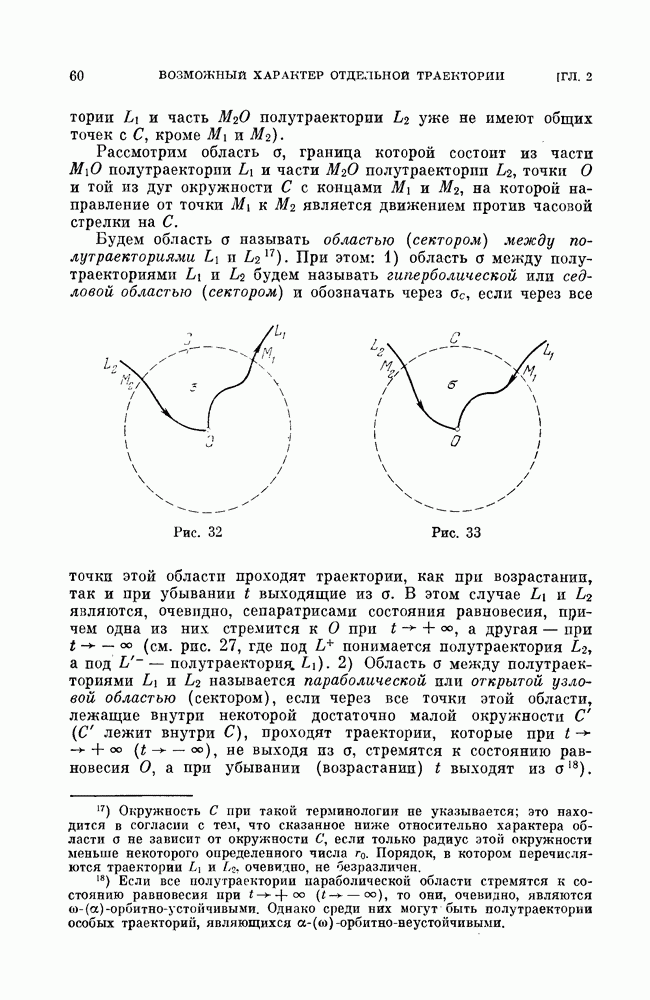
Состояние равновесия такого типа, как у данной системы, называется седлом: Траектории, стремящиеся к седлу О, в данном случае четыре полуоси  называются сепаратрисами седла.
называются сепаратрисами седла.
Траектории, сколь угодно близкие к точке сепаратрисы, стремящейся к О при  при неограниченном возрастании (убывании)
при неограниченном возрастании (убывании)  удаляются от этой сепаратрисы. Обратим внимание на то, что такое поведение траекторий, очевидно, ни в какой мере не противоречит теореме 5 § 7 (о непрерывной зависимости от начальных условий), так как эта теорема рассматривает поведение близких траекторий только на Кои очном
удаляются от этой сепаратрисы. Обратим внимание на то, что такое поведение траекторий, очевидно, ни в какой мере не противоречит теореме 5 § 7 (о непрерывной зависимости от начальных условий), так как эта теорема рассматривает поведение близких траекторий только на Кои очном
промежутке значений  Нетрудно убедиться в том, что если взять за исходную траекторию сепаратрису, то для любого конечного промежутка значений
Нетрудно убедиться в том, что если взять за исходную траекторию сепаратрису, то для любого конечного промежутка значений  теорема о непрерывной зависимости от начальных условий, очевидно, выполняется. Но при увеличении рассматриваемого промежутка величину
теорема о непрерывной зависимости от начальных условий, очевидно, выполняется. Но при увеличении рассматриваемого промежутка величину  (теоремы 5 § 7) нужно брать все меньше и меньше.
(теоремы 5 § 7) нужно брать все меньше и меньше.
Рассмотрение интегральных крпвых системы (22) в пространстве  аналогично приведенному в предыдущих примерах, и мы его опускаем.
аналогично приведенному в предыдущих примерах, и мы его опускаем.
Пример 7.

Полагая  или
или  найдем
найдем

Интегрируя последнее уравнение, получим

Это — уравнение траекторий в полярных координатах. При этом  очевидно, является решением (27), соответствующим
очевидно, является решением (27), соответствующим  т. е. траекторией. Траектории, проходящей через точку
т. е. траекторией. Траектории, проходящей через точку  соответствует значение
соответствует значение  Если
Если  то
то  при
при  при
при  (Очевидно, при этом
(Очевидно, при этом  изменяется в интервале
изменяется в интервале  Если
Если  то
то  Тогда
Тогда  при
при  при
при  Отсюда следует, что траектории системы имеют вид, указанный на рис. 14. Второе из уравнений (26) показывает, что если траектория проходит через точку
Отсюда следует, что траектории системы имеют вид, указанный на рис. 14. Второе из уравнений (26) показывает, что если траектория проходит через точку  при
при  то
то  Состояние равновесия
Состояние равновесия  так же как в случае линейной системы (12) примера 4, является фокусом, причем неустойчивым.
так же как в случае линейной системы (12) примера 4, является фокусом, причем неустойчивым.

Рис. 14
Траектория  т. е.
т. е.  (в отличие от того, что было в примере 6), не окружена замкнутыми траекториями. Она
(в отличие от того, что было в примере 6), не окружена замкнутыми траекториями. Она
является изолированной замкнутой траекторией, и все траектории, проходящие через точки достаточно малой ее окрестности, стремятся к ней при  Такая замкнутая траектория называется предельным циклом.
Такая замкнутая траектория называется предельным циклом.
Несколько более сложные примеры, исследующиеся в основном непосредственным интегрированием, см. в [12].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. АВТОНОМНЫЕ СИСТЕМЫ ВТОРОГО ПОРЯДКА С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- § 1. Автономная динамическая система на плоскости.
- § 2. Теорема существования и единственности решения.
- § 3. Простейшие свойства решений системы (А).
- § 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
- § 5. Сопоставление геометрической интерпретации системы (А) в пространстве (x, y, t) с интерпретацией на фазовой плоскости.
- § 6. Некоторые термины.
- § 7. Теорема о непрерывной зависимости решения от начальных условий.
- § 8. Направление на траекториях. Изменение параметризации.
- § 9. Дифференциальное уравнение, соответствующее динамической системе.
- § 10. Понятие интегральной кривой и интеграла в случае аналитических правых частей Р(х,у) и Q(x,y) системы (А).
- § 11. Что значит «найти решение динамической системы»?
- § 12. Примеры.
- § 13. Замечания по поводу примеров § 12.
- § 14. Математическое определение качественной (топологической) структуры разбиения на траектории и качественного исследования динамической системы.
- ГЛАВА 2. ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ — БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ
- § 2. Цикл без контакта.
- § 3. Предельная точка полутраектории и траектории. Предельная траектория.
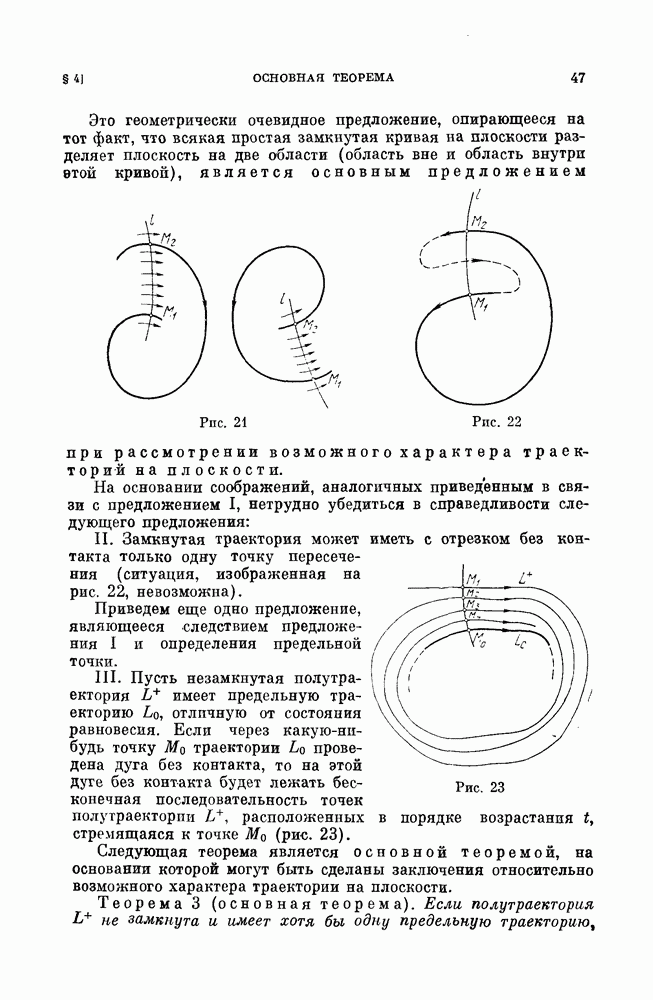
- § 4. Основная теорема.
- § 5. Возможные типы полутраекторий и их предельных множеств.
- § 6. Особые и неособые полутраектории и траектории.
- § 7. Возможные типы особых и неособых траекторий.
- § 8. Случай конечного числа особых траекторий. Элементарные ячейки.
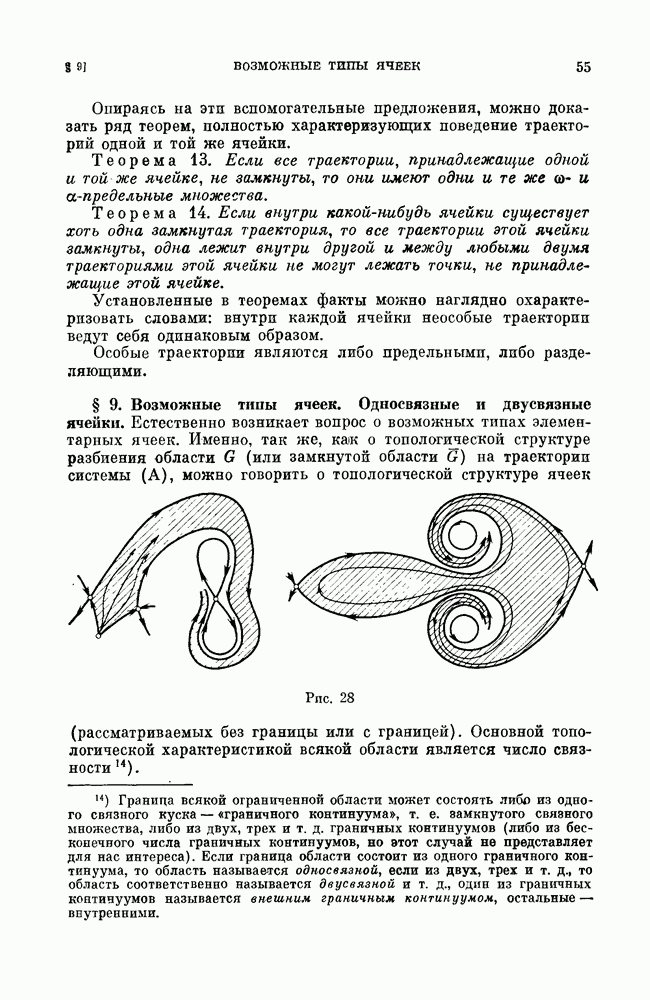
- § 9. Возможные типы ячеек. Односвязные и двусвязные ячейки.
- § 10. Два подхода к описанию качественной структуры.
- § 11. Качественная (топологическая) структура состояния равновесия в случае конечного числа особых траекторий. Схема динамической системы.
- § 12. Устойчивость по Ляпунову.
- ГЛАВА 3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННОЙ СТРУКТУРЫ ОКРЕСТНОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (ОСОБОЙ ТОЧКИ)
- § 2. Приведение динамической системы к каноническому виду.
- § 3. Возможный характер простых состояний равновесия.
- § 4. Замечания о методах установления характера грубых состояний равновесия.
- § 5. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 6. Направления, в которых траектории стремятся к простым состояниям равновесия.
- § 7. Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия.
- § 8. Сводка сведений о грубых состояниях равновесия.
- ГЛАВА 4. КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ
- § 1. Направления, в которых траектории стремятся к сложному состоянию равновесия.
- § 2. Сложное состояние равновесия (особая точка) с нулевыми характеристическими корнями.
- § 3. Примеры.
- § 4. Нормальные формы.
- ГЛАВА 5. ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ
- § 2. Условия устойчивости и неустойчивости неподвижной точки точечного отображения.
- § 3. Функция соответствия.
- § 4. Изучение окрестности замкнутой траектории. Простые и сложные предельные циклы.
- § 5. Аналитические выражения для коэффициентов функции последования. Характеристический показатель замкнутой траектории.
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЕМЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 2. Изучение поведения интегральных кривых в бесконечности. Сфера Пуанкаре.
- § 3. Примеры исследования в бесконечности [93].
- § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов.
- 1. Некоторые видоизменения критериев Бендиксона и Дюлака.
- 2. Индексы Пуанкаре. Распределение особых точек [77, 117].
- 3. Условия сосуществования замкнутых траекторий и особых точек.
- 4. Две общие теоремы Пуанкаре.
- § 5. Топографическая система Пуанкаре. Функция Ляпунова. Кривые контактов.
- ЧАСТЬ II. ТЕОРИЯ БИФУРКАЦИЙ
- § 1. Свойства консервативных систем на плоскости [2, 3].
- § 2. Динамические системы, характерные для теории колебаний.
- § 3. Измененные системы. Системы, правые части которых зависят от параметра.
- § 4. Основные теоремы о зависимости решения от изменения правых частей динамической системы.
- § 5. Грубость динамической системы и теоремы о непрерывной зависимости решения от изменения правых частей.
- ГЛАВА 8. ГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
- § 2. Состояния равновесия, возможные в грубой динамической системе.
- § 3. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 4. Замкнутые траектории, возможные в грубой системе.
- § 5. Поведение сепаратрис седел в грубых системах.
- § 6. Необходимые условия грубости. Достаточность этих условий для грубости системы.
- § 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем.
- § 8. Понятие грубости при более общих предположениях относительно правых частей динамической системы.
- § 9. Типы особых траекторий и ячеек в грубых системах.
- § 10. Замечания по поводу определения грубой системы.
- ГЛАВА 9. ПРОСТЕЙШИЕ НЕГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ — СИСТЕМЫ ПЕРВОЙ СТЕПЕНИ НЕГРУБОСТИ
- § 2. Системы первой степени негрубости.
- § 3. Состояния равновесия, возможные в системе первой степени негрубости.
- § 4. Замкнутые траектории, возможные в системе первой степени негрубости.
- § 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости.
- § 6. Необходимые и достаточные условия первой степени негрубости.
- § 7. Динамические системы более высокой степени негрубости.
- ГЛАВА 10. БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- § 1. Определение бифуркации.
- § 2. Бифуркации систем первой степени негрубости.
- § 3. Бифуркации некоторых типов сложных особых точек.
- § 4. Бифуркации двукратной точки, для которой …
- § 5. Рождение предельных циклов из особых траекторий степени негрубости выше первой.
- ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
- § 1. Возможный характер зависимости правых частей динамической системы от параметров.
- § 2. Смена качественных структур при изменении параметров.
- § 3. Случай, когда правые части зависят более чем от одного параметра.
- § 4. Бифуркации «от бесконечности».
- § 5. Условия существования седло-узла и сложного фокуса первого порядка.
- § 6. Поворот векторного поля.
- § 7. Метод малого параметра. Метод Понтрягина.
- ГЛАВА 12. ДИНАМИЧЕСКИЕ СИСТЕМЫ С ЦИЛИНДРИЧЕСКОЙ ФАЗОВОЙ ПОВЕРХНОСТЬЮ
- § 1. Цилиндрическая фазовая поверхность и характер траекторий, возможных на цилиндрической фазовой поверхности.
- § 2. Замкнутые траектории, охватывающие цилиндр.
- § 3. Приемы исследования качественной структуры динамической системы на цилиндре.
- § 4. Понятие грубости и степени негрубости для динамических систем на цилиндре. Бифуркации на цилиндре. Поворот поля.
- § 5. Динамические системы на цилиндре, близкие к гамильтоновым (метод Понтрягина).
- ГЛАВА 13. АДЕКВАТНОЕ ИСТОЛКОВАНИЕ НЕЛИНЕЙНЫХ ФИЗИЧЕСКИХ ЯВЛЕНИЙ ФАКТАМИ КАЧЕСТВЕННОЙ ТЕОРИИ И ТЕОРИИ БИФУРКАЦИЙ ДИНАМИЧЕСКИХ СИСТЕМ
- § 1. Мягкий и жесткий режимы.
- § 2. Замечания о границах области устойчивости различных стационарных режимов.
- § 3. Мягкое и жесткое возникновение колебаний.
- § 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
- § 5. Замечания по поводу других границ области устойчивости.
- ЧАСТЬ III. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- ГЛАВА 14. ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 1. Некоторые рецептурные указания.
- § 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
- § 3. Некоторые простые примеры динамических систем на цилиндре.
- ГЛАВА 15. ИССЛЕДОВАНИЕ МЕТОДОМ МАЛОГО ПАРАМЕТРА (МЕТОДОМ ПОНТРЯГИНА)
- § 2. Примеры рассмотрения методом Понтрягина (полное исследование).
- § 3. Исследование методом Понтрягина с привлечением вычислительных методов.
- ГЛАВА 16. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ
- § 2. Электрическая цепь с туннельным диодом.
- § 3. Двумерная модель динамики твердотельного лазера [119].
- § 4. Симметричный полет самолета в вертикальной плоскости (задача Н. Е. Жуковского).
- § 5. Система, описывающая динамику проточного химического реактора.
- § 6. Фазовая автоподстройка частоты.
- § 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов).
- § 8. Синхронный генератор с асинхронной характеристикой.
- ЧАСТЬ IV. КУСОЧНО-СШИТЫЕ СИСТЕМЫ
- ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ
- § 1. Сшитые системы. Доопределение на линиях сшивания.
- § 2. Возможные типы полутраекторий сшитых систем.
- § 3. Особые траектории сшитых систем.
- § 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
- ГЛАВА 18. ИССЛЕДОВАНИЕ КУСОЧНО-СШИТЫХ СИСТЕМ МЕТОДОМ ПОНТРЯГИНА
- § 2. Автоподстройка при кусочно-постоянной аппроксимации характеристики.
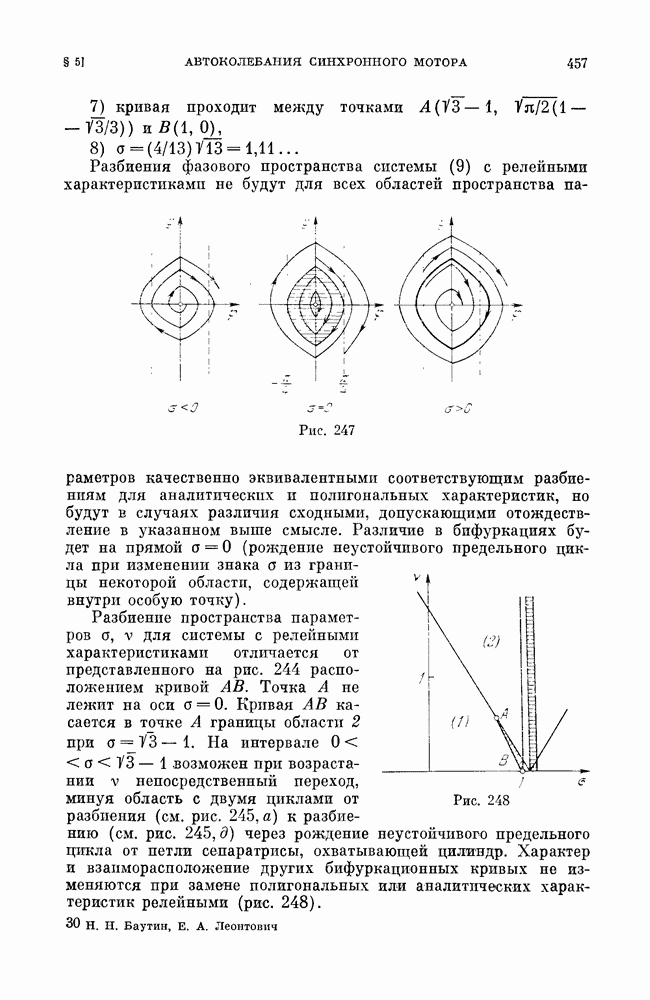
- § 3. Автоколебания синхронного мотора.
- ГЛАВА 19. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ
- § 2. Следящая система с люфтом.
- § 3. Электрическая цепь с туннельным диодом.
- § 4. Система со скачками на линии сшивания.
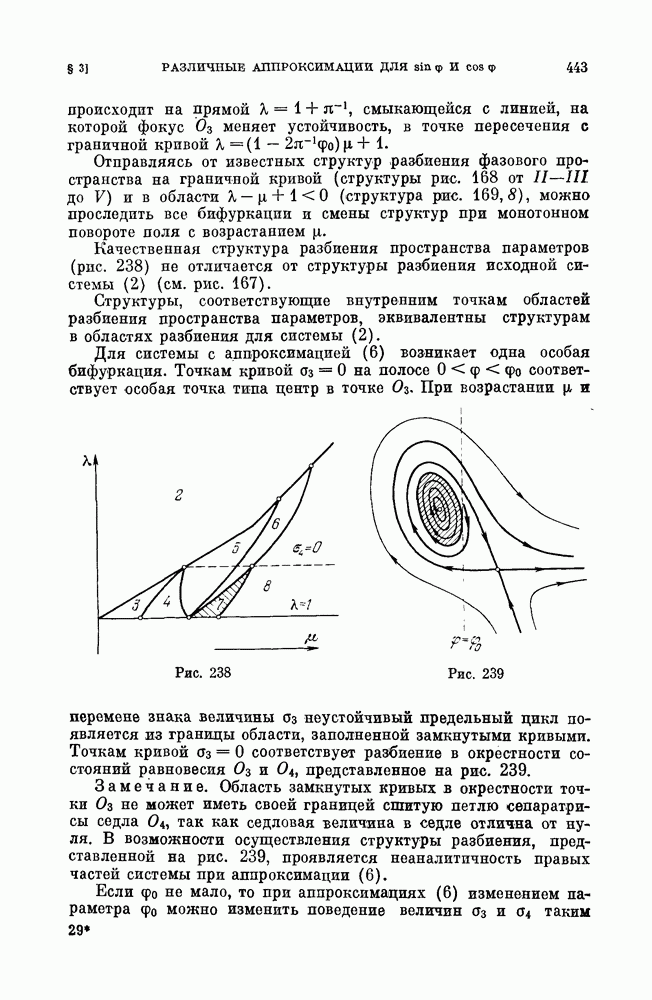
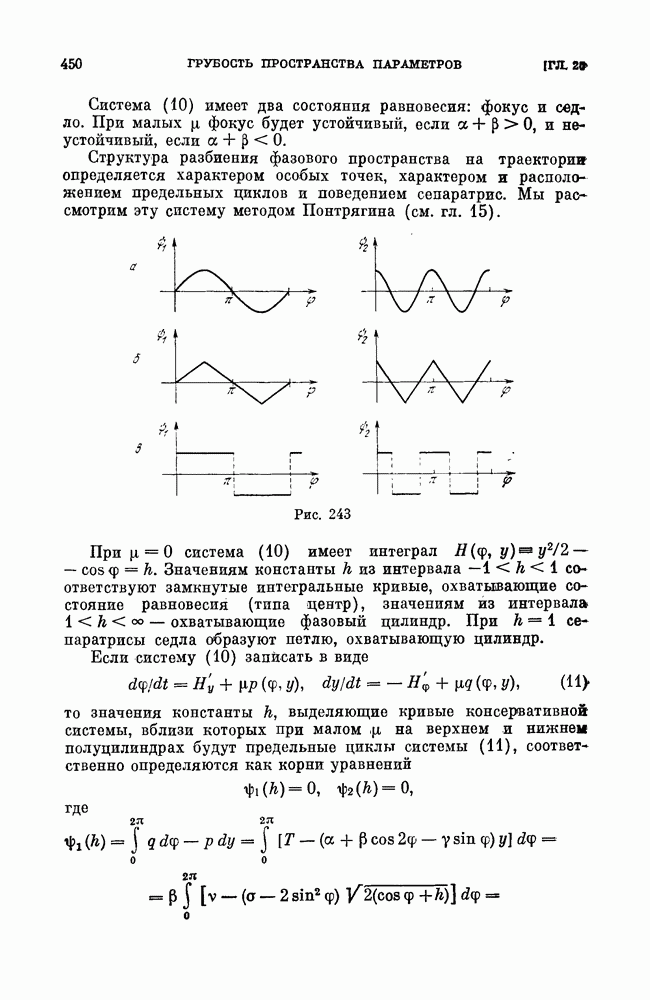
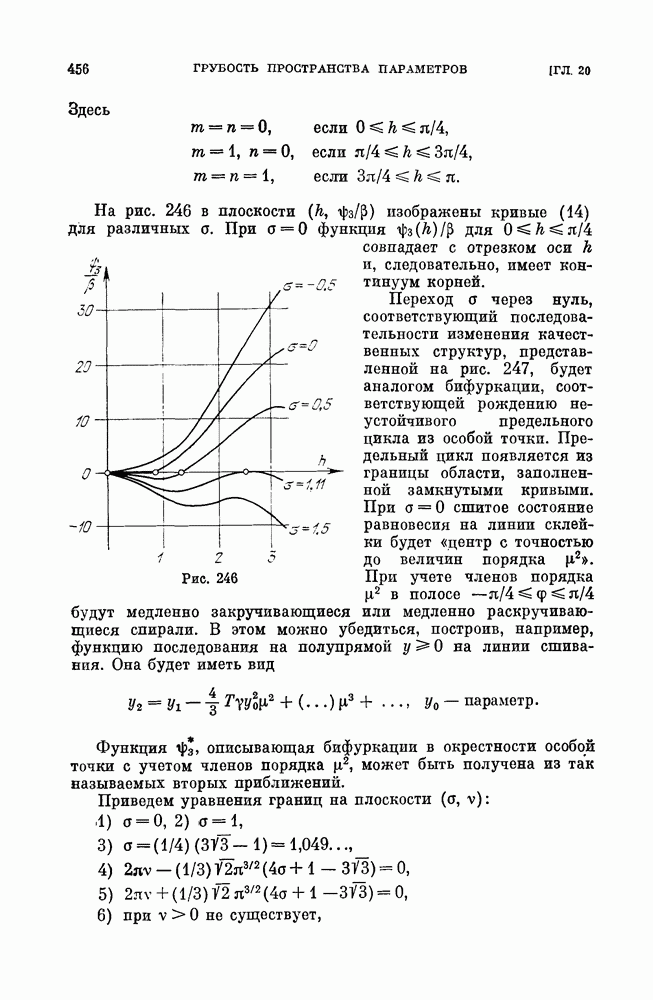
- ГЛАВА 20. ОБ АППРОКСИМАЦИЯХ И ГРУБОСТИ ПРОСТРАНСТВА ПАРАМЕТРОВ [39, 41, 42]
- § 1. Рассмотрение системы (2) при аппроксимациях пилообразными функциями.
- § 2. Рассмотрение системы (2) при аппроксимации, включающей отрезок параболы.
- § 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin f, и пилообразной для cos f функциями.
- § 4. Исследование роли аппроксимаций для уравнения маятникового типа.
- § 5. Динамическая система, описывающая автоколебания синхронного мотора.
- § 6. Динамическая система, описывающая симметричный полет самолета.
- ДОПОЛНЕНИЕ
- § 1. Динамическое системы на двумерных поверхностях.
- § 2. Динамические системы в n-мерном евклидовом пространстве.
- СПИСОК ЛИТЕРАТУРЫ