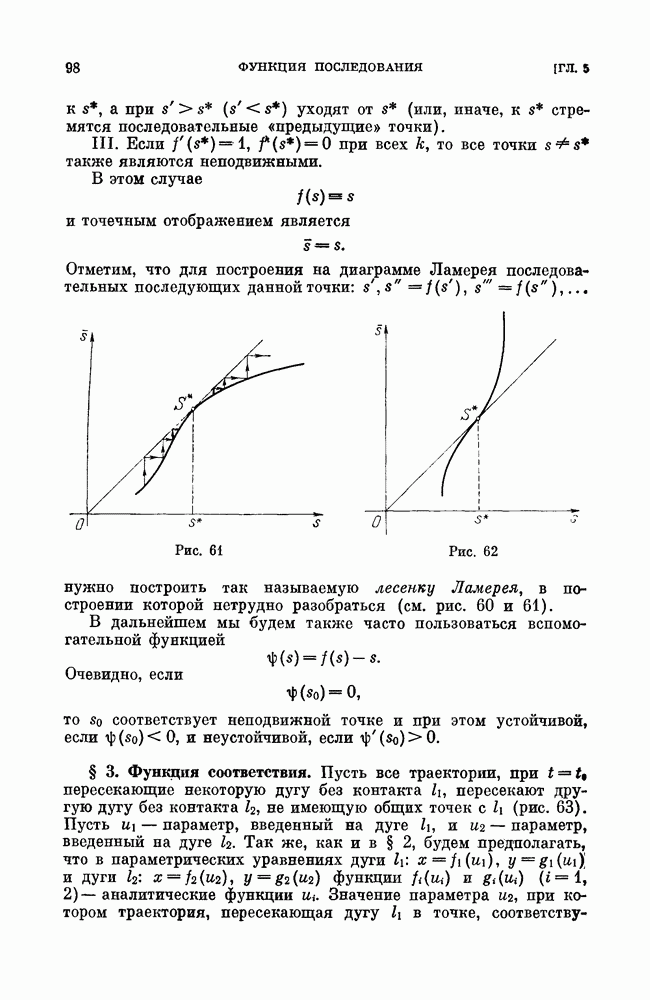
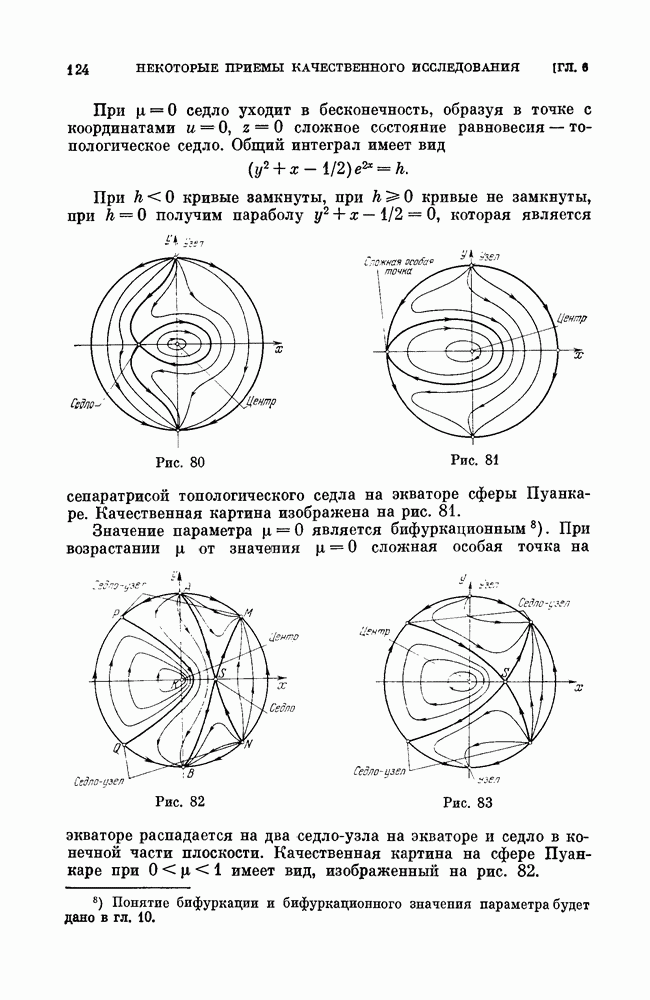
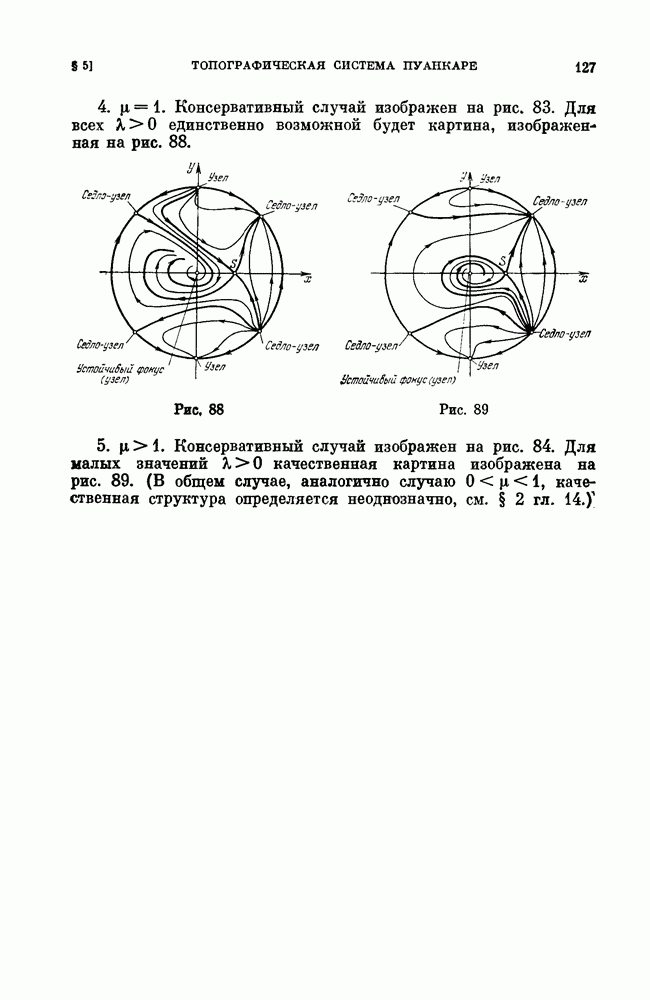
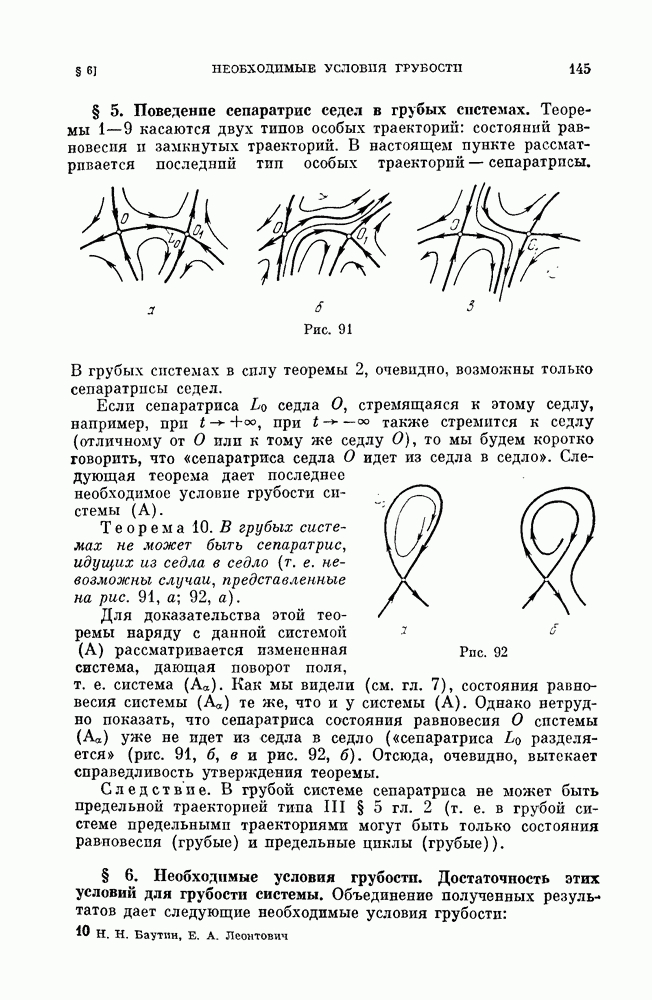
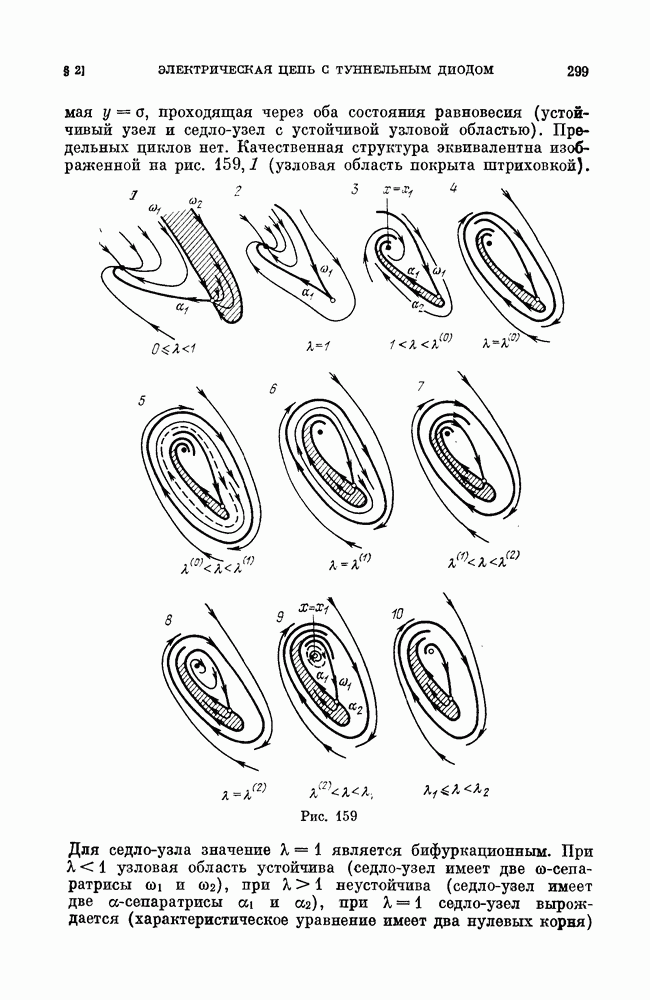
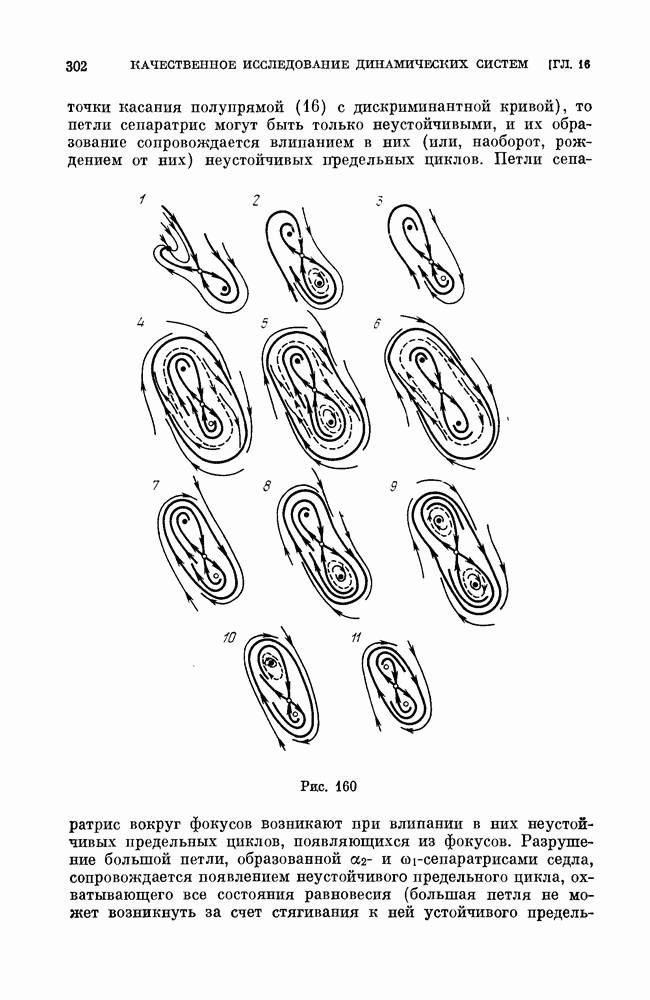
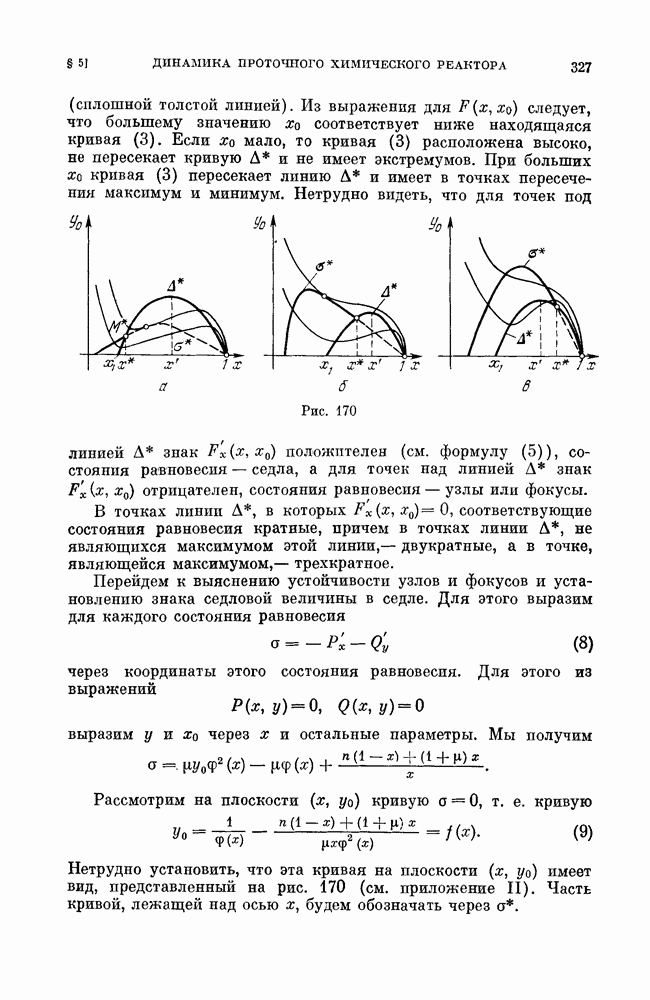
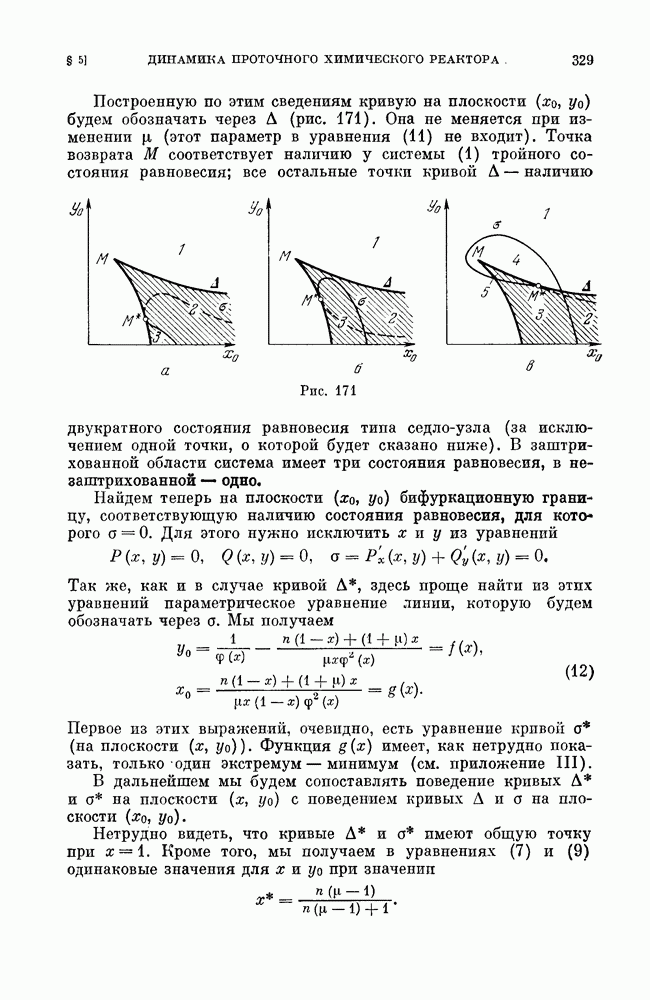
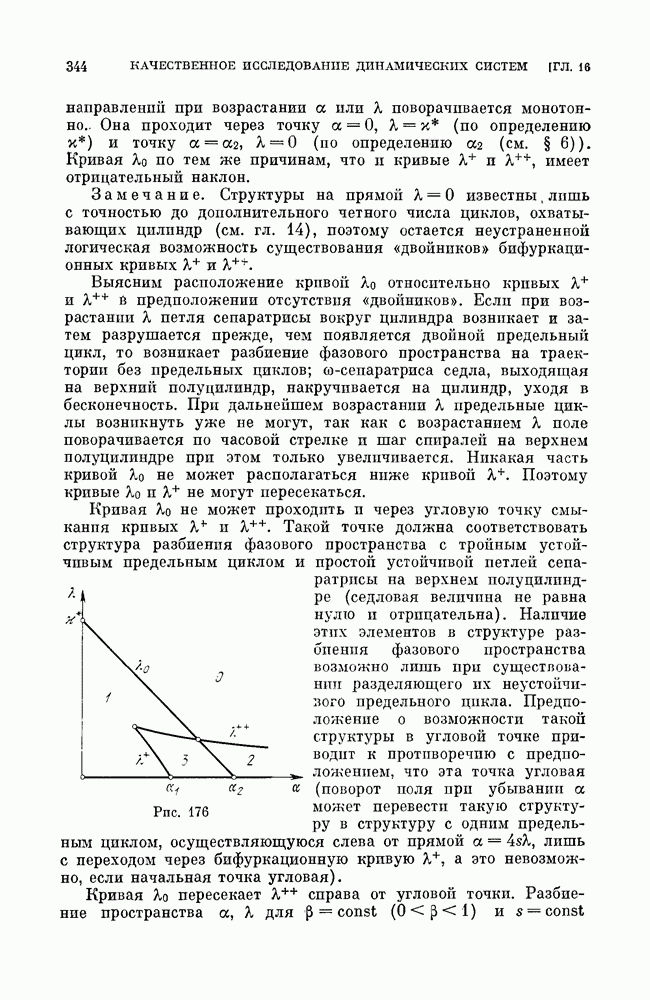
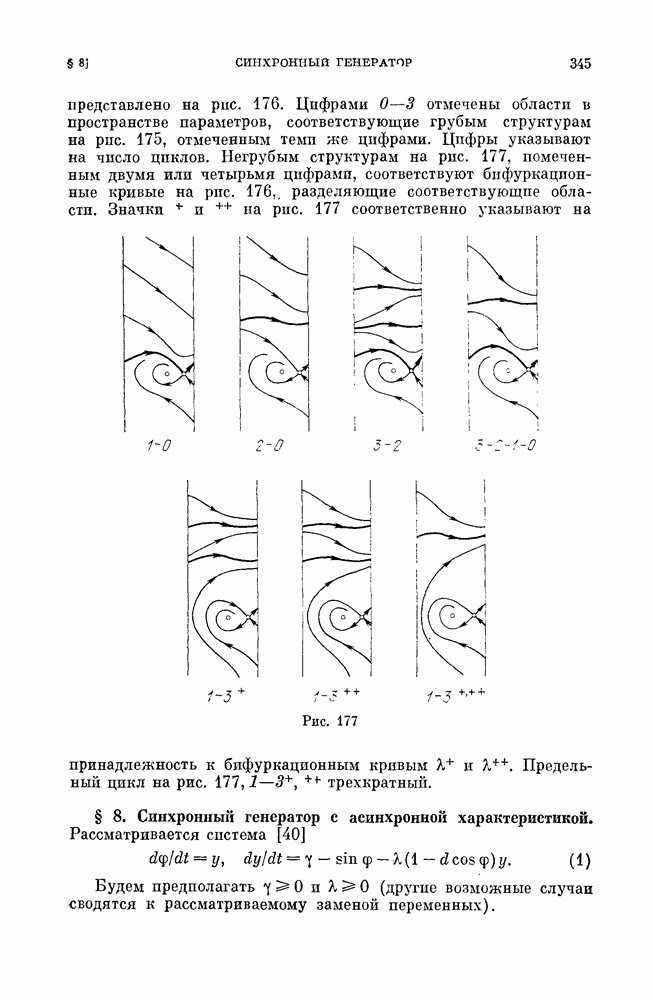
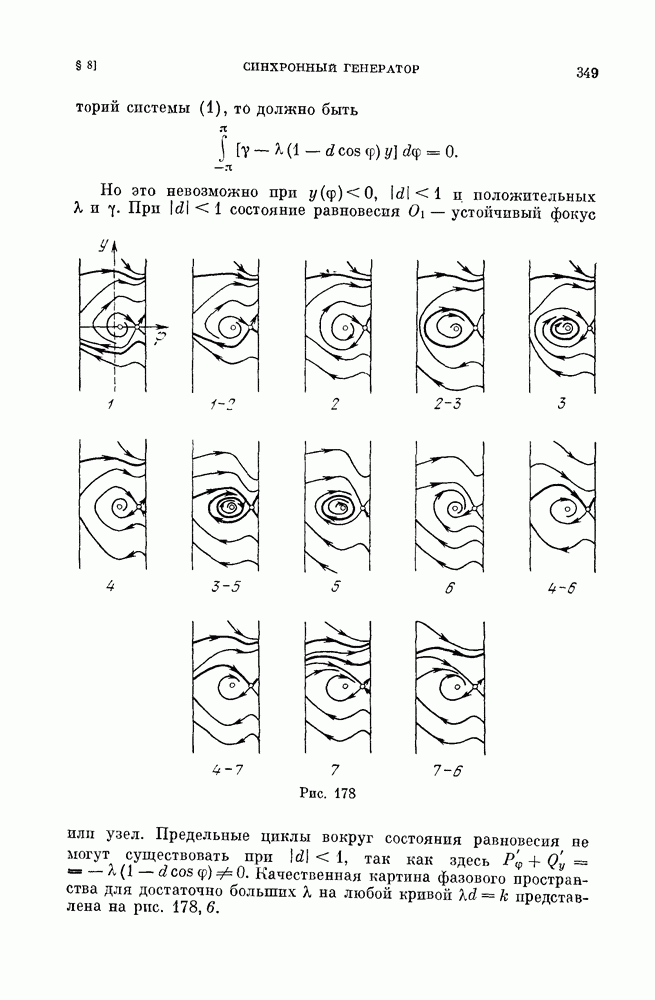
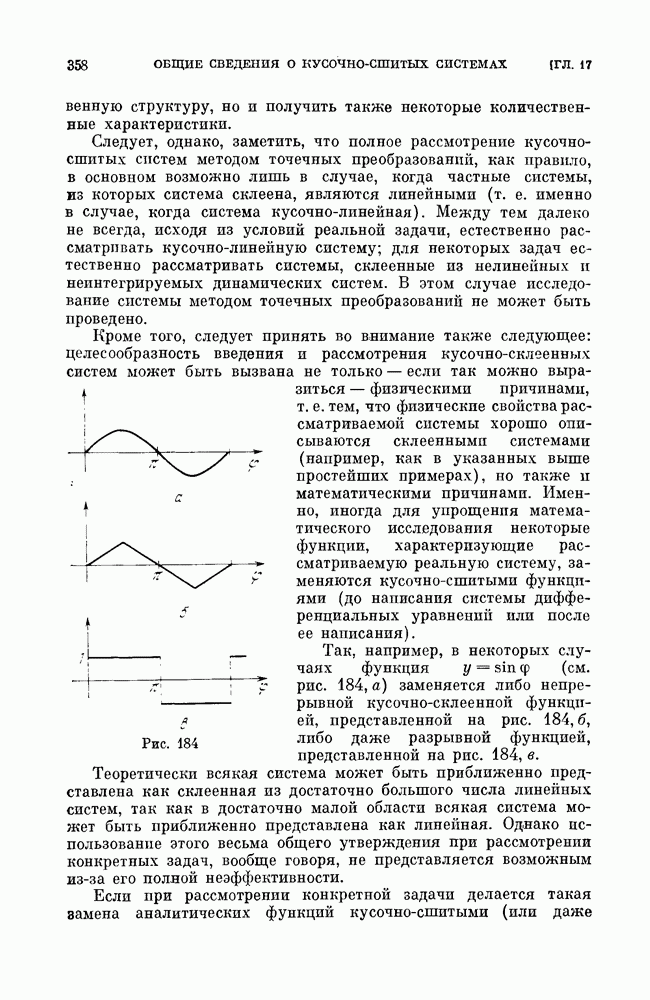
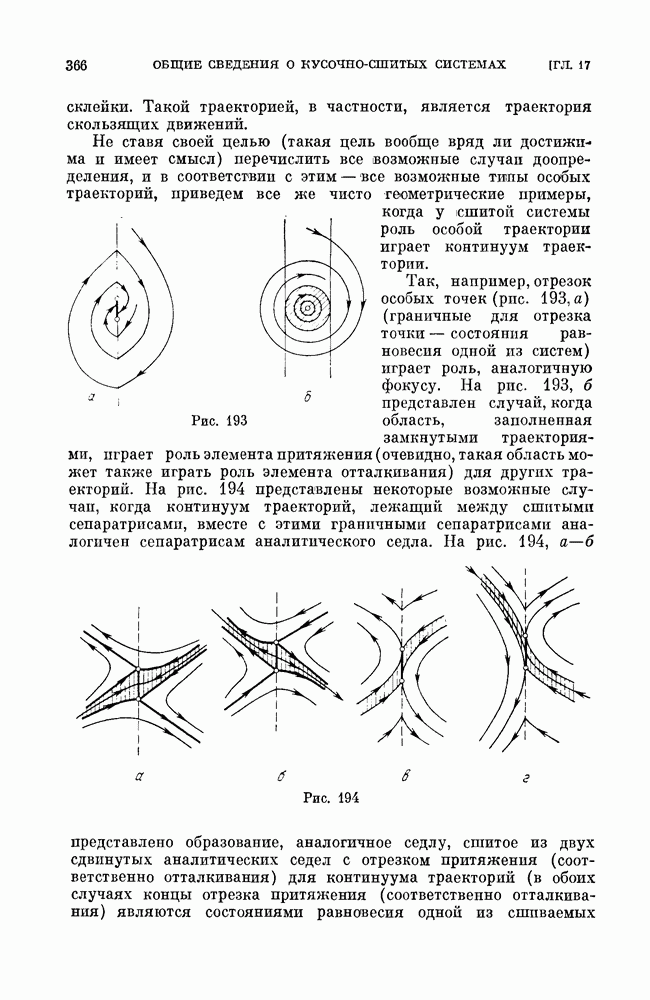
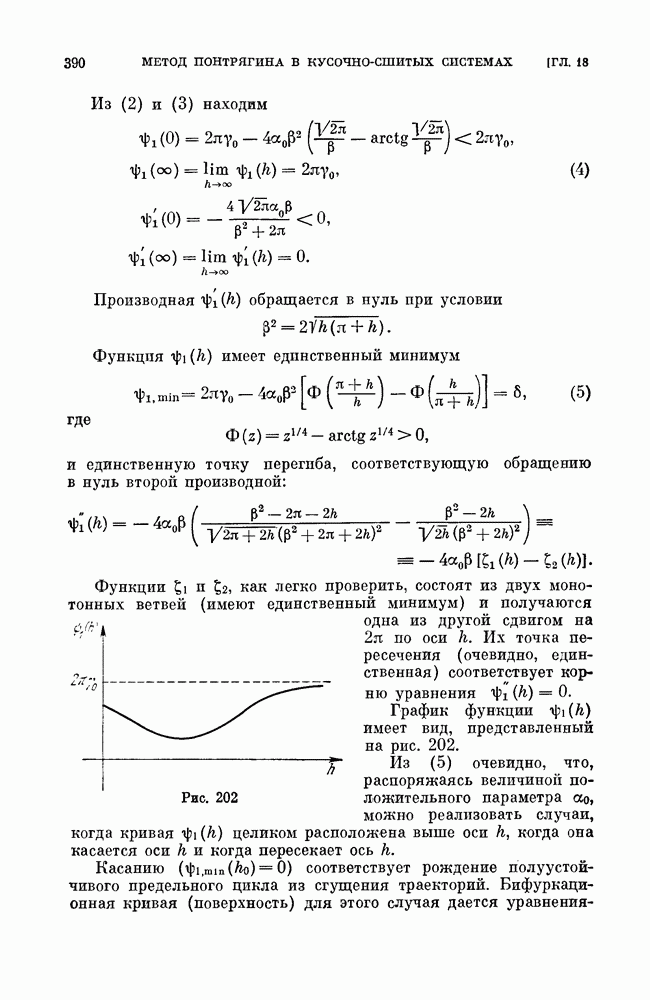
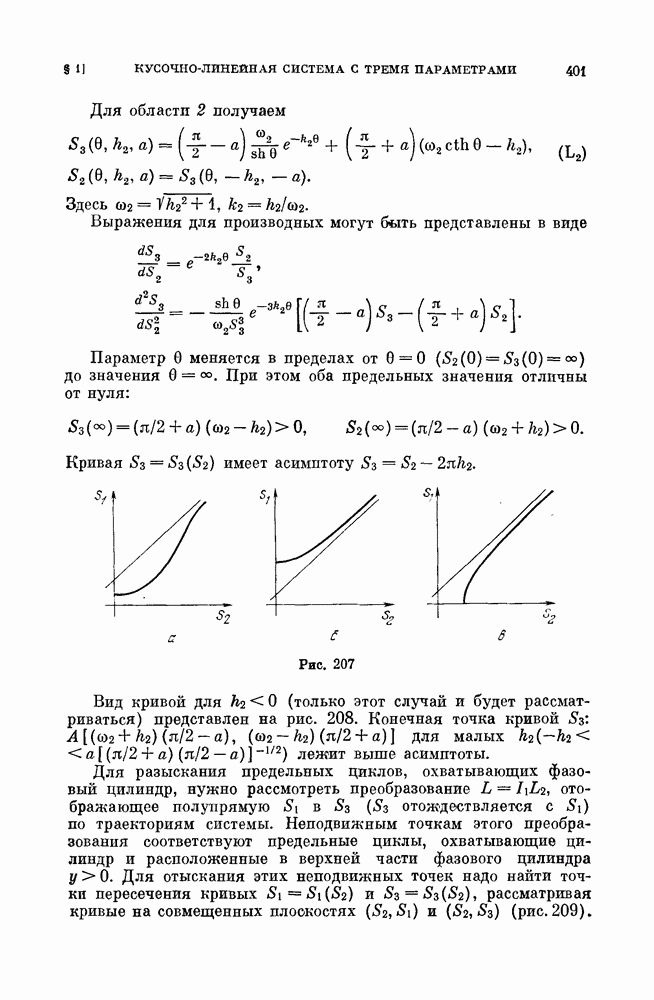
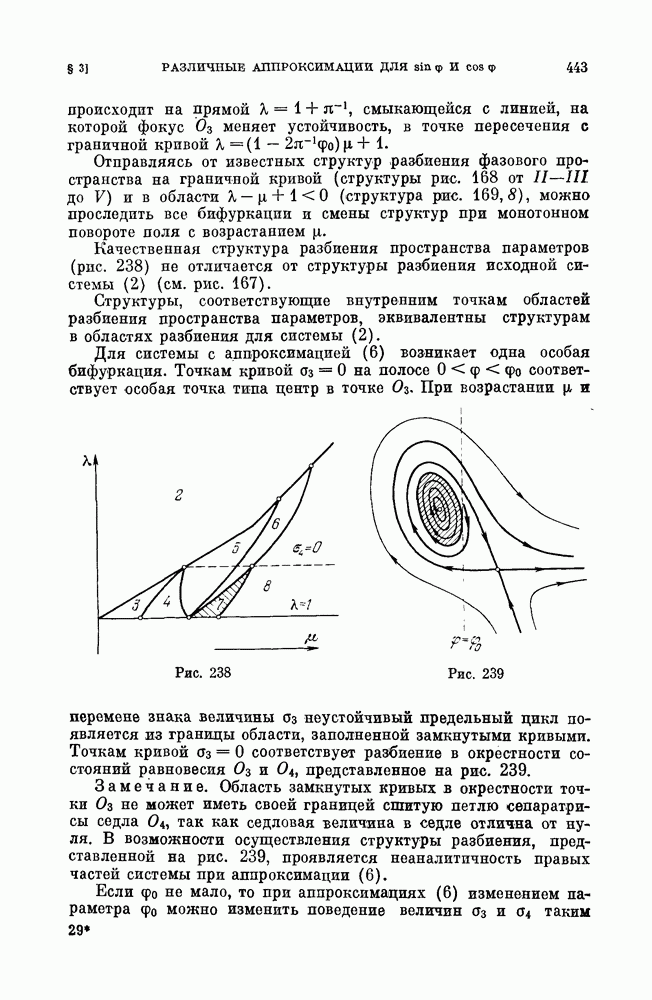
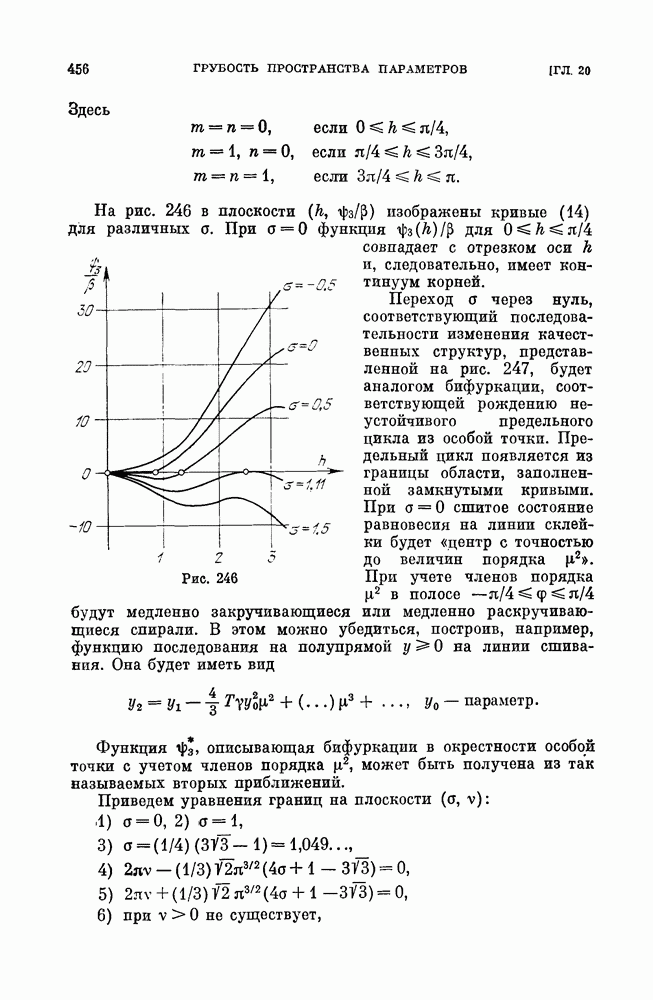
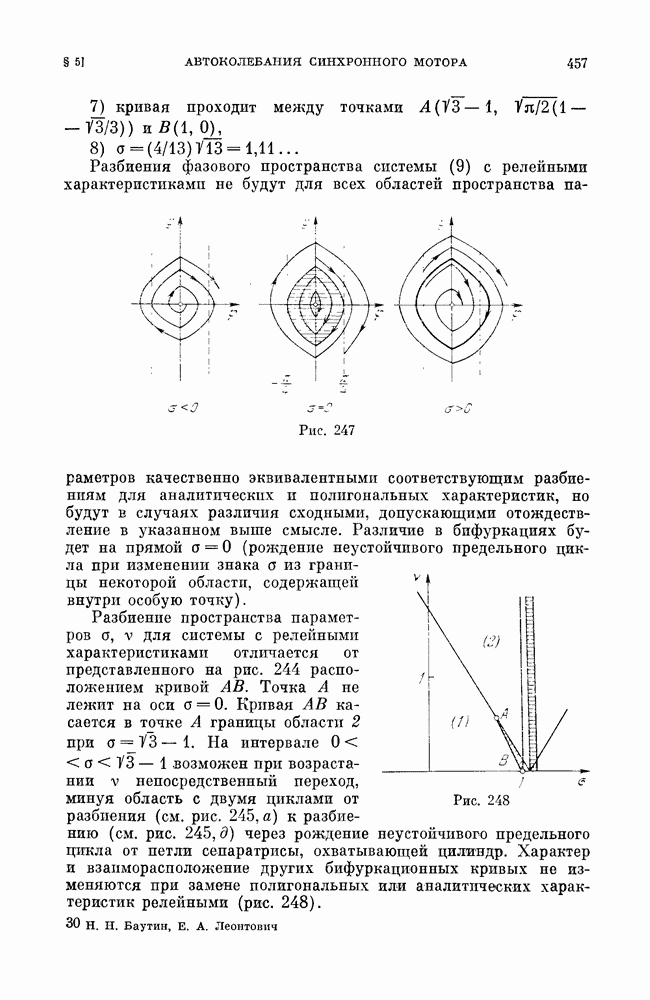
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
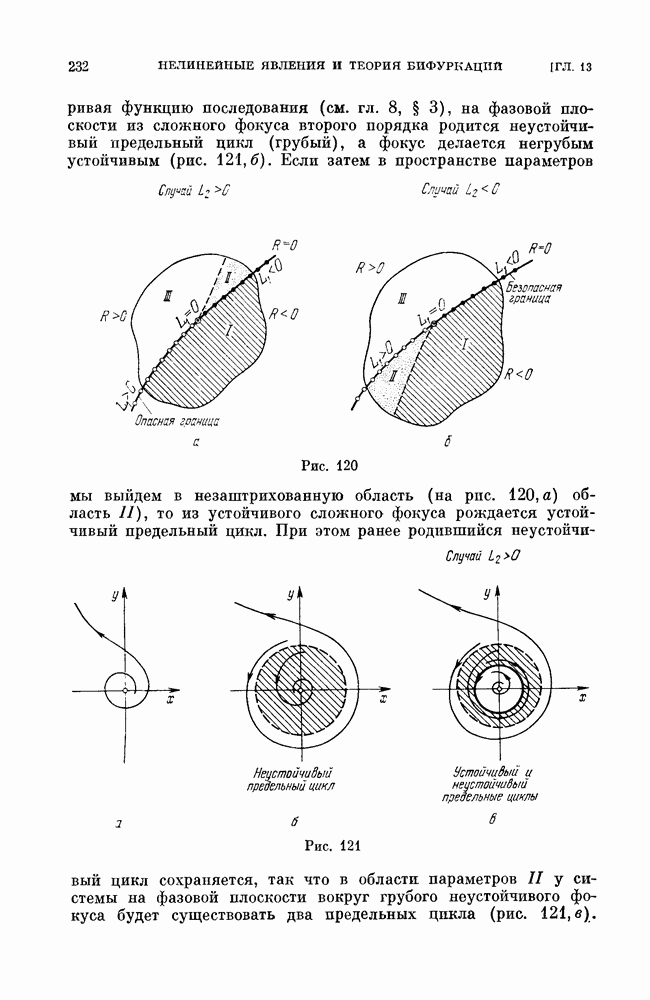
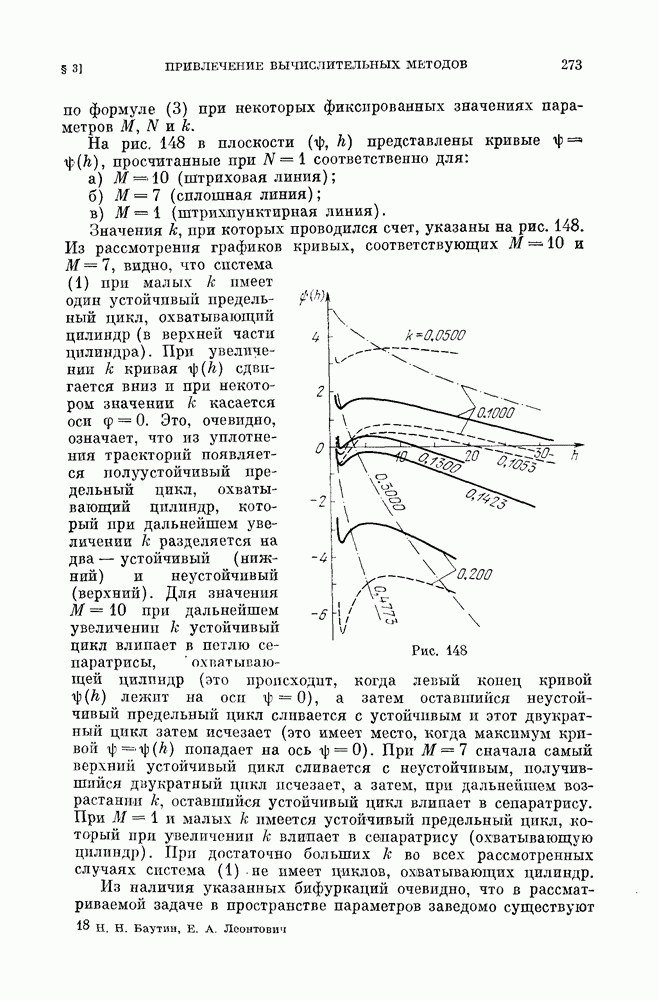
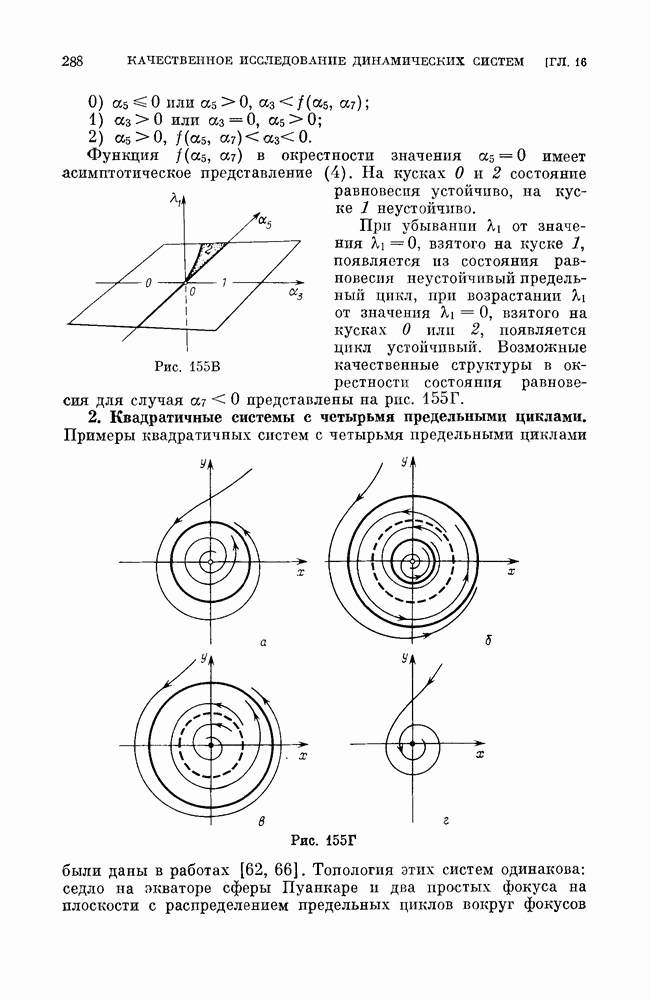
§ 2. Примеры рассмотрения методом Понтрягина (полное исследование).
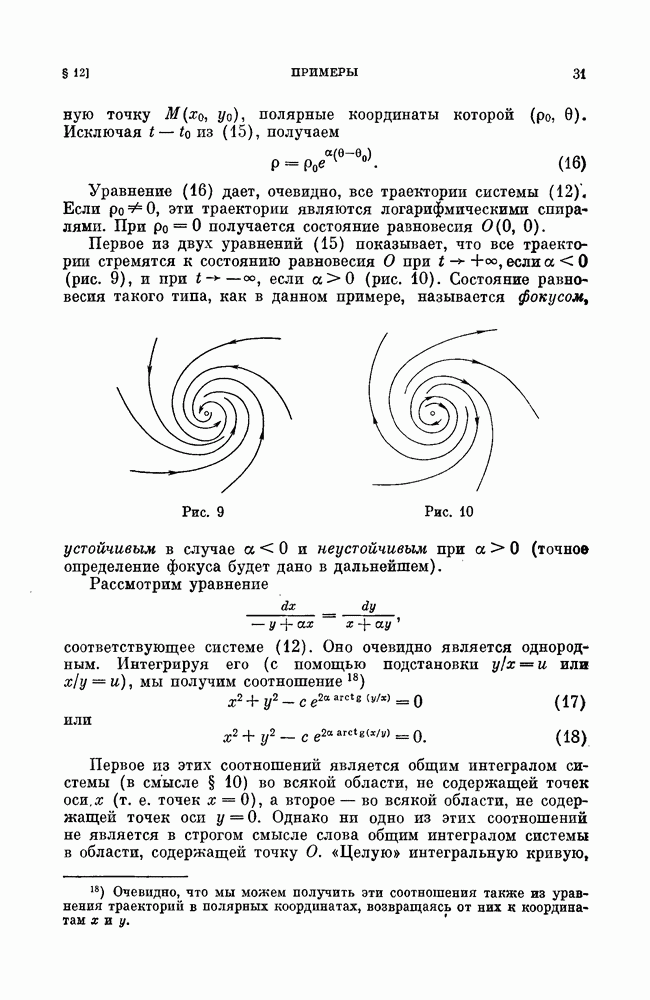
Пример 1. Рассмотрим систему, которая (при предположении малости некоторых параметров) может служить моделью частотно-фазовой автоподстройки частоты (см. 

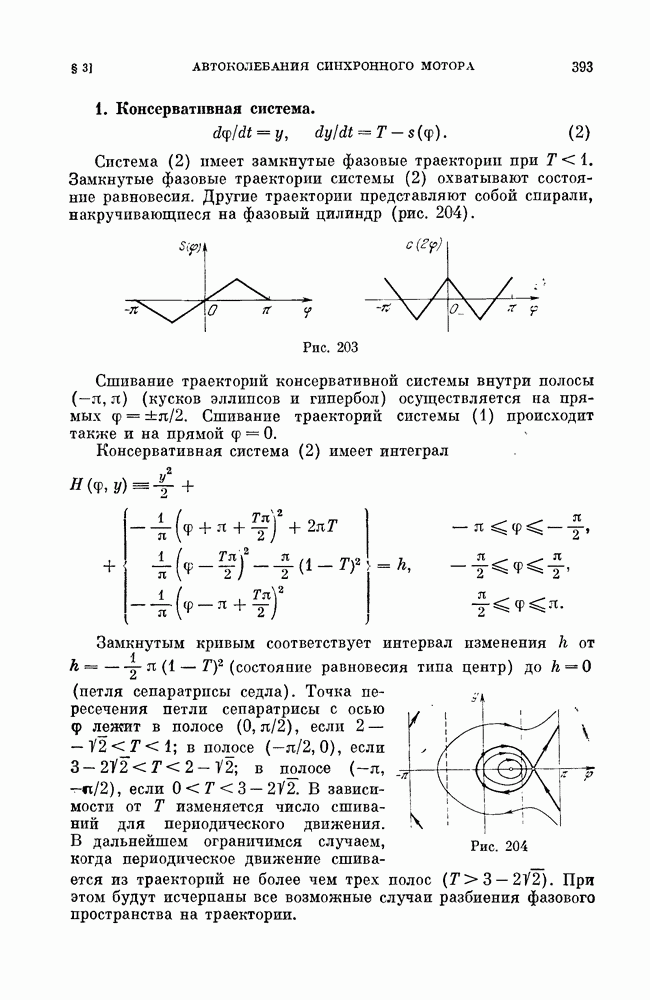
Очевидно, эта система является близкой к очень простой консервативной системе на цилиндре

интеграл которой

На плоскости  это — прямые, параллельные оси
это — прямые, параллельные оси  на фазовом цилиндре все кривые замкнуты (окружности). Составим
на фазовом цилиндре все кривые замкнуты (окружности). Составим
выражение для  Так как в рассматриваемом случае
Так как в рассматриваемом случае

то

где, очевидно, 
Мы получаем

или, вводя обозначение  будем иметь
будем иметь

Для того чтобы найти значения  при которых от кривой консервативной системы рождается предельный цикл, нужно, очевидно, рассмотреть уравнение (которое мы получим, если приравнять нулю числитель
при которых от кривой консервативной системы рождается предельный цикл, нужно, очевидно, рассмотреть уравнение (которое мы получим, если приравнять нулю числитель  выражения
выражения 

Это — кубическое уравнение, которое может быть исследовано известными методами. Мы, однако, не будем останавливаться на его исследовании подробно, а покажем только, что существуют как значения параметров  и [5, при которых это уравнение имеет только один корень, так и значения параметров, при которых это уравнение имеет три корня. Очевидно, случай, когда уравнение (3) имеет один корень, соответствует случаю (при достаточно малых
и [5, при которых это уравнение имеет только один корень, так и значения параметров, при которых это уравнение имеет три корня. Очевидно, случай, когда уравнение (3) имеет один корень, соответствует случаю (при достаточно малых  когда существует один устойчивый предельный цикл, а случай, когда это уравнение имеет три корня, соответствует случаю, когда система (1) имеет три предельных цикла — два устойчивых и между ними неустойчивый.
когда существует один устойчивый предельный цикл, а случай, когда это уравнение имеет три корня, соответствует случаю, когда система (1) имеет три предельных цикла — два устойчивых и между ними неустойчивый.
При граничном значении  (по смыслу константы
(по смыслу константы  всегда
всегда  уравнение (3) превращается в уравнение
уравнение (3) превращается в уравнение

имеющее единственный действительный корень  Очевидно, уравнение (3) будет иметь единственный действительный корень и при всех достаточно малых
Очевидно, уравнение (3) будет иметь единственный действительный корень и при всех достаточно малых  При достаточно больших
При достаточно больших  (член наивысшей степени по
(член наивысшей степени по  при
при  он отрицателен). В нуле
он отрицателен). В нуле  функции
функции  очевидно,
очевидно,
 что и означает, что соответствующий предельный цикл устойчив.
что и означает, что соответствующий предельный цикл устойчив.
Для доказательства существования значений параметров, при которых у системы (1) существует три цикла, найдем сначала значения параметров, при которых уравнение  имеет трехкратный корень. При этих значениях параметров должны удовлетворяться следующие три уравнения:
имеет трехкратный корень. При этих значениях параметров должны удовлетворяться следующие три уравнения:

Из последнего уравнения находим

Подставляя это значение  в первые два из уравнений (4) (и сокращая первое уравнение на
в первые два из уравнений (4) (и сокращая первое уравнение на  получаем следующие два соотношения для параметров, при которых
получаем следующие два соотношения для параметров, при которых  имеет тройной корень (а система
имеет тройной корень (а система  -трехкратный цикл):
-трехкратный цикл):

Отсюда мы получаем значения для  при которых выполняются условия (4) (т. е. уравнение
при которых выполняются условия (4) (т. е. уравнение  имеет трехкратный корень):
имеет трехкратный корень):

Представим теперь  в следующем виде, раскладывая
в следующем виде, раскладывая  по степеням
по степеням  и принимая во внимание, что
и принимая во внимание, что

где  когда
когда 
Но, очевидно, мы всегда можем, принимая во внимание выражение (5) и полагая

т. е. выбирая  так, чтобы
так, чтобы  взять
взять  таким, чтобы
таким, чтобы

было бы не равно нулю и знака, противоположного знаку  Тогда, очевидно, уравнение (6), которое принимает вид
Тогда, очевидно, уравнение (6), которое принимает вид

будет иметь, кроме  еще два различных корня,
еще два различных корня,  Нетрудно, принимая во внимание вид
Нетрудно, принимая во внимание вид  а значит, и знак
а значит, и знак  убедиться в том, что больший и меньший корни соответствуют устойчивым предельным циклам, а средний — неустойчивому предельному циклу.
убедиться в том, что больший и меньший корни соответствуют устойчивым предельным циклам, а средний — неустойчивому предельному циклу.
Пример 2 (динамическая система, описывающая динамику синхронного мотора в простейшей идеализации). Соответствующее дифференциальное уравнение имеет вид

Полагая  и записывая уравнение (7) в виде системы, получаем
и записывая уравнение (7) в виде системы, получаем

где  Семейство кривых
Семейство кривых

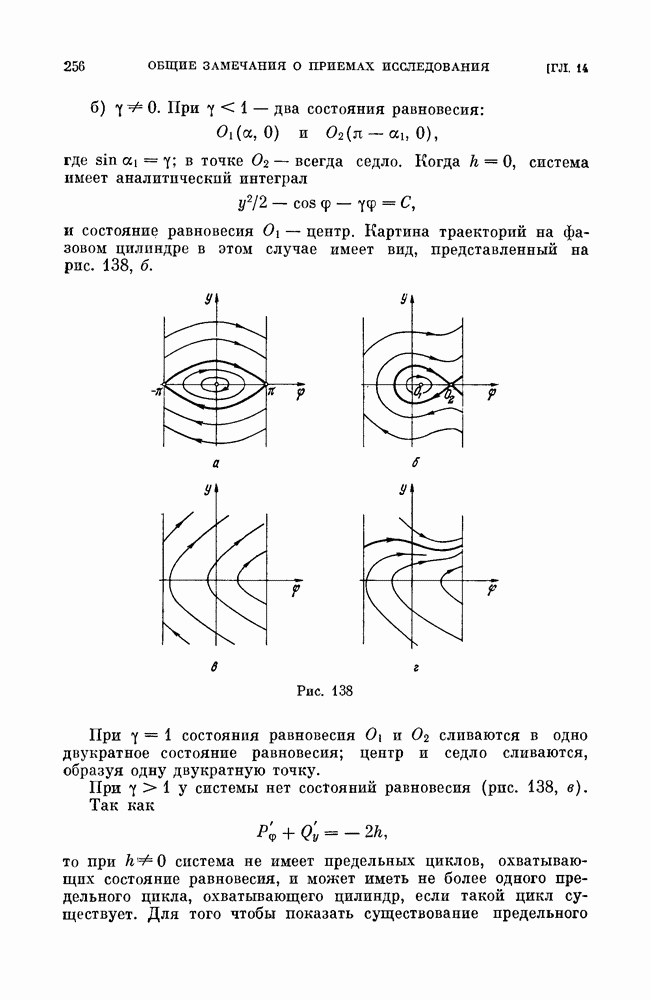
имеет вид, представленный на рис. 138, а.
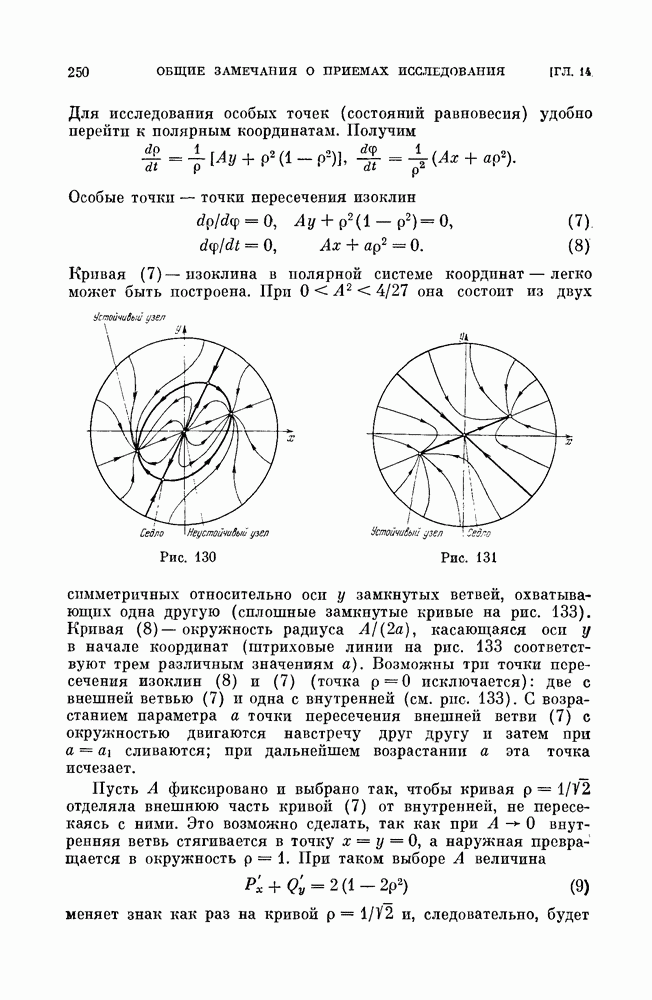
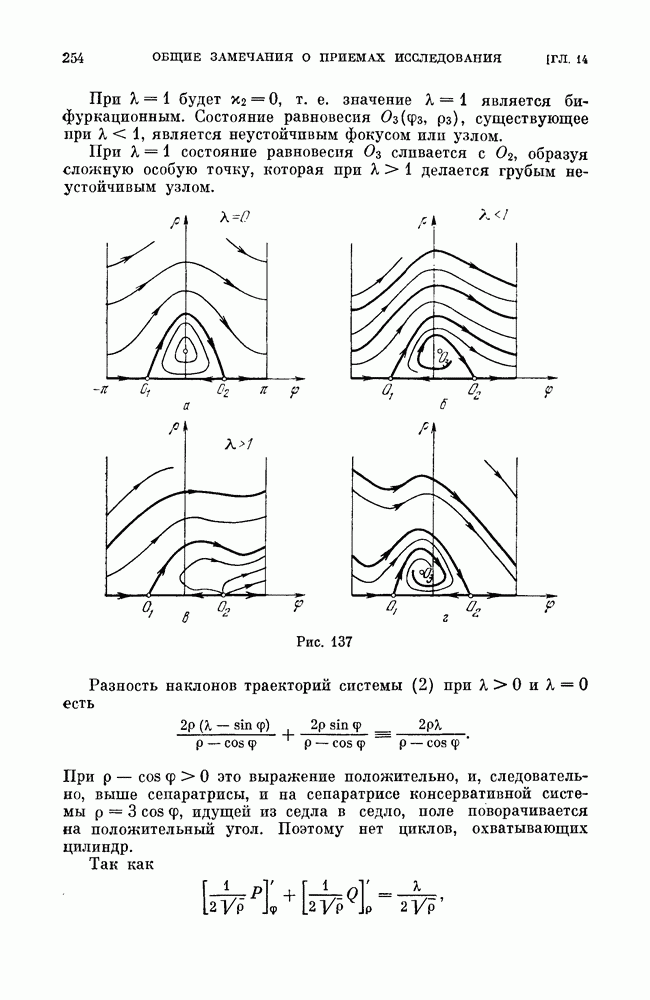
Значениям  из интервала
из интервала  соответствуют замкнутые траектории, охватывающие состояние равновесия типа центра, значениям
соответствуют замкнутые траектории, охватывающие состояние равновесия типа центра, значениям  из интервала
из интервала  замкнутые траектории, охватывающие цилиндр; при
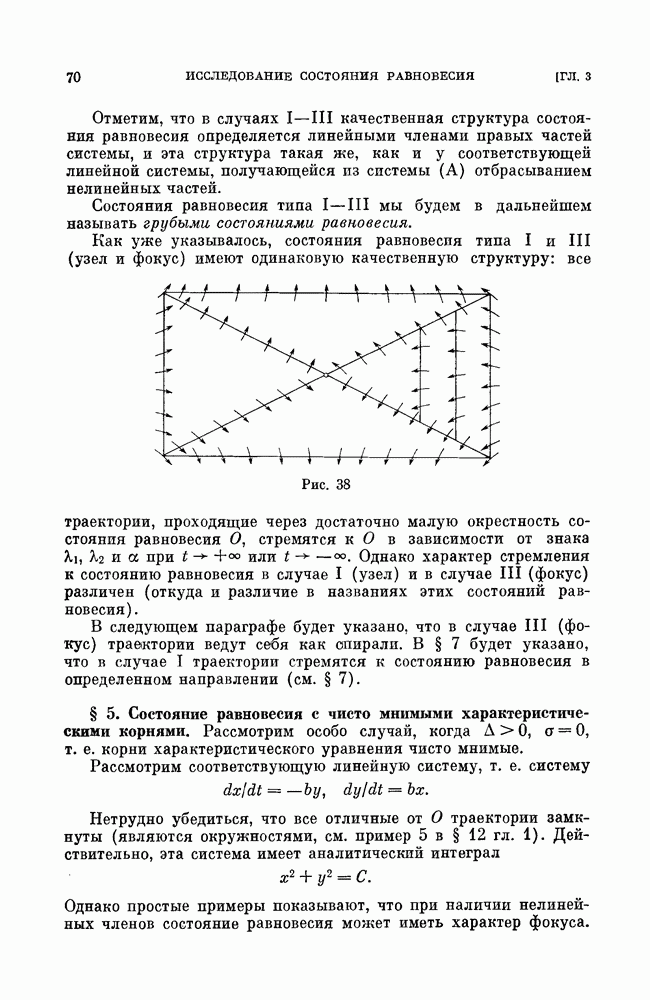
замкнутые траектории, охватывающие цилиндр; при  сепаратрисы седла образуют петлю, охватывающую цилиндр (см. рис. 138, а).
сепаратрисы седла образуют петлю, охватывающую цилиндр (см. рис. 138, а).
По критерию Бендиксона  циклов, охватывающих состояние равновесия, нет. Функция Понтрягина для верхнего полуцилиндра имеет вид
циклов, охватывающих состояние равновесия, нет. Функция Понтрягина для верхнего полуцилиндра имеет вид

Для нижнего полуцилиндра соответствующая функция будет отличаться знаком перед радикалом и, следовательно, всегда будет положительной. Поэтому на нижнем полуцилиндре циклов нет. Полагая  мы получим
мы получим

где  полный эллиптический интеграл второго рода:
полный эллиптический интеграл второго рода:

Далее мы имеем

где F - полный эллиптический интеграл первого рода и

Используя разложения (8) и (9), мы, очевидно, получаем

Для существования циклов необходимо, чтобы

или

Очевидно, нули этого уравнения будут абсциссами точек пересечения кривой  и прямой
и прямой  (рис. 139). Уравнение может иметь не более одного корня
(рис. 139). Уравнение может иметь не более одного корня  так как
так как  при
при 

Рис. 139

Рис. 140
Из условия  находим границу области существования предельного цикла:
находим границу области существования предельного цикла:

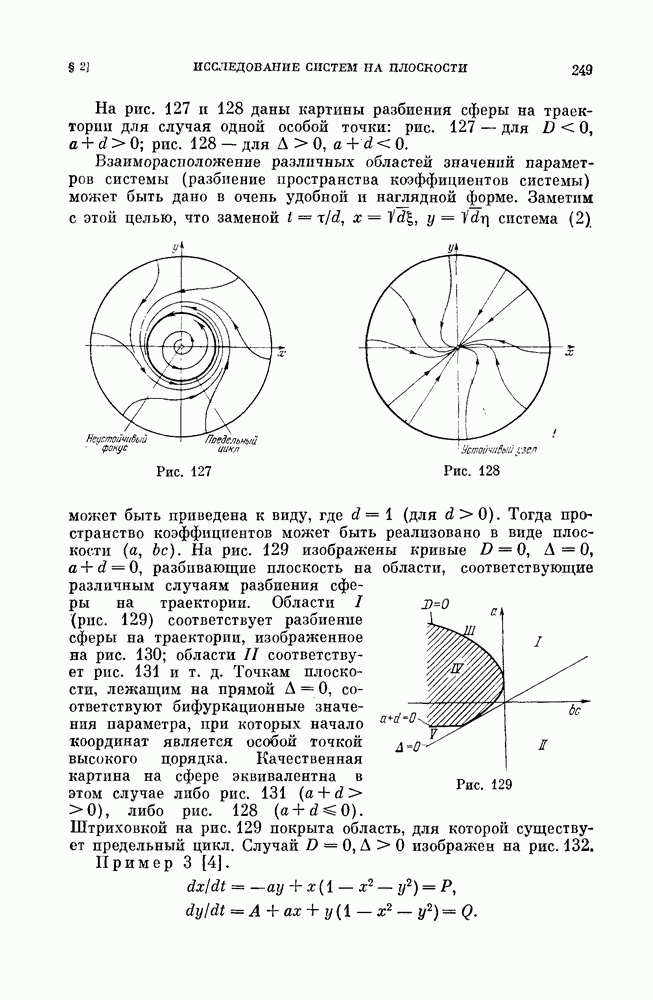
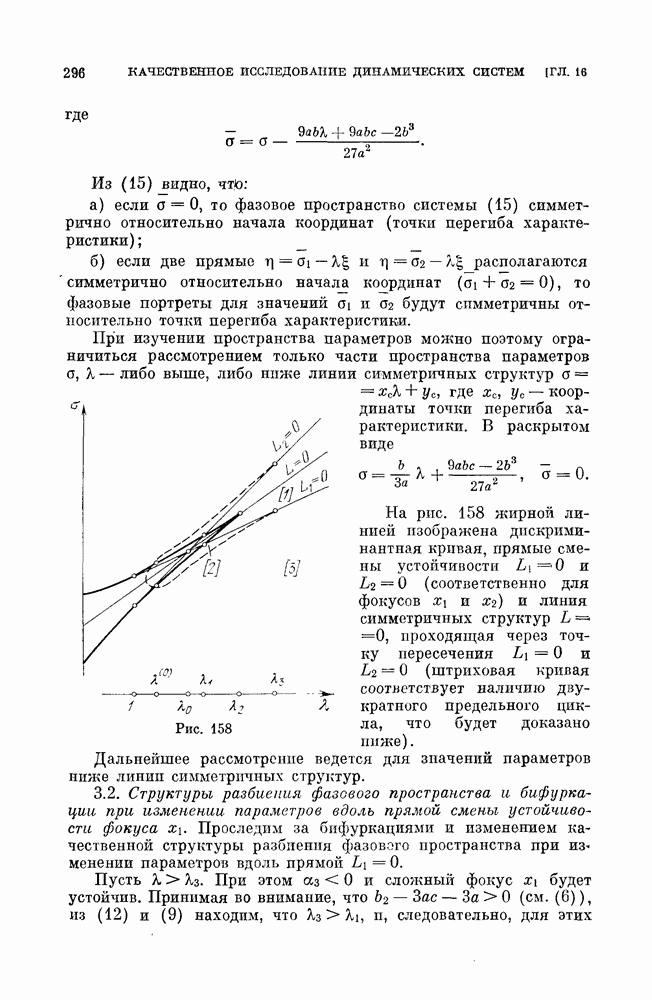
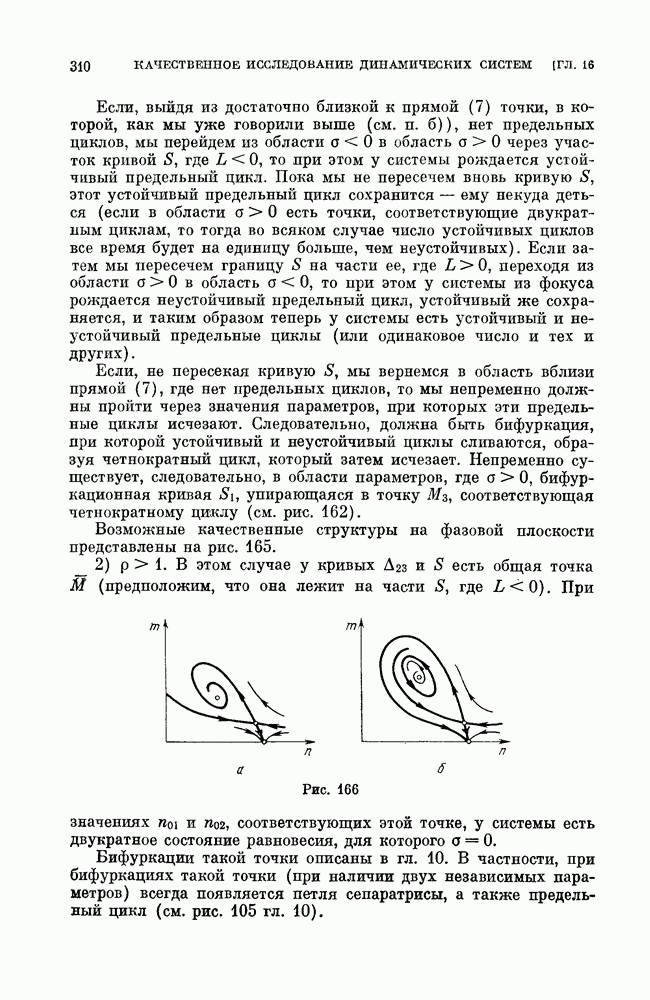
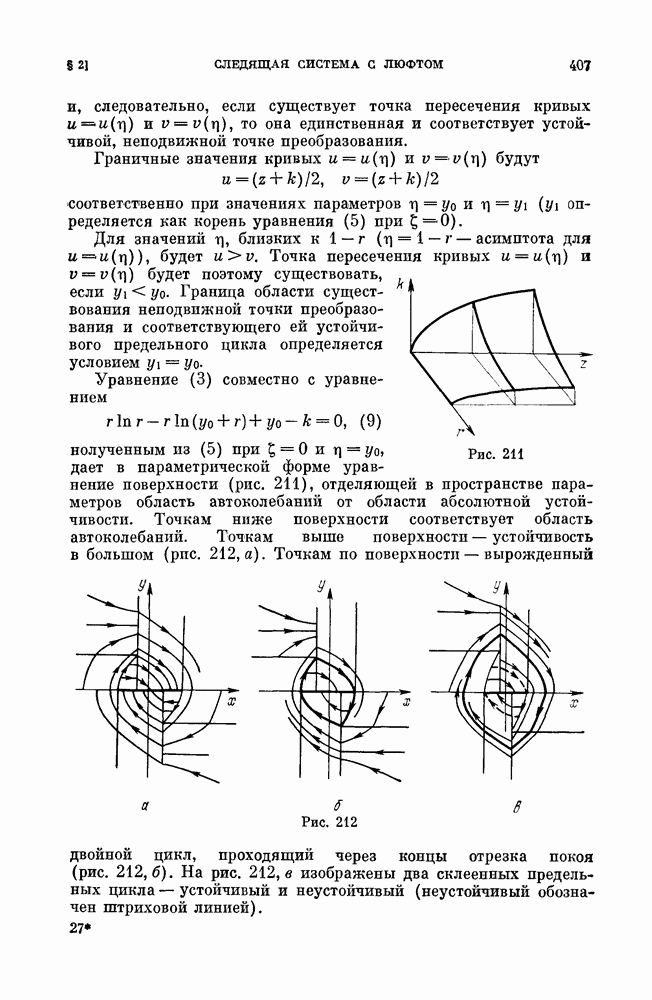
Плоскость параметров представлена на рис. 140. Заштрихованная область соответствует значениям параметров, при которых есть цикл.
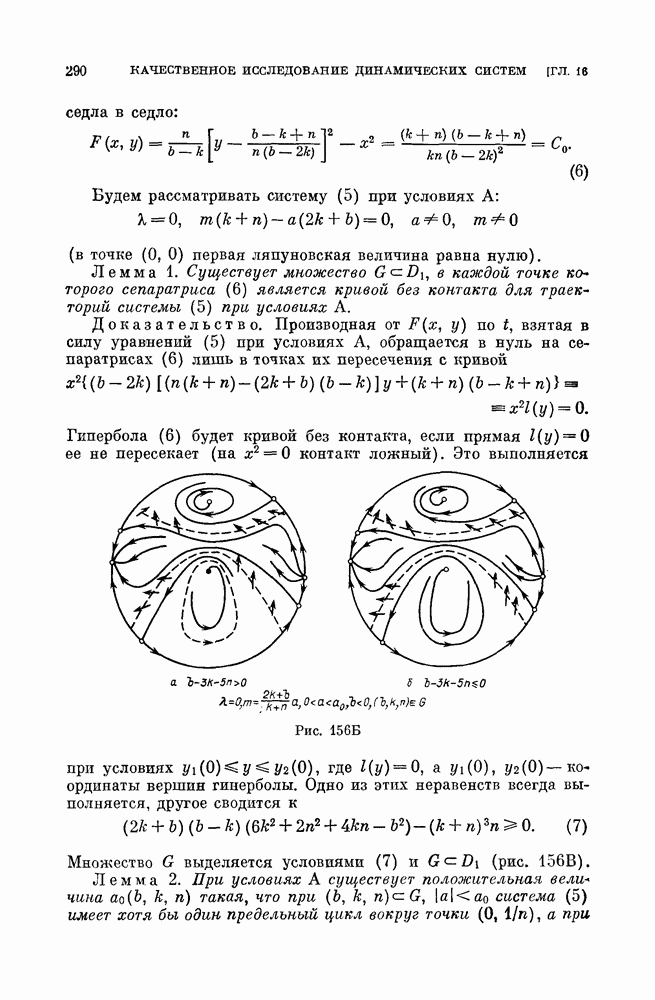
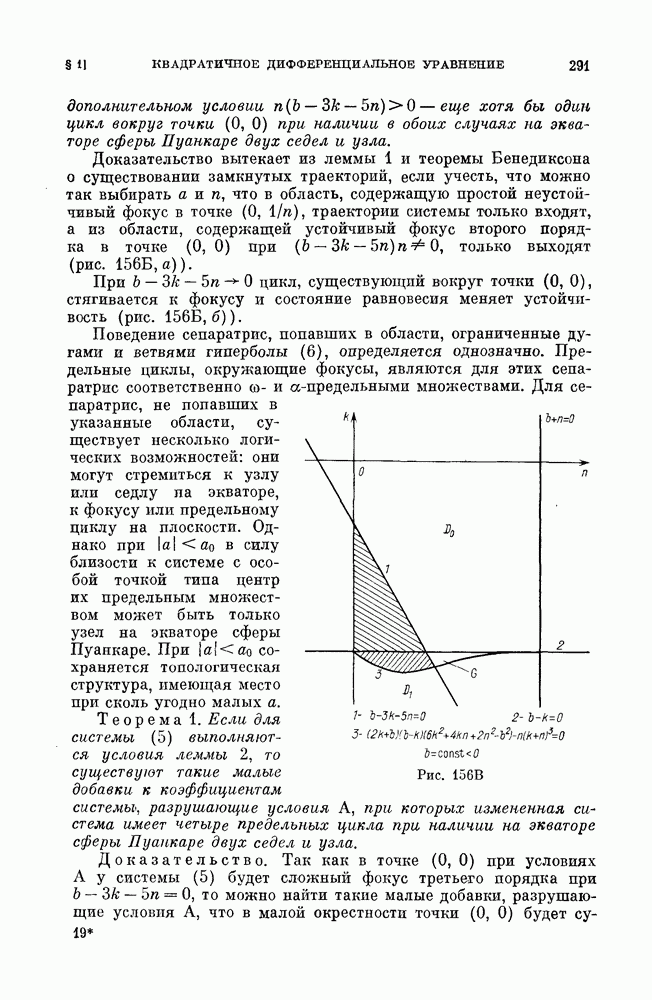
Пример 3 (фазовая автоподстройка частоты). Рассмотрим динамическую систему

которая является одной из моделей фазовой автоподстройки частоты. Мы рассмотрим эту систему в предположении, что  малы. Заменяя 4 на
малы. Заменяя 4 на  и
и  на
на  получим систему с малым параметром
получим систему с малым параметром 

которую рассмотрим методом Понтрягина как близкую к консервативной, получающейся из (11) при  При
При  система (11) имеет интеграл
система (11) имеет интеграл

и семейство кривых имеет вид, представленный на рис. 138, а. Если систему (11) записать в виде

то значения константы  выделяющие кривые консервативной системы, вблизи которых при малом
выделяющие кривые консервативной системы, вблизи которых при малом  на верхнем и нижнем полуцилиндрах будут предельные циклы системы, соответственно определяют как корни уравнений
на верхнем и нижнем полуцилиндрах будут предельные циклы системы, соответственно определяют как корни уравнений

т. е.

Для  уравнения замкнутых кривых
уравнения замкнутых кривых  охватывающих цилиндр, будут
охватывающих цилиндр, будут  а для
а для  будут
будут 
Полагая  мы получим
мы получим

Здесь  -полные эллиптические интегралы соответственно первого и второго рода и к изменяется в интервале
-полные эллиптические интегралы соответственно первого и второго рода и к изменяется в интервале  Верхний знак соответствует индексу 1 в обозначении 1,2, а нижний — индексу 2.
Верхний знак соответствует индексу 1 в обозначении 1,2, а нижний — индексу 2.
Значения константы  выделяющие кривые
выделяющие кривые  консервативной системы, охватывающие состояние равновесия, определяются как корни уравнения
консервативной системы, охватывающие состояние равновесия, определяются как корни уравнения

Здесь

 одна из кривых
одна из кривых  при
при 
Как нетрудно видеть,

где  корень уравнения
корень уравнения  (геометрический смысл
(геометрический смысл  см. рис. 141).
см. рис. 141).
Полагая  (в интервале
(в интервале  для функции Понтрягина
для функции Понтрягина  окончательно получаем
окончательно получаем

Корни уравнений  зависят от параметров
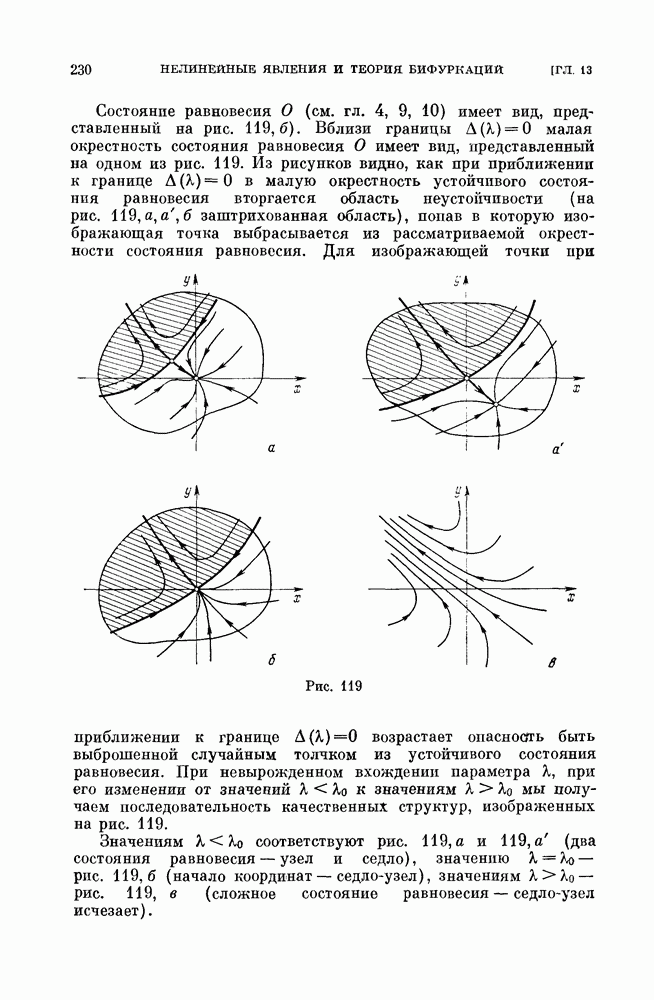
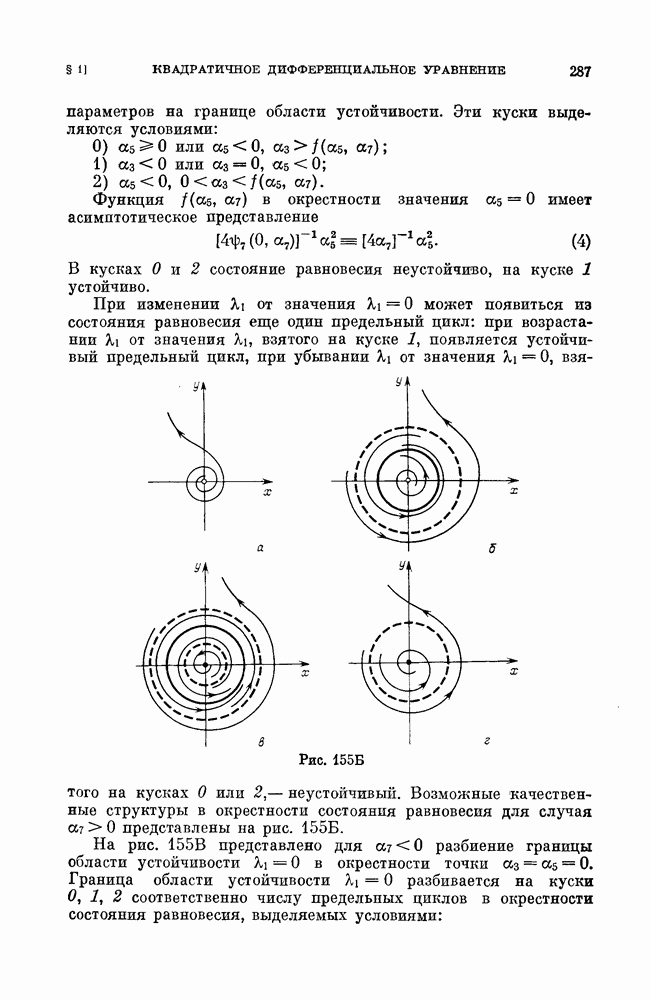
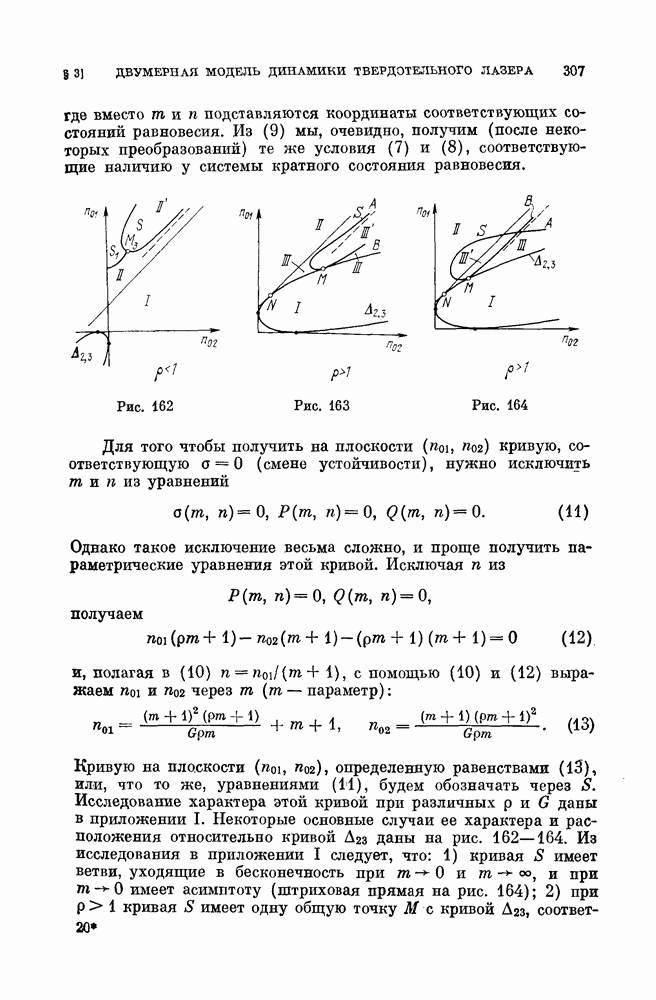
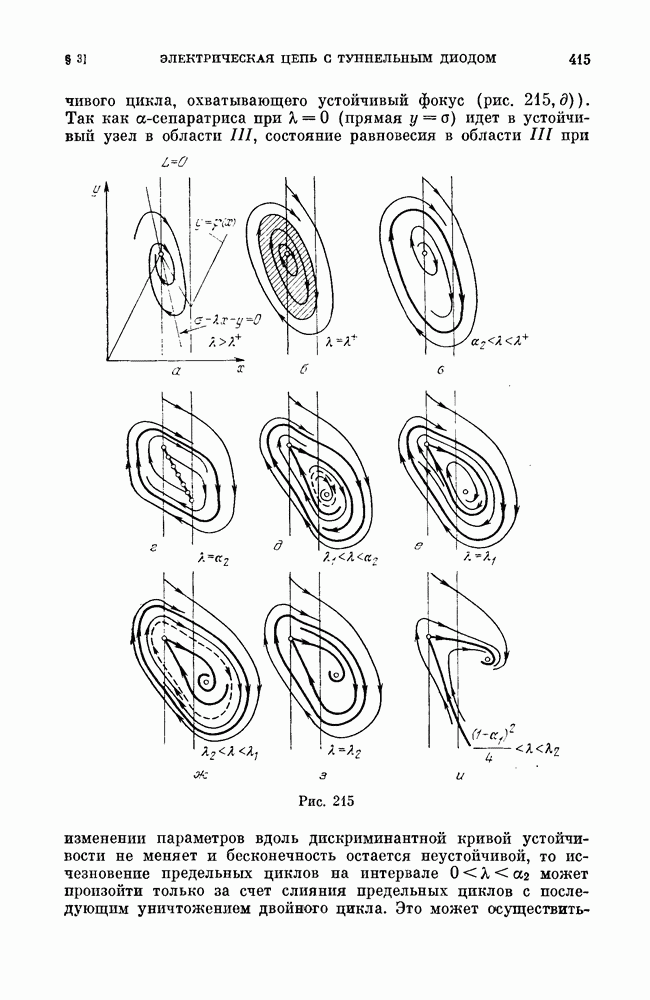
зависят от параметров  Пространство параметров можно разбить на области, соответствующие различным возможным распределениям корней уравнений. Каждому такому распределению будет соответствовать определенная структура разбиения фазового пространства на траектории. Условия появления или исчезновения корней (бифуркации) дают уравнения граничных поверхностей, разбивающих пространство параметров на области.
Пространство параметров можно разбить на области, соответствующие различным возможным распределениям корней уравнений. Каждому такому распределению будет соответствовать определенная структура разбиения фазового пространства на траектории. Условия появления или исчезновения корней (бифуркации) дают уравнения граничных поверхностей, разбивающих пространство параметров на области.

Рис. 141
Для исследования поведения функций Понтрягина вычислим их производные по k. Принимая во внимание, что

из (13) получим

Здесь, как и в (13), верхний знак соответствует индексу 1 и введено обозначение

Заметим, что  для х О всегда положительно (приложение I).
для х О всегда положительно (приложение I).
Вторая производная будет

Для  находим
находим

В дальнейшем будем считать фиксированным  и проследим за возможными бифуркациями в плоскости параметров
и проследим за возможными бифуркациями в плоскости параметров 
1. Бифуркации, связанные с поведением функции ...
Рассмотрим поведение  на интервале
на интервале  Используя разложения
Используя разложения

для малых х из (13) находим

где невыиисанные члены уже не содержат х в знаменателе. Из (22) следует, что

Заметив, что  но
но  при
при  из (13) находим
из (13) находим

Представим выражение для  из (16) в виде
из (16) в виде

из (25) получаем

Покажем, что  может иметь не более одного экстремума (максимума). Это будет следовать из того, что при условии
может иметь не более одного экстремума (максимума). Это будет следовать из того, что при условии  будет всегда
будет всегда  Из (16), (17) видно, что
Из (16), (17) видно, что  обращается в нуль при значении
обращается в нуль при значении

Для  из (18) и (27) находим
из (18) и (27) находим

так как выражения в квадратных скобках положительны в интервале  (приложения I и II).
(приложения I и II).
Сопоставляя (23), (26) и (28), заключаем, что при  функция
функция  будет монотонной (возрастающей); при
будет монотонной (возрастающей); при  она будет иметь один максимум.
она будет иметь один максимум.
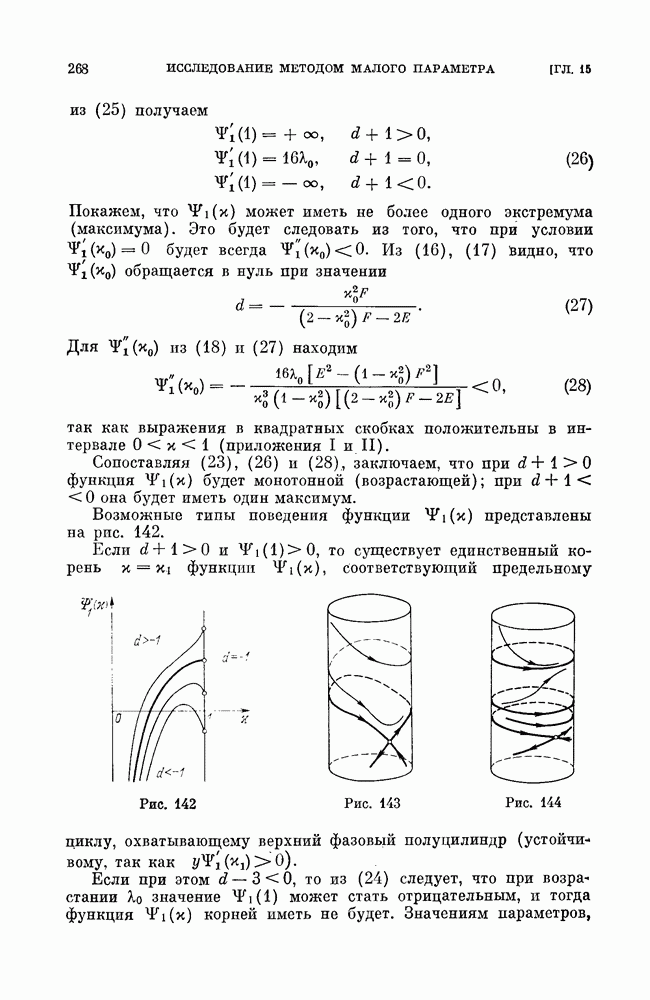
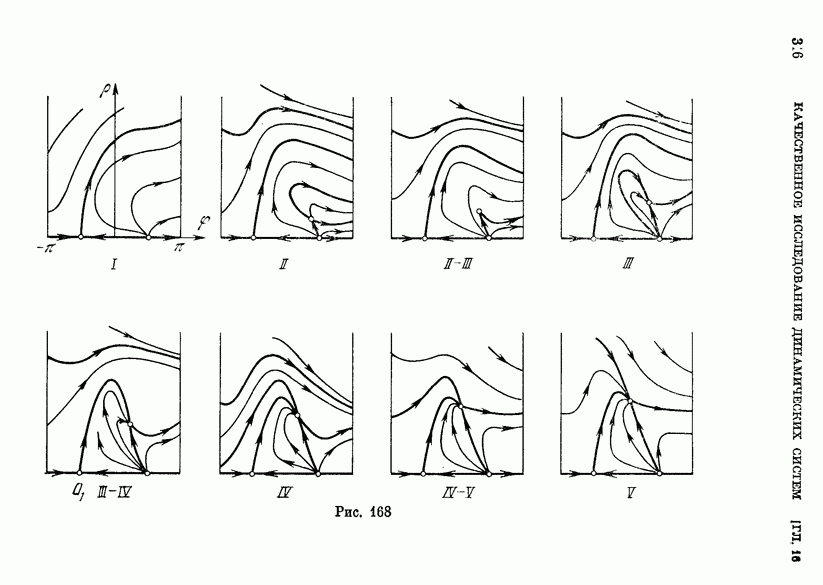
Возможные типы поведения функции  представлены на рис. 142.
представлены на рис. 142.
Если  то существует единственный корень
то существует единственный корень  функции
функции  соответствующий предельному циклу, охватывающему верхний фазовый полуцилиндр (устойчивому, так как
соответствующий предельному циклу, охватывающему верхний фазовый полуцилиндр (устойчивому, так как 

Рис. 142

Рис. 143

Рис. 144
Если при этом  то из (24) следует, что при возрастании ко значение
то из (24) следует, что при возрастании ко значение  может стать отрицательным, и тогда функция
может стать отрицательным, и тогда функция  корней иметь не будет. Значениям параметров,
корней иметь не будет. Значениям параметров,
при которых  соответствует стягивание устойчивого предельного цикла к петле сепаратрисы седла, охватывающей верхний фазовый полуцилиндр (рис. 143).
соответствует стягивание устойчивого предельного цикла к петле сепаратрисы седла, охватывающей верхний фазовый полуцилиндр (рис. 143).
Если  (и, следовательно,
(и, следовательно,  то при
то при  опять существует единственный корень
опять существует единственный корень  но теперь функция
но теперь функция  имеет один максимум и при перемене знака
имеет один максимум и при перемене знака  (при возрастании
(при возрастании  из точки
из точки  появляется второй корень функции
появляется второй корень функции  соответствующий неустойчивому предельному циклу на верхнем фазовом полуцилиндре.
соответствующий неустойчивому предельному циклу на верхнем фазовом полуцилиндре.
На верхнем фазовом полуцилиндре будет два предельных цикла (рис. 144).
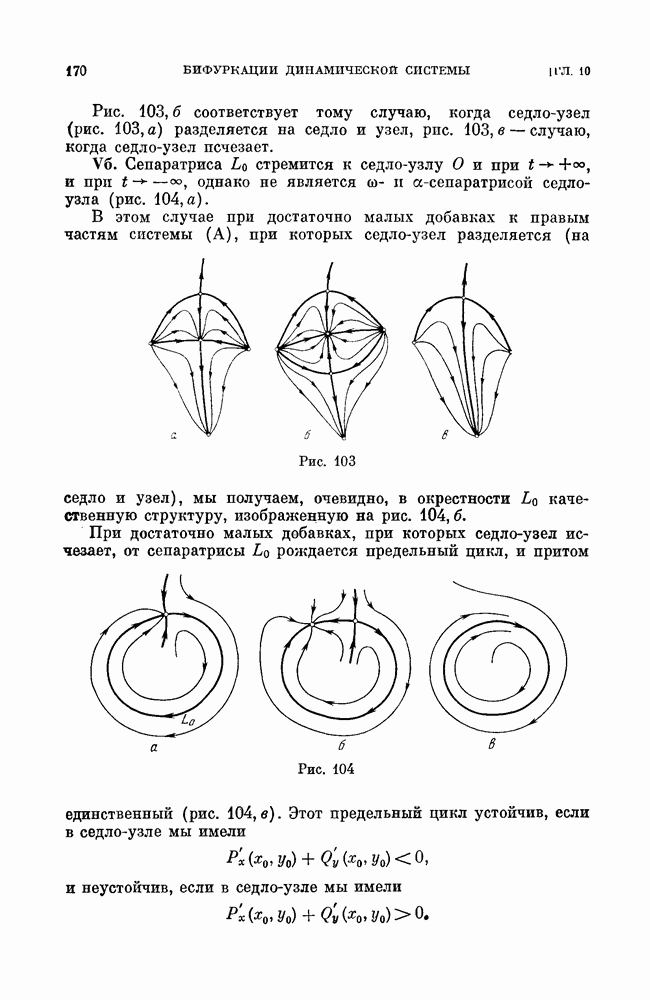
При дальнейшем возрастании  эти циклы сближаются, сливаются в двойной (полуустойчивый) и затем исчезают.
эти циклы сближаются, сливаются в двойной (полуустойчивый) и затем исчезают.
Бифуркационная кривая, соответствующая существованию двойного цикла, определяется условиями

или в параметрическом виде

где  то же, что в (13) и (17).
то же, что в (13) и (17).
Нетрудно обнаружить, что бифуркационная кривая двойных циклов (28) при  уходит в бесконечность (прямая
уходит в бесконечность (прямая  будет асимптотой), а при
будет асимптотой), а при  имеет предельную точку
имеет предельную точку  расположенную на бифуркационной кривой петель сепаратрис
расположенную на бифуркационной кривой петель сепаратрис

2. Бифуркации, связанные с поведением функции ...
Для  из (13) имеем
из (13) имеем

Из (16) видно, что  отличается от
отличается от  только знаком. Поэтому в силу (26) будет
только знаком. Поэтому в силу (26) будет

Кривая  будет иметь экстремум (минимум) лишь для отрицательных значений
будет иметь экстремум (минимум) лишь для отрицательных значений  но из (13) непосредственно обнаруживается, что в этом случае
но из (13) непосредственно обнаруживается, что в этом случае  обращаться в нуль не может, так как квадратная скобка в (13) положительна (приложение III).
обращаться в нуль не может, так как квадратная скобка в (13) положительна (приложение III).
Функция будет иметь единственный корень, соответствующий устойчивому предельному циклу, охватывающему
нижний фазовый полуцилиндр, если  Из условия
Из условия  вытекает, что
вытекает, что  следовательно, выражение (33) при убывании X может менять знак. Обращению в нуль величины
следовательно, выражение (33) при убывании X может менять знак. Обращению в нуль величины  при убывании X соответствует стягивание устойчивого предельного цикла к сепаратрисе седла, охватывающей нижний фазовый полуцилиндр (рис. 145).
при убывании X соответствует стягивание устойчивого предельного цикла к сепаратрисе седла, охватывающей нижний фазовый полуцилиндр (рис. 145).
3. Бифуркации, связанные с поведением функции ...
Перейдем теперь к рассмотрению предельных циклов, рождающихся на кривых центра. Из (15) непосредственно обнаруживается, что при  функция обращаться в нуль не может, так как выражение в квадратных скобках в (15) положительно (приложения I и IV). По критерию Бендиксона при
функция обращаться в нуль не может, так как выражение в квадратных скобках в (15) положительно (приложения I и IV). По критерию Бендиксона при  циклов нет
циклов нет  поэтому
поэтому  при
при  корней также не имеет. Проследим поведение
корней также не имеет. Проследим поведение  при
при 

Рис. 145
Из (15), (19) и (20) получаем

Из (34) и (35) следует, что при любых положительных  кривой
кривой  в интервале
в интервале  существует по крайней мере один экстремум. Нетрудно убедиться, что экстремум (максимум) может быть только один. Мы будем иметь, очевидно,
существует по крайней мере один экстремум. Нетрудно убедиться, что экстремум (максимум) может быть только один. Мы будем иметь, очевидно,  если
если  такое, что обращается в нуль выражение в квадратной скобке в (19), т. е. если
такое, что обращается в нуль выражение в квадратной скобке в (19), т. е. если

Нетрудно видеть, что при условии (36) будет

так как квадратная скобка знака не меняет (дискриминант отрицателен) и 
Так как  то экстремум кривой
то экстремум кривой  является максимумом.
является максимумом.
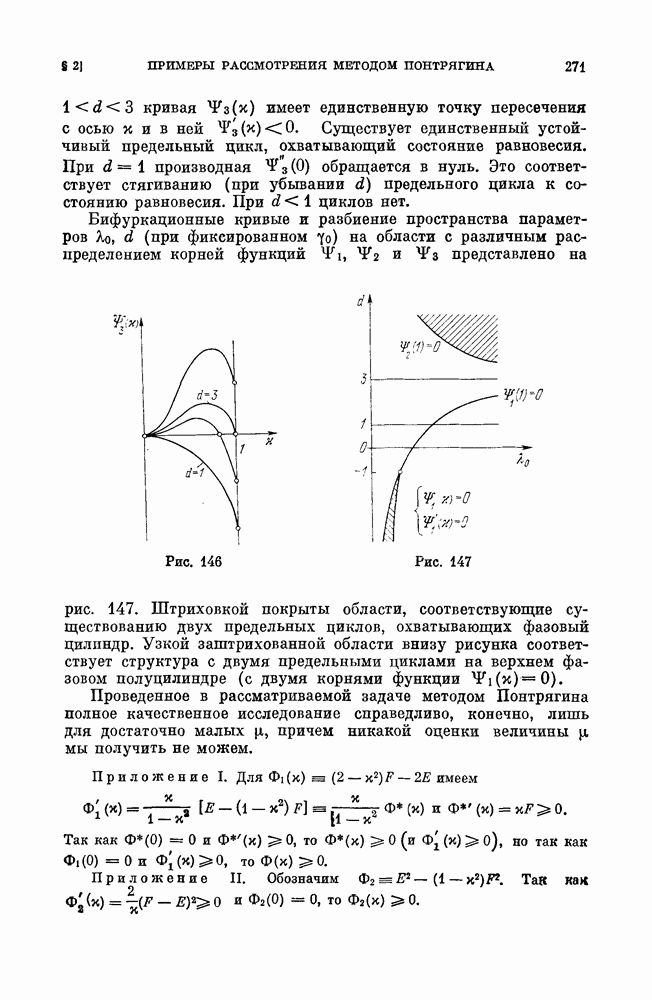
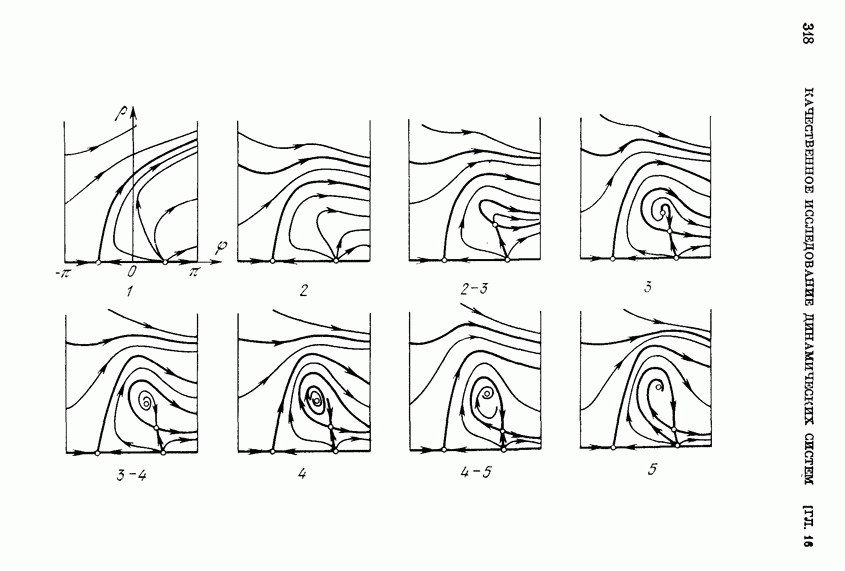
Вид кривой при различных  приведен на рис. 146. При
приведен на рис. 146. При  кривая не пересекает ось к — циклов нет. При
кривая не пересекает ось к — циклов нет. При  будет
будет  это соответствует возникновению предельного цикла, охватывающего состояние равновесия. При
это соответствует возникновению предельного цикла, охватывающего состояние равновесия. При
 кривая имеет единственную точку пересечения с осью х и в ней
кривая имеет единственную точку пересечения с осью х и в ней  Существует единственный устойчивый предельный цикл, охватывающий состояние равновесия. При
Существует единственный устойчивый предельный цикл, охватывающий состояние равновесия. При  производная
производная  обращается в нуль. Это соответствует стягиванию (при убывании
обращается в нуль. Это соответствует стягиванию (при убывании  ) предельного цикла к состоянию равновесия. При
) предельного цикла к состоянию равновесия. При  циклов нет.
циклов нет.
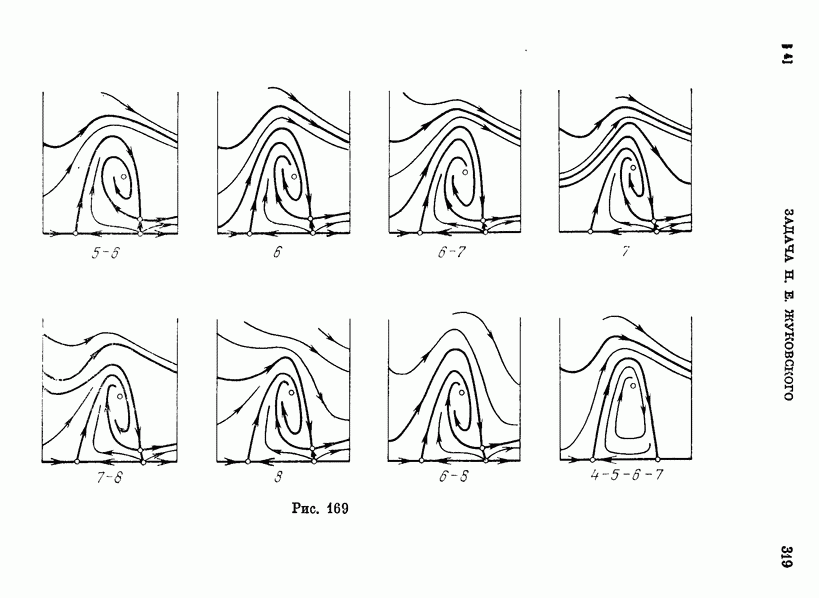
Бифуркационные кривые и разбиение пространства параметров  (при фиксированном
(при фиксированном  на области с различным распределением корней функций
на области с различным распределением корней функций  представлено на рис. 147.
представлено на рис. 147.

Рис. 146

Рис. 147
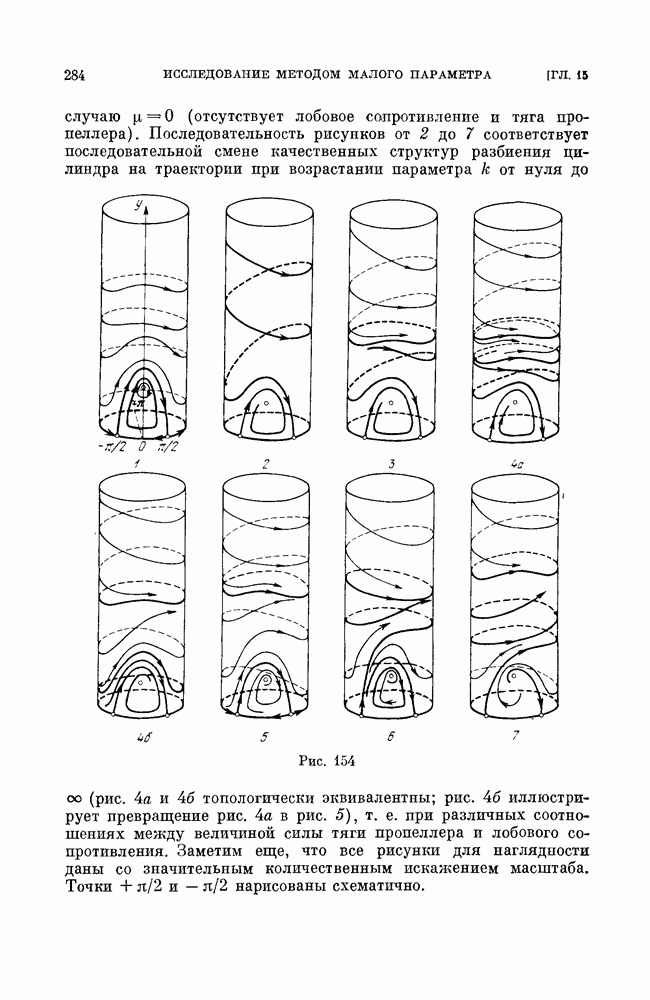
Штриховкой покрыты области, соответствующие существованию двух предельных циклов, охватывающих фазовый цилиндр. Узкой заштрихованной области внизу рисунка соответствует структура с двумя предельными циклами на верхнем фазовом полуцилиндре (с двумя корнями функции  ).
).
Проведенное в рассматриваемой задаче методом Понтрягина полное качественное исследование справедливо, конечно, лишь для достаточно малых  причем никакой оценки величины
причем никакой оценки величины  мы получить не можем.
мы получить не можем.
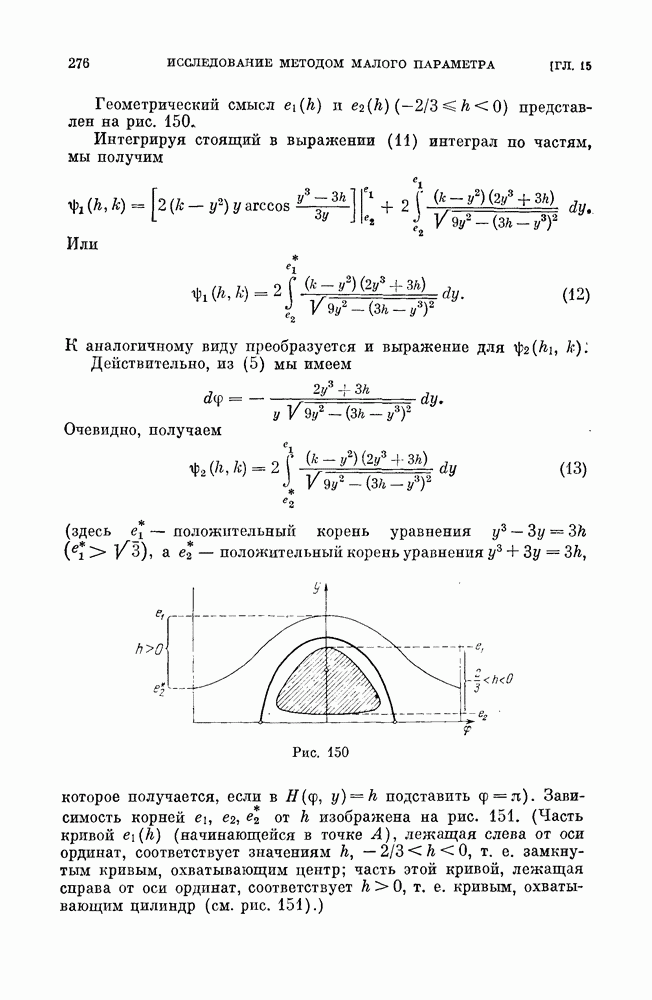
Приложение I. Для  имеем
имеем

Так как  то
то  но так как
но так как 
Приложение II. Обозначим  Так как
Так как  то
то 
Приложение III. Обозначим  Так как
Так как

Приложение IV. Обозначим  имеем
имеем

Функция  принимает на концах интервала
принимает на концах интервала  значения
значения  и 1 и имеет внутри интервала единственный максимум
и 1 и имеет внутри интервала единственный максимум  . Следовательно,
. Следовательно,  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. АВТОНОМНЫЕ СИСТЕМЫ ВТОРОГО ПОРЯДКА С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- § 1. Автономная динамическая система на плоскости.
- § 2. Теорема существования и единственности решения.
- § 3. Простейшие свойства решений системы (А).
- § 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
- § 5. Сопоставление геометрической интерпретации системы (А) в пространстве (x, y, t) с интерпретацией на фазовой плоскости.
- § 6. Некоторые термины.
- § 7. Теорема о непрерывной зависимости решения от начальных условий.
- § 8. Направление на траекториях. Изменение параметризации.
- § 9. Дифференциальное уравнение, соответствующее динамической системе.
- § 10. Понятие интегральной кривой и интеграла в случае аналитических правых частей Р(х,у) и Q(x,y) системы (А).
- § 11. Что значит «найти решение динамической системы»?
- § 12. Примеры.
- § 13. Замечания по поводу примеров § 12.
- § 14. Математическое определение качественной (топологической) структуры разбиения на траектории и качественного исследования динамической системы.
- ГЛАВА 2. ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ — БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ
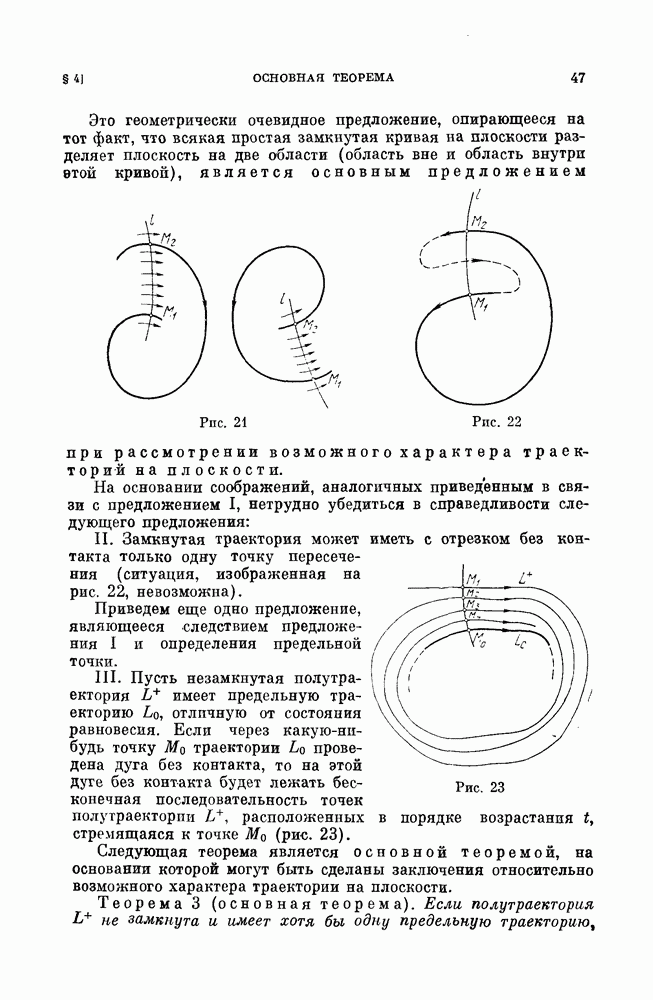
- § 2. Цикл без контакта.
- § 3. Предельная точка полутраектории и траектории. Предельная траектория.
- § 4. Основная теорема.
- § 5. Возможные типы полутраекторий и их предельных множеств.
- § 6. Особые и неособые полутраектории и траектории.
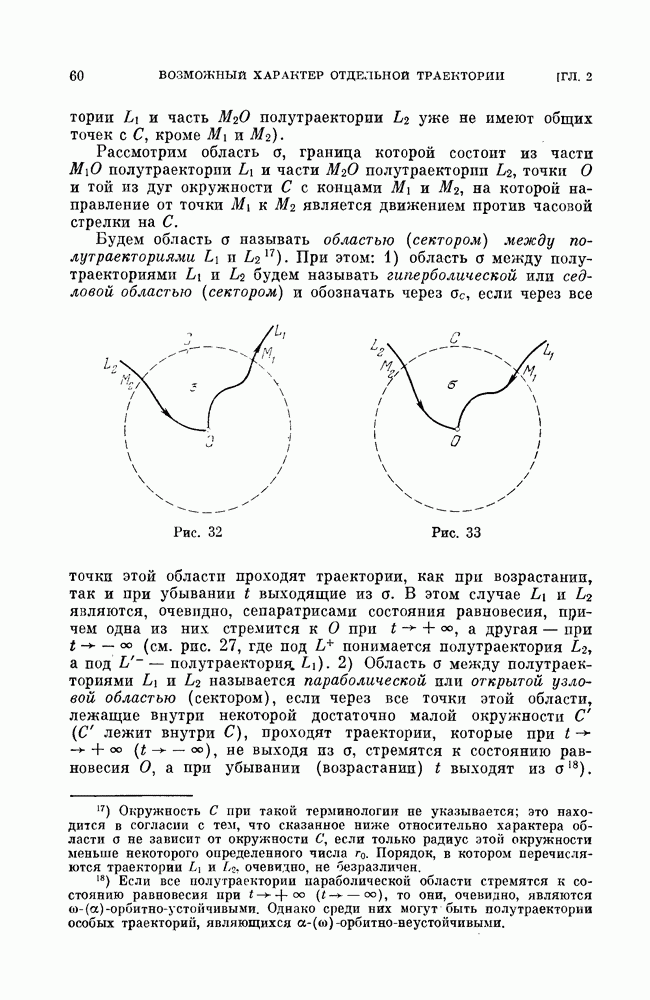
- § 7. Возможные типы особых и неособых траекторий.
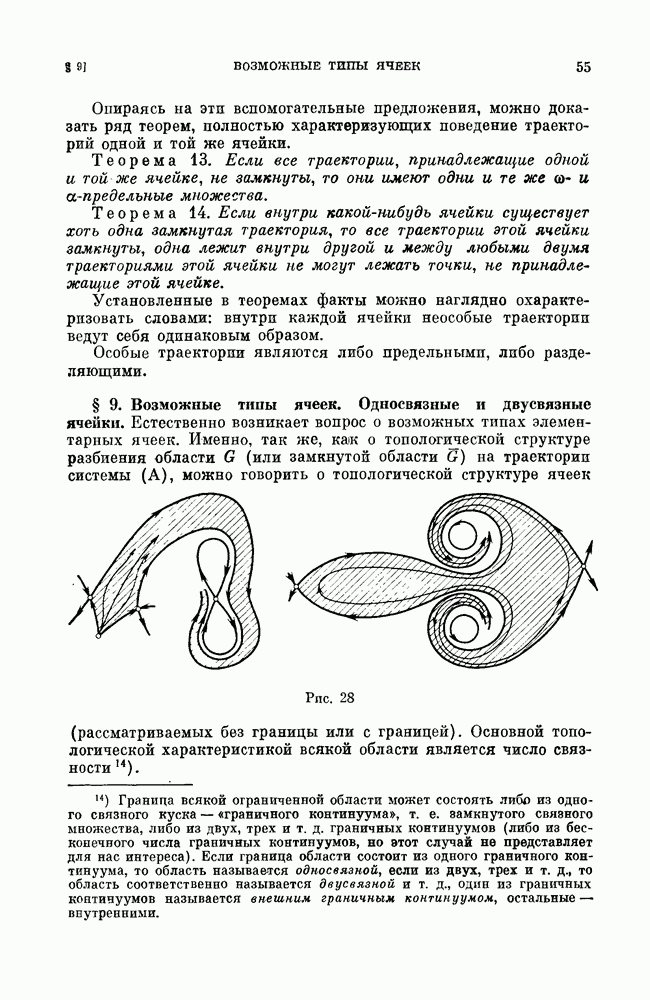
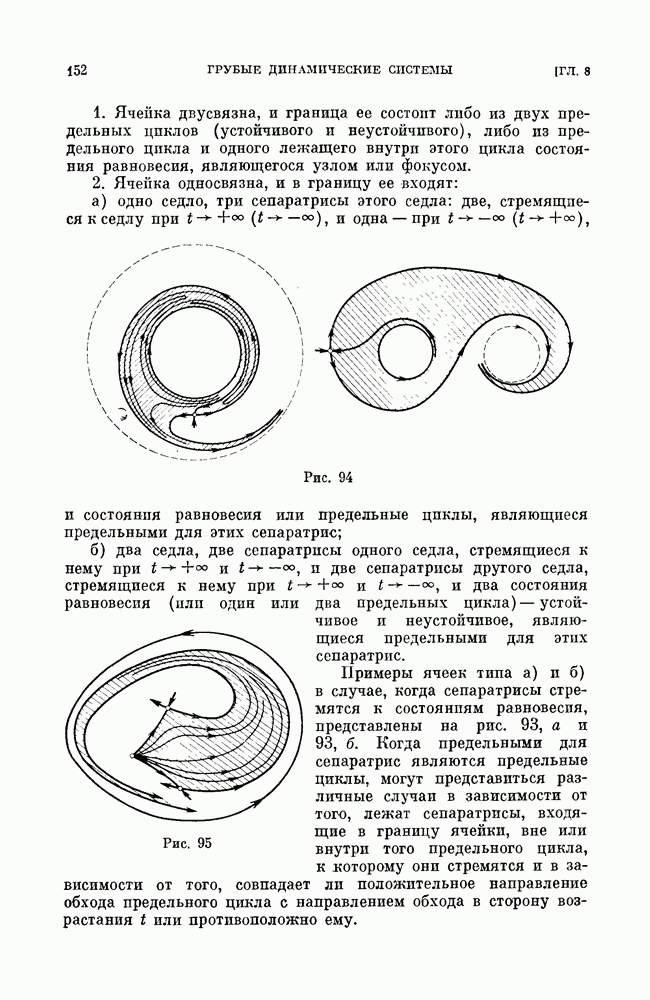
- § 8. Случай конечного числа особых траекторий. Элементарные ячейки.
- § 9. Возможные типы ячеек. Односвязные и двусвязные ячейки.
- § 10. Два подхода к описанию качественной структуры.
- § 11. Качественная (топологическая) структура состояния равновесия в случае конечного числа особых траекторий. Схема динамической системы.
- § 12. Устойчивость по Ляпунову.
- ГЛАВА 3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННОЙ СТРУКТУРЫ ОКРЕСТНОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (ОСОБОЙ ТОЧКИ)
- § 2. Приведение динамической системы к каноническому виду.
- § 3. Возможный характер простых состояний равновесия.
- § 4. Замечания о методах установления характера грубых состояний равновесия.
- § 5. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 6. Направления, в которых траектории стремятся к простым состояниям равновесия.
- § 7. Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия.
- § 8. Сводка сведений о грубых состояниях равновесия.
- ГЛАВА 4. КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ
- § 1. Направления, в которых траектории стремятся к сложному состоянию равновесия.
- § 2. Сложное состояние равновесия (особая точка) с нулевыми характеристическими корнями.
- § 3. Примеры.
- § 4. Нормальные формы.
- ГЛАВА 5. ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ
- § 2. Условия устойчивости и неустойчивости неподвижной точки точечного отображения.
- § 3. Функция соответствия.
- § 4. Изучение окрестности замкнутой траектории. Простые и сложные предельные циклы.
- § 5. Аналитические выражения для коэффициентов функции последования. Характеристический показатель замкнутой траектории.
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЕМЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 2. Изучение поведения интегральных кривых в бесконечности. Сфера Пуанкаре.
- § 3. Примеры исследования в бесконечности [93].
- § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов.
- 1. Некоторые видоизменения критериев Бендиксона и Дюлака.
- 2. Индексы Пуанкаре. Распределение особых точек [77, 117].
- 3. Условия сосуществования замкнутых траекторий и особых точек.
- 4. Две общие теоремы Пуанкаре.
- § 5. Топографическая система Пуанкаре. Функция Ляпунова. Кривые контактов.
- ЧАСТЬ II. ТЕОРИЯ БИФУРКАЦИЙ
- § 1. Свойства консервативных систем на плоскости [2, 3].
- § 2. Динамические системы, характерные для теории колебаний.
- § 3. Измененные системы. Системы, правые части которых зависят от параметра.
- § 4. Основные теоремы о зависимости решения от изменения правых частей динамической системы.
- § 5. Грубость динамической системы и теоремы о непрерывной зависимости решения от изменения правых частей.
- ГЛАВА 8. ГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
- § 2. Состояния равновесия, возможные в грубой динамической системе.
- § 3. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 4. Замкнутые траектории, возможные в грубой системе.
- § 5. Поведение сепаратрис седел в грубых системах.
- § 6. Необходимые условия грубости. Достаточность этих условий для грубости системы.
- § 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем.
- § 8. Понятие грубости при более общих предположениях относительно правых частей динамической системы.
- § 9. Типы особых траекторий и ячеек в грубых системах.
- § 10. Замечания по поводу определения грубой системы.
- ГЛАВА 9. ПРОСТЕЙШИЕ НЕГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ — СИСТЕМЫ ПЕРВОЙ СТЕПЕНИ НЕГРУБОСТИ
- § 2. Системы первой степени негрубости.
- § 3. Состояния равновесия, возможные в системе первой степени негрубости.
- § 4. Замкнутые траектории, возможные в системе первой степени негрубости.
- § 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости.
- § 6. Необходимые и достаточные условия первой степени негрубости.
- § 7. Динамические системы более высокой степени негрубости.
- ГЛАВА 10. БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- § 1. Определение бифуркации.
- § 2. Бифуркации систем первой степени негрубости.
- § 3. Бифуркации некоторых типов сложных особых точек.
- § 4. Бифуркации двукратной точки, для которой …
- § 5. Рождение предельных циклов из особых траекторий степени негрубости выше первой.
- ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
- § 1. Возможный характер зависимости правых частей динамической системы от параметров.
- § 2. Смена качественных структур при изменении параметров.
- § 3. Случай, когда правые части зависят более чем от одного параметра.
- § 4. Бифуркации «от бесконечности».
- § 5. Условия существования седло-узла и сложного фокуса первого порядка.
- § 6. Поворот векторного поля.
- § 7. Метод малого параметра. Метод Понтрягина.
- ГЛАВА 12. ДИНАМИЧЕСКИЕ СИСТЕМЫ С ЦИЛИНДРИЧЕСКОЙ ФАЗОВОЙ ПОВЕРХНОСТЬЮ
- § 1. Цилиндрическая фазовая поверхность и характер траекторий, возможных на цилиндрической фазовой поверхности.
- § 2. Замкнутые траектории, охватывающие цилиндр.
- § 3. Приемы исследования качественной структуры динамической системы на цилиндре.
- § 4. Понятие грубости и степени негрубости для динамических систем на цилиндре. Бифуркации на цилиндре. Поворот поля.
- § 5. Динамические системы на цилиндре, близкие к гамильтоновым (метод Понтрягина).
- ГЛАВА 13. АДЕКВАТНОЕ ИСТОЛКОВАНИЕ НЕЛИНЕЙНЫХ ФИЗИЧЕСКИХ ЯВЛЕНИЙ ФАКТАМИ КАЧЕСТВЕННОЙ ТЕОРИИ И ТЕОРИИ БИФУРКАЦИЙ ДИНАМИЧЕСКИХ СИСТЕМ
- § 1. Мягкий и жесткий режимы.
- § 2. Замечания о границах области устойчивости различных стационарных режимов.
- § 3. Мягкое и жесткое возникновение колебаний.
- § 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
- § 5. Замечания по поводу других границ области устойчивости.
- ЧАСТЬ III. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- ГЛАВА 14. ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 1. Некоторые рецептурные указания.
- § 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
- § 3. Некоторые простые примеры динамических систем на цилиндре.
- ГЛАВА 15. ИССЛЕДОВАНИЕ МЕТОДОМ МАЛОГО ПАРАМЕТРА (МЕТОДОМ ПОНТРЯГИНА)
- § 2. Примеры рассмотрения методом Понтрягина (полное исследование).
- § 3. Исследование методом Понтрягина с привлечением вычислительных методов.
- ГЛАВА 16. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ
- § 2. Электрическая цепь с туннельным диодом.
- § 3. Двумерная модель динамики твердотельного лазера [119].
- § 4. Симметричный полет самолета в вертикальной плоскости (задача Н. Е. Жуковского).
- § 5. Система, описывающая динамику проточного химического реактора.
- § 6. Фазовая автоподстройка частоты.
- § 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов).
- § 8. Синхронный генератор с асинхронной характеристикой.
- ЧАСТЬ IV. КУСОЧНО-СШИТЫЕ СИСТЕМЫ
- ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ
- § 1. Сшитые системы. Доопределение на линиях сшивания.
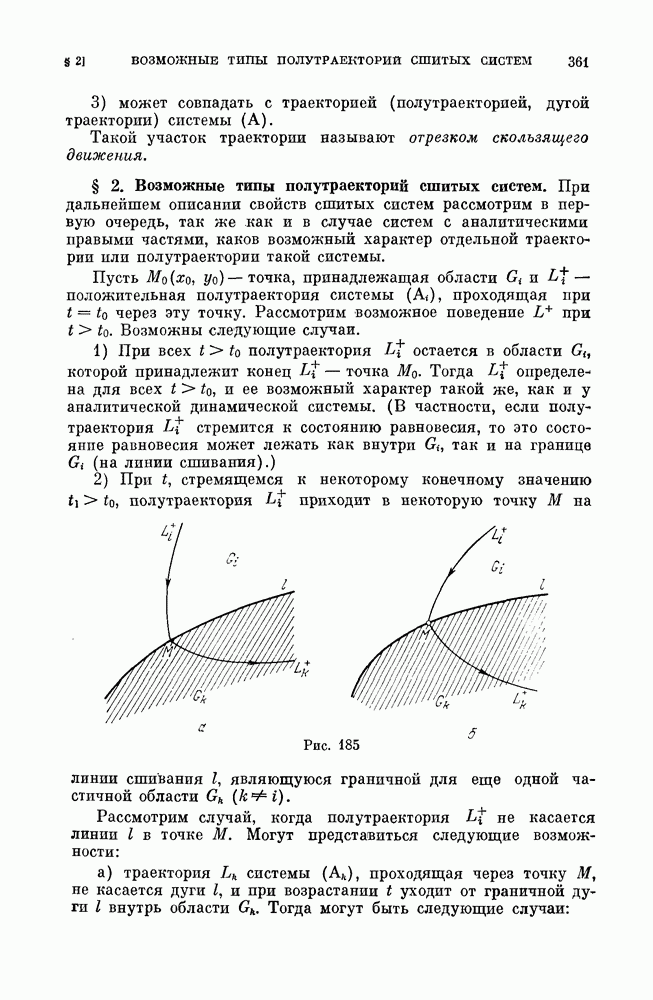
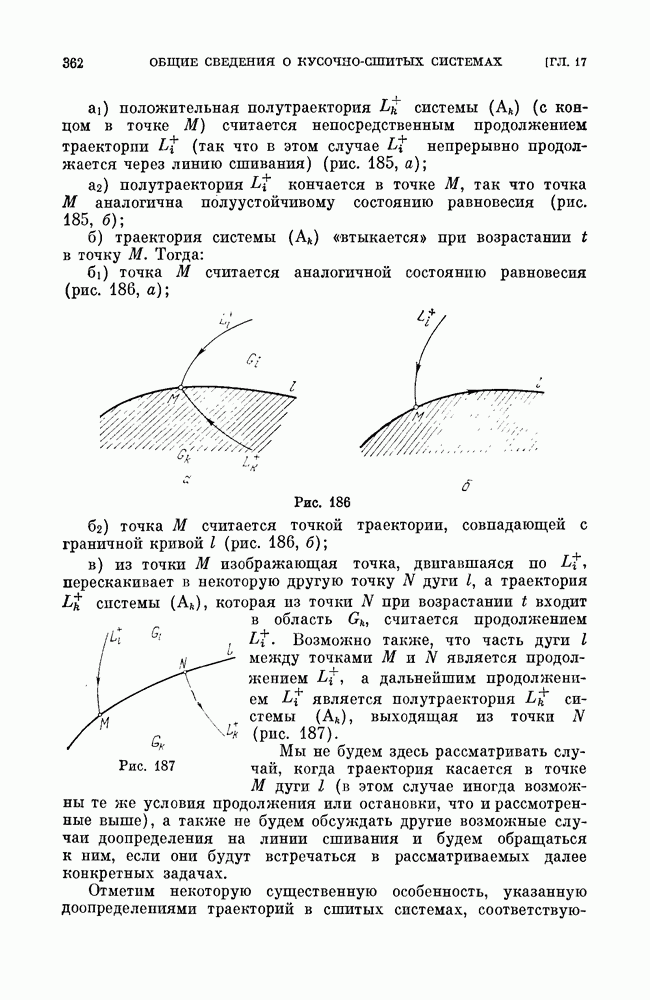
- § 2. Возможные типы полутраекторий сшитых систем.
- § 3. Особые траектории сшитых систем.
- § 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
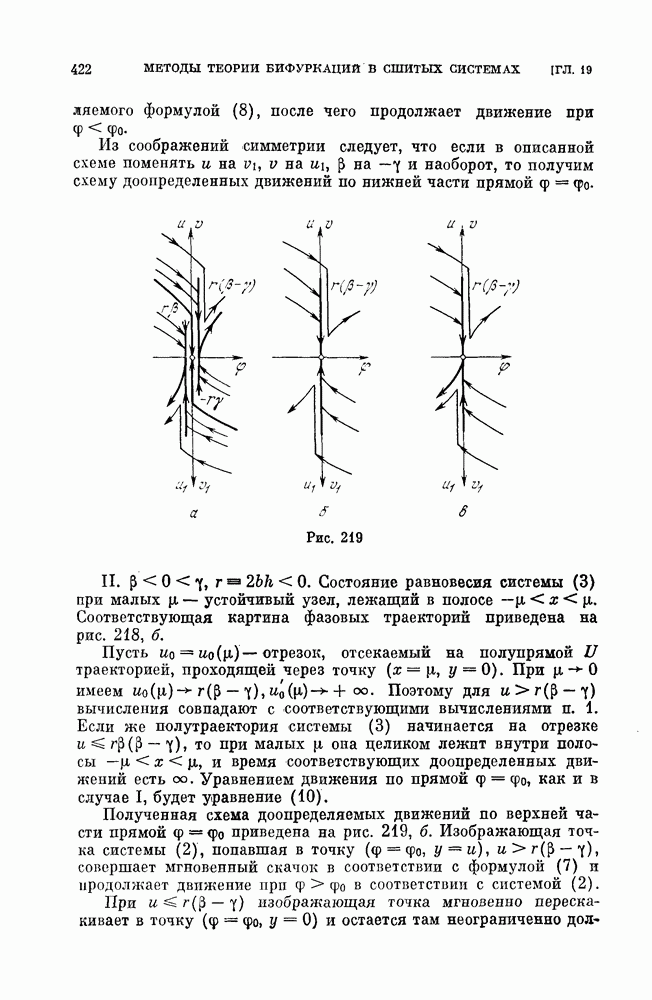
- ГЛАВА 18. ИССЛЕДОВАНИЕ КУСОЧНО-СШИТЫХ СИСТЕМ МЕТОДОМ ПОНТРЯГИНА
- § 2. Автоподстройка при кусочно-постоянной аппроксимации характеристики.
- § 3. Автоколебания синхронного мотора.
- ГЛАВА 19. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ
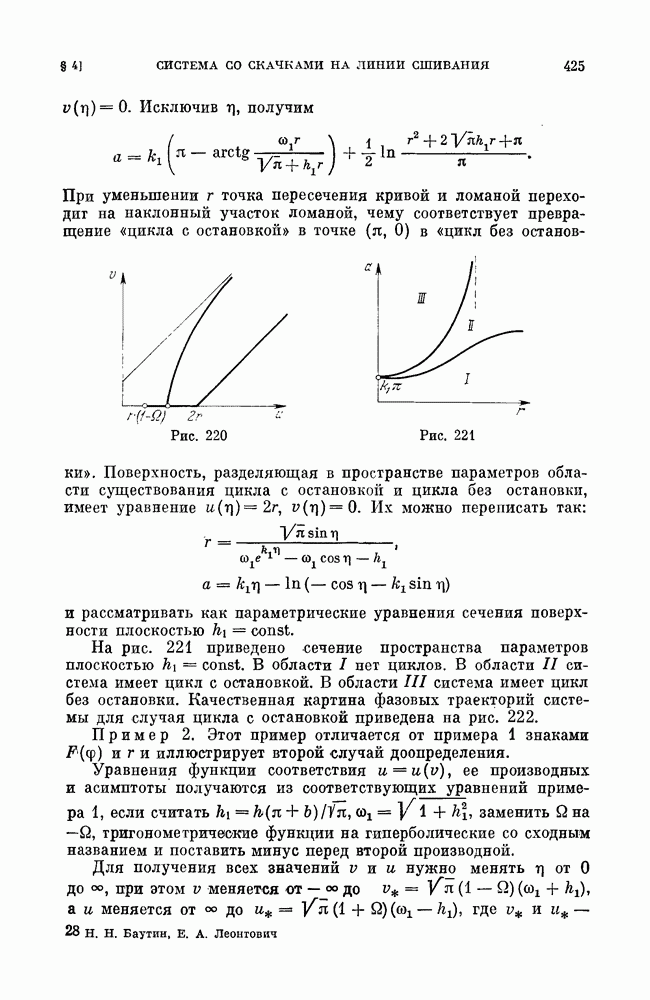
- § 2. Следящая система с люфтом.
- § 3. Электрическая цепь с туннельным диодом.
- § 4. Система со скачками на линии сшивания.
- ГЛАВА 20. ОБ АППРОКСИМАЦИЯХ И ГРУБОСТИ ПРОСТРАНСТВА ПАРАМЕТРОВ [39, 41, 42]
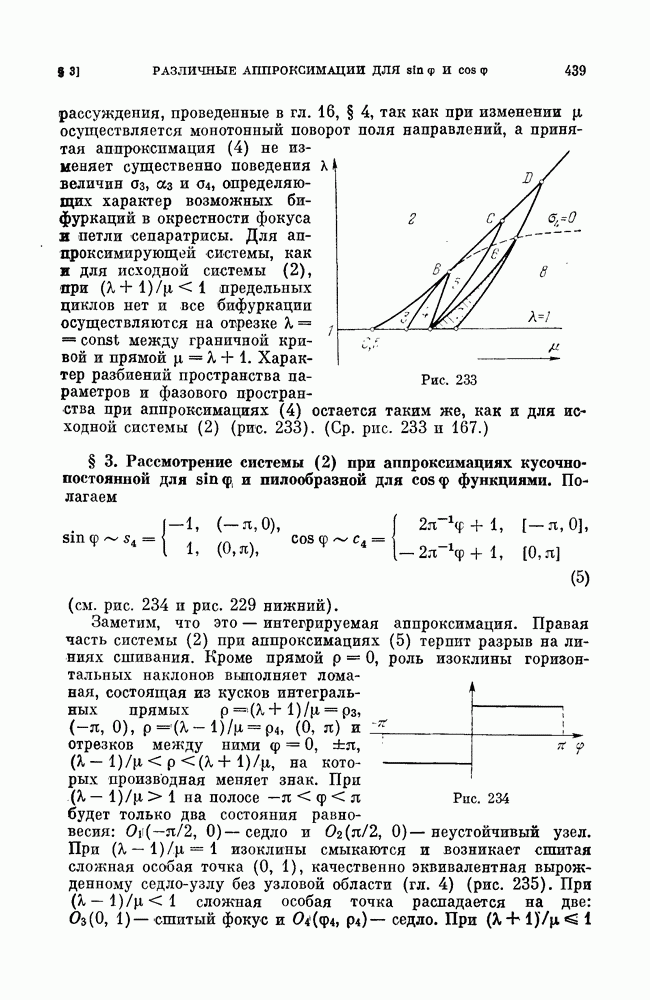
- § 1. Рассмотрение системы (2) при аппроксимациях пилообразными функциями.
- § 2. Рассмотрение системы (2) при аппроксимации, включающей отрезок параболы.
- § 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin f, и пилообразной для cos f функциями.
- § 4. Исследование роли аппроксимаций для уравнения маятникового типа.
- § 5. Динамическая система, описывающая автоколебания синхронного мотора.
- § 6. Динамическая система, описывающая симметричный полет самолета.
- ДОПОЛНЕНИЕ
- § 1. Динамическое системы на двумерных поверхностях.
- § 2. Динамические системы в n-мерном евклидовом пространстве.
- СПИСОК ЛИТЕРАТУРЫ