| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Динамические системы в n-мерном евклидовом пространстве.
Существенные отличия от систем на плоскости и от систем на поверхностях обнаруживаются уже при  . В трехмерной
. В трехмерной
системе

наряду с состояниями равновесия и замкнутыми траекториями возможны траектории всех тех типов, что и на двумерных поверхностях и, в частности, незамкнутые устойчивые по Пуассону (незамкнутые самопредельные).
Однако установление всех возможных типов траекторий, аналогичное теории Пуанкаре — Бендиксона  для случая
для случая  значительно сложнее. У динамической системы на плоскости, если траектория
значительно сложнее. У динамической системы на плоскости, если траектория  имеет незамкнутую предельную траекторию
имеет незамкнутую предельную траекторию  то
то  среди своих предельных точек может иметь только состояния равновесия. В динамических системах числа измерений
среди своих предельных точек может иметь только состояния равновесия. В динамических системах числа измерений  возможна бесконечная цепочка траекторий, обладающих тем свойством, что все они отличны от состояния равновесия и каждая траектория
возможна бесконечная цепочка траекторий, обладающих тем свойством, что все они отличны от состояния равновесия и каждая траектория  является предельной для
является предельной для  Пример такой динамической системы с неаналитической правой частью см. [96]. Вопрос о возможности такой же ситуации в аналитической системе остается открытым.
Пример такой динамической системы с неаналитической правой частью см. [96]. Вопрос о возможности такой же ситуации в аналитической системе остается открытым.
Обратимся к вопросу о перенесении понятий, введенных для двумерных систем, на трехмерные и большего числа измерений. Рассмотрим, какой характер имеют простейшие «грубые» состояния равновесия и предельные циклы трехмерной системы. Возможны следующие случаи грубых состояний равновесия:
а) узел и фокус, устойчивый или неустойчивый, когда все траектории, достаточно близкие к состоянию равновесия, стремятся к нему при  или
или 
б) седло и седло-фокус у седла и седло-фокуса есть двумерная сепаратрисная поверхность и две изолированные сепаратрисы (по разные стороны от сепаратрисной поверхности); на сепаратрисной поверхности седла есть узел, а на сепаратрисной поверхности седло-фокуса — фокус; все другие траектории, проходящие через достаточно малую окрестность седла и седло-фокуса, выходят из его окрестности и при возрастании, и при убывании 
Качественный характер седла и седло-фокуса тождествен (в смысле, полностью аналогичном такому понятию, введенному для двумерных систем).
Характер указанных состояний равновесия наглядно и просто можно посмотреть на примере линейных систем. Для системы

в начале координат при  будет седло, а при
будет седло, а при  седло-фокус.
седло-фокус.
Аналогично тому, как окрестность предельного цикла двумерной динамической системы изучается с помощью функции последования, в трехмерном пространстве окрестность замкнутой траектории изучается с помощью «отображения Пуанкаре»
отображения в себя трансверсальной к циклу площадки а. Точка пересечения площадки с циклом есть инвариантная точка отображения.
Возможны следующие случаи грубых предельных циклов: устойчивый (неустойчивый) предельный цикл, когда все достаточно близкие к циклу траектории стремятся к нему при  и седловой предельный цикл, который может быть двух типов. У седлового предельного цикла первого типа есть четыре двумерные сепаратрисные поверхности: две примыкающие к нему трубки и два примыкающих к нему кольца. На двух из сепаратрисных поверхностей (ю-сепаратрисах) все траектории вида спиралей стремятся к циклу при
и седловой предельный цикл, который может быть двух типов. У седлового предельного цикла первого типа есть четыре двумерные сепаратрисные поверхности: две примыкающие к нему трубки и два примыкающих к нему кольца. На двух из сепаратрисных поверхностей (ю-сепаратрисах) все траектории вида спиралей стремятся к циклу при  на двух других (
на двух других ( -сепаратрисах) — при
-сепаратрисах) — при  седлового цикла второго типа сепаратрисными поверхностями являются два листа Мёбиуса
седлового цикла второго типа сепаратрисными поверхностями являются два листа Мёбиуса  и
и  -сепаратрисные поверхности). Все остальные траектории из окрестности седлового предельного цикла выходят из окрестности и при возрастании, и при убывании
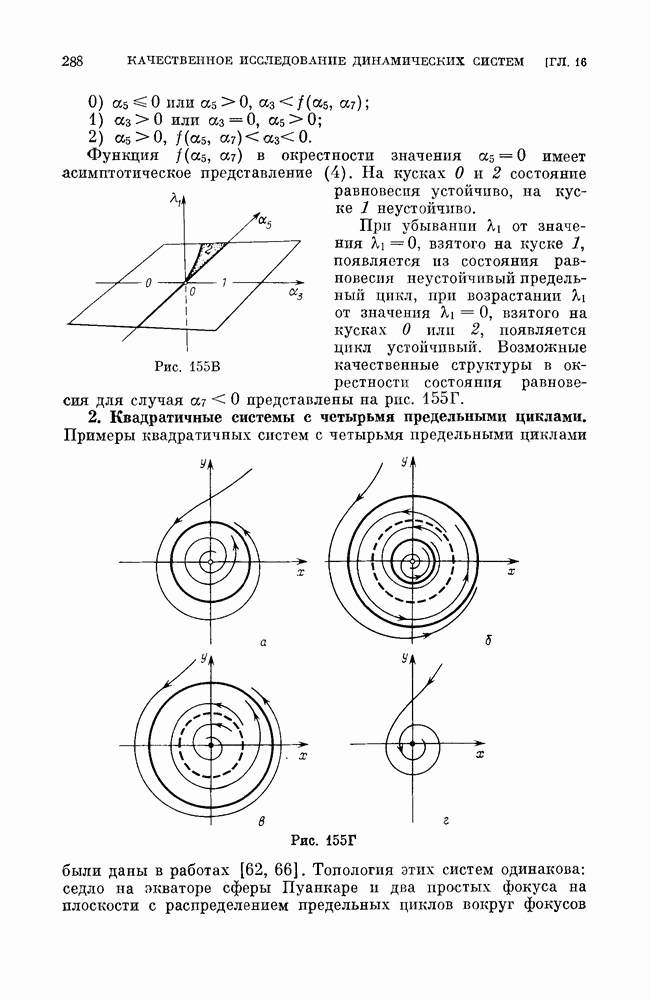
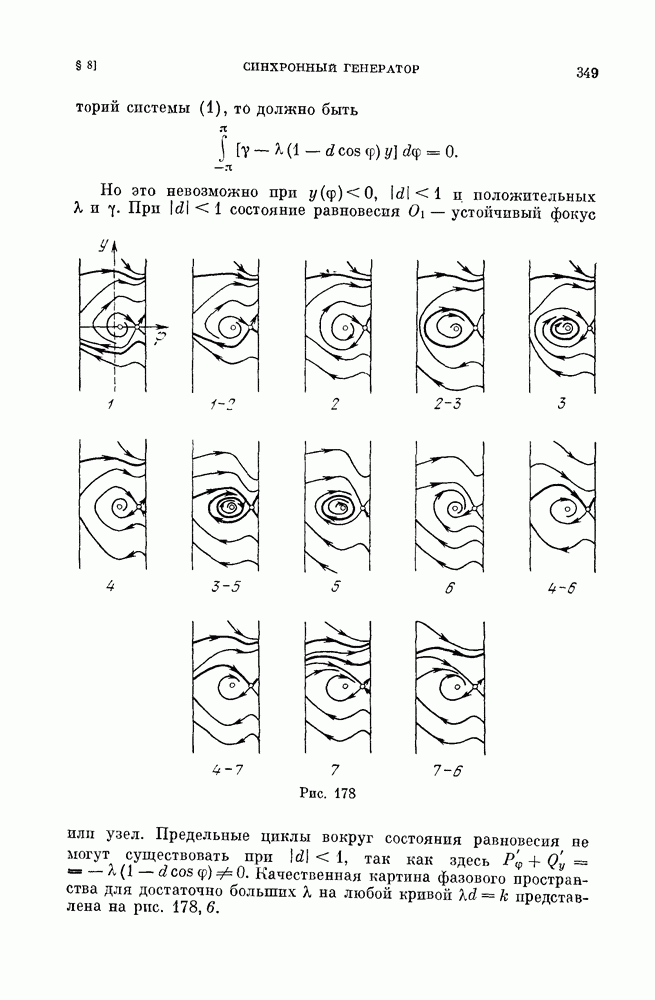
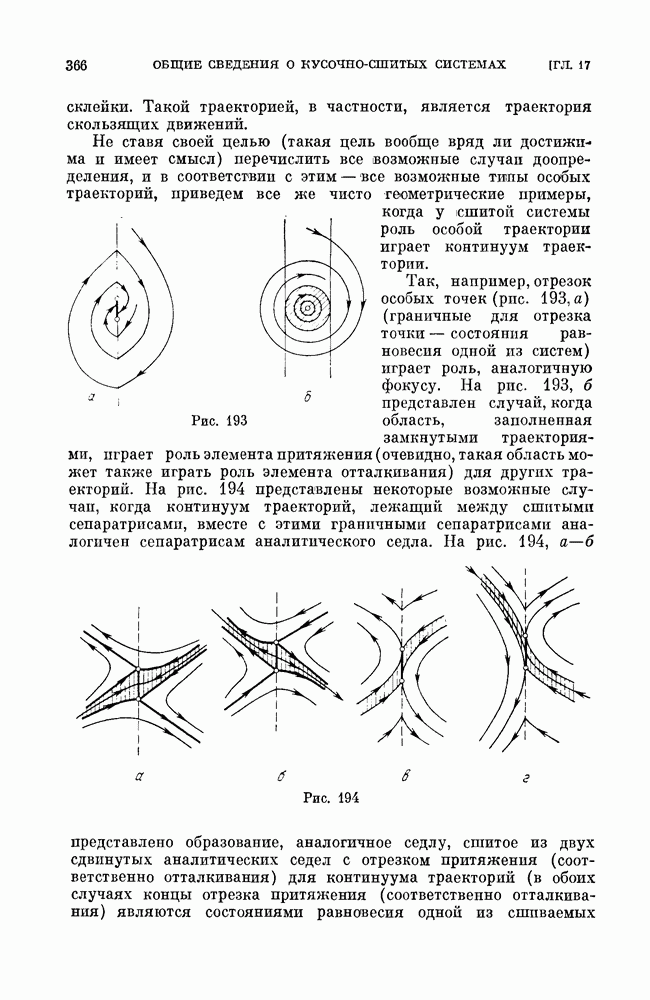
-сепаратрисные поверхности). Все остальные траектории из окрестности седлового предельного цикла выходят из окрестности и при возрастании, и при убывании  На рис. 252 представлен седловой предельный цикл первого типа (сепаратрисные поверхности не показаны).
На рис. 252 представлен седловой предельный цикл первого типа (сепаратрисные поверхности не показаны).

Рис. 252
Подчеркнем одно характерное для многомерных систем свойство: сепаратрисные поверхности разных седел и седловых предельных циклов могут пересекаться или касаться по общей для них траектории. Случай их трансверсального (без касания) пересечения является грубым.
Обратимся теперь к вопросу о перенесении понятий, введенных для двумерных систем, на трехмерные и большего числа измерений и в первую очередь — понятия грубости. И здесь ситуация осложняется. Надо иметь в виду, что рассмотрение вопроса о грубости трехмерных систем тесно связано с рассмотрением грубости отображения плоской области в себя или плоскости в плоскость. Полностью необходимые и достаточные условия грубости трехмерных систем еще не установлены. Выделены только классы грубых систем, удовлетворяющих некоторым достаточным условиям грубости. Это, в первую очередь, системы Морса — Смейла, удовлетворяющие условиям:
1) число состояний равновесия конечно и все состояния равновесия грубые;
2) число замкнутых траекторий конечно и все траектории грубые;
3) сепаратрисные поверхности различных седел и седловых предельных циклов пересекаются трансверсально (без касания).
Несмотря на простую и естественную формулировку этих достаточных условий, возможная качественная структура систем Морса — Смейла может быть очень сложной. У таких систем может быть счетное множество «ячеек». Существуют также примеры грубых динамических систем со счетным множеством седловых предельных циклов с неограниченно увеличивающимся периодом. Впервые такой пример был построен американским математиком Смейлом (см. список дополнительной литературы [42]). Примеры грубых систем со счетным множеством устойчивых или неустойчивых циклов с неограниченно увеличивающимся периодом отсутствуют. Доказательство того, что в грубых многомерных системах не может существовать счетного множества предельных циклов с ограниченными периодами, не представляет затруднений.
Понятие грубости динамической системы в многомерных системах не играет той роли, которую оно играет для двумерных динамических систем. Именно, метеорологом Лоренцем для целей предсказания погоды была выведена очень простая система трех дифференциальных уравнений

с постоянными параметрами  (см. [36]). Оказалось, что при некоторых значениях параметров при отсутствии каких-либо устойчивых состояний равновесия или устойчивых предельных циклов у этой системы существует двумерное притягивающее множество «аттрактор» - множество чрезвычайно сложной структуры, к которому все траектории из некоторой его окрестности стремятся при
(см. [36]). Оказалось, что при некоторых значениях параметров при отсутствии каких-либо устойчивых состояний равновесия или устойчивых предельных циклов у этой системы существует двумерное притягивающее множество «аттрактор» - множество чрезвычайно сложной структуры, к которому все траектории из некоторой его окрестности стремятся при 
В системе (1) есть седло, и это седло принадлежит аттрактору вместе со своими двумя изолированными сепаратрисами  Аттрактору же принадлежит и счетное всюду плотное множество седловых предельных циклов с неограниченно увеличивающимся периодом и всюду плотное множество устойчивых по Пуассону траекторий. А главное, этот аттрактор негрубый: при сколь угодно малых изменениях параметра сепаратрисы
Аттрактору же принадлежит и счетное всюду плотное множество седловых предельных циклов с неограниченно увеличивающимся периодом и всюду плотное множество устойчивых по Пуассону траекторий. А главное, этот аттрактор негрубый: при сколь угодно малых изменениях параметра сепаратрисы  входящего в него седла меняют свое расположение — они то включаются в сепаратрисные поверхности одного из седловых циклов, входящих в аттрактор, то отделяются от нее. Так как седловые циклы всюду плотны в аттракторе, то при непрерывном изменении параметров аттрактор сохраняется, но его структура в силу описанного поведения сепаратрис
входящего в него седла меняют свое расположение — они то включаются в сепаратрисные поверхности одного из седловых циклов, входящих в аттрактор, то отделяются от нее. Так как седловые циклы всюду плотны в аттракторе, то при непрерывном изменении параметров аттрактор сохраняется, но его структура в силу описанного поведения сепаратрис  непрерывно меняется. Таким образом, аттрактор Лоренца негрубый. Сложные режимы были обнаружены Лоренцем счетом на ЭВМ. Впоследствии структура аттрактора Лоренца была рассмотрена в ряде работ, например в [25]. Полное рассмотрение см. [9, 10].
непрерывно меняется. Таким образом, аттрактор Лоренца негрубый. Сложные режимы были обнаружены Лоренцем счетом на ЭВМ. Впоследствии структура аттрактора Лоренца была рассмотрена в ряде работ, например в [25]. Полное рассмотрение см. [9, 10].
Аттрактор Лоренца и его негрубость сохраняются и вообще при всех достаточно малых изменениях правых частей уравнения (1). А отсюда, очевидно, следует, что не существует сколь угодно близкой к системе (1) грубой системы и, следовательно, грубые системы не всюду плотны в пространстве трехмерных систем. Так как для двумерных систем всюду плотность грубых систем в пространстве динамических систем была чрезвычайно важным свойством, то в этом кардинальном вопросе разница между двумерными и многомерными динамическими системами очень существенна. Тем не менее понятие грубости динамических систем трех и большего числа измерений — в простейшем случае систем Морса — Смейла или даже в еще более упрощенной ситуации, например, в случае систем Морса — Смейла с конечным числом ячеек, все же сохраняет свое значение. Большое значение (как математическое, так и для приложений) имеет также рассмотрение бифуркаций многомерных динамических систем через негрубые системы. Мы сделаем по этому поводу некоторые краткие замечания.
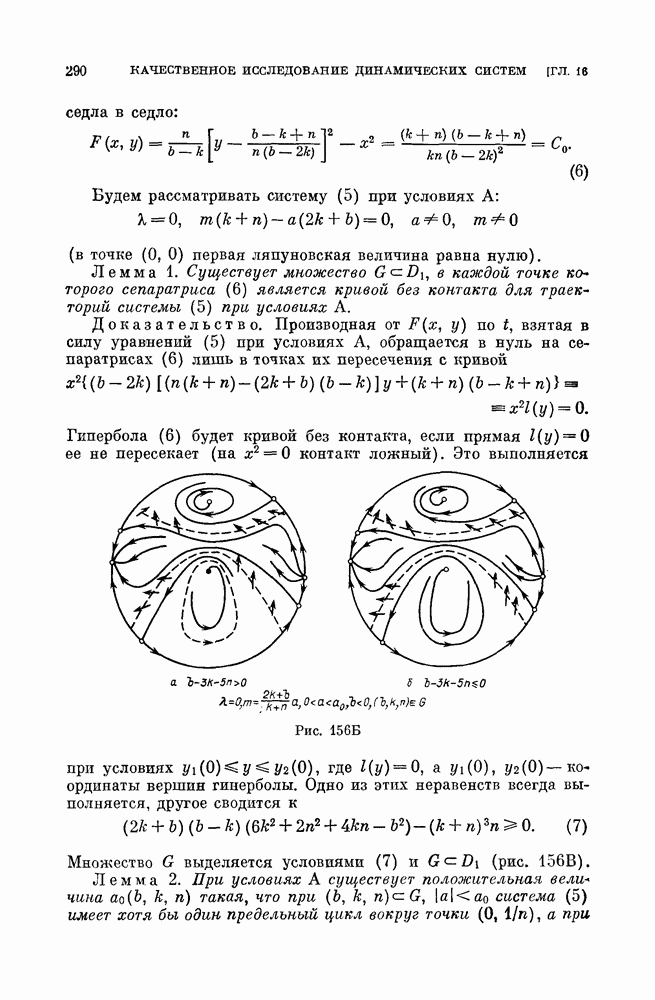
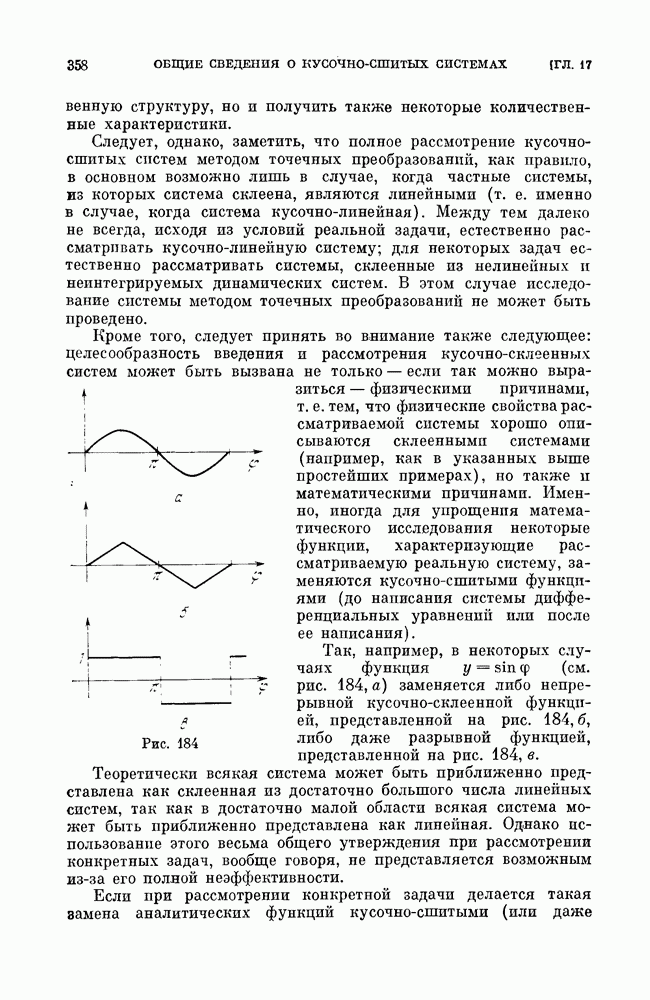
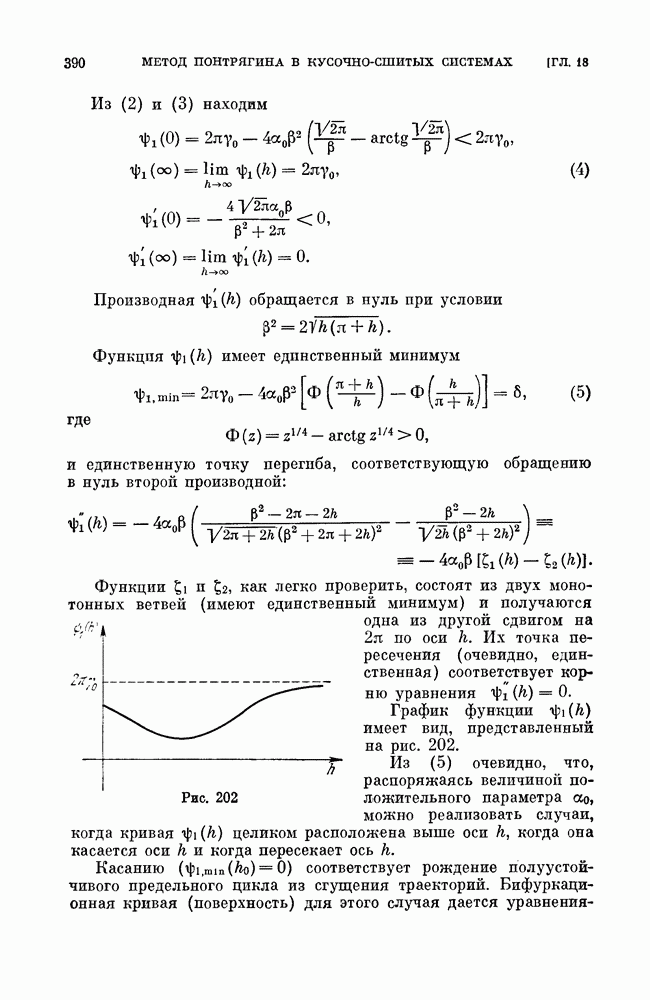
Естественно рассмотреть в первую очередь бифуркации простейших негрубых элементов и, прежде всего, простейших негрубых состояний равновесия. В трехмерных системах, так же как и в двумерных, простейшими негрубыми являются состояния равновесия с двумя чисто мнимыми характеристическими корнями. Для них Ляпуновым аналогично двумерным системам введены «ляпуновские величины». В простейших из этих состояний равновесия первая ляпуновская величина отлична от нуля. В этом простейшем случае в трехмерных системах состояния равновесия могут быть двух типов: сложным фокусом (устойчивым или неустойчивым) и сложным седло-фокусом. Далее, простейшими негрубыми состояниями равновесия в трехмерных системах могут быть двукратные состояния равновесия, возникшие в результате слияния двух простых. На рис. 253 показано образование двукратного состояния равновесия седло-фокус — фокус в результате слияния двух простых — седло-фокуса и устойчивого фокуса. При надлежащих изменениях правых частей системы двукратные состояния равновесия либо опять разделяются на простые, либо исчезают (см. [38]). На рис. 254
показано исчезновение двукратного состояния равновесия седло-узел, возникшего в результате слияния двух простых — седла и устойчивого узла. В двумерных системах два седла не могут слиться, образуя двукратное состояние равновесия, но такая возможность появляется в системах с числом измерений, большим двух.
Возможные бифуркации простейшего сложного фокуса с отличной от нуля первой ляпуновской величиной: либо фокус становится грубым той же устойчивости, что и сложный фокус, либо из сложного фокуса рождается предельный цикл, а сложный фокус превращается в седло-фокус (см. [37]).

Рис. 253
Аналогичны бифуркации для сложного седло-фокуса: либо он делается грубым, либо из него рождается седловой предельный цикл, а седло-фокус становится грубым фокусом, устойчивым или неустойчивым (см. [37]).
Возможны бифуркации, полностью аналогичные бифуркациям седло-узла на плоскости. Если сепаратриса седло-узла или седло-фокуса-фокуса идет в него же и при  и при
и при  то при исчезновении состояния равновесия появляется единственный предельный цикл, устойчивый или неустойчивый в зависимости от того, был ли неустойчив или устойчив узел или соответственно фокус, от слияния с которым был получен седло-узел или седло-фокус-фокус.
то при исчезновении состояния равновесия появляется единственный предельный цикл, устойчивый или неустойчивый в зависимости от того, был ли неустойчив или устойчив узел или соответственно фокус, от слияния с которым был получен седло-узел или седло-фокус-фокус.
Если одна из сепаратрис седло-седла возвращается в него же, то при исчезновении седло-седла появляется единственный седловой предельный цикл [137, 47].
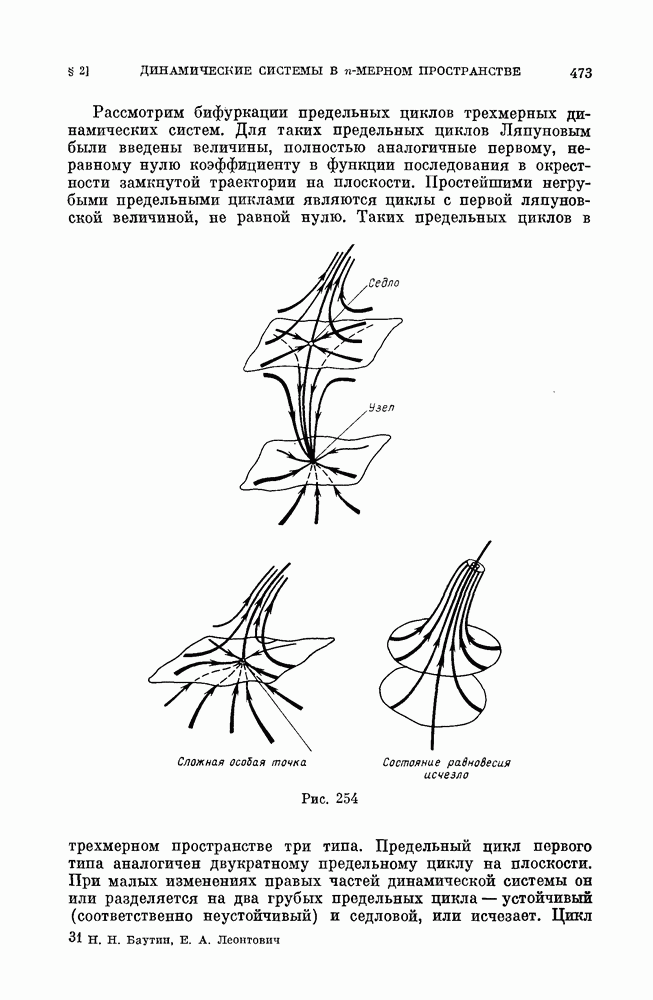
Рассмотрим бифуркации предельных циклов трехмерных динамических систем. Для таких предельных циклов Ляпуновым были введены величины, полностью аналогичные первому, неравному нулю коэффициенту в функции последования в окрестности замкнутой траектории на плоскости. Простейшими негрубыми предельными циклами являются циклы с первой ляпуновской величиной, не равной нулю. Таких предельных циклов в трехмерном пространстве три типа.
Рис. 254 (см. скан)
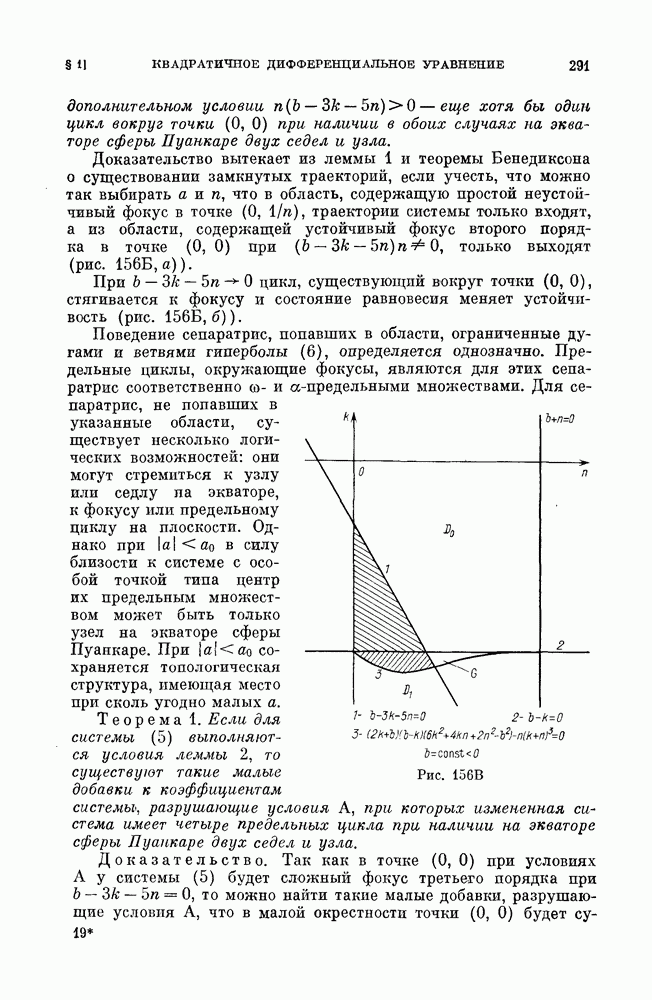
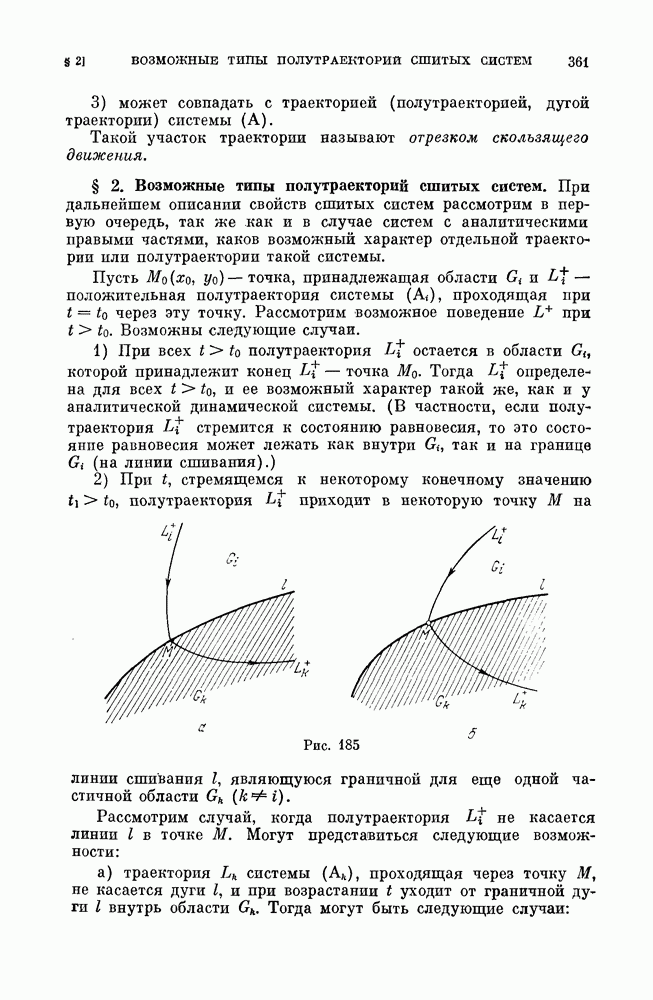
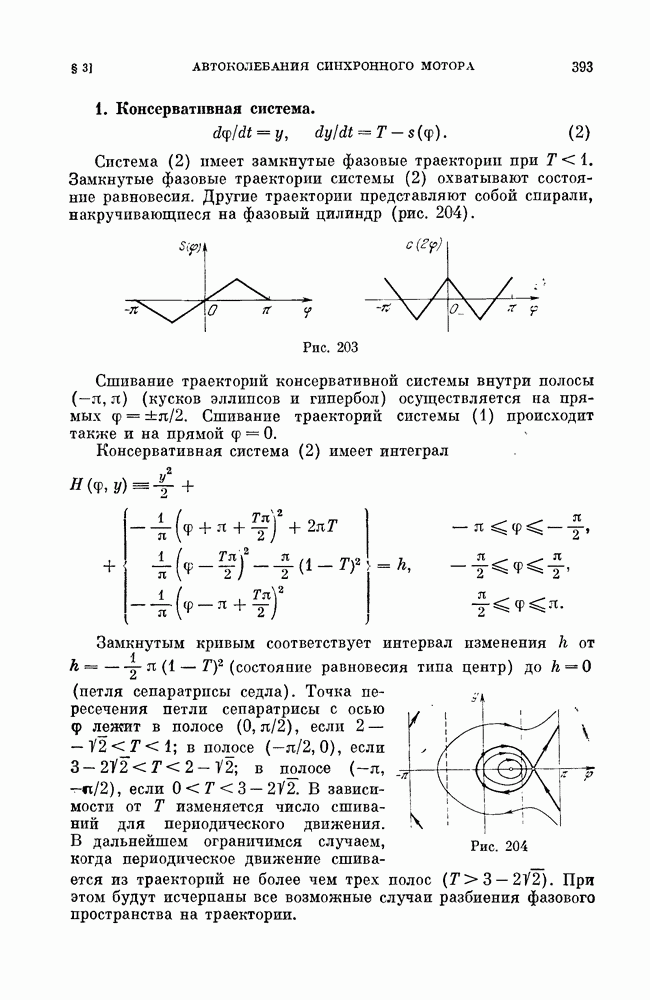
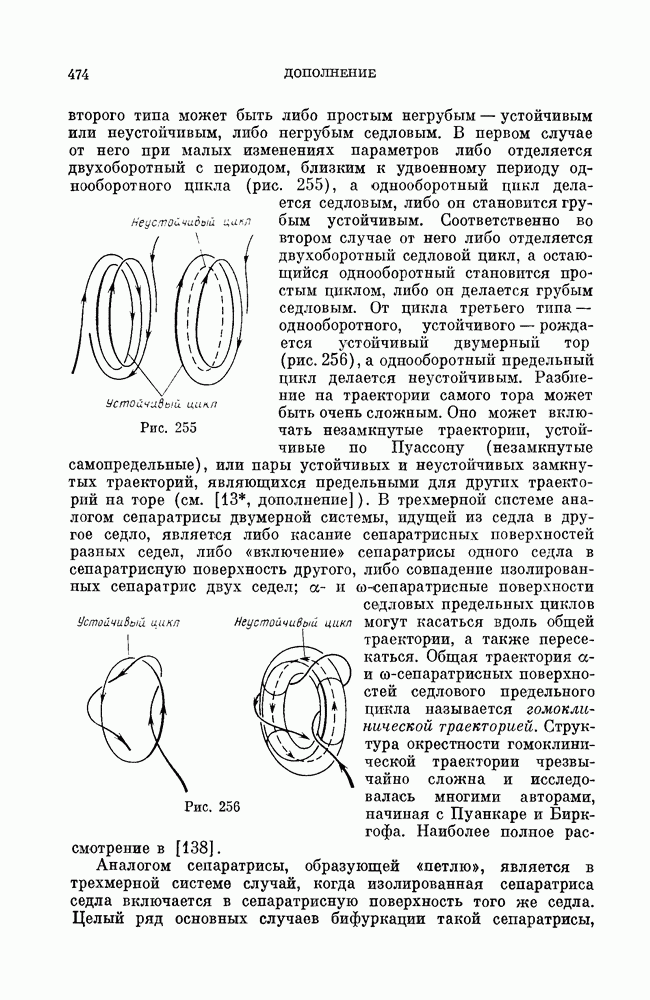
Предельный цикл первого типа аналогичен двукратному предельному циклу на плоскости. При малых изменениях правых частей динамической системы он или разделяется на два грубых предельных цикла — устойчивый (соответственно неустойчивый) и седловой, или исчезает. Цикл
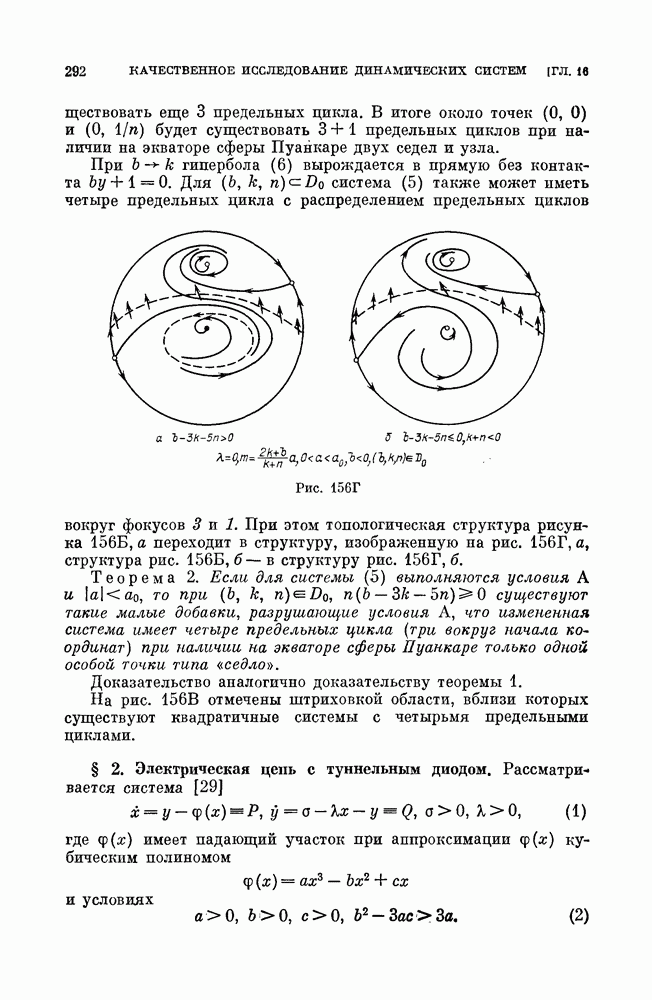
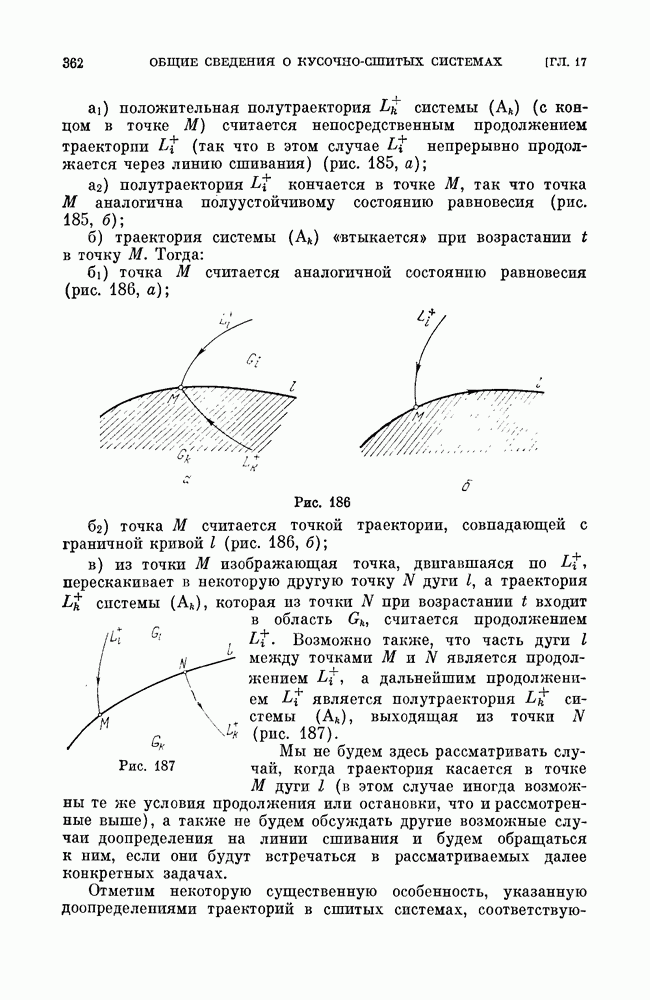
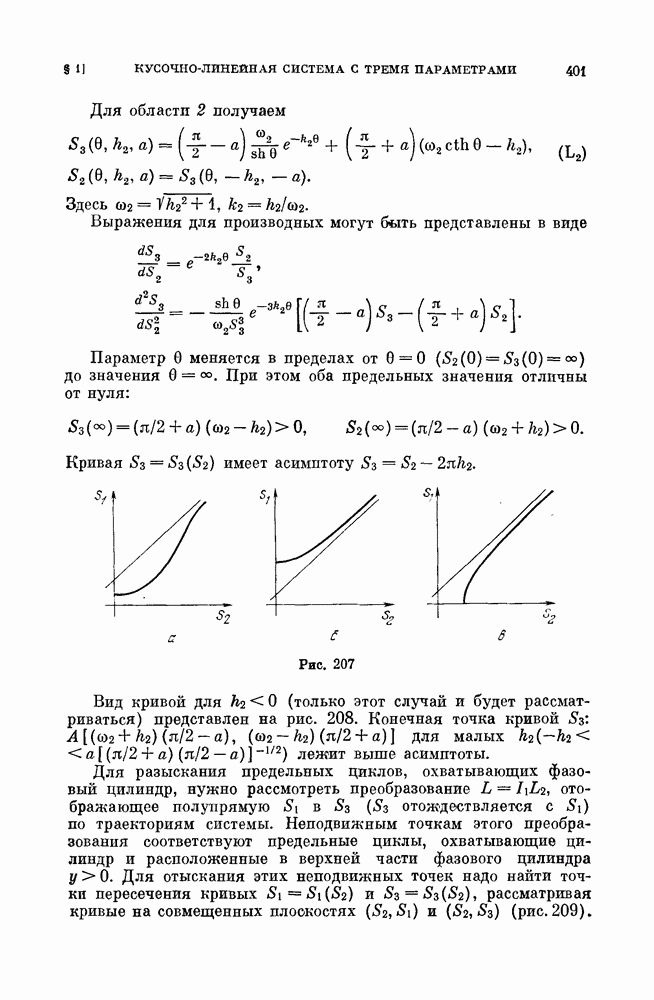
второго типа может быть либо простым негрубым — устойчивым или неустойчивым, либо негрубым седловым. В первом случае от него при малых изменениях параметров либо отделяется двухоборотный с периодом, близким к удвоенному периоду однооборотного цикла (рис. 255), а однооборотный цикл делается седловым, либо он становится грубым устойчивым. Соответственно во втором случае от него либо отделяется двухоборотный седловой цикл, а остающийся однооборотный становится простым циклом, либо он делается грубым седловым. От цикла третьего типа — однооборотного, устойчивого — рождается устойчивый двумерный тор (рис. 256), а однооборотный предельный цикл делается неустойчивым. Разбиение на траектории самого тора может быть очень сложным. Оно может включать незамкнутые траектории, устойчивые по Пуассону (незамкнутые самопредельные), или пары устойчивых и неустойчивых замкнутых траекторий, являющихся предельными для других траекторий на торе (см. [13, дополнение]). В трехмерной системе аналогом сепаратрисы двумерной системы, идущей из седла в другое седло, является либо касание сепаратрисных поверхностей разных седел, либо «включение» сепаратрисы одного седла в сепаратрисную поверхность другого, либо совпадение изолированных сепаратрис двух седел;  и
и  -сепаратрисные поверхности седловых предельных циклов могут касаться вдоль общей траектории, а также пересекаться. Общая траектория
-сепаратрисные поверхности седловых предельных циклов могут касаться вдоль общей траектории, а также пересекаться. Общая траектория  (
( -сепаратрисных поверхностей седлового предельного цикла называется гомоклинической траекторией. Структура окрестности гомоклинической траектории чрезвычайно сложна и исследовалась многими авторами, начиная с Пуанкаре и Биркгофа. Наиболее полное рассмотрение в [138].
-сепаратрисных поверхностей седлового предельного цикла называется гомоклинической траекторией. Структура окрестности гомоклинической траектории чрезвычайно сложна и исследовалась многими авторами, начиная с Пуанкаре и Биркгофа. Наиболее полное рассмотрение в [138].
Аналогом сепаратрисы, образующей «петлю», является в трехмерной системе случай, когда изолированная сепаратриса седла включается в сепаратрисную поверхность того же седла. Целый ряд основных случаев бифуркации такой сепаратрисы,

Рис. 255

Рис. 256
«образующей петлю», исследован в работе [139]. Для трехмерных систем введено понятие «седловой величины о», полностью аналогичное седловой величине двумерной системы. Некоторые случаи рождения предельных циклов из петли сепаратрисы трехмерной системы аналогичны рождению цикла из петли двумерной системы. Так, если седловая величина  и выполняется еще одно требование типа неравенства, то из петли сепаратрисы трехмерной системы при изменении параметров может родиться единственный устойчивый предельный цикл. При некоторых дополнительных условиях (типа неравенств) из петли сепаратрисы рождается единственный седловой предельный цикл. Однако если
и выполняется еще одно требование типа неравенства, то из петли сепаратрисы трехмерной системы при изменении параметров может родиться единственный устойчивый предельный цикл. При некоторых дополнительных условиях (типа неравенств) из петли сепаратрисы рождается единственный седловой предельный цикл. Однако если  то ситуация становится неизмеримо более сложной: в окрестности петли существует счетное множество седловых предельных циклов с неограниченно возрастающим периодом ([46]). (Более подробные сведения о многомерных системах и их бифуркациях см., например, [111, 140, 16-19, 24, 38, 46, 48].)
то ситуация становится неизмеримо более сложной: в окрестности петли существует счетное множество седловых предельных циклов с неограниченно возрастающим периодом ([46]). (Более подробные сведения о многомерных системах и их бифуркациях см., например, [111, 140, 16-19, 24, 38, 46, 48].)
В заключение скажем еще несколько слов о фундаментальном понятии, лежащем в основе качественного рассмотрения двумерных систем, — о классификации с точки зрения топологической тождественности разбиения на траектории: в случае многомерных систем этот подход также требует пересмотра и модификации. Однако на этих важных и тонких вопросах мы здесь не имеем возможности останавливаться и отсылаем читателя к специальной литературе (см. [63]).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. АВТОНОМНЫЕ СИСТЕМЫ ВТОРОГО ПОРЯДКА С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- § 1. Автономная динамическая система на плоскости.
- § 2. Теорема существования и единственности решения.
- § 3. Простейшие свойства решений системы (А).
- § 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
- § 5. Сопоставление геометрической интерпретации системы (А) в пространстве (x, y, t) с интерпретацией на фазовой плоскости.
- § 6. Некоторые термины.
- § 7. Теорема о непрерывной зависимости решения от начальных условий.
- § 8. Направление на траекториях. Изменение параметризации.
- § 9. Дифференциальное уравнение, соответствующее динамической системе.
- § 10. Понятие интегральной кривой и интеграла в случае аналитических правых частей Р(х,у) и Q(x,y) системы (А).
- § 11. Что значит «найти решение динамической системы»?
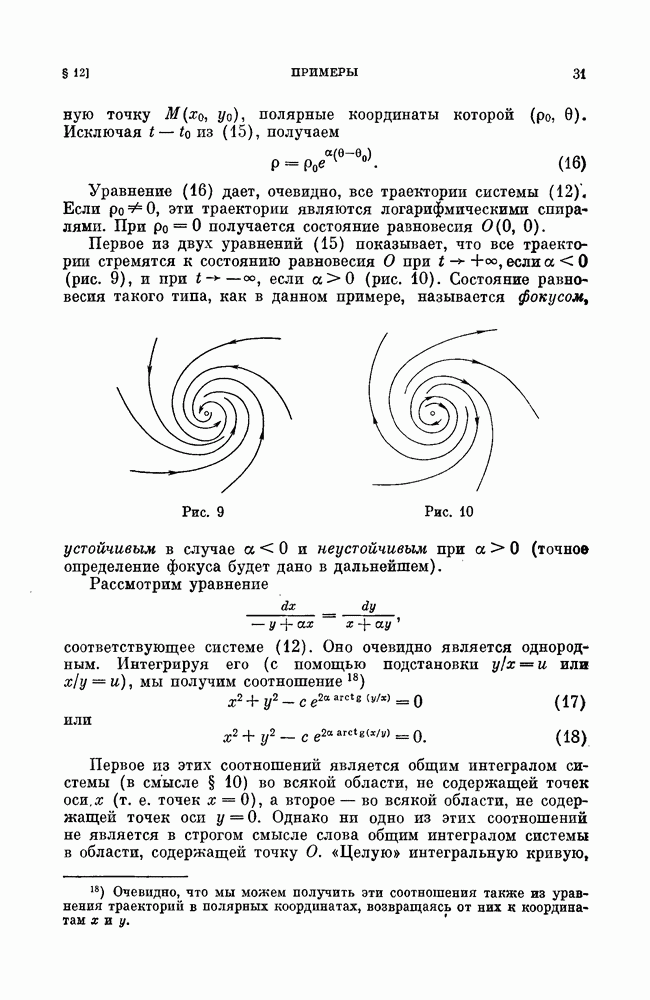
- § 12. Примеры.
- § 13. Замечания по поводу примеров § 12.
- § 14. Математическое определение качественной (топологической) структуры разбиения на траектории и качественного исследования динамической системы.
- ГЛАВА 2. ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ — БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ
- § 2. Цикл без контакта.
- § 3. Предельная точка полутраектории и траектории. Предельная траектория.
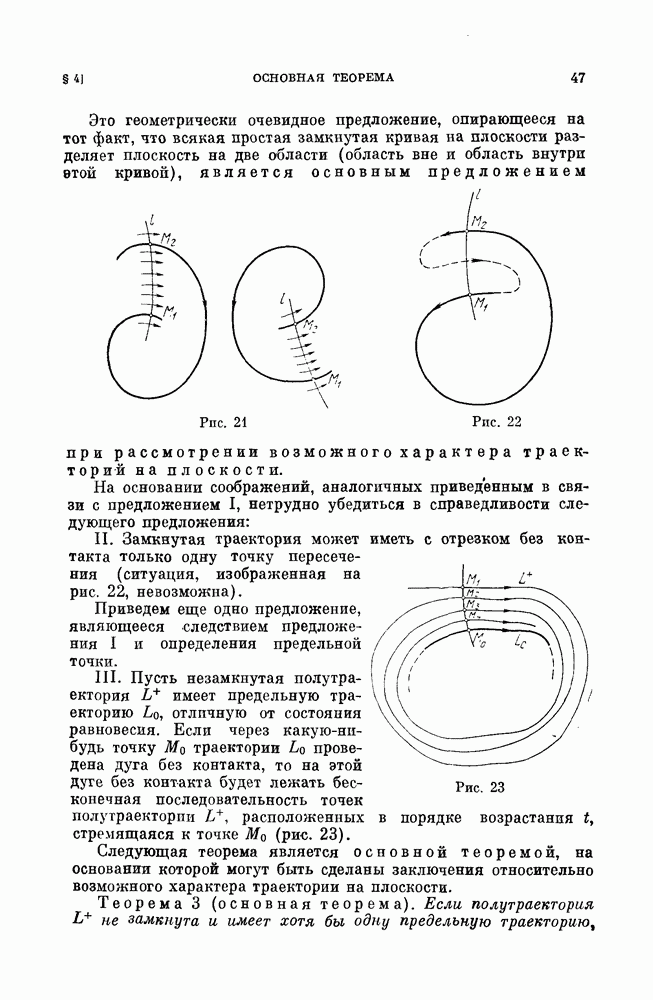
- § 4. Основная теорема.
- § 5. Возможные типы полутраекторий и их предельных множеств.
- § 6. Особые и неособые полутраектории и траектории.
- § 7. Возможные типы особых и неособых траекторий.
- § 8. Случай конечного числа особых траекторий. Элементарные ячейки.
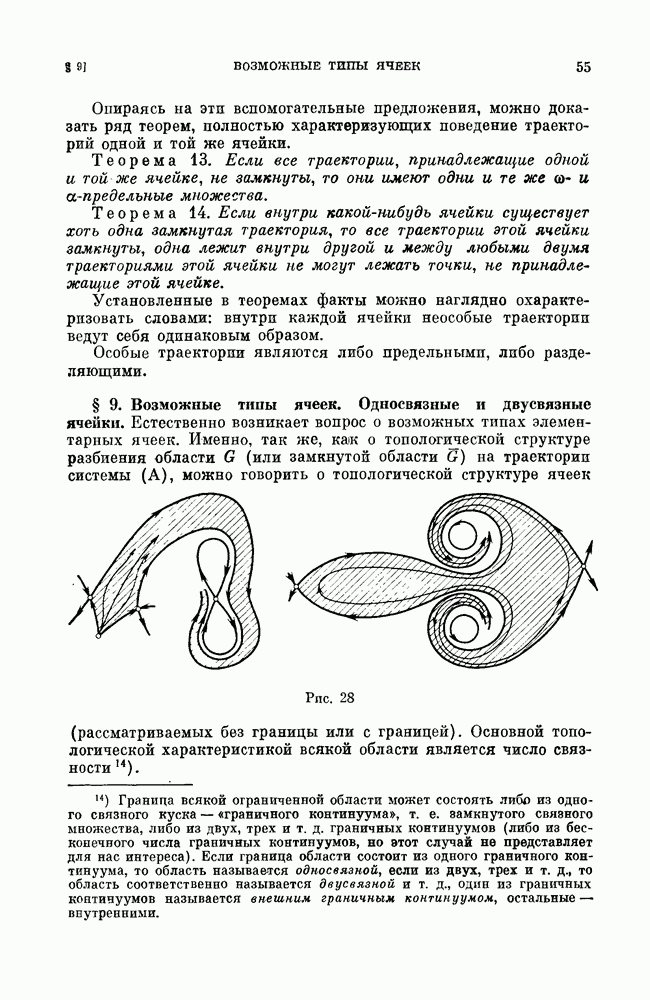
- § 9. Возможные типы ячеек. Односвязные и двусвязные ячейки.
- § 10. Два подхода к описанию качественной структуры.
- § 11. Качественная (топологическая) структура состояния равновесия в случае конечного числа особых траекторий. Схема динамической системы.
- § 12. Устойчивость по Ляпунову.
- ГЛАВА 3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННОЙ СТРУКТУРЫ ОКРЕСТНОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (ОСОБОЙ ТОЧКИ)
- § 2. Приведение динамической системы к каноническому виду.
- § 3. Возможный характер простых состояний равновесия.
- § 4. Замечания о методах установления характера грубых состояний равновесия.
- § 5. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 6. Направления, в которых траектории стремятся к простым состояниям равновесия.
- § 7. Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия.
- § 8. Сводка сведений о грубых состояниях равновесия.
- ГЛАВА 4. КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ
- § 1. Направления, в которых траектории стремятся к сложному состоянию равновесия.
- § 2. Сложное состояние равновесия (особая точка) с нулевыми характеристическими корнями.
- § 3. Примеры.
- § 4. Нормальные формы.
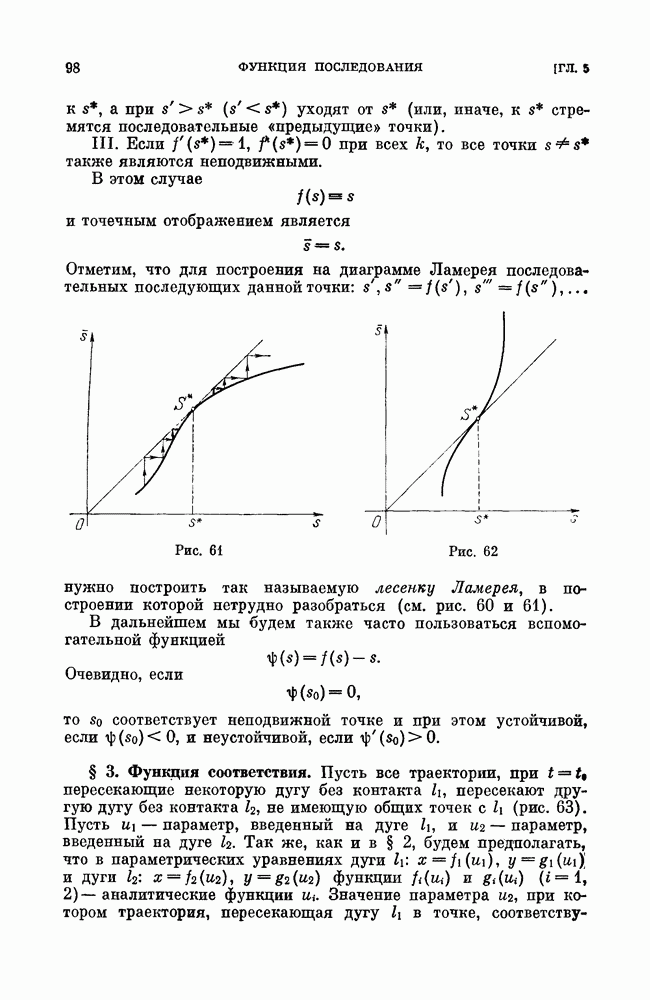
- ГЛАВА 5. ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ
- § 2. Условия устойчивости и неустойчивости неподвижной точки точечного отображения.
- § 3. Функция соответствия.
- § 4. Изучение окрестности замкнутой траектории. Простые и сложные предельные циклы.
- § 5. Аналитические выражения для коэффициентов функции последования. Характеристический показатель замкнутой траектории.
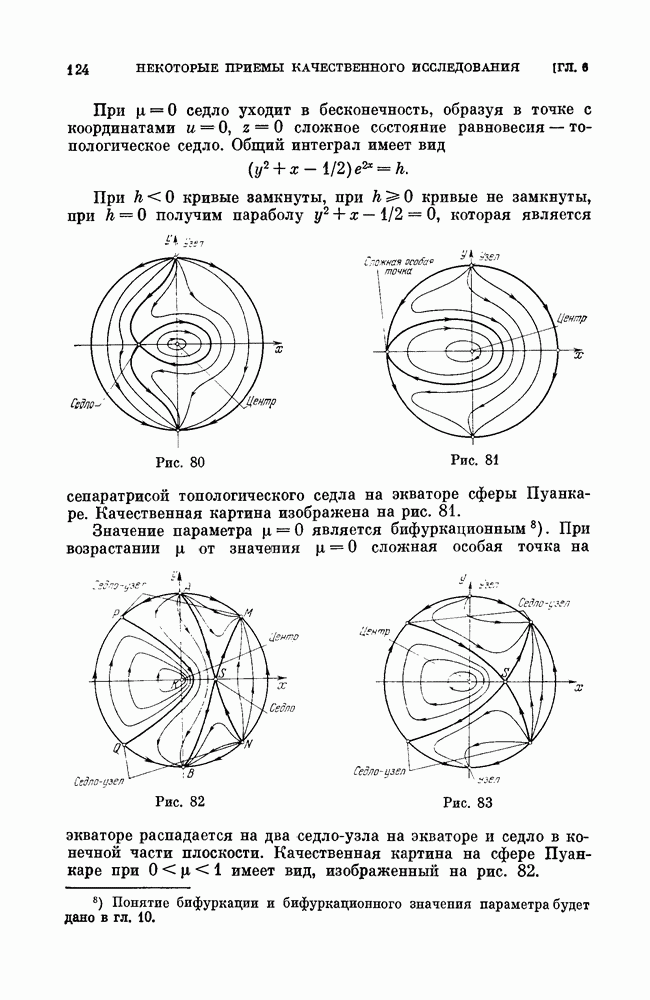
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЕМЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 2. Изучение поведения интегральных кривых в бесконечности. Сфера Пуанкаре.
- § 3. Примеры исследования в бесконечности [93].
- § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов.
- 1. Некоторые видоизменения критериев Бендиксона и Дюлака.
- 2. Индексы Пуанкаре. Распределение особых точек [77, 117].
- 3. Условия сосуществования замкнутых траекторий и особых точек.
- 4. Две общие теоремы Пуанкаре.
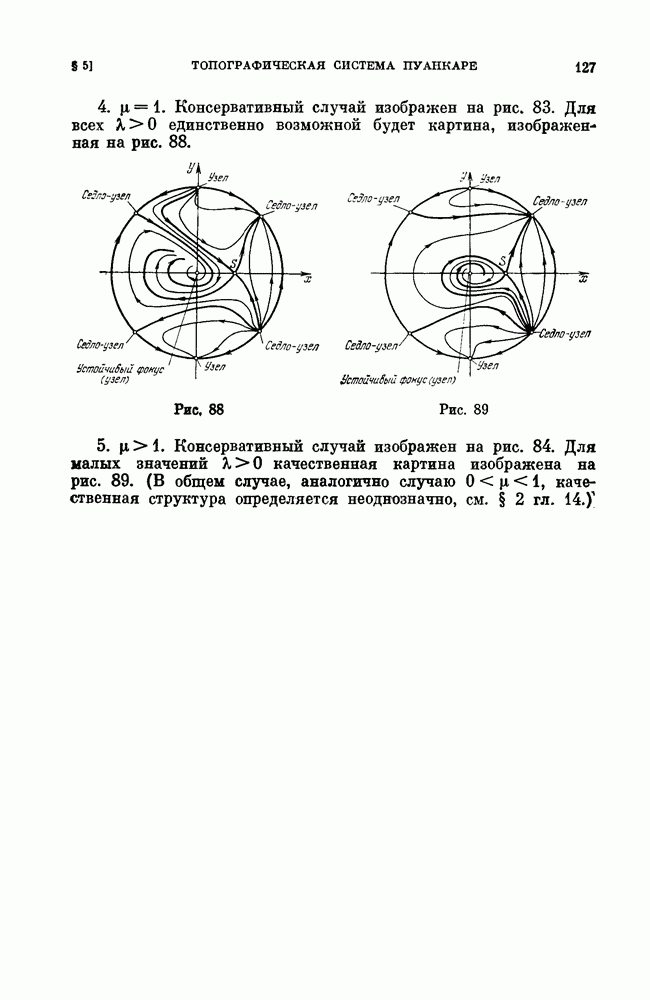
- § 5. Топографическая система Пуанкаре. Функция Ляпунова. Кривые контактов.
- ЧАСТЬ II. ТЕОРИЯ БИФУРКАЦИЙ
- § 1. Свойства консервативных систем на плоскости [2, 3].
- § 2. Динамические системы, характерные для теории колебаний.
- § 3. Измененные системы. Системы, правые части которых зависят от параметра.
- § 4. Основные теоремы о зависимости решения от изменения правых частей динамической системы.
- § 5. Грубость динамической системы и теоремы о непрерывной зависимости решения от изменения правых частей.
- ГЛАВА 8. ГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
- § 2. Состояния равновесия, возможные в грубой динамической системе.
- § 3. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 4. Замкнутые траектории, возможные в грубой системе.
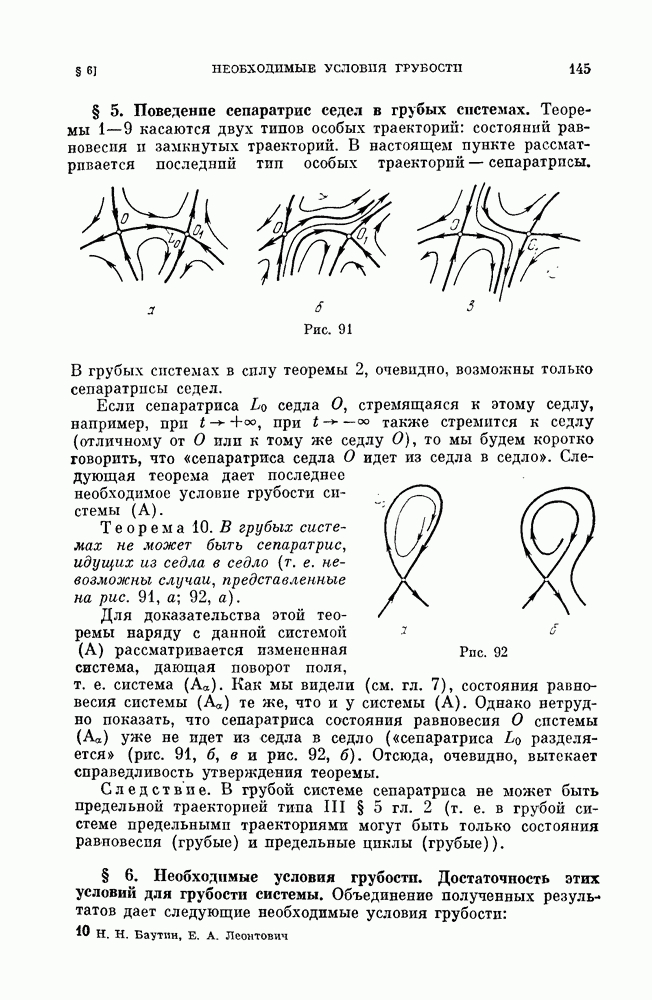
- § 5. Поведение сепаратрис седел в грубых системах.
- § 6. Необходимые условия грубости. Достаточность этих условий для грубости системы.
- § 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем.
- § 8. Понятие грубости при более общих предположениях относительно правых частей динамической системы.
- § 9. Типы особых траекторий и ячеек в грубых системах.
- § 10. Замечания по поводу определения грубой системы.
- ГЛАВА 9. ПРОСТЕЙШИЕ НЕГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ — СИСТЕМЫ ПЕРВОЙ СТЕПЕНИ НЕГРУБОСТИ
- § 2. Системы первой степени негрубости.
- § 3. Состояния равновесия, возможные в системе первой степени негрубости.
- § 4. Замкнутые траектории, возможные в системе первой степени негрубости.
- § 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости.
- § 6. Необходимые и достаточные условия первой степени негрубости.
- § 7. Динамические системы более высокой степени негрубости.
- ГЛАВА 10. БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- § 1. Определение бифуркации.
- § 2. Бифуркации систем первой степени негрубости.
- § 3. Бифуркации некоторых типов сложных особых точек.
- § 4. Бифуркации двукратной точки, для которой …
- § 5. Рождение предельных циклов из особых траекторий степени негрубости выше первой.
- ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
- § 1. Возможный характер зависимости правых частей динамической системы от параметров.
- § 2. Смена качественных структур при изменении параметров.
- § 3. Случай, когда правые части зависят более чем от одного параметра.
- § 4. Бифуркации «от бесконечности».
- § 5. Условия существования седло-узла и сложного фокуса первого порядка.
- § 6. Поворот векторного поля.
- § 7. Метод малого параметра. Метод Понтрягина.
- ГЛАВА 12. ДИНАМИЧЕСКИЕ СИСТЕМЫ С ЦИЛИНДРИЧЕСКОЙ ФАЗОВОЙ ПОВЕРХНОСТЬЮ
- § 1. Цилиндрическая фазовая поверхность и характер траекторий, возможных на цилиндрической фазовой поверхности.
- § 2. Замкнутые траектории, охватывающие цилиндр.
- § 3. Приемы исследования качественной структуры динамической системы на цилиндре.
- § 4. Понятие грубости и степени негрубости для динамических систем на цилиндре. Бифуркации на цилиндре. Поворот поля.
- § 5. Динамические системы на цилиндре, близкие к гамильтоновым (метод Понтрягина).
- ГЛАВА 13. АДЕКВАТНОЕ ИСТОЛКОВАНИЕ НЕЛИНЕЙНЫХ ФИЗИЧЕСКИХ ЯВЛЕНИЙ ФАКТАМИ КАЧЕСТВЕННОЙ ТЕОРИИ И ТЕОРИИ БИФУРКАЦИЙ ДИНАМИЧЕСКИХ СИСТЕМ
- § 1. Мягкий и жесткий режимы.
- § 2. Замечания о границах области устойчивости различных стационарных режимов.
- § 3. Мягкое и жесткое возникновение колебаний.
- § 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
- § 5. Замечания по поводу других границ области устойчивости.
- ЧАСТЬ III. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- ГЛАВА 14. ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 1. Некоторые рецептурные указания.
- § 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
- § 3. Некоторые простые примеры динамических систем на цилиндре.
- ГЛАВА 15. ИССЛЕДОВАНИЕ МЕТОДОМ МАЛОГО ПАРАМЕТРА (МЕТОДОМ ПОНТРЯГИНА)
- § 2. Примеры рассмотрения методом Понтрягина (полное исследование).
- § 3. Исследование методом Понтрягина с привлечением вычислительных методов.
- ГЛАВА 16. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ
- § 2. Электрическая цепь с туннельным диодом.
- § 3. Двумерная модель динамики твердотельного лазера [119].
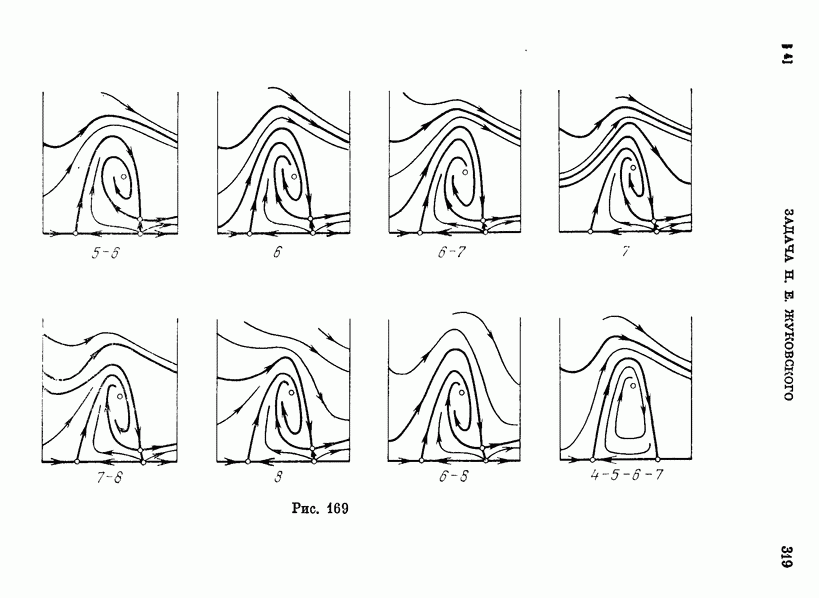
- § 4. Симметричный полет самолета в вертикальной плоскости (задача Н. Е. Жуковского).
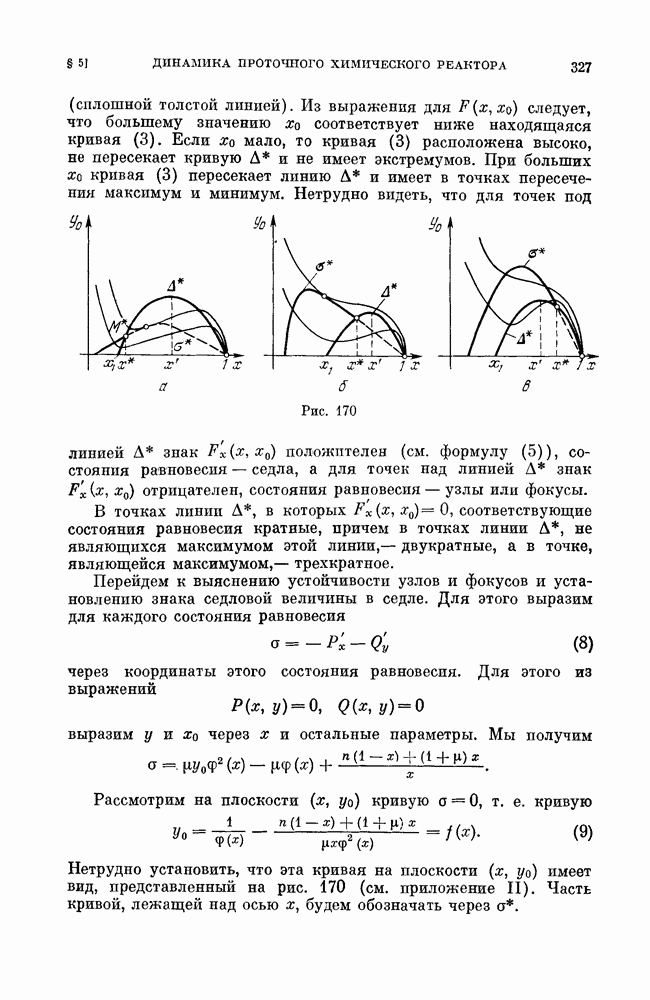
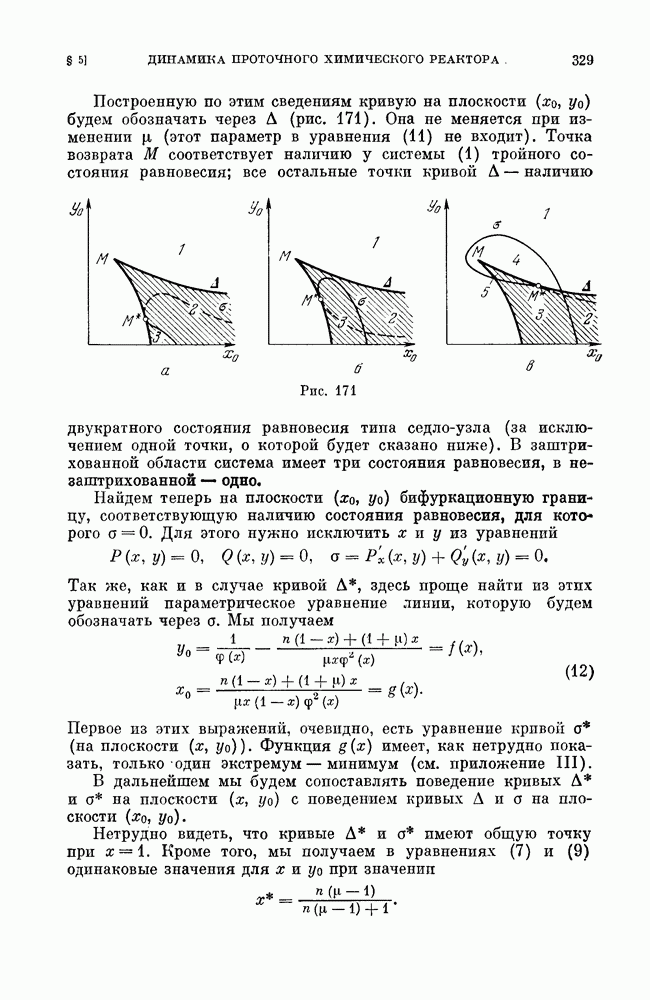
- § 5. Система, описывающая динамику проточного химического реактора.
- § 6. Фазовая автоподстройка частоты.
- § 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов).
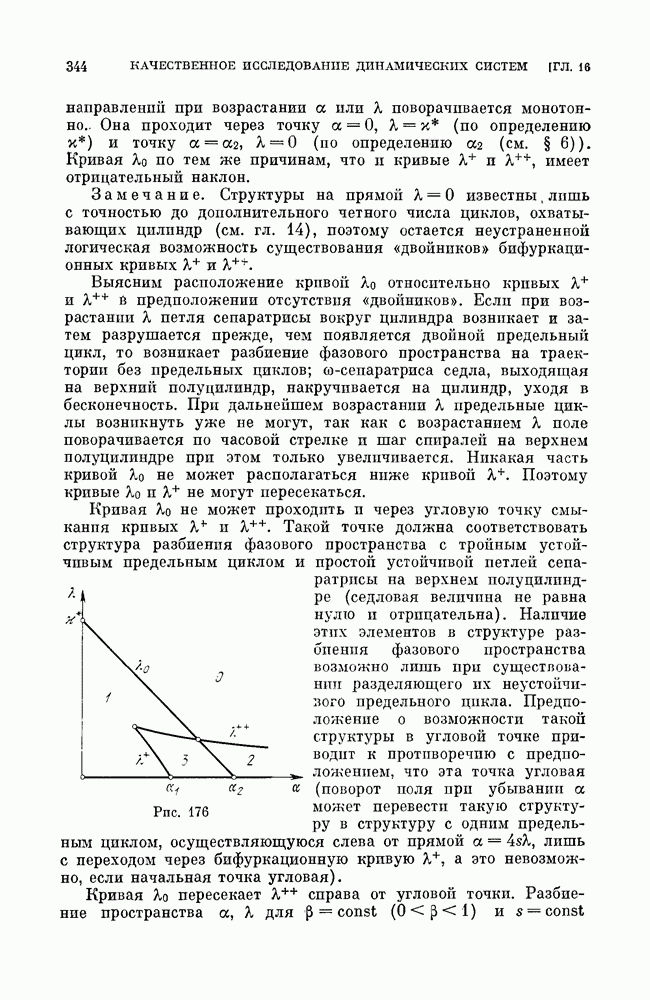
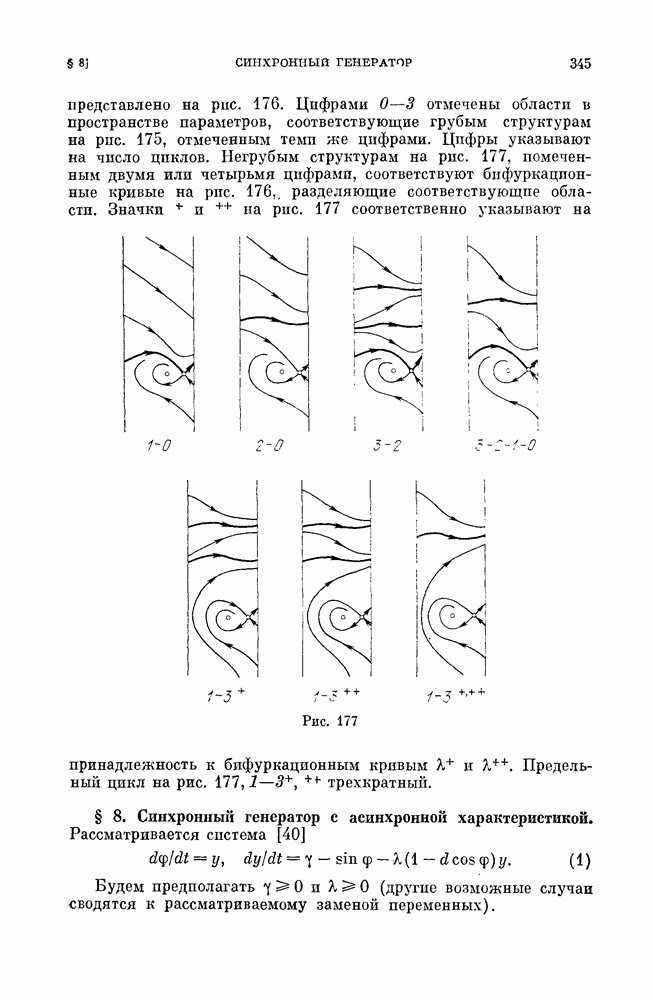
- § 8. Синхронный генератор с асинхронной характеристикой.
- ЧАСТЬ IV. КУСОЧНО-СШИТЫЕ СИСТЕМЫ
- ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ
- § 1. Сшитые системы. Доопределение на линиях сшивания.
- § 2. Возможные типы полутраекторий сшитых систем.
- § 3. Особые траектории сшитых систем.
- § 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
- ГЛАВА 18. ИССЛЕДОВАНИЕ КУСОЧНО-СШИТЫХ СИСТЕМ МЕТОДОМ ПОНТРЯГИНА
- § 2. Автоподстройка при кусочно-постоянной аппроксимации характеристики.
- § 3. Автоколебания синхронного мотора.
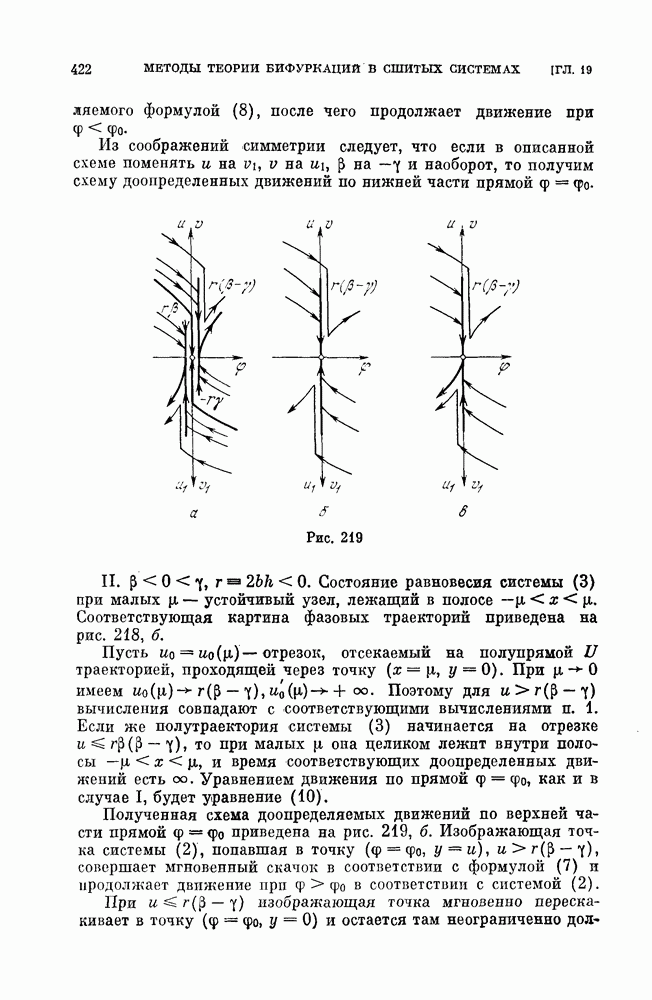
- ГЛАВА 19. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ
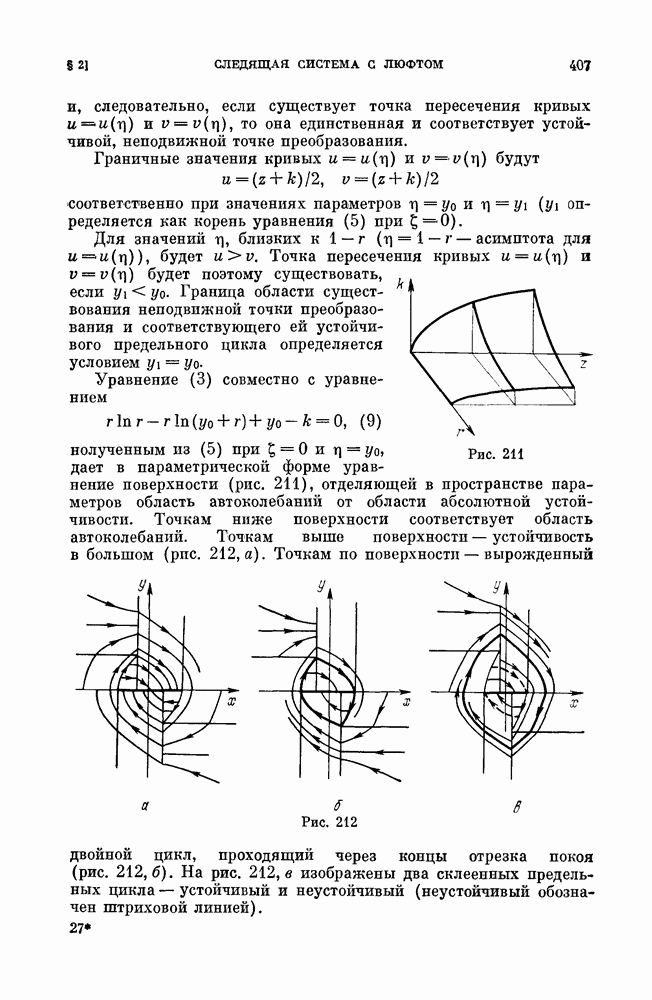
- § 2. Следящая система с люфтом.
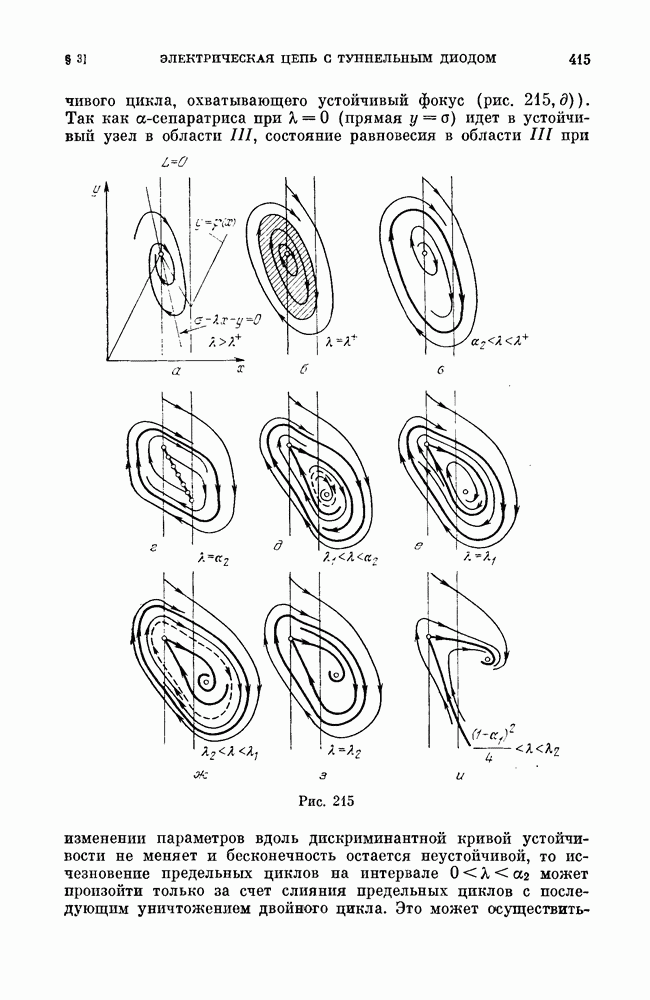
- § 3. Электрическая цепь с туннельным диодом.
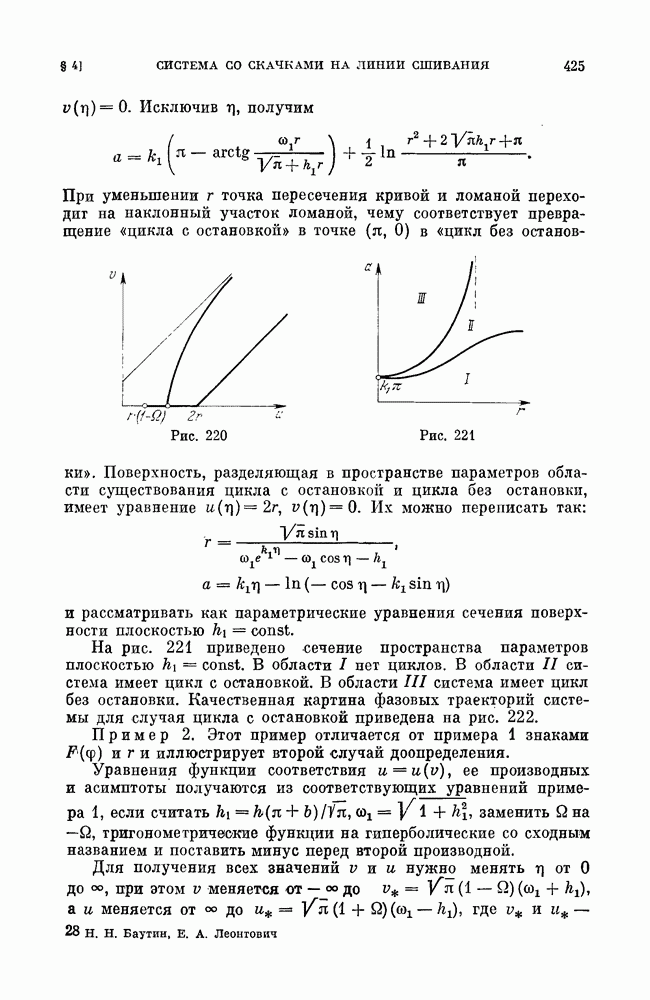
- § 4. Система со скачками на линии сшивания.
- ГЛАВА 20. ОБ АППРОКСИМАЦИЯХ И ГРУБОСТИ ПРОСТРАНСТВА ПАРАМЕТРОВ [39, 41, 42]
- § 1. Рассмотрение системы (2) при аппроксимациях пилообразными функциями.
- § 2. Рассмотрение системы (2) при аппроксимации, включающей отрезок параболы.
- § 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin f, и пилообразной для cos f функциями.
- § 4. Исследование роли аппроксимаций для уравнения маятникового типа.
- § 5. Динамическая система, описывающая автоколебания синхронного мотора.
- § 6. Динамическая система, описывающая симметричный полет самолета.
- ДОПОЛНЕНИЕ
- § 1. Динамическое системы на двумерных поверхностях.
- § 2. Динамические системы в n-мерном евклидовом пространстве.
- СПИСОК ЛИТЕРАТУРЫ