| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
§ 1. Возможный характер зависимости правых частей динамической системы от параметров.
Динамические системы, правые части которых зависят от того или другого числа параметров, всегда естественно возникают при рассмотрении различных задач из приложений.
Пусть правые части динамической системы зависят от  параметров, т. е. имеют вид
параметров, т. е. имеют вид

Мы будем предполагать, что правые части являются аналитическими функциями не только переменных х, у, но и параметров 
Если обратиться к рассмотрению одного из общих пространств динамических систем  (см. гл. 8), то, очевидно, при каждом наборе значений параметров
(см. гл. 8), то, очевидно, при каждом наборе значений параметров  - мы получаем точку в этом пространстве, а при всевозможных значениях параметров
- мы получаем точку в этом пространстве, а при всевозможных значениях параметров  в пространстве
в пространстве  выделяется
выделяется  -мерпое подпространство динамических систем
-мерпое подпространство динамических систем 
Очевидно, что, в частности, система  может быть негрубой при всех значениях параметров 7. Так, например, мы можем рассматривать систему вида
может быть негрубой при всех значениях параметров 7. Так, например, мы можем рассматривать систему вида

которая является гамильтоновой системой при всех значениях параметров (т. е. с точки зрения введенной классификации — бесконечной степени негрубости).
Очевидно, также возможны системы вида  не являющиеся гамильтоновыми, но являющиеся негрубыми при всех значениях параметров. Например, при всех значениях параметров у системы может быть сложное состояние равновесия, сепаратриса, идущая из седла в седло, и т. д.
не являющиеся гамильтоновыми, но являющиеся негрубыми при всех значениях параметров. Например, при всех значениях параметров у системы может быть сложное состояние равновесия, сепаратриса, идущая из седла в седло, и т. д.
Однако в дальнейшем мы будем предполагать, что у рассматриваемых систем, правые части которых зависят от  параметров:
параметров:  в пространстве параметров (являющемся
в пространстве параметров (являющемся  -мерным пространством) не существует никакой
-мерным пространством) не существует никакой  -мерной области, всем точкам которой соответствуют негрубые системы.
-мерной области, всем точкам которой соответствуют негрубые системы.
Это предположение является существенным для рассмотрения настоящей главы.
Можно считать, что это предположение является предположением о некотором общем случае расположения многообразия размерности  (выделенного в пространстве
(выделенного в пространстве  системой
системой  правые части которой зависят от
правые части которой зависят от  параметров
параметров  по отношению к тем подпространствам пространства
по отношению к тем подпространствам пространства  которые соответствуют негрубым динамическим системам. Именно такой характер вхождения параметра типичен для задач теории колебаний.
которые соответствуют негрубым динамическим системам. Именно такой характер вхождения параметра типичен для задач теории колебаний.
При этом предположении грубые системы в пространстве параметров заполняют области. Действительно, если в n-мерном пространстве параметров существует хотя бы одна точка, которой соответствует грубая динамическая система, то тогда, очевидно, в пространстве параметров непременно будет существовать и целая  -мерная область, заполненная грубыми системами. Так как грубые системы выделяются условиями типа неравенств, полное качественное исследование системы типа
-мерная область, заполненная грубыми системами. Так как грубые системы выделяются условиями типа неравенств, полное качественное исследование системы типа  сводится к установлению разбиения пространства параметров на области с одинаковой — грубой — качественной структурой и к установлению этой качественной структуры. Значения параметров
сводится к установлению разбиения пространства параметров на области с одинаковой — грубой — качественной структурой и к установлению этой качественной структуры. Значения параметров  соответствующее грубым системам, будем называть грубыми значениями параметров, а области, заполненные грубыми значениями параметров, — грубыми областями.
соответствующее грубым системам, будем называть грубыми значениями параметров, а области, заполненные грубыми значениями параметров, — грубыми областями.
Области, заполненные грубыми системами с различными качественными структурами, разделяются  -мерными «пленками», точкам которых соответствуют негрубые системы, причем в общем случае — это системы первой степени негрубости.
-мерными «пленками», точкам которых соответствуют негрубые системы, причем в общем случае — это системы первой степени негрубости.
Действительно, системы первой степени негрубости — это системы, которые выделяются одним (и только одним) условием типа равенства (например)

или

или

Это условие в пространстве параметров выделяет в общем случае  -мерную поверхность — «пленку».
-мерную поверхность — «пленку».
В математической литературе в настоящее время при рассмотрении функциональных пространств, а также введенного в гл. 8 пространства динамических систем, используется понятие «коразмерность». Не давая точного определения, поясним смысл этого понятия. В элементарном случае евклидова трехмерного пространства: «коразмерность  -множество точек (гладкая поверхность), задаваемое функцией
-множество точек (гладкая поверхность), задаваемое функцией  с градиентом, не равным нулю; «коразмерность 2» соответствует трансверсальным (без касания) пересечениям двух гладких поверхностей; «коразмерность 3» соответствует точке. В
с градиентом, не равным нулю; «коразмерность 2» соответствует трансверсальным (без касания) пересечениям двух гладких поверхностей; «коразмерность 3» соответствует точке. В  -мерном пространстве: коразмерность 1 задается одним условием
-мерном пространстве: коразмерность 1 задается одним условием  это гладкая гиперповерхность с числом измерений
это гладкая гиперповерхность с числом измерений  коразмерность 2 — гладкая гиперповерхность с числом измерений
коразмерность 2 — гладкая гиперповерхность с числом измерений  и т. д. Таким образом, в евклидовом пространстве понятие коразмерности не вносит ничего нового по сравнению с числом измерений. Когда рассматривается функциональное пространство, точками которого являются, например, динамические системы, о числе измерений, как правило, говорить уже невозможно. Однако можно (по аналогии с конечномерными) ввести понятия: «гладкое функциональное соотношение», «гладкая гиперповерхность», удовлетворяющая одному функциональному соотношению между элементами этого пространства, а также понятие «трансверсальное» пересечение. Тогда множество элементов этого пространства, удовлетворяющее одному функциональному соотношению, — это множество коразмерности 1. Множество элементов, удовлетворяющих
и т. д. Таким образом, в евклидовом пространстве понятие коразмерности не вносит ничего нового по сравнению с числом измерений. Когда рассматривается функциональное пространство, точками которого являются, например, динамические системы, о числе измерений, как правило, говорить уже невозможно. Однако можно (по аналогии с конечномерными) ввести понятия: «гладкое функциональное соотношение», «гладкая гиперповерхность», удовлетворяющая одному функциональному соотношению между элементами этого пространства, а также понятие «трансверсальное» пересечение. Тогда множество элементов этого пространства, удовлетворяющее одному функциональному соотношению, — это множество коразмерности 1. Множество элементов, удовлетворяющих  функциональным соотношениям, определяющим
функциональным соотношениям, определяющим  гладких гиперповерхностей, пересекающихся трансверсально, — множество коразмерности
гладких гиперповерхностей, пересекающихся трансверсально, — множество коразмерности  Пусть у динамической системы
Пусть у динамической системы  есть единственный негрубый элемент — простое состояние равновесия с чисто мнимыми характеристическими корнями и не равной нулю первой ляпуновской величиной. Если рассматривать всевозможные системы
есть единственный негрубый элемент — простое состояние равновесия с чисто мнимыми характеристическими корнями и не равной нулю первой ляпуновской величиной. Если рассматривать всевозможные системы  близкие к данной, на которые накладывается единственное требование сохранения чисто мнимых корней для близкого состояния равновесия (т. е. требование
близкие к данной, на которые накладывается единственное требование сохранения чисто мнимых корней для близкого состояния равновесия (т. е. требование  то динамические системы, удовлетворяющие этому условию, лежат на гиперповерхности коразмерности 1 в пространстве динамических систем («гладкость» этой поверхности устанавливается с использованием понятия «обобщенный градиент»). На гиперповерхности коразмерности 2 лежат,
то динамические системы, удовлетворяющие этому условию, лежат на гиперповерхности коразмерности 1 в пространстве динамических систем («гладкость» этой поверхности устанавливается с использованием понятия «обобщенный градиент»). На гиперповерхности коразмерности 2 лежат,
например, динамические системы с состоянием равновесия с чисто мнимыми корнями и равной нулю первой ляпуновской величиной 
С «порядком» коразмерности  как и со «степенями» негрубости
как и со «степенями» негрубости  связываются представления о возможных в системе при изменениях правых частей наборах бифуркаций. Понятия степеней негрубости связаны с этим более органично.
связываются представления о возможных в системе при изменениях правых частей наборах бифуркаций. Понятия степеней негрубости связаны с этим более органично.
Как мы впдели, при рассмотрении систем первой степени негрубости для такпх систем запрещаются: а) случай, когда существует двукратный предельный цикл, на который извне и изнутри накручиваются сепаратрисы, и б) случай, когда на петлю сепаратрисы накручивается хотя бы одна сепаратриса. Оба эти случая невозможны в системах первой степени негрубости в силу данного определения таких систем, так что при наличии таких образований система рассматривается как система более высокой степени негрубости.
Между тем динамические системы, для которых осуществляется случай а) или б), в общем пространстве динамических систем заполняют пленки, т. е. имеют коразмерность 1. Действительно, в случае а) эта пленка выделяется условием наличия двукратного цикла, а в случае б) — условием наличия петли сепаратрисы. Однако эти пленки существенно отличаются от пленок, соответствующих системам первой степени негрубости: в любой  окрестности существуют другие негрубые пленки; как в случае а), так и в случае
окрестности существуют другие негрубые пленки; как в случае а), так и в случае  -это пленки, соответствующие сепаратрисе, идущей из одного седла в другое седло. Можно показать, что в указанных случаях а) и б) пленка является недостижимой границей области, заполненной грубыми системами, т. е. не существует простой дуги, соединяющей сколь угодно близкую точку грубой области с указанной пленкой, не пересекающей других пленок.
-это пленки, соответствующие сепаратрисе, идущей из одного седла в другое седло. Можно показать, что в указанных случаях а) и б) пленка является недостижимой границей области, заполненной грубыми системами, т. е. не существует простой дуги, соединяющей сколь угодно близкую точку грубой области с указанной пленкой, не пересекающей других пленок.
Мы уже отмечали, что понятия грубости и степени негрубости могут быть полностью аналогично введены и в других математических объектах. Рассмотрим, например, пространство кривых

где  аналитическая функция.
аналитическая функция.
Для таких кривых можно ввести понятие «грубой кривой» и кривой «первой степени негрубости», «второй степени негрубости» и т. д. Однако при этом возникает существенное различие с динамическими системами. Можно показать, что в пространстве кривых  множество кривых первой степени негрубости (и только кривых первой степени негрубости) является пленкой, и всякая такая пленка является достижимой в множестве грубых кривых. Множество кривых более высокой степени является пересечением двух (или более) пленок и всегда имеет
множество кривых первой степени негрубости (и только кривых первой степени негрубости) является пленкой, и всякая такая пленка является достижимой в множестве грубых кривых. Множество кривых более высокой степени является пересечением двух (или более) пленок и всегда имеет
размерность меньшую, чем множество кривых первой степени негрубости. Можно показать, что все границы грубых областей пространства  достижимы.
достижимы.
Указанная разница между свойствами границ грубых областей в пространстве кривых  и в пространстве динамических систем
и в пространстве динамических систем  является несомненным отражением того обстоятельства, что, наряду с большими аналогиями, между ними существуют и существенные различия. Мы не можем здесь останавливаться на этих, с нашей точки зрения, весьма интересных вопросах.
является несомненным отражением того обстоятельства, что, наряду с большими аналогиями, между ними существуют и существенные различия. Мы не можем здесь останавливаться на этих, с нашей точки зрения, весьма интересных вопросах.
Значения параметров  соответствующие негрубой системе (при которых точка
соответствующие негрубой системе (при которых точка  лежит хотя бы на одной пленке, разделяющей две различные грубые области), будем называть бифуркационными значениями параметров, а изменение качественной структуры, которое пропсходит в системе
лежит хотя бы на одной пленке, разделяющей две различные грубые области), будем называть бифуркационными значениями параметров, а изменение качественной структуры, которое пропсходит в системе  при переходе от бифуркационных значений параметров к грубым значениям параметров, как и в гл. 10, будем называть бифуркацией. Разбиение пространства параметров на «грубые области» и разделяющие их пленки, соответствующие негрубым системам, называется бифуркационной диаграммой.
при переходе от бифуркационных значений параметров к грубым значениям параметров, как и в гл. 10, будем называть бифуркацией. Разбиение пространства параметров на «грубые области» и разделяющие их пленки, соответствующие негрубым системам, называется бифуркационной диаграммой.
В § 2 гл. 10, рассматривая исходную негрубую систему, мы устанавливали все возможные бифуркации при переходе от этой негрубой системы к любым достаточно близким грубым системам пространства.
Однако для задач из приложений при рассмотрении бифуркаций основной интерес представляет следующий вопрос: какова последовательная смена качественных структур при изменении параметров вдоль кривой в пространстве параметров, проходящей через бифуркационное значение параметров и переходящей из одной грубой области в другую?
Следующий параграф посвящен рассмотрению указанной смены качественных структур.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. АВТОНОМНЫЕ СИСТЕМЫ ВТОРОГО ПОРЯДКА С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- § 1. Автономная динамическая система на плоскости.
- § 2. Теорема существования и единственности решения.
- § 3. Простейшие свойства решений системы (А).
- § 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
- § 5. Сопоставление геометрической интерпретации системы (А) в пространстве (x, y, t) с интерпретацией на фазовой плоскости.
- § 6. Некоторые термины.
- § 7. Теорема о непрерывной зависимости решения от начальных условий.
- § 8. Направление на траекториях. Изменение параметризации.
- § 9. Дифференциальное уравнение, соответствующее динамической системе.
- § 10. Понятие интегральной кривой и интеграла в случае аналитических правых частей Р(х,у) и Q(x,y) системы (А).
- § 11. Что значит «найти решение динамической системы»?
- § 12. Примеры.
- § 13. Замечания по поводу примеров § 12.
- § 14. Математическое определение качественной (топологической) структуры разбиения на траектории и качественного исследования динамической системы.
- ГЛАВА 2. ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ — БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ
- § 2. Цикл без контакта.
- § 3. Предельная точка полутраектории и траектории. Предельная траектория.
- § 4. Основная теорема.
- § 5. Возможные типы полутраекторий и их предельных множеств.
- § 6. Особые и неособые полутраектории и траектории.
- § 7. Возможные типы особых и неособых траекторий.
- § 8. Случай конечного числа особых траекторий. Элементарные ячейки.
- § 9. Возможные типы ячеек. Односвязные и двусвязные ячейки.
- § 10. Два подхода к описанию качественной структуры.
- § 11. Качественная (топологическая) структура состояния равновесия в случае конечного числа особых траекторий. Схема динамической системы.
- § 12. Устойчивость по Ляпунову.
- ГЛАВА 3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННОЙ СТРУКТУРЫ ОКРЕСТНОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (ОСОБОЙ ТОЧКИ)
- § 2. Приведение динамической системы к каноническому виду.
- § 3. Возможный характер простых состояний равновесия.
- § 4. Замечания о методах установления характера грубых состояний равновесия.
- § 5. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 6. Направления, в которых траектории стремятся к простым состояниям равновесия.
- § 7. Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия.
- § 8. Сводка сведений о грубых состояниях равновесия.
- ГЛАВА 4. КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ
- § 1. Направления, в которых траектории стремятся к сложному состоянию равновесия.
- § 2. Сложное состояние равновесия (особая точка) с нулевыми характеристическими корнями.
- § 3. Примеры.
- § 4. Нормальные формы.
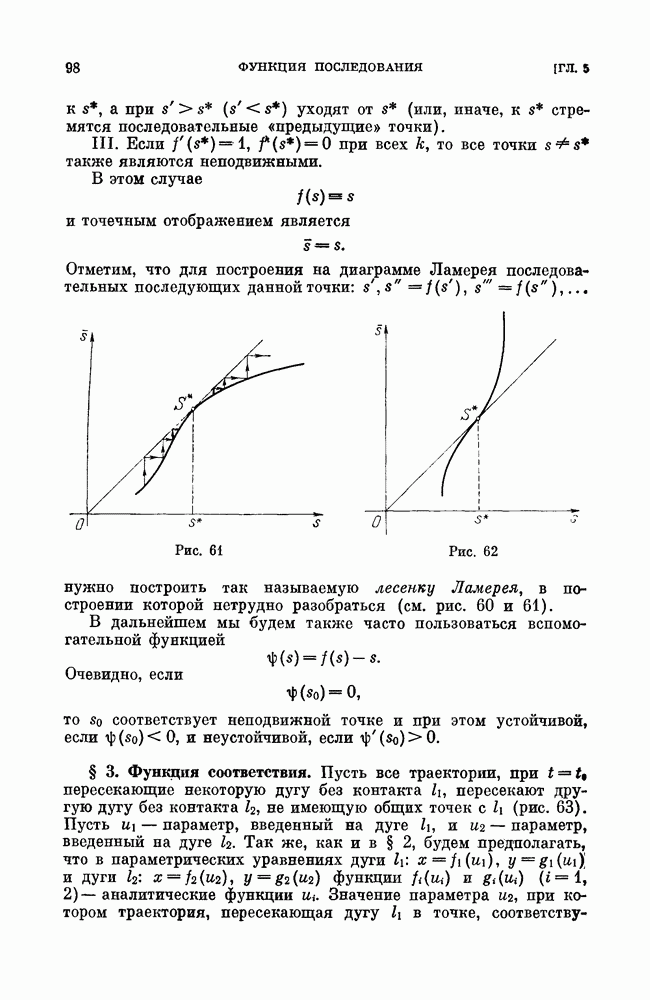
- ГЛАВА 5. ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ
- § 2. Условия устойчивости и неустойчивости неподвижной точки точечного отображения.
- § 3. Функция соответствия.
- § 4. Изучение окрестности замкнутой траектории. Простые и сложные предельные циклы.
- § 5. Аналитические выражения для коэффициентов функции последования. Характеристический показатель замкнутой траектории.
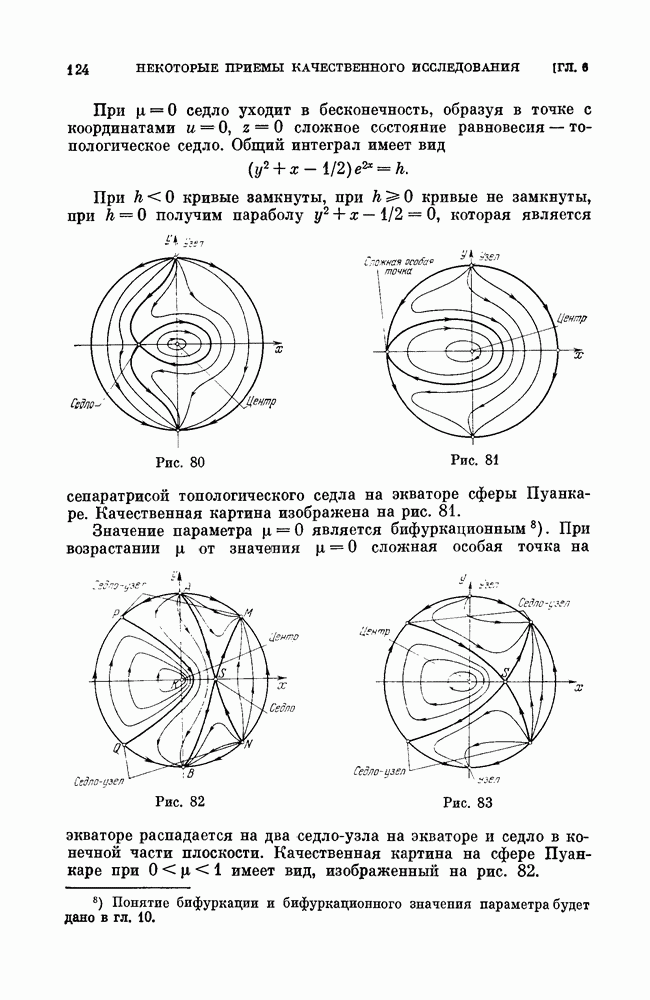
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЕМЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 2. Изучение поведения интегральных кривых в бесконечности. Сфера Пуанкаре.
- § 3. Примеры исследования в бесконечности [93].
- § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов.
- 1. Некоторые видоизменения критериев Бендиксона и Дюлака.
- 2. Индексы Пуанкаре. Распределение особых точек [77, 117].
- 3. Условия сосуществования замкнутых траекторий и особых точек.
- 4. Две общие теоремы Пуанкаре.
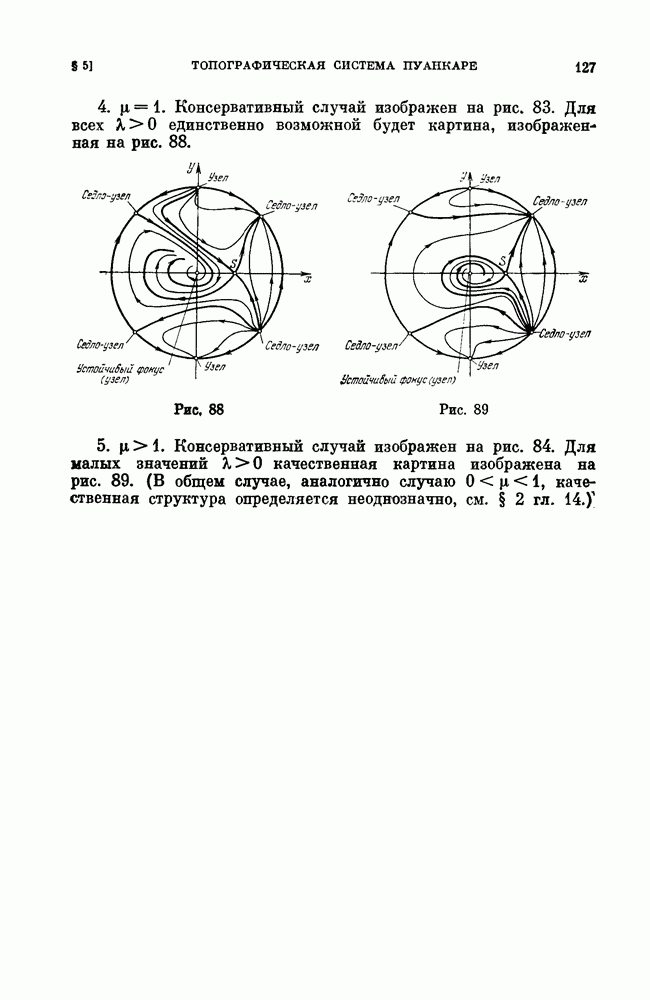
- § 5. Топографическая система Пуанкаре. Функция Ляпунова. Кривые контактов.
- ЧАСТЬ II. ТЕОРИЯ БИФУРКАЦИЙ
- § 1. Свойства консервативных систем на плоскости [2, 3].
- § 2. Динамические системы, характерные для теории колебаний.
- § 3. Измененные системы. Системы, правые части которых зависят от параметра.
- § 4. Основные теоремы о зависимости решения от изменения правых частей динамической системы.
- § 5. Грубость динамической системы и теоремы о непрерывной зависимости решения от изменения правых частей.
- ГЛАВА 8. ГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
- § 2. Состояния равновесия, возможные в грубой динамической системе.
- § 3. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 4. Замкнутые траектории, возможные в грубой системе.
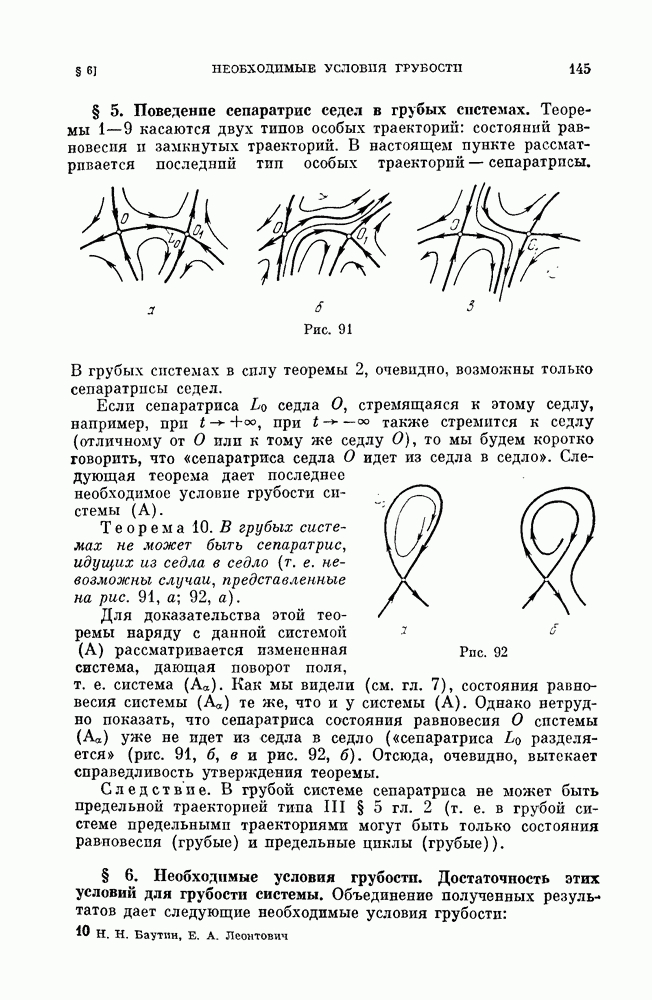
- § 5. Поведение сепаратрис седел в грубых системах.
- § 6. Необходимые условия грубости. Достаточность этих условий для грубости системы.
- § 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем.
- § 8. Понятие грубости при более общих предположениях относительно правых частей динамической системы.
- § 9. Типы особых траекторий и ячеек в грубых системах.
- § 10. Замечания по поводу определения грубой системы.
- ГЛАВА 9. ПРОСТЕЙШИЕ НЕГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ — СИСТЕМЫ ПЕРВОЙ СТЕПЕНИ НЕГРУБОСТИ
- § 2. Системы первой степени негрубости.
- § 3. Состояния равновесия, возможные в системе первой степени негрубости.
- § 4. Замкнутые траектории, возможные в системе первой степени негрубости.
- § 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости.
- § 6. Необходимые и достаточные условия первой степени негрубости.
- § 7. Динамические системы более высокой степени негрубости.
- ГЛАВА 10. БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- § 1. Определение бифуркации.
- § 2. Бифуркации систем первой степени негрубости.
- § 3. Бифуркации некоторых типов сложных особых точек.
- § 4. Бифуркации двукратной точки, для которой …
- § 5. Рождение предельных циклов из особых траекторий степени негрубости выше первой.
- ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
- § 1. Возможный характер зависимости правых частей динамической системы от параметров.
- § 2. Смена качественных структур при изменении параметров.
- § 3. Случай, когда правые части зависят более чем от одного параметра.
- § 4. Бифуркации «от бесконечности».
- § 5. Условия существования седло-узла и сложного фокуса первого порядка.
- § 6. Поворот векторного поля.
- § 7. Метод малого параметра. Метод Понтрягина.
- ГЛАВА 12. ДИНАМИЧЕСКИЕ СИСТЕМЫ С ЦИЛИНДРИЧЕСКОЙ ФАЗОВОЙ ПОВЕРХНОСТЬЮ
- § 1. Цилиндрическая фазовая поверхность и характер траекторий, возможных на цилиндрической фазовой поверхности.
- § 2. Замкнутые траектории, охватывающие цилиндр.
- § 3. Приемы исследования качественной структуры динамической системы на цилиндре.
- § 4. Понятие грубости и степени негрубости для динамических систем на цилиндре. Бифуркации на цилиндре. Поворот поля.
- § 5. Динамические системы на цилиндре, близкие к гамильтоновым (метод Понтрягина).
- ГЛАВА 13. АДЕКВАТНОЕ ИСТОЛКОВАНИЕ НЕЛИНЕЙНЫХ ФИЗИЧЕСКИХ ЯВЛЕНИЙ ФАКТАМИ КАЧЕСТВЕННОЙ ТЕОРИИ И ТЕОРИИ БИФУРКАЦИЙ ДИНАМИЧЕСКИХ СИСТЕМ
- § 1. Мягкий и жесткий режимы.
- § 2. Замечания о границах области устойчивости различных стационарных режимов.
- § 3. Мягкое и жесткое возникновение колебаний.
- § 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
- § 5. Замечания по поводу других границ области устойчивости.
- ЧАСТЬ III. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- ГЛАВА 14. ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 1. Некоторые рецептурные указания.
- § 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
- § 3. Некоторые простые примеры динамических систем на цилиндре.
- ГЛАВА 15. ИССЛЕДОВАНИЕ МЕТОДОМ МАЛОГО ПАРАМЕТРА (МЕТОДОМ ПОНТРЯГИНА)
- § 2. Примеры рассмотрения методом Понтрягина (полное исследование).
- § 3. Исследование методом Понтрягина с привлечением вычислительных методов.
- ГЛАВА 16. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ
- § 2. Электрическая цепь с туннельным диодом.
- § 3. Двумерная модель динамики твердотельного лазера [119].
- § 4. Симметричный полет самолета в вертикальной плоскости (задача Н. Е. Жуковского).
- § 5. Система, описывающая динамику проточного химического реактора.
- § 6. Фазовая автоподстройка частоты.
- § 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов).
- § 8. Синхронный генератор с асинхронной характеристикой.
- ЧАСТЬ IV. КУСОЧНО-СШИТЫЕ СИСТЕМЫ
- ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ
- § 1. Сшитые системы. Доопределение на линиях сшивания.
- § 2. Возможные типы полутраекторий сшитых систем.
- § 3. Особые траектории сшитых систем.
- § 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
- ГЛАВА 18. ИССЛЕДОВАНИЕ КУСОЧНО-СШИТЫХ СИСТЕМ МЕТОДОМ ПОНТРЯГИНА
- § 2. Автоподстройка при кусочно-постоянной аппроксимации характеристики.
- § 3. Автоколебания синхронного мотора.
- ГЛАВА 19. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ
- § 2. Следящая система с люфтом.
- § 3. Электрическая цепь с туннельным диодом.
- § 4. Система со скачками на линии сшивания.
- ГЛАВА 20. ОБ АППРОКСИМАЦИЯХ И ГРУБОСТИ ПРОСТРАНСТВА ПАРАМЕТРОВ [39, 41, 42]
- § 1. Рассмотрение системы (2) при аппроксимациях пилообразными функциями.
- § 2. Рассмотрение системы (2) при аппроксимации, включающей отрезок параболы.
- § 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin f, и пилообразной для cos f функциями.
- § 4. Исследование роли аппроксимаций для уравнения маятникового типа.
- § 5. Динамическая система, описывающая автоколебания синхронного мотора.
- § 6. Динамическая система, описывающая симметричный полет самолета.
- ДОПОЛНЕНИЕ
- § 1. Динамическое системы на двумерных поверхностях.
- § 2. Динамические системы в n-мерном евклидовом пространстве.
- СПИСОК ЛИТЕРАТУРЫ