| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Электрическая цепь с туннельным диодом.
Рассматривается система [29]

где  имеет падающий участок при аппроксимации
имеет падающий участок при аппроксимации  кубическим полиномом
кубическим полиномом

и условиях

Последнее эквивалентно условию  при котором в системе возможны разнообразные бифуркации. В случае
при котором в системе возможны разнообразные бифуркации. В случае  возможными бифуркациями являются только появление и исчезновение состояний равновесия, так как на всей плоскости
возможными бифуркациями являются только появление и исчезновение состояний равновесия, так как на всей плоскости 
1. Состояния равновесия и их бифуркации. Возможны одно или три грубых состояния равновесия. В случае одного состояния равновесия имеем фокус (узел), устойчивый, если в точке пересечения изоклин выполняется условие  и неустойчивый в противоположном случае. В случае трех состояний равновесия между фокусами (узлами) лежит седло.
и неустойчивый в противоположном случае. В случае трех состояний равновесия между фокусами (узлами) лежит седло.
Дискриминантная кривая в плоскости  отделяющая область трех состояний равновесия от области одного состояния равновесия, получается из условия соприкосновения прямой
отделяющая область трех состояний равновесия от области одного состояния равновесия, получается из условия соприкосновения прямой  и кривой
и кривой  и в параметрическом виде дается уравнениями
и в параметрическом виде дается уравнениями

где  координата точки касания.
координата точки касания.
Значению  определяемому из условия
определяемому из условия  соответствует точка возврата дискриминантной кривой. Дискриминантная кривая располагается слева от точки возврата и обращена выпуклостью в сторону области трех состояний равновесия (вторая производная имеет значение
соответствует точка возврата дискриминантной кривой. Дискриминантная кривая располагается слева от точки возврата и обращена выпуклостью в сторону области трех состояний равновесия (вторая производная имеет значение  и меняет знак, когда параметр
и меняет знак, когда параметр  переходит через значение, соответствующее точке возврата).
переходит через значение, соответствующее точке возврата).
Исключая из (3) параметр  уравнение дискриминантной кривой получим в виде
уравнение дискриминантной кривой получим в виде

Координаты точки возврата будут

Точкам дискриминантной кривой соответствуют два состояния равновесия системы (1): фокус (узел) и сложное состояние равновесия седло-узел. Точке возврата соответствует слияние трех состояний равновесия.
Система (1) будет иметь сложный фокус  на прямых, выходящих по касательной из точек дискриминантной кривой при
на прямых, выходящих по касательной из точек дискриминантной кривой при  в область
в область 
Для координат состояний равновесия имеем уравнение

Условие  дает
дает

откуда 

Подставляя (6) в (5), находим для состояния равновесия 

для состояния равновесия 

В плоскости параметров А, а прямые (7) и (8) касаются верхнех! и нижней ветвей дискриминантной кривой при  пересекаются в точке
пересекаются в точке

и пересекают ветви дискриминантной кривой при 

Координаты  могут соответствовать как фокусу, так и седлу, и поэтому при переходе через прямые (7) и (8) может менять знак или фокусная, или седловая величины
могут соответствовать как фокусу, так и седлу, и поэтому при переходе через прямые (7) и (8) может менять знак или фокусная, или седловая величины  .
.
Перенесем начало координат в состояние равновесия  где
где  одно из чисел
одно из чисел  или
или  определяемых выражением (6). Полагая
определяемых выражением (6). Полагая  получим вместо (1) систему
получим вместо (1) систему

Для системы (10) будет

Состоянием равновесия в начале координат будет сложный фокус, если  или седло, если
или седло, если 
Первая ляпуновская величина для системы (10) имеет вид

 обращается в нуль при
обращается в нуль при 

Сложный фокус устойчив  при
при  и неустойчив
и неустойчив  при
при  При
При  устойчивость сложного фокуса определяется знаком второй ляпуновской величины
устойчивость сложного фокуса определяется знаком второй ляпуновской величины 
Для ее вычисления перейдем в уравнениях (10) к новым переменным  по формулам
по формулам

В новых переменных уравнения (10) примут вид  За
За 

Для уравнений (13) величина  может быть подсчитана по готовой формуле
может быть подсчитана по готовой формуле  Получаем
Получаем

Отметим, что в выражения (11) и (14) для  не входит величина
не входит величина  следовательно, полученные выражения относятся как к левому
следовательно, полученные выражения относятся как к левому  так и к правому
так и к правому  сложным фокусам для значений параметров на прямых (7) и (8) при
сложным фокусам для значений параметров на прямых (7) и (8) при 

Рис. 157
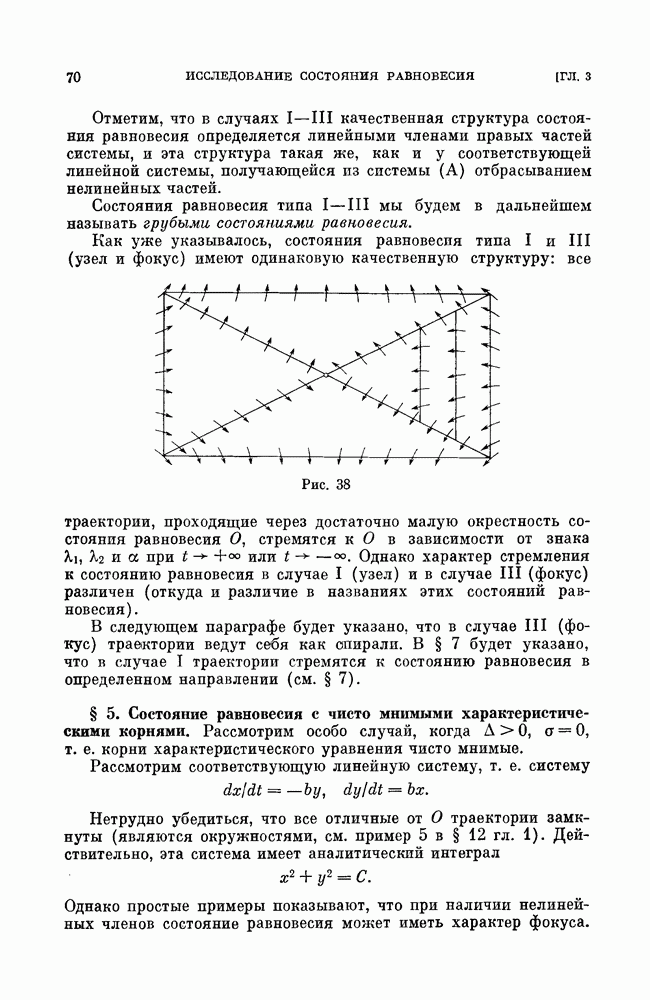
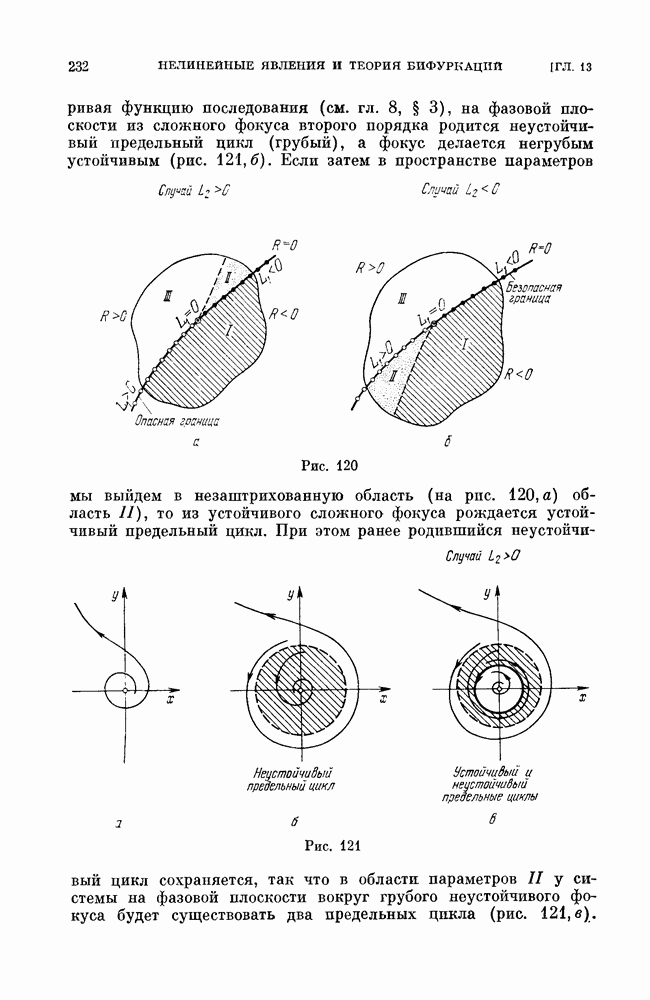
2. Поведение в бесконечности. Построим на плоскости  прямоугольник со сторонами, параллельными координатным осям, для которого изоклина
прямоугольник со сторонами, параллельными координатным осям, для которого изоклина  служит диагональю. Если такой прямоугольник взять достаточно большим, то изоклина
служит диагональю. Если такой прямоугольник взять достаточно большим, то изоклина  порядок роста которой выше, чем у прямой, стороны, параллельные оси у, не будет пересекать, а каждую из других сторон пересечет в одной точке. Все траектории системы (1) будут с возрастанием
порядок роста которой выше, чем у прямой, стороны, параллельные оси у, не будет пересекать, а каждую из других сторон пересечет в одной точке. Все траектории системы (1) будут с возрастанием  входить внутрь такого прямоугольника. Бесконечность при любых значениях параметров системы будет неустойчивой (рис. 157).
входить внутрь такого прямоугольника. Бесконечность при любых значениях параметров системы будет неустойчивой (рис. 157).
3. Качественная структура фазового пространства и пространства параметров.
3.1. Симметрия в фазовом пространстве. Перенесем начало координат в точку перегиба характеристики  Система (1) примет вид
Система (1) примет вид

где

Из (15) видно, 
а) если  то фазовое пространство системы (15) симметрично относительно начала координат (точки перегиба характеристики)
то фазовое пространство системы (15) симметрично относительно начала координат (точки перегиба характеристики) 
б) если две прямые  располагаются симметрично относительно начала координат
располагаются симметрично относительно начала координат  то фазовые портреты для значений
то фазовые портреты для значений  будут симметричны относительно точки перегиба характеристики.
будут симметричны относительно точки перегиба характеристики.
При изучении пространства параметров можно поэтому ограничиться рассмотрением только части пространства параметров а, А — либо выше, либо ниже линии симметричных структур  где
где  — координаты точки перегиба характеристики. В раскрытом виде
— координаты точки перегиба характеристики. В раскрытом виде


Рис. 158
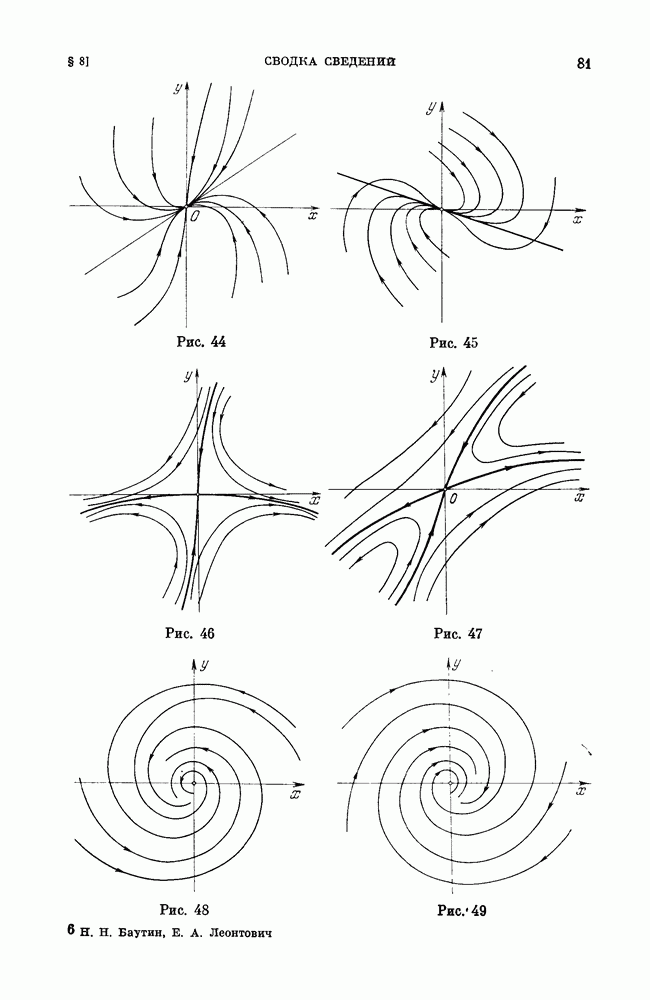
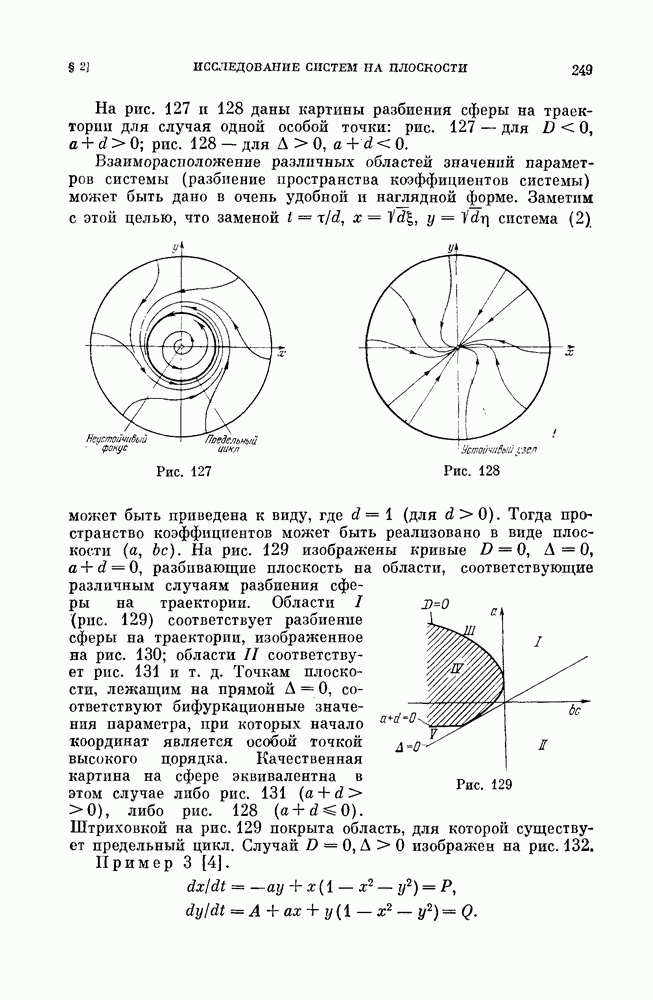
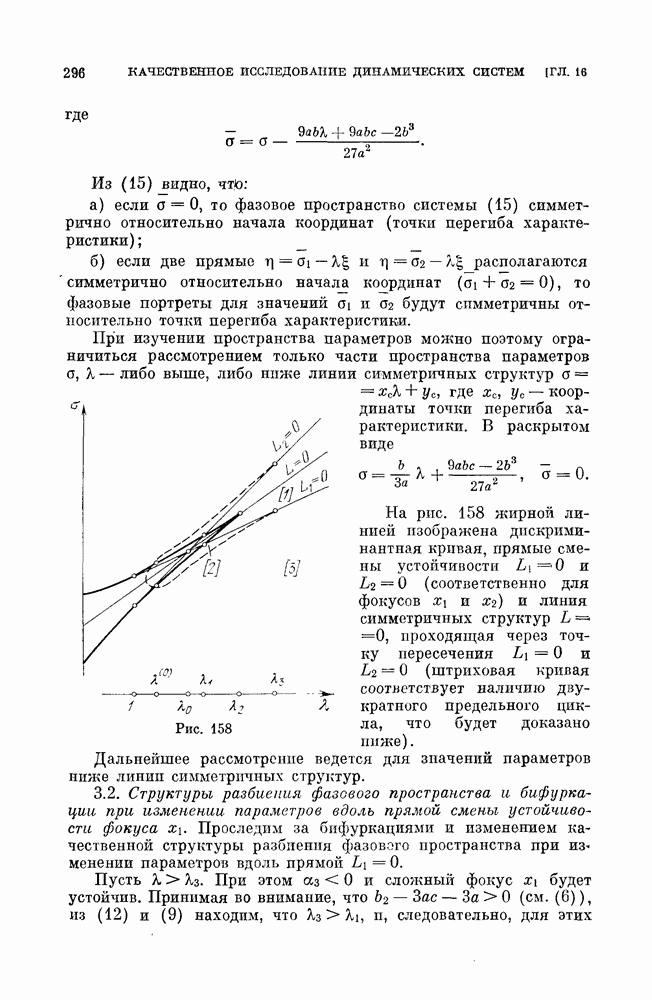
На рис. 158 жирной линией изображена дискриминантная кривая, прямые смены устойчивости  (соответственно для фокусов
(соответственно для фокусов  и линия симметричных структур
и линия симметричных структур  проходящая через точку пересечения
проходящая через точку пересечения  (штриховая кривая соответствует наличию двукратного предельного цикла, что будет доказано ниже).
(штриховая кривая соответствует наличию двукратного предельного цикла, что будет доказано ниже).
Дальнейшее рассмотрение ведется для значений параметров ниже линии симметричных структур.
3.2. Структуры разбиения фазового пространства и бифуркации при изменении параметров вдоль прямой смены устойчивости фокуса  Проследим за бифуркациями и изменением качественной структуры разбиения фазового пространства при
Проследим за бифуркациями и изменением качественной структуры разбиения фазового пространства при  менении параметров вдоль прямой
менении параметров вдоль прямой 
Пусть  При этом
При этом  и сложный фокус
и сложный фокус  будет устойчив. Принимая во внимание, что
будет устойчив. Принимая во внимание, что  (см. (6)), из (12) и (9) находим, что
(см. (6)), из (12) и (9) находим, что  следовательно, для этих
следовательно, для этих
значений параметров система (1) имеет одно состояние равновесия. При уменьшении X от значения  меняет знак
меняет знак  сложный фокус меняет устойчивость (оставаясь сложным) и от него рождается устойчивый предельный цикл. При дальнейшем уменьшении X на интервале
сложный фокус меняет устойчивость (оставаясь сложным) и от него рождается устойчивый предельный цикл. При дальнейшем уменьшении X на интервале  устойчивый цикл сохраняется. Значение
устойчивый цикл сохраняется. Значение  соответствует касанию прямой
соответствует касанию прямой  и характеристики
и характеристики  При этом на фазовой плоскости возникает седло-узел с неустойчивой узловой областью
При этом на фазовой плоскости возникает седло-узел с неустойчивой узловой областью  в седло-узле) и, как можно убедиться, при любых характеристиках, соответствующих определенному выбору коэффициентов
в седло-узле) и, как можно убедиться, при любых характеристиках, соответствующих определенному выбору коэффициентов  именно внутри предельного цикла.
именно внутри предельного цикла.
Еслп для некоторых аппроксимаций седло-узел возникает внутри цикла, а для других вне его, то по непрерывности должна существовать и такая характеристика, для которой седло-узел возникает на предельном цикле. Но седло-узел с неустойчивой узловой областью не может возникнуть на устойчивом предельном цикле 
Таким образом, достаточно знать взаимное расположение цикла и седло-узла для какой-либо одной конкретной аппроксимации. Для системы (1) с аппроксимацией  и параметрами
и параметрами  (соответствующими состояниям равновесия сложный фокус и седло-узел) численным методом установлено, что цикл охватывает седло-узел. Следовательно, это имеет место для любых кубических аппроксимаций.
(соответствующими состояниям равновесия сложный фокус и седло-узел) численным методом установлено, что цикл охватывает седло-узел. Следовательно, это имеет место для любых кубических аппроксимаций.
При дальнейшем продвижении вдоль прямой  внутрь области, ограниченной дискриминантной кривой, седло-узел распадается на седло и неустойчивый узел, который затем превращается в фокус. Точке пересечения
внутрь области, ограниченной дискриминантной кривой, седло-узел распадается на седло и неустойчивый узел, который затем превращается в фокус. Точке пересечения  прямой
прямой  с линией симметричных структур
с линией симметричных структур  соответствует фазовое пространство, содержащее два сложных фокуса, расположенных симметрично относительно седла (
соответствует фазовое пространство, содержащее два сложных фокуса, расположенных симметрично относительно седла ( -сепаратрисы седла идут к устойчивому циклу, охватывающему все три состояния равновесия,
-сепаратрисы седла идут к устойчивому циклу, охватывающему все три состояния равновесия,  -сепаратрисы скручиваются с неустойчивых! сложных фокусов).
-сепаратрисы скручиваются с неустойчивых! сложных фокусов).
Замечание. Качественная структура разбиения фазового пространства на траектории по использованной информации описывается лишь с точностью до дополнительного четного числа предельных циклов, возможно, возникших из сгущения траекторий. Такая неполнота и в дальнейшем не может быть устранена.
3.3. Структура разбиения фазового пространства и бифуркации при изменении параметров вдоль линии симметричных структур. Проследим за бифуркациями и изменением структуры фазового пространства вдоль линии симметричных структур  Пусть
Пусть  определяется выражением (4)). Единственное состояние равновесия системы — неустойчивый фокус (узел). Бесконечность неустойчива. Вокруг фокуса существует
определяется выражением (4)). Единственное состояние равновесия системы — неустойчивый фокус (узел). Бесконечность неустойчива. Вокруг фокуса существует
устойчивый предельный цикл. Убыванию А вдоль прямой  соответствует поворот прямой
соответствует поворот прямой  вокруг состояния равновесия в точке перегиба характеристики
вокруг состояния равновесия в точке перегиба характеристики  При
При  прямая будет касаться характеристики в точке перегиба
прямая будет касаться характеристики в точке перегиба  пересекает дискриминантную кривую в точке возврата) и возникнет сложное состояние равновесия, распадающееся при убывании к от значения
пересекает дискриминантную кривую в точке возврата) и возникнет сложное состояние равновесия, распадающееся при убывании к от значения  на три простых: два неустойчивых узла (фокуса) и седло между ними. На интервале
на три простых: два неустойчивых узла (фокуса) и седло между ними. На интервале  бифуркаций состояния равновесия не происходит. При
бифуркаций состояния равновесия не происходит. При  оба фокуса становятся сложными, и при убывании
оба фокуса становятся сложными, и при убывании  от значения
от значения  из них рождаются неустойчивые предельные циклы (первая фокусная величина
из них рождаются неустойчивые предельные циклы (первая фокусная величина  положительна). Возникает структура фазового пространства с тремя предельными циклами,
положительна). Возникает структура фазового пространства с тремя предельными циклами,  -сепаратрисы седла идут к устойчивому циклу, охватывающему все три состояния равновесия,
-сепаратрисы седла идут к устойчивому циклу, охватывающему все три состояния равновесия,  -сепаратрисы скручиваются с неустойчивых циклов, охватывающих устойчивые фокусы.
-сепаратрисы скручиваются с неустойчивых циклов, охватывающих устойчивые фокусы.
При дальнейшем убывании к на интервале  смены устойчивости состояний равновесия не происходит, но при
смены устойчивости состояний равновесия не происходит, но при  циклов уже нет (при
циклов уже нет (при  существует интегральная прямая
существует интегральная прямая  проходящая через все состояния равновесия). Предельные циклы могут исчезнуть, только превратившись в петли сепаратрис или слившись с циклами, вновь возникшими из петель сепаратрис. Существенно, что циклы вокруг фокусов и цикл, охватывающий все три состояния равновесия, имеют разную устойчивость. В соответствии со знаком седловой величины
проходящая через все состояния равновесия). Предельные циклы могут исчезнуть, только превратившись в петли сепаратрис или слившись с циклами, вновь возникшими из петель сепаратрис. Существенно, что циклы вокруг фокусов и цикл, охватывающий все три состояния равновесия, имеют разную устойчивость. В соответствии со знаком седловой величины  только неустойчивые циклы, охватывающие состояния равновесия, могут превратиться (и обязательно превратятся при некотором
только неустойчивые циклы, охватывающие состояния равновесия, могут превратиться (и обязательно превратятся при некотором  в петли сепаратрис. Эти две петли (возникающие одновременно, так как
в петли сепаратрис. Эти две петли (возникающие одновременно, так как  линия симметричных структур) можно рассматривать как одну вырожденную большую петлю, от которой при ее разрушении с убыванием к возникает неустойчивый же предельный цикл, охватывающий три состояния равновесия. При некотором
линия симметричных структур) можно рассматривать как одну вырожденную большую петлю, от которой при ее разрушении с убыванием к возникает неустойчивый же предельный цикл, охватывающий три состояния равновесия. При некотором  предельные циклы, охватывающие три состояния равновесия, сливаются и при убывании к исчезают.
предельные циклы, охватывающие три состояния равновесия, сливаются и при убывании к исчезают.
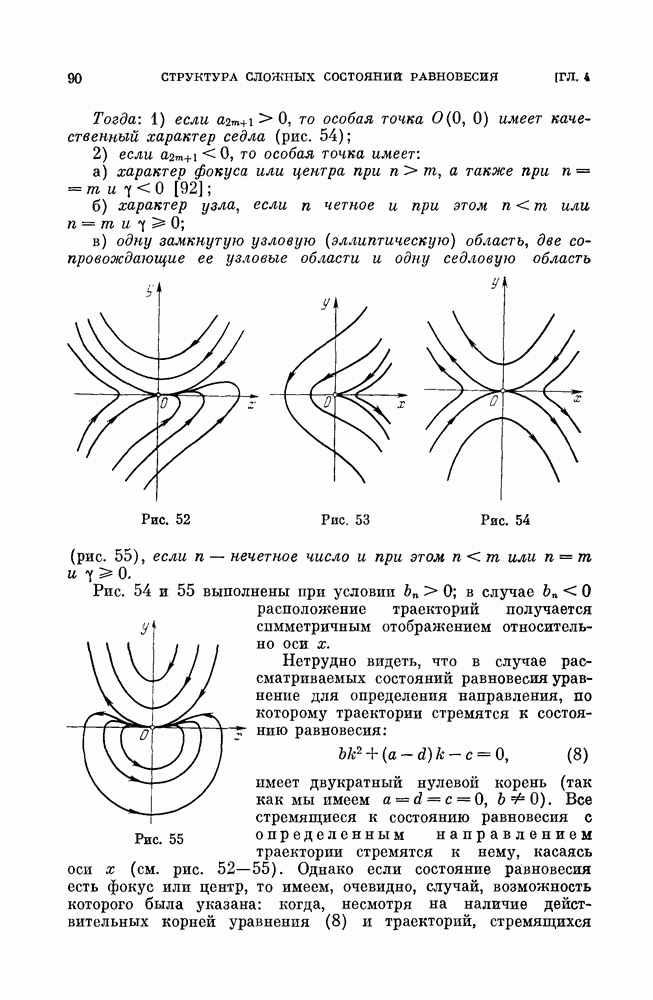
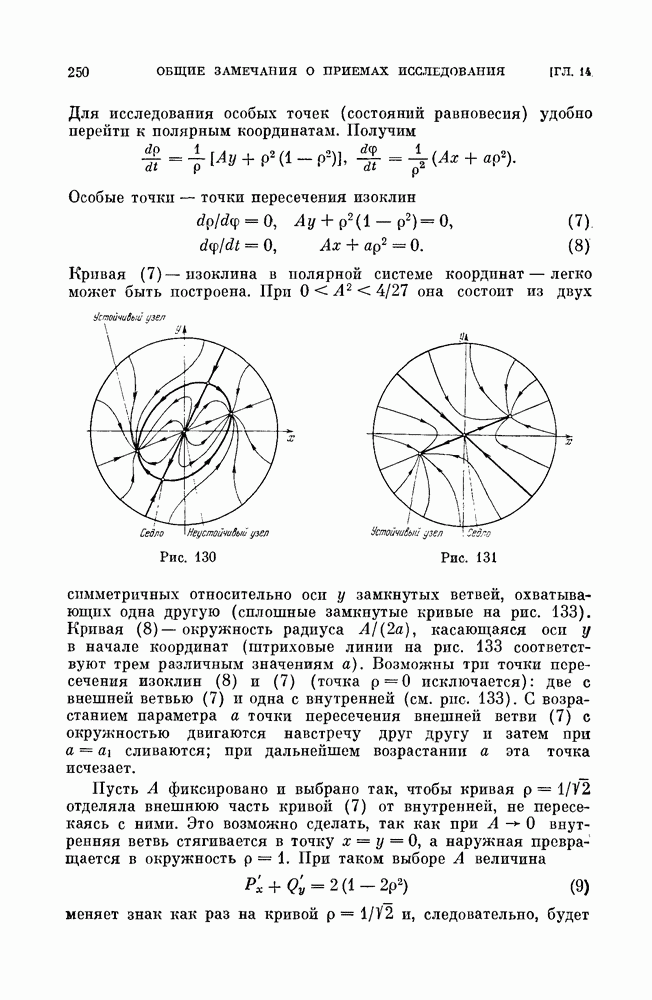
3.4. Структуры разбиения фазового пространства и бифуркации при изменении параметров вдоль дискриминантной кривой. Проследим за бифуркациями и изменением структуры фазового пространства вдоль нижней ветви дискриминантной кривой, начиная от точки возврата  На интервале
На интервале  будет существовать структура с неустойчивым фокусом и седло-узлом
будет существовать структура с неустойчивым фокусом и седло-узлом  неустойчивой узловой областью внутри устойчивого предельного цикла (рис. 159,10). При убывании А от значения
неустойчивой узловой областью внутри устойчивого предельного цикла (рис. 159,10). При убывании А от значения  фокус
фокус  меняет устойчивость и, так как
меняет устойчивость и, так как  из него рождается неустойчивый предельный цикл (рис. 159,5). Чтобы проследить за дальнейшими бифуркациями при убывании А до нуля, следует прежде всего выяснить структуру при
из него рождается неустойчивый предельный цикл (рис. 159,5). Чтобы проследить за дальнейшими бифуркациями при убывании А до нуля, следует прежде всего выяснить структуру при  Она легко определяется, так как при
Она легко определяется, так как при  существует интегральная
существует интегральная
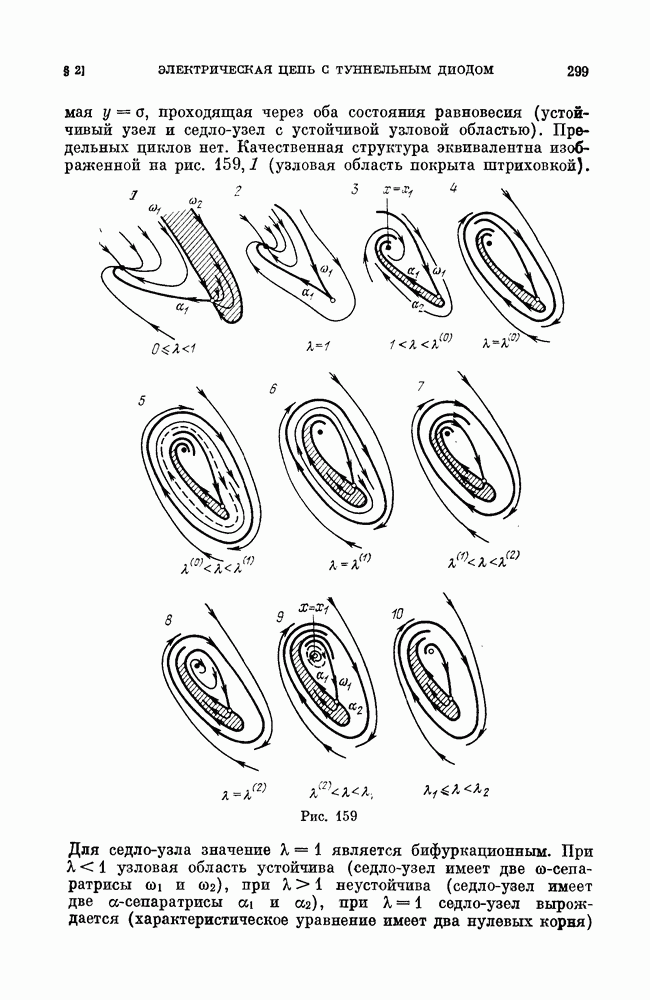
прямая  проходящая через оба состояния равновесия (устойчивый узел и седло-узел с устойчивой узловой областью). Предельных циклов нет. Качественная структура эквивалентна изображенной на рис. 159,7 (узловая область покрыта штриховкой).
проходящая через оба состояния равновесия (устойчивый узел и седло-узел с устойчивой узловой областью). Предельных циклов нет. Качественная структура эквивалентна изображенной на рис. 159,7 (узловая область покрыта штриховкой).
Рис. 159 (см. скан)
Для седло-узла значение  является бифуркационным. При
является бифуркационным. При  узловая область устойчива (седло-узел имеет две ю-сепа-ратрисы
узловая область устойчива (седло-узел имеет две ю-сепа-ратрисы  , при
, при  неустойчива (седло-узел имеет две
неустойчива (седло-узел имеет две  -сепаратрисы
-сепаратрисы  при
при  седло-узел вырождается (характеристическое уравнение имеет два нулевых корня)
седло-узел вырождается (характеристическое уравнение имеет два нулевых корня)
и узловая область исчезает (состояние равновесия имеет одну  и одну (
и одну ( -сеиератрису). Структура с сохранением типа состояний равновесия, как на рис. 159,1, осуществляется на интервале
-сеиератрису). Структура с сохранением типа состояний равновесия, как на рис. 159,1, осуществляется на интервале 
Для прослеживания бифуркаций вдоль дискриминантной кривой существенным является установление качественной структуры при  Как будет видно из дальнейшего, при возрастании к от нуля необходимо возникает из сгущения траекторий двойной предельный цикл, охватывающий состояния равновесия, однако не существует способов обнаружить точные значения параметров, при которых он возникает. В дальнейшем будем предполагать, что при
Как будет видно из дальнейшего, при возрастании к от нуля необходимо возникает из сгущения траекторий двойной предельный цикл, охватывающий состояния равновесия, однако не существует способов обнаружить точные значения параметров, при которых он возникает. В дальнейшем будем предполагать, что при  предельных циклов еще нет и осуществляется структура рис. 159, 2 (изменения в результатах, отвечающие предположению о существовании предельных циклов уже при
предельных циклов еще нет и осуществляется структура рис. 159, 2 (изменения в результатах, отвечающие предположению о существовании предельных циклов уже при  будут в дальнейшем указаны)).
будут в дальнейшем указаны)).
При возрастании к от значения к — 1 возникает структура, качественно эквивалентная представленной на рис. 159,5. Возникает неустойчивая узловая область седло-узла (обе  -сепаратрисы выходят по направлению
-сепаратрисы выходят по направлению  -сепаратриса входит по направлению
-сепаратриса входит по направлению  Узел становится фокусом при
Узел становится фокусом при  где
где 
Сопоставим теперь расположение а- и  -сепаратрис для структур на рис. 159, 9 и 159, 3. Отметим точки пересечения с
-сепаратрис для структур на рис. 159, 9 и 159, 3. Отметим точки пересечения с  и
и  -сепаратрисами на отрезке прямой
-сепаратрисами на отрезке прямой  выше фокуса (ближайшие но ходу сепаратрис от седло-узла). Для структуры на рис. 159,9 след
выше фокуса (ближайшие но ходу сепаратрис от седло-узла). Для структуры на рис. 159,9 след  -сепаратрисы на прямой
-сепаратрисы на прямой  расположен ниже следов
расположен ниже следов  -сепаратрис. Для структуры на рис. 159,5, наоборорот — выше. При убывании к последовательно должны осуществиться бифуркации, соответствующие совпадению на прямой
-сепаратрис. Для структуры на рис. 159,5, наоборорот — выше. При убывании к последовательно должны осуществиться бифуркации, соответствующие совпадению на прямой  следа
следа  -сепаратрисы со следом
-сепаратрисы со следом  -сепаратрисы (выходящей из седло-узла вверх) и со следом
-сепаратрисы (выходящей из седло-узла вверх) и со следом  -сепаратрисы (выходящей вниз). Так как седловая величина
-сепаратрисы (выходящей вниз). Так как седловая величина  при
при  положительна, то при образовании первой петли (при
положительна, то при образовании первой петли (при  к ней стягивается неустойчивый предельный цикл (см. гл. И) (рис. 159, 8). При расположении следа
к ней стягивается неустойчивый предельный цикл (см. гл. И) (рис. 159, 8). При расположении следа  -сепаратрисы между следами
-сепаратрисы между следами  и
и  -сепаратрис будет существовать замкнутый контур, образованный
-сепаратрис будет существовать замкнутый контур, образованный  -сепаратрисой седло-узла (рис. 159,7). При совпадении следов
-сепаратрисой седло-узла (рис. 159,7). При совпадении следов  и
и  -сепаратрис при
-сепаратрис при  возникает петля сепаратрисы (рис. 159,б), от которой при ее разрушении с уменьшением к рождается неустойчивый предельный цикл, охватывающий оба состояния равновесия, и возникает
возникает петля сепаратрисы (рис. 159,б), от которой при ее разрушении с уменьшением к рождается неустойчивый предельный цикл, охватывающий оба состояния равновесия, и возникает
структура рис. 159,5 с двумя предельными циклами, между которыми нет состояний равновесия. На интервале  при некотором
при некотором  предельные циклы сливаются в двойной полуустойчивый предельный цикл (рис. 159,4) и затем исчезают. Последовательность структур вдоль нижней ветви дискриминантной кривой представлена на рис.
предельные циклы сливаются в двойной полуустойчивый предельный цикл (рис. 159,4) и затем исчезают. Последовательность структур вдоль нижней ветви дискриминантной кривой представлена на рис. 
3.5. Структуры разбиения фазового пространства и бифуркации внутри дискриминантной кривой в области трех состояний равновесия. Дискриминантная кривая, представленная в параметрическом виде уравнениями (3), может рассматриваться как огибающая семейства прямых  в плоскости
в плоскости  Полупрямые
Полупрямые

касающиеся в точке  дискриминантной кривой, однократно покрывают область, ограниченную линией симметричных структур и нижней ветвью дискриминантной кривой, при
дискриминантной кривой, однократно покрывают область, ограниченную линией симметричных структур и нижней ветвью дискриминантной кривой, при  изменяющемся от точки перегиба до минимума характеристики
изменяющемся от точки перегиба до минимума характеристики  (при
(при  Зас). Движение в пространстве параметров А, о вдоль полупрямых (16) от точки касания соответствует для системы (1) повороту против часовой стрелки изоклины
Зас). Движение в пространстве параметров А, о вдоль полупрямых (16) от точки касания соответствует для системы (1) повороту против часовой стрелки изоклины  вокруг седла, возникшего в точке
вокруг седла, возникшего в точке  при разделении седло-узла на седло и узел.
при разделении седло-узла на седло и узел.
Рассмотрим бифуркации, осуществляющиеся при движении по полупрямым (16), касающимся дискриминантной кривой на интервале  Здесь возникнут как бифуркации состояний равновесия, так и бифуркации сепаратрис и предельных циклов.
Здесь возникнут как бифуркации состояний равновесия, так и бифуркации сепаратрис и предельных циклов.
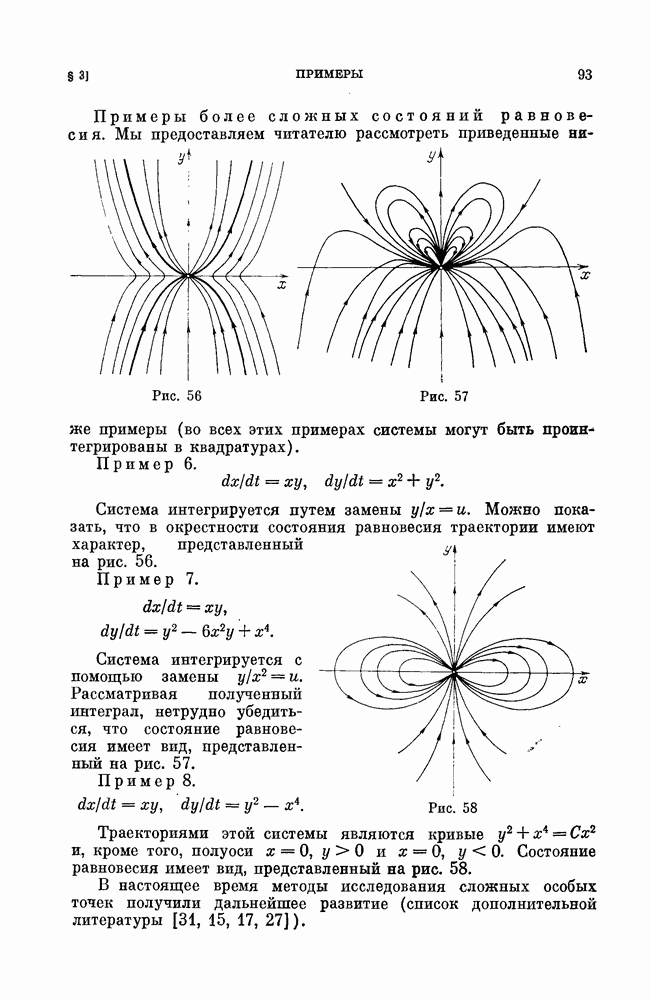
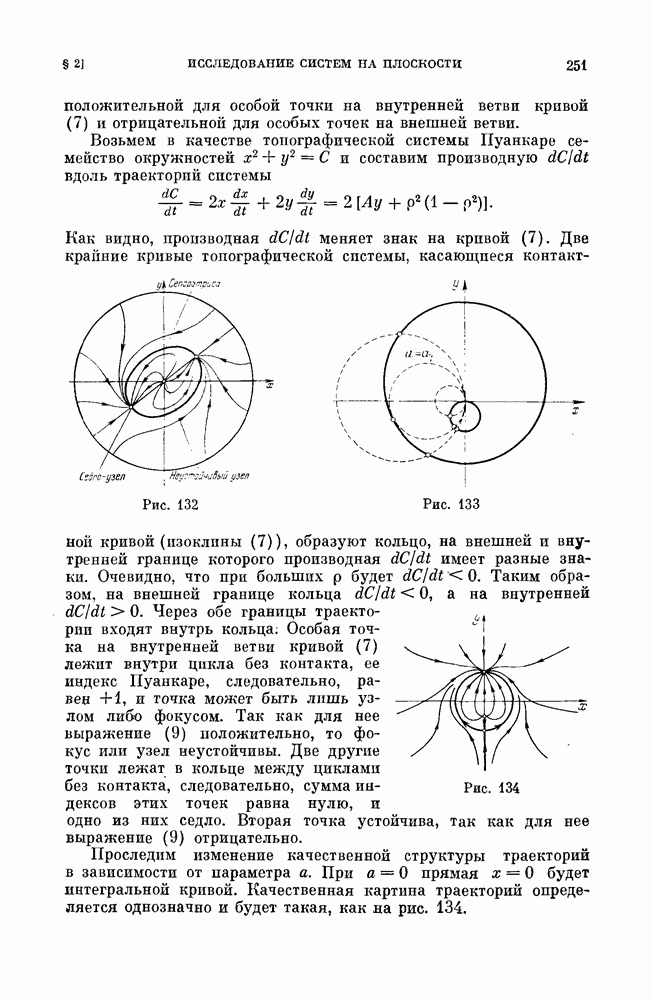
При уменьшении А состояние равновесия седло-узел внутри устойчивого предельного цикла разделяется на седло и неустойчивый узел, который при дальнейшем уменьшении А превращается в фокус (рис. 160,11).
В точках пересечения рассматриваемой полупрямой (16) с прямыми  происходят бифуркации состояний равновесия: при уменьшении А сначала из фокуса
происходят бифуркации состояний равновесия: при уменьшении А сначала из фокуса  (рис. 160,10) и затем из фокуса
(рис. 160,10) и затем из фокуса  рождаются неустойчивые предельные циклы (фокусы становятся устойчивыми) и возникает структура с тремя предельными циклами (рис. 160,9). Так как при
рождаются неустойчивые предельные циклы (фокусы становятся устойчивыми) и возникает структура с тремя предельными циклами (рис. 160,9). Так как при  предельных циклов нет
предельных циклов нет  интегральная прямая, качественная структура эквивалентна структуре рис. 160,1), то рассуждениями, аналогичными проведенным в п. 3.4, находим, что при убывании А до нуля должны осуществиться следующие бифуркации сепаратрис: возникновение петли сепаратрисы вокруг верхнего фокуса, вокруг нижнего фокуса, возникновение большой петли, содержащей внутри два состояния равновесия. Так как седловая величина положительна
интегральная прямая, качественная структура эквивалентна структуре рис. 160,1), то рассуждениями, аналогичными проведенным в п. 3.4, находим, что при убывании А до нуля должны осуществиться следующие бифуркации сепаратрис: возникновение петли сепаратрисы вокруг верхнего фокуса, вокруг нижнего фокуса, возникновение большой петли, содержащей внутри два состояния равновесия. Так как седловая величина положительна  координата
координата
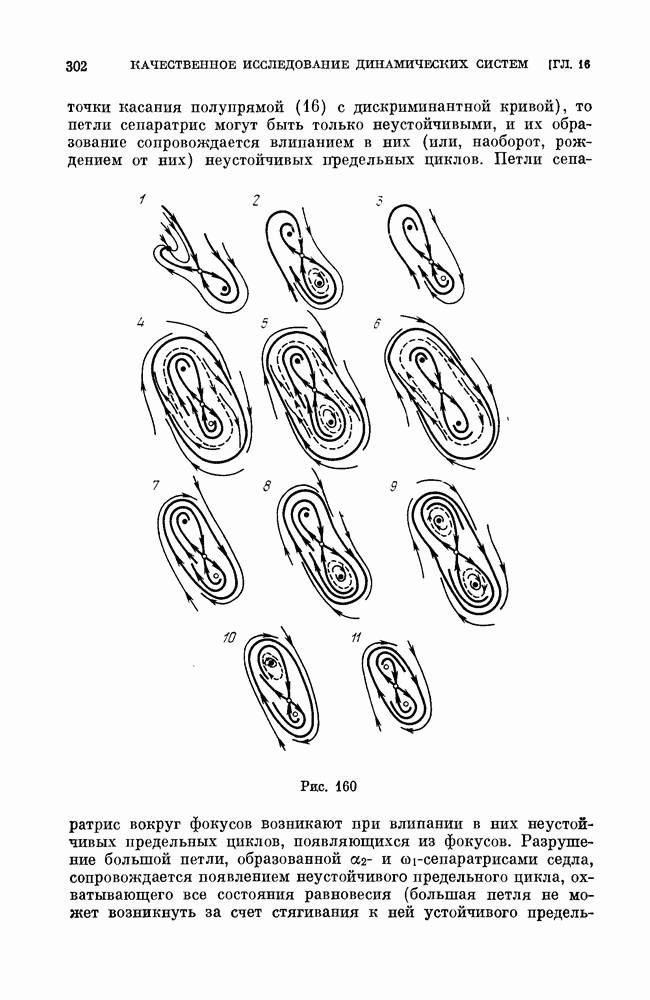
точки касания полупрямой (16) с дискриминантной кривой), то петли сепаратрис могут быть только неустойчивыми, и их образование сопровождается влипанием в них (или, наоборот, рождением от них) неустойчивых предельных циклов.
Рис. 160 (см. скан)
Петли сепаратрис вокруг фокусов возникают при влипании в них неустойчивых предельных циклов, появляющихся из фокусов. Разрушение большой петли, образованной  и
и  -сепаратрисами седла, сопровождается появлением неустойчивого предельного цикла, охватывающего все состояния равновесия (большая петля не может возникнуть за счет стягивания к ней устойчивого
-сепаратрисами седла, сопровождается появлением неустойчивого предельного цикла, охватывающего все состояния равновесия (большая петля не может возникнуть за счет стягивания к ней устойчивого
предельного цикла, так как это запрещает знак седловой величины (см. гл. 11)). Так как при  циклов нет, то при дальнейшем уменьшении X из слияния устойчивого и неустойчивого предельных циклов должен возникнуть двойной предельный цикл и затем исчезнуть. Точки бифуркаций на полупрямых (16), соответствующие петлям сепаратрис вокруг верхнего и нижнего фокусов, либо могут совпадать, либо должны разделяться точкой бифуркации, соответствующей большой петле.
циклов нет, то при дальнейшем уменьшении X из слияния устойчивого и неустойчивого предельных циклов должен возникнуть двойной предельный цикл и затем исчезнуть. Точки бифуркаций на полупрямых (16), соответствующие петлям сепаратрис вокруг верхнего и нижнего фокусов, либо могут совпадать, либо должны разделяться точкой бифуркации, соответствующей большой петле.
Для полупрямых (16), касающихся нижней границы дискриминантной кривой на интервалах  бифуркации будут аналогичными, но число их от интервала к интервалу будет уменьшаться за счет того, что некоторые бифуркации уже произошли при движении вдоль дискриминантной кривой.
бифуркации будут аналогичными, но число их от интервала к интервалу будет уменьшаться за счет того, что некоторые бифуркации уже произошли при движении вдоль дискриминантной кривой.

Рис. 161
Так как указанные бифуркации имеют место на прямых, целиком заполняющих рассматриваемую область внутри дискриминантной кривой, то существуют непрерывные кривые, на которых осуществляются бифуркации. Их начальные и конечные точки располагаются на линии симметричных структур и на дискриминантной кривой. Все три бифуркационные кривые, соответствующие трем типам петель сепаратрис, пересекаются в точке  линии симметричных структур (рис. 161). Они заканчиваются в точках
линии симметричных структур (рис. 161). Они заканчиваются в точках  на дискриминантной кривой. В точках
на дискриминантной кривой. В точках  осуществляются структуры с петлями сепаратрис. В точке
осуществляются структуры с петлями сепаратрис. В точке  сепаратрисы вырожденного седло-узла (см. гл. 4) нужно рассматривать как вырождение петли сепаратрисы вокруг верхнего фокуса, стягивающейся вместе с фокусом в одну точку. Кривая двойных циклов проходит между точкой
сепаратрисы вырожденного седло-узла (см. гл. 4) нужно рассматривать как вырождение петли сепаратрисы вокруг верхнего фокуса, стягивающейся вместе с фокусом в одну точку. Кривая двойных циклов проходит между точкой  на линии симметричных структур и точкой
на линии симметричных структур и точкой  на дискриминантной кривой слева от кривой, на которой осуществляется большая петля.
на дискриминантной кривой слева от кривой, на которой осуществляется большая петля.
Некоторые из бифуркационных кривых могут пересекаться, и поэтому последовательность качественных структур и бифуркаций при изменении параметра X вдоль отрезков касательных внутри дискриминантной крривой может быть различной.
3.6. Структуры разбиения фазового пространства и бифуркации вне дискриминантной кривой (в области одного состояния
равновесия). Здесь возможны три структуры: неустойчивый фокус внутри устойчивого предельного цикла, устойчивый фокус, окруженный двумя предельными циклами, и устойчивый фокус (узел), к которому траектории идут из бесконечности. Первая из перечисленных структур существует для точек вне дискриминантной кривой в области между прямыми  область [2] на рис. 158, 161). Область существования двух предельных циклов примыкает на интервале
область [2] на рис. 158, 161). Область существования двух предельных циклов примыкает на интервале  к куску дискриминантной кривой и к прямой
к куску дискриминантной кривой и к прямой  На интервале
На интервале  при смещении с дискриминантной кривой в область одного состояния равновесия (см. рис.
при смещении с дискриминантной кривой в область одного состояния равновесия (см. рис.  исчезает состояние равновесия седло-узел и остаются два предельных цикла вокруг устойчивого фокуса (на рис. 159, 6—8 неустойчивый предельный цикл при исчезновении седло-узла возникает из замкнутой траектории, образованной
исчезает состояние равновесия седло-узел и остаются два предельных цикла вокруг устойчивого фокуса (на рис. 159, 6—8 неустойчивый предельный цикл при исчезновении седло-узла возникает из замкнутой траектории, образованной  -сеиаратрисой седло-узла). На интервале
-сеиаратрисой седло-узла). На интервале  при переходе из области
при переходе из области  в область
в область  убыванием
убыванием  из фокуса появляется второй неустойчивый предельный цикл
из фокуса появляется второй неустойчивый предельный цикл  при
при  Бифуркационная кривая (штриховая на рис. 158, 161), соответствующая слиянию устойчивого и неустойчивого предельных циклов, начинается в точке
Бифуркационная кривая (штриховая на рис. 158, 161), соответствующая слиянию устойчивого и неустойчивого предельных циклов, начинается в точке  на прямой
на прямой  и пересекает дискриминантную кривую при
и пересекает дискриминантную кривую при  выделяя некоторую окрестность дискриминантной кривой и прямой
выделяя некоторую окрестность дискриминантной кривой и прямой  для точек которой есть одно устойчивое состояние равновесия и два предельных цикла (область [2] на рис. 158, 161). При переходе из области
для точек которой есть одно устойчивое состояние равновесия и два предельных цикла (область [2] на рис. 158, 161). При переходе из области  в область
в область  при
при  устойчивый цикл стягивается к фокусу
устойчивый цикл стягивается к фокусу  и возникает структура без предельных циклов (область [5] на рис. 158, 161). Границами области без предельных циклов служат кусок дискриминантной кривой
и возникает структура без предельных циклов (область [5] на рис. 158, 161). Границами области без предельных циклов служат кусок дискриминантной кривой  кривая двойных циклов
кривая двойных циклов  и прямая
и прямая 
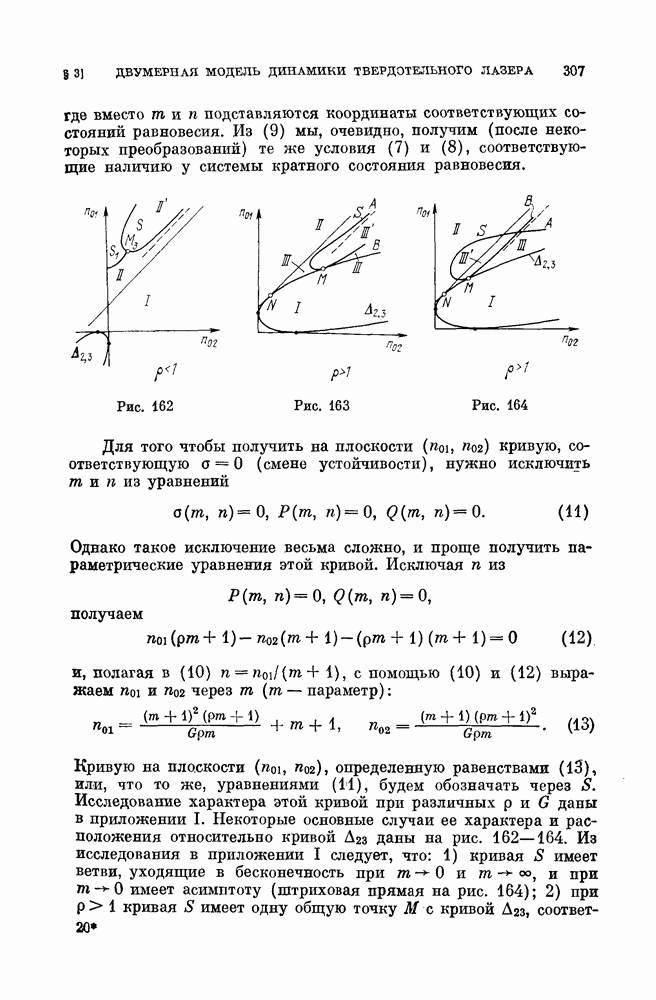
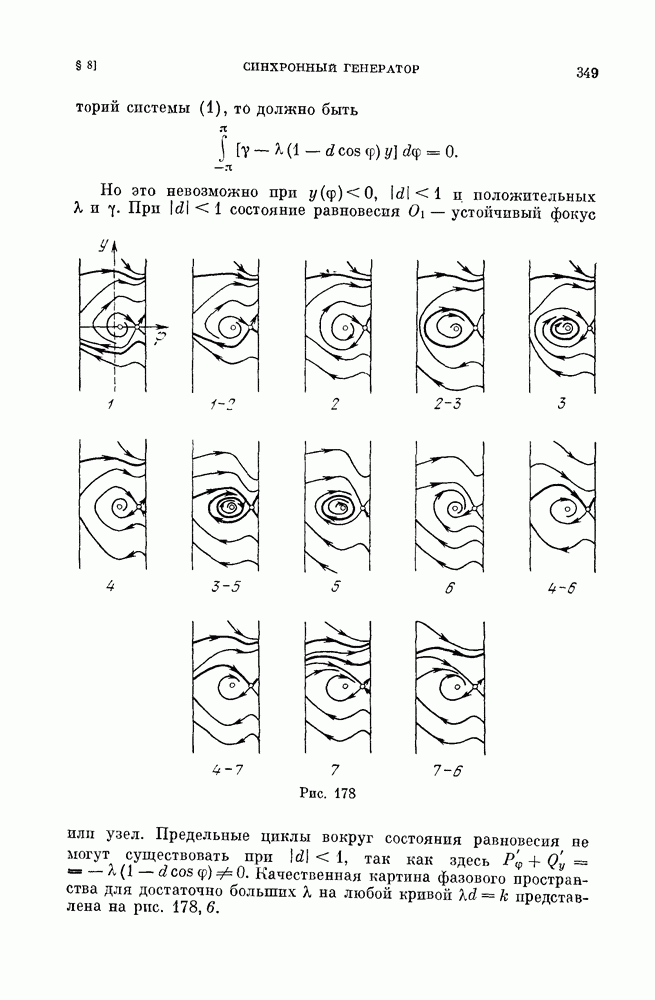
3.7. Разбиение пространства параметров. Разбиение пространства параметров на области различной качественной структуры по обе стороны линии симметричных структур  приведено на рис. 161. Соответствующие различным областям грубые структуры разбиения фазового пространства (обозначенные теми же номерами) представлены на рис. 160. Жирными линиями изображены сепаратрисы и предельные циклы, штриховой — неустойчивые предельные циклы. Устойчивые состояния равновесия — черные точки, неустойчивые — светлые.
приведено на рис. 161. Соответствующие различным областям грубые структуры разбиения фазового пространства (обозначенные теми же номерами) представлены на рис. 160. Жирными линиями изображены сепаратрисы и предельные циклы, штриховой — неустойчивые предельные циклы. Устойчивые состояния равновесия — черные точки, неустойчивые — светлые.
Разбиение на рис. 161 соответствует предположению, сделанному в п. 3.4, об отсутствии предельных циклов для структур в точке  дискриминантной кривой. Если предположение не выполняется, то кривая двойных циклов (штриховая на рис. 161) будет проходить не через точку
дискриминантной кривой. Если предположение не выполняется, то кривая двойных циклов (штриховая на рис. 161) будет проходить не через точку  а через точку
а через точку  и тогда исчезнут области [2] и [5], а на рис. 460 — соответственно структуры
и тогда исчезнут области [2] и [5], а на рис. 460 — соответственно структуры 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. АВТОНОМНЫЕ СИСТЕМЫ ВТОРОГО ПОРЯДКА С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- § 1. Автономная динамическая система на плоскости.
- § 2. Теорема существования и единственности решения.
- § 3. Простейшие свойства решений системы (А).
- § 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
- § 5. Сопоставление геометрической интерпретации системы (А) в пространстве (x, y, t) с интерпретацией на фазовой плоскости.
- § 6. Некоторые термины.
- § 7. Теорема о непрерывной зависимости решения от начальных условий.
- § 8. Направление на траекториях. Изменение параметризации.
- § 9. Дифференциальное уравнение, соответствующее динамической системе.
- § 10. Понятие интегральной кривой и интеграла в случае аналитических правых частей Р(х,у) и Q(x,y) системы (А).
- § 11. Что значит «найти решение динамической системы»?
- § 12. Примеры.
- § 13. Замечания по поводу примеров § 12.
- § 14. Математическое определение качественной (топологической) структуры разбиения на траектории и качественного исследования динамической системы.
- ГЛАВА 2. ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ — БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ
- § 2. Цикл без контакта.
- § 3. Предельная точка полутраектории и траектории. Предельная траектория.
- § 4. Основная теорема.
- § 5. Возможные типы полутраекторий и их предельных множеств.
- § 6. Особые и неособые полутраектории и траектории.
- § 7. Возможные типы особых и неособых траекторий.
- § 8. Случай конечного числа особых траекторий. Элементарные ячейки.
- § 9. Возможные типы ячеек. Односвязные и двусвязные ячейки.
- § 10. Два подхода к описанию качественной структуры.
- § 11. Качественная (топологическая) структура состояния равновесия в случае конечного числа особых траекторий. Схема динамической системы.
- § 12. Устойчивость по Ляпунову.
- ГЛАВА 3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННОЙ СТРУКТУРЫ ОКРЕСТНОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (ОСОБОЙ ТОЧКИ)
- § 2. Приведение динамической системы к каноническому виду.
- § 3. Возможный характер простых состояний равновесия.
- § 4. Замечания о методах установления характера грубых состояний равновесия.
- § 5. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 6. Направления, в которых траектории стремятся к простым состояниям равновесия.
- § 7. Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия.
- § 8. Сводка сведений о грубых состояниях равновесия.
- ГЛАВА 4. КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ
- § 1. Направления, в которых траектории стремятся к сложному состоянию равновесия.
- § 2. Сложное состояние равновесия (особая точка) с нулевыми характеристическими корнями.
- § 3. Примеры.
- § 4. Нормальные формы.
- ГЛАВА 5. ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ
- § 2. Условия устойчивости и неустойчивости неподвижной точки точечного отображения.
- § 3. Функция соответствия.
- § 4. Изучение окрестности замкнутой траектории. Простые и сложные предельные циклы.
- § 5. Аналитические выражения для коэффициентов функции последования. Характеристический показатель замкнутой траектории.
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЕМЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 2. Изучение поведения интегральных кривых в бесконечности. Сфера Пуанкаре.
- § 3. Примеры исследования в бесконечности [93].
- § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов.
- 1. Некоторые видоизменения критериев Бендиксона и Дюлака.
- 2. Индексы Пуанкаре. Распределение особых точек [77, 117].
- 3. Условия сосуществования замкнутых траекторий и особых точек.
- 4. Две общие теоремы Пуанкаре.
- § 5. Топографическая система Пуанкаре. Функция Ляпунова. Кривые контактов.
- ЧАСТЬ II. ТЕОРИЯ БИФУРКАЦИЙ
- § 1. Свойства консервативных систем на плоскости [2, 3].
- § 2. Динамические системы, характерные для теории колебаний.
- § 3. Измененные системы. Системы, правые части которых зависят от параметра.
- § 4. Основные теоремы о зависимости решения от изменения правых частей динамической системы.
- § 5. Грубость динамической системы и теоремы о непрерывной зависимости решения от изменения правых частей.
- ГЛАВА 8. ГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
- § 2. Состояния равновесия, возможные в грубой динамической системе.
- § 3. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 4. Замкнутые траектории, возможные в грубой системе.
- § 5. Поведение сепаратрис седел в грубых системах.
- § 6. Необходимые условия грубости. Достаточность этих условий для грубости системы.
- § 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем.
- § 8. Понятие грубости при более общих предположениях относительно правых частей динамической системы.
- § 9. Типы особых траекторий и ячеек в грубых системах.
- § 10. Замечания по поводу определения грубой системы.
- ГЛАВА 9. ПРОСТЕЙШИЕ НЕГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ — СИСТЕМЫ ПЕРВОЙ СТЕПЕНИ НЕГРУБОСТИ
- § 2. Системы первой степени негрубости.
- § 3. Состояния равновесия, возможные в системе первой степени негрубости.
- § 4. Замкнутые траектории, возможные в системе первой степени негрубости.
- § 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости.
- § 6. Необходимые и достаточные условия первой степени негрубости.
- § 7. Динамические системы более высокой степени негрубости.
- ГЛАВА 10. БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- § 1. Определение бифуркации.
- § 2. Бифуркации систем первой степени негрубости.
- § 3. Бифуркации некоторых типов сложных особых точек.
- § 4. Бифуркации двукратной точки, для которой …
- § 5. Рождение предельных циклов из особых траекторий степени негрубости выше первой.
- ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
- § 1. Возможный характер зависимости правых частей динамической системы от параметров.
- § 2. Смена качественных структур при изменении параметров.
- § 3. Случай, когда правые части зависят более чем от одного параметра.
- § 4. Бифуркации «от бесконечности».
- § 5. Условия существования седло-узла и сложного фокуса первого порядка.
- § 6. Поворот векторного поля.
- § 7. Метод малого параметра. Метод Понтрягина.
- ГЛАВА 12. ДИНАМИЧЕСКИЕ СИСТЕМЫ С ЦИЛИНДРИЧЕСКОЙ ФАЗОВОЙ ПОВЕРХНОСТЬЮ
- § 1. Цилиндрическая фазовая поверхность и характер траекторий, возможных на цилиндрической фазовой поверхности.
- § 2. Замкнутые траектории, охватывающие цилиндр.
- § 3. Приемы исследования качественной структуры динамической системы на цилиндре.
- § 4. Понятие грубости и степени негрубости для динамических систем на цилиндре. Бифуркации на цилиндре. Поворот поля.
- § 5. Динамические системы на цилиндре, близкие к гамильтоновым (метод Понтрягина).
- ГЛАВА 13. АДЕКВАТНОЕ ИСТОЛКОВАНИЕ НЕЛИНЕЙНЫХ ФИЗИЧЕСКИХ ЯВЛЕНИЙ ФАКТАМИ КАЧЕСТВЕННОЙ ТЕОРИИ И ТЕОРИИ БИФУРКАЦИЙ ДИНАМИЧЕСКИХ СИСТЕМ
- § 1. Мягкий и жесткий режимы.
- § 2. Замечания о границах области устойчивости различных стационарных режимов.
- § 3. Мягкое и жесткое возникновение колебаний.
- § 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
- § 5. Замечания по поводу других границ области устойчивости.
- ЧАСТЬ III. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- ГЛАВА 14. ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 1. Некоторые рецептурные указания.
- § 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
- § 3. Некоторые простые примеры динамических систем на цилиндре.
- ГЛАВА 15. ИССЛЕДОВАНИЕ МЕТОДОМ МАЛОГО ПАРАМЕТРА (МЕТОДОМ ПОНТРЯГИНА)
- § 2. Примеры рассмотрения методом Понтрягина (полное исследование).
- § 3. Исследование методом Понтрягина с привлечением вычислительных методов.
- ГЛАВА 16. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ
- § 2. Электрическая цепь с туннельным диодом.
- § 3. Двумерная модель динамики твердотельного лазера [119].
- § 4. Симметричный полет самолета в вертикальной плоскости (задача Н. Е. Жуковского).
- § 5. Система, описывающая динамику проточного химического реактора.
- § 6. Фазовая автоподстройка частоты.
- § 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов).
- § 8. Синхронный генератор с асинхронной характеристикой.
- ЧАСТЬ IV. КУСОЧНО-СШИТЫЕ СИСТЕМЫ
- ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ
- § 1. Сшитые системы. Доопределение на линиях сшивания.
- § 2. Возможные типы полутраекторий сшитых систем.
- § 3. Особые траектории сшитых систем.
- § 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
- ГЛАВА 18. ИССЛЕДОВАНИЕ КУСОЧНО-СШИТЫХ СИСТЕМ МЕТОДОМ ПОНТРЯГИНА
- § 2. Автоподстройка при кусочно-постоянной аппроксимации характеристики.
- § 3. Автоколебания синхронного мотора.
- ГЛАВА 19. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ
- § 2. Следящая система с люфтом.
- § 3. Электрическая цепь с туннельным диодом.
- § 4. Система со скачками на линии сшивания.
- ГЛАВА 20. ОБ АППРОКСИМАЦИЯХ И ГРУБОСТИ ПРОСТРАНСТВА ПАРАМЕТРОВ [39, 41, 42]
- § 1. Рассмотрение системы (2) при аппроксимациях пилообразными функциями.
- § 2. Рассмотрение системы (2) при аппроксимации, включающей отрезок параболы.
- § 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin f, и пилообразной для cos f функциями.
- § 4. Исследование роли аппроксимаций для уравнения маятникового типа.
- § 5. Динамическая система, описывающая автоколебания синхронного мотора.
- § 6. Динамическая система, описывающая симметричный полет самолета.
- ДОПОЛНЕНИЕ
- § 1. Динамическое системы на двумерных поверхностях.
- § 2. Динамические системы в n-мерном евклидовом пространстве.
- СПИСОК ЛИТЕРАТУРЫ