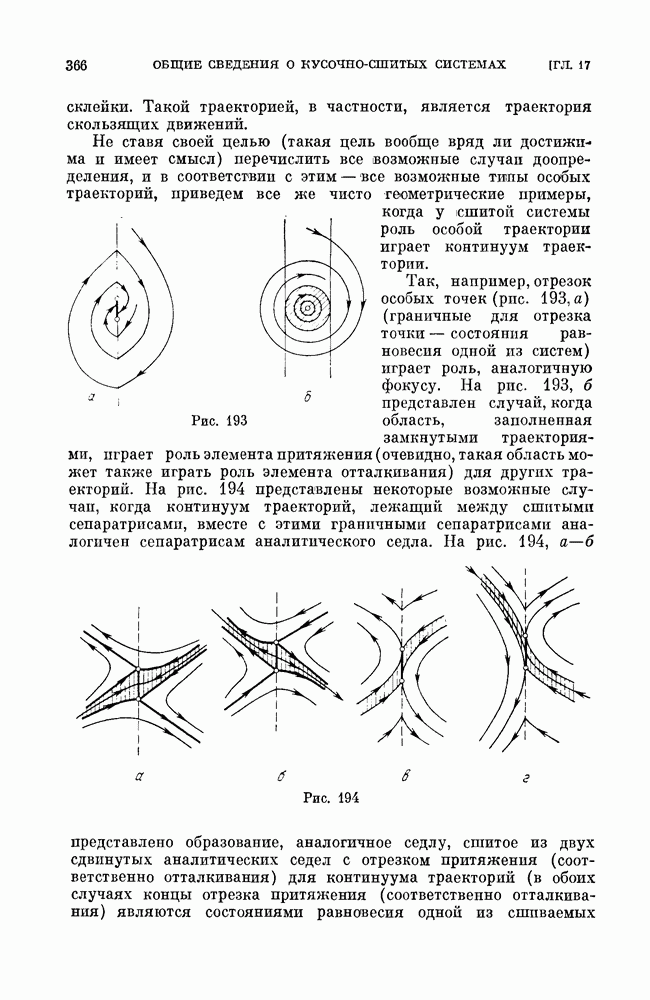
§ 5. Замечания по поводу других границ области устойчивости.

Мы рассмотрели части границы области устойчивости в случае, когда эти части соответствуют негрубым состояниям равновесия. Очевидно, аналогично могут быть рассмотрены границы области устойчивости, соответствующие еще и другим системам первой степени негрубости; именно в нумерации § 6 гл. 9: 3)-системе, имеющей двукратный предельный цикл; 4)- системе, имеющей сепаратрису, идущую из седла в седло.

Случай 3) естественным образом имеет место, когда при изменении параметра к устойчивому предельному циклу приближается неустойчивый предельный цикл (как в рассмотренном в § 3 случае жесткого возбуждения колебаний), который сливается с устойчивым циклом. Образуется двукратный цикл, который при дальнейшем изменении параметра исчезает. Изображающая точка «срывается» и стремится либо к устойчивому состоянию равновесия, либо к другому устойчивому предельному циклу.

Граница опасная. Нетрудно убедиться, что система при любой ее качественной структуре в этом случае ведет себя необратимо.

В случае 4) предположим, что изображающая точка при значениях двигается по устойчивому предельному циклу, который при влипает в сепаратрису. Очевидно, по мере образования петли сепаратрисы период предельного цикла, влипающего в эту петлю, неограниченно увеличивается. Когда после образования петли петля разрушается без образования предельного цикла, что всегда имеет место при общем вхождении параметра, изображающая точка стремится к тому устойчивому

состоянию равновесия или предельному циклу, к которому стремилась -сепаратриса седла. При обратном изменении имеет место необратимость (изображающая точка, находящаяся около устойчивого состояния равновесия или предельного цикла, к которому стремилась указанная -сепаратриса седла, не реагирует на образование петли сепаратрисы).

Мы остановимся сейчас еще на весьма интересных случаях, связанных с опасной границей, возникающей при существовании сложного фокуса и двукратного цикла, в которых можем однозначно указать поведение системы после прохождения через границу области Рауса — Гурвица.

Предположим, что неустойчивый предельный цикл, на который навивается при несколько сепаратрис, входящих в границы ячеек с различными центрами притяжения, устойчивыми состояниями равновесия или предельными циклами (рис. 123, а), при возрастании параметра стягивается к устойчивому фокусу, в окрестности которого находилась изображающая точка.

Рис. 123

Пусть при (рис. 123,б) предельный цикл влипает в состояние равновесия, которое делается сложным неустойчивым фокусом, а затем грубым неустойчивым фокусом. При сепаратрисы стремятся к этому фокусу, и, очевидно, нет возможности однозначно указать, к центру притяжения какой из ячеек (для всех этих ячеек фокус является теперь граничным) будет стремиться изображающая точка (см. [141]).

Полностью аналогичная ситуация имеет место также, например, в случае, когда изображающая точка двигается по

устойчивому предельному циклу внутри которого находится единственное неустойчивое состояние равновесия типа узел или фокус.

К циклу приближается неустойчивый предельный цикл являющийся предельным для ряда сепаратрис, входящих в границы ячеек с различными центрами притяжения. При некотором значении параметра цикл сливается с циклом и исчезает.

В рассматриваемом случае, так же как и в предыдущем, нет возможности однозначно указать поведение изображающей точки при