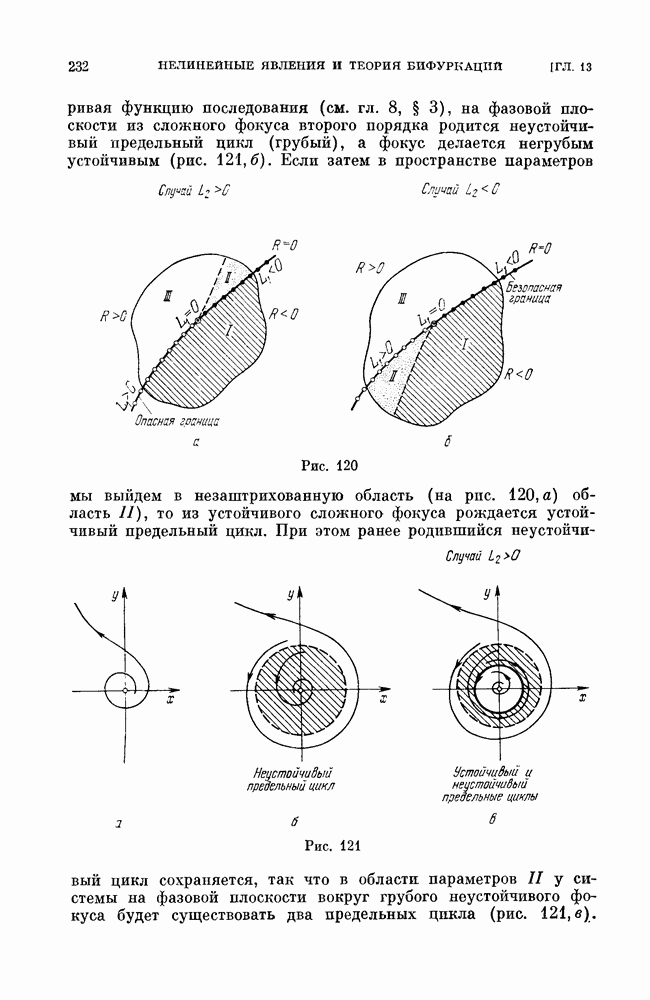
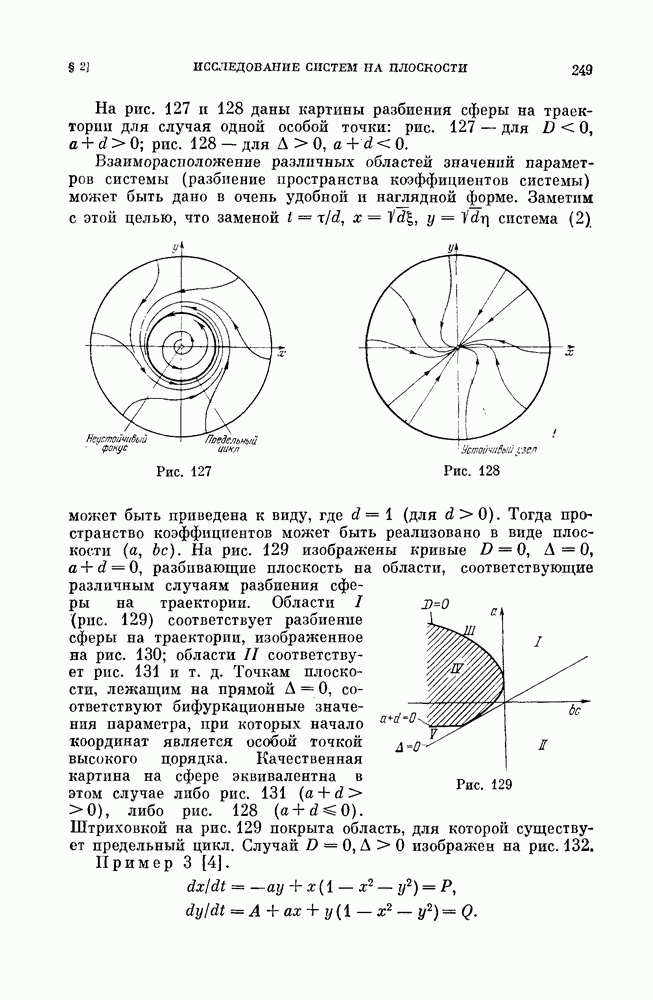
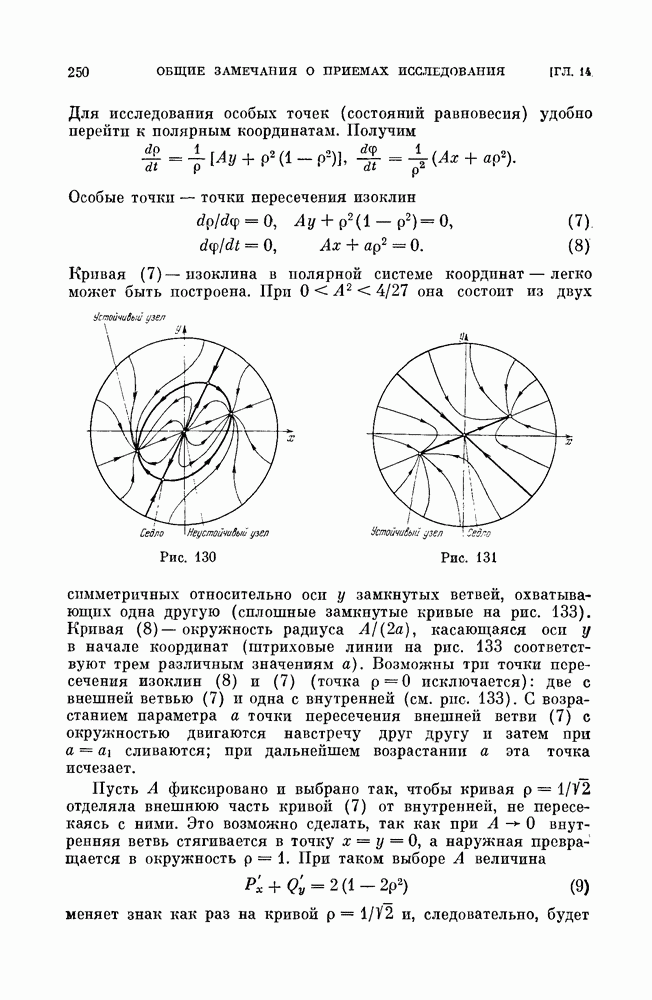
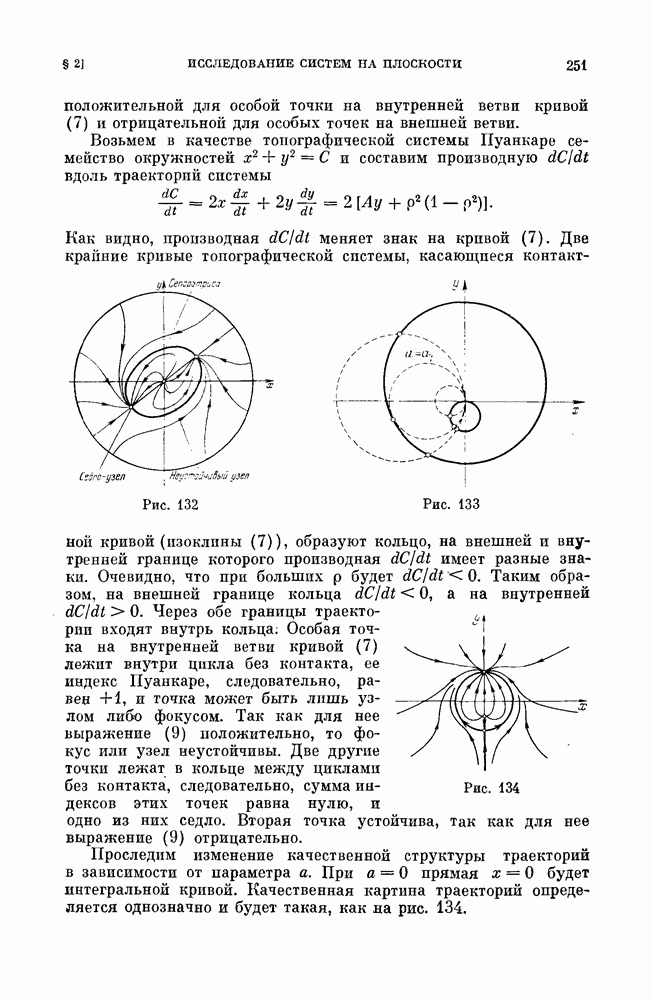
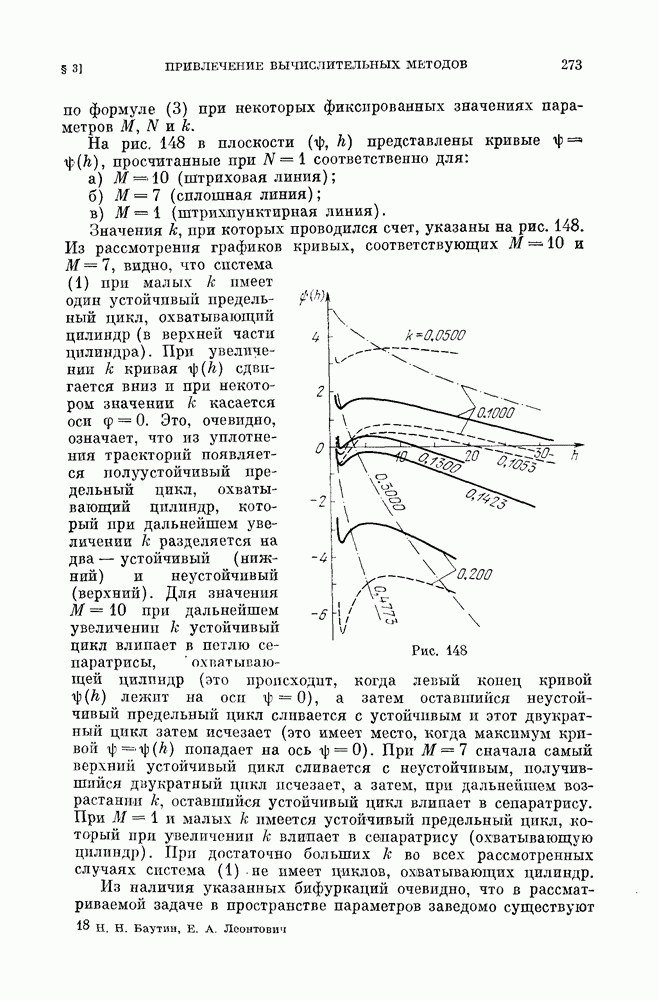
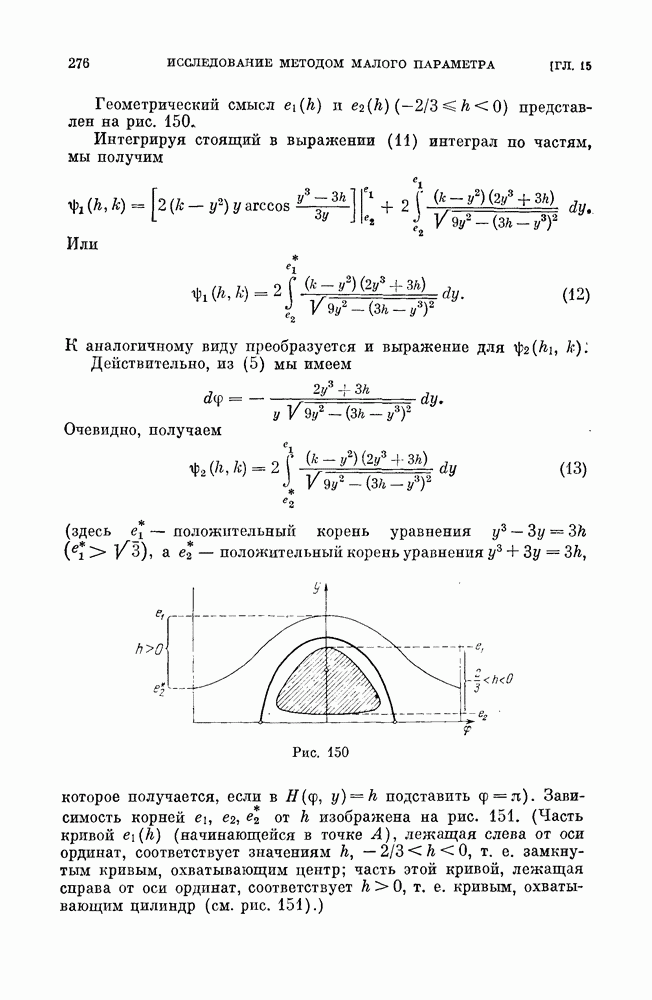
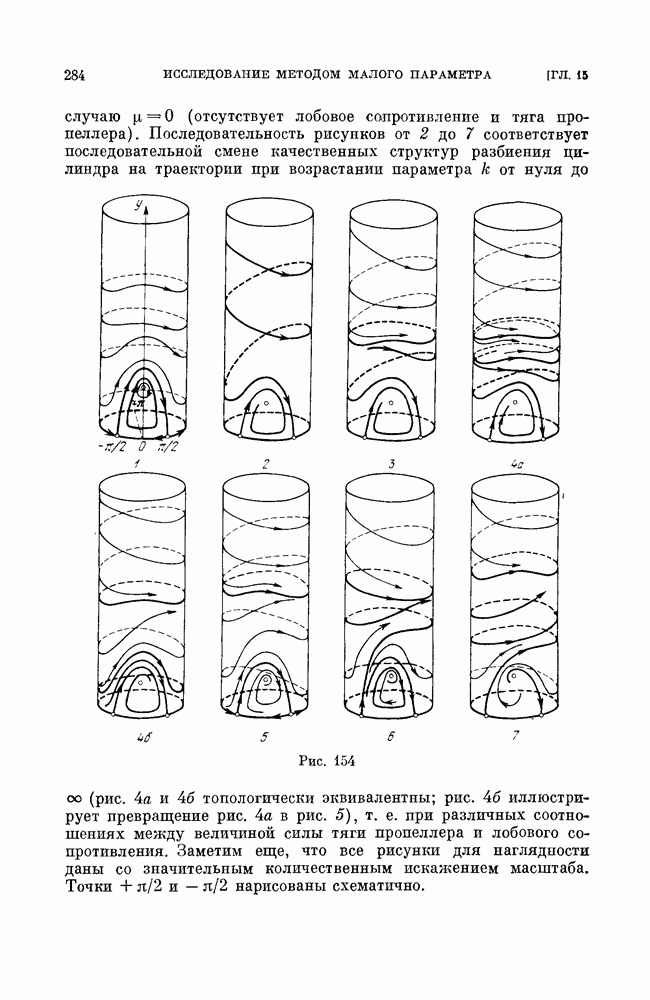
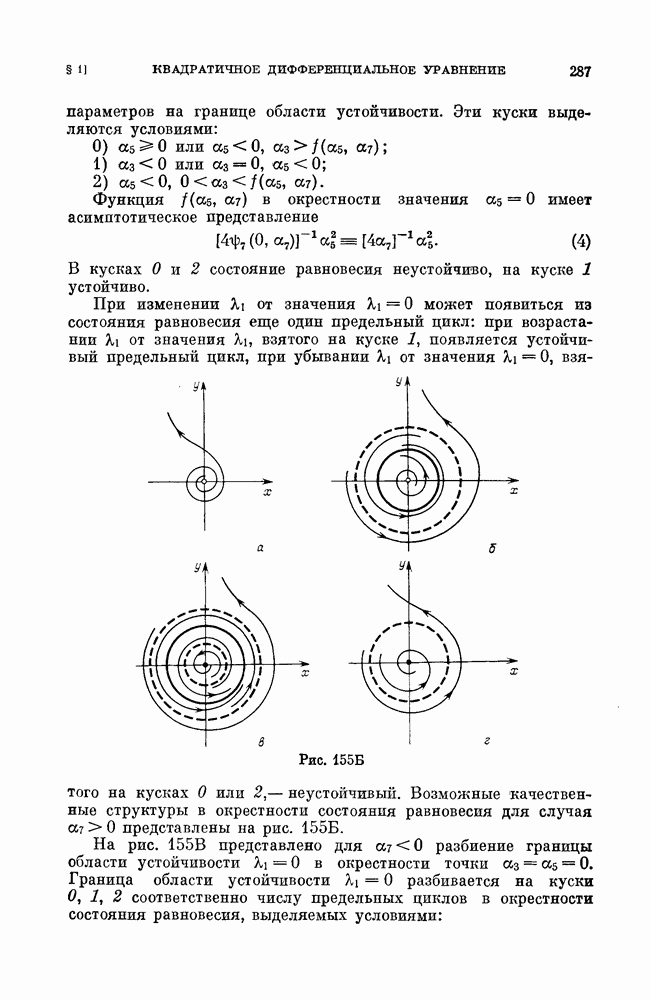
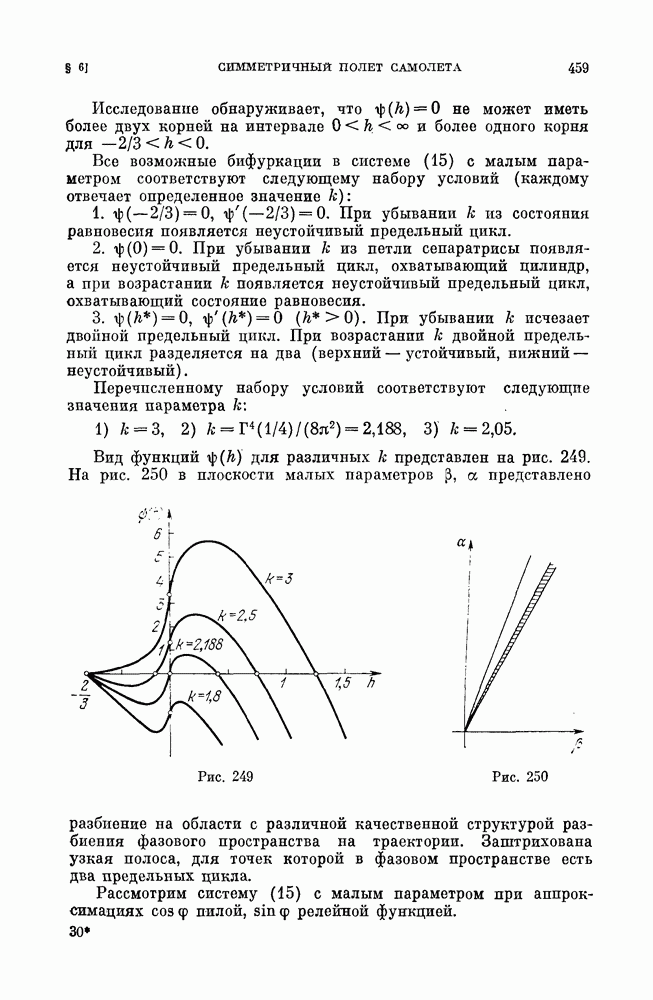
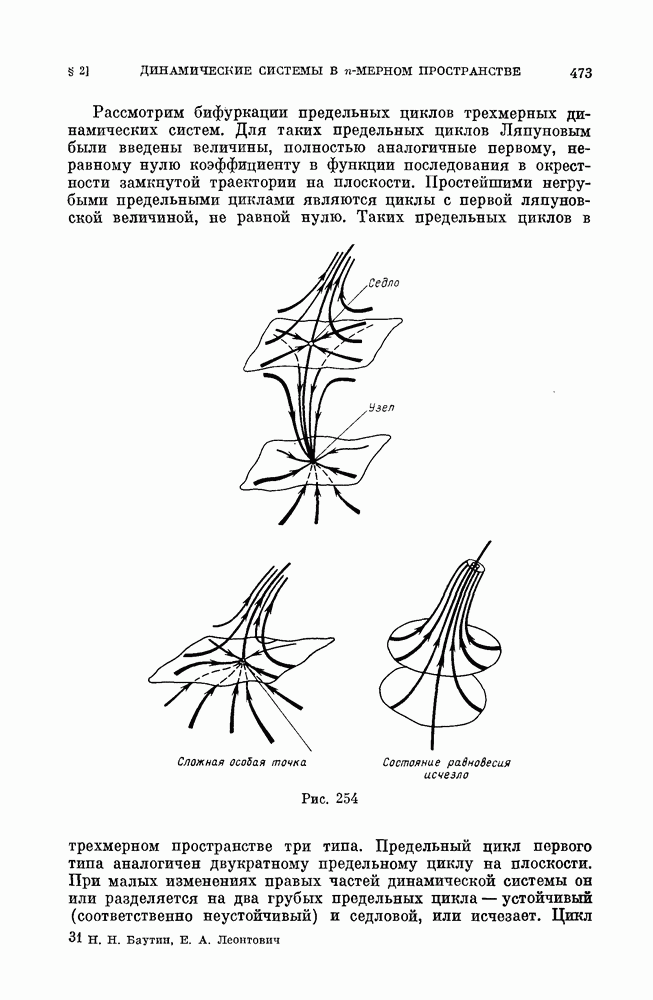
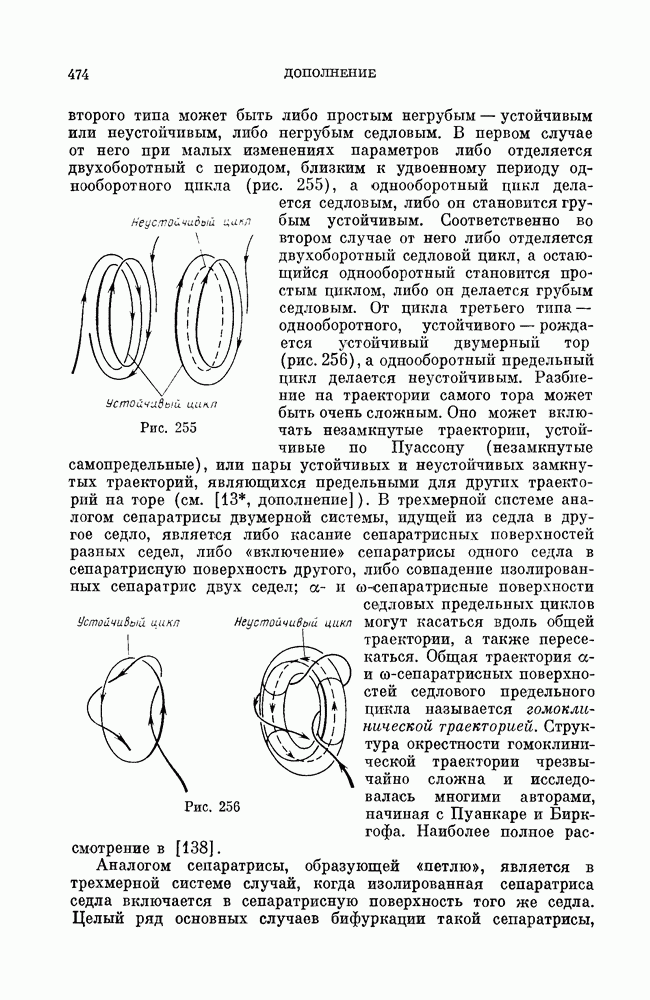
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
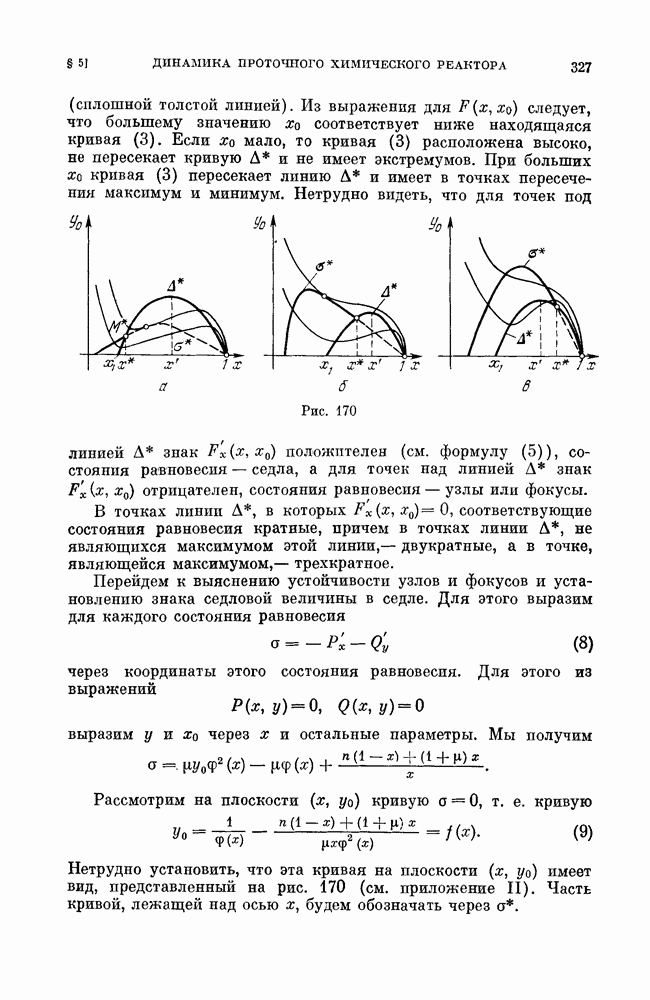
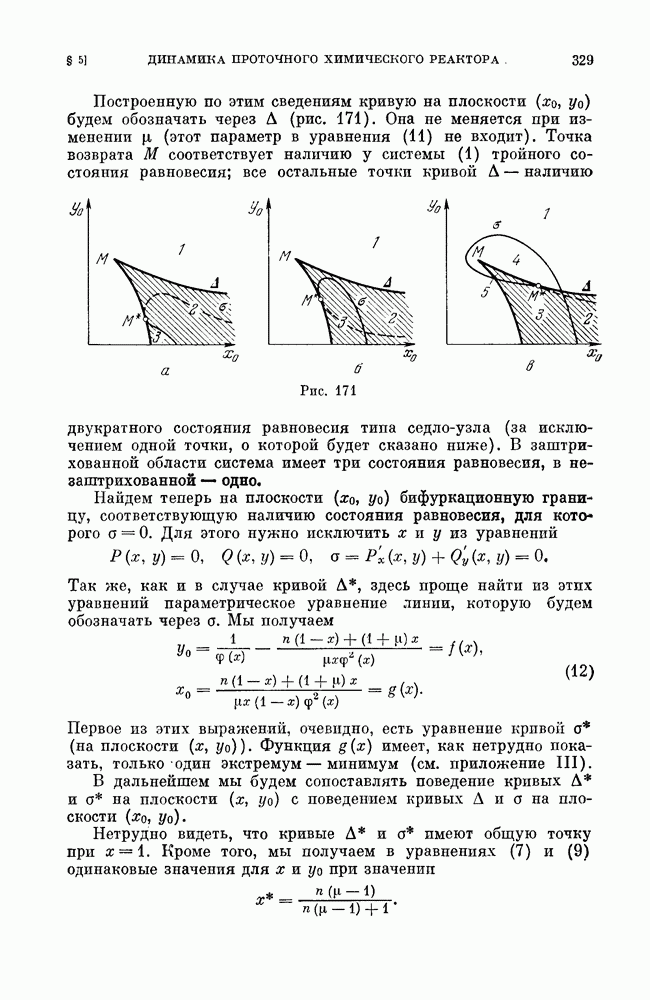
Сшитые динамические системы, возникающие из приложений, всегда содержат параметры, и при изменении параметров качественная структура рассматриваемой системы может, очевидно, изменяться.
Мы рассмотрим простейшие возможные в сшитых системах бифуркации (изменения качественной структуры) при естественном предположении, что при всех рассматриваемых значениях параметров линии сшивания остаются неизменными.
При этом, очевидно, нам достаточно рассмотреть только бифуркации сшитых особых траекторий, так как бифуркации траекторий, целиком лежащих в какой-либо из частных областей  те же, что и описанные в гл. 10, 11.
те же, что и описанные в гл. 10, 11.
Естественно выделить и рассмотреть следующие простейшие бифуркации, аналогичные простейшим бифуркациям аналитических динамических систем:
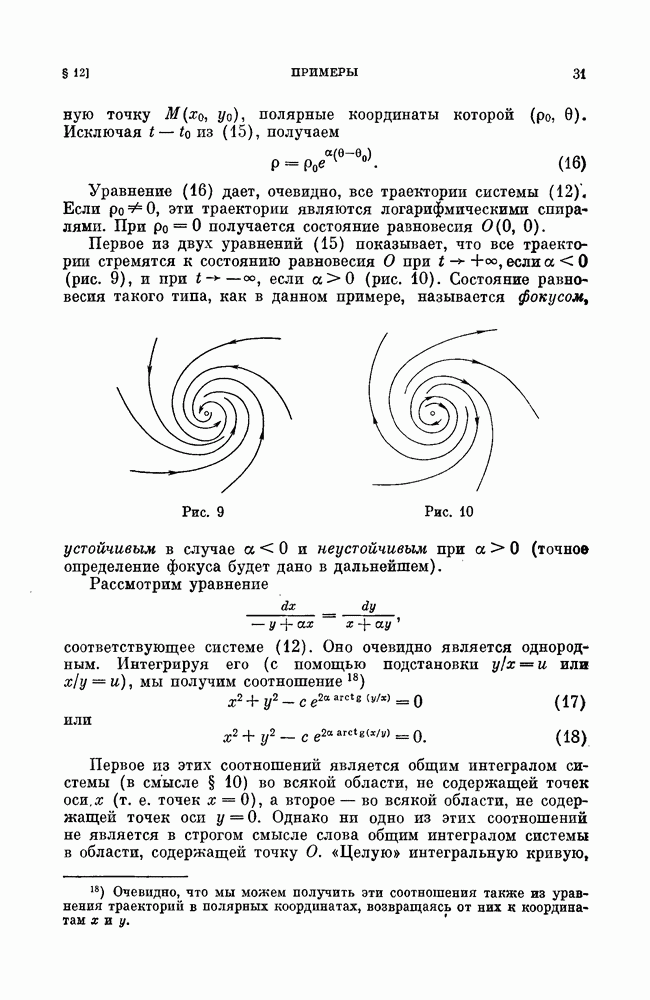
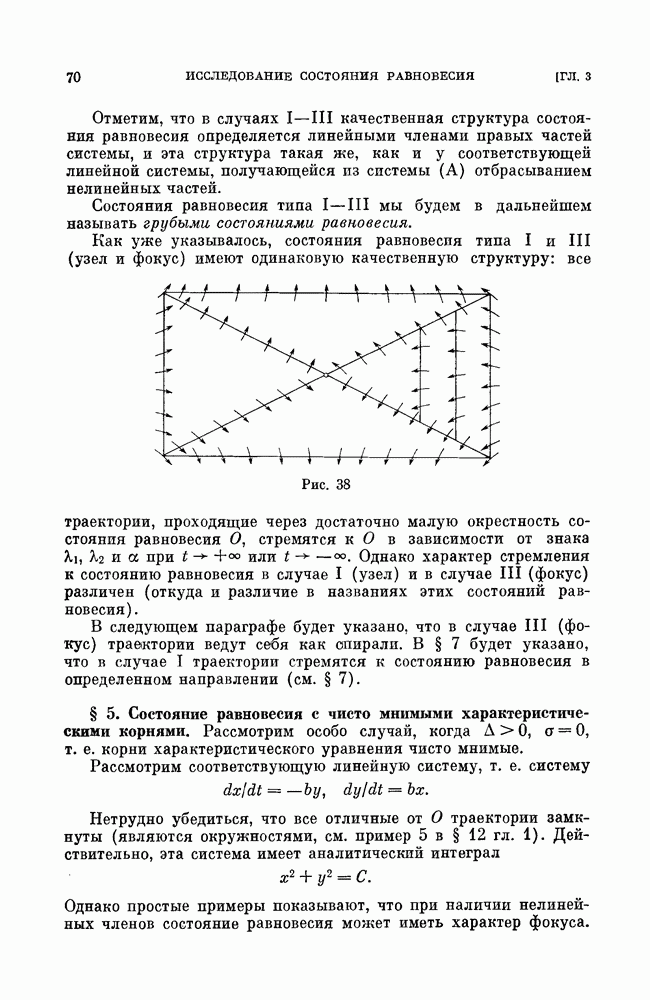
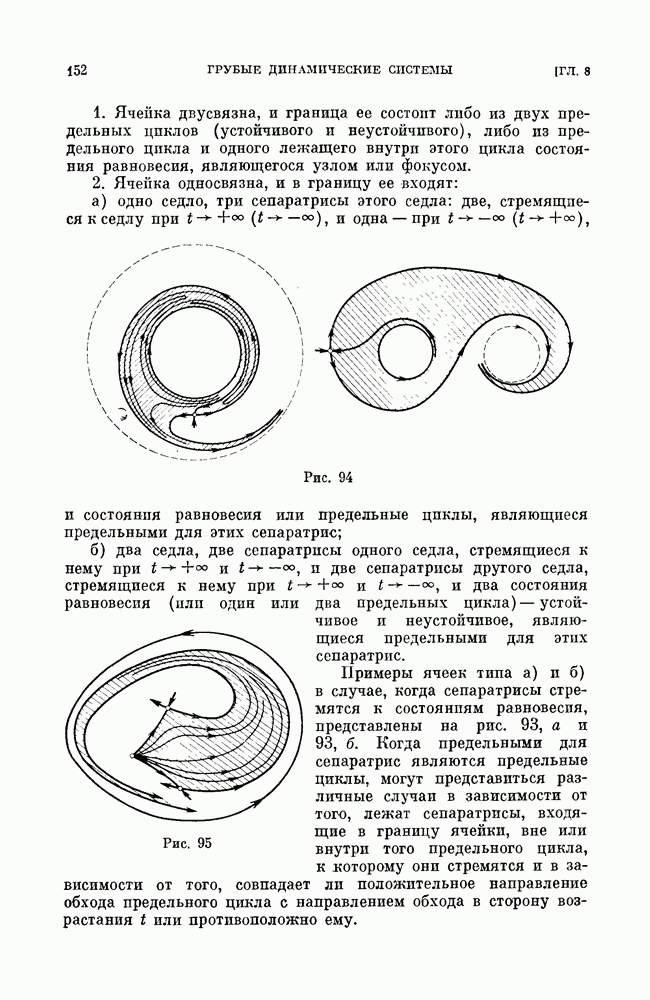
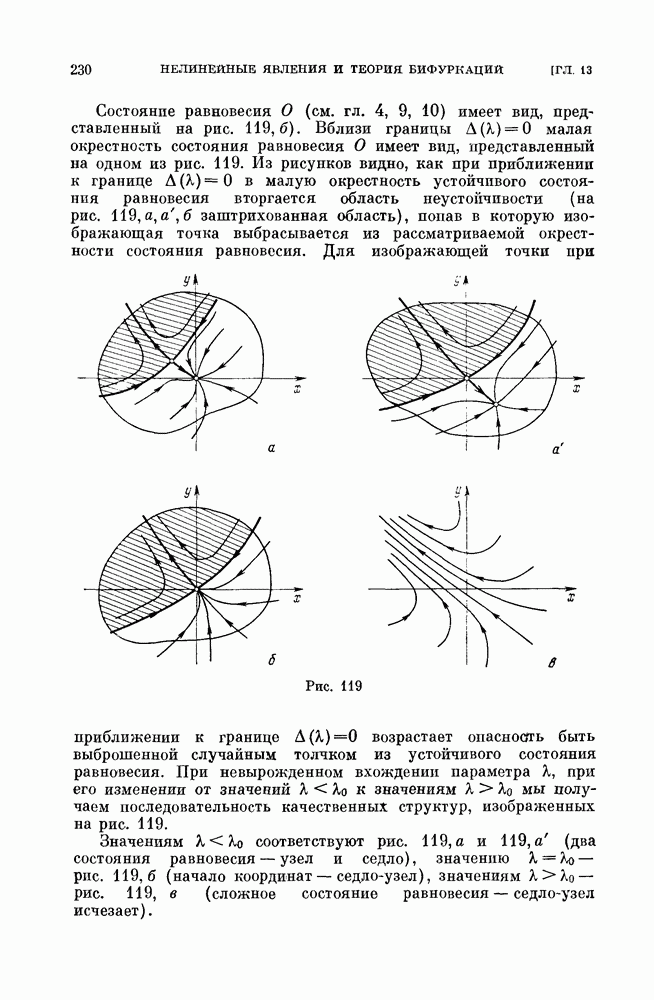
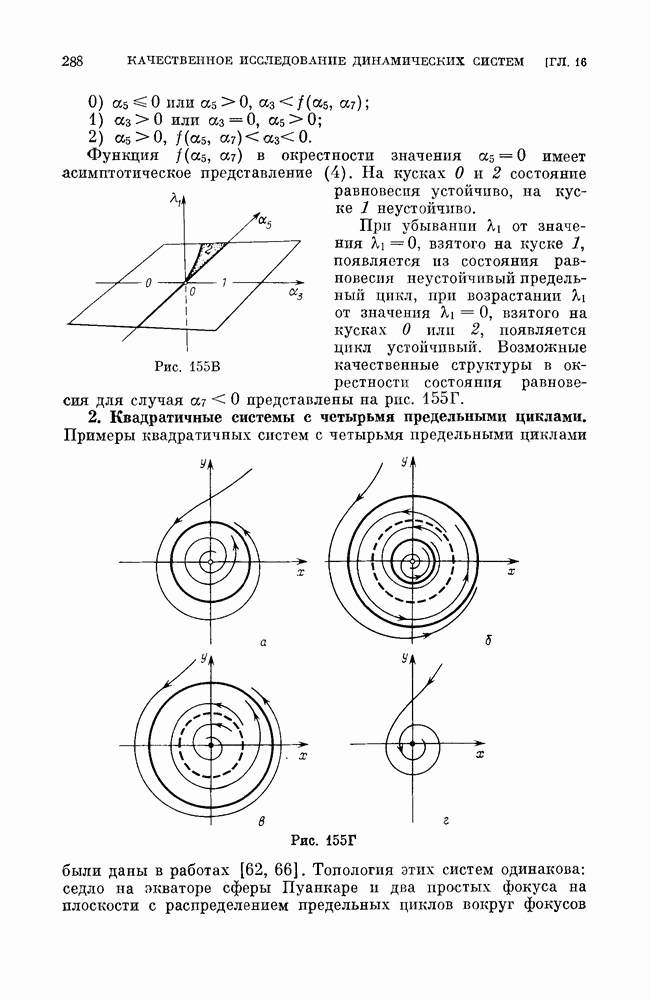
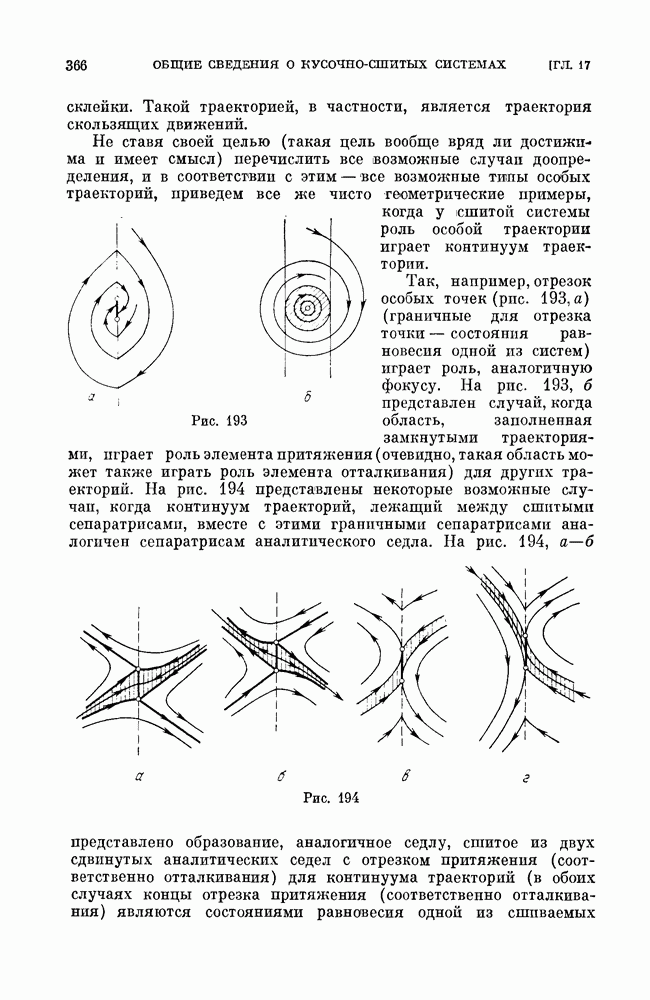
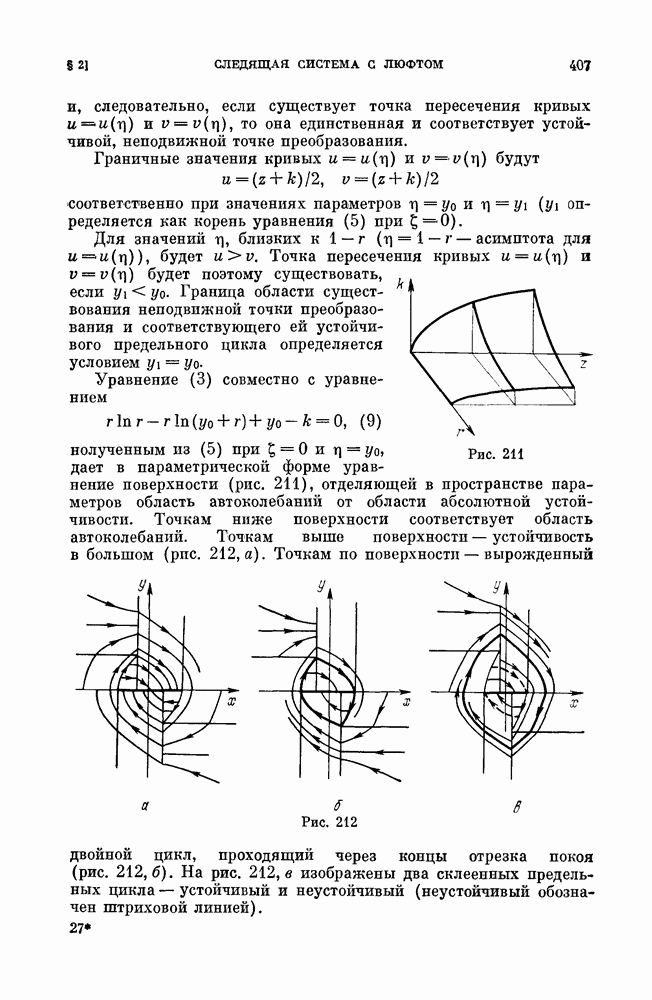
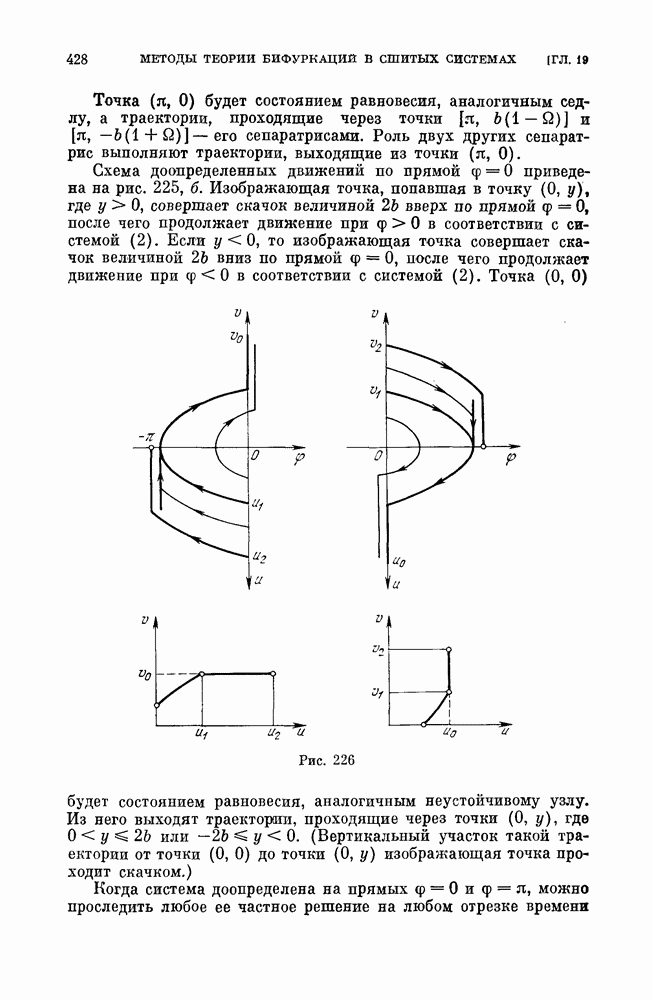
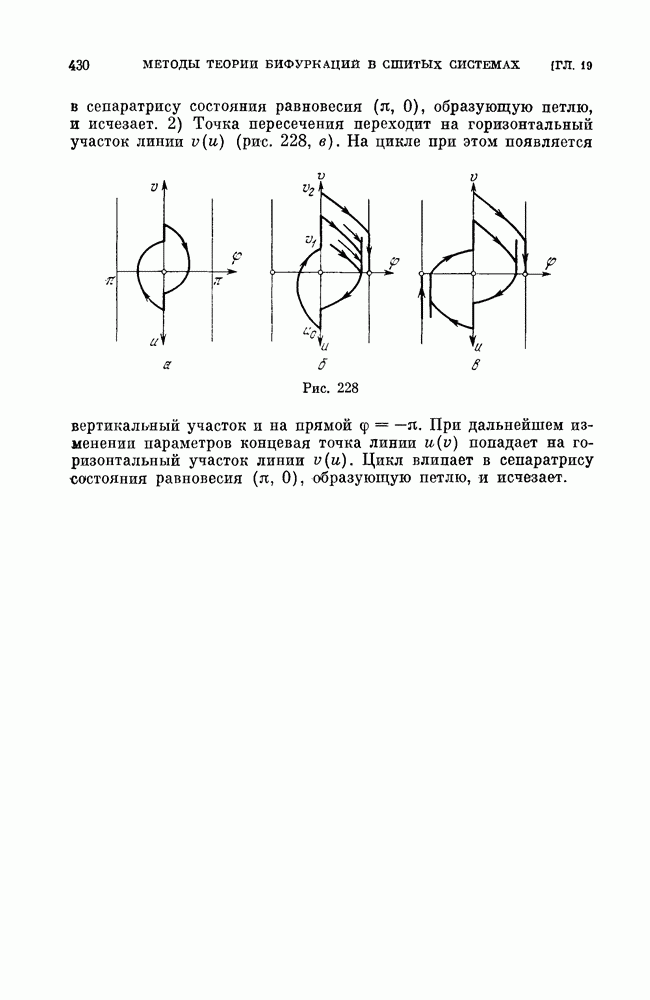
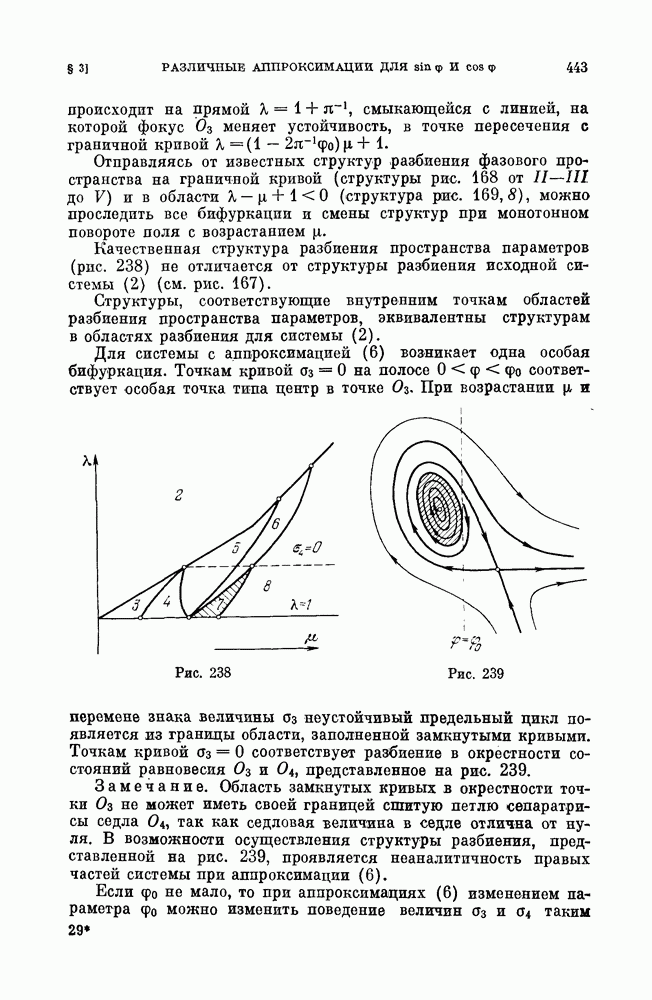
a) бифуркации сшитого состояния равновесия типа фокус (см. рис. 188);
а) бифуркации неподвижной точки типа фокус — квазифокуса (см. рис. 192, а);
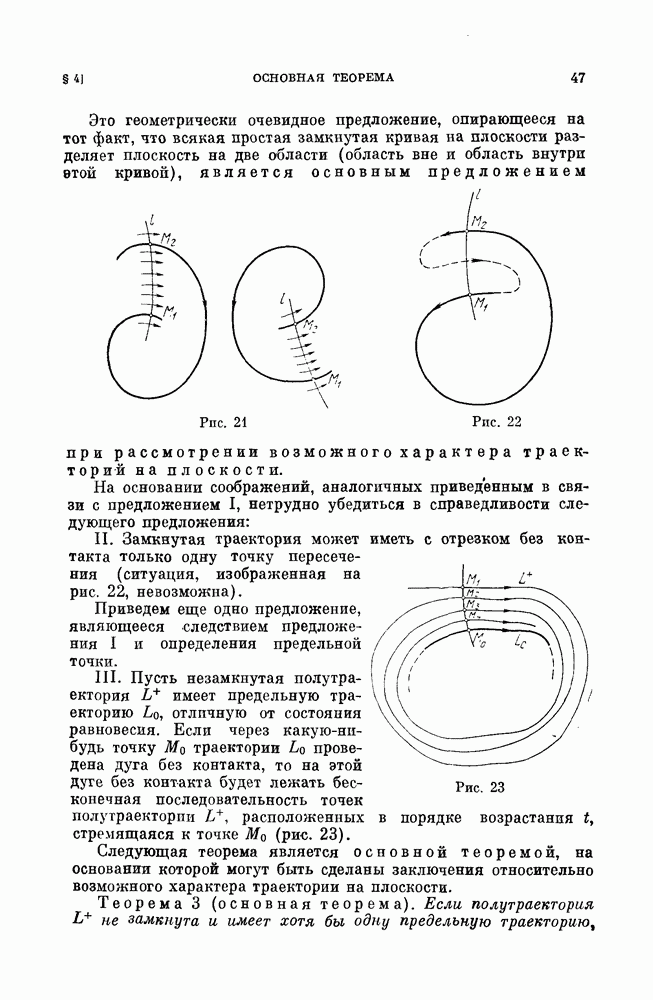
б) бифуракции сшитых предельных циклов;
в) бифуркации сшитых сепаратрис, идущих из седла в седло (седла могут быть как сшитыми, так и несшитыми);
в) бифуркации сепаратрис седлообразных точек покоя (сшитых  несшитых), идущих из седлообразной точки покоя в такую же точку покоя или седло (сшитое или несшитое);
несшитых), идущих из седлообразной точки покоя в такую же точку покоя или седло (сшитое или несшитое);
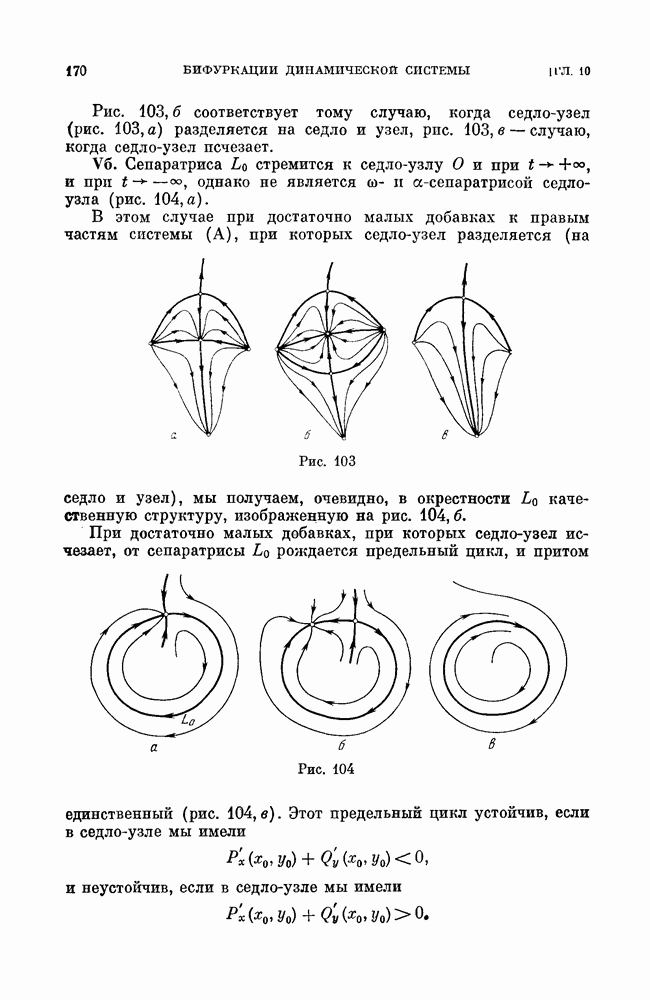
г) бифуркации сшитого седло-узла;
г) бифуркации сшитых сепаратрис седло-узла (сшптого или несшитого), выходящих из седло-узла и возвращающихся в него же.
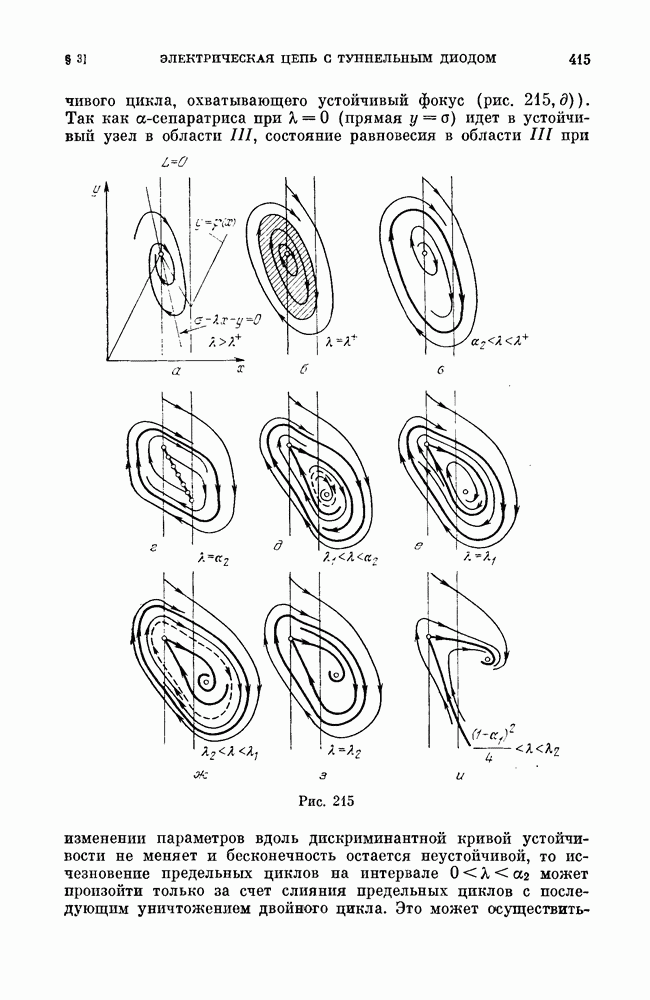
Кроме указанных бифуркаций, в сшитых системах могут быть также некоторые специфические для таких систем бифуркации. В силу того, что в сшитых системах аналогами состояний равновесия могут быть дуги притяжения или отталкивания (см. рис. 193, а), состоящие из неподвижных точек, или область, заполненная замкнутыми траекториями, и т. п., то, естественно, встречаются также бифуркации таких образований, аналогичные рождению предельного цикла из фокуса. Однако мы не будем их здесь рассматривать особо, а рассмотрим их, если они встретятся в конкретных примерах. Ниже мы приведем рассмотрение некоторых из перечисленных выше простейших бифуркаций.
1. Сложный сшитый фокус и рождение из него предельного цикла [22].
Пусть дана сшитая система

Приведенная система имеет частный вид, ввиду того, что у обеих систем  и
и  второе уравнение одно и то же. Однако такого вида сшитые системы часто встречаются. Так, например, если рассматривается уравнение второго порядка
второе уравнение одно и то же. Однако такого вида сшитые системы часто встречаются. Так, например, если рассматривается уравнение второго порядка

в котором  кусочно-непрерывны, то оно приводится к системе вида
кусочно-непрерывны, то оно приводится к системе вида  ; одно из уравнений будет одним и тем же во всех областях сшивания. Отметим, что сшивание вдоль отрезка прямой
; одно из уравнений будет одним и тем же во всех областях сшивания. Отметим, что сшивание вдоль отрезка прямой  не носит частного характера, т. е. к этому случаю мы всегда можем прийти, делая надлежащую замену переменных. Если уравнение дуги сшивания, являющейся аналитической дугой, есть
не носит частного характера, т. е. к этому случаю мы всегда можем прийти, делая надлежащую замену переменных. Если уравнение дуги сшивания, являющейся аналитической дугой, есть

то нужно ввести новое переменное

Сшитая система, заданная с помощью  имеет точку
имеет точку  сшитым состоянием равновесия. Функции
сшитым состоянием равновесия. Функции 
 ,
,  -степенные ряды, начинающиеся с квадратичных членов:
-степенные ряды, начинающиеся с квадратичных членов:

Предположим, что для системы  (продолженной на линию сшивания
(продолженной на линию сшивания  ) состояние равновесия
) состояние равновесия  является фокусом, т. е. корни соответствующего системе
является фокусом, т. е. корни соответствующего системе  характеристического уравнения
характеристического уравнения

— комплексные сопряженные:

Линейным преобразованием

приводим систему  (рассматриваемую в некоторой окрестности начала) к каноническому виду:
(рассматриваемую в некоторой окрестности начала) к каноническому виду:

Предположим, что и для системы  продолженной за линию сшивания
продолженной за линию сшивания  начало О также является фокусом, т. е. соответствующее системе
начало О также является фокусом, т. е. соответствующее системе  характеристическое уравнение
характеристическое уравнение

имеет комплексные сопряженные корни

Линейным преобразованием

приводим систему  к виду каноническому:
к виду каноническому:

Очевидно, принимая во внимание замены переменных, с помощью которых мы пришли к системам  соответственно, система
соответственно, система  рассматривается при
рассматривается при  а система
а система  при
при  При этом
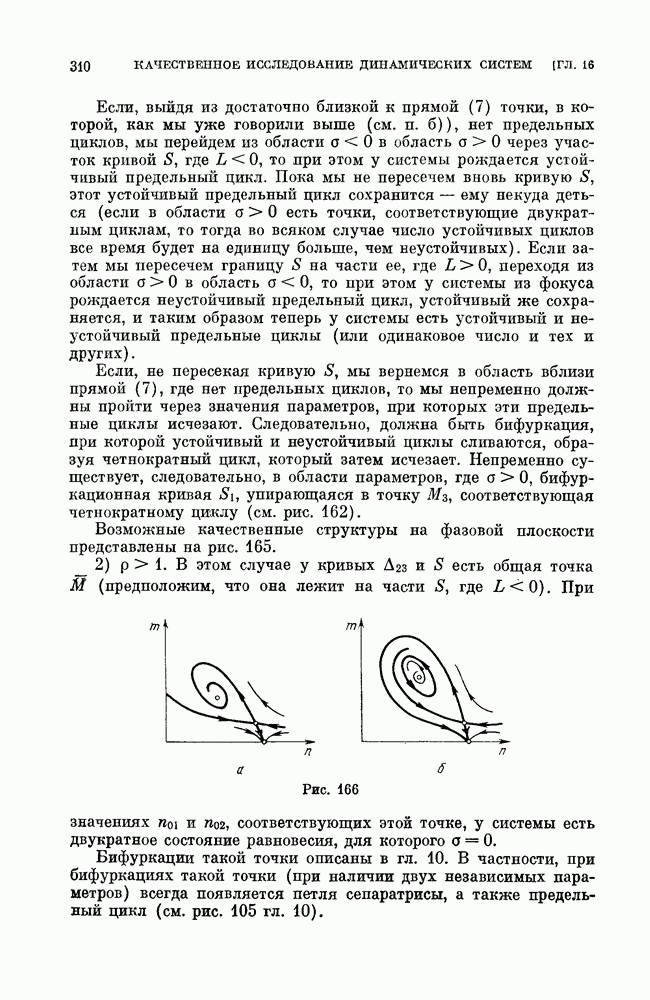
При этом

где

Выражения для  могут быть получены из выражений для
могут быть получены из выражений для  соответственно заменой
соответственно заменой  через
через  . Переходя к полярным координатам соответственно как в системе
. Переходя к полярным координатам соответственно как в системе  так и в системе
так и в системе  полагая
полагая

и соответственно

мы получим два уравнения в полярных координатах: одно — для системы 

определенной при значениях  и другое — для системы
и другое — для системы 

определенной при значениях  Здесь
Здесь

где

Решение уравнения  определяемое начальными условиями
определяемое начальными условиями  при
при  может быть записано в виде ряда по степеням
может быть записано в виде ряда по степеням  сходящегося при всех
сходящегося при всех 

Подставляя правую часть (3) в уравнение  мы для определения
мы для определения  получим рекуррентные дифференциальные уравнения
получим рекуррентные дифференциальные уравнения

с начальными условиями (см. гл. 3 § 5)

В частности,

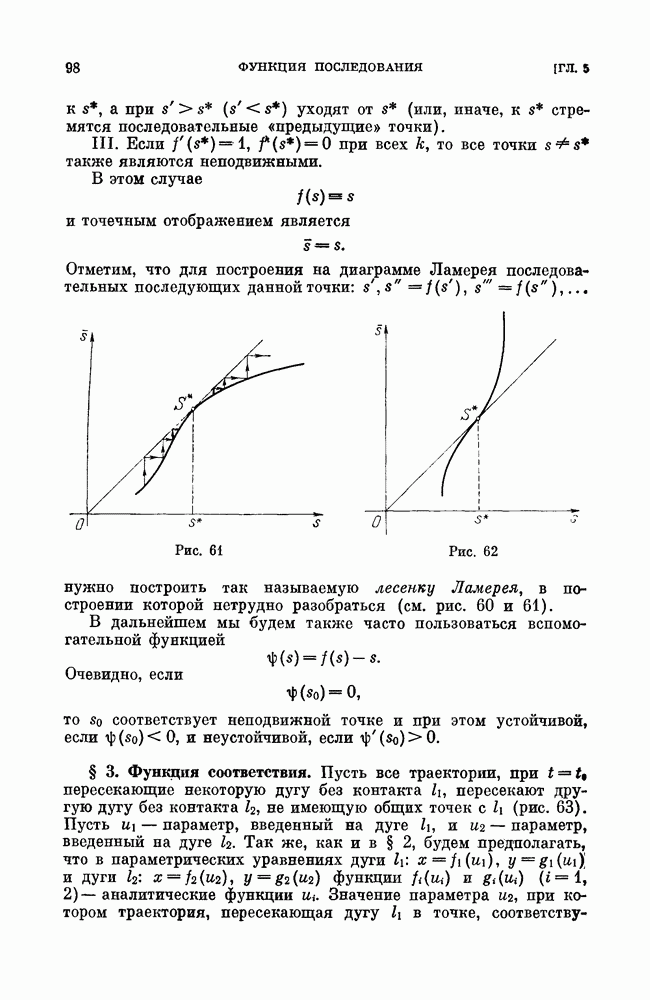
Полагая в решении  получим функцию соответствия между отрезками полупрямых (с концом в начале О)
получим функцию соответствия между отрезками полупрямых (с концом в начале О) 

Решение уравнения  с начальными условиями
с начальными условиями  при
при  и также ищем в виде ряда
и также ищем в виде ряда

где  находятся из рекуррентных уравнении, полностью аналогичных уравнениям (4). Подставляя
находятся из рекуррентных уравнении, полностью аналогичных уравнениям (4). Подставляя  получим функцию соответствия между отрезками полупрямых
получим функцию соответствия между отрезками полупрямых 

Из формул линейных преобразований (1) и (2) очевидно, что при  Отсюда
Отсюда
нетрудно видеть, что

Подставляя в (6) с учетом формул (7) выражение (5), мы получим, как нетрудно видеть, функцию последования на отрезке прямой  (с концом в начале) для сшитой системы в окрестности сшитого фокуса:
(с концом в начале) для сшитой системы в окрестности сшитого фокуса:

Вычисления дают

Очевидно, сшитое состояние равновесия О будет негрубым, сложным сшитым фокусом, если

и существует хотя бы один коэффициент функции последования  Характер устойчивости сшитого фокуса при
Характер устойчивости сшитого фокуса при  определяется первым не равны нулю коэффициентом
определяется первым не равны нулю коэффициентом  (к 2). Отметим, что, в то время как в силу теоремы Ляпунова для аналитических систем в случае, когда фокус сложный, т. е. первый коэффициент функции последования
(к 2). Отметим, что, в то время как в силу теоремы Ляпунова для аналитических систем в случае, когда фокус сложный, т. е. первый коэффициент функции последования  равен единице, одновременно обращается в нуль и второй
равен единице, одновременно обращается в нуль и второй  (так что ляпуновская величина, которая определяет устойчивость и неустойчивость сложного фокуса, может быть только
(так что ляпуновская величина, которая определяет устойчивость и неустойчивость сложного фокуса, может быть только  в случае сшитого фокуса из обращения
в случае сшитого фокуса из обращения  в единицу не следует одновременное обращение в нуль
в единицу не следует одновременное обращение в нуль  при
при  может быть как не равным нулю, так и равным нулю. Отметим также, что сложный сшитый фокус может сшиваться как из двух сложных (аналитических) фокусов, так и из двух грубых фокусов, для которых
может быть как не равным нулю, так и равным нулю. Отметим также, что сложный сшитый фокус может сшиваться как из двух сложных (аналитических) фокусов, так и из двух грубых фокусов, для которых

Приведем выражение для  через коэффициенты частичных систем
через коэффициенты частичных систем  и (II):
и (II):

Используя построенную вокруг сшитого фокуса функцию последования, нетрудно видеть, что, когда

(т. е. когда мы имеем простейший сложный фокус), при изменении коэффициентов  (так, чтобы выражение
(так, чтобы выражение  сделалось не равным нулю
сделалось не равным нулю  надлежащего знака) из сложного сшитого фокуса рождается сшитый предельный цикл (и только один) той же устойчивости, что и сложный сшитый фокус.
надлежащего знака) из сложного сшитого фокуса рождается сшитый предельный цикл (и только один) той же устойчивости, что и сложный сшитый фокус.
Если при изменении коэффициентов  сшитый фокус из устойчивого делается неустойчивым, то здесь возможна та же смена качественных структур, что и рассмотренная в гл. 11, 13 при смене устойчивости фокуса аналитической системы.
сшитый фокус из устойчивого делается неустойчивым, то здесь возможна та же смена качественных структур, что и рассмотренная в гл. 11, 13 при смене устойчивости фокуса аналитической системы.
Пусть теперь у рассматриваемого сложного (сшитого) фокуса первый не равный нулю коэффициент —  где
где 
Тогда без труда можно установить, что в случае, когда коэффициенты  аналитически зависят от параметров (это, очевидно, будет всегда, когда правые части сшиваемых динамических систем—аналитические функции параметров), то из такого фокуса может при сколь угодно малых изменениях параметров родиться не более к предельных циклов. То или другое число
аналитически зависят от параметров (это, очевидно, будет всегда, когда правые части сшиваемых динамических систем—аналитические функции параметров), то из такого фокуса может при сколь угодно малых изменениях параметров родиться не более к предельных циклов. То или другое число  к предельных циклов рождается при том или другом характере зависимости коэффициентов
к предельных циклов рождается при том или другом характере зависимости коэффициентов  от параметров.
от параметров.
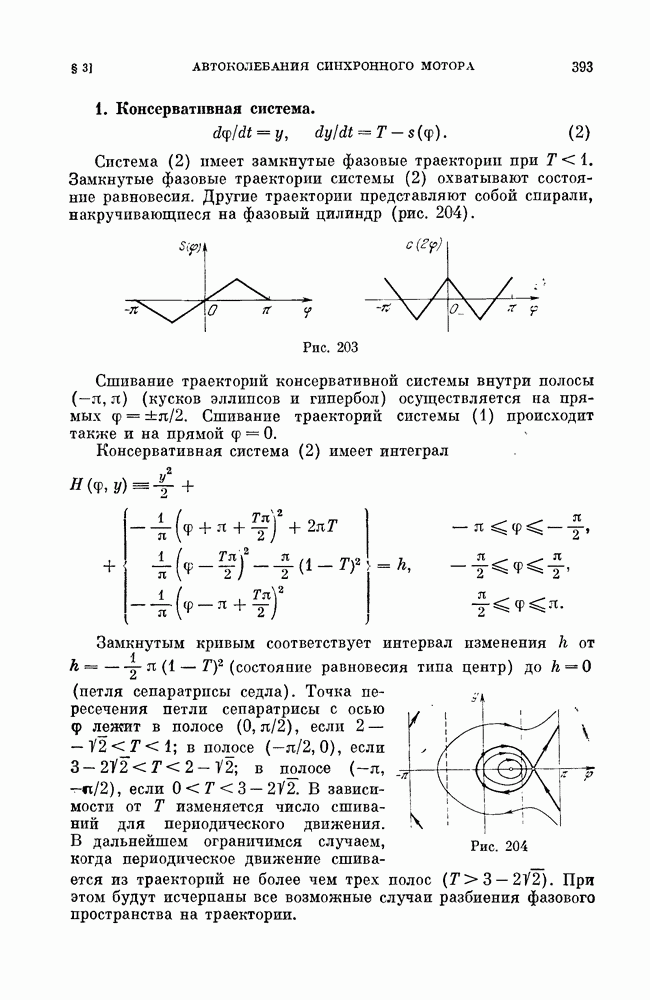
2. Сшитый из обыкновенных траекторий «квазифокус» и рождение предельных циклов из такого фокуса [72]. Пусть линия сшивания есть  и в некоторой окрестности точки
и в некоторой окрестности точки  определена сшптая система
определена сшптая система

Тогда  не является состоянием равновесия ни для одной из систем (8) и (9).
не является состоянием равновесия ни для одной из систем (8) и (9).
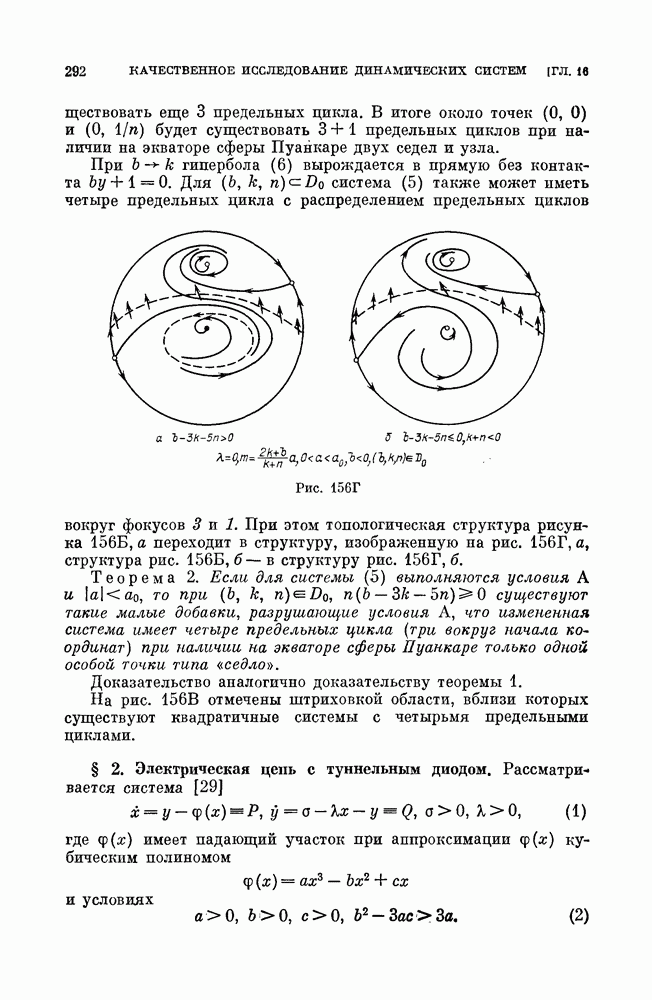
Нетрудно показать, что расположение траекторий в окрестности начала координат будет таким, как представлено на рис. 197 (если  или таким, как представлено на рис.
или таким, как представлено на рис.  если выполнены следующие условия:
если выполнены следующие условия:

Условие  есть условие касания траекторий соответственно систем (8) и (9) оси
есть условие касания траекторий соответственно систем (8) и (9) оси  Условие (11) может
Условие (11) может
быть получено, если для определения вогнутости интегральной кривой, предполагая ее заданной в виде  подсчитать
подсчитать  пользуясь системой (8) или соответственно (9), записанными в виде одного уравнения
пользуясь системой (8) или соответственно (9), записанными в виде одного уравнения  соответственно
соответственно 

Рис. 197

Рис. 198
Неподвижная точка  (квазифокус) обладает свойствами, аналогичными фокусу.
(квазифокус) обладает свойствами, аналогичными фокусу.
Для исследования свойств и бифуркаций такого квазифокуса построим в его окрестности на линии сшивания  функцию последования (точечное отображение), как и в случае настоящего сшитого фокуса (см. § 4, п. 1). Будем строить эту функцию последования из двух функций соответствия между положительной и отрицательной полуосью у. одной — по траекториям системы (8) и другой — по траекториям системы (9). Будем строить эти функции соответствия, используя общпе интегралы систем (8) и (9), в окрестности точки
функцию последования (точечное отображение), как и в случае настоящего сшитого фокуса (см. § 4, п. 1). Будем строить эту функцию последования из двух функций соответствия между положительной и отрицательной полуосью у. одной — по траекториям системы (8) и другой — по траекториям системы (9). Будем строить эти функции соответствия, используя общпе интегралы систем (8) и (9), в окрестности точки  Так как точка
Так как точка  является неособой точкой для систем (8) и (9), и (по условию) каждая из этих систем определена в некоторой полной окрестности точки
является неособой точкой для систем (8) и (9), и (по условию) каждая из этих систем определена в некоторой полной окрестности точки  то в силу общих теорем (см. гл. 1) в окрестности этой точки (локально) существуют интегралы этих систем вида
то в силу общих теорем (см. гл. 1) в окрестности этой точки (локально) существуют интегралы этих систем вида

где  и
и  аналитические функции.
аналитические функции.
Установим прежде всего некоторые элементарные свойства этих интегралов в рассматриваемом нами случае. Так как мы имеем

то, в частности,

Но в силу предположения  мы должны иметь
мы должны иметь

А тогда, очевидно, что  (так как точка
(так как точка  не является особой точкой систем (8) и (9) и не может, следовательно, быть особой точкой интегральных кривых, проходящих через эти точки). Так как (12) выполняется тождественно, то, продифференцировав его по
не является особой точкой систем (8) и (9) и не может, следовательно, быть особой точкой интегральных кривых, проходящих через эти точки). Так как (12) выполняется тождественно, то, продифференцировав его по  мы также получим тождество
мы также получим тождество

В частности, при  мы получаем в силу того, что
мы получаем в силу того, что  следующее выражение:
следующее выражение:

Но так как  то очевидно, что
то очевидно, что

Таким образом, из сделанных нами предположений (10) и (11) вытекает условие на функции 

При этих условиях мы будем строить функцию последования.
Для построения функции соответствия (согласно § 3 гл. 5) между положительной и отрицательной полуосью у введем на них параметры так, чтобы углы между траекторией и соответствующей той и другой полуосью, на которых положительное направление есть направление возрастания параметра, были одного знака.
Такими параметрами, очевидно, будут у — и на положительной и  на отрицательной полуосях. Функции соответствия по траекториям систем (8) и (9) могут быть заданы следующими неявными уравнениями:
на отрицательной полуосях. Функции соответствия по траекториям систем (8) и (9) могут быть заданы следующими неявными уравнениями:

Как мы видели (см. § 1 гл. 5), производная от функции соответствия всегда положительна. Но неявные уравнения (15), (16)
всегда, очевидно, имеют решение

которое является «паразитным». Однако кроме этого решения, это неявное уравнение имеет еще одно решение. Действительно, кривая

в силу условия  очевидно, имеет в точке
очевидно, имеет в точке  особую точку (речь идет об особой точке кривой, а не динамической системы):
особую точку (речь идет об особой точке кривой, а не динамической системы):

Эта особая точка есть узел кривой, так как в окрестности точки  принимая во внимание условия (14), мы можем записать
принимая во внимание условия (14), мы можем записать

Следовательно, для второй ветви кривой  проходящей через начало координат,
проходящей через начало координат,  (это и дает нам искомую функцию соответствия):
(это и дает нам искомую функцию соответствия):

Таким образом, из двух неявных уравнений (15) и (16) мы получаем две функции соответствия

Будем рассматривать также функцию

Очевидно, что отличным от  нулям этой функции соответствуют предельные циклы сшитой системы.
нулям этой функции соответствуют предельные циклы сшитой системы.
Перечислим некоторые свойства функций  и функции
и функции 
1) Последовательные производные от функций  при
при  очевидно, находятся следующим образом. В разложение функции
очевидно, находятся следующим образом. В разложение функции

подставляем разложение для функции  по степеням
по степеням 

В результате несложных вычислений получим

Можно показать, что при  производные нечетного порядка от функций выражаются через производные предшествующих порядков, и поэтому первая не равная нулю производная — четного порядка.
производные нечетного порядка от функций выражаются через производные предшествующих порядков, и поэтому первая не равная нулю производная — четного порядка.
2) Функция  в точке
в точке  имеет нуль четной кратности. При рассмотрении функций соответствия
имеет нуль четной кратности. При рассмотрении функций соответствия  и функции
и функции  по смыслу этих функций мы можем ограничиться рассмотрением только значений
по смыслу этих функций мы можем ограничиться рассмотрением только значений  Если же рассматривать как
Если же рассматривать как  так и
так и  то можно сформулировать еще следующее свойство функции
то можно сформулировать еще следующее свойство функции 
3) Функция  всегда имеет одинаковое число корней, меньших нуля и больших нуля. Очевидно, каждой сшитой замкнутой траектории в окрестности сшитого фокуса соответствуют два корня: один — больший нуля, другой — меньший нуля.
всегда имеет одинаковое число корней, меньших нуля и больших нуля. Очевидно, каждой сшитой замкнутой траектории в окрестности сшитого фокуса соответствуют два корня: один — больший нуля, другой — меньший нуля.
Разложение функции  по степеням и имеет вид
по степеням и имеет вид

Знак коэффициента  вместе со знаком величины
вместе со знаком величины  определяет устойчивость или неустойчивость сшитого фокуса, именно:
определяет устойчивость или неустойчивость сшитого фокуса, именно:
а) если и  имеют разные знаки, то сшитый фокус устойчив;
имеют разные знаки, то сшитый фокус устойчив;
б) если и  имеют одинаковые знаки, то сшитый фокус неустойчив. В случае, когда
имеют одинаковые знаки, то сшитый фокус неустойчив. В случае, когда  сшитый фокус аналогичен грубому;
сшитый фокус аналогичен грубому;
в) коэффициенты при  играют роль ляпуновских величин: если первый не равный нулю коэффициент есть
играют роль ляпуновских величин: если первый не равный нулю коэффициент есть  то мы будем говорить: сшитый фокус является сложным
то мы будем говорить: сшитый фокус является сложным  -кратным.
-кратным.
Предположим теперь, что правые части динамических систем (8) и (9) зависят от параметров  и при всех рассматриваемых значениях этих параметров линией сшивания остается
и при всех рассматриваемых значениях этих параметров линией сшивания остается  Предположим, что при значениях параметров
Предположим, что при значениях параметров  сшитый фокус является
сшитый фокус является  -кратным. Тогда справедливы также утверждения, полностью аналогичные
-кратным. Тогда справедливы также утверждения, полностью аналогичные
утверждениям, касающимся фокуса аналитической системы, а также сшитых «истинных» фокусов, рассмотренных в § 4.
Пусть при  сшитый квазифокус О является
сшитый квазифокус О является  -крат-ным. Тогда при всех близких к
-крат-ным. Тогда при всех близких к  значениях
значениях  из квазифокуса может родиться не более к сшитых предельных циклов, и при надлежащем характере зависимости коэффициентов
из квазифокуса может родиться не более к сшитых предельных циклов, и при надлежащем характере зависимости коэффициентов  от параметров
от параметров  может родиться к предельных циклов.
может родиться к предельных циклов.
Рассмотрим простейший сложный квазифокус, именно такой, для которого

Из такого квазифокуса при изменении параметров  может появиться один и только один сшитый предельный цикл, и притом той же устойчивости, что и фокус. Предположим, в частности, что в правые части входит только один параметр
может появиться один и только один сшитый предельный цикл, и притом той же устойчивости, что и фокус. Предположим, в частности, что в правые части входит только один параметр  Нетрудно рассмотреть разные случаи, которые при этом могут представиться, и указать возможную смену качественных структур (см. гл. 11) полностью аналогично тому, как это было сделано для случая аналитических систем, именно: пусть
Нетрудно рассмотреть разные случаи, которые при этом могут представиться, и указать возможную смену качественных структур (см. гл. 11) полностью аналогично тому, как это было сделано для случая аналитических систем, именно: пусть

тогда при возрастании  к устойчивому сложному квазифокусу стягивается неустойчивый предельный цикл, и квазифокус делается простым неустойчивым (опасная граница области устойчивости).
к устойчивому сложному квазифокусу стягивается неустойчивый предельный цикл, и квазифокус делается простым неустойчивым (опасная граница области устойчивости).
Пусть

Тогда при возрастании  из устойчивого сложного квазифокуса рождается устойчивый предельный цикл и квазифокус делается простым неустойчивым (безопасная граница области устойчивости). Отметим, кроме того, что величины
из устойчивого сложного квазифокуса рождается устойчивый предельный цикл и квазифокус делается простым неустойчивым (безопасная граница области устойчивости). Отметим, кроме того, что величины  могут быть выражены через значения
могут быть выражены через значения  и их производных при
и их производных при 
3. Сложный предельный цикл (сшитый) и рождение из него предельного цикла (сшитого). Пусть рассматриваемая сшитая система имеет сшитый предельный цикл. Рассмотрим простейший случай, когда дуги траекторий частичных систем, из которых сшит предельный цикл, пересекают линии сшивания на участках, являющихся дугами без контакта для траекторий частичных систем, и через линию сшивания продолжаются по непрерывности (пример такого сшивания предельного цикла представлен на рис. 212,в).
В этом случае, очевидно, в окрестности предельного цикла на одной из линий сшивания (безразлично какой), часть которой в окрестности точки пересечения со сшитым циклом является
дугой без контакта, может быть определена функция последования (точечное отображение). Эта функция последования, очевидно, может быть составлена из нескольких функций соответствия между дугами линий сшивания, которые последовательно пересекает рассматриваемый сшитый предельный цикл. Пусть и — параметр, на одной из этих дуг линии сшивания строится функция последования и

эта функция последования в окрестности предельного цикла при сделанных нами предположениях является аналитической функцией.
Пусть предельному циклу соответствует значение 

Так же, как и в случае предельного цикла аналитической системы (см. гл. 5), сшитый предельный цикл является грубым, если  Сшитый грубый цикл устойчив, если
Сшитый грубый цикл устойчив, если  и неустойчив, если
и неустойчив, если  Если
Если  то сшитый предельный цикл является сложным, и так же, как и в случае аналитической системы, мы можем говорить о кратности сшитого предельного цикла. Именно, если
то сшитый предельный цикл является сложным, и так же, как и в случае аналитической системы, мы можем говорить о кратности сшитого предельного цикла. Именно, если

а среди следующих производных от функции последования первая, не равная нулю производная есть

то будем говорить, что рассматриваемый сложный цикл является  -кратным.
-кратным.
Пусть сшитая динамическая система зависит от параметров  Как и выше, мы будем предполагать, что правые части частичных динамических систем
Как и выше, мы будем предполагать, что правые части частичных динамических систем  зависят от параметров
зависят от параметров  аналитически, и линии сшивания не зависят от параметров.
аналитически, и линии сшивания не зависят от параметров.
Пусть при значениях  параметров у рассматриваемой системы существует сшитый предельный цикл, и пусть
параметров у рассматриваемой системы существует сшитый предельный цикл, и пусть

— функция последования в его окрестности, определенная на некоторой линии сшивания при значениях  причем предельный цикл соответствует значению
причем предельный цикл соответствует значению  Тогда на той же линии сшивания при тех же значениях
Тогда на той же линии сшивания при тех же значениях  и всех достаточно близких к
и всех достаточно близких к  значениях
значениях  также существует функция последования, и эта функция является аналитической функцией
также существует функция последования, и эта функция является аналитической функцией  В отношении сшитого
В отношении сшитого  -кратного предельного цикла
-кратного предельного цикла
справедливы утверждения, полностью аналогичные утверждениям, сделанным по поводу кратного цикла аналитической системы.
Именно, из такого цикла при изменении  может рождаться не более к предельных циклов, и при некотором вхождении параметров в правые части может рождаться к предельных циклов.
может рождаться не более к предельных циклов, и при некотором вхождении параметров в правые части может рождаться к предельных циклов.
Если рассматриваемый сложный цикл  четнократный
четнократный  в частности, двукратный
в частности, двукратный  то, так же как и в случае аналитической системы, при изменении
то, так же как и в случае аналитической системы, при изменении  от него может либо родиться два предельных цикла, либо он остается двукратным, либо в окрестности
от него может либо родиться два предельных цикла, либо он остается двукратным, либо в окрестности  не будет ни одного цикла — двукратный цикл исчезает. Очевидно, таким образом, что сшитый двукратный цикл, так же как и аналитический, может возникнуть из уплотнения траекторий.
не будет ни одного цикла — двукратный цикл исчезает. Очевидно, таким образом, что сшитый двукратный цикл, так же как и аналитический, может возникнуть из уплотнения траекторий.
4. Сепаратриса, идущая из седла в то же седло (образующая петлю сшитой системы) и ее бифуркации. Предположим, как и в предыдущем случае, что при неизменных линиях сшивания частные системы зависят от параметров  Пусть при значениях
Пусть при значениях  . У рассматриваемой сшитой системы существует сшитая сепаратриса, идущая из седла
. У рассматриваемой сшитой системы существует сшитая сепаратриса, идущая из седла  в седло 0. Тогда по поводу возможных бифуркаций при изменении параметра такой сепаратрисы можно повторить все сказанное относительно аналогичной сепаратрисы аналитической системы.
в седло 0. Тогда по поводу возможных бифуркаций при изменении параметра такой сепаратрисы можно повторить все сказанное относительно аналогичной сепаратрисы аналитической системы.
Пусть теперь при значениях  рассматриваемой сшитой системы существует сепаратриса (сшитая), идущая из седла
рассматриваемой сшитой системы существует сепаратриса (сшитая), идущая из седла  и возвращающаяся в то же седло 0, т. е. сепаратриса, образующая петлю.
и возвращающаяся в то же седло 0, т. е. сепаратриса, образующая петлю.
Мы предположим, кроме того, что седло  либо лежит целиком в одной из областей
либо лежит целиком в одной из областей  либо лежит на границе
либо лежит на границе  но седловая область, принадлежащая внутренности петли, является сшитой.
но седловая область, принадлежащая внутренности петли, является сшитой.
Пусть седло О, входящее в рассматриваемую сшитую петлю сепаратрисы, принадлежит системе

пусть  — его координаты.
— его координаты.
Рассмотрим седловую величину седла  :
:

и предположим, что

Тогда относительно рассматриваемой сшитой сепаратрисы, образующей петлю, могут быть сделаны те же утверждения, что и относительно петли сепаратрисы аналитической системы. (Доказательство этих утверждений может быть проведено совершенно так же, как и в случае аналитической системы, на основании рассмотрения функции последования, построенной в окрестности петли из нескольких функций соответствия.) Именно, имеют место такие утверждения:
1) Сшитая сепаратриса, образующая петлю, устойчива, если седловая величина  и неустойчива, если
и неустойчива, если 
2) Если  то при изменении из петли сепаратрисы может рождаться не более одного предельного цикла: устойчивого, если
то при изменении из петли сепаратрисы может рождаться не более одного предельного цикла: устойчивого, если  и неустойчивого, если
и неустойчивого, если  При одном характере разделения сепаратрисы рождается предельный цикл, при другом — нет. Соответственно при
При одном характере разделения сепаратрисы рождается предельный цикл, при другом — нет. Соответственно при  в петлю сепаратрисы может «влипнуть» только устойчивый предельный цикл, если
в петлю сепаратрисы может «влипнуть» только устойчивый предельный цикл, если  и только неустойчивый, если
и только неустойчивый, если 
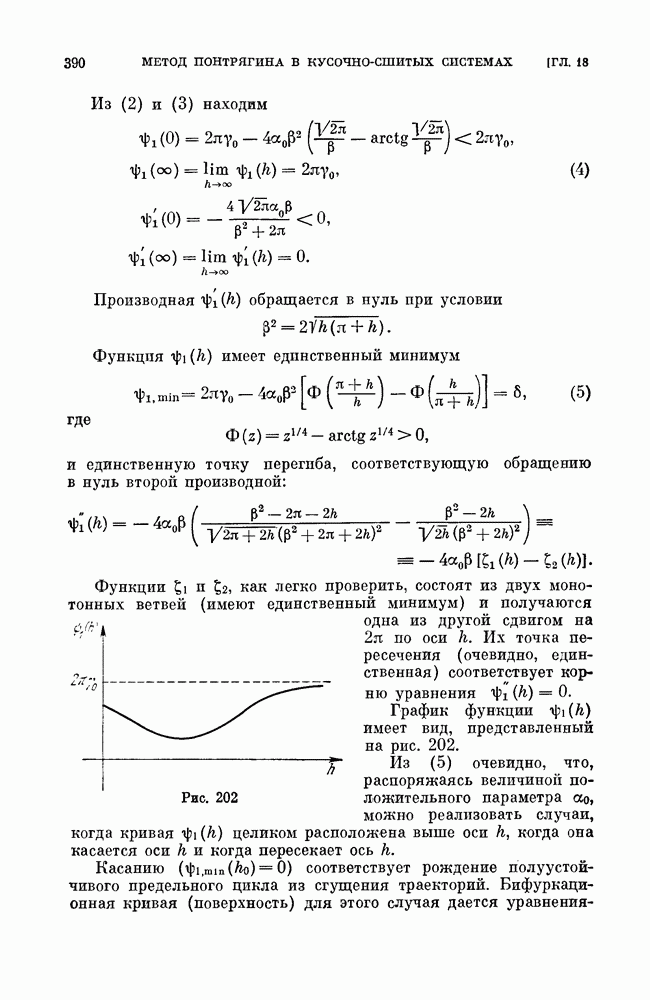
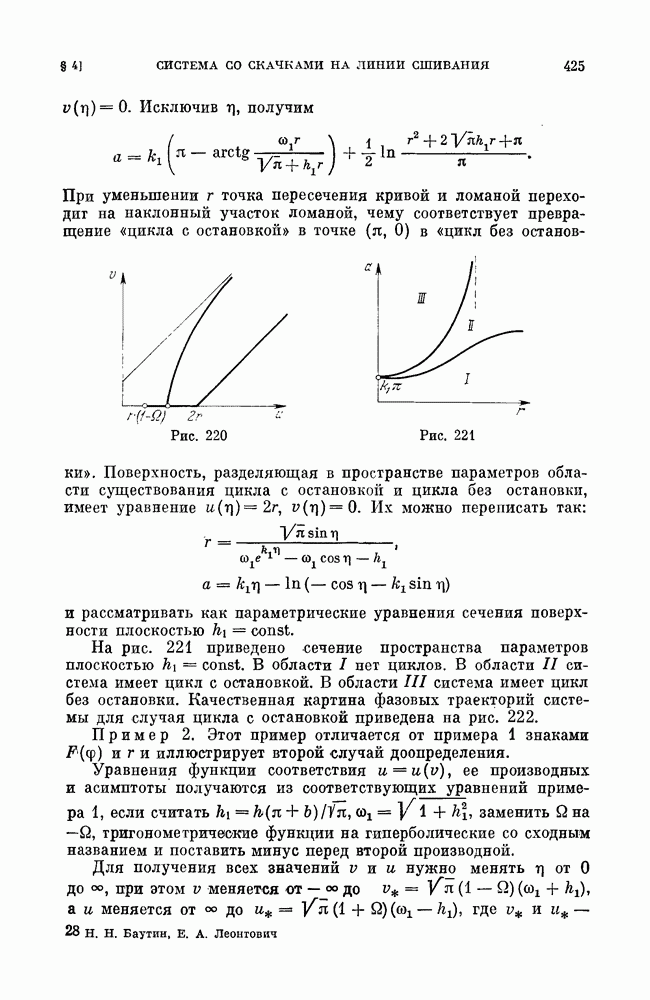
5. Метод Понтрягина для сшитых систем. Пусть Н(х,у)  семейство замкнутых кривых
семейство замкнутых кривых  зависящих от параметра
зависящих от параметра  сшитых из кусков
сшитых из кусков  на интервалах Функции
на интервалах Функции  аналитические по каждому из аргументов.
аналитические по каждому из аргументов.
Тогда система

имеет при  единственный предельный цикл в окрестности замкнутой кривой
единственный предельный цикл в окрестности замкнутой кривой  , если
, если  непрерывна в точках сшивания
непрерывна в точках сшивания 
Здесь  и
и  -аналитические функции в каждом из интервалов
-аналитические функции в каждом из интервалов  корень уравнения
корень уравнения

Предельный цикл будет устойчивым, если  , и неустойчивым, если
, и неустойчивым, если  Фазовое пространство может быть как плоским, так и цилиндрическим.
Фазовое пространство может быть как плоским, так и цилиндрическим.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. АВТОНОМНЫЕ СИСТЕМЫ ВТОРОГО ПОРЯДКА С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- § 1. Автономная динамическая система на плоскости.
- § 2. Теорема существования и единственности решения.
- § 3. Простейшие свойства решений системы (А).
- § 4. Геометрическая интерпретация системы (А) на фазовой плоскости (х, у).
- § 5. Сопоставление геометрической интерпретации системы (А) в пространстве (x, y, t) с интерпретацией на фазовой плоскости.
- § 6. Некоторые термины.
- § 7. Теорема о непрерывной зависимости решения от начальных условий.
- § 8. Направление на траекториях. Изменение параметризации.
- § 9. Дифференциальное уравнение, соответствующее динамической системе.
- § 10. Понятие интегральной кривой и интеграла в случае аналитических правых частей Р(х,у) и Q(x,y) системы (А).
- § 11. Что значит «найти решение динамической системы»?
- § 12. Примеры.
- § 13. Замечания по поводу примеров § 12.
- § 14. Математическое определение качественной (топологической) структуры разбиения на траектории и качественного исследования динамической системы.
- ГЛАВА 2. ВОЗМОЖНЫЙ ХАРАКТЕР ОТДЕЛЬНОЙ ТРАЕКТОРИИ. ТЕОРИЯ ПУАНКАРЕ — БЕНДИКСОНА. ОСОБЫЕ ТРАЕКТОРИИ
- § 2. Цикл без контакта.
- § 3. Предельная точка полутраектории и траектории. Предельная траектория.
- § 4. Основная теорема.
- § 5. Возможные типы полутраекторий и их предельных множеств.
- § 6. Особые и неособые полутраектории и траектории.
- § 7. Возможные типы особых и неособых траекторий.
- § 8. Случай конечного числа особых траекторий. Элементарные ячейки.
- § 9. Возможные типы ячеек. Односвязные и двусвязные ячейки.
- § 10. Два подхода к описанию качественной структуры.
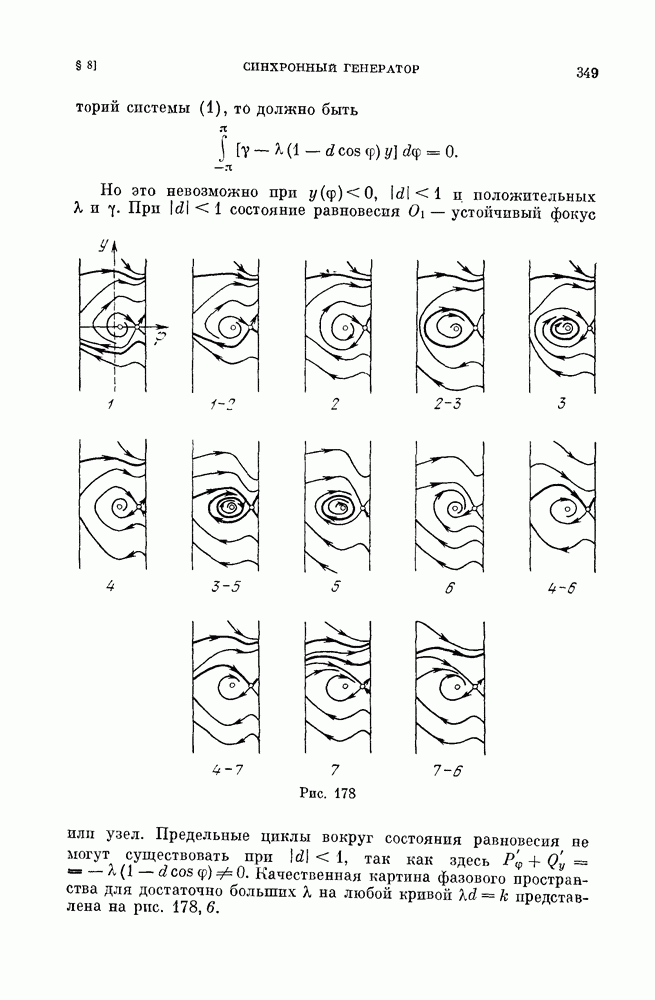
- § 11. Качественная (топологическая) структура состояния равновесия в случае конечного числа особых траекторий. Схема динамической системы.
- § 12. Устойчивость по Ляпунову.
- ГЛАВА 3. ИССЛЕДОВАНИЕ КАЧЕСТВЕННОЙ СТРУКТУРЫ ОКРЕСТНОСТИ СОСТОЯНИЯ РАВНОВЕСИЯ (ОСОБОЙ ТОЧКИ)
- § 2. Приведение динамической системы к каноническому виду.
- § 3. Возможный характер простых состояний равновесия.
- § 4. Замечания о методах установления характера грубых состояний равновесия.
- § 5. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 6. Направления, в которых траектории стремятся к простым состояниям равновесия.
- § 7. Угловой коэффициент направления, в котором траектория может стремиться к простому состоянию равновесия.
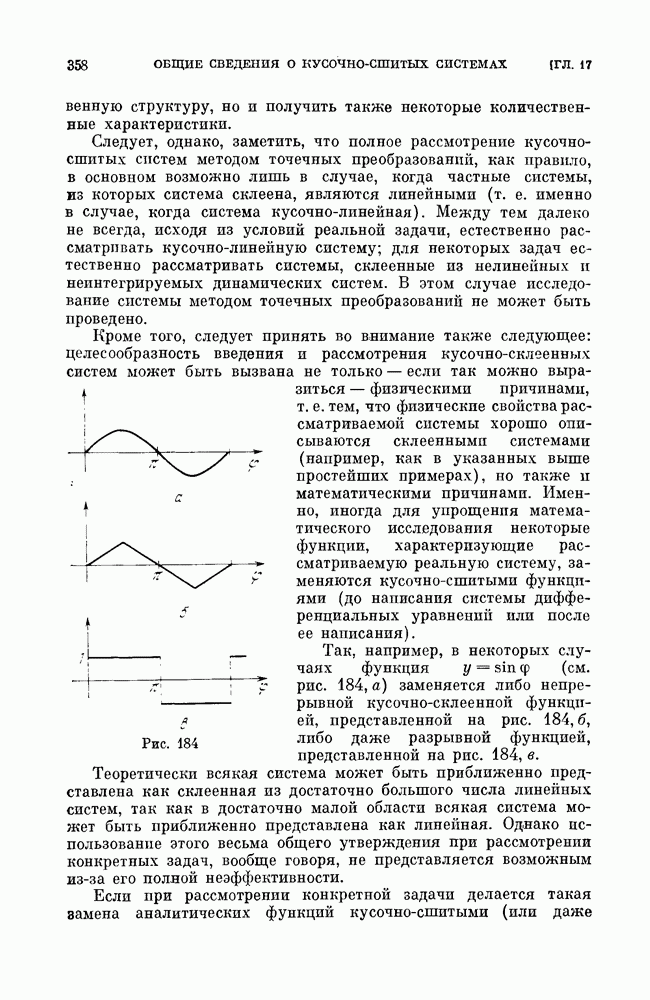
- § 8. Сводка сведений о грубых состояниях равновесия.
- ГЛАВА 4. КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ
- § 1. Направления, в которых траектории стремятся к сложному состоянию равновесия.
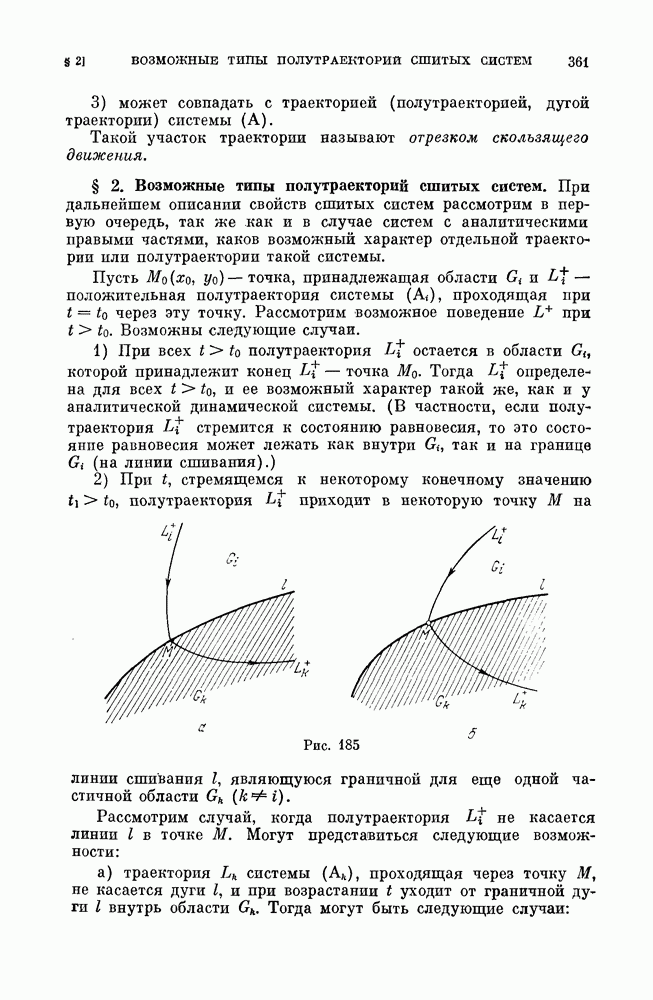
- § 2. Сложное состояние равновесия (особая точка) с нулевыми характеристическими корнями.
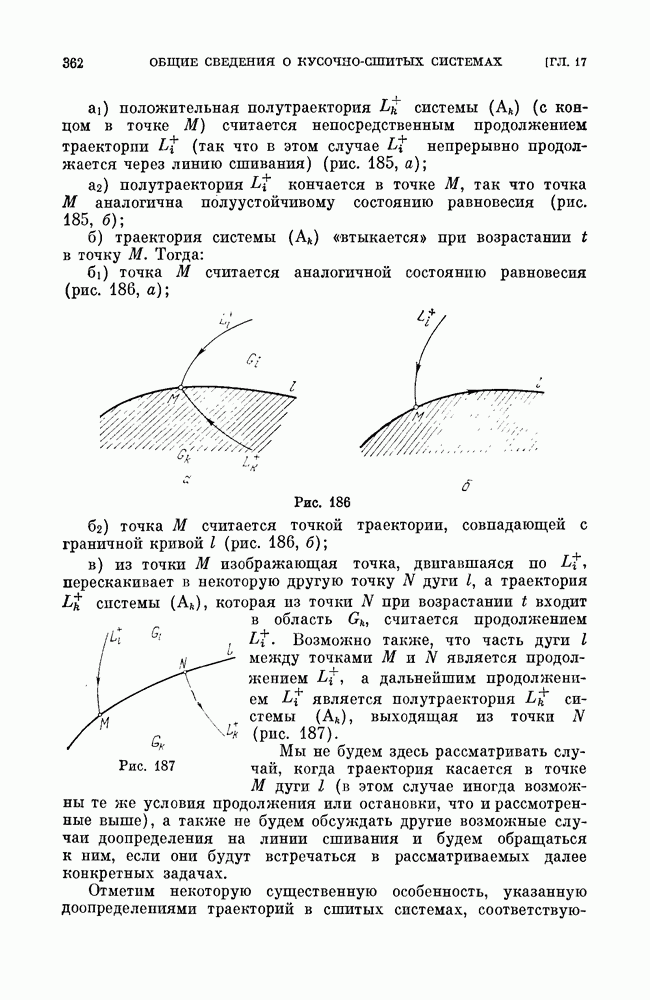
- § 3. Примеры.
- § 4. Нормальные формы.
- ГЛАВА 5. ФУНКЦИЯ ПОСЛЕДОВАНИЯ. ПРОСТЫЕ И СЛОЖНЫЕ ПРЕДЕЛЬНЫЕ ЦИКЛЫ
- § 2. Условия устойчивости и неустойчивости неподвижной точки точечного отображения.
- § 3. Функция соответствия.
- § 4. Изучение окрестности замкнутой траектории. Простые и сложные предельные циклы.
- § 5. Аналитические выражения для коэффициентов функции последования. Характеристический показатель замкнутой траектории.
- ГЛАВА 6. НЕКОТОРЫЕ ПРИЕМЫ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 2. Изучение поведения интегральных кривых в бесконечности. Сфера Пуанкаре.
- § 3. Примеры исследования в бесконечности [93].
- § 4. Критерии Бендиксона и Дюлака отсутствия предельных циклов.
- 1. Некоторые видоизменения критериев Бендиксона и Дюлака.
- 2. Индексы Пуанкаре. Распределение особых точек [77, 117].
- 3. Условия сосуществования замкнутых траекторий и особых точек.
- 4. Две общие теоремы Пуанкаре.
- § 5. Топографическая система Пуанкаре. Функция Ляпунова. Кривые контактов.
- ЧАСТЬ II. ТЕОРИЯ БИФУРКАЦИЙ
- § 1. Свойства консервативных систем на плоскости [2, 3].
- § 2. Динамические системы, характерные для теории колебаний.
- § 3. Измененные системы. Системы, правые части которых зависят от параметра.
- § 4. Основные теоремы о зависимости решения от изменения правых частей динамической системы.
- § 5. Грубость динамической системы и теоремы о непрерывной зависимости решения от изменения правых частей.
- ГЛАВА 8. ГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ
- § 2. Состояния равновесия, возможные в грубой динамической системе.
- § 3. Состояние равновесия с чисто мнимыми характеристическими корнями.
- § 4. Замкнутые траектории, возможные в грубой системе.
- § 5. Поведение сепаратрис седел в грубых системах.
- § 6. Необходимые условия грубости. Достаточность этих условий для грубости системы.
- § 7. Пространство динамических систем. Всюду плотность грубых (двумерных) динамических систем.
- § 8. Понятие грубости при более общих предположениях относительно правых частей динамической системы.
- § 9. Типы особых траекторий и ячеек в грубых системах.
- § 10. Замечания по поводу определения грубой системы.
- ГЛАВА 9. ПРОСТЕЙШИЕ НЕГРУБЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ — СИСТЕМЫ ПЕРВОЙ СТЕПЕНИ НЕГРУБОСТИ
- § 2. Системы первой степени негрубости.
- § 3. Состояния равновесия, возможные в системе первой степени негрубости.
- § 4. Замкнутые траектории, возможные в системе первой степени негрубости.
- § 5. Условия на сепаратрисы седел и седло-узлов в системе первой степени негрубости.
- § 6. Необходимые и достаточные условия первой степени негрубости.
- § 7. Динамические системы более высокой степени негрубости.
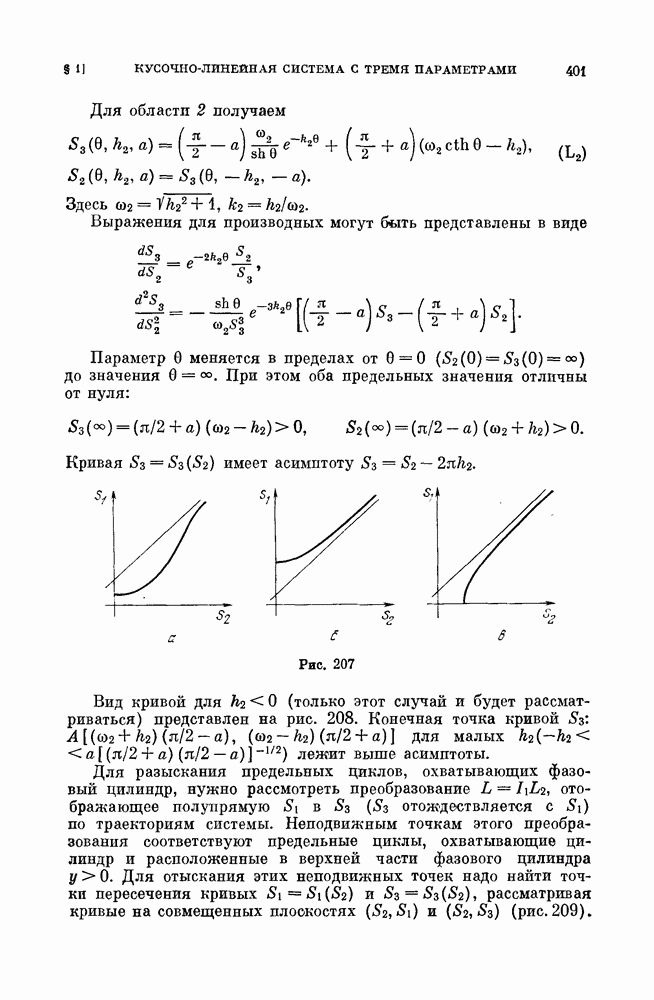
- ГЛАВА 10. БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
- § 1. Определение бифуркации.
- § 2. Бифуркации систем первой степени негрубости.
- § 3. Бифуркации некоторых типов сложных особых точек.
- § 4. Бифуркации двукратной точки, для которой …
- § 5. Рождение предельных циклов из особых траекторий степени негрубости выше первой.
- ГЛАВА 11. ДИНАМИЧЕСКИЕ СИСТЕМЫ, ПРАВЫЕ ЧАСТИ КОТОРЫХ СОДЕРЖАТ ПАРАМЕТРЫ
- § 1. Возможный характер зависимости правых частей динамической системы от параметров.
- § 2. Смена качественных структур при изменении параметров.
- § 3. Случай, когда правые части зависят более чем от одного параметра.
- § 4. Бифуркации «от бесконечности».
- § 5. Условия существования седло-узла и сложного фокуса первого порядка.
- § 6. Поворот векторного поля.
- § 7. Метод малого параметра. Метод Понтрягина.
- ГЛАВА 12. ДИНАМИЧЕСКИЕ СИСТЕМЫ С ЦИЛИНДРИЧЕСКОЙ ФАЗОВОЙ ПОВЕРХНОСТЬЮ
- § 1. Цилиндрическая фазовая поверхность и характер траекторий, возможных на цилиндрической фазовой поверхности.
- § 2. Замкнутые траектории, охватывающие цилиндр.
- § 3. Приемы исследования качественной структуры динамической системы на цилиндре.
- § 4. Понятие грубости и степени негрубости для динамических систем на цилиндре. Бифуркации на цилиндре. Поворот поля.
- § 5. Динамические системы на цилиндре, близкие к гамильтоновым (метод Понтрягина).
- ГЛАВА 13. АДЕКВАТНОЕ ИСТОЛКОВАНИЕ НЕЛИНЕЙНЫХ ФИЗИЧЕСКИХ ЯВЛЕНИЙ ФАКТАМИ КАЧЕСТВЕННОЙ ТЕОРИИ И ТЕОРИИ БИФУРКАЦИЙ ДИНАМИЧЕСКИХ СИСТЕМ
- § 1. Мягкий и жесткий режимы.
- § 2. Замечания о границах области устойчивости различных стационарных режимов.
- § 3. Мягкое и жесткое возникновение колебаний.
- § 4. «Безопасные» и «опасные» границы области устойчивости состояний равновесия.
- § 5. Замечания по поводу других границ области устойчивости.
- ЧАСТЬ III. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ КОНКРЕТНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С АНАЛИТИЧЕСКИМИ ПРАВЫМИ ЧАСТЯМИ
- ГЛАВА 14. ОБЩИЕ ЗАМЕЧАНИЯ О ПРИЕМАХ КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ
- § 1. Некоторые рецептурные указания.
- § 2. Некоторые простые примеры качественного исследования динамических систем на плоскости.
- § 3. Некоторые простые примеры динамических систем на цилиндре.
- ГЛАВА 15. ИССЛЕДОВАНИЕ МЕТОДОМ МАЛОГО ПАРАМЕТРА (МЕТОДОМ ПОНТРЯГИНА)
- § 2. Примеры рассмотрения методом Понтрягина (полное исследование).
- § 3. Исследование методом Понтрягина с привлечением вычислительных методов.
- ГЛАВА 16. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ПРИЕМОВ, ОПИРАЮЩИХСЯ НА ТЕОРИЮ БИФУРКАЦИЙ
- § 2. Электрическая цепь с туннельным диодом.
- § 3. Двумерная модель динамики твердотельного лазера [119].
- § 4. Симметричный полет самолета в вертикальной плоскости (задача Н. Е. Жуковского).
- § 5. Система, описывающая динамику проточного химического реактора.
- § 6. Фазовая автоподстройка частоты.
- § 7. Частотно-фазовая автоподстройка частоты (случай существования трех предельных циклов).
- § 8. Синхронный генератор с асинхронной характеристикой.
- ЧАСТЬ IV. КУСОЧНО-СШИТЫЕ СИСТЕМЫ
- ГЛАВА 17 ОБЩИЕ СВЕДЕНИЯ О КУСОЧНО-СШИТЫХ СИСТЕМАХ
- § 1. Сшитые системы. Доопределение на линиях сшивания.
- § 2. Возможные типы полутраекторий сшитых систем.
- § 3. Особые траектории сшитых систем.
- § 4. Бифуркации в сшитых системах. Метод Понтрягина для сшитых систем.
- ГЛАВА 18. ИССЛЕДОВАНИЕ КУСОЧНО-СШИТЫХ СИСТЕМ МЕТОДОМ ПОНТРЯГИНА
- § 2. Автоподстройка при кусочно-постоянной аппроксимации характеристики.
- § 3. Автоколебания синхронного мотора.
- ГЛАВА 19. КАЧЕСТВЕННОЕ ИССЛЕДОВАНИЕ СШИТЫХ СИСТЕМ МЕТОДАМИ ТЕОРИИ БИФУРКАЦИИ
- § 2. Следящая система с люфтом.
- § 3. Электрическая цепь с туннельным диодом.
- § 4. Система со скачками на линии сшивания.
- ГЛАВА 20. ОБ АППРОКСИМАЦИЯХ И ГРУБОСТИ ПРОСТРАНСТВА ПАРАМЕТРОВ [39, 41, 42]
- § 1. Рассмотрение системы (2) при аппроксимациях пилообразными функциями.
- § 2. Рассмотрение системы (2) при аппроксимации, включающей отрезок параболы.
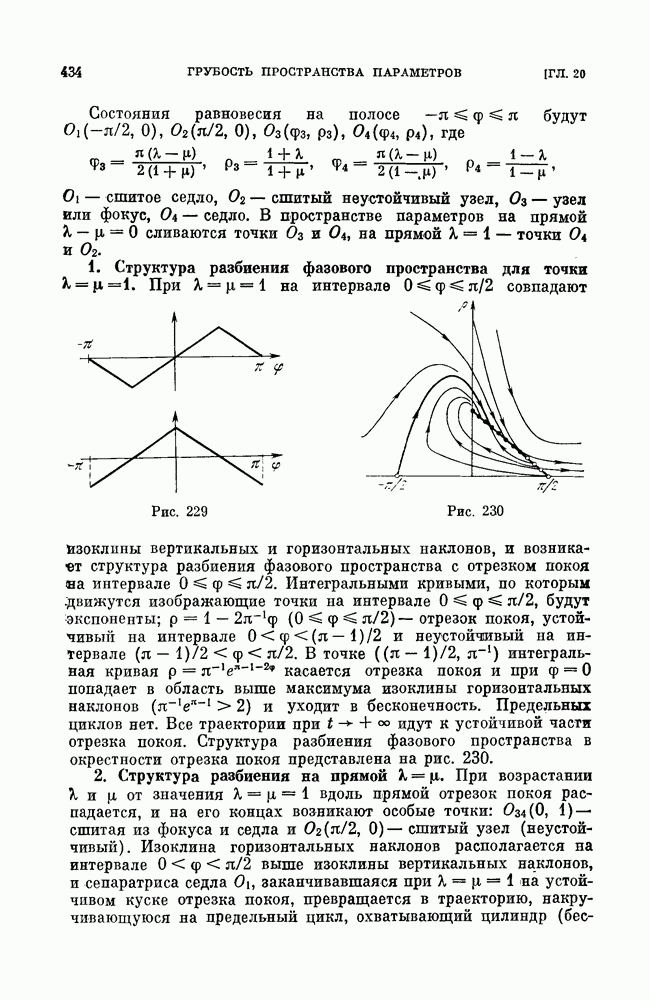
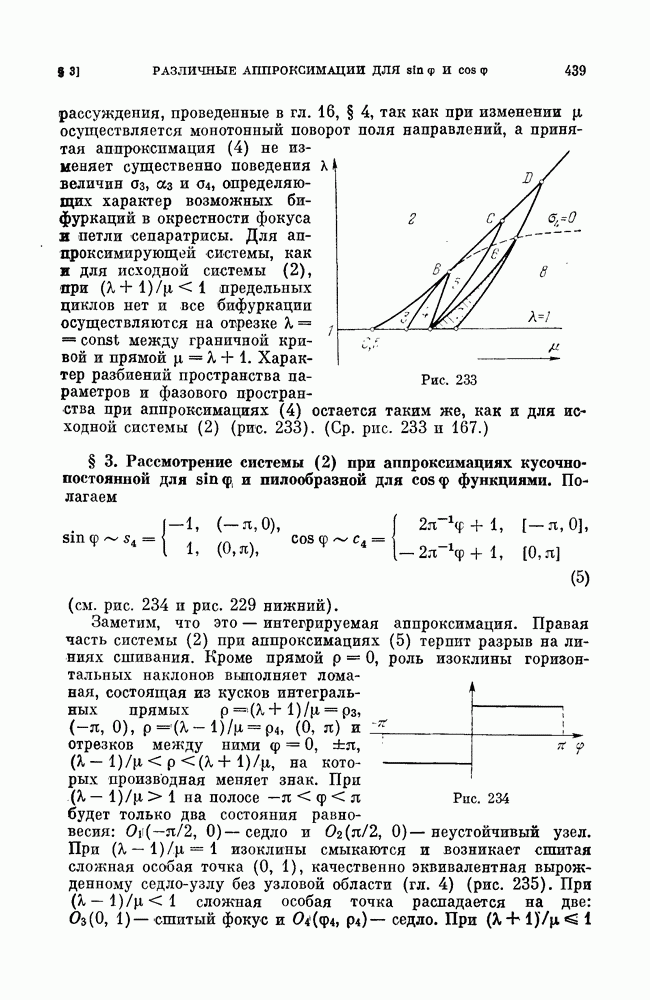
- § 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin f, и пилообразной для cos f функциями.
- § 4. Исследование роли аппроксимаций для уравнения маятникового типа.
- § 5. Динамическая система, описывающая автоколебания синхронного мотора.
- § 6. Динамическая система, описывающая симметричный полет самолета.
- ДОПОЛНЕНИЕ
- § 1. Динамическое системы на двумерных поверхностях.
- § 2. Динамические системы в n-мерном евклидовом пространстве.
- СПИСОК ЛИТЕРАТУРЫ