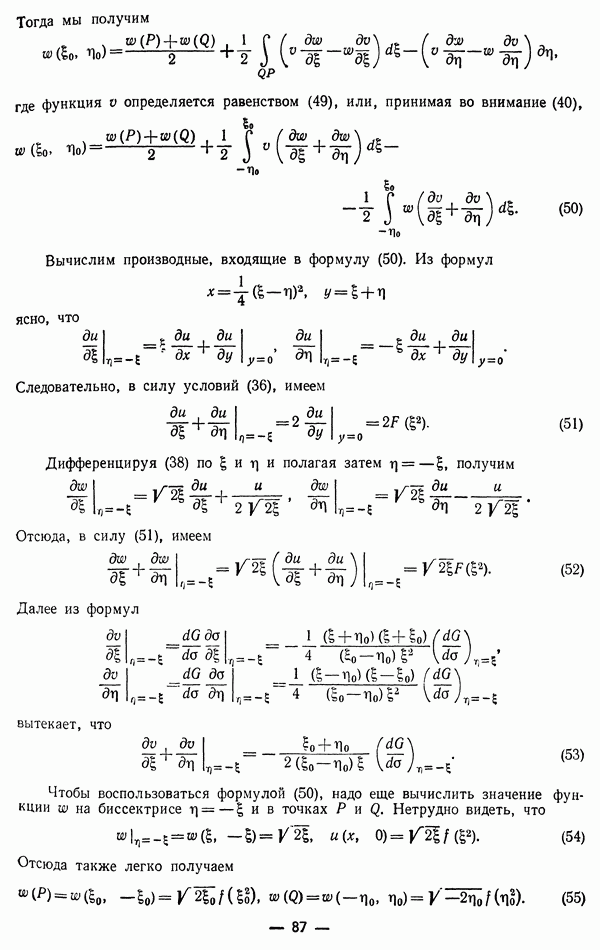| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЧАСТЬ ПЕРВАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
К уравнениям гиперболического типа приводят задачи, связанные с процессами колебаний, например, задача о колебаниях струны, мембраны, газа, электромагнитных колебаниях и т. д. Характерной особенностью процессов, описываемых такими уравнениями, является конечная скорость их распространения.
Глава IV. ПРИМЕНЕНИЕ МЕТОДА ХАРАКТЕРИСТИК К ИЗУЧЕНИЮ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ
§ 1. Уравнение колебаний струны. Решение Даламбера
1. Неограниченная струна.
Уравнение свободных колебаний однородной струны имеет вид

Положим

Нетрудно видеть, что  суть характеристики уравнения (1). Уравнение (1) в новых переменных запишется в виде
суть характеристики уравнения (1). Уравнение (1) в новых переменных запишется в виде

или, переписав его в виде

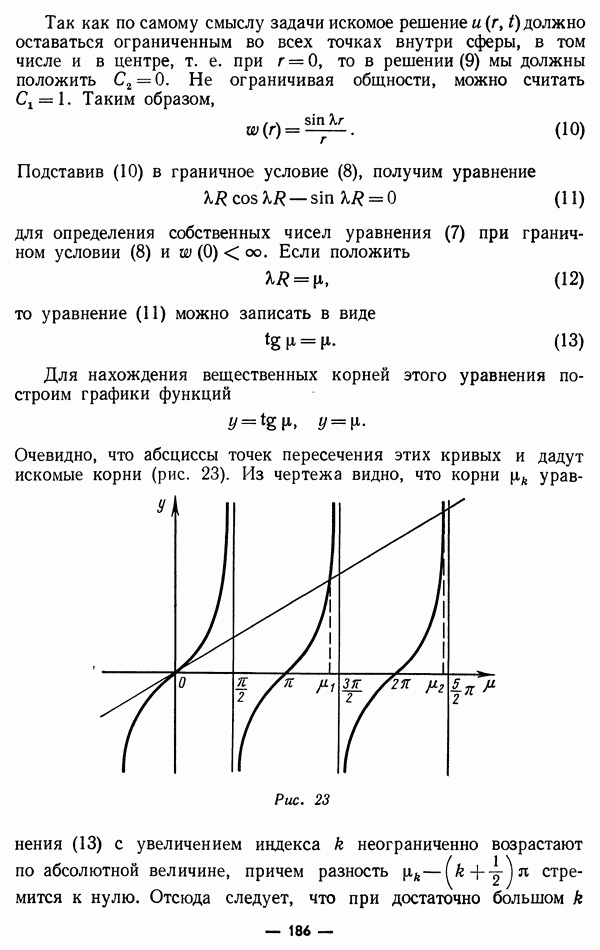
получим

где со  произвольная функция Интегрируя полученное уравнение по рассматривая
произвольная функция Интегрируя полученное уравнение по рассматривая  как параметр, найдем, что
как параметр, найдем, что

где  произвольная функция
произвольная функция  Полагая теперь
Полагая теперь

получим

Возвращаясь к старым переменным  будем иметь
будем иметь

Нетрудно проверить, что функция  определяемая формулой (3), есть решение уравнения (1), если
определяемая формулой (3), есть решение уравнения (1), если  произвольные дважды непрерывно дифференцируемые функции. Решение (3) уравнения (1) называется решением Даламбера.
произвольные дважды непрерывно дифференцируемые функции. Решение (3) уравнения (1) называется решением Даламбера.
Выясним физический смысл решения (3).
Рассмотрим сначала частный случай колебания струны, когда  т. е. когда смещение струны определяется формулой
т. е. когда смещение струны определяется формулой

Положим, что наблюдатель, выйдя в начальный момент времени  из точки
из точки  струны, передвигается в положительном направлении оси
струны, передвигается в положительном направлении оси  со скоростью а, т. е. его абсцисса меняется по закону
со скоростью а, т. е. его абсцисса меняется по закону  или
или  Для такого наблюдателя смещение струны, определяемое формулой (4), будет оставаться все время постоянным, равным
Для такого наблюдателя смещение струны, определяемое формулой (4), будет оставаться все время постоянным, равным  Самое явление, описываемое функцией
Самое явление, описываемое функцией  называется распространением прямой волны. Таким образом, решение (4) представляет прямую волну, которая распространяется в положительном направлении оси х со скоростью а. Точно так же решение
называется распространением прямой волны. Таким образом, решение (4) представляет прямую волну, которая распространяется в положительном направлении оси х со скоростью а. Точно так же решение  представляет обратную волну, которая распространяется в отрицательном направлении оси х со скоростью а.
представляет обратную волну, которая распространяется в отрицательном направлении оси х со скоростью а.
Таким образом, решение (3) является суммой прямой и обратной волн.
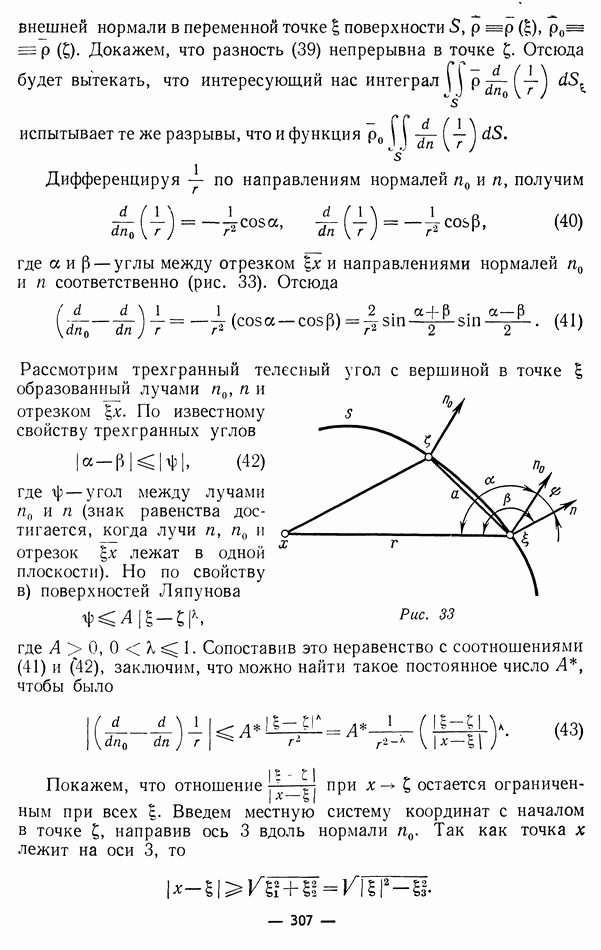
Это приводит к следующему графическому способу построения формы струны в любой момент времени  Строим кривые
Строим кривые

изображающие прямую и обратные волны в начальный момент времени  и затем, не изменяя их формы, передвигаем их одновременно со скоростью а в разные стороны:
и затем, не изменяя их формы, передвигаем их одновременно со скоростью а в разные стороны:  вправо,
вправо,
 влево. Чтобы получить теперь график струны, достаточно построить алгебраические суммы ординат раздвинутых кривых.
влево. Чтобы получить теперь график струны, достаточно построить алгебраические суммы ординат раздвинутых кривых.

Рис. 3
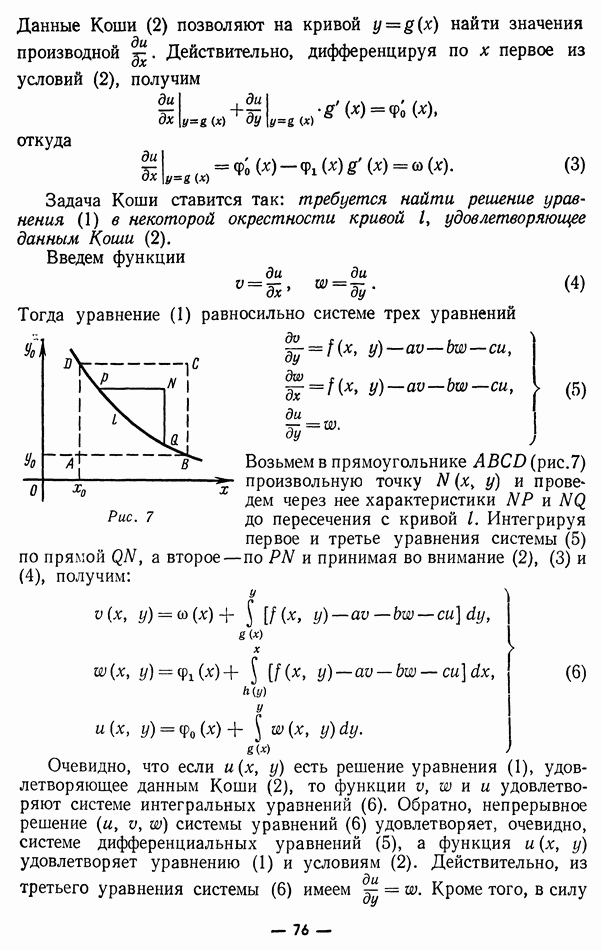
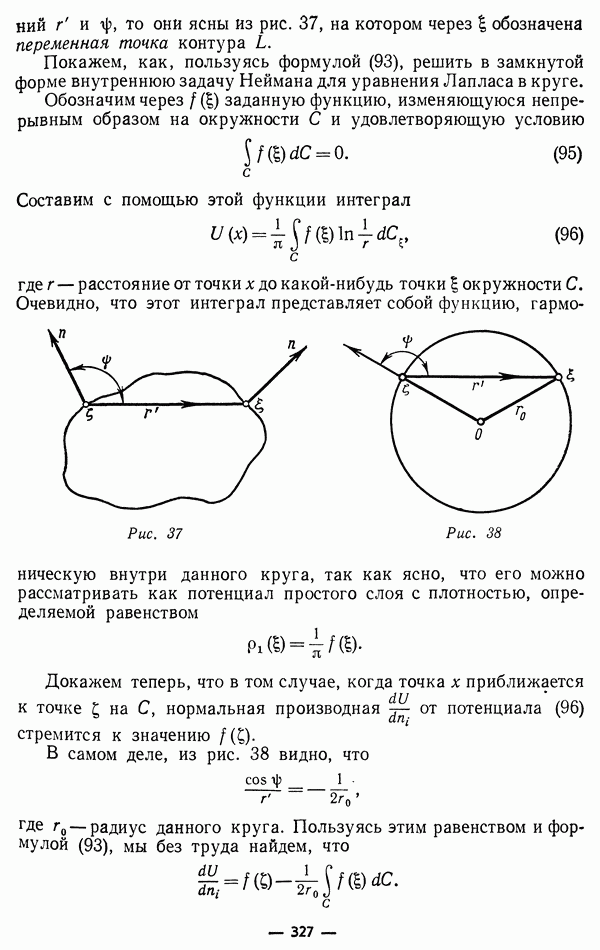
Рассмотрим верхнюю полуплоскость  в которой ось
в которой ось  соответствует положению струны в начальный момент времени
соответствует положению струны в начальный момент времени  Всякая точка
Всякая точка  нашей полуплоскости характеризует определенную точку х струны в определенный момент времени Нетрудно при этом найти графически те точки струны начальные возмущения которых дошли в момент времени
нашей полуплоскости характеризует определенную точку х струны в определенный момент времени Нетрудно при этом найти графически те точки струны начальные возмущения которых дошли в момент времени  до точки
до точки  Это будут, согласно предыдущему, точки с абсциссами
Это будут, согласно предыдущему, точки с абсциссами  так как а есть скорость распространения колебаний. Для нахождения их на оси х достаточно провести через точку
так как а есть скорость распространения колебаний. Для нахождения их на оси х достаточно провести через точку  две характеристики
две характеристики

и в пересечении их с осью  и получаются искомые точки (рис. 3).
и получаются искомые точки (рис. 3).
Вдоль первой характеристики  сохраняет постоянное значение, т. е. эта прямая дает те значения
сохраняет постоянное значение, т. е. эта прямая дает те значения  при которых прямая волна дает то же отклонение, что и при значениях
при которых прямая волна дает то же отклонение, что и при значениях  Вторая характеристика из (5) играет ту же роль для обратной волны
Вторая характеристика из (5) играет ту же роль для обратной волны  Можно сказать коротко, что возмущения распространяются по характеристикам.
Можно сказать коротко, что возмущения распространяются по характеристикам.
2. Задача Коши.
Найти решение уравнения (1), удовлетворяющее начальным условиям

Ввиду неограниченности струны функции  заданы в
заданы в 
В решении (3) уравнения (1) нужно выбрать функции  так, чтобы удовлетворить начальным условиям (6). Из начальных условий (6) имеем:
так, чтобы удовлетворить начальным условиям (6). Из начальных условий (6) имеем:

откуда, интегрируя второе равенство, получим:

где С — произвольная постоянная.
Из равенств (7) находим

Подставив (8) в (3), будем иметь

или окончательно

Формула (9) дает решение задачи Коши (1), (6), если  имеет непрерывные производные до второго порядка включительно, а
имеет непрерывные производные до второго порядка включительно, а  первого.
первого.
Задача Коши (1), (6) поставлена корректно. Действительно, полученное решение единственно, что следует из способа вывода формулы (9). Несомненна далее непрерывная зависимость решения (9) от начальных данных. В самом деле, для любого  можно указать такое
можно указать такое  что если заменить
что если заменить  на
на  так, что
так, что

то разность между новым решением  и первоначальным
и первоначальным  будет по абсолютной величине меньше
будет по абсолютной величине меньше  на любом конечном отрезке времени. Это утверждение легко следует из формулы (9). Рассмотрим два частных случая.
на любом конечном отрезке времени. Это утверждение легко следует из формулы (9). Рассмотрим два частных случая.
I) Начальные скорости точек струны равны нулю, а начальное смещение имеет место лишь в конечном промежутке  струны, т. е.
струны, т. е.  вне этого промежутка. Решение (9) выражается при этом формулой
вне этого промежутка. Решение (9) выражается при этом формулой

Решение (10) является суммой двух волн, распространяющихся направо и налево со скоростью а, причем начальная форма обеих волн определяется функцией  равной половине начального
равной половине начального
смещения. Пусть точка х струны лежит правее промежутка  При
При  из вида функции
из вида функции  и формулы (10) следует, что и
и формулы (10) следует, что и  т. е. до точки х волна еще не дошла. С момента времени
т. е. до точки х волна еще не дошла. С момента времени  — точка х начнет колебаться (момент прохождения переднего фронта прямой волны). При
— точка х начнет колебаться (момент прохождения переднего фронта прямой волны). При  из формулы (10) следует, что
из формулы (10) следует, что  Моменту времени
Моменту времени  соответствует прохождение заднего фронта прямой волны через точку
соответствует прохождение заднего фронта прямой волны через точку  после чего в этой точке
после чего в этой точке  обращается в нуль. Аналогичные рассуждения можно провести для точек струны, лежащих внутри промежутка
обращается в нуль. Аналогичные рассуждения можно провести для точек струны, лежащих внутри промежутка  или левее его. Таким образом, в каждой точке струны после прохождения обеих волн (а для точек, лежащих вне области начального смещения, после прохождения только одной) наступает покой.
или левее его. Таким образом, в каждой точке струны после прохождения обеих волн (а для точек, лежащих вне области начального смещения, после прохождения только одной) наступает покой.
2) Начальное смещение равно нулю,  отлична от нуля лишь в конечном промежутке
отлична от нуля лишь в конечном промежутке  В таком случае говорят, что струна имеет только начальный импульс. Решение (9) принимает следующий вид:
В таком случае говорят, что струна имеет только начальный импульс. Решение (9) принимает следующий вид:

или, полагая

получим

т. е. по струне распространяются две волны — одна прямая и одна обратная. Исследуем решение (11) более подробно. Пусть точка х струны лежит правее промежутка  При
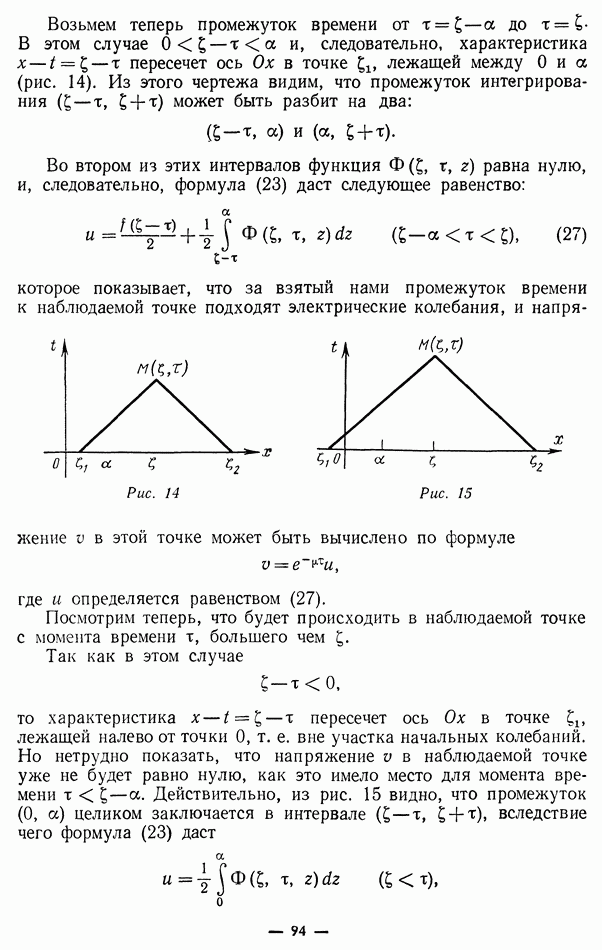
При  промежуток интегрирования
промежуток интегрирования  вырождается в точку х, а затем при увеличении
вырождается в точку х, а затем при увеличении  он расширяется в обе стороны со скоростью а.
он расширяется в обе стороны со скоростью а.
При  он не будет иметь общих точек с
он не будет иметь общих точек с  функция
функция  в нем равна нулю, и формула (11) даст и
в нем равна нулю, и формула (11) даст и  т. е. покой в точке х. Начиная с момента времени
т. е. покой в точке х. Начиная с момента времени  промежуток
промежуток  будет налегать на
будет налегать на  , в котором
, в котором  отлична от нуля, и точка начнет колебаться (момент прохождения переднего фронта волны через точку
отлична от нуля, и точка начнет колебаться (момент прохождения переднего фронта волны через точку  Наконец, при
Наконец, при  промежуток
промежуток  будет содержать целиком промежуток
будет содержать целиком промежуток  , интегрирование по
, интегрирование по  будет сводиться к
будет сводиться к
интегрированию по  так как вне его
так как вне его  при
при  мы имеем постоянное значение
мы имеем постоянное значение  равное
равное

Момент времени  есть момент прохождения заднего фронта волны через точку х.
есть момент прохождения заднего фронта волны через точку х.
Таким образом, действие начального импульса приводит к тому, что с течением времени точки струны сдвигаются на отрезок, длина которого выражается интегралом (12), и остаются без движения в этом новом положении. Волны оставляют после себя как бы след своего прохождения.
3. Ограниченная струна.
Рассмотрим теперь струну длины  закрепленную на концах. Задача о колебании такой струны сводится к нахождению решения волнового уравнения
закрепленную на концах. Задача о колебании такой струны сводится к нахождению решения волнового уравнения

при граничных условиях

и начальных условиях

Решение Даламбера

конечно, годится в этом случае, но определение  по формулам
по формулам

встречает здесь то затруднение, что функции  а следовательно,
а следовательно,  определены лишь в промежутке
определены лишь в промежутке  согласно физическому смыслу задачи, а аргументы
согласно физическому смыслу задачи, а аргументы  в формуле (16) могут лежать и вне этого промежутка. Стало быть, для возможного применения решения (16) нужно продолжить функции
в формуле (16) могут лежать и вне этого промежутка. Стало быть, для возможного применения решения (16) нужно продолжить функции  или, что вполне эквивалентно, функции
или, что вполне эквивалентно, функции  вне промежутка (
вне промежутка ( С точки зрения физической, это продолжение сводится к определению такого начального возмущения
С точки зрения физической, это продолжение сводится к определению такого начального возмущения
бесконечной струны, чтобы движение ее участка  было то же самое, как если бы он, был закреплен на концах, а оставшаяся часть струны была бы отброшена.
было то же самое, как если бы он, был закреплен на концах, а оставшаяся часть струны была бы отброшена.
Для продолжения функций  воспользуемся граничными условиями (14). Подставляя в правую часть
воспользуемся граничными условиями (14). Подставляя в правую часть  и принимая во внимание граничные условия (14), получим:
и принимая во внимание граничные условия (14), получим:

или, обозначая  через х,
через х,

Когда х изменяется в промежутке ( то первая из формул (18) определяет функцию
то первая из формул (18) определяет функцию  в промежутке
в промежутке  вторая — функцию
вторая — функцию  в промежутке
в промежутке  Стало быть, обе функции
Стало быть, обе функции  вполне определяются на промежутке длины 21. Далее из равенств (18) следует, что
вполне определяются на промежутке длины 21. Далее из равенств (18) следует, что

т. е. функции  являются функциями периодическими с периодом 21. Итак, функции
являются функциями периодическими с периодом 21. Итак, функции  определены при всех вещественных х.
определены при всех вещественных х.
Принимая во внимание, что

найдем

Эти формулы показывают, что функции  продолжаются из промежутка
продолжаются из промежутка  в промежуток
в промежуток  нечетным образом, а затем с периодом 21.
нечетным образом, а затем с периодом 21.
Чтобы полученное решение имело непрерывные производные до второго порядка включительно, нужно, помимо условий дифференцируемости функций  потребовать еще выполнения условий
потребовать еще выполнения условий

Это есть условия согласования начальных и граничных условий.
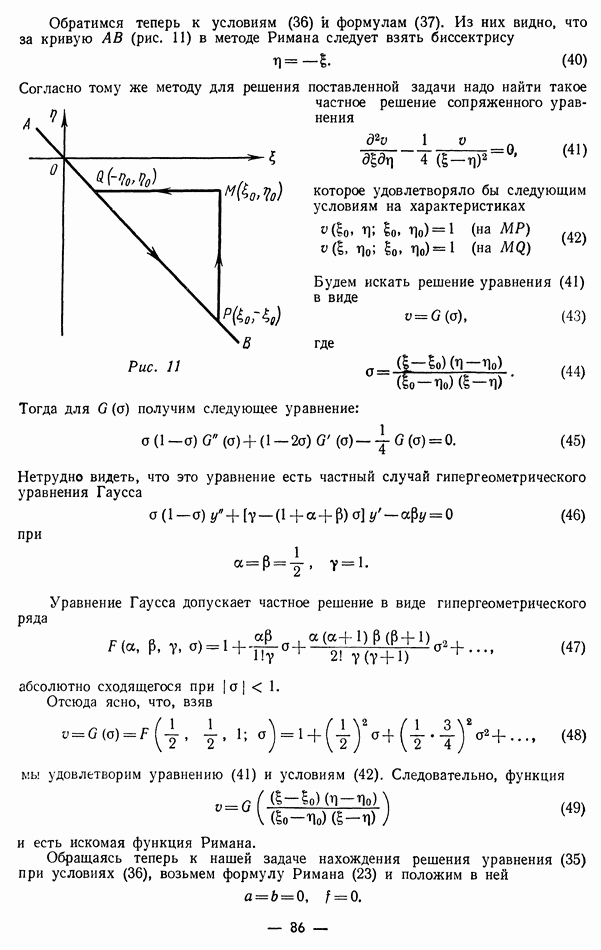
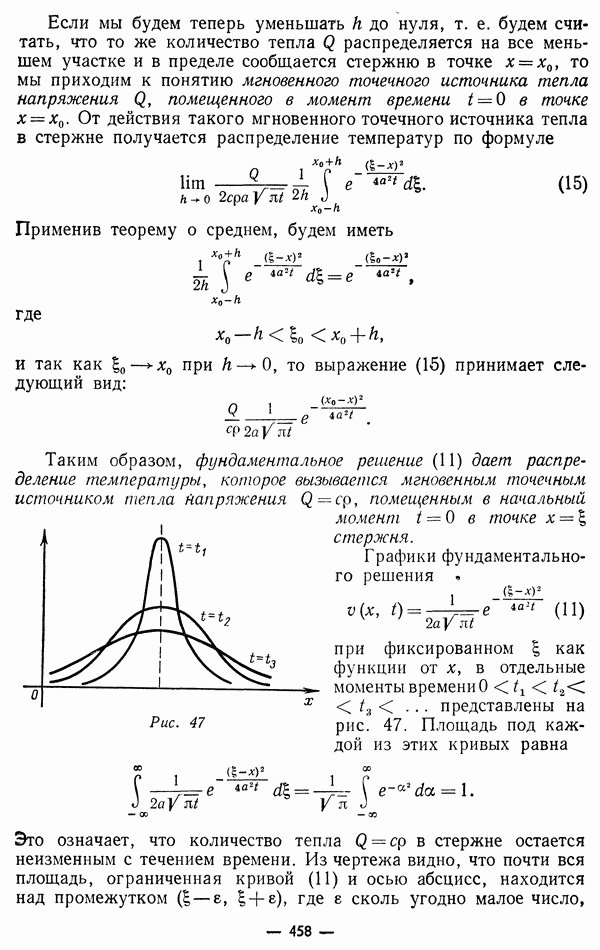
Выясним, какое действие оказывают закрепленные концы струны на ее колебания. Для этого обратимся к полуплоскости  Ввиду ограниченности струны надо рассматривать только полосу верхней полуплоскости
Ввиду ограниченности струны надо рассматривать только полосу верхней полуплоскости  заключающуюся между прямыми
заключающуюся между прямыми  (рис. 4). Проведем через точки
(рис. 4). Проведем через точки  характеристики до встречи с противоположными границами полосы и т. д. Мы разобьем, таким образом, полосу на области (I), (II), (III), ...
характеристики до встречи с противоположными границами полосы и т. д. Мы разобьем, таким образом, полосу на области (I), (II), (III), ...
Точки области (I) соответствуют тем моментам времени  когда к точкам х струны доходят прямая и обратная волны, вошедшие в начальный момент времени из внутренних точек струны. Следовательно, фиктивно добавленные бесконечные части струны еще на процесс колебания не влияют.
когда к точкам х струны доходят прямая и обратная волны, вошедшие в начальный момент времени из внутренних точек струны. Следовательно, фиктивно добавленные бесконечные части струны еще на процесс колебания не влияют.

Рис. 4
Точки вне области (I) соответствуют тем моментам времени когда к точкам х струны доходят уже волны, вышедшие в начальный момент времени из фиктивной части струны. Возьмем, например, точку  в области (II). Так как
в области (II). Так как

то в этой точке имеются две волны: одна — прямая, дошедшая от начально возмущенной точки  струны с абсциссой
струны с абсциссой  другая - обратная из точки
другая - обратная из точки  с абсциссой
с абсциссой  причем в данном случае
причем в данном случае  есть реальная точка струны,
есть реальная точка струны,  фиктивная. Нетрудно заменить ее реальной точкой, заметив, что, в силу (18),
фиктивная. Нетрудно заменить ее реальной точкой, заметив, что, в силу (18),

и, таким образом, обратная волна  есть не что иное, как прямая волна —
есть не что иное, как прямая волна —  вышедшая в начальный момент времени из точки
вышедшая в начальный момент времени из точки  (симметричной с
(симметричной с  относительно точки
относительно точки  которая, дойдя до конца струны
которая, дойдя до конца струны  в момент
в момент

изменила свое направление и знак на обратный и к моменту времени  дошла в таком виде до точки
дошла в таком виде до точки 
Таким образом, действие закрепленного конца  свелось к отражению волны смещения, связанному с переменой знака смещения и с сохранением его абсолютной величины.
свелось к отражению волны смещения, связанному с переменой знака смещения и с сохранением его абсолютной величины.
То же явление мы обнаружим и для волн, дошедших до конца  в точках области
в точках области  мы будем иметь две волны: обратную и прямую, отраженную от конца
мы будем иметь две волны: обратную и прямую, отраженную от конца  В точках областей (IV), (V), (VI), ... получим волны, которые претерпели несколько таких отражений от обоих концов струны.
В точках областей (IV), (V), (VI), ... получим волны, которые претерпели несколько таких отражений от обоих концов струны.
Из предыдущих рассуждений следует, что колебание струны, закрепленной на концах, будет периодическим с периодом 
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Уравнение колебаний струны
- § 2. Уравнение колебаний мембраны
- § 3. Уравнения гидродинамики и звуковых волн
- § 4. Уравнение распространения тепла в изотропном твердом теле
- § 5. Задачи, приводящие к уравнению Лапласа
- Глава II. КЛАССИФИКАЦИЯ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
- § 1. Типы уравнений второго порядна
- § 2. Приведение к каноническому виду уравнения второго порядка с постоянными коэффициентами
- § 3. Приведение к каноническому виду уравнения второго порядка с двумя независимыми переменными
- Глава III. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- § 1. Квазилинейные дифференциальные уравнения с двумя независимыми переменными
- § 2. Нелинейные дифференциальные уравнения с двумя независимыми переменными
- § 3. Нелинейные дифференциальные уравнения с n независимыми переменными
- ЧАСТЬ ПЕРВАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 1. Уравнение колебаний струны. Решение Даламбера
- § 2. Понятие об обобщенных решениях
- Глава V. ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
- § 1. Дифференциальное уравнение продольных колебаний однородного стержня постоянного сечения. Начальные и граничные условия
- § 2. Колебания стержня с одним закрепленным концом
- § 3. Продольный удар груза по стержню
- Глава VI. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. Задача Гурса
- § 3. Метод Римана
- § 4. Примеры на приложение метода Римана
- Глава VII. ПРИМЕНЕНИЕ МЕТОДА ХАРАКТЕРИСТИК К ИЗУЧЕНИЮ КОЛЕБАНИЙ В ЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- § 1. Дифференциальные уравнения свободных электрических колебаний
- § 2. Телеграфное уравнение
- § 3. Интегрирование телеграфного уравнения по методу Римана
- § 4. Электрические колебания в бесконечном проводе
- § 5. Колебания в линии, свободной от искажения
- § 6. Граничные условия для провода конечной длины
- Глава VIII. ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. Цилиндрические волны
- § 3. Непрерывная зависимость решения от начальных данных
- § 4. Теорема единственности
- § 5. Неоднородное волновое уравнение
- § 6. Точечный источник
- Глава IX. НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 2. Бихарактеристики
- § 3. Слабый разрыв. Фронт волны
- § 4. Распространение разрывов по лучам
- Глава X. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К ИЗУЧЕНИЮ СВОБОДНЫХ КОЛЕБАНИЙ СТРУН И СТЕРЖНЕЙ
- § 1. Метод Фурье для уравнения свободных колебаний струны
- § 2. Колебания защепленной струны
- § 3. Колебания струны под действием удара
- § 4. Продольные колебания стержня
- § 5. Общая схема метода Фурье
- Глава XI. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТРУН И СТЕРЖНЕЙ
- § 1. Вынужденные колебания струны, закрепленной на концах
- § 2. Вынужденные колебания тяжелого стержня
- § 3. Вынужденные колебания струны с подвижными концами
- § 4. Единственность решения смешанной задачи
- Глава XII. КРУТИЛЬНЫЕ КОЛЕБАНИЯ ОДНОРОДНОГО СТЕРЖНЯ
- § 1. Дифференциальное уравнение крутильных колебаний цилиндрического стержня
- § 2. Колебания стержня с одним прикрепленным диском
- Глава XIII. ФУНКЦИИ БЕССЕЛЯ
- § 1. Уравнение Бесселя
- § 2. Некоторые частные случаи функций Бесселя
- § 3. Ортогональность функций Бесселя и их корни
- § 4. Разложение произвольной функции в ряд по функциям Бесселя
- § 5. Некоторые интегральные представления функций Бесселя
- § 6. Функции Ханкеля
- § 7. Функции Бесселя мнимого аргумента
- Глава XIV. МАЛЫЕ КОЛЕБАНИЯ НИТИ, ПОДВЕШЕННОЙ ЗА ОДИН КОНЕЦ
- § 1. Свободные колебания подвешенной нити
- § 2. Вынужденные колебания подвешенной нити
- Глава XV. МАЛЫЕ РАДИАЛЬНЫЕ КОЛЕБАНИЯ ГАЗА
- § 1. Радиальные колебания газа в сфере
- § 2. Радиальные колебания газа в неограниченной цилиндрической трубке
- Глава XVI. ПОЛИНОМЫ ЛЕЖАНДРА
- § 1. Дифференциальное уравнение Лежандра
- § 2. Ортогональность полиномов Лежандра и их норма
- § 3. Некоторые свойства полиномов Лежандра
- § 4. Интегральные представления полиномов Лежандра
- § 5. Производящая функция
- § 6. Рекуррентные соотношения между полиномами Лежандра и их производными
- § 7. Функция Лежандра второго рода
- § 8. Малые колебания вращающейся струны
- Глава XVII. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К ИССЛЕДОВАНИЮ МАЛЫХ КОЛЕБАНИЙ ПРЯМОУГОЛЬНОЙ И КРУГЛОЙ МЕМБРАНЫ
- § 1. Свободные колебания прямоугольной мембраны
- § 2. Свободные колебания круглой мембраны
- § 3. Метод Фурье в многомерном случае
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- Глава XVIII. ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ, ПРИМЕНЯЕМЫЕ В ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 2. Формулы Остроградского — Гаусса и Грина
- § 3. Преобразование формулы Грина
- § 4. Функции Леви
- § 5. Формула Грина — Стокса
- § 6. Формула Грина — Стокса в случае двух измерений
- § 7. Представление некоторых дифференциальных выражений в ортогональных системах координат
- Глава XIX. УРАВНЕНИЯ ЛАПЛАСА И ПУАССОНА
- § 1. Уравнения Лапласа и Пуассона. Примеры задач, приводящих к уравнению Лапласа
- § 2. Граничные задачи
- § 3. Гармонические функции
- § 4. Единственность решений граничных задач
- § 5. Фундаментальные решения уравнения Лапласа. Основная формула теории гармонических функций
- § 6. Формула Пуассона. Решение задачи Дирихле для шара
- § 7. Функция Грина
- § 8. Гармонические функции на плоскости
- Глава XX. ТЕОРИЯ ПОТЕНЦИАЛА
- § 1. Ньютоновский потенциал
- § 2. Потенциалы разных порядков
- § 3. Мультиполи
- § 4. Разложение потенциала по мультиполям. Сферические функции
- § 5. Потенциалы простого и двойного слоя
- § 6. Поверхности Ляпунова
- § 7. Сходимость инепрерывная зависимость несобственных интегралов от параметров
- § 8. Поведение потенциала простого слоя и его нормальных производных при пересечении слоя
- § 9. Тангенциальные производные потенциала простого слоя и производные по любому направлению
- § 10. Поведение потенциала двойного слоя при пересечении слоя
- § 11. Уровенные распределения
- § 12. Энергия гравитационного поля. Задача Гаусса
- § 13. Поле тяжести. Теорема Стокса
- § 14. Логарифмический потенциал
- Глава XXI. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 1. Построение системы линейно-независимых сферических функций
- § 2. Ортогональность сферических функций
- § 3. Разложение по сферическим функциям
- § 4. Применение сферических функций для решения граничных задач
- § 5. Функция Грина задачи Дирихле для шара
- § 6. Функция Грина задачи Неймана для шара
- Глава XXII. ПРИЛОЖЕНИЕ ТЕОРИИ СФЕРИЧЕСКИХ ФУНКЦИЙ К РЕШЕНИЮ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Электростатический потенциал проводящего шара, разделенного слоем диэлектрика на два полушария
- § 2. Задача о стационарном распределении температуры в шаре
- § 3. Задача о распределении электричества на индуктивно заряженном шаре
- § 4. Обтекание шара потоком несжимаемой жидкости
- Глава XXIII. ГРАВИТАЦИОННЫЕ ВОЛНЫ НА ПОВЕРХНОСТИ ЖИДКОСТИ
- § 2. Двумерные волны в бассейне ограниченной глубины
- § 3. Кольцевые волны
- § 4. Метод станционарной фазы
- Глава XXIV. УРАВНЕНИЕ ГЕЛЬМГОЛЬЦА
- § 1. Связь уравнения Гельмгольца с некоторыми уравнениями гиперболического и параболического типов
- § 2. Сферически симметричные решения уравнения Гельмгольца в ограниченной области
- § 3. Собственные числа и собственные функции граничной задачи общего вида. Разложения по собственным функциям
- § 4. Разделение переменных в уравнении Гельмгольца в цилиндрических и сферических координатах
- § 5. Сферически симметричные решения уравнения Гельмгольца в бесконечной области
- § 6. Интегральные формулы
- § 7. Разложения в ряды по частным решениям уравнения Гельмгольца в бесконечной области
- § 8. Вопросы единственности решений внешних граничных задач для уравнения Гельмгольца
- Глава XXV. ИЗЛУЧЕНИЕ И РАССЕЯНИЕ ЗВУКА
- § 1. Основные зависимости для звуковых полей
- § 2. Звуковое поле вибрирующего цилиндра
- § 3. Звуковое поле пульсирующего шара. Точечный источник
- § 4. Излучение из отверстия в плоском экране
- § 5. Звуковое поле при произвольном колебании поверхности шара
- § 6. Исследование поля шара при произвольном колебании его поверхности. Акустические или колебательные мультиполи
- § 7. Рассеяние звука
- ДОПОЛНЕНИЕ К ЧАСТИ ВТОРОЙ. СВЕДЕНИЯ ОБ УРАВНЕНИЯХ ЭЛЛИПТИЧЕСКОГО ТИПА ОБЩЕГО ВИДА
- § 1. Общий вид уравнения эллиптического типа
- § 2. Основные граничные задачи
- § 3. Сопряженные граничные задачи
- § 4. Фундаментальные решения. Функция Грина
- § 5. Теоремы единственности
- § 6. Условия разрешимости граничных задач
- ЧАСТЬ ТРЕТЬЯ. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. Первая граничная задача. Теорема о максимуме и минимуме
- § 2. Задача Коши
- Глава XXVII. РАСПРОСТРАНЕНИЕ ТЕПЛА В БЕСКОНЕЧНОМ СТЕРЖНЕ
- § 1. Распространение тепла в неограниченном стержне
- § 2. Распространение тепла в полуограниченном стержне
- Глава XXVIII. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ
- § 1. Распространение тепла в ограниченном стержне
- § 2. Неоднородное уравнение теплопроводности
- § 3. Распространение тепла в бесконечном цилиндре
- § 4. Распространение тепла в цилиндре конечных размеров
- § 5. Распространение тепла в однородном шаре
- § 6. Распространение тепла в прямоугольной пластинке
- ЧАСТЬ ЧЕТВЕРТАЯ. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
- Глава XXIX. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 2. Уравнения Лоренца — Максвелла
- § 3. Уравнения Максвелла
- § 4. Уравнения магнитной гидродинамики
- § 5. Потенциалы электромагнитного поля
- § 6. Периодические по времени электромагнитные поля
- § 7. Условия на бесконечности и граничные условия
- § 8. Представление электромагнитного поля с помощью двух скалярных функций
- § 9. Теорема единственности
- Глава XXX. НАПРАВЛЯЕМЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 1. Поперечно-электрические, поперечно-магнитные и поперечно-электромагнитные волны
- § 2. Волны между идеально проводящими плоскостями, разделенными диэлектриком
- § 3. Дальнейшее рассмотрение направляемых волн
- § 4. ТМ-волны в волноводе круглого сечения
- § 5. ТЕ-волны в волноводе круглого сечения
- § 6. Волны в коаксиальном кабеле
- § 7. Волны в диэлектрическом стержне
- Глава XXXI. ЭЛЕКТРОМАГНИТНЫЕ РУПОРЫ И РЕЗОНАТОРЫ
- § 1. Секториалькый рупор и секториальный резонатор
- § 2. Сферический резонатор
- Глава XXXII. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА—ЛИУВИЛЛЯ
- § 2. Задача Штурма — Лиувилля
- § 3. Функция Грина
- § 4. Экстремальные свойства собственных функций
- § 5. Разложение по собственным функциям задачи Штурма — Лиувнлля на конечном интервале
- § 6. Сингулярная задача Штурма-Лиувилля
- § 7. Разложение по собственным функциям сингулярной задачи Штурма — Лиувилля на полубесконечном интервале
- § 8. Вычисление спектральной функции (полубесконечный интервал)
- § 9. Разложение по собственным функциям сингулярной задачи Штурма — Лиувилля на интервале, бесконечном в обе стороны
- § 10. Разложение по бесселевым функциям
- Глава XXXIII. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ РЕШЕНИЯ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 2. Условия, обеспечивающие возможность интегрального преобразования
- § 3. Интегральные преобразования в конечных пределах
- § 4. Интегральные преобразования с бесконечными пределами (общий случай)
- § 5. Некоторые часто применяемые преобразования с бесконечными пределами
- Глава XXXIV. ПРИМЕРЫ ПРИМЕНЕНИЯ КОНЕЧНЫХ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- § 1. Колебания тяжелой нити
- § 2. Колебания мембраны
- § 3. Распределение тепла в цилиндрическом стержне
- § 4. Распространение тепла в круглой трубе
- § 5. Поток тепла в шаре
- § 6. Стационарный поток тепла в параллелепипеде
- Глава XXXV. ПРИМЕРЫ ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
- § 1. Задача о колебаниях бесконечной струны
- § 2. Линейный поток тепла в полуограниченном стержне
- § 3. Распределение тепла в цилиндрическом стержне, поверхность которого поддерживается при двух различных температурах
- § 4. Установившееся тепловое состояние бесконечного клина
- Глава XXXVI. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
- § 2. Вертикальный излучатель в однородной среде над идеально проводящей плоскостью
- § 3. Вертикальный излучатель в однородной среде над средой с конечной электропроводностью
- § 4. Магнитная антенна над средой с конечной электропроводностью
- § 5. Поле произвольной системы излучателей
- § 6. Горизонтальный излучатель над средой с конечной электропроводностью
- Глава XXXVII. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
- § 1. Уравнения движения вязкой жидкости
- § 2. Движение вязкой жидкости в полупространстве над вращающимся диском бесконечного радиуса
- § 3. Движение вязкой жидкости в плоском диффузоре