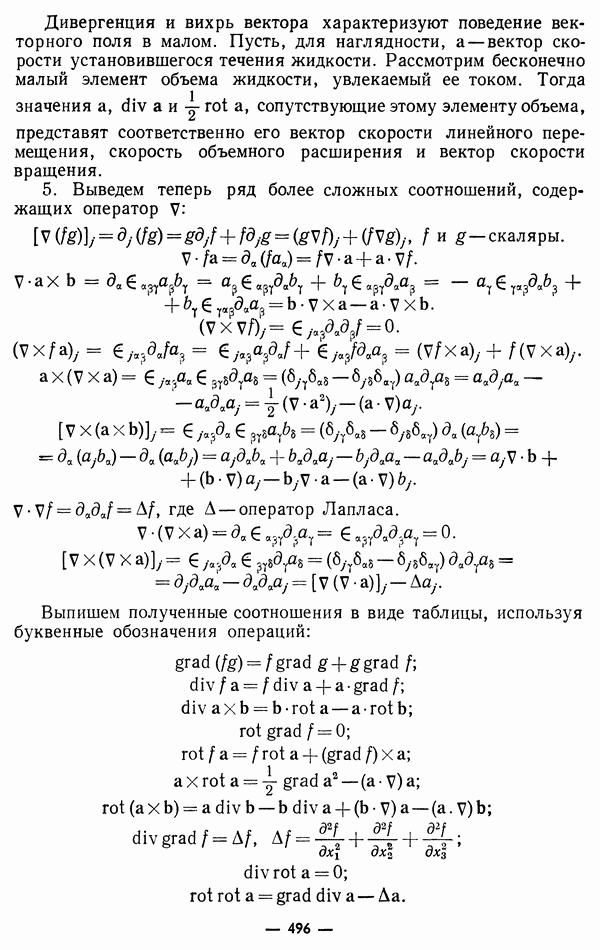| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
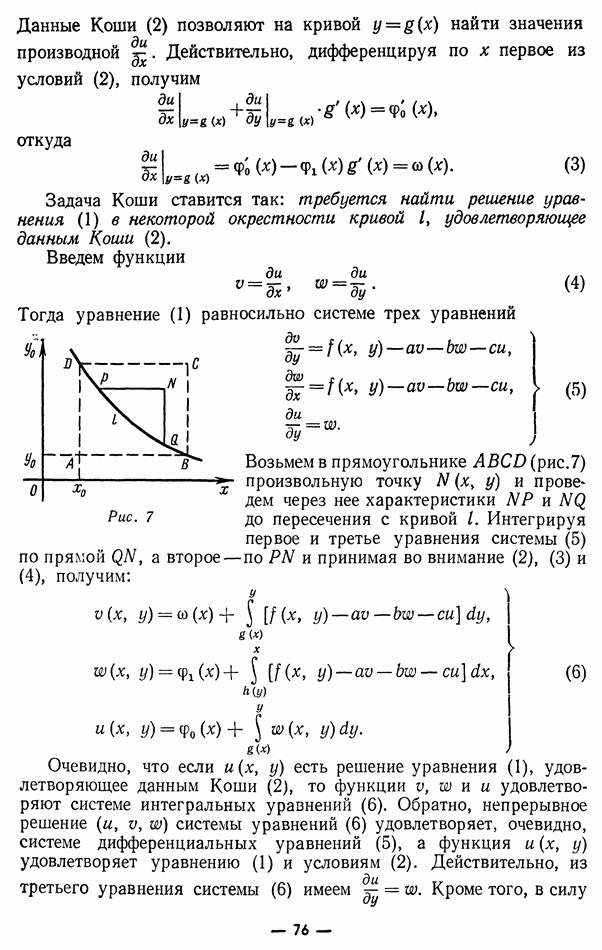
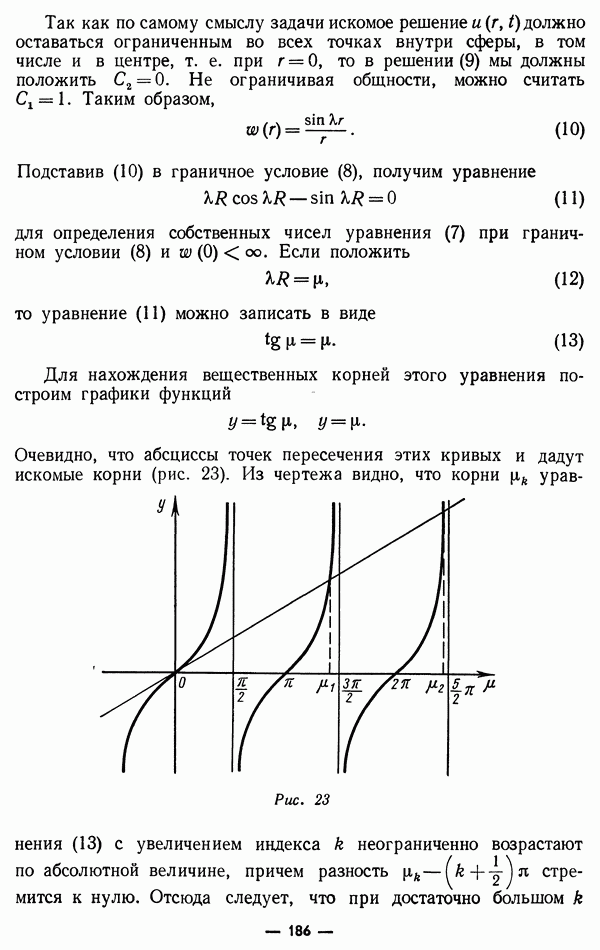
§ 5. Фундаментальные решения уравнения Лапласа. Основная формула теории гармонических функций
Как мы видели в § 1, функция

где  — координаты двух точек
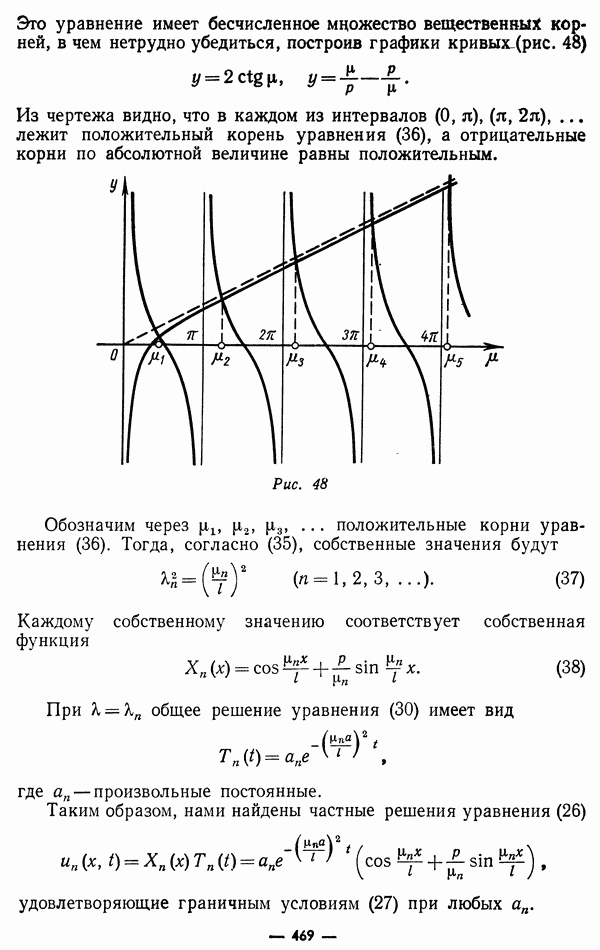
— координаты двух точек  при
при  удовлетворяет уравнению Лапласа. Так как выражение — симметрично относительно координат точек
удовлетворяет уравнению Лапласа. Так как выражение — симметрично относительно координат точек  это справедливо при дифференцировании по координатам как точки так и точки х.
это справедливо при дифференцировании по координатам как точки так и точки х.
При  функция у испытывает бесконечный разрыв.
функция у испытывает бесконечный разрыв.
Если функция  в области V гармонична по координатам точки
в области V гармонична по координатам точки  и непрерывна вместе со своими первыми производными, то функцию
и непрерывна вместе со своими первыми производными, то функцию

будем называть фундаментальным решением уравнения Лапласа в области 
Используя свойства фундаментальных решений, можно вывести важные интегральные формулы, связывающие значение произвольной достаточно гладкой функции в какой-либо точке внутри или на границе области ее определения с совокупностью значений этой функции и ее нормальной производной на границе рассматриваемой области.
Рассмотрим сначала ограниченные области. Пусть V — такая область. Когда точка х лежит вне области У, фундаментальное решение  в этой области гармонично, вследствие чего, положив в формуле Грина (7), гл. XVIII,
в этой области гармонично, вследствие чего, положив в формуле Грина (7), гл. XVIII,

получим:

где через обозначено все пространство, а точка  рассматривается как параметр. Когда точка х лежит внутри области V, то формулу Грина можно применить в области
рассматривается как параметр. Когда точка х лежит внутри области V, то формулу Грина можно применить в области  где
где  лежащий в области
лежащий в области  произвольно малого радиуса
произвольно малого радиуса  с центром в точке х. При этом вместо соотношения (38) получим:
с центром в точке х. При этом вместо соотношения (38) получим:

При  интеграл
интеграл  стремится к несобственному интегралу
стремится к несобственному интегралу  если последний существует. Интеграл
если последний существует. Интеграл  стремится к нулю, поскольку производная непрерывна (по предположению, принятому при выводе формулы Грина) и, следовательно, ограничена, а функция
стремится к нулю, поскольку производная непрерывна (по предположению, принятому при выводе формулы Грина) и, следовательно, ограничена, а функция  растет на
растет на  как
как  тогда как площадь поверхности
тогда как площадь поверхности  убывает как
убывает как  Рассмотрим поведение интеграла от а
Рассмотрим поведение интеграла от а  В силу равенства (37):
В силу равенства (37):

Первый из интегралов в правой части при  обращается в нуль, так как подынтегральное выражение ограничено. Подынтегральное выражение во втором интеграле преобразуем, воспользовавшись тем, что на шаровой поверхности
обращается в нуль, так как подынтегральное выражение ограничено. Подынтегральное выражение во втором интеграле преобразуем, воспользовавшись тем, что на шаровой поверхности  так как внешняя нормаль к границе области
так как внешняя нормаль к границе области  направлена вдоль радиуса
направлена вдоль радиуса  внутрь шара
внутрь шара  . Это даст:
. Это даст:

По теореме о среднем

где  значение функции и в некоторой точке, принадлежащей шару
значение функции и в некоторой точке, принадлежащей шару  Заметив, что интеграл
Заметив, что интеграл  равен площади
равен площади 
поверхности  а при
а при  величина
величина  стремится к
стремится к  так как функция и непрерывна, получим
так как функция и непрерывна, получим

Учтя найденные значения пределов, окончательно получим:

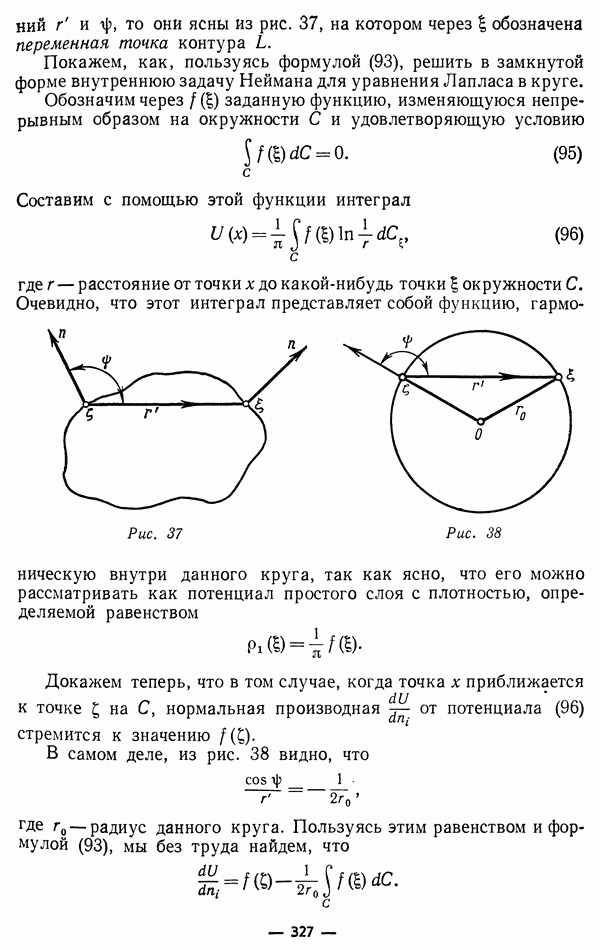
Предположим, наконец, что точка х расположена на граничной поверхности  Применив формулу Грина в области
Применив формулу Грина в области  где
где  лежащая в области V часть шара
лежащая в области V часть шара  описанного малым радиусом
описанного малым радиусом  из точки х, получим
из точки х, получим

где  часть граничной поверхности
часть граничной поверхности  лежащая в шаре
лежащая в шаре  часть поверхности шара лежащая в области
часть поверхности шара лежащая в области  При
При  интеграл в левой части этого соотношения стремится к несобственному интегралу по
интеграл в левой части этого соотношения стремится к несобственному интегралу по  За его значение примем предел правой части, при вычислении которого мы можем повторить все рассуждения предыдущего случая, за тем исключением, что теперь в формуле (39) вместо интеграла
За его значение примем предел правой части, при вычислении которого мы можем повторить все рассуждения предыдущего случая, за тем исключением, что теперь в формуле (39) вместо интеграла  будет фигурировать интеграл
будет фигурировать интеграл  равный площади той части поверхности шара
равный площади той части поверхности шара  которая лежит в области
которая лежит в области 
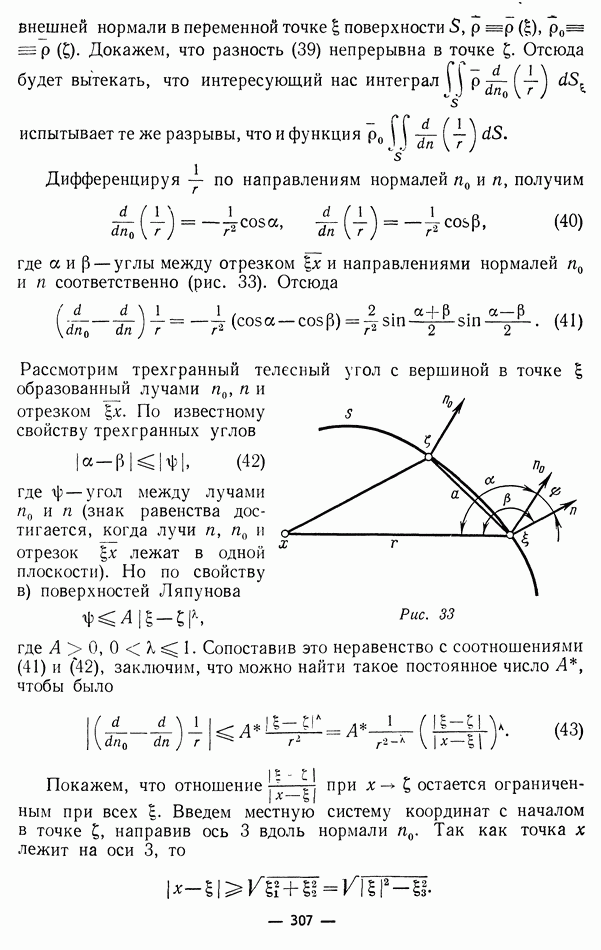
Введем в точке х местную декартову систему координат  направив ось 3 вдоль внешней нормали к поверхности
направив ось 3 вдоль внешней нормали к поверхности  в точке х. По предположению (гл. XVIII, § 1), внутри некоторого шара с центром в точке х уравнение поверхности
в точке х. По предположению (гл. XVIII, § 1), внутри некоторого шара с центром в точке х уравнение поверхности  можно записать в виде
можно записать в виде

где функция  и ее производные первого порядка непрерывны и обращаются в точке х в нуль. Вследствие этого, по определению дифференцируемой функции, в малой окрестности точки х имеет место соотношение:
и ее производные первого порядка непрерывны и обращаются в точке х в нуль. Вследствие этого, по определению дифференцируемой функции, в малой окрестности точки х имеет место соотношение:

где величины и  обращаются в нуль одновременно с
обращаются в нуль одновременно с  Введем сферические координаты
Введем сферические координаты  положив
положив

Подставив эти выражения в найденное выше соотношение, получим

где  функция, ограниченная и обращающаяся в нуль одновременно с
функция, ограниченная и обращающаяся в нуль одновременно с  угловая координата точки на поверхности
угловая координата точки на поверхности  Воспользовавшись этим выражением, придем к следующей оценке интересующего нас интеграла
Воспользовавшись этим выражением, придем к следующей оценке интересующего нас интеграла

где  ограниченная функция, обращающаяся в нуль одновременно с
ограниченная функция, обращающаяся в нуль одновременно с  Вследствие этого
Вследствие этого

что приведет нас к соотношению

Объединив формулы (38), (40) и (42) в одну, можем записать:

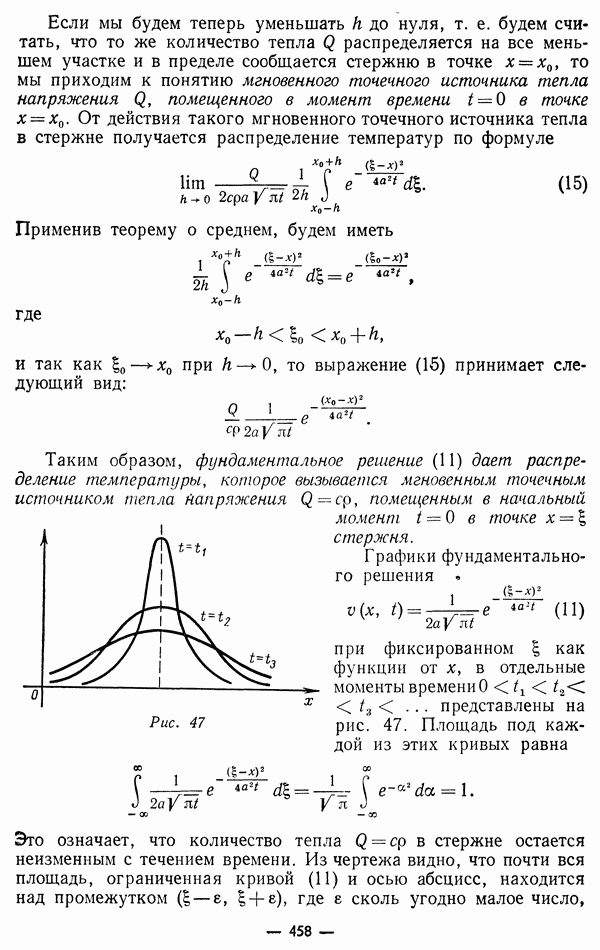
Если функция и гармонична в области У, то формула (43) примет вид:

Это соотношение называют основной формулой теории гармонических функций.
Она переносится и на бесконечные области. Пусть  -бесконечная область с конечной границей
-бесконечная область с конечной границей  а
а  — часть области V, лежащая в шаре
— часть области V, лежащая в шаре  конечного радиуса
конечного радиуса  содержащем границу
содержащем границу  внутри себя. Применив формулу (44) в области К, придем к формуле, левая часть которой по виду будет отличаться от левой части формулы (44) тем, что в ней добавится интеграл
внутри себя. Применив формулу (44) в области К, придем к формуле, левая часть которой по виду будет отличаться от левой части формулы (44) тем, что в ней добавится интеграл

При неограниченном возрастании радиуса шара этот интеграл стремится к нулю, так как, в силу леммы § 3 о поведении гармонической функции на бесконечности и определения фундаментального решения  подынтегральное выражение при этом убывает как
подынтегральное выражение при этом убывает как  тогда как площадь поверхности
тогда как площадь поверхности  шара
шара  растет лишь как
растет лишь как  Перейдя к пределу при
Перейдя к пределу при  снова получим формулу
снова получим формулу

совпадающую с формулой (44) для ограниченных областей.
Опираясь на формулы (44) и (45) покажем, что внутри области гармоничности любая гармоническая функция дифференцируема неограниченное число раз. Для этого положим: 
Фундаментальное решение  в любой области, не содержащей точку
в любой области, не содержащей точку  дифференцируемо по координатам точки х неограниченное число раз, причем результат дифференцирования всякий раз представляет ограниченную функцию переменной
дифференцируемо по координатам точки х неограниченное число раз, причем результат дифференцирования всякий раз представляет ограниченную функцию переменной  Если
Если  внутренняя точка области V, то
внутренняя точка области V, то  когда
когда  Следовательно, интегралы (44) и (45) можно дифференцировать по координатам точки х, как по параметрам, неограниченное число раз. Это доказывает высказанное утверждение, когда гармоническая функция и непрерывна в области V вместе со своими первыми производными. Если непрерывность первых производных не имеет места, высказанное утверждение все же справедливо, так как в формулах (44) и (45) от интегрирования по поверхности
Следовательно, интегралы (44) и (45) можно дифференцировать по координатам точки х, как по параметрам, неограниченное число раз. Это доказывает высказанное утверждение, когда гармоническая функция и непрерывна в области V вместе со своими первыми производными. Если непрерывность первых производных не имеет места, высказанное утверждение все же справедливо, так как в формулах (44) и (45) от интегрирования по поверхности  можно перейти к интегрированию по поверхности
можно перейти к интегрированию по поверхности  лежащей целиком внутри области V и заключающей точку х внутри себя. Так как внутри области гармоничности всякая гармоническая функция дважды дифференцируема, то формула, содержащая
лежащей целиком внутри области V и заключающей точку х внутри себя. Так как внутри области гармоничности всякая гармоническая функция дважды дифференцируема, то формула, содержащая
интеграл по поверхности  будет иметь смысл и, следовательно из нее снова будет следовать неограниченная дифференцируемость функции
будет иметь смысл и, следовательно из нее снова будет следовать неограниченная дифференцируемость функции 
Пусть  — шар, описанный радиусом а из точки
— шар, описанный радиусом а из точки  и целиком лежащий в области гармоничности функции
и целиком лежащий в области гармоничности функции  . На поверхности шара
. На поверхности шара  : Положим как и выше:
: Положим как и выше:  Тогда, в силу соотношения (34), формула (44) примет вид:
Тогда, в силу соотношения (34), формула (44) примет вид:

т. е. среднее арифметическое значение гармонической функции на поверхности шара равно ее значению в его центре. Это утверждение носит название теоремы о среднем значении гармонической функ 
ЗАДАЧИ
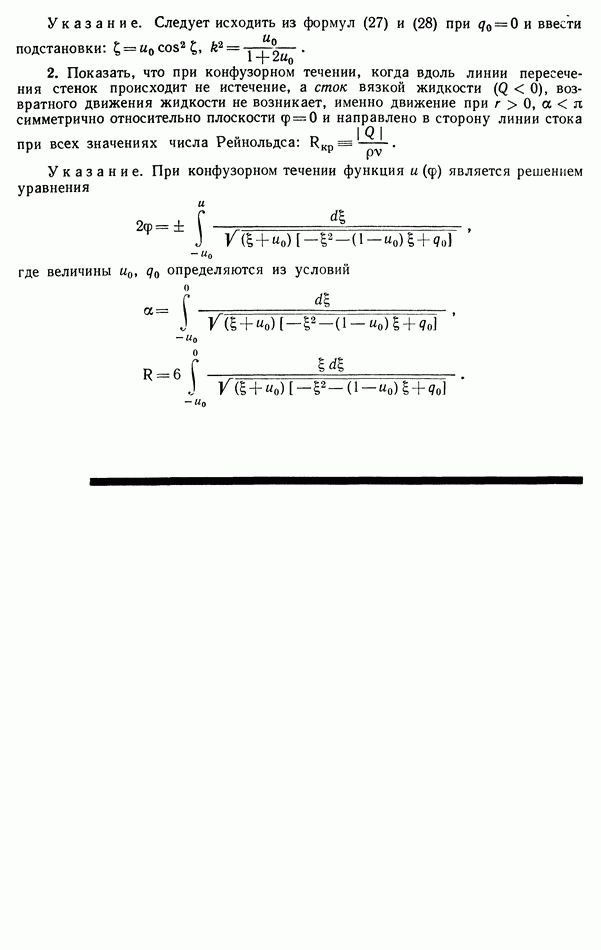
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава I. ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Уравнение колебаний струны
- § 2. Уравнение колебаний мембраны
- § 3. Уравнения гидродинамики и звуковых волн
- § 4. Уравнение распространения тепла в изотропном твердом теле
- § 5. Задачи, приводящие к уравнению Лапласа
- Глава II. КЛАССИФИКАЦИЯ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
- § 1. Типы уравнений второго порядна
- § 2. Приведение к каноническому виду уравнения второго порядка с постоянными коэффициентами
- § 3. Приведение к каноническому виду уравнения второго порядка с двумя независимыми переменными
- Глава III. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- § 1. Квазилинейные дифференциальные уравнения с двумя независимыми переменными
- § 2. Нелинейные дифференциальные уравнения с двумя независимыми переменными
- § 3. Нелинейные дифференциальные уравнения с n независимыми переменными
- ЧАСТЬ ПЕРВАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 1. Уравнение колебаний струны. Решение Даламбера
- § 2. Понятие об обобщенных решениях
- Глава V. ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
- § 1. Дифференциальное уравнение продольных колебаний однородного стержня постоянного сечения. Начальные и граничные условия
- § 2. Колебания стержня с одним закрепленным концом
- § 3. Продольный удар груза по стержню
- Глава VI. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. Задача Гурса
- § 3. Метод Римана
- § 4. Примеры на приложение метода Римана
- Глава VII. ПРИМЕНЕНИЕ МЕТОДА ХАРАКТЕРИСТИК К ИЗУЧЕНИЮ КОЛЕБАНИЙ В ЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- § 1. Дифференциальные уравнения свободных электрических колебаний
- § 2. Телеграфное уравнение
- § 3. Интегрирование телеграфного уравнения по методу Римана
- § 4. Электрические колебания в бесконечном проводе
- § 5. Колебания в линии, свободной от искажения
- § 6. Граничные условия для провода конечной длины
- Глава VIII. ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. Цилиндрические волны
- § 3. Непрерывная зависимость решения от начальных данных
- § 4. Теорема единственности
- § 5. Неоднородное волновое уравнение
- § 6. Точечный источник
- Глава IX. НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 2. Бихарактеристики
- § 3. Слабый разрыв. Фронт волны
- § 4. Распространение разрывов по лучам
- Глава X. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К ИЗУЧЕНИЮ СВОБОДНЫХ КОЛЕБАНИЙ СТРУН И СТЕРЖНЕЙ
- § 1. Метод Фурье для уравнения свободных колебаний струны
- § 2. Колебания защепленной струны
- § 3. Колебания струны под действием удара
- § 4. Продольные колебания стержня
- § 5. Общая схема метода Фурье
- Глава XI. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТРУН И СТЕРЖНЕЙ
- § 1. Вынужденные колебания струны, закрепленной на концах
- § 2. Вынужденные колебания тяжелого стержня
- § 3. Вынужденные колебания струны с подвижными концами
- § 4. Единственность решения смешанной задачи
- Глава XII. КРУТИЛЬНЫЕ КОЛЕБАНИЯ ОДНОРОДНОГО СТЕРЖНЯ
- § 1. Дифференциальное уравнение крутильных колебаний цилиндрического стержня
- § 2. Колебания стержня с одним прикрепленным диском
- Глава XIII. ФУНКЦИИ БЕССЕЛЯ
- § 1. Уравнение Бесселя
- § 2. Некоторые частные случаи функций Бесселя
- § 3. Ортогональность функций Бесселя и их корни
- § 4. Разложение произвольной функции в ряд по функциям Бесселя
- § 5. Некоторые интегральные представления функций Бесселя
- § 6. Функции Ханкеля
- § 7. Функции Бесселя мнимого аргумента
- Глава XIV. МАЛЫЕ КОЛЕБАНИЯ НИТИ, ПОДВЕШЕННОЙ ЗА ОДИН КОНЕЦ
- § 1. Свободные колебания подвешенной нити
- § 2. Вынужденные колебания подвешенной нити
- Глава XV. МАЛЫЕ РАДИАЛЬНЫЕ КОЛЕБАНИЯ ГАЗА
- § 1. Радиальные колебания газа в сфере
- § 2. Радиальные колебания газа в неограниченной цилиндрической трубке
- Глава XVI. ПОЛИНОМЫ ЛЕЖАНДРА
- § 1. Дифференциальное уравнение Лежандра
- § 2. Ортогональность полиномов Лежандра и их норма
- § 3. Некоторые свойства полиномов Лежандра
- § 4. Интегральные представления полиномов Лежандра
- § 5. Производящая функция
- § 6. Рекуррентные соотношения между полиномами Лежандра и их производными
- § 7. Функция Лежандра второго рода
- § 8. Малые колебания вращающейся струны
- Глава XVII. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К ИССЛЕДОВАНИЮ МАЛЫХ КОЛЕБАНИЙ ПРЯМОУГОЛЬНОЙ И КРУГЛОЙ МЕМБРАНЫ
- § 1. Свободные колебания прямоугольной мембраны
- § 2. Свободные колебания круглой мембраны
- § 3. Метод Фурье в многомерном случае
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- Глава XVIII. ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ, ПРИМЕНЯЕМЫЕ В ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 2. Формулы Остроградского — Гаусса и Грина
- § 3. Преобразование формулы Грина
- § 4. Функции Леви
- § 5. Формула Грина — Стокса
- § 6. Формула Грина — Стокса в случае двух измерений
- § 7. Представление некоторых дифференциальных выражений в ортогональных системах координат
- Глава XIX. УРАВНЕНИЯ ЛАПЛАСА И ПУАССОНА
- § 1. Уравнения Лапласа и Пуассона. Примеры задач, приводящих к уравнению Лапласа
- § 2. Граничные задачи
- § 3. Гармонические функции
- § 4. Единственность решений граничных задач
- § 5. Фундаментальные решения уравнения Лапласа. Основная формула теории гармонических функций
- § 6. Формула Пуассона. Решение задачи Дирихле для шара
- § 7. Функция Грина
- § 8. Гармонические функции на плоскости
- Глава XX. ТЕОРИЯ ПОТЕНЦИАЛА
- § 1. Ньютоновский потенциал
- § 2. Потенциалы разных порядков
- § 3. Мультиполи
- § 4. Разложение потенциала по мультиполям. Сферические функции
- § 5. Потенциалы простого и двойного слоя
- § 6. Поверхности Ляпунова
- § 7. Сходимость инепрерывная зависимость несобственных интегралов от параметров
- § 8. Поведение потенциала простого слоя и его нормальных производных при пересечении слоя
- § 9. Тангенциальные производные потенциала простого слоя и производные по любому направлению
- § 10. Поведение потенциала двойного слоя при пересечении слоя
- § 11. Уровенные распределения
- § 12. Энергия гравитационного поля. Задача Гаусса
- § 13. Поле тяжести. Теорема Стокса
- § 14. Логарифмический потенциал
- Глава XXI. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 1. Построение системы линейно-независимых сферических функций
- § 2. Ортогональность сферических функций
- § 3. Разложение по сферическим функциям
- § 4. Применение сферических функций для решения граничных задач
- § 5. Функция Грина задачи Дирихле для шара
- § 6. Функция Грина задачи Неймана для шара
- Глава XXII. ПРИЛОЖЕНИЕ ТЕОРИИ СФЕРИЧЕСКИХ ФУНКЦИЙ К РЕШЕНИЮ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Электростатический потенциал проводящего шара, разделенного слоем диэлектрика на два полушария
- § 2. Задача о стационарном распределении температуры в шаре
- § 3. Задача о распределении электричества на индуктивно заряженном шаре
- § 4. Обтекание шара потоком несжимаемой жидкости
- Глава XXIII. ГРАВИТАЦИОННЫЕ ВОЛНЫ НА ПОВЕРХНОСТИ ЖИДКОСТИ
- § 2. Двумерные волны в бассейне ограниченной глубины
- § 3. Кольцевые волны
- § 4. Метод станционарной фазы
- Глава XXIV. УРАВНЕНИЕ ГЕЛЬМГОЛЬЦА
- § 1. Связь уравнения Гельмгольца с некоторыми уравнениями гиперболического и параболического типов
- § 2. Сферически симметричные решения уравнения Гельмгольца в ограниченной области
- § 3. Собственные числа и собственные функции граничной задачи общего вида. Разложения по собственным функциям
- § 4. Разделение переменных в уравнении Гельмгольца в цилиндрических и сферических координатах
- § 5. Сферически симметричные решения уравнения Гельмгольца в бесконечной области
- § 6. Интегральные формулы
- § 7. Разложения в ряды по частным решениям уравнения Гельмгольца в бесконечной области
- § 8. Вопросы единственности решений внешних граничных задач для уравнения Гельмгольца
- Глава XXV. ИЗЛУЧЕНИЕ И РАССЕЯНИЕ ЗВУКА
- § 1. Основные зависимости для звуковых полей
- § 2. Звуковое поле вибрирующего цилиндра
- § 3. Звуковое поле пульсирующего шара. Точечный источник
- § 4. Излучение из отверстия в плоском экране
- § 5. Звуковое поле при произвольном колебании поверхности шара
- § 6. Исследование поля шара при произвольном колебании его поверхности. Акустические или колебательные мультиполи
- § 7. Рассеяние звука
- ДОПОЛНЕНИЕ К ЧАСТИ ВТОРОЙ. СВЕДЕНИЯ ОБ УРАВНЕНИЯХ ЭЛЛИПТИЧЕСКОГО ТИПА ОБЩЕГО ВИДА
- § 1. Общий вид уравнения эллиптического типа
- § 2. Основные граничные задачи
- § 3. Сопряженные граничные задачи
- § 4. Фундаментальные решения. Функция Грина
- § 5. Теоремы единственности
- § 6. Условия разрешимости граничных задач
- ЧАСТЬ ТРЕТЬЯ. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. Первая граничная задача. Теорема о максимуме и минимуме
- § 2. Задача Коши
- Глава XXVII. РАСПРОСТРАНЕНИЕ ТЕПЛА В БЕСКОНЕЧНОМ СТЕРЖНЕ
- § 1. Распространение тепла в неограниченном стержне
- § 2. Распространение тепла в полуограниченном стержне
- Глава XXVIII. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ
- § 1. Распространение тепла в ограниченном стержне
- § 2. Неоднородное уравнение теплопроводности
- § 3. Распространение тепла в бесконечном цилиндре
- § 4. Распространение тепла в цилиндре конечных размеров
- § 5. Распространение тепла в однородном шаре
- § 6. Распространение тепла в прямоугольной пластинке
- ЧАСТЬ ЧЕТВЕРТАЯ. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
- Глава XXIX. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 2. Уравнения Лоренца — Максвелла
- § 3. Уравнения Максвелла
- § 4. Уравнения магнитной гидродинамики
- § 5. Потенциалы электромагнитного поля
- § 6. Периодические по времени электромагнитные поля
- § 7. Условия на бесконечности и граничные условия
- § 8. Представление электромагнитного поля с помощью двух скалярных функций
- § 9. Теорема единственности
- Глава XXX. НАПРАВЛЯЕМЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 1. Поперечно-электрические, поперечно-магнитные и поперечно-электромагнитные волны
- § 2. Волны между идеально проводящими плоскостями, разделенными диэлектриком
- § 3. Дальнейшее рассмотрение направляемых волн
- § 4. ТМ-волны в волноводе круглого сечения
- § 5. ТЕ-волны в волноводе круглого сечения
- § 6. Волны в коаксиальном кабеле
- § 7. Волны в диэлектрическом стержне
- Глава XXXI. ЭЛЕКТРОМАГНИТНЫЕ РУПОРЫ И РЕЗОНАТОРЫ
- § 1. Секториалькый рупор и секториальный резонатор
- § 2. Сферический резонатор
- Глава XXXII. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА—ЛИУВИЛЛЯ
- § 2. Задача Штурма — Лиувилля
- § 3. Функция Грина
- § 4. Экстремальные свойства собственных функций
- § 5. Разложение по собственным функциям задачи Штурма — Лиувнлля на конечном интервале
- § 6. Сингулярная задача Штурма-Лиувилля
- § 7. Разложение по собственным функциям сингулярной задачи Штурма — Лиувилля на полубесконечном интервале
- § 8. Вычисление спектральной функции (полубесконечный интервал)
- § 9. Разложение по собственным функциям сингулярной задачи Штурма — Лиувилля на интервале, бесконечном в обе стороны
- § 10. Разложение по бесселевым функциям
- Глава XXXIII. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ РЕШЕНИЯ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 2. Условия, обеспечивающие возможность интегрального преобразования
- § 3. Интегральные преобразования в конечных пределах
- § 4. Интегральные преобразования с бесконечными пределами (общий случай)
- § 5. Некоторые часто применяемые преобразования с бесконечными пределами
- Глава XXXIV. ПРИМЕРЫ ПРИМЕНЕНИЯ КОНЕЧНЫХ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- § 1. Колебания тяжелой нити
- § 2. Колебания мембраны
- § 3. Распределение тепла в цилиндрическом стержне
- § 4. Распространение тепла в круглой трубе
- § 5. Поток тепла в шаре
- § 6. Стационарный поток тепла в параллелепипеде
- Глава XXXV. ПРИМЕРЫ ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
- § 1. Задача о колебаниях бесконечной струны
- § 2. Линейный поток тепла в полуограниченном стержне
- § 3. Распределение тепла в цилиндрическом стержне, поверхность которого поддерживается при двух различных температурах
- § 4. Установившееся тепловое состояние бесконечного клина
- Глава XXXVI. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
- § 2. Вертикальный излучатель в однородной среде над идеально проводящей плоскостью
- § 3. Вертикальный излучатель в однородной среде над средой с конечной электропроводностью
- § 4. Магнитная антенна над средой с конечной электропроводностью
- § 5. Поле произвольной системы излучателей
- § 6. Горизонтальный излучатель над средой с конечной электропроводностью
- Глава XXXVII. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
- § 1. Уравнения движения вязкой жидкости
- § 2. Движение вязкой жидкости в полупространстве над вращающимся диском бесконечного радиуса
- § 3. Движение вязкой жидкости в плоском диффузоре