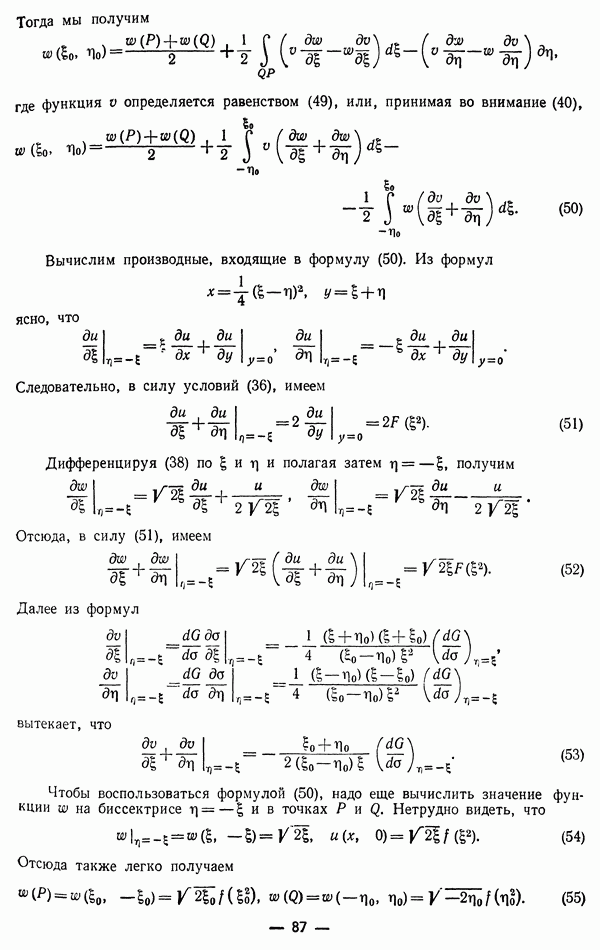| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Уравнения Максвелла
В предыдущем параграфе под  понимались истинные поля, как бы быстро они ни менялись во времени и пространстве. Если к уравнениям (1)-(2) присоединить уравнения движения истинных зарядов—электронов и ионов, то, очевидно,
понимались истинные поля, как бы быстро они ни менялись во времени и пространстве. Если к уравнениям (1)-(2) присоединить уравнения движения истинных зарядов—электронов и ионов, то, очевидно,
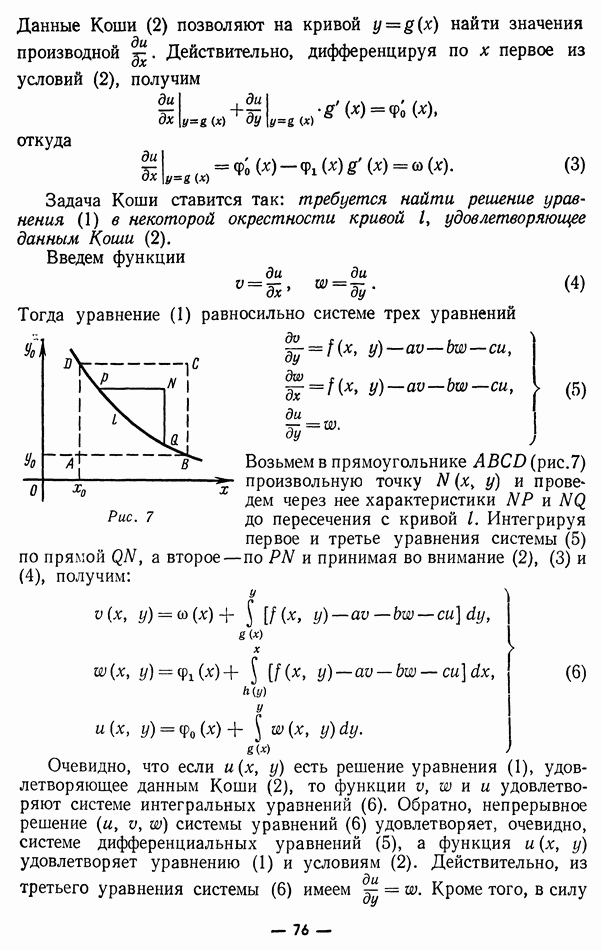
о фактическом решении уравнений не может быть речи. Поэтому возникает необходимость перехода от рассмотрения истинных к рассмотрению макроскопических полей и токов, т. е. полей и токов, усредненных по большому числу элементов микроструктуры вещества (молекул, ячеек кристалла и т. п.). Разумеется, этот подход к делу есть обычная процедура, которая ведет от физики микропроцессов к физике сплошных сред, оперирующей только с макроскопическими величинами.
Задача, таким образом, состоит в том, чтобы из уравнений (1) -(4) для истинного электромагнитного поля получить уравнения для макроскопического электромагнитного поля в среде.
Формальная замена величин, входящих в уравнения Лоренца — Максвелла, их средними значениями приводит к появлению в правых частях уравнений средних значений  плотностей заряда и тока, которые не соответствуют никаким макроскопическим физическим величинам, поскольку, как будет видно из дальнейшего, они не могут быть непосредственно макроскопически измерены.
плотностей заряда и тока, которые не соответствуют никаким макроскопическим физическим величинам, поскольку, как будет видно из дальнейшего, они не могут быть непосредственно макроскопически измерены.
Это объясняется тем, что токи и электрические заряды, являющиеся элементами микроструктуры, в зависимости от их особенностей и характера взаимодействия с другими элементами микроструктуры и электромагнитным полем, формируются в различные макроскопические величины, т. е. проявляются в различных макроскопических свойствах тел.
В среде под воздействием электромагнитного поля возможны три основных процесса:
1. Перенос заряженных частиц. Макроскопическое проявление этого явления называют конвективным электрическим током. Заряженные частицы, могущие перемещаться на макроскопические расстояния, называют свободными зарядами.
2. Смещение заряженных частиц разных знаков, входящих в один элемент структуры, в целом электрически нейтральный (молекула, ячейка кристалла и т. п.). Электрическое поле, смещая связанные в единый элемент структуры разноименные частицы в разных направлениях, вызывает: а) деформацию этого элемента и появление (или изменение имевшегося) дипольного электрического момента, направленного вдоль поля, б) поворот элементов микроструктуры, обладающих дипольным моментом, в направлении, соответствующем ориентации дипольных моментов вдоль электрического поля. Если изменения электромагнитного поля в пространстве и времени не слишком резки, то рассматриваемые процессы в соседних элементах микроструктуры протекают в одном направлении, приводя к электрической поляризации среды,
т. е. к появлению у макроскопически различимых объемов среды дипольных электрических моментов. Электрическая поляризация может быть охарактеризована вектором плотности дипольного момента  называемым также вектором плотности поляризации или просто поляризацией.
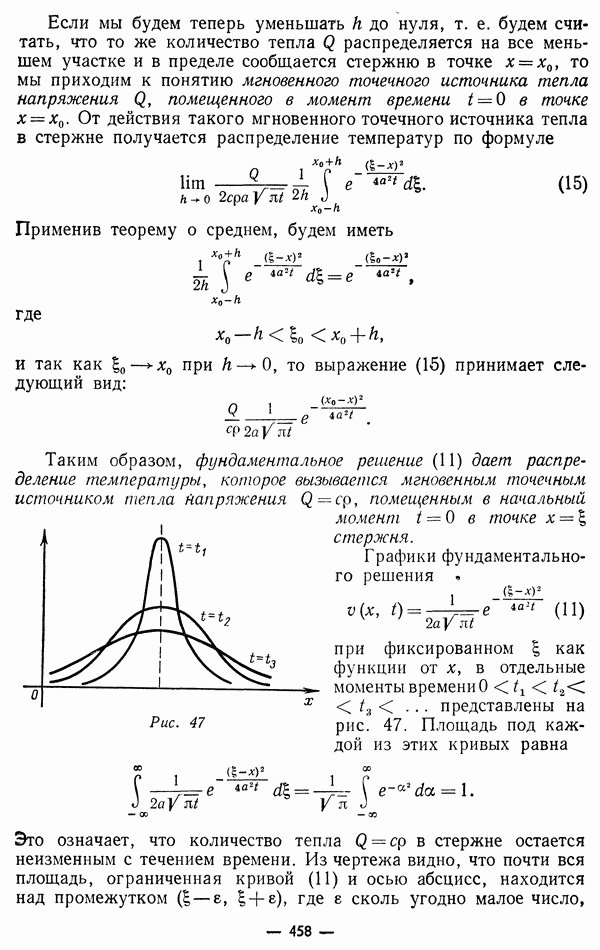
называемым также вектором плотности поляризации или просто поляризацией.
Вектор дипольного момента двух разноименных одинаковых по величине зарядов  равен
равен  где 1 — вектор, соединяющий отрицательный и положительный заряды. При изменении дипольного момента заряды смещаются в противоположных направлениях со скоростью
где 1 — вектор, соединяющий отрицательный и положительный заряды. При изменении дипольного момента заряды смещаются в противоположных направлениях со скоростью  что соответствует току
что соответствует току 
Отсюда очевидно, что изменение плотности дипольного момента сопровождается макроскопическим током с плотностью который называют током поляризации. Конвективный ток при определенных условиях можно отличить от тока поляризации, поскольку последний равен нулю в постоянном электромагнитном поле, сохраняющем поляризацию  неизменной.
неизменной.
3. Поворот дипольных магнитных моментов частиц среды в направлении, соответствующем ориентации магнитных моментов вдоль магнитного поля. Протекание этого процесса для соседних частиц среды в одном направлении приводит к макроскопическому эффекту, который может быть назван магнитной поляризацией или намагничением среды.
Магнитные моменты частиц среды (молекул, атомов, ионов) обусловлены орбитальным движением электронов и наличием спина у элементарных частиц. Формально возникновение магнитных моментов можно рассматривать как следствие существования замкнутых микротоков. Полный ток сквозь любую замкнутую поверхность  в среде, обусловленной замкнутыми токами, очевидно, равен нулю. При усреднении эти токи дадут составляющую
в среде, обусловленной замкнутыми токами, очевидно, равен нулю. При усреднении эти токи дадут составляющую  средней плотности тока, обладающую этим же свойством, т. е.
средней плотности тока, обладающую этим же свойством, т. е.

где  нормаль к
нормаль к  Поэтому поле вектора
Поэтому поле вектора  соленоидально (см. § 1) и его можно представить как вихрь некоторого вектора, который принято обозначать символом
соленоидально (см. § 1) и его можно представить как вихрь некоторого вектора, который принято обозначать символом 

Вектор  называют намагниченностью среды, а вектор
называют намагниченностью среды, а вектор  плотностью тока намагничения.
плотностью тока намагничения.
Таким образом, в общем случае усредненную плотность тока можно представить в виде суммы

плотностей  тока конвекции,
тока конвекции,  тока поляризации и
тока поляризации и  тока намагничения.
тока намагничения.
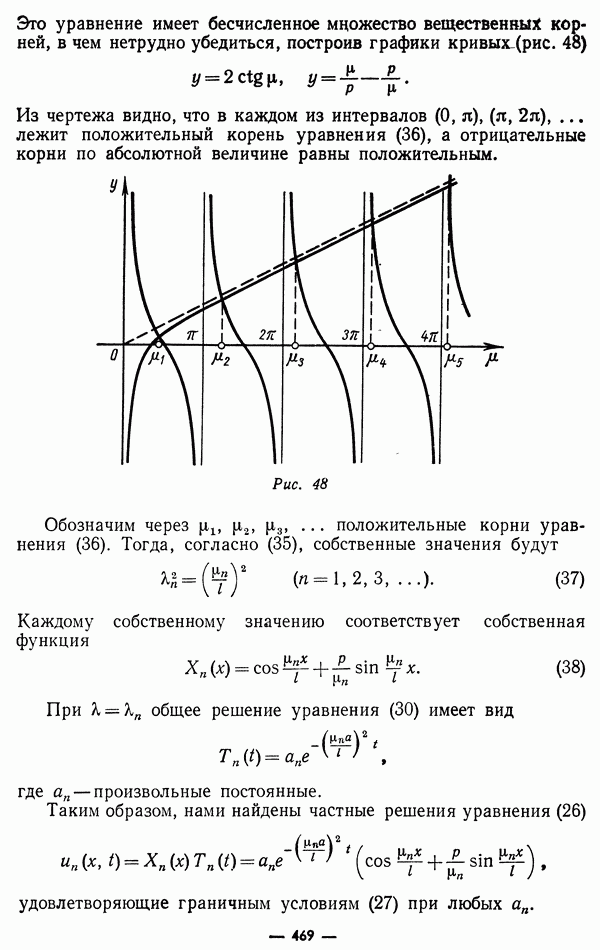
Предположим далее, что число заряженных частиц, которые могут переноситься полем, остается при действии поля неизменным, вследствие чего имеет место закон сохранения

Тогда, усреднив закон сохранения (5), используя (6) и приняв во внимание, что расходимость соленоидального поля равна нулю, получим

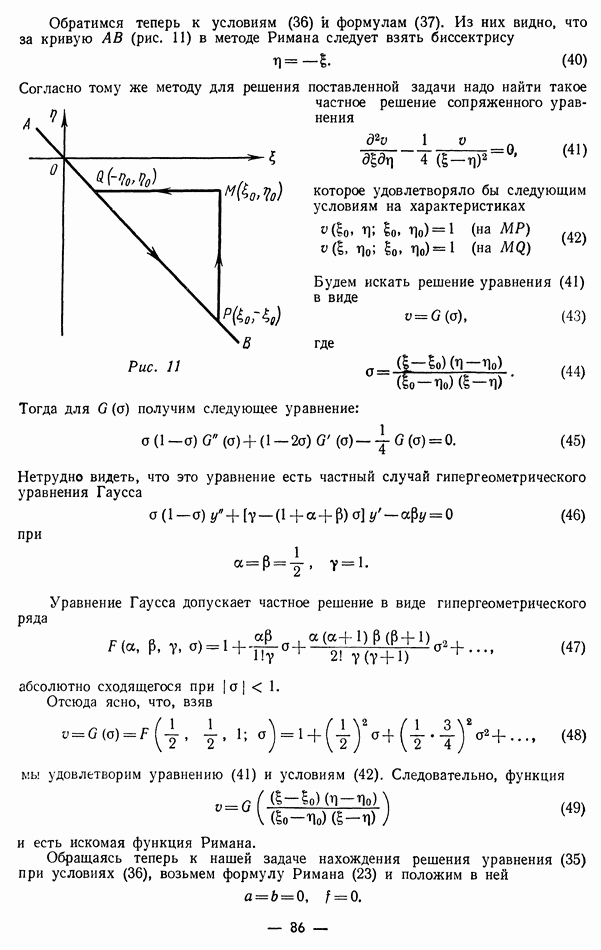
откуда

 плотность электрического заряда, распределение которого не зависит от времени и, следовательно, не меняется под действием поля. Этот заряд может быть интерпретирован как заряд, механически удерживаемый в фиксированных точках пространства. Ниже будем считать
плотность электрического заряда, распределение которого не зависит от времени и, следовательно, не меняется под действием поля. Этот заряд может быть интерпретирован как заряд, механически удерживаемый в фиксированных точках пространства. Ниже будем считать  Восстановление значения
Восстановление значения  может быть достигнуто простой заменой
может быть достигнуто простой заменой 
Используя полученные выражения для  и заменив
и заменив  в системе уравнений Лоренца-Максвелла (1) -(4) усредненными величинами
в системе уравнений Лоренца-Максвелла (1) -(4) усредненными величинами  получим
получим

Вектор  называют вектором электрической индукции, а вектор
называют вектором электрической индукции, а вектор  вектором магнитной индукции. Вектор
вектором магнитной индукции. Вектор  обозначаемый ниже символом
обозначаемый ниже символом  и вектор
и вектор  обозначаемый ниже символом
обозначаемый ниже символом  называют соответственно электрическим и магнитным векторами или, что то же, напряженностями электрического и магнитного полей в среде. Вектор
называют соответственно электрическим и магнитным векторами или, что то же, напряженностями электрического и магнитного полей в среде. Вектор  и скаляр
и скаляр  ниже будут обозначаться символами
ниже будут обозначаться символами  и называться просто плотностями тока и заряда. Выразим более наглядно произведенную замену обозначений:
и называться просто плотностями тока и заряда. Выразим более наглядно произведенную замену обозначений:

В этих обозначениях существует некоторая исторически сложившаяся непоследовательность, поскольку усредненными значениями истинных полей являются векторы, обозначаемые символами  тогда как вместо В естественно было бы писать
тогда как вместо В естественно было бы писать 
векторами, включающими индуцированные поля  являются векторы, обозначаемые символами
являются векторы, обозначаемые символами  тогда как символ
тогда как символ  было бы естественней отнести к усредненному истинному полю. Та же несообразность и в названиях: средними значениями истинных напряженностей являются электрический вектор и вектор магнитной индукции, тогда как индуцированные поля включают вектор электрической индукции и магнитный вектор. Что же касается до использования обозначений
было бы естественней отнести к усредненному истинному полю. Та же несообразность и в названиях: средними значениями истинных напряженностей являются электрический вектор и вектор магнитной индукции, тогда как индуцированные поля включают вектор электрической индукции и магнитный вектор. Что же касается до использования обозначений  совпадающих с обозначениями в (1) -(4), но имеющих иной смысл, то это практически при некоторой осмотрительности не ведет к недоразумениям.
совпадающих с обозначениями в (1) -(4), но имеющих иной смысл, то это практически при некоторой осмотрительности не ведет к недоразумениям.
Усредненные уравнения Лоренца-Максвелла называют уравнениями Максвелла. В новых обозначениях (7) они имеют вид:

Можно показать, что все входящие в эти уравнения величины могут быть независимо измерены макроскопическими методами и, следовательно, имеют физический смысл, как макроскопические величины.
В отсутствии поляризующейся среды  и уравнения Максвелла приобретают вид уравнений (1) -(4).
и уравнения Максвелла приобретают вид уравнений (1) -(4).
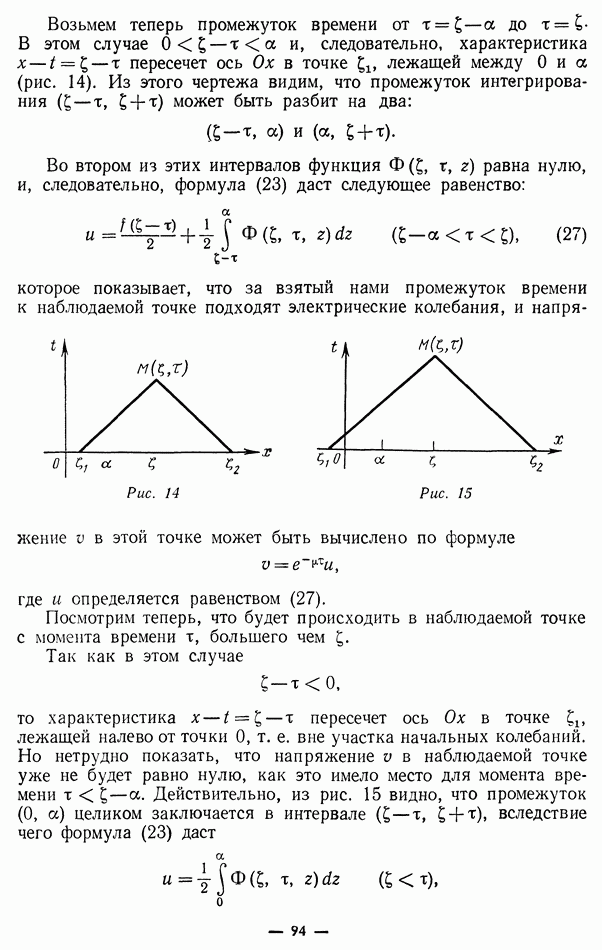
Из уравнений Максвелла, так же как из уравнений Лоренца — Максвелла, следует закон сохранения электрического заряда в форме (5) и, наоборот, из уравнений (5) и (9) с точностью до константы интегрирования следует уравнение (10). Аналогично из (8) следует, что  следовательно, уравнение (11) определяет лишь константу интегрирования. Поэтому, как и в отношении уравнений Лоренца-Максвелла, можно сказать, что, по существу, уже два первых уравнения Максвелла (8) и (9) образуют полную систему уравнений электромагнитного поля, уравнения же (10) и (11), являясь следствием закона сохранения электрического заряда и отсутствия магнитного заряда, выражают ограничения на возможные распределения электромагнитного поля в пространстве, что должно быть учтено при задании начальных условий.
следовательно, уравнение (11) определяет лишь константу интегрирования. Поэтому, как и в отношении уравнений Лоренца-Максвелла, можно сказать, что, по существу, уже два первых уравнения Максвелла (8) и (9) образуют полную систему уравнений электромагнитного поля, уравнения же (10) и (11), являясь следствием закона сохранения электрического заряда и отсутствия магнитного заряда, выражают ограничения на возможные распределения электромагнитного поля в пространстве, что должно быть учтено при задании начальных условий.
Система (8) -(9) содержит шесть уравнений для пятнадцати компонент векторов  В действительности, из рассмотрения процессов поляризации и возникновения тока следует, что между векторами
В действительности, из рассмотрения процессов поляризации и возникновения тока следует, что между векторами  между векторами
между векторами  а также между векторами
а также между векторами  должны существовать
должны существовать
функциональные связи, вследствие чего из этих пяти векторов только два независимы; за них принимают обычно векторы  Если электромагнитное поле изменяется достаточно медленно, так что процессы поляризации успевают следовать за изменениями поля, то соотношения между рассматриваемыми пятью векторами не зависят от производных этих векторов по времени. Удовлетворяющие этому условию поля будем называть квазистационарными. В подавляющем большинстве сред при
Если электромагнитное поле изменяется достаточно медленно, так что процессы поляризации успевают следовать за изменениями поля, то соотношения между рассматриваемыми пятью векторами не зависят от производных этих векторов по времени. Удовлетворяющие этому условию поля будем называть квазистационарными. В подавляющем большинстве сред при  при отсутствии внешнего макроскопического поля, векторы
при отсутствии внешнего макроскопического поля, векторы  равны нулю. Для таких сред, если, кроме того, они однородны и изотропны в отношении электромагнитных свойств, и квазистационарных полей с хорошей точностью соблюдаются соотношения
равны нулю. Для таких сред, если, кроме того, они однородны и изотропны в отношении электромагнитных свойств, и квазистационарных полей с хорошей точностью соблюдаются соотношения

где  — не зависящие от
— не зависящие от  постоянные, получившие наименования соответственно электрической и магнитной проницаемостей среды. Соотношения (12), (13) перестают быть верными для очень сильных полей, приближающихся к микрополям в среде. Для плотности тока
постоянные, получившие наименования соответственно электрической и магнитной проницаемостей среды. Соотношения (12), (13) перестают быть верными для очень сильных полей, приближающихся к микрополям в среде. Для плотности тока  та же степень приближения, что в (12), (13), дается законом Ома, который может быть сформулирован как утверждение, что плотность тока в данной точке среды пропорциональна силе, с которой усредненное по микроструктуре электромагнитное поле действовало бы в этой точке среды на единичный положительный заряд, движущийся вместе со средой. Если среда неподвижна, то на единичный положительный заряд действует сила, равная напряженности
та же степень приближения, что в (12), (13), дается законом Ома, который может быть сформулирован как утверждение, что плотность тока в данной точке среды пропорциональна силе, с которой усредненное по микроструктуре электромагнитное поле действовало бы в этой точке среды на единичный положительный заряд, движущийся вместе со средой. Если среда неподвижна, то на единичный положительный заряд действует сила, равная напряженности  Если же в рассматриваемой точке среда движется со скоростью
Если же в рассматриваемой точке среда движется со скоростью  то на заряд действует также сила —
то на заряд действует также сила —  обусловленная магнитным полем, так что в общем случае, с учетом (13), закон Ома может быть выражен соотношением
обусловленная магнитным полем, так что в общем случае, с учетом (13), закон Ома может быть выражен соотношением

где  постоянная, называемая электропроводностью среды.
постоянная, называемая электропроводностью среды.
Во многих практических задачах, как об этом упоминалось в предыдущем параграфе, удобно считать, что кроме токов, обусловленных электропроводностью среды, в среде существует еще заданное поле  сторонних токов, создаваемых некоторым известным процессом (например, в антенне передатчика). Заменив в уравнениях Максвелла
сторонних токов, создаваемых некоторым известным процессом (например, в антенне передатчика). Заменив в уравнениях Максвелла  на
на  и подставив в них
и подставив в них  приведем их к виду
приведем их к виду

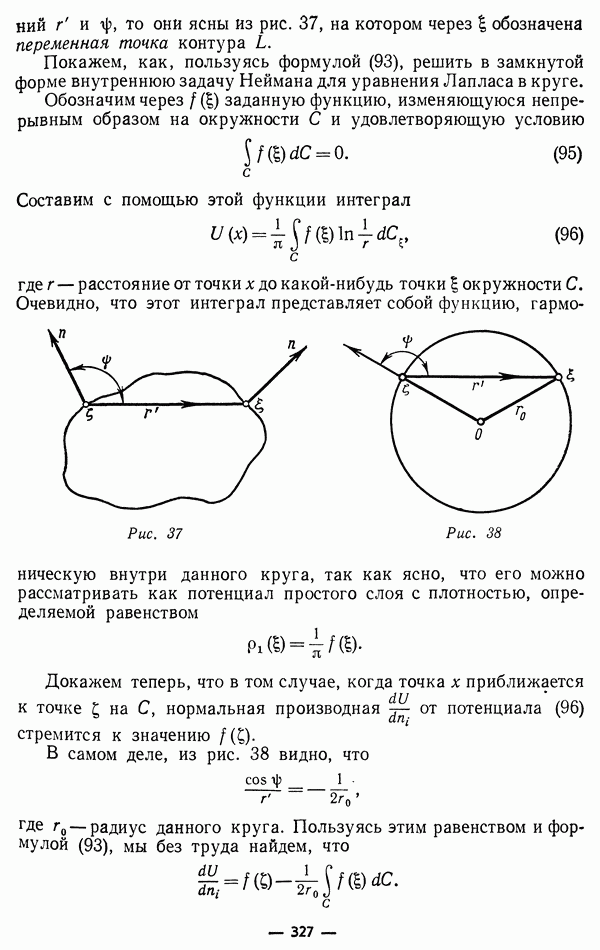
Здесь число неизвестных уже равно числу уравнений, если скорость среды  считать известной.
считать известной.
Существуют два важных класса сред, называемых проводниками и диэлектриками. Проводниками называют среды с высокой электропроводностью. Перемещение зарядов в проводнике, помещенном во внешнее электрическое поле, создает поле, обратное внешнему (поляризация проводника). В частности, как известно из электростатики, статическое электрическое поле в проводнике всегда равно нулю. Если внешнее поле меняется настолько медленно, что процесс поляризации успевает следовать за его изменениями (внешнее поле при этом называют квазистационарным), то внутри проводника существует только электрическое поле, индуцированное изменениями магнитного поля в соответствии с первым из уравнений Максвелла (15). При этом оказывается, что член во втором уравнении (15) очень мал и в пределах точности, обеспечиваемой описанием среды соотношениями (12)-(14), его можно опустить. Применив операцию  ко второму из уравнений (15) и подставив значение
ко второму из уравнений (15) и подставив значение  в первое из них, получим
в первое из них, получим

откуда, ввиду  с помощью формул § 1 найдем, что в средах с высокой электропроводностью
с помощью формул § 1 найдем, что в средах с высокой электропроводностью

где  оператор Лапласа.
оператор Лапласа.
Если скорость среды  то из (16) для каждой из компонент вектора
то из (16) для каждой из компонент вектора  (в прямоугольной прямолинейной системе координат) получается уравнение теплопроводности и диффузии. Таким образом, процесс распространения магнитного поля в электропроводной среде носит тот же характер, что и процессы диффузии и распространения тепла, изученные в части III. В связи с этим ниже они детально рассматриваться не будут.
(в прямоугольной прямолинейной системе координат) получается уравнение теплопроводности и диффузии. Таким образом, процесс распространения магнитного поля в электропроводной среде носит тот же характер, что и процессы диффузии и распространения тепла, изученные в части III. В связи с этим ниже они детально рассматриваться не будут.
Диэлектриками называют среды, не содержащие свободных зарядов и, вследствие этого, не обладающие электропроводностью. Для таких сред уравнения Максвелла (15) приводятся к виду

Продифференцировав одно из этих уравнений по  и подставив результат во второе уравнение, можно разделить переменные и
и подставив результат во второе уравнение, можно разделить переменные и
получить уравнения

Таким образом, электрическое и магнитное поля в диэлектриках (и, в частности, в пустоте) удовлетворяют волновым уравнениям (гл: I, § 1) и, следовательно, процессы распространения электромагнитного поля в диэлектриках носят волновой характер, детально изучавшийся в гл. VIII. Ниже результаты гл. VIII будут дополнены рассмотрением ряда задач, относящихся к стационарным периодическим электромагнитным процессам, играющим исключительно важную роль в технике.
Соотношения  справедливы для однородных и изотропных сред. Из
справедливы для однородных и изотропных сред. Из  легко вывести уравнения для сред, в которых проницаемости меняются от точки к точке. Эти уравнения, однако, практически менее употребительны, так как более сложны для решения. Чаще рассматривается случай, когда две или несколько однородных сред соприкасаются между собой на некоторых граничных поверхностях. Для точек граничных поверхностей соотношения
легко вывести уравнения для сред, в которых проницаемости меняются от точки к точке. Эти уравнения, однако, практически менее употребительны, так как более сложны для решения. Чаще рассматривается случай, когда две или несколько однородных сред соприкасаются между собой на некоторых граничных поверхностях. Для точек граничных поверхностей соотношения  неприменимы и должны быть заменены граничными условиями:
неприменимы и должны быть заменены граничными условиями:

Индексами  здесь отмечены предельные значения векторов поля при приближении к поверхности раздела соответственно со стороны среды
здесь отмечены предельные значения векторов поля при приближении к поверхности раздела соответственно со стороны среды  и среды
и среды  единичный вектор нормали к поверхности раздела, направленный от среды
единичный вектор нормали к поверхности раздела, направленный от среды  к среде
к среде  и рпов — поверхностные плотности тока и заряда. Эти же условия должны быть, естественно, соблюдены и на границах области, занятой электромагнитным полем в однородной среде. Это показывает, что электромагнитное поле, вообще говоря, проникает за любую границу, отделяющую различные среды.
и рпов — поверхностные плотности тока и заряда. Эти же условия должны быть, естественно, соблюдены и на границах области, занятой электромагнитным полем в однородной среде. Это показывает, что электромагнитное поле, вообще говоря, проникает за любую границу, отделяющую различные среды.
Граничные условия (20) являются следствием уравнений Максвелла (8) -(9) и легко выводятся с помощью формул Остроградского-Гаусса и Стокса. В § 7 в несколько преобразованной форме они будут выведены из уравнений Максвелла.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Глава I. ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Уравнение колебаний струны
- § 2. Уравнение колебаний мембраны
- § 3. Уравнения гидродинамики и звуковых волн
- § 4. Уравнение распространения тепла в изотропном твердом теле
- § 5. Задачи, приводящие к уравнению Лапласа
- Глава II. КЛАССИФИКАЦИЯ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
- § 1. Типы уравнений второго порядна
- § 2. Приведение к каноническому виду уравнения второго порядка с постоянными коэффициентами
- § 3. Приведение к каноническому виду уравнения второго порядка с двумя независимыми переменными
- Глава III. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- § 1. Квазилинейные дифференциальные уравнения с двумя независимыми переменными
- § 2. Нелинейные дифференциальные уравнения с двумя независимыми переменными
- § 3. Нелинейные дифференциальные уравнения с n независимыми переменными
- ЧАСТЬ ПЕРВАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 1. Уравнение колебаний струны. Решение Даламбера
- § 2. Понятие об обобщенных решениях
- Глава V. ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
- § 1. Дифференциальное уравнение продольных колебаний однородного стержня постоянного сечения. Начальные и граничные условия
- § 2. Колебания стержня с одним закрепленным концом
- § 3. Продольный удар груза по стержню
- Глава VI. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. Задача Гурса
- § 3. Метод Римана
- § 4. Примеры на приложение метода Римана
- Глава VII. ПРИМЕНЕНИЕ МЕТОДА ХАРАКТЕРИСТИК К ИЗУЧЕНИЮ КОЛЕБАНИЙ В ЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- § 1. Дифференциальные уравнения свободных электрических колебаний
- § 2. Телеграфное уравнение
- § 3. Интегрирование телеграфного уравнения по методу Римана
- § 4. Электрические колебания в бесконечном проводе
- § 5. Колебания в линии, свободной от искажения
- § 6. Граничные условия для провода конечной длины
- Глава VIII. ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. Цилиндрические волны
- § 3. Непрерывная зависимость решения от начальных данных
- § 4. Теорема единственности
- § 5. Неоднородное волновое уравнение
- § 6. Точечный источник
- Глава IX. НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 2. Бихарактеристики
- § 3. Слабый разрыв. Фронт волны
- § 4. Распространение разрывов по лучам
- Глава X. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К ИЗУЧЕНИЮ СВОБОДНЫХ КОЛЕБАНИЙ СТРУН И СТЕРЖНЕЙ
- § 1. Метод Фурье для уравнения свободных колебаний струны
- § 2. Колебания защепленной струны
- § 3. Колебания струны под действием удара
- § 4. Продольные колебания стержня
- § 5. Общая схема метода Фурье
- Глава XI. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТРУН И СТЕРЖНЕЙ
- § 1. Вынужденные колебания струны, закрепленной на концах
- § 2. Вынужденные колебания тяжелого стержня
- § 3. Вынужденные колебания струны с подвижными концами
- § 4. Единственность решения смешанной задачи
- Глава XII. КРУТИЛЬНЫЕ КОЛЕБАНИЯ ОДНОРОДНОГО СТЕРЖНЯ
- § 1. Дифференциальное уравнение крутильных колебаний цилиндрического стержня
- § 2. Колебания стержня с одним прикрепленным диском
- Глава XIII. ФУНКЦИИ БЕССЕЛЯ
- § 1. Уравнение Бесселя
- § 2. Некоторые частные случаи функций Бесселя
- § 3. Ортогональность функций Бесселя и их корни
- § 4. Разложение произвольной функции в ряд по функциям Бесселя
- § 5. Некоторые интегральные представления функций Бесселя
- § 6. Функции Ханкеля
- § 7. Функции Бесселя мнимого аргумента
- Глава XIV. МАЛЫЕ КОЛЕБАНИЯ НИТИ, ПОДВЕШЕННОЙ ЗА ОДИН КОНЕЦ
- § 1. Свободные колебания подвешенной нити
- § 2. Вынужденные колебания подвешенной нити
- Глава XV. МАЛЫЕ РАДИАЛЬНЫЕ КОЛЕБАНИЯ ГАЗА
- § 1. Радиальные колебания газа в сфере
- § 2. Радиальные колебания газа в неограниченной цилиндрической трубке
- Глава XVI. ПОЛИНОМЫ ЛЕЖАНДРА
- § 1. Дифференциальное уравнение Лежандра
- § 2. Ортогональность полиномов Лежандра и их норма
- § 3. Некоторые свойства полиномов Лежандра
- § 4. Интегральные представления полиномов Лежандра
- § 5. Производящая функция
- § 6. Рекуррентные соотношения между полиномами Лежандра и их производными
- § 7. Функция Лежандра второго рода
- § 8. Малые колебания вращающейся струны
- Глава XVII. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К ИССЛЕДОВАНИЮ МАЛЫХ КОЛЕБАНИЙ ПРЯМОУГОЛЬНОЙ И КРУГЛОЙ МЕМБРАНЫ
- § 1. Свободные колебания прямоугольной мембраны
- § 2. Свободные колебания круглой мембраны
- § 3. Метод Фурье в многомерном случае
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- Глава XVIII. ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ, ПРИМЕНЯЕМЫЕ В ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 2. Формулы Остроградского — Гаусса и Грина
- § 3. Преобразование формулы Грина
- § 4. Функции Леви
- § 5. Формула Грина — Стокса
- § 6. Формула Грина — Стокса в случае двух измерений
- § 7. Представление некоторых дифференциальных выражений в ортогональных системах координат
- Глава XIX. УРАВНЕНИЯ ЛАПЛАСА И ПУАССОНА
- § 1. Уравнения Лапласа и Пуассона. Примеры задач, приводящих к уравнению Лапласа
- § 2. Граничные задачи
- § 3. Гармонические функции
- § 4. Единственность решений граничных задач
- § 5. Фундаментальные решения уравнения Лапласа. Основная формула теории гармонических функций
- § 6. Формула Пуассона. Решение задачи Дирихле для шара
- § 7. Функция Грина
- § 8. Гармонические функции на плоскости
- Глава XX. ТЕОРИЯ ПОТЕНЦИАЛА
- § 1. Ньютоновский потенциал
- § 2. Потенциалы разных порядков
- § 3. Мультиполи
- § 4. Разложение потенциала по мультиполям. Сферические функции
- § 5. Потенциалы простого и двойного слоя
- § 6. Поверхности Ляпунова
- § 7. Сходимость инепрерывная зависимость несобственных интегралов от параметров
- § 8. Поведение потенциала простого слоя и его нормальных производных при пересечении слоя
- § 9. Тангенциальные производные потенциала простого слоя и производные по любому направлению
- § 10. Поведение потенциала двойного слоя при пересечении слоя
- § 11. Уровенные распределения
- § 12. Энергия гравитационного поля. Задача Гаусса
- § 13. Поле тяжести. Теорема Стокса
- § 14. Логарифмический потенциал
- Глава XXI. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 1. Построение системы линейно-независимых сферических функций
- § 2. Ортогональность сферических функций
- § 3. Разложение по сферическим функциям
- § 4. Применение сферических функций для решения граничных задач
- § 5. Функция Грина задачи Дирихле для шара
- § 6. Функция Грина задачи Неймана для шара
- Глава XXII. ПРИЛОЖЕНИЕ ТЕОРИИ СФЕРИЧЕСКИХ ФУНКЦИЙ К РЕШЕНИЮ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Электростатический потенциал проводящего шара, разделенного слоем диэлектрика на два полушария
- § 2. Задача о стационарном распределении температуры в шаре
- § 3. Задача о распределении электричества на индуктивно заряженном шаре
- § 4. Обтекание шара потоком несжимаемой жидкости
- Глава XXIII. ГРАВИТАЦИОННЫЕ ВОЛНЫ НА ПОВЕРХНОСТИ ЖИДКОСТИ
- § 2. Двумерные волны в бассейне ограниченной глубины
- § 3. Кольцевые волны
- § 4. Метод станционарной фазы
- Глава XXIV. УРАВНЕНИЕ ГЕЛЬМГОЛЬЦА
- § 1. Связь уравнения Гельмгольца с некоторыми уравнениями гиперболического и параболического типов
- § 2. Сферически симметричные решения уравнения Гельмгольца в ограниченной области
- § 3. Собственные числа и собственные функции граничной задачи общего вида. Разложения по собственным функциям
- § 4. Разделение переменных в уравнении Гельмгольца в цилиндрических и сферических координатах
- § 5. Сферически симметричные решения уравнения Гельмгольца в бесконечной области
- § 6. Интегральные формулы
- § 7. Разложения в ряды по частным решениям уравнения Гельмгольца в бесконечной области
- § 8. Вопросы единственности решений внешних граничных задач для уравнения Гельмгольца
- Глава XXV. ИЗЛУЧЕНИЕ И РАССЕЯНИЕ ЗВУКА
- § 1. Основные зависимости для звуковых полей
- § 2. Звуковое поле вибрирующего цилиндра
- § 3. Звуковое поле пульсирующего шара. Точечный источник
- § 4. Излучение из отверстия в плоском экране
- § 5. Звуковое поле при произвольном колебании поверхности шара
- § 6. Исследование поля шара при произвольном колебании его поверхности. Акустические или колебательные мультиполи
- § 7. Рассеяние звука
- ДОПОЛНЕНИЕ К ЧАСТИ ВТОРОЙ. СВЕДЕНИЯ ОБ УРАВНЕНИЯХ ЭЛЛИПТИЧЕСКОГО ТИПА ОБЩЕГО ВИДА
- § 1. Общий вид уравнения эллиптического типа
- § 2. Основные граничные задачи
- § 3. Сопряженные граничные задачи
- § 4. Фундаментальные решения. Функция Грина
- § 5. Теоремы единственности
- § 6. Условия разрешимости граничных задач
- ЧАСТЬ ТРЕТЬЯ. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. Первая граничная задача. Теорема о максимуме и минимуме
- § 2. Задача Коши
- Глава XXVII. РАСПРОСТРАНЕНИЕ ТЕПЛА В БЕСКОНЕЧНОМ СТЕРЖНЕ
- § 1. Распространение тепла в неограниченном стержне
- § 2. Распространение тепла в полуограниченном стержне
- Глава XXVIII. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ
- § 1. Распространение тепла в ограниченном стержне
- § 2. Неоднородное уравнение теплопроводности
- § 3. Распространение тепла в бесконечном цилиндре
- § 4. Распространение тепла в цилиндре конечных размеров
- § 5. Распространение тепла в однородном шаре
- § 6. Распространение тепла в прямоугольной пластинке
- ЧАСТЬ ЧЕТВЕРТАЯ. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
- Глава XXIX. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 2. Уравнения Лоренца — Максвелла
- § 3. Уравнения Максвелла
- § 4. Уравнения магнитной гидродинамики
- § 5. Потенциалы электромагнитного поля
- § 6. Периодические по времени электромагнитные поля
- § 7. Условия на бесконечности и граничные условия
- § 8. Представление электромагнитного поля с помощью двух скалярных функций
- § 9. Теорема единственности
- Глава XXX. НАПРАВЛЯЕМЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 1. Поперечно-электрические, поперечно-магнитные и поперечно-электромагнитные волны
- § 2. Волны между идеально проводящими плоскостями, разделенными диэлектриком
- § 3. Дальнейшее рассмотрение направляемых волн
- § 4. ТМ-волны в волноводе круглого сечения
- § 5. ТЕ-волны в волноводе круглого сечения
- § 6. Волны в коаксиальном кабеле
- § 7. Волны в диэлектрическом стержне
- Глава XXXI. ЭЛЕКТРОМАГНИТНЫЕ РУПОРЫ И РЕЗОНАТОРЫ
- § 1. Секториалькый рупор и секториальный резонатор
- § 2. Сферический резонатор
- Глава XXXII. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА—ЛИУВИЛЛЯ
- § 2. Задача Штурма — Лиувилля
- § 3. Функция Грина
- § 4. Экстремальные свойства собственных функций
- § 5. Разложение по собственным функциям задачи Штурма — Лиувнлля на конечном интервале
- § 6. Сингулярная задача Штурма-Лиувилля
- § 7. Разложение по собственным функциям сингулярной задачи Штурма — Лиувилля на полубесконечном интервале
- § 8. Вычисление спектральной функции (полубесконечный интервал)
- § 9. Разложение по собственным функциям сингулярной задачи Штурма — Лиувилля на интервале, бесконечном в обе стороны
- § 10. Разложение по бесселевым функциям
- Глава XXXIII. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ РЕШЕНИЯ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 2. Условия, обеспечивающие возможность интегрального преобразования
- § 3. Интегральные преобразования в конечных пределах
- § 4. Интегральные преобразования с бесконечными пределами (общий случай)
- § 5. Некоторые часто применяемые преобразования с бесконечными пределами
- Глава XXXIV. ПРИМЕРЫ ПРИМЕНЕНИЯ КОНЕЧНЫХ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- § 1. Колебания тяжелой нити
- § 2. Колебания мембраны
- § 3. Распределение тепла в цилиндрическом стержне
- § 4. Распространение тепла в круглой трубе
- § 5. Поток тепла в шаре
- § 6. Стационарный поток тепла в параллелепипеде
- Глава XXXV. ПРИМЕРЫ ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
- § 1. Задача о колебаниях бесконечной струны
- § 2. Линейный поток тепла в полуограниченном стержне
- § 3. Распределение тепла в цилиндрическом стержне, поверхность которого поддерживается при двух различных температурах
- § 4. Установившееся тепловое состояние бесконечного клина
- Глава XXXVI. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
- § 2. Вертикальный излучатель в однородной среде над идеально проводящей плоскостью
- § 3. Вертикальный излучатель в однородной среде над средой с конечной электропроводностью
- § 4. Магнитная антенна над средой с конечной электропроводностью
- § 5. Поле произвольной системы излучателей
- § 6. Горизонтальный излучатель над средой с конечной электропроводностью
- Глава XXXVII. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
- § 1. Уравнения движения вязкой жидкости
- § 2. Движение вязкой жидкости в полупространстве над вращающимся диском бесконечного радиуса
- § 3. Движение вязкой жидкости в плоском диффузоре