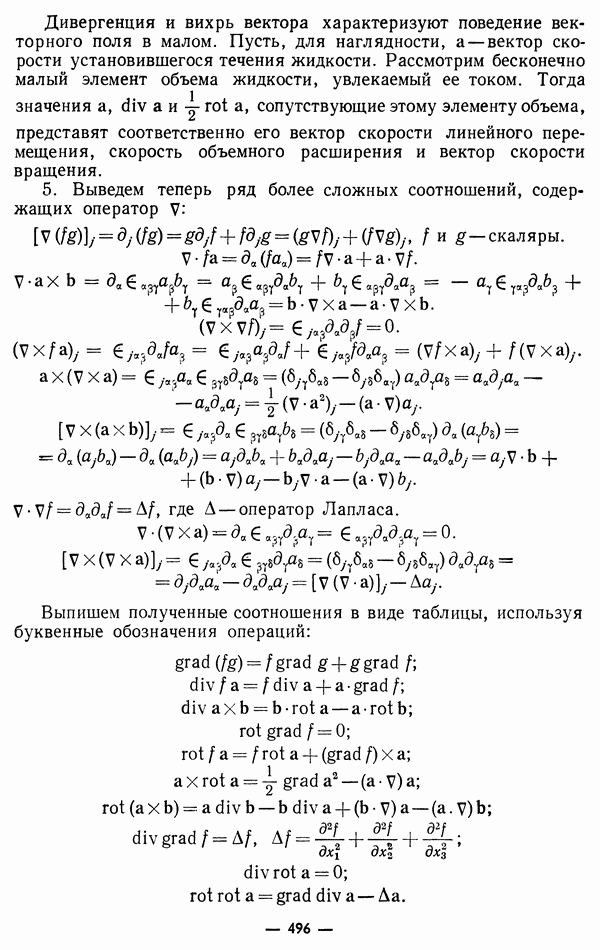ЧАСТЬ ЧЕТВЕРТАЯ. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ

Глава XXIX. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

§ 1. Векторные поля

Этот параграф имеет целью систематизировать и дополнить известные читателю из курса анализа сведения о векторном исчислении.

1. Физическое пространство в математической физике рассматривается как некоторый данный неизменный объект, характеризуемый евклидовой геометрией. В таком пространстве всегда может быть введена ортогональная декартова система координат, которая каждой точке пространства сопоставляет три числа — координаты этой точки, представляющие расстояния этой точки от соответствующих координатных плоскостей. Ниже будут рассматриваться только координатные системы, обладающие этими свойствами. Если одна из них задана, то любая другая может быть получена с помощью: а) движения, т. е. переноса начала и поворота системы координат и б) отражения (в координатной плоскости), как будем называть преобразование, состоящее в изменении направления одной из осей координат. При отражении правая система координат переходит в левую и наоборот. Эти два типа преобразований, т. е. движение и отражение, содержатся в изометрическом преобразовании:

где соответственно старые и новые координаты, постоянные, определяющие перенос начала координат, постоянные коэффициенты, удовлетворяющие условиям:

Из этих условий следует, что определитель преобразования Если то рассматриваемое преобразование представляет движение. Если то преобразование не сводится только к движению, но включает еще и отражение, вследствие чего меняется ориентация системы координат: правая система переходит в левую, а левая — в правую.

Свойства физической среды, очевидно, не могут зависеть от выбора той или иной системы координат. Между тем, в общем случае, в зависимости от выбора системы координат они выражаются различными функциями координат. Для того, чтобы эти функции определяли одно и то же физическое свойство, они должны при преобразованиях координат также преобразовываться по определенному закону.

Пусть, например, некоторая физическая величина в каждой фиксированной точке пространства характеризуется числом (плотность, заряд, температура, концентрация и т. п.). При данном фиксированном выборе системы координат такая величина представляет некоторую принимающую числовые значения функцию трех вещественных переменных координат точек пространства. Пусть система координат преобразована так, что точке, которая в старой системе имела координаты теперь отвечают координаты Так как значение физической величины не зависит от выбора системы координат, то ее зависимость от новых координат представляется функцией удовлетворяющей условию

Функцию, которая при преобразовании координат преобразуется по закону, выраженному этим соотношением, называют скаляром. Область пространства, в каждой точке которой задан скаляр, называют скалярным полем.

Не все физические величины могут быть представлены одной числовой функцией. В частности, это относится к двум важным группам величин. К одной из них принадлежат такие величины, как ускорение, скорость, линейное перемещение, сила и т. п., которые в каждой точке пространства характеризуются не только численным значением, но и направлением в пространстве. Эти

величины за малый промежуток времени всегда проявляются как линейное перемещение и могут быть измерены как линейное перемещение (скорость — перемещение за единицу времени, сила — причина, вызывающая линейное перемещение, она может быть измерена перемещением соответствующего пробного тела и т. д.). К другой группе принадлежат такие величины, как угловое ускорение, угловая скорость, момент сил и т. п. Эти величины за малый промежуток времени всегда проявляются как угловое перемещение (поворот) и могут быть измерены угловым перемещением. Величины этой группы кроме численной величины характеризуются плоскостью поворота и направлением поворота в этой плоскости.

Величины первой группы могут быть изображены направленным отрезком («стрелкой»), длина которого в определенном масштабе соответствует численному значению величины, а направление — направлению, характеризующему данную величину. Чтобы аналитически задать отрезок, соответствующий некоторой физической величине, можно использовать ту же систему координат, что и для описания физического пространства. Именно, зададим направленный отрезок его проекциями на координатные оси. Тем самым физические величины первой группы в данной фиксированной системе координат аналитически будут заданы тремя функциями координат, принимающими числовые значения, равные взятым с соответствующим знаком длинам проекций изображающего отрезка. Эти три функции назовем компонентами физической величины в данной системе координат.

Как именно преобразуются компоненты при преобразовании координат, вытекает из свойств рассматриваемых физических величин. Именно, они должны преобразоваться по тому же закону, как проекции линейных перемещений, т. е. как разность координат двух точек. В свою очередь при поворотах и изменении направления осей разности координат преобразуются по тому же закону, как координаты, и не меняются при переносе начала координат.

Пусть, например, физическая величина рассматриваемого типа, а ее компоненты в некоторой системе координат. В соответствии со сказанным, компоненты величины в новой системе координат определяются соотношениями:

Совокупность трех функций координат, которые при преобразованиях координат преобразуются по закону, выраженному этими соотношениями, т. е. как разности координат, называют полярным вектором или просто вектором. Функции, образующие вектор, называют его компонентами.

Обратимся к величинам второй группы. Аналогично тому, как величины первой группы в данной точке пространства могли быть изображены отрезком, величины второй группы могут быть изображены отнесенной к данной точке пространства плоской площадкой, ограниченной выпуклым контуром с заданным направлением обхода. Площадка предполагается ориентированной параллельно плоскости характеризующего величину углового перемещения, направление обхода контура — выбранным соответственно направлению углового перемещения, а площадь площадки — равной абсолютному численному значению величины. Спроектируем площадку на координатную плоскость, образованную осями 2, 3 системы координат. Направление обхода контура площадки определяет направление обхода контура проекции. Будем говорить, что это направление положительно, если оно соответствует направлению поворота от оси к оси 3 (по кратчайшему угловому расстоянию). Площадь проекции, взятую со знаком «плюс», если направление обхода проекции положительно, и со знаком «минус» в противном случае, назовем первой компонентой физической величины второй группы. Аналогично проекциями на плоскости осей 3, 1 и 1, 2 определим вторую и третью компоненты. При этом за положительное примем направление поворота от оси 3 к оси 1 и от оси 1 к оси Таким образом, в данной фиксированной системе координат физическая величина окажется заданной тремя компонентами, являющимися функциями координат.

Из определения компонент физической величины второй группы следует, что при изменении направления осей системы координат, они преобразуются следующим образом:

При изменении направления одноименной оси компонента не изменяется, так как знак компоненты определяется расположением неодноименных ей осей. При изменении направления одной из неодноименных осей знак компоненты меняется. Заметим, что компоненты вектора преобразуются иначе: они меняют знак при изменении направления одноименной оси и не зависят от направления неодноименных осей. Что же касается поворотов и переноса начала системы координат, то при этих преобразованиях компоненты величин второй группы преобразуются по тому же закону, что и компоненты векторов.

Совокупность трех функций координат, которые при движениях преобразуются как компоненты векторов, а при отражениях — по указанному выше правилу, называют аксиальным или осевым вектором, употребительно также название псевдовектор. Функции, образующие осевой вектор, называют его компонентами.

Легко видеть, что направленный отрезок, проекции которого на оси координат равны компонентам аксиального вектора, перпендикулярен площадке, изображающей аксиальный вектор.

Направление отрезка совпадает с направлением поступательного перемещения правого винта, который вращают в направлении обхода контура площадки, если система координат правая, и в противоположном направлении, если система координат левая. Длина отрезка равна площади площадки. Практически для графического изображения аксиального вектора обычно пользуются таким отрезком («стрелкой»), что позволяет полярные и аксиальные векторы изображать одинаковым образом. Этот способ вполне оправдан, если при описании физических явлений используются только системы координат, которые можно совместить движением, т. е. системы координат одной ориентации, правые или левые. При преобразованных же, включающих отражение, отрезок приходится заменять другим отрезком, соответственно правилу преобразования компонент аксиального вектора.

Сходство полярных и аксиальных векторов в особенности проявляется в общности алгебраических и дифференциальных операций с ними. Различие природы этих векторов сказывается только в одном случае: сложение полярного и аксиального вектора представляет операцию, не имеющую смысла. Практически, когда это не может повести к недоразумениям, определения «полярный» и «аксиальный» всегда опускают, говоря просто о векторах. Область пространства, в каждой точке которой задан полярный или аксиальный вектор, называют векторным полем. Существует простое правило, позволяющее отличить полярные и аксиальные векторы. Изучаемое физическое явление надо зеркально отразить в плоскости, нормальной рассматриваемому вектору. Если направление, в котором протекает явление, при отражении изменяется на обратное, то характеризующая его физическая величина — полярный вектор. В противном случае явление характеризуется аксиальным вектором.

Скаляры и векторы представляют величины, с помощью которых осуществляется инвариантное, т. е. не зависящее от выбора системы координат, описание физических явлений. В этом состоит значение этих величин в физике. Скаляры и векторы являются частным случаем тензоров — величин, широко используемых в физике, но рассмотрение которых выходит за рамки этой книги.

2. Примем в дальнейшем следующие обозначения. Векторы будем обозначать буквами латинского алфавита, набранными жирным шрифтом, компоненты векторов-—теми же, но набранными курсивом буквами с соответствующими индексами. Например, векторы, компоненты вектора а и т. п. Чтобы обозначить компоненту сложного выражения, представляющего вектор, будем заключать это выражение в круглые скобки и снизу, справа, ставить индекс, обозначающий номер компоненты.

В отношении всех векторов, которые будут рассматриваться в этом параграфе, будем предполагать, что они заданы в каждой точке некоторой области, т. е. образуют векторное поле.

Определение вектора, данное в п. 1, без труда обобщается на случай любых криволинейных координат. Однако для простоты в этом параграфе будем предполагать, что компоненты векторов заданы в ортогональной декартовой системе координат. В этом случае уравнения векторных линий поля, т. е. линий, касающихся в каждой точке векторов а поля, имеют вид

где компоненты — вообще говоря, функции координат. Многообразие векторных линий представляет инвариантную характеристику, не зависящую от используемых координат.

3. Введем символику, удобную при выкладках с векторами. Примем обозначение суммирования, предложенное Эйнштейном: если в некотором одночленном выражении один и тот же индекс встречается дважды, то это выражение понимается как сумма выражений того же вида по всем значениям, которые может иметь указанный индекс. Например, вместо опуская символ суммирования, будем писать Индекс, по которому осуществляется суммирование, называют индексом суммирования. Ради наглядности для индексов суммирования ниже используются буквы греческого алфавита, а индексы, по которым суммирование не производится, обозначаются буквами латинского алфавита. Отметим, что замена обозначения индекса суммирования не меняет значения суммы, аналогично тому, как изменение обозначения для переменной интегрирования не меняет значения интеграла. Например, При рассмотрении векторов в трехмерном пространстве возможными значениями индексов являются числа 1, 2, 3, что ниже будет всюду подразумеваться. Введем символ Кронекера

Легко видеть, что

Введем далее символ

Напомним, что четными являются перестановки нечетными — перестановки Круговая

перестановка индексов не меняет четности перестановки. Следовательно,

Легко проверить, что (по греческим индексам суммирование!)

4. Перейдем к определению основных действий с векторами. Суммой а двух векторов называют вектор с компонентами равными сумме одноименных компонент векторов Понятие суммы векторов имеет смысл только тогда, когда оба вектора одной природы, т. е. оба полярные или оба аксиальные.

Для векторов определены три операции, называемые умножением.

Скалярное произведение векторов определяется равенством

Принято обозначение Скалярное произведение двух полярных или двух аксиальных векторов представляет скаляр, т. е. величину, принимающую в каждой точке пространства, где заданы оба вектора, определенное численное значение, независящее от выбора системы координат. Скалярное произведение разноименных векторов имеет разные знаки в правых и левых системах координат. Такие величины называют псевдоскалярами.

Произведение вектора а на скаляр (псевдоскаляр) определяется как вектор с компонентами Если а — полярный (аксиальный) вектор, скаляр (псевдоскаляр), то — полярный вектор. В противном случае — аксиальный вектор.

Векторное произведение двух векторов определяется равенством

Например, Если оба вектора одноименны, то их векторное произведение — аксиальный вектор, в противном случае — полярный.

Смешанное произведение а определяется равенством

Так как значение при круговой перестановке индексов не меняется, то отсюда, в частности, ясно, что при круговой перестановке векторов с значение смешанного произведения

не меняется. Если все векторы одноименны, то смешанное произведение — псевдоскаляр.

Операцию дифференцирования по координате будем обозначать символом так что, например, и Построим символический полярный вектор V с компонентами который назовем дифференциальным оператором V (набла). Говоря, что оператор V есть вектор, подразумевают, что алгебраические операции с символами производятся как с компонентами векторов, в окончательных же выражениях им придается смысл соответствующих дифференцирований. При этом, очевидно, не безразлично, в каком порядке стоят оператор V и остальные символы. Например,

— также дифференциальный оператор (скалярный). Его применение к вектору дает вектор

называемый градиентом вектора по вектору а. Наоборот, выражение а есть, как будет показано ниже, скаляр, или псевдоскаляр.

Сочетание оператора V с тремя операциями умножения дает три оператора: которые символически могут быть обозначены как

Первый из них (градиент) соответствует умножению V на скаляр (псевдоскаляр), второй (дивергенция) — скалярному умножению V на вектор, третий (ротор или вихрь) — векторному умножению V на вектор. Применив эти операторы к скаляру и вектору а соответственно получим:

а) вектор с компонентами

называемый градиентом скаляра

б) скаляр (псевдоскаляр)

называемый дивергенцией или расхождением вектора а,

в) вектор с компонентами

называемый ротором или вихрем вектора а.

В каких случаях определенные выше векторы являются полярными, а в каких — аксиальными, легко разобраться по аналогии с произведениями векторов.

Дивергенция и вихрь вектора характеризуют поведение векторного поля в малом. Пусть, для наглядности, а — вектор скорости установившегося течения жидкости. Рассмотрим бесконечно малый элемент объема жидкости, увлекаемый ее током. Тогда значения сопутствующие этому элементу объема, представят соответственно его вектор скорости линейного перемещения, скорость объемного расширения и вектор скорости вращения.

5. Выведем теперь ряд более сложных соотношений, содержащих оператор V

Выпишем полученные соотношения в виде таблицы, используя буквенные обозначения операций:

6. Рассмотрим далее некоторые интегральные формулы.

Формула Гаусса — Остроградского (1) гл. XVIII в векторных обозначениях имеет вид:

где единичный вектор, направленный вдоль внешней нормали к поверхности ограничивающей объем Произведение есть проекция вектора а на внешнюю нормаль. Интеграл справа называют потоком вектора а сквозь

Вообще, если произвольная, не обязательно замкнутая поверхность, целиком принадлежащая полю, то интеграл

называют потоком вектора а сквозь или числом векторных линий, пересекающих

Если в объеме то в силу формулы Остроградского-Гаусса число векторных линий, входящих в объем У, равно числу линий, выходящих из него. Если в некоторой части поля разобьем ее на области, в которых сохраняет знак. Тогда из формулы Остроградского-Гаусса следует, что в областях, где число векторных линий возрастает, а там, где -убывает.

Об областях, где говорят, что они лишены источников поля. В этих областях векторные линии не могут ни начинаться, ни кончаться.

Формула Стокса (гл. XVIII, § 7) в векторных обозначениях имеет вид:

где единичный вектор, направленный вдоль нормали к кусочно-гладкой поверхности единичный вектор, касающийся границы поверхности Направление выбирается так, что если смотреть из конца какого-либо из векторов то указывает направление обхода контура против часовой стрелки. Интеграл слева представляет поток вихря вектора а, интеграл справа называют циркуляцией вектора а вдоль контура

7. Векторное поле называют безвихревым, если Из формулы Стокса следует, что если контур может быть границей поверхности, целиком принадлежащей полю, то циркуляция вектора а безвихревого поля равна нулю. Если область, занятая полем, односвязна, т. е. любой контур непрерывной деформацией можно стянуть в точку, принадлежащую области, то любой контур может служить границей поверхности, целиком принадлежащей полю,

Векторное поле а называют потенциальным, если существует дифференцируемое скалярное поле такое, что Ввиду того, что потенциальное поле безвихревое. Обратное верно, если область, занятая полем, односвязна. Скаляр называют скалярным потенциалом поля

Векторное поле, дивергенция которого во всех точках равна нулю, называют соленоидальным. Всякое соленоида ьное поле а может быть представлено в виде где А — вектор, называемый векторным потенциалом поля а. Поскольку соленоидальное поле лишено источников, то его векторные линии либо замкнуты, либо имеют бесконечную длину.

Теорема Гельмгольца утверждает, что всякое однозначное и непрерывное во всем пространстве векторное поле представимо в виде

где скалярное поле, векторное поле, т. е. любое достаточно гладкое векторное поле может быть представлено как сумма потенциального и соленоидального полей. Функцию называют скалярным потенциалом у а вектор к векторным потенциалом. Векторный потенциал А можно выбрать так, чтобы Так как то источники а векторного поля всегда выражаются через лапласиан скалярного потенциала и не зависят от векторного потенциала.