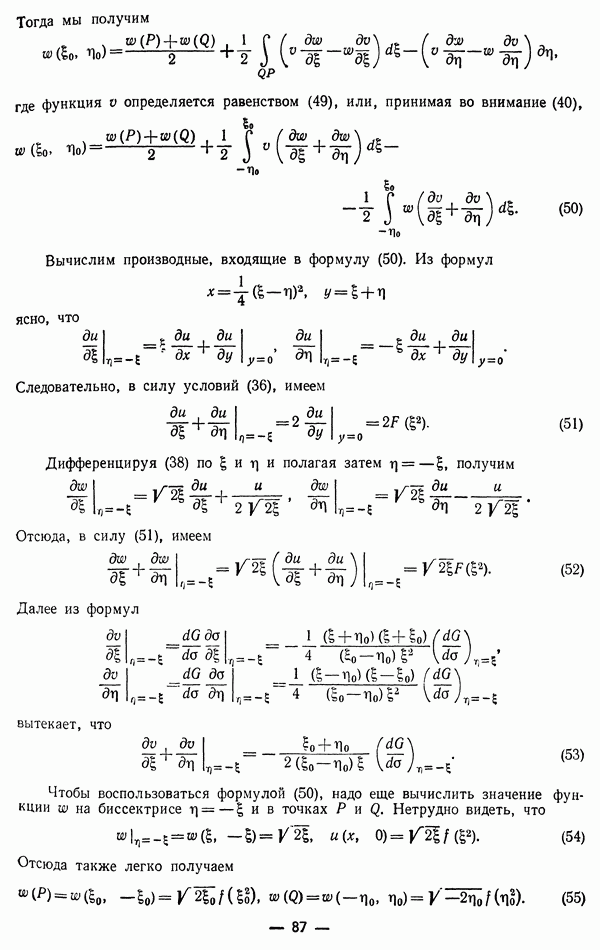| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
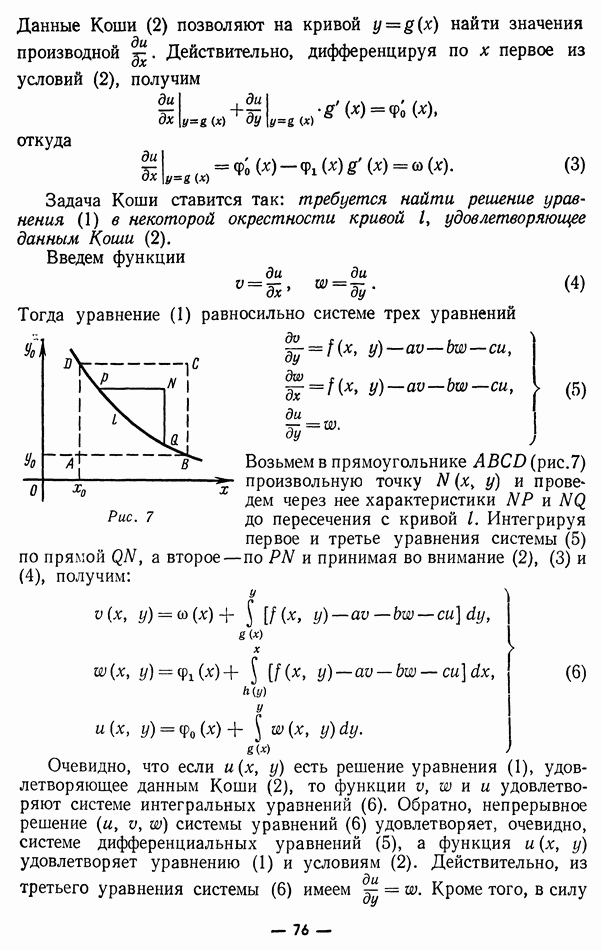
§ 3. Интегрирование телеграфного уравнения по методу Римана
Применим метод Римана к нахождению решения уравнения (9), удовлетворяющего начальным условиям

Прежде всего преобразуем это уравнение к каноническому виду, введя новые независимые переменные  по формулам
по формулам

Тогда уравнение (9) примет вид

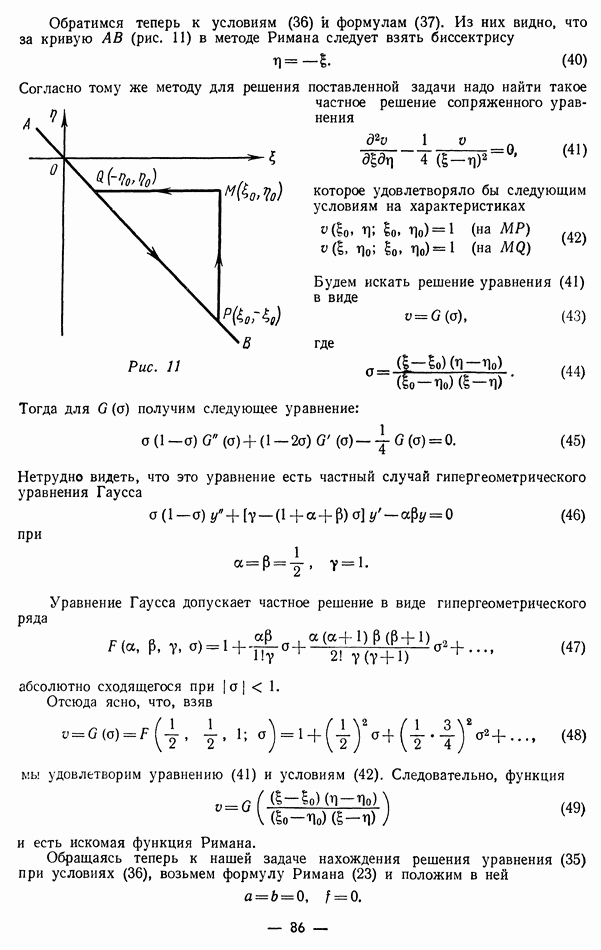
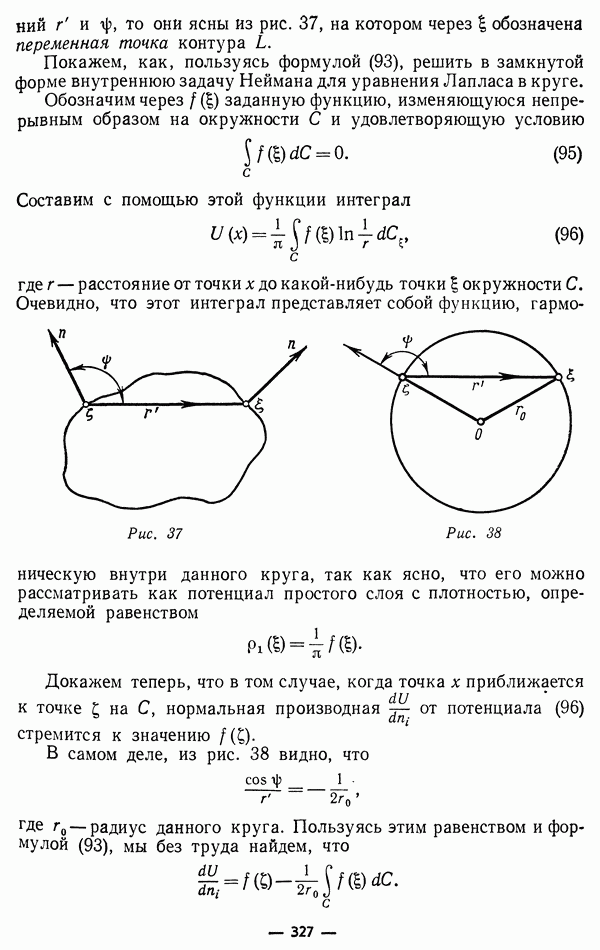
Прямая  в новых переменных будет биссектрисой (рис. 12):
в новых переменных будет биссектрисой (рис. 12):


Рис. 12
Далее, из формул (12) вытекает, что

откуда следует, что

или, в силу начальных условий (11), имеем

а также

Полагая в формуле Римана  и приняв во внимание (14), получим
и приняв во внимание (14), получим

Найдем теперь функцию Римана ту,  Она должна удовлетворять сопряженному уравнению
Она должна удовлетворять сопряженному уравнению

и обращаться на характеристиках  и
и  в единицу. Будем искать решение уравнения (18) в виде
в единицу. Будем искать решение уравнения (18) в виде

Подставив это выражение в уравнение (18) и обозначив через К корень  найдем, что функция
найдем, что функция  удовлетворяет обыкновенному дифференциальному уравнению
удовлетворяет обыкновенному дифференциальному уравнению

частным решением которого является функция Бесселя нулевого порядка:

Отсюда ясно, что, взяв

получим решение уравнения (18), которое обращается на характеристиках  в единицу, так как здесь
в единицу, так как здесь 
Таким образом, функция Римана найдена, она имеет следующий вид:

Отсюда легко получим:

и, следовательно,

Подставив теперь (15) (16) и (22) в формулу (17) и приняв во внимание, что

получим

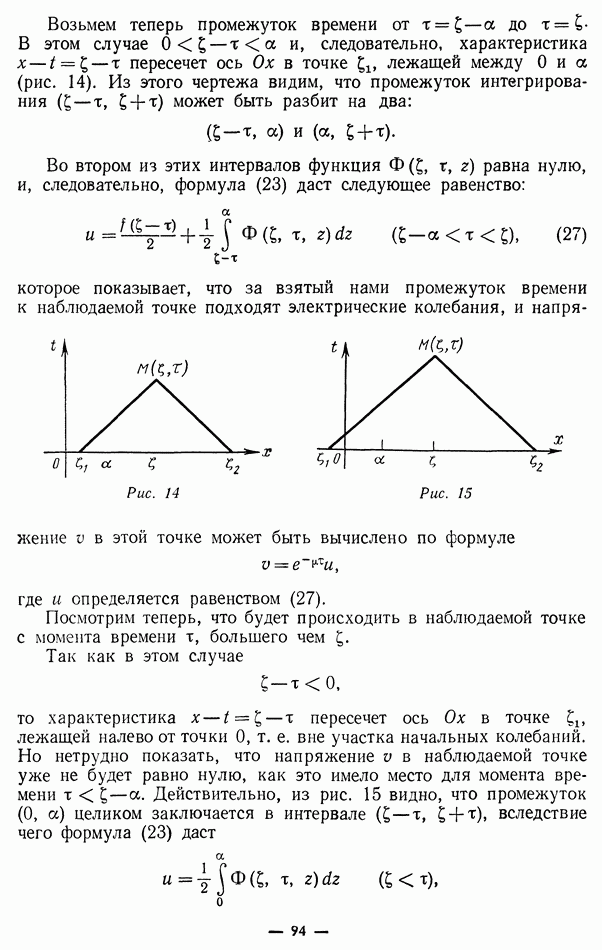
Возвращаясь теперь к старым переменным  (значки О опущены) и вводя новую переменную интегрирования
(значки О опущены) и вводя новую переменную интегрирования  получим
получим

где

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Глава I. ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Уравнение колебаний струны
- § 2. Уравнение колебаний мембраны
- § 3. Уравнения гидродинамики и звуковых волн
- § 4. Уравнение распространения тепла в изотропном твердом теле
- § 5. Задачи, приводящие к уравнению Лапласа
- Глава II. КЛАССИФИКАЦИЯ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
- § 1. Типы уравнений второго порядна
- § 2. Приведение к каноническому виду уравнения второго порядка с постоянными коэффициентами
- § 3. Приведение к каноническому виду уравнения второго порядка с двумя независимыми переменными
- Глава III. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- § 1. Квазилинейные дифференциальные уравнения с двумя независимыми переменными
- § 2. Нелинейные дифференциальные уравнения с двумя независимыми переменными
- § 3. Нелинейные дифференциальные уравнения с n независимыми переменными
- ЧАСТЬ ПЕРВАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 1. Уравнение колебаний струны. Решение Даламбера
- § 2. Понятие об обобщенных решениях
- Глава V. ПРОДОЛЬНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
- § 1. Дифференциальное уравнение продольных колебаний однородного стержня постоянного сечения. Начальные и граничные условия
- § 2. Колебания стержня с одним закрепленным концом
- § 3. Продольный удар груза по стержню
- Глава VI. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА С ДВУМЯ НЕЗАВИСИМЫМИ ПЕРЕМЕННЫМИ
- § 2. Задача Гурса
- § 3. Метод Римана
- § 4. Примеры на приложение метода Римана
- Глава VII. ПРИМЕНЕНИЕ МЕТОДА ХАРАКТЕРИСТИК К ИЗУЧЕНИЮ КОЛЕБАНИЙ В ЭЛЕКТРИЧЕСКИХ ЛИНИЯХ
- § 1. Дифференциальные уравнения свободных электрических колебаний
- § 2. Телеграфное уравнение
- § 3. Интегрирование телеграфного уравнения по методу Римана
- § 4. Электрические колебания в бесконечном проводе
- § 5. Колебания в линии, свободной от искажения
- § 6. Граничные условия для провода конечной длины
- Глава VIII. ВОЛНОВОЕ УРАВНЕНИЕ
- § 2. Цилиндрические волны
- § 3. Непрерывная зависимость решения от начальных данных
- § 4. Теорема единственности
- § 5. Неоднородное волновое уравнение
- § 6. Точечный источник
- Глава IX. НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО ТИПА
- § 2. Бихарактеристики
- § 3. Слабый разрыв. Фронт волны
- § 4. Распространение разрывов по лучам
- Глава X. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К ИЗУЧЕНИЮ СВОБОДНЫХ КОЛЕБАНИЙ СТРУН И СТЕРЖНЕЙ
- § 1. Метод Фурье для уравнения свободных колебаний струны
- § 2. Колебания защепленной струны
- § 3. Колебания струны под действием удара
- § 4. Продольные колебания стержня
- § 5. Общая схема метода Фурье
- Глава XI. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТРУН И СТЕРЖНЕЙ
- § 1. Вынужденные колебания струны, закрепленной на концах
- § 2. Вынужденные колебания тяжелого стержня
- § 3. Вынужденные колебания струны с подвижными концами
- § 4. Единственность решения смешанной задачи
- Глава XII. КРУТИЛЬНЫЕ КОЛЕБАНИЯ ОДНОРОДНОГО СТЕРЖНЯ
- § 1. Дифференциальное уравнение крутильных колебаний цилиндрического стержня
- § 2. Колебания стержня с одним прикрепленным диском
- Глава XIII. ФУНКЦИИ БЕССЕЛЯ
- § 1. Уравнение Бесселя
- § 2. Некоторые частные случаи функций Бесселя
- § 3. Ортогональность функций Бесселя и их корни
- § 4. Разложение произвольной функции в ряд по функциям Бесселя
- § 5. Некоторые интегральные представления функций Бесселя
- § 6. Функции Ханкеля
- § 7. Функции Бесселя мнимого аргумента
- Глава XIV. МАЛЫЕ КОЛЕБАНИЯ НИТИ, ПОДВЕШЕННОЙ ЗА ОДИН КОНЕЦ
- § 1. Свободные колебания подвешенной нити
- § 2. Вынужденные колебания подвешенной нити
- Глава XV. МАЛЫЕ РАДИАЛЬНЫЕ КОЛЕБАНИЯ ГАЗА
- § 1. Радиальные колебания газа в сфере
- § 2. Радиальные колебания газа в неограниченной цилиндрической трубке
- Глава XVI. ПОЛИНОМЫ ЛЕЖАНДРА
- § 1. Дифференциальное уравнение Лежандра
- § 2. Ортогональность полиномов Лежандра и их норма
- § 3. Некоторые свойства полиномов Лежандра
- § 4. Интегральные представления полиномов Лежандра
- § 5. Производящая функция
- § 6. Рекуррентные соотношения между полиномами Лежандра и их производными
- § 7. Функция Лежандра второго рода
- § 8. Малые колебания вращающейся струны
- Глава XVII. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К ИССЛЕДОВАНИЮ МАЛЫХ КОЛЕБАНИЙ ПРЯМОУГОЛЬНОЙ И КРУГЛОЙ МЕМБРАНЫ
- § 1. Свободные колебания прямоугольной мембраны
- § 2. Свободные колебания круглой мембраны
- § 3. Метод Фурье в многомерном случае
- ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
- Глава XVIII. ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ, ПРИМЕНЯЕМЫЕ В ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 2. Формулы Остроградского — Гаусса и Грина
- § 3. Преобразование формулы Грина
- § 4. Функции Леви
- § 5. Формула Грина — Стокса
- § 6. Формула Грина — Стокса в случае двух измерений
- § 7. Представление некоторых дифференциальных выражений в ортогональных системах координат
- Глава XIX. УРАВНЕНИЯ ЛАПЛАСА И ПУАССОНА
- § 1. Уравнения Лапласа и Пуассона. Примеры задач, приводящих к уравнению Лапласа
- § 2. Граничные задачи
- § 3. Гармонические функции
- § 4. Единственность решений граничных задач
- § 5. Фундаментальные решения уравнения Лапласа. Основная формула теории гармонических функций
- § 6. Формула Пуассона. Решение задачи Дирихле для шара
- § 7. Функция Грина
- § 8. Гармонические функции на плоскости
- Глава XX. ТЕОРИЯ ПОТЕНЦИАЛА
- § 1. Ньютоновский потенциал
- § 2. Потенциалы разных порядков
- § 3. Мультиполи
- § 4. Разложение потенциала по мультиполям. Сферические функции
- § 5. Потенциалы простого и двойного слоя
- § 6. Поверхности Ляпунова
- § 7. Сходимость инепрерывная зависимость несобственных интегралов от параметров
- § 8. Поведение потенциала простого слоя и его нормальных производных при пересечении слоя
- § 9. Тангенциальные производные потенциала простого слоя и производные по любому направлению
- § 10. Поведение потенциала двойного слоя при пересечении слоя
- § 11. Уровенные распределения
- § 12. Энергия гравитационного поля. Задача Гаусса
- § 13. Поле тяжести. Теорема Стокса
- § 14. Логарифмический потенциал
- Глава XXI. СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 1. Построение системы линейно-независимых сферических функций
- § 2. Ортогональность сферических функций
- § 3. Разложение по сферическим функциям
- § 4. Применение сферических функций для решения граничных задач
- § 5. Функция Грина задачи Дирихле для шара
- § 6. Функция Грина задачи Неймана для шара
- Глава XXII. ПРИЛОЖЕНИЕ ТЕОРИИ СФЕРИЧЕСКИХ ФУНКЦИЙ К РЕШЕНИЮ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Электростатический потенциал проводящего шара, разделенного слоем диэлектрика на два полушария
- § 2. Задача о стационарном распределении температуры в шаре
- § 3. Задача о распределении электричества на индуктивно заряженном шаре
- § 4. Обтекание шара потоком несжимаемой жидкости
- Глава XXIII. ГРАВИТАЦИОННЫЕ ВОЛНЫ НА ПОВЕРХНОСТИ ЖИДКОСТИ
- § 2. Двумерные волны в бассейне ограниченной глубины
- § 3. Кольцевые волны
- § 4. Метод станционарной фазы
- Глава XXIV. УРАВНЕНИЕ ГЕЛЬМГОЛЬЦА
- § 1. Связь уравнения Гельмгольца с некоторыми уравнениями гиперболического и параболического типов
- § 2. Сферически симметричные решения уравнения Гельмгольца в ограниченной области
- § 3. Собственные числа и собственные функции граничной задачи общего вида. Разложения по собственным функциям
- § 4. Разделение переменных в уравнении Гельмгольца в цилиндрических и сферических координатах
- § 5. Сферически симметричные решения уравнения Гельмгольца в бесконечной области
- § 6. Интегральные формулы
- § 7. Разложения в ряды по частным решениям уравнения Гельмгольца в бесконечной области
- § 8. Вопросы единственности решений внешних граничных задач для уравнения Гельмгольца
- Глава XXV. ИЗЛУЧЕНИЕ И РАССЕЯНИЕ ЗВУКА
- § 1. Основные зависимости для звуковых полей
- § 2. Звуковое поле вибрирующего цилиндра
- § 3. Звуковое поле пульсирующего шара. Точечный источник
- § 4. Излучение из отверстия в плоском экране
- § 5. Звуковое поле при произвольном колебании поверхности шара
- § 6. Исследование поля шара при произвольном колебании его поверхности. Акустические или колебательные мультиполи
- § 7. Рассеяние звука
- ДОПОЛНЕНИЕ К ЧАСТИ ВТОРОЙ. СВЕДЕНИЯ ОБ УРАВНЕНИЯХ ЭЛЛИПТИЧЕСКОГО ТИПА ОБЩЕГО ВИДА
- § 1. Общий вид уравнения эллиптического типа
- § 2. Основные граничные задачи
- § 3. Сопряженные граничные задачи
- § 4. Фундаментальные решения. Функция Грина
- § 5. Теоремы единственности
- § 6. Условия разрешимости граничных задач
- ЧАСТЬ ТРЕТЬЯ. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
- § 1. Первая граничная задача. Теорема о максимуме и минимуме
- § 2. Задача Коши
- Глава XXVII. РАСПРОСТРАНЕНИЕ ТЕПЛА В БЕСКОНЕЧНОМ СТЕРЖНЕ
- § 1. Распространение тепла в неограниченном стержне
- § 2. Распространение тепла в полуограниченном стержне
- Глава XXVIII. ПРИМЕНЕНИЕ МЕТОДА ФУРЬЕ К РЕШЕНИЮ ГРАНИЧНЫХ ЗАДАЧ
- § 1. Распространение тепла в ограниченном стержне
- § 2. Неоднородное уравнение теплопроводности
- § 3. Распространение тепла в бесконечном цилиндре
- § 4. Распространение тепла в цилиндре конечных размеров
- § 5. Распространение тепла в однородном шаре
- § 6. Распространение тепла в прямоугольной пластинке
- ЧАСТЬ ЧЕТВЕРТАЯ. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ
- Глава XXIX. УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- § 2. Уравнения Лоренца — Максвелла
- § 3. Уравнения Максвелла
- § 4. Уравнения магнитной гидродинамики
- § 5. Потенциалы электромагнитного поля
- § 6. Периодические по времени электромагнитные поля
- § 7. Условия на бесконечности и граничные условия
- § 8. Представление электромагнитного поля с помощью двух скалярных функций
- § 9. Теорема единственности
- Глава XXX. НАПРАВЛЯЕМЫЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 1. Поперечно-электрические, поперечно-магнитные и поперечно-электромагнитные волны
- § 2. Волны между идеально проводящими плоскостями, разделенными диэлектриком
- § 3. Дальнейшее рассмотрение направляемых волн
- § 4. ТМ-волны в волноводе круглого сечения
- § 5. ТЕ-волны в волноводе круглого сечения
- § 6. Волны в коаксиальном кабеле
- § 7. Волны в диэлектрическом стержне
- Глава XXXI. ЭЛЕКТРОМАГНИТНЫЕ РУПОРЫ И РЕЗОНАТОРЫ
- § 1. Секториалькый рупор и секториальный резонатор
- § 2. Сферический резонатор
- Глава XXXII. РАЗЛОЖЕНИЕ ПО СОБСТВЕННЫМ ФУНКЦИЯМ ЗАДАЧИ ШТУРМА—ЛИУВИЛЛЯ
- § 2. Задача Штурма — Лиувилля
- § 3. Функция Грина
- § 4. Экстремальные свойства собственных функций
- § 5. Разложение по собственным функциям задачи Штурма — Лиувнлля на конечном интервале
- § 6. Сингулярная задача Штурма-Лиувилля
- § 7. Разложение по собственным функциям сингулярной задачи Штурма — Лиувилля на полубесконечном интервале
- § 8. Вычисление спектральной функции (полубесконечный интервал)
- § 9. Разложение по собственным функциям сингулярной задачи Штурма — Лиувилля на интервале, бесконечном в обе стороны
- § 10. Разложение по бесселевым функциям
- Глава XXXIII. ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ РЕШЕНИЯ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 2. Условия, обеспечивающие возможность интегрального преобразования
- § 3. Интегральные преобразования в конечных пределах
- § 4. Интегральные преобразования с бесконечными пределами (общий случай)
- § 5. Некоторые часто применяемые преобразования с бесконечными пределами
- Глава XXXIV. ПРИМЕРЫ ПРИМЕНЕНИЯ КОНЕЧНЫХ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
- § 1. Колебания тяжелой нити
- § 2. Колебания мембраны
- § 3. Распределение тепла в цилиндрическом стержне
- § 4. Распространение тепла в круглой трубе
- § 5. Поток тепла в шаре
- § 6. Стационарный поток тепла в параллелепипеде
- Глава XXXV. ПРИМЕРЫ ПРИМЕНЕНИЯ ИНТЕГРАЛЬНЫХ ПРЕОБРАЗОВАНИЙ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
- § 1. Задача о колебаниях бесконечной струны
- § 2. Линейный поток тепла в полуограниченном стержне
- § 3. Распределение тепла в цилиндрическом стержне, поверхность которого поддерживается при двух различных температурах
- § 4. Установившееся тепловое состояние бесконечного клина
- Глава XXXVI. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
- § 2. Вертикальный излучатель в однородной среде над идеально проводящей плоскостью
- § 3. Вертикальный излучатель в однородной среде над средой с конечной электропроводностью
- § 4. Магнитная антенна над средой с конечной электропроводностью
- § 5. Поле произвольной системы излучателей
- § 6. Горизонтальный излучатель над средой с конечной электропроводностью
- Глава XXXVII. ДВИЖЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
- § 1. Уравнения движения вязкой жидкости
- § 2. Движение вязкой жидкости в полупространстве над вращающимся диском бесконечного радиуса
- § 3. Движение вязкой жидкости в плоском диффузоре