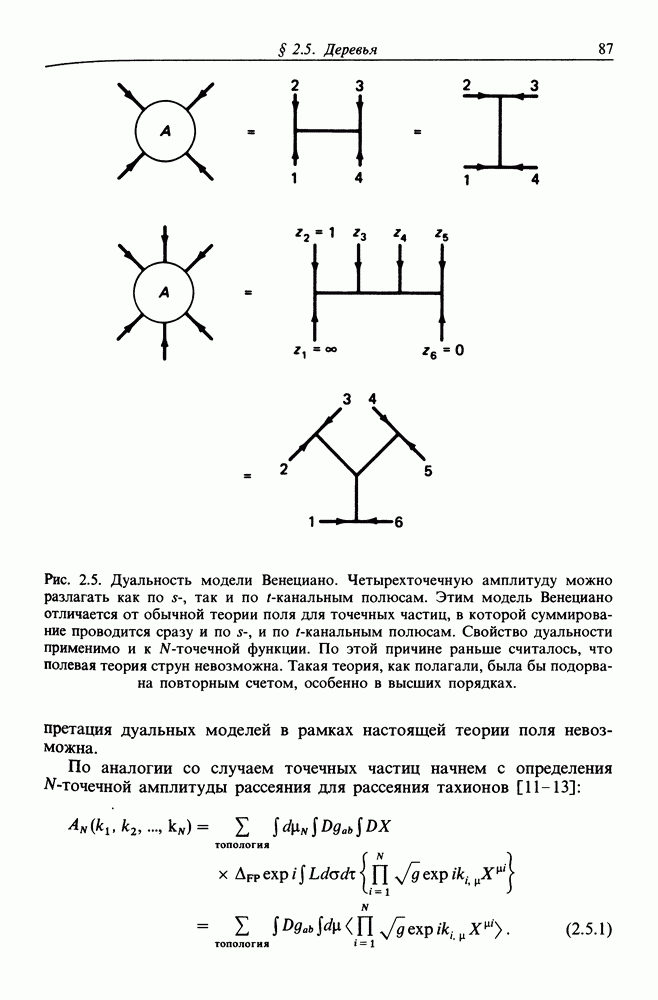
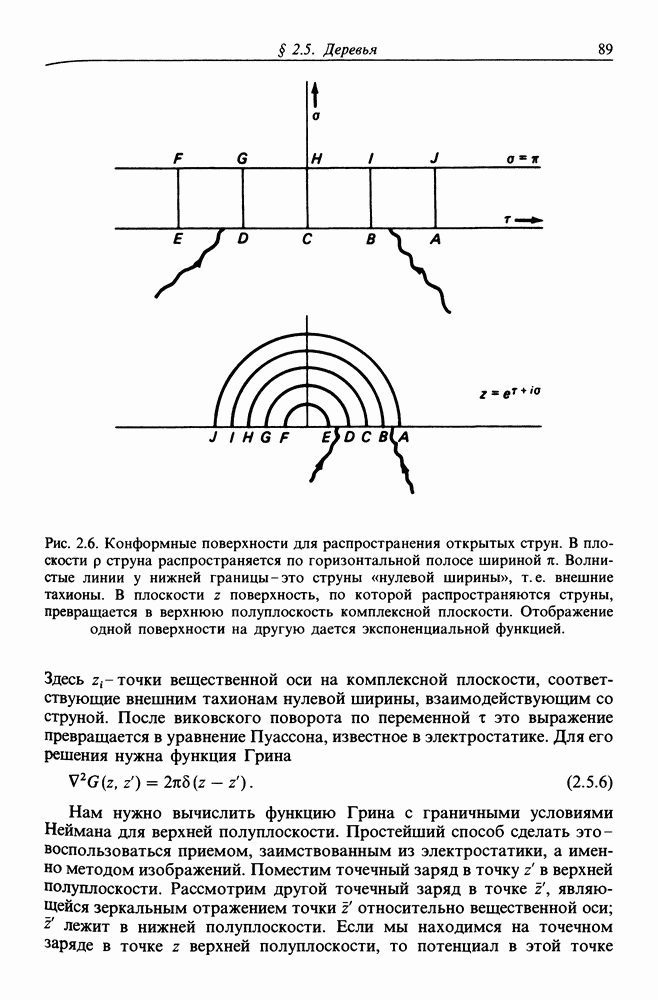
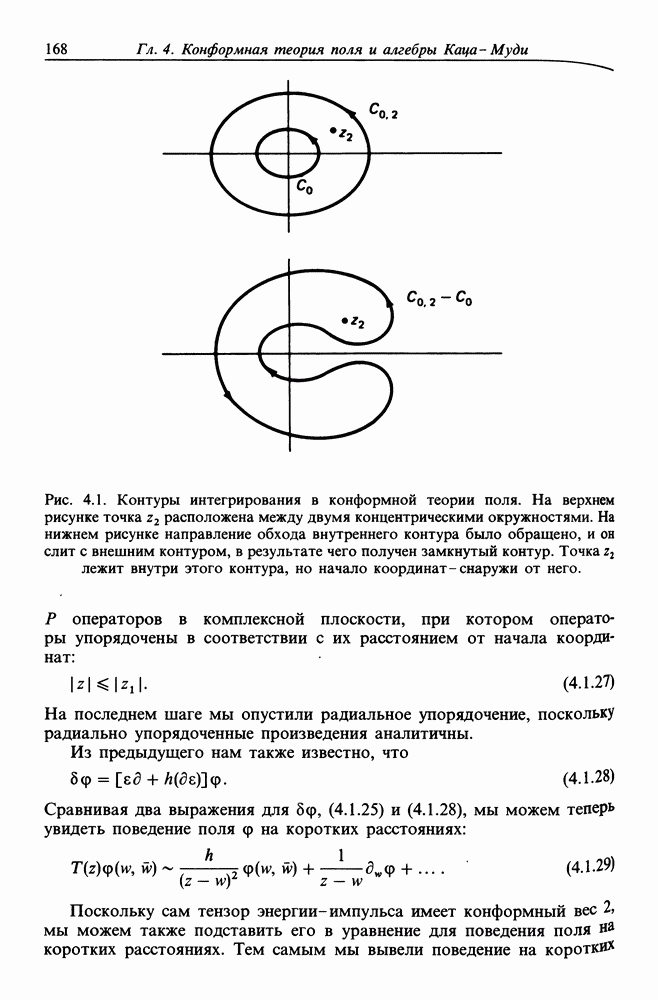
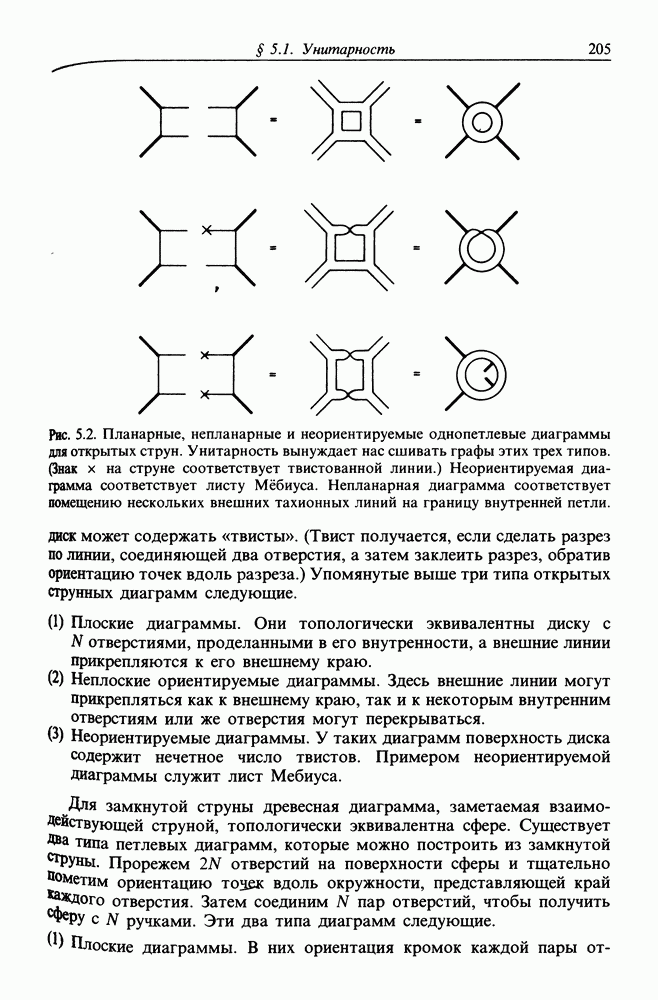
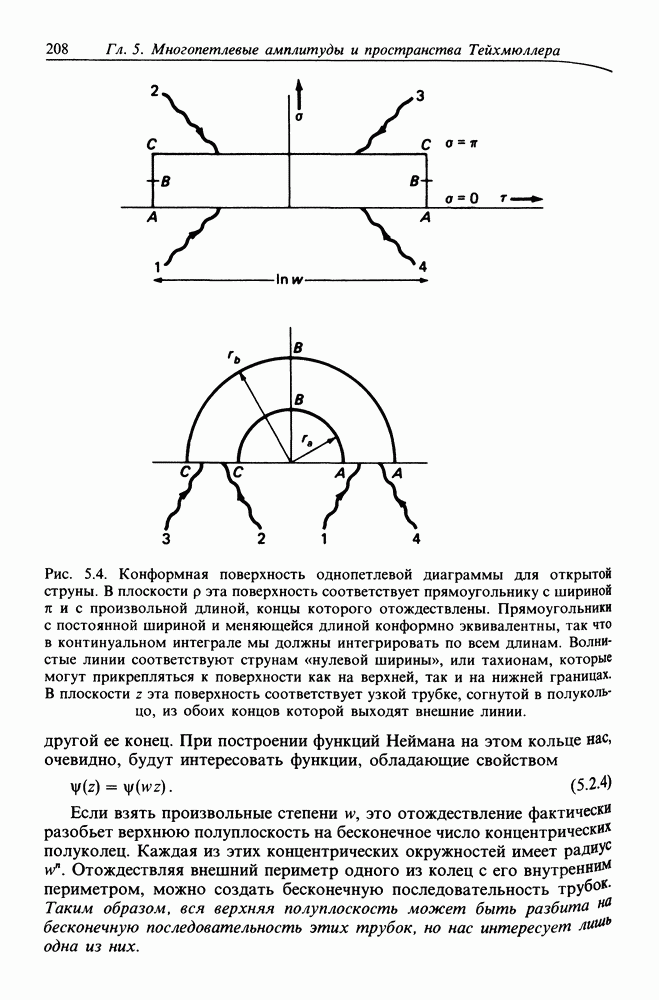
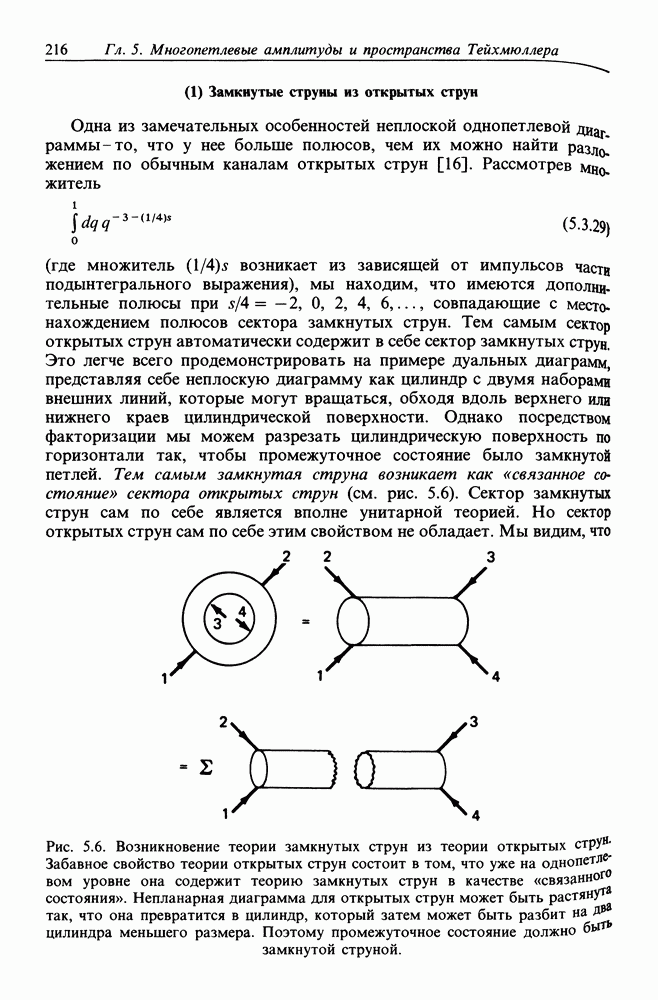
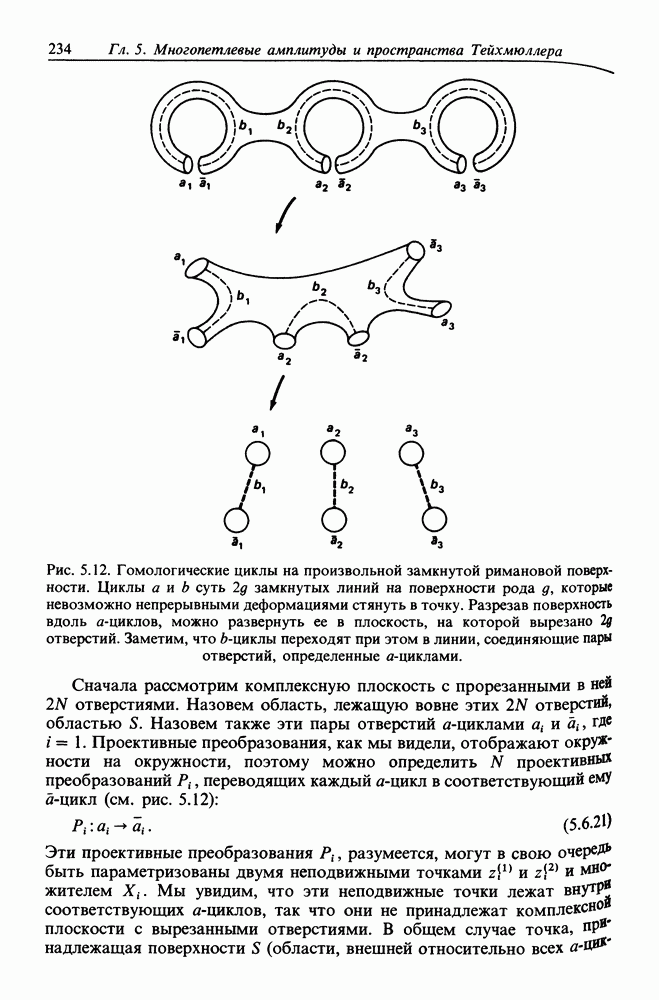
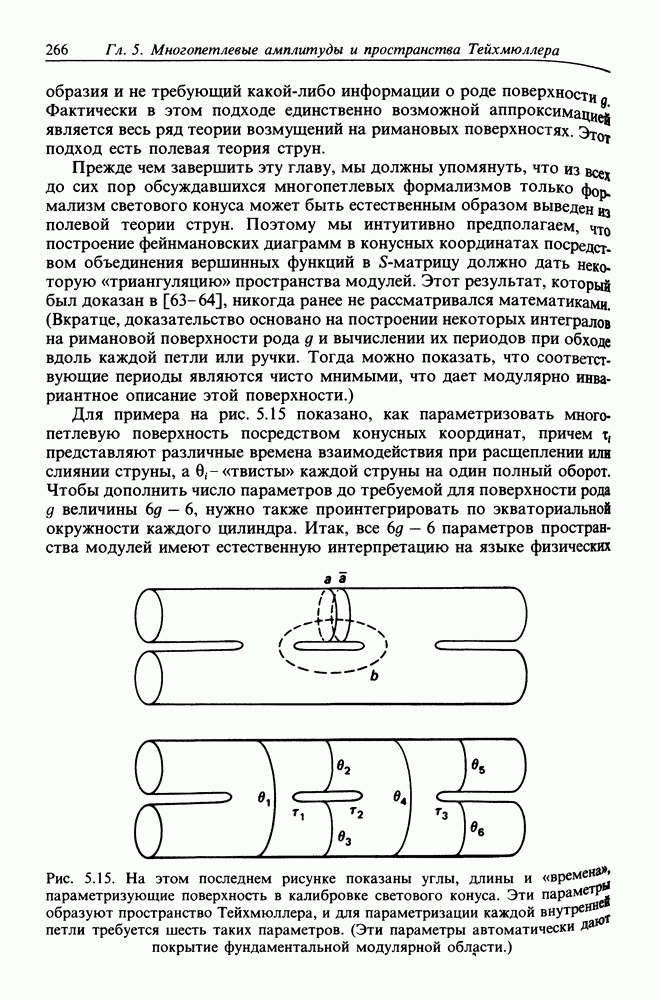
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 11.4. КЭЛЕРОВЫ МНОГООБРАЗИЯ
До сих пор наше обсуждение касалось в основном вещественных многообразий. Однако эти результаты довольно легко обобщаются на комплексные многообразия.
Для того чтобы определить  -мерное комплексное многообразие, нам понадобится
-мерное комплексное многообразие, нам понадобится  -мерное вещественное многообразие и обобщение
-мерное вещественное многообразие и обобщение
обычного определения комплексного числа:  где
где  Если мы имеем
Если мы имеем  -мерное вещественное многообразие, то при наличии на нем
-мерное вещественное многообразие, то при наличии на нем  тензорного поля
тензорного поля  заменяющего мнимую единицу
заменяющего мнимую единицу  и удовлетворяющего матричному уравнению
и удовлетворяющего матричному уравнению

можно определить комплексное число как

Многообразия, на которых задано такое тензорное поле  называются почти комплексными.
называются почти комплексными.
Однако мы хотим большего, нежели только существования тензорного поля  Мы хотели бы диагонализовать
Мы хотели бы диагонализовать  Если мы используем комплексные координаты
Если мы используем комплексные координаты

то хотелось бы произвести такую замену переменных, чтобы

Вопрос стоит так: всегда ли мы можем диагонализовать  в окрестности точки
в окрестности точки  используя преобразование координат
используя преобразование координат

(которое не является функцией от  Такое преобразование координат называется голоморфным, что является обобщением понятия аналитичности. Для разных точек
Такое преобразование координат называется голоморфным, что является обобщением понятия аналитичности. Для разных точек  мы, конечно, должны будем склеивать эти окрестности друг с другом, используя различные голоморфные преобразования, до тех пор, пока не покроем ими всю поверхность.
мы, конечно, должны будем склеивать эти окрестности друг с другом, используя различные голоморфные преобразования, до тех пор, пока не покроем ими всю поверхность.
Если всегда можно найти такие голоморфные преобразования, которые диагонализуют  в окрестности каждой точки
в окрестности каждой точки  многообразия, то мы будем говорить, что многообразие имеет комплексную структуру и является комплексным многообразием.
многообразия, то мы будем говорить, что многообразие имеет комплексную структуру и является комплексным многообразием.
Итак, имеем следующие аналогии:

(Интуитивно, процесс склеивания окрестностей, в которых  является диагональным, напоминает «проблему лифта» в общей теории относительности. С помощью общекоординатного преобразования в любой выбранной точке мы всегда можем локально обратить символы
является диагональным, напоминает «проблему лифта» в общей теории относительности. С помощью общекоординатного преобразования в любой выбранной точке мы всегда можем локально обратить символы
Кристоффеля в нуль, что соответствует свободному падению в лифте и отсутствию гравитации. Но, вообще говоря, мы не можем глобально обратить в нуль символы Кристоффеля, иначе пространство будет плоским, однако в каждой точке многообразия мы можем перейти в систему отсчета, связанную с лифтом.)
На первый взгляд, данное выше определение комплексного многообразия может показаться слишком многословным для столь интуитивного понятия. Однако можно привести примеры  -мерных вещественных многообразий, для которых используемый в определении критерий не выполняется. Например, сферы
-мерных вещественных многообразий, для которых используемый в определении критерий не выполняется. Например, сферы  не являются комплексными многообразиями (за исключением
не являются комплексными многообразиями (за исключением  так как
так как  Таким образом, отнюдь не очевидно, что произвольное
Таким образом, отнюдь не очевидно, что произвольное  -мерное вещественное многообразие может быть представлено как
-мерное вещественное многообразие может быть представлено как  -мерное комплексное многообразие.
-мерное комплексное многообразие.
Обсудим дифференциальные формы на комплексных многообразиях. Комплексифицируем наши базисные дифференциалы следующим образом:

Понятие  -формы теперь может быть обобщено до понятия
-формы теперь может быть обобщено до понятия  -формы
-формы

 ненадчеркнутыми и
ненадчеркнутыми и  надчеркнутыми индексами. Теперь мы можем определить две внешние производные:
надчеркнутыми индексами. Теперь мы можем определить две внешние производные:

Свойства этих производных таковы: 

Каждая форма теперь характеризуется двумя индексами  Следовательно, можно определить новую группу когомологий. Вместо когомологий де Рама, строящихся с помощью оператора
Следовательно, можно определить новую группу когомологий. Вместо когомологий де Рама, строящихся с помощью оператора  мы будем иметь дело с когомологиями Дольбо, использующих оператор
мы будем иметь дело с когомологиями Дольбо, использующих оператор  . Как и прежде, можно определить замкнутые и точные
. Как и прежде, можно определить замкнутые и точные  -формы, используя
-формы, используя  вместо
вместо 

Как и прежде, можно ввести сопряженный оператор и лапласиан. В комплексном случае мы на самом деле имеем два лапласиана:

Теперь можно сформулировать комплексную версию теоремы Ходжа:
Теорема Ходжа. Каждая комплексная  -форма имеет единственное разложение
-форма имеет единственное разложение

где а - гармоническая форма:

а Р, у - формы типов  соответственно.
соответственно.
Можно ввести обобщение чисел Бетти формулой

Связь с прежними числами Бетти дается формулой

Применяя комплексное сопряжение, получаем соотношение

и свойство дуальности Пуанкаре

Дадим теперь определение кэлерова многообразия. Если мы имеем комплексное многообразие с эрмитовой метрикой  то всегда можно ввести два-форму
то всегда можно ввести два-форму

называемую кэлеровой формой. Комплексное многообразие называется кэлеровым, если

Кэлерово многообразие характеризуется тем, что его кэлерова форма замкнута.
Кэлерово многообразие вследствие данного выше определения имеет много замечательных свойств, делающих его наиболее привлекательным среди всех комплексных многообразий. Мы просто перечислим некоторые из этих свойств:
(1) Можно показать, что эрмитова метрика на кэлеровом многообразии
может быть записана через производные от одной функции, кэлерова потенциала 

(2) Непосредственным вычислением легко показать, что на кэлеровом многообразии выполняется

В силу этих тождеств различные лапласианы, которые можно задать на кэлеровом многообразии, совпадают. Таким образом, на кэлеровом многообразии не возникает путаницы при использовании разных лапласианов.
(3) Если многообразие допускает кэлерову метрику, то числа Бетти четной степени должны быть больше или равны единице, а числа Бетти нечетной степени должны принимать четные значения:

для натуральных чисел  (Этот простой критерий исключает из рассмотрения большой класс многообразий. Например,
(Этот простой критерий исключает из рассмотрения большой класс многообразий. Например,  не допускает кэлеровой метрики, поскольку
не допускает кэлеровой метрики, поскольку  Критерий (11.4.21) исключает также
Критерий (11.4.21) исключает также  но допускает кэлерову структуру на
но допускает кэлерову структуру на 
(4) Если  ковариантно постоянный тензор, то метрика кэлерова. Для комплексных многообразий верно и обратное утверждение:
ковариантно постоянный тензор, то метрика кэлерова. Для комплексных многообразий верно и обратное утверждение:

(5) Если два-форма кручения, которую можно ввести на комплексном многообразии, равна нулю, то метрика будет кэлеровой.
(6) Единственные ненулевые символы Кристоффеля на кэлеровом многообразии равны

Единственные ненулевые компоненты тензора кривизны даются формулой

а другие компоненты можно получить, используя симметрии тензора кривизны и комплексное сопряжение. Компоненты тензора Риччй становятся равны

Два-форма

замкнута: 
(7) В качестве прямого следствия можно показать, что группой голономии кэлеровых многообразий служит  Это может быть использовано как альтернативное определение кэлерова многообразия. Отметим, что группа голономии есть группа вращения, генерируемая движениями по замкнутым путям на многообразии и зависящая от
Это может быть использовано как альтернативное определение кэлерова многообразия. Отметим, что группа голономии есть группа вращения, генерируемая движениями по замкнутым путям на многообразии и зависящая от

где  - матрицы алгебры Ли некоторой группы вращений
- матрицы алгебры Ли некоторой группы вращений  -мерного касательного пространства. Коэффициенты при
-мерного касательного пространства. Коэффициенты при  как видим, зависят от антисимметричного тензора Римана
как видим, зависят от антисимметричного тензора Римана  и
и  можно теперь рассматривать как антисимметричные
можно теперь рассматривать как антисимметричные  -матрицы алгебры Ли группы вращений. При этом для произвольного многообразия группой голономии будет
-матрицы алгебры Ли группы вращений. При этом для произвольного многообразия группой голономии будет  Однако если многообразие кэлерово, то можно показать, что ограничения на тензор кривизны, которые мы нашли ранее, редуцируют группу
Однако если многообразие кэлерово, то можно показать, что ограничения на тензор кривизны, которые мы нашли ранее, редуцируют группу  к группе
к группе  являющуюся подгруппой в
являющуюся подгруппой в  Ограничение, состоящее в том, что (11.4.24) есть единственные ненулевые компоненты тензора кривизны, нарушает
Ограничение, состоящее в том, что (11.4.24) есть единственные ненулевые компоненты тензора кривизны, нарушает  (
( -симметрию.
-симметрию.
(8) Класс кэлеровых многообразий, имеющих  группу голономии, может быть еще более сужен, если мы потребуем, чтобы многообразия имели нулевой первый класс Черна. В этом случае группа голономии
группу голономии, может быть еще более сужен, если мы потребуем, чтобы многообразия имели нулевой первый класс Черна. В этом случае группа голономии  редуцируется до
редуцируется до  Действительно, для любого
Действительно, для любого  выполняется теорема Калаби-Яу, утверждающая, что кэлерово многообразие с нулевым первым классом Черна всегда допускает кэлерову метрику с группой голономии
выполняется теорема Калаби-Яу, утверждающая, что кэлерово многообразие с нулевым первым классом Черна всегда допускает кэлерову метрику с группой голономии  Можно показать, что исчезновение первого класса Черна эквивалентно тому, что на многообразии существует риччи-плоская метрика. Поэтому мы будем использовать эти два понятия как взаимозаменяемые.
Можно показать, что исчезновение первого класса Черна эквивалентно тому, что на многообразии существует риччи-плоская метрика. Поэтому мы будем использовать эти два понятия как взаимозаменяемые.
Теперь будет полезно рассмотреть конкретные примеры кэлеровых многообразий.
(1) Римановы поверхности
Любая ориентируемая риманова поверхность допускает кэлерову метрику. Поскольку квадрат элемента длины на любой римановой поверхности может быть представлен в виде

то поверхность будет кэлеровым многообразием, потому что всегда Можно подобрать кэлеров потенциал  так, чтобы выполнялось
так, чтобы выполнялось

Кэлеровость римановых поверхностей очевидна, так как любая  -форма на римановой поверхности, включая и кэлерову
-форма на римановой поверхности, включая и кэлерову  -форму, является замкнутой.
-форму, является замкнутой.
(2) Комплексное N-мерное пространство
Очевидно, что комплексное  -мерное пространство
-мерное пространство  кэлерово, так как его стандартная билинейная форма
кэлерово, так как его стандартная билинейная форма

всегда может быть приведена к кэлерову виду.
(3) Сфера
Заметим, что  вообще говоря, не допускает кэлеровой метрики. Это связано с тем, что числа Бетти четной степени
вообще говоря, не допускает кэлеровой метрики. Это связано с тем, что числа Бетти четной степени  для
для  равного ненулевому целому числу, обычно все равны нулю. Следовательно, они не могут быть больше или равны единице, что было одним из необходимых условий для кэлеровых многообразий. Исключением служит двумерная сфера
равного ненулевому целому числу, обычно все равны нулю. Следовательно, они не могут быть больше или равны единице, что было одним из необходимых условий для кэлеровых многообразий. Исключением служит двумерная сфера  которая не имеет ненулевых чисел Бетти четной степени. Чтобы показать, что два-сфера допускает кэлерову метрику, заметим, что
которая не имеет ненулевых чисел Бетти четной степени. Чтобы показать, что два-сфера допускает кэлерову метрику, заметим, что  имеет квадрат элемента длины следующего вида:
имеет квадрат элемента длины следующего вида:

Если переписать это в комплексной форме, то мы можем записать кэлерову форму в виде

Эта кэлерова форма точна, и, следовательно,  допускает кэлерову метрику. Хотя
допускает кэлерову метрику. Хотя  и является кэлеровым многообразием, нетрудно показать, что
и является кэлеровым многообразием, нетрудно показать, что  и поэтому
и поэтому  не является риччи-плоским многообразием.
не является риччи-плоским многообразием.
Заметим, что  комплексное многообразие, если
комплексное многообразие, если  и
и  нечетные числа. Однако это не означает, что многообразия
нечетные числа. Однако это не означает, что многообразия  кэлеровы. Действительно,
кэлеровы. Действительно,  - комплексные многообразия, но они не являются кэлеровыми.
- комплексные многообразия, но они не являются кэлеровыми.  - кэлерово (но не риччи-плоское).
- кэлерово (но не риччи-плоское).
(4) Комплексное проективное N-мерное пространство
Для доказательства кэлеровости пространства  заметим, что его метрика может быть записана как метрика Фубини-Штуди на
заметим, что его метрика может быть записана как метрика Фубини-Штуди на  :
:

(5) Комплексные подмногообразия в СРN
Легко видеть, что комплексные подмногообразия в  также являются кэлеровыми многообразиями. Фактически для подмногообразий мы используем метрику, определенную для
также являются кэлеровыми многообразиями. Фактически для подмногообразий мы используем метрику, определенную для  выбирая только те компоненты метрического тензора, индексы которых пробегают касательное к подмногообразию пространство. Поскольку исходная метрика кэлерова, метрика на подмногообразии (совпадающая с исходной) также должна быть кэлеровой.
выбирая только те компоненты метрического тензора, индексы которых пробегают касательное к подмногообразию пространство. Поскольку исходная метрика кэлерова, метрика на подмногообразии (совпадающая с исходной) также должна быть кэлеровой.
(6) Торы
Двумерный тор  имеет равный нулю первый класс Черна:
имеет равный нулю первый класс Черна:  Можно также показать, что четырехмерный тор
Можно также показать, что четырехмерный тор  кэлеров. И, наконец, можно показать, что шестимерный тор
кэлеров. И, наконец, можно показать, что шестимерный тор  одновременно является кэлеровым и риччи-плоским. Таким образом, компактификация на шестимерный тор, похоже, обладает тем желательным свойством, что
одновременно является кэлеровым и риччи-плоским. Таким образом, компактификация на шестимерный тор, похоже, обладает тем желательным свойством, что  -суперсимметрия сохраняется. Однако недостатком шестимерного тора является сохранение слишком большого числа симметрий. Действительно, на
-суперсимметрия сохраняется. Однако недостатком шестимерного тора является сохранение слишком большого числа симметрий. Действительно, на  сохраняется
сохраняется  -суперсимметрия, что делает его неприемлемым с точки зрения феноменологии.
-суперсимметрия, что делает его неприемлемым с точки зрения феноменологии.
Соберем некоторые из полученных выше результатов в таблицу:

Здесь  -кэлерово означает риччи-плоское и кэлерово,
-кэлерово означает риччи-плоское и кэлерово,  равно эйлеровой характеристике и
равно эйлеровой характеристике и 
Отметим, что условие равенства нулю тензора Риччи налагает Дополнительные ограничения на кэлерово многообразие. Например, кэлерово многообразие комплексной размерности три имеет  тогда и только тогда, когда на нем существует ковариантно постоянная Ненулевая голоморфная три-форма
тогда и только тогда, когда на нем существует ковариантно постоянная Ненулевая голоморфная три-форма  . Это доказывает, в частности, что
. Это доказывает, в частности, что  не допускает риччи-плоской кэлеровой метрики. (Мы знаем, что это многообразие имеет
не допускает риччи-плоской кэлеровой метрики. (Мы знаем, что это многообразие имеет  Значит, по определению на нем не существует гармонических три-форм. Но это также означает, что не
Значит, по определению на нем не существует гармонических три-форм. Но это также означает, что не
существует и голоморфных три-форм. Следовательно,  допускает риччи-плоской кэлеровой метрики.)
допускает риччи-плоской кэлеровой метрики.)
Другое простое следствие этого заключается в том, что любая гармоническая  -форма в трех комплексных измерениях может быть умножена на
-форма в трех комплексных измерениях может быть умножена на  , что даст в результате гармоническую
, что даст в результате гармоническую  -форму:
-форму:

Это равенство выполняется в силу, что со ковариантно постоянна и, следовательно, под знаком лапласиана ведет себя как константа. Так что гармоническая форма остается гармонической после умножения на  При этом
При этом  -форма становится (0,3 —
-форма становится (0,3 —  -формой, поскольку мы свертываем с эрмитовым метрическим тензором
-формой, поскольку мы свертываем с эрмитовым метрическим тензором  а не с
а не с 
Изложенное выше позволяет избавиться почти ото всех чисел Ходжа. Используя различные симметрии относительно отражений и предыдущую симметрию, можно показать, что лишь  остаются как независимые компоненты на многообразии с
остаются как независимые компоненты на многообразии с 
 -голономией. Среди них можно также вычеркнуть
-голономией. Среди них можно также вычеркнуть  по следующей причине. Мы знаем, что лапласиан всегда можно разложить, представив его в виде
по следующей причине. Мы знаем, что лапласиан всегда можно разложить, представив его в виде

При действии на  -форму различные члены, содержащие тензор кривизны, сворачиваются в тензор Риччи. Но тензор Риччи равен нулю на риччи-плоском многообразии. Следовательно, гармоническая
-форму различные члены, содержащие тензор кривизны, сворачиваются в тензор Риччи. Но тензор Риччи равен нулю на риччи-плоском многообразии. Следовательно, гармоническая  -форма должна быть ковариантно постоянной. Это означает, что число Бетти гармонических
-форма должна быть ковариантно постоянной. Это означает, что число Бетти гармонических  -форм должно равняться нулю:
-форм должно равняться нулю:  . Но это также означает, что
. Но это также означает, что  в силу (11.4.15). Собирая все сказанное вместе, можно показать, что для риччи-плоского многообразия
в силу (11.4.15). Собирая все сказанное вместе, можно показать, что для риччи-плоского многообразия

Последнее равенство, выполняющееся для риччи-плоской метрики, станет чрезвычайно важным, когда мы будем обсуждать проблему поколений. Оказывается, что  связаны с числом фермионов положительной и отрицательной киральности, которые можно ввести на многообразии, так что уравнение (11.4.36) констатирует, что число поколений равно половине эйлеровой характеристики:
связаны с числом фермионов положительной и отрицательной киральности, которые можно ввести на многообразии, так что уравнение (11.4.36) констатирует, что число поколений равно половине эйлеровой характеристики:

Таким образом мы получаем, что число поколений имеет топологическое происхождение!
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Часть I. ПЕРВИЧНОЕ КВАНТОВАНИЕ И КОНТИНУАЛЬНЫЕ ИНТЕГРАЛЫ
- Глава 1 КОНТИНУАЛЬНЫЕ ИНТЕГРАЛЫ И ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 1.2. ИСТОРИЧЕСКИЙ ОБЗОР КАЛИБРОВОЧНОЙ ТЕОРИИ
- § 1.3. КОНТИНУАЛЬНЫЙ ИНТЕГРАЛ И ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 1.4. РЕЛЯТИВИСТСКИЕ ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 1.5. ПЕРВИЧНОЕ И ВТОРИЧНОЕ КВАНТОВАНИЕ
- § 1.6. КВАНТОВАНИЕ ФАДДЕЕВА-ПОПОВА
- § 1.7. ВТОРИЧНОЕ КВАНТОВАНИЕ
- § 1.8. ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
- § 1.9. ТОКИ И ВТОРИЧНОЕ КВАНТОВАНИЕ
- § 1.10. РЕЗЮМЕ
- Глава 2. СТРУНЫ НАМБУ-ГОТО
- § 2.1. БОЗОННЫЕ СТРУНЫ
- § 2.2. КВАНТОВАНИЕ ГУПТЫ-БЛЕЙЛЕРА
- § 2.3. КВАНТОВАНИЕ В КАЛИБРОВКЕ СВЕТОВОГО КОНУСА
- § 2.4. BRST-КВАНТОВАНИЕ
- § 2.5. ДЕРЕВЬЯ
- § 2.6. ОТ КОНТИНУАЛЬНОГО ИНТЕГРАЛА К ОПЕРАТОРАМ
- § 2.7. ПРОЕКТИВНАЯ ИНВАРИАНТНОСТЬ И ТВИСТЫ
- § 2.8. ЗАМКНУТЫЕ СТРУНЫ
- § 2.9. УНИЧТОЖЕНИЕ ДУХОВ
- § 2.10. РЕЗЮМЕ
- Глава 3. СУПЕРСТРУНЫ
- § 3.1. СУПЕРСИММЕТРИЧНЫЕ ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 3.2. ДВУМЕРНАЯ СУПЕРСИММЕТРИЯ
- § 3.3. ДЕРЕВЬЯ
- § 3.4. ЛОКАЛЬНАЯ ДВУМЕРНАЯ СУПЕРСИММЕТРИЯ
- § 3.5. КВАНТОВАНИЕ
- § 3.6. ПРОЕКЦИЯ GSO
- § 3.7. СУПЕРСТРУНЫ
- § 3.8. КВАНТОВАНИЕ ДЕЙСТВИЯ ГРИНА-ШВАРЦА В КОНУСНЫХ ПЕРЕМЕННЫХ
- § 3.9. ВЕРШИНЫ И ДЕРЕВЬЯ
- § 3.10 РЕЗЮМЕ
- Глава 4. КОНФОРМНАЯ ТЕОРИЯ ПОЛЯ И АЛГЕБРЫ КАЦА-МУДИ
- § 4.2. СУПЕРКОНФОРМНАЯ ТЕОРИЯ ПОЛЯ
- § 4.3. СПИНОВЫЕ ПОЛЯ
- § 4.4. СУПЕРКОНФОРМНЫЕ ДУХИ
- § 4.5. ФЕРМИОННЫЙ ВЕРШИННЫЙ ОПЕРАТОР
- § 4.6. СПИНОРЫ И ДЕРЕВЬЯ
- § 4.7. АЛГЕБРЫ КАЦА-МУДИ
- § 4.8. СУПЕРСИММЕТРИЯ
- § 4.9. РЕЗЮМЕ
- Глава 5. МНОГОПЕТЛЕВЫЕ АМПЛИТУДЫ И ПРОСТРАНСТВА ТЕЙХМЮЛЛЕРА
- § 5.2. ОДНОПЕТЛЕВЫЕ АМПЛИТУДЫ
- § 5.3. ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
- § 5.4. ОДНОПЕТЛЕВЫЕ АМПЛИТУДЫ СУПЕРСТРУН
- § 5.5. ОДНОПЕТЛЕВЫЕ ДИАГРАММЫ ЗАМКНУТЫХ СТРУН
- § 5.6. МНОГОПЕТЛЕВЫЕ АМПЛИТУДЫ
- § 5.7. РИМАНОВЫ ПОВЕРХНОСТИ И ПРОСТРАНСТВА ТЕЙХМЮЛЛЕРА
- § 5.8. КОНФОРМНАЯ АНОМАЛИЯ
- § 5.9. СУПЕРСТРУНЫ
- § 5.10. ДЕТЕРМИНАНТЫ И СИНГУЛЯРНОСТИ
- § 5.11. ПРОСТРАНСТВА МОДУЛЕЙ И ГРАССМАНИАНЫ
- § 5.12. РЕЗЮМЕ
- Часть II. ВТОРИЧНОЕ КВАНТОВАНИЕ И ПОИСКИ ГЕОМЕТРИИ
- Глава 6. ПОЛЕВАЯ ТЕОРИЯ В КАЛИБРОВКЕ СВЕТОВОГО КОНУСА
- § 6.2 ВЫВОД ПОЛЕВОЙ ТЕОРИИ ТОЧЕЧНЫХ ЧАСТИЦ
- § 6.3. ПОЛЕВАЯ ТЕОРИЯ В КАЛИБРОВКЕ СВЕТОВОГО КОНУСА
- § 6.4. ВЗАИМОДЕЙСТВИЯ
- § 6.5. МЕТОД ФУНКЦИЙ НЕЙМАНА
- § 6.6. ЭКВИВАЛЕНТНОСТЬ АМПЛИТУД РАССЕЯНИЯ
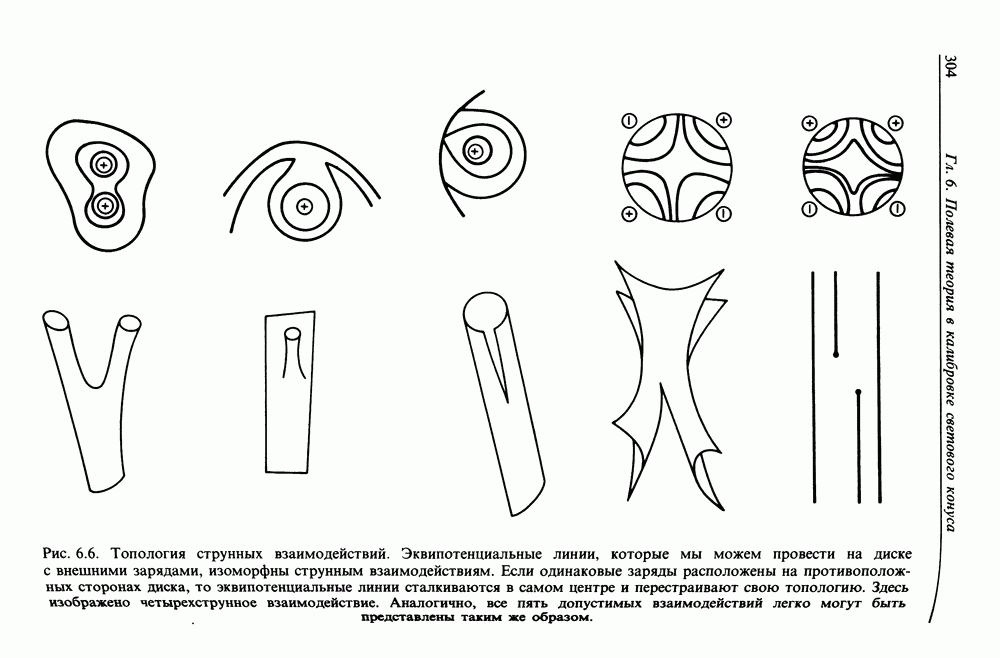
- § 6.7. ЧЕТЫРЕХСТРУННОЕ ВЗАИМОДЕЙСТВИЕ
- § 6.8. ПОЛЕВАЯ ТЕОРИЯ СУПЕРСТРУН
- § 6.9. РЕЗЮМЕ
- Глава 7. ПОЛЕВАЯ ТЕОРИЯ BRST
- § 7.1. КОВАРИАНТНАЯ ПОЛЕВАЯ ТЕОРИЯ СТРУН
- § 7.2. ПОЛЕВАЯ ТЕОРИЯ BRST
- § 7.3. ФИКСАЦИЯ КАЛИБРОВКИ
- § 7.4. ВЗАИМОДЕЙСТВИЯ
- § 7.5. АКСИОМАТИЧЕСКАЯ ФОРМУЛИРОВКА
- § 7.6. ДОКАЗАТЕЛЬСТВО ЭКВИВАЛЕНТНОСТИ
- § 7.7. ЗАМКНУТЫЕ СТРУНЫ И СУПЕРСТРУНЫ
- § 7.8. РЕЗЮМЕ
- Глава 8. ГЕОМЕТРИЧЕСКАЯ ПОЛЕВАЯ ТЕОРИЯ СТРУН
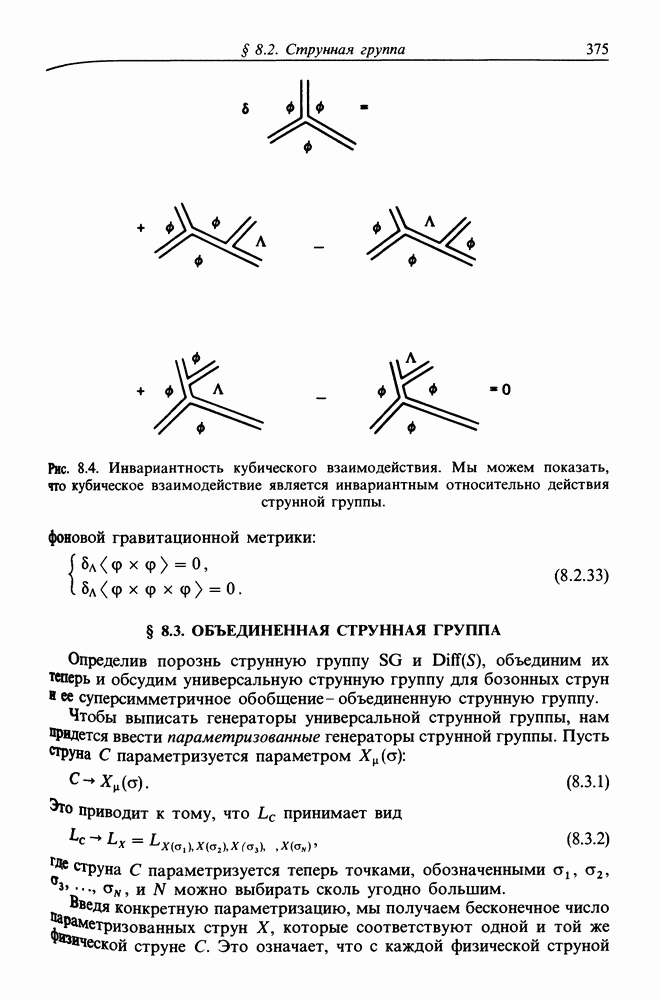
- § 8.2. СТРУННАЯ ГРУППА
- § 8.3. ОБЪЕДИНЕННАЯ СТРУННАЯ ГРУППА
- § 8.4. ПРЕДСТАВЛЕНИЯ ГРУППЫ USG
- § 8.5. ДУХОВЫЙ СЕКТОР И КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
- § 8.6. СВЯЗНОСТИ И КОВАРИАНТНЫЕ ПРОИЗВОДНЫЕ
- § 8.7. ГЕОМЕТРИЧЕСКИЙ ВЫВОД ДЕЙСТВИЯ
- § 8.8. ИНТЕРПОЛЯЦИОННАЯ КАЛИБРОВКА
- § 8.9. ЗАМКНУТЫЕ СТРУНЫ И СУПЕРСТРУНЫ
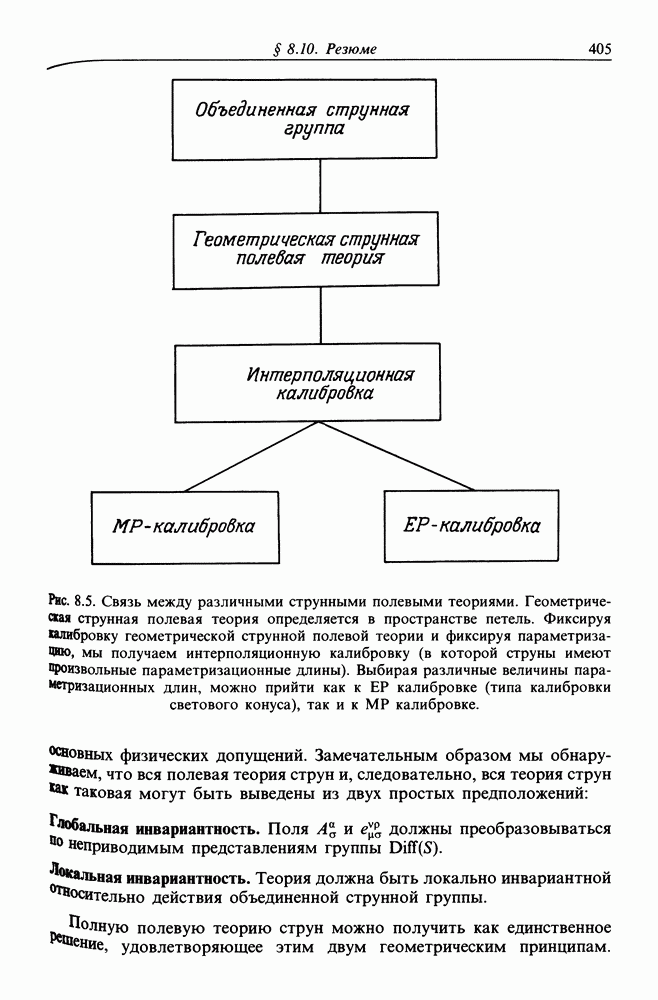
- § 8.10. РЕЗЮМЕ
- Часть III. ФЕНОМЕНОЛОГИЯ И ПОСТРОЕНИЕ МОДЕЛЕЙ
- Глава 9. АНОМАЛИИ И ТЕОРЕМА АТЬИ-ЗИНГЕРА
- § 9.2. АНОМАЛИИ И ФЕЙНМАНОВСКИЕ ДИАГРАММЫ
- § 9.3. АНОМАЛИИ В ФУНКЦИОНАЛЬНОМ ФОРМАЛИЗМЕ
- § 9.4. АНОМАЛИИ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
- § 9.5. ИНДЕКС ОПЕРАТОРА ДИРАКА
- § 9.6. ГРАВИТАЦИОННЫЕ И КАЛИБРОВОЧНЫЕ АНОМАЛИИ
- § 9.7. СОКРАЩЕНИЕ АНОМАЛИЙ В ТЕОРИИ СТРУН
- § 9.8. ПРОСТОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ АТЬИ-ЗИНГЕРА ОБ ИНДЕКСЕ
- § 9.9. РЕЗЮМЕ
- Глава 10. ГЕТЕРОТИЧЕСКИЕ СТРУНЫ И КОМПАКТИФИКАЦИЯ
- § 10.2. ГЕТЕРОТИЧЕСКАЯ СТРУНА
- § 10.3. СПЕКТР СОСТОЯНИЙ
- § 10.4. КОВАРИАНТНАЯ И ФЕРМИОННАЯ ФОРМУЛИРОВКИ
- § 10.5. ДЕРЕВЬЯ
- § 10.6. ОДНОПЕТЛЕВАЯ АМПЛИТУДА
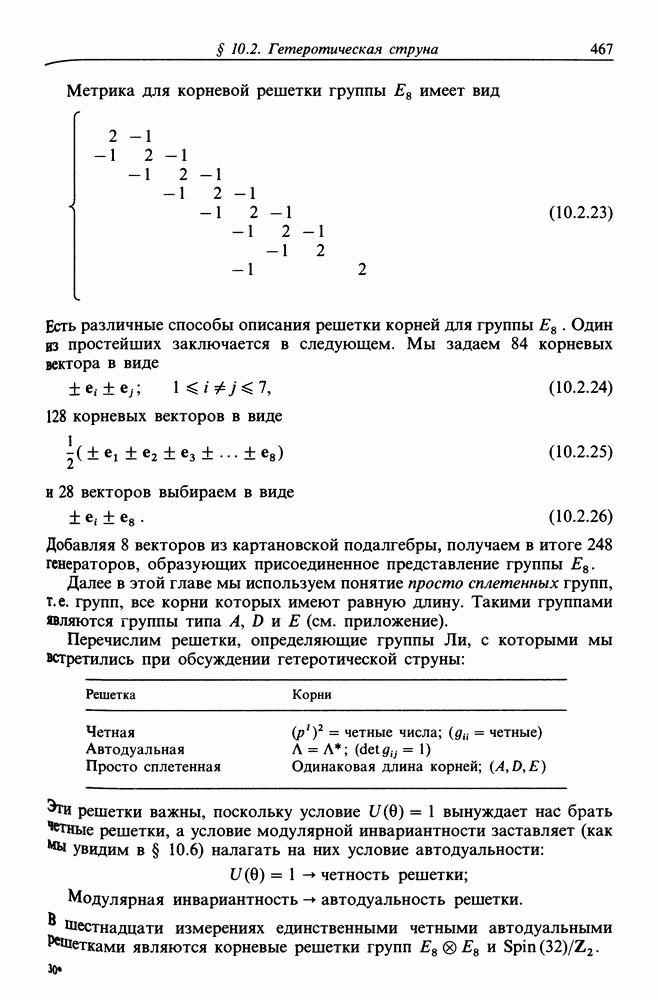
- § 10.7. ГРУППА Е8 И АЛГЕБРЫ КАЦА-МУДИ
- § 10.8. ДЕСЯТИМЕРНАЯ ТЕОРИЯ БЕЗ СУПЕРСИММЕТРИИ
- § 10.9. ЛОРЕНЦЕВЫ РЕШЕТКИ
- § 10.10. РЕЗЮМЕ
- Глава 11. ПРОСТРАНСТВА КАЛАБИ-ЯУ И ОРБИОБРАЗИЯ
- § 11.2. ОБЗОР ТЕОРИИ КОГОМОЛОГИЙ ДЕ РАМА
- § 11.3. КОГОМОЛОГИИ И ГОМОЛОГИИ
- § 11.4. КЭЛЕРОВЫ МНОГООБРАЗИЯ
- § 11.5. ВЛОЖЕНИЕ СПИНОВОЙ СВЯЗНОСТИ
- § 11.6. ПОКОЛЕНИЯ ФЕРМИОНОВ
- § 11.7. ВИЛЬСОНОВСКИЕ ЛИНИИ
- § 11.8. ОРБИОБРАЗИЯ
- § 11.9. ЧЕТЫРЕХМЕРНЫЕ СУПЕРСТРУНЫ
- § 11.10. РЕЗЮМЕ
- § 11.11. ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЕ
- § П.1. КРАТКОЕ ВВЕДЕНИЕ В ТЕОРИЮ ГРУПП
- СОВПАДЕНИЯ
- § П.2. КРАТКОЕ ВВЕДЕНИЕ В ОБЩУЮ ТЕОРИЮ ОТНОСИТЕЛЬНОСТИ
- § П.3. КРАТКОЕ ВВЕДЕНИЕ В ТЕОРИЮ ФОРМ
- § П.4. КРАТКОЕ ВВЕДЕНИЕ В СУПЕРСИММЕТРИЮ
- § П.5. КРАТКОЕ ВВЕДЕНИЕ В ТЕОРИЮ СУПЕРГРАВИТАЦИИ
- § П.6. СЛОВАРИК ТЕРМИНОВ
- П.7. ОБОЗНАЧЕНИЯ