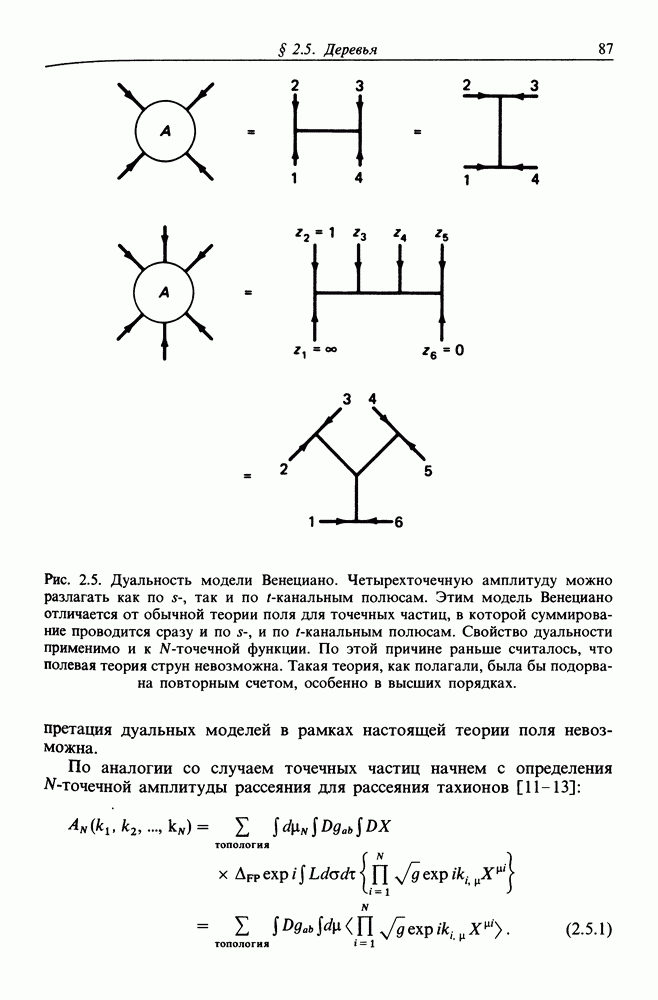
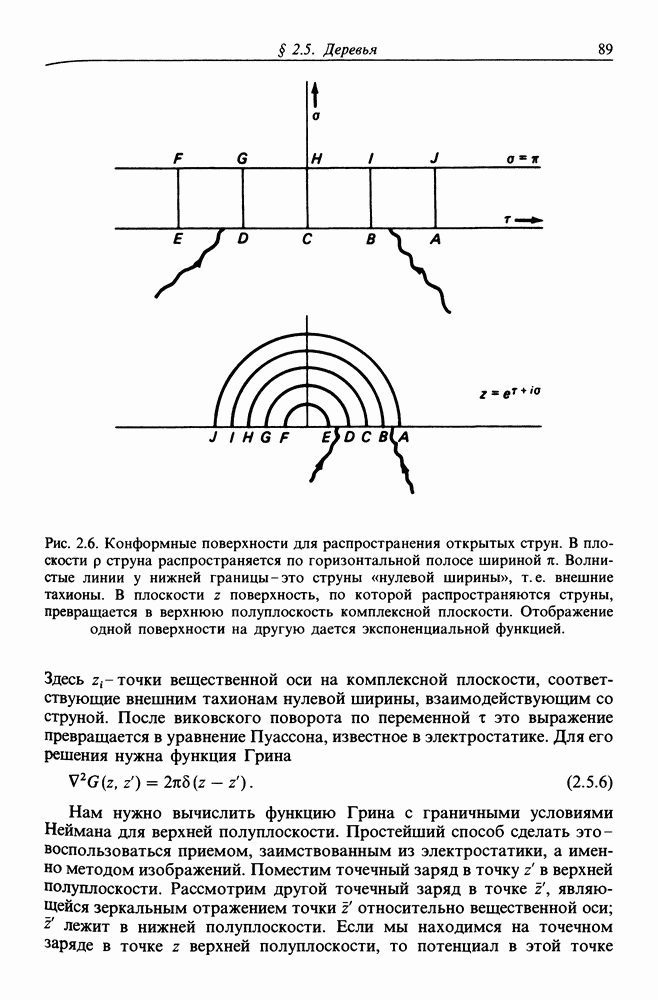
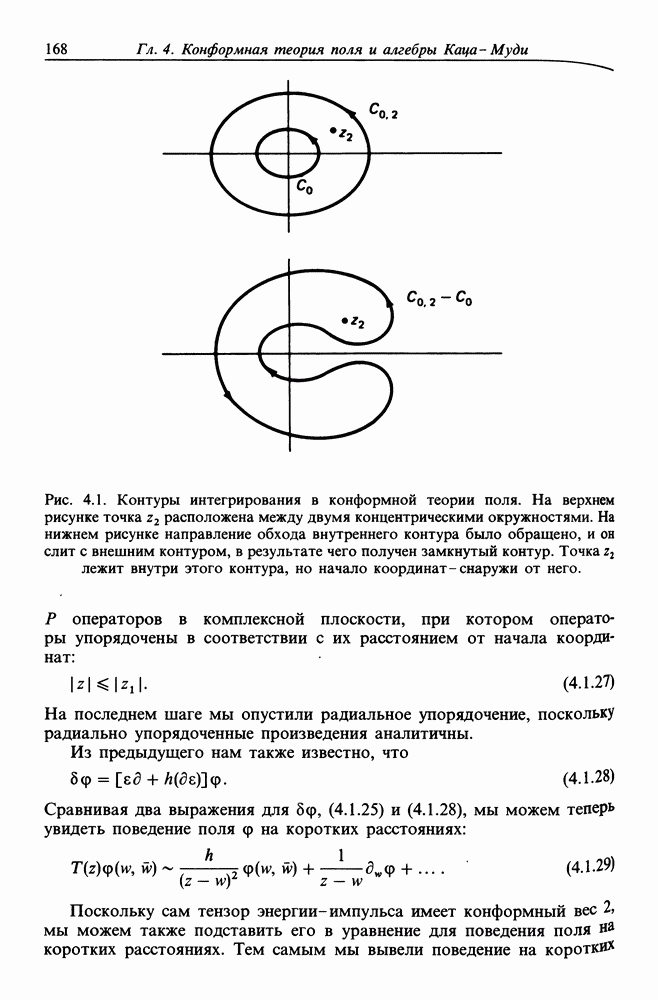
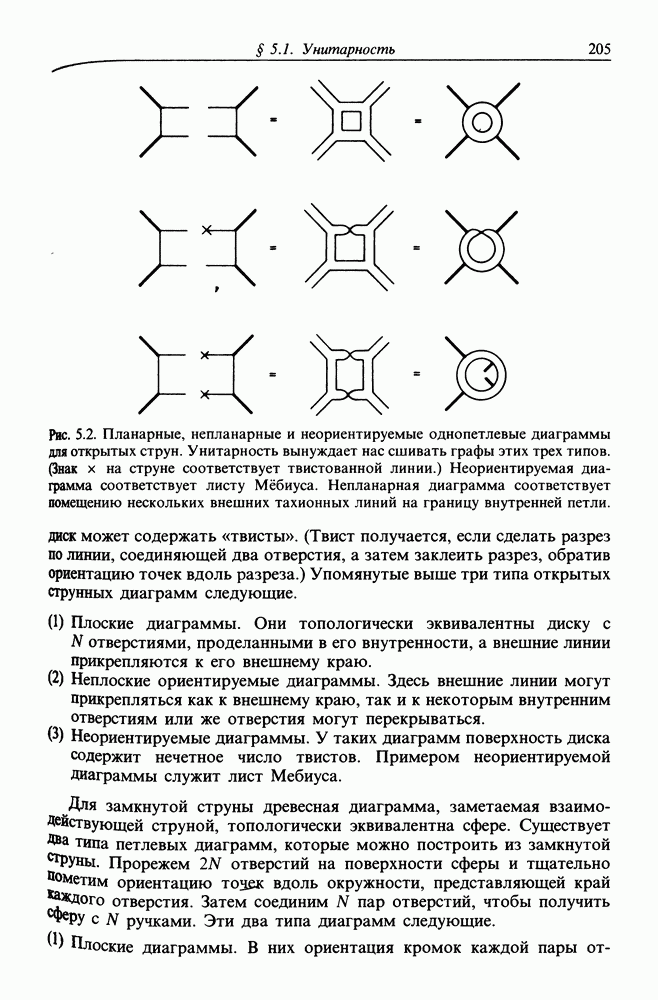
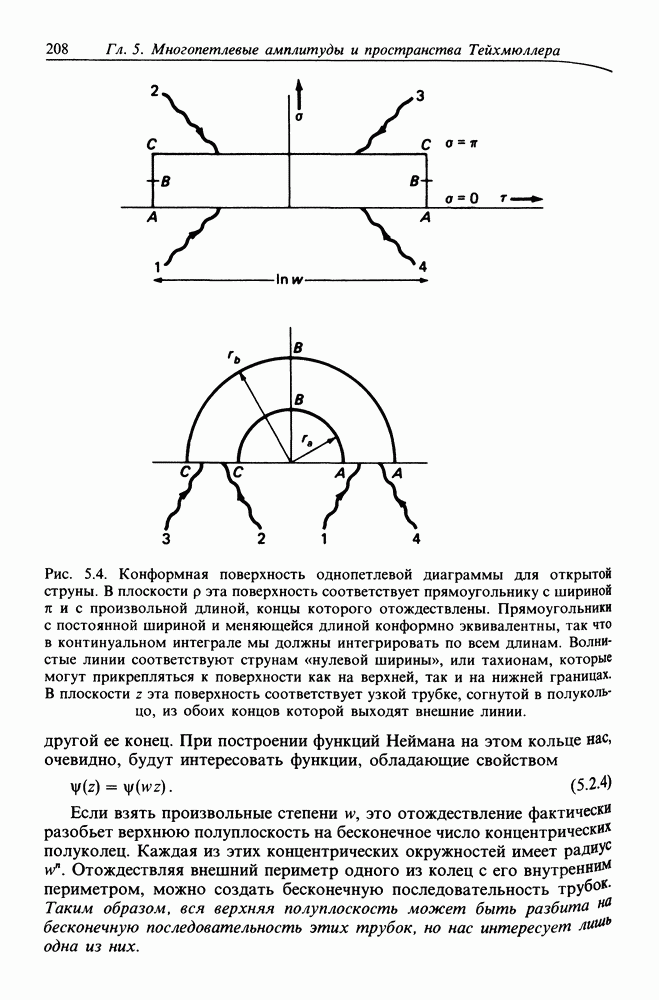
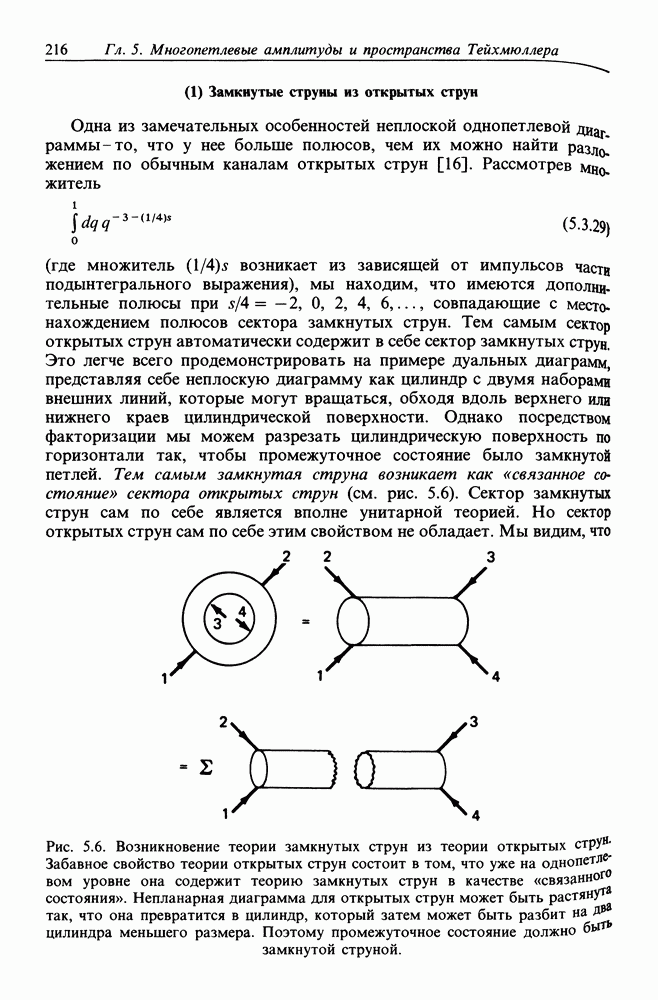
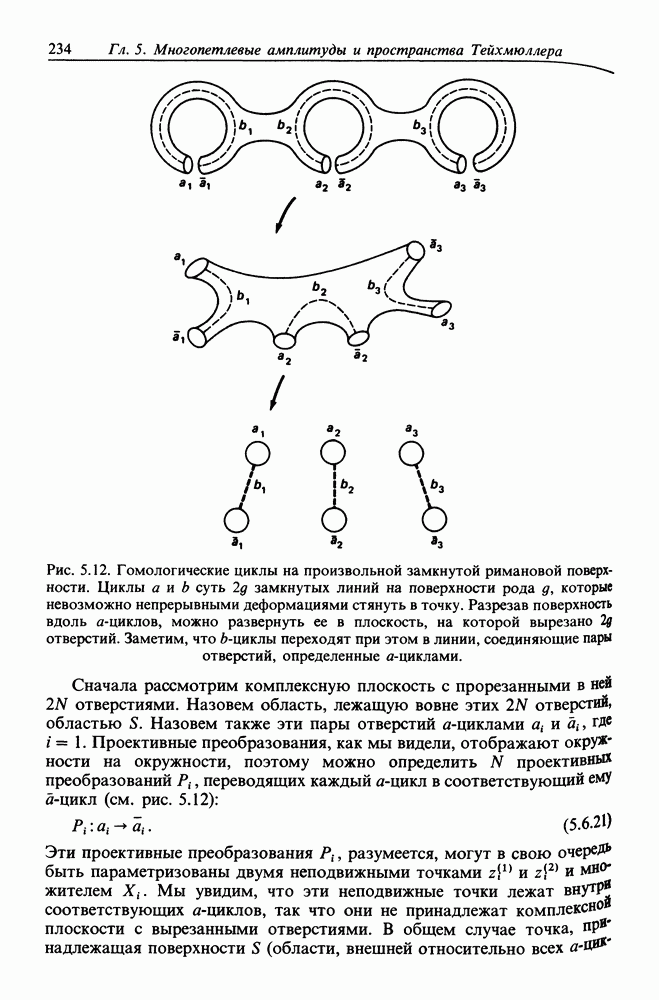
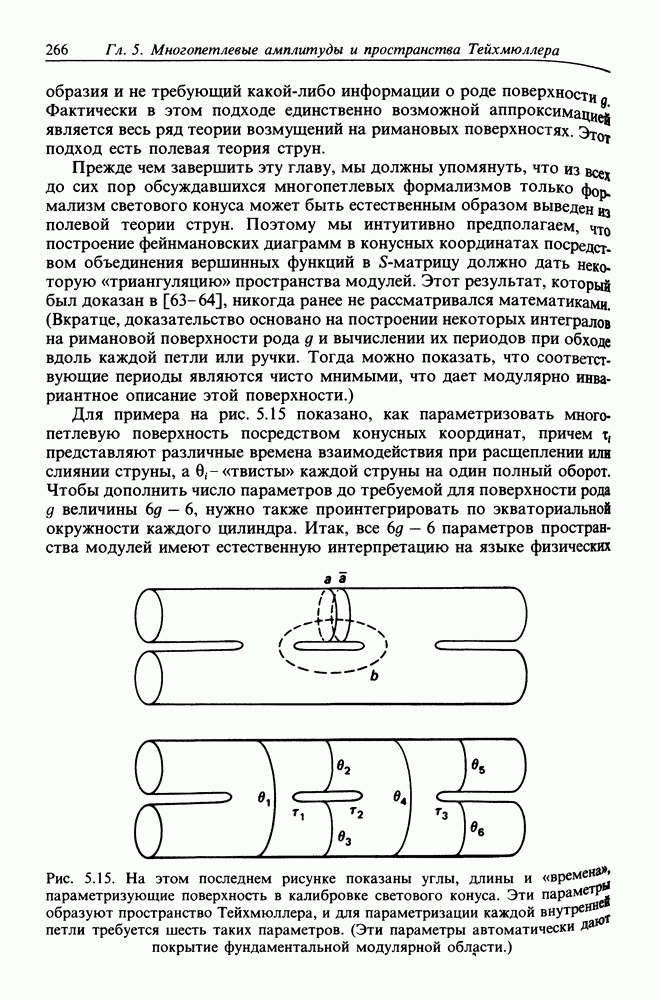
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9.4. АНОМАЛИИ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
При изучении характеристических классов [10,11] (это даст нам систематический анализ всех возможных топологических членов) мы используем язык форм (см. приложение). В некотором смысле теория дифференциальных форм только воспроизводит результаты, которые могут быть получены и при использовании обычных аналитических методов вычислений. Однако в большом числе измерений число индексов быстро увеличивается. Сильное сокращение обозначений в теории форм позволяет нам быстро манипулировать тензорами произвольного ранга в любой размерности, что затруднительно при использовании стандартного тензорного исчисления. В гл. 11 мы увидим, что теория форм является наиболее удобным языком для теории гомологий и когомологий.
Вооруженные теорией дифференциальных форм, мы построим ряд характеристических классов, что позволит нам записать множество всех топологических членов практически для любой размерности и любой группы.
Определим инвариантный полином, удовлетворяющий условию

где  матрицы группы Ли. Примерами инвариантных полиномов служат
матрицы группы Ли. Примерами инвариантных полиномов служат

Пусть  - два-форма кривизны
- два-форма кривизны

удовлетворяющая тождествам Бьянки

В приложении мы доказываем два важных свойства для инвариантных
полиномов, а именно что

для некоторой формы  т. е. инвариантный полином от форм кривизны является одновременно замкнутой и точной формой. Теория форм дает явное выражение для
т. е. инвариантный полином от форм кривизны является одновременно замкнутой и точной формой. Теория форм дает явное выражение для  Например, в приложении мы показываем, что
Например, в приложении мы показываем, что

Таким образом, след произведения два-форм кривизны является точной и замкнутой формой. Это представляет собой обобщение на языке форм предыдущих тождеств, которые были доказаны непосредственно. Например, в четырех измерениях мы имеем (9.2.7) и (9.2.17). Для произвольной размерности мы имеем (9.2.16). Эта новая форма, с которой мы встречались в (9.2.8), называется формой Черна-Саймонса.
Все это важно, поскольку ранее мы видели, что в двух и четырех измерениях существуют полиномы от тензора кривизны, являющиеся полными производными. Но мы были не в состоянии построить эти топологические инварианты в более высоких размерностях. Тождество (9.4.6) подводит итог решения данной проблемы.
Используя язык форм, можно также найти удобное выражение для условия согласованности Весса-Зумино. В  -мерном пространстве формально определим произведение форм кривизны, которое обозначим
-мерном пространстве формально определим произведение форм кривизны, которое обозначим  (Конечно, эта форма равна нулю
(Конечно, эта форма равна нулю  измерениях, но мы оставим в стороне это обстоятельство.) Эта форма по построению является точной:
измерениях, но мы оставим в стороне это обстоятельство.) Эта форма по построению является точной:

где  — форма Черна-Саймонса.
— форма Черна-Саймонса.  является также калибровочно инвариантной, поскольку построена из форм кривизны. То обстоятельно, что она одновременно и калибровочно-инвариантна, и точна, позволяет нам написать
является также калибровочно инвариантной, поскольку построена из форм кривизны. То обстоятельно, что она одновременно и калибровочно-инвариантна, и точна, позволяет нам написать

Таким образом, мы видим, что калибровочная вариация формы Черна-Саймонса замкнута. Локально можно написать

Цель этой конструкции - найти форму для аномалии  такую, чтобы была явной калибровочной вариацией от некоторой другой формы.
такую, чтобы была явной калибровочной вариацией от некоторой другой формы.
Запишем

Используя теорему Стокса, можно показать, что

где многообразия  и
и  связаны следующим образом:
связаны следующим образом: 
Это и есть нужный нам результат. Мы сейчас показали, что аномальный член  является калибровочной вариацией другой формы. Таким образом,
является калибровочной вариацией другой формы. Таким образом,  автоматически удовлетворяет условию согласованности Весса-Зумино, поскольку
автоматически удовлетворяет условию согласованности Весса-Зумино, поскольку

Мы будем использовать эту конструкцию, когда начнем сокращать аномалии в теории суперструн.
Вооружившись теорией дифференциальных форм, можно построить характеристические полиномы.
Мы найдем четыре основных характеристических класса:
(1) классы Черна;
(2) классы Понтрягина;
(3) классы Эйлера;
(4) классы Штифеля-Уитни.
Ограничимся формой кривизны  принимающей значение в алгебре
принимающей значение в алгебре  , т.е. произвольной
, т.е. произвольной  -матрицей с комплексными элементами. Определим полную форму Черна для этой алгебры как
-матрицей с комплексными элементами. Определим полную форму Черна для этой алгебры как

где мы использовали разложение по степеням  Обрывающееся в конечном счете разложение имеет следующие слагаемые:
Обрывающееся в конечном счете разложение имеет следующие слагаемые:


где

Заметим, что ряд в конечном счете обрывается, потому что  в достаточно высокой степени равна нулю в силу того, что
в достаточно высокой степени равна нулю в силу того, что  являются образующими грассмановой алгебры. В дополнение к классам Черна с, можно также ввести характер Черна
являются образующими грассмановой алгебры. В дополнение к классам Черна с, можно также ввести характер Черна

Всегда можно диагонализировать матрицу  так, что на ее диагонали будут стоять собственные значения
так, что на ее диагонали будут стоять собственные значения  То есть всегда можно найти матрицу
То есть всегда можно найти матрицу  такую что
такую что

После диагонализации  и с
и с  приобретают простой вид:
приобретают простой вид:

Заметим, что в пространстве четырех измерений топологический инвариант для группы  имеет вид
имеет вид

Кроме классов Черна существуют тесно связанные с ними классы Понтрягина. Пусть  принадлежит алгебре Ли
принадлежит алгебре Ли  ; тогда определим форму Понтрягина
; тогда определим форму Понтрягина

Класс Эйлера, однако, определяется несколько иначе. Его определение основывается не на детерминанте, как в случае классов Черна а Понтрягина, а на пфаффиане. Рассмотрим два-форму

Возьмем ее в  степень:
степень:

Заметим, что  является антисимметричной матрицей. Мы не можем диагонализировать антисимметричную матрицу так, чтобы ее диагональные элементы совпадали с ее собственными значениями Однако ее можно записать в виде
является антисимметричной матрицей. Мы не можем диагонализировать антисимметричную матрицу так, чтобы ее диагональные элементы совпадали с ее собственными значениями Однако ее можно записать в виде

Инвариант  , который строится по антисимметричной матрице а, называется пфаффианом. В терминах собственных значений пфаффиан равен
, который строится по антисимметричной матрице а, называется пфаффианом. В терминах собственных значений пфаффиан равен

Легко видеть, что пфаффиан  является квадратным корнем из старшего класса Понтрягина:
является квадратным корнем из старшего класса Понтрягина:

Приведем некоторые примеры классов Эйлера:

Они представляют собой не что иное, как упоминавшиеся ранее в (9.2.18) и (9.2.19) тождества, причем

В заключение выпишем некоторые другие представляющие интерес характеристические полиномы. Если через  обозначить собственные значения формы кривизны, то
обозначить собственные значения формы кривизны, то

Мы увидим, что  -полином, например, играет решающую
-полином, например, играет решающую 
вычислении аномалии для взаимодействующих с гравитацией частиц спина 1/2.
Наконец, можно определить классы Штифеля-Уитни, которые, к сожалению, не связаны с какой-либо формой кривизны. В то же время классы Штифеля-Уитни необходимы, чтобы определить, является ли данное многообразие спинорным многообразием, т.е. допускающим введение спиноров. Многие многообразия, которые, как кажется на первый взгляд, допускают спиноры, на самом деле не являются спинорными многообразиями. Приведем важные факты, касающиеся связи свойств многообразий с индексами классов Штифеля-Уитни. Обращение в нуль индекса первого класса Штифеля-Уитни означает, что многообразие является ориентируемым:

Наиболее важный факт заключается в том, что многообразие М допускает спиноры, если индекс его второго класса Штифеля-Уитни равен нулю:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- Часть I. ПЕРВИЧНОЕ КВАНТОВАНИЕ И КОНТИНУАЛЬНЫЕ ИНТЕГРАЛЫ
- Глава 1 КОНТИНУАЛЬНЫЕ ИНТЕГРАЛЫ И ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 1.2. ИСТОРИЧЕСКИЙ ОБЗОР КАЛИБРОВОЧНОЙ ТЕОРИИ
- § 1.3. КОНТИНУАЛЬНЫЙ ИНТЕГРАЛ И ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 1.4. РЕЛЯТИВИСТСКИЕ ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 1.5. ПЕРВИЧНОЕ И ВТОРИЧНОЕ КВАНТОВАНИЕ
- § 1.6. КВАНТОВАНИЕ ФАДДЕЕВА-ПОПОВА
- § 1.7. ВТОРИЧНОЕ КВАНТОВАНИЕ
- § 1.8. ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
- § 1.9. ТОКИ И ВТОРИЧНОЕ КВАНТОВАНИЕ
- § 1.10. РЕЗЮМЕ
- Глава 2. СТРУНЫ НАМБУ-ГОТО
- § 2.1. БОЗОННЫЕ СТРУНЫ
- § 2.2. КВАНТОВАНИЕ ГУПТЫ-БЛЕЙЛЕРА
- § 2.3. КВАНТОВАНИЕ В КАЛИБРОВКЕ СВЕТОВОГО КОНУСА
- § 2.4. BRST-КВАНТОВАНИЕ
- § 2.5. ДЕРЕВЬЯ
- § 2.6. ОТ КОНТИНУАЛЬНОГО ИНТЕГРАЛА К ОПЕРАТОРАМ
- § 2.7. ПРОЕКТИВНАЯ ИНВАРИАНТНОСТЬ И ТВИСТЫ
- § 2.8. ЗАМКНУТЫЕ СТРУНЫ
- § 2.9. УНИЧТОЖЕНИЕ ДУХОВ
- § 2.10. РЕЗЮМЕ
- Глава 3. СУПЕРСТРУНЫ
- § 3.1. СУПЕРСИММЕТРИЧНЫЕ ТОЧЕЧНЫЕ ЧАСТИЦЫ
- § 3.2. ДВУМЕРНАЯ СУПЕРСИММЕТРИЯ
- § 3.3. ДЕРЕВЬЯ
- § 3.4. ЛОКАЛЬНАЯ ДВУМЕРНАЯ СУПЕРСИММЕТРИЯ
- § 3.5. КВАНТОВАНИЕ
- § 3.6. ПРОЕКЦИЯ GSO
- § 3.7. СУПЕРСТРУНЫ
- § 3.8. КВАНТОВАНИЕ ДЕЙСТВИЯ ГРИНА-ШВАРЦА В КОНУСНЫХ ПЕРЕМЕННЫХ
- § 3.9. ВЕРШИНЫ И ДЕРЕВЬЯ
- § 3.10 РЕЗЮМЕ
- Глава 4. КОНФОРМНАЯ ТЕОРИЯ ПОЛЯ И АЛГЕБРЫ КАЦА-МУДИ
- § 4.2. СУПЕРКОНФОРМНАЯ ТЕОРИЯ ПОЛЯ
- § 4.3. СПИНОВЫЕ ПОЛЯ
- § 4.4. СУПЕРКОНФОРМНЫЕ ДУХИ
- § 4.5. ФЕРМИОННЫЙ ВЕРШИННЫЙ ОПЕРАТОР
- § 4.6. СПИНОРЫ И ДЕРЕВЬЯ
- § 4.7. АЛГЕБРЫ КАЦА-МУДИ
- § 4.8. СУПЕРСИММЕТРИЯ
- § 4.9. РЕЗЮМЕ
- Глава 5. МНОГОПЕТЛЕВЫЕ АМПЛИТУДЫ И ПРОСТРАНСТВА ТЕЙХМЮЛЛЕРА
- § 5.2. ОДНОПЕТЛЕВЫЕ АМПЛИТУДЫ
- § 5.3. ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
- § 5.4. ОДНОПЕТЛЕВЫЕ АМПЛИТУДЫ СУПЕРСТРУН
- § 5.5. ОДНОПЕТЛЕВЫЕ ДИАГРАММЫ ЗАМКНУТЫХ СТРУН
- § 5.6. МНОГОПЕТЛЕВЫЕ АМПЛИТУДЫ
- § 5.7. РИМАНОВЫ ПОВЕРХНОСТИ И ПРОСТРАНСТВА ТЕЙХМЮЛЛЕРА
- § 5.8. КОНФОРМНАЯ АНОМАЛИЯ
- § 5.9. СУПЕРСТРУНЫ
- § 5.10. ДЕТЕРМИНАНТЫ И СИНГУЛЯРНОСТИ
- § 5.11. ПРОСТРАНСТВА МОДУЛЕЙ И ГРАССМАНИАНЫ
- § 5.12. РЕЗЮМЕ
- Часть II. ВТОРИЧНОЕ КВАНТОВАНИЕ И ПОИСКИ ГЕОМЕТРИИ
- Глава 6. ПОЛЕВАЯ ТЕОРИЯ В КАЛИБРОВКЕ СВЕТОВОГО КОНУСА
- § 6.2 ВЫВОД ПОЛЕВОЙ ТЕОРИИ ТОЧЕЧНЫХ ЧАСТИЦ
- § 6.3. ПОЛЕВАЯ ТЕОРИЯ В КАЛИБРОВКЕ СВЕТОВОГО КОНУСА
- § 6.4. ВЗАИМОДЕЙСТВИЯ
- § 6.5. МЕТОД ФУНКЦИЙ НЕЙМАНА
- § 6.6. ЭКВИВАЛЕНТНОСТЬ АМПЛИТУД РАССЕЯНИЯ
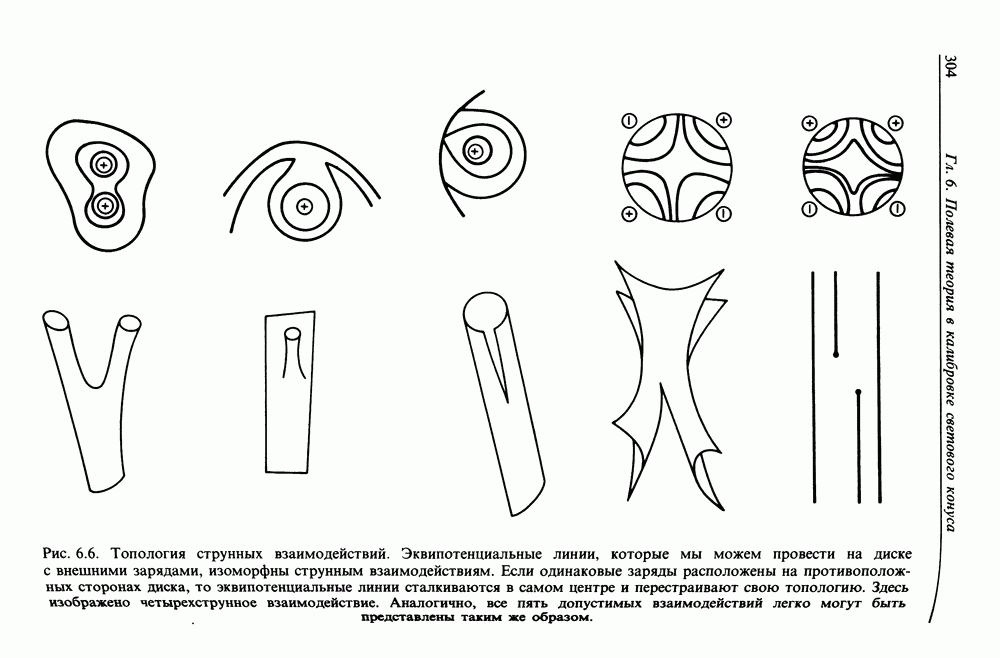
- § 6.7. ЧЕТЫРЕХСТРУННОЕ ВЗАИМОДЕЙСТВИЕ
- § 6.8. ПОЛЕВАЯ ТЕОРИЯ СУПЕРСТРУН
- § 6.9. РЕЗЮМЕ
- Глава 7. ПОЛЕВАЯ ТЕОРИЯ BRST
- § 7.1. КОВАРИАНТНАЯ ПОЛЕВАЯ ТЕОРИЯ СТРУН
- § 7.2. ПОЛЕВАЯ ТЕОРИЯ BRST
- § 7.3. ФИКСАЦИЯ КАЛИБРОВКИ
- § 7.4. ВЗАИМОДЕЙСТВИЯ
- § 7.5. АКСИОМАТИЧЕСКАЯ ФОРМУЛИРОВКА
- § 7.6. ДОКАЗАТЕЛЬСТВО ЭКВИВАЛЕНТНОСТИ
- § 7.7. ЗАМКНУТЫЕ СТРУНЫ И СУПЕРСТРУНЫ
- § 7.8. РЕЗЮМЕ
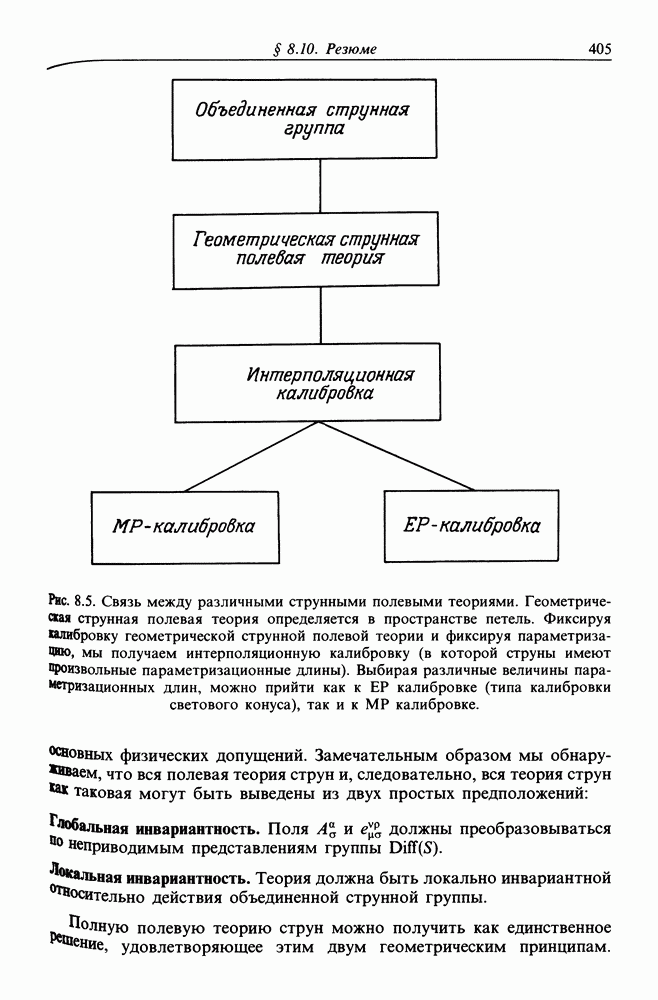
- Глава 8. ГЕОМЕТРИЧЕСКАЯ ПОЛЕВАЯ ТЕОРИЯ СТРУН
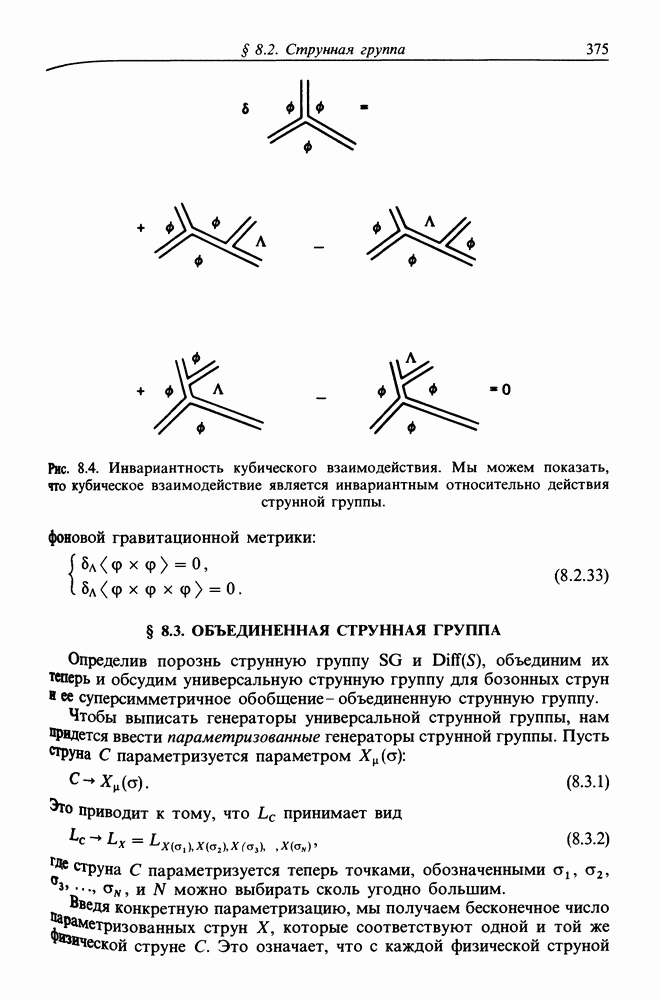
- § 8.2. СТРУННАЯ ГРУППА
- § 8.3. ОБЪЕДИНЕННАЯ СТРУННАЯ ГРУППА
- § 8.4. ПРЕДСТАВЛЕНИЯ ГРУППЫ USG
- § 8.5. ДУХОВЫЙ СЕКТОР И КАСАТЕЛЬНОЕ ПРОСТРАНСТВО
- § 8.6. СВЯЗНОСТИ И КОВАРИАНТНЫЕ ПРОИЗВОДНЫЕ
- § 8.7. ГЕОМЕТРИЧЕСКИЙ ВЫВОД ДЕЙСТВИЯ
- § 8.8. ИНТЕРПОЛЯЦИОННАЯ КАЛИБРОВКА
- § 8.9. ЗАМКНУТЫЕ СТРУНЫ И СУПЕРСТРУНЫ
- § 8.10. РЕЗЮМЕ
- Часть III. ФЕНОМЕНОЛОГИЯ И ПОСТРОЕНИЕ МОДЕЛЕЙ
- Глава 9. АНОМАЛИИ И ТЕОРЕМА АТЬИ-ЗИНГЕРА
- § 9.2. АНОМАЛИИ И ФЕЙНМАНОВСКИЕ ДИАГРАММЫ
- § 9.3. АНОМАЛИИ В ФУНКЦИОНАЛЬНОМ ФОРМАЛИЗМЕ
- § 9.4. АНОМАЛИИ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
- § 9.5. ИНДЕКС ОПЕРАТОРА ДИРАКА
- § 9.6. ГРАВИТАЦИОННЫЕ И КАЛИБРОВОЧНЫЕ АНОМАЛИИ
- § 9.7. СОКРАЩЕНИЕ АНОМАЛИЙ В ТЕОРИИ СТРУН
- § 9.8. ПРОСТОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ АТЬИ-ЗИНГЕРА ОБ ИНДЕКСЕ
- § 9.9. РЕЗЮМЕ
- Глава 10. ГЕТЕРОТИЧЕСКИЕ СТРУНЫ И КОМПАКТИФИКАЦИЯ
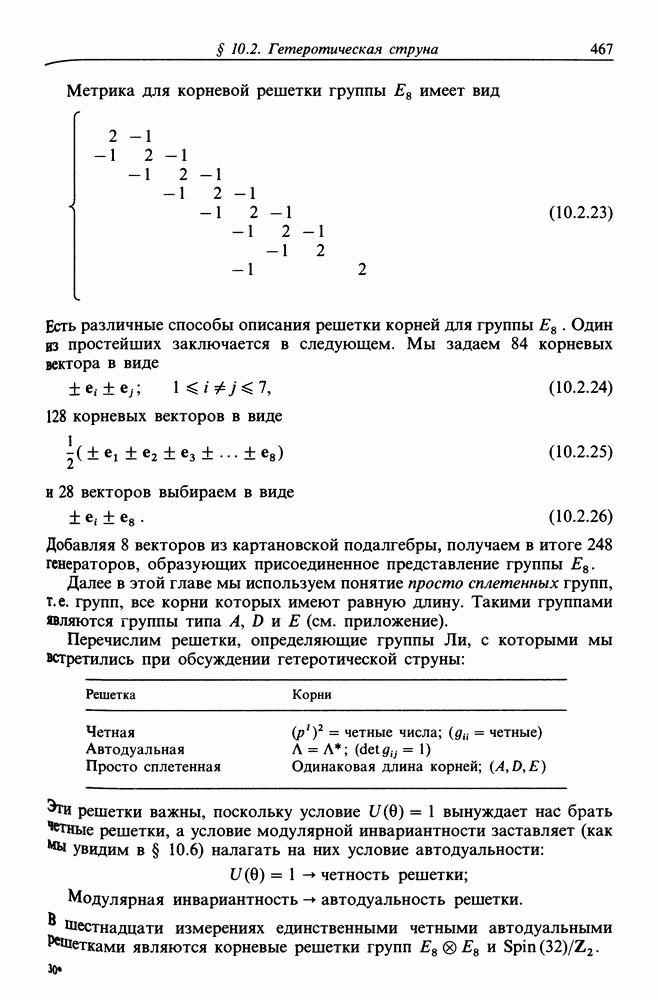
- § 10.2. ГЕТЕРОТИЧЕСКАЯ СТРУНА
- § 10.3. СПЕКТР СОСТОЯНИЙ
- § 10.4. КОВАРИАНТНАЯ И ФЕРМИОННАЯ ФОРМУЛИРОВКИ
- § 10.5. ДЕРЕВЬЯ
- § 10.6. ОДНОПЕТЛЕВАЯ АМПЛИТУДА
- § 10.7. ГРУППА Е8 И АЛГЕБРЫ КАЦА-МУДИ
- § 10.8. ДЕСЯТИМЕРНАЯ ТЕОРИЯ БЕЗ СУПЕРСИММЕТРИИ
- § 10.9. ЛОРЕНЦЕВЫ РЕШЕТКИ
- § 10.10. РЕЗЮМЕ
- Глава 11. ПРОСТРАНСТВА КАЛАБИ-ЯУ И ОРБИОБРАЗИЯ
- § 11.2. ОБЗОР ТЕОРИИ КОГОМОЛОГИЙ ДЕ РАМА
- § 11.3. КОГОМОЛОГИИ И ГОМОЛОГИИ
- § 11.4. КЭЛЕРОВЫ МНОГООБРАЗИЯ
- § 11.5. ВЛОЖЕНИЕ СПИНОВОЙ СВЯЗНОСТИ
- § 11.6. ПОКОЛЕНИЯ ФЕРМИОНОВ
- § 11.7. ВИЛЬСОНОВСКИЕ ЛИНИИ
- § 11.8. ОРБИОБРАЗИЯ
- § 11.9. ЧЕТЫРЕХМЕРНЫЕ СУПЕРСТРУНЫ
- § 11.10. РЕЗЮМЕ
- § 11.11. ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЕ
- § П.1. КРАТКОЕ ВВЕДЕНИЕ В ТЕОРИЮ ГРУПП
- СОВПАДЕНИЯ
- § П.2. КРАТКОЕ ВВЕДЕНИЕ В ОБЩУЮ ТЕОРИЮ ОТНОСИТЕЛЬНОСТИ
- § П.3. КРАТКОЕ ВВЕДЕНИЕ В ТЕОРИЮ ФОРМ
- § П.4. КРАТКОЕ ВВЕДЕНИЕ В СУПЕРСИММЕТРИЮ
- § П.5. КРАТКОЕ ВВЕДЕНИЕ В ТЕОРИЮ СУПЕРГРАВИТАЦИИ
- § П.6. СЛОВАРИК ТЕРМИНОВ
- П.7. ОБОЗНАЧЕНИЯ