| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.6. Грассманово описание для произвольной компактной группы Ли
Изучая  для компактной полупростой группы
для компактной полупростой группы  можно считать центр этой группы тривиальным. Действительно, если группа
можно считать центр этой группы тривиальным. Действительно, если группа  накрытие
накрытие  то многообразие
то многообразие  это объединение нескольких связных компонент пространства
это объединение нескольких связных компонент пространства  Если центр тривиален, то G является связной компонентой единицы в группе автоморфизмов своей алгебры Ли
Если центр тривиален, то G является связной компонентой единицы в группе автоморфизмов своей алгебры Ли 
Самое очевидное гильбертово пространство, на котором действует  пространство
пространство  Это, в сущности, присоединенное представление. Мы отождествим
Это, в сущности, присоединенное представление. Мы отождествим  где
где  размерность
размерность  Таким образом, мы отождествляем
Таким образом, мы отождествляем  с подгруппой группы
с подгруппой группы  с помощью присоединенного представления группы G на
с помощью присоединенного представления группы G на  Пространство петель
Пространство петель  является подмногообразием в
является подмногообразием в  следовательно, может быть отождествлено с подмногообразием в
следовательно, может быть отождествлено с подмногообразием в 
Определение (8.6.1).  это подмногообразие в
это подмногообразие в  состоящее из подпространств
состоящее из подпространств  таких, что
таких, что

Здесь обозначает подпространство гладких функций из  которое, как нам известно, плотно. Тот факт, что оно является алгеброй Ли, означает, что
которое, как нам известно, плотно. Тот факт, что оно является алгеброй Ли, означает, что  замкнуто относительно поточечного коммутатора
замкнуто относительно поточечного коммутатора  -значных функций.
-значных функций.
Теорема (8.6.2). Действие группы  на
на  сохраняет
сохраняет  если центр G тривиален, соответствие
если центр G тривиален, соответствие  определяет диффеоморфизм
определяет диффеоморфизм 
Доказательство. Первое утверждение очевидно, так как любая группа действует на своей алгебре Ли автоморфизмами (алгебр Ли). (Условие (ii) возникает, как и в (8.5.1), из-за того, что присоединенное действие сохраняет форму Киллинга, так что  лежит в ортогональной группе
лежит в ортогональной группе 
Обратно, пусть  удовлетворяет условиям определения (8.6.1). Из (ii) получаем
удовлетворяет условиям определения (8.6.1). Из (ii) получаем  Мы знаем,
Мы знаем,  состоит из гладких функций. Для любой точки z на окружности отображение вычисления: сопоставляющее функции ее значение в точке z, является изоморфизмом не только линейных пространств, но и алгебр Ли. Оно коммутирует также с комплексным сопряжением. Если петля у определена формулой
состоит из гладких функций. Для любой точки z на окружности отображение вычисления: сопоставляющее функции ее значение в точке z, является изоморфизмом не только линейных пространств, но и алгебр Ли. Оно коммутирует также с комплексным сопряжением. Если петля у определена формулой  то она является петлей со значениями в группе автоморфизмов алгебры Ли
то она является петлей со значениями в группе автоморфизмов алгебры Ли  Для группы с тривиальным центром это означает, что у принадлежит
Для группы с тривиальным центром это означает, что у принадлежит  По уже знакомым соображениям
По уже знакомым соображениям 
Как и в предыдущем разделе, из теоремы (8.6.2) можно получить, что умножение  является диффеоморфизмом, а умножение
является диффеоморфизмом, а умножение  диффеоморфизмом на плотное открытое подмножество связной компоненты единицы. Сейчас мы определим стратификацию и клеточное разбиение для
диффеоморфизмом на плотное открытое подмножество связной компоненты единицы. Сейчас мы определим стратификацию и клеточное разбиение для  по аналогии с теоремами, доказанными ранее для
по аналогии с теоремами, доказанными ранее для 
Выберем максимальный тор  и систему положительных корней. Тогда мы можем определить нильпотентные подгруппы
и систему положительных корней. Тогда мы можем определить нильпотентные подгруппы  в
в  алгебры Ли которых порождены корневыми векторами из
алгебры Ли которых порождены корневыми векторами из  связанными с положительными (отрицательными) корнями. Мы определим также подгруппы
связанными с положительными (отрицательными) корнями. Мы определим также подгруппы  состоит из петель
состоит из петель  таких, что
таких, что  Таким образом,
Таким образом, 
Сформулируем результат, который мы хотим доказать.
Теорема (8.6.3). (i)  является объединением стратов которые занумерованы решеткой
является объединением стратов которые занумерованы решеткой  состоящей из гомоморфизмов
состоящей из гомоморфизмов 
(ii) Страт  является орбитой точки
является орбитой точки  относительно действия
относительно действия  и представляет собой локально замкнутое стягиваемое комплексное подмногообразие в
и представляет собой локально замкнутое стягиваемое комплексное подмногообразие в  конечной коразмерности
конечной коразмерности  диффеоморфное
диффеоморфное  .
.
(iii) Орбита точки  относительно действия
относительно действия  является комплексной клеткой
является комплексной клеткой  размерности
размерности  которая диффеоморфна
которая диффеоморфна  и трансверсально пересекается с в единственной точке
и трансверсально пересекается с в единственной точке  .
.
(iv) Орбита точки  относительно действия
относительно действия  является открытым подмножеством в
является открытым подмножеством в  Умножение
Умножение  задает диффеоморфизм
задает диффеоморфизм 
Объединение клеток  совпадает с
совпадает с 
Вновь стратификация подмножества  оказывается индуцированной стратификацией грассманиана
оказывается индуцированной стратификацией грассманиана  Для определения последней мы должны выбрать ортонормированный базис
Для определения последней мы должны выбрать ортонормированный базис  занумерованный целыми числами. Мы сделаем это таким образом, чтобы подпространство
занумерованный целыми числами. Мы сделаем это таким образом, чтобы подпространство  оказалось порожденным множеством
оказалось порожденным множеством  при
при  и чтобы
и чтобы  Отсюда
Отсюда  что
что  базис для
базис для  Мы выберем его так, чтобы он состоял из собственных векторов относительно действия группы
Мы выберем его так, чтобы он состоял из собственных векторов относительно действия группы  Каждый вектор (для
Каждый вектор (для  является весовым относительно действия Т: это корневой вектор группы G или вектор веса нуль. Мы выберем нумерацию для
является весовым относительно действия Т: это корневой вектор группы G или вектор веса нуль. Мы выберем нумерацию для  так, чтобы вектор предшествовал вектору всякий раз, когда разность между весом вектора
так, чтобы вектор предшествовал вектору всякий раз, когда разность между весом вектора  и весом вектора является суммой положительных корней. В частности, набор
и весом вектора является суммой положительных корней. В частности, набор  где
где  ранг группы
ранг группы  состоит из всех отрицательных корневых векторов и порождает алгебру Ли
состоит из всех отрицательных корневых векторов и порождает алгебру Ли  порождает алгебру Ли
порождает алгебру Ли 
В базисе группа  действует на
действует на  нижними треугольными матрицами из подгруппы
нижними треугольными матрицами из подгруппы  см. (7.3.3).
см. (7.3.3).
Страты и клетки для  нумеруются подмножествами
нумеруются подмножествами  множества
множества  Среди них встречаются множества соответствующие решетке Т гомоморфизмов
Среди них встречаются множества соответствующие решетке Т гомоморфизмов  эти множества определяются соотношением
эти множества определяются соотношением

Мы будем писать  вместо
вместо  В нашем доказательстве теоремы (8.6.3) используется следующая
В нашем доказательстве теоремы (8.6.3) используется следующая
Лемма (8.6.4). Страты  и клетки
и клетки  для
для  пересекающиеся с
пересекающиеся с  совпадают с
совпадают с  для
для 
Мы отложим доказательство этой леммы до конца раздела, а. сейчас займемся доказательством теоремы (8.6.3).
Доказательство теоремы (8.6.3). Положим

Лемма (8.6.4) показывает, что  является объединением стратов
является объединением стратов  Так как
Так как  лежит в
лежит в  ясно, что орбита точки
ясно, что орбита точки  относительно
относительно  лежит в
лежит в  Поэтому основное — это доказать, что
Поэтому основное — это доказать, что  транзитивно действует на 2. Из предложения (8.4.1) мы знаем, что любое единственным образом представляется в виде
транзитивно действует на 2. Из предложения (8.4.1) мы знаем, что любое единственным образом представляется в виде  где у принадлежит
где у принадлежит  Так как
Так как  -является пересечением
-является пересечением  достаточно показать, что у принадлежит
достаточно показать, что у принадлежит  Конструкция у из (8.4.1) может быть сформулирована следующим образом. Если
Конструкция у из (8.4.1) может быть сформулирована следующим образом. Если  лежит в
лежит в  размерность
размерность  равна
равна  и отображение вычисления
и отображение вычисления  является изоморфизмом для любой точки
является изоморфизмом для любой точки  Ортогональная проекция
Ортогональная проекция  также является изоморфизмом. Само
также является изоморфизмом. Само  разлагается в композицию
разлагается в композицию

Каждое из трех встречающихся здесь линейных пространств является алгеброй Ли для  заметим, что
заметим, что  Более того, каждое отображение является гомоморфизмом алгебр Ли, ибо отображение
Более того, каждое отображение является гомоморфизмом алгебр Ли, ибо отображение  индуцировано проекцией
индуцировано проекцией  на
на  идеал в
идеал в  Итак,
Итак,  гомоморфизм алгебр Ли и, следовательно, лежит в
гомоморфизм алгебр Ли и, следовательно, лежит в  как и хотелось.
как и хотелось.
Остаток доказательства повторяет аналогичные рассуждения для  и мы не будем останавливаться на нем подробнее.
и мы не будем останавливаться на нем подробнее.
Орбиты действия  на
на  получаются, как
получаются, как  раньше, объединением
раньше, объединением  которые нумеруются классами сопряженности гомоморфизмов
которые нумеруются классами сопряженности гомоморфизмов  или, эквивалентно, множеством орбит
или, эквивалентно, множеством орбит  группы Вейля
группы Вейля  группы
группы 
ствующей на решетке  Это множество
Это множество  можно упорядочить по правилу:
можно упорядочить по правилу:  если выпуклая оболочка орбиты
если выпуклая оболочка орбиты  содержится в выпуклой оболочке орбиты
содержится в выпуклой оболочке орбиты  . (Здесь Т рассматривается как решетка в векторном пространстве
. (Здесь Т рассматривается как решетка в векторном пространстве  ) Не продолжая обсуждения, мы сформулируем
) Не продолжая обсуждения, мы сформулируем
Предложение (8.6.5). (i)  трансверсально пересекает
трансверсально пересекает  по множеству состоящему из гомоморфизмов
по множеству состоящему из гомоморфизмов  которые сопряжены к А.
которые сопряжены к А.

Так как имеется клеточное разбиение множества  на клетки четной размерности, фундаментальная группа
на клетки четной размерности, фундаментальная группа  должна быть тривиальной. Теперь рассмотрим
должна быть тривиальной. Теперь рассмотрим  как пространство полиномиальных петель
как пространство полиномиальных петель  Фундаментальная группа пространства
Фундаментальная группа пространства  равна второй гомотопической группе
равна второй гомотопической группе  Если мы покажем, что пространство
Если мы покажем, что пространство  гомотопически эквивалентно
гомотопически эквивалентно  то получим доказательство хорошо известного, но важного факта:
то получим доказательство хорошо известного, но важного факта:  равна нулю для любой компактной группы Ли
равна нулю для любой компактной группы Ли  По существу это доказательство совпадает с доказательством Ботта, основанным на теории Морса [14].
По существу это доказательство совпадает с доказательством Ботта, основанным на теории Морса [14].
Предложение (8.6.6). Включение  или, эквивалентно,
или, эквивалентно,  является гомотопической эквивалентностью.
является гомотопической эквивалентностью.
Следствие (8.6.7). Гомотопическая группа  равна нулю.
равна нулю.
Доказательство (8.6.6). Идея доказательства состоит в том,  обладают согласованными стратификациями с помощью гомотопически эквивалентных подмножеств.
обладают согласованными стратификациями с помощью гомотопически эквивалентных подмножеств.
Расположим элементы решетки Т в виде последовательности, начинающейся с нуля, так, чтобы А, предшествовало  если
если  содержится в замыкании страта
содержится в замыкании страта  (мы будем выражать это формулой
(мы будем выражать это формулой  . Пусть
. Пусть  обозначает объединение всех открытых множеств
обозначает объединение всех открытых множеств  для которых
для которых  объединение
объединение  таких, что
таких, что  Мы будем писать также
Мы будем писать также  для соответствующих частей множества
для соответствующих частей множества  Нам достаточно показать, что
Нам достаточно показать, что  является гомотопической эквивалентностью для всех А (ср. [114, приложение]).
является гомотопической эквивалентностью для всех А (ср. [114, приложение]).
Итак,  — это объединение и
— это объединение и  а пересечение этих множеств равно
а пересечение этих множеств равно  . (Тот факт, что все точки
. (Тот факт, что все точки  лежат в стратах следует из аналогичного факта для
лежат в стратах следует из аналогичного факта для
 доказанного в (7.3.3).) Множество
доказанного в (7.3.3).) Множество  стягиваемо, a
стягиваемо, a  диффеоморфно
диффеоморфно  и, следовательно, гомотопически эквивалентно
и, следовательно, гомотопически эквивалентно 
Аналогично, пространство  является объединением множеств
является объединением множеств  пересечение которых равно
пересечение которых равно  то время как
то время как  диффеоморфно
диффеоморфно  множество
множество  гомеоморфно
гомеоморфно  мы не знаем, является ли
мы не знаем, является ли  многообразием и, следовательно,
многообразием и, следовательно,  гомеоморф но
гомеоморф но  Далее,
Далее,  и
и  стягиваемы по тем же причинам, что и
стягиваемы по тем же причинам, что и  а пространство
а пространство  о гомотопически эквивалентно пространству
о гомотопически эквивалентно пространству  По индукции мы можем получить, что пространство
По индукции мы можем получить, что пространство  гомотопически эквивалентно
гомотопически эквивалентно  (Мы использовали следующий факт: если
(Мы использовали следующий факт: если  где
где  открытые подмножества, и отображение
открытые подмножества, и отображение  индуцирует гомотопические эквивалентности
индуцирует гомотопические эквивалентности  и
и  то оно является гомотопической эквивалентностью.
то оно является гомотопической эквивалентностью. 
Доказательство (8.6.4). Мы закончим этот раздел отложенным доказательством леммы (8.6.4).
Определим действие окружности Т на  следующим образом. Выберем некоторый гомоморфизм
следующим образом. Выберем некоторый гомоморфизм  что рлежит в положительной камере Вейля в
что рлежит в положительной камере Вейля в  т. е.
т. е.  для любого корня а. Для любого достаточно большого целого
для любого корня а. Для любого достаточно большого целого  совпадает с централизатором элемента
совпадает с централизатором элемента  Действие
Действие  которое мы хотим определить, получается одновременным, вращением со скоростью
которое мы хотим определить, получается одновременным, вращением со скоростью  и сопряжением с помощью
и сопряжением с помощью 

при этом  переходит в
переходит в  где
где

Это действие распространяется на все гильбертово пространство  и диагонально в базисе
и диагонально в базисе  . А именно,
. А именно,  где числа
где числа  монотонно возрастают с ростом
монотонно возрастают с ростом  для достаточно больших
для достаточно больших  Далее, Т действует и на
Далее, Т действует и на  и это действие распространяется до действия
и это действие распространяется до действия  (см. разд. 7.6). Кроме того, это действие сохраняет подмногообразие
(см. разд. 7.6). Кроме того, это действие сохраняет подмногообразие  а также страты
а также страты  Для любого
Для любого  точка
точка  стремится к некоторому пределу при
стремится к некоторому пределу при  этот предел, очевидно, является неподвижной точкой относительно действия Т и содержится в том же страте, что и
этот предел, очевидно, является неподвижной точкой относительно действия Т и содержится в том же страте, что и  (Это происходит потому, что страты характеризуются предложением (7.5.4),
(Это происходит потому, что страты характеризуются предложением (7.5.4),  просто умножает плюккерову координату
просто умножает плюккерову координату  на
на  где
где  монотонно возрастает с ростом
монотонно возрастает с ростом 
стремится к  при
при  Однако неподвижные точки действия Т на
Однако неподвижные точки действия Т на  это только под пространства
это только под пространства  для
для  . В самом деле, если подпространство
. В самом деле, если подпространство  неподвижно для некоторого
неподвижно для некоторого  то
то

для всех  Положив
Положив  мы обнаружим, что
мы обнаружим, что  коммутирует с
коммутирует с  так что
так что  лежит в
лежит в  Равенство (8.6.8) сводится теперь к условию, что отображение
Равенство (8.6.8) сводится теперь к условию, что отображение  является гомоморфизмом. Итак, любой страт содержит точку
является гомоморфизмом. Итак, любой страт содержит точку  а значит, имеет вид
а значит, имеет вид 
Рассуждения для клеток  по существу такие же: рассматривается
по существу такие же: рассматривается  при и
при и 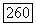
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- Глава 1. Введение
- ЧАСТЬ I
- 2.1. Алгебра Ли
- 2.2. Комплексные группы
- 2.3. Компактные группы Ли
- 2.4. Система корней
- 2.5. Группы с простыми связями
- 2.6. Группа Вейля и камеры Вейля: положительные корни
- 2.7. Неприводимые представления и антидоминантные веса
- 2.8. Комплексные однородные пространства
- 2.9. Теорема Бореля — Вейля
- Глава 3. Группы гладких отображений
- 3.1. Бесконечномерные многообразия
- 3.2. Группы отображений как бесконечномерные группы Ли
- 3.3. Группы диффеоморфизмов
- 3.4. Некоторые теоретико-групповые свойства группы Мар(Х; G)
- 3.5. Подгруппы в LG: полиномиальные петли
- 3.6. Максимальные абелевы подгруппы в LG
- 3.7. Скрученные группы петель
- Глава 4. Центральные расширения
- 4.2. Расширения алгебр Ли
- 4.3. Коприсоединенное действие группы LG на … и его орбиты
- 4.4. Групповые расширения в случае односвязной группы G
- 4.5. Расслоения со слоем окружность, связности и кривизна
- 4.6. Групповые расширения в случае полупростой, но не односвязной группы G
- 4.7. Основное центральное расширение группы LUn
- 4.8. Ограничение расширения на подгруппу LT
- 4.9. Скалярное произведение на …
- 4.10. Расширения группы Map(X; G)
- 4.11. Дополнение: когомологии группы LG и ее алгебры Ли
- Глава 5. Система корней: алгебры Каца-Муди
- 5.1. Система корней и аффинная группа Вейля
- 5.2. Образующие и соотношения
- 5.3. Алгебры Каца — Муди
- Глава 6. Группы петель как группы операторов в гильбертовом пространстве
- 6.1. Петли как операторы умножения
- 6.2. Ограниченная полная линейная группа гильбертова пространства
- 6.3. Отображение …
- 6.4. Периодичность Ботта
- 6.5. Изоморфизм .. и вложение …
- 6.6. Центральное расширение группы …
- 6.7. Центральное расширение группы …
- 6.8. Вложение группы …
- 6.9. Другие поляризации пространства Н: замена окружности прямой и введение «массы»
- 6.10. Обобщения на другие группы отображений
- Глава 7. Грассманиан гильбертова пространства и детерминантное линейное расслоение
- 7.2. Некоторые плотные подмногообразия в Gr(H)
- 7.3. Стратификация многообразия Gr(H)
- 7.4. Клеточное разбиение пространства Gr(H)
- 7.5. Плюккерово вложение
- 7.6. Действие полугруппы …
- 7.7. Детерминантное расслоение
- 7.8. Пространство Gr(H) как кэлерово многообразие и симплектическое многообразие
- Глава 8. Основное однородное пространство
- 8.2. Два приложения разложения Биркгофа
- 8.3. Грассманово описание …
- 8.4. Стратификация Gr(n): разложения Биркгофа и Брюа
- 8.5. Грассманово описание для других классических групп
- 8.6. Грассманово описание для произвольной компактной группы Ли
- 8.7. Однородное пространство LG/T и многообразие периодических флагов
- 8.8. Периодичность Ботта
- 8.9. «Омега-G» как кэлерово многообразие: поток энергии
- 8.10. «Омега-G» и голоморфные расслоения
- 8.11. Однородное пространство, связанное с римановой поверхностью: пространства модулей векторных расслоений
- 8.12. Дополнение: теория рассеяния
- ЧАСТЬ II
- Глава 9. Теория представлений
- 9.1. Общие замечания о представлениях
- 9.2. Условие положительности энергии
- 9.3. Классификация и основные свойства представлений с положительной энергией
- 9.4. Оператор Казимира и инфинитезимальное действие группы диффеоморфизмов
- 9.5. Группы Гейзенберга и их стандартные представления
- Глава 10. Фундаментальное представление
- 10.1. Г как внешняя алгебра: фермнонное пространство Фока
- 10.2. Структура гильбертова пространства
- 10.3. Кольцо симметрических многочленов
- 10.4. Г как сумма симметрических алгебр
- 10.5. Тройное тождество Якоби
- 10.6. Базисные представления групп LUn и LSUn
- 10.7. Двумерная квантовая теория поля
- Глава 11. Теория Бореля-Вейля
- 11.1. Пространство голоморфных сечений однородного линейного расслоения
- 11.2. Разложение представлений: полная приводимость
- 11.3. Существование голоморфных сечений
- 11.4. Условие гладкости
- Глава 12. Спинорное представление
- 12.1. Алгебра Клиффорда
- 12.2. Вторая конструкция спинорного представления
- 12.3. Спинорное представление как сечения голоморфного линейного расслоения
- 12.4. Бесконечномерное спинорное представление
- 12.5. Базисное представление группы LO2
- 12.6. Аналогия: экстраспециальная 2-группа
- Глава 13. Блипы, или вертексные операторы
- 13.2. Действие … на …
- 13.3. Представления уровня 1 группы LG для группы G с простыми связями
- 13.4. Действие … на представлениях групп петель с положительной энергией
- 13.5. Общие замечания: случай общей максимальной абелевой подгруппы в LG
- Глава 14. Формула Каца для характеров и резольвента Бернштейна — Гельфанда — Гельфанда
- 14.2. Мотивировка формулы для характеров: формула Вейля для компактной группы
- 14.3. Формула для характера
- 14.4. Алгебраическое доказательство формулы для характеров
- 14.5. Резольвента Бернштейна — Гельфанда — Гельфанда
- 14.6. Приложения резольвенты: когомологии Lg
- Добавление А. Разложение петель: образующие и соотношения для …
- Добавление В. Гармонические отображения
- Дополнение. Группы петель и уравнения типа КдФ
- 3. Детерминантное расслоение и «тау»-функция
- 4. Обобщенные уравнения КдФ и формальная функция Бейкера
- 5. Функция Бейкера
- 6. Алгебраические кривые: конструкция Кричевера
- 7. Рациональные кривые
- 8. Функции Шура и «тау»-функция
- 9. Тэта-функция и «тау»-функция
- 10. Приложение: теория представлений групп петель






















































































































































































































































































































































































































































