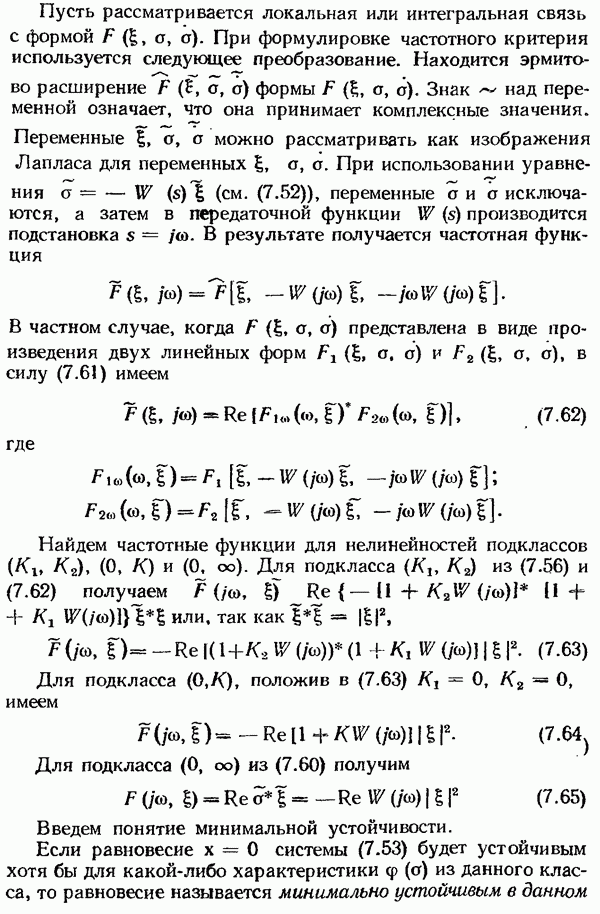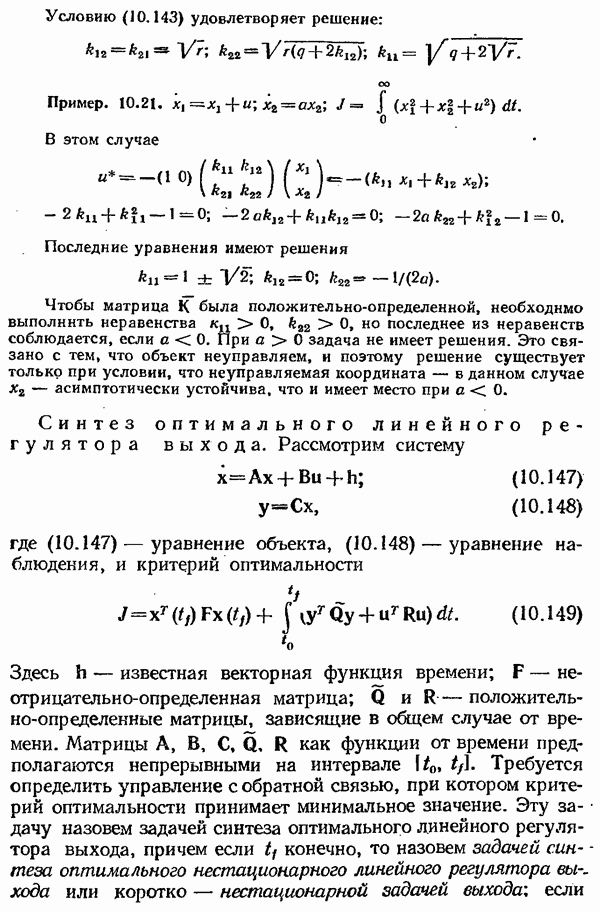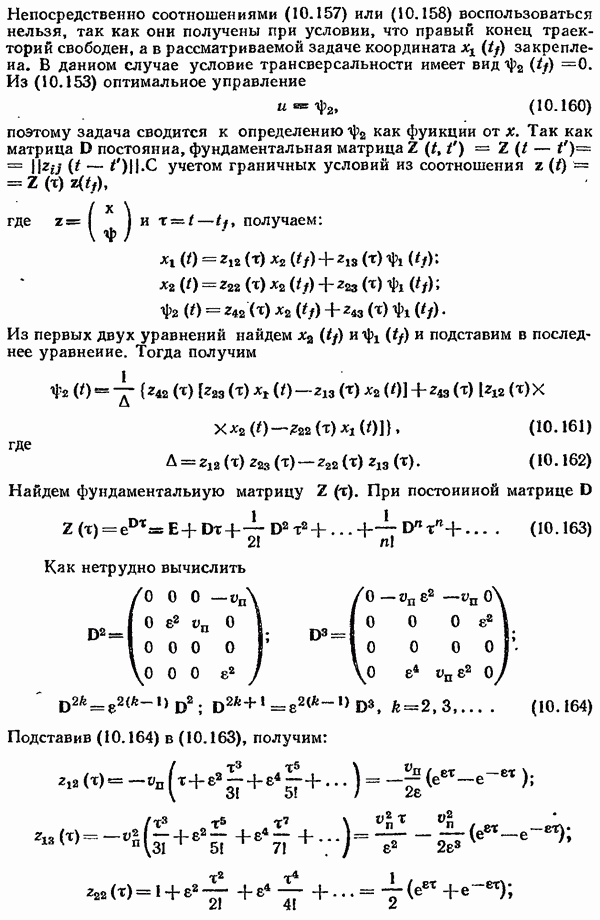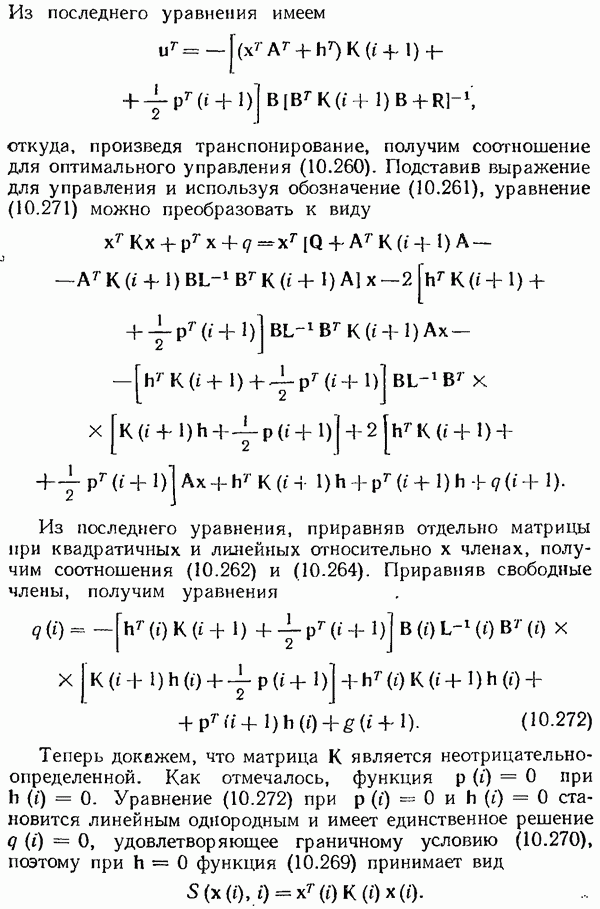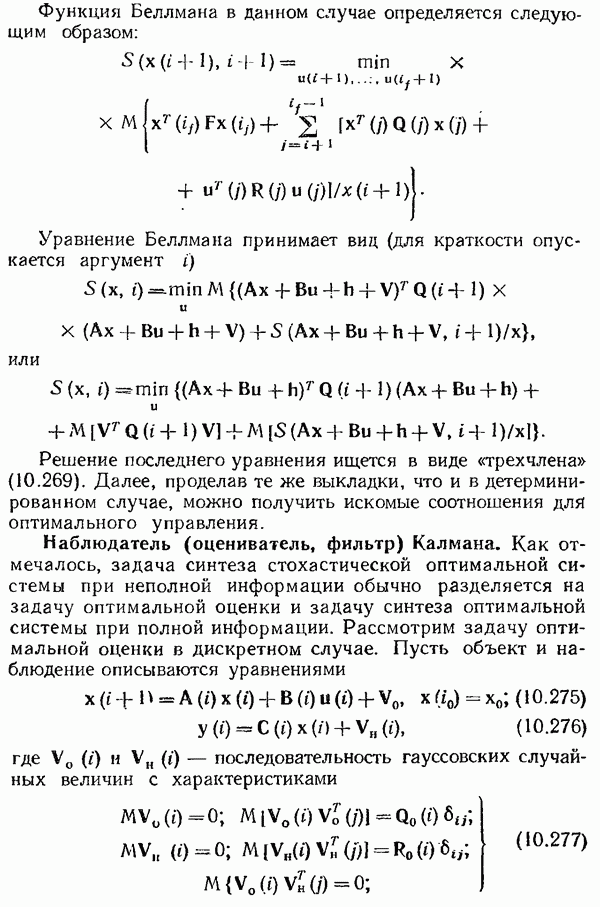| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Синтез оптимального линейного регулятора выхода.
Рассмотрим систему

где (10.147) — уравнение объекта, (10.148) — уравнение наблюдения, и критерий оптимальности

Здесь  — известная векторная функция времени;
— известная векторная функция времени;  — неотрицательно-определенная матрица;
— неотрицательно-определенная матрица;  — положительно-определенные матрицы, зависящие в общем случае от времени. Матрицы А, В, С, Q, R как функции от времени предполагаются непрерывными на интервале
— положительно-определенные матрицы, зависящие в общем случае от времени. Матрицы А, В, С, Q, R как функции от времени предполагаются непрерывными на интервале  Требуется определить управление с обратной связью, при котором критерий оптимальности принимает минимальное значение. Эту задачу назовем задачей синтеза оптимального линейного регулятора выхода, причем если
Требуется определить управление с обратной связью, при котором критерий оптимальности принимает минимальное значение. Эту задачу назовем задачей синтеза оптимального линейного регулятора выхода, причем если  конечно, то назовем задачей синтеза оптимального нестационарного линейного регулятора выхода или коротко — нестационарной задачей выхода; если
конечно, то назовем задачей синтеза оптимального нестационарного линейного регулятора выхода или коротко — нестационарной задачей выхода; если
 и матрицы А, В, С, Q, R постоянны, то назовем задачей синтеза оптимального стационарного линейного регулятора выхода или коротко — стационарной задачей выхода. В стационарной задаче выхода дополнительно требуется, чтобы замкнутая система была асимптотически устойчива.
и матрицы А, В, С, Q, R постоянны, то назовем задачей синтеза оптимального стационарного линейного регулятора выхода или коротко — стационарной задачей выхода. В стационарной задаче выхода дополнительно требуется, чтобы замкнутая система была асимптотически устойчива.
Задача синтеза оптимального линейного регулятора выхода отличается от рассмотренной задачи синтеза оптимального линейного регулятора состояния тем, что в критерии оптимальности (10.149) входит интегральная квадратичная ошибка выходного (наблюдаемого) вектора, а не вектора состояния, и условие задачи дополняется уравнением наблюдения.
Подставив выражение (10.148) для выходного вектора в функционал (10.149), получим

Таким образом, формально приходим к задаче синтеза оптимального линейного регулятора состояния (10.147), (10.150). Отличие этой задачи от ранее рассмотренной заключается в том, что здесь роль матрицы Q играет произведение  поэтому решение задачи синтеза оптимального нестационарного линейного регулятора выхода совпадает с решением (10.122)-(10.125) задачи синтеза оптимального нестационарного линейного регулятора состояния при условии, что в матричном уравнении Риккати
поэтому решение задачи синтеза оптимального нестационарного линейного регулятора выхода совпадает с решением (10.122)-(10.125) задачи синтеза оптимального нестационарного линейного регулятора состояния при условии, что в матричном уравнении Риккати  . И решение существует и единственно независимо от свойств стабилизируемости и обнаруживаемости системы. Существование и единственность решения следует из существования и единственности решения уравнений (10.123), (10.124) при граничных условиях (10.125).
. И решение существует и единственно независимо от свойств стабилизируемости и обнаруживаемости системы. Существование и единственность решения следует из существования и единственности решения уравнений (10.123), (10.124) при граничных условиях (10.125).
Решение задачи синтеза оптимального стационарного линейного регулятора выхода совпадает с решением (10.140), (10.141) задачи синтеза оптимального стационарного линейного регулятора состояния при условии, что в алгебраическом уравнении Риккати  . Это решение существует и единственно в том и только в том случае, если система (10.147), (10.148) стабилизируема и обнаруживаема [10].
. Это решение существует и единственно в том и только в том случае, если система (10.147), (10.148) стабилизируема и обнаруживаема [10].
На строгом доказательстве последнего утверждения останавливаться не будем. Ограничимся общими рассуждениями. Так как на неуправляемые координаты воздействовать нельзя, Для возможности решения задачи синтеза асимптотически устойчивой системы необходимо, чтобы они стремились со
временем к нулю. Точно так же, нельзя воздействовать должным образом на невосстанавливаемые координаты, так как неизвестно, как они изменяются. Поэтому необходимо, чтобы они также стремились со временем к нулю (обнаруживаемость). То, что обнаруживаемость и восстанавливаемость являются достаточным условием существования решения, следует из того, что всегда можно выбрать такое управление с обратной связью, при котором восстанавливаемые и управляемые координаты стремятся асимптотически к нулю.
Теперь рассмотрим алгебраическое уравнение Риккати

которое необходимо решить, чтобы определить оптимальный закон управления в задаче синтеза регулятора выхода. Матрица  в общем случае является неотрицательно-определенной, хотя матрица Q положительно определена. Очевидно, она является положительно-определенной в том и только в том случае, если
в общем случае является неотрицательно-определенной, хотя матрица Q положительно определена. Очевидно, она является положительно-определенной в том и только в том случае, если  только при
только при 
В том случае, когда матрица  не является положительно-определенной, искомым решением уравнения (10.151), т. е. решением, определяющим оптимальный закон управления, может быть неотрицательно-определенная матрица. При этом уравнение (10.151) не имеет решения, которое было бы положительно-определенной матрицей. Как увидим на примере, из того, что матрица
не является положительно-определенной, искомым решением уравнения (10.151), т. е. решением, определяющим оптимальный закон управления, может быть неотрицательно-определенная матрица. При этом уравнение (10.151) не имеет решения, которое было бы положительно-определенной матрицей. Как увидим на примере, из того, что матрица  не является положительно-определенной, не следует, что и искомое решение уравнения
не является положительно-определенной, не следует, что и искомое решение уравнения  также не является положительно-определенной матрицей. Можно показать [10], что искомое решение (10.151) является положительно-определенной матрицей в том и только в том случае, если система (10.147), (10.148) вполне восстанавливаема.
также не является положительно-определенной матрицей. Можно показать [10], что искомое решение (10.151) является положительно-определенной матрицей в том и только в том случае, если система (10.147), (10.148) вполне восстанавливаема.
Таким образом, если уравнение (10.151) не имеет положительно-определенного решения, т. е. решения, которое является положительно-определенной матрицей, следует искать неотрицательно-определенное решение.
Критерий неотрицательной определенности. Для того чтобы симметричная матрица К была неотрицательно определена, необходимо и достаточно, чтобы все главные миноры определителя  (т. е. все миноры, получающиеся из этого определителя вычеркиванием строк и столбцов с одними и теми же номерами, или, иначе говоря, все
(т. е. все миноры, получающиеся из этого определителя вычеркиванием строк и столбцов с одними и теми же номерами, или, иначе говоря, все
миноры, симметричные относительно главной диагонали этого определителя) были неотрицательны.
Пример 10.22.  .
.
В данном случае

Алгебраическое уравнение Риккати имеет вид

или в скалярной форме

Оно имеет положительно-определенное решение

хотя матрица  не ивляется положительно-определенной.
не ивляется положительно-определенной.
Метод решения алгебраического уравнения Риккати. Алгебраическое уравнение Риккати является нелинейным, и в общем случае аналитически решить его не удается. Как было показано, решение этого уравнения совпадает с установившимся решением (дифференциального) матричного уравнения Риккати. Поэтому один из возможных способов его решения основан на нахождении установившегося решения матричного уравнения Риккати (10.137), записанного в обратном времени, при начальном условии  , где
, где  — произвольная неотрицательно-определенная симметричная матрица.
— произвольная неотрицательно-определенная симметричная матрица.
Рассмотрим еще численный метод Ньютона-Рафсона [10]. Запишем алгебраическое уравнение Риккати в виде

где  — в общем случае неотрицательно-определенная матрица (в частности, она может быть равна
— в общем случае неотрицательно-определенная матрица (в частности, она может быть равна  . Введем матричную функцию
. Введем матричную функцию

Задача заключается в том, чтобы определить неотрицательноопределенную матрицу К, удовлетворяющую условию  . Построим итерационную процедуру. Пусть
. Построим итерационную процедуру. Пусть  решение, которое получается на
решение, которое получается на  шаге. Положим
шаге. Положим

Предполагая, что  является малой величиной, и пренебрегая квадратичным относительно
является малой величиной, и пренебрегая квадратичным относительно  членом, получим
членом, получим

Приравняв правую часть нулю, получим линейное уравнение

откуда находится 
Таким образом, имеем следующую итерационную процедуру:
а) вначале полагается  и выбирается
и выбирается 
б) из последнего уравнения находится 
в) если  не превышает допустимой ошибки (допустимая ошибка задается), то итерационная процедура заканчивается; в противном случае увеличивается
не превышает допустимой ошибки (допустимая ошибка задается), то итерационная процедура заканчивается; в противном случае увеличивается  на единицу и по формуле (10.152) вычйсляется
на единицу и по формуле (10.152) вычйсляется  соответствующее новому значению
соответствующее новому значению  а затем происходит возврат к
а затем происходит возврат к  .
.
Процедура сходится, если правильно выбрать начальное приближение  Справедливо следующее утверждение 1101: если алгебраическое уравнение Риккати имеет единственное неотрицательно-определенное решение, то
Справедливо следующее утверждение 1101: если алгебраическое уравнение Риккати имеет единственное неотрицательно-определенное решение, то

при условии, что начальное приближение  выбрано таким образом, что матрица
выбрано таким образом, что матрица  асимптотически устойчива (т. е. ее собственные значения имеют отрицательные вещественные части).
асимптотически устойчива (т. е. ее собственные значения имеют отрицательные вещественные части).
Если начальное приближение выбрано неудачно, то может наблюдаться сходимость к произвольному решению алгебраического уравнения Риккати или вообще не сходится. Если матрица А асимптотически устойчива, то целесообразно принять 
Метод прогонки решения задачи синтеза оптимальной линейной системы. Выше задача синтеза оптимальной линейной системы (при  ) методом динамического программирования была сведена
) методом динамического программирования была сведена
на к решению матричного уравнения иккати. Здесь рассматривается еще один метод решения этой задачи, основанной на вариационном методе и прогонке (переносе) граничных условий с одного конца на другой. Этот метод, как увидим на примере, иногда позволяет получить аналитическое выражение для оптимального закона управления и тогда, когда матричное уравнение Риккати аналитически решить не удается.
Итак, рассмотрим задачу синтеза оптимальной линейной системы при условии, что уравнение объекта, граничные условия и критерий оптимальности имеют следующий вид:

Здесь для удобства в качестве критерия оптимальности принят функционал (10.121), поделенный на два. Это, очевидно, не должно сказаться на решении задачи, т. е. на оптимальном законе управления.
Составим гамильтониан (принимаем 

Найдем уравнения Эйлера-Лагранжа:

Из последнего уравнения

Подставив это выражение, запишем уравнение объекта совместно с первым уравнением Эйлера—Лагранжа:

или  где
где 
Условие трансверсальности (10.40) принимает вид

Запишем решение уравнения (10.154), используя его нормированную фундаментальную матрицу  удовлетворяющую условию
удовлетворяющую условию  при любом
при любом 

Представим фундаментальную матрицу в соответствии со структурой уравнения (10.154) в виде

где  матрицы размерности
матрицы размерности 
Используя это представление и приняв  из (10.156) получим
из (10.156) получим

или после подстановки (10.155)

Исключим из полученной системы уравнений 

При этом, по существу, граничное условие из точки  на временной оси переносится в точку
на временной оси переносится в точку  Сравнивая оптимальный закон управления (10.153) после подстановки в него последнего выражения для
Сравнивая оптимальный закон управления (10.153) после подстановки в него последнего выражения для  с оптимальным законом управления (10.138), получаем
с оптимальным законом управления (10.138), получаем

и в частном случае, когда 

Соотношения (10.157) и (10.158) определяют решение матричного уравнения Риккати через фундаментальную матрицу системы, состоящей из уравнения объекта и уравнения Эйлера—Лагранжа для сопряженной координаты. Они могут быть - использованы для определения матрицы  при решении задач синтеза оптимального линейного регулятора.
при решении задач синтеза оптимального линейного регулятора.

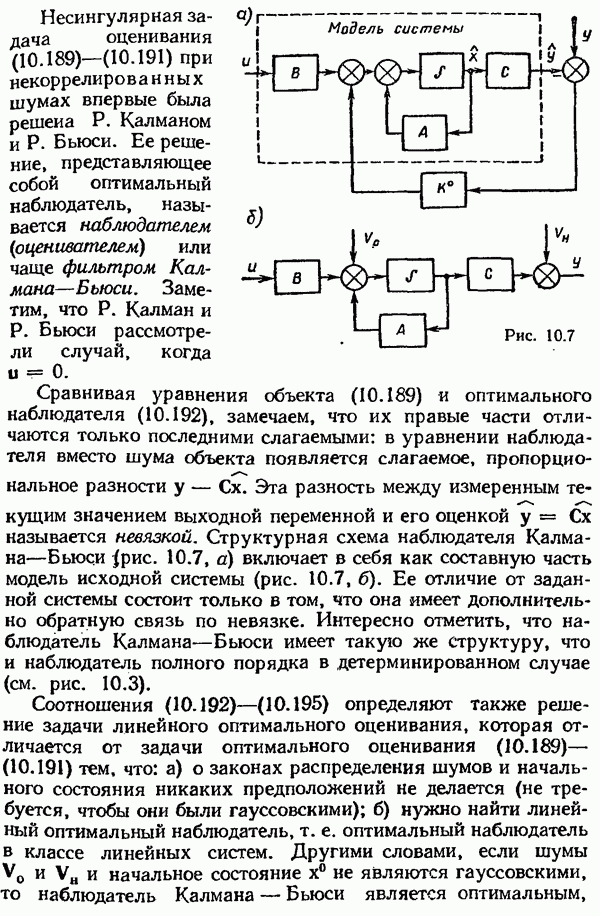
Рис. 10,б
Пример 10.23. Простейшая задача перехвата. Решим изложенным методом прогонки задачу перехвата, несколько отличную от задачи, рассмотренной в [5].
Пусть цель движется равномерно и прямолинейно со скоростью  . Перехватчик движется с постоянной скоростью
. Перехватчик движется с постоянной скоростью  Курсовые углы цели
Курсовые углы цели  и перехватчика
и перехватчика  (рис. 10.6) достаточно малы:
(рис. 10.6) достаточно малы:

При этом условии в первом приближении можно записать  где
где  — угловая скорость перехватчика. Принимая угловую скорость
— угловая скорость перехватчика. Принимая угловую скорость  за управление и введя обозначения
за управление и введя обозначения  можно записать
можно записать

где

Примем за начальное время  . Время перехвата
. Время перехвата  начальное расстояние,
начальное расстояние,  — скорость сближения перехватчика и цели. В силу (10 159) в первом приближении
— скорость сближения перехватчика и цели. В силу (10 159) в первом приближении

и промахом будет  . Потребуем, чтобы промах был равен нулю. Тогда граничные условия имеют вид
. Потребуем, чтобы промах был равен нулю. Тогда граничные условия имеют вид

Рассмотрим задачу синтеза оптимального управления с обратной связью при двух разных критериях оптимальности.
1. Пусть критерий оптимальности имеет вид

В этом случае

и матрица  принимает вид
принимает вид

Непосредственно соотношениями (10.157) или (10.158) воспользоваться нельзя, так как они получены при условии, что правый конец траекторий свободен, а в рассматриваемой задаче координата  закреплена. В данном случае условие трансверсальности имеет вид
закреплена. В данном случае условие трансверсальности имеет вид  Из (10.153) оптимальное управление
Из (10.153) оптимальное управление

поэтому задача сводится к определению  как функции от х. Так как матрица
как функции от х. Так как матрица  постоянна, фундаментальная матрица
постоянна, фундаментальная матрица  учетом граничных условий из соотношения
учетом граничных условий из соотношения  где
где  получаем:
получаем:

Из первых двух уравнений найдем  и подставим в последнее уравнение. Тогда получим
и подставим в последнее уравнение. Тогда получим

где

Найдем фундаментальную матрицу  При постоиииой матрице
При постоиииой матрице 

Как нетрудно вычислить

Подставив (10.164) в (10.163), получим:


Подставив эти выражения в (10.160)-(10.162), оптимальный закон управления можно записать следующим образом:

При  разложив экспоненциальные функции в ряд и отбросив члены, содержащие множитель
разложив экспоненциальные функции в ряд и отбросив члены, содержащие множитель  выше пятой степени, получим
выше пятой степени, получим

В исходных переменных это соотношение принимает вид

С учетом (10.159) имеем (см. рис. 10.6)

или

Используя это соотношение, оптимальный закон управления можио записать в виде

Это соотношение определяет закон пропорционального сближения с переменным коэффициентом навигации.
2. Пусть теперь критерий оптимальности имеет, вид

В этом случае

и, как легко проверить, имеем:

Точное выражение для фундаментальной матрицы получить не удается. При  , используя (10.163) и отбрасывая малые члены более высокого порядка, чем
, используя (10.163) и отбрасывая малые члены более высокого порядка, чем  получим:
получим:

После подстановки этих выражений в (10.160)-(10.161) оптимальный закон управления записывается в виде

или в исходных переменных

Используя (10.165), получаем

или, учитывай, что 

Таким образом, опять оптимальное управление определяет закон пропорционального сближения с переменным коэффициентом навигации. При  оба оптимальных закона управления совпадают и приобретают вид
оба оптимальных закона управления совпадают и приобретают вид

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
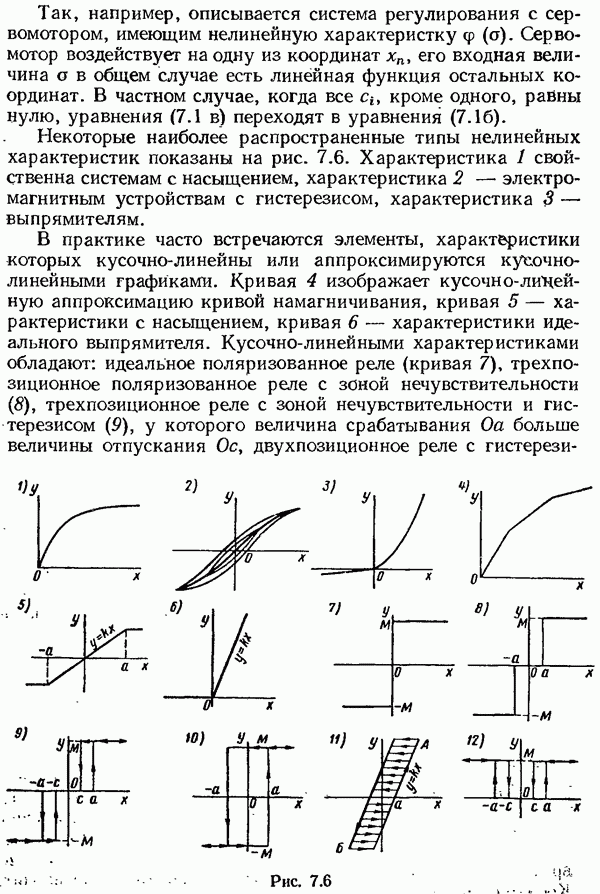
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
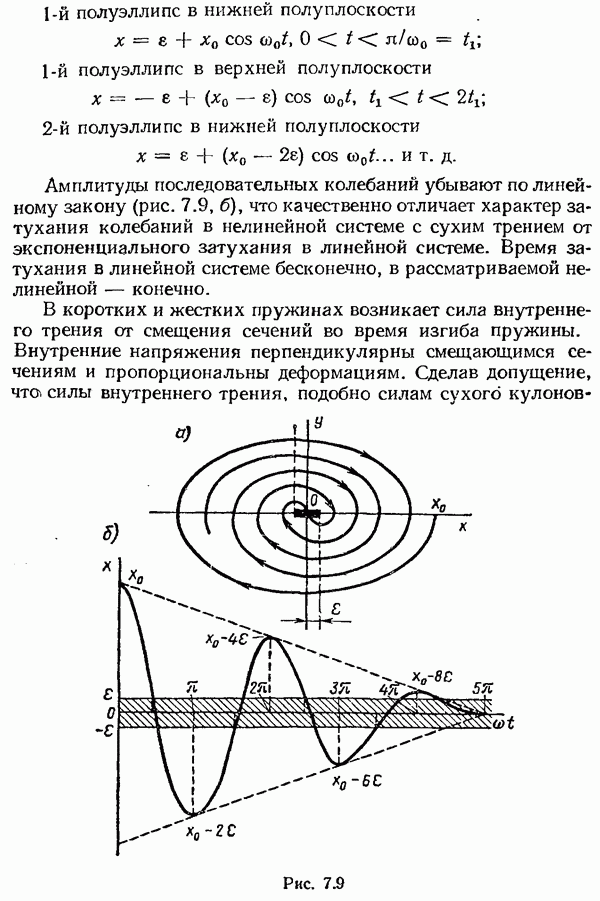
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
- § 7.3. Автоколебания. Метод точечных преобразований
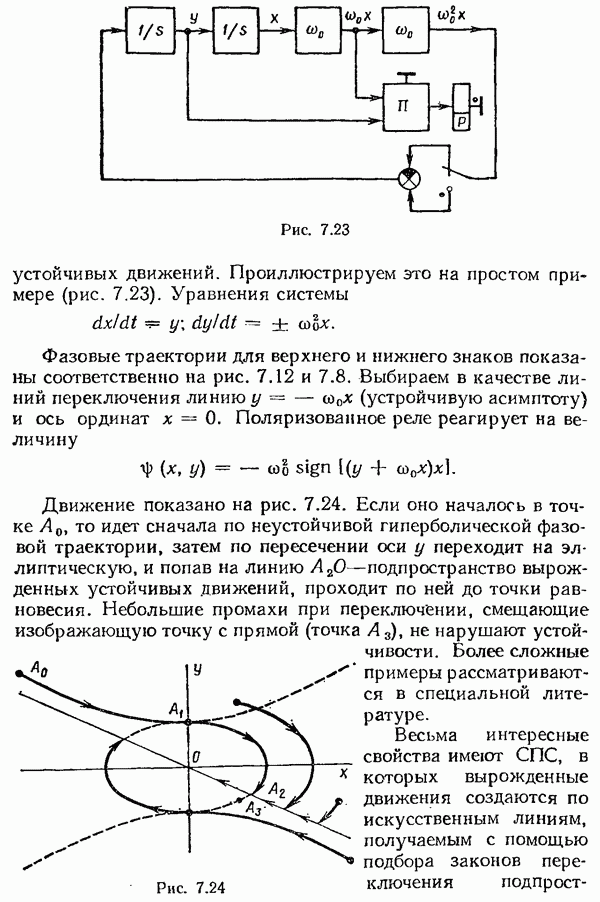
- § 7.4. Системы с переменной структурой
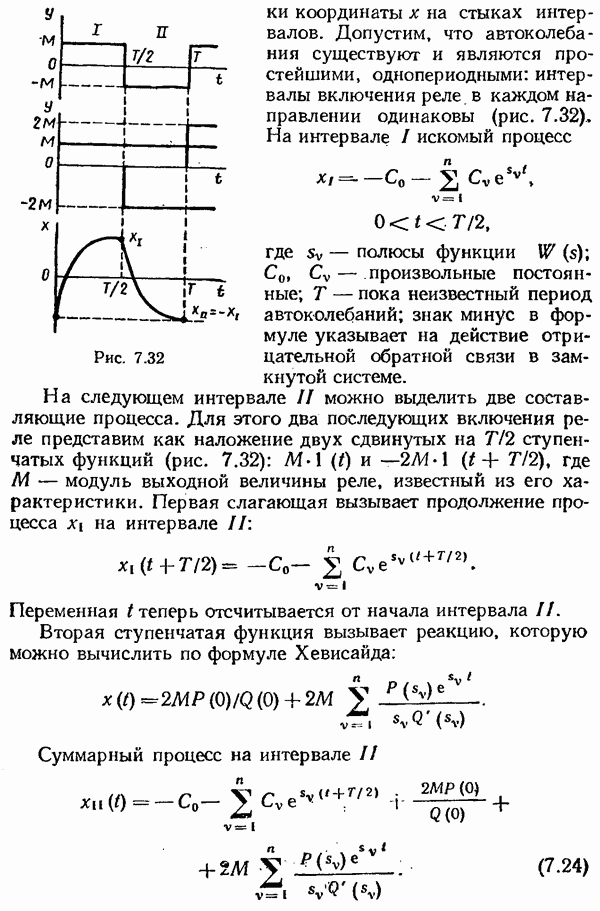
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
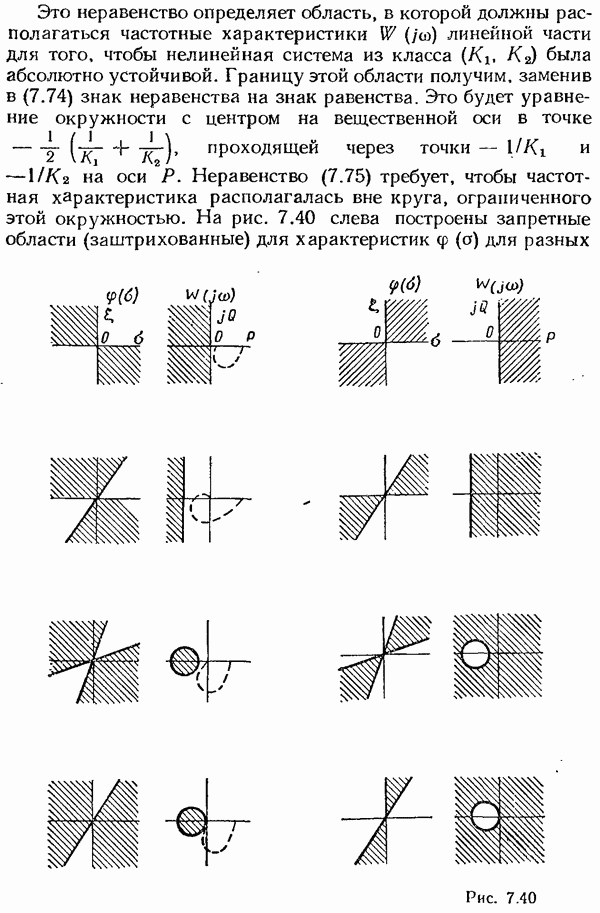
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
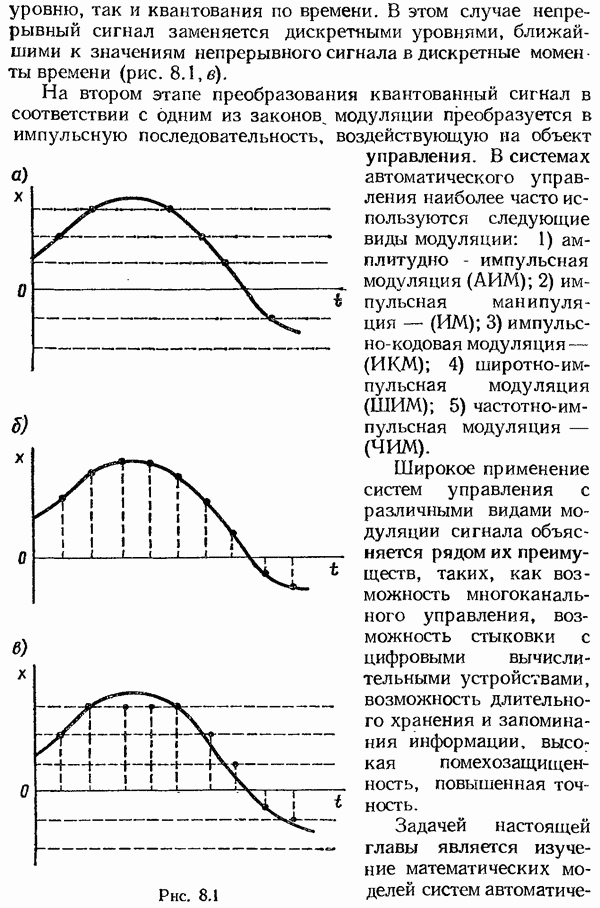
- Структурная схема амплитудно-импульсного модулятора.
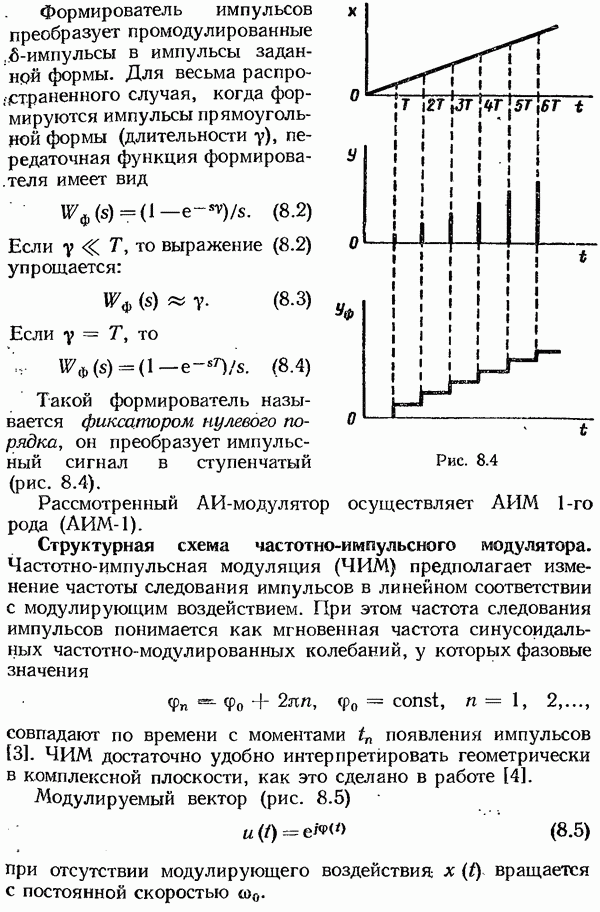
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
- Исследование периодических режимов в системах с ИЧИМ.
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
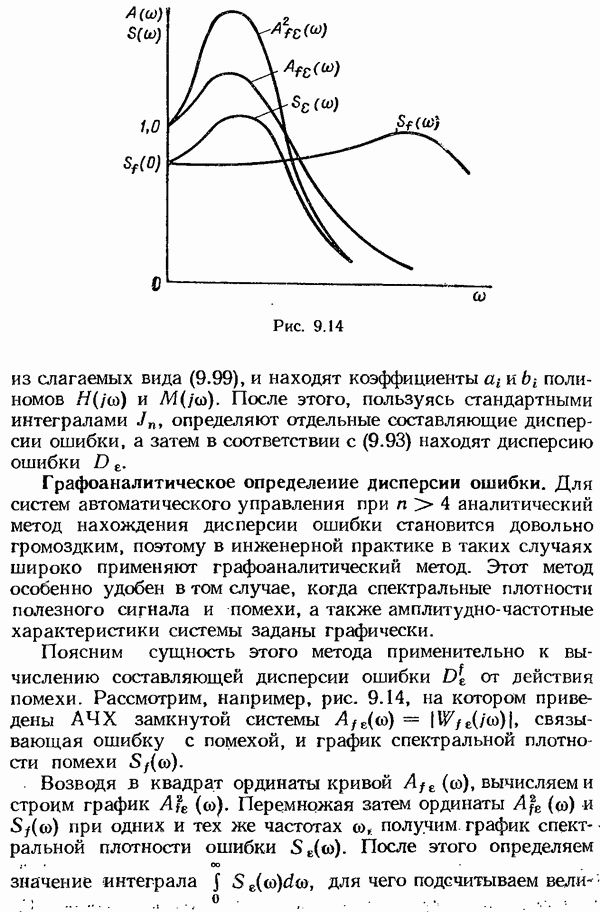
- Аналитический метод определения дисперсии ошибки.
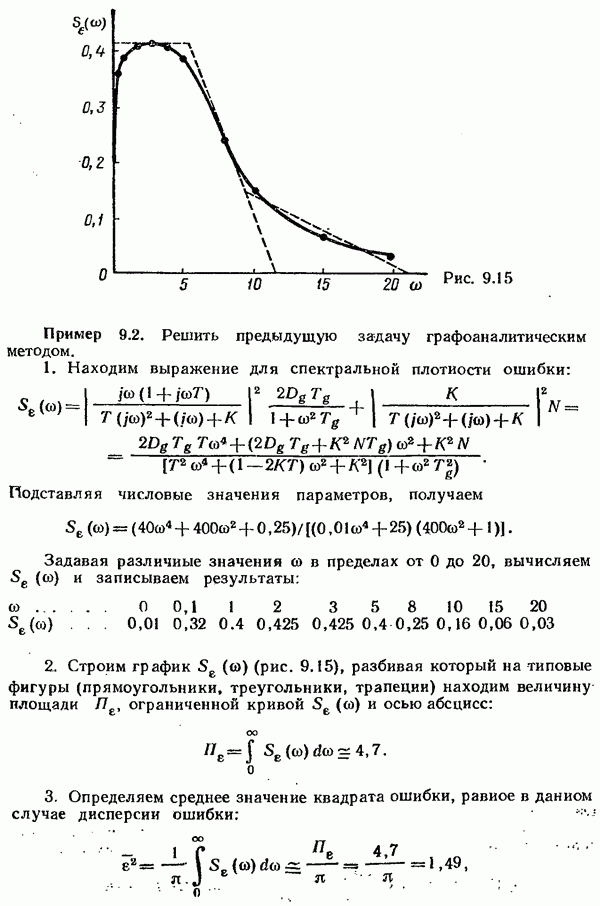
- Графоаналитическое определение дисперсии ошибки.
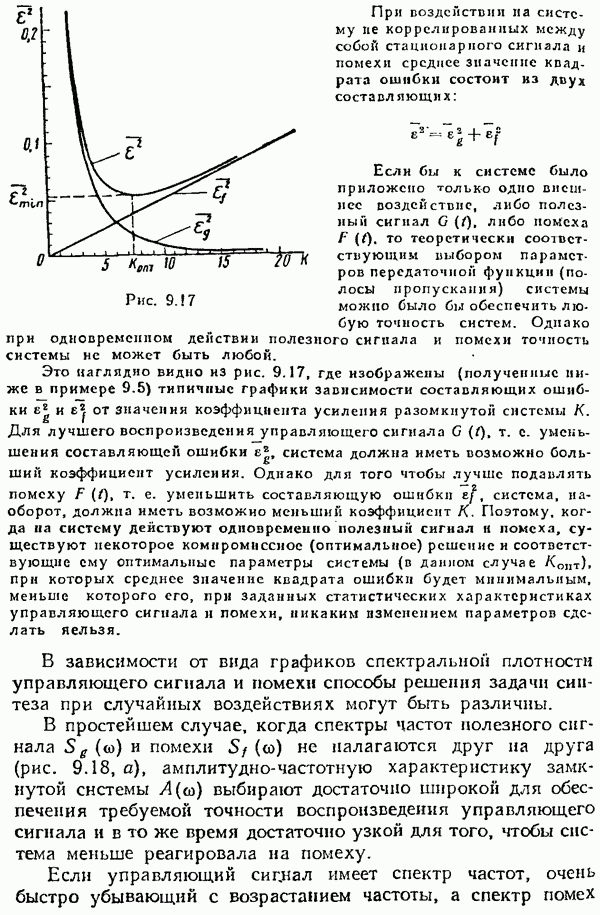
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
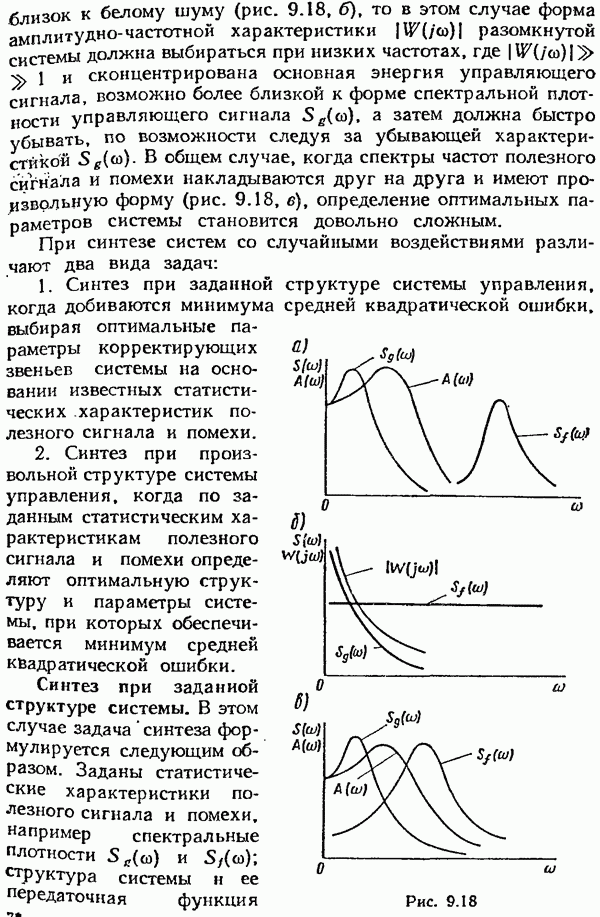
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
- § 9.9. Нелинейное преобразование случайных сигналов
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
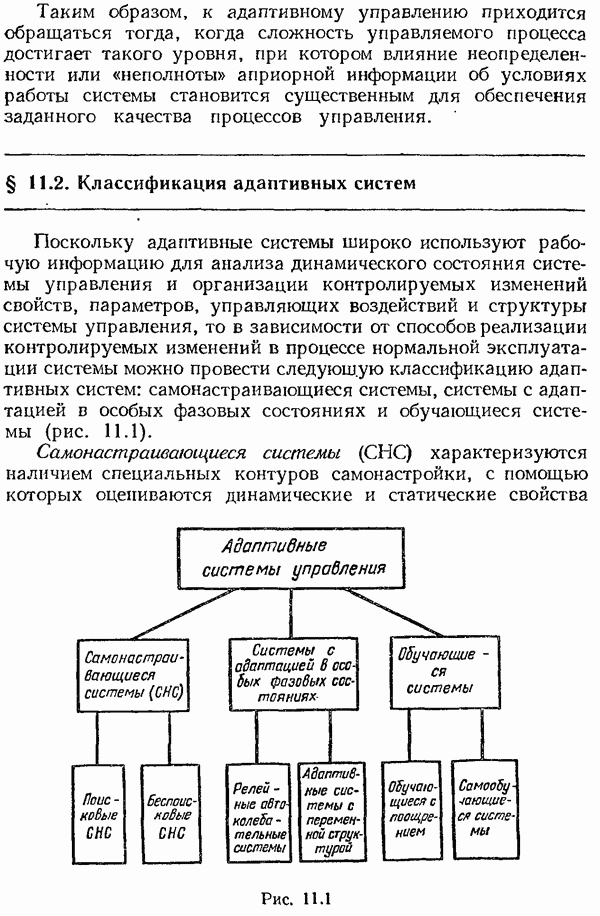
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
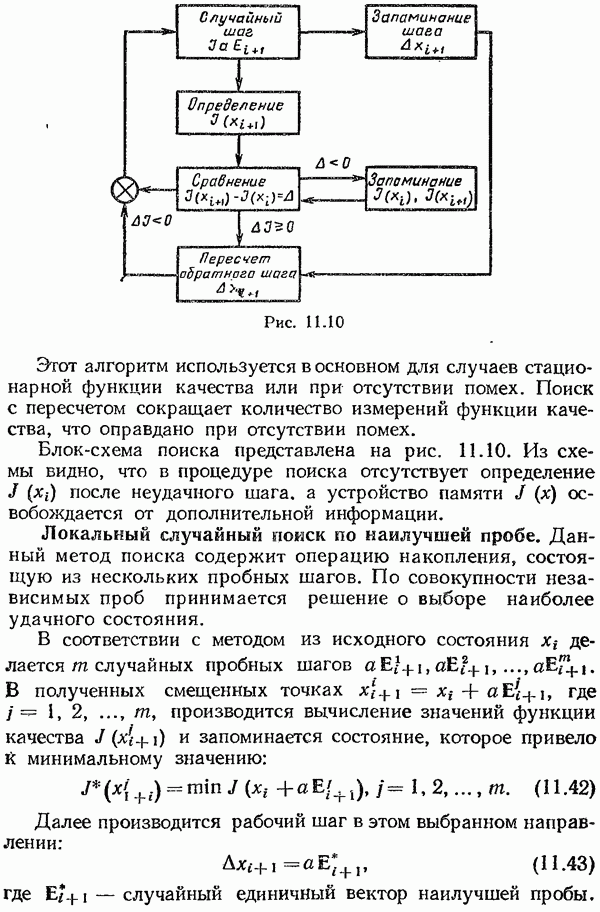
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
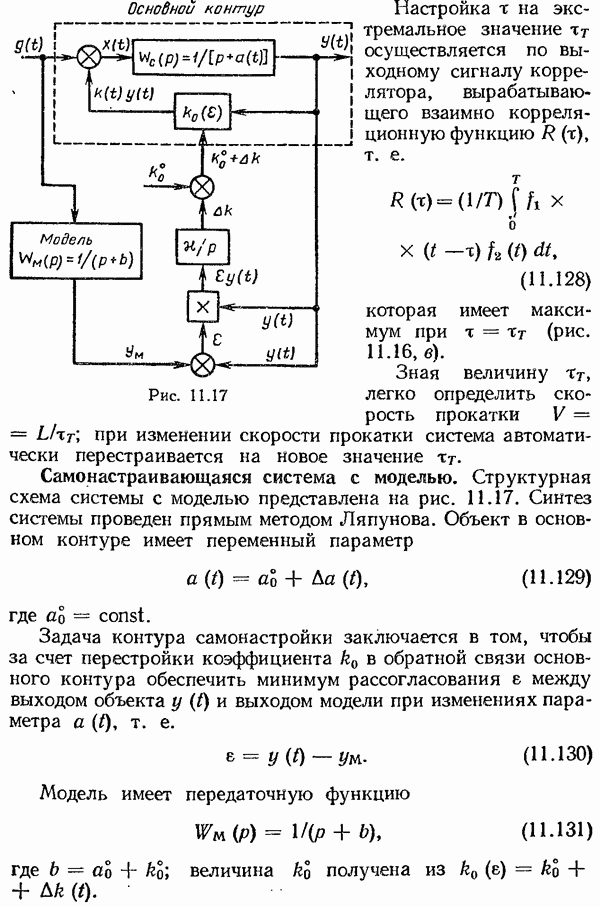
- Самонастраивающаяся система с моделью.
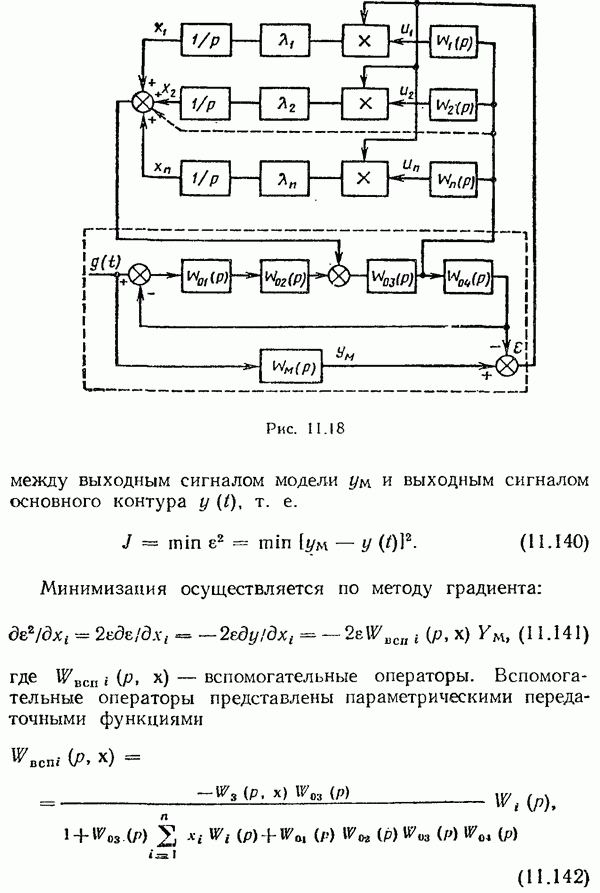
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
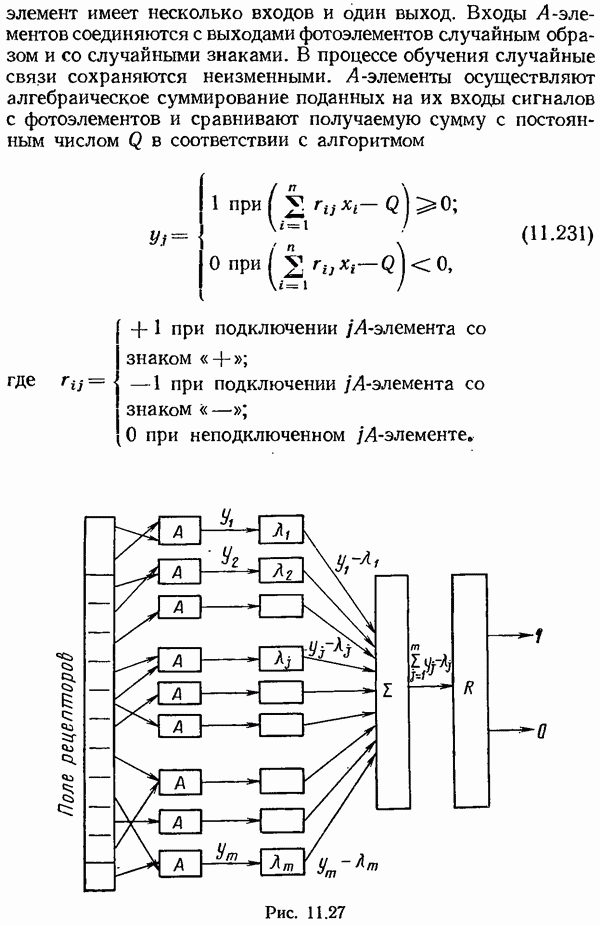
- Персептронная модель автоматической классификации.
- § 11.6. Адаптивные робототехнические системы
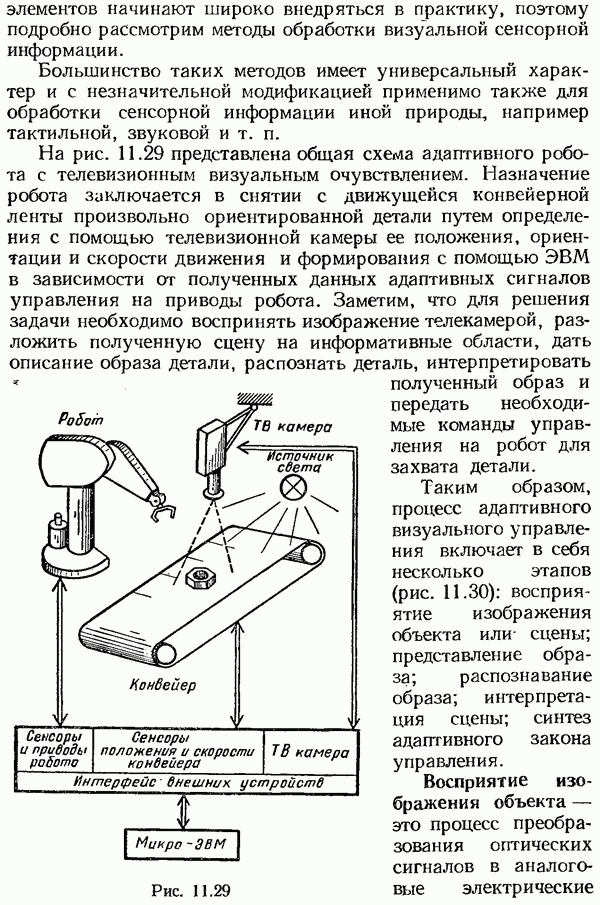
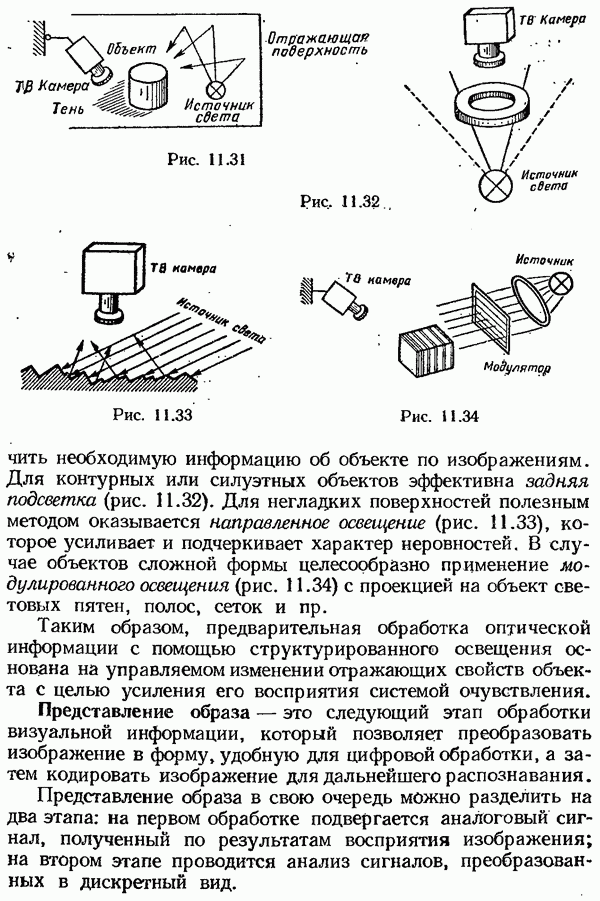
- Методы обработки сенсорной информации для адаптивного управления роботами.
- Восприятие изображения объекта
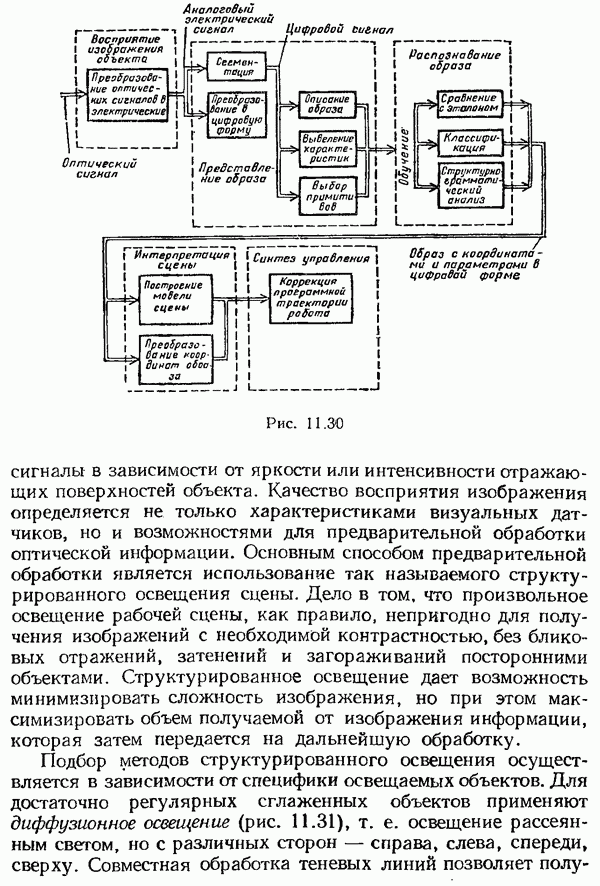
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ