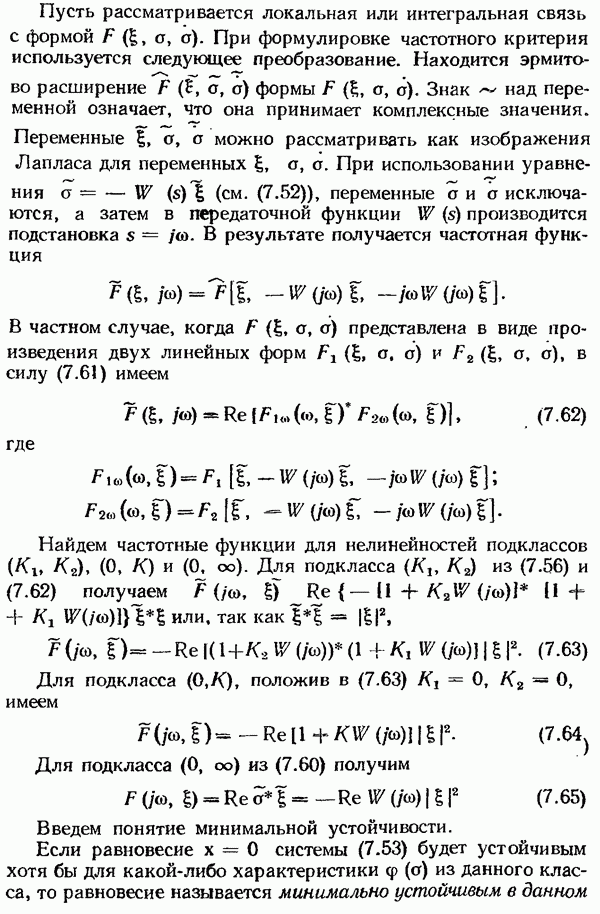| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
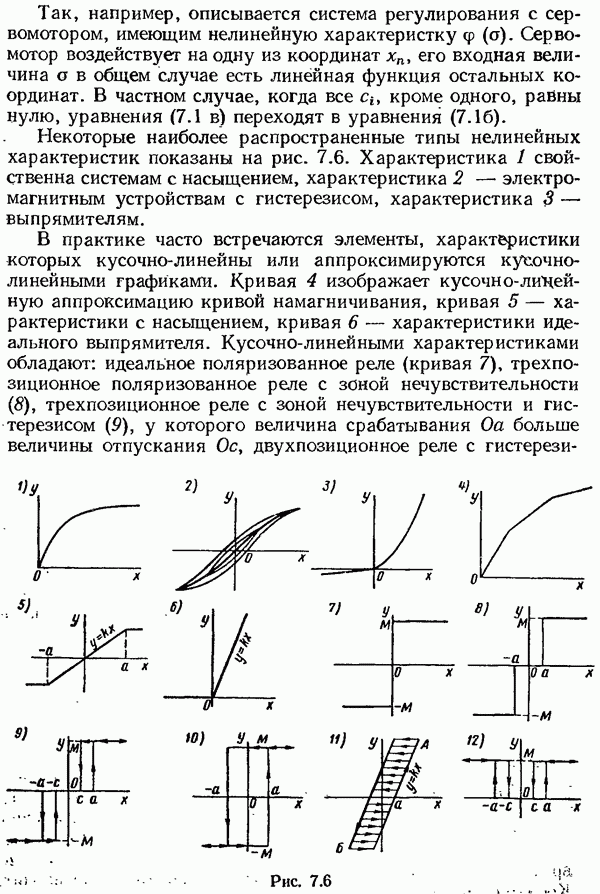
Исследование качества систем с амплитудно-импульсной модуляцией.
При исследовании качества систем автоматического управления возникают, как правило, три рода задач: 1) оценка установившегося значения сигнала ошибки системы

Рис. 8.19

Рис. 8.20
(установившееся значение отклонения входного сигнала импульсного элемента х (см. рис. 8.12); 2) построение кривой переходного процесса в моменты съема  косвенная оценка параметров переходного процесса, в первую очередь оценка перерегулирования и времени регулирования.
косвенная оценка параметров переходного процесса, в первую очередь оценка перерегулирования и времени регулирования.
Рассмотрим задачу оценки установившегося сигнала ошибки системы. Сигнал на входе импульсного элемента и входной сигнал системы  (см. рис. 8.12) связаны соотношением (8.35):
(см. рис. 8.12) связаны соотношением (8.35):

Запишем передаточную функцию (8.35) в виде отношения двух многочленов  , где
, где  — многочлен степени
— многочлен степени  — характеристический многочлен степени
— характеристический многочлен степени  . Предположим, что
. Предположим, что  имеет вид единичного скачка, т. е.
имеет вид единичного скачка, т. е.

Тогда сигнал  в дискретные моменты времени будет определяться выражением
в дискретные моменты времени будет определяться выражением

где

Если система устойчива, то действительные части корней  характеристического уравнения отрицательны и все слагаемые в (8.51) с ростом
характеристического уравнения отрицательны и все слагаемые в (8.51) с ростом  будут стремиться к нулю. Таким образом,
будут стремиться к нулю. Таким образом,

Значение (8.52) характеризует установившееся значение ошибки в системе с АИМ. Значение  , если
, если  и обращается в нуль в астатической системе, т. е. в том случае, когда в контуре системы имеется интегрирующее звено (например, исполнительный элемент). Это несложно показать, если проанализировать соотношение (8.52) с учетом (8.32).
и обращается в нуль в астатической системе, т. е. в том случае, когда в контуре системы имеется интегрирующее звено (например, исполнительный элемент). Это несложно показать, если проанализировать соотношение (8.52) с учетом (8.32).
Задачу построения кривой переходного процесса можно решить с помощью соотношения (8.51), однако данный подход весьма неудобен уже при степени характеристического уравнения  поскольку требует вычисления корней уравнения
поскольку требует вычисления корней уравнения 
Рассмотрим предложенные в [1] более удобные способы, не требующие вычисления корней и позволяющие построить процесс при любом внешнем воздействии.
Пусть передаточная функция замкнутой системы представлена в виде

Разлагая ее в ряд по степеням  и применяя обратное дискретное преобразование Лапласа, можно получить
и применяя обратное дискретное преобразование Лапласа, можно получить

где коэффициенты  определяются из рекуррентного соотношения:
определяются из рекуррентного соотношения:

Выражение (8.54) позволяет определить процесс регулирования (для  ) при любой форме
) при любой форме  . Если
. Если  имеет вид единичного скачка, то
имеет вид единичного скачка, то  Равно единице при
Равно единице при  и нулю при
и нулю при  а значения процесса находятся суммированием коэффициента
а значения процесса находятся суммированием коэффициента 

Рис. 8.21

Рис. 8.22
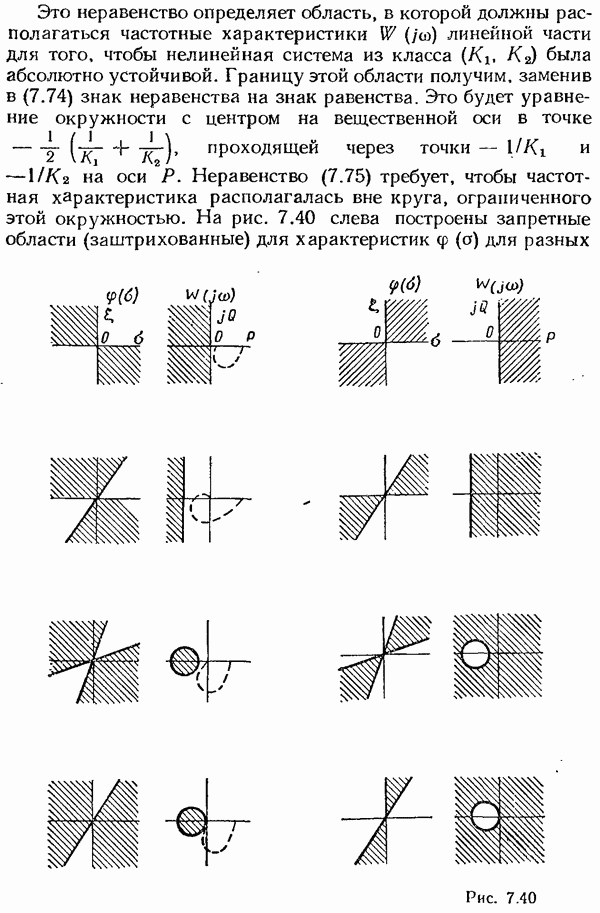
Второй способ построения кривой переходного процесса основан на использовании частотных характеристик. По известной  строится вещественная частотная характеристика
строится вещественная частотная характеристика  . Если представить ее в виде суммы типовых трапецеидальных характеристик (рис. 8.21), то искомую величину
. Если представить ее в виде суммы типовых трапецеидальных характеристик (рис. 8.21), то искомую величину  можно выразить в виде
можно выразить в виде

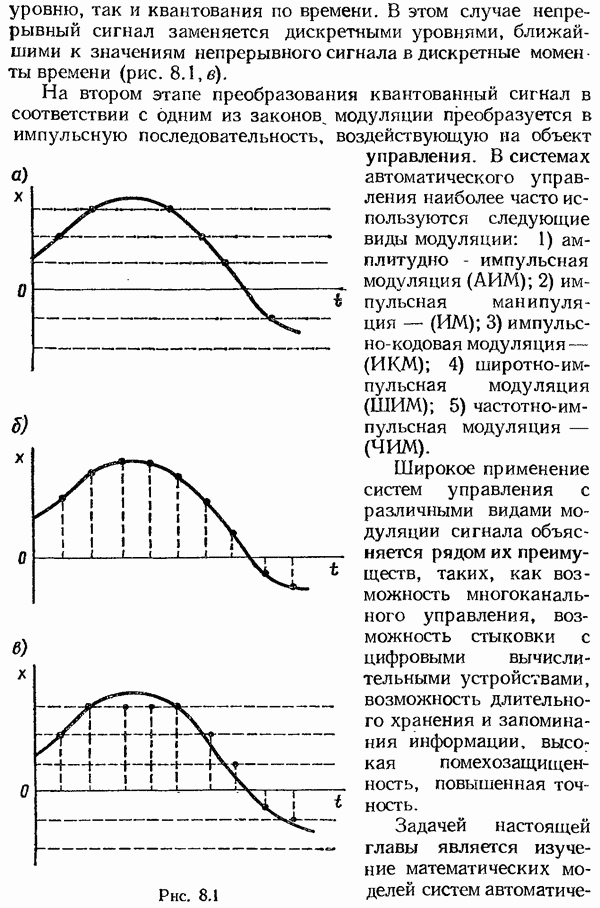
Здесь  — площадь трапеции. Параметры произвольной
— площадь трапеции. Параметры произвольной  трапеции обозначены на рис. 8.22. Пользуясь таблицами
трапеции обозначены на рис. 8.22. Пользуясь таблицами  определяем
определяем  а затем по соотношению (8.54) строим кривую переходного процесса
а затем по соотношению (8.54) строим кривую переходного процесса 
Косвенные методы оценки показателей качества процесса регулирования в системах с АИМ играют такую же важную роль, как и в системах непрерывного регулирования. Рассмотрим следующие основные косвенные оценки: степень устойчивости, степень колебательности и интегральные оценки.
Степенью устойчивости  будем называть минимальную вещественную часть корня характеристического уравнения
будем называть минимальную вещественную часть корня характеристического уравнения  замкнутой системы:
замкнутой системы:

Так как исследуемые процессы выражаются в функции относительного времени  то и степень устойчивости
то и степень устойчивости  является относительной величиной. Примем обозначение для абсолютной величины степени устойчивости
является относительной величиной. Примем обозначение для абсолютной величины степени устойчивости  , т. е.
, т. е.  Для определения степени устойчивости достаточно в передаточную
Для определения степени устойчивости достаточно в передаточную
функцию разомкнутой системы  подставить
подставить  вместо
вместо  и полученную таким образом передаточную функцию рассматривать как передаточную функцию некоторой «фиктивной» системы, граница устойчивости которой соответствует линии, равной степени устойчивости исследуемой системы.. Задача, таким образом, сводится к тому, чтобы определить параметры, при которых «фиктивная» система находится на границе устойчивости. В этом случае исследуемая система будет иметь заданную степень устойчивости. Исследование системы с позиций устойчивости может быть проведено по любому из приведенных выше критериев.
и полученную таким образом передаточную функцию рассматривать как передаточную функцию некоторой «фиктивной» системы, граница устойчивости которой соответствует линии, равной степени устойчивости исследуемой системы.. Задача, таким образом, сводится к тому, чтобы определить параметры, при которых «фиктивная» система находится на границе устойчивости. В этом случае исследуемая система будет иметь заданную степень устойчивости. Исследование системы с позиций устойчивости может быть проведено по любому из приведенных выше критериев.
Рассмотрим случай, характерный именно для систем с АИМ. Пусть характеристическое уравнение замкнутой системы

Если параметры системы таковы, что выполняется условие

то

Так как корни уравнения (8.60) равны  то степень устойчивости рассматриваемой системы равна бесконечности. Если известна передаточная функция разомкнутой системы
то степень устойчивости рассматриваемой системы равна бесконечности. Если известна передаточная функция разомкнутой системы

то условие бесконечной степени устойчивости, аналогичное (8.59), можно записать с учетом (8.59), (8.61):

Физически бесконечная степень устойчивости означает, что при возмущениях типа единичного скачка процесс регулирования заканчивается за конечное число тактов работы импульсного элемента. Действительно, если справедливо соотношение (8.59), то из рекуррентного соотношения (8.55) получаем

В этом случае в соответствии с формулой (8.54)  принимает значение
принимает значение

Очевидно, что  при
при  не зависит от
не зависит от  . В частности, если
. В частности, если  то
то  при
при  Рассмотренное свойство систем с АИМ можно использовать при построении оптимальных по быстродействию систем. Принципиально можно добиться того, чтобы переходный процесс заканчивался за один такт работы импульсного элемента.
Рассмотренное свойство систем с АИМ можно использовать при построении оптимальных по быстродействию систем. Принципиально можно добиться того, чтобы переходный процесс заканчивался за один такт работы импульсного элемента.
Степенью колебательности  устойчивой импульсной системы будем называть абсолютную величину отношения мнимой части ближайшего к оси корня характеристического уравнения к действительной части (рис. 8.23), т. е.
устойчивой импульсной системы будем называть абсолютную величину отношения мнимой части ближайшего к оси корня характеристического уравнения к действительной части (рис. 8.23), т. е.

При расчете степени колебательности можно Пользоваться тем же подходом, что и при расчете степени устойчивости. Разница состоит в том, что в передаточную функцию системы подставляется

Применяя для исследования устойчивости «фиктивной» системы один из известных критериев, можно определить, обладает ли данная система заданной величиной  или подобрать параметры системы, при которых
или подобрать параметры системы, при которых  равно заданной величине. Отметим, что степень колебательности относится к дискретным значениям процесса в моменты съема.
равно заданной величине. Отметим, что степень колебательности относится к дискретным значениям процесса в моменты съема.
Связь  с показателями качества переходного процесса (в частности, с перерегулированием и временем регулирования) подробно рассмотрена в гл. 4 при исследовании качества линейных непрерывных систем.
с показателями качества переходного процесса (в частности, с перерегулированием и временем регулирования) подробно рассмотрена в гл. 4 при исследовании качества линейных непрерывных систем.

Рис. 8.23
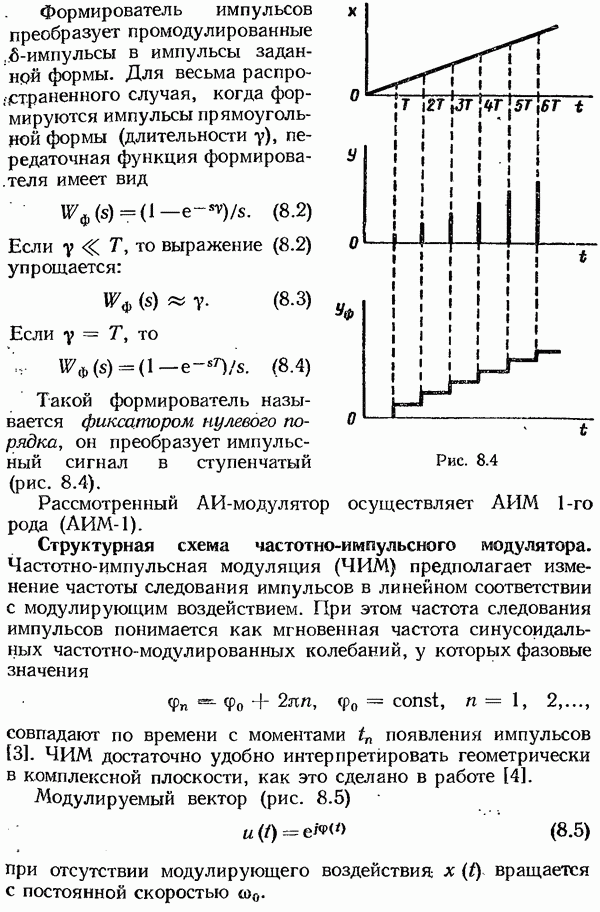
Интегральные оценки. Динамические свойства переходного процесса в системе с АИМ, возникающего от воздействия вида единичного скачка, по аналогии с непрерывными системами можно охарактеризовать интегральными оценками вида

Оценка выражает собой площадь, заключенную между графиком ступенчатой функции, образующейся из решетчатой функции  и графиком ее установившегося значения, т. е. площадь отклонения ступенчатой функции от ее предельного значения. Эта площадь на рис. 8.24 показана штриховкой. Очевидно, что оценку следует применять только к неколебательным процессам. Используя теорему о площади [1], выражение для вычисления оценки
и графиком ее установившегося значения, т. е. площадь отклонения ступенчатой функции от ее предельного значения. Эта площадь на рис. 8.24 показана штриховкой. Очевидно, что оценку следует применять только к неколебательным процессам. Используя теорему о площади [1], выражение для вычисления оценки  при
при  можно получить в виде
можно получить в виде

Оценку  можно использовать и для колебательных процессов. Вычисляют
можно использовать и для колебательных процессов. Вычисляют  непосредственно по коэффициентам передаточной функции замкнутой системы. Для воздействия вида единичного скачка полиномы числителя
непосредственно по коэффициентам передаточной функции замкнутой системы. Для воздействия вида единичного скачка полиномы числителя  и знаменателя
и знаменателя  передаточной функции запишутся в виде
передаточной функции запишутся в виде

тогда при 

при

Оценку  можно также определить, пользуясь частотной характеристикой замкнутой системы:
можно также определить, пользуясь частотной характеристикой замкнутой системы:


Рис. 8.24
т. е. оценка  равна площади квадрата модуля
равна площади квадрата модуля 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
- § 7.3. Автоколебания. Метод точечных преобразований
- § 7.4. Системы с переменной структурой
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
- Исследование периодических режимов в системах с ИЧИМ.
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
- Графоаналитическое определение дисперсии ошибки.
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
- § 9.9. Нелинейное преобразование случайных сигналов
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
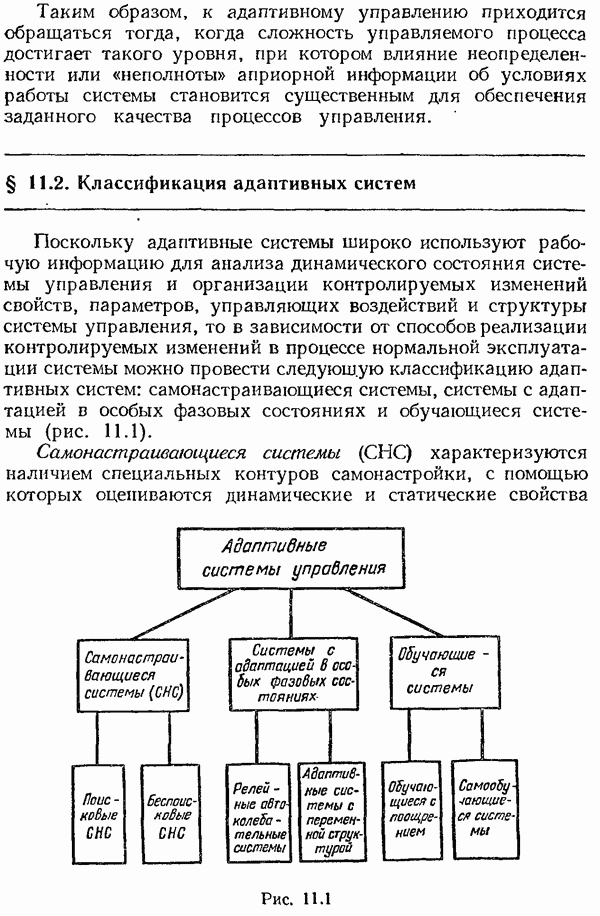
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
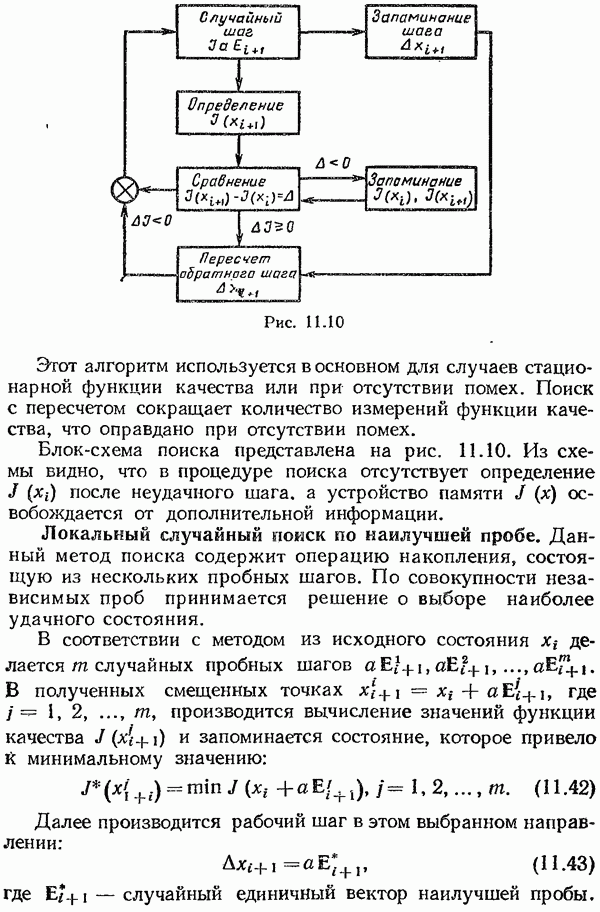
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
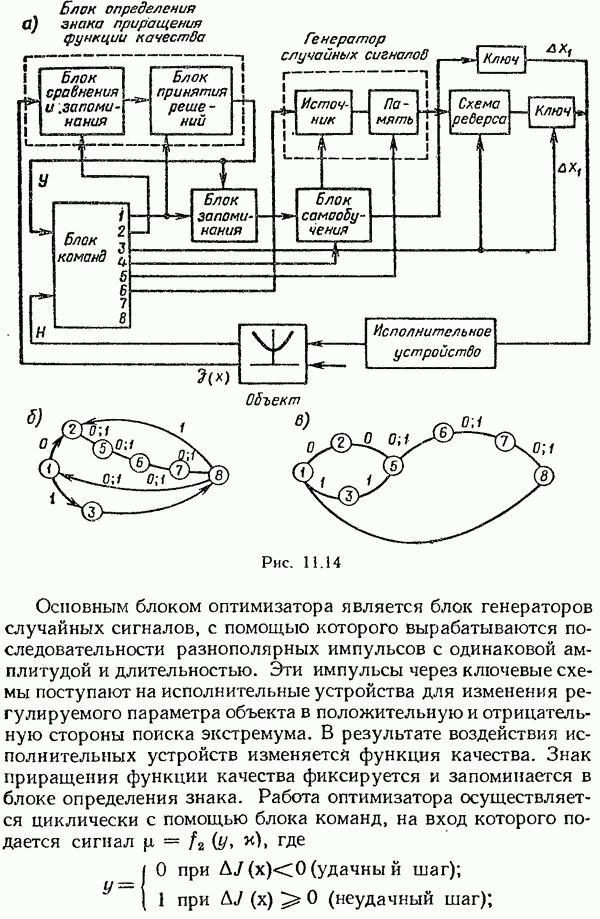
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
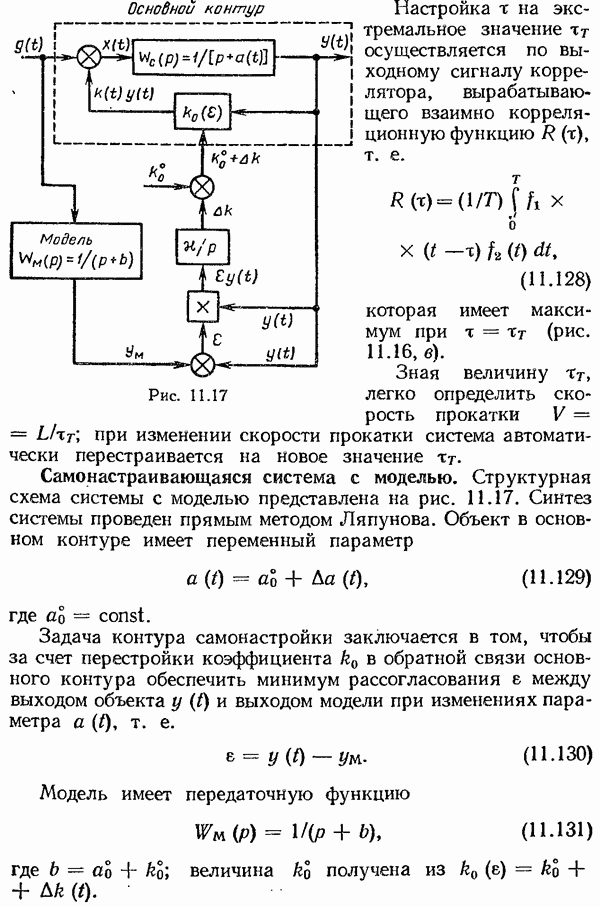
- Самонастраивающаяся система с моделью.
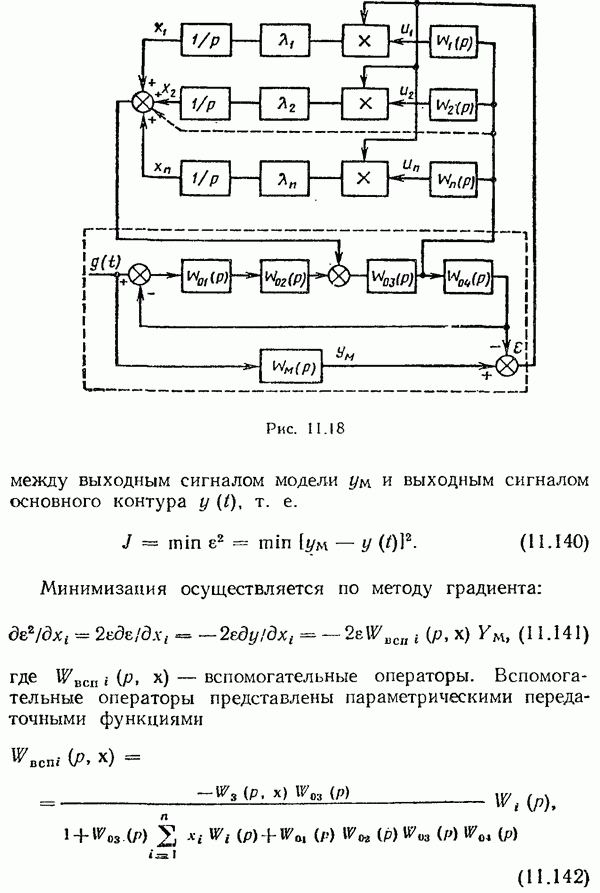
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
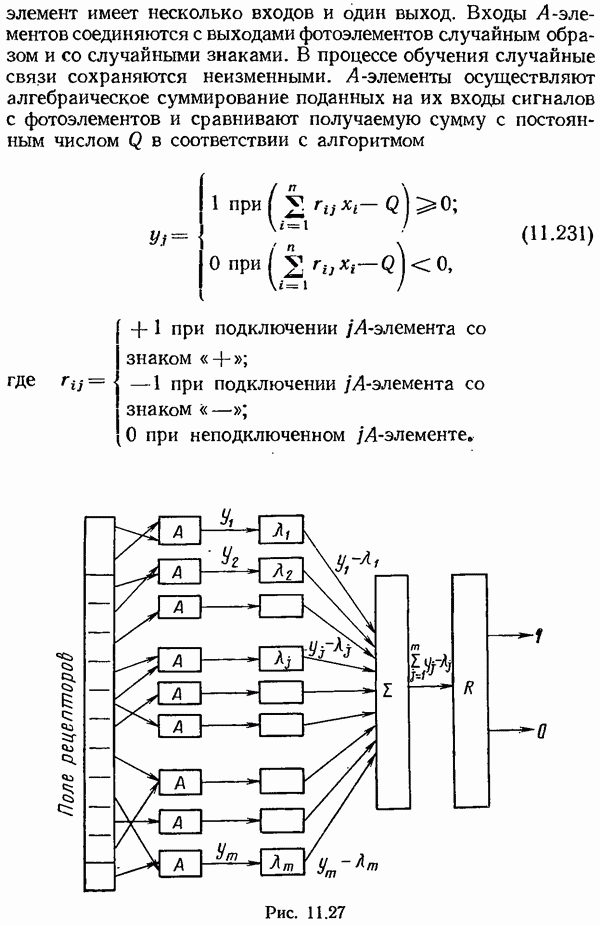
- Персептронная модель автоматической классификации.
- § 11.6. Адаптивные робототехнические системы
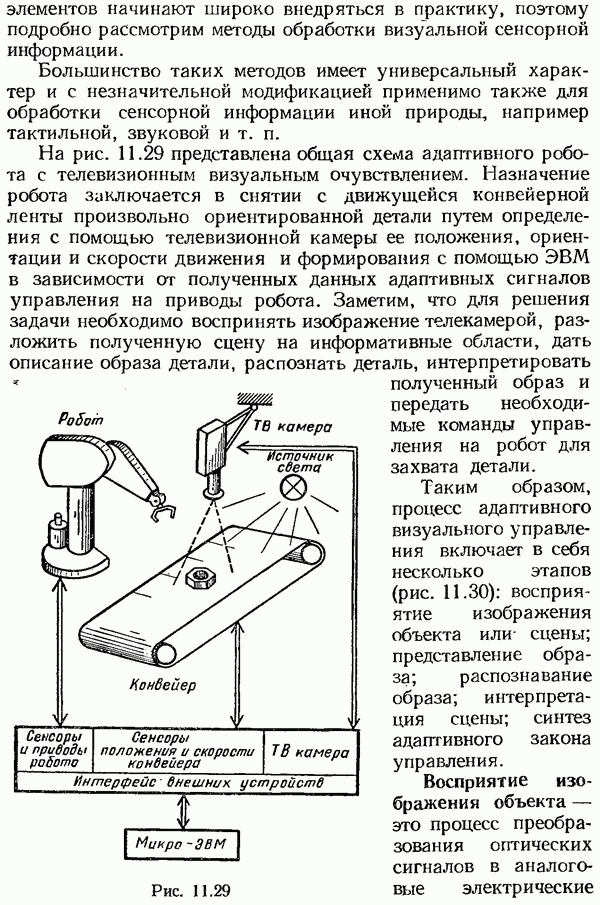
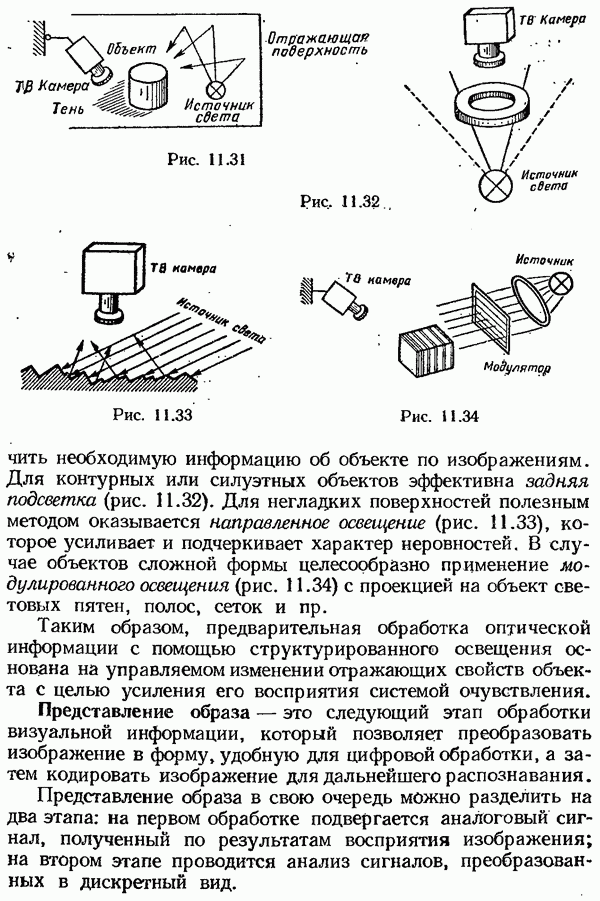
- Методы обработки сенсорной информации для адаптивного управления роботами.
- Восприятие изображения объекта
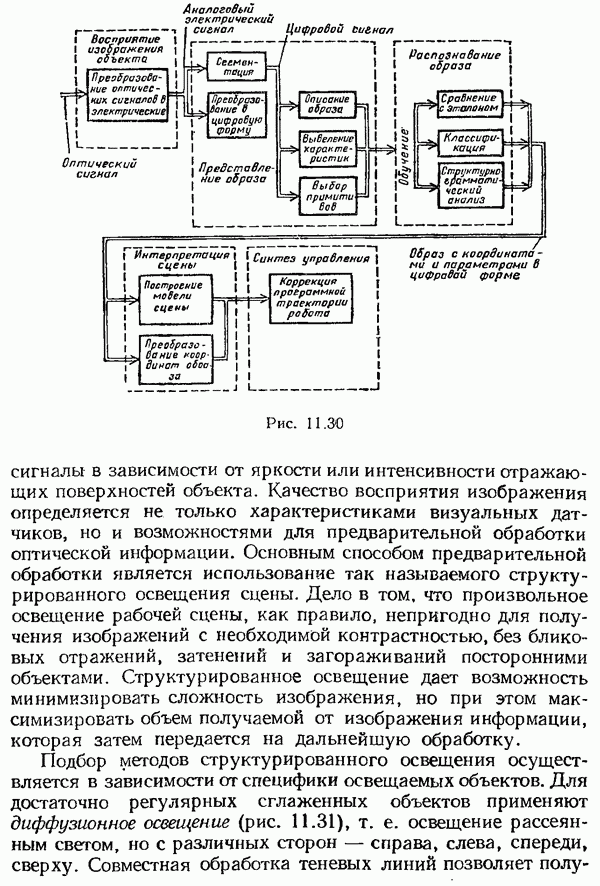
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ