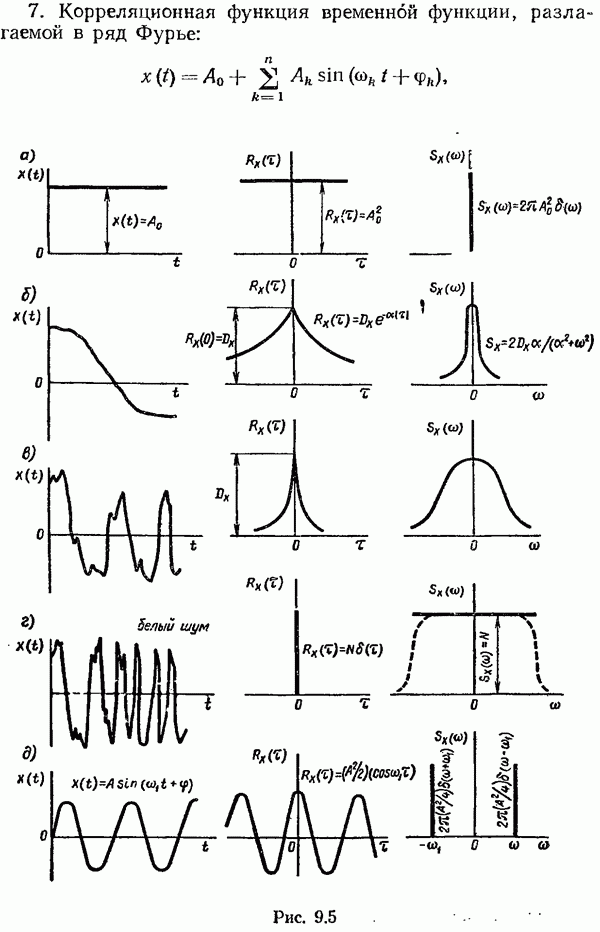
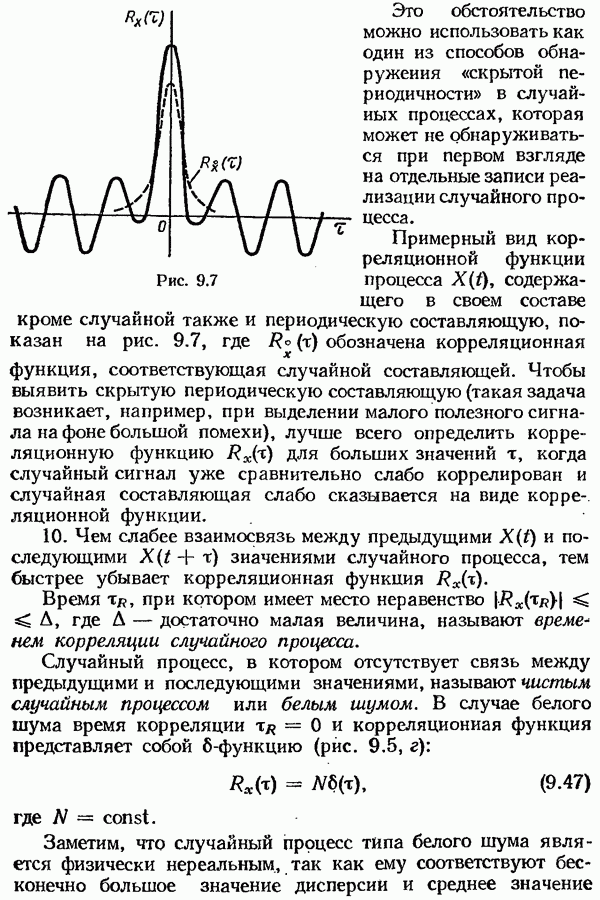
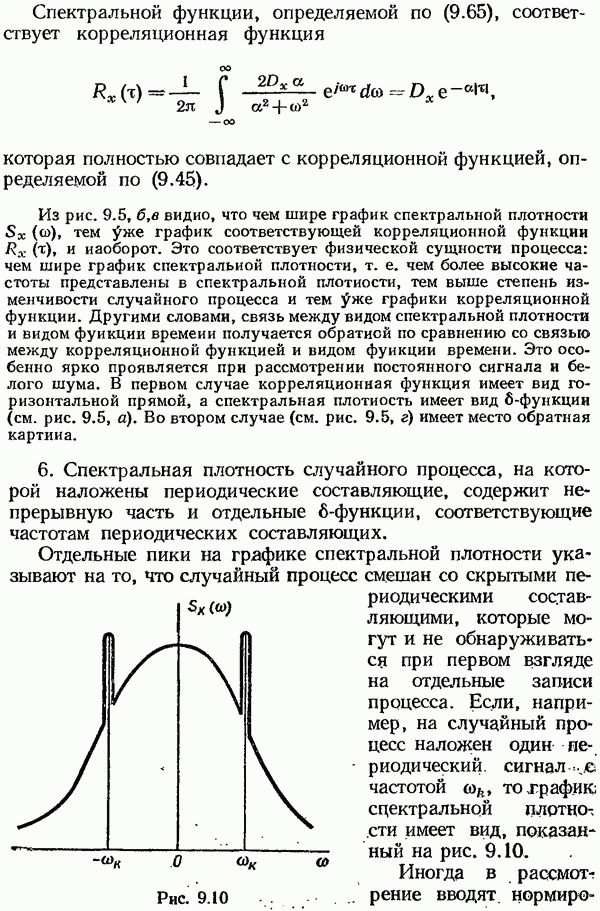
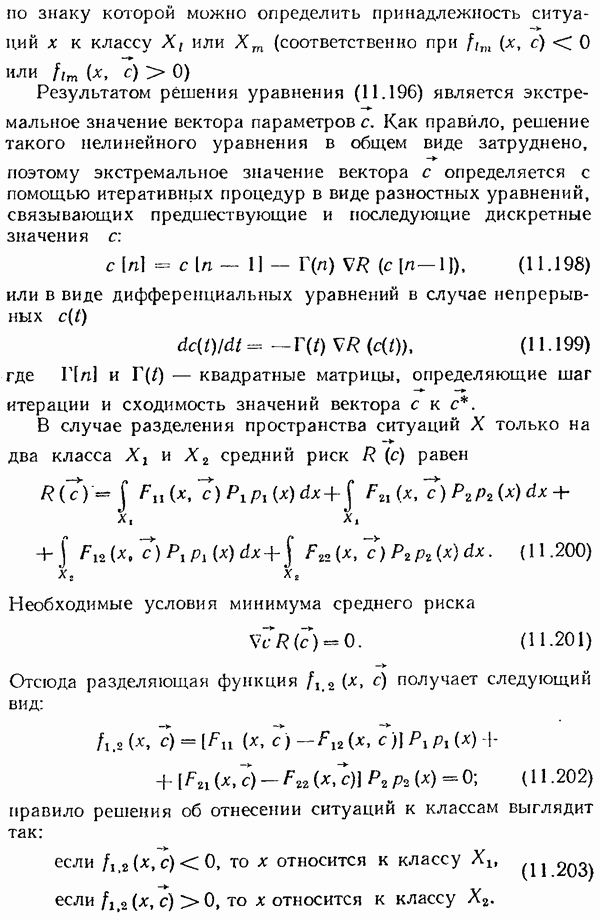| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
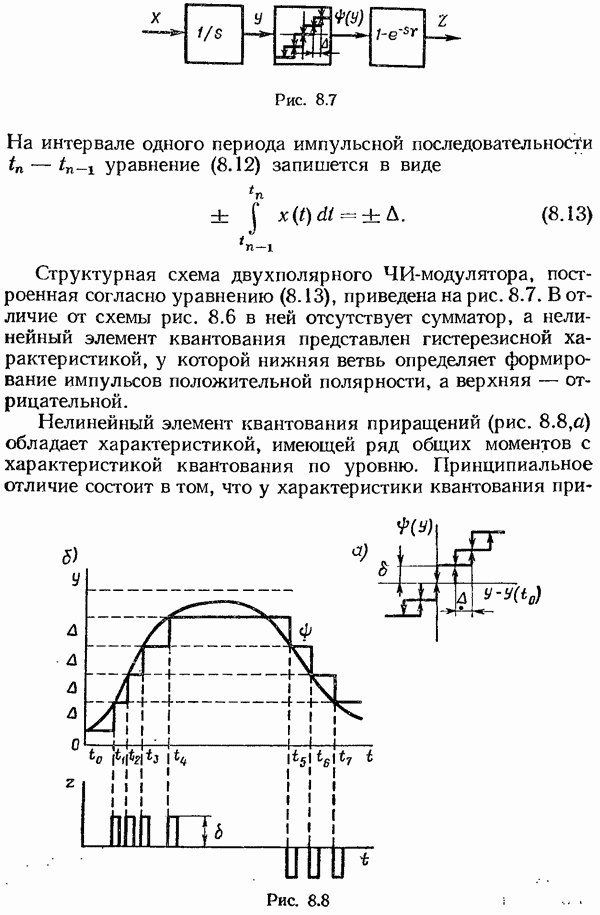
Синтез при произвольной структуре системы.
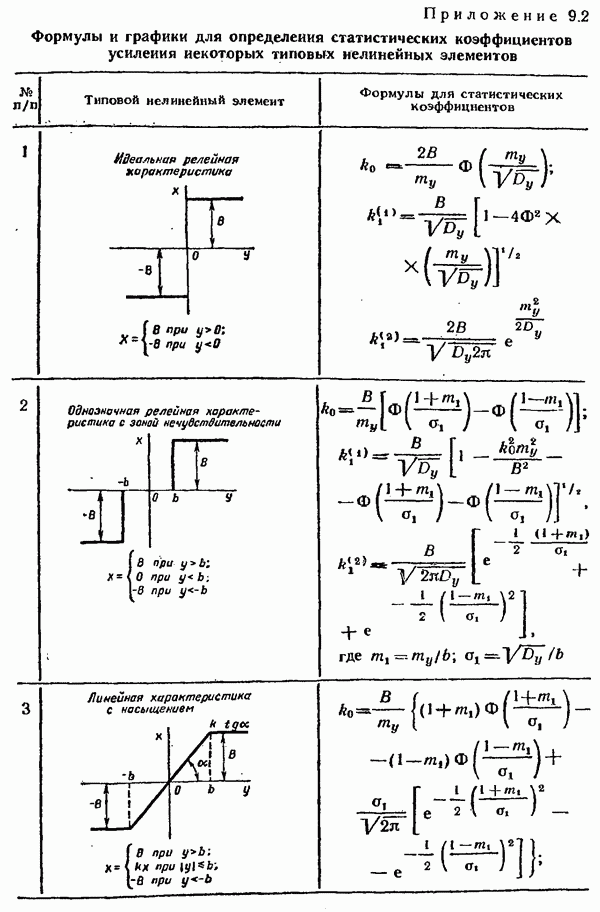
Пусть на систему действуют полезный сигнал  и помеха
и помеха  которые приложены к одному и тому же входу (см. рис. 9.16) и являются стационарными случайными процессами с равными нулю средними значениями. Если полезный сигнал и помеха приложены к разным входам, то методом эквивалентных преобразований
которые приложены к одному и тому же входу (см. рис. 9.16) и являются стационарными случайными процессами с равными нулю средними значениями. Если полезный сигнал и помеха приложены к разным входам, то методом эквивалентных преобразований  всегда можно привести к одному входу. Таким образом, суммарный сигнал на входе системы будет равен
всегда можно привести к одному входу. Таким образом, суммарный сигнал на входе системы будет равен

Выходной сигнал системы  связан с входным сигналом
связан с входным сигналом  уравнением
уравнением

где  — передаточная функция замкнутой системы.
— передаточная функция замкнутой системы.
Допустим, что система должна воспроизводить некоторую функцию от управляющего сигнала

Ошибка воспроизведения равна

Задача синтеза в случае произвольной структуры линейной системы состоит в том, чтобы при известных статистических характеристиках полезного сигнала и помехи найти такую физически реализуемую оптимальную передаточную функцию замкнутой системы  при которой среднее значение квадрата суммарной ошибки было бы минимально, т. е.
при которой среднее значение квадрата суммарной ошибки было бы минимально, т. е.

Рассмотрим задачу синтеза оптимальной передаточной функции  считая, что нам заданы спектральные плотности полезного сигнала
считая, что нам заданы спектральные плотности полезного сигнала  и помехи
и помехи  а также преобразующий оператор (алгоритм преобразования)
а также преобразующий оператор (алгоритм преобразования)  Решение проведем для упрощенного, но часто встречающегося случая, когда полезный сигнал и помеха не коррелированы.
Решение проведем для упрощенного, но часто встречающегося случая, когда полезный сигнал и помеха не коррелированы.
Выражение для любой реализации случайной суммарной ошибки можно записать следующим образом:

Выражение для спектральной плотности ошибки

а среднее значение квадрата ошибки

Для минимизации ошибки  необходимо выбрать соответствующую частотную передаточную функцию системы
необходимо выбрать соответствующую частотную передаточную функцию системы 
Основная трудность в минимизации выражения (9.113) связана с учетом условий физической осуществимости передаточной функции системы  Найдем сначала
Найдем сначала  без учета этого условия, а затем на основе полученного решения построим лучшую из физически реализуемых систем.
без учета этого условия, а затем на основе полученного решения построим лучшую из физически реализуемых систем.
Записав частотные передаточные функции  в виде
в виде

вычислим

Тогда (9.113) принимает вид

Из (9.114) необходимо найти такие значения  при которых выполнялось бы условие
при которых выполнялось бы условие  Это типичная вариационная задача, решаемая, например, с помощью Уравнений Эйлера.
Это типичная вариационная задача, решаемая, например, с помощью Уравнений Эйлера.
Учитывая, что  положительны при любом значении со, для минимизации
положительны при любом значении со, для минимизации  необходимо, чтобы член
необходимо, чтобы член  был наибольшим, т. е. чтобы
был наибольшим, т. е. чтобы

Тогда (9.114) примет вид

Так как все члены в последнем подынтегральном выражении положительны, то минимум среднего значения квадрата ошибки будет при минимальном значении функции 
Приравнивая  получаем
получаем

откуда находим выражение для оптимальной амплитудно-частотной характеристики замкнутой системы:

Имея в виду, что  выражения (9.115) и (9.116) можно объединить в одно уравнение:
выражения (9.115) и (9.116) можно объединить в одно уравнение:

Как следует из (9.117), единственными статистическими характеристиками полезного сигнала и помехи, необходимыми для определения оптимальной частотой передаточной функции замкнутой системы, являются их спектральные плотности.
Оптимальная частотная передаточная функция системы, определяемая по (9.117), была найдена без учета возможности ее физической реализуемости.
Условием физической реализуемости системы является равенство

т. е. реакция системы на  -фуикцию, действующую в момент
-фуикцию, действующую в момент  равна нулю при
равна нулю при 
Частотная передаточная функция  физически реализуемой системы должна иметь все полюсы в верхней полуплоскости корней,
физически реализуемой системы должна иметь все полюсы в верхней полуплоскости корней,
ней, а соответствующая ей передаточная функция  должна иметь только левые корни. Однако оптимальная частотная передаточная функция, определяемая (9.117), может оказаться в общем случае физически нереализуемой. Это можно показать на частном простейшем примере. Пусть решается задача воспроизведения, т. е.
должна иметь только левые корни. Однако оптимальная частотная передаточная функция, определяемая (9.117), может оказаться в общем случае физически нереализуемой. Это можно показать на частном простейшем примере. Пусть решается задача воспроизведения, т. е.  и пусть помеха представляет собой единичный белый шум, т. е.
и пусть помеха представляет собой единичный белый шум, т. е.  . Тогда
. Тогда

и так как  — положительная величина, то она раскладывается на комплексные множители, один из которых всегда будет иметь полюсы в нижней полуплоскость корней. Импульсная переходная функция
— положительная величина, то она раскладывается на комплексные множители, один из которых всегда будет иметь полюсы в нижней полуплоскость корней. Импульсная переходная функция  найденная для такой частотной передаточной функции, будет существовать и для отрицательных значений времени
найденная для такой частотной передаточной функции, будет существовать и для отрицательных значений времени  т. е. до приложения возмущения. Это и свидетельствует о нереализуемости
т. е. до приложения возмущения. Это и свидетельствует о нереализуемости 
Оптимальная частотная передаточная функция, определяемая (9.117), оказалась физически нереализуемой потому, что в реальных системах всегда существует связь между амплитудно-частотной  и фазовой
и фазовой  характеристиками, которая не была учтена при выводе формулы (9.117). При выводе (9.117) решались уравнения (9.115) и (9.116), которые, как правило, являются несовместимыми, т. е. нельзя найти одно решение, одновременно удовлетворяющее обоим этим уравнениям.
характеристиками, которая не была учтена при выводе формулы (9.117). При выводе (9.117) решались уравнения (9.115) и (9.116), которые, как правило, являются несовместимыми, т. е. нельзя найти одно решение, одновременно удовлетворяющее обоим этим уравнениям.
Для того чтобы реализовать функцию, наиболее близкую к оптимальной, необходимо из  выделить физически реализуемую часть с полюсами, находящимися в верхней полуплоскости корней, а остальные члены отбросить.
выделить физически реализуемую часть с полюсами, находящимися в верхней полуплоскости корней, а остальные члены отбросить.
Для этого, пользуясь методикой, предложенной Г. Боде и К. Шенноном, разлагают сначала знаменатель выражения (9.117) на комплексные множители (операции «факторизации»):

где  — функция, все нули и полюсы которой лежат в верхней полуплоскости комплексного переменного
— функция, все нули и полюсы которой лежат в верхней полуплоскости комплексного переменного  — функция, комплексно-сопряженная с
— функция, комплексно-сопряженная с  все нули и полюсы которой лежат в нижней полуплоскости комплексного переменного
все нули и полюсы которой лежат в нижней полуплоскости комплексного переменного 
Затем производят разделение  на реализуемые и нереализуемые слагаемые (операция «расщепления»):
на реализуемые и нереализуемые слагаемые (операция «расщепления»):

причем реализуемая часть отмечается знаком плюс, а нереализуемая — знаком минус.
Отбрасывая члены, соответствующие нереализуемой части, условие оптимальности с учетом физической реализуемости записывают следующим образом:

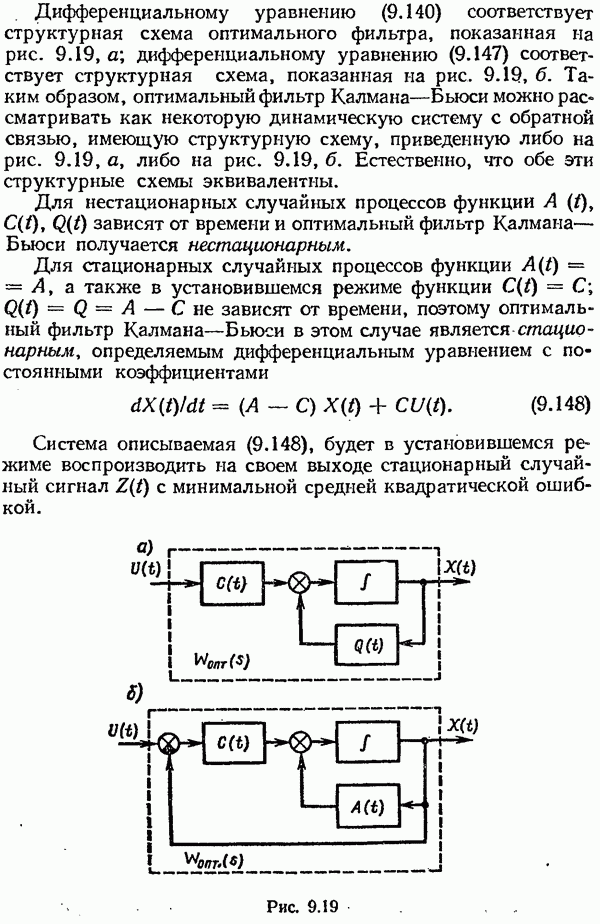
Физически реализуемая частотная передаточная функция оказывается уже неоптимальной в прежнем понимании, но среди физически реализуемых функций в соответствии с принятым критерием она является наилучшей.
Таким образом, когда полезный сигнал и помеха некоррелированы, нахождение оптимальной физически реализуемой частотной передаточной функции  производится в следующем порядке:
производится в следующем порядке:
1. Вычисляем суммарную спектральную плотность управляющего сигнала и помехи и представляем эту сумму в виде двух комплексных сомножителей:

2. Выделяем составляющую 
3. Раскладываем на простейшие слагаемые выражение  , отбрасывая члены с полюсами, расположенными в нижней полуплоскости корней, т. е.
, отбрасывая члены с полюсами, расположенными в нижней полуплоскости корней, т. е.  выделяем из него физически реализуемую часть
выделяем из него физически реализуемую часть 
4. Определяем оптимальную физически реализуемую частотную передаточную функцию системы:

Можно показать, что при наличии взаимной корреляции полезного сигнала и помехи оптимальная частотная передаточная функция

где  — взаимные спектральные плотности управляющего сигнала и помехи.
— взаимные спектральные плотности управляющего сигнала и помехи.
Оптимальную передаточную функцию  получают по найденной оптимальной частотой передаточной функции
получают по найденной оптимальной частотой передаточной функции  подставляя в последнюю
подставляя в последнюю  вместо
вместо 
Затем в соответствии с полученной передаточной функцией  выбирают элементы системы. Если часть элементов задана и изменить их параметры не представляется возможным, то в таких случаях задача сводится к выбору параметров корректирующих цепей при найденной оптимальной передаточной функции системы управления в целом и известных передаточных функциях отдельных заданных элементов системы.
выбирают элементы системы. Если часть элементов задана и изменить их параметры не представляется возможным, то в таких случаях задача сводится к выбору параметров корректирующих цепей при найденной оптимальной передаточной функции системы управления в целом и известных передаточных функциях отдельных заданных элементов системы.
В системе, имеющей оптимальную передаточную функцию, получается теоретически достижимый минимум среднего квадрата ошибки:

Пример 9.6. На входе следящей системы действует случайный полезный сигнал  имеющий спектральную плотность
имеющий спектральную плотность

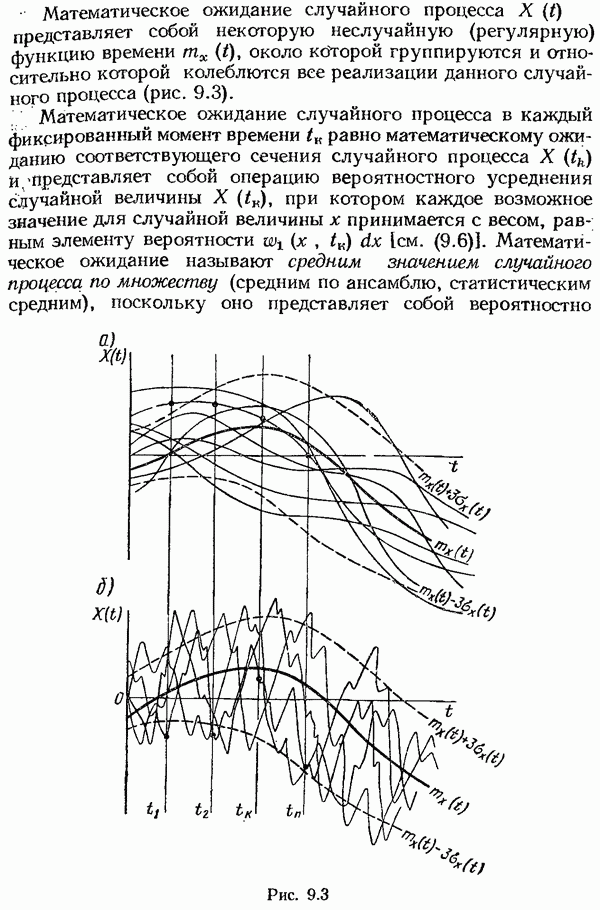
где  — значение спектральной плотности полезного сигнала на нулевой частоте.
— значение спектральной плотности полезного сигнала на нулевой частоте.
На полезный сигнал наложена случайная помеха  типа «бeлый шум», спектральная плотность которой равна
типа «бeлый шум», спектральная плотность которой равна  , где
, где  — значение спектральной плотности помехи на нулевой частоте. Корреляция между полезным сигналом и помехой отсутствует.
— значение спектральной плотности помехи на нулевой частоте. Корреляция между полезным сигналом и помехой отсутствует.
Требуется определить оптимальную передаточную функцию следящей системы и соответствующую ей дисперсию суммарной ошибки
1. Вычисляем спектральную плотность суммарного входного сигнала  и представляем ее в виде произведения комплексных сомножителей:
и представляем ее в виде произведения комплексных сомножителей:

2. Определяем  для чего раскладываем полученное выражение на комплексно-сопряженные множители:
для чего раскладываем полученное выражение на комплексно-сопряженные множители:

где 
Следовательно,

3. Находим составляющую  . В нашем случае для следящей системы
. В нашем случае для следящей системы  поэтому получаем
поэтому получаем

4. Раскладываем последнее выражение на простые слагаемые:

отбрасывая члены с полюсами, расположенными в правой полуплоскости, выделим физически реализуемую часть:

5. Находим оптимальную частотную передаточную функцию физически реализуемой системы:

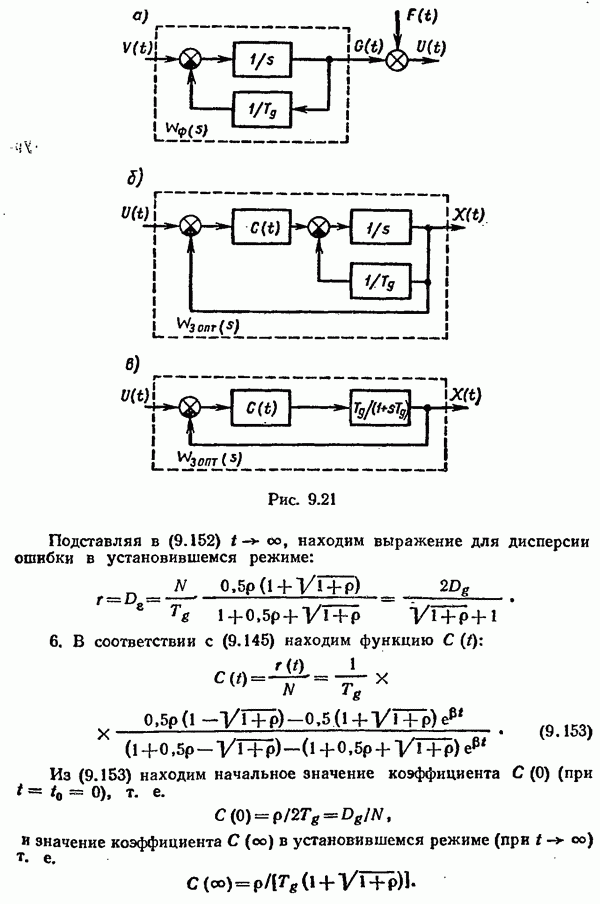
где  коэффициент усиления замкнутой оптимальной системы;
коэффициент усиления замкнутой оптимальной системы;  — постоянная времени замкнутой оптимальной системы.
— постоянная времени замкнутой оптимальной системы.
6. Подставляя в последнее выражение  вместо
вместо  находим оптимальную передаточную функцию замкнутой системы:
находим оптимальную передаточную функцию замкнутой системы:

Подставляя числовые значения коэффициентов, получаем

Следовательно, в нашем случае оптимальная передаточная функция замкнутой системы

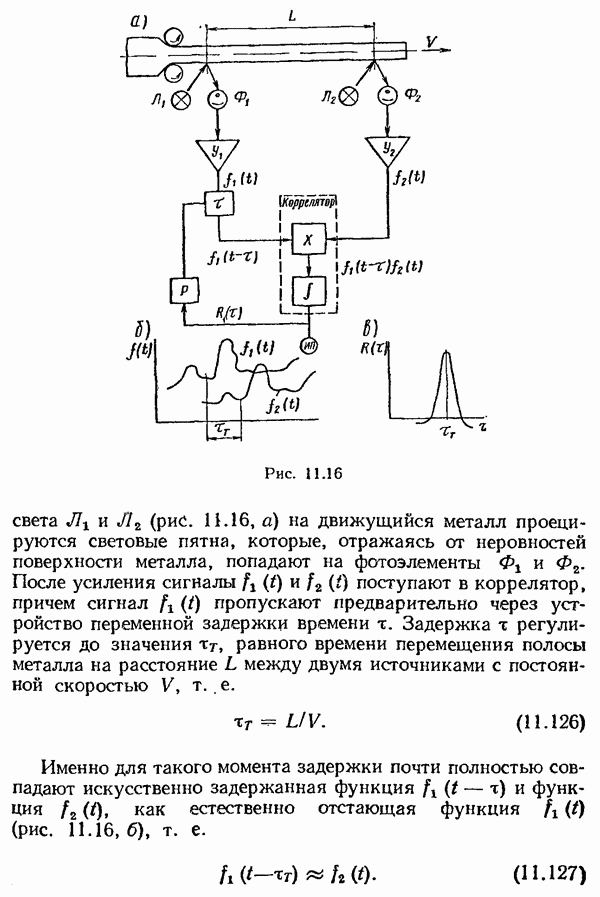
7. Определяем оптимальную передаточную функцию разомкнутой системы:

8. Определяем передаточную функцию замкнутой системы по ошибке:

9. Определяем спектральную плотность ошибки:

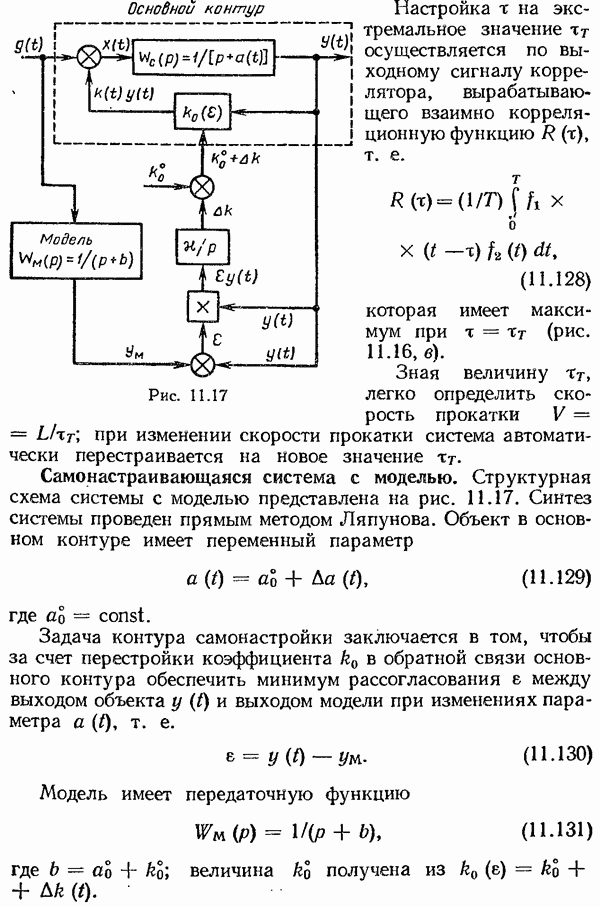
60. Определяем дисперсию ошибки:

Средняя квадратическая ошибка, совпадающая в данном случае со средним квадратическим отклонением, равна

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
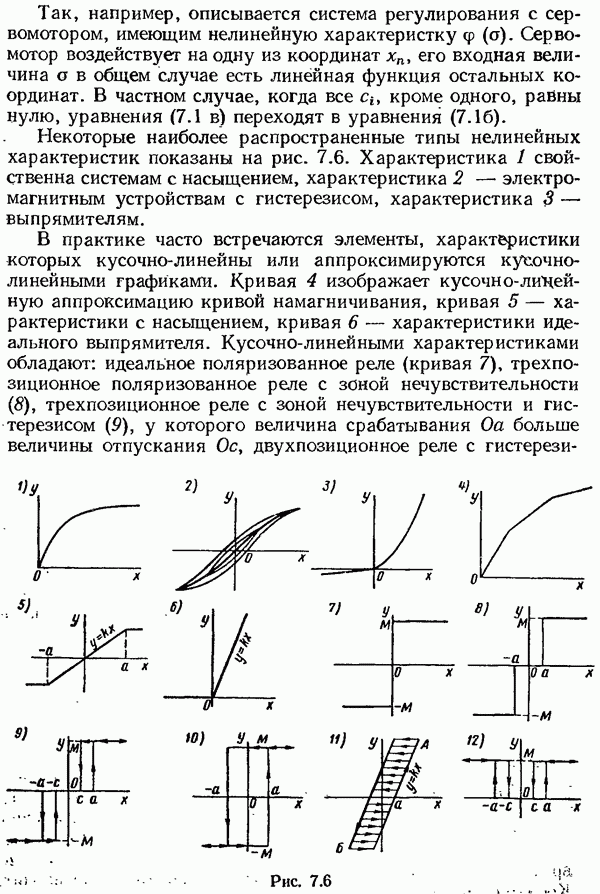
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
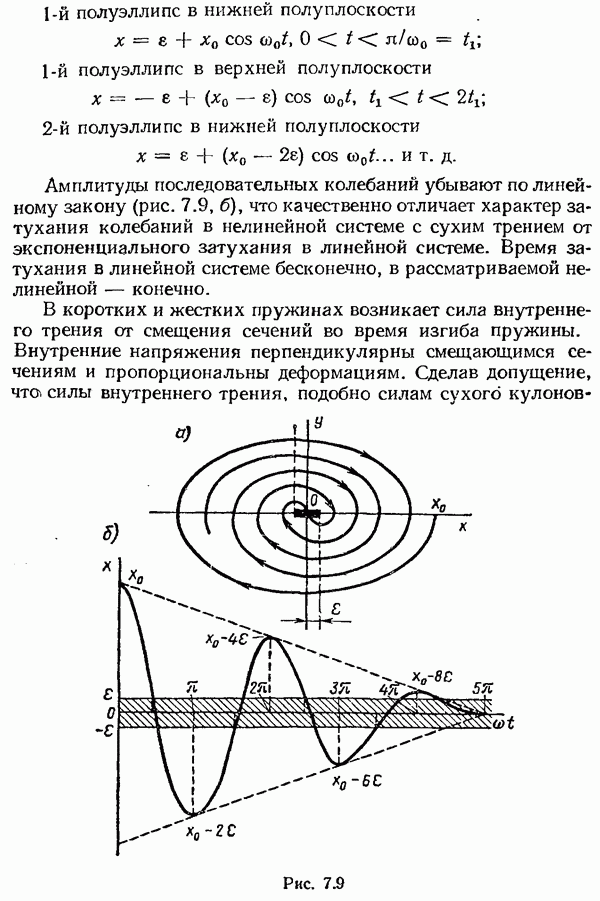
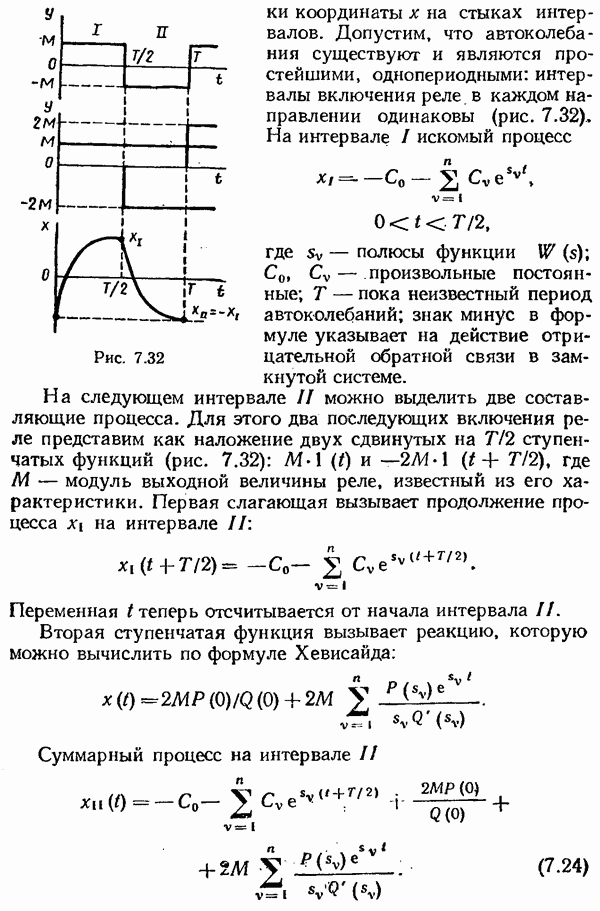
- § 7.3. Автоколебания. Метод точечных преобразований
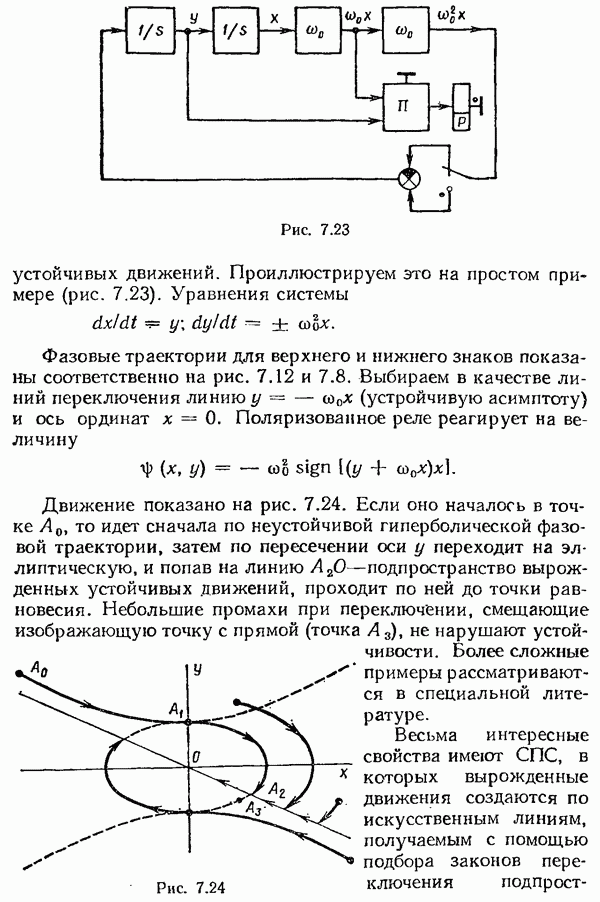
- § 7.4. Системы с переменной структурой
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
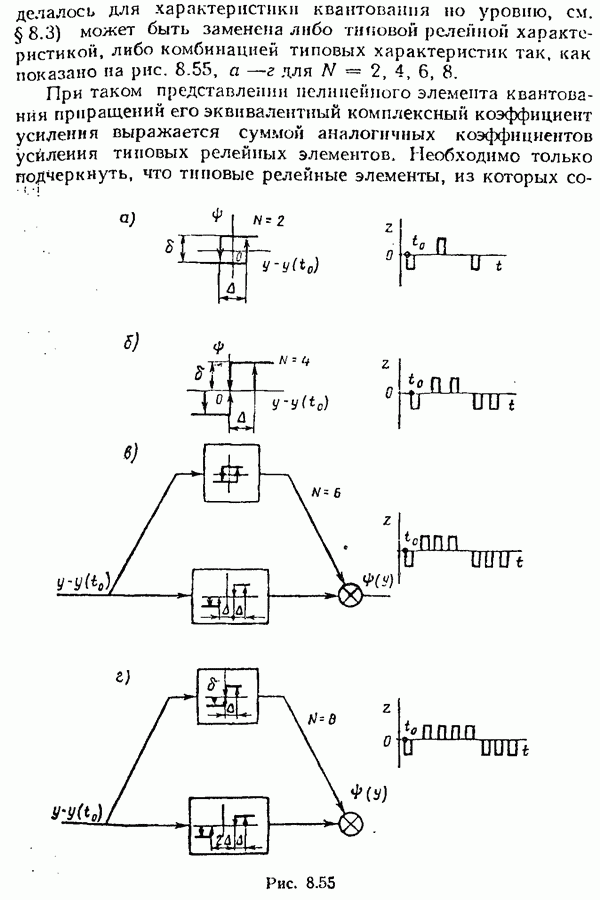
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
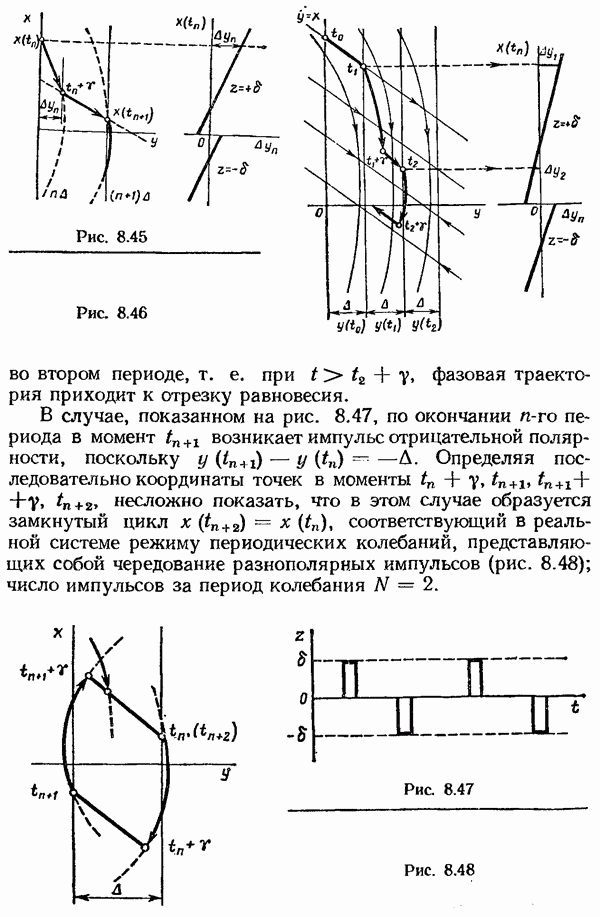
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
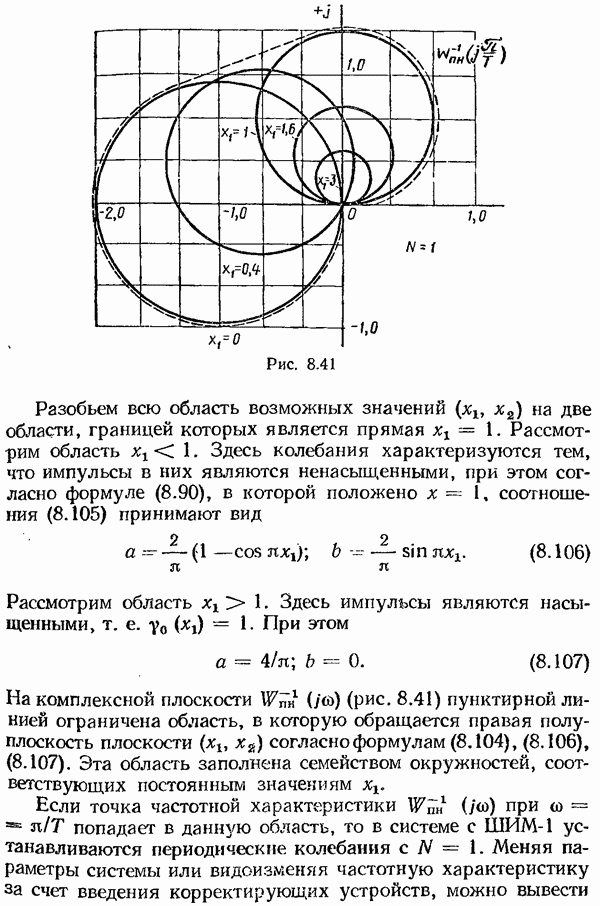
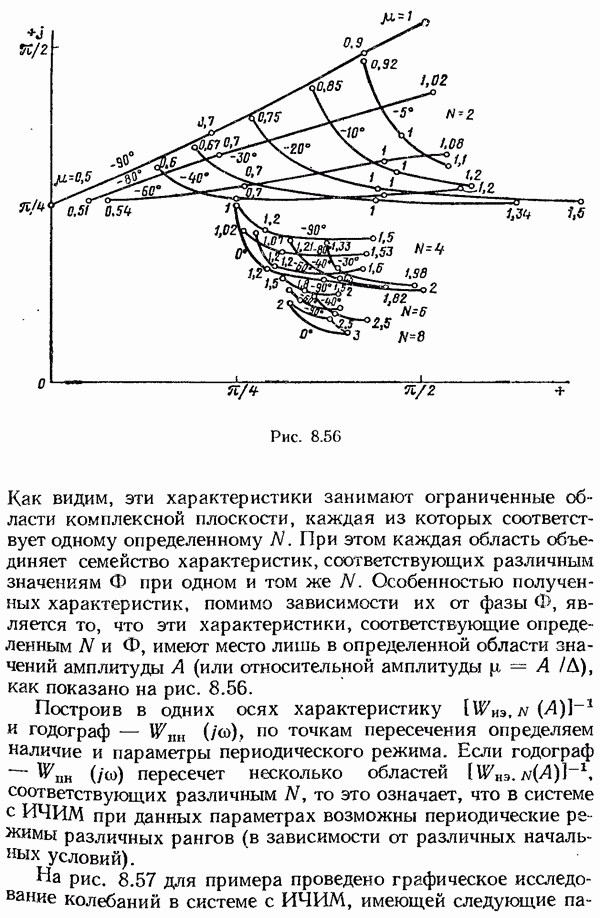
- Исследование периодических режимов в системах с ИЧИМ.
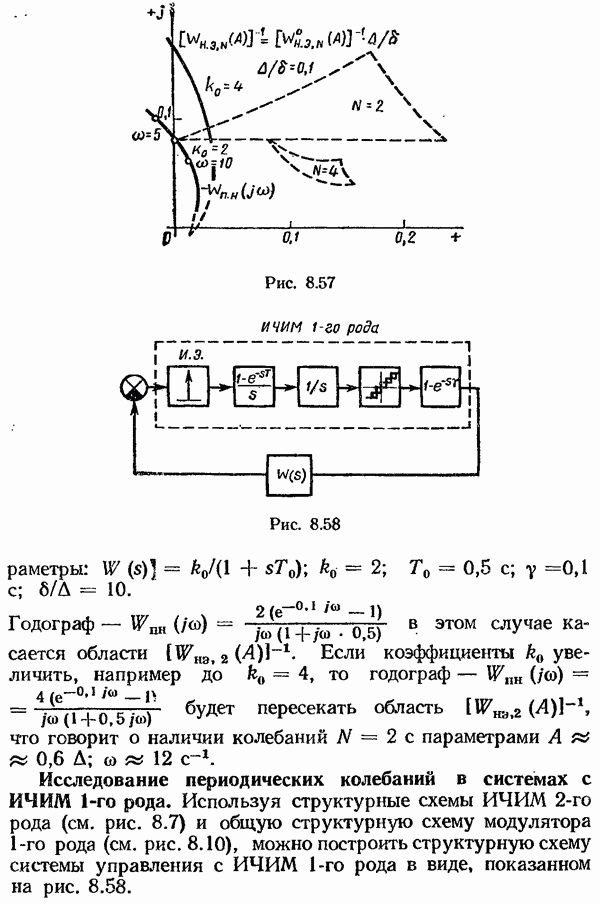
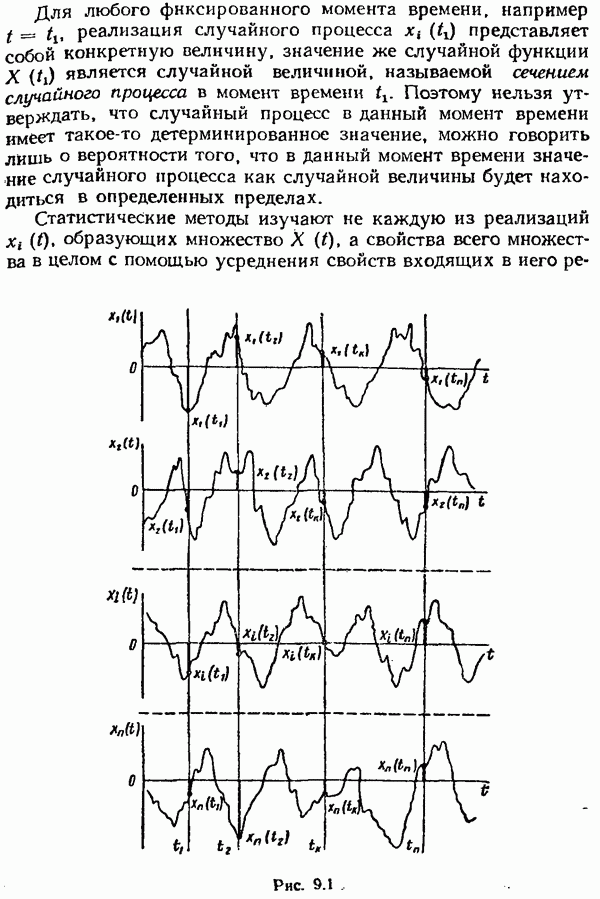
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
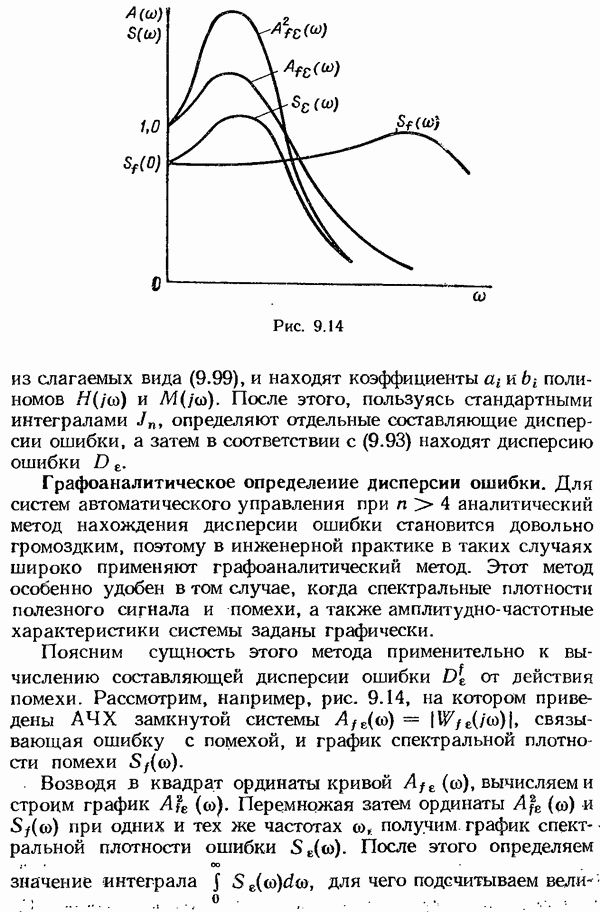
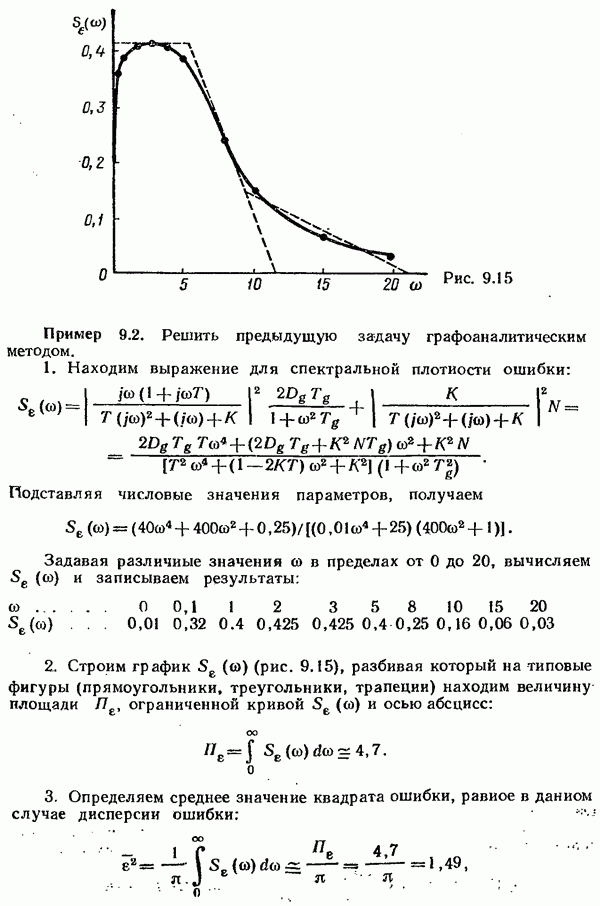
- Графоаналитическое определение дисперсии ошибки.
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
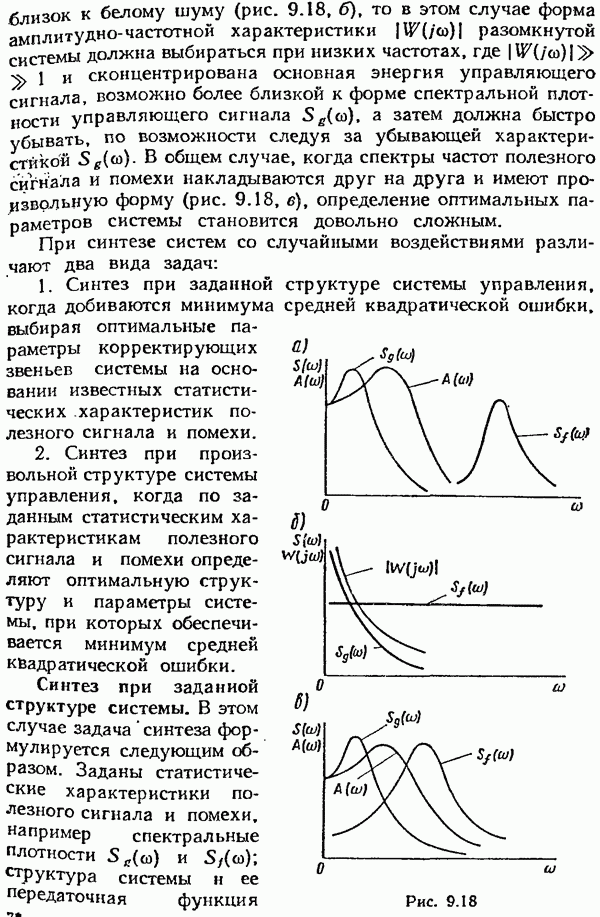
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
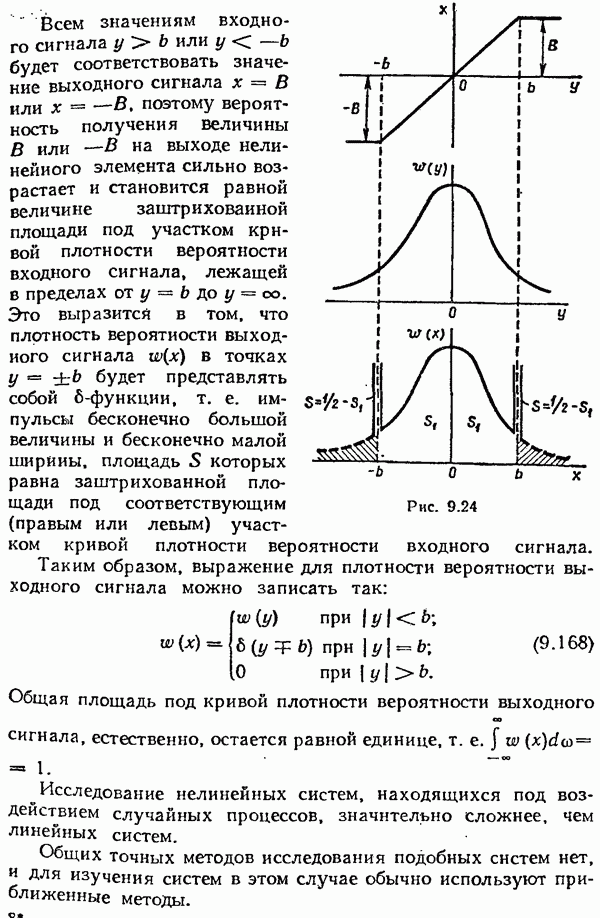
- § 9.9. Нелинейное преобразование случайных сигналов
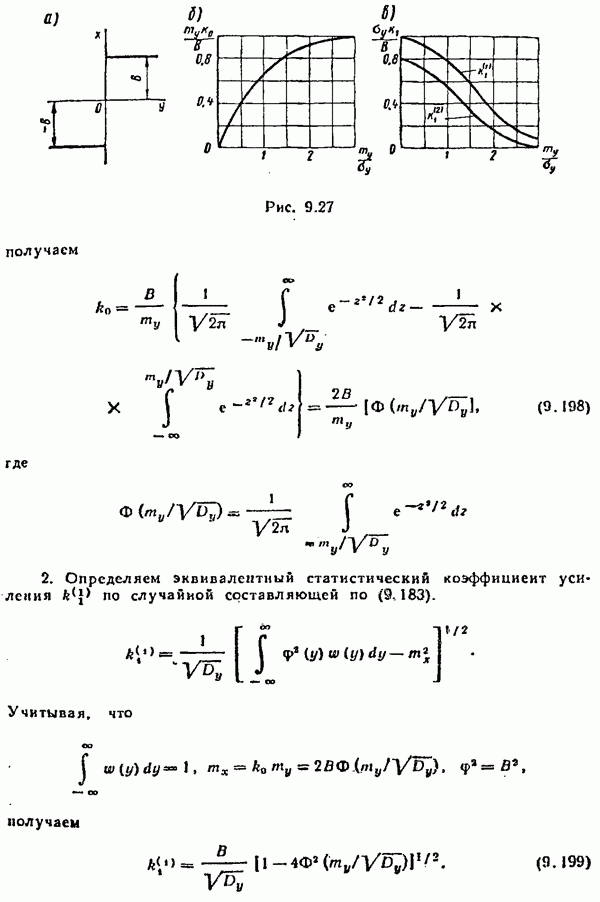
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
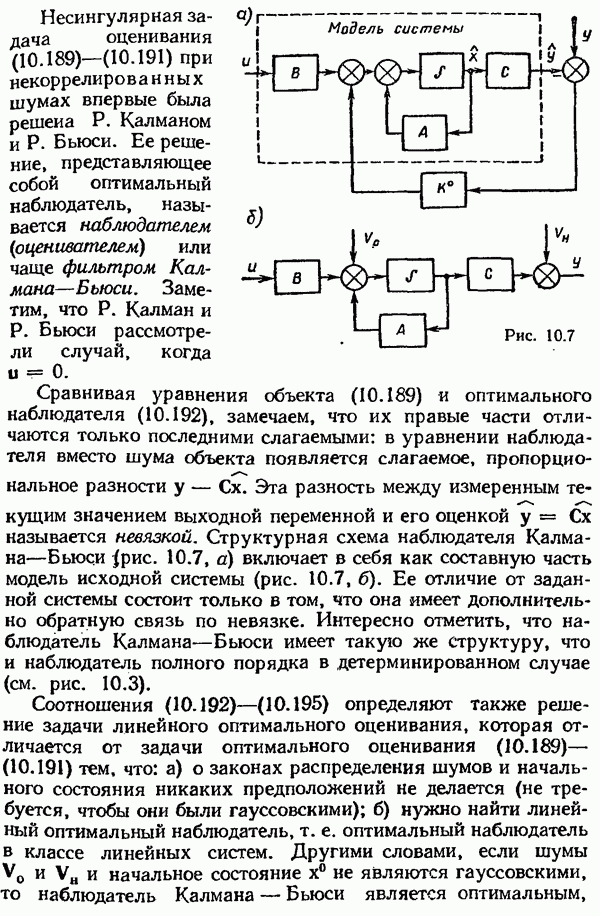
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
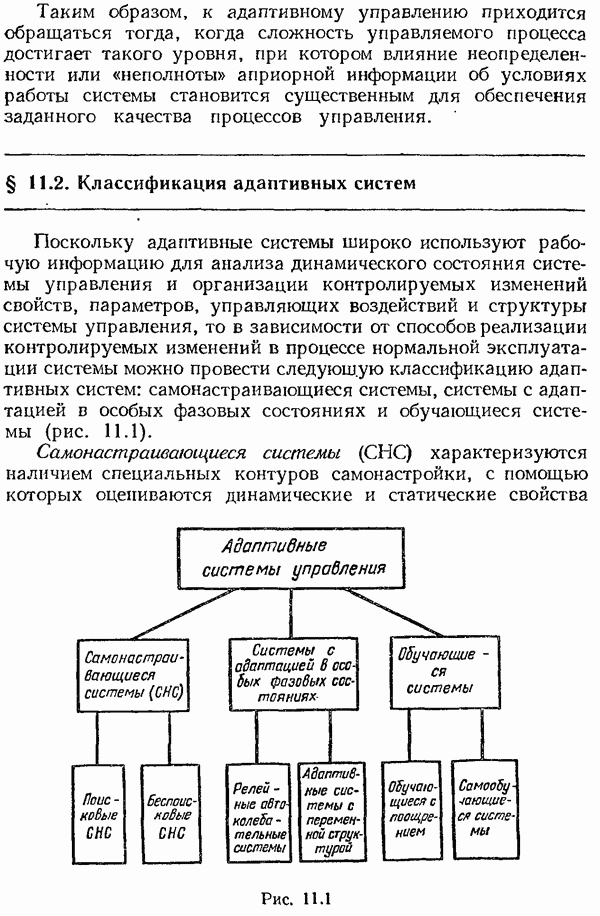
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
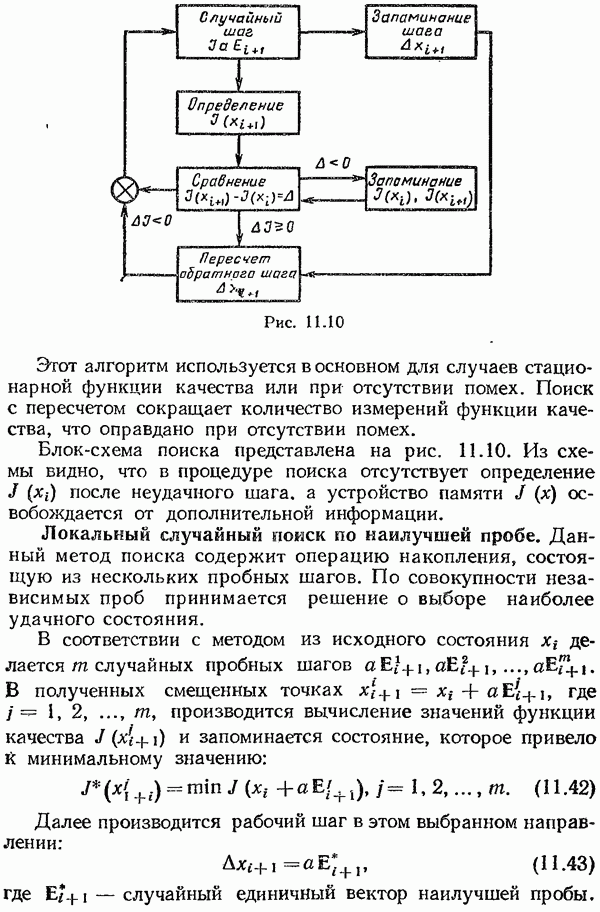
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
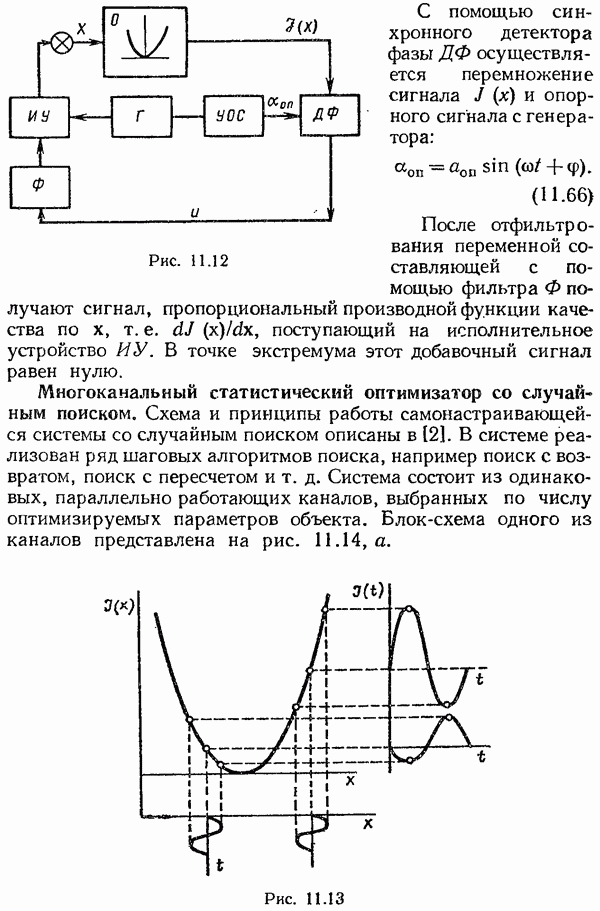
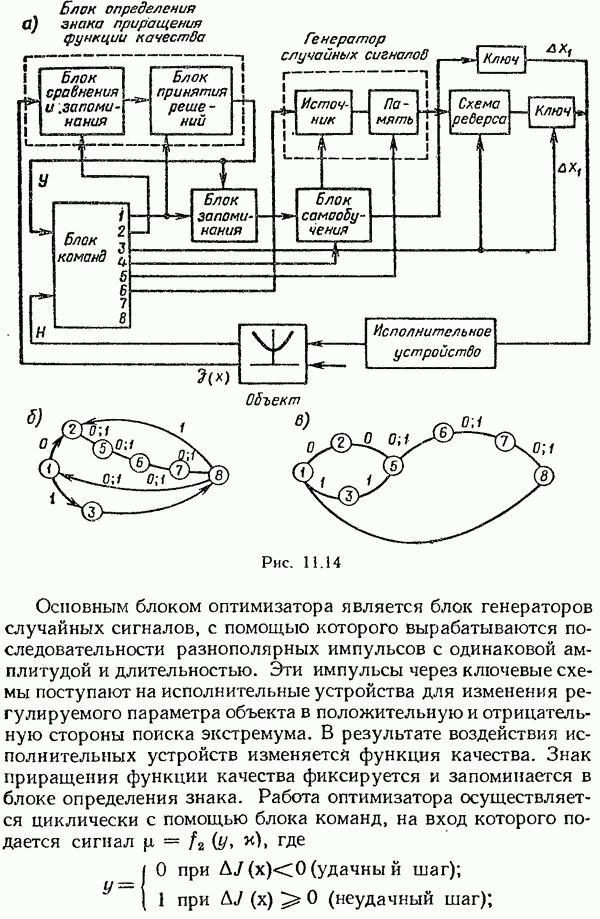
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
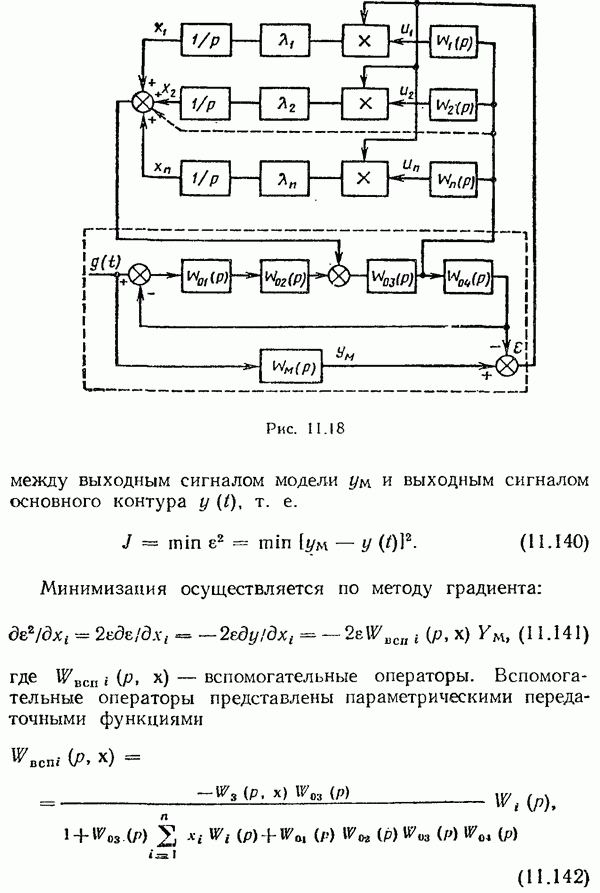
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
- Самонастраивающаяся система с моделью.
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
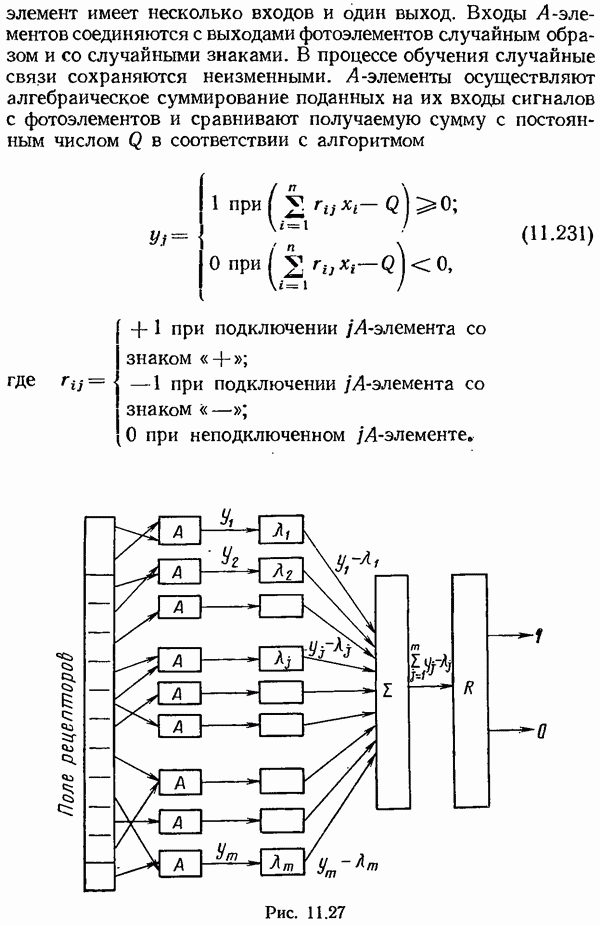
- Персептронная модель автоматической классификации.
- § 11.6. Адаптивные робототехнические системы
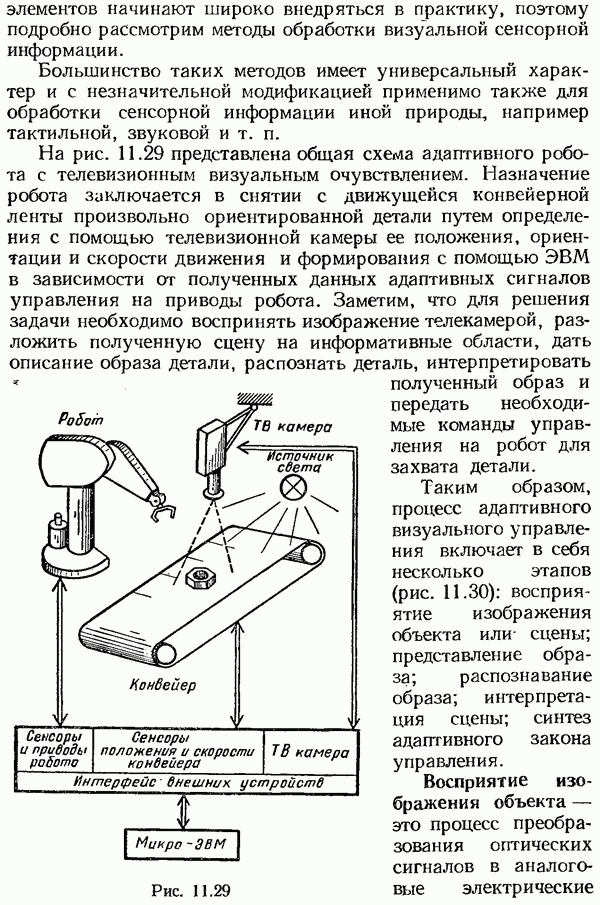
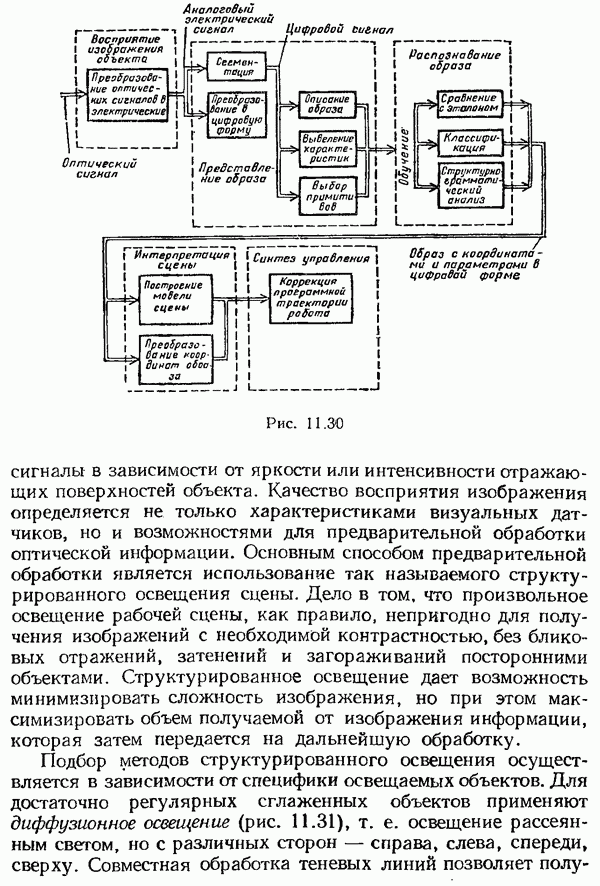
- Методы обработки сенсорной информации для адаптивного управления роботами.
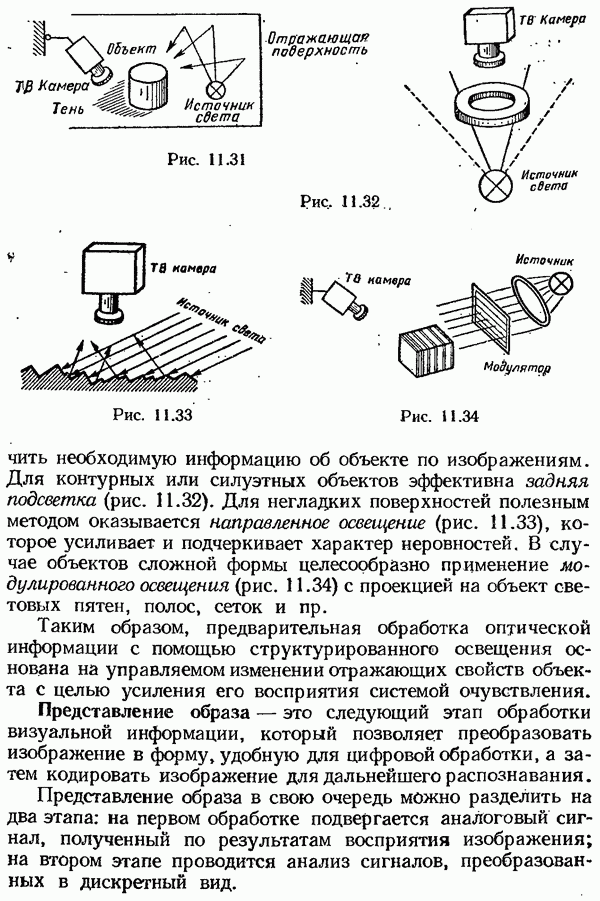
- Восприятие изображения объекта
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ