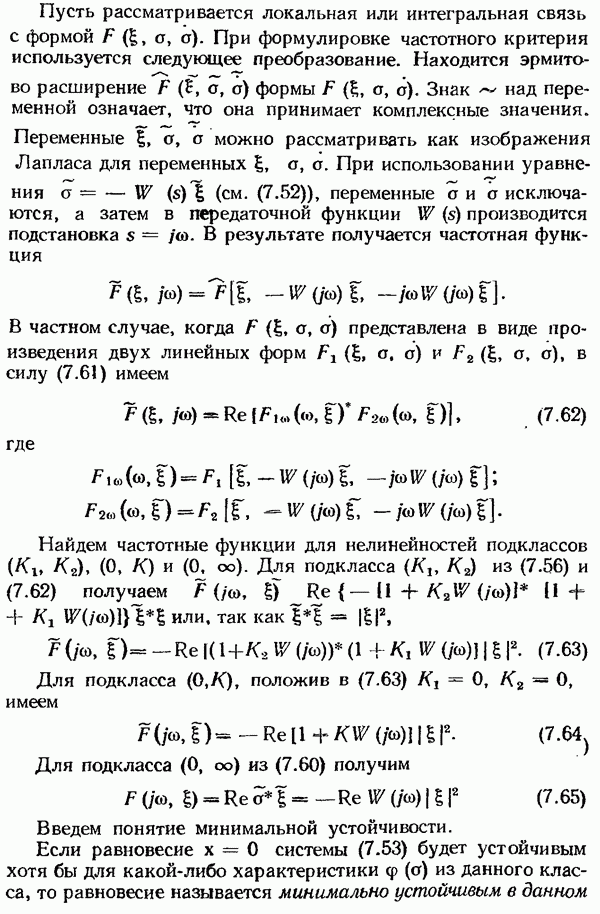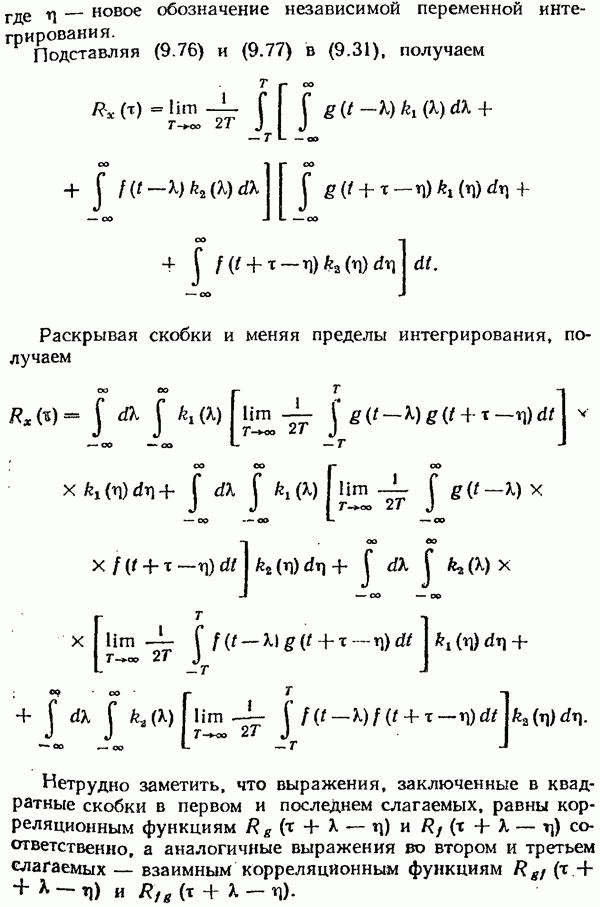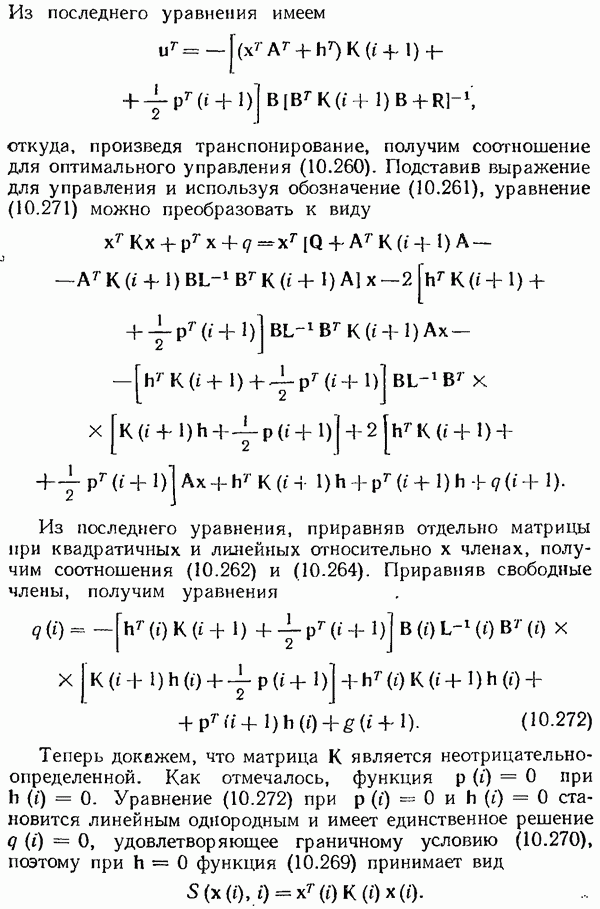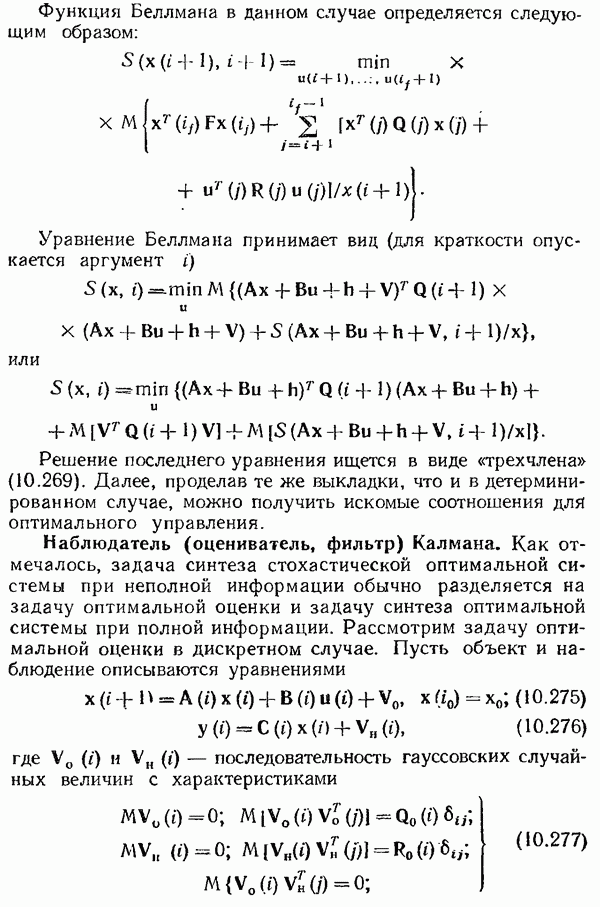| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
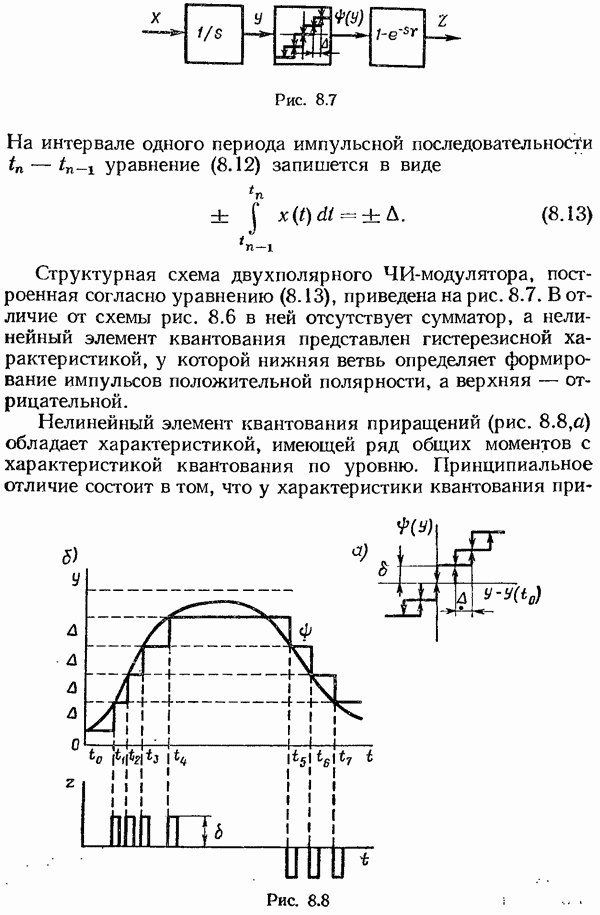
Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
На основании

Рис. 11.23
(11.165) поверхность скольжения  формируется из
формируется из  фазовых координат системы
фазовых координат системы  Поэтому при создании системы с переменной структурой требуется информация о производных сигнала ошибки х. Количество производных определяется порядком исходного дифференциального уравнения. Хорошо известно, что получение точных значений производных высокого порядка путем многократного дифференцирования сигнала х является сложной технической задачей. На практике при высокой размерности исходных уравнений приходится заменять часть недоступных точному измерению фазовых координат
Поэтому при создании системы с переменной структурой требуется информация о производных сигнала ошибки х. Количество производных определяется порядком исходного дифференциального уравнения. Хорошо известно, что получение точных значений производных высокого порядка путем многократного дифференцирования сигнала х является сложной технической задачей. На практике при высокой размерности исходных уравнений приходится заменять часть недоступных точному измерению фазовых координат  различными внутренними координатами системы, связанными с фазовыми координатами через параметры объекта управления или регулятора. При этом удается получить преимущество в точности воспроизведения значений координат и снизить влияние помех на систему.
различными внутренними координатами системы, связанными с фазовыми координатами через параметры объекта управления или регулятора. При этом удается получить преимущество в точности воспроизведения значений координат и снизить влияние помех на систему.
Однако в системах с переменной структурой указанная замена часто оказывается неэквивалентной. На рис. 11.23 представлена система с переменной структурой. В управляющем устройстве  формируется закон управления
формируется закон управления

где

 — поверхность скольжения,
— поверхность скольжения,  — постоянные величины;
— постоянные величины;  — постоянные коэффициенты.
— постоянные коэффициенты.
Для формирования закона управления (11.170) необходимо продифференцировать сигнал ошибки  два раза и получить фазовые координаты
два раза и получить фазовые координаты  где
где  После двукратного дифференцирования сигнала ошибки
После двукратного дифференцирования сигнала ошибки  с помощью реальных дифференциаторов уровень помех на выходе второго дифференциатора может возрасти до недопустимых значений. В этом случае может оказаться более выгодным использовать вместо координаты
с помощью реальных дифференциаторов уровень помех на выходе второго дифференциатора может возрасти до недопустимых значений. В этом случае может оказаться более выгодным использовать вместо координаты  внутреннюю координату 23, доступную для точного измерения непосредственно с объекта управления.
внутреннюю координату 23, доступную для точного измерения непосредственно с объекта управления.
Тогда поверхность скольжения будет иметь следующий вид:

Внутренняя координата  связана с координатой ошибки х, соотношением
связана с координатой ошибки х, соотношением

Подставив (11.172) в (11.171), получим

где 
Таким образом, после замены  на
на  положение поверхности скольжения в фазовом пространстве определяется в зависимости от переменных параметров объекта управления
положение поверхности скольжения в фазовом пространстве определяется в зависимости от переменных параметров объекта управления  Следовательно, движение в скользящем режиме, происходящее по указанной поверхности, теперь уже не будет независимым от параметрических возмущений, поскольку сама поверхность скольжения при изменениях указанных параметров будет подвижна. Это приведет к тому, что качество переходных процессов в системе будет существенно изменяться при параметрических воздействиях. Например, при значительных диапазонах изменения параметров
Следовательно, движение в скользящем режиме, происходящее по указанной поверхности, теперь уже не будет независимым от параметрических возмущений, поскольку сама поверхность скольжения при изменениях указанных параметров будет подвижна. Это приведет к тому, что качество переходных процессов в системе будет существенно изменяться при параметрических воздействиях. Например, при значительных диапазонах изменения параметров  длительность переходных процессов может изменяться в несколько раз. Если показатели качества должны поддерживаться в жестких пределах независимо от изменяющихся пара-. метров, тогда произвольные смещения поверхности скольжения должны устраняться, т. е. поверхность скольжения должна
длительность переходных процессов может изменяться в несколько раз. Если показатели качества должны поддерживаться в жестких пределах независимо от изменяющихся пара-. метров, тогда произвольные смещения поверхности скольжения должны устраняться, т. е. поверхность скольжения должна
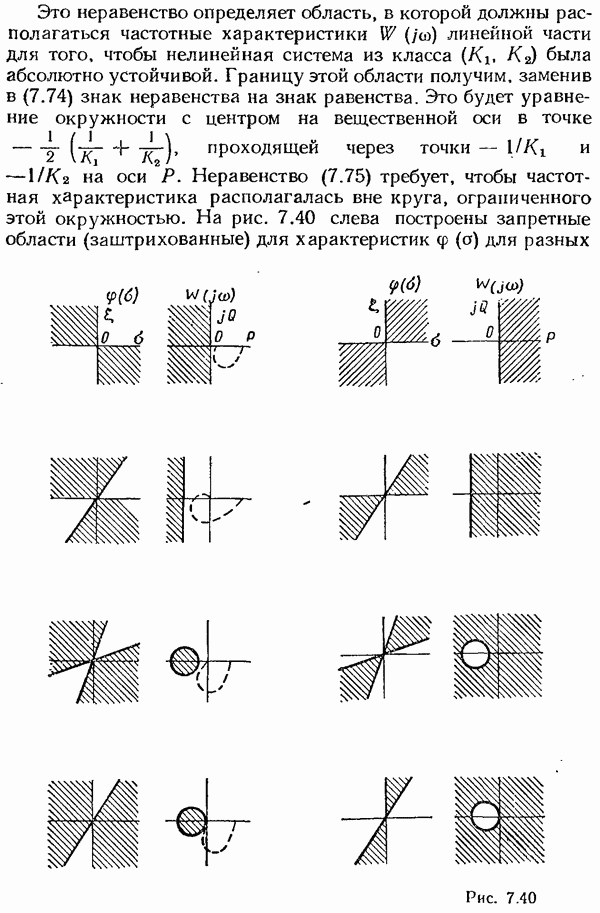
в процессе изменении возвращаться в исходное состояние. Однако такой способ адаптации требует дополнительной информации об изменяющихся параметрах объекта управления. Обычно возможности для получения такой информации ограничены. Поэтому возможен другой способ адаптации характеристик системы в условиях действия параметрических возмущений, который базируется на использовании не только разрывных коэффициентов в функции управления и, но и разрывных поверхностей скольжения  . В фазовом пространстве системы (рис. 11.24) формируются две поверхности скольжения, так же как и в случае (11.173), т. е. с помощью внутренней координаты
. В фазовом пространстве системы (рис. 11.24) формируются две поверхности скольжения, так же как и в случае (11.173), т. е. с помощью внутренней координаты 

Причем коэффициенты  подбирают, исходя из заданных требований к качеству переходных процессов, но так, чтобы во всем диапазоне изменения параметров объекта траектории движения в скользящем режиме по поверхности были только апериодические, что соответствует сильно демпфированному движению. Коэффициенты
подбирают, исходя из заданных требований к качеству переходных процессов, но так, чтобы во всем диапазоне изменения параметров объекта траектории движения в скользящем режиме по поверхности были только апериодические, что соответствует сильно демпфированному движению. Коэффициенты  поверхности
поверхности  наоборот, подбирают из условия слабо демпфированных движений по траекториям скольжения на
наоборот, подбирают из условия слабо демпфированных движений по траекториям скольжения на 
Адаптивный закон управления позволяет объединить обе поверхности скольжения в одну, но разрывную поверхность скольжения, что эквивалентно скачкообразному изменению положения поверхности скольжения в фазовом пространстве:

где


Рис. 11.24
Все коэффициенты  являются постоянными величинами. Только коэффициенты
являются постоянными величинами. Только коэффициенты  — переменные в силу связи внутренней координаты
— переменные в силу связи внутренней координаты  выбирают из условий перехода изображающей точки с
выбирают из условий перехода изображающей точки с  на
на  Разрыв поверхности скольжения
Разрыв поверхности скольжения  производится в месте пересечения
производится в месте пересечения  с плоскостью
с плоскостью  Все постоянные коэффициенты (в частности, коэффициент
Все постоянные коэффициенты (в частности, коэффициент  выбирают как из условия попадания изображающей точки из любых начальных положений на обе поверхности скольжения, так и из условий обеспечения скользящих режимов на каждой поверхности скольжения
выбирают как из условия попадания изображающей точки из любых начальных положений на обе поверхности скольжения, так и из условий обеспечения скользящих режимов на каждой поверхности скольжения  при всех изменениях параметров объекта внутри заданного диапазона. На рис. 11.24 показана фазовая траектория, начинающаяся в точке М. Изображающая точка, попав на поверхность скольжения
при всех изменениях параметров объекта внутри заданного диапазона. На рис. 11.24 показана фазовая траектория, начинающаяся в точке М. Изображающая точка, попав на поверхность скольжения  далее перемещается но этой поверхности в скользящем режиме вплоть до плоскости В. В этот момент происходит разрыв и перемещение поверхности скольжения [изменение
далее перемещается но этой поверхности в скользящем режиме вплоть до плоскости В. В этот момент происходит разрыв и перемещение поверхности скольжения [изменение  на
на  . В результате этого скользящий режим прекращается изображающая точка в силу уравнений одной из структур движется в направлении измененной поверхности скольжения, попадает на эту поверхность и заканчивает движение в скользящем режиме уже по поверхности
. В результате этого скользящий режим прекращается изображающая точка в силу уравнений одной из структур движется в направлении измененной поверхности скольжения, попадает на эту поверхность и заканчивает движение в скользящем режиме уже по поверхности  Эффект адаптации здесь проявляется за счет того, что, хотя обе поверхности скольжения
Эффект адаптации здесь проявляется за счет того, что, хотя обе поверхности скольжения  в результате параметрических возмущений смещаются в фазовом пространстве, это практически не сказывается на показателях качества переходных процессов, поскольку заключительный этап движения всегда происходит по сильно демпфированной траектории скольжения на поверхности
в результате параметрических возмущений смещаются в фазовом пространстве, это практически не сказывается на показателях качества переходных процессов, поскольку заключительный этап движения всегда происходит по сильно демпфированной траектории скольжения на поверхности 
При очень больших диапазонах изменения параметров объекта разрыв поверхности скольжения  на пересечении с неподвижной плоскостью
на пересечении с неподвижной плоскостью  оказывается эффективным только для части диапазона изменения параметров.
оказывается эффективным только для части диапазона изменения параметров.
Этот недостаток устраняется за счет формирования подвижной плоскости  обеспечивающей разрыв и переключение
обеспечивающей разрыв и переключение  Такой эффект получается при введении в уравнение плоскости разрыва В внутренней координаты
Такой эффект получается при введении в уравнение плоскости разрыва В внутренней координаты  вместо фазовой координаты
вместо фазовой координаты  . Плоскость В, перемещаясь вверх или вниз однозначно с изменениями параметров объекта, вносит соответствующее Опережение или запаздывание по моменту разрыва плоскости скольжения
. Плоскость В, перемещаясь вверх или вниз однозначно с изменениями параметров объекта, вносит соответствующее Опережение или запаздывание по моменту разрыва плоскости скольжения  тем самым улучшаются условия для попадания изображающей точки после разрыва с поверхности скольжения
тем самым улучшаются условия для попадания изображающей точки после разрыва с поверхности скольжения  на поверхность
на поверхность  Закон управления в этом случае приобретает следующий вид:
Закон управления в этом случае приобретает следующий вид:

Все коэффициенты являются постоянными величинами, а  такие же, как и в (11.175)
такие же, как и в (11.175)
К преимуществу адаптивных систем с переменной структурой указанных типов следует отнести высокую эффективность адаптации при простом конструктивном исполнении системы. Выбор постоянных настроек регулятора и логическая коррекция структуры в зависимости только от фазового состояния системы управления существенно упрощают ее синтез.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
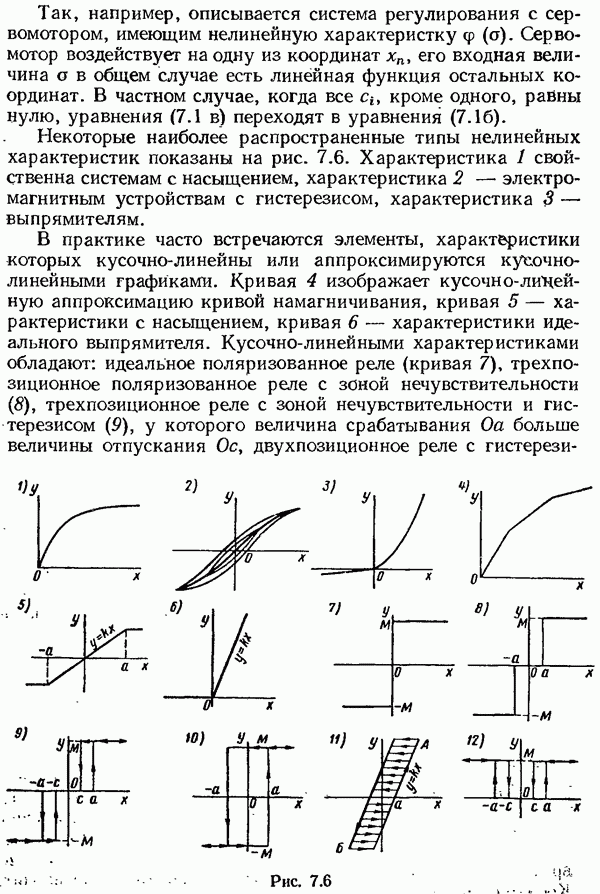
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
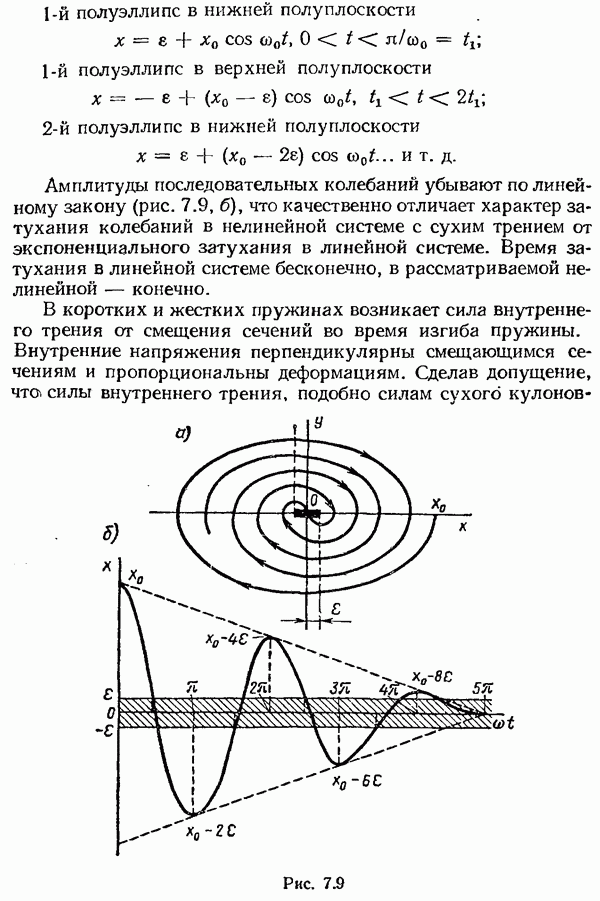
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
- § 7.3. Автоколебания. Метод точечных преобразований
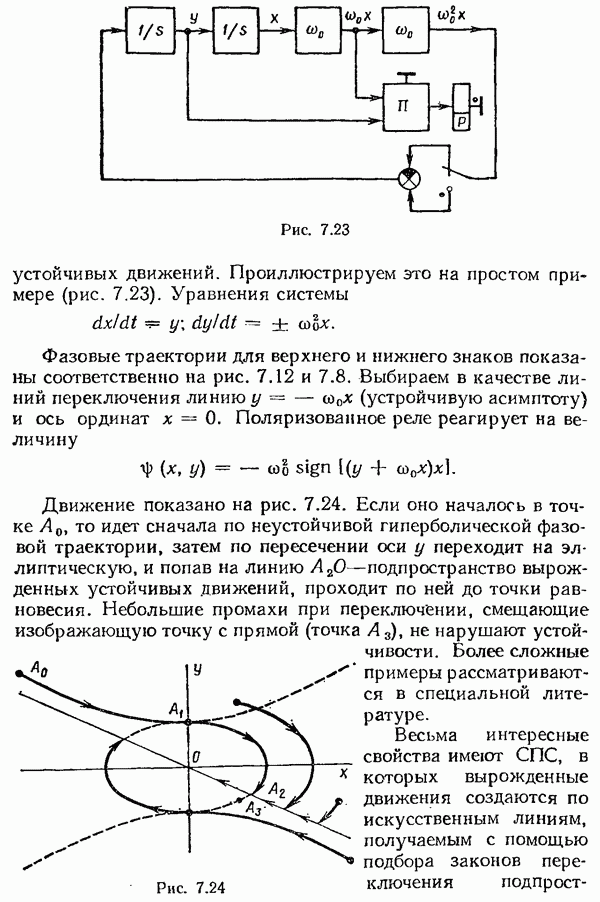
- § 7.4. Системы с переменной структурой
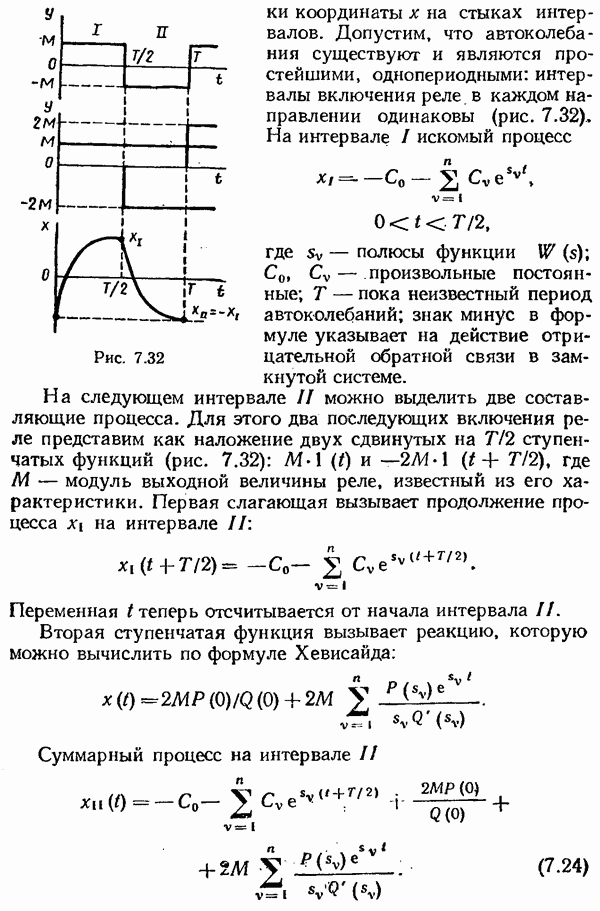
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 8.1. Понятие об импульсных системах автоматического управления
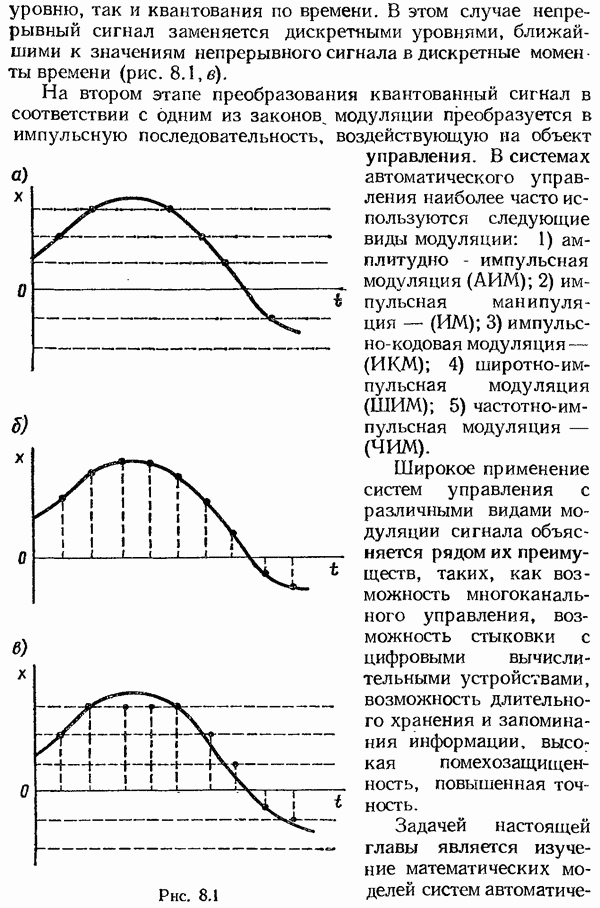
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
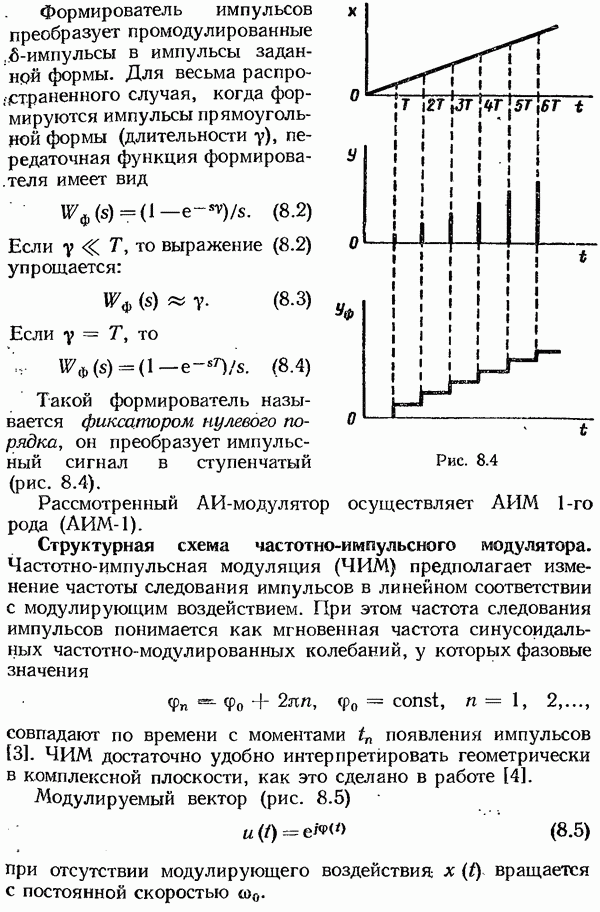
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
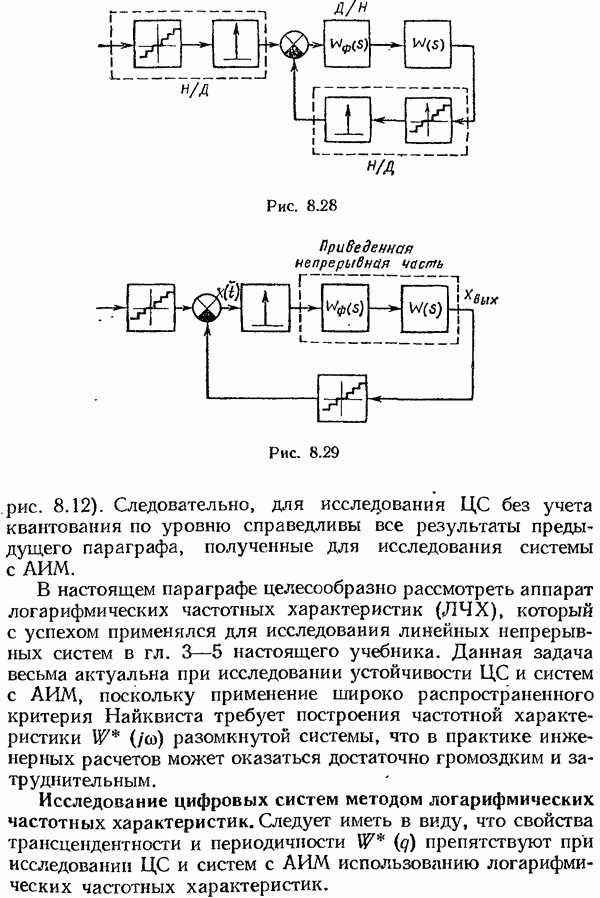
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
- Исследование периодических режимов в системах с ИЧИМ.
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
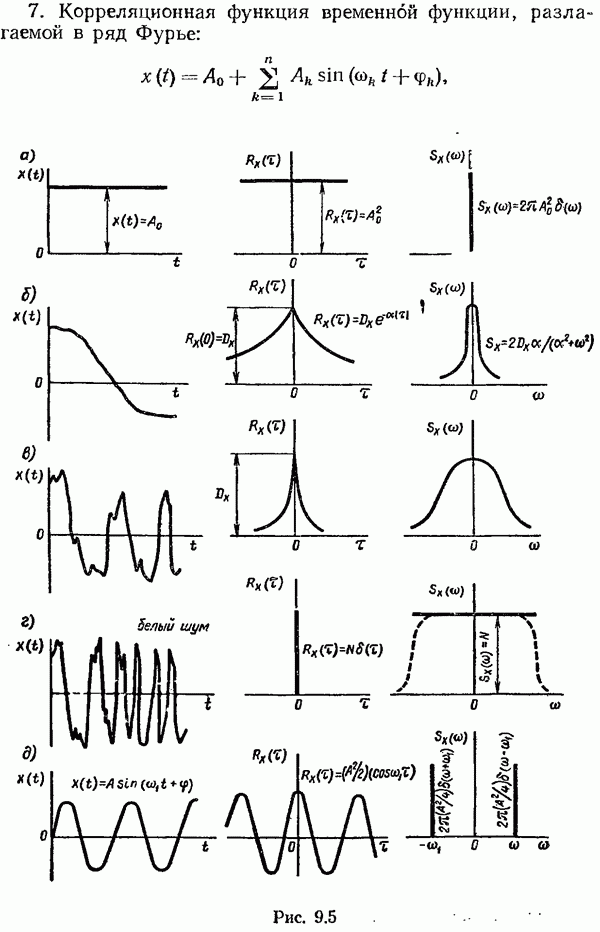
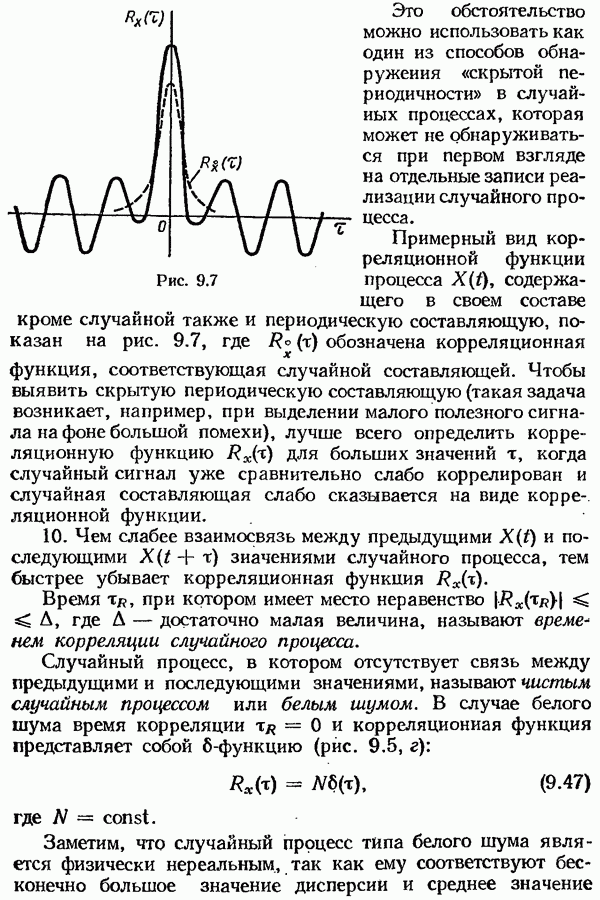
- § 9.3. Корреляционные функции случайных процессов
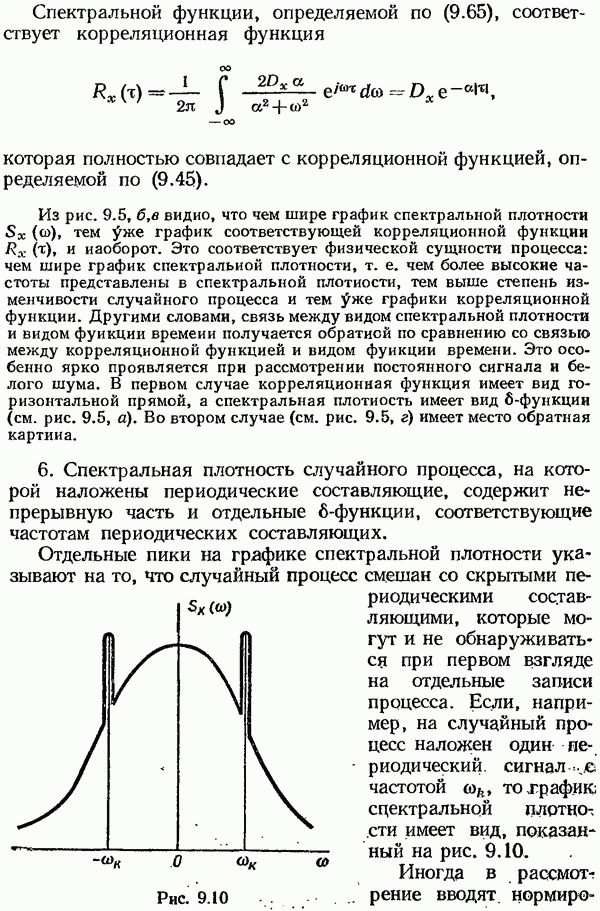
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
- Графоаналитическое определение дисперсии ошибки.
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
- § 9.9. Нелинейное преобразование случайных сигналов
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
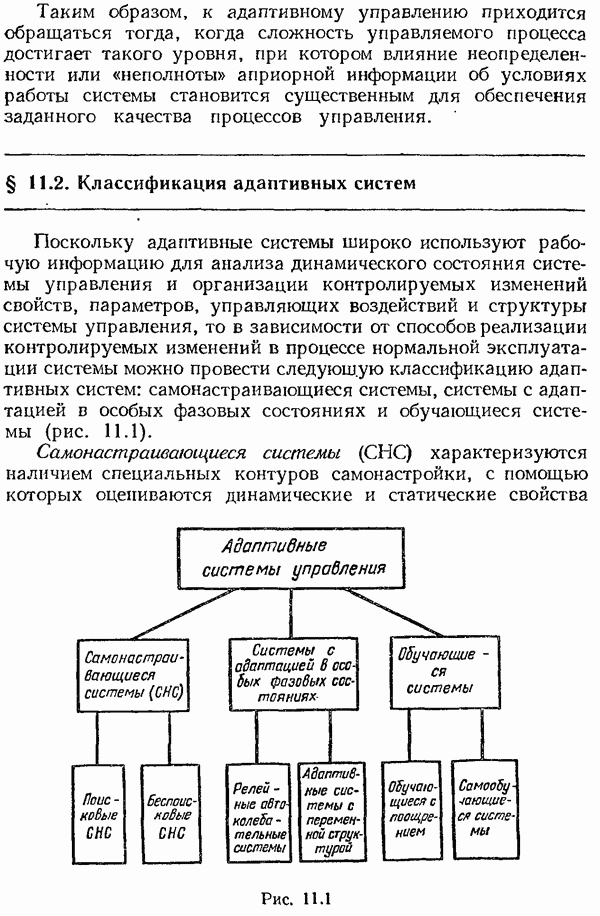
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
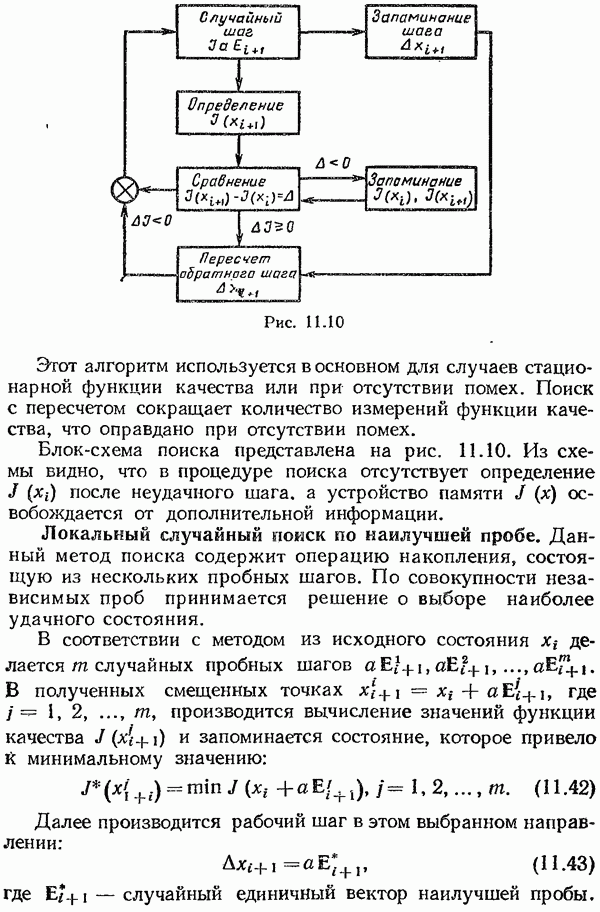
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
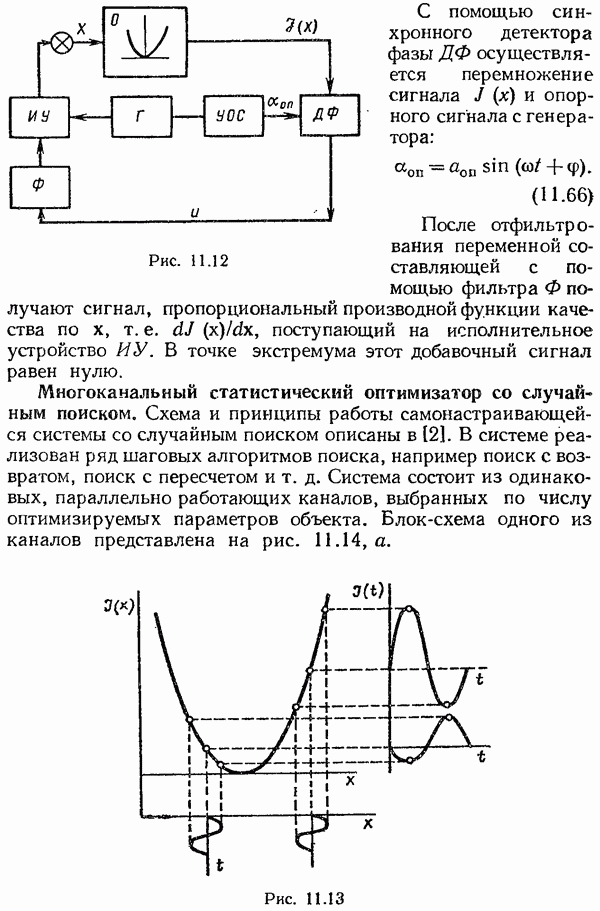
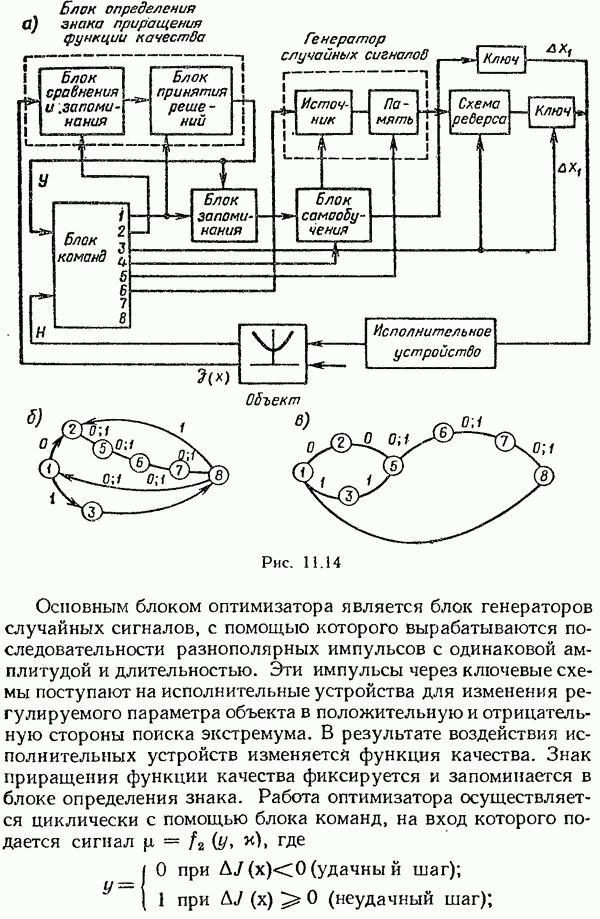
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
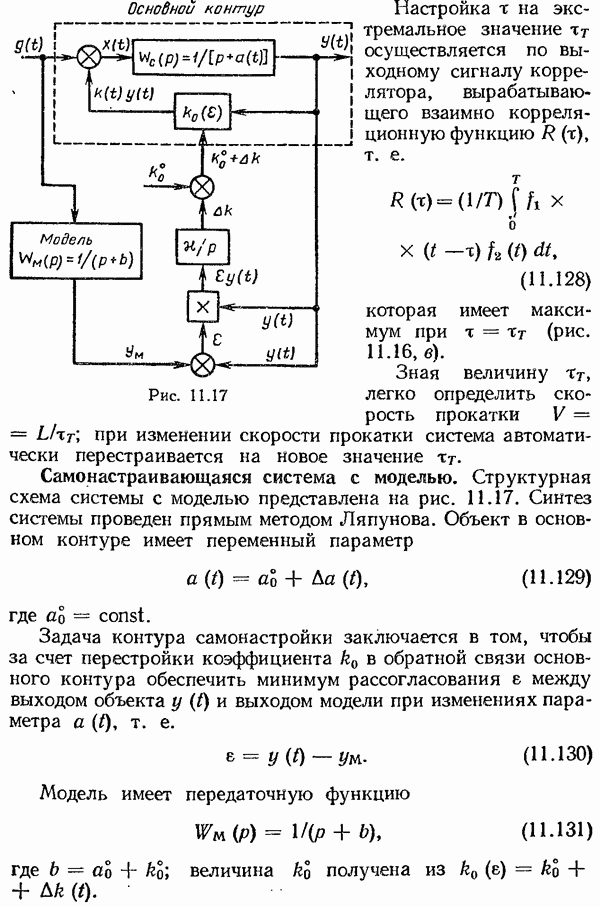
- Самонастраивающаяся система с моделью.
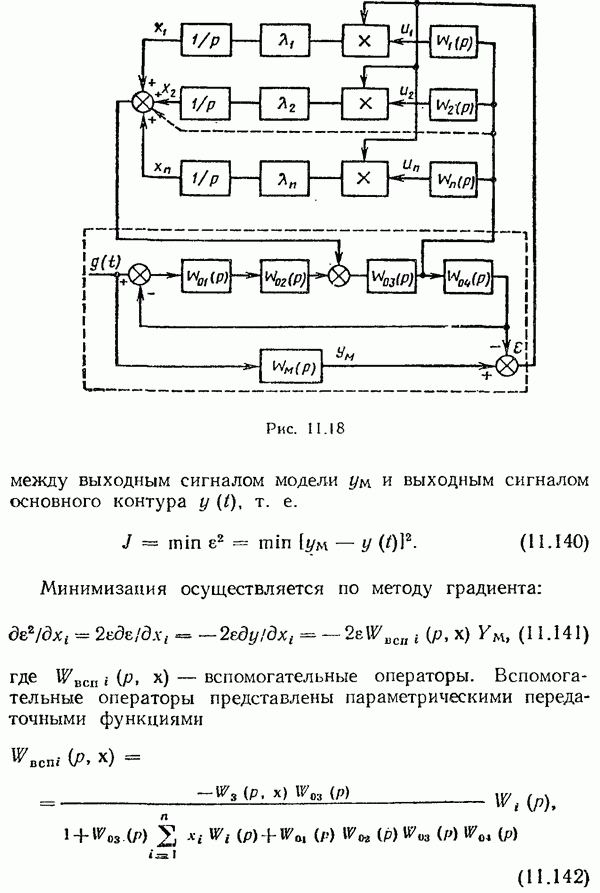
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
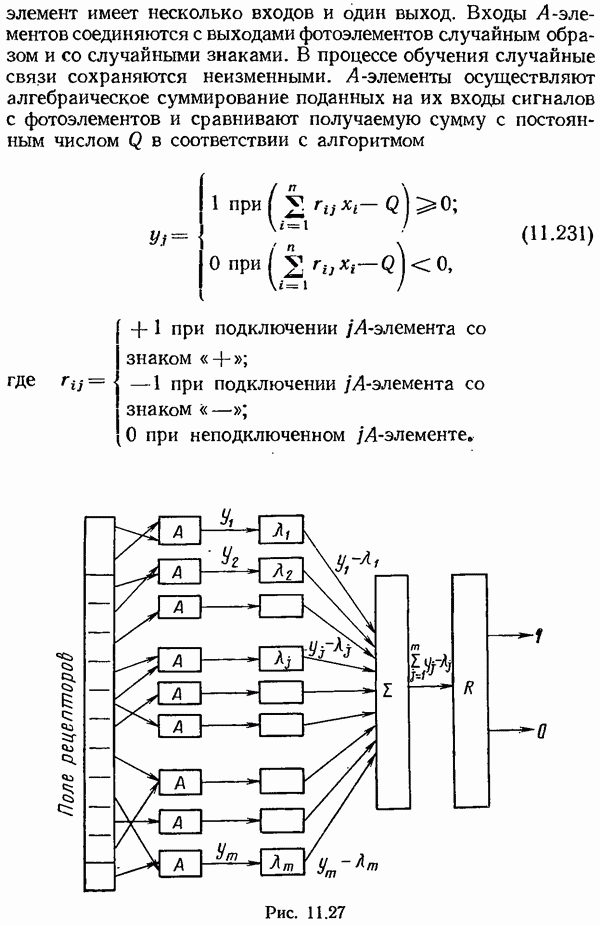
- Персептронная модель автоматической классификации.
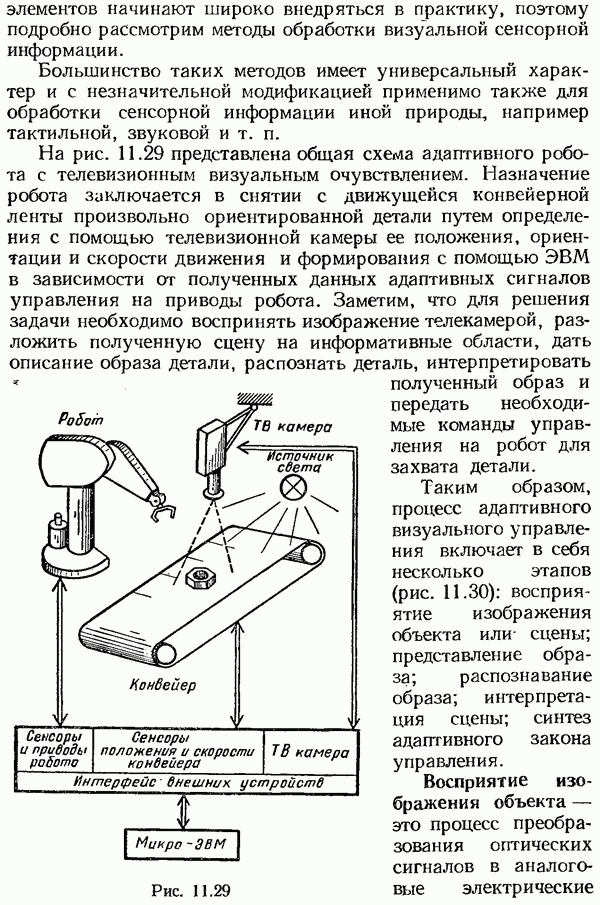
- § 11.6. Адаптивные робототехнические системы
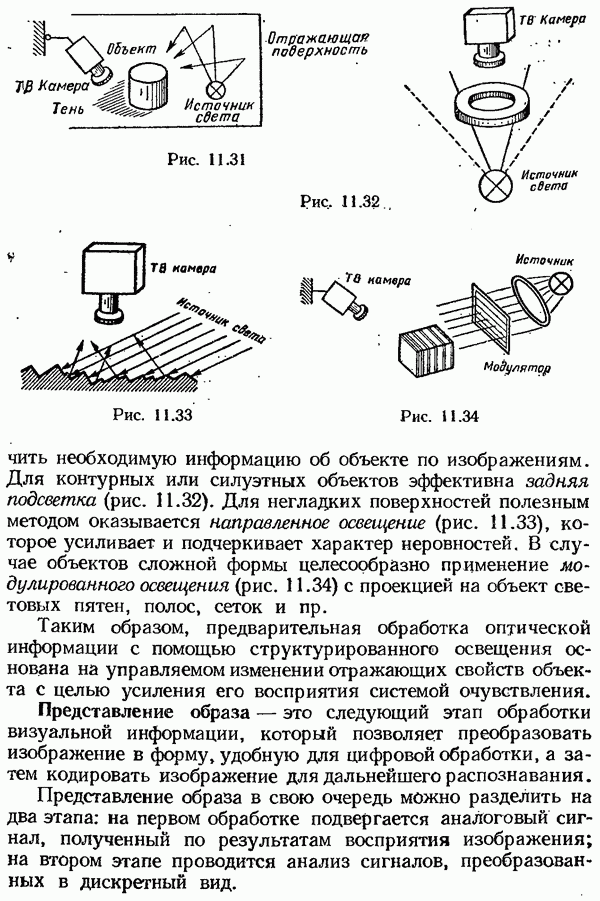
- Методы обработки сенсорной информации для адаптивного управления роботами.
- Восприятие изображения объекта
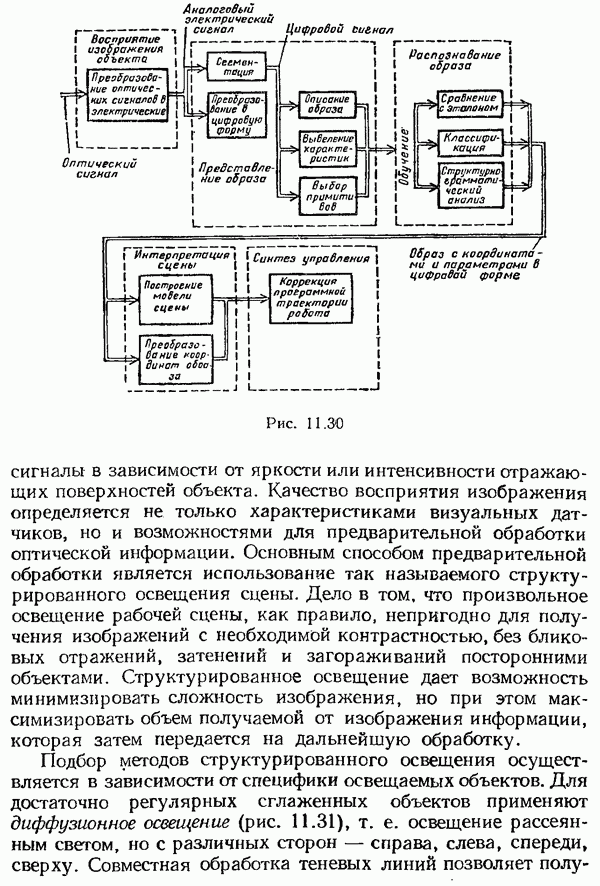
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ