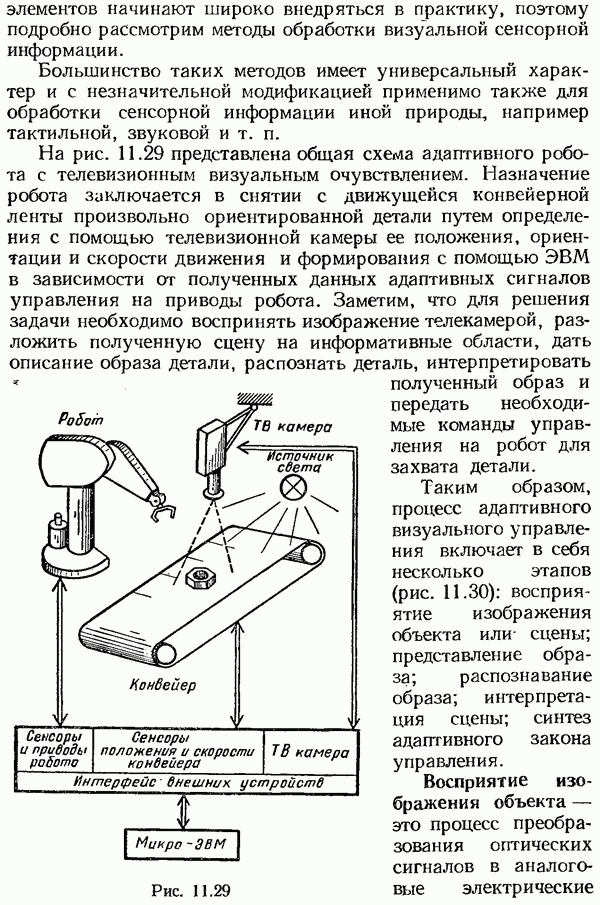
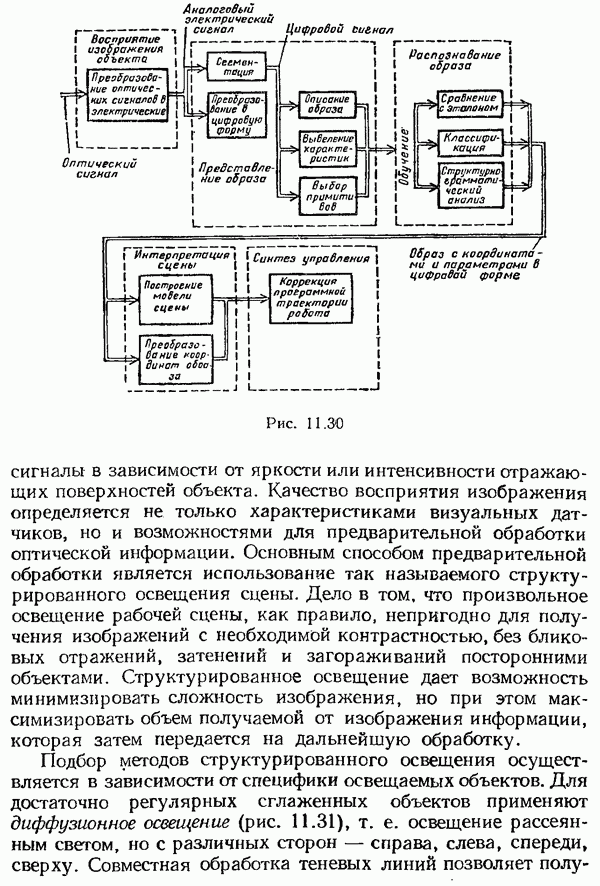
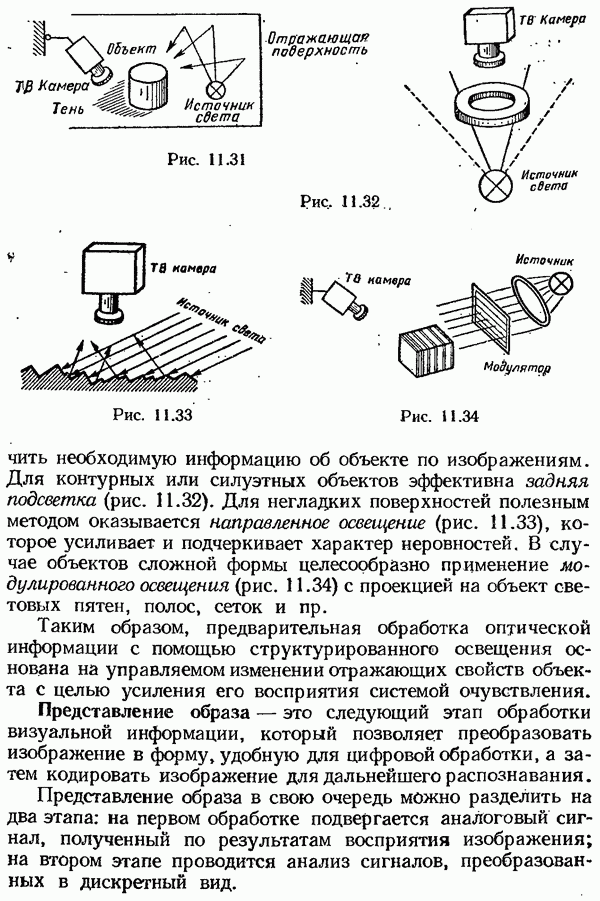
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
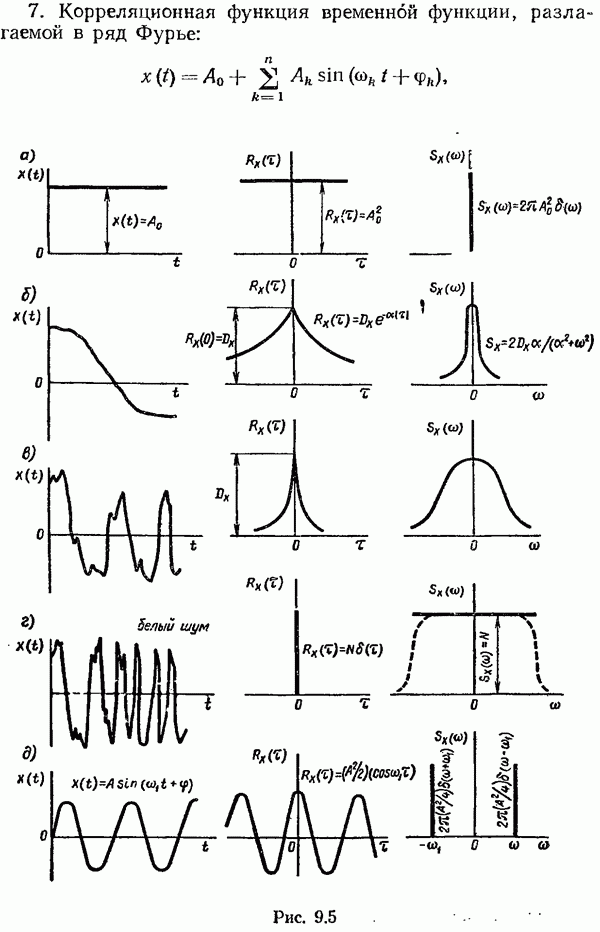
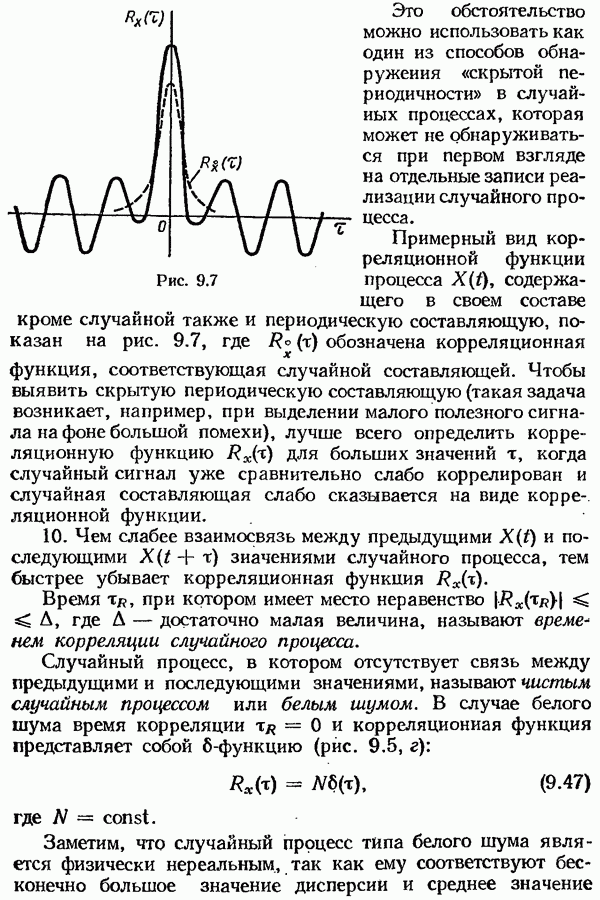
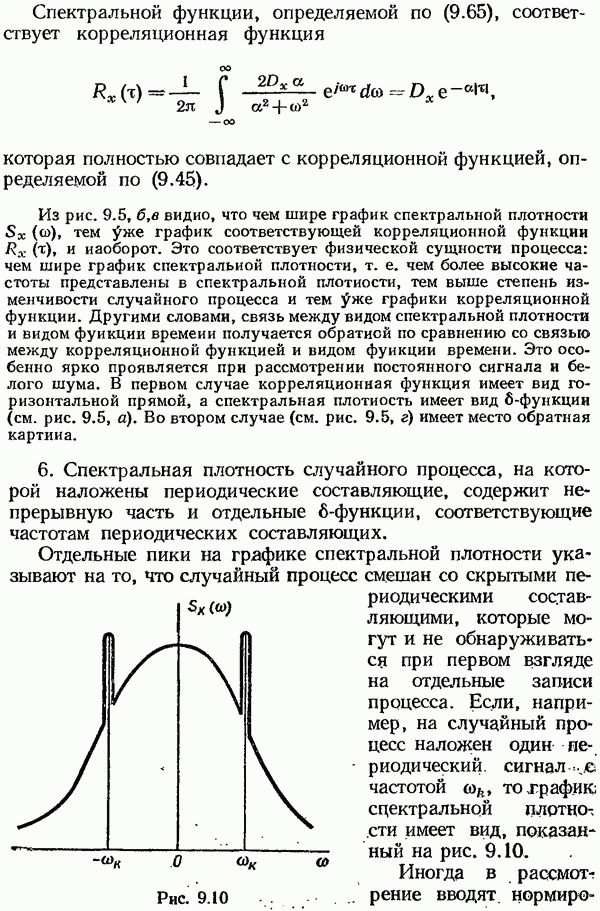
§ 9.10. Статистическая линеаризация нелинейных элементов
Наибольшее распространение в практике расчета нелинейных систем при случайных воздействиях получил приближенный метод, называемый методом статистической линеаризации, разработанный в 1954 г. одновременно И. Е. Казаковым в СССР и Р. Бутоном в США.
Идея метода основана на приближенной замене нелинейных преобразований процессов, происходящих в системе, статистически эквивалентными им линейными преобразованиями, при этом нелинейный элемент заменяется статистически эквивалентным линейным элементом. В результате такой замены система в целом линеаризуется и для ее исследования можно применять аппарат линейной теории.
Возможны различные критерии статистической эквивалентности, которые могут быть положены в основу метода статистической линеаризации. В тех случаях, когда линеаризуют безынерционный нелинейный элемент, у которого нелинейная зависимость между входным  и выходным
и выходным  сигналами имеет вид
сигналами имеет вид

где  — статическая характеристика нелинейного элемента, применяют следующие два критерия:
— статическая характеристика нелинейного элемента, применяют следующие два критерия:
1. Критерий равенства математического ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента.
2. Критерий минимума математического ожидания квадрата разности случайных процессов на выходе нелинейного элемента и эквивалентного ему линейного элемента.
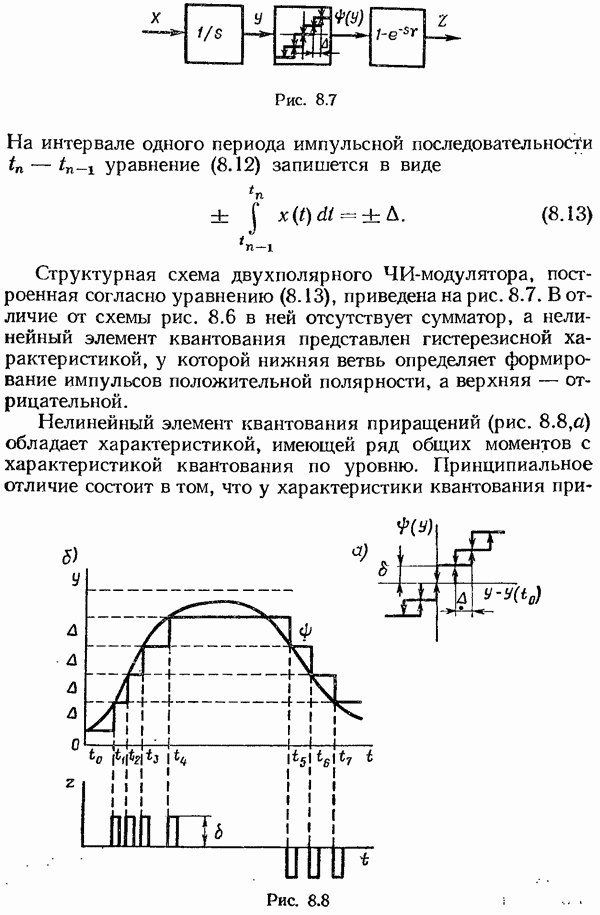
Познакомимся с этими критериями, ограничиваясь рассмотрением только однозначных нелинейных характеристик, которые могут быть либо нечетными, либо четными.
Напомним, что для нечетных и четных характеристик соответственно справедливы соотношения

Случайные процессы на входе и выходе нелинейного элемента могут быть представлены следующим образом:

где  — математические ожидания входного и выходного сигналов соответственно, включающие медленно меняющиеся регулярные составляющие;
— математические ожидания входного и выходного сигналов соответственно, включающие медленно меняющиеся регулярные составляющие;  — центрированные случайные составляющие процессов на входе и выходе нелинейного элемента соответственно.
— центрированные случайные составляющие процессов на входе и выходе нелинейного элемента соответственно.
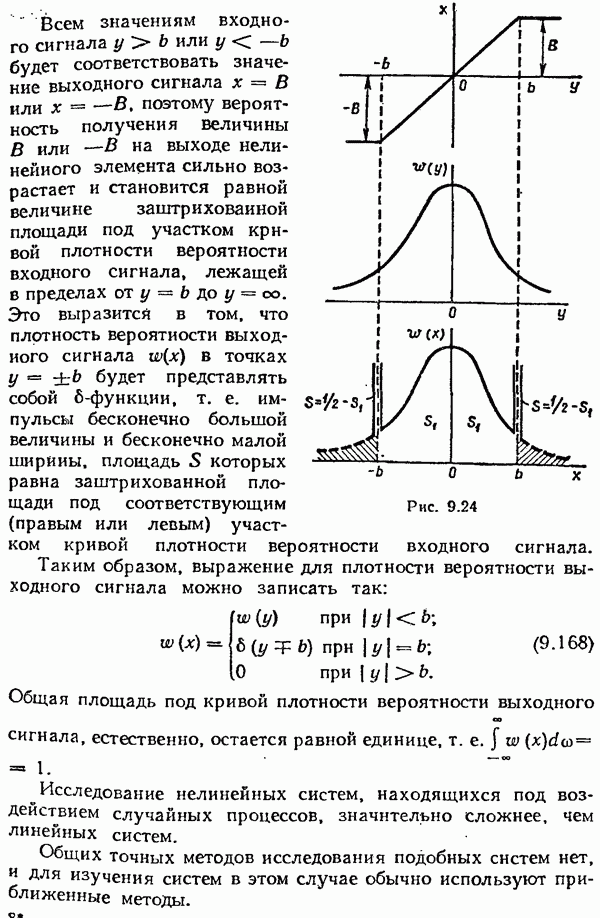
Заметим, что для четных нелинейных характеристик, обладающих выпрямляющими свойствами, математическое ожидание  отлично от нуля даже при
отлично от нуля даже при 
В общем случае для однозначной нелинейной функции  произвольного внда сигнал на выходе эквивалентного линеаризованного элемента
произвольного внда сигнал на выходе эквивалентного линеаризованного элемента

где  — математическое ожидание нелинейной функции
— математическое ожидание нелинейной функции  — эквивалентный статистический коэффициент усиления по случайной центрированной составляющей.
— эквивалентный статистический коэффициент усиления по случайной центрированной составляющей.
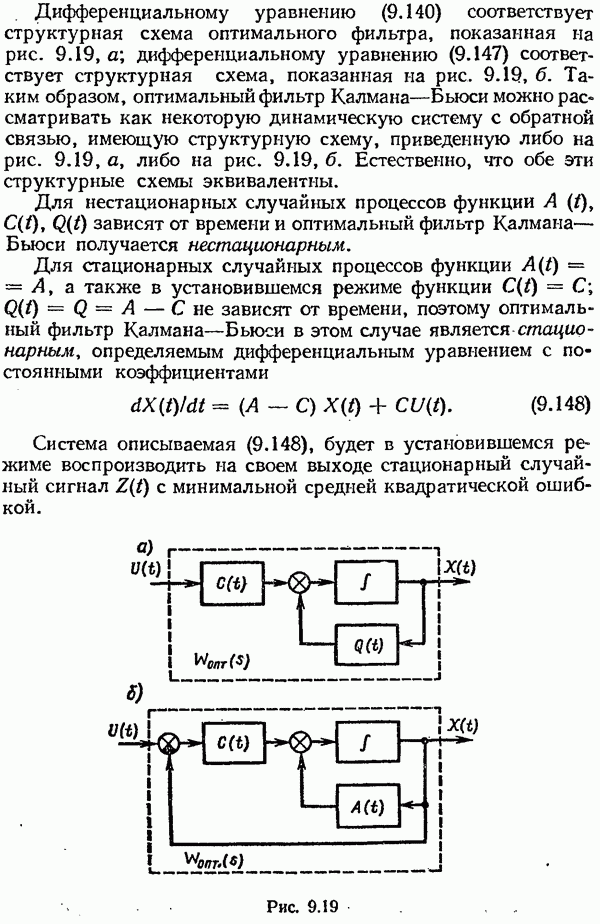
Таким образом, в общем случае нелинейный безынерционный элемент (рис. 9.25, а) заменяют двумя безынерционными элементами: нелинейным по математическому ожиданию и линейным по случайной центрированной составляющей (рис. 9.25, б).
В частном случае, когда нелинейный безынерционный элемент имеет нечетную характеристику, функция  может быть представлена в виде
может быть представлена в виде

где  — эквивалентный статистический коэффициент усиления нелинейного элемента по математическому ожиданию (по средней составляющей).
— эквивалентный статистический коэффициент усиления нелинейного элемента по математическому ожиданию (по средней составляющей).
В этом случае нелинейный элемент можно эквивалентно заменить двумя линейными элементами с коэффициентами усиления  (рис. 9.26). Числовые значения этих коэффициентов при заданной нелинейной зависимости
(рис. 9.26). Числовые значения этих коэффициентов при заданной нелинейной зависимости  определяются значениями математического ожидания и дисперсии случайного сигнала на входе нелинейного элемента.
определяются значениями математического ожидания и дисперсии случайного сигнала на входе нелинейного элемента.
Покажем сначала, как находят коэффициенты  в случае статистической линеаризации, основанной на первом
в случае статистической линеаризации, основанной на первом

Рис. 9.25

Рис. 9.26
критерии статистической эквивалентности, состоящем в выполнении равенства математического ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента, т. е. когда

Принимая во внимание (9.174), получаем

Для нечетных нелинейностей, учитывая (9.175), получим

Чтобы найти статистически эквивалентный коэффициент  перепишем (9.177) следующим образом:
перепишем (9.177) следующим образом:

откуда

Обозначение  показывает, что коэффициент кг найден по первому критерию эквивалентности.
показывает, что коэффициент кг найден по первому критерию эквивалентности.
Статистические коэффициенты  можно также выразить через нелинейную зависимость
можно также выразить через нелинейную зависимость  и плотность вероятности
и плотность вероятности  случайного сигнала
случайного сигнала  на входе нелинейного элемента:
на входе нелинейного элемента:


Знаки в (9.180) и (9.183) следует выбирать такими, чтобы знаки  совпадали.
совпадали.
Второй критерий статистической эквивалентности требует выполнения условия минимума математического ожидания квадрата разности процессов на выходе нелинейного элемента и эквивалентного линейного элемента, т. е.

Подставляя в (9.184) значения  определяемые по (9.173) и (9.174), получим
определяемые по (9.173) и (9.174), получим

После выполнения операции возведения в квадрат и вычисления математического ожидания имеем

где  — математическое ожидание случайного процесса на выходе нелинейного элемента;
— математическое ожидание случайного процесса на выходе нелинейного элемента;  — дисперсия центрированного случайного процесса на входе и выходе нелинейного элемента соответственно;
— дисперсия центрированного случайного процесса на входе и выходе нелинейного элемента соответственно;  — математическое ожидание (среднее значение) произведения двух случайных функций
— математическое ожидание (среднее значение) произведения двух случайных функций  равное начальному значению взаимной корреляционной функции
равное начальному значению взаимной корреляционной функции 
При заданных значениях  величина
величина  является функцией параметров
является функцией параметров 
Значения  , при которых выполняется (9.184), найдем, если приравняем нулю частные производные функции
, при которых выполняется (9.184), найдем, если приравняем нулю частные производные функции  по параметрам
по параметрам  Имеем
Имеем  откуда
откуда

В случае нечетной нелинейной характеристики  учитывая (9.175), получаем следующее выражение для коэффициента
учитывая (9.175), получаем следующее выражение для коэффициента 

Значение коэффициента  находим из
находим из

откуда

Обозначение  показывает, что коэффициент найден по второму критерию эквивалентности.
показывает, что коэффициент найден по второму критерию эквивалентности.
Статистический коэффициент  можно выразить также через плотность вероятности
можно выразить также через плотность вероятности  входного случайного сигнала
входного случайного сигнала  и нелинейную зависимость
и нелинейную зависимость  т. е.
т. е.

Обычно значение коэффициента  определенное из первого критерия по (9.180), является несколько завышенным,
определенное из первого критерия по (9.180), является несколько завышенным,  определенное из второго критерия по (9.188), — несколько заниженным, поэтому при расчетах рекомендуется брать их среднее арифметическое значение, т. е.
определенное из второго критерия по (9.188), — несколько заниженным, поэтому при расчетах рекомендуется брать их среднее арифметическое значение, т. е.

Сравнивая (9.178), и (9.179) с (9.186) и (9.187), видим, что коэффициенты  получаются одинаковыми при статистической линеаризации как по первому, так и по второму критерию.
получаются одинаковыми при статистической линеаризации как по первому, так и по второму критерию.
Из (9.181), (9.182), (9.183) и (9.189) видно, что статистически эквивалентные коэффициенты усиления зависят не только от вида характеристики нелинейного элемента  но и от закона распределения (плотности вероятности) случайного процесса на входе нелинейного элемента
но и от закона распределения (плотности вероятности) случайного процесса на входе нелинейного элемента  .
.
При использовании метода статистической линеаризации приближенно полагают, что закон распределения случайного процесса является нормальным. Такое предположение можно сделать потому, что при прохождении случайного сигнала с
любым законом распределения через линейные инерционные звенья на выходе последних закон распределения случайного сигнала оказывается близким к нормальному. При этом чем инерционнее система, тем закон распределения случайного сигнала на ее выходе ближе к нормальному. Наличие нелинейного элемента в системе нарушает это, однако при достаточно узкой полосе пропускания линейной части системы имеется тенденция к восстановлению нормального закона распределения.
При нормальном законе распределения плотность вероятности однозначно определяется математическим ожиданием и дисперсией случайного процесса, поэтому в этом случае коэффициенты  будут лишь функциями математического ожидания
будут лишь функциями математического ожидания  и дисперсии
и дисперсии  входного сигнала, т. е.
входного сигнала, т. е.

То обстоятельство, что коэффициенты  зависят от параметров ту и
зависят от параметров ту и  входного сигнала, отражено на рис. 9.26 пунктирными линиями.
входного сигнала, отражено на рис. 9.26 пунктирными линиями.
Формулы (9.181), (9.182), (9.183) и (9.189) при нормальном законе распределения будут иметь следующий вид:

Если умножить выражение (9.193) на ту, затем продифференцировать произведение  по
по  и сопоставить полученное выражение с (9.195), то можно убедиться в выполнении следующего равенства:
и сопоставить полученное выражение с (9.195), то можно убедиться в выполнении следующего равенства:

Соотношение (9.196) может быть использовано как для нахождения коэффициента  вместо (9.195), так и для проверки правильности определения коэффициентов
вместо (9.195), так и для проверки правильности определения коэффициентов 
Пример 9.9. На входе нелинейного элемента, имеющего статическую квадратичную зависимость  между входным и выходным сигналами, действует случайный сигнал
между входным и выходным сигналами, действует случайный сигнал  имеющий нормальный закон распределения. Определить эквивалентные статистические коэффициенты усиления
имеющий нормальный закон распределения. Определить эквивалентные статистические коэффициенты усиления 
1. Так как характеристика нелинейного элемента является четной, то в соответствии с (9.181) функция  равна
равна

2. На основании (9.196), дифференцируя полученное выражение для  определяем коэффициент
определяем коэффициент 

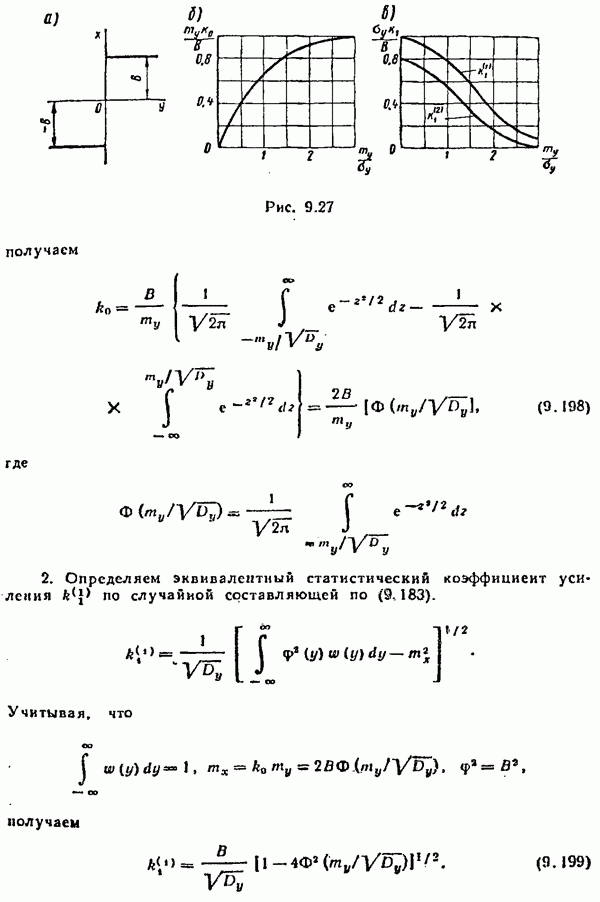
Пример 9.10. На входе нелинейного элемента типа идеального реле (рис. 9.27, а) с характеристикой

действует случайный сигнал  имеющий нормальный закон распределения. Определить эквивалентные статистические коэффициенты усиления нелинейного элемента
имеющий нормальный закон распределения. Определить эквивалентные статистические коэффициенты усиления нелинейного элемента 
1. Определяем эквивалентный статистический коэффициент усиления по математическому ожиданию  по (9.193), т. е.
по (9.193), т. е.

Вводя обозначение


(кликните для просмотра скана)
3. Определяем эквивалентный статистический коэффициент усиления  по случайной составляющей по (9.195):
по случайной составляющей по (9.195):

Учитывая (9.197), получаем

Из (9.198), (9.199) и (9.200) видно, что при нормальном законе распределения коэффициенты  выражаются через функцию Крампа (нормированный интеграл плотности вероятности)
выражаются через функцию Крампа (нормированный интеграл плотности вероятности)

Для вычисления коэффициентов статистической линеаризации достаточно знать математическое ожидание ту и дисперсию  случайного процесса на входе нелинейного элемента и значения функции Крампа для аргументов, определяемых через
случайного процесса на входе нелинейного элемента и значения функции Крампа для аргументов, определяемых через  .
.
Построенные по (9.198), (9.199), (9.200) графики коэффициентов  статистической линеаризации идеального реле приведены на рис 9 27, б, в. Из этих графиков видно, что релейный элемент по отношению к среднему значению входного сигнала ту ведет себя как линейное звено, коэффициент усиления которого
статистической линеаризации идеального реле приведены на рис 9 27, б, в. Из этих графиков видно, что релейный элемент по отношению к среднему значению входного сигнала ту ведет себя как линейное звено, коэффициент усиления которого  зависит от величины ту
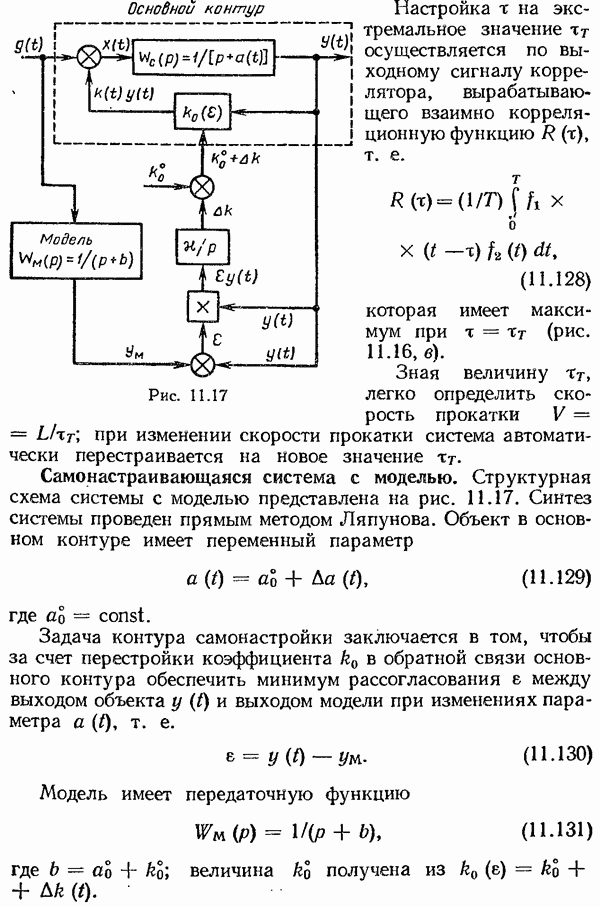
зависит от величины ту  .
.
Таким образом, случайная составляющая входного сигнала создает эффект линеаризации нелинейного элемента для регулярной составляющей (среднего значения) сигнала. Метод статистической линеаризации формально похож на метод вибрационной линеаризации нелинейного элемента колебаниями высокой частоты постоянной амплитуды.
В свою очередь, регулярная составляющая входного сигнала оказывает влияние на прохождение случайной составляющей. Так, например, для рассмотренного нелинейного элемента типа идеального реле передача случайной составляющей ослабляется за счет насыщения нелинейного элемента регулярной составляющей сигнала, поскольку коэффициенты  уменьшаются с ростом
уменьшаются с ростом  .
.
Ограничения в использовании метода статистической линеаризации обусловлены требованиями нормального закона распределения случайного процесса на входе нелинейного элемента, что выполняется достаточно хорошо, если линейная часть системы будет обладать свойствами низкочастотного фильтра.
Для нормального закона распределения значения коэффициентов  для различных типовых нелинейных элементов заранее определены по (9.192), (9.193), (9.194), (9.195) и приведены в виде графиков зависимости этих коэффициентов от математического ожидания
для различных типовых нелинейных элементов заранее определены по (9.192), (9.193), (9.194), (9.195) и приведены в виде графиков зависимости этих коэффициентов от математического ожидания  и дисперсии
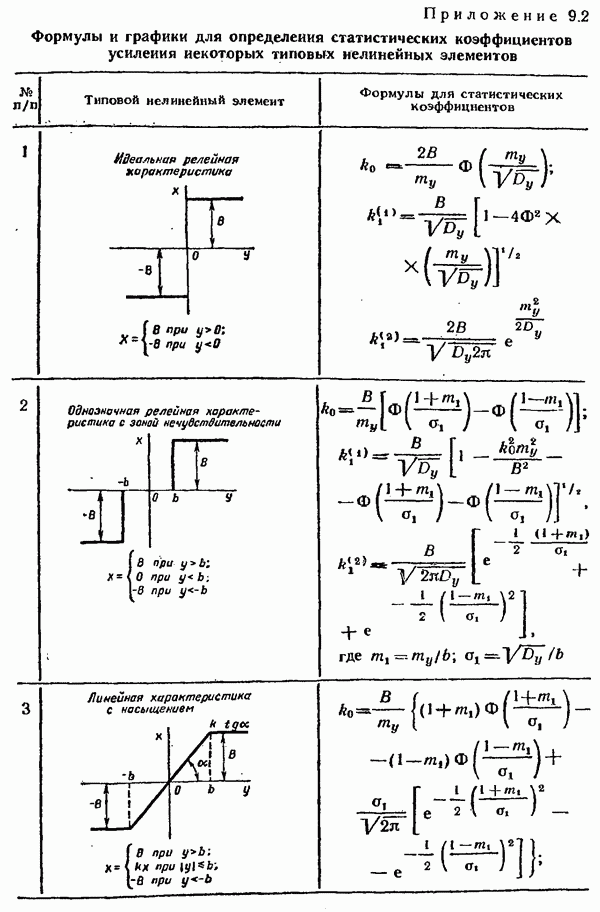
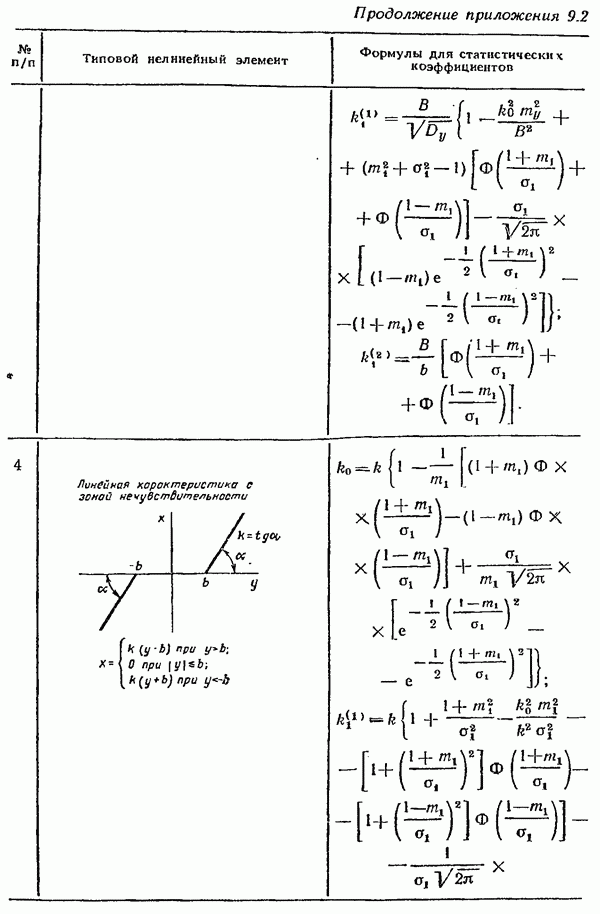
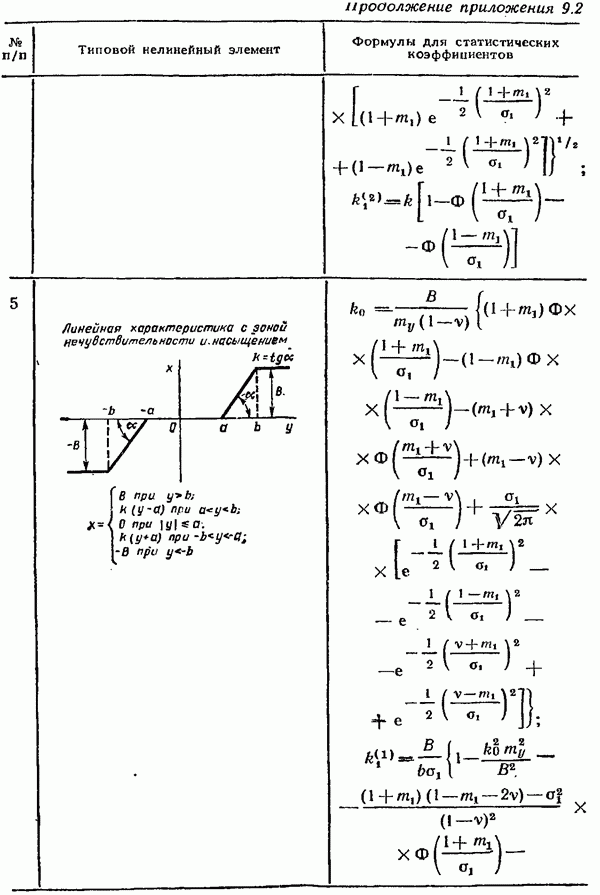
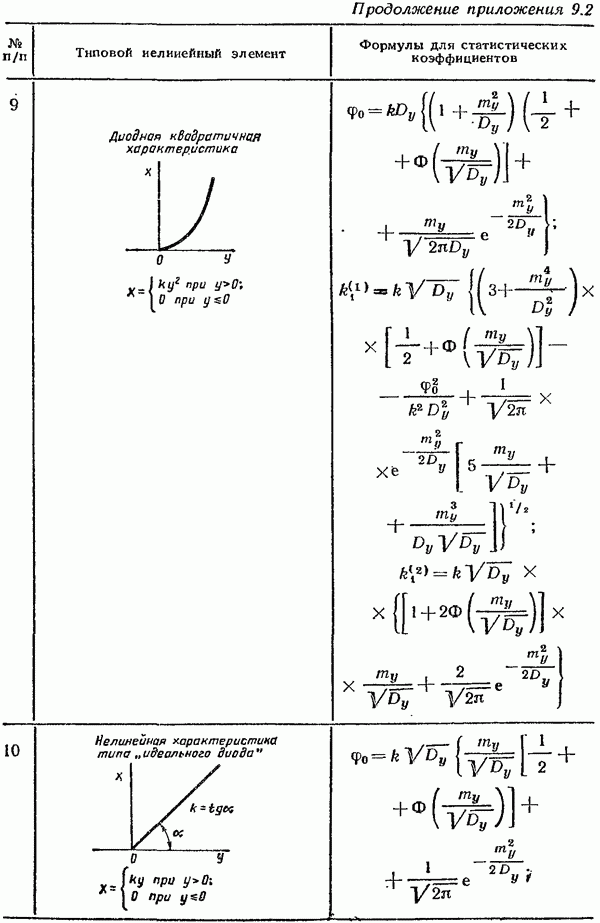
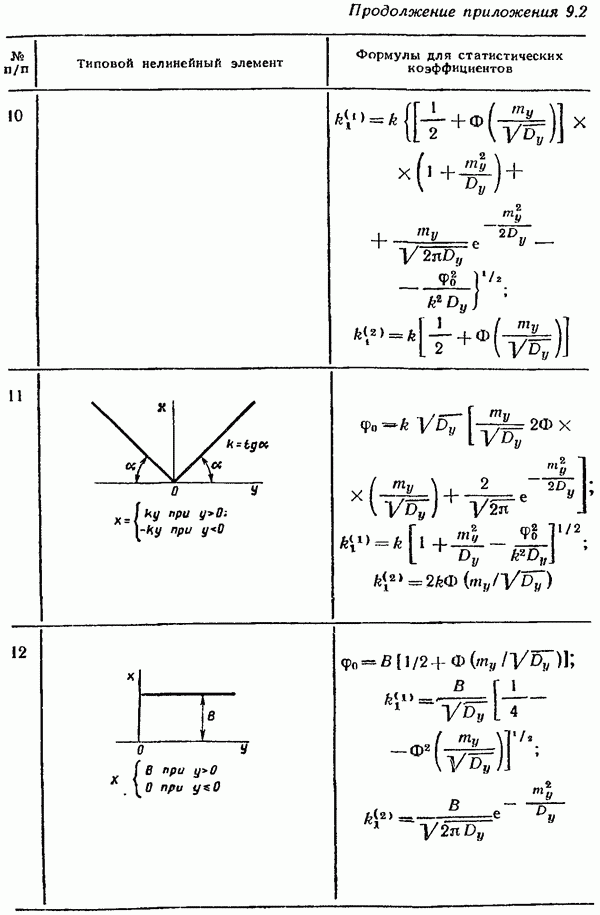
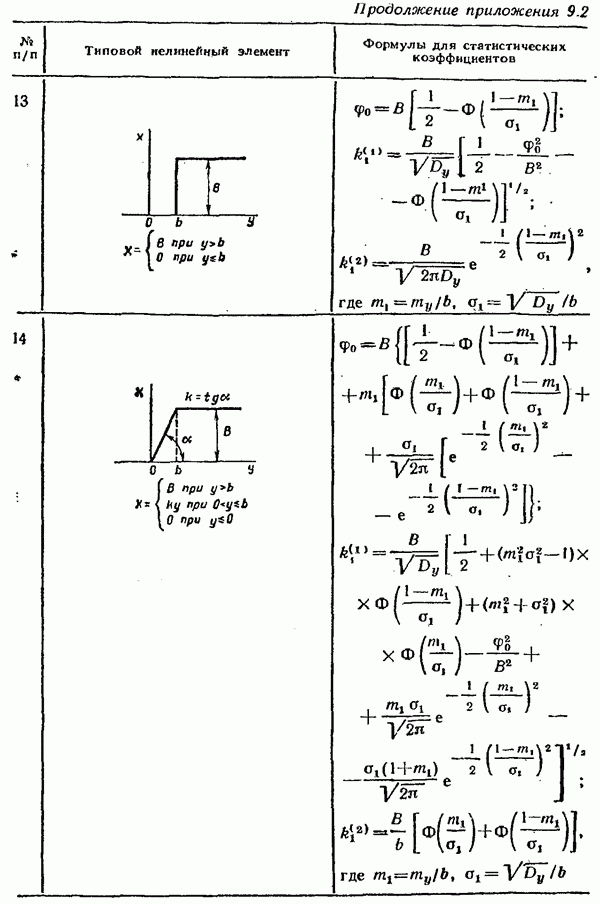
и дисперсии  входного случайного сигнала. Использование этих графиков значительно упрощает расчет конкретных систем автоматического управления методом статистической линеаризации. В приложении 9.2 приведены для примера формулы и графики
входного случайного сигнала. Использование этих графиков значительно упрощает расчет конкретных систем автоматического управления методом статистической линеаризации. В приложении 9.2 приведены для примера формулы и графики  для некоторых наиболее часто встречающихся типовых нелинейностей.
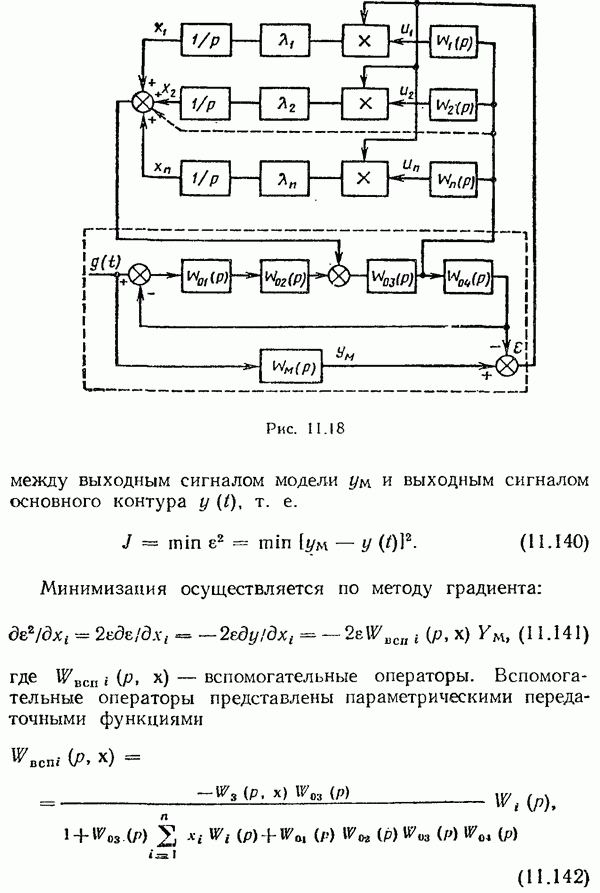
для некоторых наиболее часто встречающихся типовых нелинейностей.
Метод статистической линеаризации особенно эффективен при анализе стационарного режима работы системы автоматического управления. В этом случае  и коэффициенты статистической линеаризации не зависят от времени. Линеаризованная система является при этом системой с постоянными параметрами и ее исследование может быть проведено сравнительно просто.
и коэффициенты статистической линеаризации не зависят от времени. Линеаризованная система является при этом системой с постоянными параметрами и ее исследование может быть проведено сравнительно просто.
В нестационарном режиме, который может быть вызван, например, переходным процессом, нестационарностью воздействий или самой системы, коэффициенты статистической линеаризации изменяются во времени. Линеаризованная система оказывается при этом системой с переменными параметрами
и ее исследование усложняется. Исследования системы в этом случае могут производиться с помощью аналоговых или цифровых вычислительных машин.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
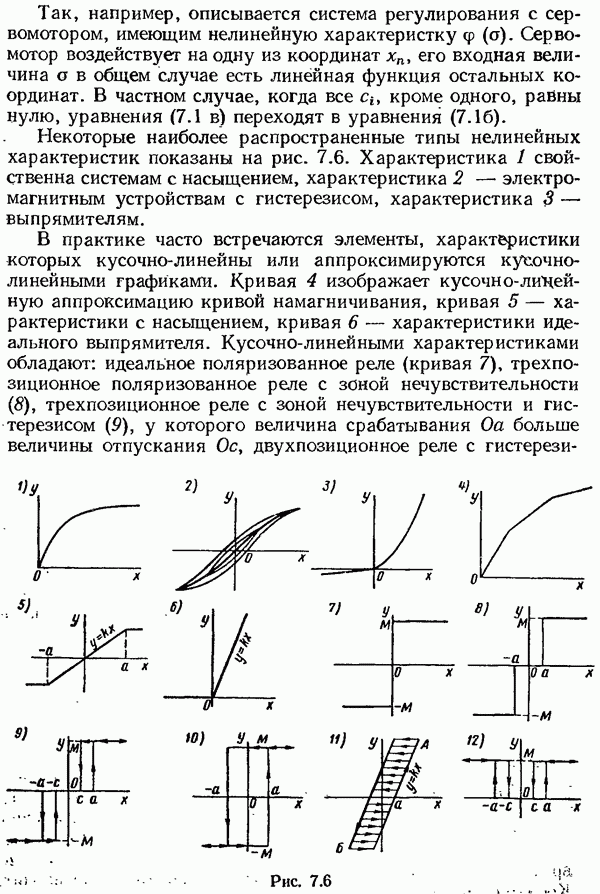
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
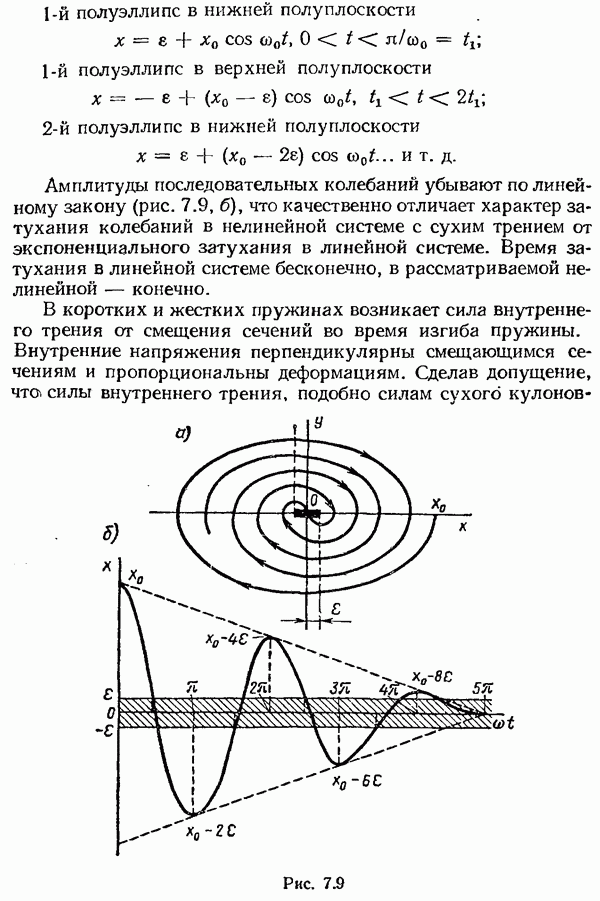
- § 7.3. Автоколебания. Метод точечных преобразований
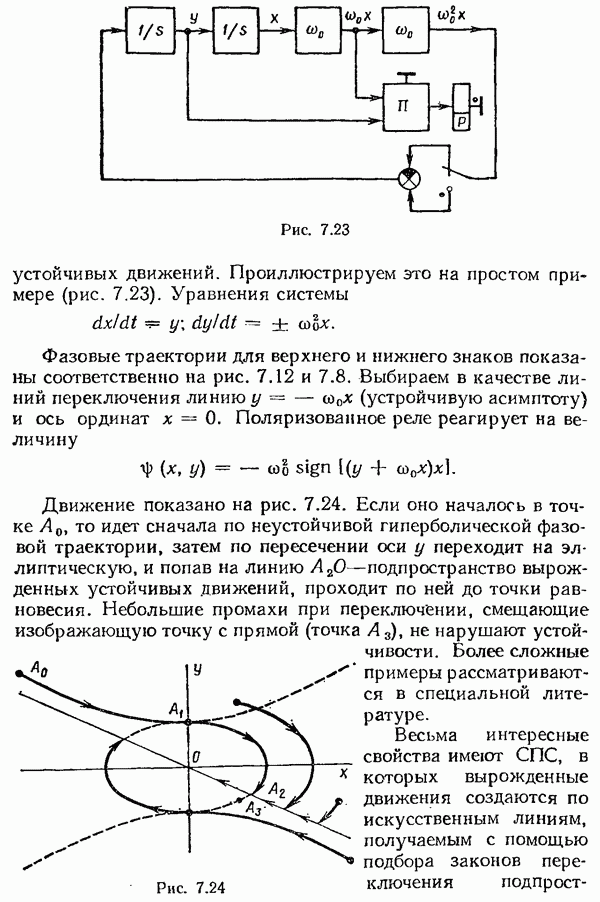
- § 7.4. Системы с переменной структурой
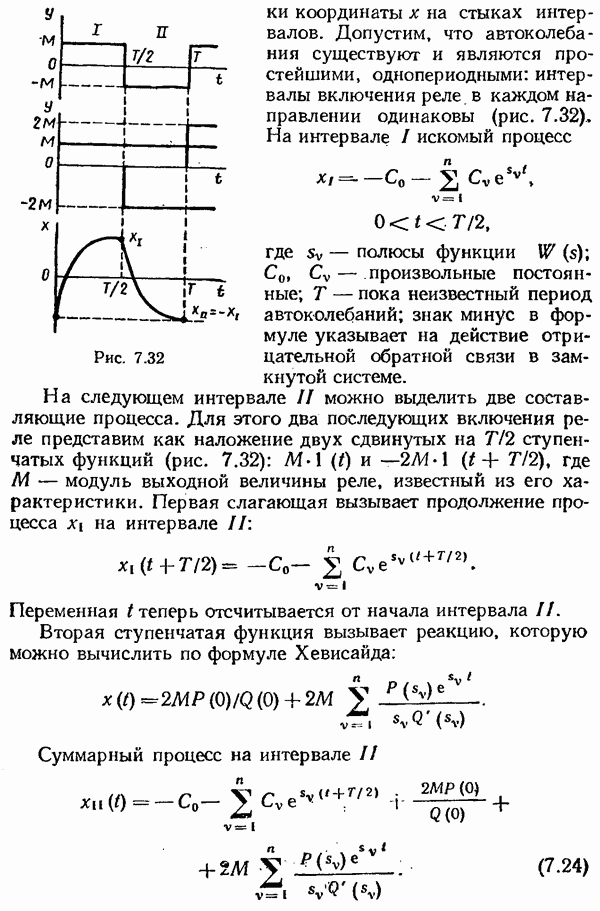
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
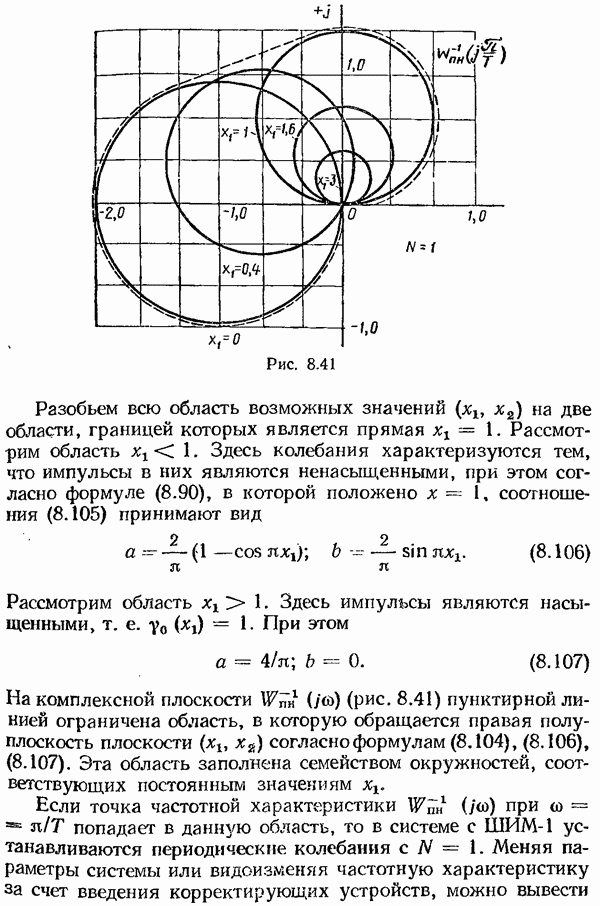
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
- Исследование периодических режимов в системах с ИЧИМ.
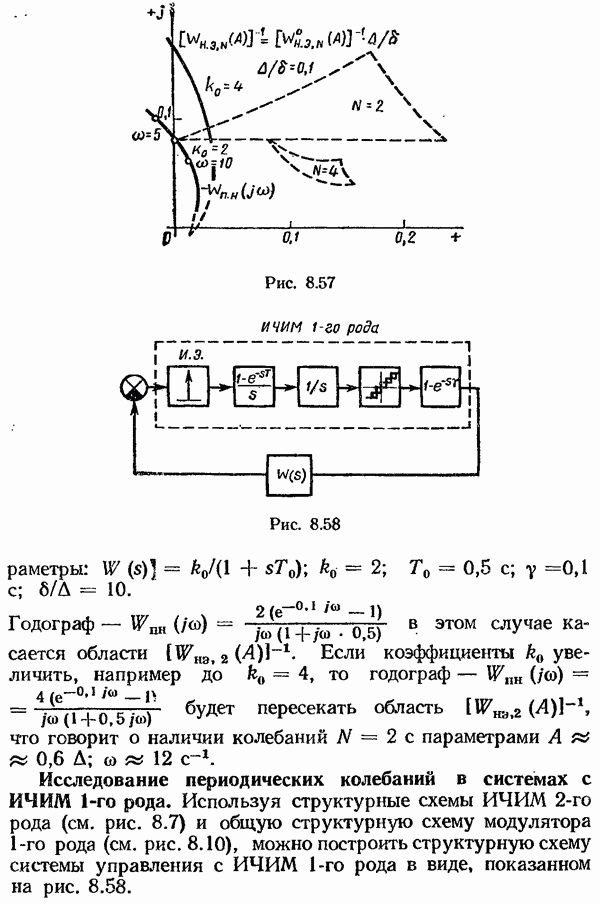
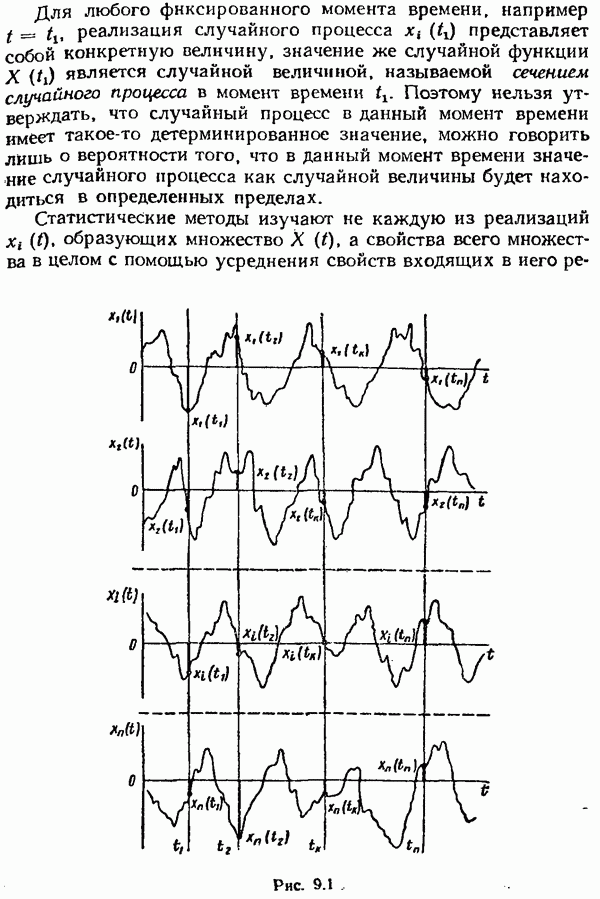
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
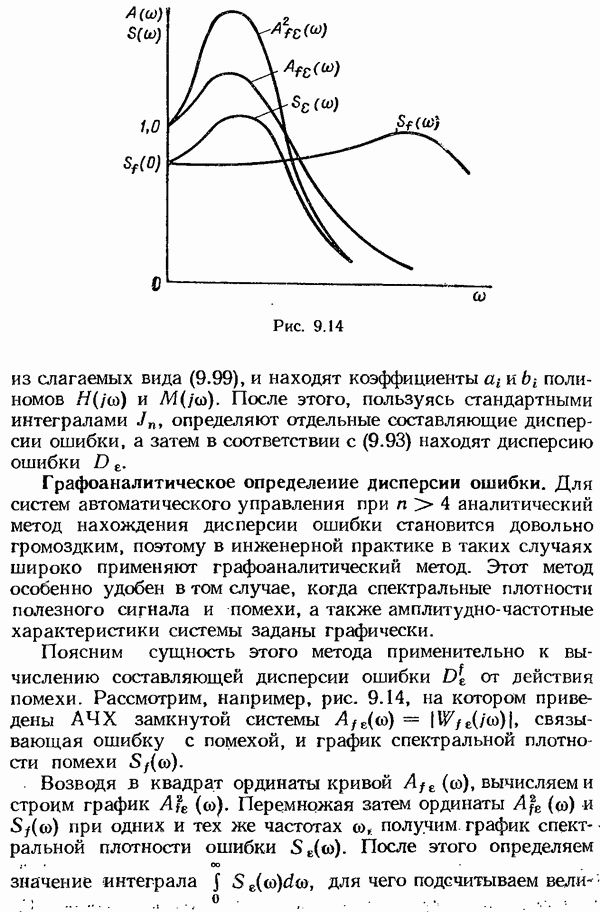
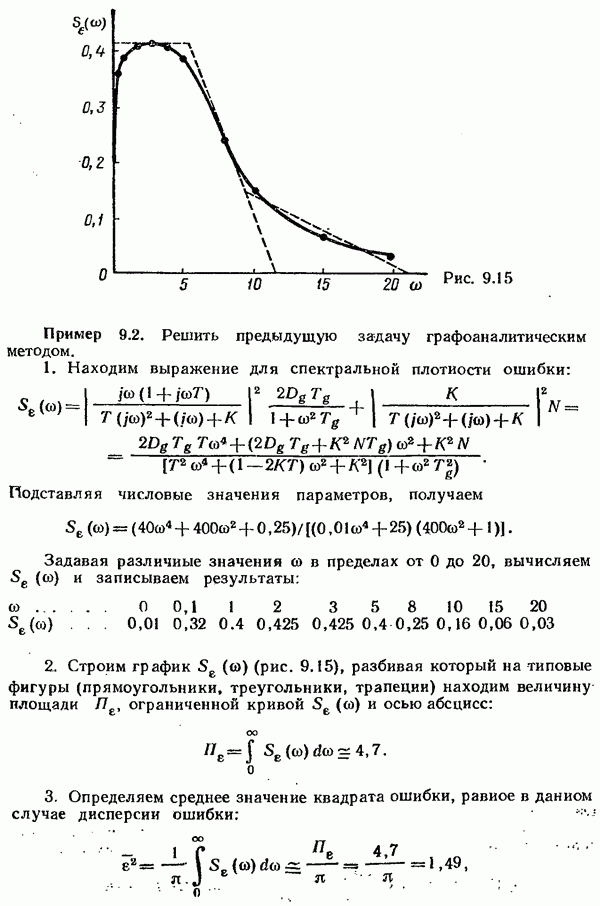
- Графоаналитическое определение дисперсии ошибки.
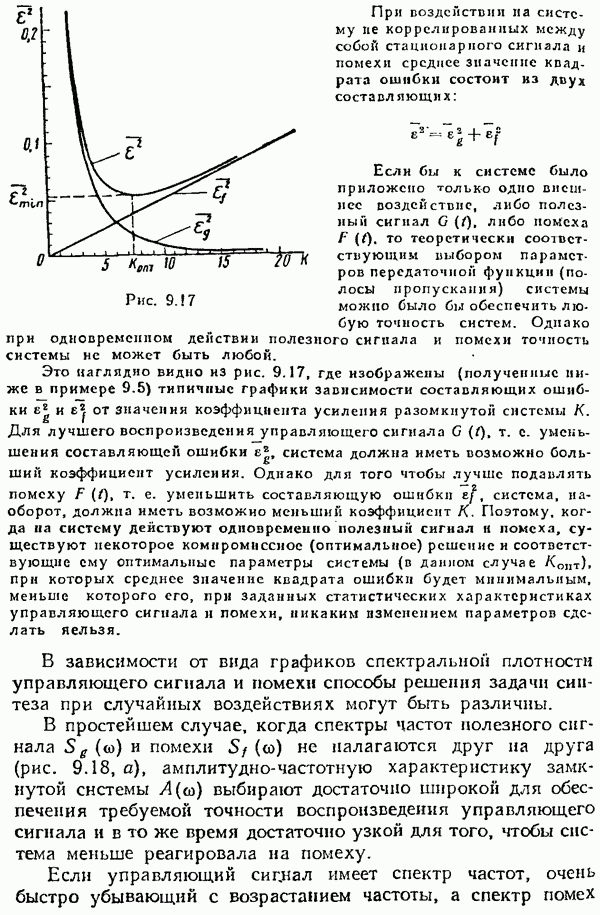
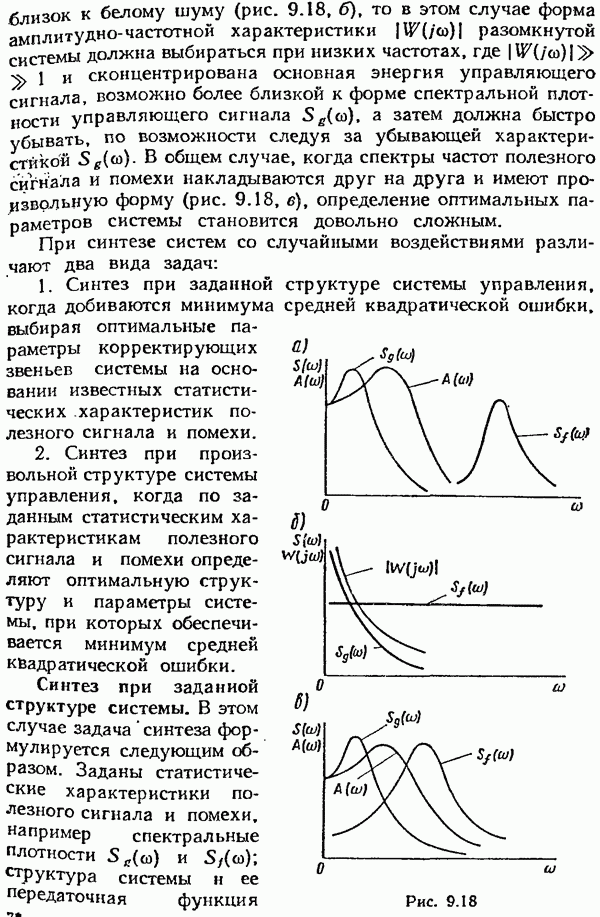
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
- § 9.9. Нелинейное преобразование случайных сигналов
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
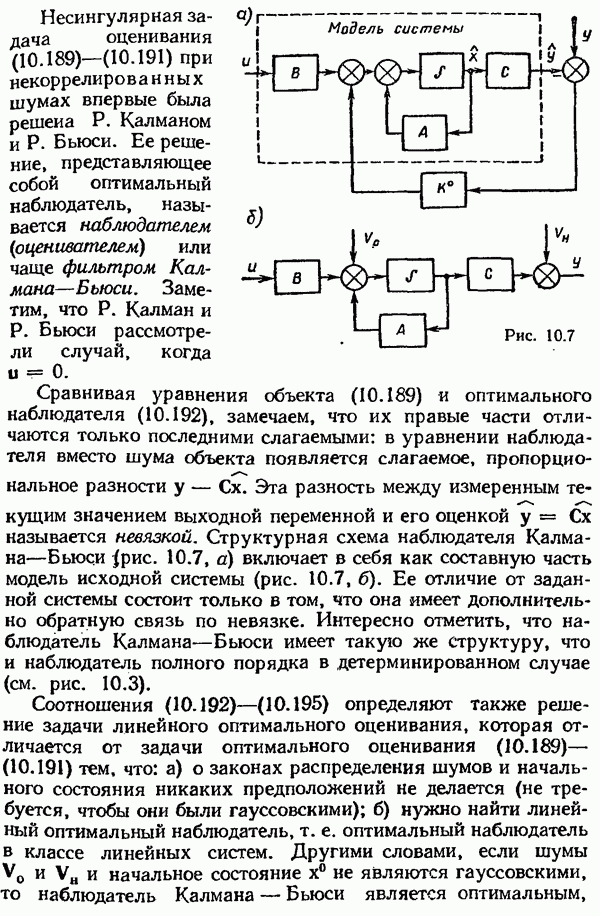
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
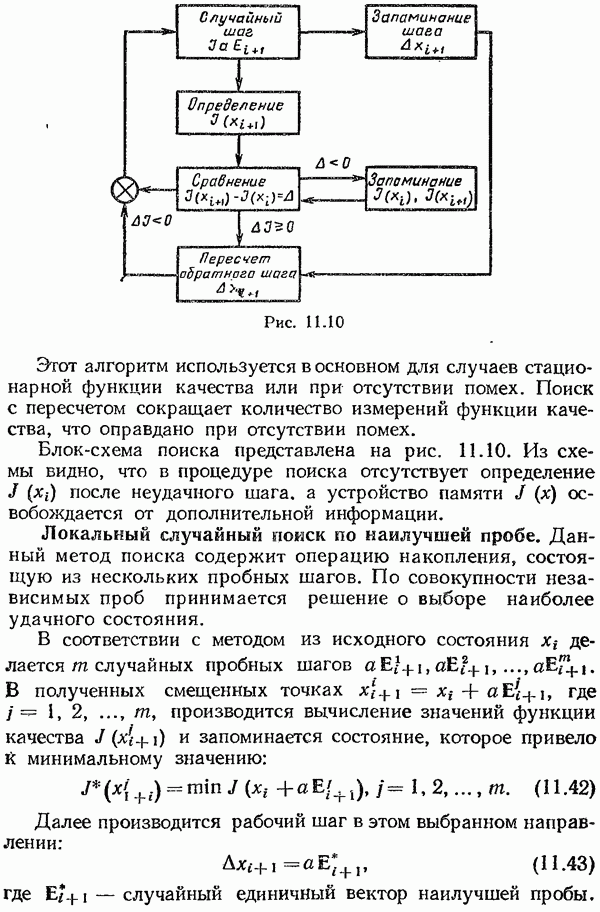
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
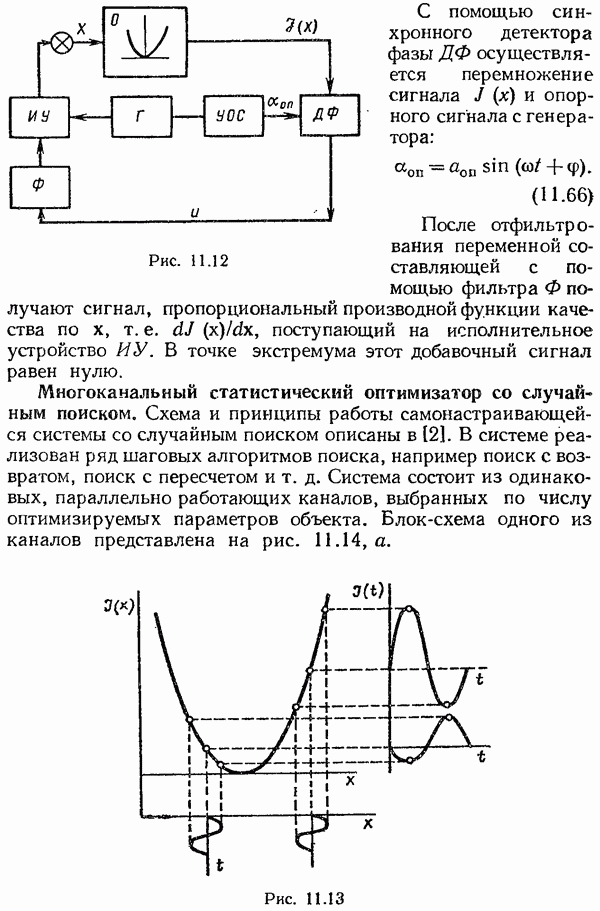
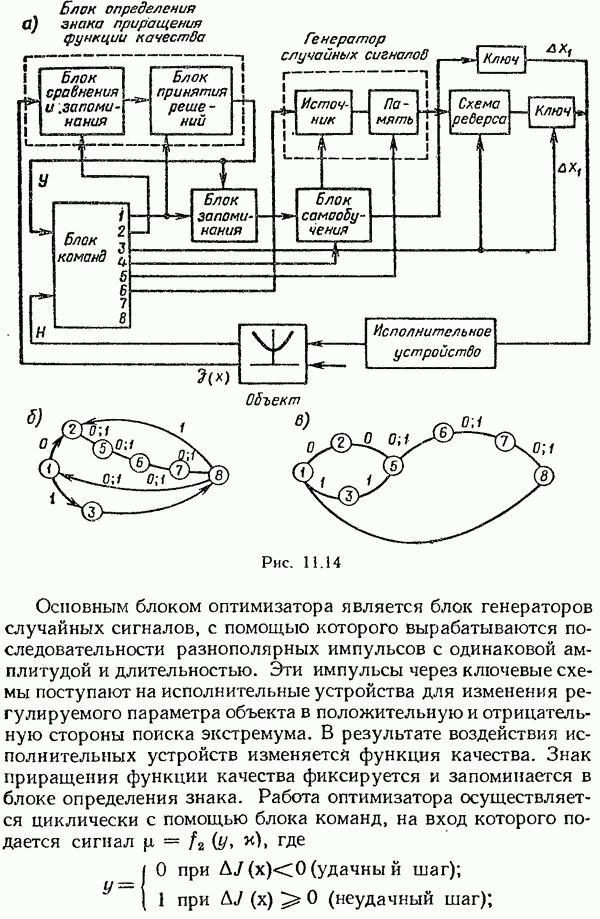
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
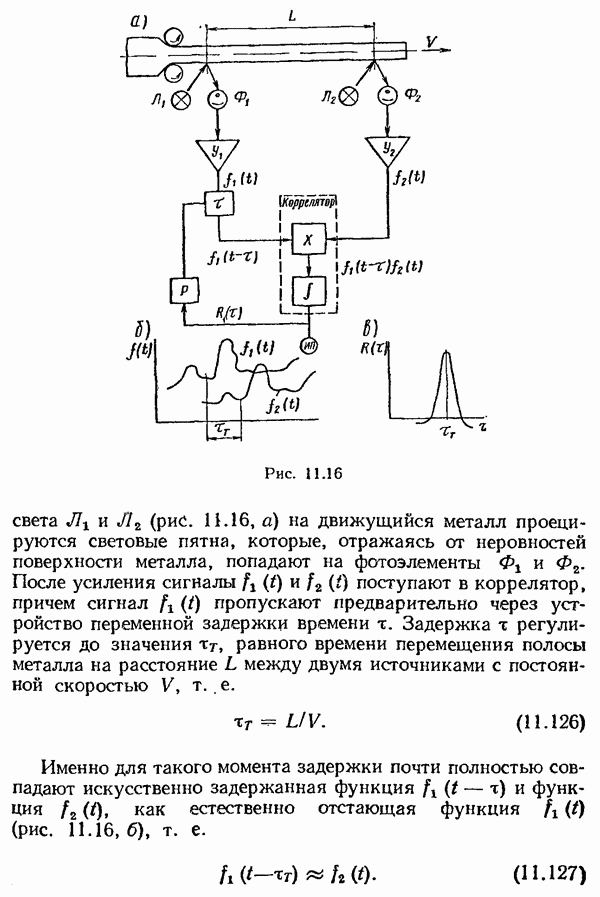
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
- Самонастраивающаяся система с моделью.
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
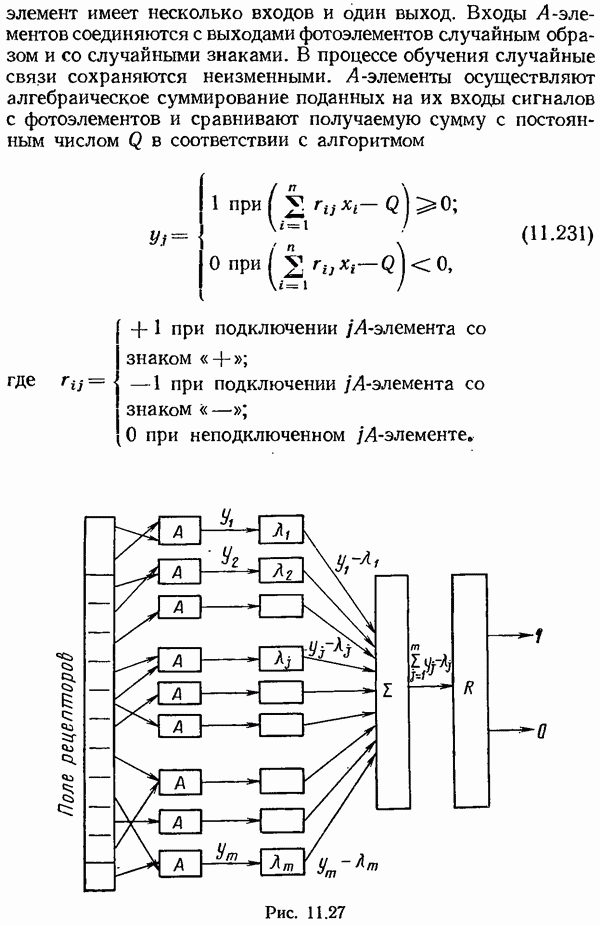
- Персептронная модель автоматической классификации.
- § 11.6. Адаптивные робототехнические системы
- Методы обработки сенсорной информации для адаптивного управления роботами.
- Восприятие изображения объекта
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ