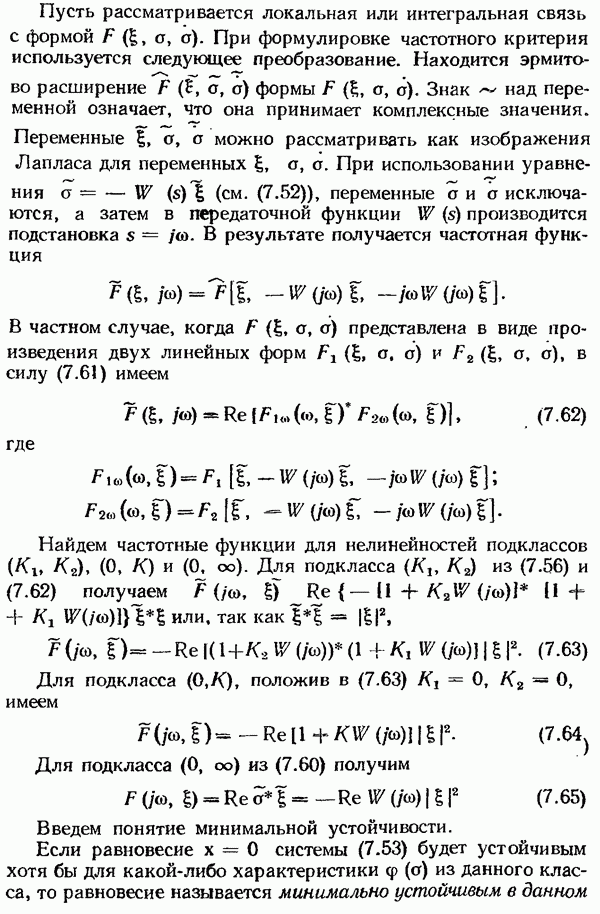| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9.8. Случайные процессы в линейных импульсных системах
Аналогом непрерывной реализации  случайного процесса
случайного процесса  для импульсных систем является дискретная (решетчатая) реализация
для импульсных систем является дискретная (решетчатая) реализация  (рис. 9.22, а), представляющая собой последовательность ординат, совпадающих с соответствующим значением непрерывной реализации
(рис. 9.22, а), представляющая собой последовательность ординат, совпадающих с соответствующим значением непрерывной реализации  в дискретные моменты относительного времени
в дискретные моменты относительного времени  , где Т — период квантования.
, где Т — период квантования.
Совокупность решетчатых реализаций  называют дискретным (решетчатым) случайным процессом
называют дискретным (решетчатым) случайным процессом  Дискретные случайные процессы, по аналогии с непрерывными случайными
Дискретные случайные процессы, по аналогии с непрерывными случайными

Рис. 9.22
процессами, могут характеризоваться такими статистическими характеристиками, как математическое ожидание (момент первого порядка), корреляционная функция (момент второго порядка) и т. д.
Математическое ожидание и корреляционная функция (а также любые моменты  порядка) дискретного случайного процесса равны математическому ожиданию и корреляционной функции (моменту
порядка) дискретного случайного процесса равны математическому ожиданию и корреляционной функции (моменту  порядка) соответствующего непрерывного случайного процесса, взятым в дискретные моменты времени
порядка) соответствующего непрерывного случайного процесса, взятым в дискретные моменты времени 
В дальнейшем будем рассматривать стационарные эргодические случайные процессы. В этом случае среднее значение по множеству (математическое ожидание) равно среднему значению по времени, которое определяется следующей суммой:

где  — любая реализация дискретного случайного процесса.
— любая реализация дискретного случайного процесса.
Среднее значение квадрата стационарного случайного процесса (с равным нулю средним значением) называют дисперсией дискретного случайного процесса:

Корреляционной функцией стационарного дискретного случайного процесса (с равным нулю средним значением)  является неслучайная дискретная (решетчатая) функция
является неслучайная дискретная (решетчатая) функция

где  — дискретные значения относительного времени.
— дискретные значения относительного времени.
Дискретная корреляционная функция обладает следующими основными свойствами:
1. Начальное значение дискретной корреляционной функции (при  равно дисперсии дискретного случайного процесса:
равно дисперсии дискретного случайного процесса:

2. Дискретная корреляционная функция при  достигает наибольшего значения:
достигает наибольшего значения:

3. Дискретная корреляционная функция является четной:

При наличии двух дискретных случайных процессов,  вводят понятие взаимной корреляционной функции
вводят понятие взаимной корреляционной функции

свойства которой схожи со свойствами взаимной корреляционной функции для непрерывных случайных процессов. Так, например,

а в случае, если  статистически независимы (взаимно некоррелированы), имеем
статистически независимы (взаимно некоррелированы), имеем 

Спектральная плотность дискретного случайного процесса по аналогии с обычной спектральной плотностью находится как дискретное преобразование Фурье от ординат дискретной корреляционной функции:

где  — относительная круговая частота.
— относительная круговая частота.
Спектральная плотность  дискретного случайного процесса связана со спектральной плотностью
дискретного случайного процесса связана со спектральной плотностью  соответствующего ему непрерывного случайного процесса:
соответствующего ему непрерывного случайного процесса:

Из (9.159) видно, что спектральная плотность дискретного случайного процесса является периодической функцией частоты 
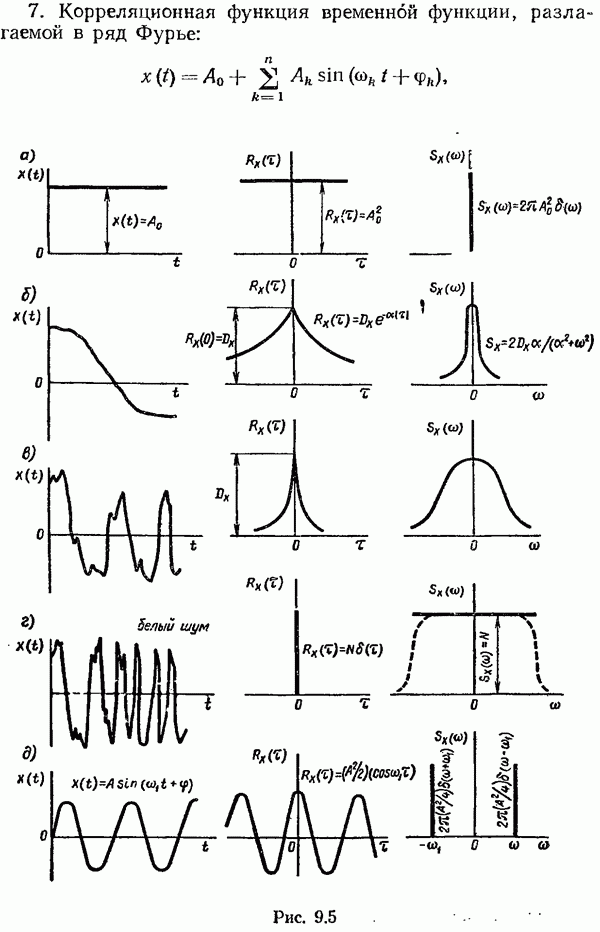
Графики типичной корреляционной функции  дискретного стационарного случайного процесса и соответствующей ему спектральной плотности
дискретного стационарного случайного процесса и соответствующей ему спектральной плотности  приведены на рис. 9.22, б, в.
приведены на рис. 9.22, б, в.
Взаимную спектральную плотность двух дискретных случайных процессов можно определить через взаимную корреляционную функцию:

Корреляционные функции и спектральные плотности дискретного случайного процесса связаны следующими зависимостями:

На основании (9.161) полагая  , получаем
, получаем

Из (9.163) видно, что дисперсия дискретной случайной функции пропорциональна значению интеграла от 0 до  от ее спектральной плотности.
от ее спектральной плотности.
Методы расчета импульсных систем автоматического управления при случайных воздействиях аналогичны методам расчета непрерывных систем. Как и в непрерывных системах (см. § 9.6), каждую координату линейной импульсной системы можно представить в виде двух составляющих: эквивалентной регулярной составляющей и центрированной случайной составляющей. Каждую из составляющих находят отдельно, а затем на основании принципа суперпозиции складывают. По аналогии с непрерывными системами чаще всего при практических расчетах используют зависимости между спектральными плотностями дискретных случайных сигналов входной величины  и ошибки
и ошибки 
Рассмотрим линейную импульсную систему, дискретная передаточная функция которой, связывающая входной сигнал в ошибку, равна  Пусть на вход этой системы поступает стационарный случайный процесс
Пусть на вход этой системы поступает стационарный случайный процесс  равный
равный  , где
, где  — математическое ожидание (среднее значение) стационарного случайного процесса;
— математическое ожидание (среднее значение) стационарного случайного процесса;  — центрированная составляющая случайного процесса. Для центрированной составляющей случайного процесса должна быть задана спектральная плотность
— центрированная составляющая случайного процесса. Для центрированной составляющей случайного процесса должна быть задана спектральная плотность  зная которую, можно определить по (9.159) спектральную плотность
зная которую, можно определить по (9.159) спектральную плотность 
Тогда дискретная спектральная плотность  ошибки импульсной системы определяется по формуле
ошибки импульсной системы определяется по формуле

где  — частотная передаточная функция замкнутой импульсной системы по ошибке.
— частотная передаточная функция замкнутой импульсной системы по ошибке.
Зная спектральную плотность ошибки  можно по (9.163) определить дисперсию ошибки
можно по (9.163) определить дисперсию ошибки  .
.
Регулярная составляющая (математическое ожидание) дискретной случайной ошибки в данном случае определяется через частотную передаточную функцию замкнутой импульсной системы по ошибке: 1

В общем случае, когда эквивалентная регулярная составляющая входного сигнала  (включающая в себя как математическое ожидание входного случайного процесса, так и регулярный внешний сигнал) изменяется во времени, регулярная составляющая ошибки
(включающая в себя как математическое ожидание входного случайного процесса, так и регулярный внешний сигнал) изменяется во времени, регулярная составляющая ошибки  также будет изменяться во времени.
также будет изменяться во времени.
Регулярную составляющую дискретной ошибки  обусловленную, например, действием регулярного входного сигнала
обусловленную, например, действием регулярного входного сигнала  можно определить, используя различные способы. В общем случае по известной дискретной передаточной функции
можно определить, используя различные способы. В общем случае по известной дискретной передаточной функции  сначала находят Z-изображение регулярной составляющей ошибки
сначала находят Z-изображение регулярной составляющей ошибки  а затем находят регулярную составляющую (оригинал) ошибки, вычисляя интеграл обращения с помощью теоремы вычетов.
а затем находят регулярную составляющую (оригинал) ошибки, вычисляя интеграл обращения с помощью теоремы вычетов.
При медленно изменяющемся входном сигнале  установившееся значение регулярной составляющей ошибки
установившееся значение регулярной составляющей ошибки  можно определить, например, способом, аналогичным способу коэффициентов ошибок для непрерывных систем, разлагая изображение регулярной составляющей ошибки
можно определить, например, способом, аналогичным способу коэффициентов ошибок для непрерывных систем, разлагая изображение регулярной составляющей ошибки  в степенной ряд.
в степенной ряд.
Расчет дисперсии по формуле (9.163) существенно упрощается в тех случаях, когда случайная функция  представляет собой центрированный случайный процесс, эффективное время корреляции которого меньше периода квантования. В этом случае считают, что
представляет собой центрированный случайный процесс, эффективное время корреляции которого меньше периода квантования. В этом случае считают, что

и представляют случайный процесс как белый шум с корреляционной функцией

где  — дисперсия входного воздействия;
— дисперсия входного воздействия;  — единичная решетчатая импульсная функция, равная единице при
— единичная решетчатая импульсная функция, равная единице при  и равная нулю при
и равная нулю при  Этому белому шуму соответствует спектральная плотность
Этому белому шуму соответствует спектральная плотность

При расчете замкнутых импульсных систем, на которые одновременно воздействуют полезный сигнал и помеха, часто интересуются точностью системы, характеризующейся средним значением квадрата дискретной случайной ошибки и определяемой по формулам, аналогичным по своей структуре
соответствующим формулам для непрерывных стационарных систем.
Например, если на вход импульсной системы поступают случайные стационарные статистически не связанные (некоррелированные) полезный сигнал  и помеха
и помеха  то спектральная плотность
то спектральная плотность  дискретной случайной ошибки
дискретной случайной ошибки

где  — дискретные спектральные плотности входного сигнала и помехи;
— дискретные спектральные плотности входного сигнала и помехи;  — частотные передаточные функции замкнутой импульсной системы, связывающие соответственно полезный сигнал и помеху с ошибкой.
— частотные передаточные функции замкнутой импульсной системы, связывающие соответственно полезный сигнал и помеху с ошибкой.
Дисперсию дискретной ошибки определяют через спектральную плотность по формуле (9.163).
Среднее значение квадрата установившейся дискретной ошибки

где  — эквивалентная регулярная составляющая ошибки;
— эквивалентная регулярная составляющая ошибки;  — дисперсия ошибки.
— дисперсия ошибки.
Аналитические вычисления по (9.165) в общем случае являются достаточно трудоемкими, однако при определенных условиях их можно свести к вычислению табличных стандартных интегралов, с помощью которых, аналогично тому, как это делается для непрерывных систем, можно выразить значение дисперсии ошибки через параметры импульсной системы и дискретных спектральных плотностей внешних воздействий.
Приведенные выше формулы записаны для дискретных относительных моментов времени (моментов квантования), соответствующих значениям  Однако они могут быть записаны не только для моментов квантования, но и для любого момента времени между ними
Однако они могут быть записаны не только для моментов квантования, но и для любого момента времени между ними  , где
, где  . В последнем случае рассматривают смещенные дискретные (решетчатые) функции
. В последнем случае рассматривают смещенные дискретные (решетчатые) функции  соответствующие передаточные функции импульсной системы
соответствующие передаточные функции импульсной системы  и корреляционные функции
и корреляционные функции 
Следует отметить, что имеются также аналитические метода решения задач оптимизации импульсных систем при случайных воздействиях, которые аналогичны методам оптимизации для непрерывных систем, однако они применимы только
для ограниченного класса систем и довольно громоздки. Поэтому на практике в большинстве случаев исследования импульсных систем при случайных воздействиях проводят методами моделирования.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
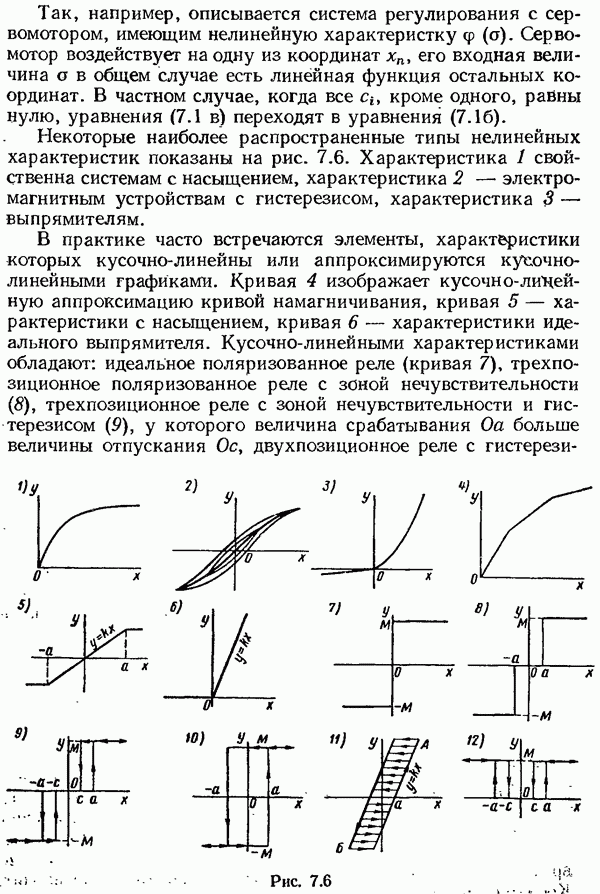
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
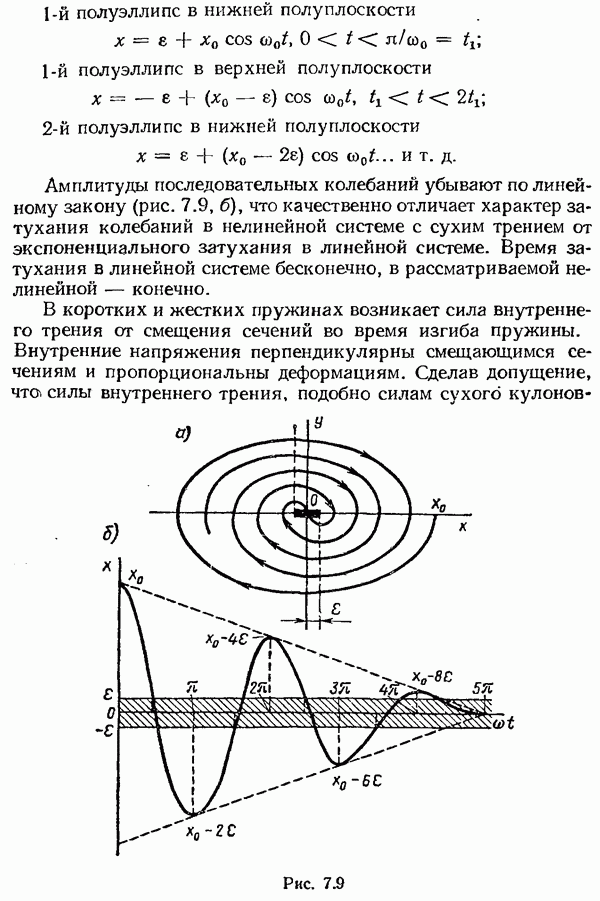
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
- § 7.3. Автоколебания. Метод точечных преобразований
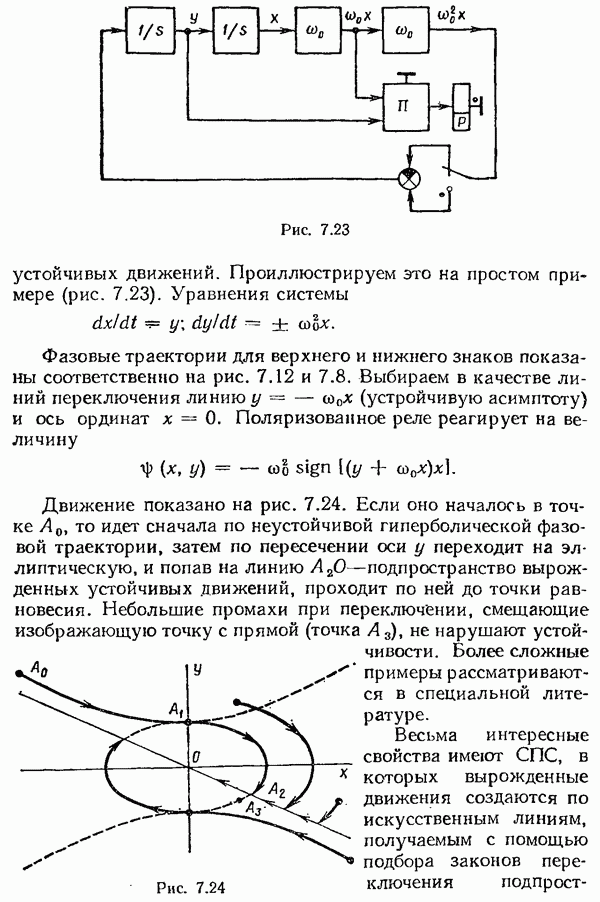
- § 7.4. Системы с переменной структурой
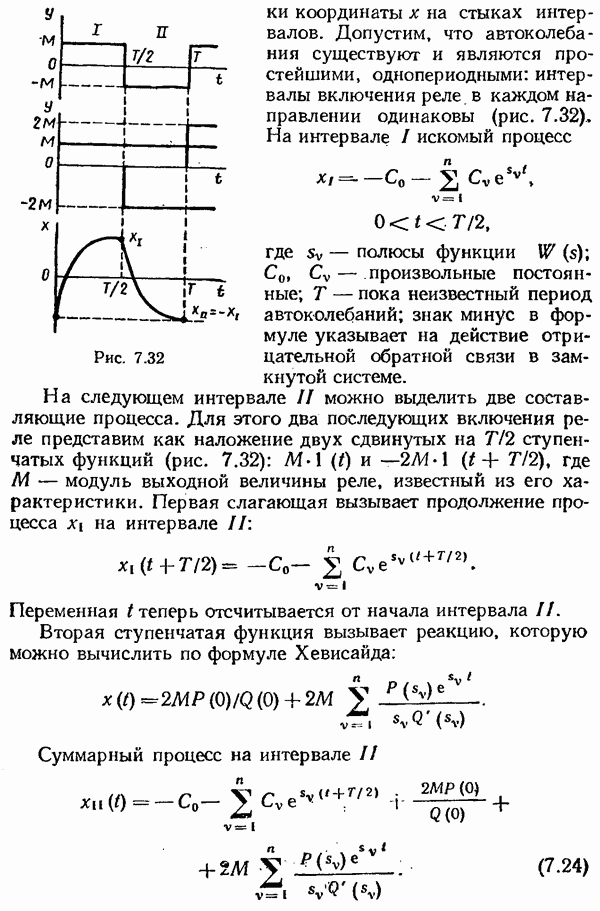
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
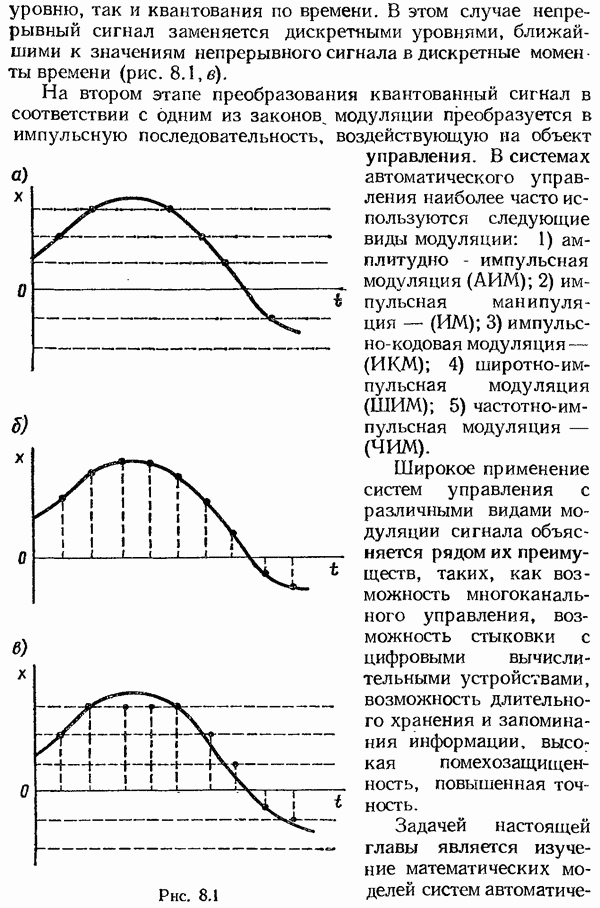
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
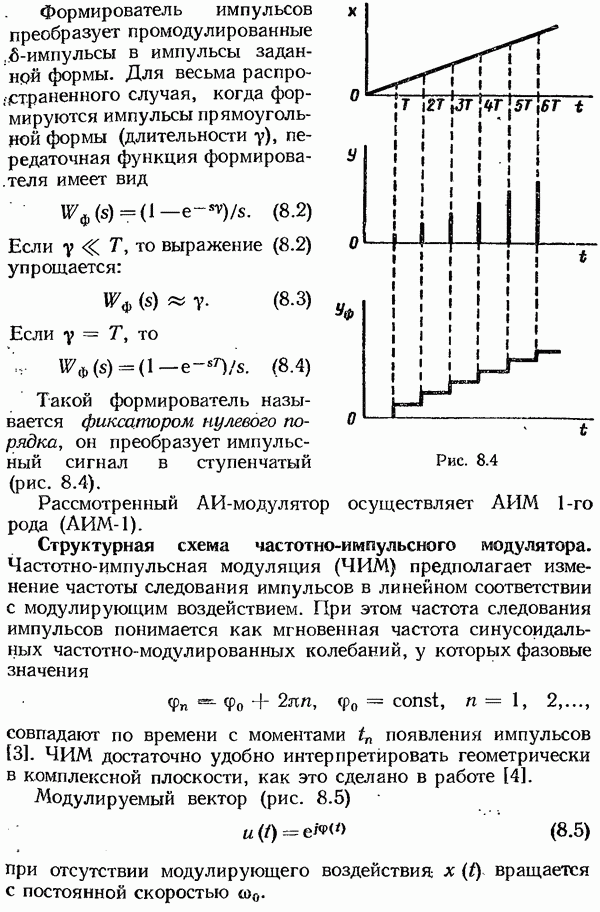
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
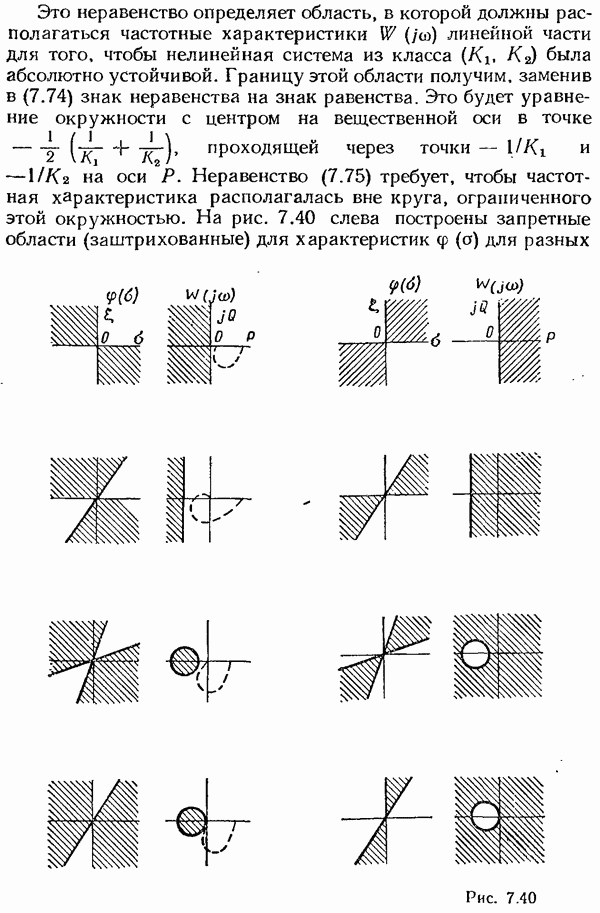
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
- Исследование периодических режимов в системах с ИЧИМ.
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
- Графоаналитическое определение дисперсии ошибки.
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
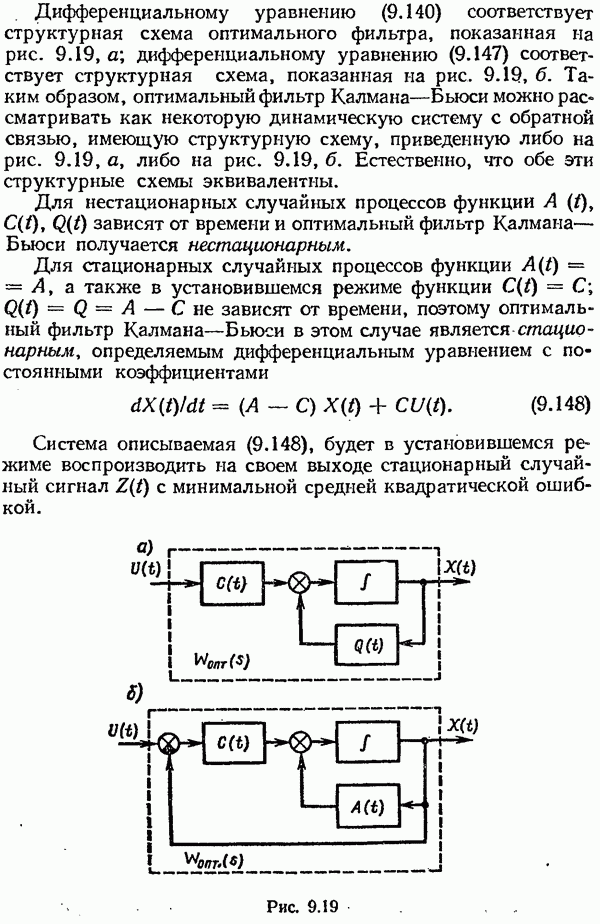
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
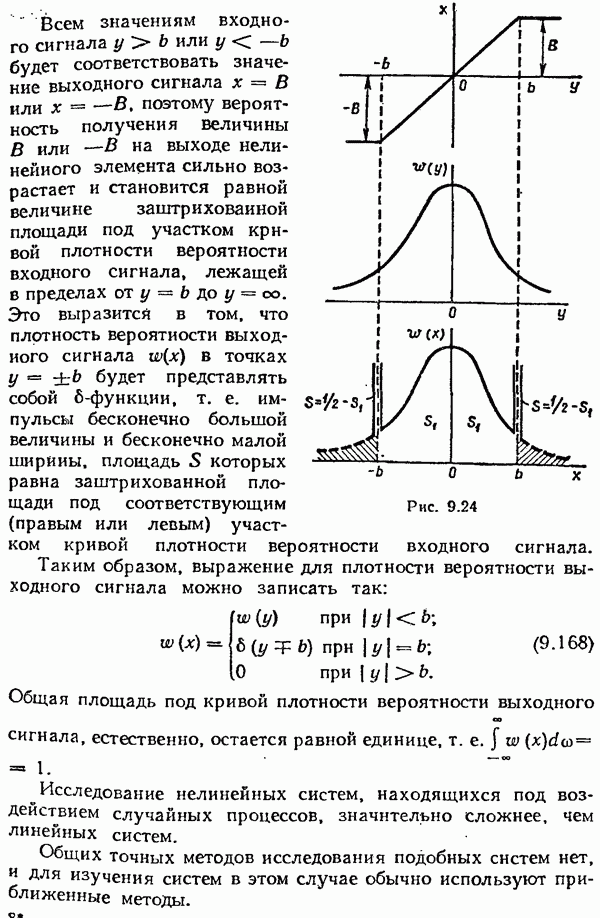
- § 9.9. Нелинейное преобразование случайных сигналов
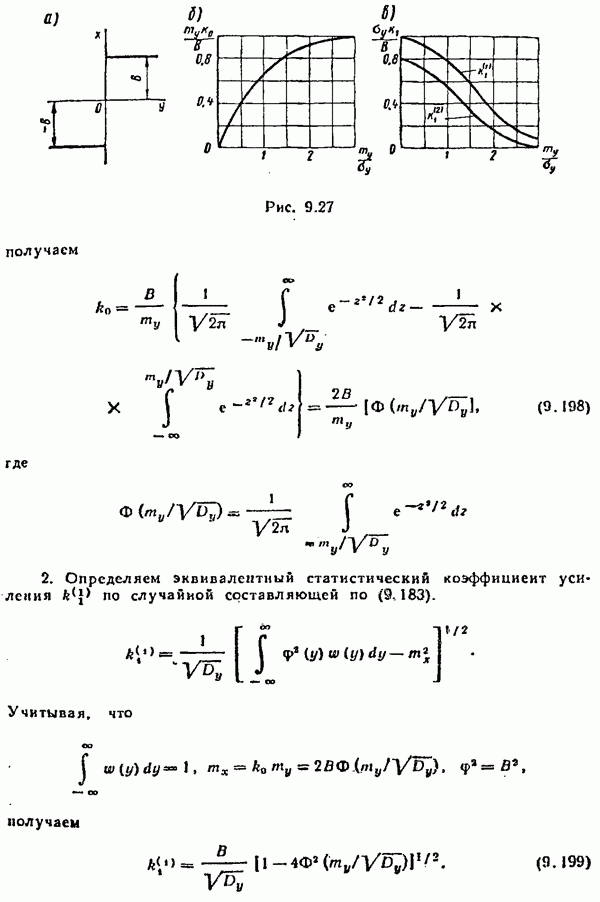
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
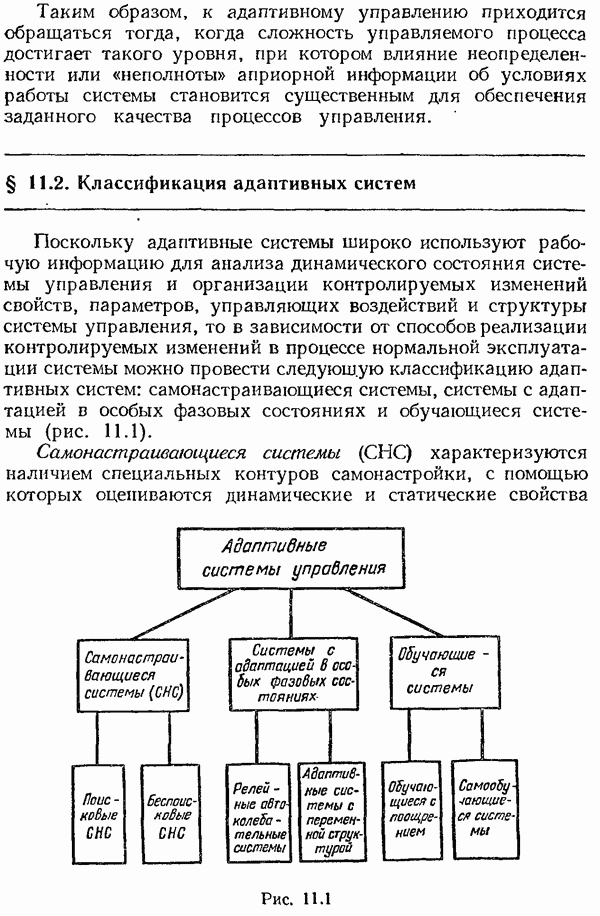
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
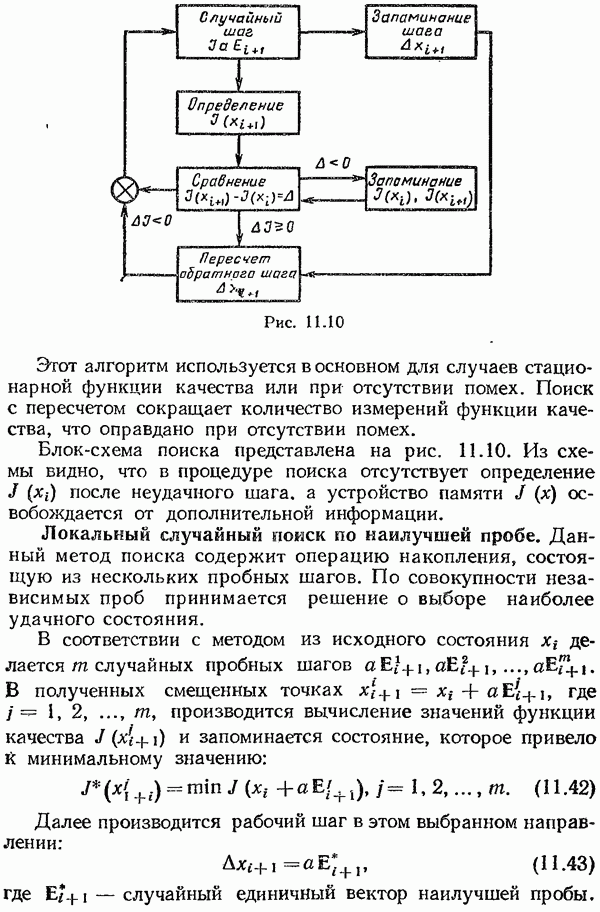
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
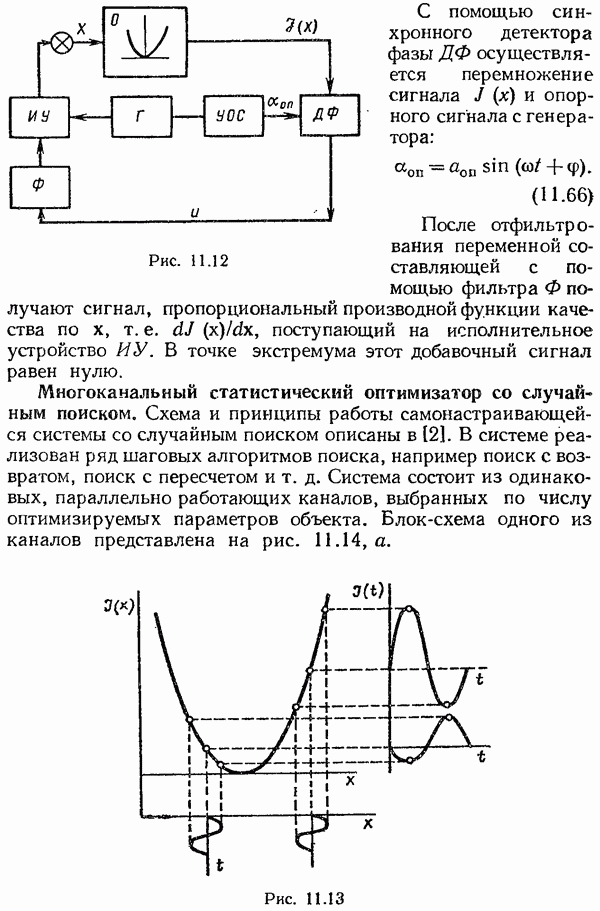
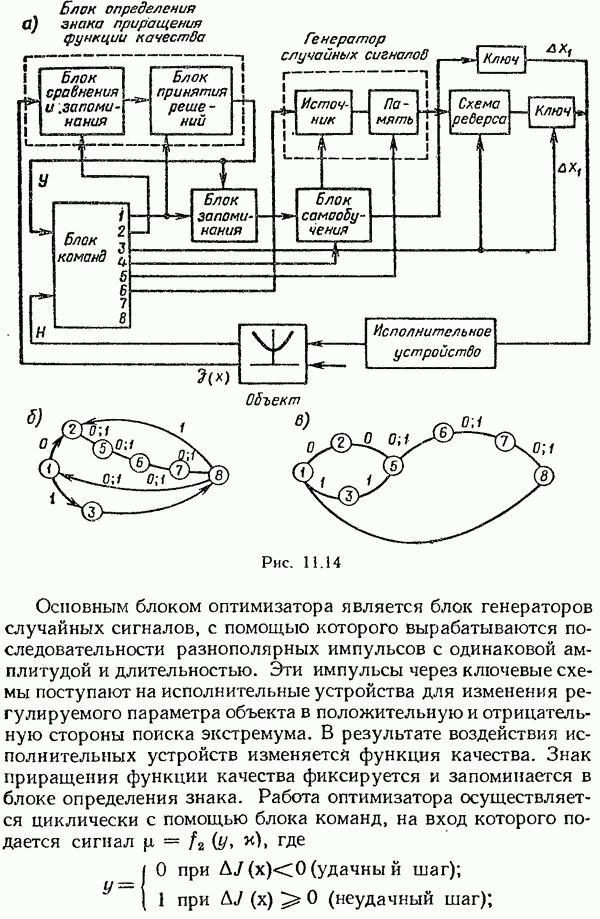
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
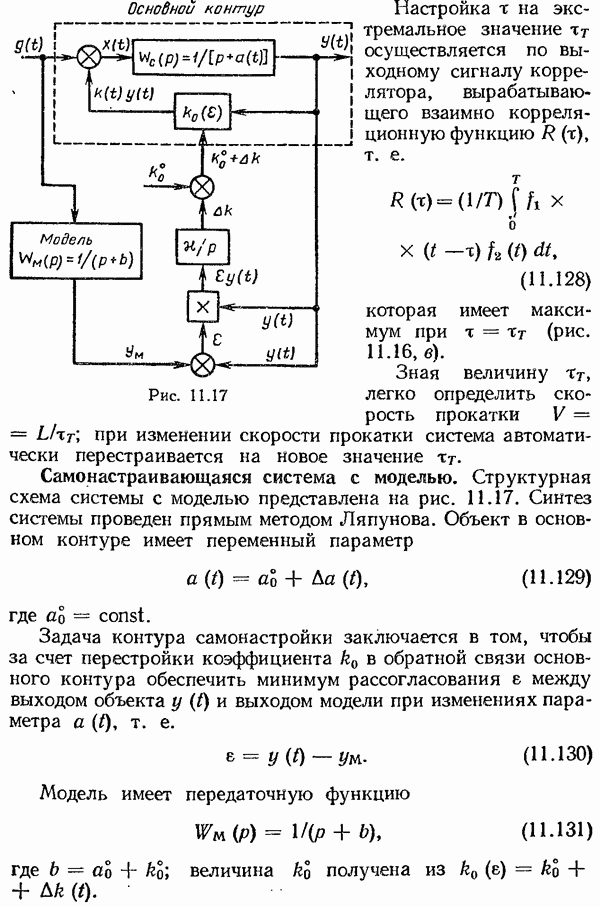
- Самонастраивающаяся система с моделью.
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
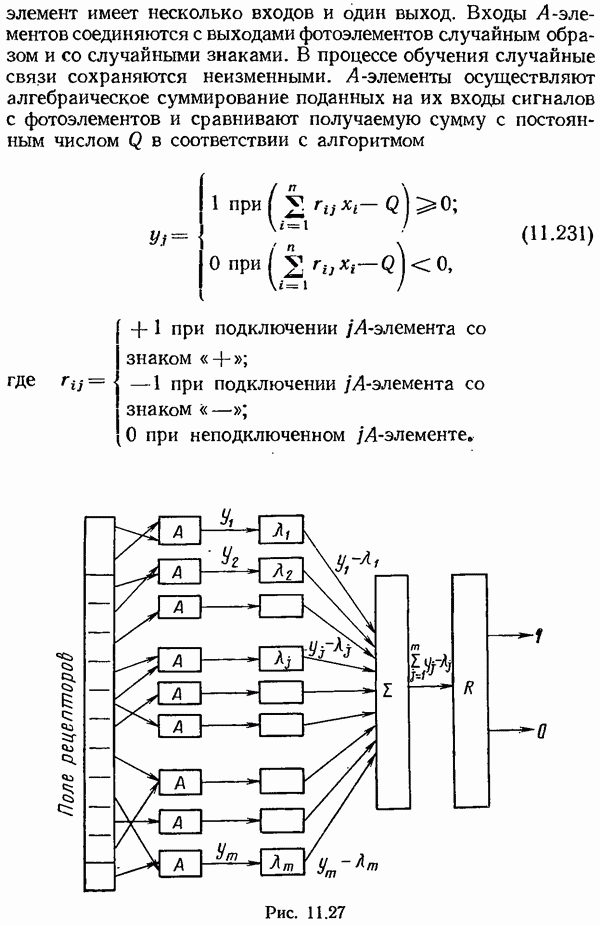
- Персептронная модель автоматической классификации.
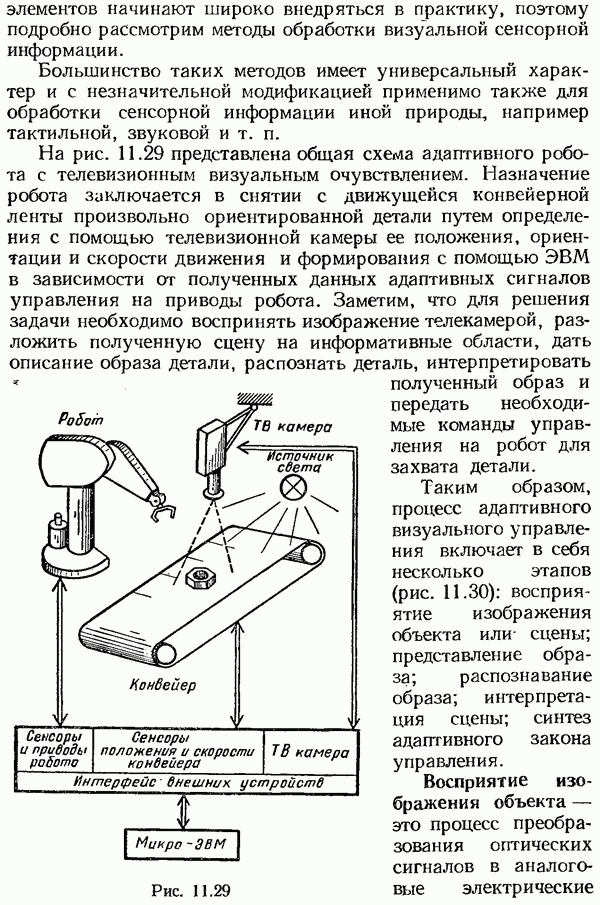
- § 11.6. Адаптивные робототехнические системы
- Методы обработки сенсорной информации для адаптивного управления роботами.
- Восприятие изображения объекта
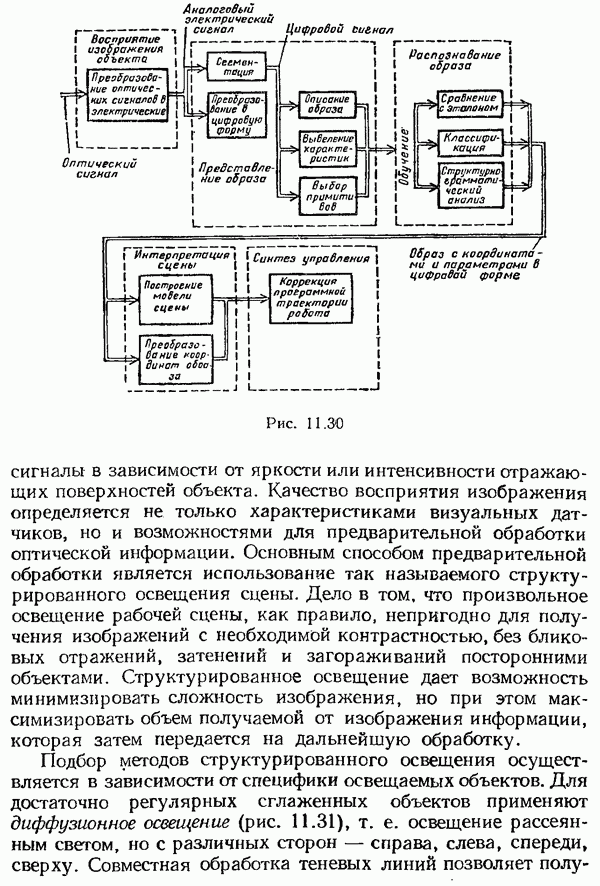
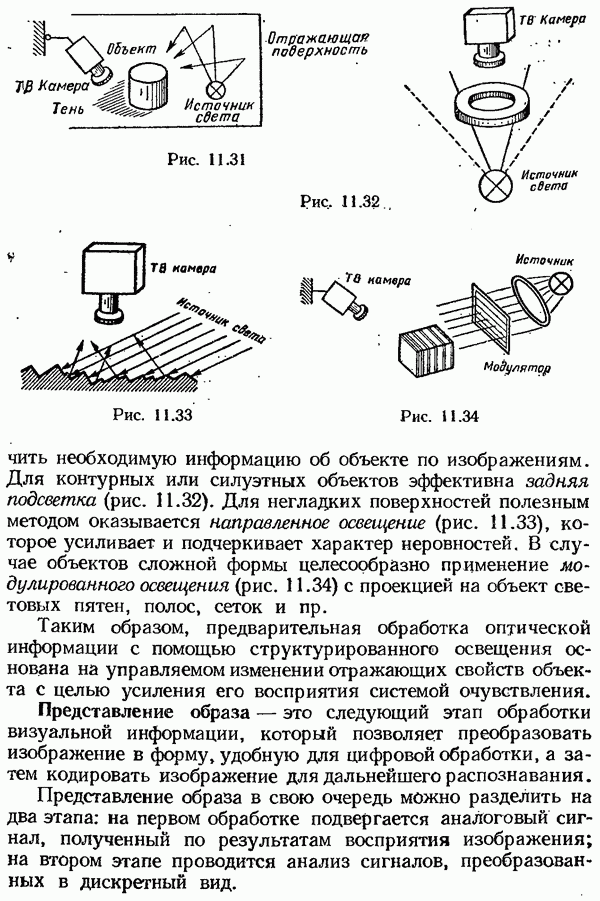
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ