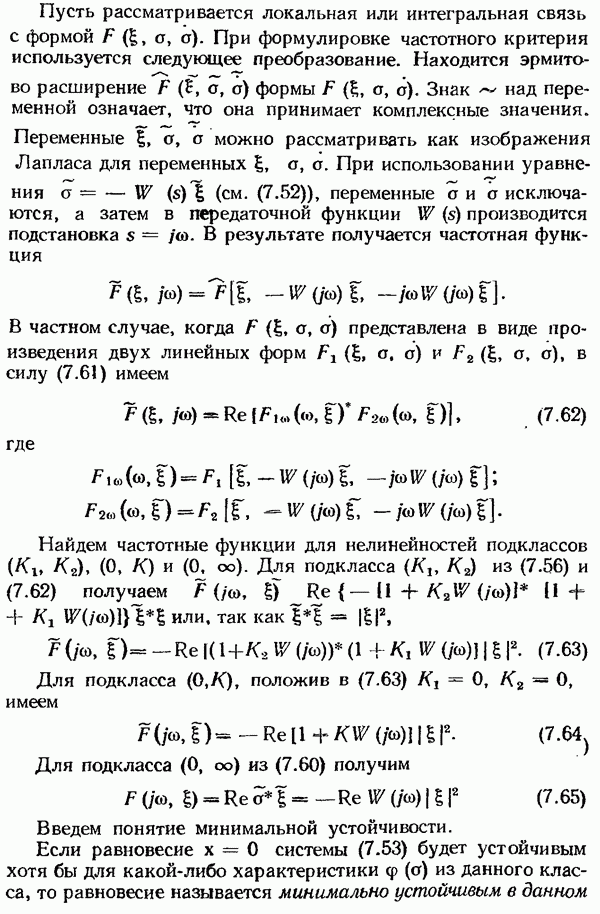| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
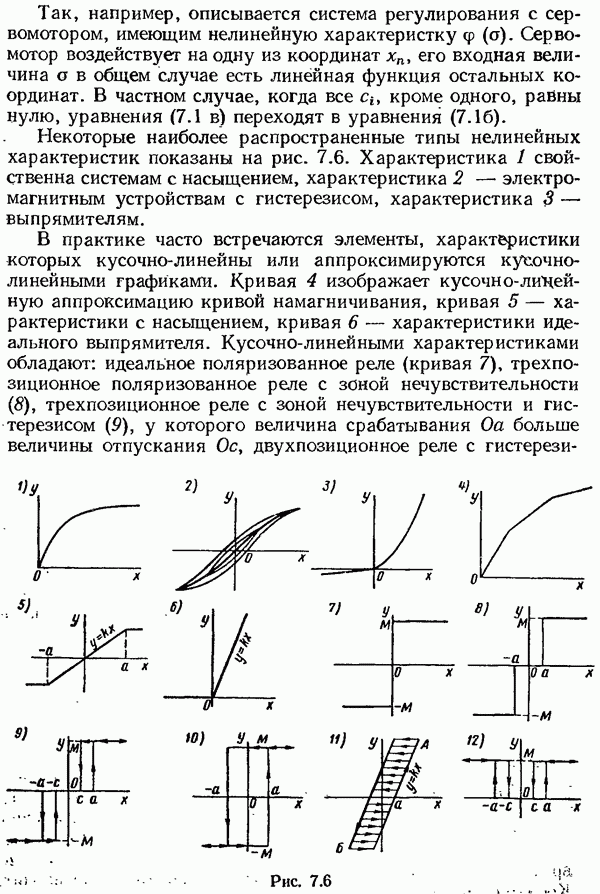
§ 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
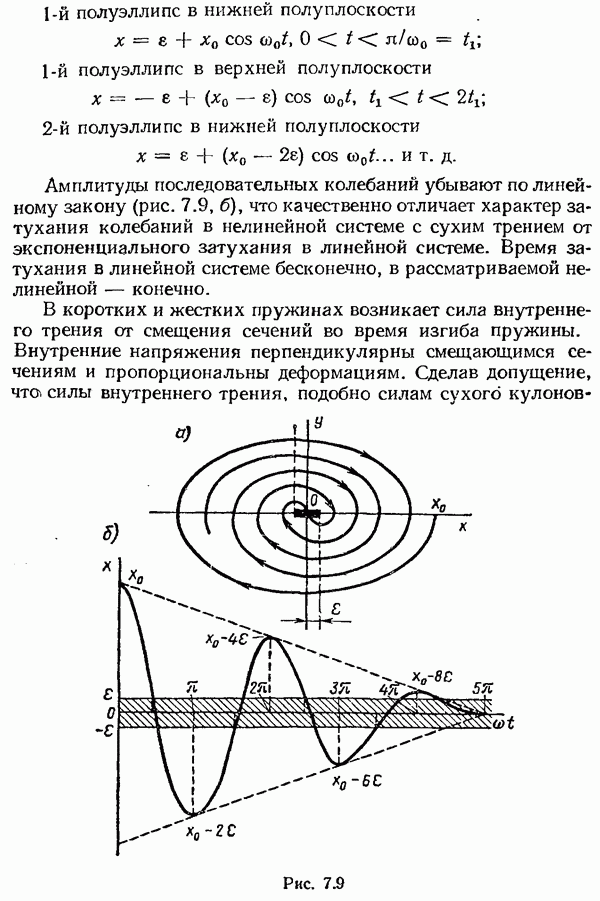
Во многих динамических нелинейных системах периодические движения на выходе инерционной линейной части, возникли ли они в результате воздействия периодической, но не синусоидальной, внешней силы или же возбудились как автоколебания, оказываются близкими к синусоидальным. Это дает основание считать, что система обладает свойством низкочастотного фильтра, пропускающего без ослабления основную и существенно ослабляющего высшие гармонические. «Гипотеза
фильтра», принимаемая по отношению к нелинейным системам с близкими к синусоидальным периодическими режимами лежит в основе приближенных методов. По отношению к близким к синусоидальным автоколебательным режимам принимается другая гипотеза наряду с гипотезой фильтра — гипотеза «авторезонанса», или «порождающей системы». В самом деле, если нет вынуждающей периодической внешней силы, но автоколебания возникают, причем по форме они близки к колебаниям в линейных системах, то естественно предположить, что по отношению к периодическому режиму, наблюдаемому в нелинейной системе, последняя близка к линейной, в которой могут возбуждаться незатухающие колебания. Такую близкую линейную систему называют порождающей. Если порождающая система существует, то нелинейное дифференциальное уравнение может быть разложено на сумму линейного с чисто мнимыми корнями и нелинейного уравнения, которое обычно представляют как нелинейную функцию координаты и ее производных, умноженную на «малый параметр». При обращении малого параметра в нуль уравнение вырождается в порождающее линейное.
Для приближенного анализа периодических режимов Пуанкаре, Ван-дер-Полем и другими были разработаны методы малого параметра, строго обоснованные для нелинейностей, выражаемых аналитическими функциями. Но в теории управления в большинстве случаев приходится иметь дело с неаналитическими, разрывными и неоднозначными нелинейностями. Для таких систем получили распространение два типа приближенных методов: эквивалентной линеаризации и гармонического баланса. Для безынерционных нелинейных элементов обе этй группы методов по существу идентичны и дают совпадающие результаты.
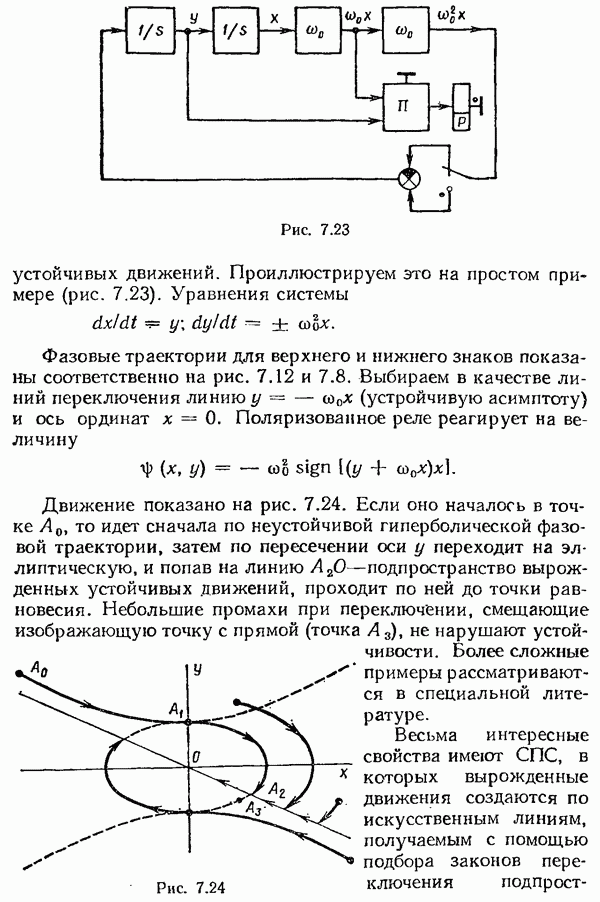
Метод эквивалентной линеаризации в применении к однозначным безынерционным нелинейностям состоит в следующем. Пусть передаточная функция линейной части замкнутой системы (рис. 7.1)

Если трактовать  как символ дифференцирования
как символ дифференцирования  то дифференциальное уравнение замкнутой нелинейной системы
то дифференциальное уравнение замкнутой нелинейной системы

Пусть  однозначная функция. Заменим ее суммой линейной функции и «малого» нелинейного слагаемого;
однозначная функция. Заменим ее суммой линейной функции и «малого» нелинейного слагаемого;

Выберем с так, чтобы уравнение

получающееся при  было порождающим, т. е. имело бы чисто мнимые корни
было порождающим, т. е. имело бы чисто мнимые корни  Такую линеаризацию и называют эквивалентной (она не обязательно совпадает с линеаризацией посредством отбрасывания нелинейной части ряда Тейлора:
Такую линеаризацию и называют эквивалентной (она не обязательно совпадает с линеаризацией посредством отбрасывания нелинейной части ряда Тейлора:  может отличаться от линейного члена ряда, а
может отличаться от линейного члена ряда, а  может содержать и линейный член). Эквивалентную линеаризацию удавалось иногда успешно применять и в таких случаях, когда
может содержать и линейный член). Эквивалентную линеаризацию удавалось иногда успешно применять и в таких случаях, когда  не являлась малой или когда функция
не являлась малой или когда функция  не была аналитической и не разлагалась в ряд Тейлора.
не была аналитической и не разлагалась в ряд Тейлора.
В очень многих практических задачах при этом получалось удовлетворительное приближение к истинному решению, но строгого обоснования метода для таких задач в общем случае найти еще не удалось.
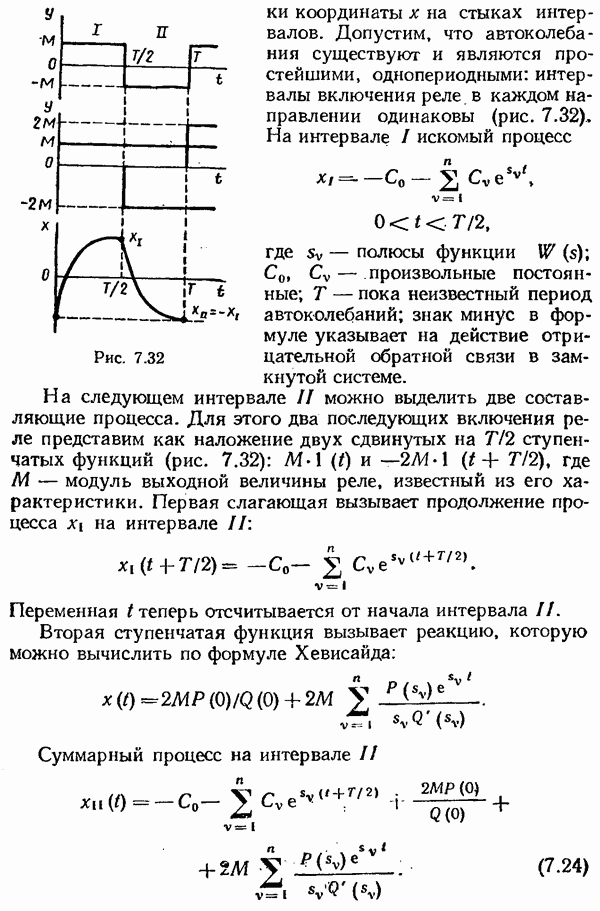
Периодическое решение уравнения (7.31) приближенно представляют так:

Выбор начала отсчета времени, при котором в решении строят только синусную составляющую, не снижает общности, если система стационарна. Амплитуда А пока не известна и не может быть найдена из линейного уравнения. Получим ее из нелинейного уравнения, воспользовавшись на этот раз гипотезой фильтра.
В соответствии с этой гипотезой высшими гармониками на выходе линейной части можно пренебречь и считать выход равным  . Тогда на вход нелинейного элемента поступает синусоидальный сигнал
. Тогда на вход нелинейного элемента поступает синусоидальный сигнал  , а выходная его величина будет
, а выходная его величина будет

Коэффициенты  о при основной гармонике и
о при основной гармонике и  находят по формулам Фурье, так как (7.33) есть часть ряда Фурье:
находят по формулам Фурье, так как (7.33) есть часть ряда Фурье:

где 
При симметричных нелинейных характеристиках, проходящих через начало координат, величина  равна нулю. Ограничимся в основном рассмотрением только таких характеристик, Далее, так как
равна нулю. Ограничимся в основном рассмотрением только таких характеристик, Далее, так как  однозначна, то
однозначна, то  совпадает по фазе с
совпадает по фазе с  , в соответствии с (7.32) не содержит, косинусных составляющих, т. е.
, в соответствии с (7.32) не содержит, косинусных составляющих, т. е.

Так как высшие гармоники, пройдя через линейную часть, в соответствии с гипотезой фильтра практически исчезнут и на вход нелинейного элемента не пройдут, то при нахождении х мы их можем не принимать во внимание и подставить в уравнение (7.29) только  . При этом
. При этом

Таким образом, коэффициент с эквивалентной линеаризации равен  Так как
Так как  — функция амплитуды А, характеристика
— функция амплитуды А, характеристика  в результате линеаризации заместилась пучком прямых, проходящих через начало координат и имеющих наклоны, различные для разных А. Из пучка надлежит выбрать ту прямую, при которой уравнение (7.31) становится порождающим с частотой решения, равной частоте автоколебаний. Подставляя в
в результате линеаризации заместилась пучком прямых, проходящих через начало координат и имеющих наклоны, различные для разных А. Из пучка надлежит выбрать ту прямую, при которой уравнение (7.31) становится порождающим с частотой решения, равной частоте автоколебаний. Подставляя в  получим
получим

откуда


Рис. 7.33
 — это обратная амплитуднофазовая характеристика линейной части. Так как
— это обратная амплитуднофазовая характеристика линейной части. Так как  в рассматриваемом случае — действительное число, то частота
в рассматриваемом случае — действительное число, то частота  определяется точкой пересечения характеристики —
определяется точкой пересечения характеристики —  с действительной осью. Приравняв
с действительной осью. Приравняв  длине отрезка от начала координат до пересечения
длине отрезка от начала координат до пересечения  с действительной осью, получим уравнение, из которого можно найти А. Но в общем случае эту задачу удобнее решать графоаналитически. Один из методов графоаналитического решения рассмотрен в следующем параграфе.
с действительной осью, получим уравнение, из которого можно найти А. Но в общем случае эту задачу удобнее решать графоаналитически. Один из методов графоаналитического решения рассмотрен в следующем параграфе.
Если характеристика  неоднозначна, то b отличен от нуля, в выражении (7.33) присутствует косинусная составляющая и выразить
неоднозначна, то b отличен от нуля, в выражении (7.33) присутствует косинусная составляющая и выразить  как линейную функцию х с действительным коэффициентом нельзя. Заменив в (7.33) х и у относительными переменными
как линейную функцию х с действительным коэффициентом нельзя. Заменив в (7.33) х и у относительными переменными  после несложных преобразований получим
после несложных преобразований получим

Это уравнение эллипса, пересекающего ось  в точках
в точках  , а ось
, а ось  в точках
в точках  . С помощью этого эллипса можно определить значения g и b из опыта. Например, сняв на осциллографе в осях
. С помощью этого эллипса можно определить значения g и b из опыта. Например, сняв на осциллографе в осях  гистерезисную петлю при воздействии на вход синусоидального напряжения, заменим ее приближенно эллипсом, проходящим через точки пересечения петли с осями координат (рис. 7.33). Из приведенных выше соотношений найдем
гистерезисную петлю при воздействии на вход синусоидального напряжения, заменим ее приближенно эллипсом, проходящим через точки пересечения петли с осями координат (рис. 7.33). Из приведенных выше соотношений найдем

Поскольку линеаризация  посредством функции
посредством функции  в данном случае невозможна, то порождающего решения в указанном выше смысле не существует.
в данном случае невозможна, то порождающего решения в указанном выше смысле не существует.
Но для установившегося периодического движения эквивалентную линеаризацию дифференциального уравнения все же можно формально выполнить, если аппроксимировать  линейной функцией не только х, но и его производной по времени.
линейной функцией не только х, но и его производной по времени.
Так, в литературе получил широкое распространение следующий способ линеаризации. Представим у в виде

Тогда (7 29) с учетом, что  можно привести к виду
можно привести к виду

Поскольку (7.32) удовлетворяет этому уравнению, то характеристическое уравнение последнего имеет пару чисто мнимых корней  и уравнение (7.37) можно в этом смысле назвать порождающим. Но таких «порождающих» уравнений можно написать бесчисленное множество, поскольку «линеаризующих» уравнений нелинейного элемента
и уравнение (7.37) можно в этом смысле назвать порождающим. Но таких «порождающих» уравнений можно написать бесчисленное множество, поскольку «линеаризующих» уравнений нелинейного элемента

которым удовлетворяли бы соотношения (7.32) и (7 33) также существует бесконечно много. Для этого достаточно выбирать коэффициенты полиномов  так, чтобы соблюдались равенства
так, чтобы соблюдались равенства

где

Так, например, пусть нелинейный элемент замещается звеном второго порядка с передаточной функцией

Для данной функции  Подставляя последние выражения в (7.39), получим
Подставляя последние выражения в (7.39), получим

Для нахождения четырех неизвестных  имея два уравнения, двумя параметрами задаемся произвольно, а из уравнений находим два остальные
имея два уравнения, двумя параметрами задаемся произвольно, а из уравнений находим два остальные
Подстановка (7.38) в (7.29) дает «порождающее» уравнение

Среди этих уравнений могут быть уравнения, имеющие устойчивые и неустойчивые решения с различными переходными процессами. Любое из них пригодно для нахождения автоколебаний, но, если не дано специального обоснования для каждого конкретного случая, в общем не позволяет исследовать устойчивость и неустановившиеся режимы. Поэтому эквивалентная линеаризация по рассмотренному выше способу для нелинейных элементов с неоднозначными характеристиками может быть использована только для нахождения параметров первых гармоник автоколебаний, исследования же переходных процессов, иногда рекомендуемые в литературе, с помощью описания нелинейного элемента уравнением (7.37) в общем случае необоснованны.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
- § 7.3. Автоколебания. Метод точечных преобразований
- § 7.4. Системы с переменной структурой
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
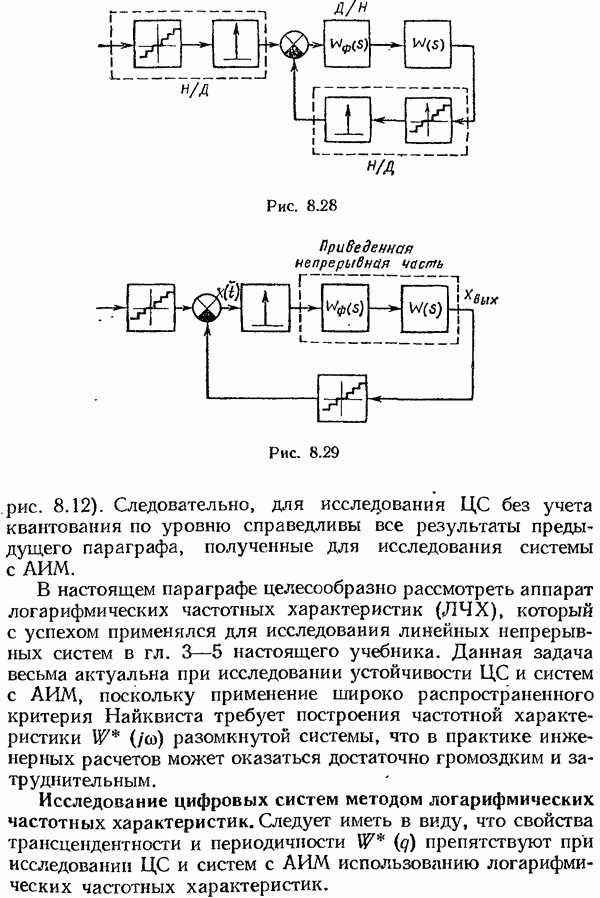
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
- Исследование периодических режимов в системах с ИЧИМ.
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
- Графоаналитическое определение дисперсии ошибки.
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
- § 9.9. Нелинейное преобразование случайных сигналов
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
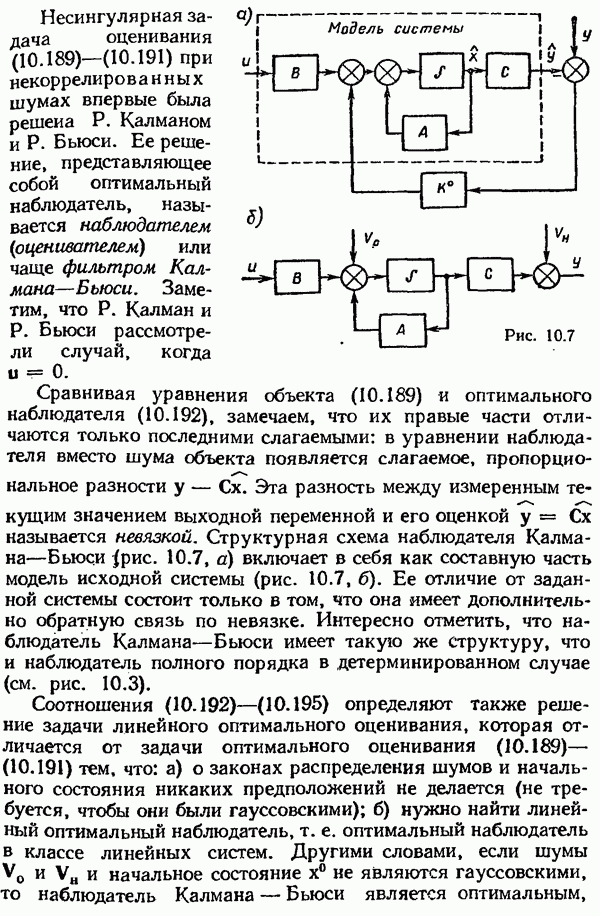
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
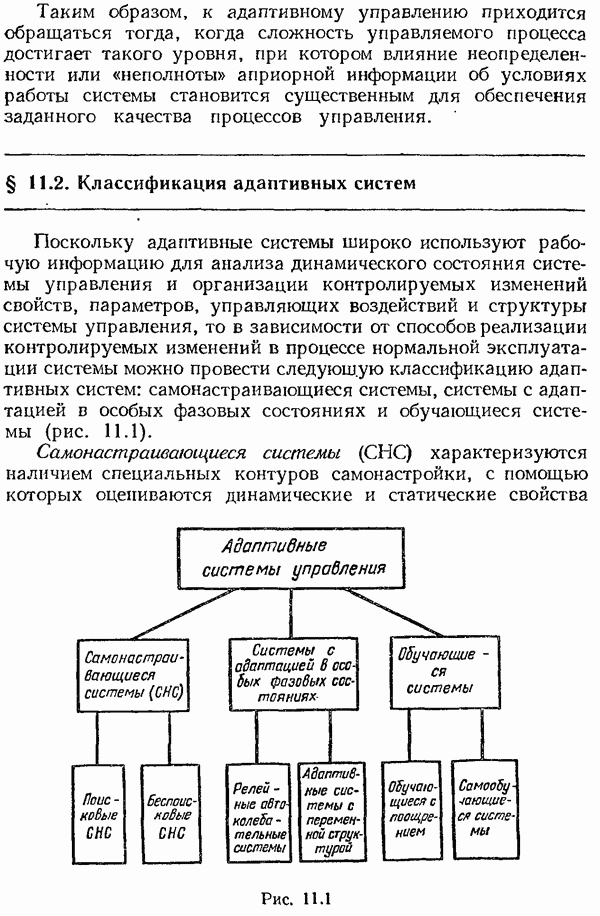
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
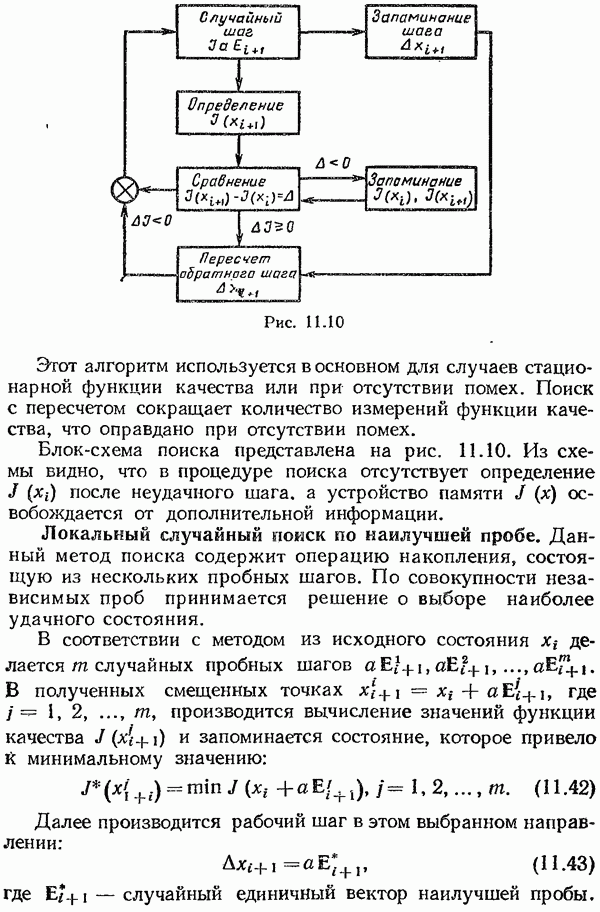
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
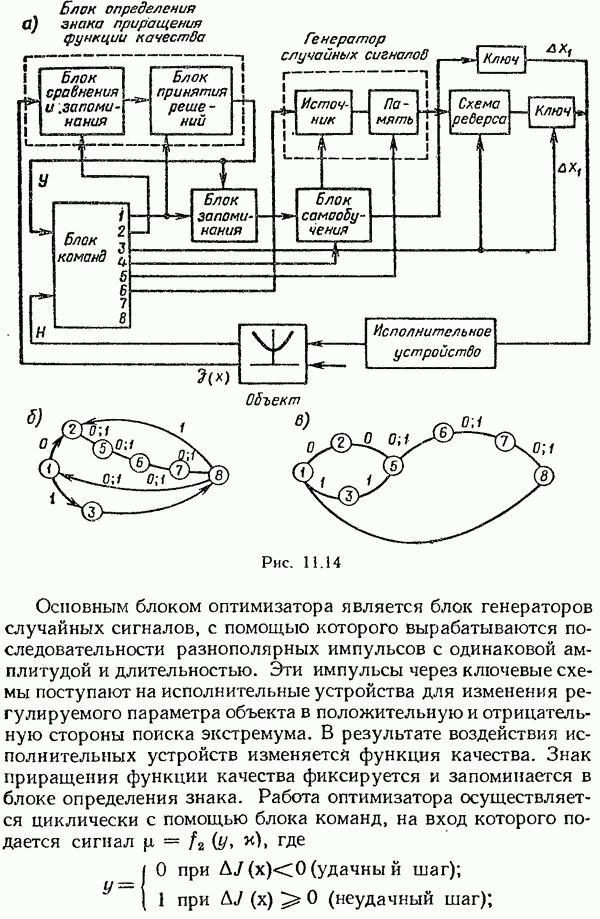
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
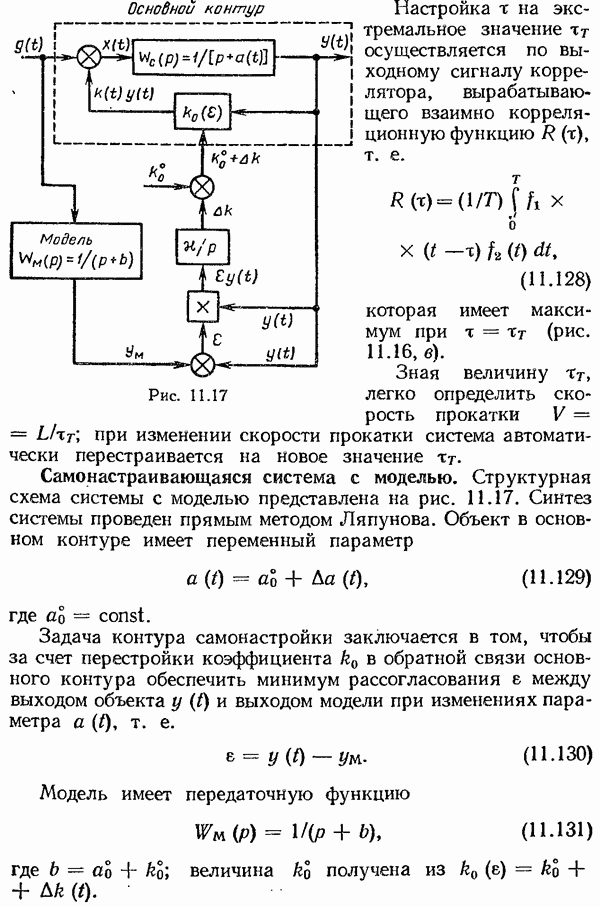
- Самонастраивающаяся система с моделью.
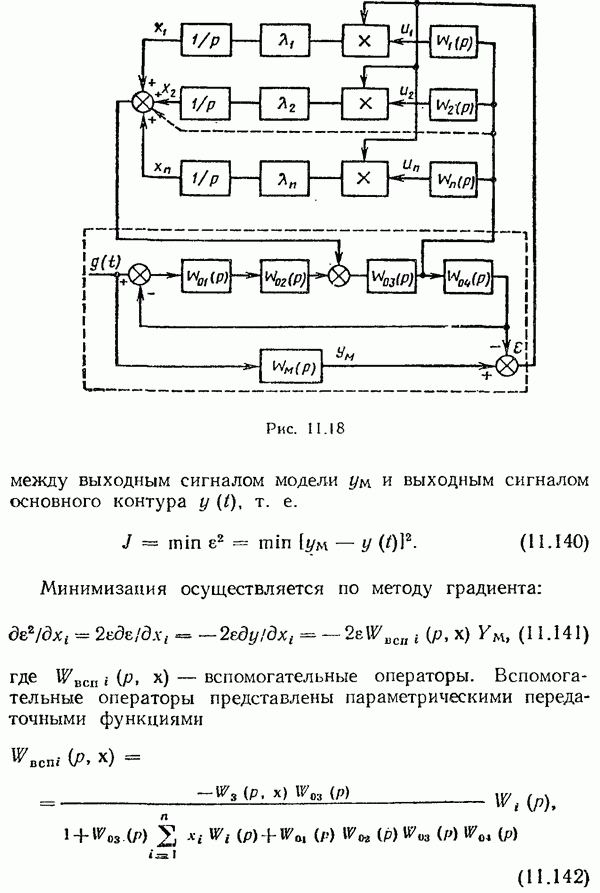
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
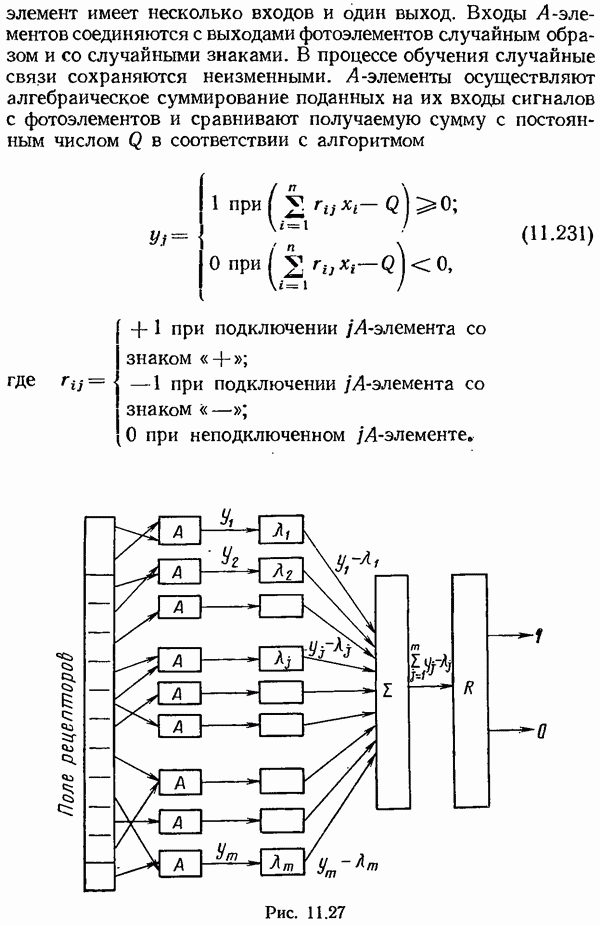
- Персептронная модель автоматической классификации.
- § 11.6. Адаптивные робототехнические системы
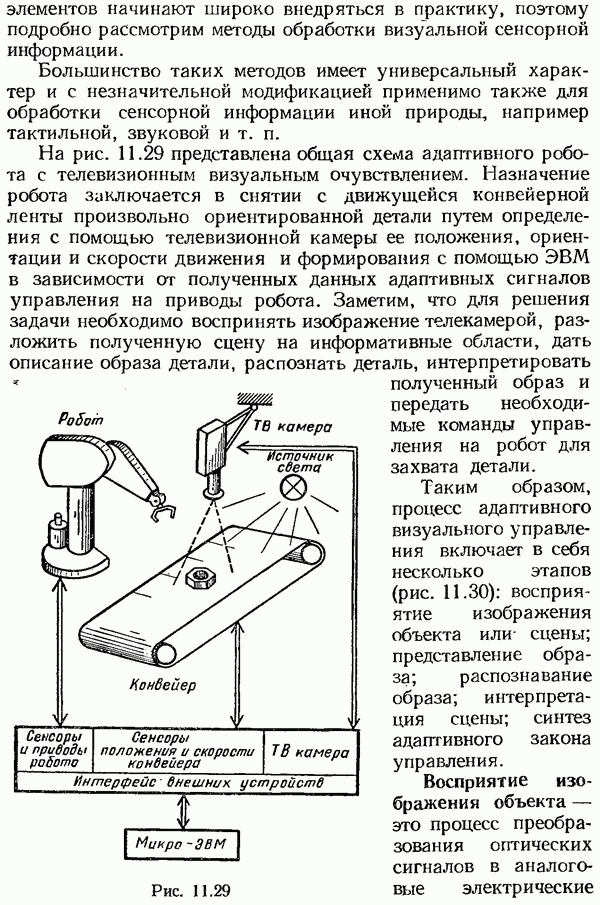
- Методы обработки сенсорной информации для адаптивного управления роботами.
- Восприятие изображения объекта
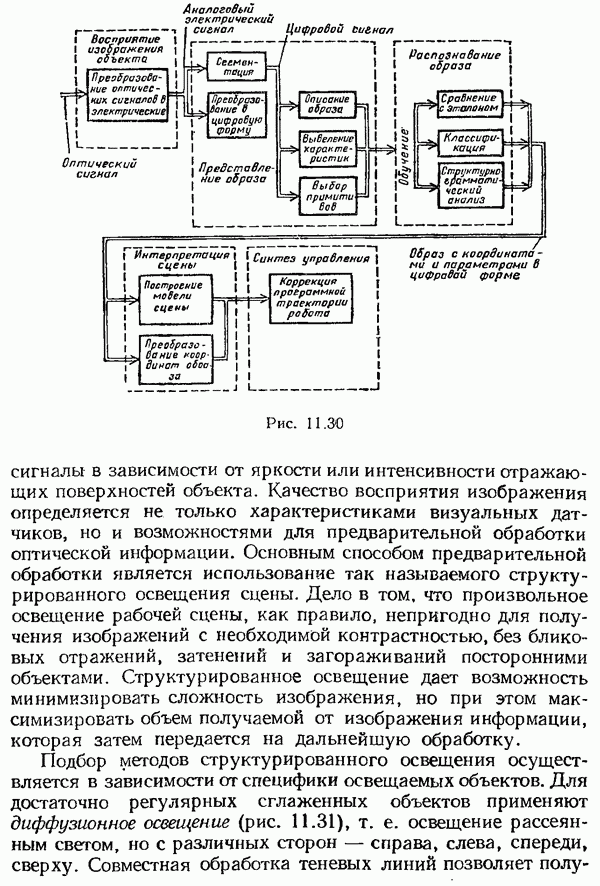
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ