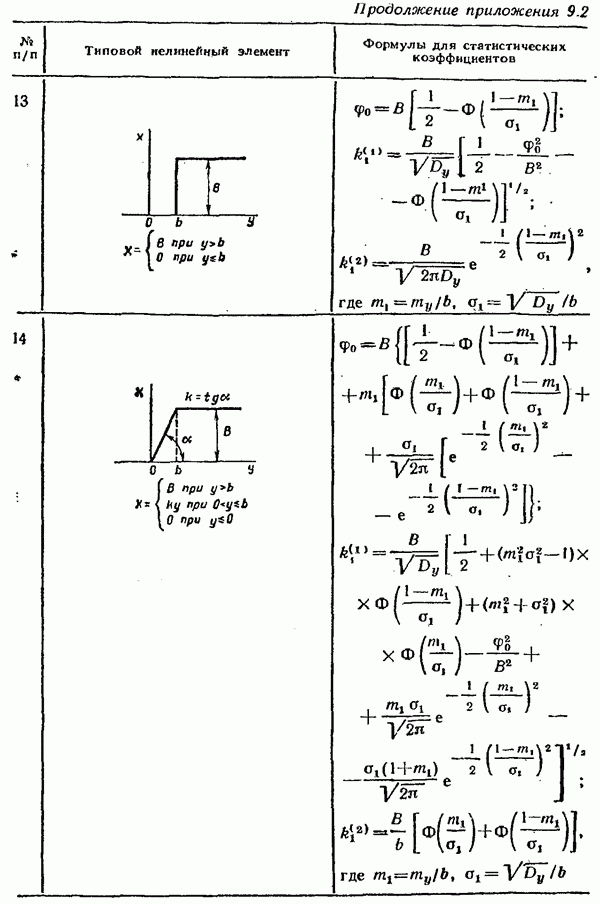
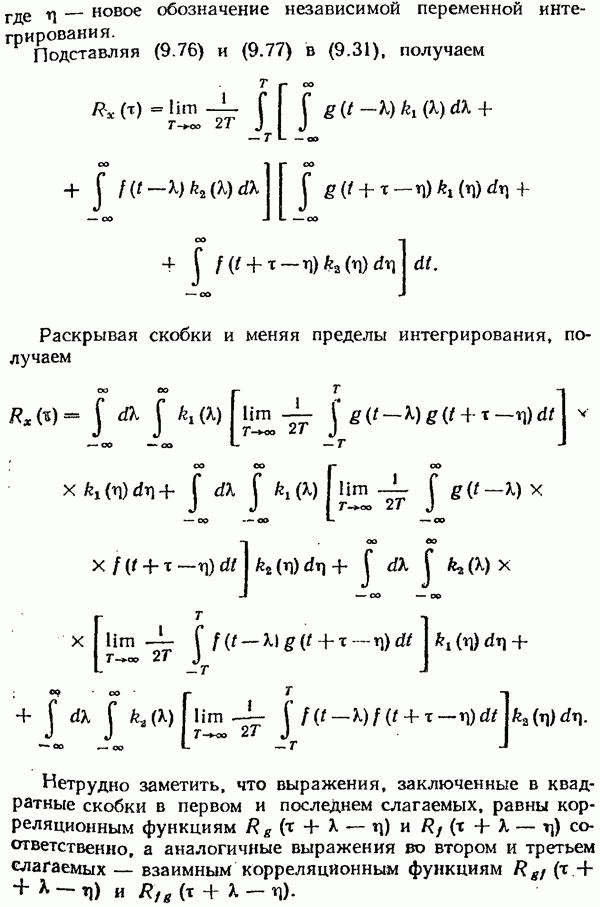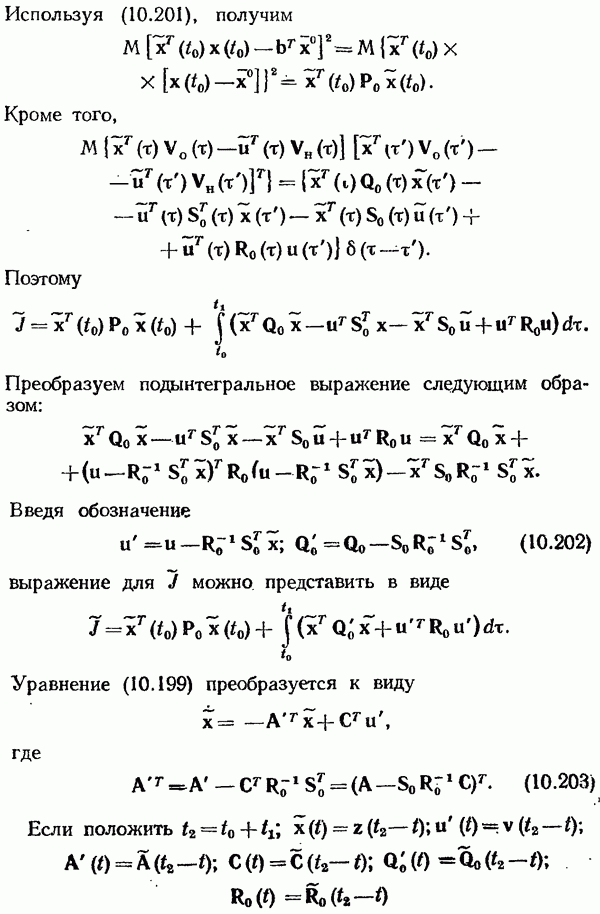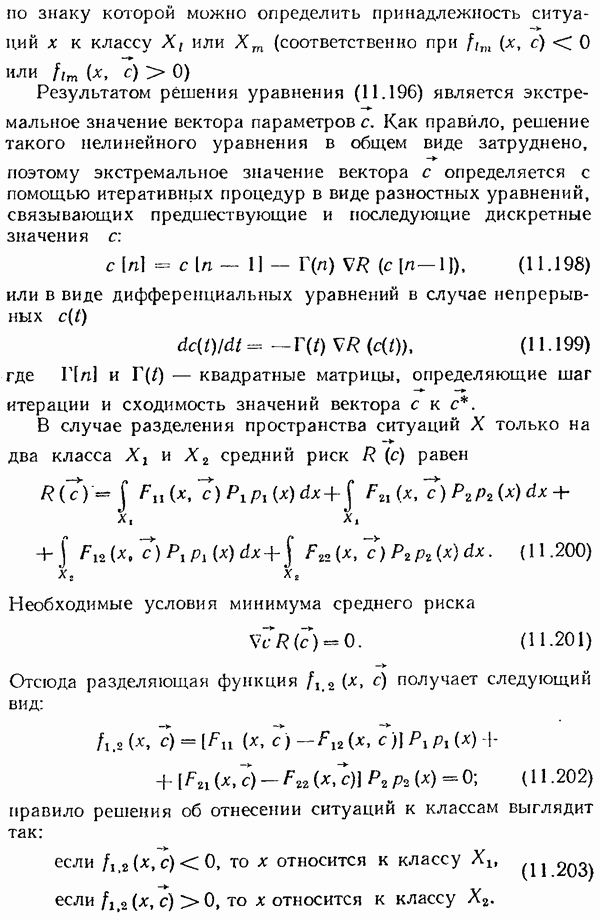| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Задачи с подвижными концами и фиксированным временем
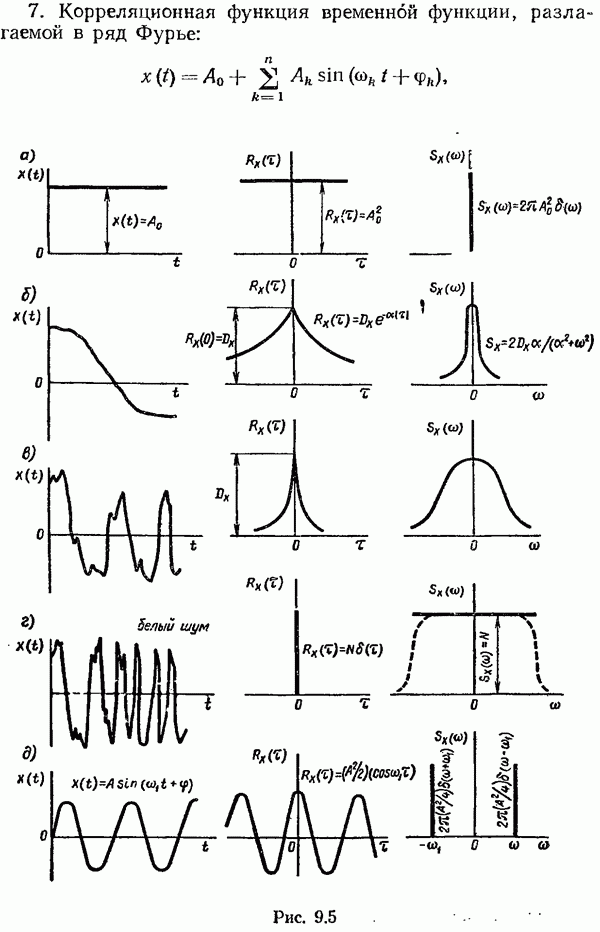
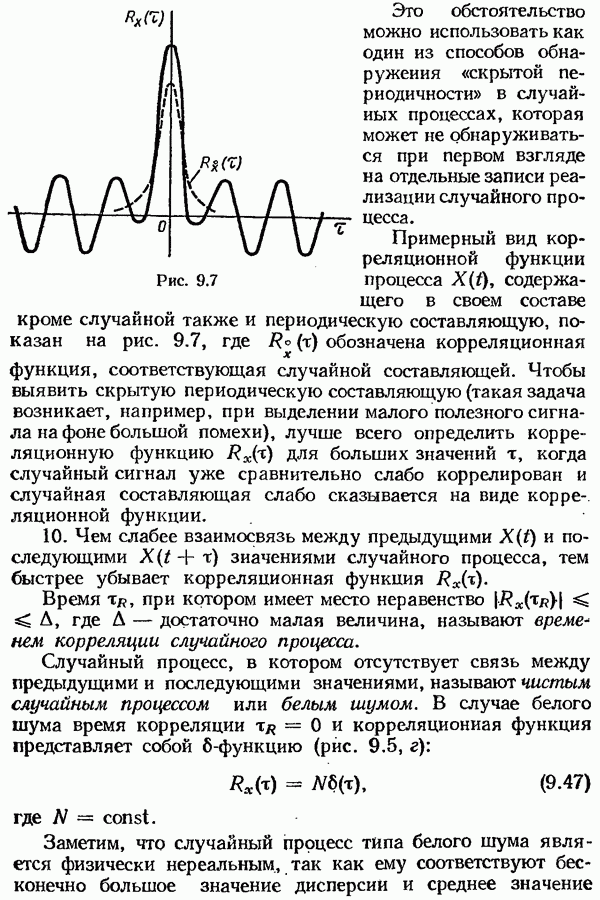
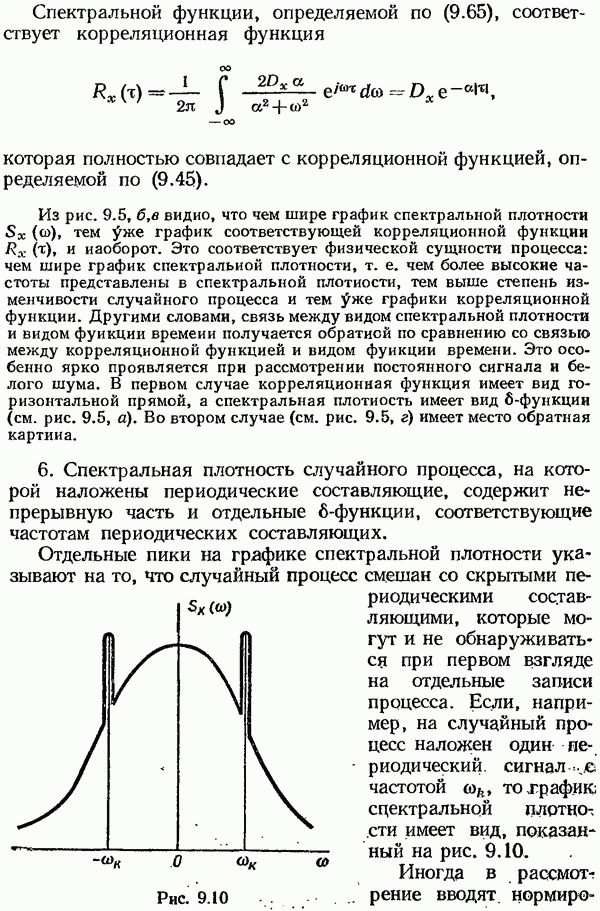
Если концы подвижны, то в классическом случае задача оптимального управления отличается от задачи  тем, что изменяются краевые условия и критерий оптимальности может иметь любой из указанных при классификации видов, т. е. в этом случае задача оптимального управления может быть задачей Лагранжа, Больца и Майера. Когда концы закреплены и время фиксировано, задача оптимального управления может быть только задачей Лагранжа.
тем, что изменяются краевые условия и критерий оптимальности может иметь любой из указанных при классификации видов, т. е. в этом случае задача оптимального управления может быть задачей Лагранжа, Больца и Майера. Когда концы закреплены и время фиксировано, задача оптимального управления может быть только задачей Лагранжа.
Получим необходимые условия. Начнем с простейшей вариационной задачи с подвижными концами и фиксированным временем  функции
функции  непрерывны и дифференцируемы по всем своим аргументам. Порядок вывода необходимых условий такой же, как и в случае задачи с фиксированными концами. Некоторые
непрерывны и дифференцируемы по всем своим аргументам. Порядок вывода необходимых условий такой же, как и в случае задачи с фиксированными концами. Некоторые
особенности появляются из-за того, что в силу подвижности граничных точек их также нужно варьировать. Опять все выкладки будем выполнять, предполагая, что  принадлежит к классу гладких функций:
принадлежит к классу гладких функций: 
Пусть экстремум достигается в точке  При произвольной фиксированной точке
При произвольной фиксированной точке  функционал
функционал

является функцией от числового аргумента е. Эта функция достигает экстремума при  -Поэтому по теореме Ферма
-Поэтому по теореме Ферма

Интегрируя по частям второе слагаемое под интегралом получим

Функция  должна доставлять экстремум функционалу
должна доставлять экстремум функционалу  при фиксированных граничных точках
при фиксированных граничных точках  поэтому она должна удовлетворять уравнению Эйлера
поэтому она должна удовлетворять уравнению Эйлера

С учетом этого уравнения имеем

В силу произвольности и независимости  из последнего равенства получаем соотношения
из последнего равенства получаем соотношения

которые называются условиями трансверсальности. Если  — вектор, то условия трансверсальности в скалярной форме принимают вид
— вектор, то условия трансверсальности в скалярной форме принимают вид

Уравнения Эйлера в скалярной форме были уже приведены [см. (10.21)]. Итак, решение вариационной задачи с подвижными концами кроме уравнений Эйлера должно удовлетворять условиям трансверсальности.
Получим необходимые условия оптимальности для задачи оптимального управления:

Граничные условия (10.38) предполагаются независимыми, функции  — непрерывными и дифференцируемыми по всем своим аргументам. На остальные функции накладываются такие же требования, как и в случае задачи с фиксированными концами. Используя прием Лагранжа, преобразуем эту задачу в простейшую задачу Больца:
— непрерывными и дифференцируемыми по всем своим аргументам. На остальные функции накладываются такие же требования, как и в случае задачи с фиксированными концами. Используя прием Лагранжа, преобразуем эту задачу в простейшую задачу Больца:

где

Уравнения Эйлера—Лагранжа для этой задачи совпадают с уравнением (10.32) или (10.33) и (10,34).
С учетом равенств  условия трансверсальности принимают вид
условия трансверсальности принимают вид

Отдельные координаты граничных точек могут быть фиксированы. Соотношения, определяющие эти координаты, в выражение для  не включаются, и так как при определении необходимых условий они не варьируются, то в условия трансверсальности не должны входить соотношения, содержащие частные производные по этим координатам; их из (10.40) нужно исключить. В частности, если начальная точка фиксирована, т. е. фиксированы все координаты точки
не включаются, и так как при определении необходимых условий они не варьируются, то в условия трансверсальности не должны входить соотношения, содержащие частные производные по этим координатам; их из (10.40) нужно исключить. В частности, если начальная точка фиксирована, т. е. фиксированы все координаты точки  то условия трансверсальности (10.40) принимают вид
то условия трансверсальности (10.40) принимают вид

Если часть координат точки  также фиксирована, то в последнем условии
также фиксирована, то в последнем условии  пробегает только значения индексов нефиксированных координат.
пробегает только значения индексов нефиксированных координат.
Правило множителей Лагранжа для задачи с подвижными концами и фиксированным временем.
Если допустимая пара  является решением задачи (10.36)-(10.39), то существуют такие не равные одновременно нулю множители Лагранжа, что эта пара удовлетворяет уравнениям Эйлера—Лагранжа (10.33), (10.34) и условиям трансверсальности (10.40).
является решением задачи (10.36)-(10.39), то существуют такие не равные одновременно нулю множители Лагранжа, что эта пара удовлетворяет уравнениям Эйлера—Лагранжа (10.33), (10.34) и условиям трансверсальности (10.40).
Если управление терпит разрыв, то решение  должно удовлетворять уравнениям Эйлера—Лагранжа в точка непрерывности управления. В угловых точках (в точках разрыва управления) должно выполняться условие Вейерштрасса—Эрдмана (10.35).
должно удовлетворять уравнениям Эйлера—Лагранжа в точка непрерывности управления. В угловых точках (в точках разрыва управления) должно выполняться условие Вейерштрасса—Эрдмана (10.35).
Таким образом, чтобы получить решение задачи (10.36)- (10.39), нужно решить уравнения (10.36) и (10.37) совместно с уравнениями Эйлера—Лагранжа при краевых условиях (10.38) и условиях трансверсальности (10.40). Этих соотношений достаточно, чтобы определить все неизвестные величины.
Пример 10.2. Рассмотрим задачу

Эта задача отличается от задачи, рассмотренной в примере 10.1, только тем, что правый конец не закреплен: координата  не фиксирована. Поэтому уравнения Эйлера—Лаграижа и их решения получаются такими же, что и в примере 10.1:
не фиксирована. Поэтому уравнения Эйлера—Лаграижа и их решения получаются такими же, что и в примере 10.1:

Функция  и условия трансверсальности принимают вид
и условия трансверсальности принимают вид

С учетом этого условия имеем  Подставив полученное выражение для управления в уравнения объекта и решив их при заданных краевых условиях, получим:
Подставив полученное выражение для управления в уравнения объекта и решив их при заданных краевых условиях, получим:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
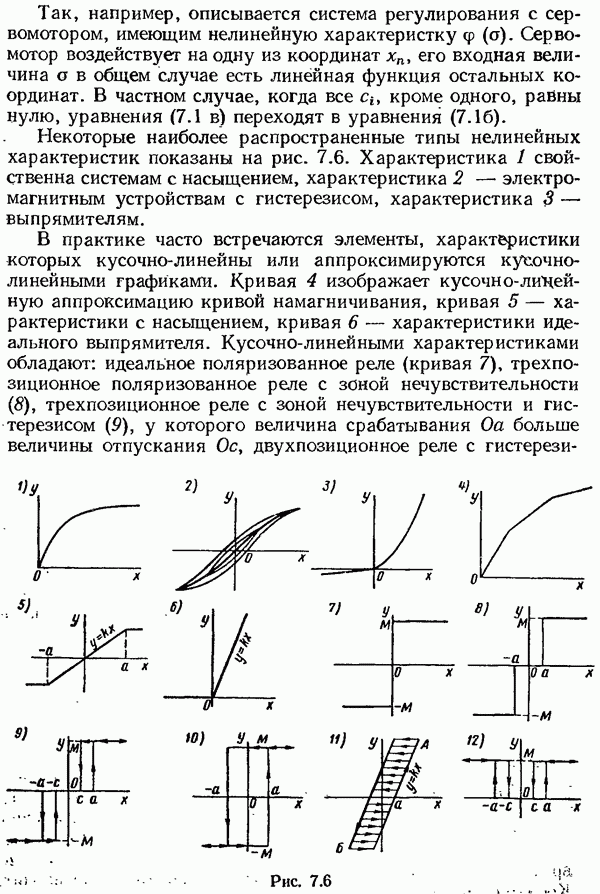
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
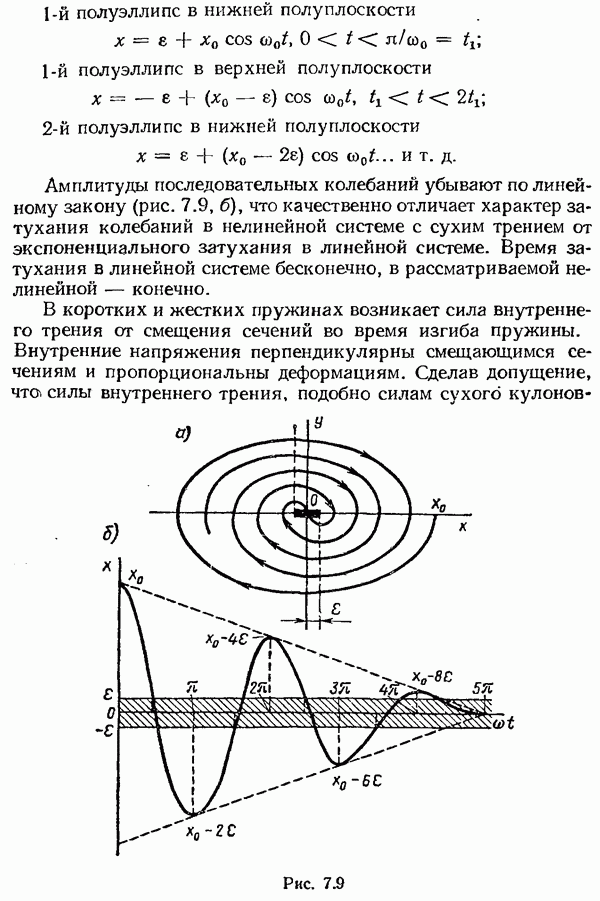
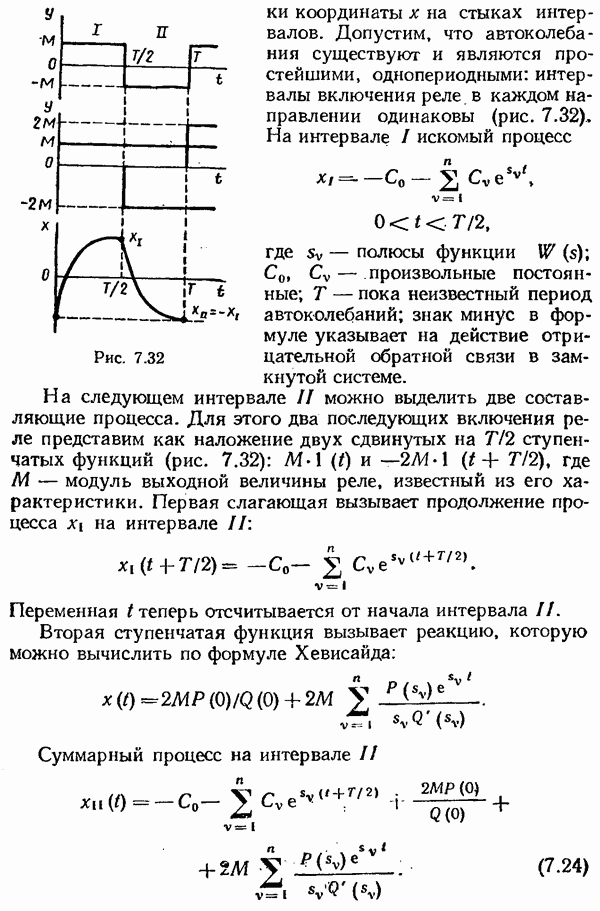
- § 7.3. Автоколебания. Метод точечных преобразований
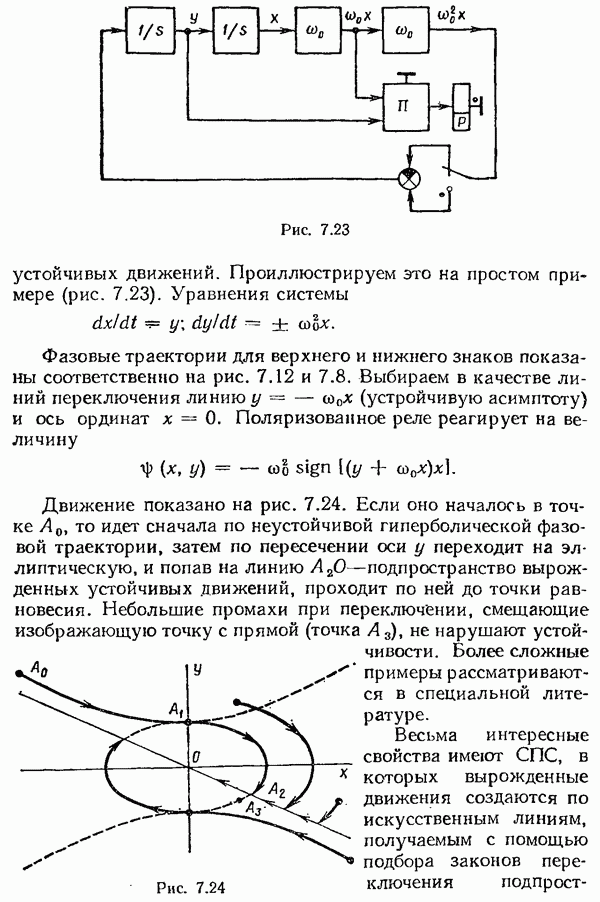
- § 7.4. Системы с переменной структурой
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
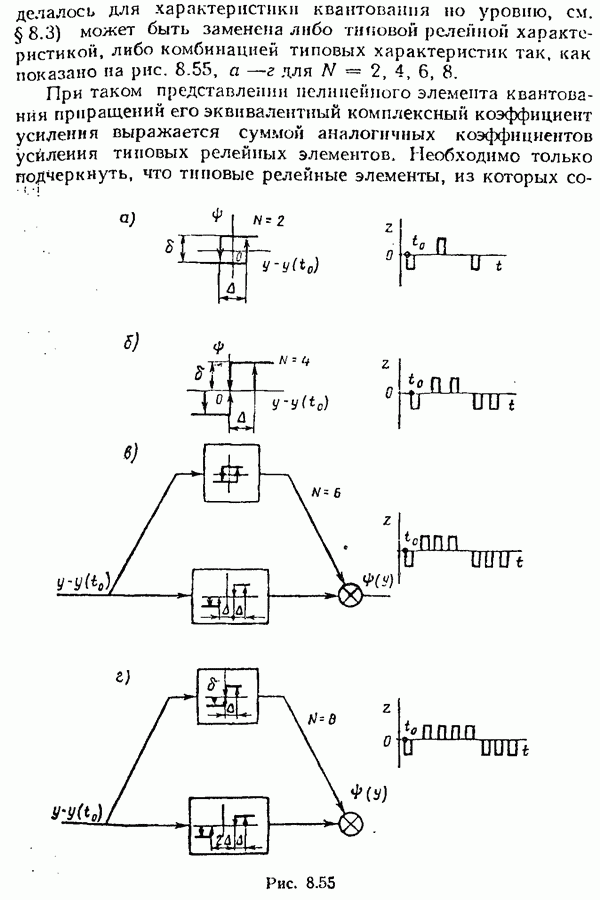
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
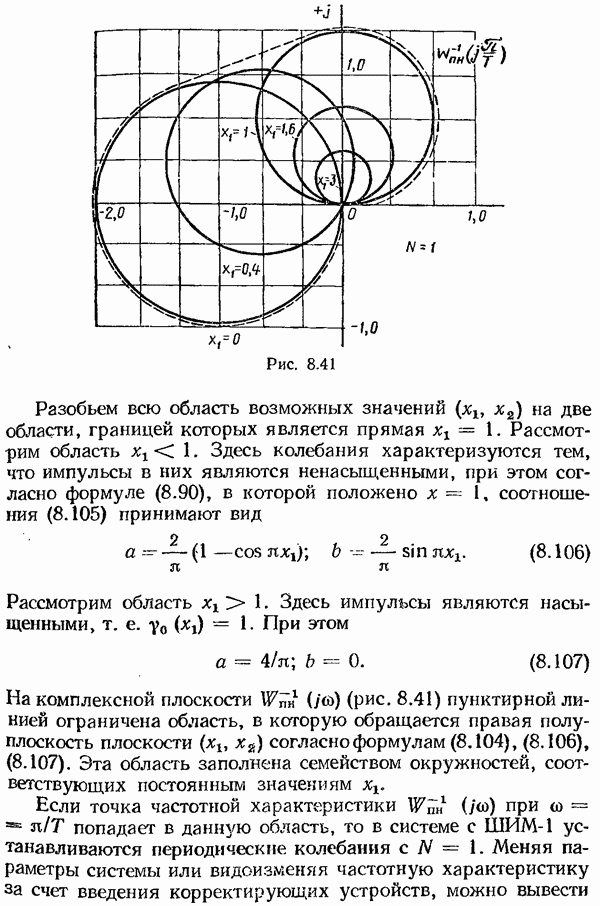
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
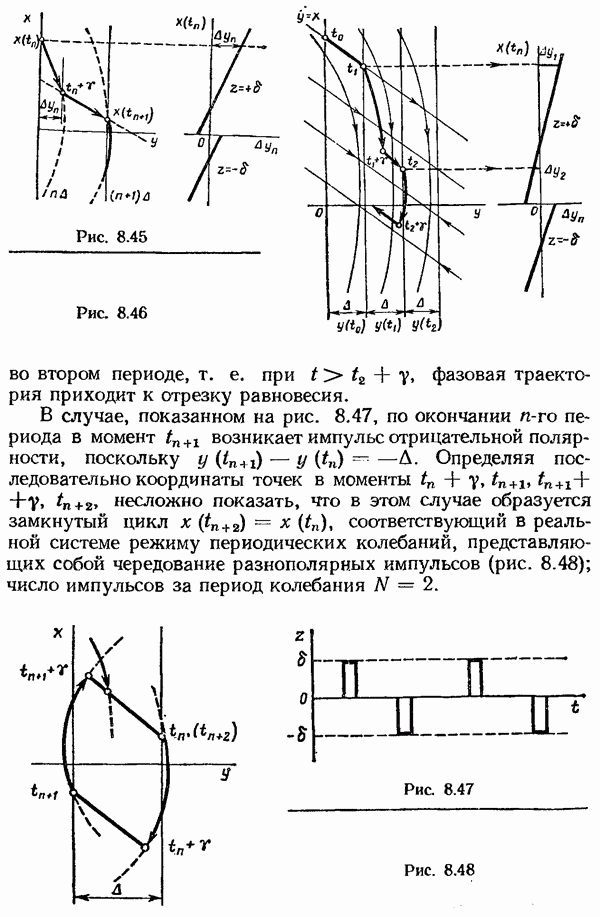
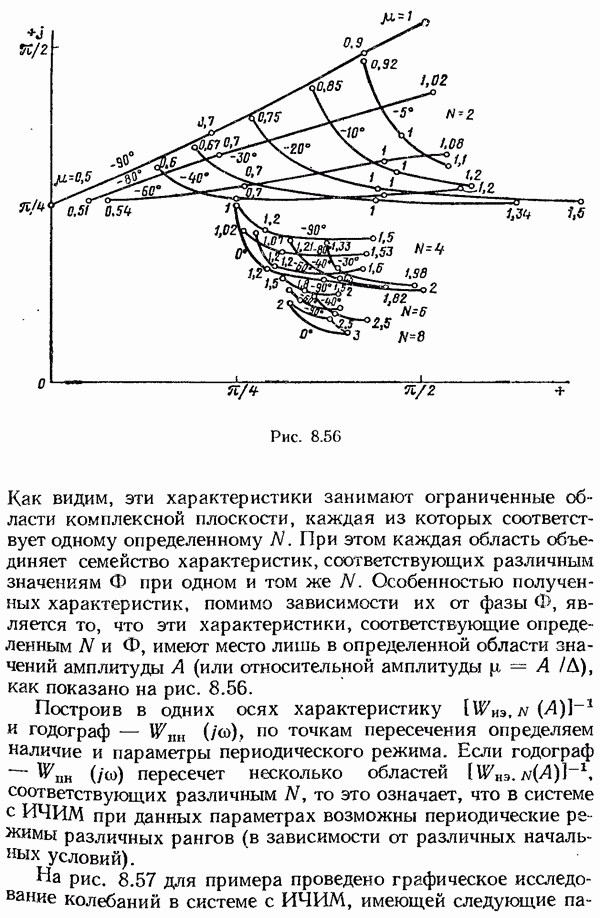
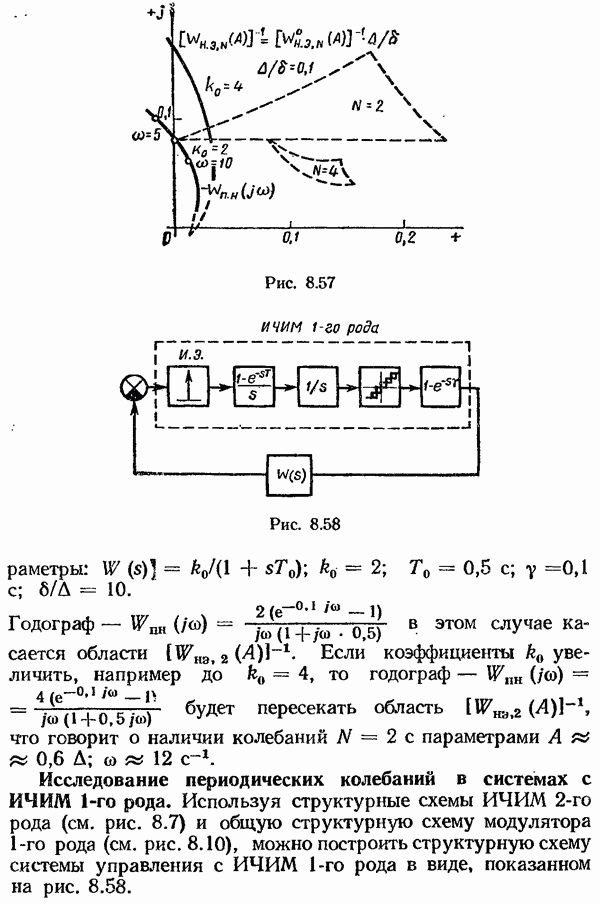
- Исследование периодических режимов в системах с ИЧИМ.
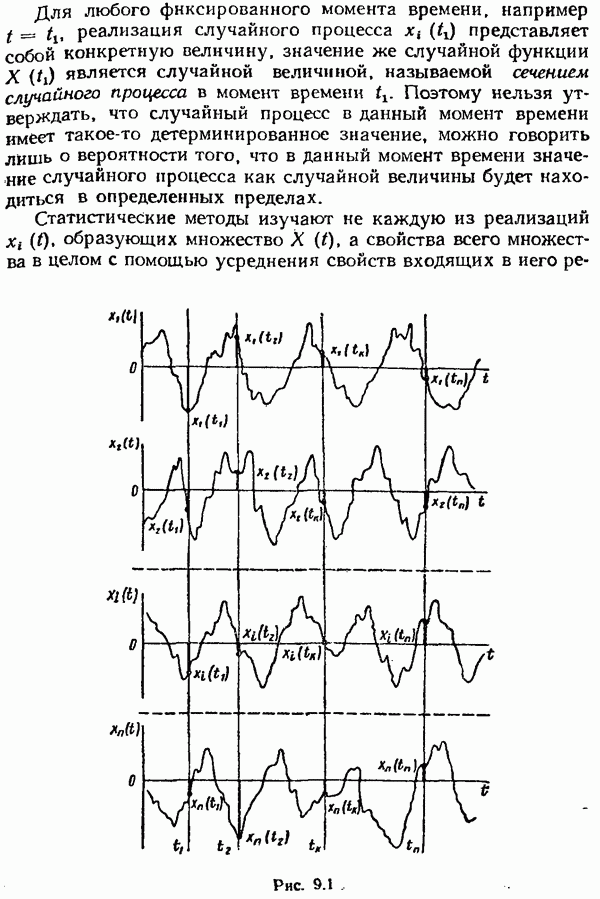
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
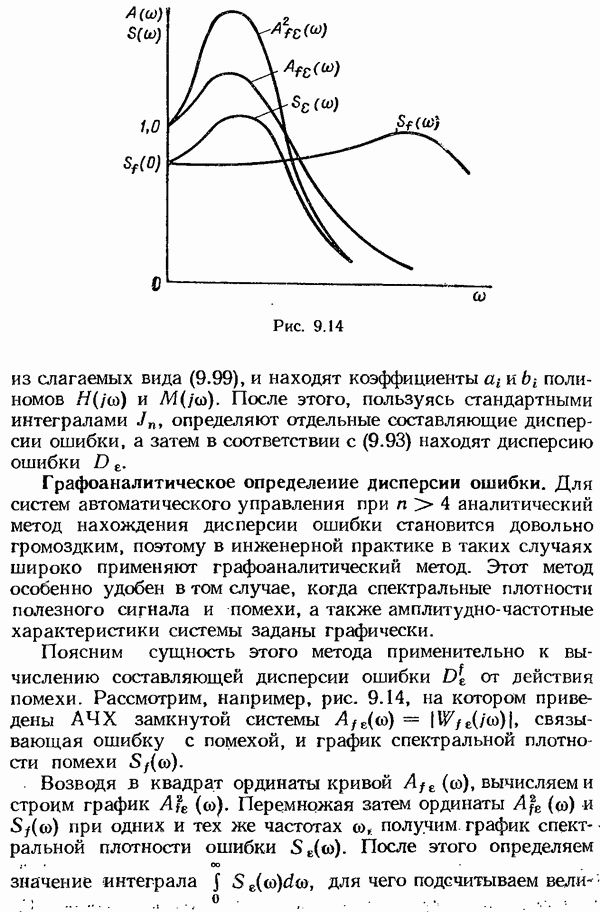
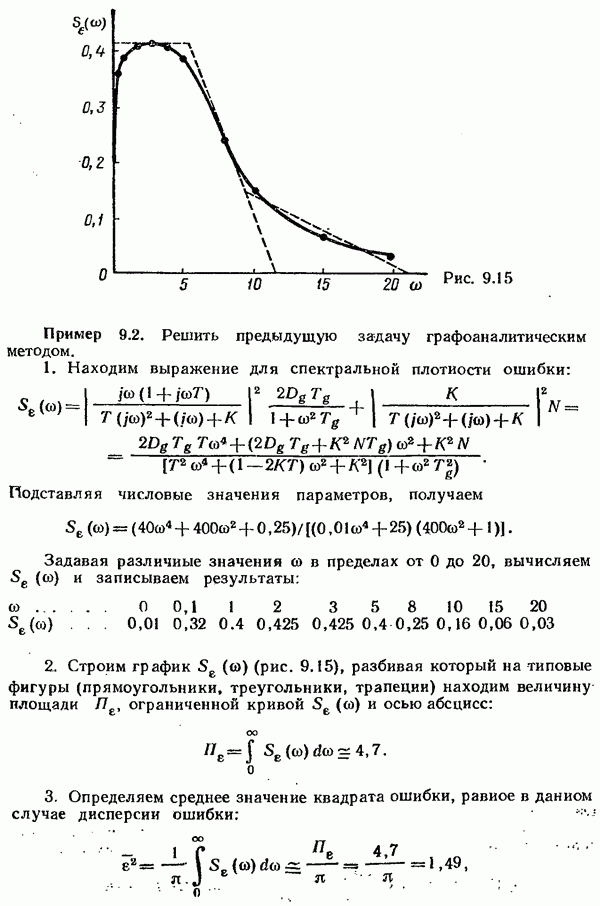
- Графоаналитическое определение дисперсии ошибки.
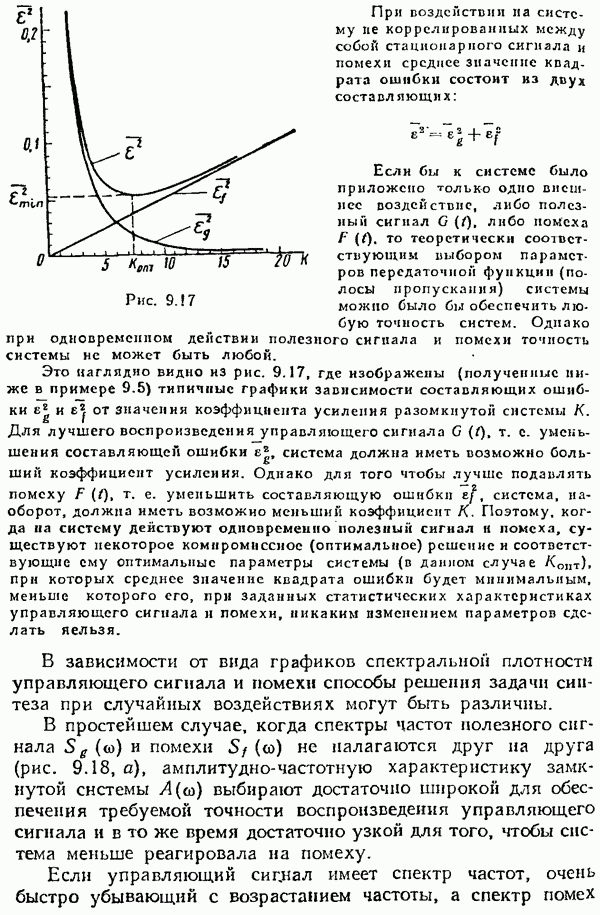
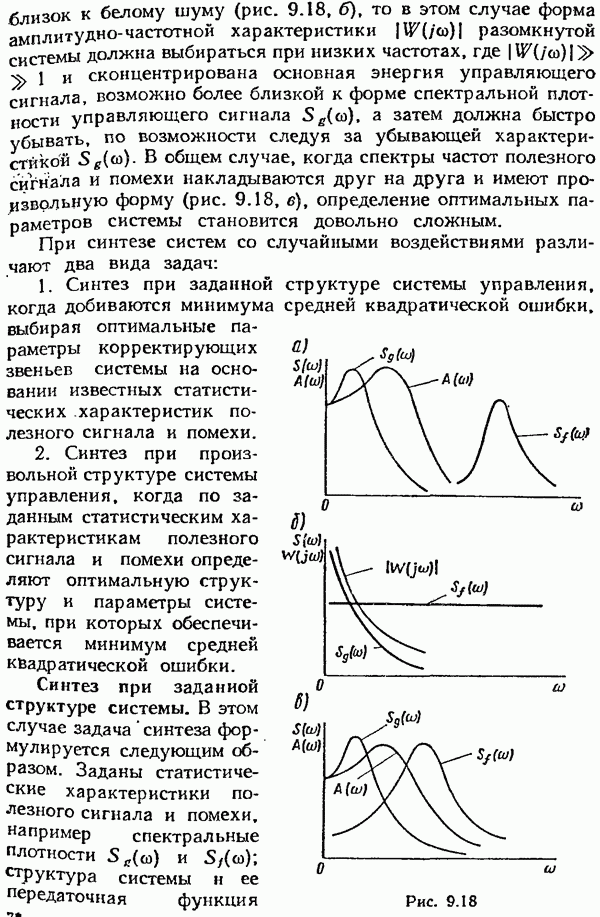
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
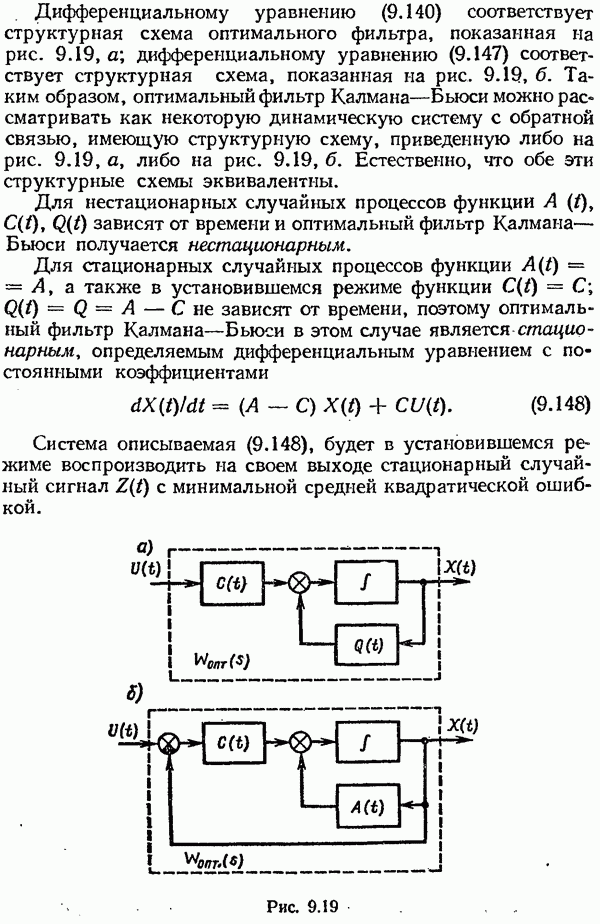
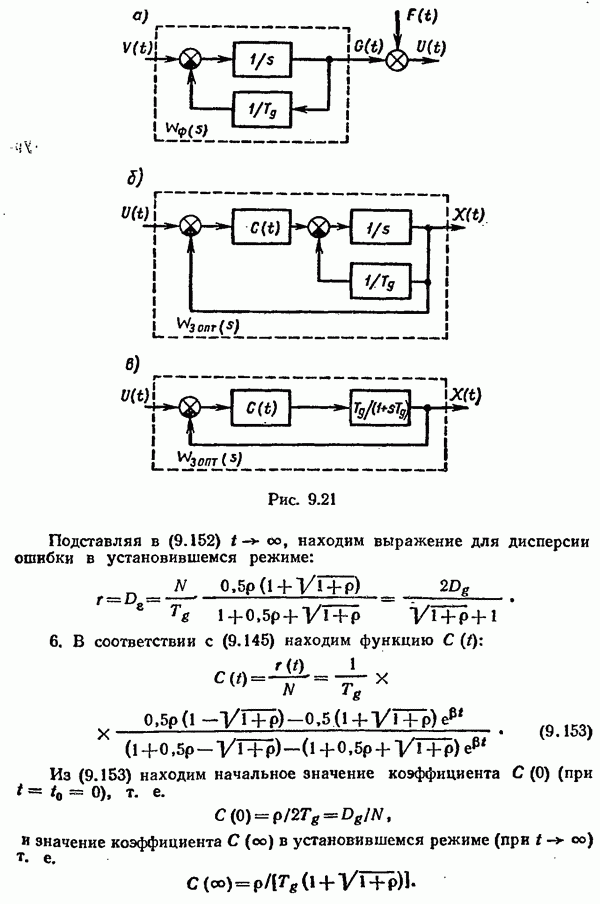
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
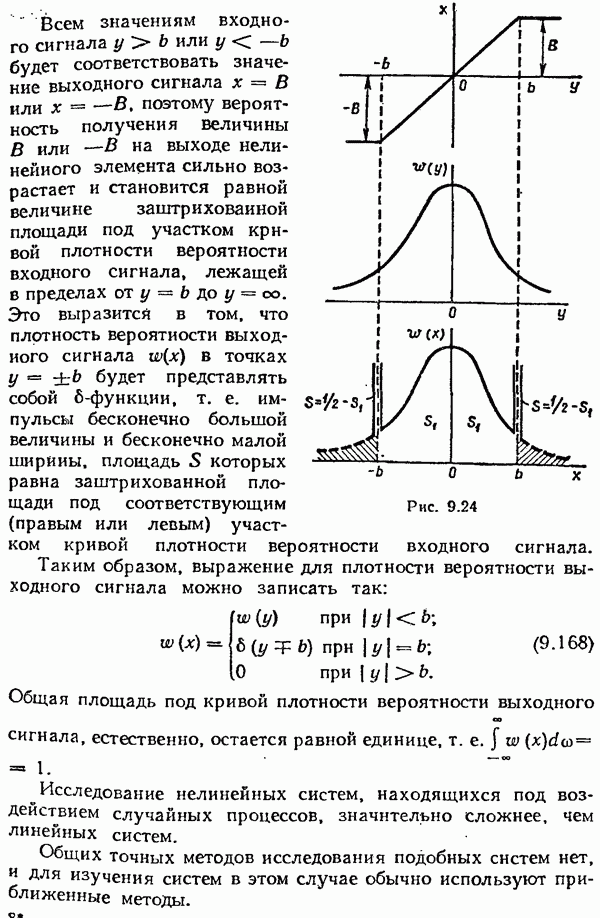
- § 9.9. Нелинейное преобразование случайных сигналов
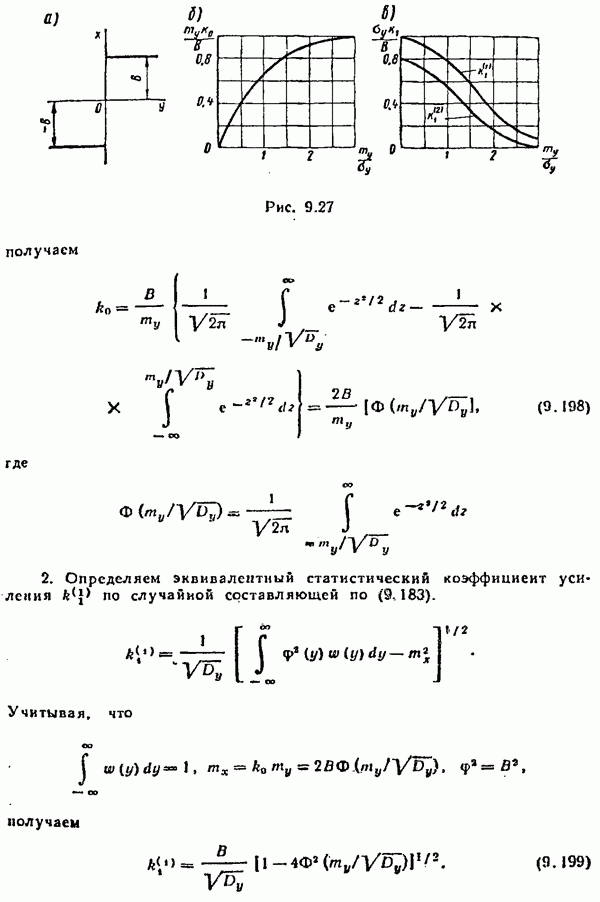
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
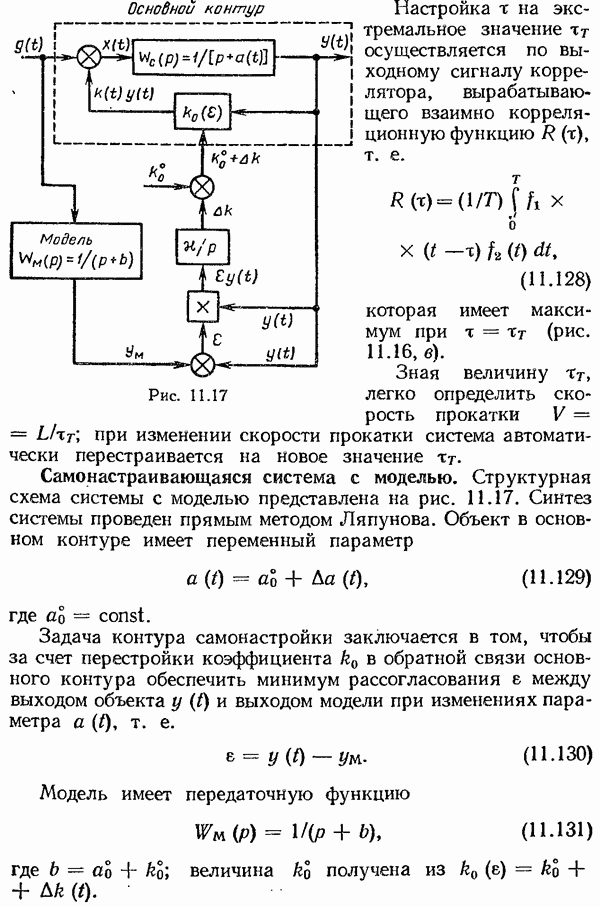
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
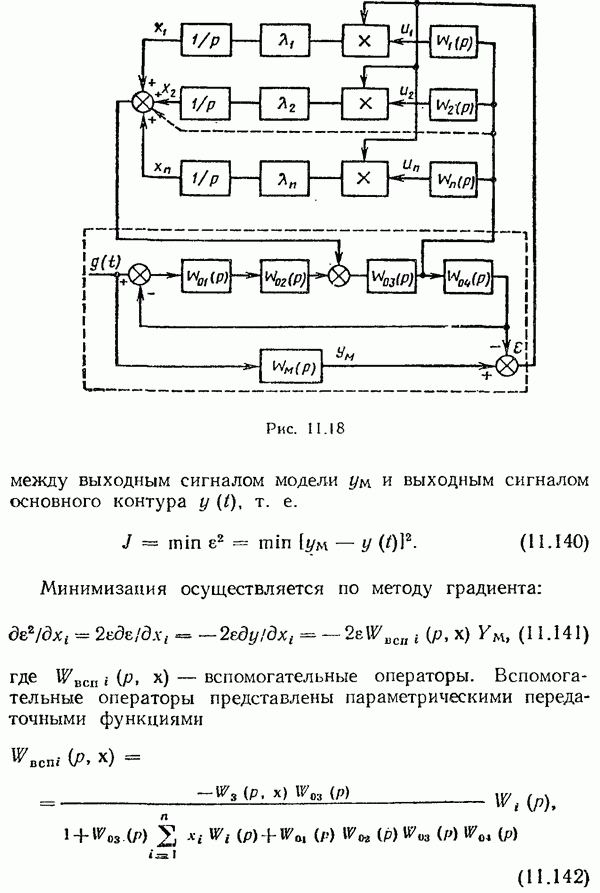
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
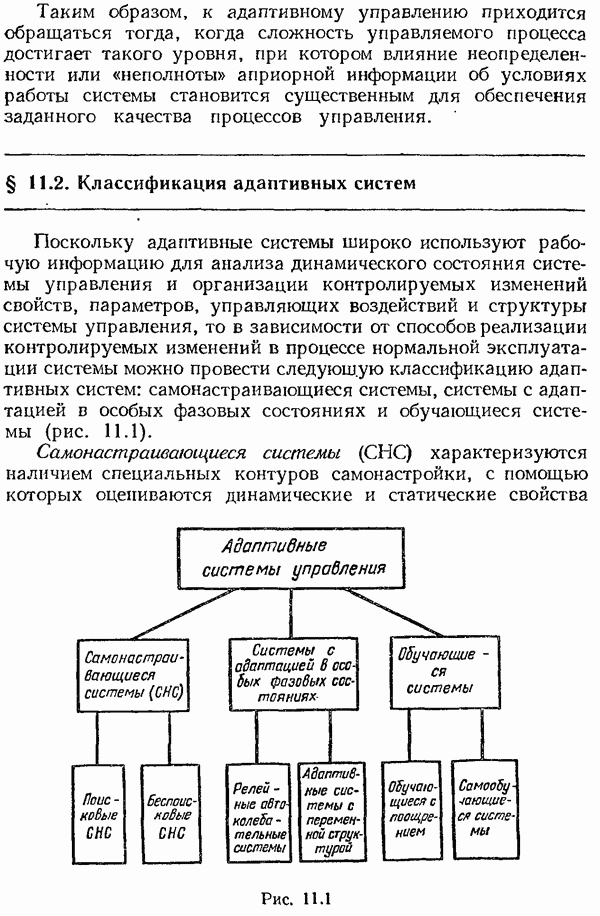
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
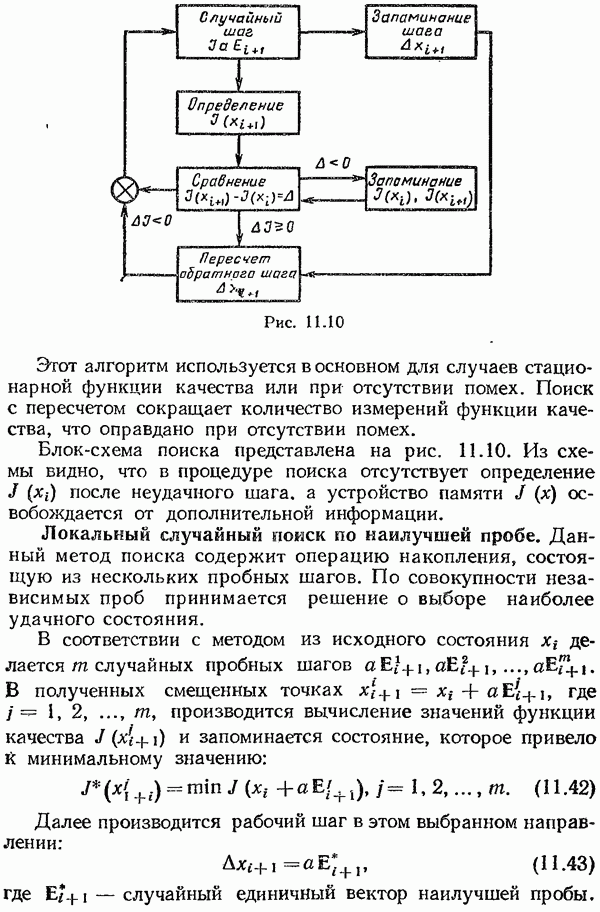
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
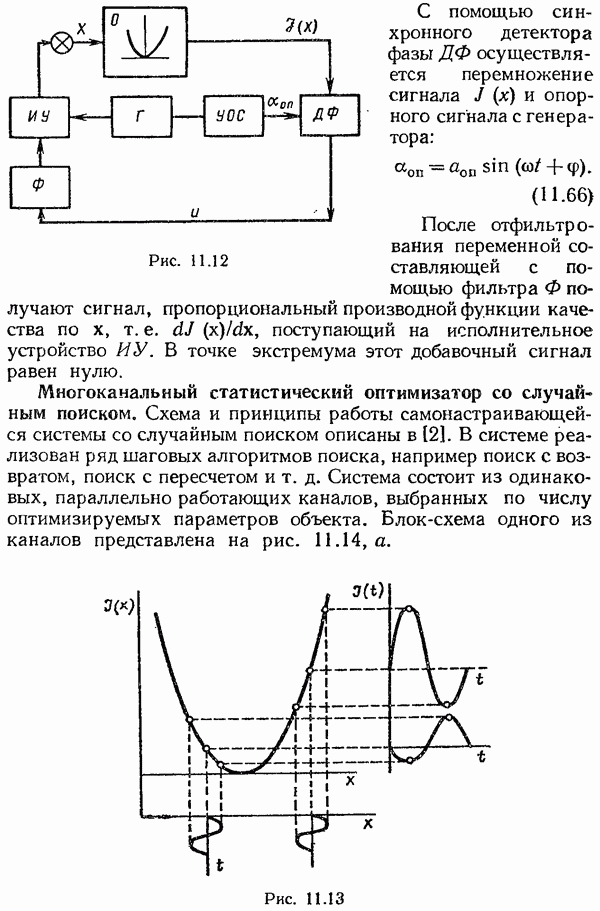
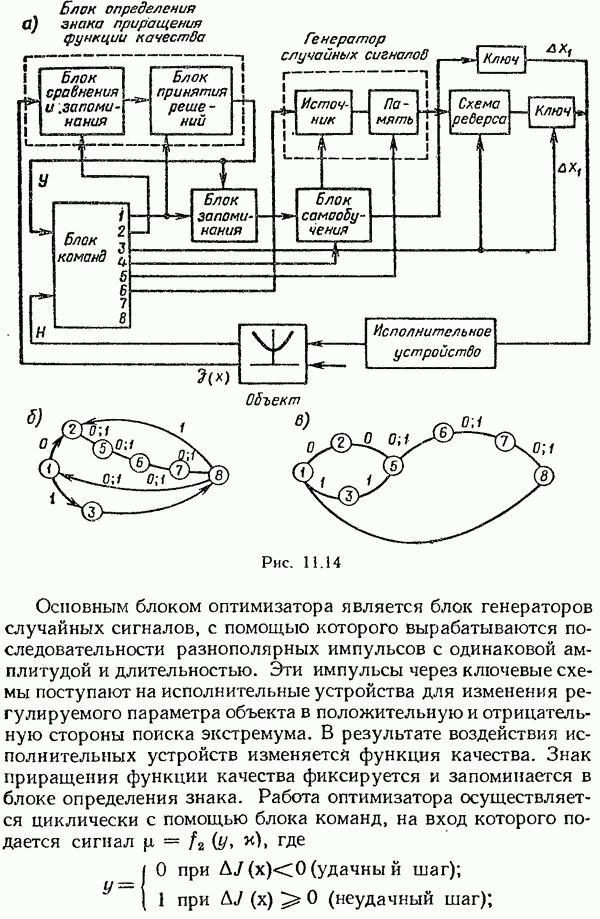
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
- Самонастраивающаяся система с моделью.
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
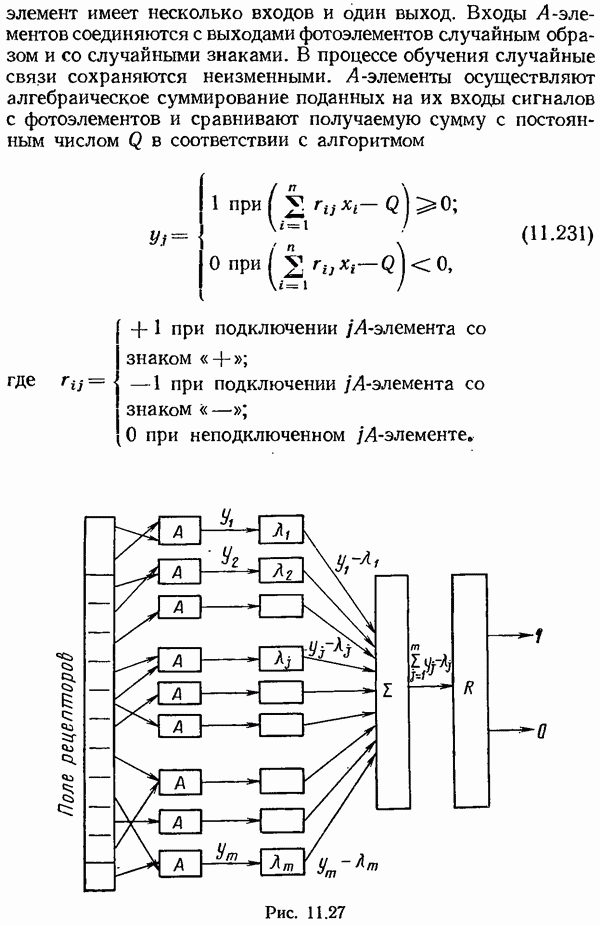
- Персептронная модель автоматической классификации.
- § 11.6. Адаптивные робототехнические системы
- Методы обработки сенсорной информации для адаптивного управления роботами.
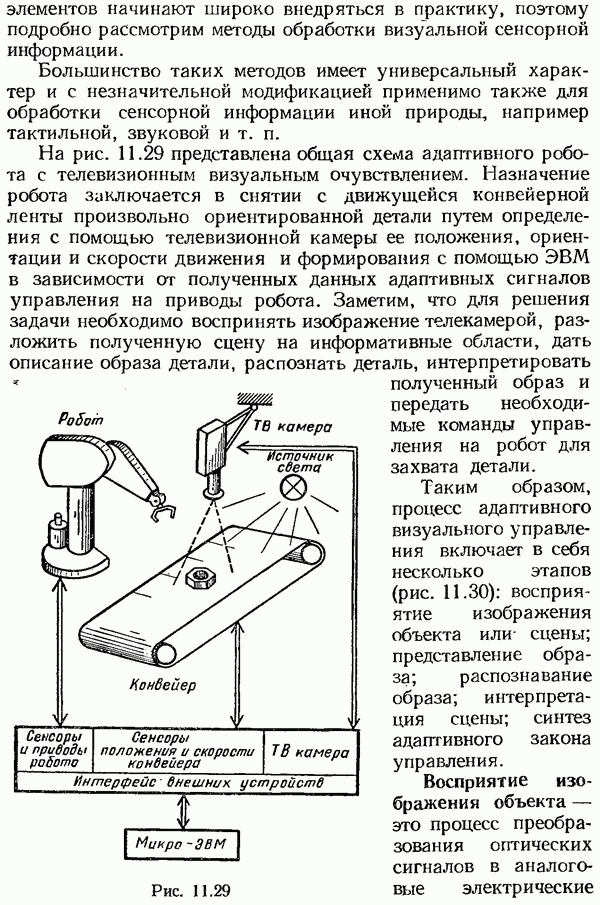
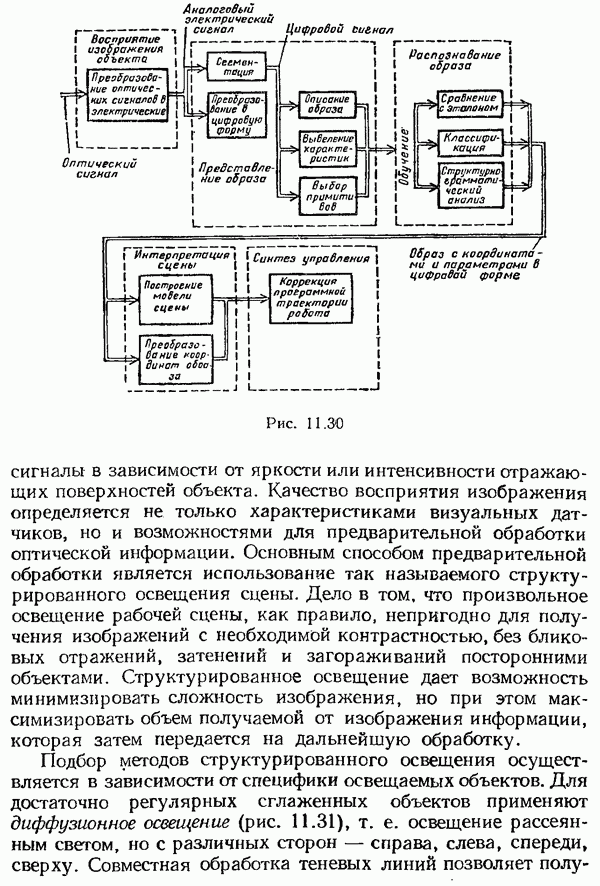
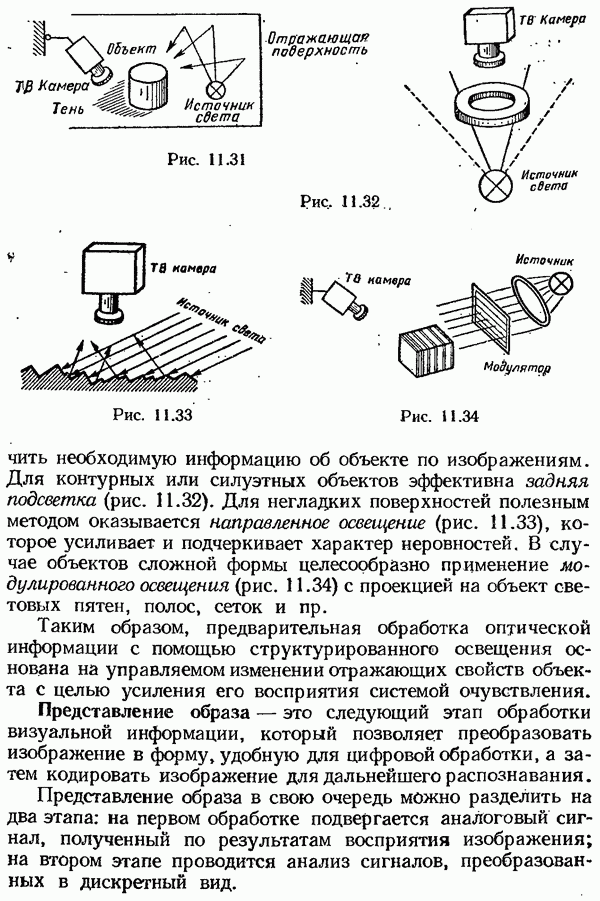
- Восприятие изображения объекта
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ