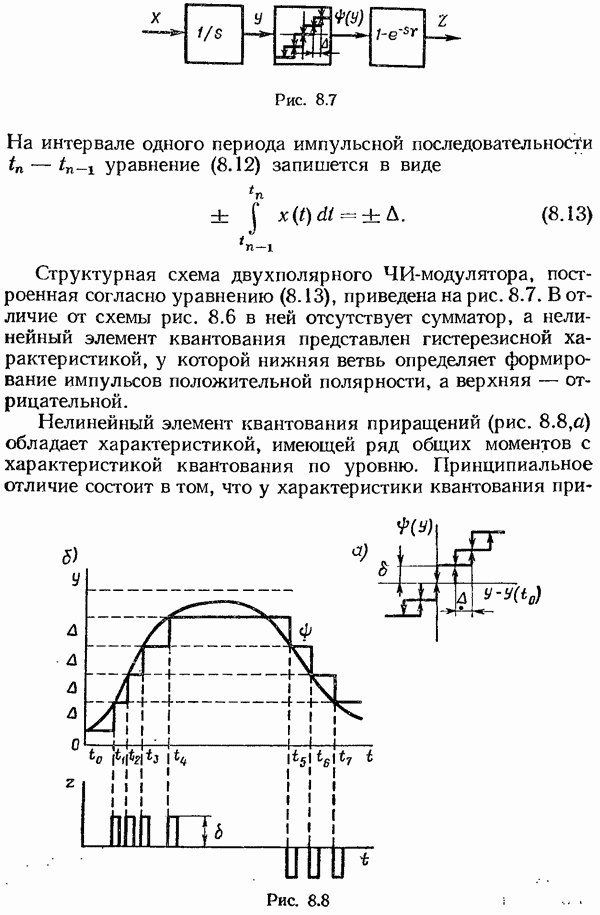
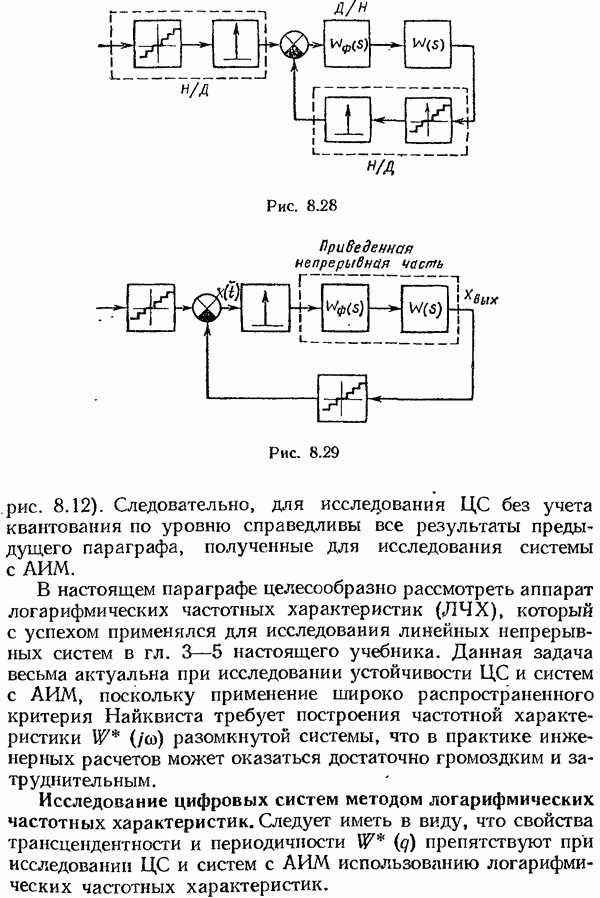
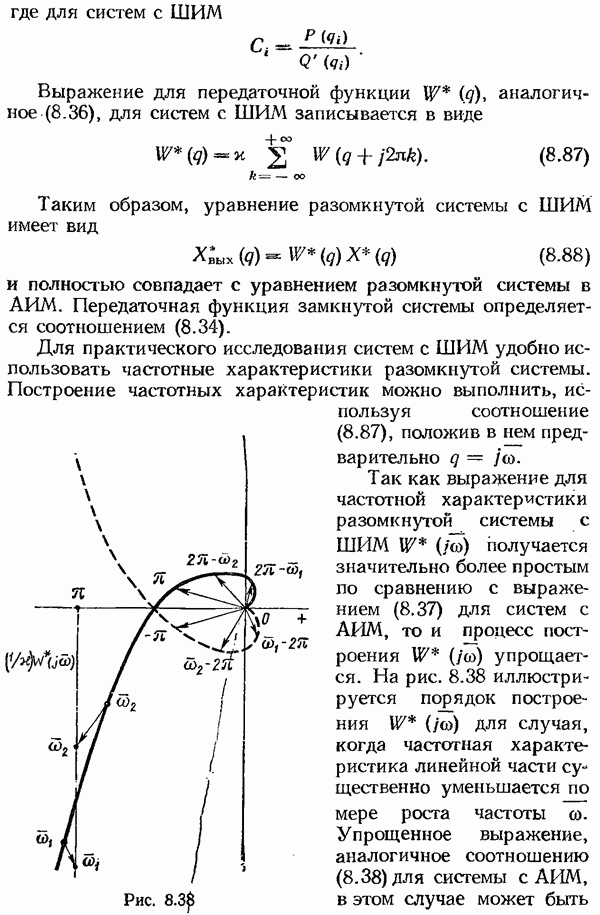
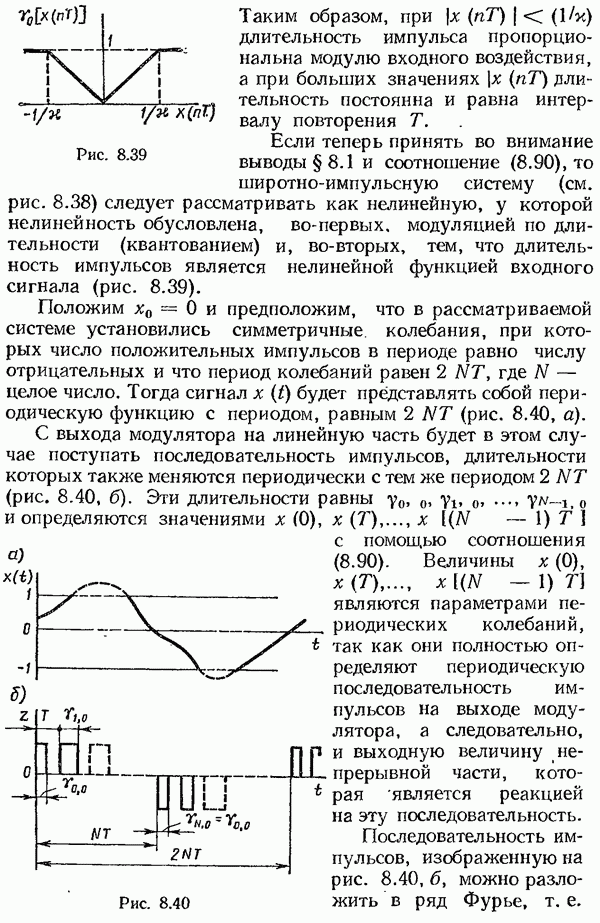
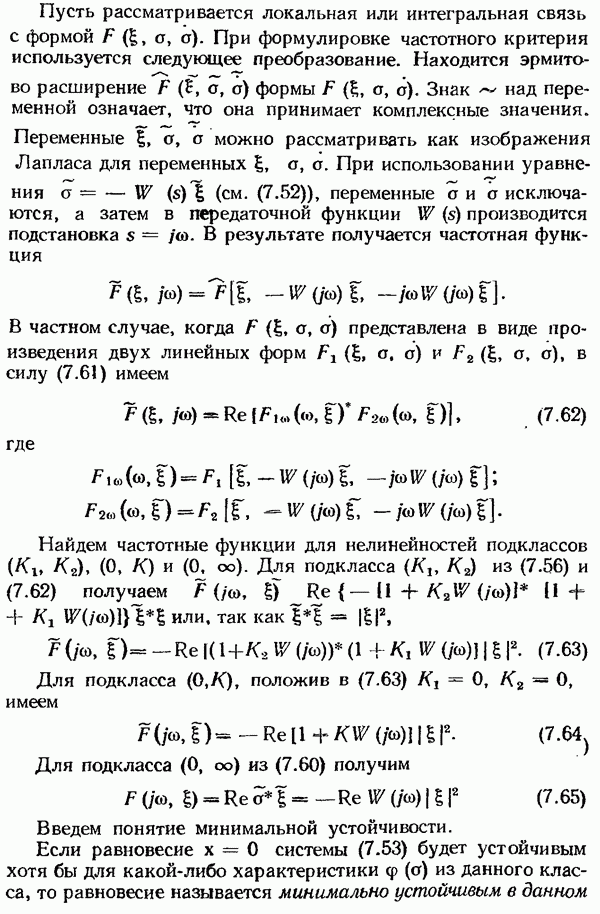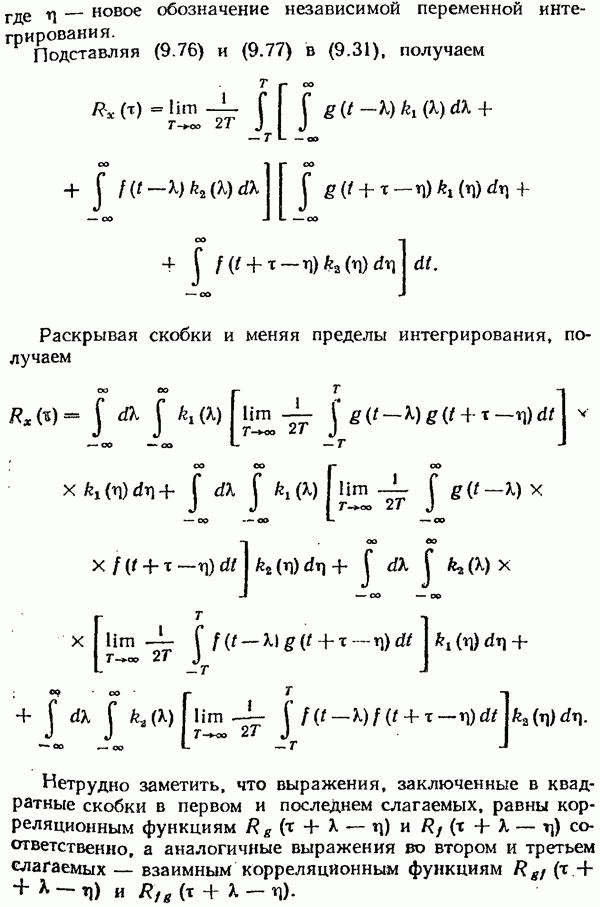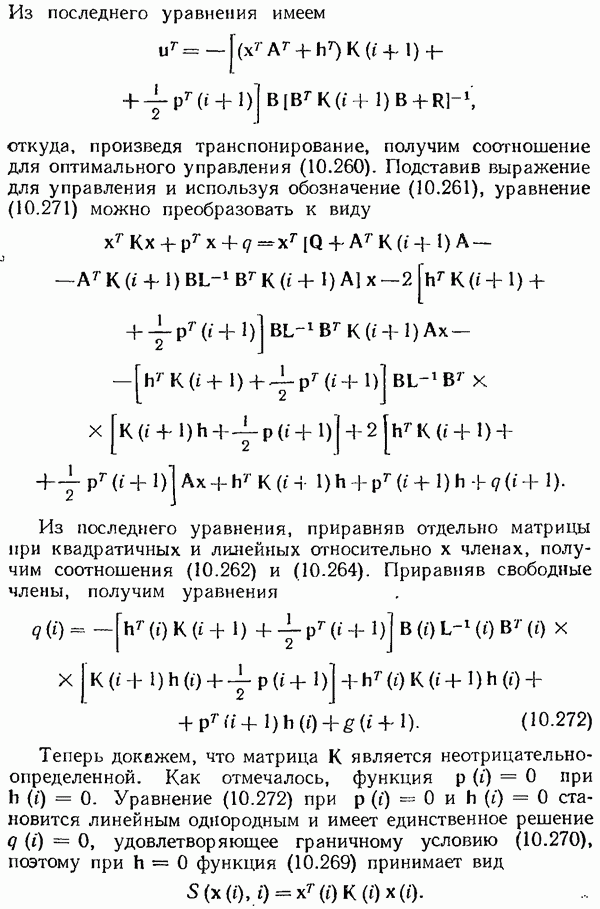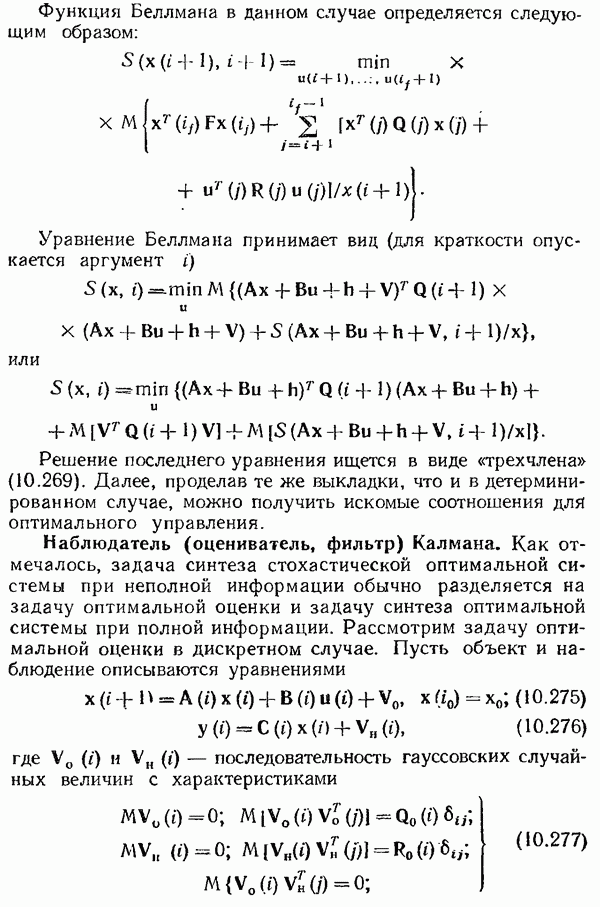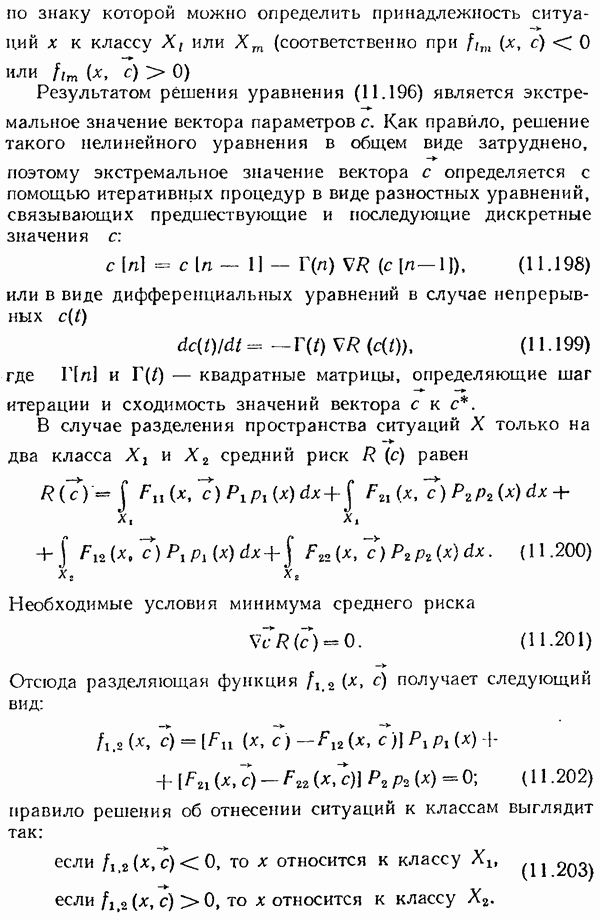| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
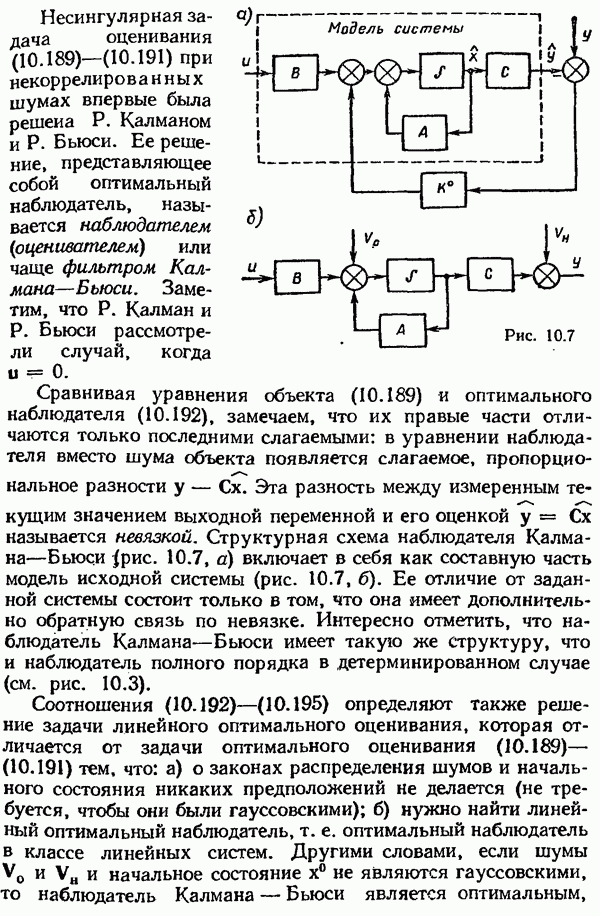
Оптимальный фильтр Калмана—Бьюси.
Нахождение оптимального фильтра Винера основывалось на использовании интегрального уравнения Винера — Хопфа, при решении которого стационарные случайные процессы рассматривались в частотной области. В 1960 г. Р. Калман и Р. Бьюси рассмотрели проблему линейной фильтрации во временной области и, используя концепцию «пространства состояний», предложили новый эффективный метод синтеза оптимальных систем по критерию минимума математического ожидания квадрата случайной ошибки, применимый как для стационарных, так и для нестационарных марковских случайных процессов. Так как в основе используемой Калманом и Бьюси концепции «пространства состояний» лежит предположение о том, что случайный процесс является марковским, то их подход к синтезу оптимальных линейных систем иногда называют марковской теорией оптимальной линейной фильтрации.
Описывая все случайные процессы не с помощью корреляционных функций или спектральных плотностей, а с помощью дифференциальных уравнений или уравнений состояния, Калман и Бьюси показали, что при случайных воздействиях оптимальная линейная система (оптимальный фильтр Калмана — Бьюси) должна удовлетворять некоторой системе неоднородных линейных дифференциальных уравнений. Нахождение оптимальной системы по этим дифференциальным уравнениям намного легче, чем по интегральным уравнениям Винера — Хопфа, особенно в случае нестационарных случайных процессов.
Вывод уравнений оптимального фильтра был выполнен Калманом и Бьюси для многомерных случайных процессов. Познакомимся с основной идеей метода Калмана — Бьюси на примере более простых, но часто встречающихся на практике одномерных фильтров.
Допустим, что синтезируемая система должна воспроизводить некоторый сигнал  представляющий собой в общем случае нестационарный случайный процесс. Пусть на входе системы кроме этого сигнала действует также помеха
представляющий собой в общем случае нестационарный случайный процесс. Пусть на входе системы кроме этого сигнала действует также помеха 
представляющая собой в общем случае нестационарный случайный процесс типа «белый шум» с нулевым средним значением. Таким образом, суммарный входной сигнал

Для вывода уравнения одномерного оптимального фильтра Калмана — Бьюси существенным является то, что случайный процесс  должен быть сначала представлен дифференциальным уравнением первого порядка следующего вида:
должен быть сначала представлен дифференциальным уравнением первого порядка следующего вида:

где  — некоторая функция времени, зависящая от статистических характеристик случайного процесса
— некоторая функция времени, зависящая от статистических характеристик случайного процесса  — нестационарный случайный процесс типа «белый шум» с нулевым средним значением.
— нестационарный случайный процесс типа «белый шум» с нулевым средним значением.
Корреляционные функции нестационарных случайных процессов  имеют вид
имеют вид

где  — непрерывные, непрерывно дифференцируемые функции времени, причем
— непрерывные, непрерывно дифференцируемые функции времени, причем

В частном случае для стационарных случайных процессов  их корреляционные функции
их корреляционные функции

где
Если случайный процесс на выходе системы равен  , то случайная ошибка системы
, то случайная ошибка системы  равная разности между воспроизводимым сигналом
равная разности между воспроизводимым сигналом  и выходным сигналом
и выходным сигналом  имеет вид
имеет вид

Калман и Бьюси показали, что оптимальная система (оптимальный фильтр Калмана—Бьюси), обеспечивающая в любой момент времени  воспроизведение сигнала
воспроизведение сигнала  при минимуме математического ожидания квадрата случайной ошибки, должна описываться неоднородным дифференциальным уравнением вида
при минимуме математического ожидания квадрата случайной ошибки, должна описываться неоднородным дифференциальным уравнением вида

Таким образом, при синтезе оптимального фильтра Калмана — Быоси задача сводится к нахождению таких функций времени  в дифференциальном уравнении (9.140), при которых обеспечивался бы минимум математического ожидания квадрата случайной ошибки, т. е.
в дифференциальном уравнении (9.140), при которых обеспечивался бы минимум математического ожидания квадрата случайной ошибки, т. е.

Предполагая, что случайный процесс  представлен в виде (9.135), приведем без доказательства формулы для нахождения функций
представлен в виде (9.135), приведем без доказательства формулы для нахождения функций  при которых обеспечивается минимум (9.141).
при которых обеспечивается минимум (9.141).
Прежде чем определить функции  находят некоторую функцию времени
находят некоторую функцию времени  равную математическому ожиданию квадрата случайной ошибки (дисперсии ошибки):
равную математическому ожиданию квадрата случайной ошибки (дисперсии ошибки):

она определяется как решение следующего дифференциального уравнения Риккати:

Для решения (9.143) нужно знать начальное значение  при
при  Обычно
Обычно  поэтому
поэтому

После нахождения функции  определяют функцию
определяют функцию  по формуле
по формуле

и функцию  по формуле
по формуле

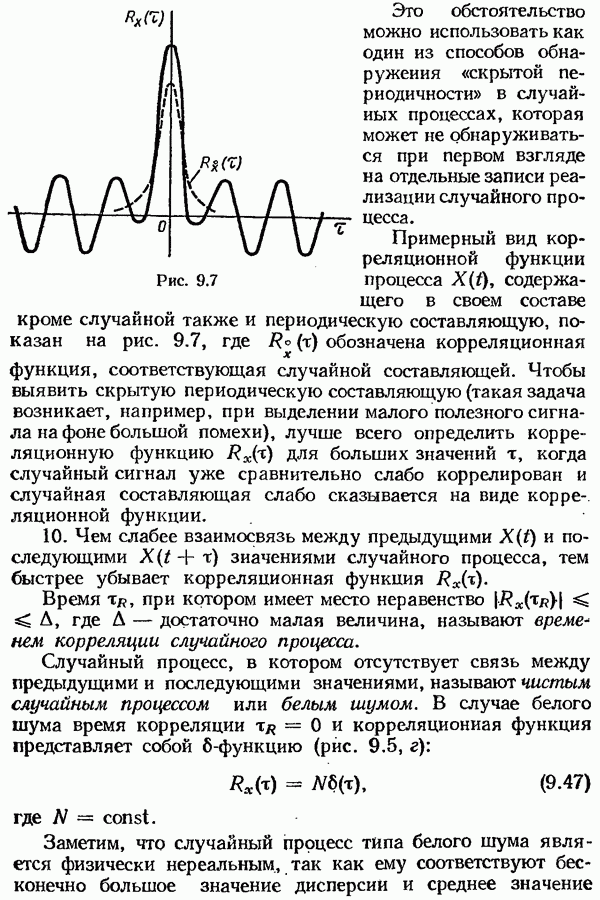
Наиболее сложным этапом синтеза оптимальных фильтров методом Калмана — Бьюси является решение уравнения Риккати (9.143). В общем случае оно требует применения ЭВМ.
Важное самостоятельное значение имеют также вопросы исследования существования решения уравнения (9.143), его единственности и устойчивости.
Учитывая (9.146), уравнение оптимального фильтра Калмана—Бьюси иногда записывают в следующем виде:

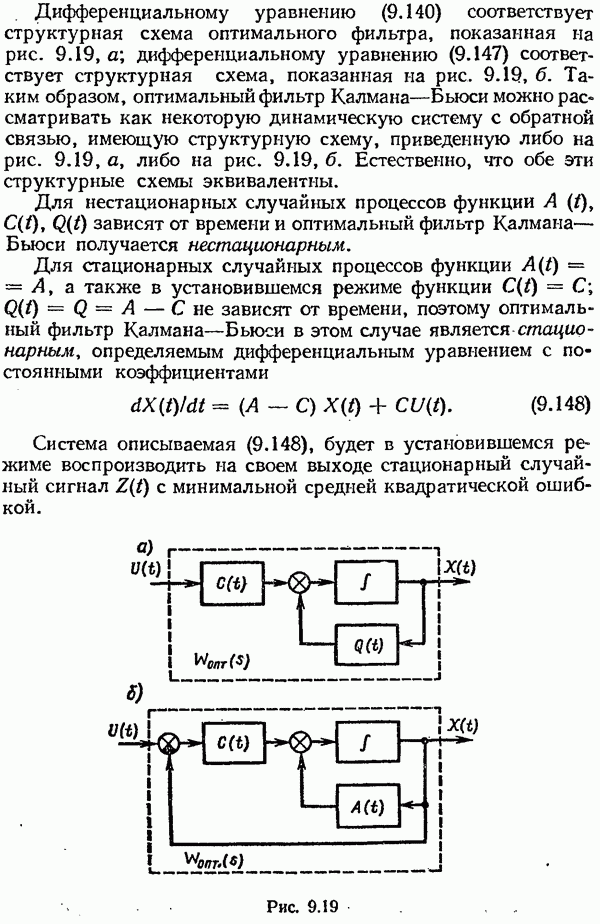
Дифференциальному уравнению (9.140) соответствует структурная схема оптимального фильтра, показанная на рис. 9.19, а; дифференциальному уравнению (9.147) соответствует структурная схема, показанная на рис. 9.19, б. Таким образом, оптимальный фильтр Калмана—Бьюси можно рассматривать как некоторую динамическую систему с обратной связью, имеющую структурную схему, приведенную либо на рис. 9.19, а, либо на рис. 9.19, б. Естественно, что обе эти структурные схемы эквивалентны.
Для нестационарных случайных процессов функции  зависят от времени и оптимальный фильтр Калмана—Бьюси получается нестационарным.
зависят от времени и оптимальный фильтр Калмана—Бьюси получается нестационарным.
Для стационарных случайных процессов функции  а также в установившемся режиме функции
а также в установившемся режиме функции  не зависят от времени, поэтому оптимальный фильтр Калмана—Бьюси в этом случае является стационарным, определяемым дифференциальным уравнением с постоянными коэффициентами
не зависят от времени, поэтому оптимальный фильтр Калмана—Бьюси в этом случае является стационарным, определяемым дифференциальным уравнением с постоянными коэффициентами

Система описываемая (9.148), будет в установившемся режиме воспроизводить на своем выходе стационарный случайный сигнал  с минимальной средней квадратической ошибкой.
с минимальной средней квадратической ошибкой.

Рис. 9.19

Рис. 9.20
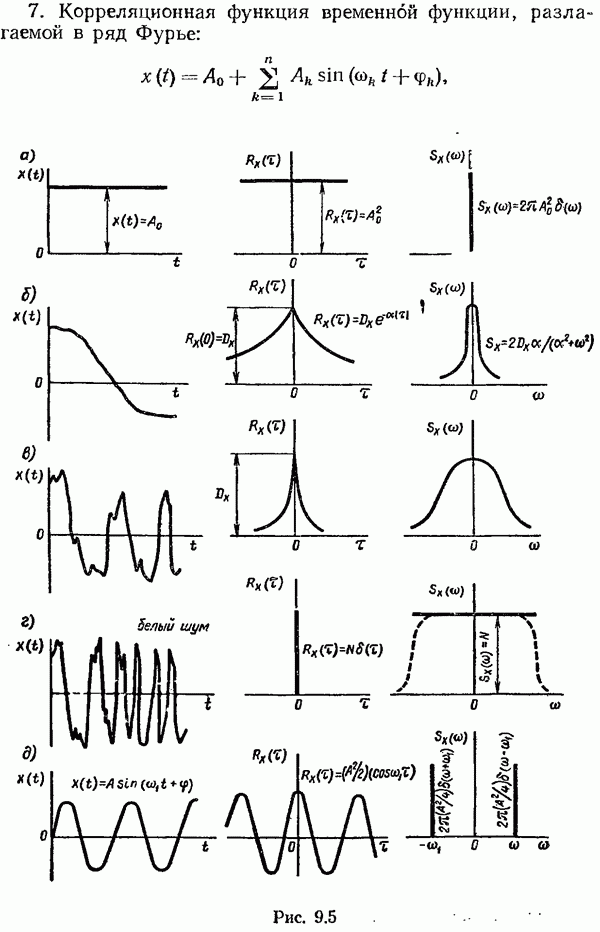
Естественно, что для стационарных процессов результаты, полученные методом Калмана—Бьюси и методом Винера, совпадают. Уравнение (9.148), полученное во временной области, эквивалентно оптимальному фильтру Винера, определяемому в частотной области уравнением (9.125).
Остановимся кратко на очень существенном для фильтров Калмана—Бьюси вопросе о возможности представления случайного процесса  в виде дифференциального уравнения (9,135).
в виде дифференциального уравнения (9,135).
Нахождение (9.135) связано с задачей определения формирующего фильтра (стационарного или нестационарного), который при воздействии на его вход белого шума  позволяет получить на своем выходе заданный случайный процесс
позволяет получить на своем выходе заданный случайный процесс  Структурную схему такого формирующего фильтра в соответствии с (9.135) можно представить так, как показано на рис. 9.20.
Структурную схему такого формирующего фильтра в соответствии с (9.135) можно представить так, как показано на рис. 9.20.
Для стационарных случайных процессов методы определения параметров формирующих фильтров разработаны хорошо. В этих случаях формирующий фильтр можно описать обыкновенным дифференциальным уравнением с постоянными коэффициентами или соответствующей передаточной функцией формирующего фильтра  . Особенно просто находится передаточная функция формирующего фильтра в том случае, когда выражение для спектральной плотности
. Особенно просто находится передаточная функция формирующего фильтра в том случае, когда выражение для спектральной плотности  стационарного случайного процесса
стационарного случайного процесса  имеет вид дробно-рациональной функции частоты, т. е. когда выражение для спектральной плотности может быть представлено в виде произведения двух комплексно-сопряженных множителей:
имеет вид дробно-рациональной функции частоты, т. е. когда выражение для спектральной плотности может быть представлено в виде произведения двух комплексно-сопряженных множителей:

Пусть на входе формирующего фильтра действует стационарный случайный сигнал  типа «белый шум», имеющий спектральную плотность
типа «белый шум», имеющий спектральную плотность  тогда спектральная плотность сигнала на выходе формирующего фильтра
тогда спектральная плотность сигнала на выходе формирующего фильтра

Учитывая (9.149), можно записать

откуда частотная передаточная функция формирующего фильтра

Подставляя в последнее выражение  получаем выражение для передаточной функции формирующего фильтра
получаем выражение для передаточной функции формирующего фильтра

Зная передаточную функцию формирующего фильтра, находим дифференциальное уравнение вида (9.135), связывающее случайные процессы 
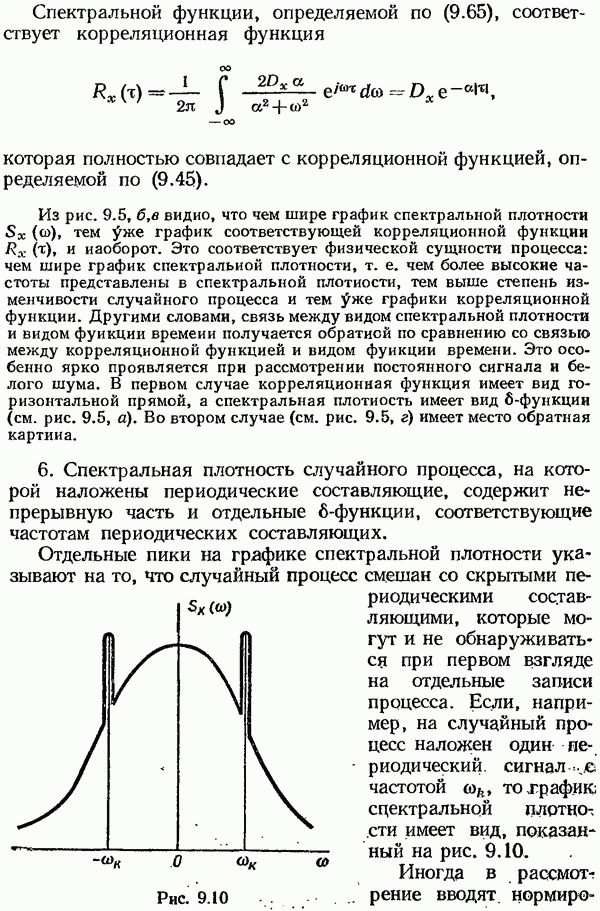
Если спектральная плотность  не является дробнорациональной функцией частоты или получена экспериментально, то для нахождения формирующего фильтра ее нужно сначала аппроксимировать дробно-рациональной функцией частоты.
не является дробнорациональной функцией частоты или получена экспериментально, то для нахождения формирующего фильтра ее нужно сначала аппроксимировать дробно-рациональной функцией частоты.
В заключение следует отметить, что если входные воздействия являются стационарными случайными процессами, то метод Калмана—Бьюси не имеет преимуществ перед методом синтеза оптимальных фильтров Винера. Этот метод в основном применяют для синтеза оптимальных нестационарных линейных фильтров.
Он позволяет также достаточно просто находить структуру и параметры оптимального фильтра и в том случае, когда воспроизводимый сигнал  описывается полиномом со случайными коэффициентами:
описывается полиномом со случайными коэффициентами:

где  — случайные величины с известными статистическими характеристиками.
— случайные величины с известными статистическими характеристиками.
Синтез оптимальных линейных фильтров Калмана—Бьюси, проведенный первоначально для помехи в виде белого шума, был в дальнейшем развит на более общие случаи, например на случай коррелированных помех, имеющих неравномерную спектральную плотность, на случай нелинейной фильтрации и др. Заметим, наконец, что оптимальные фильтры Калмана—Бьюси, как и оптимальные фильтры Винера, позволяют решать не только задачу оптимального воспроизведения
сигнала на фоне помех (фильтрации), но и задачи статистического упреждения, статистического дифференцирования и т. д.
Пример 9.8. На входе линейной следящей системы действует стационарный случайный процесс  спектральная плотность которого
спектральная плотность которого

и случайная помеха  типа «белый шум», имеющая спектральную плотность
типа «белый шум», имеющая спектральную плотность

Числовые значения коэффициентов

Определить методом Калмана—Бьюси оптимальную передаточную функцию системы, обеспечивающую минимум средней квадратической ошибки.
1. Так как система предназначена для воспроизведения полезного сигнала  то преобразующий оператор
то преобразующий оператор  воспроизводимый сигнал
воспроизводимый сигнал  , следовательно,
, следовательно, 
В соответствии с (9.149) представляем выражение для спектральной плотности  в виде произведения комплексно-сопряженных сомножителей
в виде произведения комплексно-сопряженных сомножителей

и находим

2. Рассматривая заданный стационарный случайный процесс  как реакцию некоторого формирующего фильтра на стационарный случайный процесс
как реакцию некоторого формирующего фильтра на стационарный случайный процесс  типа «белый шум», имеющий спектральную плотность
типа «белый шум», имеющий спектральную плотность  находим частотную передаточную функцию этого формирующего фильтра по (9.150):
находим частотную передаточную функцию этого формирующего фильтра по (9.150):

3. Находим передаточную функцию формирующего фильтра:

4. Полученной передфаточной функции формирующего фильтра соответствует следующее дифференциальное уравнение, связывающее случайные процессы 

Чтобы привести последнее дифференциальное уравнение к виду (9.135), примем, что спектральная плотность белого шума равна  тогда
тогда  и окончательно случайный процесс
и окончательно случайный процесс  можно представить как
можно представить как

где 
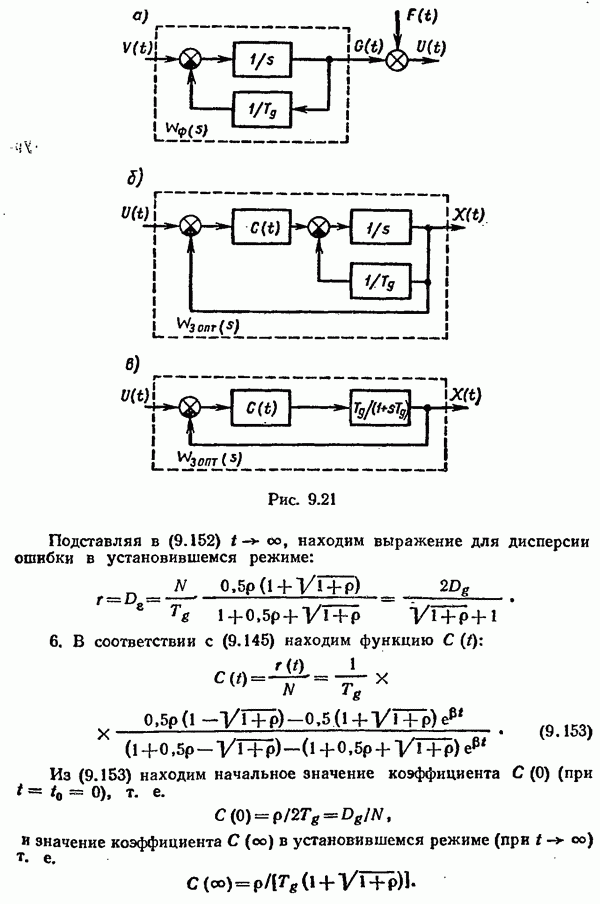
Соответствующая этому дифференциальному уравнению структурная схема формирующего фильтра показана на рис. 9.21, а.
5. Уравнение (9.143) в данном случае имеет вид

При постоянных значениях коэффициентов  это дифференциальное уравнение является уравнением с разделяющимися переменными и приводится к следующему виду:
это дифференциальное уравнение является уравнением с разделяющимися переменными и приводится к следующему виду:

Интегрируя по общим правилам, получаем

где  — постоянная интегрирования.
— постоянная интегрирования.
Последнее выражение можно переписать следующим образом:

Новую постоянную интегрирования С находят из начальных условий при  . В соответствии с (9.144), начальное значение дисперсии ошибки
. В соответствии с (9.144), начальное значение дисперсии ошибки  поэтому постоянная интегрирования получается равной
поэтому постоянная интегрирования получается равной

Таким образом, можно записать

Учитывая, что  и производя соответствующие преобразования, окончательно получаем
и производя соответствующие преобразования, окончательно получаем

где  — отношение спектральных плотностей воспро» изводимого сигнала и помехи, на нулевой частоте.
— отношение спектральных плотностей воспро» изводимого сигнала и помехи, на нулевой частоте.

Рис. 9.21
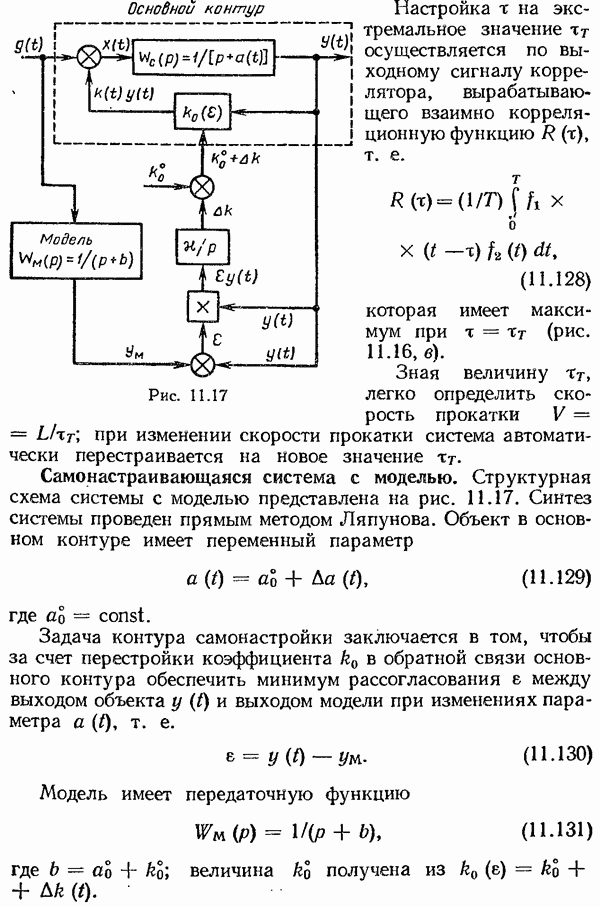
Подставляя в (9.152)  , находим выражение для дисперсии ошибки в установившемся режиме:
, находим выражение для дисперсии ошибки в установившемся режиме:

6. В соответствии с (9.145) находим функцию 

Из (9.153) находим начальное значение коэффициента С (0) (при  т. е.
т. е.

в значение коэффициента  в установившемся режиме (при
в установившемся режиме (при  т. е.
т. е.

7. Дифференциальное уравнение оптимального фильтра Калмана—Бьюси в соответствии с (9.147) имеет вид

Структурная схема, соответствующая этому дифференциальному уравнению, приведена на рис. 9.21, б. Заменяя интегрирующее звено, охваченное обратной связью, инерционным звеном, можно представить структурную схему так, как показано на рис. 9.21, в. Используя эту структурную схему и значения передаточных функций отдельных ее динамических звеньев, определяем для установившегося режима передаточную функцию замкнутой оптимальной системы:

где

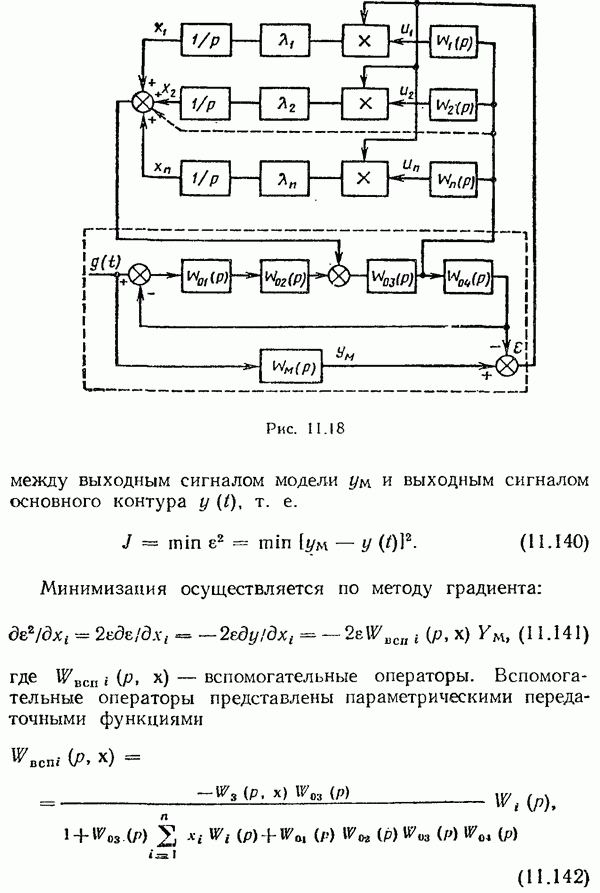
Полученное выражение для передаточной функции оптимального фильтра Калмана—Бьюси полностью совпадают с выражением для передаточной функции фильтра Винера, найденного в примерах 9.6 и 9.7.
Следует обратить внимание на то, что даже при стационарных случайных воздействиях в переходном режиме оптимальный фильтр Калмана—Бьюси является нестационарным, поскольку коэффициент  изменяется во времени.
изменяется во времени.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
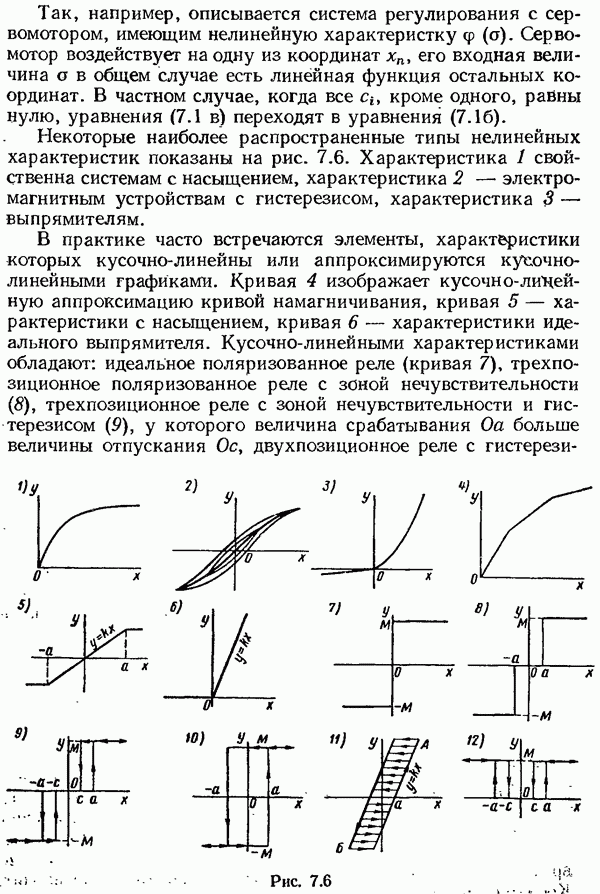
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
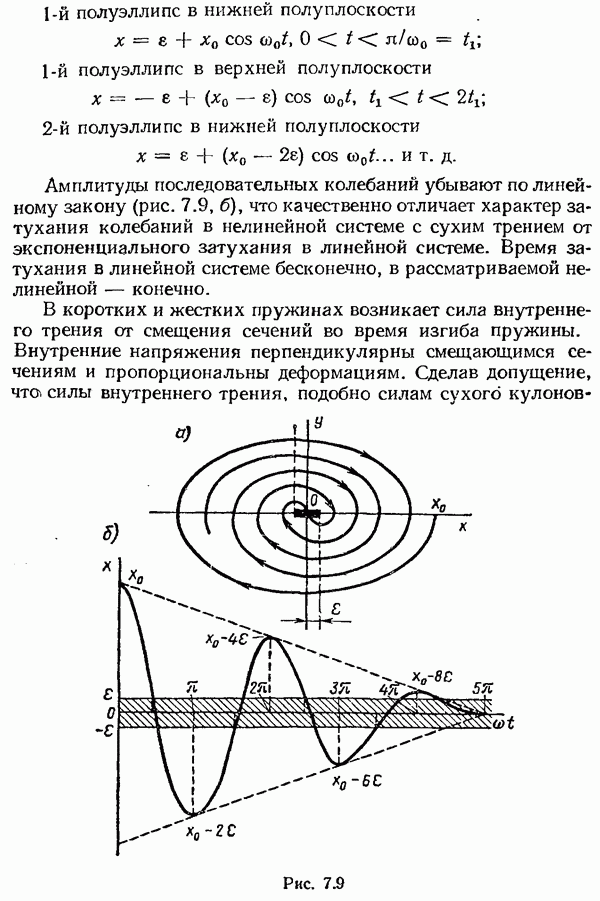
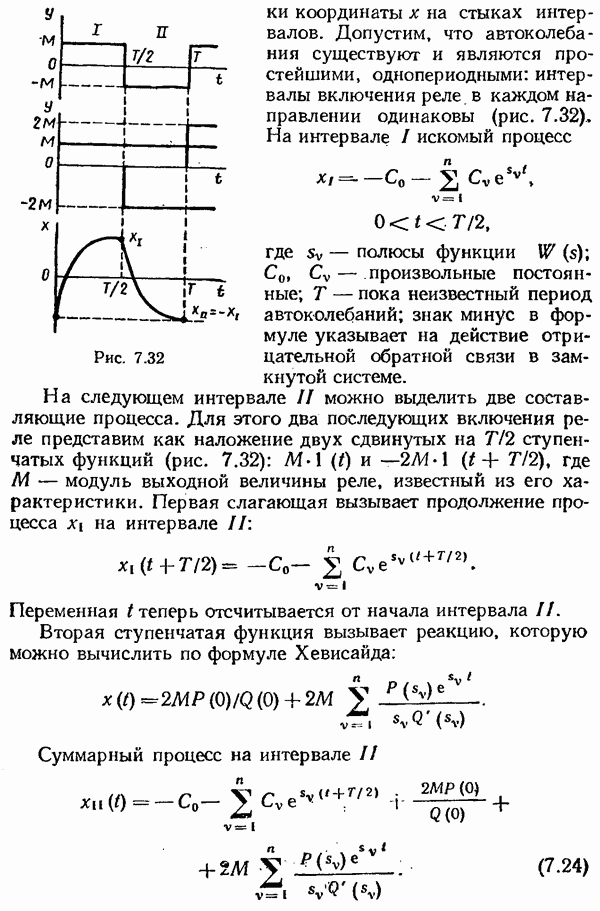
- § 7.3. Автоколебания. Метод точечных преобразований
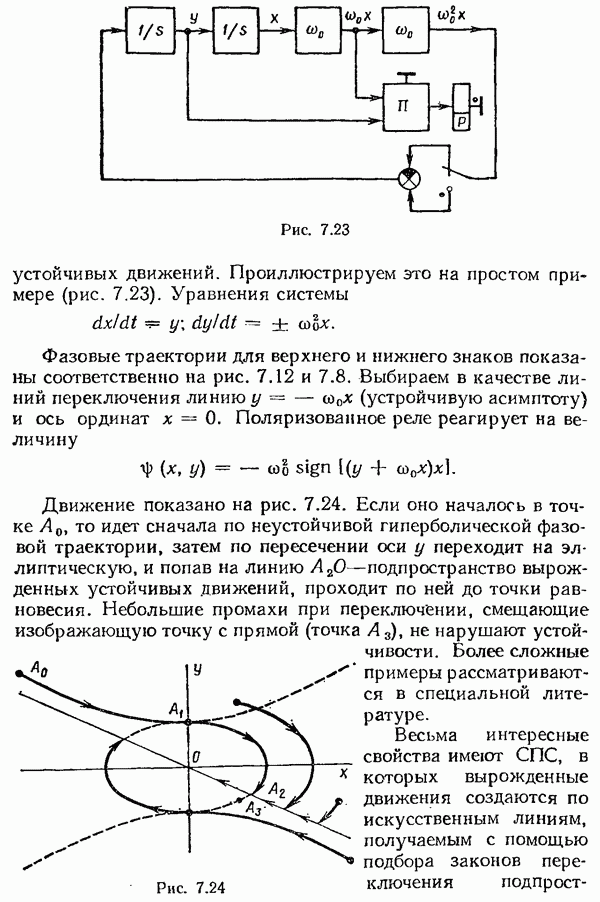
- § 7.4. Системы с переменной структурой
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
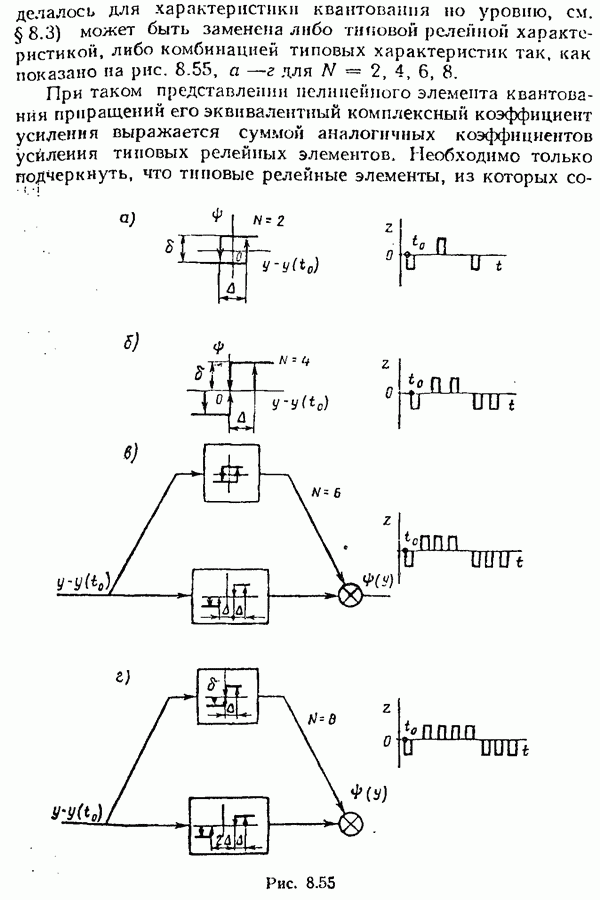
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
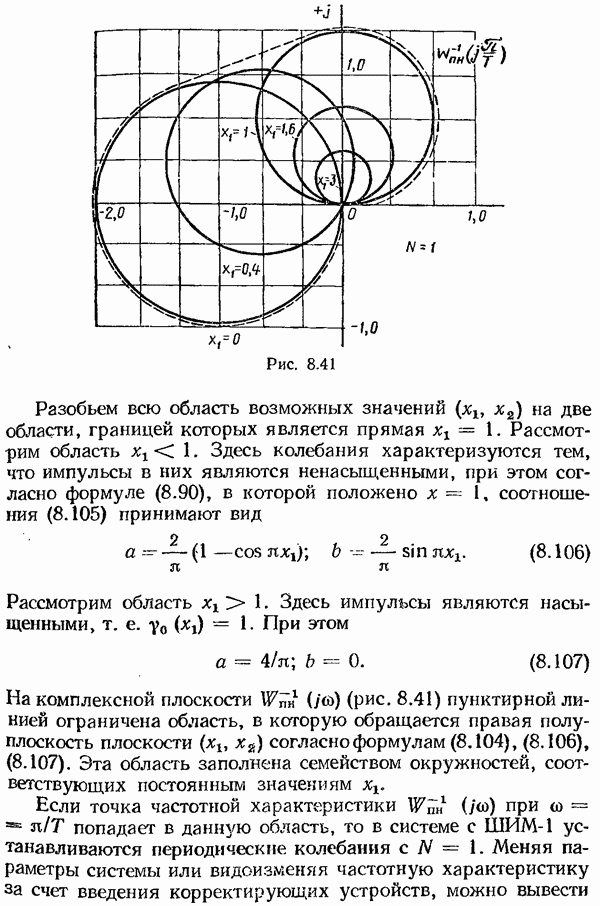
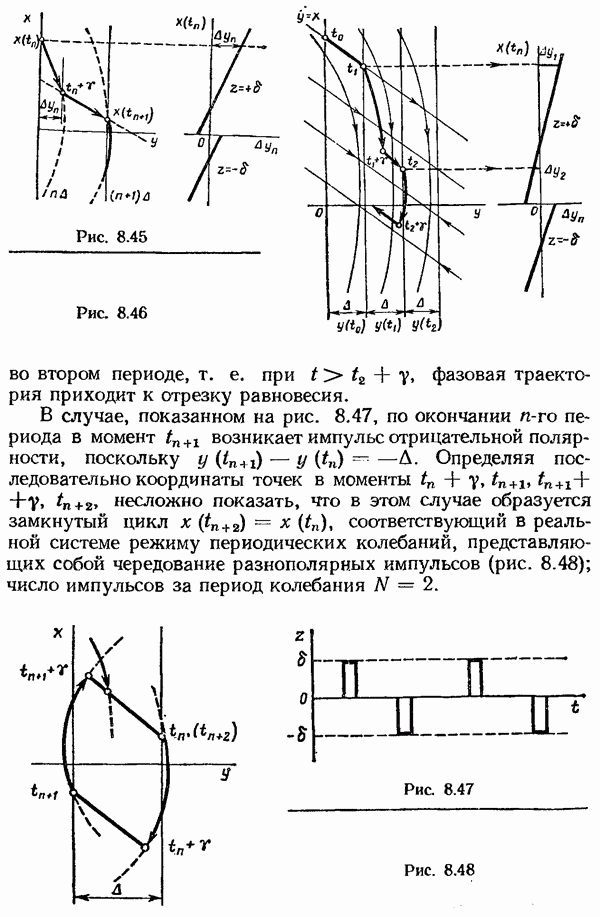
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
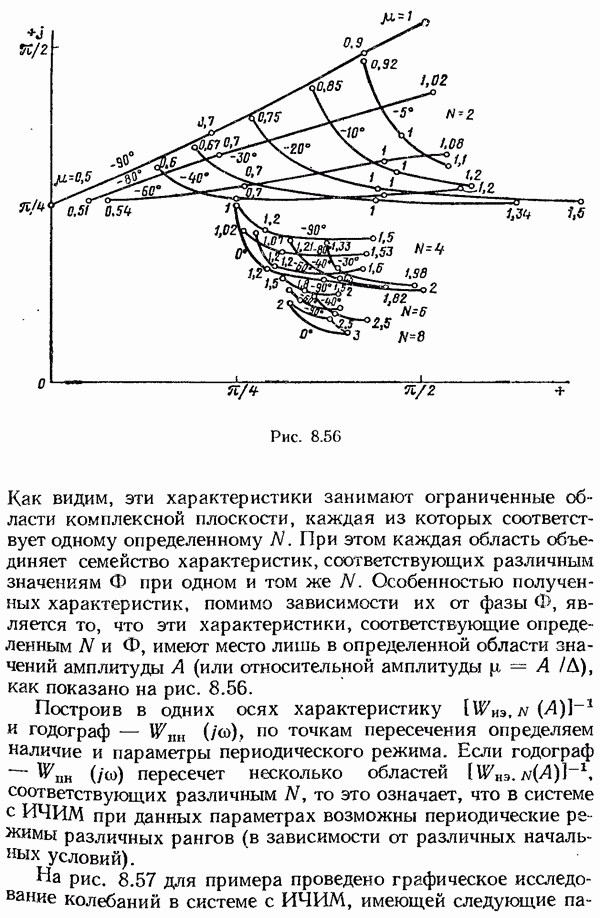
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
- Исследование периодических режимов в системах с ИЧИМ.
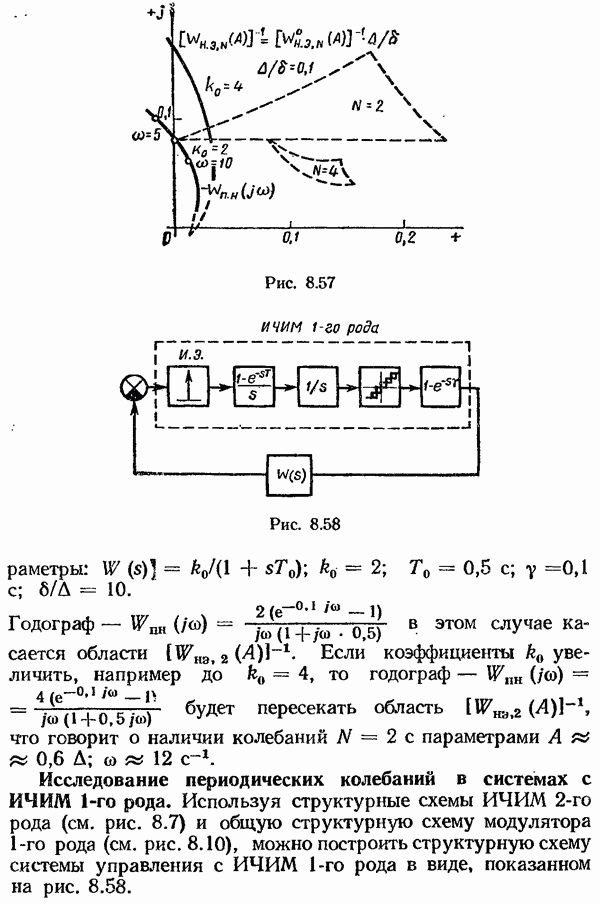
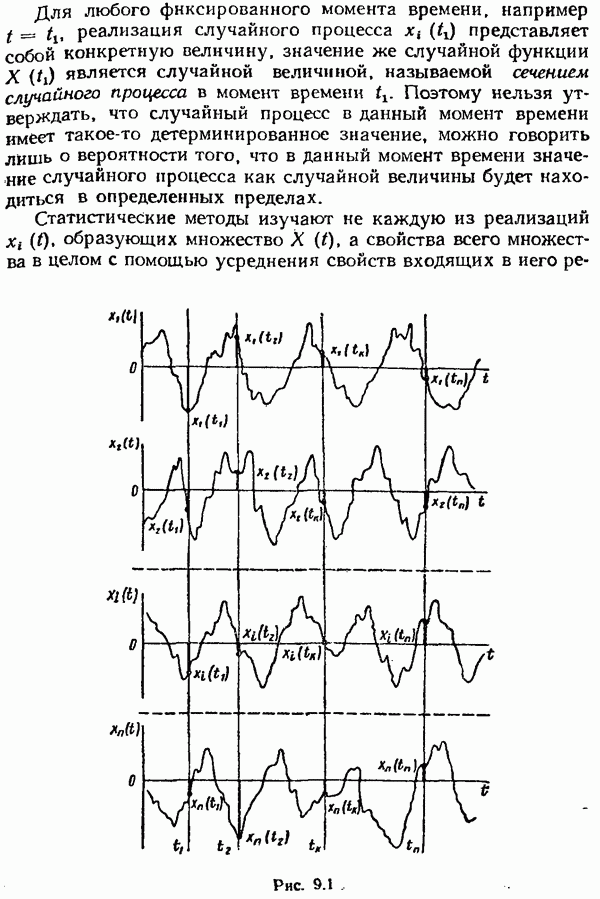
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
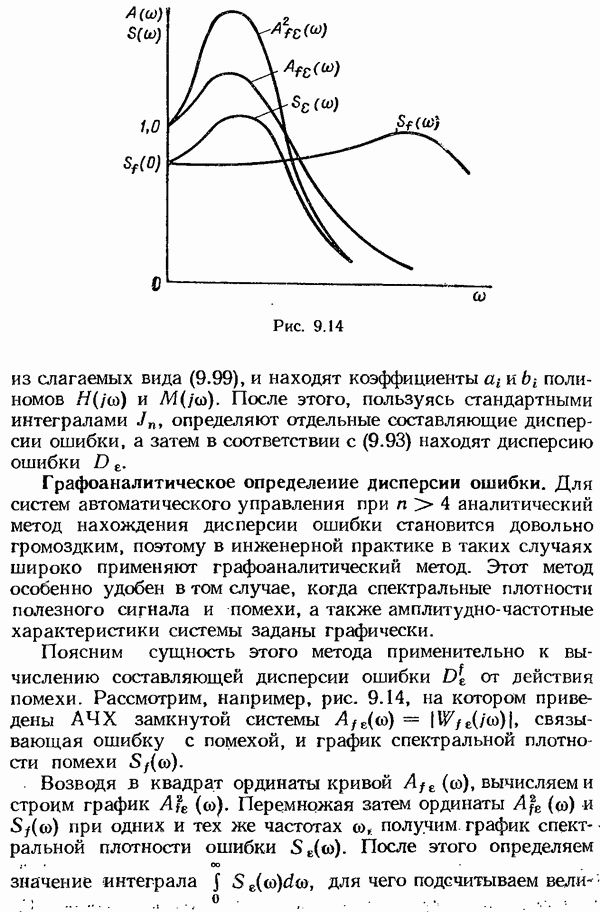
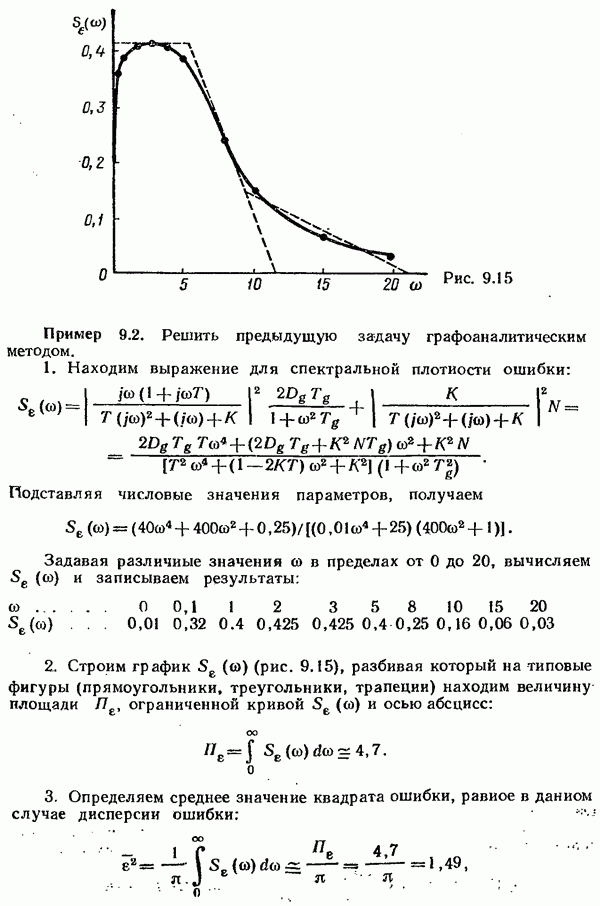
- Графоаналитическое определение дисперсии ошибки.
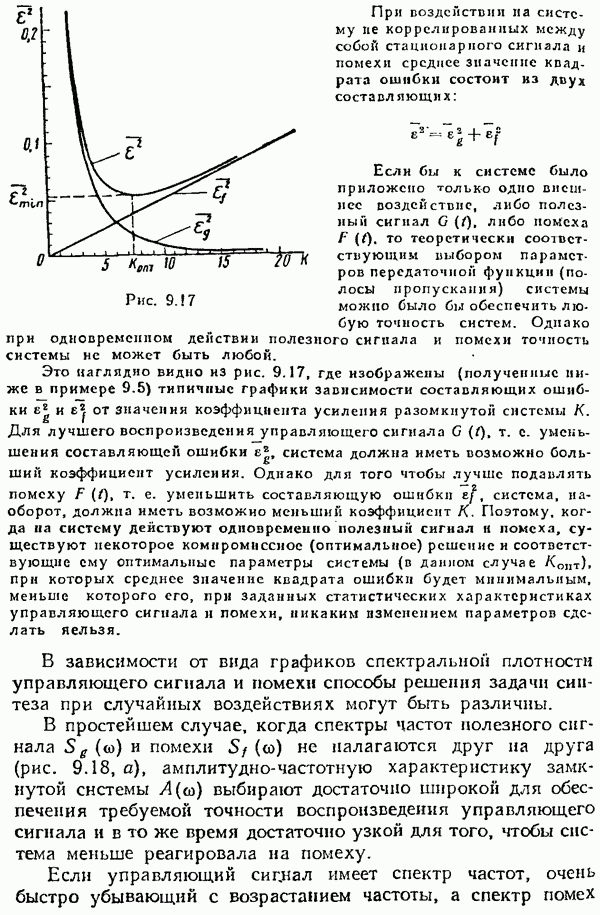
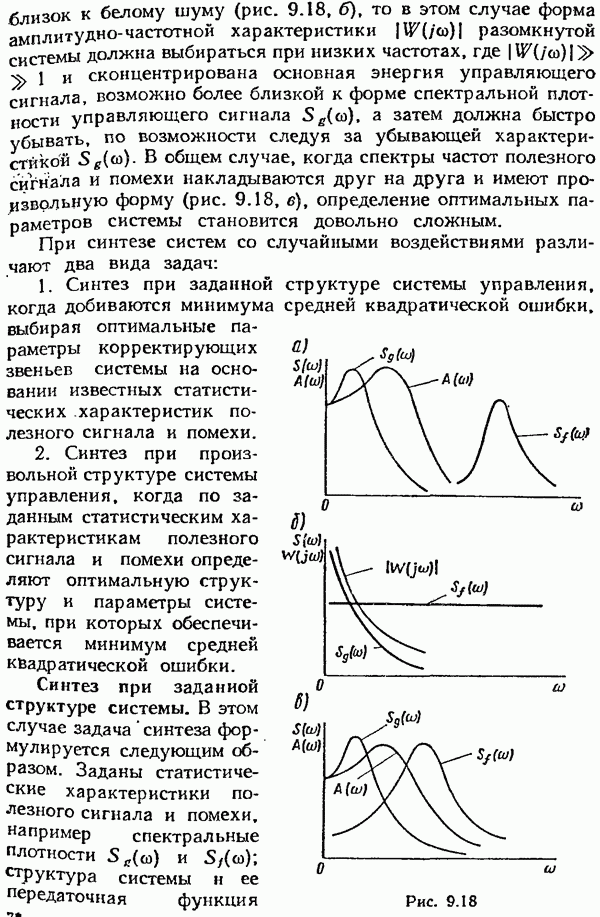
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
- § 9.9. Нелинейное преобразование случайных сигналов
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
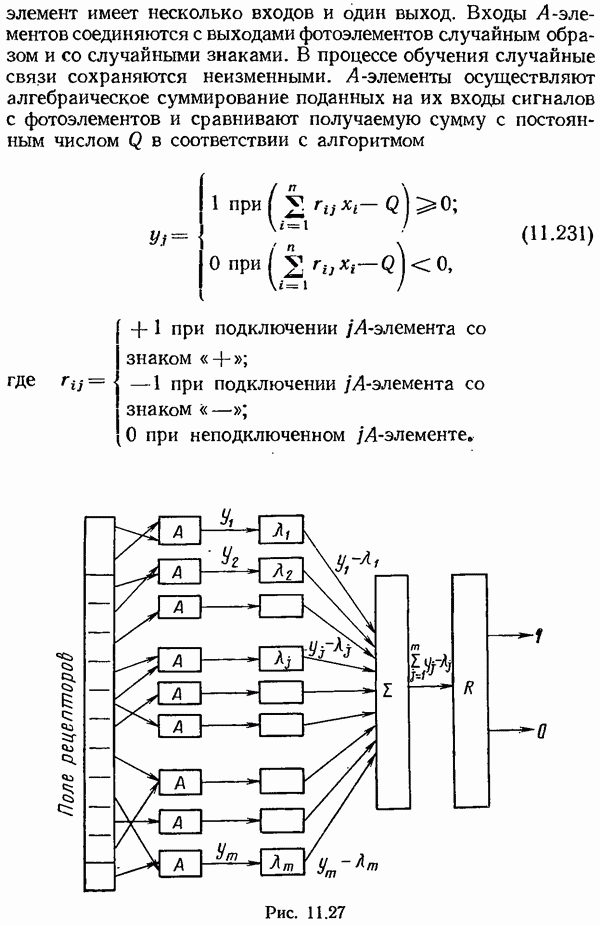
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
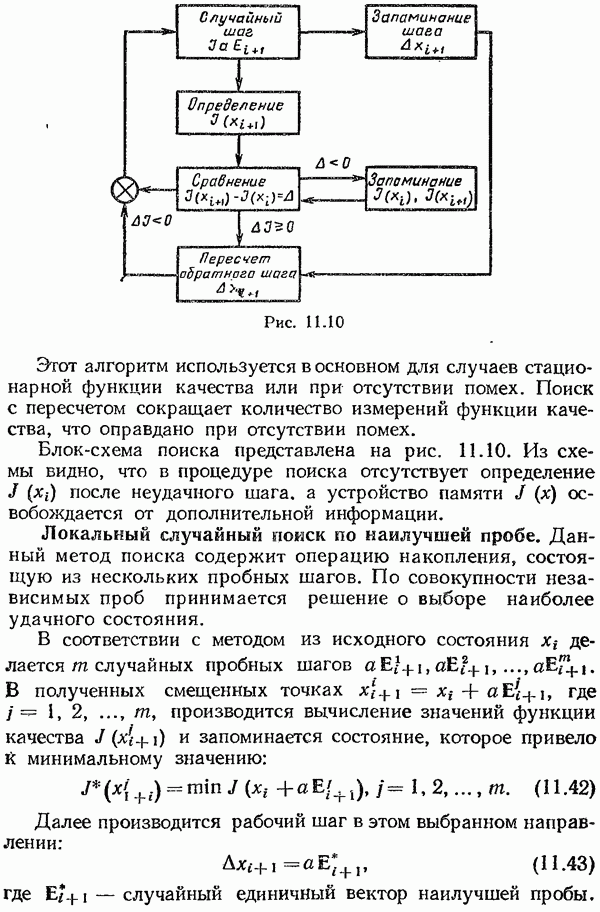
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
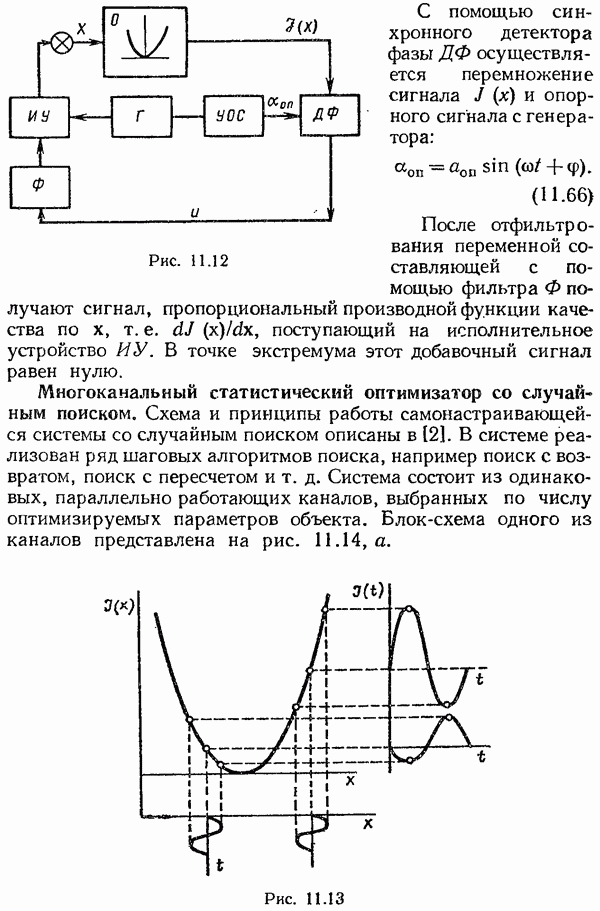
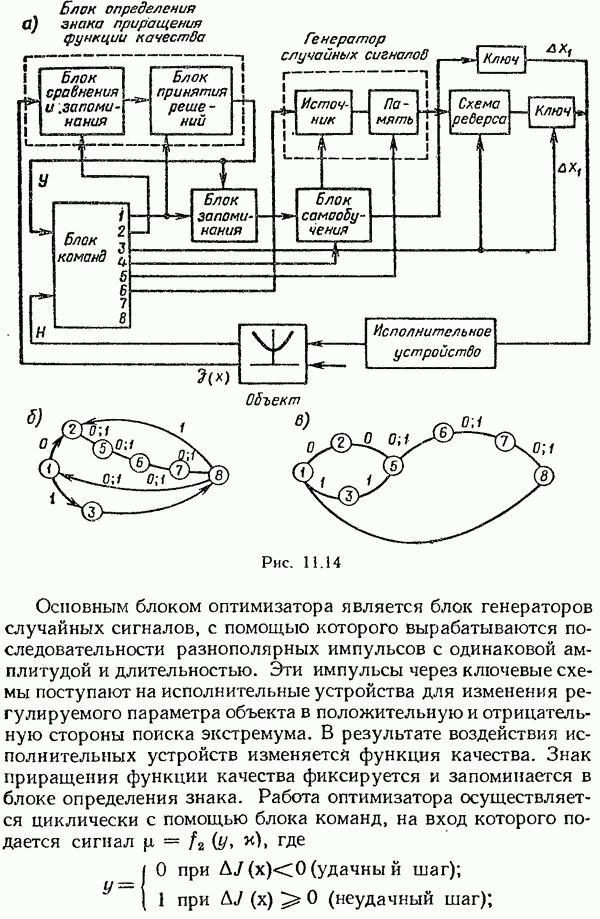
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
- Самонастраивающаяся система с моделью.
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
- Персептронная модель автоматической классификации.
- § 11.6. Адаптивные робототехнические системы
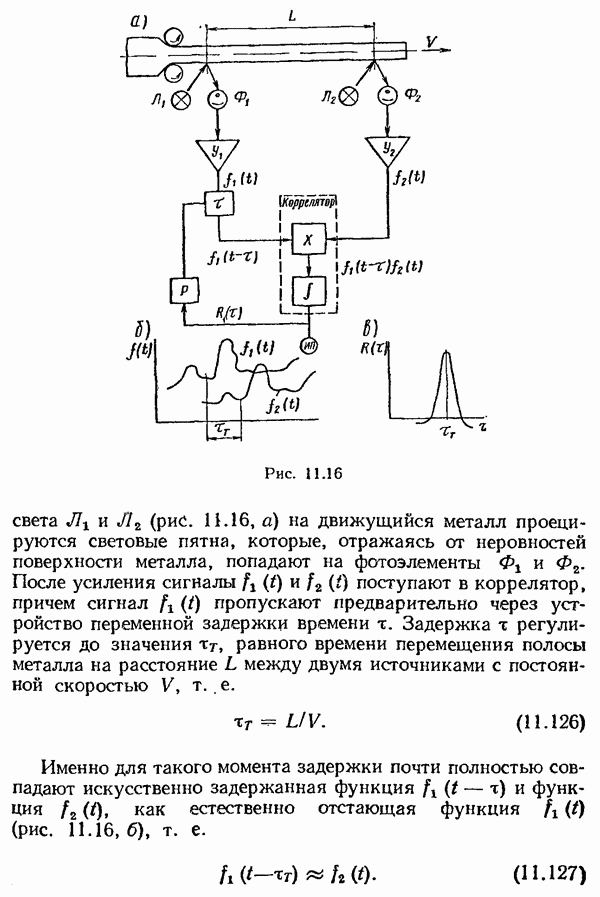
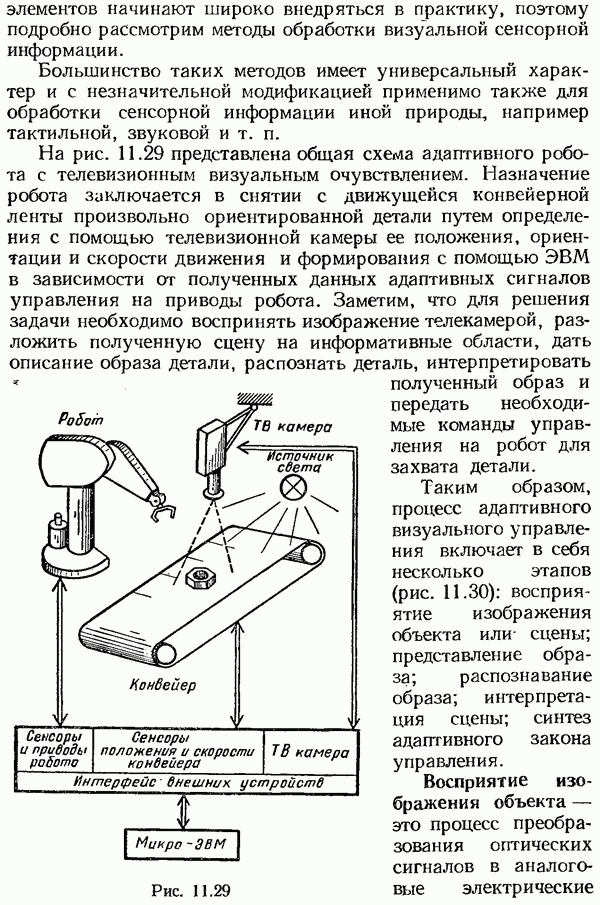
- Методы обработки сенсорной информации для адаптивного управления роботами.
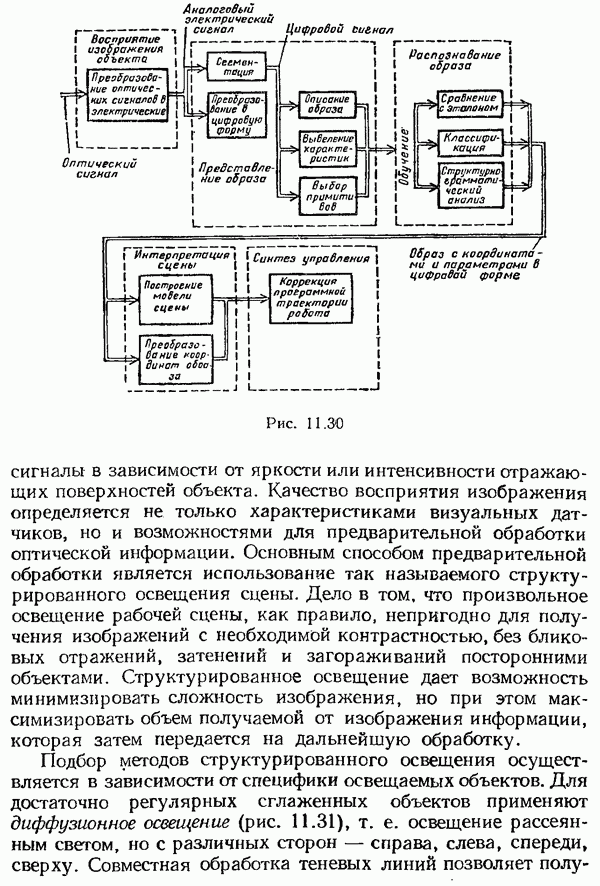
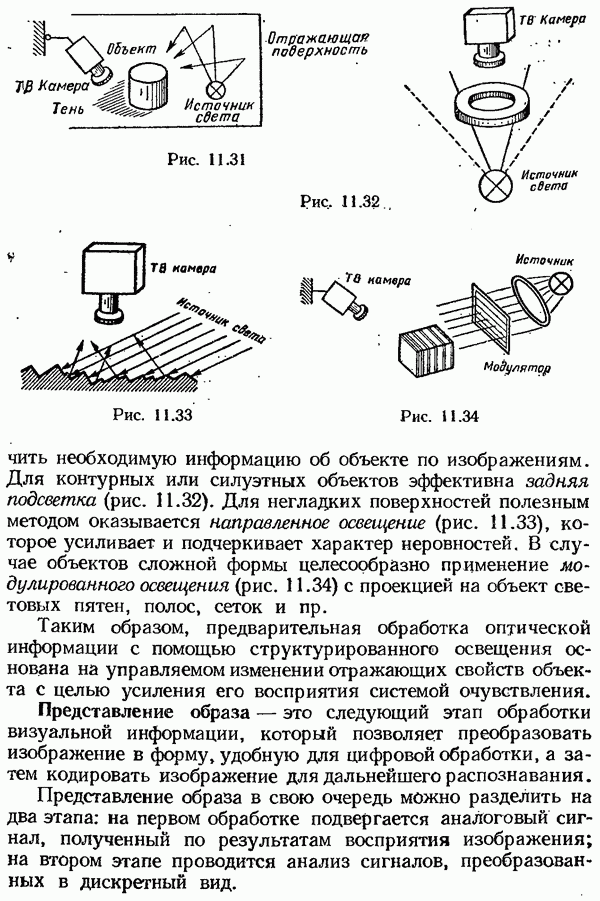
- Восприятие изображения объекта
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ