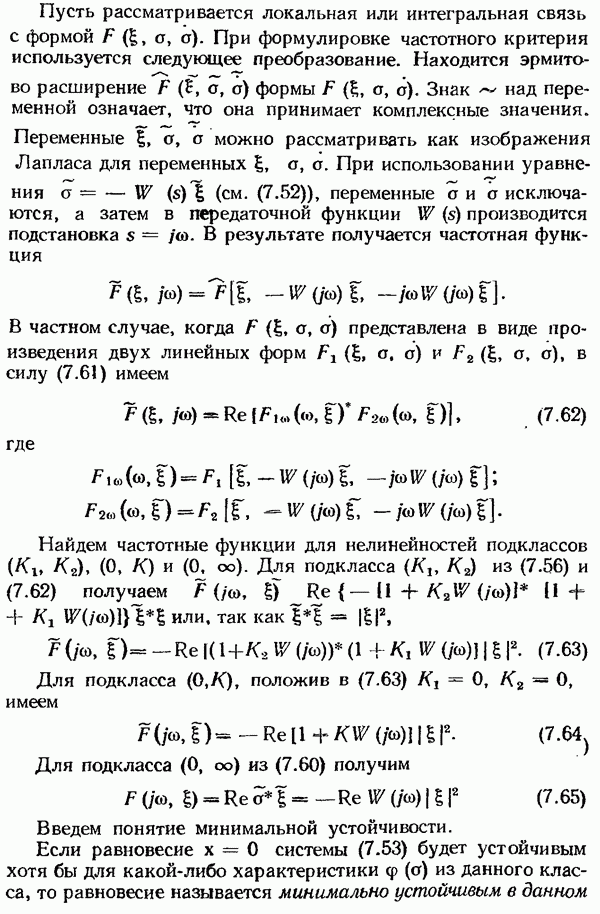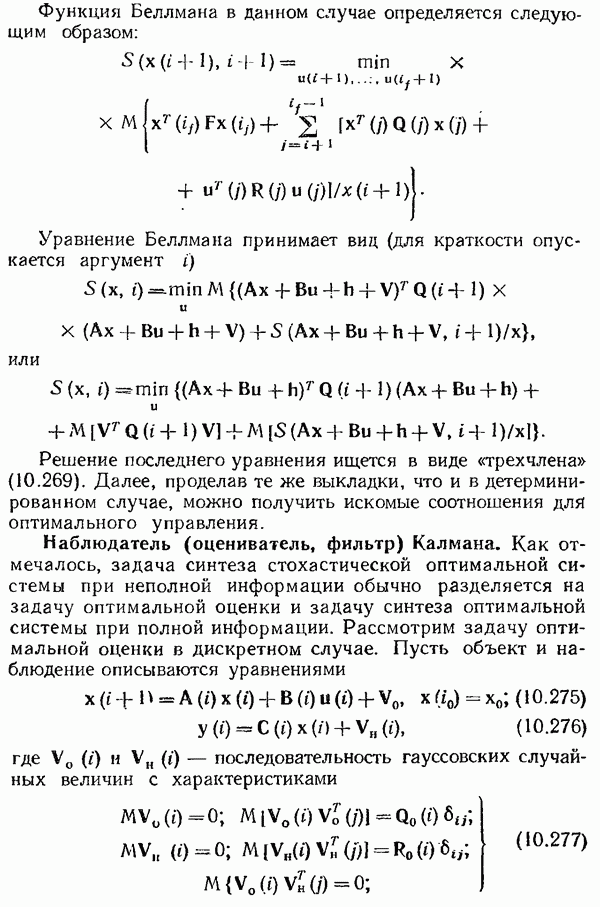| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
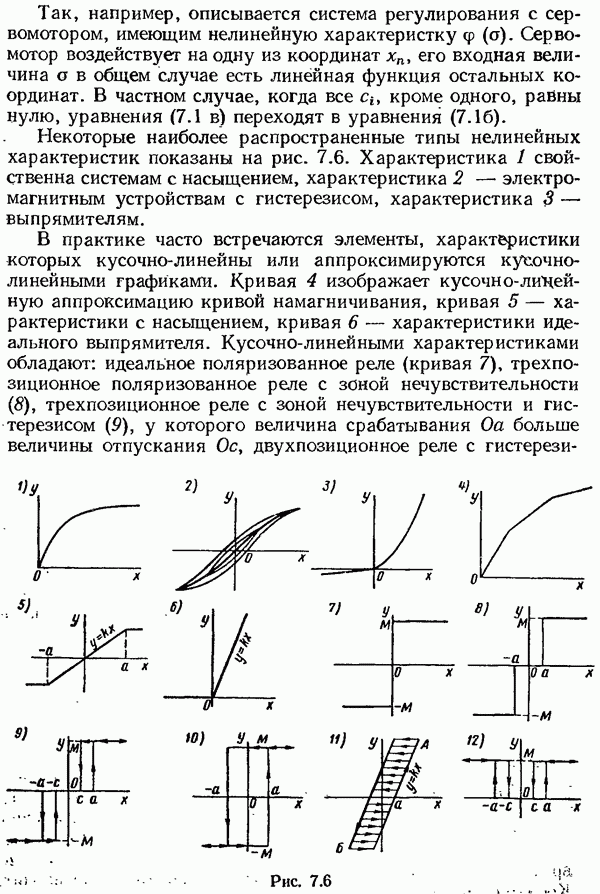
§ 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
Рассмотрим систему автоматического управления с пере даточной функцией  служащую для усиления и преобразования управляющего полезного сигнала
служащую для усиления и преобразования управляющего полезного сигнала  при наличии случайной помехи
при наличии случайной помехи  Это преобразование в общем случае производится в соответствии с некоторым заданным оператором (алгоритмом преобразования)
Это преобразование в общем случае производится в соответствии с некоторым заданным оператором (алгоритмом преобразования)  (рис. 9.16).
(рис. 9.16).
В общем случае система должна возможно более точно воспроизводить на своем выходе не само управляющее воздействие  а некоторую функцию от управляющего воздействия
а некоторую функцию от управляющего воздействия

В системах, находящихся под воздействием случайного (или регулярного) полезного сигнала и случайной помехи, возникает задача отделения полезного сигнала от помехи и подавления (фильтрации) последней. Эту задачу называют задачей фильтрации или сглаживания.
Введение преобразующего оператора  обобщает задачу не только на обычные следящие системы, у которых
обобщает задачу не только на обычные следящие системы, у которых  т. е.
т. е.  но и на другие классы систем, выполняющие различные преобразования управляющего сигнала.
но и на другие классы систем, выполняющие различные преобразования управляющего сигнала.

Рис. 9.16
В зависимости от вида оператора  задача фильтрации сочетается с задачей воспроизведения
задача фильтрации сочетается с задачей воспроизведения  упреждения (предсказания), или экстраполяции
упреждения (предсказания), или экстраполяции  интегрирования
интегрирования  дифференцирования
дифференцирования  и др. В общем случае преобразующий оператор
и др. В общем случае преобразующий оператор  может быть произвольным. Идеальное преобразование полезного сигнала в соответствии с (9.107) невозможно из-за динамических ошибок системы, а также из-за наличия возмущающих воздействий (помех). Поэтому выходной сигнал (регулируемая величина)
может быть произвольным. Идеальное преобразование полезного сигнала в соответствии с (9.107) невозможно из-за динамических ошибок системы, а также из-за наличия возмущающих воздействий (помех). Поэтому выходной сигнал (регулируемая величина)  будет отличаться от воспроизводимого сигнала
будет отличаться от воспроизводимого сигнала  Разность
Разность

называют случайной ошибкой системы.
Синтез систем при случайных воздействиях заключается в определении динамических характеристик системы, наилучшим образом обеспечивающих выполнение некоторого статистического критерия оптимальности. Существуют различные статистические критерии оптимальности. Однако наиболее часто за статистический критерий оптимальности принимают критерий минимума средней квадратической ошибки [см. (9.95)]:

где  — любая реализация случайной ошибки.
— любая реализация случайной ошибки.
В этом случае задача синтеза состоит в том, чтобы найти такую физически реализуемую оптимальную передаточную функцию замкнутой системы  при которой было бы минимальным среднее значение квадрата ошибки:
при которой было бы минимальным среднее значение квадрата ошибки:

Согласно критерию средней квадратической ошибки оценка точности системы производится в зависимости от среднего, а не мгновенного значения ошибки, что не всегда является достаточным, например тогда, когда требуется, чтобы ошибка не выходила за заданные пределы. Применение этого критерия может оказаться нерациональным и в тех случаях, когда требования к величине ошибки в разные моменты времени неодинаковы.
Однако несмотря на то, что этот критерий, впрочем, как и всякий другой косвенный критерий, не является универсальным, он благодаря своей  простоте получил широкое практическое применение.
простоте получил широкое практическое применение.

Рис. 9.17
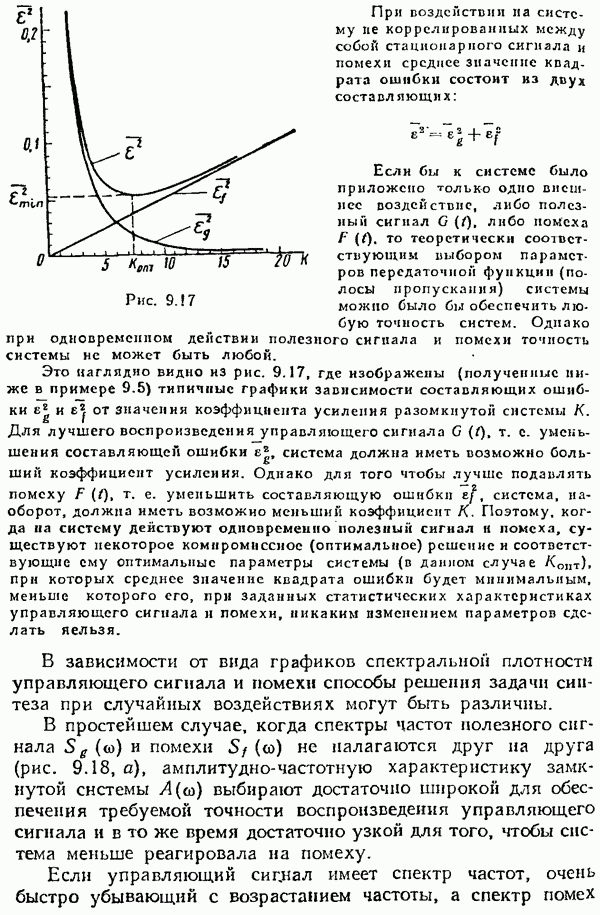
При воздействии на систему не коррелированных между собой стационарного сигнала и помехи среднее значение квадрата ошибки состоит из двух составляющих:

Если бы к системе было приложено только одно внешнее воздействие, либо полезный сигнал  либо помеха
либо помеха  , то теоретически соответствующим выбором параметров передаточной функции (полосы пропускания) системы можно было бы обеспечить любую точность систем. Однако при одновременном действии полезного сигнала и помехи точность системы не может быть любой.
, то теоретически соответствующим выбором параметров передаточной функции (полосы пропускания) системы можно было бы обеспечить любую точность систем. Однако при одновременном действии полезного сигнала и помехи точность системы не может быть любой.
Это наглядно видно из рис. 9.17, где изображены (полученные ниже в примере 9.5) типичные графики зависимости составляющих ошибки и от значения коэффициента усиления разомкнутой системы К. Для лучшего воспроизведения управляющего сигнала  , т. е. уменьшения составляющей ошибки
, т. е. уменьшения составляющей ошибки  система должна иметь возможно больший коэффициент усиления. Однако для того чтобы лучше подавлять помеху
система должна иметь возможно больший коэффициент усиления. Однако для того чтобы лучше подавлять помеху  , т. е. уменьшить составляющую ошибки
, т. е. уменьшить составляющую ошибки  система, наоборот, должна иметь возможно меньший коэффициент К. Поэтому, когда на систему действуют одновременно полезный сигнал и помеха, существуют некоторое компромиссное (оптимальное) решение и соответствующие ему оптимальные параметры системы (в данном случае
система, наоборот, должна иметь возможно меньший коэффициент К. Поэтому, когда на систему действуют одновременно полезный сигнал и помеха, существуют некоторое компромиссное (оптимальное) решение и соответствующие ему оптимальные параметры системы (в данном случае  при которых среднее значение квадрата ошибки будет минимальным, меньше которого его, при заданных статистических характеристиках управляющего сигнала и помехи, никаким изменением параметров сделать нельзя.
при которых среднее значение квадрата ошибки будет минимальным, меньше которого его, при заданных статистических характеристиках управляющего сигнала и помехи, никаким изменением параметров сделать нельзя.
В зависимости от вида графиков спектральной плотности управляющего сигнала и помехи способы решения задачи синтеза при случайных воздействиях могут быть различны.
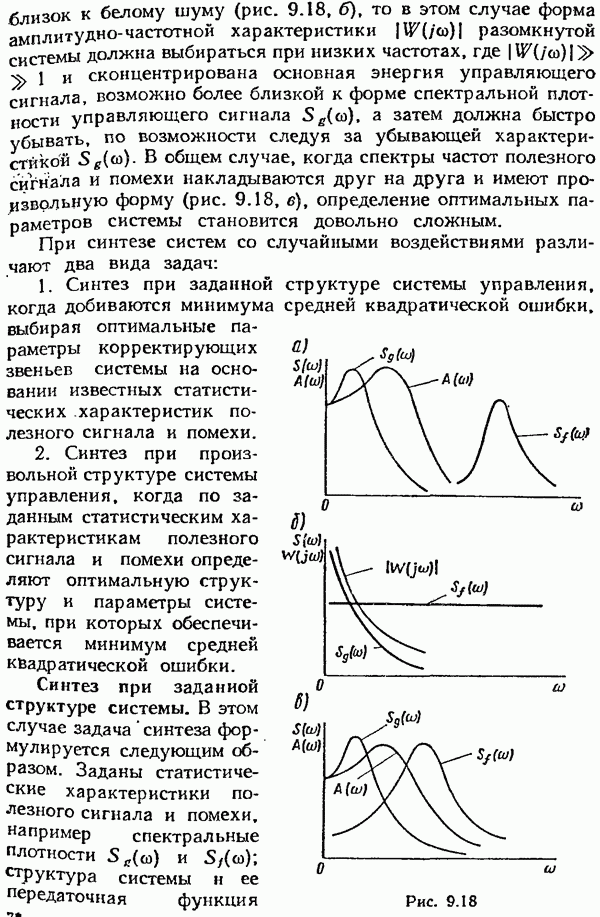
В простейшем случае, когда спектры частот полезного сигнала  и помехи
и помехи  не налагаются друг на друга (рис. 9.18, а), амплитудно-частотную характеристику замкнутой системы
не налагаются друг на друга (рис. 9.18, а), амплитудно-частотную характеристику замкнутой системы  выбирают достаточно широкой для обеспечения требуемой точности воспроизведения управляющего сигнала и в то же время достаточно узкой для того, чтобы система меньше реагировала на помеху.
выбирают достаточно широкой для обеспечения требуемой точности воспроизведения управляющего сигнала и в то же время достаточно узкой для того, чтобы система меньше реагировала на помеху.
Если управляющий сигнал имеет спектр частот, очень быстро убывающий с возрастанием частоты, а спектр помех
близок К белому шуму (рис. 9.18, б), то в этом случае форма амплитудно-частотной характеристики  разомкнутой системы должна выбираться при низких частотах, где
разомкнутой системы должна выбираться при низких частотах, где  и сконцентрирована основная энергия управляющего сигнала, возможно более близкой к форме спектральной плотности управляющего сигнала
и сконцентрирована основная энергия управляющего сигнала, возможно более близкой к форме спектральной плотности управляющего сигнала  а затем должна быстро убывать, по возможности следуя за убывающей характеристикой
а затем должна быстро убывать, по возможности следуя за убывающей характеристикой  . В общем случае, когда спектры частот полезного сигнала и помехи накладываются друг на друга и имеют произвольную форму (рис. 9.18, в), определение оптимальных параметров системы становится довольно сложным.
. В общем случае, когда спектры частот полезного сигнала и помехи накладываются друг на друга и имеют произвольную форму (рис. 9.18, в), определение оптимальных параметров системы становится довольно сложным.
При синтезе систем со случайными воздействиями различают два вида задач:
1. Синтез при заданной структуре системы управления, когда добиваются минимума средней квадратической ошибки, выбирая оптимальные параметры корректирующих звеньев системы на основании известных статистических характеристик полезного сигнала и помехи.
2. Синтез при произвольной структуре системы управления, когда по заданным статистическим характеристикам полезного сигнала и помехи определяют оптимальную структуру и параметры системы, при которых обеспечивается минимум средней кьадрэтической ошибки.
Синтез при заданной структуре системы. В этом случае задача синтеза формулируется следующим образом. Заданы статистические характеристики полезного сигнала и помехи, например спектральные плотности  структура системы и ее передаточная функция
структура системы и ее передаточная функция

Рис. 9.18
 , где
, где  — параметры системы.
— параметры системы.
Требуется найти оптимальные параметры системы  которых обеспечивается минимум средней квадратической ошибки.
которых обеспечивается минимум средней квадратической ошибки.
Эта задача решается следующим образом: зная спектральные плотности  и передаточную функцию системы, определяют спектральную плотность ошибки
и передаточную функцию системы, определяют спектральную плотность ошибки  а затем, пользуясь табличными интегралами, находят аналитическое выражение среднего значения квадрата ошибки
а затем, пользуясь табличными интегралами, находят аналитическое выражение среднего значения квадрата ошибки  которое получается зависящим от параметров системы:
которое получается зависящим от параметров системы:

Дифференцируя (9.111) по  , где
, где  и приравнивая нулю частные производные, находят
и приравнивая нулю частные производные, находят  уравнений, из которых определяют оптимальные параметры системы
уравнений, из которых определяют оптимальные параметры системы  обеспечивающие минимум средней квадратической ошибки.
обеспечивающие минимум средней квадратической ошибки.
Как правило, большинство, параметров системы изменять трудно либо невозможно, так как они определяются заданными техническими или конструктивными соображениями. Поэтому обычно выбирают два-три параметра, например постоянные времени корректирующих звеньев, коэффициент усиления разомкнутой системы и др. Если число переменных  невелико, то отыскание экстремума функции не вызывает затруднений. При большем числе
невелико, то отыскание экстремума функции не вызывает затруднений. При большем числе  когда явное выражение среднего значения квадрата ошибки через параметры системы определить затруднительно либо оно слишком громоздко, используют приближенные методы отыскания минимума выражения (9.111) путем числового задания интересующих параметров и построения соответствующих графиков.
когда явное выражение среднего значения квадрата ошибки через параметры системы определить затруднительно либо оно слишком громоздко, используют приближенные методы отыскания минимума выражения (9.111) путем числового задания интересующих параметров и построения соответствующих графиков.
Параметры системы, выбранные по критерию минимума средней квадратической ошибки, оценивают затем, исходя из возможности их технической реализации и допустимых динамических показателей системы (времени регулирования, наличия и величины перерегулирования и т. д.).
Заметим, что указанная выше методика выбора оптимальных параметров системы может применяться и при одновременном воздействии на систему регулярных и случайных сигналов.
Пример 9.4. Условия задачи такие же. как и примере 9.1. Требуется определить оптимальное значение коэффициента усиления разомкнутой системы  соответствующее минимуму средней квадратической ошибки, и вычислить среднюю квадратическую ошибку при
соответствующее минимуму средней квадратической ошибки, и вычислить среднюю квадратическую ошибку при 
Ранее (в примере 9.1) было получено выражение для среднего значения квадрата ошибки

Для исследования на минимум средней квадратической ошибки необходимо приравнять нулю производную от этого выражения по коэффициелту усиления разомкнутой системы. В результате получаем

Из последнего уравнения определяем оптимальное значение коэффициента усиления разомкнутой системы:

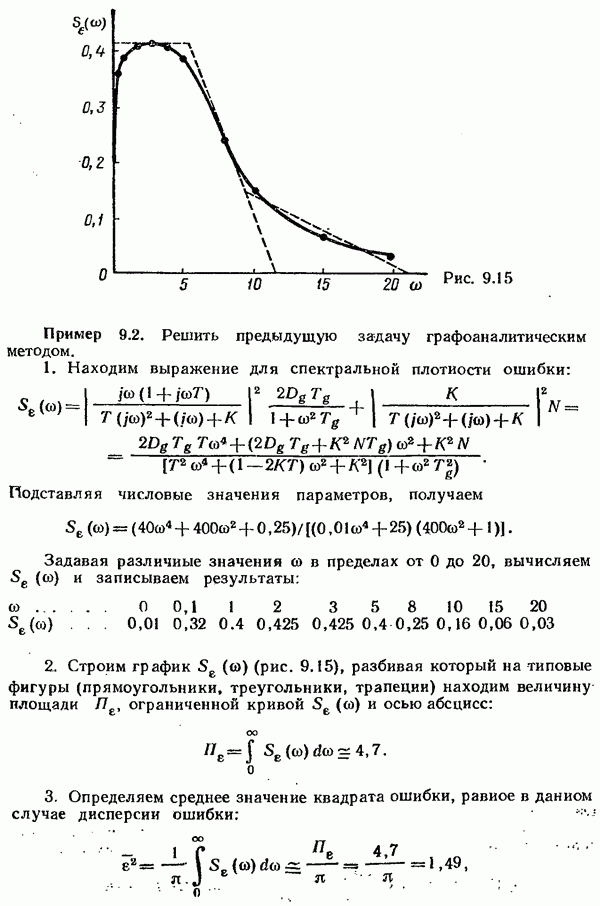
Подставляя числовые значении параметров, получаем

Подставляя  в выражение для среднего значения квадрата ошибки, получаем
в выражение для среднего значения квадрата ошибки, получаем

Средняя квадратическая ошибка, соответствующая 

Пример 9.5. Условия задачи такие же, как и в примере 9,3. Требуется определить оптимальное значение коэффициента усиления разомкнутой системы  и вычислить среднюю квадратическую ошибку при
и вычислить среднюю квадратическую ошибку при 
Ранее (в примере 9.3) было получено выражение для среднего значения квадрата ошибки

Приравниваем нулю производную от этого выражения по коэффициенту усиления разомкнутой системы:

Из последнего выражения определяем Копт  Подставляя числовые значения параметров, получаем
Подставляя числовые значения параметров, получаем

Среднее значение квадрата ошибки; соответствующее 

Средняя квадратическая ошибка

Графики изменения  в функции коэффициента усиления системы К приведены на рис. 9.17.
в функции коэффициента усиления системы К приведены на рис. 9.17.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
- § 7.3. Автоколебания. Метод точечных преобразований
- § 7.4. Системы с переменной структурой
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
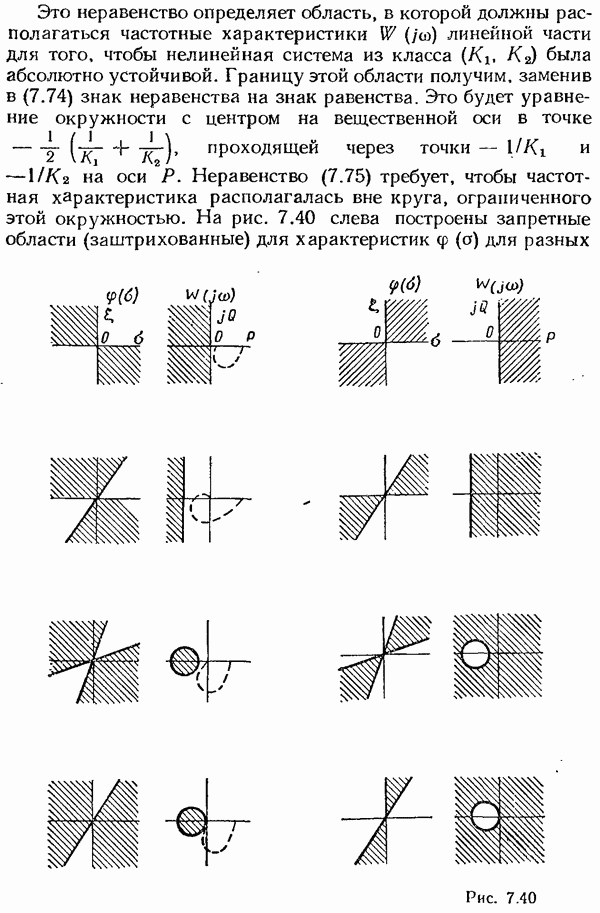
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
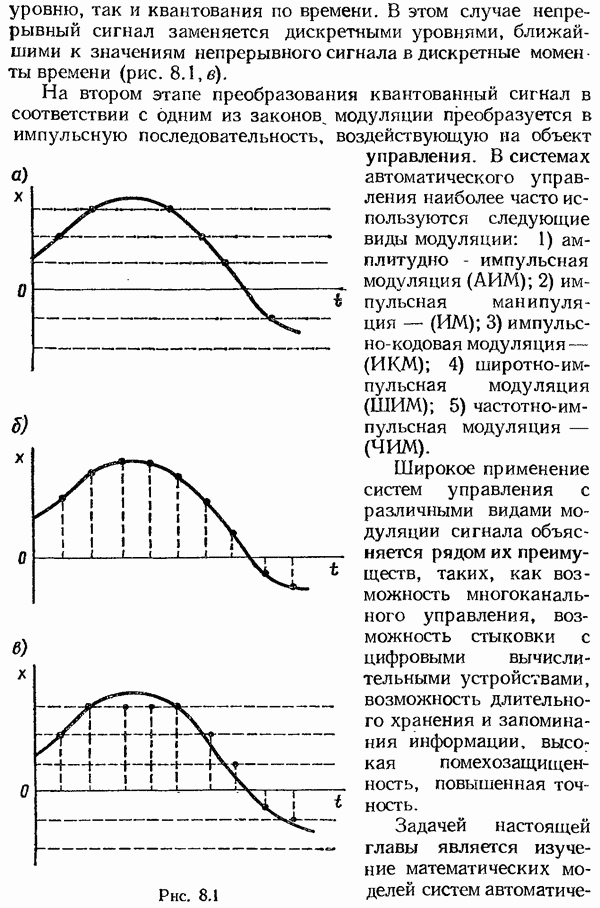
- § 8.1. Понятие об импульсных системах автоматического управления
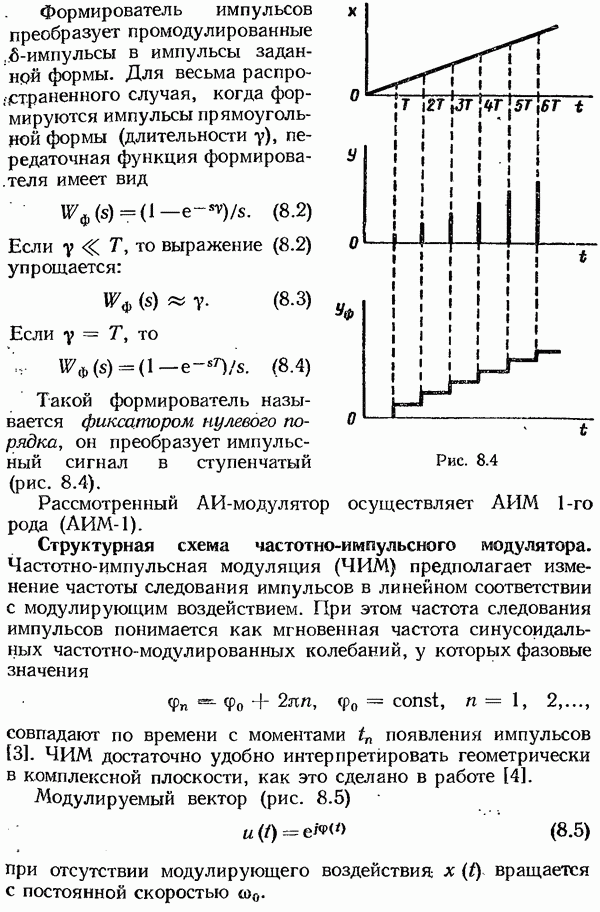
- Структура и уравнения импульсных модуляторов.
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
- Исследование периодических режимов в системах с ИЧИМ.
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
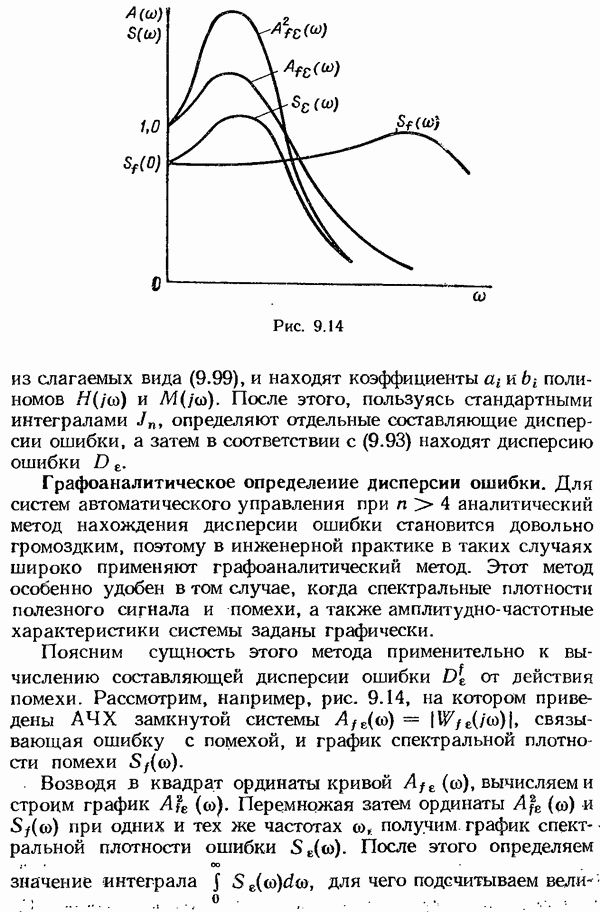
- Аналитический метод определения дисперсии ошибки.
- Графоаналитическое определение дисперсии ошибки.
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
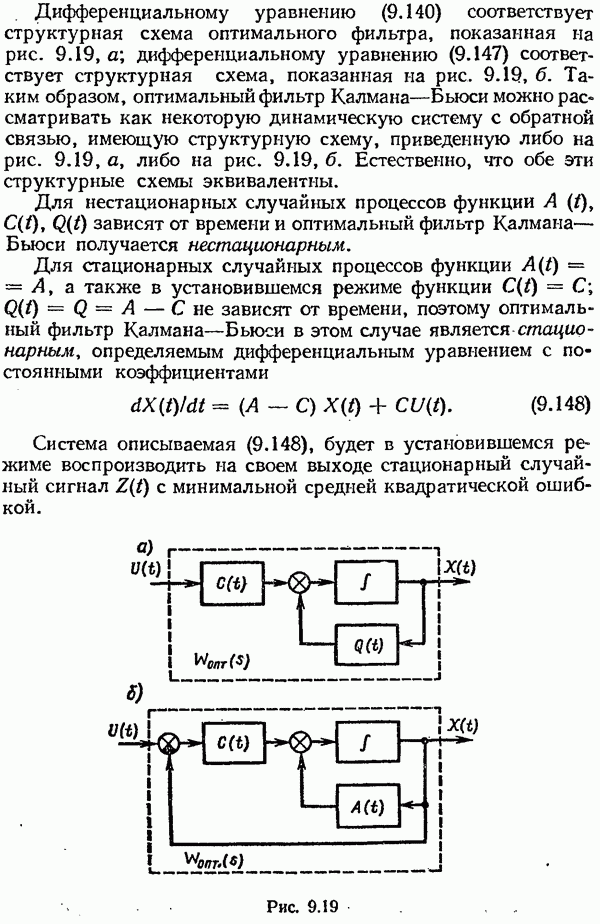
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
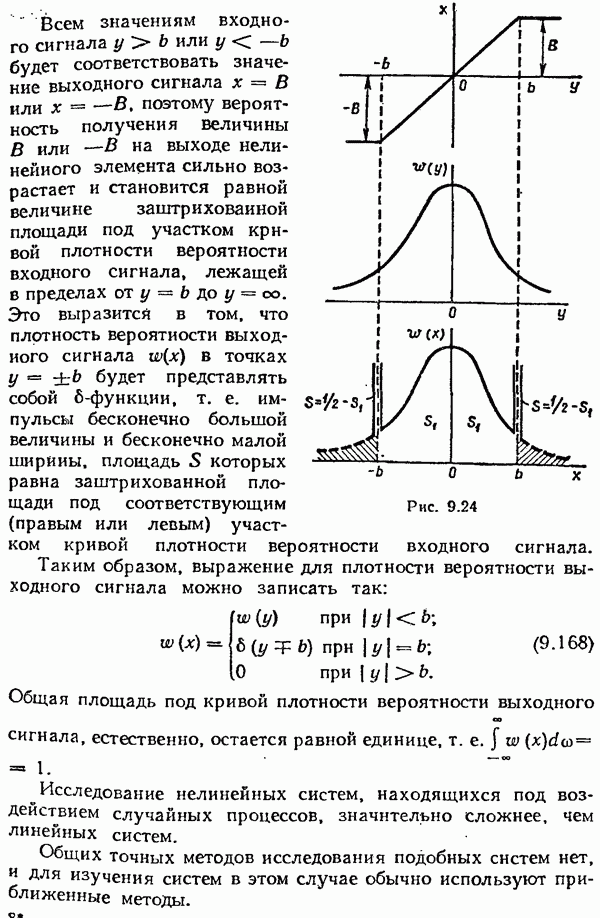
- § 9.9. Нелинейное преобразование случайных сигналов
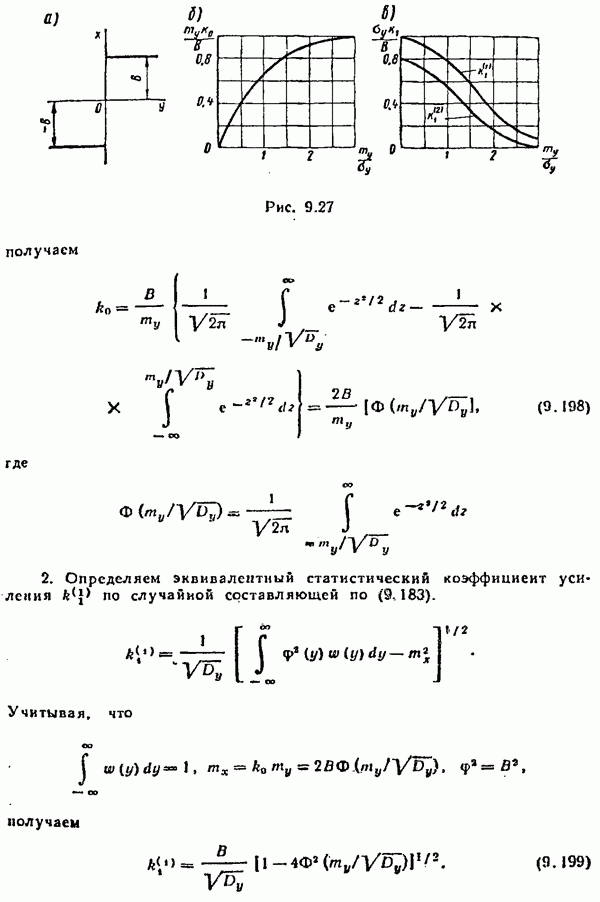
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
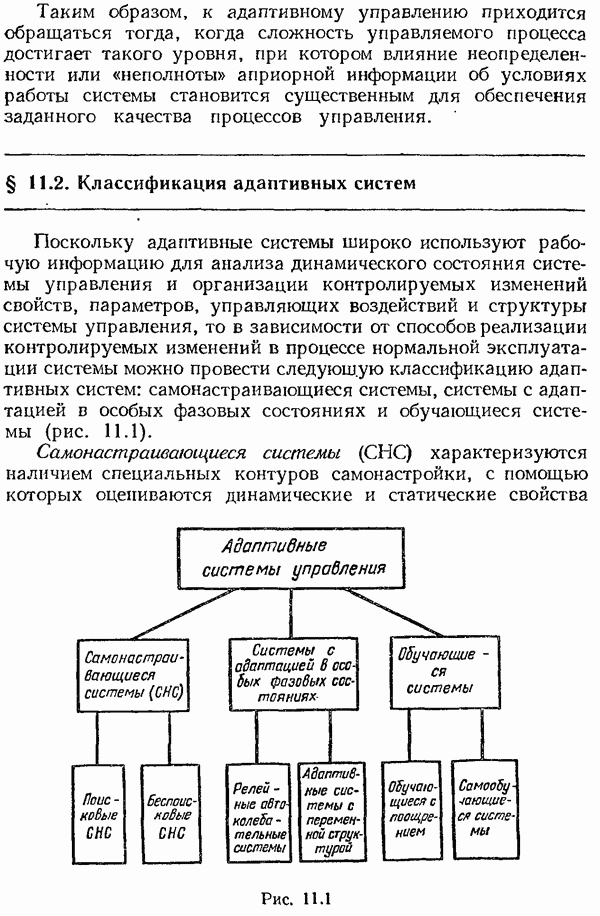
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
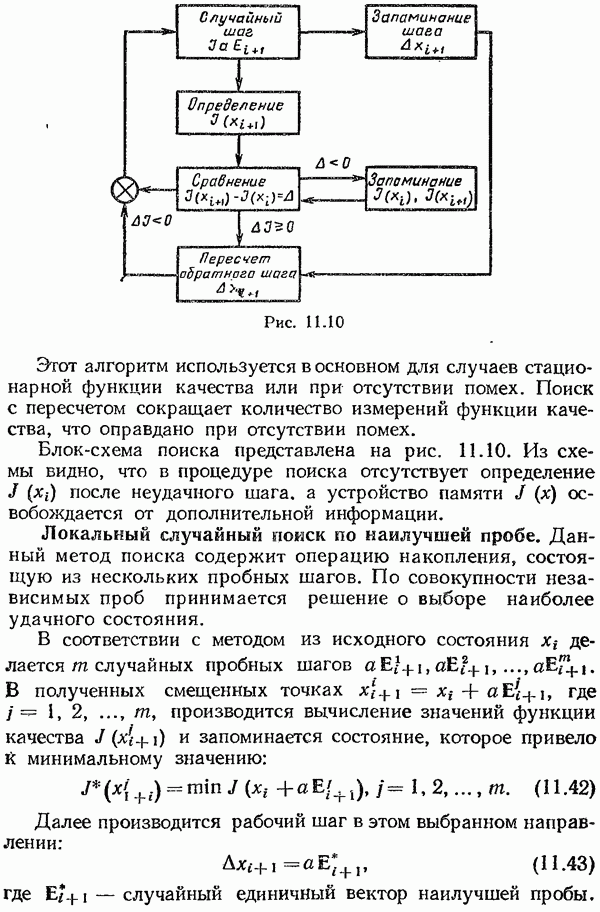
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
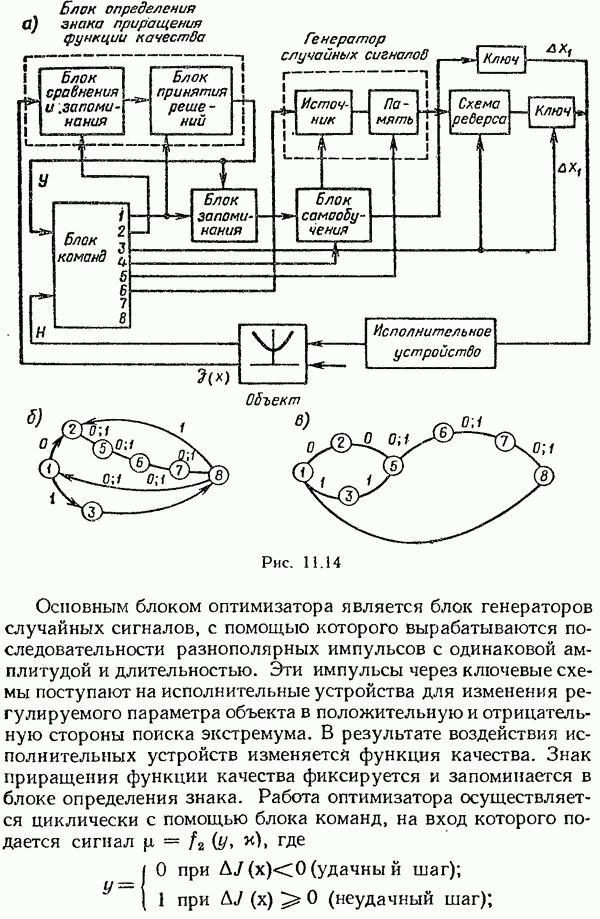
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
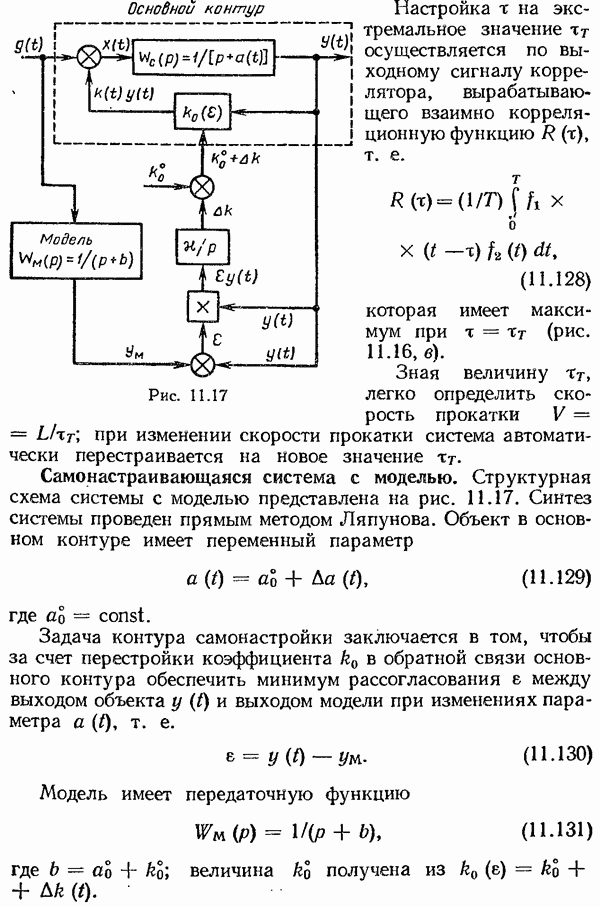
- Самонастраивающаяся система с моделью.
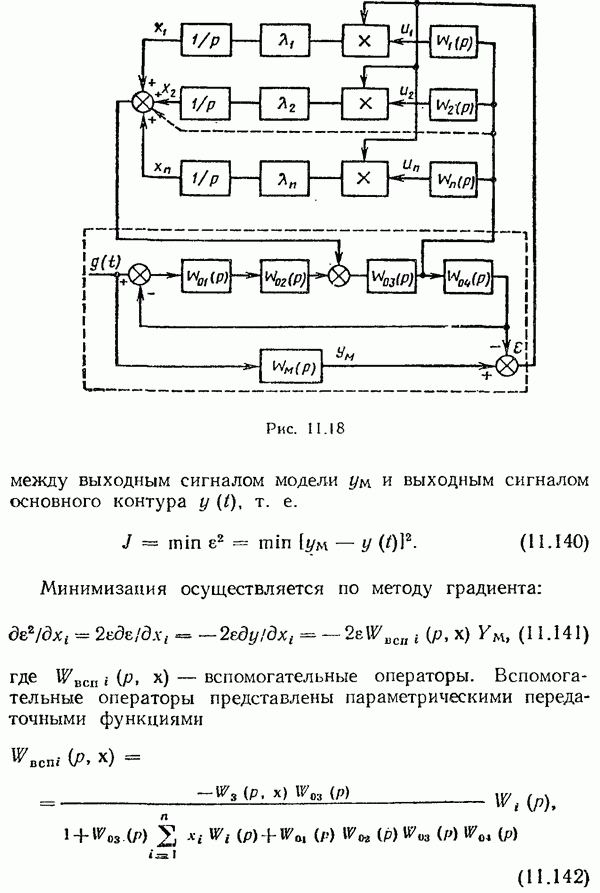
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
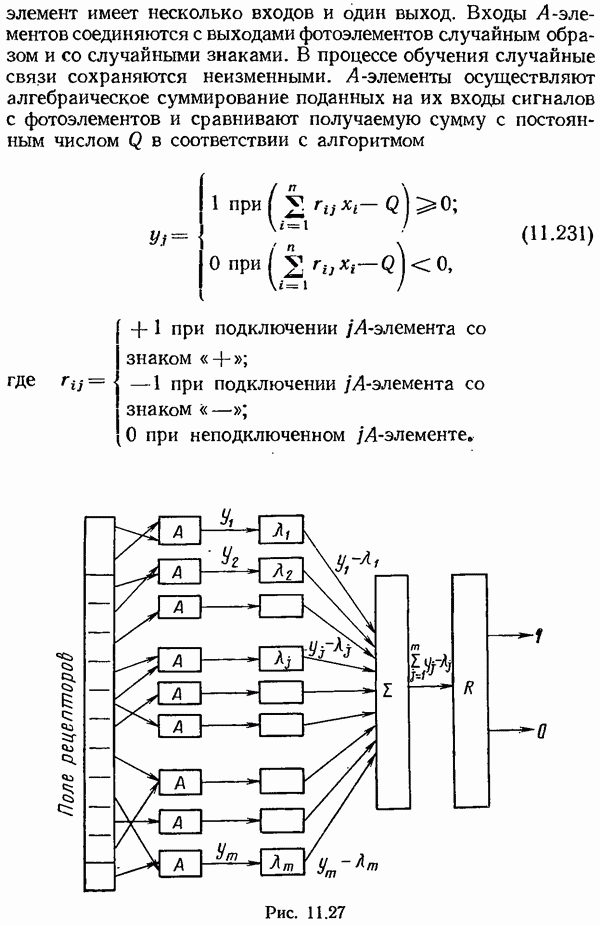
- Персептронная модель автоматической классификации.
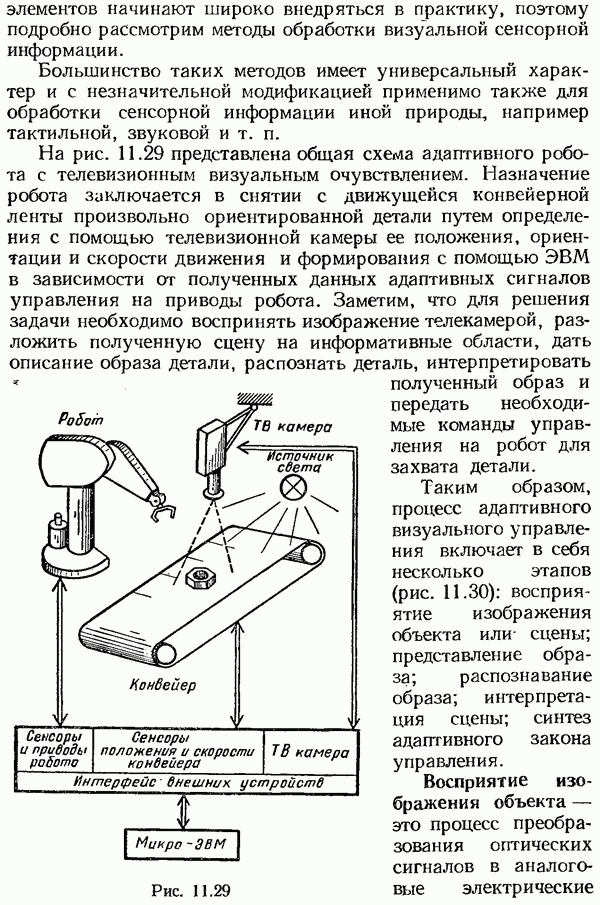
- § 11.6. Адаптивные робототехнические системы
- Методы обработки сенсорной информации для адаптивного управления роботами.
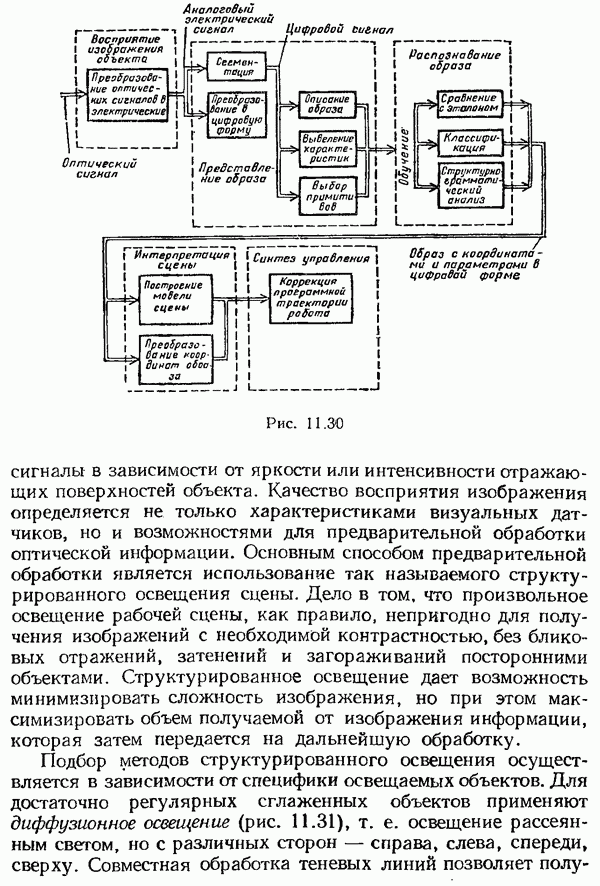
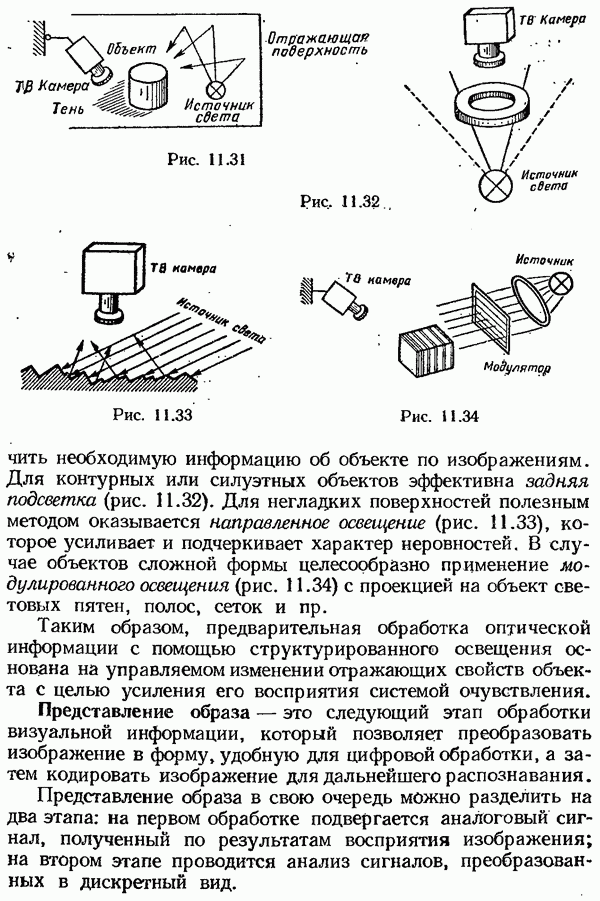
- Восприятие изображения объекта
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ