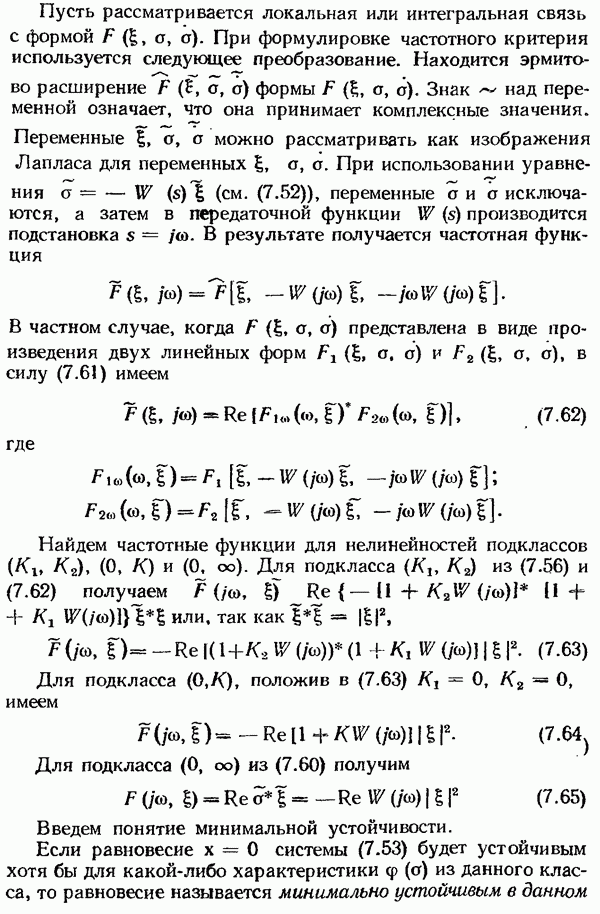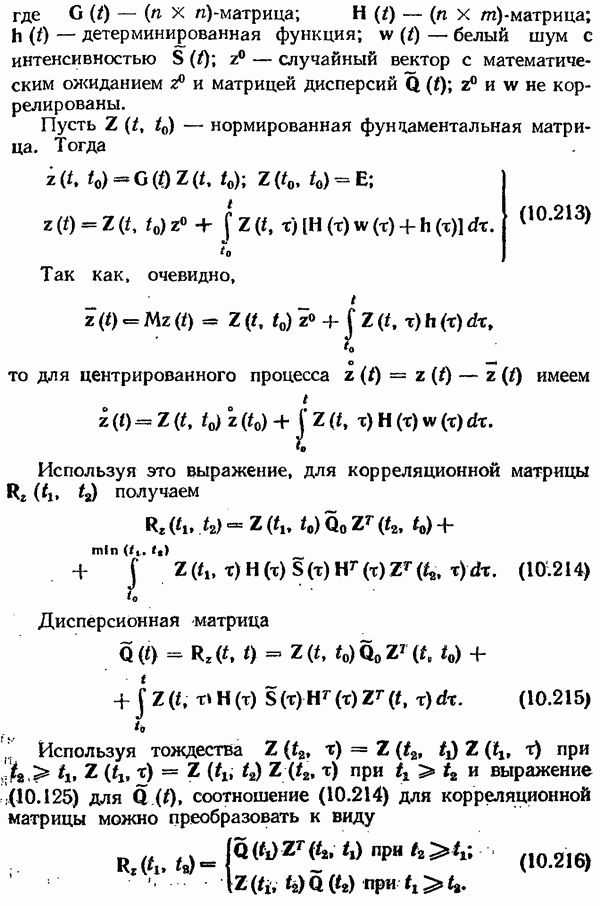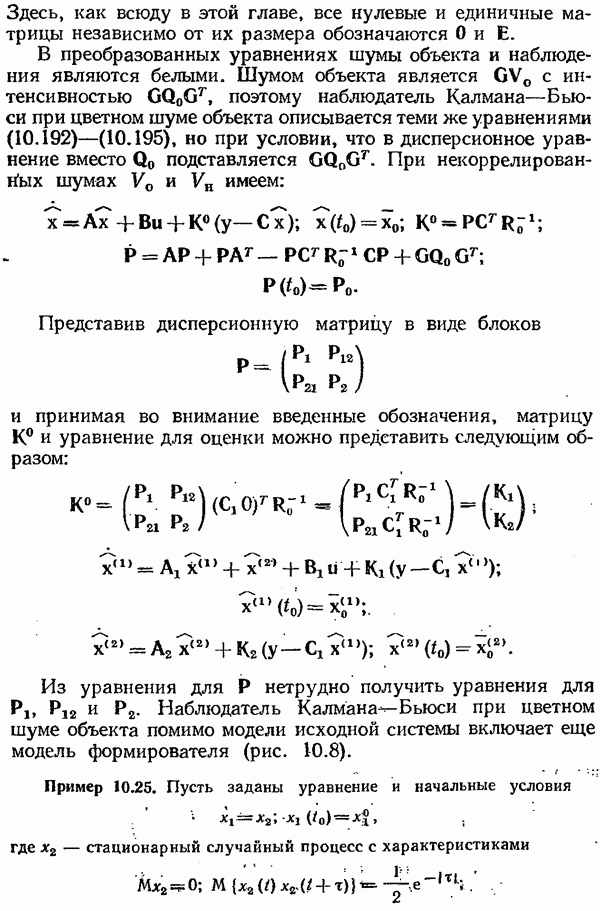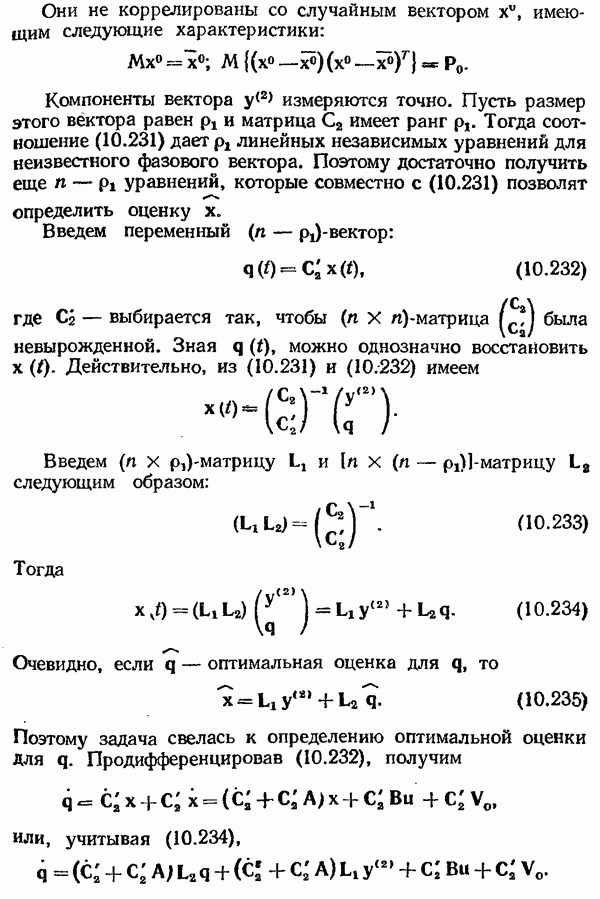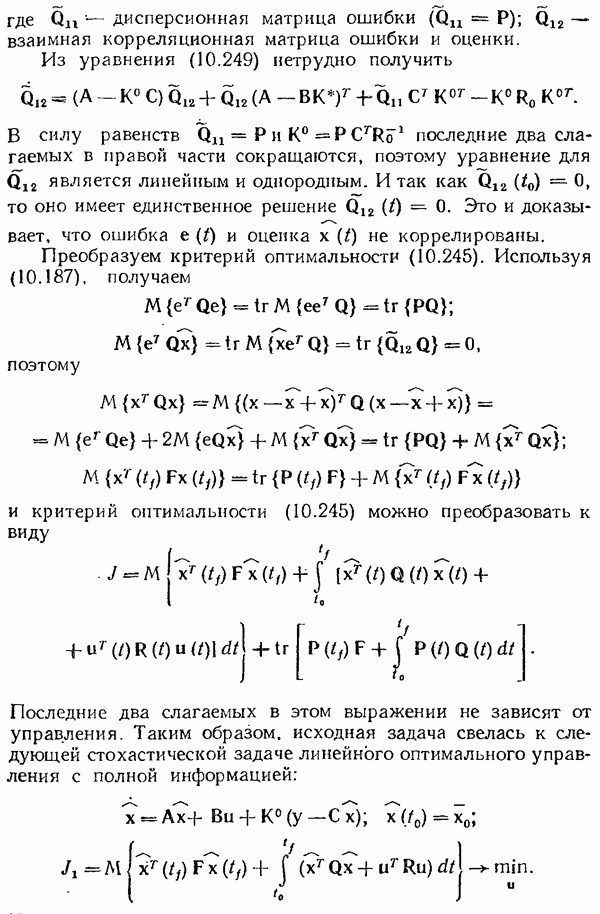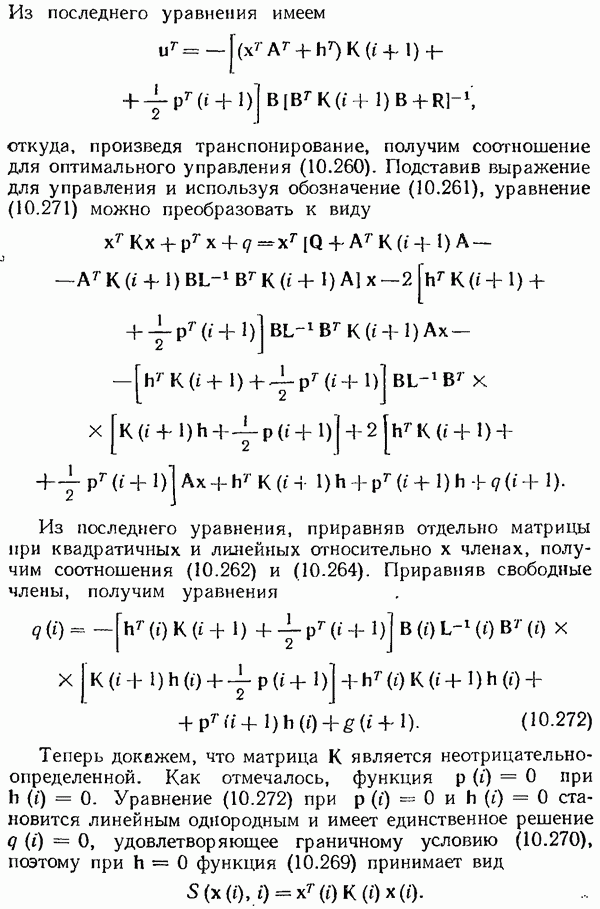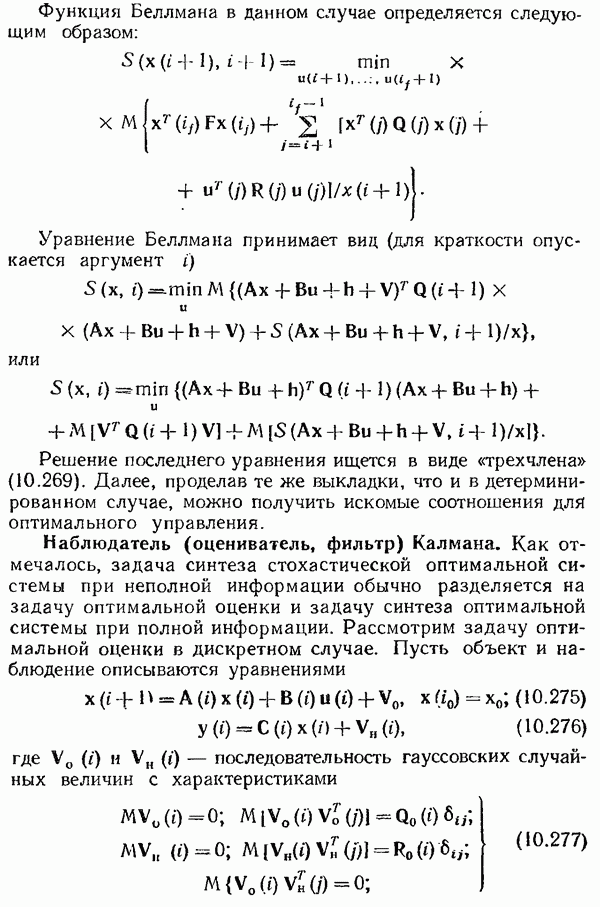| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
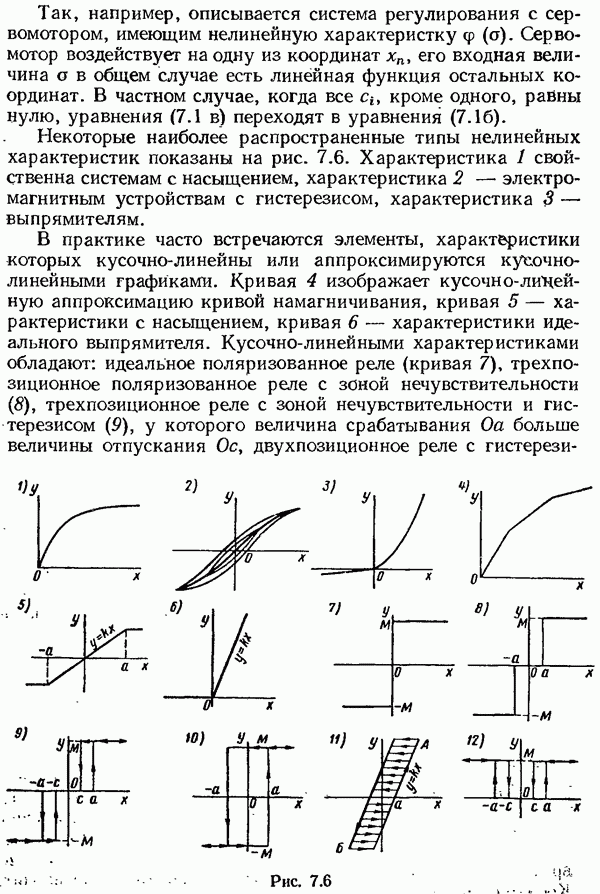
§ 7.8. Устойчивость в малом, большом и целом
В нелинейных системах движение или равновесие, устойчивое в малом, может оказаться неустойчивым при больших отклонениях и первый метод Ляпунова, рассмотренный в гл. 3 для исследования устойчивости на основе уравнений линейного приближения, уже недостаточен для полного исследования устойчивости в нелинейных системах.
Анализ устойчивости движения можно свести к анализу устойчивости равновесия (тривиального решения) в преобразованном фазовом пространстве отклонений. Исследуемое движение и его траекторию считают невозмущенными; предполагается, что к моменту времени, принимаемому за начало отсчета, возмущающие силы сместили изображающую точку с невозмущенной траектории на другую — возмущенную, после чего их действие прекратилось. Отклонения координат изображающей точки  на возмущенной траектории в каждый момент
на возмущенной траектории в каждый момент  от тех координат точки на невозмущенной траектории в тот же момент, которые имели бы место при отсутствии возмущений, принимают за координаты нового фазового пространства. На основе исходных уравнений движения составляют уравнения в этих отклонениях. Но если для линейных систем уравнения в отклонениях были подобны исходным или даже несколько проще их, то для нелинейных систем форма уравнения в отклонениях может оказаться значительно более сложной, чем у исходных уравнений. Начало координат нового пространства будет устойчивой точкой равновесия, если устойчиво невозмущенное движение.
от тех координат точки на невозмущенной траектории в тот же момент, которые имели бы место при отсутствии возмущений, принимают за координаты нового фазового пространства. На основе исходных уравнений движения составляют уравнения в этих отклонениях. Но если для линейных систем уравнения в отклонениях были подобны исходным или даже несколько проще их, то для нелинейных систем форма уравнения в отклонениях может оказаться значительно более сложной, чем у исходных уравнений. Начало координат нового пространства будет устойчивой точкой равновесия, если устойчиво невозмущенное движение.
Если точка равновесия  устойчива, то вокруг начала координат существует область притяжения траекторий — область С (на рис. 7.37 однократно заштрихована). Если известно лишь то, что область притяжения существует, то считают, что состояние равновесия устойчиво в малом, т. е. устойчивость гарантируют лишь при достаточно малых отклонениях.
устойчива, то вокруг начала координат существует область притяжения траекторий — область С (на рис. 7.37 однократно заштрихована). Если известно лишь то, что область притяжения существует, то считают, что состояние равновесия устойчиво в малом, т. е. устойчивость гарантируют лишь при достаточно малых отклонениях.
Пусть область  существует. Зададимся областью допустимых начальных отклонений
существует. Зададимся областью допустимых начальных отклонений  например, в виде гиперкуба
например, в виде гиперкуба

Рис. 7.37
с центром в начале координат, ребра которого параллельны осям координат и имеют длину  (на рис. 7.37 — дважды заштрихованный квадрат). В соответствии с определением устойчивости Ляпунова равновесие устойчиво (в малом), если можно выбрать такое К, что область
(на рис. 7.37 — дважды заштрихованный квадрат). В соответствии с определением устойчивости Ляпунова равновесие устойчиво (в малом), если можно выбрать такое К, что область  будет целиком принадлежать области
будет целиком принадлежать области  (рис. 7.37, а).
(рис. 7.37, а).
Для того чтобы определить устойчивость в большом, нужно задаться, кроме того, областью  возможных (по техническим условиям) в данной системе отклонений. Зададим
возможных (по техническим условиям) в данной системе отклонений. Зададим  также в виде соосного с
также в виде соосного с  гиперкуба с длиной ребра
гиперкуба с длиной ребра  . Если гиперкуб
. Если гиперкуб  целиком принадлежит области
целиком принадлежит области  равновесие устойчиво в большом (рис. 7.37, а), если часть его находится вне области
равновесие устойчиво в большом (рис. 7.37, а), если часть его находится вне области  равновесие устойчиво в малом, но неустойчиво в большом (рис. 7.37, б). Математически сказанное формулируется так: если при наперед заданном положительном
равновесие устойчиво в малом, но неустойчиво в большом (рис. 7.37, б). Математически сказанное формулируется так: если при наперед заданном положительном  (соответствует зачерненным квадратам
(соответствует зачерненным квадратам  на рис. 7.37, а, б) можно выбрать другое положительное число
на рис. 7.37, а, б) можно выбрать другое положительное число  такое, что при начальных отклонениях
такое, что при начальных отклонениях  удовлетворяющих условию
удовлетворяющих условию

значения  при всех
при всех  будут удовлетворять соотношению
будут удовлетворять соотношению

то равновесие устойчиво в малом.
Если, кроме того, возможные начальные отклонения удовлетворяют условиям

то равновесие устойчиво в большом.
Если область  распространяется на все пространство, равновесие называют устойчивым в целом. Так как обычно границы области
распространяется на все пространство, равновесие называют устойчивым в целом. Так как обычно границы области  установить бывает трудно, об устойчивости в целом судят по величине
установить бывает трудно, об устойчивости в целом судят по величине  если она не ограничена, т. е. условие
если она не ограничена, т. е. условие  соблюдается при любом сколь угодно большом К, имеет место устойчивость в целом.
соблюдается при любом сколь угодно большом К, имеет место устойчивость в целом.
Если приведенные условия соблюдаются при любом сколь угодно малом  говорят, что равновесие устойчиво асимптотически.
говорят, что равновесие устойчиво асимптотически.
Для исследования устойчивости в большом и целом используют специальные методы, из которых ниже коротко рассматриваются два — второй (прямой) метод А. М. Ляпунова и
метод В. М. Попова — для исследования абсолютной устойчивости (т. е. устойчивости в целом для определенного класса нелинейностей).
Пример 7.2. Получим уравнения в отклонениях для исследования устойчивости периодического движения

выражающего основную гармонику автоколебаний и являющегося точным решением уравнения (7.31)

и приближенным решением уравнения (7.29) Считая (7.44), в котором  уравнениями невозмущенного движения, зададим приращения двум основным параметрам
уравнениями невозмущенного движения, зададим приращения двум основным параметрам  :
:

Так как  зависят от А, они также получат приращения
зависят от А, они также получат приращения  но найти их непосредственно из (7.34) нельзя, так как в подынтегральные выражения теперь входит неизвестная функция времени
но найти их непосредственно из (7.34) нельзя, так как в подынтегральные выражения теперь входит неизвестная функция времени  Чтобы обойти это затруднение, прибегают к приближенному нахождению
Чтобы обойти это затруднение, прибегают к приближенному нахождению  для чего предполагают, что А изменяется настолько медленно, что в течение одного периода
для чего предполагают, что А изменяется настолько медленно, что в течение одного периода  оно мало отличается от постоянного и может быть заменено постоянным числом, равным усредненному за период значению А. Тогда по (7.34) находят
оно мало отличается от постоянного и может быть заменено постоянным числом, равным усредненному за период значению А. Тогда по (7.34) находят  и b как функцию подобного изменяющегося ступенями от периода к периоду аргумента А. Затем вводят еще одно допущение: в полученных функциях
и b как функцию подобного изменяющегося ступенями от периода к периоду аргумента А. Затем вводят еще одно допущение: в полученных функциях  аргумент А является уже не ступенчатой, а непрерывной функцией и приращения
аргумент А является уже не ступенчатой, а непрерывной функцией и приращения  выражаются через
выражаются через  следующим образом:
следующим образом:

Используя (7.45) и известные в математике выражения для преобразования действия линейного оператора  (где М — полином,
(где М — полином,  на произведения функций и
на произведения функций и 

где  , т.е. получим
, т.е. получим

где

Подставляя  вместо А и
вместо А и  вместо после преобразований и отбрасывания малых высших порядков получим
вместо после преобразований и отбрасывания малых высших порядков получим

где
Исключая уравнения установившихся автоколебаний

и приравнивая порознь нулю коэффициенты при  получим
получим

Это линеаризованные уравнения в отклонениях параметров автоколебаний — амплитуды А и фазы  Они значительно сложнее исходного уравнения (7.45). Исследование устойчивости периодического движения в малом свелось теперь к исследованию устойчивости в малом равновесия или тривиального решения
Они значительно сложнее исходного уравнения (7.45). Исследование устойчивости периодического движения в малом свелось теперь к исследованию устойчивости в малом равновесия или тривиального решения  путем при ложения любого из критериев устойчивости к характеристическому уравнению
путем при ложения любого из критериев устойчивости к характеристическому уравнению

Эквивалентную гармоническую линеаризацию можно осуществить по уравнениям (7.47).
«Медленность» изменения параметров  позволяет существенно упростить приближенное исследование переходного процесса при малых отклонениях.
позволяет существенно упростить приближенное исследование переходного процесса при малых отклонениях.

«Медленность» изменения означает, что скорость изменения функций в любой момент времени принимается малой в сравнении с  , но учитываемой величиной, высшие же производные
, но учитываемой величиной, высшие же производные  считаются
считаются
в сравнения с  малыми высших порядков и отбрасываются. Пренебрегая
малыми высших порядков и отбрасываются. Пренебрегая  оставляем в полиномах
оставляем в полиномах  свободные члены и члены, содержащие
свободные члены и члены, содержащие  в первой степени, и получаем пару уравнении первого порядка для приближенного описания изменения переменных
в первой степени, и получаем пару уравнении первого порядка для приближенного описания изменения переменных

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 7. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- § 7.1. Основные типы. нелинейных систем и характеристик
- § 7.2. Изображение движений в фазовой плоскости
- Линейная консервативная система второго порядка.
- Система с сухим кулоновским трением.
- Система с отрицательной восстанавливающей силой.
- Линейная колебательная система с вязким трением.
- Линейная апериодическая система с вязким трением.
- § 7.3. Автоколебания. Метод точечных преобразований
- § 7.4. Системы с переменной структурой
- § 7.5. Метод «припасовывания» граничных значений
- § 7.6. Приближенное исследование автоколебаний. Метод эквивалентной линеаризации
- § 7.7. Метод гармонического баланса
- § 7.8. Устойчивость в малом, большом и целом
- § 7.9. Второй (прямой) метод Ляпунова
- § 7.10. Абсолютная устойчивость
- Квадратичный критерий абсолютной устойчивости.
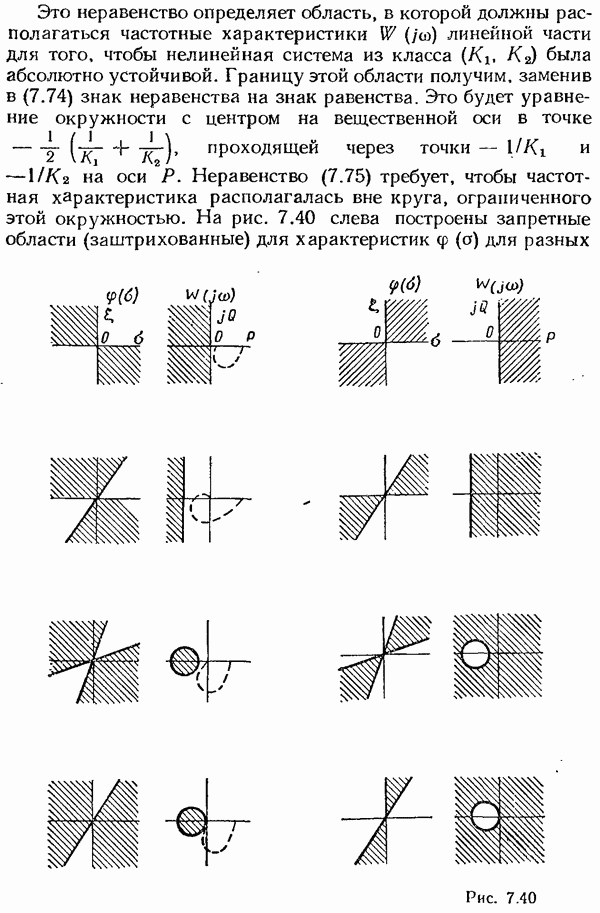
- Круговой критерий устойчивости.
- Критерий В. М. Попова.
- Примечание к критерию Попова.
- Гипотезы М. Айзермана и Р. Калмана.
- Определение автоколебаний.
- Упрощенный критерий колебательности.
- Глава 8. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
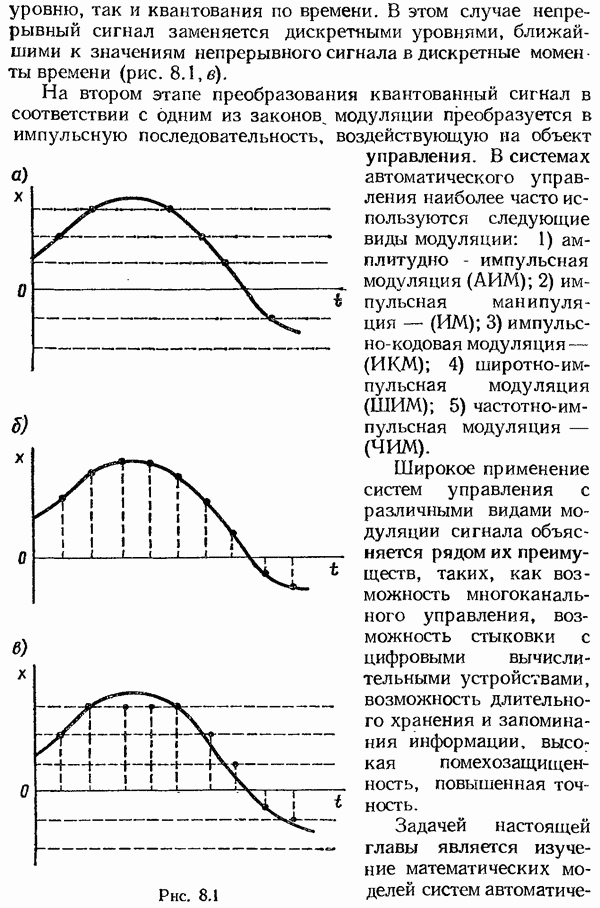
- § 8.1. Понятие об импульсных системах автоматического управления
- Структура и уравнения импульсных модуляторов.
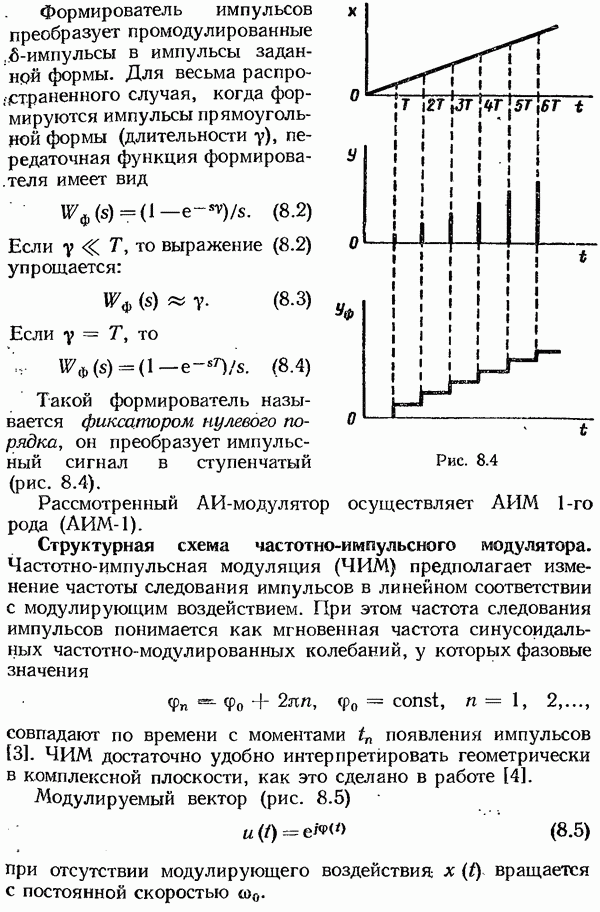
- Структурная схема амплитудно-импульсного модулятора.
- Структурная схема частотно-импульсного модулятора.
- Структурная схема широтно-импульсного модулятора.
- Структурные схемы частотно-импульсных к широтно- импульсных модуляторов 1-го рода.
- Структурная схема системы управления с импульсной модуляцией. Классификация систем управления с импульсной модуляцией.
- § 8.2. Исследование устойчивости и качества систем управления с амплитудноимпульсной модуляцией
- Передаточная функция импульсной системы.
- Дискретное преобразование Лапласа и его основные свойства.
- Частотные характеристики импульсной системы.
- Исследование устойчивости систем с амплитудно-импульсной модуляцией.
- Алгебраический критерий устойчивости (аналог критерия Гурвица).
- Частотный критерий устойчивости (аналог критерия Найквиста).
- Исследование качества систем с амплитудно-импульсной модуляцией.
- Непрерывное регулирование как граница импульсного регулирования.
- § 8.3. Исследование динамики цифровых систем автоматического управления
- Исследование цифровых систем методом логарифмических частотных характеристик.
- Исследование цифровых систем с непрерывной передачей данных.
- Исследование цифровых систем с учетом квантования по уровню и по времени.
- § 8.4. Исследование систем с широтноимпульсной модуляцией
- Исследование периодических колебаний в системах с широтно-импульсной модуляцией.
- § 8.5. Исследование систем с частотно-импульсной модуляцией
- Исследование устойчивости в целом частотно-импульсных систем 2-го рода.
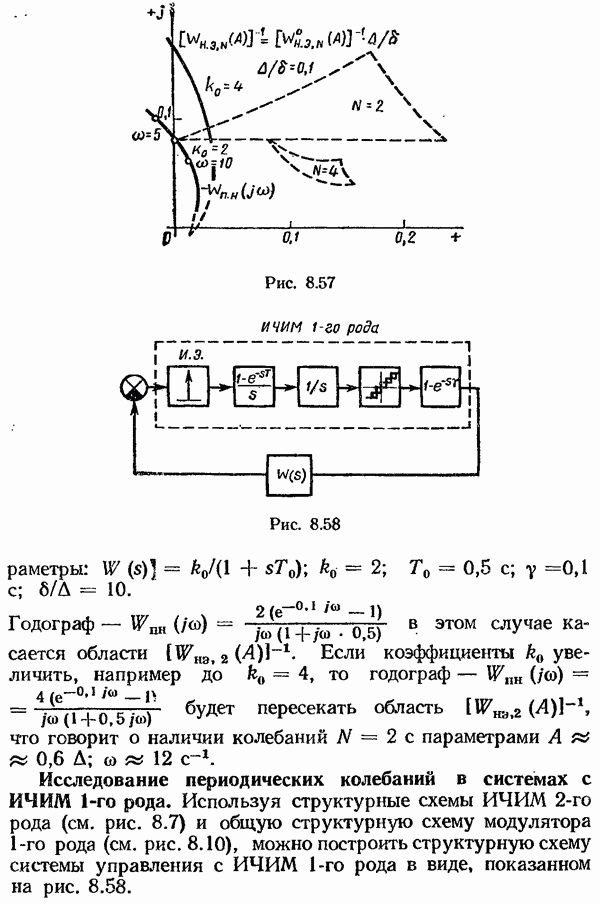
- Исследование периодических режимов в системах с ИЧИМ.
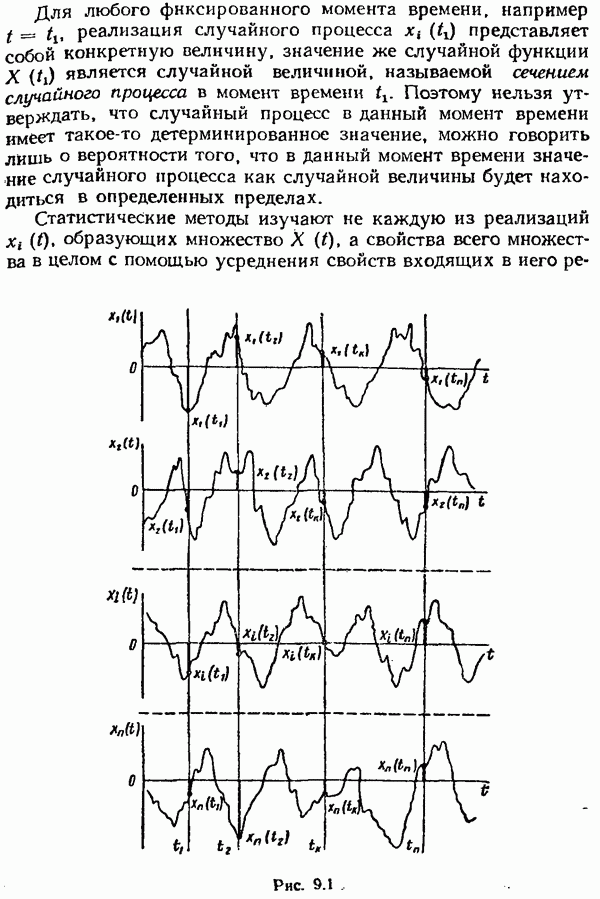
- Исследование периодических колебаний в системах с ИЧИМ 1-го рода.
- Глава 9. СЛУЧАЙНЫЕ ПРОЦЕССЫ В АВТОМАТИЧЕСКИХ СИСТЕМАХ УПРАВЛЕНИЯ
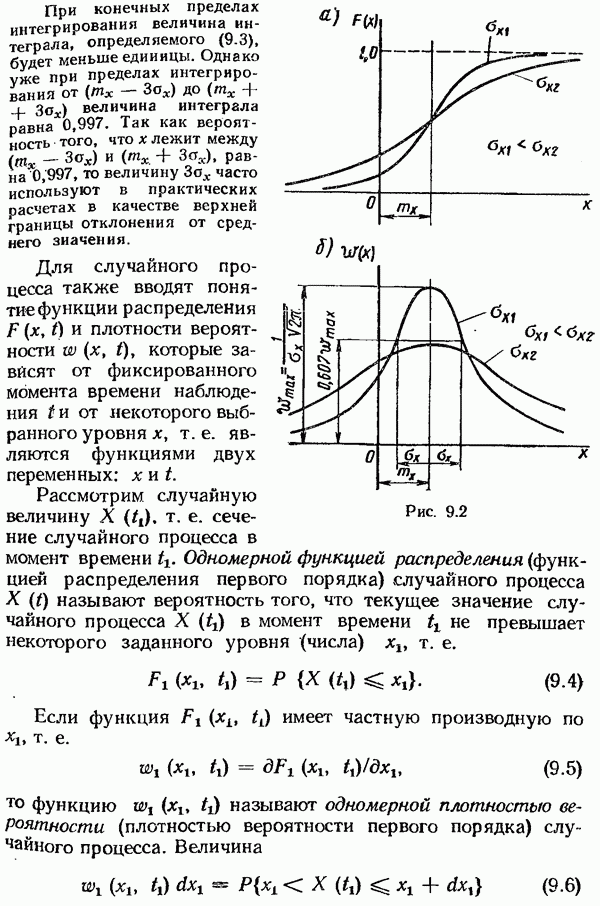
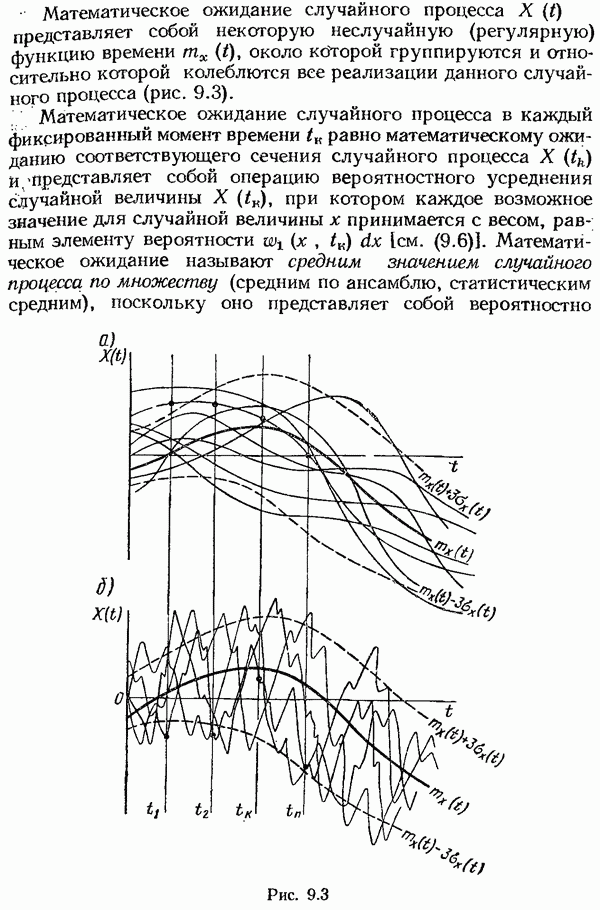
- § 9.2. Случайные процессы и их основные статистические характеристики
- § 9.3. Корреляционные функции случайных процессов
- § 9.4. Спектральные плотности случайных процессов
- § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы
- § 9.6. Расчет линейных систем при случайных воздействиях
- Аналитический метод определения дисперсии ошибки.
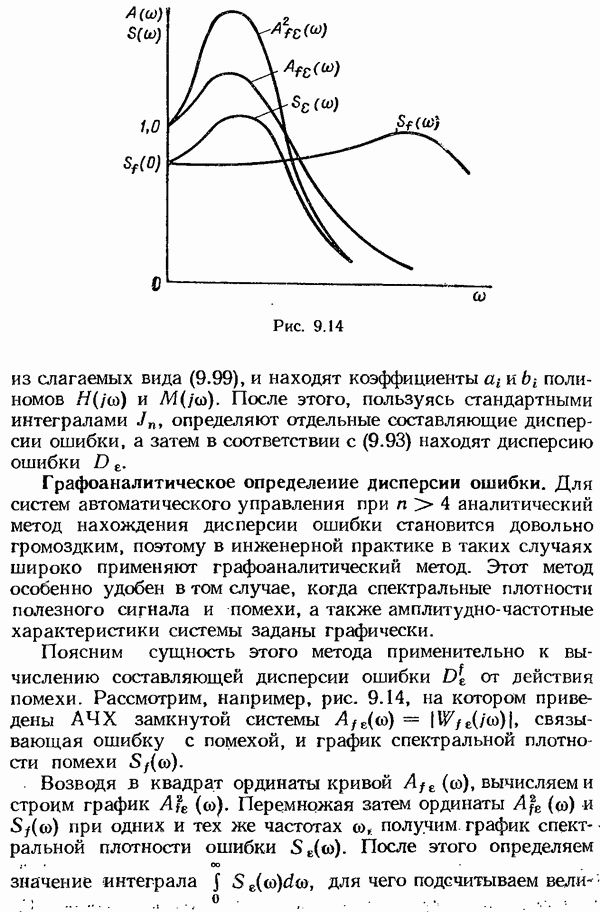
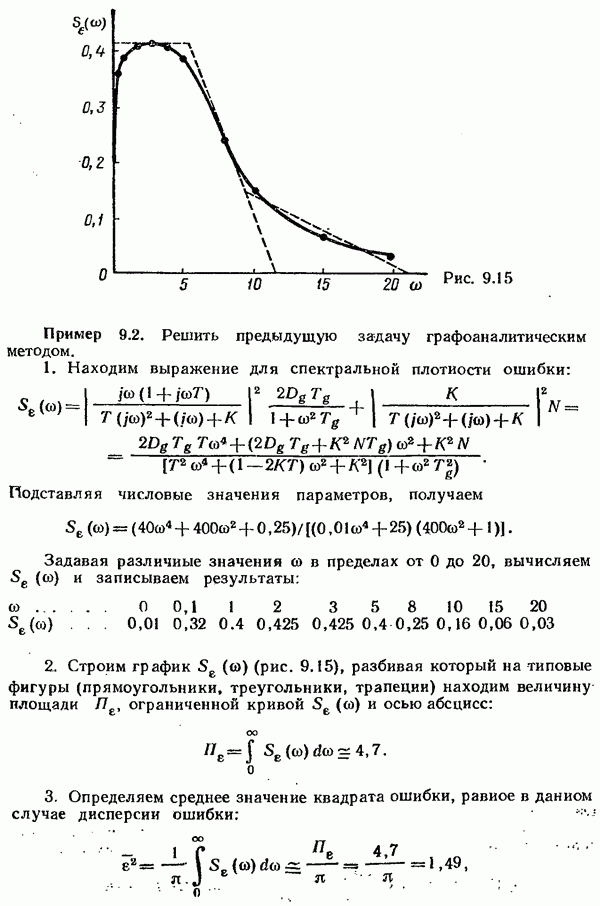
- Графоаналитическое определение дисперсии ошибки.
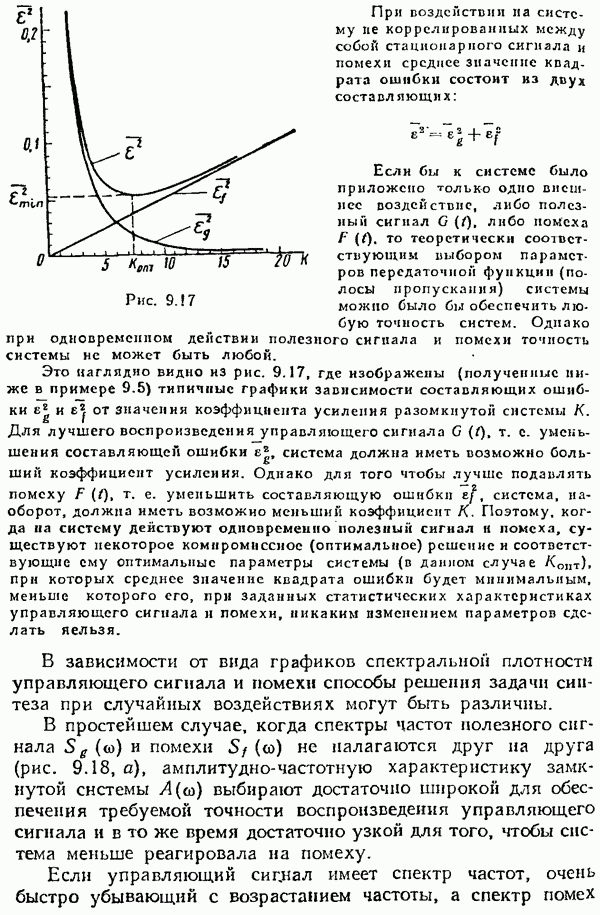
- § 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой
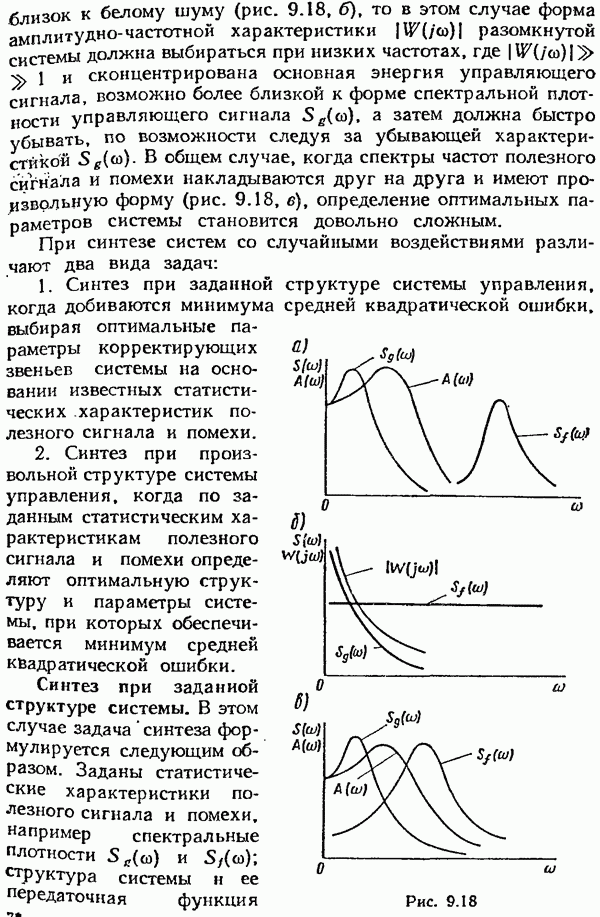
- Синтез при произвольной структуре системы.
- Оптимальный фильтр Винера.
- Оптимальный фильтр Калмана—Бьюси.
- § 9.8. Случайные процессы в линейных импульсных системах
- § 9.9. Нелинейное преобразование случайных сигналов
- § 9.10. Статистическая линеаризация нелинейных элементов
- § 9.11. Расчет нелинейных систем методом статистической линеаризации
- Расчет замкнутых нелинейных систем.
- Глава 10. МЕТОДЫ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ
- Общая постановка задачи оптимального управления
- Примеры постановки задач оптимального управления.
- Классификация задач оптимального управления
- § 10.2. Метод классического вариационного исчисления (метод множителей Лагранжа)
- Уравнения Эйлера—Лагранжа.
- Задачи с подвижными концами и фиксированным временем
- Задача с нефиксированным временем.
- § 10.3. Принцип максимума Понтрягина. Условие нормальности. Теорема об n интервалах. Вырожденные и особые задачи
- Задача с подвижными концами
- Задача максимального быстродействия
- Условие нормальности.
- Теорема об n интервалах.
- Задача с ограничением на фазовые координаты
- Вырожденные задачи
- Особые задачи
- § 10.4. Метод динамического программирования. Теорема Болтянского. Метод Кротова
- Принцип оптимальности
- Функция и уравнение Беллмана
- Проблема обоснования метода динамического программирования и достаточные условия оптимальности
- Метод Кротова [11]
- Принцип оптимальности Кротова.
- § 10.5. Управляемость и наблюдаемость. Наблюдатели
- Управляемость линейных стационарных объектов.
- Стабилизируемость.
- Управляемость при наличии ограничения на управление.
- Наблюдаемость и восстанавливаемость
- Обнаруживаемость
- Наблюдатели
- Наблюдатели пониженного порядка.
- § 10.6. Методы синтеза оптимальных систем с обратной связью. Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Синтез оптимальных линейных систем по интегральному квадратичному критерию
- Векторное дифференцирование.
- Синтез оптимального линейного регулятора выхода.
- § 10.7. Стохастические оптимальные системы. Методы синтеза. Методы оптимальной оценки состояния. Принцип разделимости
- Метод динамического программирования
- Синтез стохастической оптимальной линейной системы при полной информации о состоянии
- Синтез стохастических оптимальных систем управления при неполной информации
- Наблюдатель Калмана—Бьюси при цветном шуме объекта.
- Наблюдатель Калмана—Бьюси при цветном шуме наблюдения.
- Сингулярная (вырожденная) задача линейного оптимального оценивания.
- Линеаризованный наблюдатель Калмана—Бьюси.
- Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- § 10.8. Оптимальные дискретные системы
- Синтез оптимальной линейной системы при квадратном критерии
- Стохастическая оптимальная линейная система при полной информации о состоянии.
- Наблюдатель (оцениватель, фильтр) Калмана.
- О расходимости фильтров и методах их регуляризации.
- Глава 11. АДАПТИВНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ УПРАВЛЕНИЯ
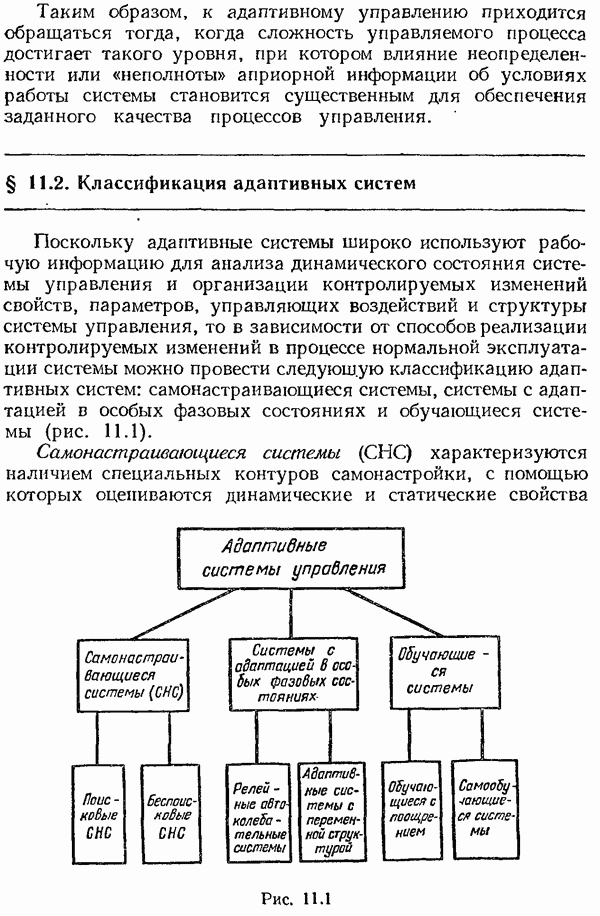
- § 11.2. Классификация адаптивных систем
- § 11.3. Самонастраивающиеся системы
- Принципы построения поисковых самонастраивающихся систем.
- Регулярные методы поиска экстремума
- Метод градиента.
- Метод наискорейшего спуска.
- Методы экстраполяционного поиска.
- Методы случайного поиска
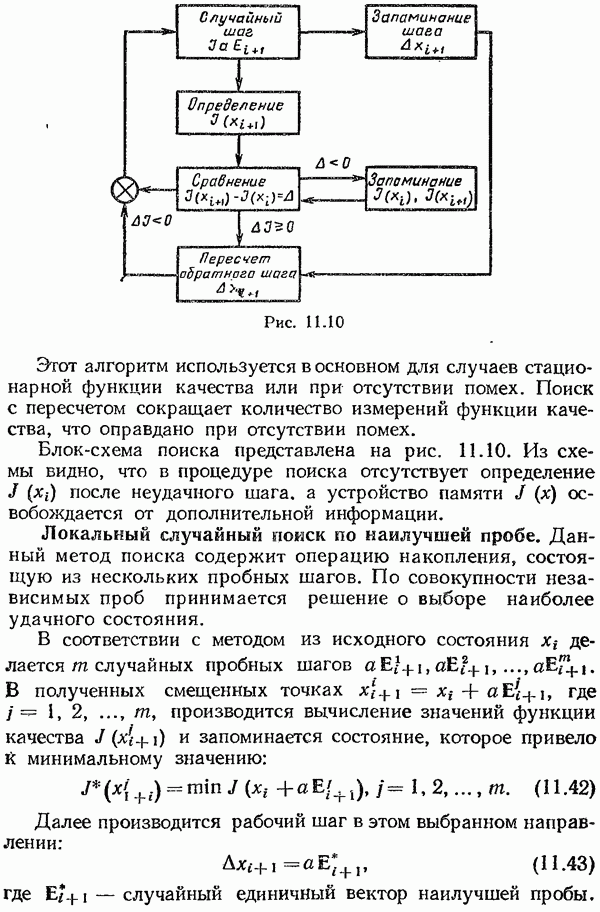
- Локальный случайный поиск с пересчетом.
- Локальный случайный поиск по наилучшей пробе.
- Локальный случайный поиск по статистическому градиенту.
- Глобальный случайный поиск с независимым выбором плотности распределения пробных шагов.
- Примеры поисковых самонастраивающихся систем
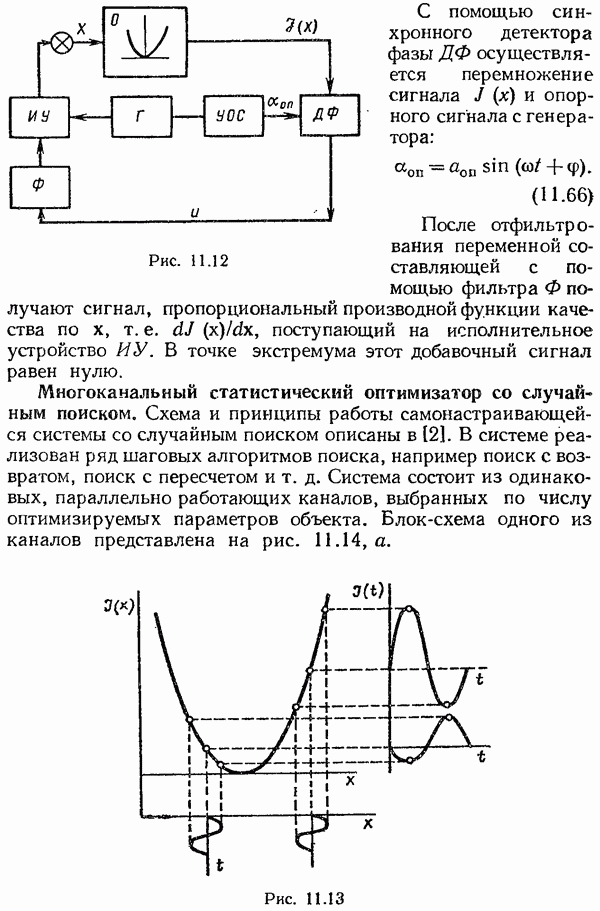
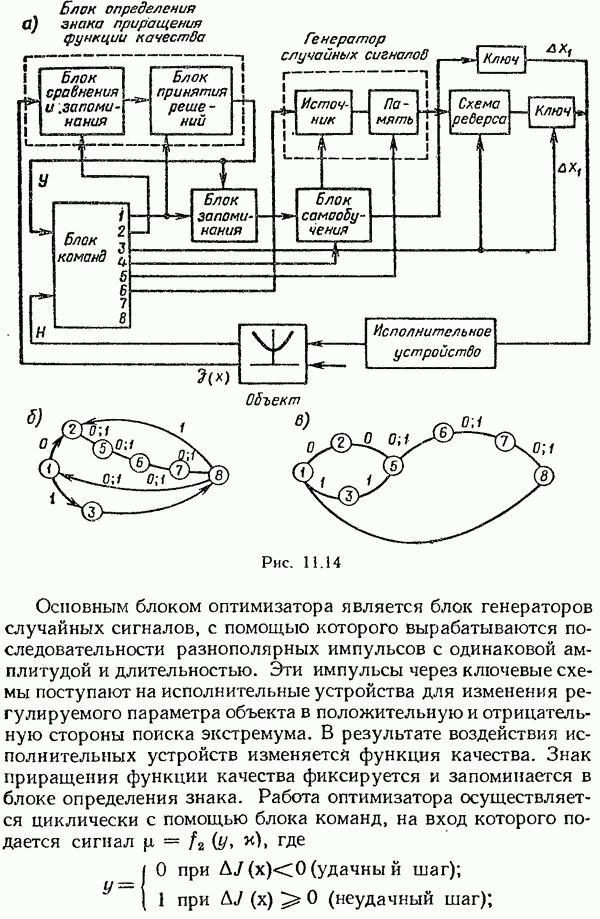
- Многоканальный статистический оптимизатор со случайным поиском.
- Принцип инвариантности.
- Принцип эталонной модели.
- Принципы определения градиента функции качества.
- Принципы идентификации динамических свойств системы управления.
- Примеры беспоисковых самонастраивающихся систем
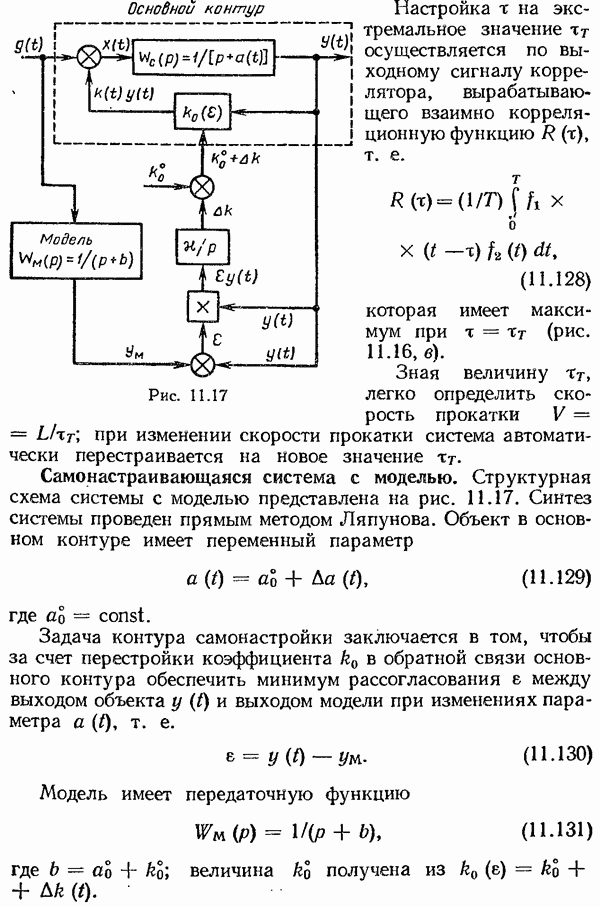
- Самонастраивающаяся система с моделью.
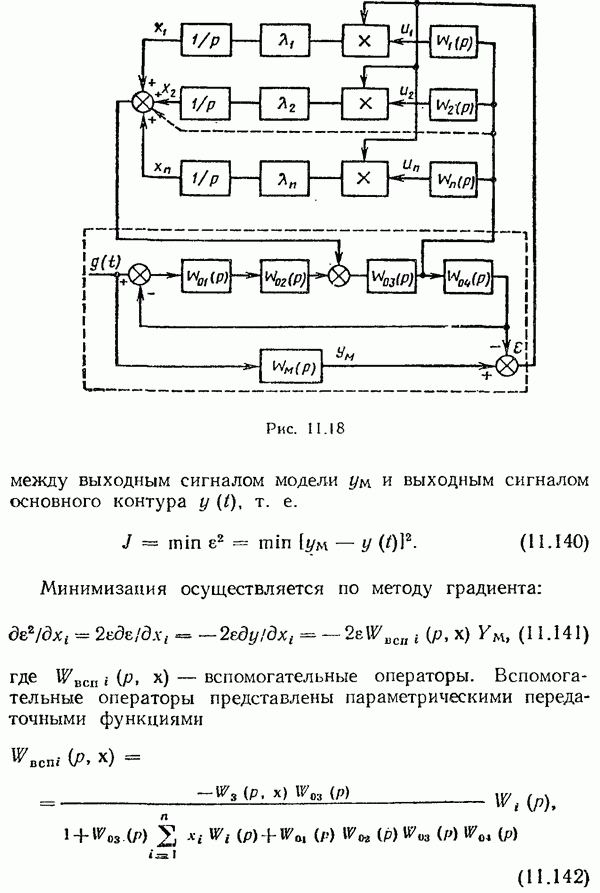
- Градиентная самонастраивающаяся система.
- § 11.4. Системы с адаптацией в особых фазовых состояниях
- Адаптивные системы с переменной структурой.
- Адаптивная система с переменной структурой, использующая информацию о внутренних координатах.
- § 11.5. Обучающиеся системы
- Метод секущих плоскостей.
- Метод потенциальных функций.
- Вероятностные алгоритмы обучения.
- Самообучение.
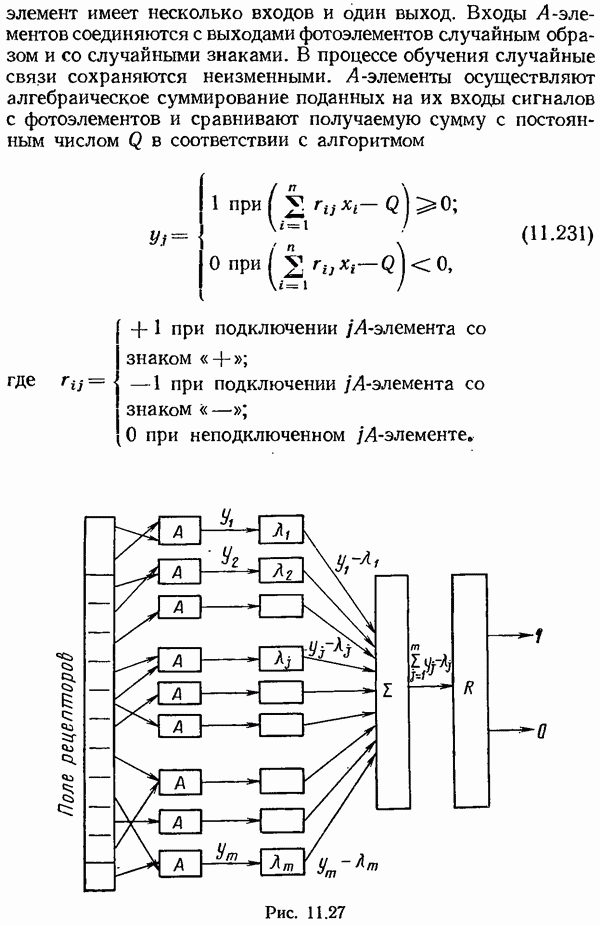
- Персептронная модель автоматической классификации.
- § 11.6. Адаптивные робототехнические системы
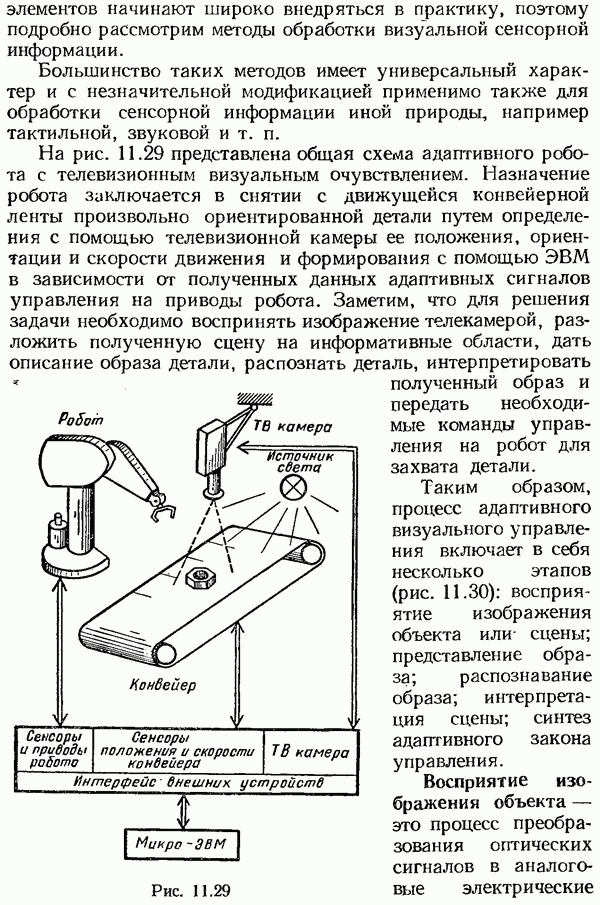
- Методы обработки сенсорной информации для адаптивного управления роботами.
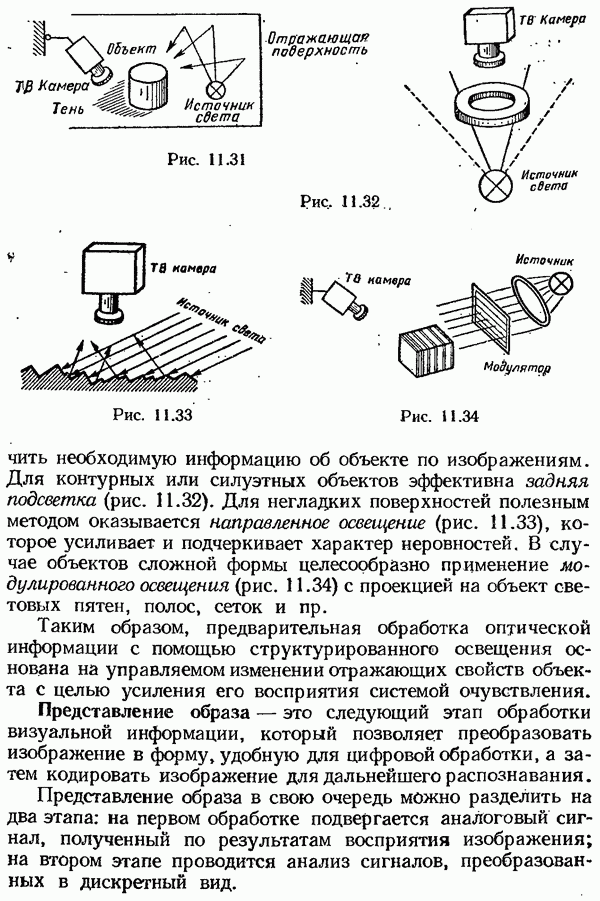
- Восприятие изображения объекта
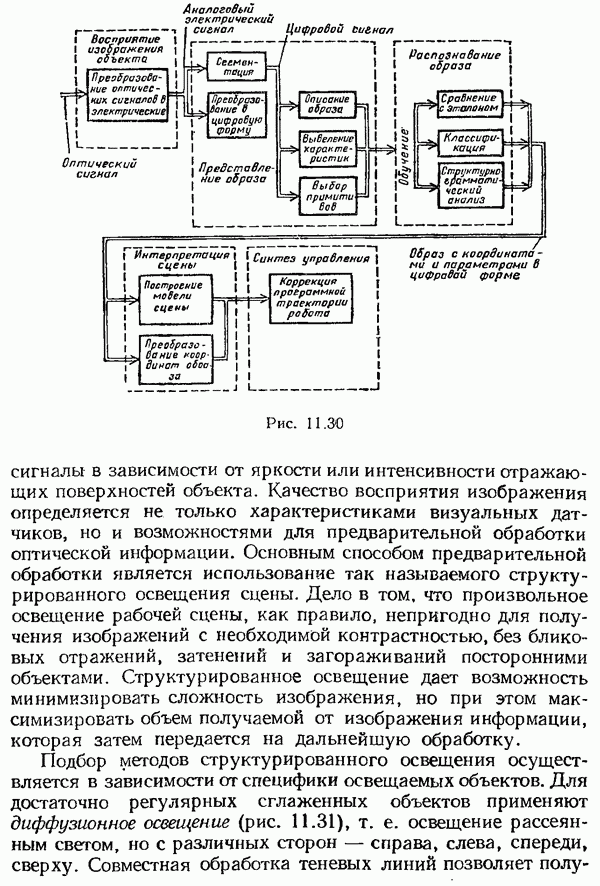
- Представление образа
- ЗАКЛЮЧЕНИЕ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ